0 引言
无刷双馈电机是一种具有广泛应用前景的新型电机,在变频调速系统、变速恒频发电、船用轴带发电、风力和水力发电系统等领域中有广泛的应用[1-2]。无刷双馈电机的特点在于取消了电刷和集电环,转子绕组形成自闭合回路,定子侧嵌有两套不同极对数定子绕组,按功能分为功率绕组和控制绕组。无刷双馈电机运行时,功率绕组直接与电网相连,控制绕组由变频电源供电,两套绕组通过电机转子的耦合作用对定子不同极数的旋转磁场进行调制,实现电机的机电能量转换[3]。无刷双馈电机发生转子偏心故障后,气隙长度发生变化,不仅会影响转子的磁场调制作用,恶化电机各项性能指标;甚至会造成转子扫膛,电机烧毁。因此,对无刷双馈电机在转子偏心故障下气隙磁场特征规律进行研究,对于探索无刷双馈电机早期故障诊断具有重要意义。
转子偏心故障作为一种常见的电机故障,国内外学者对电机偏心故障的检测与诊断问题进行了详细的研究。文献[4]提出了运用倒频谱分析与小波分解相结合的电机故障检测方法,可用于检测电机的复合故障。文献[5]采用奇异值分解滤波和Prony 结合的检测技术,提高了抗噪能力,可在短时数据下检测出转子偏心。文献[6]进行了基于定子电流分析的异步电机定转子故障诊断系统的研究。文献[7]对定子电流与电压进行Park 变化,通过对数据处理诊断感应电机是否发生偏心。文献[8]针对闭环控制的变频感应电机,利用电压空间矢量的高频成分与电流空间矢量的低频成分来诊断偏心故障。文献[9-10]采用解析法对转子偏心故障下气隙磁场进行计算,并与有限元法计算结果作对比,验证了解析法的正确性。分析发现,现有文献并未研究偏心故障对无刷双馈电机气隙磁场中时间谐波、空间谐波造成的影响。
本文采用解析法对无刷双馈电机转子偏心后的气隙磁场进行计算,并建立用于分析无刷双馈电机转子偏心的场路耦合模型,对一台45kW 无刷双馈电机转子偏心进行仿真分析,得到了偏心故障对气隙磁场空间谐波、时间谐波的影响,以及磁场谐波随气隙位置的分布规律和在不同偏心率下的变化规律,为无刷双馈电机转子偏心故障的检测和诊断提供了理论依据。
1 转子偏心故障下气隙磁场理论分析
1.1 转子偏心气隙磁导
通常将转子偏心分为静偏心、动偏心和混合偏心。静偏心,也称安装偏心,主要由于电机定子内径安装不当或不规则圆度引起的。转子静偏心时轴承位置发生变化,转子绕偏心后轴承中心旋转,气隙最小长度位置不变。动偏心,又称质量偏心,是由电机转轴发生弯曲、轴承磨损引起的。转子动偏心后转轴仍绕偏心前轴承中心旋转,气隙最小长度随着转子旋转而改变。混合偏心,又称动静混合偏心,即静偏心、动偏心故障同时发生。
无刷双馈电机转子偏心模型如图1 所示。偏心故障后转子绕转子中心B 旋转为静偏心;绕定子中心A 旋转为动偏心;既不绕定子中心A 也不绕转子中心B 旋转时为混合偏心。
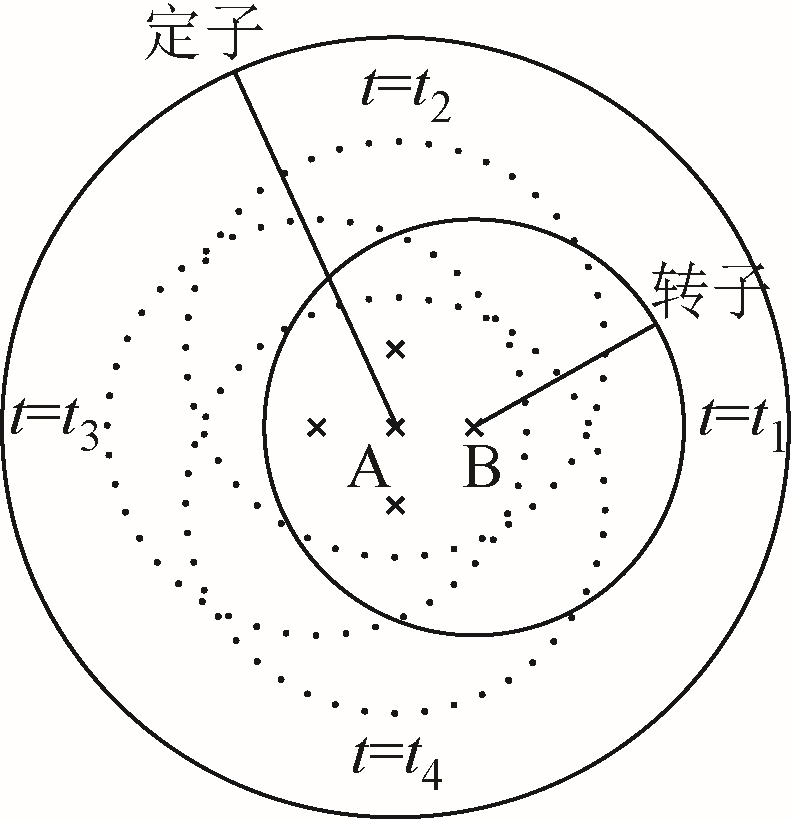
图1 转子偏心模型
Fig.1 Rotor eccentric model
当无刷双馈电机发生混合偏心时,气隙长度为时间和空间的函数。在混合偏心故障下,设按余弦规律,气隙长度表达式为[11]
式中,δ0 为均匀气隙的长度;δε 为气隙偏心的长度;θ 为机械角位移;ωε 为转子旋转时偏心气隙的旋转角速度。若转子为静偏心时,ωε=0;当转子发生动偏心时,ωε 等于转子旋转的角速度Ω2,表达式为
式中,ω1 为定子磁场旋转角速度;p 为定子绕组极对数;s 为转差率。
由传统的解析理论得知,气隙磁导和气隙长度的倒数成正比,结合式(1)可以得出,混合偏心故障下,气隙磁导的表达式为
式中,Λ0 为正常运行情况下的不变气隙磁导,即气隙磁导中的直流分量;ε 为转子偏心率,表达式为

若ωε=0,则为纯静态偏心状态,式(3)可化简为
从式(5)中可以看出,静态偏心情况下的气隙磁导表达式为一个随定子位置角变化的函数,与时间变量无关。
从上述公式推导中可以发现,无刷双馈电机发生转子偏心故障时,当偏心气隙旋转角速度ωε 等于零时,转子偏心故障为静偏心;当ωε 等于转子旋转角速度Ω2 时,偏心故障为动偏心;ωε 既不为零,也不等于转子旋转角速度Ω2 时,则为混合偏心。
1.2 转子偏心气隙磁场
无刷双馈电机气隙合成磁动势可表示为
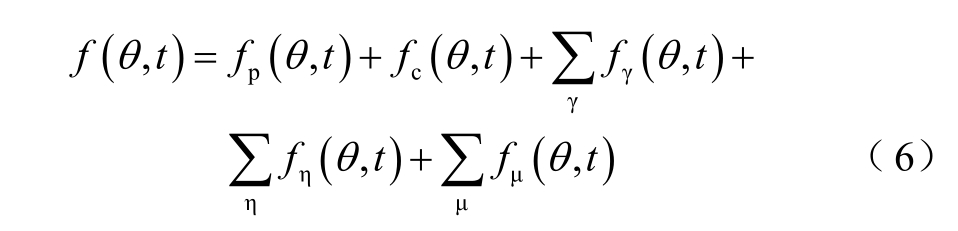
式中,f(θ,t)为气隙合成磁动势;fp(θ,t)、fc(θ,t)分别为功率绕组、控制绕组合成磁动势;fγ(θ,t)、fη(θ,t)分别为功率绕组、控制绕组谐波合成磁动势;fμ(θ,t)为转子绕组合成磁动势。将磁导表达式(3)与磁动势表达式(6)相乘,可得一系列的谐波磁场,比较重要的有
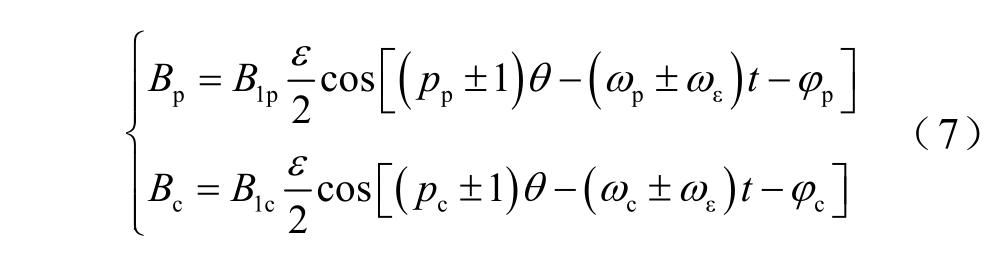
式中,Bp 为功率绕组磁感应强度;Bc 为控制绕组磁感应强度;B1p、B1c 分别为Bp 和Bc 的幅值;pp 为功率绕组极对数;pc 为控制绕组极对数;ωp 为功率绕组旋转磁场角频率;ωc 为控制绕组旋转磁场角频率;φp 为功率绕组主波合成磁动势初相角;φc 为控制绕组主波合成磁动势初相角。
从式(7)中可以看出,发生转子偏心故障后,静偏心、动偏心故障均会改变空间谐波极对数。发生偏心故障后谐波极对数为基波极对数加减1。而谐波幅值正比于偏心率ε。静偏心故障不会改变时间谐波频率,动偏心故障下时间谐波频率发生变化,结合式(2)和式(7)可得动偏心故障下时间谐波频率为
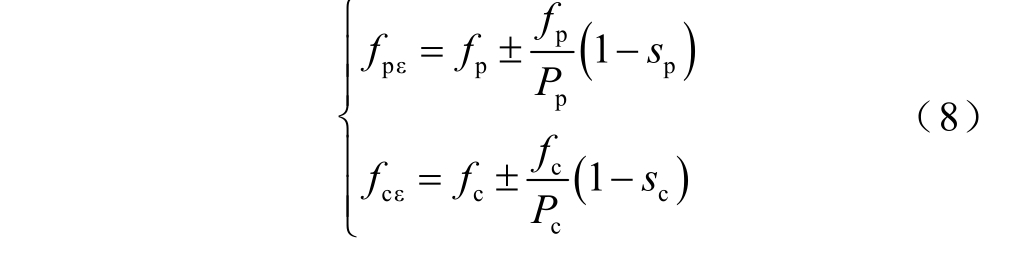
式中,fpε 为功率绕组频率在偏心故障后的畸变频率;fpε 为功率绕组频率在偏心故障后的畸变频率;sp、sc分别为功率绕组、控制绕组转差率,表达式为[12]
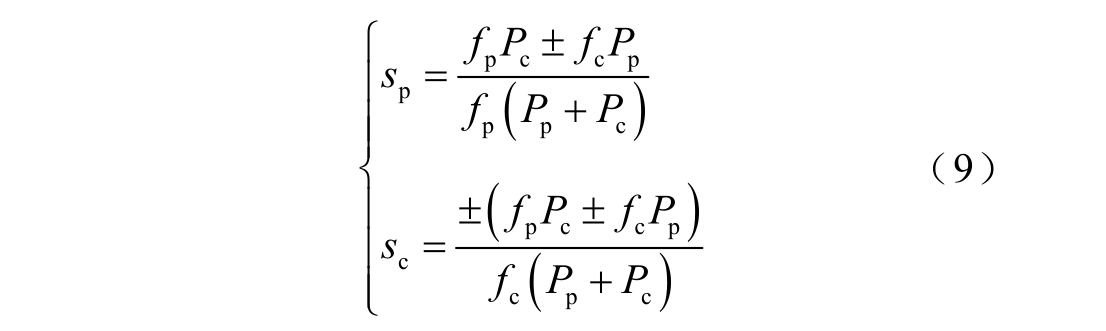
式中,功率绕组和控制绕组相序相同时取负号,反之取正号。
对于 2/4 对极无刷双馈电机,当电机转速为600r/min,功率绕组频率为50Hz,控制绕组频率为10Hz 时,通过式(8)和式(9)计算出偏心故障导致的畸变频率为20Hz、40Hz、60Hz。
2 无刷双馈电机转子偏心场路耦合模型
本文以一台45kW 无刷双馈电机为研究对象,功率绕组星形联结,控制绕组三角形联结,转子绕组按齿谐波绕组设计,其基本参数见表1。
表1 电机主要的仿真参数
Tab.1 Major simulation parameters of the machine

参 数 数 值 额定功率/kW 45 功率绕组极对数 2 控制绕组极对数 4 功率绕组电压/V 380 功率绕组频率/Hz 50 控制绕组电压/V 114 控制绕组频率/Hz 10 功率绕组并联支路数 1 定子外径/mm 491 定子内径/mm 343 转子内径/mm 342 转子外径/mm 198 铁心长度/mm 202 功率绕组线圈匝数 10 控制绕组线圈匝数 10 控制绕组并联支路数 1
本文借鉴了文献[13-14]使用的场路耦合法,以回路电流和矢量磁位作为变量,将电机的电磁场方程与反映绕组联结情况的电路方程联立起来同时求解,建立了无刷双馈电机转子偏心故障的瞬态电磁场与多回路耦合的数学模型。无刷双馈电机控制绕组连接三相对称交流电源,功率绕组带负载作为发电机运行时,整个系统的场路耦合示意图模型如图2所示。线圈直线段电阻和电感、槽漏感和谐波漏感包含于有限元模型中,图中PA、PB、PC 为功率绕组,CA、CB、CC 为控制绕组,Rps、Lps 分别为功率绕组端部电阻和漏电感,Rcs、Lcs 分别为控制绕组端部电阻和漏电感,Ua、Ub、Uc 为三相对称交流电源。
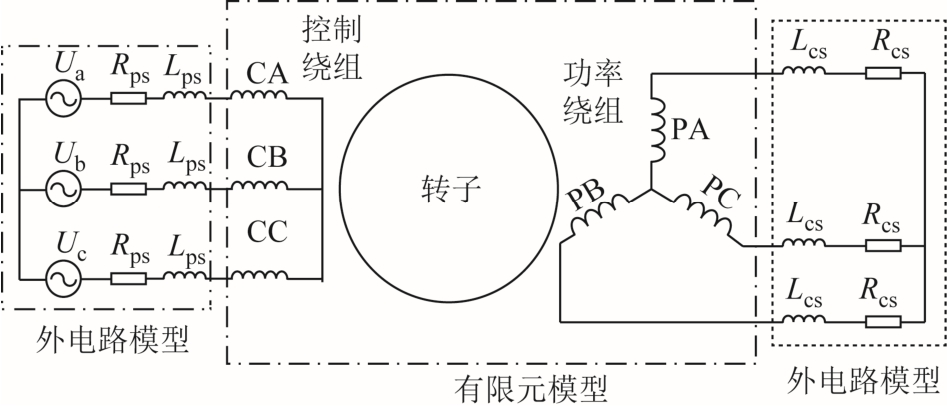
图2 场路耦合模型
Fig.2 Field coupling model
忽略位移电流及温度对绕组电阻率影响,认为电机内磁场为二维分布,则电机瞬态电磁场的微分方程可表示为
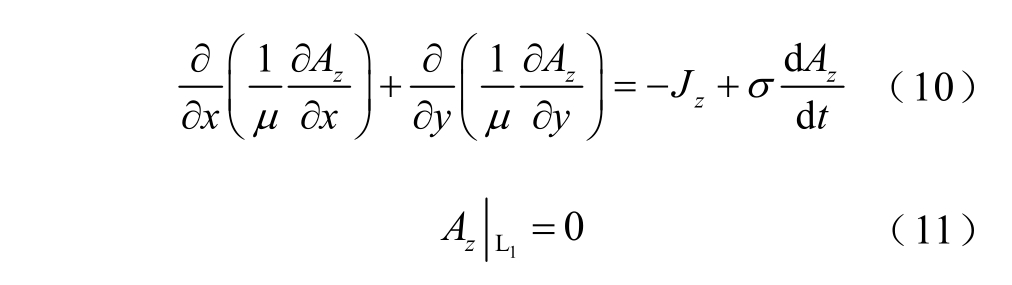
式中,Az 为矢量磁位的轴向分量;Jz 为电流密度的轴向分量;μ 为材料的磁导率;σ 为材料的电导率;L1 为定子铁心外圆。无刷双馈电机有限元模型如图3所示。
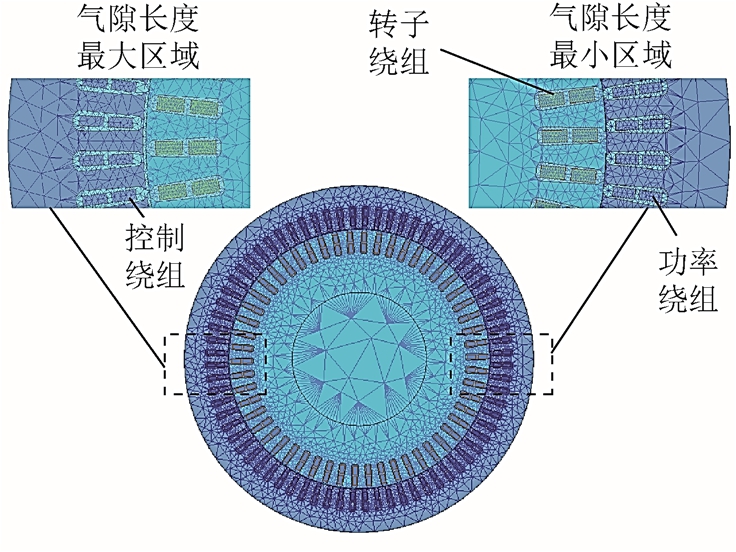
图3 45kW 无刷双馈电机有限元仿真模型
Fig.3 45kW brushless doubly-fed machine simulation model
通过场路耦合法可以将电机的直线部分与端部分开考虑,多回路模型中的漏感只剩下电机的端部漏感;直线部分用二维电磁场的有限元计算方法,端部部分通过多回路模型来计算。这样不仅能考虑绕组的空间位置、联结方式,而且免去了参数计算的困难,也简化了迭代过程[15-16]。
3 转子偏心故障下场路耦合模型仿真分析
3.1 电机偏心前后磁场分布及空间谐波分析
转子偏心率为0.8 时,对2/4 对极无刷双馈电机额定负载运行状态下的气隙磁场进行仿真计算,无刷双馈电机运行在发电机状态,电机达到稳态后,电机内的磁力线分布如图4 所示。
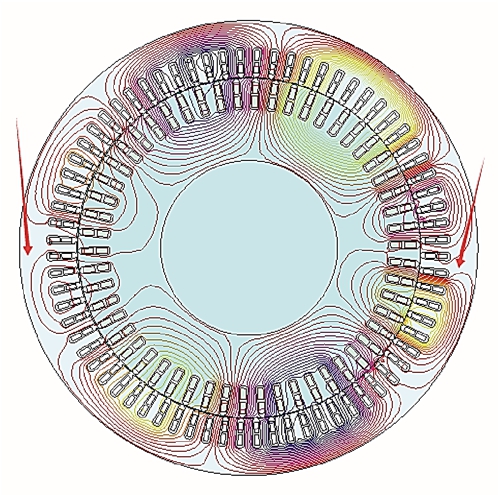
图4 静偏心下磁力线分布
Fig.4 Static eccentricity magnetic field line distribution
对某一时刻电机磁场的空间分布,可将动偏心看作不同时间的静偏心,并无本质区别。从图3 中可以看出,转子偏心故障后,气隙长度发生变化,使气隙磁导随空间位置分布而改变,进而对气隙磁场造成影响。气隙长度最小区域磁力线增多,而气隙长度最大区域磁力线减少,电机内部磁场明显不对称。可以看出,转子偏心故障对气隙磁场造成严重影响。
对气隙磁场进行快速傅里叶分析,以4 对极谐波为基准,各个极对数谐波幅值占基波幅值的百分比如图5 所示。

图5 气隙磁场空间谐波
Fig.5 Air gap magnetic field spatial harmonic
从图5 中可以看出,负载工况下电机正常运行时,除2、4 对极基波外,8、10、14、16 对极谐波较大。文献[17]指出,无刷双馈电机内除功率绕组pp对极、控制绕组pc 对极谐波外,还存在有极对数为kZr±pp、kZr±pc 的齿谐波,对本文2/4 极无刷双馈电机,转子等效齿数为6,则理论上应出现6k±2、6k±4对极谐波(k 为正整数),因此,正常运行时出现的各对极空间谐波符合理论结果,也验证了场路耦合模型的正确性。
转子偏心故障后,电机气隙中谐波极对数发生了变化,除2、4 对极基波以及提到的齿谐波外,还出现了正常运行时含量极低的1、3、5 对极谐波,谐波极对数等于基波极对数加减1,与解析法分析结果一致。转子偏心后1、3、5 对极谐波幅值达到3.89%、7.98%、13.69%。因此,空间谐波信号可用于检测转子偏心故障。
3.2 转子偏心故障后气隙磁场时间谐波分析
3.2.1 时间谐波分析仿真模型
电机气隙磁场是随时间和空间变化的函数,除去前文讨论的空间谐波外,转子偏心还会对时间谐波造成影响。采用场路耦合有限元模型计算时,并不能直接计算出气隙磁场随时间的变化规律,并且无刷双馈电机中气隙磁通密度非常小,无法通过放入霍尔元件来检测气隙磁场。本文借鉴了文献[18]使用的检测线圈法,即将一定匝数线圈放置在电机齿部,通过对线圈上感应电压的谐波分析,来间接分析气隙磁场的谐波信号。
检测线圈模型如图6 所示,将一定匝数的线圈放置在电机定子齿上。由磁路理论可知,在一个齿距范围内的主磁通从空气隙进入铁心表面后,将几乎全部从齿内通过,通过线圈的磁链为[19]
式中,Bδ(t,φ)为电机定子齿所对应的气隙磁通密度;rav 为平均气隙半径;li 为电机定子铁心长度的有效值;N 为电机定子齿上检测线圈匝数。

图6 检测线圈模型
Fig.6 Detection coil model
由法拉第电磁感应定律可得,检测线圈两端的感应电压为
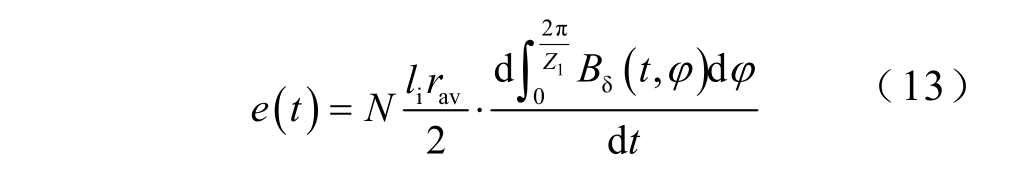
由式(13)可知,检测线圈感应电压e(t)和气隙磁通密度Bδ(t, φ)的频谱特征一致,因此,可以通过对测量线圈电压随时间变化波形的频谱来分析气隙磁场的谐波。
本文对多个定子齿上设置了检测线圈,不仅可以通过对其中一个线圈的分析得出因转子偏心故障产生的时间谐波,还可以对多个线圈联合分析,来研究时间谐波随空间位置的变化规律。
3.2.2 气隙磁场时间谐波的频谱分析
对本文无刷双馈电机内部其中一个检测线圈的感应电压进行频谱分析,来研究因转子偏心故障引入的气隙磁场时间谐波。
由1.2 节的理论分析可知,转子动偏心故障会引起气隙磁场谐波频率的变化,根据解析法分析结果,电机转速为600r/min,功率绕组50Hz,控制绕组10Hz 时,转子偏心会引入20Hz、40Hz、60Hz 谐波磁场。对比转子偏心故障前后这些频率谐波发现:转子发生偏心故障后,气隙磁场中畸变频率谐波幅值明显增大,不同偏心率下这三种频率谐波幅值如图7 所示。
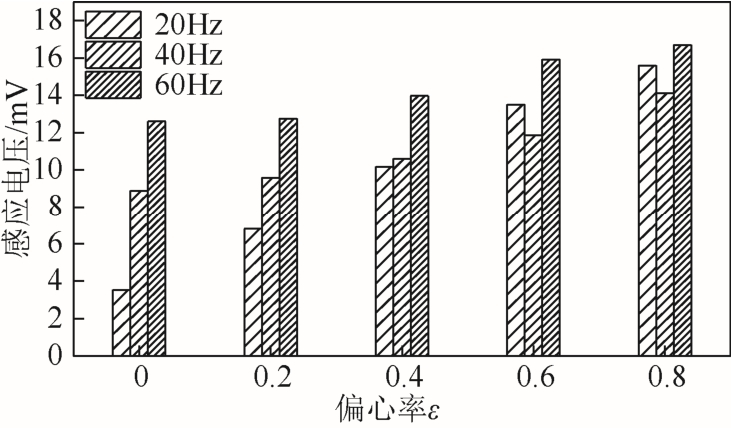
图7 时间谐波幅值随频率和偏心率变化
Fig.7 Time harmonic amplitude variation with frequency and eccentricity
正常运行时,检测线圈上相应感应电压幅值为3.53mV、8.87mV、12.60mV。当转子偏心率为0.8 时,对应频率的感应电压幅值为15.59mV、14.10mV、16.70mV,分别为正常运行的4.42 倍、1.59 倍、1.33倍。检测线圈上谐波电压的增大,反映出气隙磁场中相应频率谐波的增大。从图7 中还可以看出,随着偏心率的增大,谐波幅值随之增大,谐波磁场与偏心率呈正相关关系。因此,当气隙磁场中的检测信号幅值逐渐增大,说明电机发生动态偏心故障的程度加剧,这也为电机动态偏心故障的定量诊断提供了依据。
3.2.3 气隙磁场时间谐波随空间位置的分布规律
对无刷双馈电机内所有检测线圈取同一频率谐波幅值,可研究谐波磁场随空间位置的变化规律。从图7 中可以看出转子偏心故障后20Hz 谐波幅值增大最为明显,以20Hz 谐波为研究对象,对气隙磁场谐波随空间位置的分布规律进行研究,20Hz 谐波在不同偏心率下随空间位置的分布规律如图8 所示。

图8 时间谐波信号的空间分布
Fig.8 Spatial distribution of time harmonic signals
从图8 中可以看出,偏心故障后,各个偏心率下,感应电压幅值在不同空间位置处相差较大,总体上随空间位置变化呈正弦分布。不同偏心率下,谐波信号增大程度并不相同,在圆周角度180°位置,也是气隙长度最小区域,偏心率增加对谐波信号的影响最为明显。而在圆周角度105°、200°、328°处的谐波信号较小,若仅对这些位置检测线圈信号分析,则很难看出转子偏心对谐波信号的的影响。因此在检测转子动偏心信号时,在电机内部设置多个检测线圈联合分析,对早期故障检测具有重要意义。
4 结论
本文采用磁动势磁导法从理论上分析了无刷双馈电机转子偏心故障对气隙磁场的影响,并建立了无刷双馈电机转子偏心场路耦合模型。以一台2/4对极45kW 无刷双馈电机为例,对转子偏心故障对气隙磁场空间谐波、时间谐波的影响进行了详细的研究,得到以下结论:
1)转子偏心故障会导致气隙磁场谐波极对数的变化,增加的谐波磁场极对数为基波磁场极对数加减1。2/4 对极无刷双馈电机正常运行时气隙磁场中主要为2、4 对极基波,转子偏心后会引进1、3、5 对极谐波。
2)转子动偏心会使气隙磁场谐波频率发生变化,通过解析法给出了因转子动偏心而引进的谐波频率计算公式。
3)对于一台2/4 对极、功率绕组50Hz、控制绕组频率10Hz 的无刷双馈电机,动偏心故障会导致20Hz、40Hz、60Hz 时间谐波增大,其中20Hz 谐波幅值增加最明显,在偏心率为0.8 时达到正常运行状态下的4.42 倍。不同频率的时间谐波幅值随偏心率增加而增大。
4)转子偏心故障后,无刷双馈电机气隙谐波磁场随空间位置呈正弦分布,随着偏心率的增加,气隙长度最小区域谐波信号增加最为明显。
[1] Williamson S, Ferreira A C, Wallace A K. Generalized theory of the brushless doubly-fed machine. part I: analysis[J]. IEE Proceedings, Electrical Power Applications, 1997, 144(2): 111-122, .
[2] Williamson S, Ferreira A C, Wallace A K. Generalised theory of the brushless doubly-fed machine. 2: model verification and performance[J]. IEE Proc eedings-Electric Power Application, 1997, 144(2): 123-129.
[3] 杨顺昌. 无刷双馈电机的电磁设计特点[J]. 中国电机工程学报, 2001, 21(7): 107-110. Yang Shunchang. Feature of electromagnetic design for brushless doubly-fed machines[J]. Proceedings of the CSEE, 2001, 21(7): 107-110.
[4] 张雄希, 刘振兴. 基于倒频谱分析的电机故障检测[J].电力系统保护与控制, 2010, 38(20): 145-147. Zhang Xiongxi, Liu Zhenxing. Fault detection for motor based on cepstrum analysis[J]. Power System Protection and Control, 2010, 38(20): 145-147.
[5] 张菁菁, 王臻. 基于奇异值分解滤波的Prony 技术在异步电机偏心故障检测中的研究[J]. 电机与控制应用, 2016, 43(3): 83-88. Zhang Jingjing, Wang zhen. Research on the detecting eccentricity fault of asynchronous motor based on singular value decomposition filter and prony technique[J]. Motor and Control Applications, 2016, 43(3): 83-88.
[6] 靳彦虎. 基于定子电流信号分析的异步电机定转子故障的诊断[D]. 石家庄:河北科技大学, 2013.
[7] Cardoso A J M, Saraiva E S. Computer-aided detection of airgap eccentricity in operating threephase induction motors by Park's vector approach[J]. IEEE Transactions on Industry Applications, 2002, 29(5): 897-901.
[8] Huang Xianghui. Diagnotics of air gap eccentricity in closed-loop drive-connected induction motors[C]//4th IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives Conference, Atlanta, GA, USA 2005, DOI: 10.1109/DEMPED. 2003.1234592.
[9] 仇志坚, 李琛, 周晓燕, 等. 表贴式永磁电机转子偏心空载气隙磁场解析[J]. 电工技术学报, 2013, 28(3): 114-121. Qiu Zhijian, Li Wei, Zhou Xiaoyan, et al. Analytical calculation of no-load air-gap magnetic field in surface-mounted permanent magnet motors with rotor eccentricity[J]. Transactions of China Electrotechnical Society, 2013, 28(3): 114-121.
[10] 章跃进, 章君达. 偏心式谐波磁力齿轮气隙磁场分式线性变换解析模型[J]. 电工技术学报, 2018, 33(15): 3572-3577. Zhang Yuejin, Zhang Junda. Analytical model of magnetic field of eccentric harmonic magnetic gear using fractional linear transformation method[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3572-3577.
[11] 陈世坤. 电机设计[M]. 北京: 机械工业出版社, 1990.
[12] 邓先明, 姜建国. 无刷双馈电机的工作原理及电磁设计[J]. 中国电机工程学报, 2003, 23(11): 130-136. Deng Xianming, Jiang Jianguo. The principle and electromagnetic design of brushless doubly-fed machines[J]. Proceedings of the CSEE, 2003, 23(11): 130-136.
[13] 孙宇光, 王祥珩, 桂林, 等. 场路耦合法计算同步发电机定子绕组内部故障的暂态过程[J]. 中国电机工程学报, 2004, 24(1): 136-141. Sun Yuguang, Wang Xiangheng, Gui Lin, et al. Transient calculation of stator’s internal faults in synchronous generator using FEM coupled with multiloop method[J]. Proceedings of the CSEE, 2004, 24(1): 136-141.
[14] 赵洪森, 戈宝军, 陶大军, 等. 大型核电汽轮发电机定子内部短路故障时局部电磁力分布研究[J]. 电工技术学报, 2018, 33(7): 1497-1507. Zhao Hongsen, Ge Baojun, Tao Dajun, et al. Local electromagnetic force distribution study on giant nuclear turbo-generators with stator short-circuit fault[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1497-1507 .
[15] 赵洪森, 戈宝军, 陶大军, 等. 定子绕组匝间短路对发电机电磁转矩特性的影响[J]. 电工技术学报, 2016, 31(5): 192-198. Zhao Hongsen, Ge Baojun, Tao Dajun, et al. Influence of stator winding inter turn short circuit fault on generator electromagnetic torque characteristics[J]. Transactions of China Electrotechnical Society, 2016, 31(5): 192-198.
[16] 肖士勇, 戈宝军, 陶大军, 等. 同步发电机定子绕组匝间短路时转子动态电磁力计算[J]. 电工技术学报, 2018, 33(13): 2956-2962. Xiao Shiyong, Ge Baojun, Tao Dajun, et al. Calculation of rotor dynamic electromagnetic force of synchronous generator under the stator winding interturn short circuit fault[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 2956-2962.
[17] 贾磊. 绕线转子无刷双馈电机电磁设计与运行特性研究[D]. 武汉: 华中科技大学, 2016.
[18] 王汉丰. 潜水电机偏心故障下的磁场特性分析及其在线检测[D]. 合肥:合肥工业大学, 2016.
[19] 阚超豪, 丁少华, 刘祐良, 等. 基于气隙磁场分析的无刷双馈电机偏心故障研究[J]. 微电机, 2017, 50(3): 5-8,18. Kan Chaohao, Ding Shaohua, Liu Youliang, et al. Study on eccentricity fault of brushless doubly-fed machine based on air gap magnetic field analysis[J]. Micromotor, 2017, 50(3): 5-8,18.