0 引言
与三相感应电机相比, 无刷双馈电机(Brushless Doubly-Fed Machine,BDFM)具有运行可靠、功率因数可调、变频器容量小等优点,在变速恒频发电以及变速驱动等领域有着广泛的应用前景。BDFM 作为发电机运行时,具有良好的变速恒频恒压发电特性,可应用于风力、水力和船用轴带发电等领域,而且控制装置中的变频器容量远小于全功率逆变所需的容量[1-4];作为电动机运行时,其稳定转速为

式中,pp 和fp 分别为功率绕组的极对数和频率;pc和fc 分别为控制绕组的极对数和频率。由式(1)可知,转速只与通电频率以及两套绕组的极对数有关,与负载大小无关,其具有精确的调速性能和良好的机械特性。BDFM 定子上有两套不同极对数的绕组(功率绕组和控制绕组),功率绕组的频率与电网的频率保持一致,为恒定值。因此,只需改变控制绕组的通电频率,电机转速就会改变,可用于风机和水泵等负载的变频节能调速系统[5-7]。
目前,随着煤炭、冶金、矿山等行业的电气传动技术的不断发展,大量重型起动机和大中型电动机驱动装置需要起动电流小、起动转矩大的感应电机。因此,电气传动系统对电机提出了更高的要求,如何进一步提高电机起动性能成为本领域的研究热点。普通变频电机的变频器容量大,调速成本高,系统效率低。与普通变频电机相比,BDFM 的变频器容量低,调速范围广,效率高。BDFM 调速系统中变频器容量约占电机容量的30%,即可满足变频调速要求。若起动时采用变频起动,则变频器容量偏小,无法满足起动转矩要求。若像普通感应电机一样采用直接起动的方法,电机起动电流较大,可达到额定值的4~7 倍,对电网的冲击电流很大[8-10]。另外,绕线转子BDFM 由传统绕线转子感应电机演变而来,无集电环、电刷对外连接,将原有绕线转子绕组移到了定子上变为控制绕组,原有的定子绕组为功率绕组。原来通过转子绕组串联电阻减小起动电流、增加起动转矩的方法现在可由定子控制绕组串联起动电阻或频敏变阻器来实现,但在一些重载起动和频繁起动场合,该方式存在操作较麻烦、可靠性低、综合成本较大等问题[11-13]。
鉴于目前BDFM 存在起动电流较大且起动转矩不高,影响其工业应用等问题,本课题组将复合线圈结构引入到BDFM 转子绕组中,并与定子磁动势谐波理论相结合设计了一种绕线转子BDFM——多谐波联合起动BDFM。本文首先介绍了多谐波联合起动BDFM 结构及工作原理;然后建立多谐波联合起动BDFM 绕组磁动势数学分析模型,并对电机建立等效电路来研究多谐波联合起动对BDFM 起动电流及磁动势(Magnetomotive Force, MMF)的影响,详细分析多谐波联合起动BDFM 谐波磁场特性及起动性能;最后通过时步有限元法,并结合样机试验,验证了该电机的可行性及优越性。
1 多谐波联合起动BDFM 结构及工作原理
1.1 结构
图1 给出了所提出的多谐波联合起动BDFM的结构,该结构定子槽数Zs=36,功率绕组为4 对极,控制绕组为2 对极,转子槽数为24 的绕线转子BDFM。

图1 多谐波联合起动BDFM 结构
Fig.1 Structure diagram of BDFM with multi-harmonic combined starting
根据文献[14-16]中的设计思想,采用“槽号相位图法”设计了定子上的两套不同极对数的绕组,两套绕组在2/4 对极下均为正规60°相带,其绕组联结方式如图2 所示,该绕组的展开图如图3 所示,图中数字表示转子槽号,绕组参数见表1。
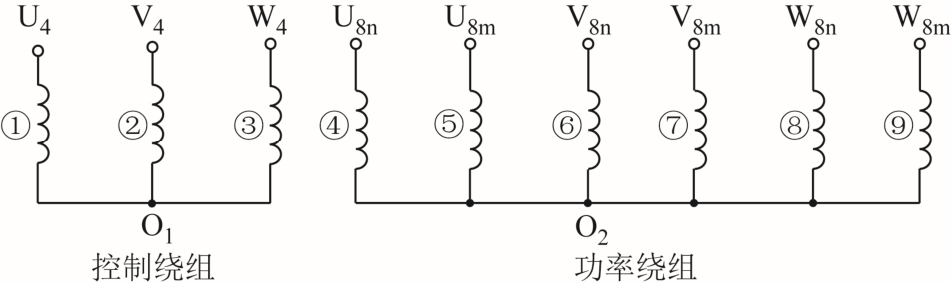
图2 定子绕组连接方式
Fig.2 Connection method of stator winding

图3 定子绕组的展开图
Fig.3 Outspread diagram of stator winding
表1 定子绕组参数
Tab.1 Parameters of the stator winding

参 数 线圈组 ①②③ ⑤⑦⑨ ④⑥⑧ 每个线圈组线圈数 12 9 3 每个线圈匝数 15 20 60 导线直径/mm 0.60 0.60 0.60 并绕导线数 2 3 1 支路串联匝数 180 180 180
为了进一步提高转子与定子上两套不同极对数绕组的耦合能力,课题组结合谐波磁动势原理与绕组设计理论,将复合线圈引入到转子绕组中,转子槽数Zr=24,其设计方案如图4 所示。黑色线圈的匝数为N1=13,灰色线圈的匝数为N2=5。


图4 转子绕组的连接方式
Fig.4 Connection method of rotor winding
1.2 工作原理
多谐波联合起动BDFM 控制结构示意图如图5所示。定子上有两套不同的绕组,控制绕组采用星形联结,功率绕组采用大小双星形联结法(Y3Y1/Y3联结),其中U4、V4、W4 为控制绕组接线端,U8m、V8m、W8m为功率绕组上大星形Y3起动接线端,U8n、V8n、W8n 为功率绕组上小星形Y1 运行接线端。起动时,将控制绕组接线端短接,功率绕组大星形Y3 起动接线端接入电网,即同时闭合S0、S1。闭合开关后接入工频电源,电机开始起动和加速,当转速上升到同步转速附近时,将控制绕组接线端接入变频器,同时将功率绕组上小星形Y1 运行接线端分别投入起动端所接入的电网中,即闭合S2,同时断开S1,完成起动过程,电机开始进入双馈运行状态。通过开关切换,无需变频起动便使得电机由起动状态进入到双馈运行状态,然后可通过变频器调节fc 实现有效的变频调速。

图5 多谐波联合起动BDFM 控制示意图
Fig.5 Control schematic of BDFM with multi-harmonic combined starting
2 多谐波联合起动BDFM 磁动势分析
由于多谐波联合起动BDFM 在起动时,定子上控制绕组短接,仅部分功率绕组接入电网,接入电网的这部分功率绕组将产生pp 对极基波磁场及其与基波磁场同转向的不同极对数下的主、副谐波磁场,转子绕组在基波及主、副谐波磁场中感应出与定子极对数相对应的基波和谐波磁动势。由于转子的磁场调制作用,转子除了产生与定子极对数相同的谐波磁场外,同时还产生一系列的齿谐波,这些磁场相当于由转子励磁产生的,部分在定子中感应出相应电流。如此不断循环,定子、转子磁场相互作用,达到一个平衡的状态,从而实现了能量转换,其能量关系为:由电网输入电机的电能=耦合磁场内储能的增加+电机内部的能量损耗+由转轴输出的机械能
2.1 定子磁动势分析
定子绕组由若干线圈组成,因此绕组的谐波磁场的分析要从一个线圈开始。当线圈中通入电流 0i ,一个线圈电流产生的磁动势沿气隙圆周的分布情况及磁动势波形如图6 所示。槽距角为αs,节距角为αc,气隙有效长度为δ,每个线圈的匝数为N。

图6 定子上线圈产生的磁场和磁动势分布规律
Fig.6 Distribution of magnetic field and magnetomotive force generated by coils on stator
对图6 中的矩形波进行傅里叶分解,可得出极对数v=1,2,3,⋅⋅⋅的所有磁动势谐波,单个线圈产生的磁动势fc 为

式中,v 为谐波极对数;kyv 为v 对极谐波绕组的短距系数;θ为沿气隙圆周的空间位置角度。
由于多谐波联合起动BDFM 时,定子上功率绕组仅部分绕组单独接入电网,而且每相有若干个槽号相串联,部分槽号之间不相邻,其采用非正规排列连接。因此得出v 对极谐波的槽矢量星形如图7所示。

图7 槽矢量星形图
Fig.7 Slot-vector star graph
现取各矢量长度为1,则对任意一个正负槽号Mx(x=1,2,⋅⋅⋅,Z)号槽的槽矢量均可用复数指数函数表示为
假设A 相占Z/3 个槽号(正负槽号均有)分别为MA1, MA2, MA3, ⋅⋅⋅, MAx, ⋅⋅⋅, MAZ/3,则A 相的合成矢量的复数表达式为

A 相磁动势如图8 所示,根据图8 可将式(6)转换为
式中


图8 A 相磁动势
Fig.8 MMF of A phase
由于各个线圈的矢量长度都一样,均为1,因而矢量和与算术和之比同矢量长度无关,则A 相绕组v 对极谐波的分布系数为
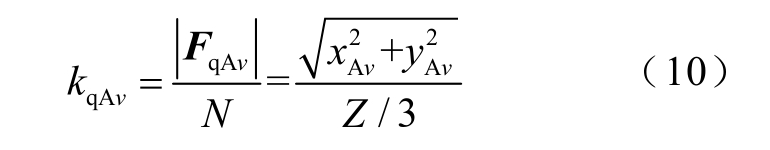
相位角为

同理可得出B、C 两相绕组的合成矢量的复数表达式为

当三个矢量相位、大小不同时,示意图如图9a所示。定子绕组中的三相电流为对称电流,三相定子绕组产生的v 对极谐波磁动势可分解为顺转、逆转两个旋转磁动势和一个零序分量磁动势,如图9b、图9c、图9d 所示。以x、y 为坐标的空间矢量,根据对称分量法可将每个矢量都分解为三个分量之和,如式(14)所示。

图9 三相绕组的磁矢量及其分解为对称分量
Fig.9 The MMF vector of three-phase winding and its
decomposition into symmetrical components

由图9 和式(14)可知,正序分量 A +vF 、 B +vF和 C +vF 三相对称,负序分量 Av-F 、 Bv-F 和 Cv-F 三相对称,可写成

由于当三相绕组通以三相对称电流时,三个零序分量 FA v 0 、 F B v 0 、 FC v 0同相位、同大小,即
当 iA + iB + iC = 0时,零序分量的合成结果为零。上述式(14)~式(16)联立可求解出正、负序分量为

由以上分析可知,每相都有一个正序分量和负序分量,且均为三相对称。正序分量大小分别为![]() 负序分量的大小分别为
负序分量的大小分别为![]()
![]() 相应地,每相都有一个正序分布系数kqv+和一个负序分布系数kqv-。显然,每相绕组v 对极谐波的分布系数是由三相绕组综合决定,故得出三相综合正序和负序分布系数,其值为
相应地,每相都有一个正序分布系数kqv+和一个负序分布系数kqv-。显然,每相绕组v 对极谐波的分布系数是由三相绕组综合决定,故得出三相综合正序和负序分布系数,其值为

由以上分析可得,当三相绕组通入对称的电流时,假设A 相的电流为 ![]() ,则A相绕组电流产生的磁动势正序和负序分量的幅值为
,则A相绕组电流产生的磁动势正序和负序分量的幅值为
则三相合成的磁动势正序和负序分量的幅值为
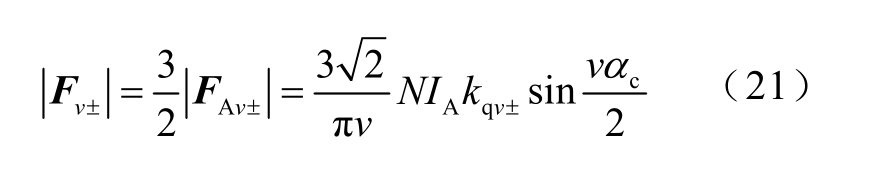
多谐波联合起动BDFM 在起动时由于定子绕组采用大小双星形联结法,控制绕组短接,功率绕组仅部分绕组单独接入电网,此时起动时,磁场和气隙磁通密度除基波外,还产生含极对数为1, 2, 3, 5, 6, …一系列磁动势谐波。其中,3 对极为主谐波,2、5 对极为副谐波。将各磁动势谐波幅值用基波幅值的百分数表示。若基波是Fp+,则各谐波幅值用基波的百分数表示为

对多谐波联合起动BDFM 定子绕组起动时大星接入电网三相所占槽号进行分析。选取基波磁动势的旋转方向为参考正方向。顺转波表示各极对数谐波磁动势与基波转向相同,反转波表示各极对数谐波磁动势与基波转向相反。则该方案在起动时的磁动势谐波分析,见表2。
表2 36 槽8 极槽号Y3Y1/Y3 联结起动时磁动势谐波分析
Tab.2 Analysis of MMF harmonics at start-up of Y3Y1/ Y3-linked(Zs=36, 2pp=8)

极对数相位/(°) 三相绕组综合 分布系数 三相绕组合成磁动势(%) A 相 B 相 C 相 kqv+ kqv- Fv+ Fv- 1 223.8 180 136.2 0.09 0.04 16.77 6.53 2 236.9 0.00 123.1 0.21 0.02 34.57 3.91 3 240 0.00 120 0.30 0.00 41.36 0.00 4 60 180 -60 0.96 0.00 100.0 0.00 5 239.3 0.00 120.7 0.26 0.03 17.76 2.25 6 240 300 120 0.15 0.07 5.22 2.61 7 247.8 180 112.2 0.05 0.09 0.26 0.46 8 120 0.00 240 0.00 0.18 0.00 3.20 9 0.00 0.00 0.00 0.00 0.00 0.00 0.00 10 7.80 0.00 352.1 0.02 0.05 0.78 1.92
从表2 中可以看出,由于3、4 对极磁动势谐波对基波而言不存在反转向负序分量,说明该绕组对3、4 对极磁动势谐波而言都是三相对称的,并且磁动势基波是圆形旋转磁动势。对于2、5 对极副谐波而言,虽然三相绕组不对称,但顺转波远大于反转波,其转向与基波磁动势转向相同,对起动转矩也具有一定的提升作用,其矢量合成图如图10所示。


图10 起动时定子绕组磁动势矢量合成图
Fig.10 Vector composition diagram of MMF of stator winding at start-up
图11 a、图11b 分别为多谐波联合起动BDFM起动时和双馈运行时定子齿部磁通密度分布图。对比图11a、图11b 可知,多谐波联合起动时定子齿部磁通密度普遍低于双馈运行时的定子齿部磁通密度,且其最大值与运行时相比约低了0.132T,磁场 饱和程度降低,说明转子绕组采用复合线圈结构有效地降低了起动电流。

图11 起动和运行时定子齿部磁通密度分布
Fig.11 Magnetic density distribution diagram of stator teeth during starting and running
2.2 转子磁动势分析
多谐波联合起动BDFM 起动时由于控制绕组短接,功率绕组仅部分绕组单独接入电网,因此,功率绕组pp 对极基波磁场在转子内感应出pc 和pp对极谐波磁场,产生感应电动势。控制绕组通过转子作用感应出 pc 对极基波磁场,从而实现了定子两套不同极对数绕组之间的耦合,实现机电能量的转换。以图4 中转子绕组Ⅰ和Ⅳ为例,其等效连接如图12 所示,带“′”为少匝,不带“′”为多匝。转子绕组Ⅰ在不同极对数磁场下的矢量相位图如图13 所示。

图12 转子绕组Ⅰ和Ⅳ
Fig.12 Rotor windings I and IV

图13 不同极对数下转子绕组Ⅰ槽号矢量相位图
Fig 13 The vector phase diagram of slot-number of rotor winding under different pole-pairs
当电机起动时,由图13 可知,转子绕组Ⅰ和Ⅳ中,(1, 2)、(3, 4)号线圈与(13, 14)、(15, 16)号线圈产生的奇极对数谐波磁动势相位相反,与其产生的偶极对数谐波磁动势相位一致。假定(1, 2)、(3, 4)号线圈与(13, 14)、(15, 16)号线圈中的多匝部分( 1=13N )产生的感应电动势之和大小均为 1E ,少匝部分( 2=5N )产生的感应电动势之和大小均为2E 。在起动时,对于奇极对数谐波磁动势而言,转子绕组Ⅰ~Ⅲ中,上、下并联支路感应电动势的大小部分抵消,均变为 E1 - E2,上、下并联支路合成感应电动势的方向相反。因此,转子绕组Ⅰ~Ⅲ中外部连接线不起作用,复合线圈内部形成环流,没有电流贯穿于整个闭合回路;而转子绕组Ⅳ~Ⅵ无外部连接线,复合线圈内存在环流。此时,转子绕组的有效匝数减少,呈现高阻态。对于偶极对数谐波磁场而言,转子绕组Ⅰ~Ⅲ中上、下并联支路感应电动势大小相互叠加变为E1+E2,与外部连接线形成闭合回路。此时,有效匝数为N1+N2。而转子绕组Ⅳ~Ⅵ没有外部接线,上、下并联支路感应电动势完全抵消,并联支路内部无电流,此时复合线圈不起作用,转子绕组的有效匝数没有变化。
当电机双馈运行时,该电机为一台普通2/4 对极BDFM 正常运行状态。由于转子绕组Ⅳ~Ⅵ的上、下并联支路感应电动势同大小、同相位,感应电动势相互抵消,此时,转子每相的有效匝数没有发生改变,对定子边而言转子呈现低阻态。
3 多谐波联合起动BDFM 起动性能分析
基于以上分析可知,多谐波联合起动 BDFM在起动时定子上功率绕组采用独特的联结方法,磁动势中除产生和电机双馈运行时与功率绕组极对数相同的基波外,还产生主谐波、多个极对数副谐波等其他一系列谐波磁场。基波磁场与它在转子绕组中感应产生的电流相互作用而产生电磁转矩;定子的谐波磁场均以不同的转速在气隙中推移,并在转子绕组中产生感应电动势和电流,从而产生转矩,这些与基波磁场同转向的谐波磁场产生的转矩均为起动转矩,从而进一步引起电机起动性能的变化[17-20]。由于多谐波联合起动 BDFM定子绕组产生较大的磁动势谐波成分(基波、主谐波和多个极对数副谐波),和常规电机的计算不同,这些谐波产生的作用不能当作漏抗处理,而把这些谐波对电机起动时产生的转矩当作起动转矩来计算。
令功率绕组和控制绕组的转差率分别为

式中,ωp 为功率绕组电角频率,ωp=2πfp;ωc 为控制绕组电角频率,ωc=2πfc;ωr 为转子旋转机械角速度,ωr=2πnr/60;pp 对极磁场在转子绕组中感应的电流频率为fpr=spfp;pc 对极磁场在转子绕组中感应的电流频率为fcr=scfc。ωp、ωc 与ωr 同方向时为正,反方向为负。图14 给出了多谐波联合起动时所存在的磁动势分量。双箭头表示两个磁动势相互作用所产生的起动转矩。图14 中上方是由功率和控制绕组的电流产生的多个磁动势,下方是由转子绕组电流产生的多个磁动势。左边框内的均是由功率绕组的电流产生以及派生出来的多个磁动势,右边框内的是由控制绕组的电流产生以及派生出来的多个磁动势[7]。

图14 各谐波磁场的相互作用
Fig.14 Interaction of harmonic magnetic fields
由于其他各极对数磁动势谐波产生的转矩都可以小到忽略不计,本文不考虑各极对数谐波转矩之间的相互影响,分别计算出基波、主谐波和副谐波磁动势的电磁转矩,然后叠加,分析电机起动过程中的转矩情况,其等效电路如图15 所示。

图15 起动时的等效电路
Fig.15 Equivalent circuit at start-up
对于vn 极谐波而言,其相对于转子的转差率![]() 由等效电路即可推出2、3、4、5 对极谐波产生的起动转矩为
由等效电路即可推出2、3、4、5 对极谐波产生的起动转矩为


其对应的转矩-转速特性曲线如图16 所示,转子电阻变化时的T-s 特性曲线如图17 所示。

图16 多谐波联合起动时的转矩特性 Fig.16 Torque characteristic at start-up

图17 转子电阻变化时的 -T s 特性
Fig.17 Torque characteristic when the rotor resistance changes at start-up
通过对比图16 和图17 可知,转子电阻 2R′增大,T-s 曲线左移,增大了起动转矩。多谐波联合起动BDFM 在起动时增大了起动转矩,且转速下降缓慢,机械特性变硬,带负载的能力增强。当控制绕组短接时,其转差率为

从式(28)可以看出,当多谐波联合起动BDFM的转速 n 达到接近功率绕组的自然同步速np=60fp/(pp+pc),则转差率sc 将趋于无穷大,由图15等效电路可知,相当于 2 c p/sR s′ 趋于无穷大,即相当于控制绕组开路。此时基波、主谐波磁动势与转子磁动势相互作用产生的转矩在np 时达到极小值。另外在该起动方式下,副谐波在起动初期协助主谐波、基波提高电机的起动转矩,但在起动后期,副谐波产生的转矩为负,反而会削弱起动转矩,因此,使得起动过程中转矩-转速曲线在功率绕组的自然同步速(500r/min)附近会出现凹陷,此时有可能将电机转速“卡”在功率绕组的自然同步速(500r/min)附近而不能继续上升,也有可能由于电机的转动惯性拖动,使得电机转速一直上升,不过电机转速增量降低, 使得电机转速会稳定在 np=60fp/pp(750r/min)。所以目前有关文献对BDFM 异步运行模式的表述不一致,控制绕组在相同联结方式下的稳态转速差异很大[23-26]。
图18a 给出的是仅有功率绕组中的部分绕组单独励磁且空载起动时的磁场分布。从图18a 中可以看出,气隙磁通密度呈不对称状态,且饱和程度较小。图18b 给出的是功率和控制绕组共同励磁且空载运行时的磁场分布。从图18b 中可以看出,双馈运行时的磁力线分布合理,能够沿着有利于机电能量转换的路径流通,而且呈对称状态。由图18 可知,BDFM 双馈运行时的磁通密度饱和程度明显高于多 谐波联合起动BDFM 的饱和程度,且有多处小范围饱和。普通感应电机在起动瞬间,起动电流很大,可达到额定值的4~7 倍,对电网的冲击电流很大。进一步说明了多谐波联合起动保持较高的起动转矩,且降低了电动机起动电流。

图18 起动和双馈运行时磁力线分布
Fig.18 Magnetic field distribution during starting and running
图19 给出了起动时多谐波联合起动BDFM 的气隙磁通密度径向分量的波形。由于气隙磁通密度径向分量对机电能量转换起关键性作用,其与励磁电流的大小有直接关系,且对电机的剪切力、饱和程度、损耗有着重要影响,因此对气隙磁通密度径向分量的大小进行研究,气隙磁通密度径向分量的计算公式为
式中, rB 为径向磁通密度; xB 为磁通密度的x 轴分量; yB 为磁通密度的y 轴分量。通过式(29)对图19 的气隙磁通密度径向分量进行分解,其快速傅里叶变换(Fast Fourier Tranform, FFT)分析示意图如图20 所示。

图19 起动时气隙磁通密度径向分量的波形
Fig.19 Waveform of radial component of air gap magnetic flux at start-up

图20 FFT 分析
Fig.20 Analysis of FFT
由图20 可以看出,气隙磁场含有不同极对数的磁动势谐波,在以4 对极磁动势为基波时,其主要产生的谐波含量2、3、5 对极谐波磁动势,在起动时产生的基波极数幅值大,而且能与主谐波、副谐波联合起来,足以抵消无用谐波对电机的影响,因此其他含量低的谐波对电机的运行性能影响较小。
4 样机仿真与试验结果比较
为了验证上述对多谐波联合起动BDFM 的分析,设计了一台2/4 对极BDFM,其设计数据见表3,根据表3 先建立试验平台,如图21 所示。利用时步有限元进行仿真计算,并通过试验进行验证。
表3 样机主要尺寸与参数
Tab.3 Prototype main size and parameters (单位:mm)

参 数 数 值 定子外径 215 定子内径 130 气隙长度 0.4 转子外径 129.2 转子内径 50 铁心长度 190

图21 试验平台 Fig.21 Test platform
当电机空载起动时的特性曲线如图22 所示。0~300ms 左右,此时BDFM 为多谐波联合起动电机,即将控制绕组短接、部分功率绕组接入工频电源(fp=50Hz),稳定状态转速为750r/min,待电机转速 稳定后,通过切换开关将样机切换至BDFM 的双馈运行状态(fp=50Hz,fc=10Hz),此时,样机稳定后的转速为600r/min。整个过程的转速和转矩波形如图22 所示。


图22 仿真曲线
Fig.22 Simulation curves
从图22a、图22b 中可以看出,多谐波联合起动在功率绕组自然同步速为500r/min 附近,电机转速与惯性共同作用,转速增量降低,但电机转速会一直上升至同步点转速750r/min。这是由于电机在500r/min 附近转矩出现塌陷所造成的结果,但是多谐波联合起动BDFM 在500r/min 之前就将其切换,缩短起动时间,进而进入变频调速状态。
为了验证多谐波联合起动的优越性,分别对BDFM 在不同起动方式下进行了仿真。图23 为不同起动方式下功率绕组的相电流仿真波形。图23a为控制绕组短接,部分功率绕组励磁的多谐波联合 起动方式;图23b 为控制绕组励磁,功率绕组全部励磁的双馈起动方式;图23c 为控制绕组短接,功率绕组全部励磁的异步起动方式。


图23 不同起动方式下功率绕组的相电流仿真波形
Fig.23 Phase current simulation waveforms of power winding under different starting methods
从图23 中可以看出,与异步起动、双馈起动相比,多谐波联合起动大大降低了起动电流,而且在切换过程中,冲击电流较小,进一步说明了采用多谐波联合起动方式在保持较高起动转矩的情况下,有效地抑制了样机的起动电流,提高了样机的起动性能。
下面通过对样机进行空载试验以验证仿真结果的正确性。在施加相同的工频激励下的功率绕组的相电流波形如图24 所示。
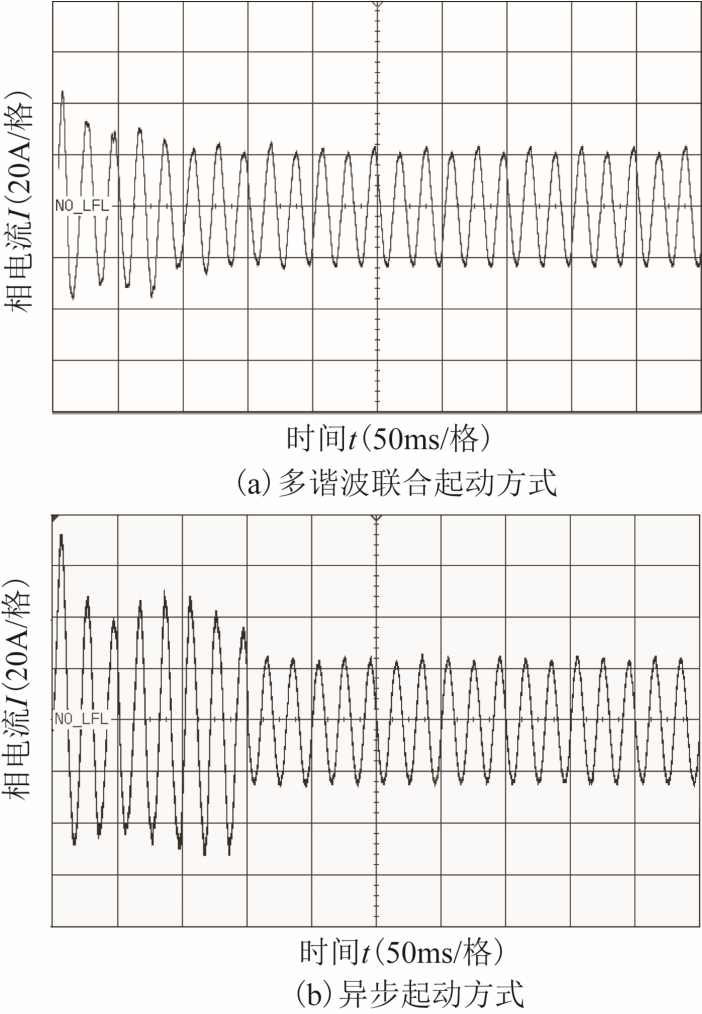
图24 空载试验功率绕组相电流波形
Fig.24 Phase current test waveform of power winding under no load condition
普通感应电机在直接起动时,起动电流通常为额定电流的4~7 倍。结合试验波形可以看出,与异步起动相比,多谐波联合BDFM 起动电流得到了有效的降低,说明采用多谐波联合起动方式在维持原有转矩大小的情况下,可以有效降低起动电流,改善电机的起动性能,进一步验证了理论的正确性。从图24 可以看出,在电机空载起动时,多谐波联合起动时功率绕组相电流峰值为45.3A;异步起动时功率绕组相电流的峰值为74.8A。对比可知,采用多谐波联合起动的最大起动电流降低了40%左右,大大减小了对电网和电机造成的冲击。通过与图23 相比可知,空载试验与仿真结果基本一致,且偏差较小,验证了仿真的正确性。
5 结论
本文通过对多谐波联合起动BDFM 的工作原理、定转子绕组磁动势、气隙磁通密度以及起动电流的分析,研究多谐波联合起动BDFM 的谐波磁场特性及起动性能,得到如下结论:
1)多谐波联合起动BDFM 转子绕组采用复合线圈结构,增大了起动电阻,从而降低了起动电流,降低了磁场饱和程度。
2)多谐波联合起动BDFM 在起动时的磁场和气隙磁通密度除基波外,还含有与基波同转向而极对数不同的谐波磁场,由于磁场之间相互作用,进一步增大电机的起动转矩。
3)多谐波联合起动BDFM 在起动时由电网直接供电,完成起动过程后,可通过开关切换至BDFM双馈运行状态,进而实现变频调速。
4)样机仿真与试验结果表明,多谐波联合起动BDFM 具有起动方便、易于切换和起动性能好等优点,对改善电动机起动性能的研究具有一定的指导作用。
[1] Zhang Fengge, Yu Siyang, Wang Xiuping, et al. Research of a novel brushless doubly-fed generator with hybrid rotor[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(7): 1-5.
[2] Wang Yunchong , Ho S L, Fu W N, et al. A novel brushless doubly-fed generator for wind power generation[J]. IEEE Transactions on Magnetics, 2012, 48(11): 4172-4175.
[3] Liu Yi, Xu Wei, Zhu Jianguo, et al. Sensorless control of standalone brushless doubly-fed induction generator feeding unbalanced loads in ship shaft power generation system[J]. IEEE Transactions on Industrial Electronics, 2019, 66(1): 739-749.
[4] 张凤阁, 王秀平, 于思洋, 等. 不同转子结构无刷双馈电动机转子耦合能力与运行性能的对比分析与实验研究[J]. 中国电机工程学报, 2016, 36(10): 2816-2826. Zhang Fengge, Wang Xiuping, Yu Siyang, et al. Comparative analysis and experimental research of coupling capability and operating characteristics for brushless doubly-fed motors with different rotor structures[J]. Proceedings of the CSEE, 2016, 36(10): 2816-2826.
[5] 阚超豪, 赵威, 储成龙, 等. 基于变极绕组的无刷双馈电机起动特性研究[J]. 电工技术学报, 2019, 34(7): 1392-1403. Kan Chaohao, Zhao Wei, Chu Chenglong, et al. Research on starting characteristics of brushless doubly-fed machines based on pole changing winding[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1392-1403.
[6] 欧先朋, 韩力, 韩雪峰, 等. 两种不同笼型转子结构无刷双馈电机的稳态运行性能对比[J]. 电工技术学报, 2017, 32(23): 61-71. Ou Xianpeng, Han Li, Han Xuefeng, et al. Comparison of steady state operating performances on brushless doubly-fed machine with two different cage rotors[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 61-71.
[7] 程源, 王雪帆, 熊飞, 等. 绕线转子无刷双馈电机开环控制下的稳定性研究[J]. 中国电机工程学报, 2013, 33(增刊1): 203-210. Cheng Yuan, Wang Xuefan, Xiong Fei, et al. Investigation of stability for a wound-rotor brushless doubly-fed machine under open-loop control [J]. Proceedings of the CSEE, 2013, 33(S1): 203-210.
[8] 黄长喜, 阚超豪, 任泰安, 等. 磁阻式无刷双馈电机的转子结构及其性能分析[J]. 电工技术学报, 2017, 32(增刊2): 26-33. Huang Changxi, Kan Chaohao, Ren Taian, et al. Performance analysis on brushless doubly-fed motor with reluctance rotor[J]. Transactions of China Electrotechnical Society, 2017, 32(S2): 26-33.
[9] 李宁, 程明, 韩鹏. 电动汽车用新型双定子无刷双馈电机转子磁链定向控制[J]. 电工技术学报, 2014, 29(增刊):115-123. Li Ning, Cheng Ming, Han Peng. Rotor flux oriented control of a new dual-stator brushless doubly-fed motor for EV/HEV applications[J]. Transactions of China Electrotechnical Society, 2014, 29(S): 115-123.
[10] 阚超豪, 鲍习昌, 王雪帆, 等. 无刷双馈电机的研究现状与最新进展[J]. 中国电机工程学报, 2018, 38(13): 3939-3959. Kan Chaohao, Bao Xichang, Wang Xuefan, et al. Overview and recent developments of brushless doubly-fed machine[J]. Proceedings of the CSEE, 2018, 38(13): 3939-3959.
[11] 辜承林, 陈乔夫, 熊永前. 电机学[M]. 武汉: 华中科技大学出版社, 2010.
[12] 邓先明, 姜建国. 无刷双馈电机的工作原理及电磁设计[J]. 中国电机工程学报, 2003, 23(11): 130-136. Deng Xianmig, Jiang Jianguo. The principle and electromagnetic design of brushless doubly-fed machine[J]. Proceedings of the CSEE, 2003, 23(11): 130-136.
[13] 杜江, 韩力, 欧先朋, 等. 笼型转子无刷双馈电机异步运行模式的实验研究[J]. 中国电机工程学报, 2016, 36(14): 3964-3972. Du Jiang, Han Li, Ou Xianpeng, et al. Experimental study of brushless doubly-fed machine with cage rotor at the asynchronous operation mode[J]. Proceedings of the CSEE, 2016, 36(14): 3964-3972.
[14] 许实章. 交流电机的绕组理论[M]. 北京: 机械工业出版社, 1985.
[15] 许实章. 新型电机绕组—理论与设计[M]. 北京: 机械工业出版社, 2001.
[16] 王雪帆, 许实章. 一种新型感应电机转子绕组—无感绕组的研究[J]. 电工技术学报, 1992, 7(4): 1-4. Wang Xuefan, Xu Shizhang. Wound-rotor induction motors with inductionless wingding[J]. Transactions of China Electrotechnical Society, 1992, 7(4): 1-4.
[17] 于克训, 汤鹏. 无刷双馈电机等效电路模型与特性分析[J]. 中国电机工程学报, 2018, 38(14): 4222-4231. Yu Kexun, Tang Peng. Equivalent circuit model and characteristic analysis of brushless doubly-fed machine[J]. Proceedings of the CSEE, 2018, 38(14): 4222-4231.
[18] 张爱玲, 熊光煜, 刘振富, 等. 无刷双馈电机传递关系和功率因数特性的试验研究[J]. 中国电机工程学报, 2011, 31(6): 92-97. Zhang Ailing, Xiong Guangyu, Liu Zhenfu, et al. Experimental study on energy transmission and power factor characteristics of brushless doubly-fed machines[J]. Proceedings of the CSEE, 2011, 31(6): 92-97.
[19] 邓先明, 姜建国, 方荣惠. 笼型转子无刷双馈电机的电磁分析和等效电路[J]. 电工技术学报, 2005, 20(8): 6-11. Deng Xianming, Jiang Jianguo, Fang Ronghui. The electromagnetic analysis and equivalent circuit of brushless doubly-fed machine with cage rotor[J]. Transaction of China Electrotechnical Society, 2005, 20(8): 6-11.
[20] 熊飞, 王雪帆, 张经纬, 等. 绕线转子无刷双馈电机的链型等效电路模型[J]. 电工技术学报, 2010, 25(2): 15-21. Xiong Fei, Wang Xuefan, Zhang Jingwei, et al. Chain equivalent circuit model of wound-rotor brushless doubly-fed machine[J]. Transactions of China Electrotechnical Society, 2010, 25(2): 15-21.