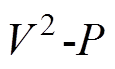的二次函数关系设计了
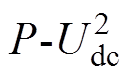下垂控制。对于连接高渗透率电网的换流站采用有功-频率（P-f）下垂控制[20]，能够较好地维持交流系统频率稳定。摘要 现有的对于直流电网的研究多集中于放射状直流电网拓扑的下垂系数计算，针对复杂直流电网的研究较少。该文提出一种基于自律分散控制的网孔型直流电网下垂系数计算方法。首先，由系统级控制采集和交换换流站信息，使各换流站获取相同的全局信息；其次，将全局信息代入最优潮流优化模型计算各换流站的有功功率和直流电压参考值；随后，定义虚拟节点并将直流电压参考值的平均值定义为虚拟电压值，取直流系统中直流电压等于虚拟电压值的点，将这些等势点合为虚拟节点从而简化网络拓扑；接着，分别计算最优潮流分布下和当前工况下各节点相对于虚拟节点的虚拟电阻和实际电阻值，此时，下垂系数等于两种电阻值差的倒数；最后，在PSCAD/EMTDC中搭建了六端直流电网。通过仿真，分析并验证了所提方法的可行性。
关键词：直流电网 自律分散控制 虚拟节点 下垂系数
随着风力发电、光伏发电站的大规模建设，含有大量新能源电源的交流电网（以下简称高渗透率电网）与主网连接的问题愈发突出[1-3]。高渗透率电网具有转动惯量较小，频率、交流电压波动较大的特点[4-5]。而柔性直流输电技术具有无功解耦控制、潮流反转且电压极性不变、稳定交流母线电压等特性[6]，可以避免高渗透率电网与主网直接相连[7]。
柔性直流换流站可组成柔性多端直流电网，主要有主从控制、裕度控制和下垂控制三种控制模 式[8-11]。主从控制模式和裕度控制模式需要设置主控站控制直流电压，主控站需要较大的容量，对器件要求较高。此外，主从控制模式对通信的依赖度较高，主控站功率越限或退出运行，需要其他换流站及时切换为主控站；裕度控制模式虽然对通信的依赖度较弱，但是各换流站之间通过预设的特性曲线运行，不利于实现直流电网的优化运行。
下垂控制是由模拟传统同步发电机的有功功率、频率下垂特性提出的，广泛应用在新能源发电、微电网中[12-17]。文献[12]指出下垂控制提供了虚拟阻抗，实现了换流站之间的功率分配。文献[13-17]将下垂控制应用于多端柔性直流输电系统中，采用下垂控制的各换流站以维持直流电压稳定和输出额定功率为目标，采用P-Udc下垂控制。文献[18-19]以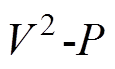的二次函数关系设计了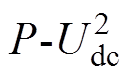下垂控制。对于连接高渗透率电网的换流站采用有功-频率（P-f）下垂控制[20]，能够较好地维持交流系统频率稳定。
此外，现有的研究对直流电网的直接控制和放射状直流电网的下垂控制研究较多。例如，文献[6]通过集中控制方式，计算各换流站的功率和直流电压参考值，直接控制直流系统的稳定运行。这种方案不但对系统通信速度和可靠性要求较高，还存在响应速度较慢、电压裕度选择困难的问题[8]。文献[21]采用定下垂系数的自律分散控制方式，实现各换流站的稳定运行。这种方法虽能保证直流电网的运行，但存在下垂系数选取困难，定下垂系数调节不够精确的问题[8]。文献[12]指出，采用下垂控制相当于加入了虚拟阻抗。由于放射状电网存在一个公共母线，则各节点相对于公共母线的虚拟阻抗即是下垂系数，如文献[18-19]均是采用这种方法，但是，此种方法局限于直流电网的拓扑，不具有一般性。对于环状或者网状电网，文献[10-11, 13-17, 22]采用功率分配的方法，下垂系数呈比例关系分配各换流站的功率，通过优化算法计算各换流站分配的功率大小，再确定下垂系数。这种方法在稳态运行下能够较好地分配换流站功率，但是当出现功率扰动时，会存在因下垂系数较小、分流精度较低，或是下垂系数较大、电压偏差较大的问题。另外，对于网孔型直流电网或是更复杂的直流电网拓扑，目前鲜有文献分析其基于虚拟阻抗的下垂系数获取方法。
为了弱化直流电网中各换流站对通信可靠性的依赖和实现最优运行控制，有学者提出了自律分散控制策略，且在微电网中有较为广泛的应用[23]。自律分散控制是一种分布式控制策略，具有通信可靠性依赖较小、网络拓展性较好和分布式控制等特点。其分为系统级和站控级两层控制，系统级控制实现信息获取、交换和最优运行方式计算。一致性算法是一种全局信息交换的方法，已有大量的文献对一致性算法展开研究。文献[24]基于一致性算法获取的全局信息，设计了U-I下垂控制以实现对各逆变器的均压、均流控制。文献[25]基于快速一致性算法，实现了全局信息交换并计算了各逆变器之间的虚拟阻抗。
本文根据张北柔性直流电网示范工程远景年规划，搭建了六端柔性直流电网拓扑，设计了自律分散控制的系统级控制和站控级控制。在自律分散控制的系统级控制中，分析了通信可靠性和各换流站获取全局信息的时间延迟，并设计了以系统损耗最小和直流电压偏差最小为目标的最优潮流优化模型。通过将目标函数和约束条件进行适当放缩和变形，以适合凸优化计算，并计算出各换流站的参考直流电压和参考有功功率。随后，在自律分散控制的站控级控制中，将直流系统中所有电压等于平均直流电压的点合并为一个虚拟节点，简化直流网络。根据最优潮流优化模型计算出的结果计算参考电阻值，同时计算各节点相对于虚拟节点的实际电阻值，下垂控制系数即为参考电阻值和实际值之差的倒数。最后，在PSCAD/EMTDC中搭建了六端直流电网模型用以验证本文所提方法的可行性。
为了发挥柔性直流输电技术的诸多优点，展示柔性直流输电技术，我国提出了张北柔直工程的远景年规划，张北地区将建成由张北地区风电厂、光伏电厂、抽水蓄能电站、冀北电网和北京电网互联形成的六端柔性直流电网。
建立如图1所示的六端柔性直流电网拓扑。该拓扑中，VSC1、VSC3、VSC5为送端换流站，汇集以风电为主的新能源电力送入直流电网；VSC2换流站连接抽水蓄能电站，在大运行方式下，将作为逆变站吸收直流电网的能量并储存起来；VSC4和VSC6分别连接一个交流系统，表示实际电网中的城市、区域负荷中心等电网，从直流系统吸收能量。
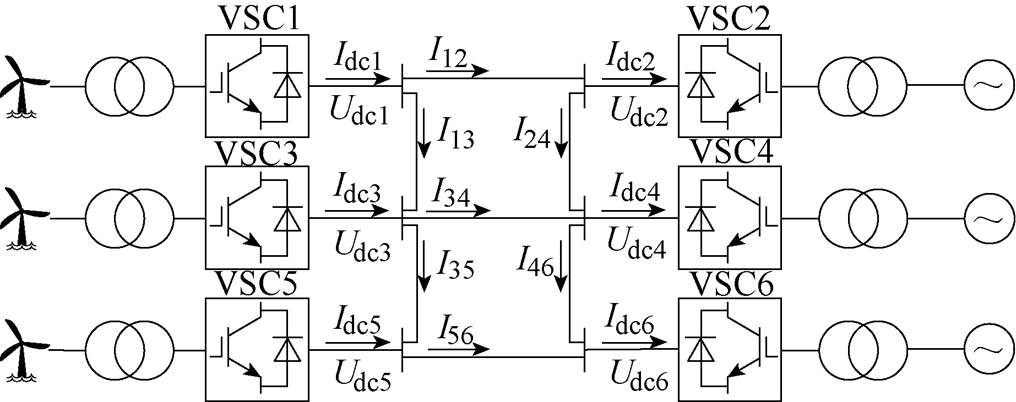
图1 张北六端柔性直流电网拓扑
Fig.1 Topology of the DC power grid
自律分散控制将在每个换流站实现交直流侧信息采集、换流站之间信息交换、潮流优化模型计算和换流站下垂控制等方法。
自律分散控制由系统级和站控级两级控制组成。系统级控制主要实现交直流侧信息采集、换流站之间信息交换、由全局信息计算最优潮流优化模型；站控级控制采用下垂控制，由潮流优化结果计算各换流站下垂系数，使直流网络运行在最优状态。总体上，自律分散控制的控制流程如图2所示。
通信可靠性和通信时延会影响控制稳定性。当发生通信中断时，不同的通信方式会影响全局信息获取的能力。信息的获取速度受通信时延影响，进而影响控制的响应速度。因此，本节将选择合理的通信方式并分析通信时延对控制稳定性的影响。
对于如图1所示直流网络拓扑中，考虑如图3 所示换流站间的四种通信方式，以实现各换流站之间的信息交换和全局信息获取。
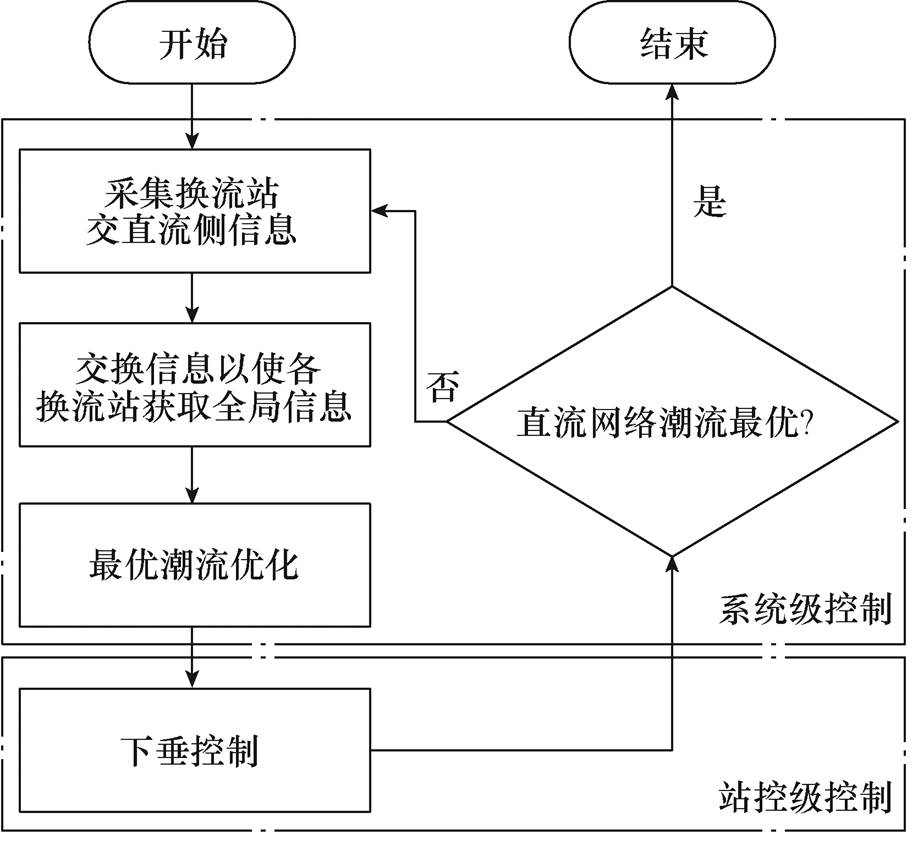
图2 自律分散控制的控制流程
Fig.2 Flow chart of autonomous decentralized control
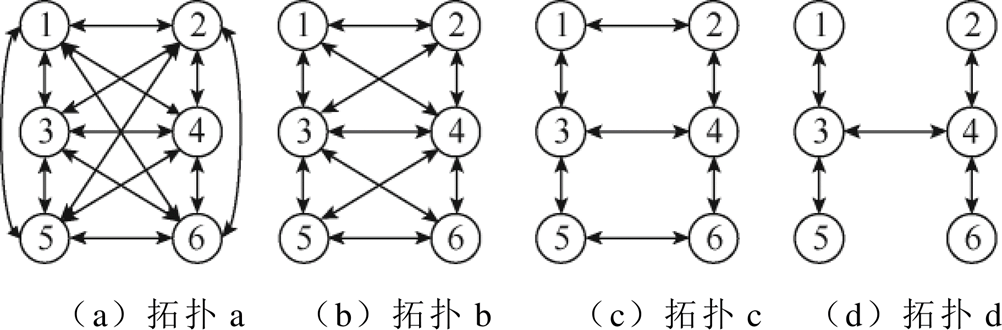
图3 换流站间的四种通信方式
Fig.3 Four types of communications among converters
本文采用一致性算法交换各换流站采集的交直流侧信息。一致性算法广泛应用于分布式控制系统的全局信息获取中，其原理本文不作详述。一致性算法的收敛速度取决于通信拉普拉斯矩阵L的非0最小特征根lmin。分别计算四种通信方式下L的非0最小特征根，通信拉普拉斯矩阵的特征参数见表1。
表1 通信拉普拉斯矩阵的特征参数
Tab.1 Characteristic parameters of communication Laplacian matrix
拓扑结构lmin a6 b2 c1 d0.438 4
综合考虑一致性算法的收敛速度、通信线路数量，选用第三种通信拓扑。即使在部分通信线路中断的情况下，只要通信拓扑仍是连通图，仍可以通过一致性算法获取全局信息。
通信拓扑确定后，可以计算自律分散控制的时间延迟。时间延迟由采样时延、通信时延和计算时延组成。对于采样延迟，实际的直流电压和直流功率与控制系统采样得到的数字反馈量之间存在的采样延迟约为100ms[26]。
通信时延考虑通信速度的影响，可表示[21]为
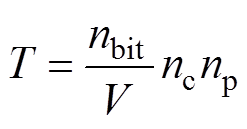(1)式中，nbit为信息位数；nc为达到收敛时的迭代次数；np为交换的信息数；V为通信速度。
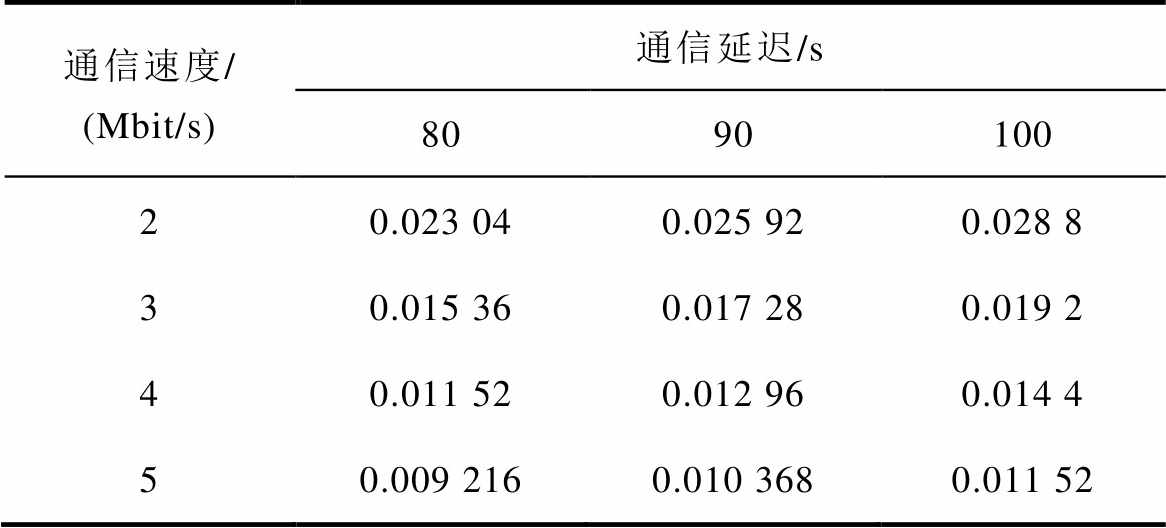
通信信息取8位有效数字，即nbit =64，此时，收敛精度取10-7即可满足要求，取迭代次数nc不小于80次。通信压力最大的换流站需要向邻近的3个换流站发送信息，内容包括直流电压、直流功率和有功功率参考值，则取np=9；通信速度V受换流站之间的距离影响。考虑不同的通信速度和迭代次数，见表2。
表2 不同通信速度和迭代次数下的通信延迟
Tab.2 Communication delay with different communication speeds and iterations
通信速度/ (Mbit/s)通信延迟/s 8090100 20.023 040.025 920.028 8 30.015 360.017 280.019 2 40.011 520.012 960.014 4 50.009 2160.010 3680.011 52
由表2可知，通信时延是远远大于采样时延的。此外，考虑现有计算机的性能，计算时延可忽略。因此，相对于整个优化运行的控制过程，自律分散控制的系统级控制是满足控制时延要求的。
如图1所示的系统，通过一致性算法使各换流站获取相同的全局信息，因此，通过潮流优化模型计算得出的最优潮流分布也是相同的。
2.2.1 最优潮流优化模型的目标函数
建立以系统损耗最小和直流电压偏差最小为目标的潮流优化模型。此时换流站的有功功率参考值Pref等于注入直流系统的有功功率参考值Pdcref减去换流站损耗Ploss_st；直流电压参考值由潮流优化模型计算获得。
应注意，连接新能源电网的换流站采用V/f控制，无法控制直流侧功率和电压；连接交流电网的换流站注入直流系统的有功功率应与参考值相同；只有连接抽水蓄能电站的换流站可以自由地控制有功功率和直流电压。因此，只需计算连接交流电网换流站的直流电压参考值和连接抽水蓄能电站换流站的有功功率、直流电压参考值。
直流功率以注入直流系统的方向为正，则整流站的直流功率为正，逆变站的直流功率为负。因此，潮流优化模型的目标函数表示为
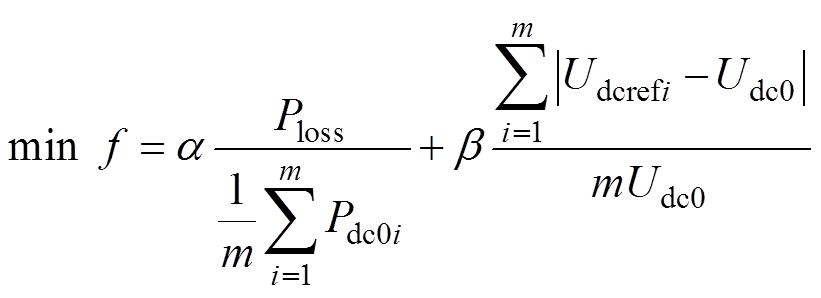(2)式中，Pdc0i为各换流站注入直流系统的额定有功功率；Udcrefi为最优潮流下各换流站端口的直流电压参考值；Udc0为直流系统的额定电压；m为换流站个数；a 和b 为系统损耗最小和直流电压偏差最小两个目标的权重系数，满足a +b =1；Ploss为系统的功率损耗，由换流站损耗Ploss_st和直流系统损耗Ploss_dc组成。直流系统损耗Ploss_dc可以表示为
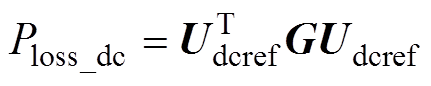(3)
式中，Udcref为最优潮流下各换流站端口的直流电压参考值列向量；G为直流网络电抗矩阵。
各换流站损耗Ploss_st可以表示[24-25, 27-28]为
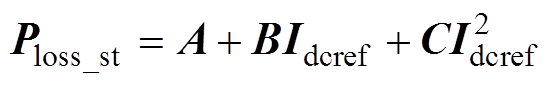(4)式中，以列向量Ploss_st、Idcref表示各换流站损耗和各换流站注入直流系统的电流；A为无负荷损耗系数列向量；B为关于直流电流的线性损耗系数的对角矩阵；C为关于直流电流的非线性损耗系数的对角矩阵，列向量和各对角矩阵中的系数计算方式如下
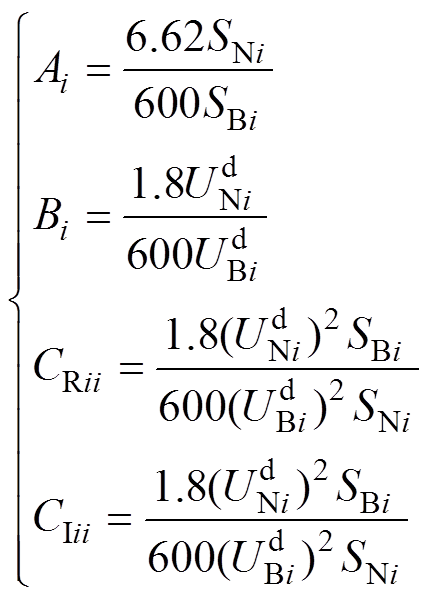(5)
式中，SNi、SBi分别为各换流站额定容量和标准系统基准容量；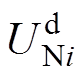
、
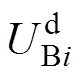分别为各换流站额定电压和标准系统基准电压；下标R、I分别表示整流侧和逆变侧；下标i表示换流站编号。
2.2.2 最优潮流优化模型的约束条件
约束条件的设置需要满足各换流站的控制方式、直流电压范围和交流侧容量限制。
由于连接新能源电网的换流站采用V/f控制，在不考虑延迟的情况下，其注入到换流站的有功功率是确定值，即
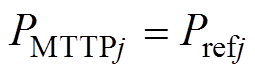(6)式中，PMTTPj为新能源电网的最大功率跟踪值；j为连接新能源电网的换流站编号。
连接交流系统的换流站注入交流系统的有功功率满足
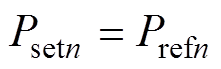(7)式中，Psetn为交流电网调度中心设置的有功功率需求；n为连接交流电网的换流站的编号。为了维持交流电网的稳定运行，连接交流电网的换流站需要按照调度指令运行。
同时，直流网络节点的电压电流满足基尔霍夫定律，即
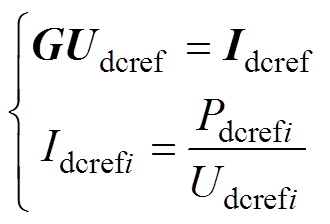(8)换流站一般控制无功功率为0，因此，注入换流站的功率和注入直流系统的功率之间的关系可以表示为
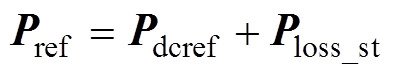(9)
此外，还应考虑节点电压的范围约束和换流站的功率上限约束，即
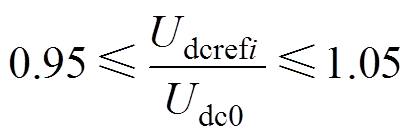(10)
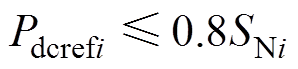(11)
式(10)中表述了各节点直流电压的运行范围不能超过0.95～1.05(pu)，即波动不超过5%。式(11)为传输功率受换流站容量的限制约束，考虑到负荷扰动和线路热稳定性限制等因素，实际传输功率会设置有一定的裕度。参考文献[25]将裕度设为20%，即得到式(11)。
2.2.3 最优潮流优化模型的计算
由2.2.2节建立的最优潮流优化模型可知，针对如图1所示的系统，需要计算逆变侧各节点的直流电压参考值，以及连接抽蓄电站的换流器有功功率参考值。为了保证各换流站自律分散控制的计算结果相同，本文采用凸优化对最优潮流优化模型进行求解。
凸优化是指[29]将目标函数限定为凸函数，优化变量的可行域限定为凸集，则最优问题为凸优化问题。凸优化问题的局部最优解一定为全局最优解。因此，对于采用自律分散控制的各换流站，采用凸优化求解最优潮流优化模型可以保证各换流站计算出的最优潮流分布相同。
首先需要检查最优潮流优化模型是否符合凸优化的形式。对于目标函数，Ploss由式(3)计算，本质上是一个二次函数；对于直流电压偏差的计算，可以变形为(Udcref -Udc0)2来计算，通过设置b 值进行放缩，其本质也是一个二次函数。对于约束条件中的等式和不等式约束显然是符合凸优化的条件的。对于式(8)，将其变形为式(12)来进行放缩，其本质也是个二次函数，符合凸优化要求。
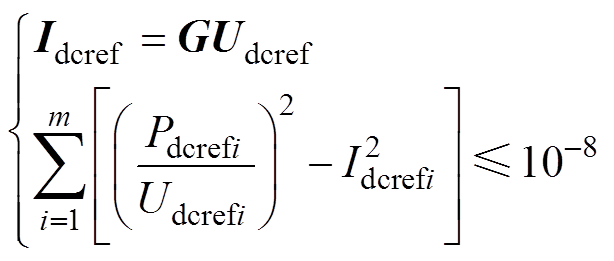(12)自律分散控制的系统级控制通过换流站间的信息交换获取系统的全局信息，并进行最优潮流计算。而站控级控制将通过最优潮流结果计算各换流站的下垂系数。
现有研究主要集中于放射状直流电网拓扑上，这种拓扑存在一个公共节点，因此，直流电网的导纳矩阵为对角矩阵，并可以通过导纳矩阵的对角元素计算下垂系数。但对于如图1所示的网孔型直流电网拓扑，由于不存在公共节点，网络的导纳矩阵存在非对角元素，计算下垂系数较为复杂。
针对复杂直流电网不易计算下垂系数的问题，本文提出了一种基于自律分散控制的网孔型直流电网的模型简化方法。
首先，定义平均直流电压Uave为
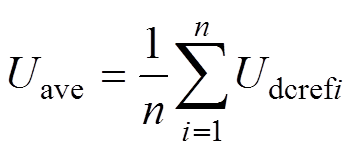(13) 考虑到在图1拓扑的运行过程中，各整流站节点的直流电压值大于各逆变站节点的直流电压值，而各整流站之间和各逆变站之间的直流电压值相差不大，则电压值等于Uave的节点将会出现在换流站1和2、3和4、5和6之间的线路上。将三条线路上的直流电压等于Uave的节点合为一个，定义为虚拟节点7，则虚拟节点7的直流电压为Uave。直流电网简化过程示意图如图4所示。
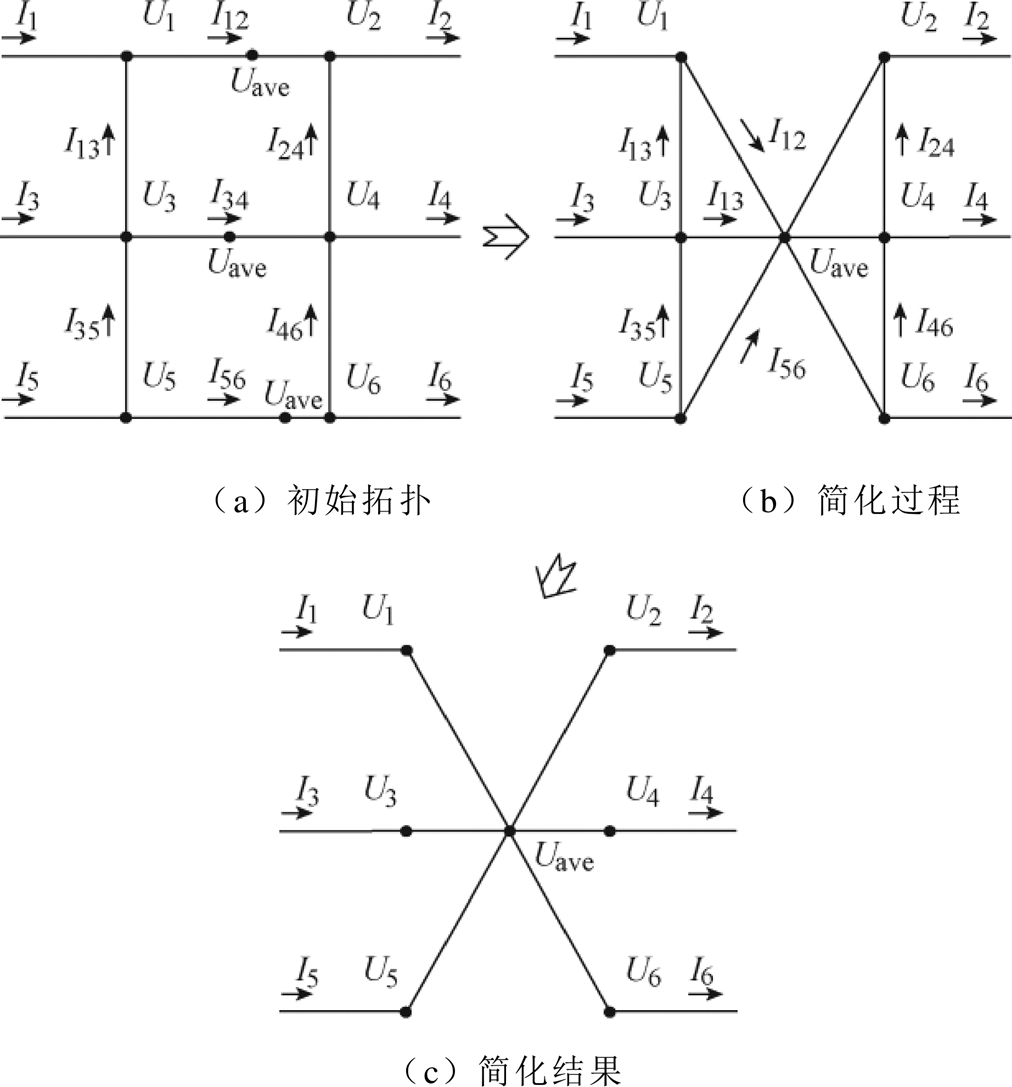
图4 直流电网简化过程示意图
Fig.4 Diagram of the DC system simplification process
此时，电网拓扑仍然不是最简形式，还需要进一步简化为图4c的形式。因此，提取出图4b中的一块基本拓扑单元，并定义其电流方向如图5所示。
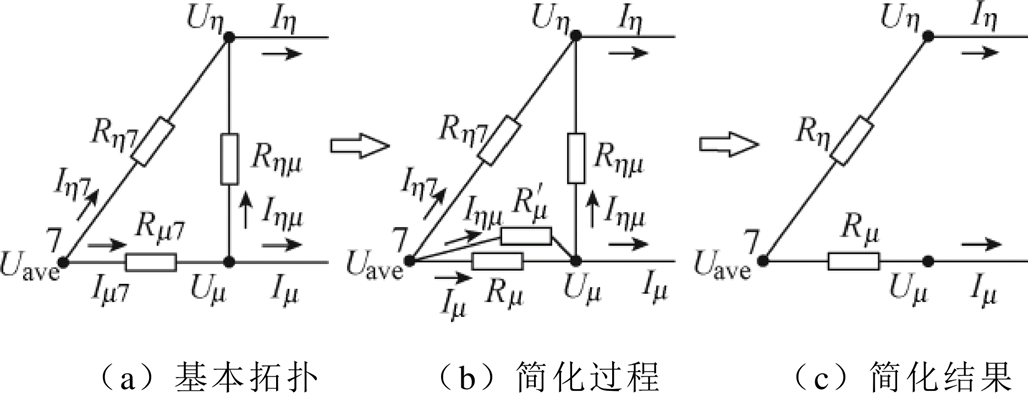
图5 图4b中的基本拓扑单元及其简化过程
Fig.5 Basic unit of the topology in Fig.4b and its simplification
首先，根据基尔霍夫定律，建立图5a中各节点的电压电流关系为
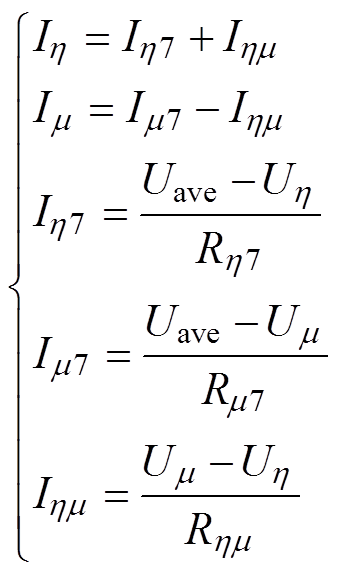(14)注意到电流Im7含有两个电流分量：一部分电流Ihm 注入节点h；另一部分电流Im 注入节点m。根据叠加定理，可将支路电阻Rm7转化为两个电阻Rm 和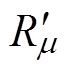
并联的形式，如图5b所示，使其满足
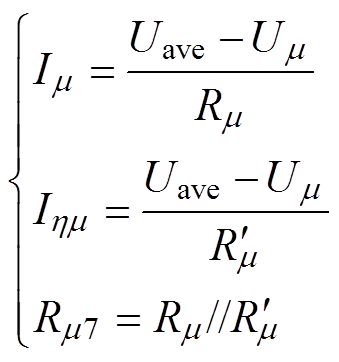(15)
则节点h、m 的直流电压Uh、Um 和虚拟节点7的直流电压Uave的关系可表示为
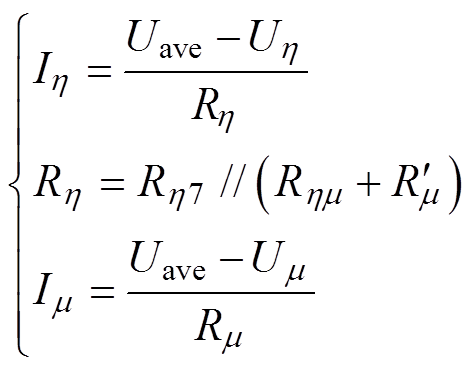(16)如此，可将图5a所示的基本单元拓扑简化为图5c所示的拓扑，直流电压电流关系如式(16)所示。根据叠加定理，上述验证过程同样适用于多端口拓扑。从而证明了由图4b到图4c的简化过程是成 立的。
3.1节验证了由图4a所示的直流电网拓扑化简为如图4c所示的拓扑是可行的。因此，通过构造虚拟节点，将网孔型直流电网化简为放射性电网拓扑，以计算各换流站的下垂系数，是本文对自律分散控制应用于复杂电网提出的改进。图6给出了获取下垂系数的计算流程。
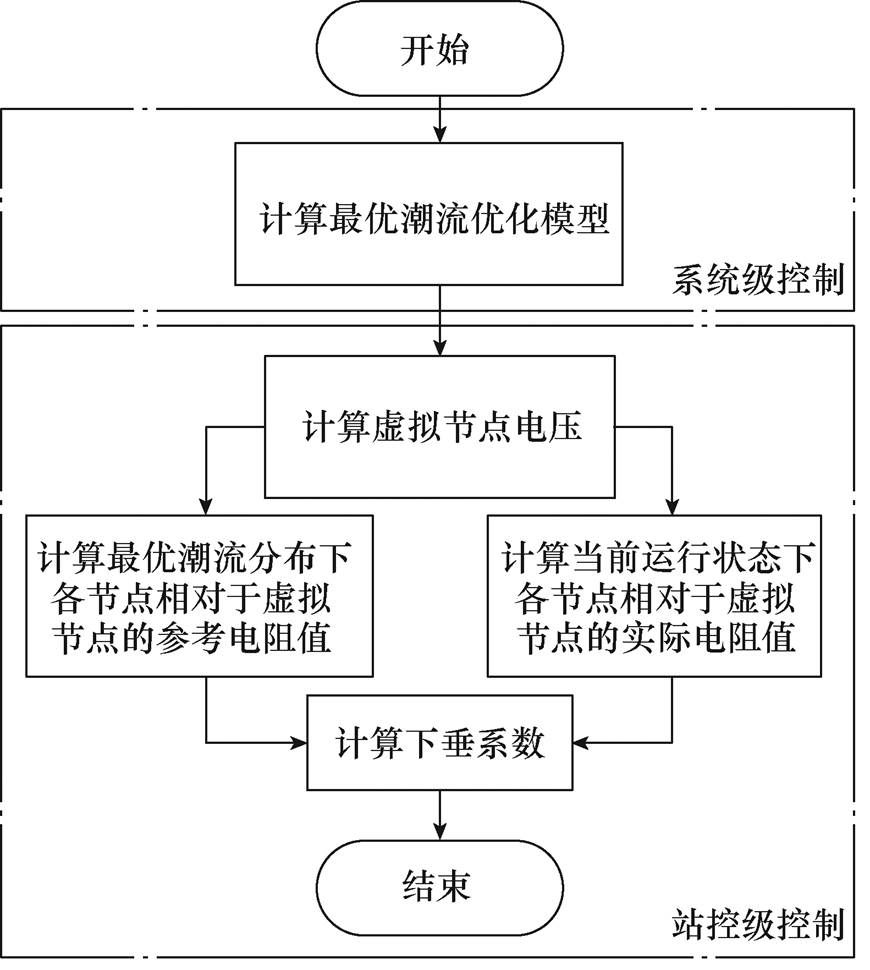
图6 下垂系数计算流程
Fig.6 Flow chart of droop coefficient calculation
首先，由自律分散控制系统级控制的最优潮流优化模型计算出各节点直流电压参考值Udcrefi和有功功率参考值Pdcrefi，并由式(13)计算出虚拟节点的直流电压。需要注意，连接新能源电网的换流站无法控制注入直流系统的有功功率和直流电压，连接交流电网的换流站无法调整有功功率参考值（由交流系统运行调度的实际工况决定），通过最优潮流优化模型计算出的参考值用于逆变站的直流电压-功率下垂控制。
然后，计算出各节点相对于虚拟节点的电阻 值，即
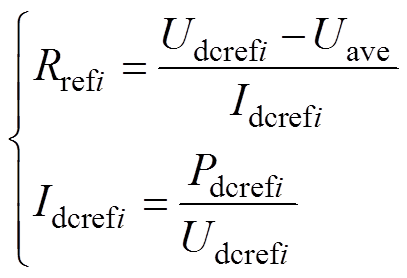(17)式中，Pdcrefi为各节点注入直流系统的有功功率参考值；Rrefi为基于最优潮流优化模型的结果计算出的各换流站节点相对于虚拟节点的最优电阻值。
最后，计算当前各换流站节点相对于虚拟节点7的电阻值，即
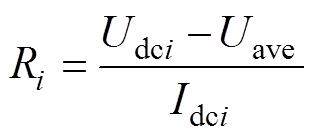(18)式中，Udci和Idci分别为各换流站节点的实测直流电压和电流值。
各换流站的下垂系数可以表示为
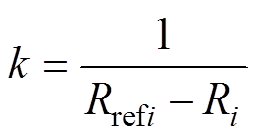(19)实际上，由于连接新能源电网的换流站采用V/f控制，控制目标为交流侧的电压和频率，所以由式(19)计算出的下垂系数不参与其控制。下垂系数只影响连接交流电网的换流站和连接抽蓄电站的换流站的控制。
在PSCAD/EMTDC仿真软件中建立如图1所示的系统模型，并搭建自律分散控制。模型中直流系统各支路阻抗参数见表3。
仿真中，0～0.7s为系统初始化阶段，连接新能源电网的换流站采用V/f控制，连接交流电网的换流站采用定有功功率控制，连接抽水蓄能电站的换流站采用定直流电压控制方式起动。系统的运行参数见表4。
表3 直流系统线路阻抗参数
Tab.3 Line parameters of the DC system
线路R/WL/H l122.00.04 l131.00.02 l241.50.03 l342.50.05 l351.50.03 l461.00.02 l561.50.03
表4 初始系统运行参数
Tab.4 Parameters of the initial operation
换流站编号控制方式控制目标 VSC1V/fPMTTP=1 000MW VSC3V/fPMTTP=900MW VSC5V/fPMTTP=1 100MW VSC2UdcUdcref =500kV VSC4PPset=800MW VSC6PPset=750MW
0.7s后，切换为自律分散控制。此时，通过自律分散控制的系统级控制，各换流站获取系统的全局信息，并通过最优潮流优化模型计算最优分布。其计算结果见表5。
表5 最优潮流优化模型计算结果
Tab.5 Results of the optimal power flow model
换流站直流电压/kV下垂系数有功功率/MW 2号493.040.275911.28 4号493.330.209— 6号494.210.180—
图7绘制了仿真时间从0.6～1.2s时段内，直流功率的变化曲线仿真波形，0.7s自律分散控制投入运行。
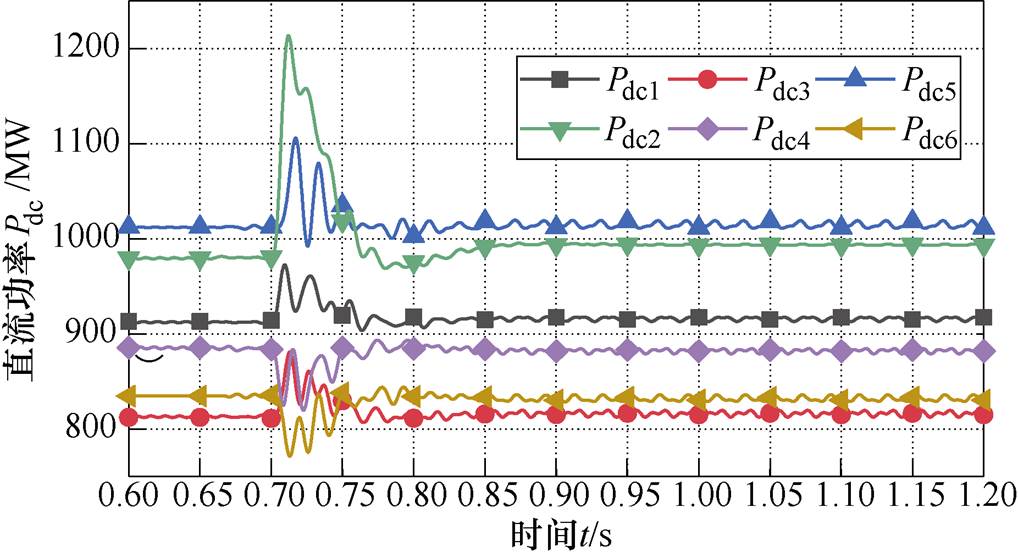
图7 直流功率仿真波形
Fig.7 Simulation waveforms of the DC power
0.7s后，逆变侧换流站切换为下垂控制，系统经过0.1s的扰动逐渐进入新的稳态。从图7可以看出，整流站和逆变4号、6号站的直流功率基本不变，逆变2站的直流功率上升，系统的损耗下降。图8给出了直流电压的仿真变化曲线波形。
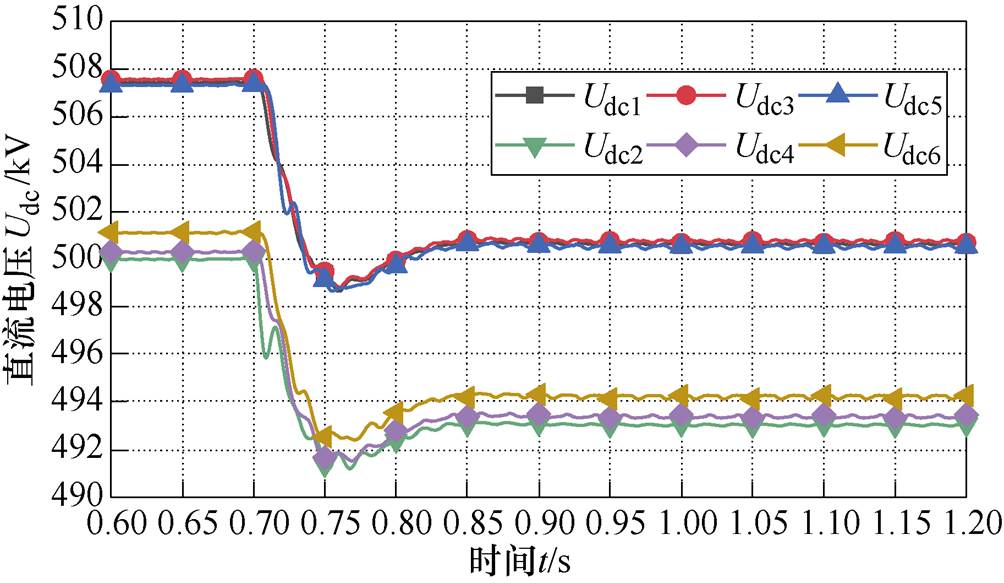
图8 直流电压仿真波形
Fig.8 Simulation waveforms of the DC voltage
由图8可以看出，逆变站电压基本按照最优运行参考值输出，整流站线路压降均高于逆变站电压，以保证功率的正常传输。图9给出了自律分散控制投入前后的系统损耗情况。
图9 系统损耗仿真波形
Fig.9 Simulation waveforms of the DC consumption
由图9可知，系统损耗有了明显的下降。0.7s前损耗平均值为557MW，0.9s进入稳态后损耗为540MW，与最优潮流优化模型计算出的理论损耗值（538.79MW）基本相同，损耗平均值下降了约17MW。图10为交流侧有功功率仿真波形，用以观察功率传输的稳定性。
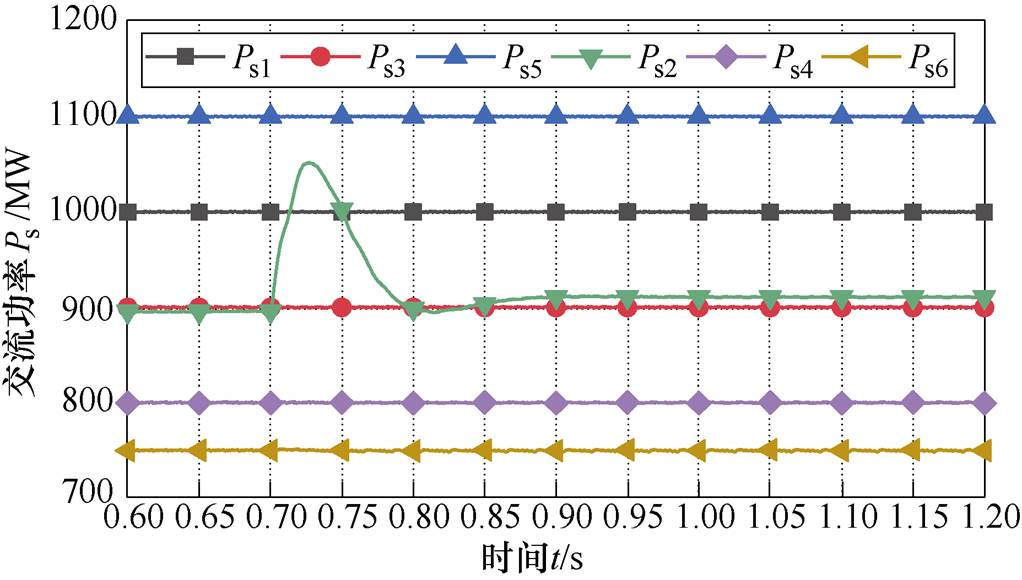
图10 交流侧有功功率仿真波形
Fig.10 Simulation waveforms of the AC active power
图10中，三个连接新能源电网的换流站因采用V/f控制策略，其注入换流站的功率在自律分散控制启动前后没有变化。Ps4、Ps6为连接交流电网的换流站注入交流系统的功率，控制切换前后两换流站送入交流电网的功率基本不变。暂态过程最大的波形为连接抽蓄电站的换流器注入交流系统的功率波形，在切换控制方式并逐渐进入稳态后，其注入交流系统的功率有明显的上升。在其他换流站功率变化不大的情况，该换流站注入交流系统的功率上升说明系统的损耗降低。
由于本文所研究的直流电网传输距离较短，因此，换流站的损耗远远大于直流网络的损耗。此时，由计算换流站的损耗的式(4)和式(5)可以发现，当直流电压降低时，由式(5)计算的系数B和C均下降，则由式(4)计算的换流站损耗也会下降。这与直流电压下降、系统损耗降低的仿真结果相同。同时，直流系统的损耗仿真结果与最优潮流优化模型的计算结果基本相同，也从侧面印证了本文所提方法的正确性。
目前研究多集中于放射状直流电网拓扑的下垂系数计算。针对这一问题，本文提出了一种基于自律分散控制的网孔型直流电网下垂系数计算方法。首先，通过自律分散控制的系统级控制收集、交换各换流站交直流侧信息，使各换流站获取相同的全局信息。然后，由考虑系统损耗最小和直流电压偏差最小的最优潮流优化模型计算各换流站的参考功率、参考直流电压和下垂系数。随后，由自律分散控制的站控级控制完成各换流站的控制切换，实现最优潮流的分布。在计算下垂系数的过程中，由参考直流电压计算直流系统平均电压，在直流系统的线路中寻找这些节点并合并为同一虚拟节点。由基尔霍夫定律能够将网孔型直流电网化简为以虚拟节点为放射中心的放射状拓扑形式。再由参考功率和实际功率计算出各换流站节点相对于虚拟节点的虚拟电阻即可计算下垂系数。本文在PSCAD/EMTDC仿真软件中搭建了基于张北示范工程远景年规划的六端柔性直流电网，验证了本文所提方法的正确性和可行性。
参考文献
[1] 叶婧, 林涛, 张磊, 等. 考虑动态频率约束的含高渗透率光伏电源的孤立电网机组组合[J]. 电工技术学报, 2017, 32(13): 194-202.
Ye Jing, Lin Tao, Zhang Lei, et al. Isolated grid unit commitment with dynamic frequency constraint considering photovoltaic power plants participating in frequency regulation[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 194-202.
[2] 陆晶晶, 贺之渊, 赵成勇, 等. 直流输电网规划关键技术与展望[J]. 电力系统自动化, 2019, 43(2): 182-191.
Lu Jingjing, He Zhiyuan, Zhao Chengyong, et al. Key technologies and prospects for DC power grid planning[J]. Automation of Electric Power Systems, 2019, 43(2): 182-191.
[3] 杨海涛, 吉平, 苗淼, 等. 未来中国特高压电网结构形态与电源组成相互关系分析[J]. 电力系统自动化, 2018, 42(6): 9-17.
Yang Haitao, Ji Ping, Miao Miao, et al. Analysis on interrelationship between future UHV power grid structural form and power source composition in China[J]. Automation of Electric Power Systems, 2018, 42(6): 9-17.
[4] 周天沛, 孙伟. 高渗透率下变速风力机组虚拟惯性控制的研究[J]. 中国电机工程学报, 2017, 37(2): 486-496.
Zhou Tianpei, Sun Wei. Study on virtual inertia control for DFIG-based wind farms with high penetration[J]. Proceedings of the CSEE, 2017, 37(2): 486-495.
[5] 施琳, 罗毅, 施念, 等. 高渗透率风电-储能孤立电网控制策略[J]. 中国电机工程学报, 2013, 33(16): 78-85, 15.
Shi Lin, Luo Yi, Shi Nian, et al. A control strategy of isolated grid with high penetration of wind and energy storage systems[J]. Proceedings of the CSEE, 2013, 33(16): 78-85, 15.
[6] 邵冰冰, 赵书强, 高本锋, 等. 连接弱交流电网的VSC-HVDC失稳机理及判据研究[J]. 电工技术学报, 2019, 34(18): 3884-3896.
Shao Bingbing, Zhao Shuqiang, Gao Benfeng, et al. Instability mechanism and criterion analysis of VSC-HVDC connected to the weak AC power grid[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3884-3896.
[7] 王一凡, 赵成勇, 郭春义. 双馈风电场孤岛经模块化多电平换流器直流输电并网系统小信号稳定性分析与振荡抑制方法[J]. 电工技术学报, 2019, 34(10): 2116-2129.
Wang Yifan, Zhao Chengyong, Guo Chunyi. Small signal stability and oscillation suppression method for islanded double fed induction generator-based wind farm integrated by modular multilevel converter based HVDC system[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2116-2129.
[8] 王渝红, 阳莉汶, 江伟, 等. 直流电网联网设备与控制策略研究综述[J]. 电网技术, 2018, 42(1): 12-24.
Wang Yuhong, Yang Liwen, Jiang Wei, et al. Review on equipment and control strategies of DC power grid[J]. Power System Technology, 2018, 42(1): 12-24.
[9] 汤广福. 基于电压源换流器的高压直流输电技术[M]. 北京: 中国电力出版社, 2010.
[10] 韩民晓, 熊凌飞, 丁辉. 利用电压倾斜控制的VSC-MTDC稳定性分析[J]. 电网技术, 2015, 39(7): 1808-1813.
Han Minxiao, Xiong Lingfei, Ding Hui. Stability analysis of VSC-MTDC with voltage droop control[J]. Power System Technology, 2015, 39(7): 1808-1813.
[11] 熊凌飞, 韩民晓. 基于组合方式的多端柔性直流输电系统控制策略[J]. 电网技术, 2015, 39(6): 1586- 1592.
Xiong Lingfei, Han Minxiao. A novel combined control strategy for VSC-MTDC[J]. Power System Technology, 2015, 39(6): 1586-1592.
[12] 朱珊珊, 汪飞, 郭慧, 等. 直流微电网下垂控制技术研究综述[J]. 中国电机工程学报, 2018, 38(1): 72-84, 344.
Zhu Shanshan, Wang Fei, Guo Hui, et al. Overview of droop control in DC microgrid[J]. Proceedings of the CSEE, 2018, 38(1): 72-84, 344.
[13] 孙黎霞, 陈宇, 宋洪刚, 等. 适用于VSC-MTDC的改进直流电压下垂控制策略[J]. 电网技术, 2016, 40(4): 1037-1043.
Sun Lixia, Chen Yu, Song Honggang, et al. Improved voltage droop control strategy for VSC-MTDC[J]. Power System Technology, 2016, 40(4): 1037-1043.
[14] 罗永捷, 李耀华, 王平, 等. 多端柔性直流输电系统直流电压自适应下垂控制策略研究[J]. 中国电机工程学报, 2016, 36(10): 2588-2599.
Luo Yongjie, Li Yaohua, Wang Ping, et al. DC voltage adaptive droop control of multi-terminal HVDC systems[J]. Proceedings of the CSEE, 2016, 36(10): 2588-2599.
[15] 刘瑜超, 武健, 刘怀远, 等. 基于自适应下垂调节的VSC-MTDC功率协调控制[J]. 中国电机工程学报, 2016, 36(1): 40-48.
Liu Yuchao, Wu Jian, Liu Huaiyuan, et al. Effective power sharing based on adaptive droop control method in VSC multi-terminal DC grids[J]. Pro- ceedings of the CSEE, 2016, 36(1): 40-48.
[16] 吴杰, 王志新. 多端柔性直流输电系统的改进下垂控制策略[J]. 电工技术学报, 2017, 32(20): 241-250.
Wu Jie, Wang Zhixin. Improved droop control strategy for multi-terminal voltage source converter- HVDC[J]. Transactions of China Electrotechnical Society, 2017, 32(20): 241-250.
[17] 阎发友, 汤广福, 贺之渊, 等. 基于MMC的多端柔性直流输电系统改进下垂控制策略[J]. 中国电机工程学报, 2014, 34(3): 397-404.
Yan Fayou, Tang Guangfu, He Zhiyuan, et al. An improved droop control strategy for MMC-based VSC-MTDC systems[J]. Proceedings of the CSEE, 2014, 34(3): 397-404.
[18] Cao Yijia, Wang Weiyu, Li Yong, et al. A virtual synchronous generator control strategy for VSC- MTDC systems[J]. IEEE Transactions on Energy Conversion, 2017, 33(2): 750-761.
[19] 王炜宇, 李勇, 曹一家, 等. 基于虚拟调速器的多端直流虚拟同步机控制策略[J]. 中国电机工程学报, 2018, 38(12): 3461-3470, 5.
Wang Weiyu, Li Yong, Cao Yijia, et al. The virtual synchronous generator technology based on virtual governor for multi-terminal direct current system[J]. Proceedings of the CSEE, 2018, 38(12): 3461-3470, 5.
[20] 韩民晓, 翟冬玲, 唐晓骏. 连接低惯量系统的柔性直流输电模型预测控制[J]. 电工技术学报, 2017, 32(22): 198-206.
Han Minxiao, Zhai Dongling, Tang Xiaojun. Model predictive control of voltage source converter-HVDC connected to low inertia system[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 198- 206.
[21] 王皓界, 韩民晓, Josep M Guerrero, 等. 基于自律分散系统的直流微电网稳定控制器优化设计[J]. 中国电机工程学报, 2016, 36(2): 360-367.
Wang Hanjie, Han Minxiao, Josep M Guerrero, et al. Optimization design of DC micro-grid stability controller based on the autonomous decentralized system[J]. Proceedings of the CSEE, 2016, 36(2): 360-367.
[22] 韩民晓, 许冬, 万磊. 基于一致性算法的混合多端直流自律分散控制[J]. 电力系统自动化, 2016, 40(12): 130-136.
Han Minxiao, Xu Dong, Wan Lei. Consensus algorithm based decentralized autonomous control of hybrid multi-terminal direct current system[J]. Automation of Electric Power Systems, 2016, 40(12): 130-136.
[23] 许冬. 混合多端直流输电运行特性研究[D]. 北京: 华北电力大学, 2017.
[24] 曾琦, 李兴源, 张立奎. 考虑运行损耗和功率裕度的VSC-MTDC系统改进优化下垂控制策略[J]. 高电压技术, 2016, 42(10): 98-106.
Zeng Qi, Li Xingyuan, Zhang Likui. Improved optimization droop control strategy taking into account the network loss and available headroom for VSC-MTDC system[J]. High Voltage Engineering, 2016, 42(10): 98-106.
[25] 邱迪. 交流/混合直流联合系统最优潮流分析[D]. 哈尔滨: 哈尔滨工业大学, 2017.
[26] 鲁挺, 赵争鸣, 张颖超, 等. 采样延迟和误差对三电平PWM整流直接功率控制性能的影响及其抑制方法[J]. 电工技术学报, 2010, 25(3): 66-72.
Lu Ting, Zhao Zhengming, Zhang Yingchao, et al. Effect of sampling delay and error on direct power control performance of three-level PWM rectifier and its restraining method[J]. Transactions of China Electrotechnical Society, 2010, 25(3): 66-72.
[27] Daelemans G, Srivastava K, Reza M, et al. Mini- mization of steady-state losses in meshed networks using VSC HVDC[C]//Power & Energy Society General Meeting, Calgary, AB, Canada, 2009: 1-5.
[28] Beerten J, Cole S, Belmans R. A sequential AC/DC power flow algorithm for networks containing multi-terminal VSC HVDC systems[J]. Power & Energy Society General Meeting, 2010, 89(1): 1-7.
[29] Boyd S, Vandenberghe L. Convex optimization[M]. Cambridge: Cambridge University Press, 2004.
A New Method to Obtain the Droop Control Coefficient in a Meshed DC System Based on Automatically Decentralized Control
Abstract Recent researches focus on droop control coefficient calculation in the radial DC system, and fewer researches investigate its calculation in complex DC systems. This paper proposed a new method for droop control coefficient calculation in a meshed DC system based on automatically decentralized control. Firstly, the information of the converter was collected and interchanged by the system control layer of the automatically decentralized control. After that, all the converters obtained the same global information by the optimal power flow model to calculate the reference values of DC voltage and active power. Then, the virtual node was defined and its voltage was equal to the average of the reference DC voltage. The nodes where the voltage is equal to the virtual voltage were selected, and the system was simplified into radial topology. Subsequently, the reference resistances between nodes and the virtual node under the optimal condition could be obtained, the real resistances between nodes and the virtual node under current condition also could be calculated. Herein, the droop control coefficients are equal to the inverse of difference between the virtual and real resistances. Finally, a 6-terminal MMC-MTDC model was established in PSCAD/EMTDC, and the simulations verified the proposed method.
keywords：DC power system, automatically decentralized control, virtual node, droop control coefficient
DOI: 10.19595/j.cnki.1000-6753.tces.191440
中图分类号：TM76
曹 昕 男，1994年生，博士研究生，研究方向为电力电子在电力系统中的应用。E-mail: caoxin_ncepu_16@163.com（通信作者）
韩民晓 男，1961年生，教授，博士生导师，研究方向为电力电子在电力系统中的应用。E-mail: hanminxiao@263.net
收稿日期 2019-11-09
改稿日期 2020-02-27
国家重点研发计划智能电网技术与装备重点专项（2016YFB0900600）和中央高校基本科研业务费专项资金（2018QN019）资助项目。
（编辑 陈 诚）