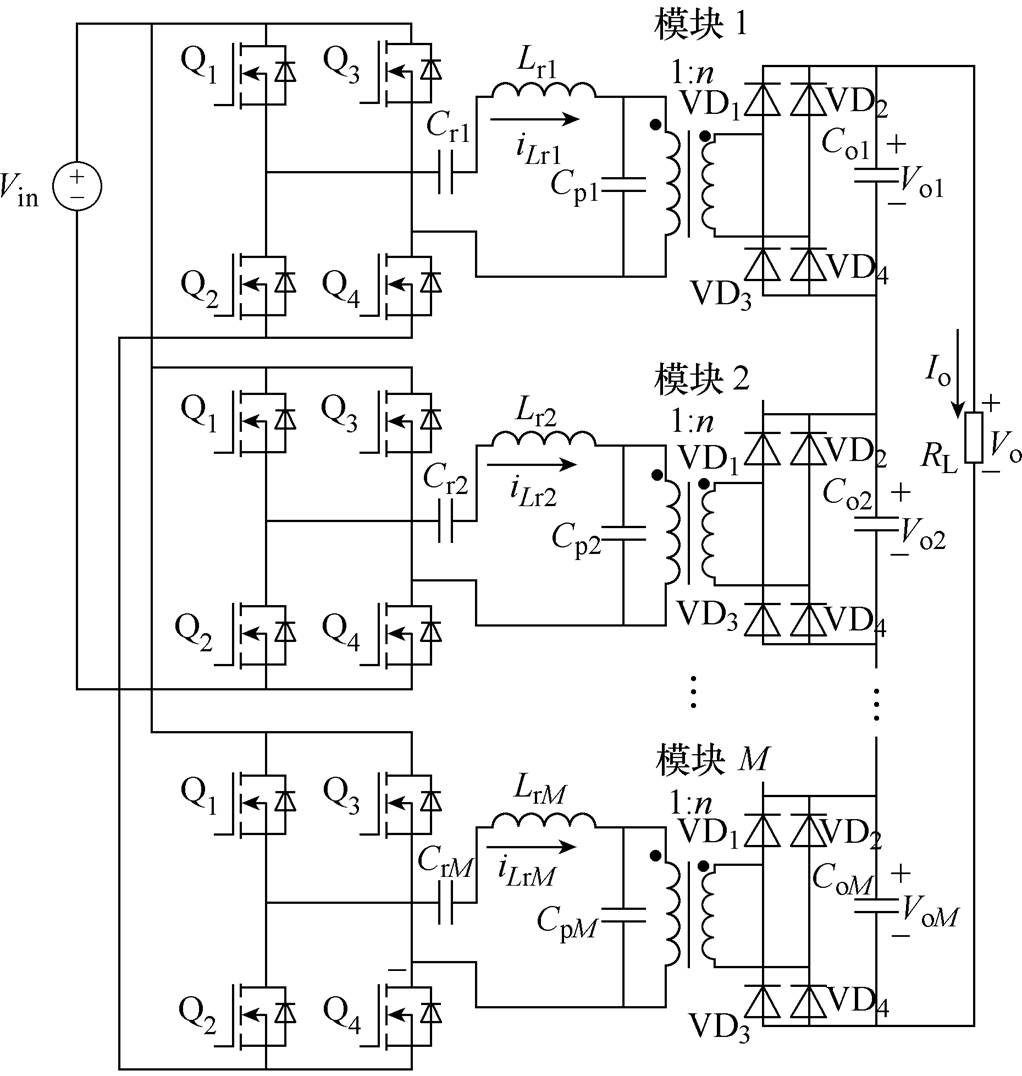
图1 多模块LCC变换器级联拓扑
Fig.1 Topology of the multi-module LCC converter
摘要 相对于单模块LCC变换器,输入并联输出串联(IPOS)多模块LCC级联变换器的拓扑具有模块化、元件电气应力小、输出纹波小、输出电压高、功率大等优势,但是各模块间谐振参数的偏差会引起模块输出电压不均衡。该文针对容性滤波的LCC谐振变换器,采用基波等效法计算出变换器电压电流的基波分量,利用广义状态空间平均法建立LCC变换器的状态方程,随后推导出单模块的LCC变换器大信号模型。在此基础上,推导出IPOS两模块LCC变换器的大信号模型,并以此模型来分析谐振参数偏差对模块间输出电压均衡的影响。最后搭建两模块LCC变换器的样机平台,验证了所提出的多模块LCC变换器大信号模型具有良好的准确度,所提模型可为谐振参数的容差分析提供依据。
关键词:多模块 LCC谐振变换器 大信号模型 谐振参数偏差 输出电压不均衡
近年来,高压直流电源广泛应用于加速器、静电除尘、医疗X光电源等领域[1-6]。串并联(LCC)谐振变换器以其能够利用变压器的寄生参数作为谐振元件和软开关的优势,在高压直流电源领域获得广泛应用[7]。利用其软开关特性,开关频率可以进一步提高,实现高效率和高功率密度[8-10]。
现有高压直流电源基本都工作于脉冲模式,脉冲的上升、下降时间和输出电压的纹波是系统的关键指标[11]。在容性输出滤波的LCC谐振变换器中,输出电压纹波和上升、下降时间均与输出滤波电容大小有关,是一对矛盾的指标,需要折中优化设计。
采用新型SiC MOSFET器件,可以进一步提高系统的开关频率,降低系统的上升、下降时间和输出电压纹波[12]。但是高频化给高压变压器、驱动、控制策略等设计提出了更高的要求,而目前SiC器件的高成本也限制了其在工业界的应用。
采用电力电子大功率领域常用的多模块策略,构成输入并联输出串联的多模块LCC级联拓扑,如图1所示。利用多模块拓扑,系统发热更平衡,通过备份冗余等策略还可提升系统的可靠性[13-14]。

图1 多模块LCC变换器级联拓扑
Fig.1 Topology of the multi-module LCC converter
同时,通过多个模块之间的移相控制,各个模块的输出纹波相互抵消,大大减小了输出纹波[15]。图2为两个LCC变换器模块进行移相控制的波形,将两个模块的导通脉冲移相90°,则两个模块的输出电压Vo1和Vo2可以叠加抵消,得到的总电压Vo如图2所示,可见输出电压纹波急剧减小。因此,多模块LCC变换器进行模块间移相可以大幅减小输出滤波电容,得到更短的上升、下降时间。
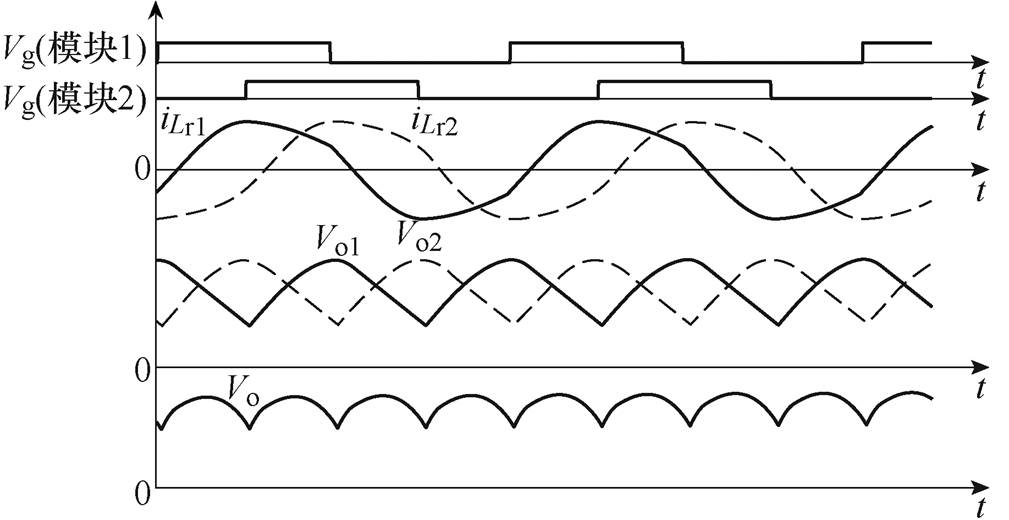
图2 两模块LCC变换器移相波形
Fig.2 Waveforms of the two-module LCC converter with phase shift
虽然多模块LCC变换器级联拓扑相对于单模块拓扑优势显著,但是也存在输出电压不均衡的挑战。在实际生产中,各个模块的谐振元件参数(谐振电感Lr、串联谐振电容Cr和并联谐振电容Cp)不可避免地与设计值有一定偏差,造成每个模块的电压增益曲线不一致。图3为不同负载Lr偏差±5%下,LCC变换器的电压增益,可见Lr的偏差会造成增益曲线的变化,进而造成模块间电压的不均衡。

图3 谐振电感偏差对LCC变换器增益的影响
Fig.3 Influence of resonant inductance deviation on voltage gain of LCC resonant converters
谐振参数偏差对LCC变换器模块输出电压的影响,国内外鲜有研究。文献[16]针对并联输出的多模块LLC变换器,提出一种输出电流均衡计算方法,但无法适用于LCC变换器。文献[17-18]研究了三相LCC变换器交错并联运行,但是没有考虑谐振参数偏差的影响。
为分析谐振参数偏差对输出电压的影响,本文提出了多模块LCC变换器的大信号模型。首先采用基波等效法和广义状态空间平均法建立了输出容性滤波LCC变换器的状态方程,随后推导出单模块的LCC变换器大信号模型。在此基础上,推导出输入并联输出串联的两模块LCC变换器的大信号模型,并以此模型来分析谐振参数偏差对模块间输出电压均衡的影响。最后搭建两模块LCC变换器的样机平台,对所提出的多模块LCC变换器大信号模型进行了验证。
单模块LCC变换器拓扑如图4所示,H桥由4个开关管Q1、Q2、Q3和Q4构成,谐振腔由谐振电感Lr、串联谐振电容Cr和并联谐振电容Cp构成,变压器的电压比为1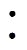 n,二次侧的整流桥由4个二极管VD1、VD2、VD3和VD4组成,使用电容Co进行输出滤波。
n,二次侧的整流桥由4个二极管VD1、VD2、VD3和VD4组成,使用电容Co进行输出滤波。
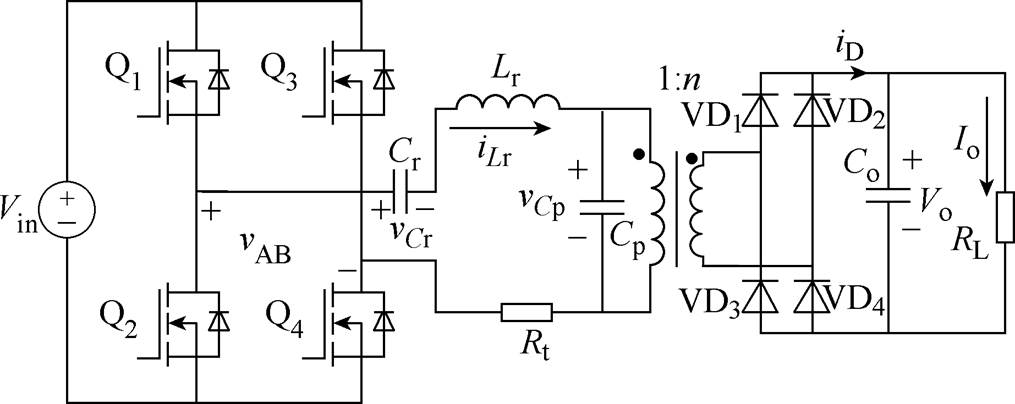
图4 单模块LCC变换器拓扑
Fig.4 Topology of LCC resonant converters
输入电压为Vin,输出电压为Vo,输出电阻为RL,H桥输出电压为vAB,电容Cr的电压为vCr,电容Cp的电压为vCp,流过电感Lr的电流为iLr。
为了便于分析建模,将变换器的损耗,包括开关管、变压器、谐振腔、整流桥和线路等,集中以电阻Rt体现。
将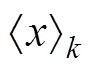 定义为变量x的第k次谐波的系数[19],有
定义为变量x的第k次谐波的系数[19],有
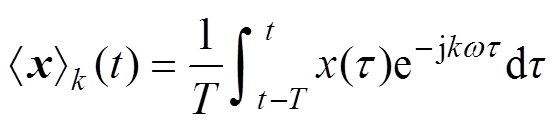 (1)
(1)式中,T为开关周期。
即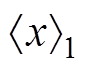 为变量x的基波分量,
为变量x的基波分量,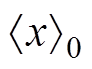 为变量x的直流分量。对
为变量x的直流分量。对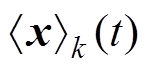 求微分[20],有
求微分[20],有
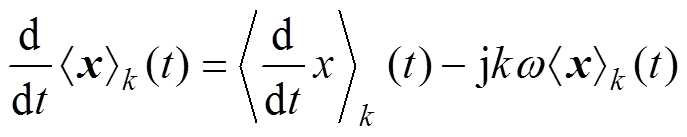 (2)
(2)LCC变换器稳态运行时的典型时域波形如图5所示,此时开关频率为fsw,角频率为w,周期为T,H桥vAB输出电压占空比为D。
在随后的建模中,对变压器一次侧的参数变量vAB、vCr、iLr和vCp,求解出其基波分量来代替;对变压器二次侧的参数变量iD和Vo,求解出直流分量来代替。假设谐振电流iLr(t)为纯正弦,有
 (3)
(3)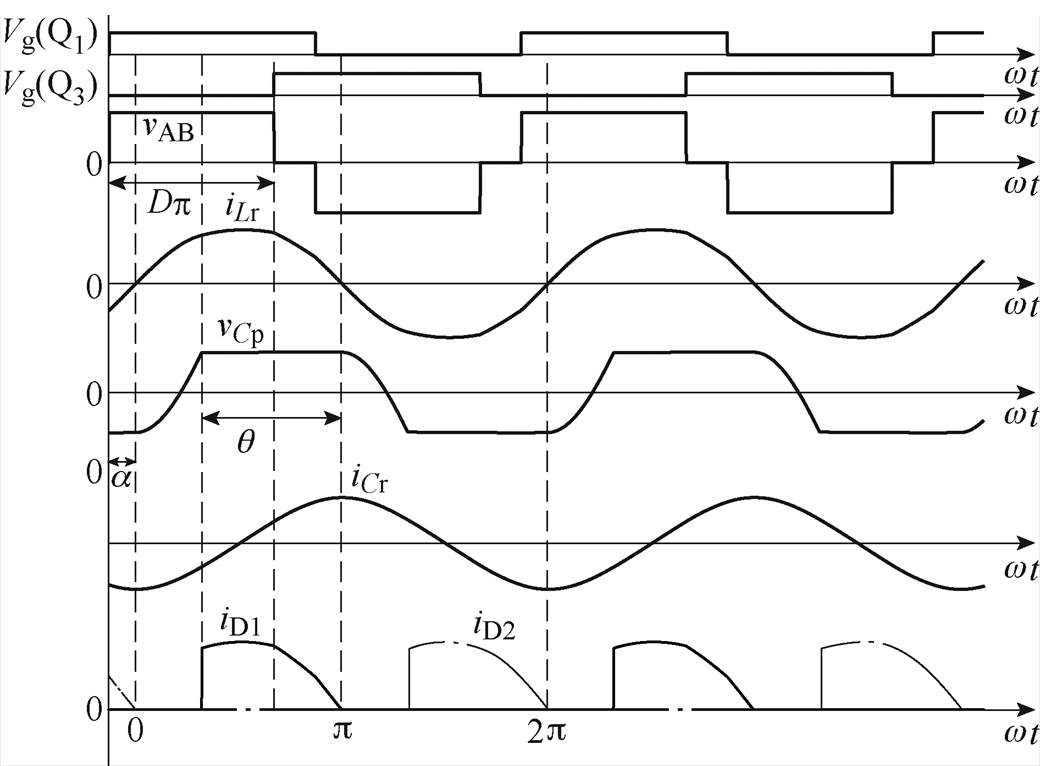
图5 LCC变换器稳态波形
Fig.5 Steady-state waveforms of the LCC resonant converter
式中,ILm为电流iLr(t)的幅值。
二极管的导通角为q,则整流桥的输出电流iD(t)为
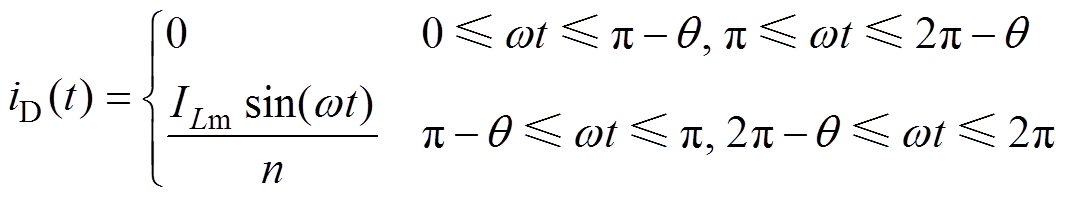 (4)
(4)在整个开关周期内,iD(t)的平均值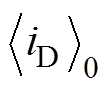 为
为
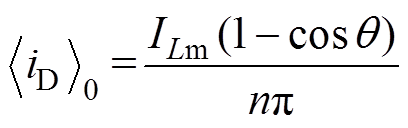 (5)
(5)
对流入电容Cp的电流进行积分,可得整个开关周期内电容Cp的电压vCp(t)为
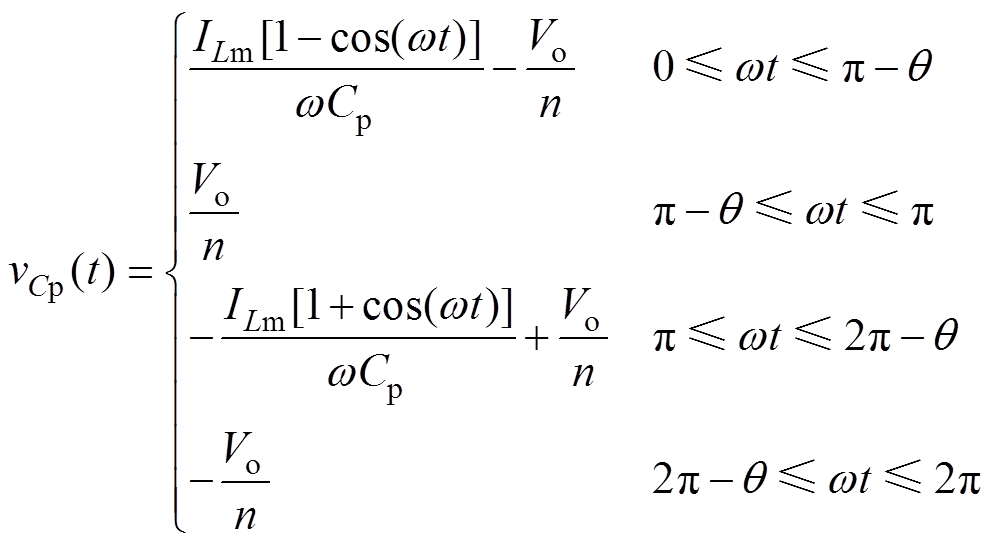 (6)
(6)在 时,电压vCp(t)连续,可得ILm为
时,电压vCp(t)连续,可得ILm为
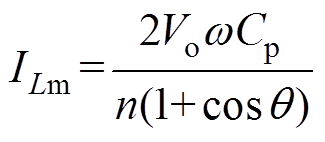 (7)
(7)
电流iLr滞后开关管开通时刻的角度为a,由图5可知,vAB(t)为
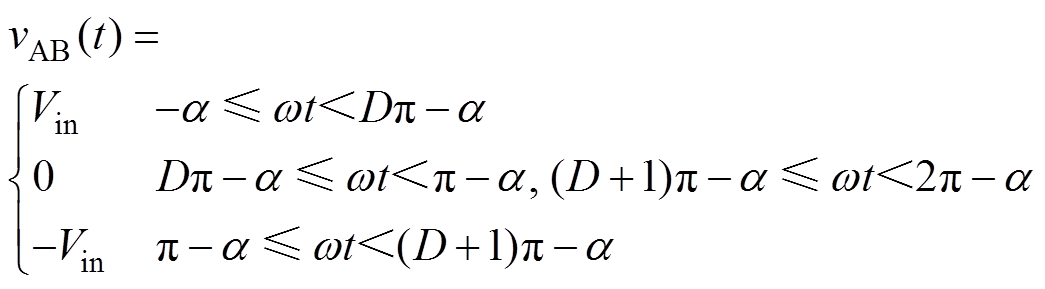 (8)
(8)利用傅里叶级数分解,vAB(t)在复数域的基波分量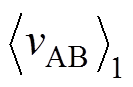 为
为
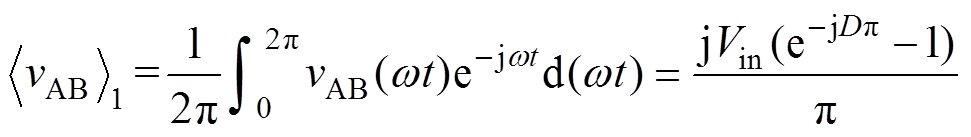 (9)
(9)
根据图4,可得LCC变换器的时域微分方程为
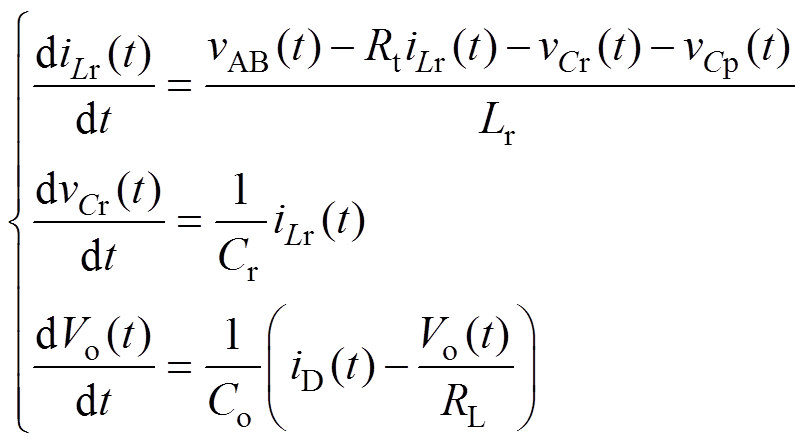 (10)
(10)将变压器二次侧的变量 、
、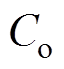 、
、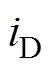 和
和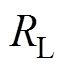 折算到一次侧,可得折算后
折算到一次侧,可得折算后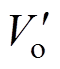 、
、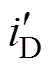 、
、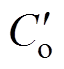 和
和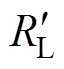 分别为
分别为
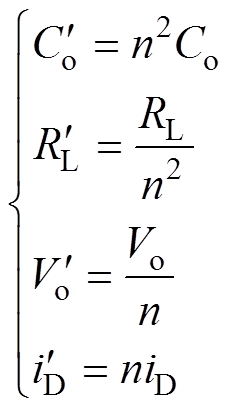 (11)
(11)
选取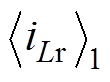 、
、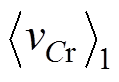 和
和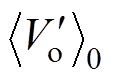 作为状态变量,根据时域微分方程式(10),结合式(2),可建立LCC变换器的状态模型,有
作为状态变量,根据时域微分方程式(10),结合式(2),可建立LCC变换器的状态模型,有
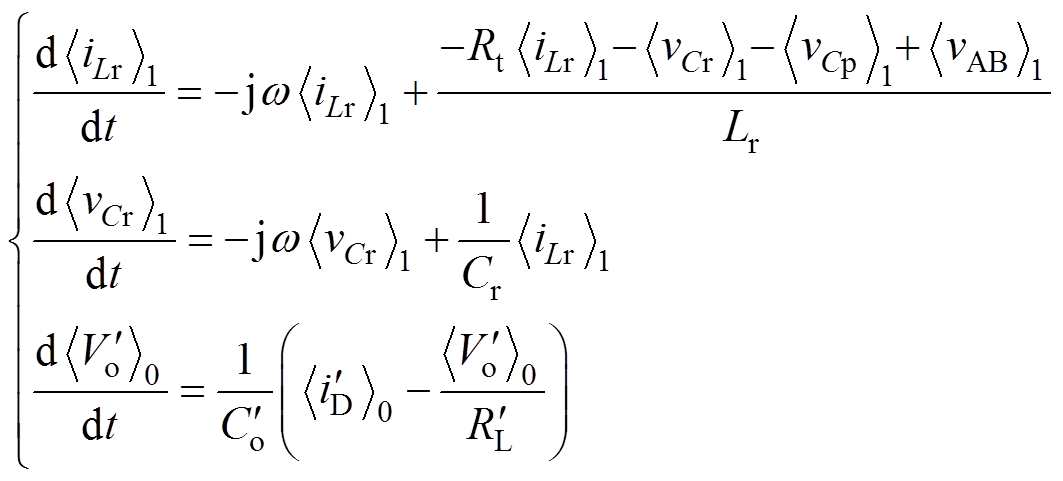 (12)
(12)式中,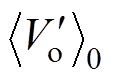 为实数,
为实数,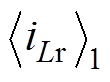 、
、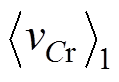 和
和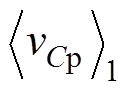 为复数,将复数状态变量的实部和虚部分开,有
为复数,将复数状态变量的实部和虚部分开,有
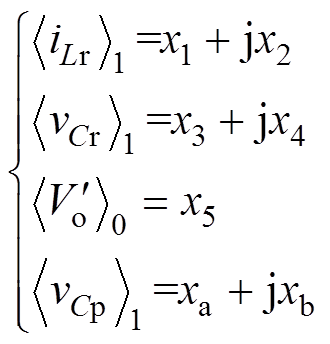 (13)
(13)
依据傅里叶级数,iLr(t)为
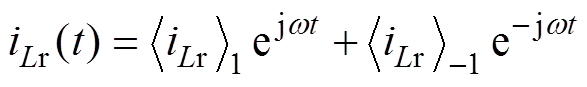 (14)
(14)式中,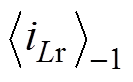 为-1次谐波的系数,
为-1次谐波的系数,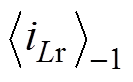 与
与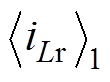 为共轭复数,比较式(14)和式(3),可得谐振电流iLr(t)幅值ILm为
为共轭复数,比较式(14)和式(3),可得谐振电流iLr(t)幅值ILm为
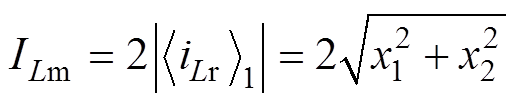 (15)
(15)
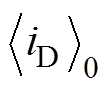 与iLr(t)的幅值ILm的关系见式(5),可得
与iLr(t)的幅值ILm的关系见式(5),可得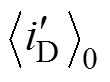 为
为
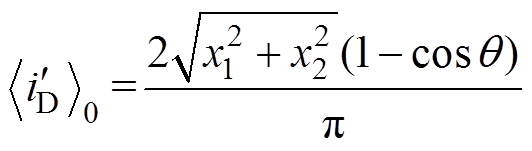 (16)
(16)
输出电压Vo与iLr(t)的幅值ILm的关系见式(7),有
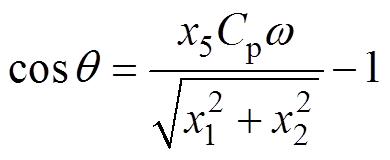 (17)
(17)vCp(t)的表达式见式(6),根据式(1)即可得到其基波分量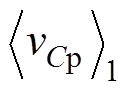 ,有
,有
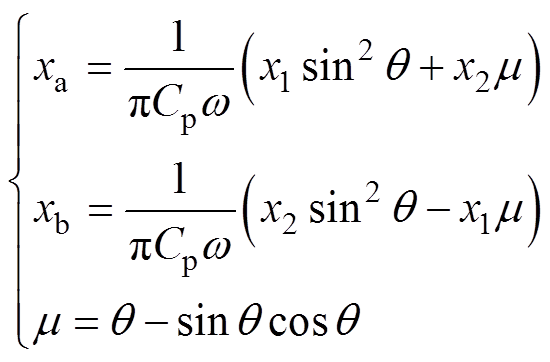 (18)
(18)
式中,m 为参数。
根据上述推导,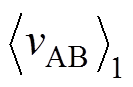 见式(9),
见式(9),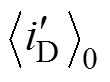 见式(16),
见式(16),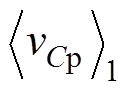 见式(18),复数域的LCC变换器状态方程式(12)可改写为实数方程,有
见式(18),复数域的LCC变换器状态方程式(12)可改写为实数方程,有
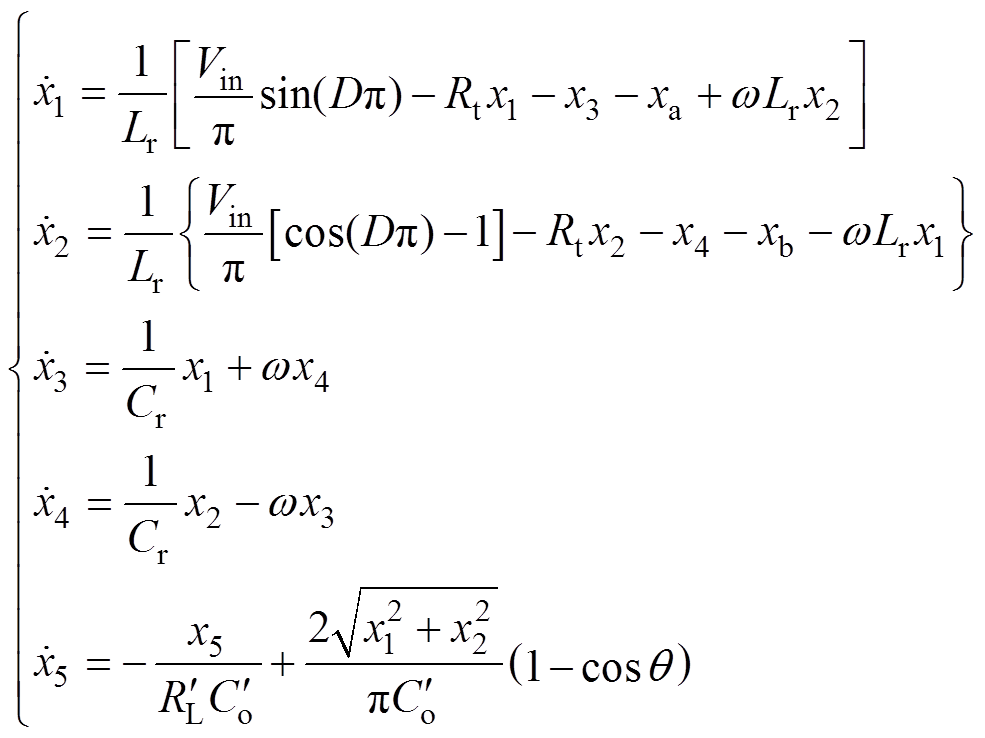 (19)
(19)其中
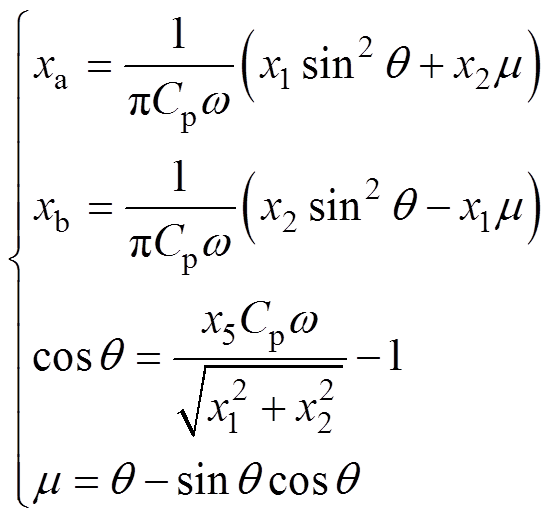 (20)
(20)
状态变量x1、x2、x3、x4和x5组成状态向量x(t),有
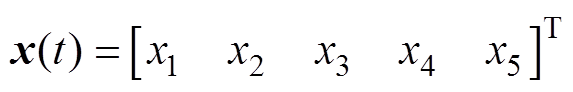 (21)
(21)输入变量w、D和Vin组成输入向量u(t),有
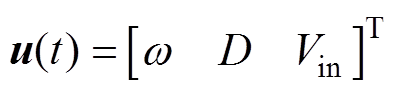 (22)
(22)
根据状态方程式(19)和式(20),在给定输入u(t)的情况下,即可求解状态x(t)。
根据上述推导出的LCC变换器状态方程,可得其大信号模型如图6所示。LCC变换器可由5阶的状态方程描述,5个状态变量中,x1和x2为电流,x3、x4和x5为电压。求解出状态变量后,可根据这些状态变量推导出LCC变换器的电压、电流等参数,即谐振电流iLr(t)幅值为 ,串联谐振电容Cr电压vCr(t)幅值为
,串联谐振电容Cr电压vCr(t)幅值为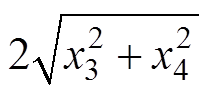 ,并联谐振电容Cp电压vCp(t)幅值为
,并联谐振电容Cp电压vCp(t)幅值为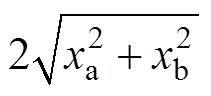 ,输出电压Vo为nx5。
,输出电压Vo为nx5。

图6 单模块LCC变换器大信号模型
Fig.6 Large-signal model of the single-module LCC resonant converter
为了简化分析,以两模块LCC变换器级联拓扑为例来分析多模块LCC变换器,所提出的分析方法可以直接推广到多模块LCC变换器级联的拓扑。
两模块LCC变换器输入并联输出串联拓扑如图7所示,模块1谐振腔的谐振元件参数分别为Lr1、Cr1和Cp1,模块2谐振腔的谐振元件参数分别为Lr2、Cr2和Cp2。两个模块的输出电压分别为Vo1、Vo2,输出总电压Vo为两模块输出电压之和,即Vo=Vo1+ Vo2。两个模块的开关角频率均为w,占空比分别为D1和D2。

图7 两模块LCC变换器输入并联输出串联拓扑
Fig.7 Topology of the two-module LCC resonant converter with input parallel and output series
根据第1节推导出的单模块LCC大信号模型,将其推广到双模块LCC变换器,其大信号模型如图8所示,而状态方程见附录。比较单模块和两模块的状态方程,相对于单模块,在两模块LCC变换器中,其输出电流为(Vo1+Vo2)/RL,两个模块之间的耦合也是通过输出电流链接的。
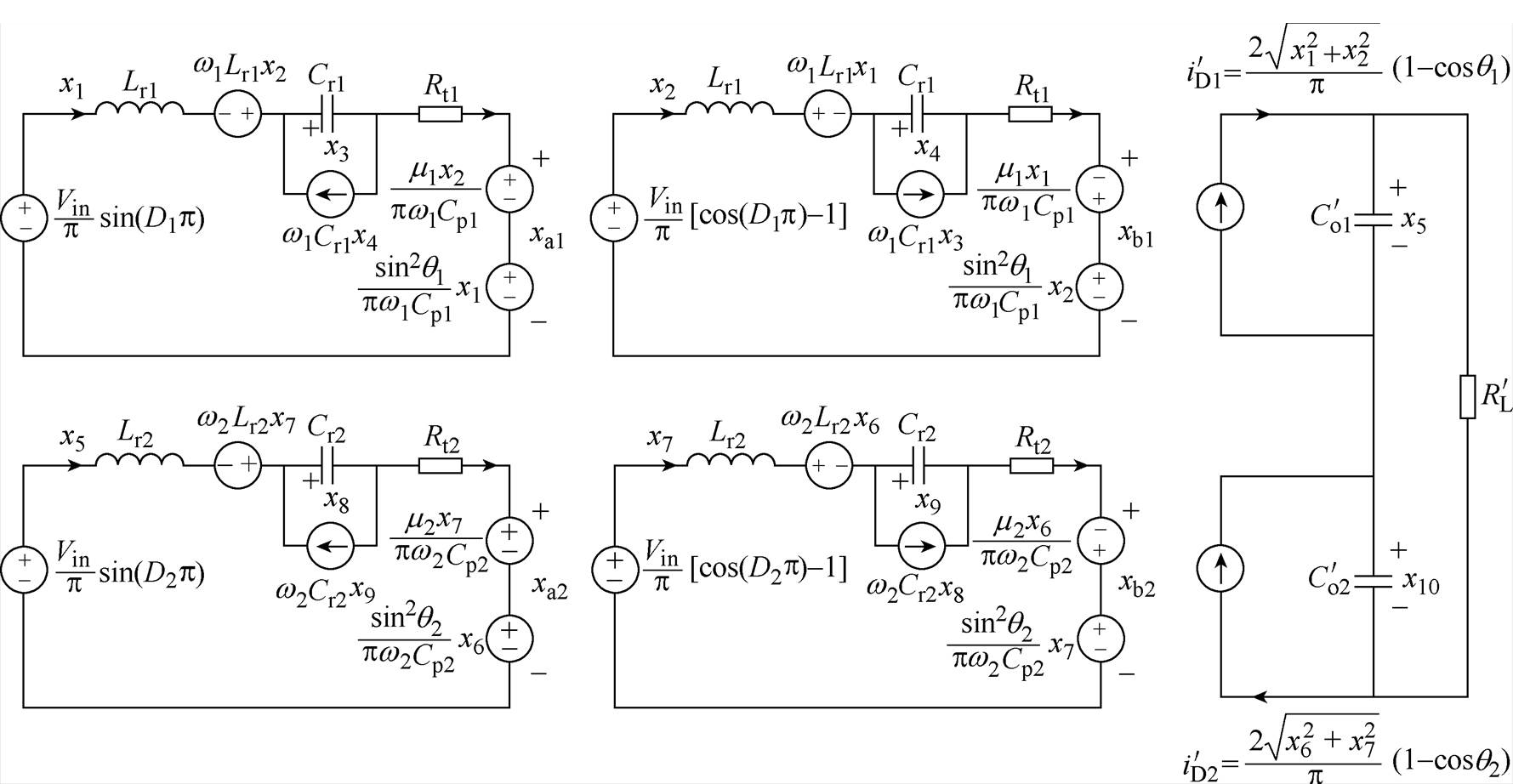
图8 两模块LCC变换器大信号模型
Fig.8 Large-signal model of the two-module LCC resonant converter
在两模块LCC变换器状态方程中,有10个状态变量,组成状态向量x(t),有
 (23)
(23)输入向量u(t)由w、D1、D2和Vin组成,有
 (24)
(24)
求解出这些状态变量后,即可得到两模块的输出电压,可知模块1的输出电压Vo1=nx5,模块2的输出电压Vo2=nx10。
为研究谐振参数偏差对两模块LCC变换器输出电压的影响,定义两模块的输出电压不平衡度dV为
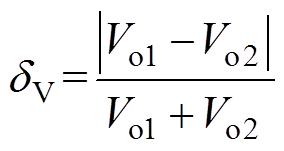 (25)
(25)为验证所提出的多模块LCC变换器大信号模型,并研究谐振元件参数偏差对输出电压的影响,搭建了两模块LCC变换器实验样机,如图9所示,样机详细参数见表1。

图9 两模块LCC变换器实验样机
Fig.9 Photo of two-module LCC resonant converter prototype
图10为单模块LCC变换器输出电压Vo与开关频率fsw的关系,负载电阻RL分别为20W 和40W。此时输入电压Vin=105V,后续实验的输入电压不变。对比所提出模型与实验结果,不同开关频率和不同负载下,模型与实验均吻合良好,验证了所提出单模块LCC大信号模型在不同负载和频率下的准确性。
表1 两模块LCC变换器实验样机参数
Tab.1 Parameters of the two-module LCC resonant converter prototype

参 数数 值 输入电压Vin/V100~120 输出电压Vo/V40~220 输出电流Io/A<4 谐振电感Lr/mH72 串联谐振电容Cr/nF52.8 并联谐振电容Cp/nF21 变压器电压比1n54 输出滤波电容Co/mF4.2 开关频率fsw/kHz120~200 占空比D1
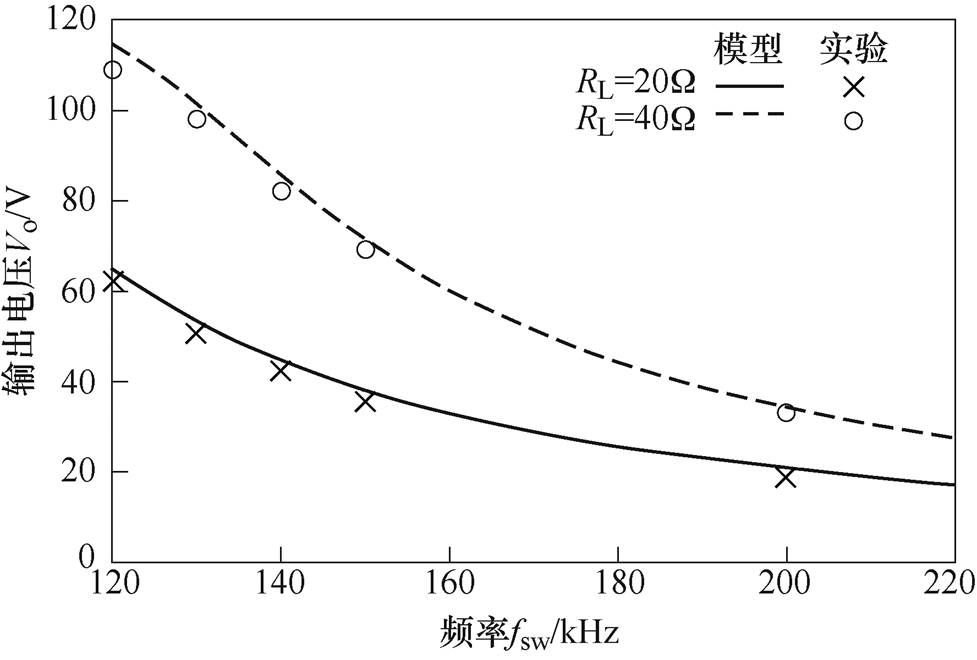
图10 单模块LCC变换器输出电压
Fig.10 Output voltage of the single-module LCC resonant converter
图11为两模块的谐振电感不一致时,输出电压Vo和谐振电流iLr的波形。其中,将模块2的谐振电感Lr2由72mH增加到76mH,开关频率为130kHz,负载RL=40W。由图11可知,谐振电感偏差5.5%将引起严重的输出电压不均衡,此时输出电压分别为84.8V和13.8V,模块1的输出电压远高于模块2,电压不均衡度dV达到72%。对比所提出模型与实验结果,模块1的谐振电流幅值和输出电压稍高于实验值,模块2则与实验值较为接近。
图12为两模块的串联谐振电容Cr不一致时,输出电压Vo和谐振电流iLr的波形。其中,将模块2的串联谐振电容Cr2由52.8nF增加到55nF,开关频率为130kHz,负载RL为40W。由图12可知,在串联谐振电容Cr偏差为4.2%时,两模块的输出电压分别为67.7V和33.3V,可见串联谐振电容Cr不一致也会引起输出电压的不平衡,电压不均衡度dV达到34%。对比所提出模型与实验结果,模块2的谐振电流幅值和输出电压稍高于实验值,模块1则与实验值较为接近。
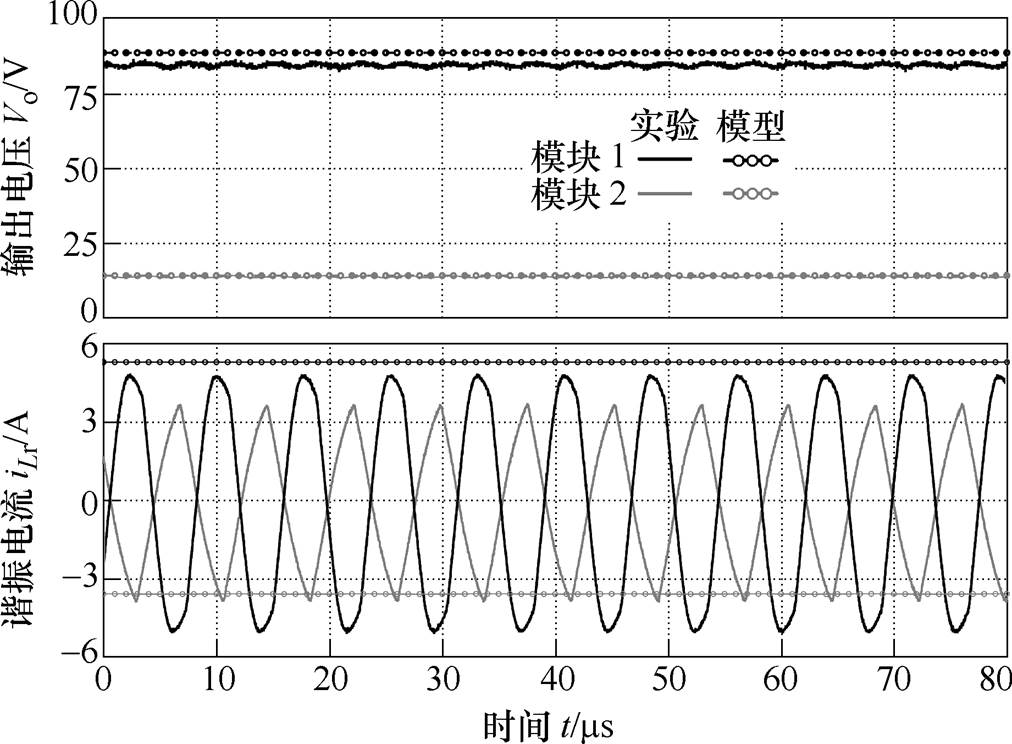
图11 谐振电感Lr不一致时两模块LCC变换器波形(Lr1=72mH,Lr2=76mH)
Fig.11 Waveforms of the two-module LCC resonant converter with unequal resonant inductance (Lr1=72mH, Lr2=76mH)
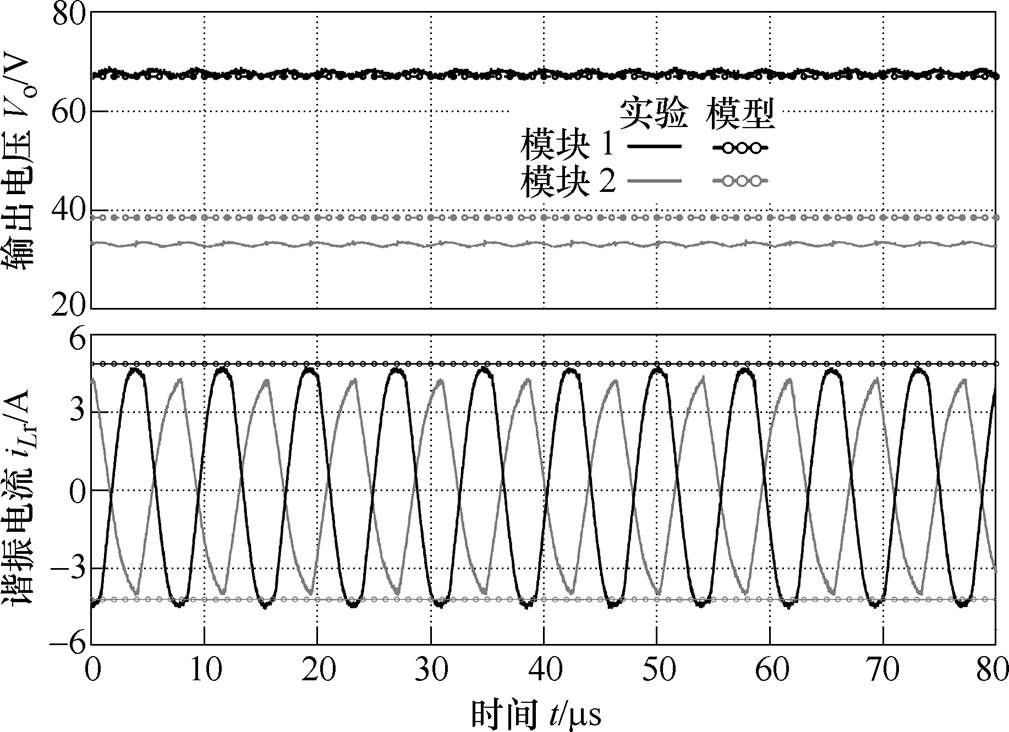
图12 串联谐振电容Cr不一致时两模块LCC变换器波形(Cr1=52.8nF,Cr2=55nF)
Fig.12 Waveforms of the two-module LCC resonant converter with unequal series resonant capacitance (Cr1=52.8nF, Cr2=55nF)
图13为两模块的并联谐振电容Cp不一致时,输出电压Vo和谐振电流iLr的波形。其中,将模块2的并联谐振电容Cp2由21nF增加到22.4nF,开关频率为140kHz,负载RL为80W。由图13可知,在并联谐振电容Cp偏差为6.1%时,两模块的输出电压分别为96V和66.9V,可见,并联谐振电容Cp不一致也会引起输出电压的不平衡,电压不均衡度dV达到18%。根据模型计算得到两模块的输出电压分别为101V和70V,稍高于实验值,同时两个模块的谐振电流幅值也稍高于实验值。
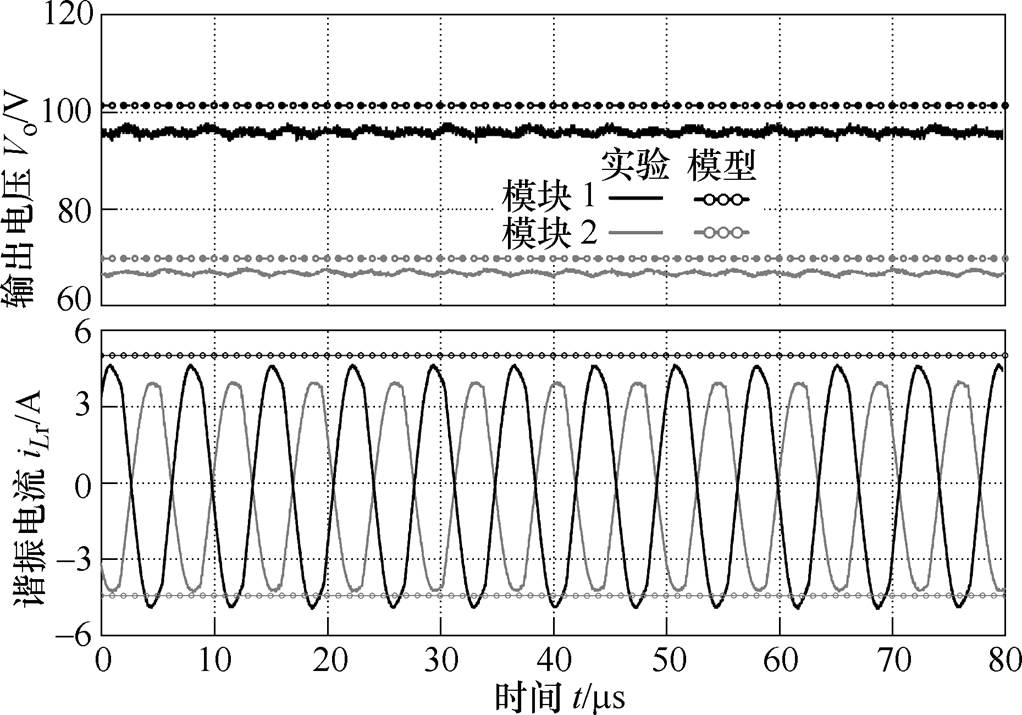
图13 并联谐振电容Cp不一致时两模块LCC变换器波形(Cp1=21nF,Cp2=22.4nF)
Fig.13 Waveforms of the two-module LCC resonant converter with unequal parallel resonant capacitance(Cp1=21nF, Cp2=22.4nF)
如图14所示为两模块的Lr和Cr不一致时,输出电压Vo和谐振电流iLr的波形。其中,将模块2的Lr2由72mH增加到76mH、Cr2由52.8nF增加到55nF,开关频率为130kHz,负载RL为40W。此时,两模块的输出电压分别为108.5V和2.6V,电压不均衡度dV达到95.3%,而所提出模型的输出电压分别为107V和2.7V。对比所提出模型与实验结果,两模块的输出电压与实验值均较为接近,模块2的谐振电流幅值稍低于实验值。
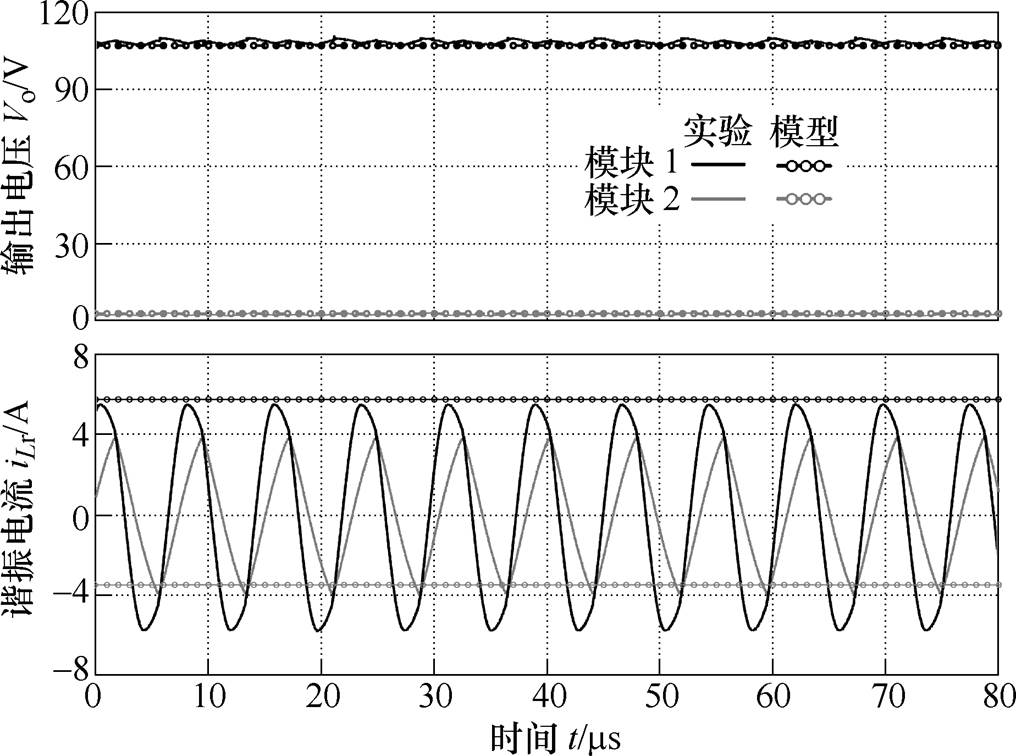
图14 谐振电感Lr和串联谐振电容Cr不一致时两模块LCC变换器波形(Lr1=72mH,Lr2=76mH;Cr1=52.8nF,Cr2=55nF)
Fig.14 Waveforms of two-module LCC resonant converter with unequal resonant inductance and series resonant capacitance(Lr1=72mH, Lr2=76mH; Cr1=52.8nF, Cr2=55nF)
图15为两模块的Lr、Cr和Cp均不一致时,输出电压Vo和谐振电流iLr的波形。其中,将模块2的Lr2由72mH增加到76mH、Cr2由52.8nF增加到55nF、Cp2由21nF增加到22.4nF,开关频率为130kHz,负载RL为40W。此时,两模块的输出电压分别为109V和2.3V,电压不均衡度dV达到95.9%,而所提出模型的输出电压分别为107.2V和2.5V。对比所提出模型与实验结果,两模块的输出电压与实验值均较为接近。
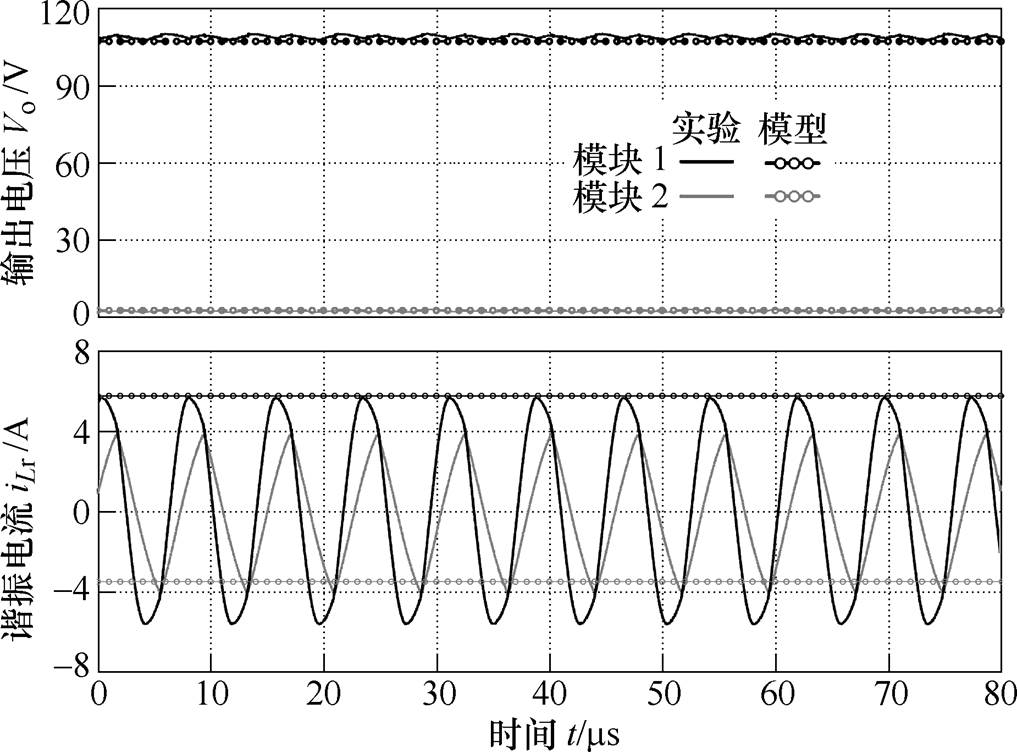
图15 谐振电感Lr、串联谐振电容Cr和并联谐振电容Cp均不一致时两模块LCC变换器波形(Lr1=72mH,Lr2=76mH;Cr1=52.8nF,Cr2=55nF;Cp1=21nF,Cp2=22.4nF)
Fig.15 Waveforms of two-module LCC resonant converter with unequal resonant inductance, series resonant capacitance and parallel resonant capacitance(Lr1=72mH, Lr2=76mH; Cr1=52.8nF, Cr2=55nF; Cp1=21nF, Cp2=22.4nF)
由以上实验结果可知,谐振参数偏差为5%左右会引起严重的输出侧不均压。在谐振参数有偏差的情况下,相同负载下,变换器的增益曲线变化较小,但是输出侧串联使得两模块输出电流必须一致,因此输出增益大的模块会有更大的等效输出电阻,而更大的等效输出电阻相当于更小的负载,由LCC增益曲线与负载的关系可知,更小的负载会导致更大的增益,最终导致增益大的模块的输出电压会进一步变大,因而较小的电压增益变化会引起极大的输出电压不均衡。
对比模型和实验结果可得,所推导的大信号模型对于单模块和多模块LCC变换器均能得到较为精确的结果,同时还能预测谐振参数偏差下,输出电压的不均衡度。
多模块LCC变换器交错并联的拓扑可以减小输出纹波,但是谐振参数的偏差会引起模块输出电压不均衡。为了分析谐振参数偏差对模块输出电压的影响,本文提出了输入并联输出串联的两模块LCC变换器的大信号模型。针对容性滤波的单模块LCC谐振变换器,本文采用基波等效法和广义状态空间平均法建立了单模块LCC变换器的大信号模型。在此基础上,扩展为多模块LCC变换器的大信号模型。最后通过搭建的两模块LCC变换器的样机平台,对所提出的多模块LCC变换器大信号模型进行了验证。实验结果显示,谐振参数偏差5%左右会引起严重的输出侧不均压,所提出的模型能精确计算谐振参数偏差导致的输出电压不均衡,可用于设计时谐振参数的容差分析。
附 录
输入并联输出串联的两模块LCC变换器的状态方程为
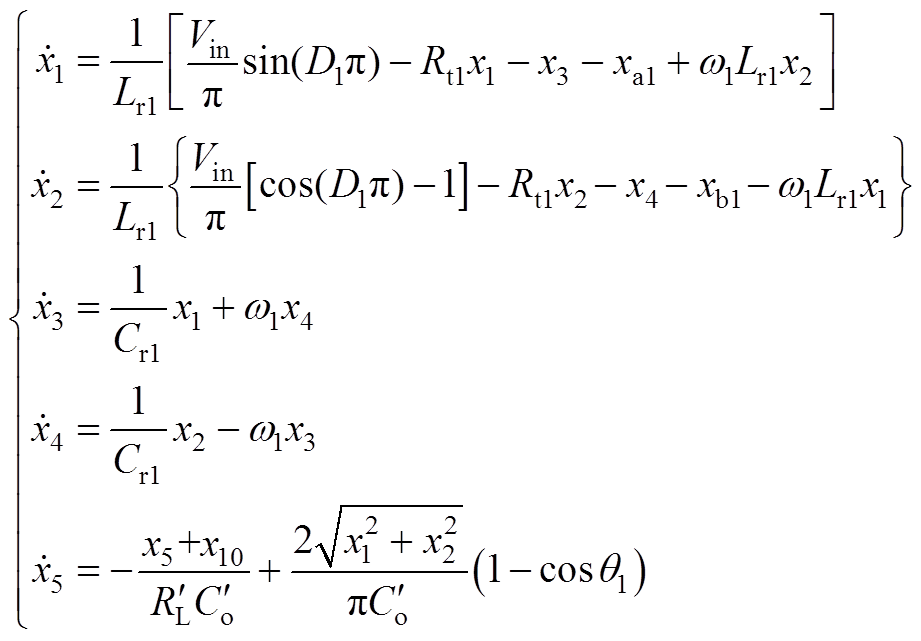 (A1)
(A1)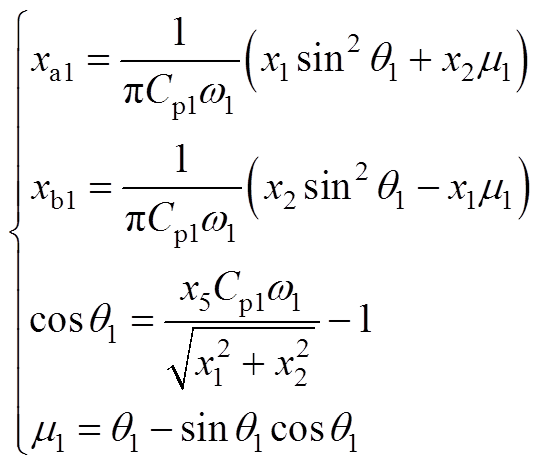 (A2)
(A2)
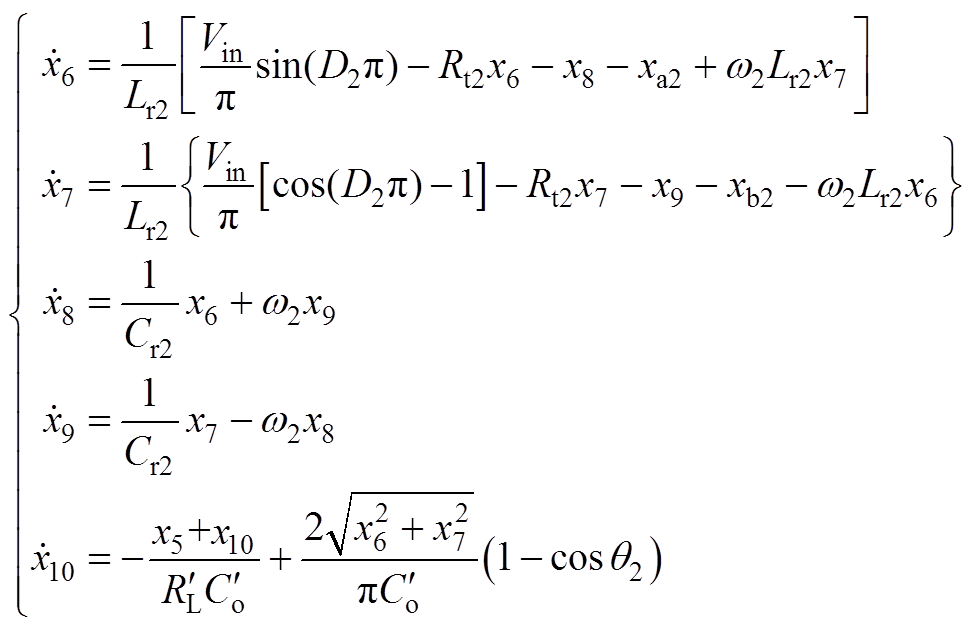 (A3)
(A3)
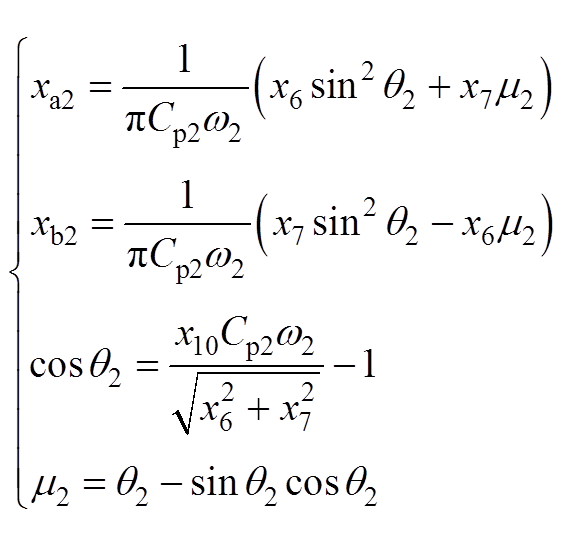 (A4)
(A4)参考文献
[1] 夏冰, 阮新波, 陈武. 高压大功率场合LCC谐振变换器的分析与设计[J]. 电工技术学报, 2009, 24(5): 60-66.
Xia Bing, Ruan Xinbo, Chen Wu. Analysis and design of LCC resonant converter for high voltage and high power applications[J]. Transactions of China Electrotechnical Society, 2009, 24(5): 60-66.
[2] Sung-Roc J, Yu Chanhun, Hong-Je R. Simplified design of a solid state pulsed power modulator based on power cell structure[J]. IEEE Transactions on Industrial Electronics, 2018, 65(3): 2112-2121.
[3] 刘国梁, 李新, 伍梁, 等. 宽范围输入输出电压LCC谐振变换器的分析设计[J]. 浙江大学学报(工学版), 2018, 52(9): 1762-1770.
Liu Guoliang, Li Xin, Wu Liang, et al. Analysis and design-optimization of LCC resonant converter oper- ating under wide range input and output voltage[J]. Journal of Zhejiang University (Engineering Science), 2018, 52(9): 1762-1770.
[4] Soeiro T B, Mühlethaler J, Linnér J, et al. Automated design of a high-power high-frequency LCC resonant converter for electrostatic precipitators[J]. IEEE Transactions on Industrial Electronics, 2013, 60(11): 4805-4819.
[5] Jang S, Seo J, Ryoo H. Development of 50kV, 100kW three-phase resonant converter for 95GHz gyrotron[J]. IEEE Transactions on Industrial Electronics, 2016, 63(11): 6674-6683.
[6] Guo Tang, Zhang Chi, Chang Lei, et al. Large-signal modeling of LCC resonant converter operating in discontinuous current mode applied to electrostatic precipitators[C]//2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition, Long Beach, CA, 2013: 2629-2635.
[7] 张治国, 谢运祥, 袁兆梅. LCC谐振变换器的电路特性分析[J]. 电工技术学报, 2013, 28(4): 50-57.
Zhang Zhiguo, Xie Yunxiang, Yuan Zhaomei. Analysis of circuit characteristics of LCC resonant con- verter[J]. Transactions of China Electrotechnical Society, 2013, 28(4): 50-57.
[8] 高铁峰, 张森, 赵剑锋, 等. LCC谐振变换器非对称移相控制及效率优化方法[J]. 电工技术学报, 2017, 32(8): 208-219.
Gao Tiefeng, Zhang Sen, Zhao Jianfeng, et al. Asymmetrical phase shift control and efficiency optimization strategy for LCC resonant converter[J]. Transactions of China Electrotechnical Society, 2017, 32(8): 208-219.
[9] 王德玉, 段元超, 高鹤, 等. LCC谐振变换器电流输出特性研究与软开关实现[J]. 电工技术学报, 2018, 33(12): 2788-2800.
Wang Deyu, Duan Yuanchao, Gao He, et al. Current output characteristics and implementation of soft switch based on LCC resonant converter[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(12): 2788-2800.
[10] Outeiro M T, Buja G, Czarkowski D. Resonant power converters: an overview with multiple elements in the resonant tank network[J]. IEEE Industrial Electronics Magazine, 2016, 10(2): 21-45.
[11] Jaritz M, Biela J. 115kV solid state long pulse modulator for the European spallation source (ESS)[C]// IEEE 21st International Conference on Pulsed Power, Brighton, 2017: 1-4.
[12] Mao Saijun, Wu Tao, Lu Xi, et al. High frequency high voltage power conversion with silicon carbide power semiconductor devices[C]//6th Electronic System- Integration Technology Conference, Grenoble, 2016: 1-5.
[13] Mao Saijun, Popovic J, Ferreira J A, et al. Comparative analysis and evaluation of high voltage power generation architectures[C]//IEEE Energy Conversion Congress and Exposition, Cincinnati, OH, 2017: 4753-4760.
[14] Mao Saijun, Li Chengmin, Li Wuhua, et al. Review of high frequency high voltage generation archite- ctures[C]//IEEE 3rd International Future Energy Electronics Conference and ECCE Asia, Kaohsiung, 2017: 2260-2266.
[15] Jaritz M, Biela J. Output voltage ripple analysis for modular series parallel resonant converter systems with capacitive output filter[C]//20th European Conference on Power Electronics and Applications, Riga, 2018: 1-10.
[16] Wang Hongliang, Chen Yang, Hu Zhiyuan, et al. An algorithm to analyze circulating current for multi- phase resonant converter[C]//IEEE Applied Power Electronics Conference and Exposition, Long Beach, CA, 2016: 899-906.
[17] 高贺. 三相LCC串并联谐振变换器的研究[D]. 哈尔滨: 哈尔滨工业大学, 2017.
[18] 石岩. 宽范围输出的三相LCC谐振变换器研究[D]. 哈尔滨: 哈尔滨工业大学, 2016.
[19] Sanders S R, Noworolski J M, Liu Xiaojun, et al. Generalized averaging method for power conversion circuits[J]. IEEE Transactions on Power Electronics, 1991, 6(2): 251-259.
[20] Maksimovic D, Stankovic A M, Thottuvelil V J, et al. Modeling and simulation of power electronic con- verters[J]. Proceedings of the IEEE, 2001, 89(6): 898-912.
Analysis of Output Voltage Imbalance for Cascaded Multi-Module LCC Converters Based on Large-Signal Model
Abstract Compared with the single-module LCC converter, the multi-module LCC converters with input parallel output series (IPOS) have the advantages of modularity, small component electrical stress, small output ripple, high output voltage and high power. However, the deviation of the resonant tank parameters between the modules will cause the unbalanced module output voltage. In this paper, for the LCC resonant converter with the capacitive filter, the fundamental components of the voltage and current of the converter were calculated by the fundamental wave approximation. The state equation of the LCC converter was established adopting the generalized state-space averaging method. Then, the large-signal model of the single-module LCC converter was derived. On this basis, the large-signal model of the two-module LCC converter with input parallel and output series was derived. Through the large-signal model, the influence of the deviation of the resonant tank parameters on the output voltage balance between modules was analyzed. Finally, a prototype of the two-module LCC converter is built, which shows that the proposed large-signal model of multi-module LCC converter has good accuracy. The proposed model can provide a basis for the tolerance analysis of resonant tank parameters.
keywords:Multi-module, LCC resonant converter, large-signal model, resonant parameters deviation, output voltage imbalance
DOI: 10.19595/j.cnki.1000-6753.tces.191461
中图分类号:TM46
伍 梁 男,1992年生,博士研究生,研究方向为LCC谐振变换器控制策略及其模块化级联技术。E-mail: wuliang2015@zju.edu.cn
陈国柱 男,1967年生,博士,教授,博士生导师,研究方向为高性能电力电子系统及其先进数字控制。E-mail: gzchen@zju.edu.cn(通信作者)
国家自然科学基金资助项目(51777186)。
收稿日期2019-11-11
改稿日期 2020-04-26
(编辑 崔文静)