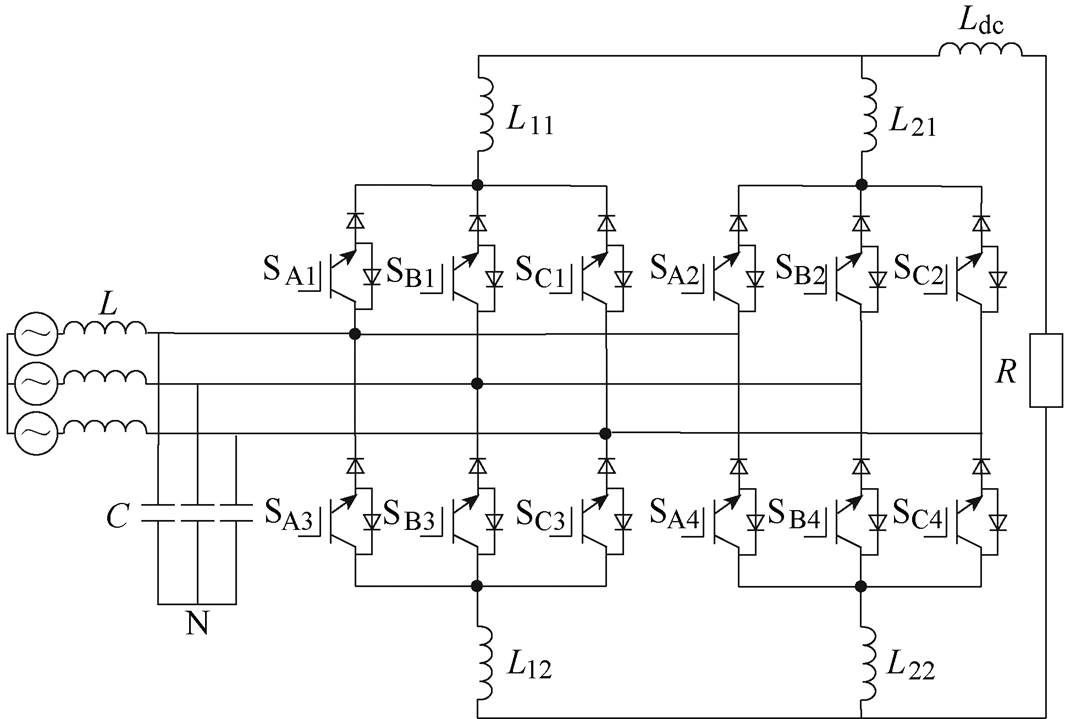
图1 三相5L-CSR主电路拓扑结构
Fig.1 Main circuit of three-phase five-level current source rectifier
摘要 针对由多个三相电流源型桥式整流器并联组成的电流型多电平整流器（MCSR），采用传统的空间矢量脉宽调制（SVPWM）算法涉及大量三角函数运算，影响控制器的运算效率。该文研究一种基于三相电流型五电平整流器（5L-CSR）的60°坐标系SVPWM算法，该方法有效地简化了基本矢量及其作用时间的计算过程。并且针对均流电感存在的电流平衡问题，提出合理分配冗余开关组合作用时间和作用顺序的方法，使得单个调制周期内均流电感承受平均电压为零，进而解决了均流电感电流不平衡问题，实现了直流侧自均流。最后，搭建三相5L-CSR的仿真模型以及实验样机进行验证。
关键词：多电平 空间矢量脉宽调制 电流型整流器 均流电感电流平衡
多电平整流器因具有输出功率大、器件开关频率低、网侧电流谐波小等特性，有效地解决了当前电力电子器件的功率处理能力与开关频率之间的矛盾[1]，从而得到了广泛关注[2-6]。
近年来，对多电平整流器的研究侧重于电压型多电平整流器（Multilevel Voltage Source Rectifier, MVSR），并且在拓扑结构、调制方法、谐波特性等方面取得了大量成果[7-12]。但是，与MVSR相比，电流型整流器（Multilevel Current Source Rectifier, MCSR）具备直流侧电压低于交流侧电压峰值的特性，在感应加热等应用场合有着独特的优势[13]。近年来，超导储能技术的发展和应用[14-15]，很好地解决了MCSR中电感储能效率低的问题[16]。MCSR因具有可四象限运行、短路保护可靠性高等优点,在高压直流输电[17-18]、新能源汽车等领域[19-20]有着良好的应用前景。当前研究中MCSR的调制策略多为载波相移正弦脉宽调制[21-23]（Carrier Phase-Shifted Sinusoidal Pulse Width Modulation, CPS-SPWM），虽然实现比较方便，但其直流电流利用率比空间矢量脉宽调制（Space Vector Pulse Width Modulation, SVPWM）低。文献[24]提出了错时采样空间矢量调制，该方法将各个整流单元的采样时间错开实现调制，但计算过程较为复杂。而SVPWM算法因其便于数字实现、电流利用率高的优点，在变流器中已经得到广泛应用，但是传统直角坐标系下的SVPWM算法，在参考矢量扇区判断及基本矢量作用时间的计算中，涉及较多的三角函数运算，会影响控制器的运算效率。
本文基于由两个三相电流型桥式整流器（整流单元）并联的电流型五电平整流器（Five-Level Current Source Rectifier, 5L-CSR）拓扑结构进行研究。首先，针对5L-CSR提出了一种60°坐标系SVPWM算法，该算法可以省去传统直角坐标系下SVPWM算法中的三角函数运算，简化了计算。同时，通过合理分配冗余开关组合作用顺序以及作用时间，保证了5L-CSR中均流电感电流平衡。最后，通过仿真和搭建实验样机对所提方法进行了验证。
三相5L-CSR主电路拓扑结构如图1所示，三相5L-CSR是由两个整流单元并联组成的，其交流侧可以直接并联，直流侧则通过均流电感并联。
图1 三相5L-CSR主电路拓扑结构
Fig.1 Main circuit of three-phase five-level current source rectifier
三相5L-CSR中，不允许电流无通路的情况，因此上、下桥臂三个开关器件在任意时刻都分别必须有且仅有一个导通。将这12个开关管分为4组，与同一个均流电感（L11、L12、L21、L22）相连的3个开关管为一组，每组有且仅有一个开关导通。定义Skj为开关器件，其中，k=A, B, C表示相位；j=1, 2, 3, 4表示组号。则开关函数skj可定义为
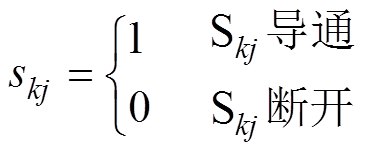（1）并且满足如下条件
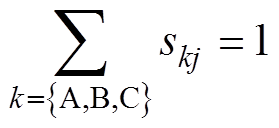（2）
根据开关状态所必需的条件，5L-CSR一共有34=81种不同的开关组合状态Em。将开关状态用一个4×1的矩阵来表示，矩阵中的元素对应各组开关状态，可表示为
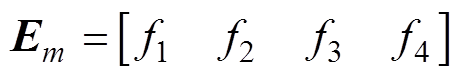（3）式中，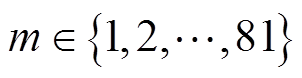
；
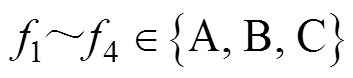，A、B、C则表示每一组开关中导通的相。例如，开关状态为[A B B C]，则ia=idc/2，ib=0，ic=-idc/2，代入空间电流矢量转换公式为
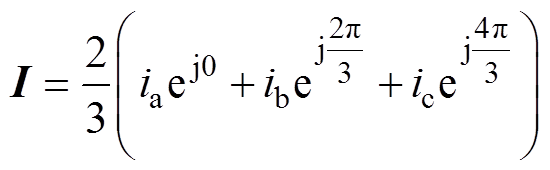（4）
可以得出，基本空间电流矢量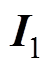
为
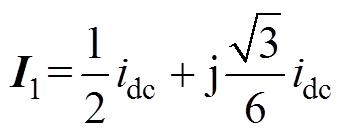（5）同理，按照上述步骤计算所有的开关组合可以得出19个不同的基本空间电流矢量，基本电流矢量对应开关组合见表1。按照基本矢量幅值的大小，可以分成大矢量、中矢量、小矢量和零矢量四类，相应的矢量长度分别为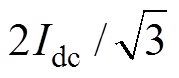
、
、
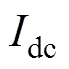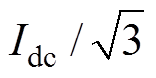和0。19个基本空间电流矢量分布如图2所示。
表1 基本电流矢量对应开关组合
Tab.1 Classification of space vector and their switching states
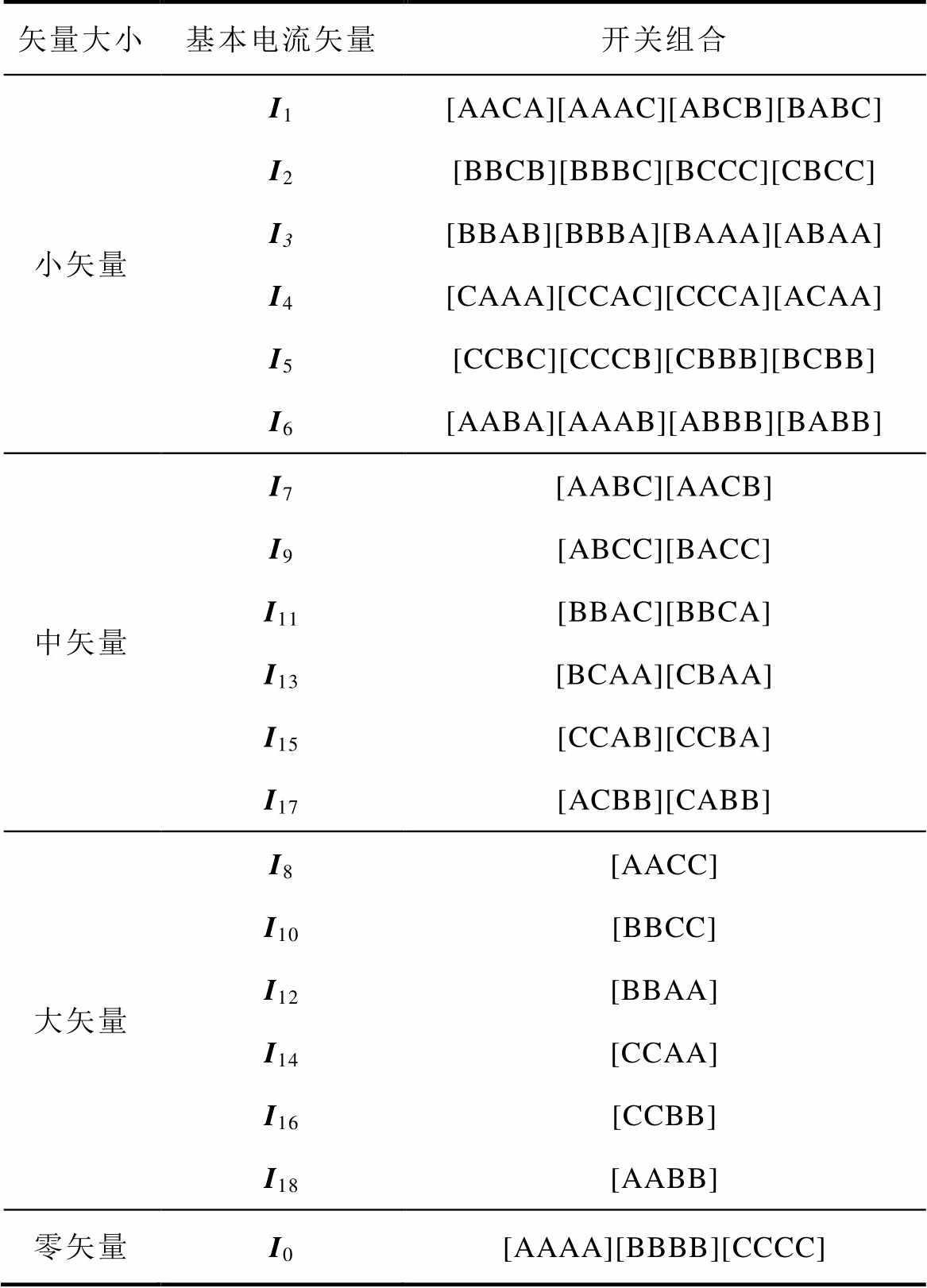
矢量大小基本电流矢量开关组合 小矢量I1[AACA][AAAC][ABCB][BABC] I2[BBCB][BBBC][BCCC][CBCC] I3[BBAB][BBBA][BAAA][ABAA] I4[CAAA][CCAC][CCCA][ACAA] I5[CCBC][CCCB][CBBB][BCBB] I6[AABA][AAAB][ABBB][BABB] 中矢量I7[AABC][AACB] I9[ABCC][BACC] I11[BBAC][BBCA] I13[BCAA][CBAA] I15[CCAB][CCBA] I17[ACBB][CABB] 大矢量I8[AACC] I10[BBCC] I12[BBAA] I14[CCAA] I16[CCBB] I18[AABB] 零矢量I0[AAAA][BBBB][CCCC]
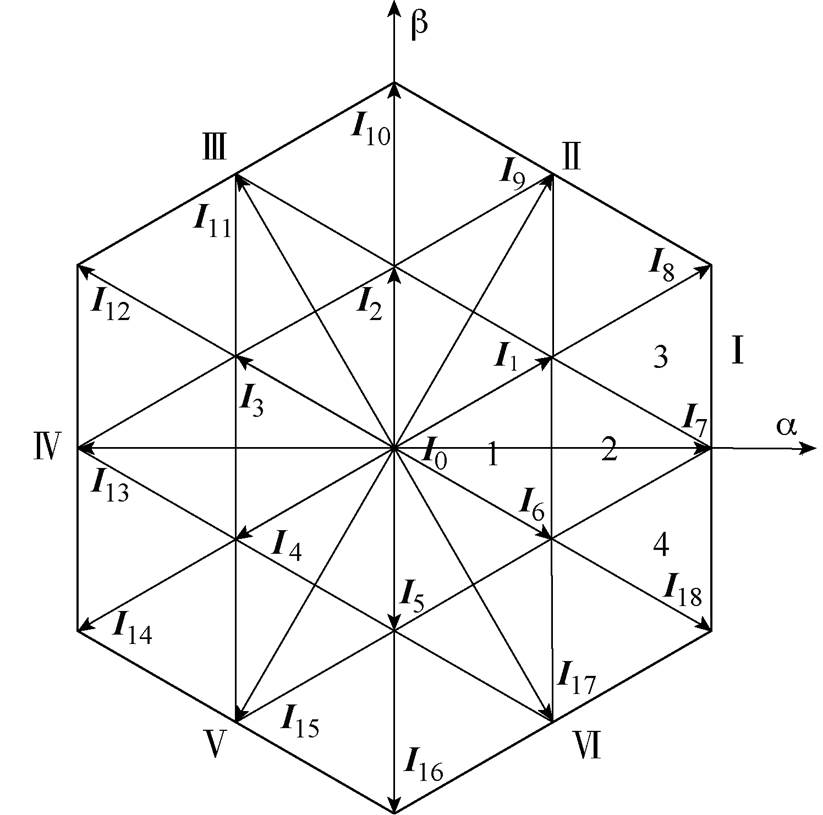
图2 空间电流矢量分布
Fig.2 Space current vector diagram
在90°坐标系中，SVPWM算法根据参考电流矢量所在扇区选择三个基本矢量，再利用伏秒平衡原理计算出各个基本矢量作用时间，采用七段式调制生成所需的PWM信号。而本文通过坐标变换，将空间电流矢量变换到60°坐标系下，优化了扇区判断和基本矢量作用时间计算过程。
定义采用的60°坐标系为gh坐标系，取a 轴顺时针旋转30°为g轴，g轴再逆时针旋转60°为h轴，ab 坐标系与gh坐标系变换如图3所示。Iref为参考电流矢量，在不同坐标系下有不同坐标描述，在ab 坐标系下表示为Ia、Ib，在gh坐标系下为Ig、Ih。
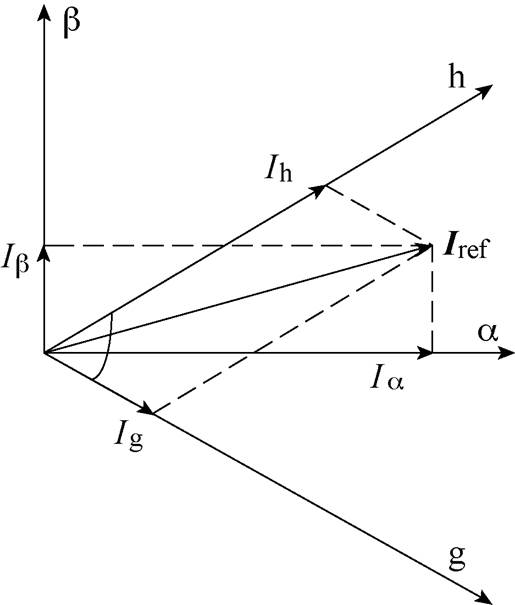
图3 ab 坐标系与gh坐标系变换
Fig.3 The transformation between ab coordinate system and gh coordinate system
根据几何关系分析，由ab 坐标系到gh坐标系的坐标变换式为
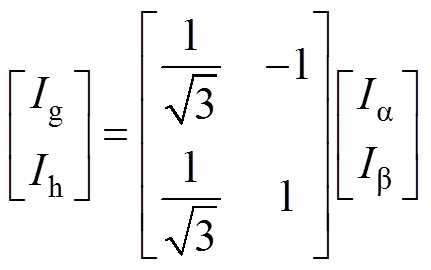（6）三相静止坐标系abc与gh坐标系的坐标变换关系为
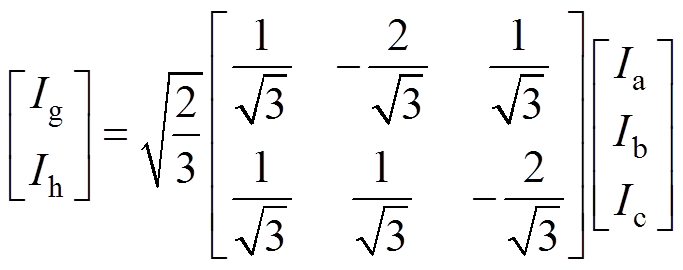（7）
为了计算方便，将参考电流矢量Iref进行标幺化处理，本文以小矢量幅值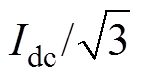
为标幺变换基准值，即
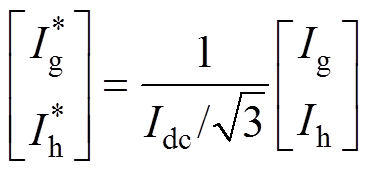（8）通过ab 坐标系到gh坐标系变换以及标幺化，可以得出gh坐标系下所有基本电流的位置坐标，gh坐标系下5L-CSR空间电流矢量如图4所示。
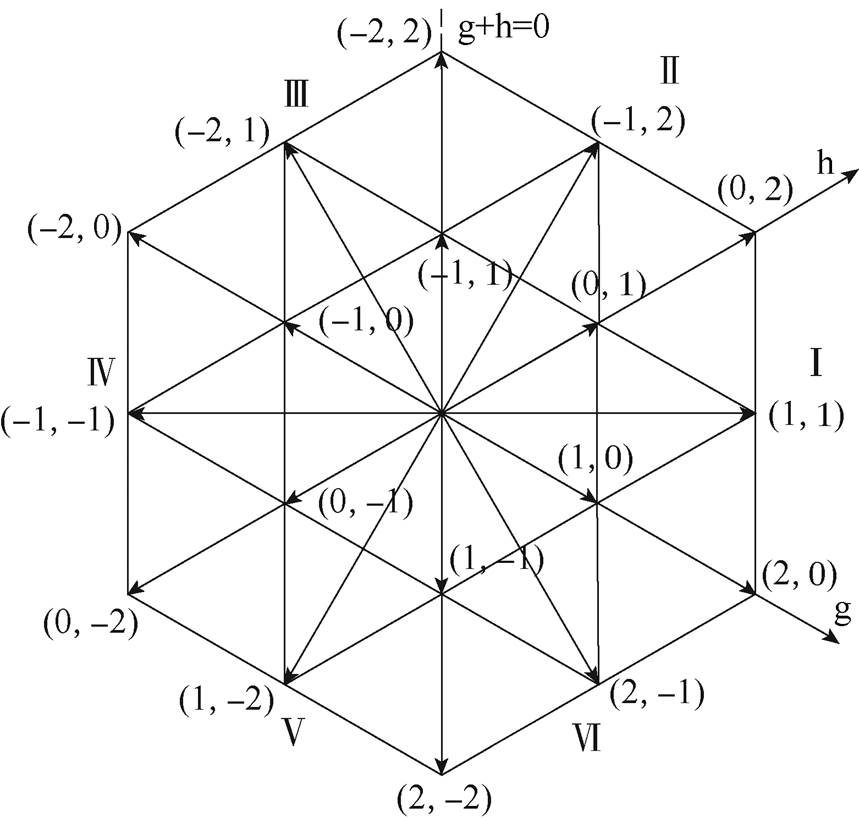
图4 gh坐标系下5L-CSR空间电流矢量
Fig.4 Space current vector diagram of 5L-CSR based on gh coordinate system
根据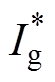
、
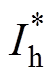的值，可以简便地判断出电流矢量所在的大扇区。但是在第Ⅱ大扇区和第Ⅲ大扇区中同时存在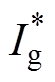＜0、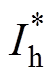＞0的情况，所以需要附加条件“g+h=0”来判断矢量的位置。大扇区划分如图4所示，划分条件见表2。
表2 大扇区判断条件
Tab.2 Judgment conditions of large sector
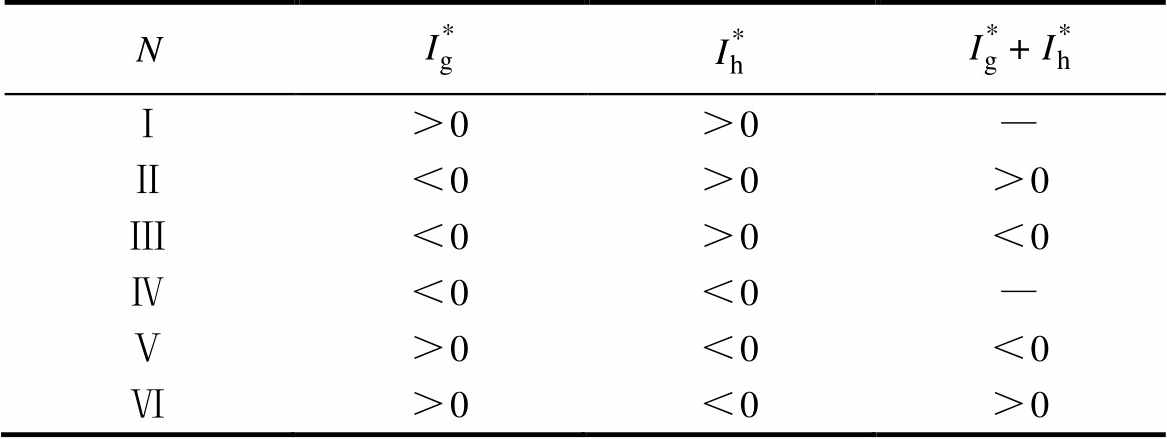
N+ Ⅰ＞0＞0— Ⅱ＜0＞0＞0 Ⅲ＜0＞0＜0 Ⅳ＜0＜0— Ⅴ＞0＜0＜0 Ⅵ＞0＜0＞0
判断出参考电流矢量所在大扇区后，根据大扇区之间一致性的特点，为了后续计算方便，可以将其余大扇区的参考矢量转换到第Ⅰ大扇区，进而可以比较方便地判断出小扇区位置。以第Ⅱ大扇区到第Ⅰ大扇区为例分析转换关系，gh坐标系下大扇区转换关系如图5所示，第Ⅱ大扇区与第Ⅰ大扇区坐标转换关系为
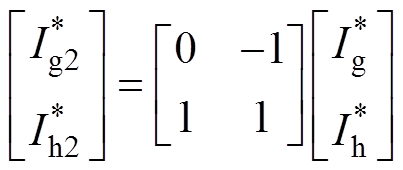（9）以此类推，其他大扇区的参考矢量也可以转换到第Ⅰ大扇区，其转换关系为
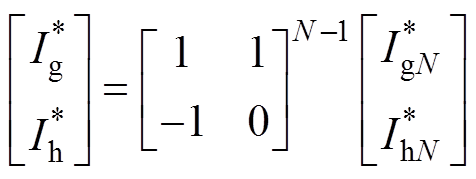（10）
式中，N为大扇区号，N=1,…,6。
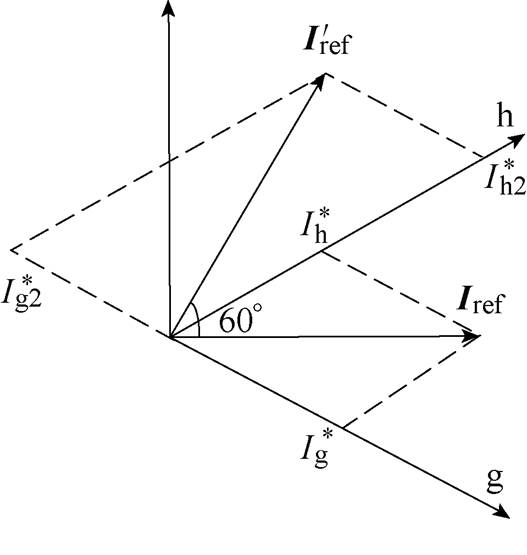
图5 gh坐标系下大扇区转换关系
Fig.5 Large sector conversion relationship ingh coordinate system
利用以上分析计算得到的参考矢量转换到第Ⅰ大扇区的分量为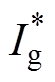和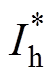，可以判断出参考矢量所在位置。以第Ⅰ大扇区4个小扇区的划分情况为例，扇区Ⅰ的小扇区划分示意图如图6所示。
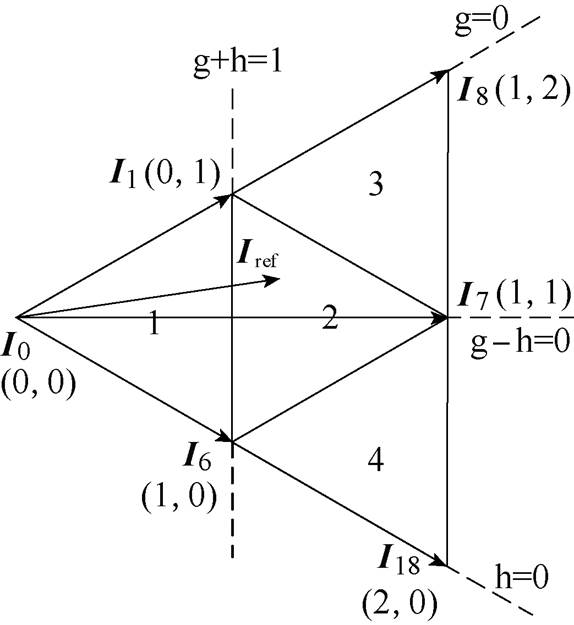
图6 扇区Ⅰ的小扇区划分示意图
Fig.6 Schematic diagram of small sector division of sector Ⅰ
通过分析可以得出参考矢量所在小扇区的判断条件，见表3。
表3 小扇区判断条件
Tab.3 Judgment conditions of small sector
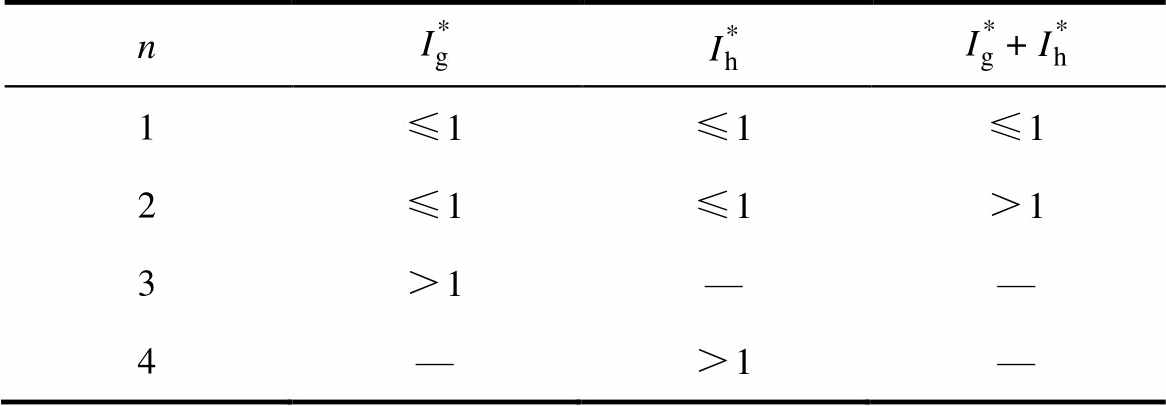
n+ 1≤1≤1≤1 2≤1≤1＞1 3＞1—— 4—＞1—
对于任意的参考电流矢量Iref都可由3个最近的基本矢量合成，确定了基本矢量之后，根据伏秒平衡原理得
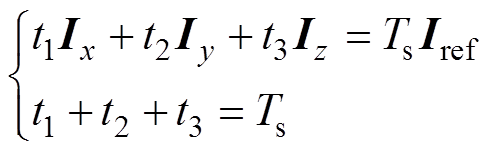（11）式中，Ix、Iy、Iz为合成Iref的基本矢量；Ts为采样周期；t1、t2、t3分别为三个基本矢量作用时间。图6中，Iref位于第Ⅰ大扇区第2小扇区，Ix、Iy、Iz分别对应I1、I6、I7，根据式（11），利用坐标变换转换到60°坐标系下，可得
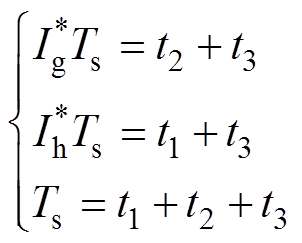（12）
求解可得基本矢量作用时间为
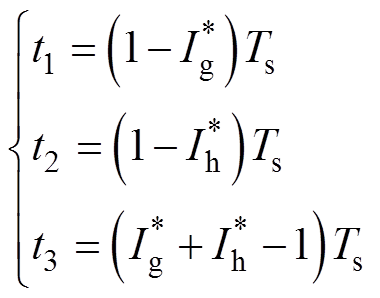（13）同理，可以求出第Ⅰ大扇区其余小扇区中的基本矢量及作用时间，见表4。
表4 基本矢量作用时间
Tab.4 Acting time of basic vector
nIx, Iy, Izt1t2t3 1I6, I1, I0 2I1, I6, I7 3I18, I7, I6 4I7, I8, I1
结合式（10）坐标旋转就可以计算出其他扇区的基本矢量作用时间。
均流电感主要起到平均直流电流和滤除电流纹波的作用，分析图1所示主电路可知：直流侧均流电感电流均衡受到均流电感两端电压的影响。直流电流分配不均将会影响整流器系统的正常工作，甚至损坏硬件电路。均流电感的选取应满足
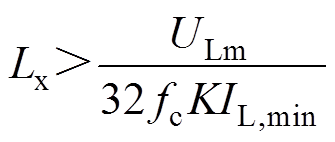（14）式中，ULm为交流侧线电压峰值；fc为开关频率；K为整流单元并联数；IL,min为最小负载电流。
由表1可知，一个基本电流矢量对应多种开关组合状态，冗余开关组合生成相同的电流矢量，但是不同开关组合状态使得均流电感两端电压有所不同。例如，I1对应的开关组合[ABCB]和[BABC]，上、下桥臂均流电感两端电压分别为-UAB/2、-UBC/2和UAB/2、UBC/2。因此，针对本文提出的调制方法，在一个调制周期内，可以采用控制这两种开关组合作用时间相等的方法，用以保持均流电感承受的平均电压为零，从而能够维持均流电感的电流平衡。
确定了各个基本电流矢量之后，为使开关器件开关损耗最小，须尽量减少开关切换次数，即每个开关器件在一个开关周期开关状态切换不能多于两次。综上分析，本文矢量合成模式采用七段式，第Ⅰ大扇区中矢量作用顺序及作用时间见表5。
表5 开关状态作用序列
Tab.5 Switching state sequence
扇区开关组合 t3/4t1/2t2/2t3/2t1/2t2/2t3/4 Ⅰ-1BCBCACBCABCBCBCBCACBBABCBCBC Ⅰ-2AACBABCBACBCAABCBABCCACBAACB Ⅰ-3ACBCAABBAACBCACBAABBAABCACBC Ⅰ-4ABCBAACBAACCBABCAABCAACCABCB
本文使用Matlab/Simulink搭建了5L-CSR模型，采样频率为5kHz。图7为5L-CSR系统的稳态仿真波形。网侧电压仿真波形有效值为220V，其余主要参数见表6。图7c中直流总电流非常平稳，整流单元电流分配均匀，为直流总电流的一半；图7d为网侧电流总谐波畸变率（Total Harmonic Distortion, THD）。
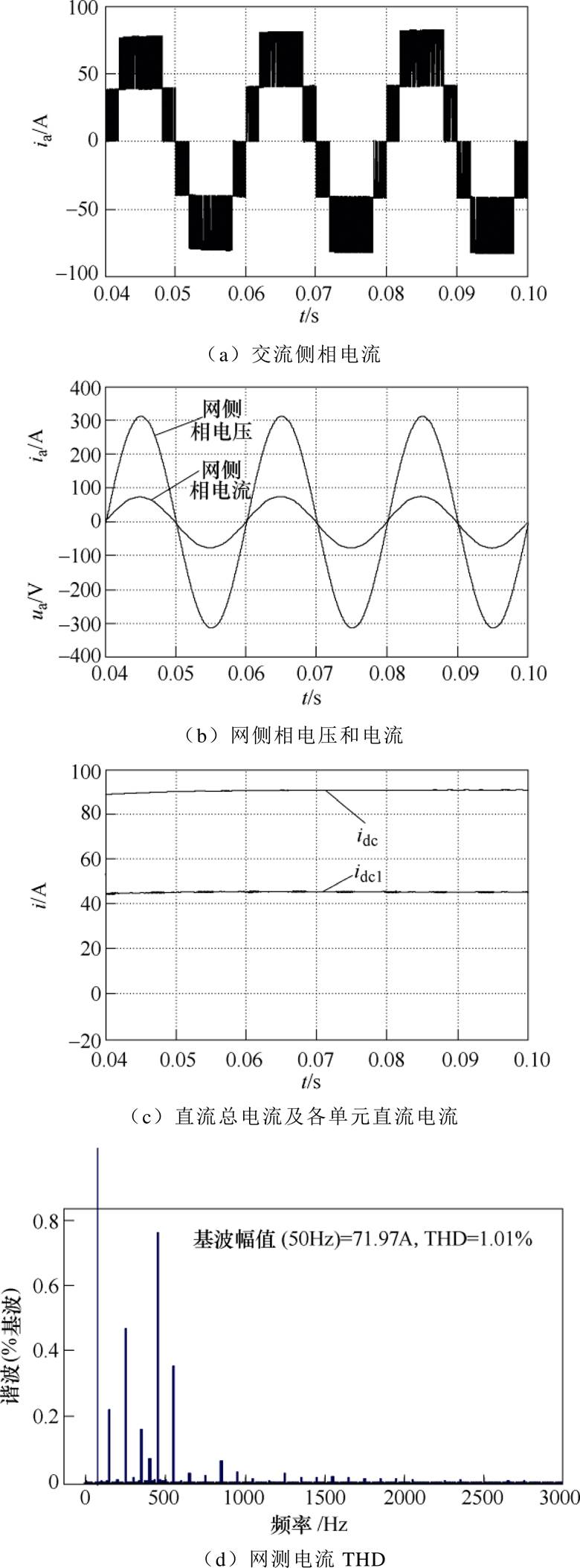
图7 整流器稳态仿真波形
Fig.7 Simulation waveforms in rectifier steady-state
表6 三相5L-CSR样机参数表
Tab.6 Parameter of three-phase 5L-CSR
参 数数 值 网侧三相电压有效值/V100 交流侧滤波电容/mF50 交流侧滤波电感/mH1 直流侧均流电感/mH5 直流侧电感/mH10 PWM开关频率/Hz5 000 直流侧负载/W3
从仿真结果可以看出，系统运行稳定，网侧电流THD仅为1.01%。同时，在相同的条件下，仿真时间设定为0.3s，传统SVPWM算法和60°坐标系下SVPWM算法实际运行时长分别为28.4s和20.6s，证明了60°坐标系下SVPWM算法运算效率较高。
为了验证本文的理论分析以及仿真结果，搭建了一台5L-CSR实验样机。由于FPGA具有强大的时序处理能力，PC/104（SCM-7018B）主板有着良好的可拓展性和数据处理能力，所以本文采用PC/104（SCM-7018B）主板和FPGA作为控制器。表6给出了实验样机主要参数。
图8给出了系统稳态时部分实验波形。由图8可以看出，整流器运行比较稳定，并且工作在单位功率因数状态；由于采用了合理分配冗余开关组合作用时间和作用顺序的措施，两个整流单元直流电流大小基本一致。上述实验结果与仿真分析基本吻合，证明了本文调制策略是正确有效的。
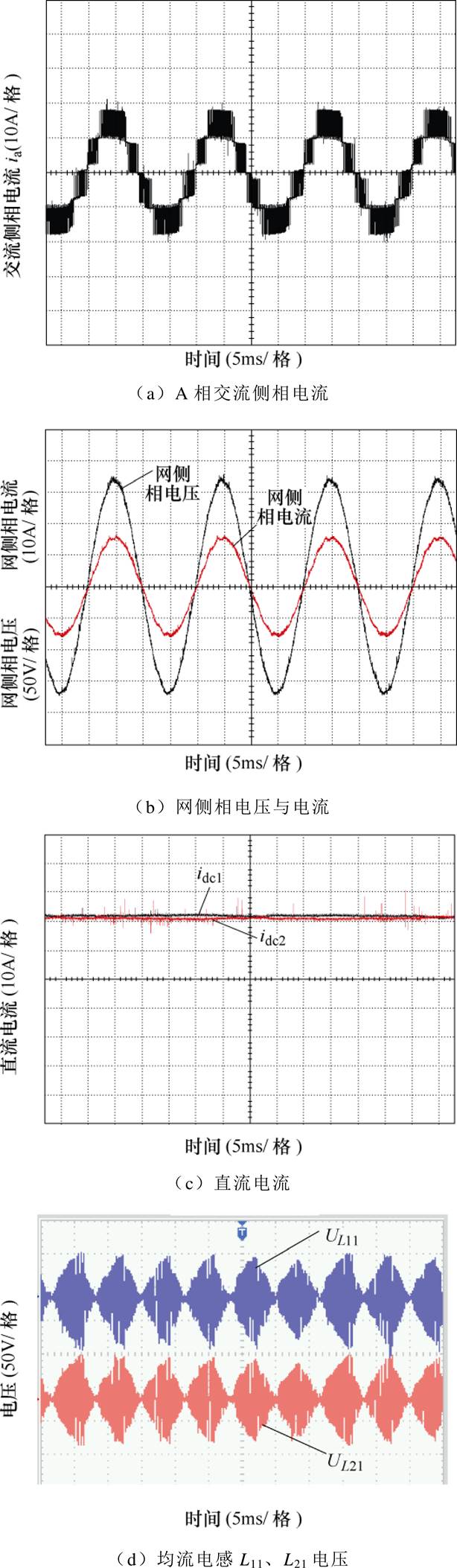
图8 稳态实验波形
Fig.8 Experimental waveforms in steady state
本文针对5L-CSR，提出了一种基于60°坐标系SVPWM算法，首先对该方法的原理以及实现过程进行了详细的分析和推导，该方法能够简便地求出基本矢量及其作用时间，与传统SVPWM算法相比，省去了大量三角函数运算。针对均流电感电流平衡问题，提出了合理分配冗余开关组合作用时间和作用顺序的方法，保证了各整流单元的直流侧电流平衡，实现了自均流。仿真和实验结果都验证了该方法的正确性和有效性。
参考文献
[1] Lai Jih-Sheng, Fang Zhengpeng. Multilevel converters- a new breed of power converters[J]. IEEE Transa- ctions on Industry Application, 1996, 32(3): 509-517.
[2] 王涛, 陈昌松, 段善旭, 等. 用于改善电流过零点畸变的Vienna整流器空间矢量调制策略[J]. 电工技术学报, 2019, 34(18): 3854-3864.
Wang Tao, Chen Changsong, Duan Shanxu, et al. An improved space-vector modulation for Vienna rectifier to eliminating current distortion around zero- crossing point[J]. Transaction of China Electro- technical Society, 2019, 34(18): 3854-3864.
[3] 康劲松, 张烨. 多电平变流器在风力发电系统中的应用[J]. 中国电机工程学报, 2009, 29(24): 20-25.
Kang Jinsong, Zhang Ye. Multi-level converter applied to wind power generation system[J]. Pro- ceedings of the CSEE, 2009, 29(24): 20-25.
[4] Li Ding, Li Yunwei. Simultaneous DC current balance and common-mode voltage control with multilevel current source inverters[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(11): 9188- 9197.
[5] 王兴贵, 薛晟, 李晓英. 模块化多电平变流器半桥串联结构微电网输出特性分析[J]. 电工技术学报, 2019, 34(10): 2130-2140.
Wang Xinggui, Xue Sheng, Li Xiaoying. Analysis of output characteristics of a microgrid based on modular multilevel converter half-bridge series structure[J]. Transaction of China Electrotechnical Society, 2019, 34(10): 2130-2140.
[6] 白志红. 电流型多电平变流器的一些相关理论以及应用技术研究[D]. 杭州: 浙江大学, 2008.
[7] 葛银波, 胡海涛, 杨孝伟, 等. 模块化多电平变流器型中压直流牵引供电系统控制方法研究[J]. 电工技术学报, 2018, 33(16): 3792-3801.
Ge Yinbo, Hu Haitao, Yang Xiaowei, et al. Research on control strategy of modular multilevel converter based medium-voltage direct current traction power supply system[J]. Transaction of China Electro- technical Society, 2018, 33(16): 3792-3801.
[8] 孙帆, 王金梅, 鲁娅楠. 模块化多电平变流器改进最近电平调制策略的研究[J]. 电气技术, 2019, 20(2): 23-27.
Sun Fan, Wang Jinmei, Lu Yanan. Research on improved nearest level modulation strategy for modular multilevel converter[J]. Electrical Engin- eering, 2019, 20(2): 23-27.
[9] 罗锐, 何英杰, 陈晖, 等. 三电平变流器中点电位平衡及低开关损耗SVPWM策略[J]. 电工技术学报, 2018, 33(14): 3245-3254.
Luo Rui, He Yingjie, Chen Hui, et al. SVPWM scheme for three-level converters with neutral-point potential balancing and switching loss reduction[J]. Transaction of China Electrotechnical Society, 2018, 33(14): 3245-3254.
[10] 葛兴来, 张晓华, 岳岩. 低载波比下三电平NPC逆变器同步SVPWM算法[J]. 电机与控制学报, 2018, 22(9): 24-32.
Ge Xinglai, Zhang Xiaohua, Yue Yan. Comparative study on synchronized space vector PWM for three level neutral point clamped VSI under low carrier ratio[J]. Electric Machines and Control, 2018, 22(9): 24-32.
[11] Lee J S, Lee K B. Carrier-based discontinuous PWM method for Vienna rectifiers[J]. IEEE Transactions on Power Electronics, 2015, 30(6): 2896-2900.
[12] 杨涛, 赵景涛, 王前双. 基于多重化DC/DC变换器的储能变流器研究[J]. 电力系统保护与控制, 2016, 44(20): 119-127.
Yang Tao, Zhao Jingtao, Wang Qianshuang. Research on power conversion system based on interleaved DC/DC converter[J]. Power System Protection and Control, 2016, 44(20): 119-127.
[13] 李玉玲. 电流型PWM整流器及其控制策略的研究[D]. 杭州: 浙江大学, 2006.
[14] Karasik V, Dixon K, Weber C, et al. SMES for power utility applications: a review of technical and cost considerations[J]. IEEE Transactions on Applied Superconductivity, 1999, 9(2): 541-546.
[15] 郭文勇, 蔡富裕, 赵闯, 等. 超导储能技术在可再生能源中的应用与展望[J]. 电力系统自动化, 2019, 43(8): 2-19.
Guo Wenyong, Cai Fuyu, Zhao Chuang, et al. Application and prospect of superconducting magnetic energy storage for renewable energy[J]. Automation of Electric Power Systems, 2019, 43(8): 2-19.
[16] 白志红, 张仲超. 一种新型超导储能多模块并联的电流型多电平变流器[J]. 中国电机工程学报, 2008, 28(9): 17-22.
Bai Zhihong, Zhang Zhongchao. A novel multi- module parallel multilevel current-source converter for super-conducting magnetic energy storage system[J]. Proceedings of the CSEE, 2008, 28(9): 17-22.
[17] 姚骏, 谭义, 裴金鑫, 等. 模块化多电平变流器高压直流输电系统直流故障改进控制策略[J]. 电工技术学报, 2018, 33(14): 3306-3318.
Yao Jun, Tan Yi, Pei Jinxin, et al. Improved control strategy for DC fault in modular multi-level converter-HVDC system[J]. Transaction of China Electrotechnical Society, 2018, 33(14): 3306-3318.
[18] 孙云龙, 李忠华, 索长友. 电导非线性对HVDC电缆绝缘空间电荷动态过程的影响[J]. 电机与控制学报, 2019, 23(7): 27-37.
Sun Yunlong, Li Zhonghua, Suo Changyou. Effect of nonlinear conductivity on dynamic process of space charge in HVDC cable insulation[J]. Electric Machines and Control, 2019, 23(7): 27-37.
[19] Soeiro T B, Heldwein M L, Kolar J W. Three-phase modular multilevel current source rectifiers for electric vehicle battery charging systems[C]//2013 Brazilian Power Electronics Conference, Gramado, 2013: 623-629.
[20] 徐歌, 肖仕武, 丛明一. 电动汽车充放电站的短路故障分析与保护[J]. 电力系统保护与控制, 2018, 46(7): 150-156.
Xu Ge, Xiao Shiwu, Cong Mingyi. Short-circuit fault analysis and protection for electric vehicle charging and discharging station[J]. Power System Protection and Control, 2018, 46(7): 150-156.
[21] 张国荣, 颜丽花. 单极倍频CPS-SPWM传输带宽的研究[J]. 电力系统保护与控制, 2018, 46(12): 1-8.
Zhang Guorong, Yan Lihua. Study on the trans- mission bandwidth of unipolar frequency doubled CPS-SPWM[J]. Power System Protection and Control, 2018, 46(12): 1-8.
[22] 李建林, 林平, 王长永, 等. 基于载波相移SPWM技术的电流型有源滤波器的研究[J]. 中国电机工程学报, 2003, 23(10): 99-103.
Li Jianlin, Lin Ping, Wang Changyong, et al. Research on current-source converter with carrier phase shifted SPWM for active power filter[J]. Proceedings of the CSEE, 2003, 23(10): 99-103.
[23] 艾永乐, 陈博, 李自清, 等. 基于调制比优化的单相逆变器主谐波滤除研究[J]. 电力系统保护与控制, 2018, 46(10): 130-135.
Ai Yongle, Chen Bo, Li Ziqing, et al. Research on single phase inverter main harmonic filter based on modulation ratio optimization[J]. Power System Protection and Control, 2018, 46(10): 130-135.
[24] 林平，王立乔，李建林, 等. 基于级联型错时采样空间矢量调制多电平变流器的APF研究[J]. 中国电机工程学报, 2005, 25(8): 71-74.
Lin Ping, Wang Liqiao, Li Jianlin, et al. Research on cascade multi-level converter with sample time stag- gered SVM and its application to APF[J]. Pro- ceedings of the CSEE, 2005, 25(8): 71-74.
Space Vector Pulse Width Modulation Strategy Based on Three-Phase Five-Level Current Source Rectifier
Abstract The multilevel current source rectifier (MCSR) consists of multiple paralleled three-phase current source bridge rectifiers. If the traditional space vector pulse width modulation (SVPWM) method is used, it involves a lot of trigonometric functions, which affects the data processing efficiency of the controller. Therefore, a space vector pulse width modulation method based on three-phase MCSR in 60° coordinate system is proposed, and the calculation process of basic vector and action time is simplified effectively. At the same time, a method for reasonably distributing the switching time and sequence of the redundant switch is proposed to balance dc current. Thus, the current balance inductance at each switching period withstands a zero average voltage, thereby solving the current imbalance problem of the balance inductance and realizing the automatic average of DC current. Finally, the simulation and experiment of three-phase 5L-CSR were carried out to verify the proposed method.
keywords：Multilevel, space vector pulse width modulation, current source rectifier, average inductor current balancing
DOI: 10.19595/j.cnki.1000-6753.tces.191449
中图分类号：TM461
张 强 男，1972年生，博士，硕士生导师，研究方向为感应加热装置的设计。E-mail: Zhangqiang_mail@126.com
吴延飞 男，1995年生，硕士研究生，研究方向为大功率PWM整流器。E-mail: wuyanfei95@163.com（通信作者）
收稿日期 2019-11-09
改稿日期 2020-01-10
（编辑 陈 诚）