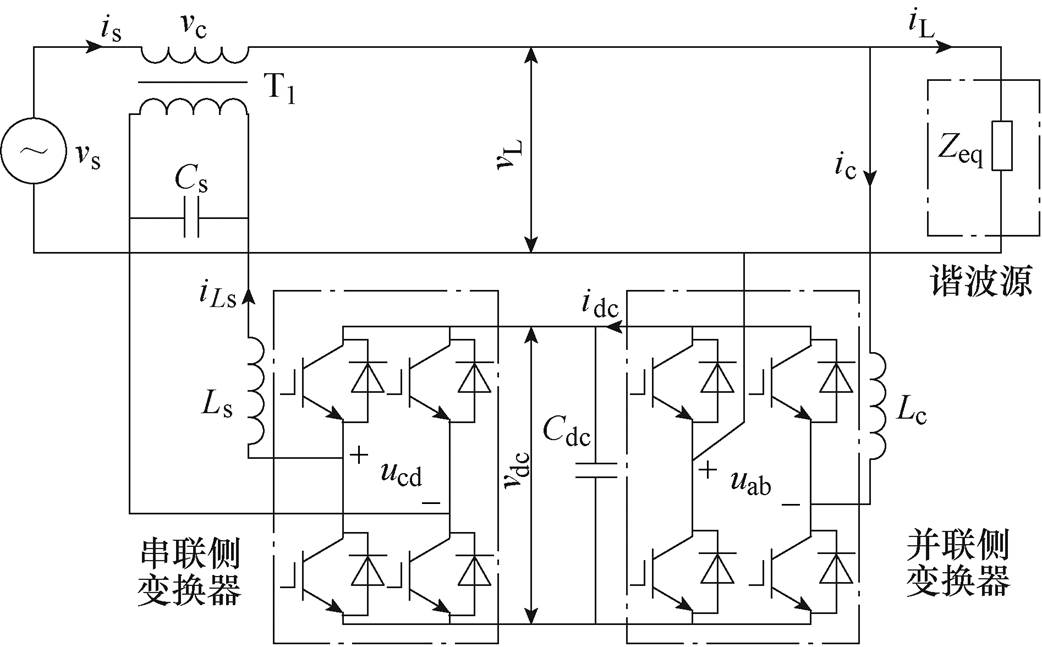
图1 单相UPQC拓扑
Fig.1 Topology of single-phase UPQC
摘要 单相统一电能质量调节器（UPQC）并联侧和串联侧变换器之间存在脉动的功率差，脉动的功率在直流电容上产生低频电压纹波并影响变换器的补偿效果。该文分析单相UPQC中并联侧变换器直流母线低频纹波产生的原因以及对补偿效果的影响。为了抑制对补偿电流的影响，在电压外环加入陷波器减少电压纹波产生谐波参考电流，在电流内环引入网侧电流特征次谐波补偿，进一步抑制电压纹波对调制信号的影响。仿真和实验验证了对低频纹波分析的正确性，以及所提控制策略抑制直流纹波影响的可行性和有效性。
关键词：单相统一电能质量调节器 低频电压纹波 纹波电压影响抑制 特征次谐波补偿
统一电能质量调节器（Unified Power Quality Conditioner, UPQC）兼具解决电压和电流两类电能质量问题的能力[1-4]，但是变换器之间脉动功率差在共用直流母线电容上形成低频电压纹波[5-7]。减小直流侧电容后低频波动更加明显[8-10]，同时对并联侧补偿效果产生影响。
针对三相UPQC系统中由于负载或电压不平衡产生的直流纹波，可以通过调整开关管作用时间抑制纹波电压对变换器性能的影响[11]。在车载逆变器输入含有2次纹波时，频率补偿算法可以有效地减小引起三相牵引电机中拍频的谐波电流含量，从而消除拍频现象[12]。上述算法在三相系统中得到了较好的应用。对于单相变换器，放宽直流母线电压波动的约束条件可以显著减小无功发生器直流侧电 容[13]。同样在输入输出同频同相的前提下，单相背靠背系统采用同步技术能够降低对直流电容的要 求[14]。但应用在单相UPQC并联变换器的补偿效果将不够理想。
为了抑制纹波电压对电流内环的影响，文献 [8, 15-16]引入比例谐振控制器、重复控制器精确追踪参考电流。在此基础上，文献[17]提取参考电流的高次谐波抑制网侧电流的畸变。但是，在直流电压波动幅值较大时，单相UPQC电压环产生的电流参考信号不直接反映补偿后网侧电流谐波，难以抑制低频纹波对网侧电流补偿的影响。同时，这些控制策略一般根据调制信号或直流电压脉动对传统控制策略进行改进，并没有根据网侧电流的实际情况进行调整，因此，减小直流电容后网侧电流谐波含量仍然明显。
除对电流内环进行改进外，也可以对电压外环进行优化。可以将直流电压取平均值或经过滑动平均滤波器[18-19]再参与运算，但是这一算法使得电压调节响应较慢，影响补偿效果。为了提高响应速度，可以将上述滤波器在电压环串入陷波器[8, 20-21]、低通滤波[22-23]等滤除低频纹波，低通滤波器（Low Pass Filter, LPF）容易滤除系统响应产生的波动，陷波器仅滤除特定谐波[24]，因此具有较好的效果。
不论电压外环还是电流内环的改进，均很难较好地抑制直流低频纹波对补偿效果的影响，因此，针对单相UPQC直流纹波对并联侧补偿电流的影响，本文在基于陷波器的电压外环基础上提出网侧电流特征次谐波补偿的内环控制策略，进而抑制低频纹波对补偿电流的影响。
单相UPQC拓扑如图1所示，串联和并联变换器共用直流母线，在不同的工况下，其网侧电源、负载以及并联侧变换器和串联侧变换器的功率流向是不同的，但始终存在动态平衡的关系。图1中，T1为隔离变压器，Zeq为等效负载，Ls和Cs为串联侧滤波器，Lc为并联侧滤波器。
图1 单相UPQC拓扑
Fig.1 Topology of single-phase UPQC
并联侧变换器不仅需要补偿负载的无功电流和谐波电流，还要起到稳定直流电压的作用。在单相UPQC正常稳态工作时，假设并联侧变换器网侧电压不含谐波，则网侧电压、补偿电流可表示为
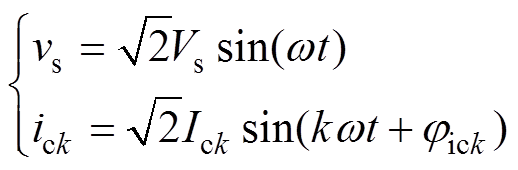（1）式中，w 为网侧电压角频率，w =2pf，f为网侧电压基波频率；Vs为网侧电压有效值；Ick为补偿电流ic中的k次电流有效值；jick为补偿电流中第k次谐波电流与输入电压的相位差；k为大于1的整数。
补偿网侧电流谐波时，并联侧变换器的有功损耗可以忽略，即UPQC不消耗网侧有功，变换器从电网获得的瞬时功率pac可以表示为
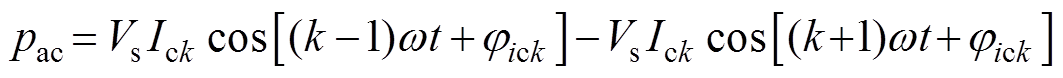（2）根据功率守恒原则，交流侧传递到直流侧功率引起的电压波动满足
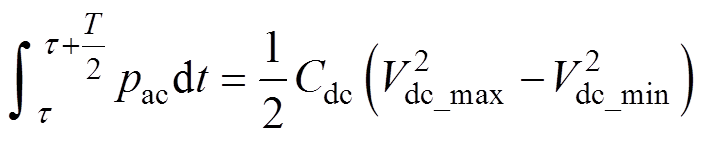（3）
式中，Cdc为直流侧电容；Vdc_max和Vdc_min分别为输出纹波电压的最大值和最小值。直流侧电容波动电压dk=vdc-Vdref，其中，vdc为直流电压，Vdcref为直流侧电压稳定值。则波动电压为
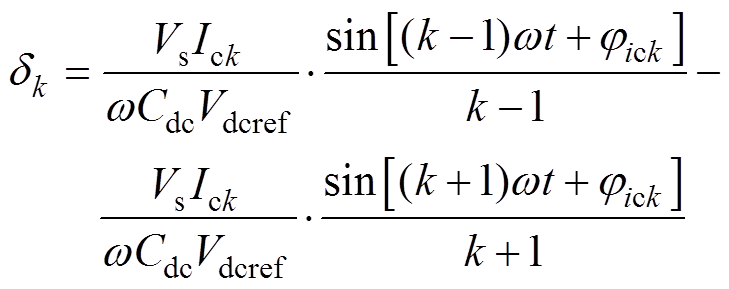（4） 从式（4）得出，补偿k次电流会引起k±1次的电压波动。单相非线性负载中电流主要含有3、5、7、…等奇次谐波，因此引起的电压波动主要为2、4、6、…等偶次谐波。又由于3次谐波含量占谐波电流的比例最大，所以补偿谐波电流主要引起直流侧电压的2次低频纹波。根据式（4）绘制直流侧电压受补偿电流影响的结果如图2所示，可得直流侧电压畸变程度随着补偿电流次数的增加而增加。
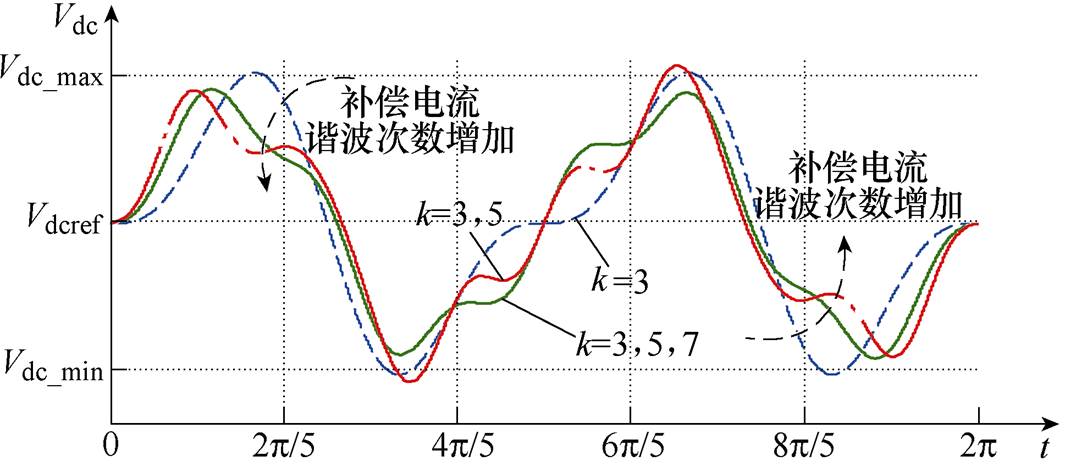
图2 补偿不同电流时的直流侧电压波形
Fig.2 DC-link voltage waveforms at different compensation current
UPQC的并联侧变换器不仅需要补偿谐波电流，还需要对负载的无功电流进行补偿。若并联侧变换器输出电流ic只含无功电流，k=1且补偿的无功电流与网侧电压相位相差90°，则有
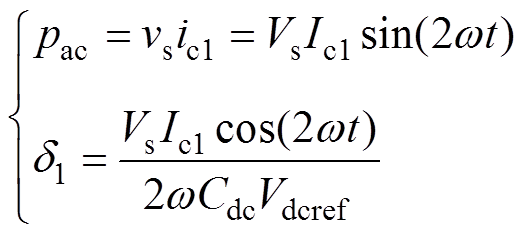（5）可以得出，补偿无功电流同样会引起直流电压2次脉动。
由于补偿电流导致的直流纹波中2次纹波占比最大，因此本文主要分析2次电压纹波影响。
传统控制中单相UPQC系统的直流侧电压误差经过比例积分（Proportional Integral, PI）控制器输出并联侧变换器有功电流幅值给定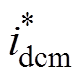
，有功电流给定幅值为
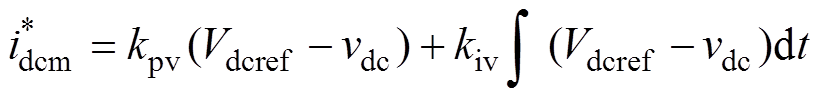（6）式中，kpv、kiv分别为电压控制器的比例和积分参数，其中，kpv主要起到调节电压的作用，忽略积分环节，将vs锁相得到的sin(wt)与有功电流幅值相乘。因此，只补偿大于等于3的奇次谐波时参考电流为
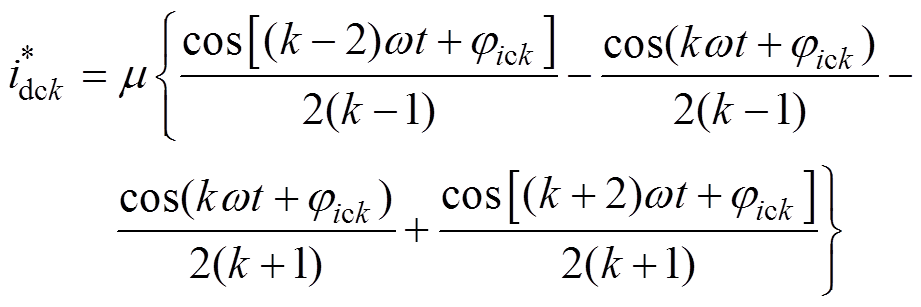（7）
其中
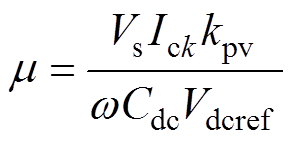
补偿无功时，电流参考值其边界条件可表示为
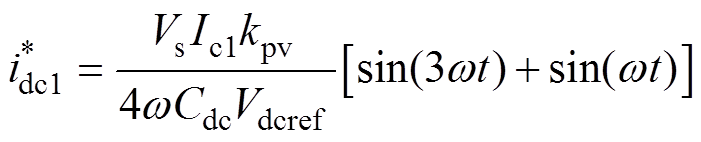（8）
结合式（7）和式（8）可以看出，传统控制主要影响补偿电流的3、5、7等奇次谐波，又由式（2）～式（4）得出谐波电流又会产生2、4、6等偶次的电压纹波。而由1.1节可知，直流纹波主要是2次纹波，影响补偿电流中的3次谐波。
现做如下假设：控制环节中直流纹波的2次纹波没有进入控制器环路，即控制环节输出的调制信号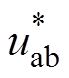
仅含有维持直流侧电压的基波分量。只补偿无功电流时，并联侧变换器输出端口电压与调制波以及并联侧变换器直流侧电容电压存在关系为
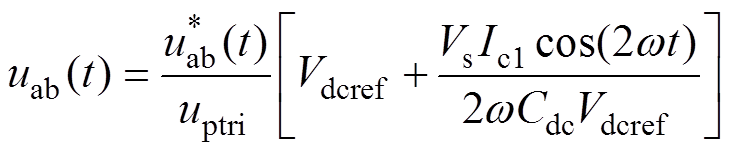（9）式中，uptri为调制中三角载波的幅值。从式（9）可得，当并联侧变换器直流电压存在2次电压纹波时，并联侧变换器端口电压uab中含有大量的3次谐波，经过与网侧连接电感Lc之后，变换器输出的电流将含有大量的3次谐波。控制环节中需要对输出电流进行采集，导致调制信号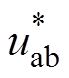中存在3次谐波，最终并联侧变换器输出电流中含有3次谐波。再根据式（4），3次谐波电流引起2、4次电压纹波。
当调制波只含有维持直流侧电压的基波分量时，忽略开关次谐波，根据式（9）绘制端口电压如图3所示，无畸变的正弦调制波会使补偿电流含有额外的畸变电流，导致端口电平不会根据负载以及直流侧电压的变化而变化。因此需要根据负载情况实时修正调制波，进而修正端口电平可以降低网侧电流总谐波畸变率（Total Harmonic Distortion, THD）。
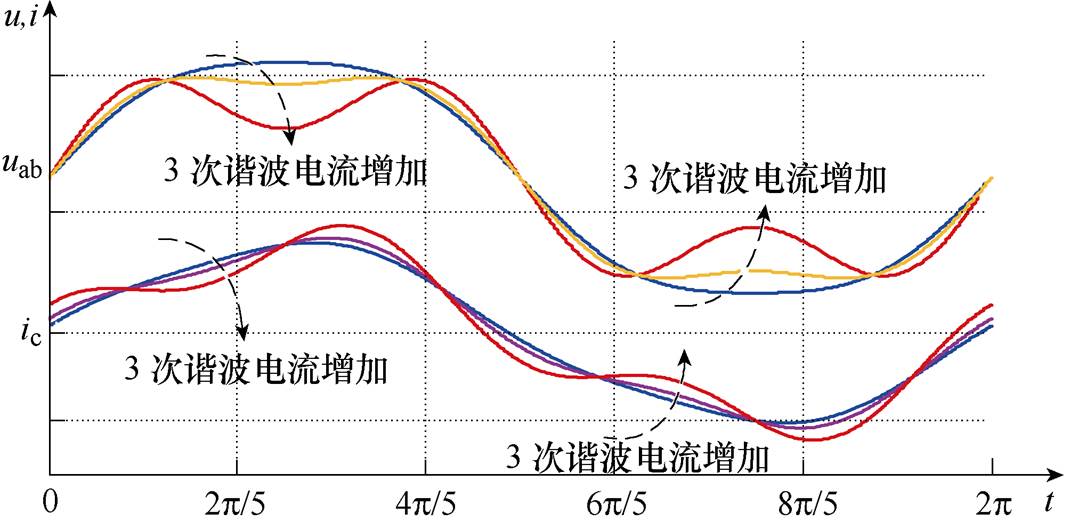
图3 负载3次谐波电流对uab、ic的影响
Fig.3 The influence of 3rd harmonic current on uab, ic
综上所述，补偿电流与直流侧电容电压相互影响的结果如图4所示，补偿无功电流会产生2次纹波电压，补偿3次谐波电流会引起2、4次纹波电压，补偿5次谐波电流会引起4、6次纹波电压等。同时直流母线电压纹波又会影响补偿电流。
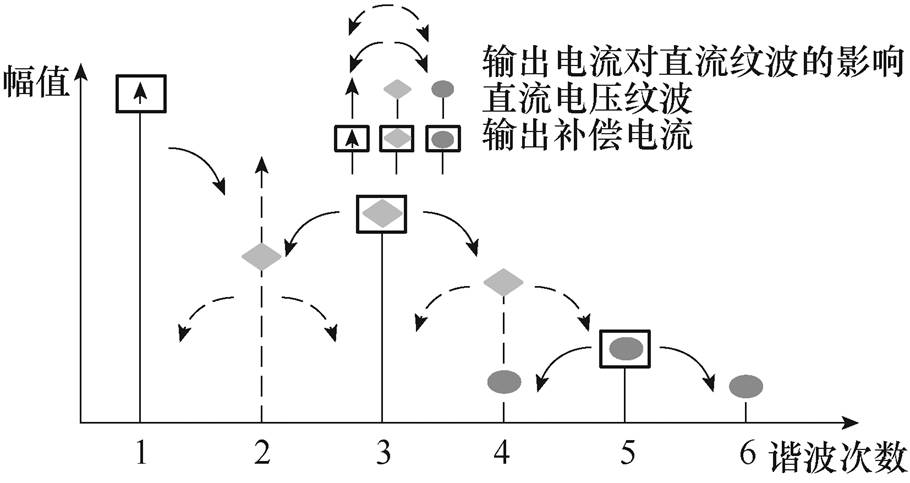
图4 补偿电流和直流纹波频谱图
Fig.4 Compensation current and DC-link voltage ripple spectrum
从上述分析可得，直流纹波电压主要是2次低频纹波，通过控制环节和调制环节影响并联侧变换器补偿电流，其中，控制环节对应到控制器中为电压外环，调制环节为电流内环，输出谐波电流含量的增加导致补偿负载谐波效果不理想。
由式（7）和式（8）可知，在补偿网侧无功和3次谐波时产生的低频纹波电压主要影响网侧电流的3次谐波，因此需要对网侧电流的3次谐波进行控制，也可以根据负载谐波次数对网侧电流中的5、7等奇次谐波加以补偿控制。
由1.2节分析可知，纹波电压通过调制环节影响网侧电流的补偿效果。为了提高补偿效果，在调制信号中引入网侧电流中的奇次谐波抵消直流侧电压中的偶次低频分量对网侧电流的影响。并联侧变换器谐波电流检测方法及电流内环控制如图5所示。本文采用有功、无功解耦的方法检测奇次谐波的有功无功分量，如图5所示，其中，ds为网侧电流的奇次谐波，由于ds为检测is中的网侧电流的奇次谐波，因此对基波和其他谐波增益几乎为0。并联变换器的脉冲宽度调制（Pulse Width Modulation, PWM）等效增益用Kpwm表示，kip为电流环比例控制器。
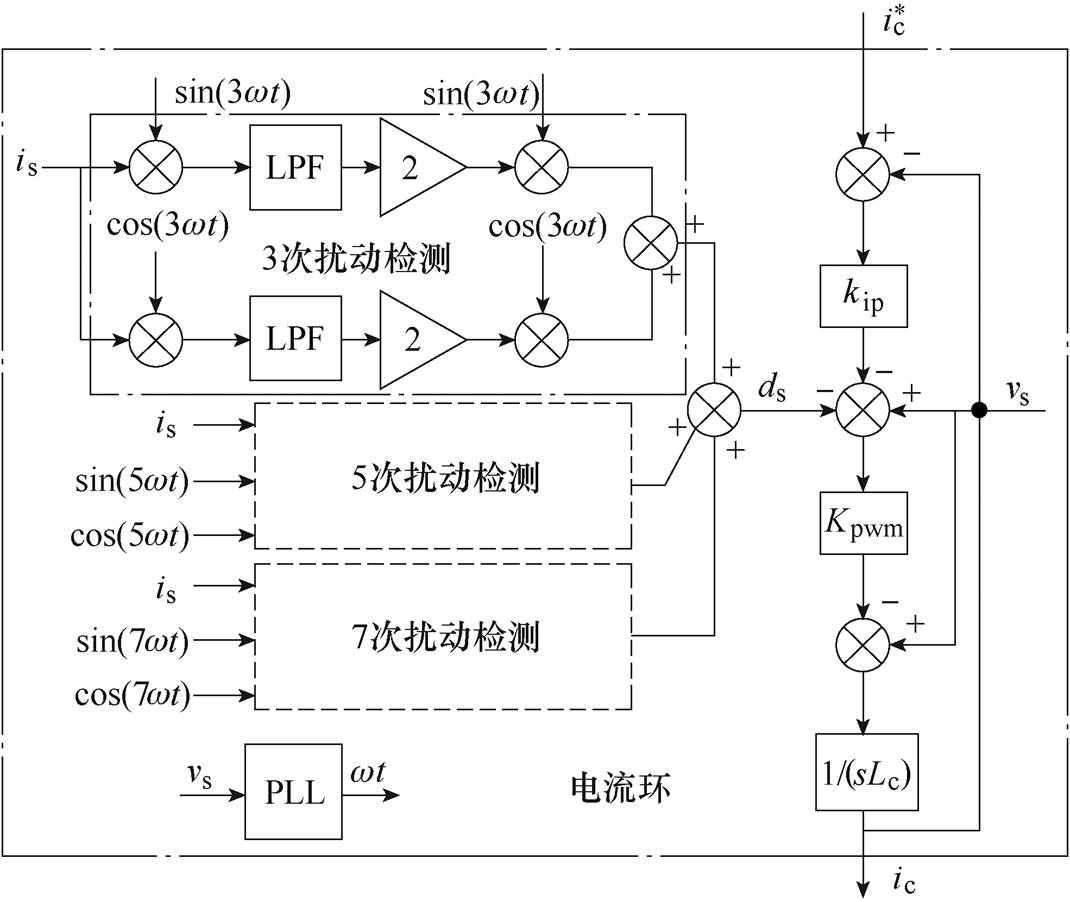
图5 并联侧变换器谐波电流检测方法及电流内环控制
Fig.5 Current detection method and inner current loop control startegy of parallel converter
根据图5推导出，并联侧变换器的补偿输出电流ic闭环传递函数为
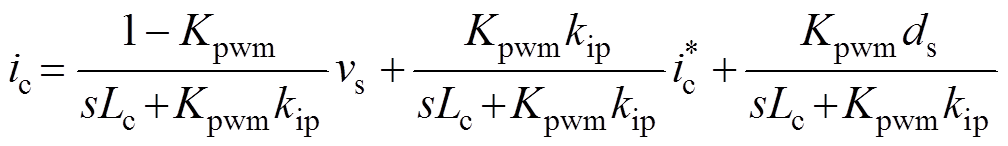（10）变换器的PWM等效增益Kpwm=1，代入式（10）可以化简为
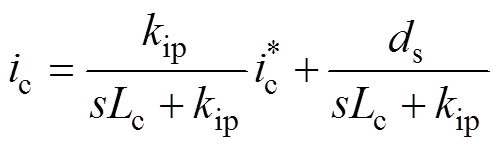（11）
可知，假定负载谐波只含有3次且电压环不对谐波补偿产生影响，在控制器中没有引入特征次谐波补偿时ds=0,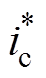 
=iL。当直流电容减小时，直流电压纹波将会明显增加，变换器仅补偿负载中的无功和3次谐波时，根据式（7）和式（8）可得，参考电流中的3次谐波明显增加，因此不引入特征次谐波补偿时，变换器补偿的谐波电流中并没有考虑因直流母线电压纹波影响产生的额外的3次谐波，因此会使得网侧电流含有一定的3次及5次谐波。
当引入特征次谐波补偿时，ds为检测到的网侧电流谐波，在负载谐波电流完全补偿时，ds即为因直流电压波动对网侧电流影响产生的谐波，将此谐波引入控制器后即可降低网侧电流中的谐波。因此，改进后的电流内环特征次谐波补偿策略有助于抑制低频纹波对补偿电流的影响。
电流内环是在直流电压纹波不通过电压外环影响补偿电流的基础上设计的，但是直流纹波同样会通过电压外环影响系统性能。因此，在抑制纹波电压通过电流内环影响补偿电流后，还需要抑制纹波电压通过电压外环对补偿电流的影响。由式（4）和式（5）可知，补偿无功和谐波时会引起直流侧2、4、6等偶次低频纹波，由于负载无功和3次谐波为主要成分，需要在电压环中滤除其中的2次低频分量，也可以根据负载谐波成分滤除其他偶次低频 分量。
滤除直流侧电压低频分量后，采用传统控制方法对输出电压调节产生的有功分量不能反映负载有功、无功情况，电压环不能根据网侧电流的特性进行调整，因此，需要引入负载电流的有功、无功分量才能进一步提高变换器补偿效果。
负载电流iL主要含有谐波电流ih、有功电流ip和无功电流iq，有
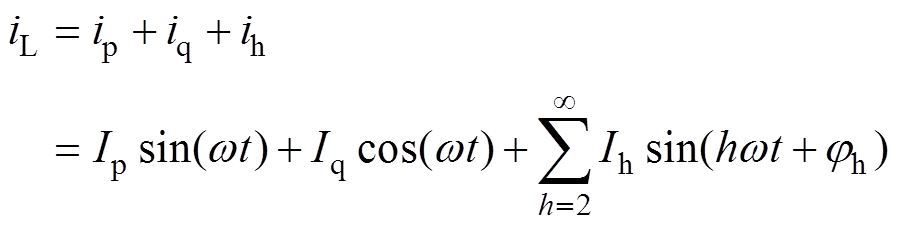（12）式中，Ip、Iq和Ih分别为负载有功电流、无功电流和谐波电流的幅值。负载电流iL分别与sin(wt)和cos(wt)相乘可得
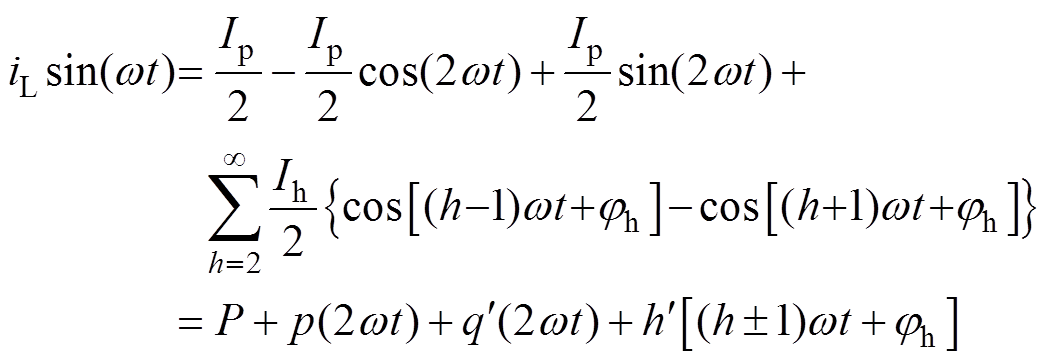（13）
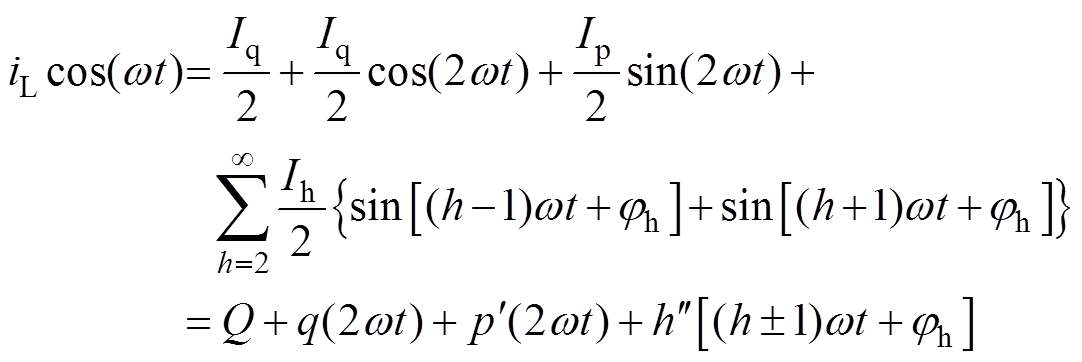（14）从式（13）中可得，负载电流中的有功电流ip转化为直流有功分量P和2倍频有功分量p(2wt)，无功电流iq转化为2倍频无功分量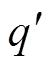
(2wt)，谐波电流ih转化为h±1次的谐波分量
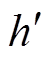，同样从式（14）中得出，负载电流的无功电流iq转变为直流无功分量Q和2倍频无功、有功分量q(2wt)和
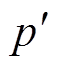(2wt)以及h±1次的谐波分量
。将式（13）、式（14）得到的结果通过低通滤波器，滤除其中的交流分量得到直流量，再将取得的直流分量乘以2得到有功电流的幅值Ip和无功电流的幅值Iq。将检测到的无功电流幅值与cos(wt)相乘得到无功电流，同理可得有功电流。根据式（12），得到谐波电流ih=iL-ip-iq。
谐波电流与检测得到的无功电流的和是并联侧变换器所需补偿电流ic的一部分给定，与计算得出的保持直流电压稳定的损耗有功电流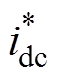
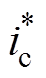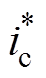相加可得补偿电流给定，即=iL-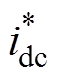。当负载不需要补偿无功电流时，闭合图6所示的无功电流分量iq，即
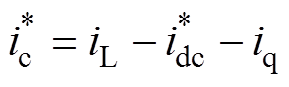（15） 综上所述，本文提出的抑制直流纹波影响控制策略如图6所示。通过陷波器阻止电压纹波进入电压外环控制器，同时特征次谐波补偿的电流内环控制策略进一步抑制直流电压纹波对补偿电流的影响。
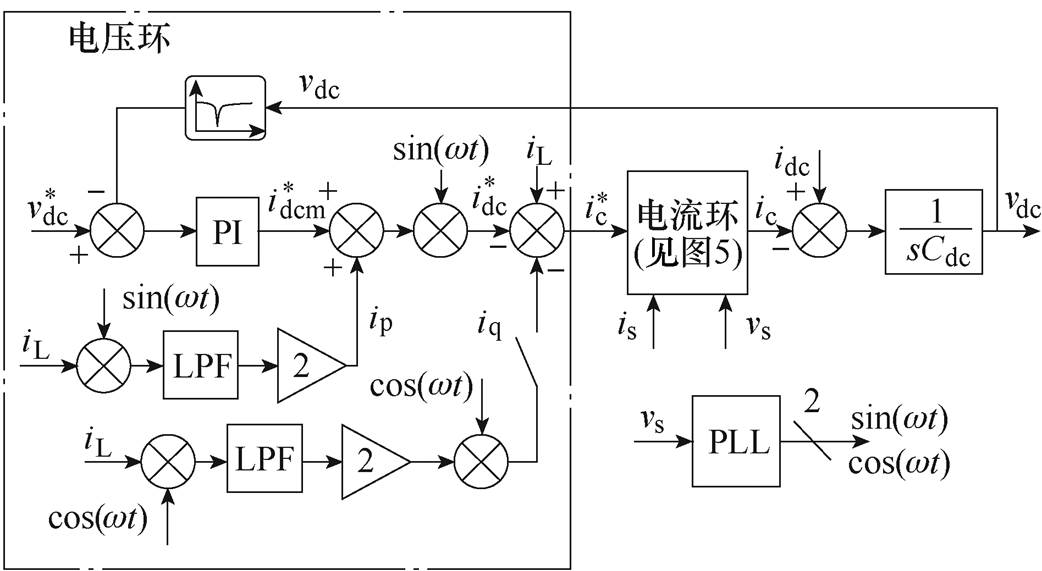
图6 抑制直流纹波影响控制策略
Fig.6 The proposed control strategy for suppressing DC-link voltage ripple influence
为了验证本文所提控制策略抑制单相UPQC低频电压纹波影响补偿电流的有效性，在Matlab/ Simulink软件中根据图1和表1搭建仿真模型，在谐波源负载条件下，测试了不同算法对网侧电流以及直流侧电容对补偿效果的影响。根据电力薄膜电容厂家推荐指导，纹波系数一般小于0.28，在实验系统留有裕度的前提下取纹波系数0.15，因此根据式（4）和式（5）取直流电容为70mF。
在不引入新的电压电流谐波，同时满足单相UPQC能量流动的要求下，串联侧控制为电压源，谐波源采用不控整流代替，参数见表1，其中，25W 电阻与2.2mF电容串联后再与25W 电阻并联。
表1 单相UPQC实验参数
Tab.1 The parameters of single-phase UPQC
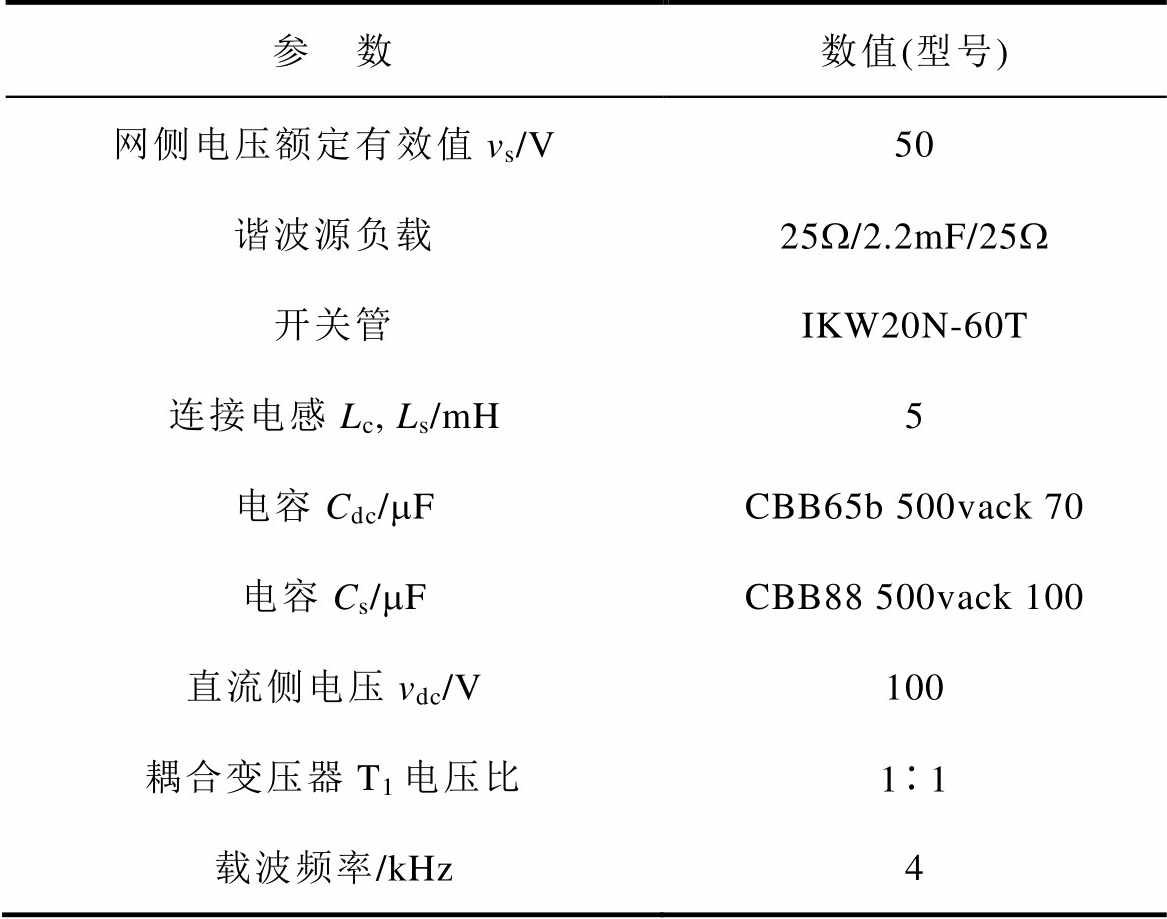
参 数数值(型号) 网侧电压额定有效值vs/V50 谐波源负载25W/2.2mF/25W 开关管IKW20N-60T 连接电感Lc, Ls/mH5 电容Cdc/mFCBB65b 500vack 70 电容Cs/mFCBB88 500vack 100 直流侧电压vdc/V100 耦合变压器T1电压比11 载波频率/kHz4
直流侧电容70mF时不同控制方法下网侧电流THD如图7所示。其中四种不同的控制方法为：传统瞬态电流控制（方法a）；在电压环加入陷波器控制（方法b）；本文方法只补偿3次谐波（方法c）；本文方法补偿3次和5次谐波（方法d）。由图7可知，单相UPQC并联侧采用传统的瞬态电流控制（方法a）时，网侧电流畸变严重，THD为10.2%；在电压外环加入陷波器（方法b）可以抑制纹波电压对补偿电流的影响，网侧电流THD降低至7.49%，电压外环引入陷波器并不能显著降低网侧电流谐波含量；当通过扰动前馈补偿（方法c）后，网侧电流3次谐波含量从6.1%降低至0.5%，THD降低至5.67%；为了进一步抑制网侧电流畸变，在电流内环引入5次扰动前馈（方法d），5次及7次谐波含量分别从3.62%、3.53%降低至0.25%和0.08%，抑制效果明显。
由1.2节分析，直流侧电压的波动会影响并联侧变换器的补偿效果。为了对比直流侧不同电容条件下传统控制方法和所提算法对网侧电流畸变的影响，在不同电容下进行仿真，具体结果如图8所示，在不同电容下，所提算法明显可以降低网侧电流THD。在500mF电容时，传统控制方法下网侧电流THD为2.8%，采用本文所提控制方法后，直流侧电容为70mF时，网侧电流THD为2.4%，在达到相同补偿效果条件下，可以大约减少85%直流母线电容。
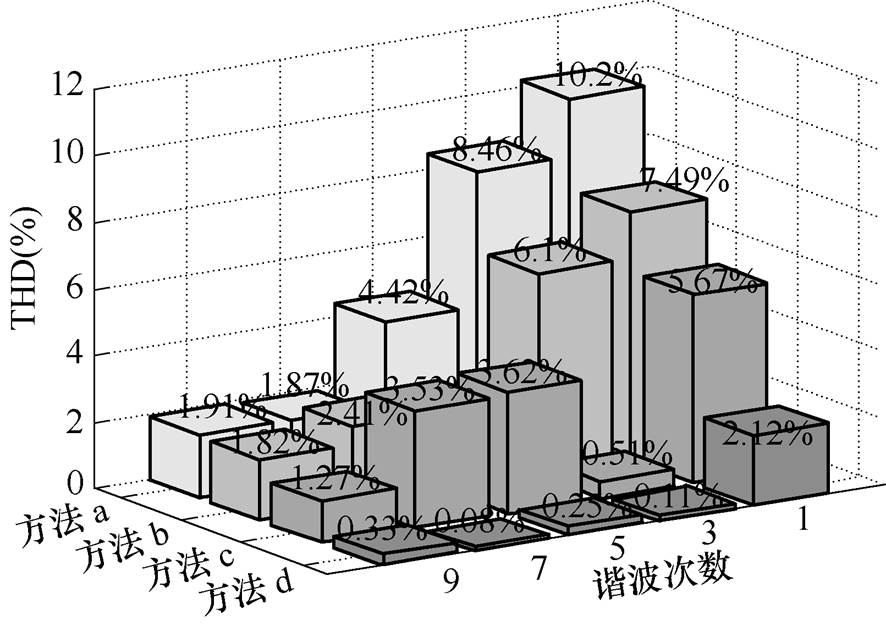
图7 直流侧电容70mF时不同控制方法下网侧电流THD
Fig.7 Gride current THD under different control startegies with 70mF DC-link capacitor
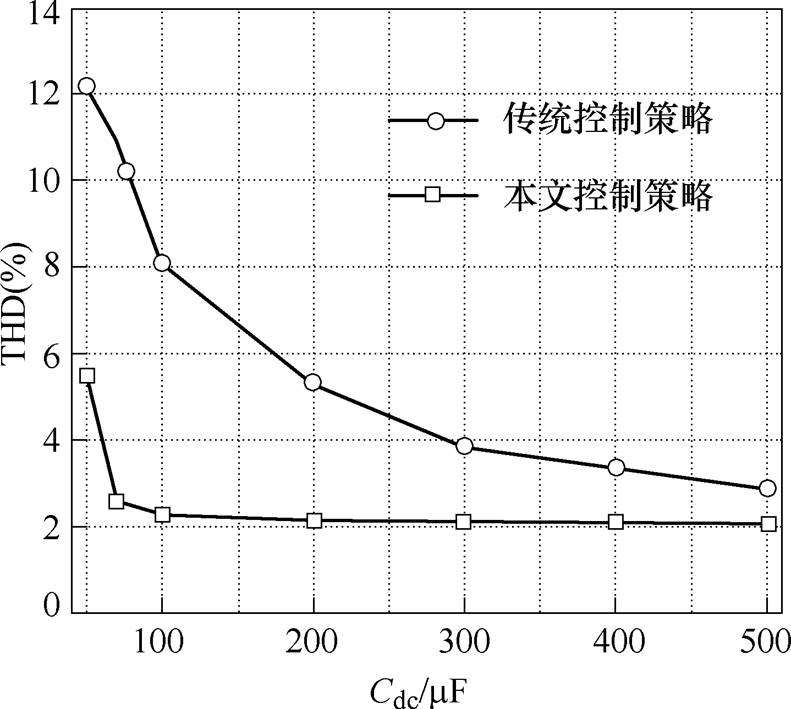
图8 两种算法下不同电容时的网侧电流THD
Fig.8 Grid current THD with different capacitances under two control strategies
参照图1中的结构和表1中的参数搭建单相两电平全桥UPQC实验平台。为验证本文所提出的抑制直流纹波影响的并联侧变换器控制方法，串联侧和谐波源与仿真保持一致。对比测试了不同电容条件下两种控制方法对并联侧电流的补偿效果。
动态测试结果如图9所示，变换器开始处于空载整流状态，切入不控整流负载后，负载电流发生突变，经过谐波检测模块和控制器的调节后，并联侧变换器输出补偿电流。约80ms后可以看到变换器输出补偿电流正常，网侧电流得到有效补偿。由空载到投入负载，引起直流侧电压跌落约为40V，超调约为20V。网侧电压暂降时UPQC补偿电压电流实验波形如图10所示。从图10可以看出，串联侧变换器网侧电压有效值为40V时，负载电压有效值维持在50V。为了进一步验证并联侧变换器控制策略不影响串联侧补偿效果，网侧电压有效值从40V突降为20V，负载电压跌落约为10V，350ms后恢复到正常。网侧电压跌落或欠电压时，负载电压几乎不变，始终维持在给定值，也就是本文所提控制策略不会对串联侧补偿产生影响。
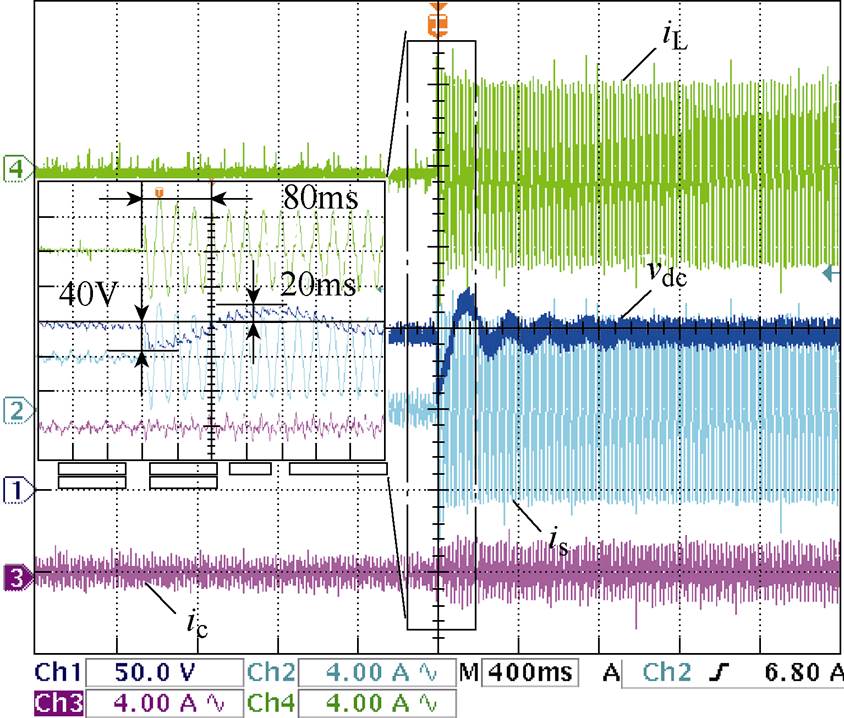
图9 负载投入后系统动态响应实验波形
Fig.9 Experimental waveforms of system dynamic response when load changes
图10 网侧电压暂降时UPQC补偿电压电流实验波形
Fig.10 Waveforms of UPQC compensation voltage and current when grid voltage sag
为了验证在直流电压波动的条件下并联侧对网侧电流补偿的效果，直流侧电容取为70mF，此时直流纹波较大，负载电流THD=22.7%。
采用传统控制策略时网侧电流的补偿效果如图11所示，在直流纹波的影响下补偿电流畸变，补偿后的网侧电流THD=10.5%。在电压外环加入陷波器后实验结果如图12所示，相对于传统控制策略，电压环加入陷波器能够将电网电流THD降低至7.7%，但是仍不能够满足工业要求。
从图11和图12的实验结果可以看出，传统控制策略以及电压环引入陷波器的控制策略在电压纹波显著时，并不能有效抑制对网侧电流的影响，因此，有必要进一步对控制策略进行优化。采用本文所提的电压外环引入陷波器并在电流内环引入特征次谐波电流补偿后，网侧电流THD降低到2.7%，如图13所示。可以看出，在小电容条件下，本文所提控制方法能够有效抑制直流纹波对并联侧变换器输出的影响，且输入功率因数较高。
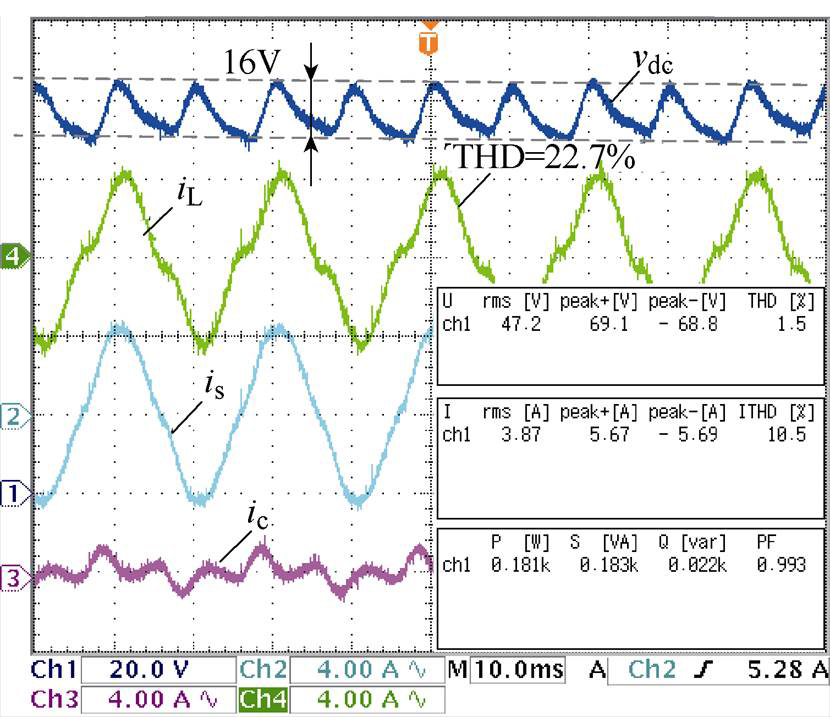
图11 传统控制策略下并联侧变换器稳态波形
Fig.11 Waveforms of parallel converter with the traditional control strategy
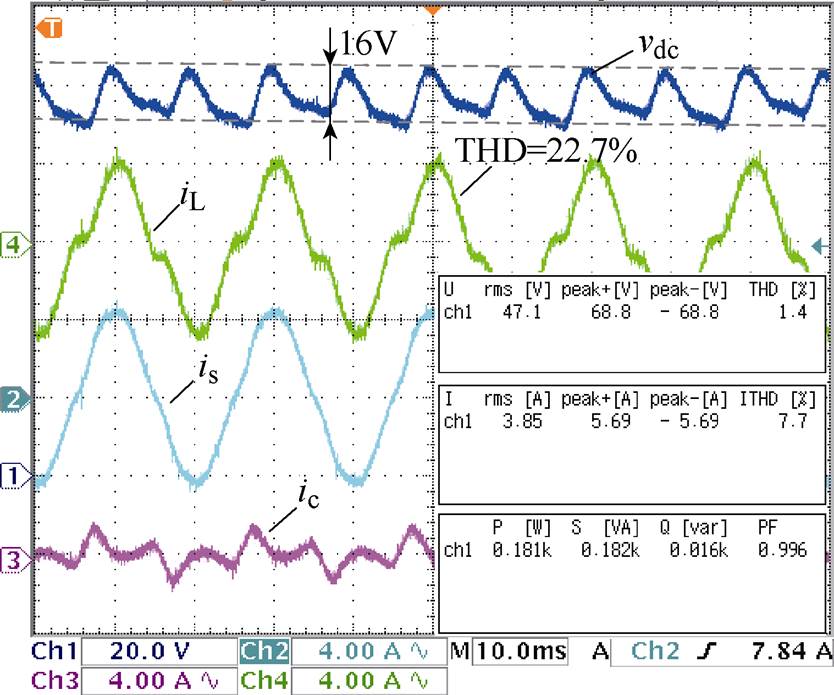
图12 电压环含有陷波器的并联侧变换器波形
Fig.12 Waveforms of parallel converter with notch filter in the voltage loop
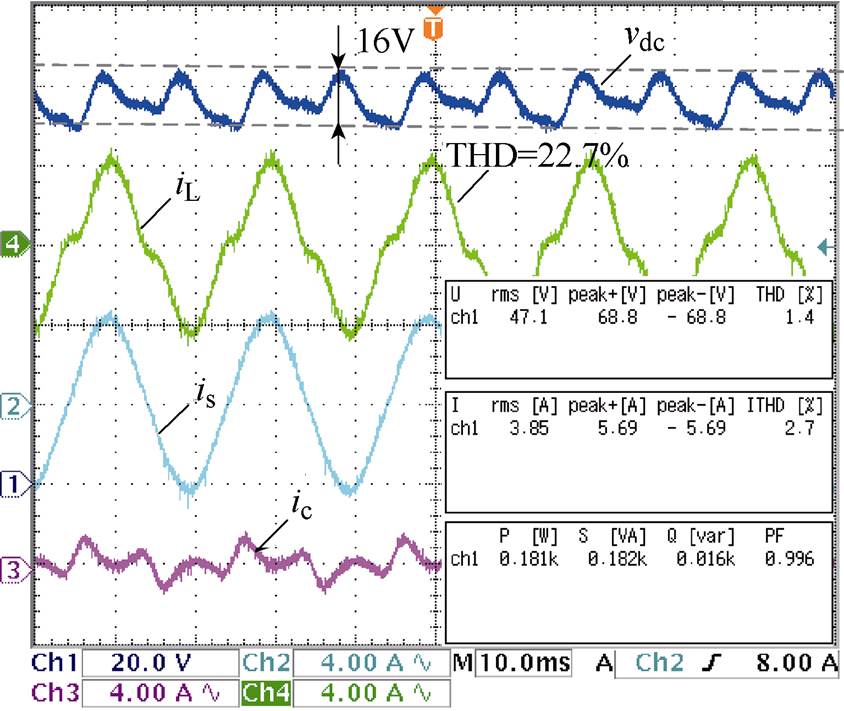
图13 所提控制策略下并联侧变换器系统稳态波形
Fig.13 Waveforms of parallel converter with the proposed control strategy
综合图11～图13实验结果可以得出，在减小单相UPQC支撑电容情况下，本文所提算法能够显著抑制低频纹波对变换器补偿电流的影响。
本文分析了单相UPQC并联侧变换器直流纹波产生的原因及其对并联侧变换器造成的影响。提出在电压外环引入陷波器的基础上，通过电流内环引入网侧电流特征次谐波补偿策略抑制直流脉动电压对补偿电流的影响。其中，电压外环的陷波器可以抑制直流脉动电压进入电压环，电流内环的特征次谐波补偿引入的奇次谐波可以抵消直流侧偶次纹波对补偿电流产生的奇次影响。仿真和实验结果表明：
1）相比于传统控制以及电压环加入陷波器的策略，本文提出的电压外环陷波器结合电流内环特征次谐波补偿的控制策略可有效降低网侧电流THD。
2）直流电容取值较小，直流电压波动明显时，相比传统方法，本文所提算法将显著降低网侧电流THD，且可以获得与大电容条件下的传统控制策略相同的补偿效果。
因此，本文所提控制策略在减小单相变换器直流母线电容上具有明显的优势。
参考文献
[1] 杨用春, 肖湘宁, 郭世枭, 等. 基于模块化多电平变流器的统一电能质量调节器工程实验装置研究[J]. 电工技术学报, 2018, 33(16): 3743-3755.
Yang Yongchun, Xiao Xiangning, Guo Shixiao, et al. Research of unified power quality conditioner engineering experiment device based on modular multilevel converter[J]. Transactions of China Elec- trotechnical Society, 2018, 33(16): 3743-3755.
[2] 慕小斌, 王久和, 孙凯, 等. 统一电能质量调节器串联变流器多频级联无源控制研究[J]. 中国电机工程学报, 2017, 37(16): 4769-4779.
Mu Xiaobin, Wang Jiuhe, Sun Kai, et al. Study on multi-frequency cascade passivity-based control for the series converter of unified power quality con- ditioner[J]. Proceedings of the CSEE, 2017, 37(16): 4769-4779.
[3] 王浩, 刘进军, 梅桂华. 一种串联侧三相解耦型统一电能质量控制器[J]. 电工技术学报, 2016, 31(2): 215-220.
Wang Hao, Liu Jinjun, Mei Guihua. A unified power quality conditioner with three-phase decoupling in series section[J]. Transactions of China Electro- technical Society, 2016, 31(2): 215-220.
[4] 陆晶晶, 肖湘宁, 张剑, 等. 基于定有功电流限值控制的MMC型UPQC协调控制方法[J]. 电工技术学报, 2015, 30(3): 196-204.
Lu Jingjing, Xiao Xiangning, Zhang Jian, et al. MMC-UPQC coordinated control method based on fixed active current limit value control[J]. Transa- ctions of China Electrotechnical Society, 2015, 30(3): 196-204.
[5] Krishnamoorthy H, Daniel M, Ramos-Ruiz J, et al. Isolated AC-DC converter using medium frequency transformer for off-shore wind turbine DC collection grid[J]. IEEE Transactions on Industrial Electronics, 2017, 64(11): 8939-8947.
[6] 于传, 徐修华, 王书征. 基波和谐波下的UPQC功率流动分析[J]. 电气技术, 2017, 18(9): 24-28, 34.
Yu Chuan, Xu Xiuhua, Wang Shuzheng. Analysis of UPQC power flow under fundamental and harmonic condition[J]. Electrical Engineering, 2017, 18(9): 24-28, 34.
[7] 殷晓东, 罗登, 李祖勇, 等. 一种双向隔离DC-DC变换器二次纹波电压抑制方法[J]. 电工技术学报, 2018, 33(6): 1356-1363.
Yin Xiaodong, Luo Deng, Li Zuyong, et al. A second-order ripple voltage suppression algorithm of bidirectional isolation DC-DC converter[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(6): 1356-1363.
[8] Su Mei, Pan Pan, Long Xi, et al. An active power-decoupling method for single-phase AC-DC converters[J]. IEEE Transactions on Industrial Informatics, 2014, 10(1): 461-468.
[9] Cai Yaping, Xu Jianping, Ping Yang, et al. Evalu- ation and suppression of a low-frequency output voltage ripple of a single-stage AC-DC converter based on an output impedance model[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4): 2803-2813.
[10] 李凯, 赵争鸣, 袁立强, 等. 基于能量平衡的降低模块化多电平变换器子模块电容电压波动控制策略[J]. 电工技术学报, 2017, 32(14): 17-26.
Li Kai, Zhao Zhengming, Yuan Liqiang, et al. Control strategy based on the energy balance for reducing sub-module capacitor voltage fluctuation of modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2017, 32(14): 17-26.
[11] 谭智力, 朱冬姣, 陈坚. 三相四线UPQC直流侧电容电压波动机理及抑制方法[J]. 电力系统自动化, 2010, 34(7): 61-65, 74.
Tan Zhili, Zhu Dongjiao, Chen Jian. DC side capacitor voltage fluctuation reason and inhibition method for three-phase four-wire UPQC[J]. Automation of Electric Power Systems, 2010, 34(7): 61-65, 74.
[12] 苟斌, 冯晓云, 宋文胜, 等. 牵引变流器-电机拍频现象及其抑制方法[J]. 中国电机工程学报, 2013, 33(9): 55-63.
Gou Bin, Feng Xiaoyun, Song Wensheng, et al. Analysis and suppression of beat phenomenon for railway traction converters and motors[J]. Pro- ceedings of the CSEE, 2013, 33(9): 55-63.
[13] Liu Yunting, Wang Xiaorui, Fang Zhengpeng. An H-bridge-based single-phase VAR generator with minimum DC capacitance[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(4): 2001-2014.
[14] Freitas I S de, Jacobina C B, Cipriano dos Santos E. Single-phase to single-phase full-bridge converter operating with reduced AC power in the DC-link capacitor[J]. IEEE Transactions on Power Electronics, 2010, 25(2): 272-279.
[15] Yang Yongheng, Zhou Keliang, Wang Huai, et al. Analysis and mitigation of dead-time harmonics in the single-phase full-bridge PWM converter with repetitive controllers[J]. IEEE Transactions on Indu- stry Applications, 2018, 54(5): 5343-5354.
[16] Alam K S, Xiao Dan, Zhang Daming, et al. Single- phase multicell AC-DC converter with optimized controller and passive filter parameters[J]. IEEE Transactions on Industrial Electronics, 2019, 66(1): 297-306.
[17] Devassy S, Singh B. Control of solar photovoltaic integrated UPQC operating in polluted utility conditions[J]. IET Power Electronics, 2017, 10(12): 1413-1421.
[18] Devassy S, Singh B. Design and performance analysis of three-phase solar PV integrated UPQC[J]. IEEE Transactions on Industry Applications, 2018, 54(1): 73-81.
[19] Liu Yonglu, Sun Yao, Su Mei. Active power com- pensation method for single-phase current source rectifier without extra active switches[J]. IET Power Electronics, 2016, 9(8): 1719-1726.
[20] Li Sinan, Qi Wenlong, Tan S C, et al. Enhanced automatic-power-decoupling control method for single-phase AC-to-DC converters[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(2): 1816-1828.
[21] She Xu, Huang A Q, Wang Gangyao. 3-D space modulation with voltage balancing capability for a cascaded seven-level converter in a solid-state trans- former[J]. IEEE Transactions on Power Electronics, 2011, 26(12): 3778-3789.
[22] Qin Hengsi, Kimball J W. Closed-loop control of DC-DC dual-active-bridge converters driving single- phase inverters[J]. IEEE Transactions on Power Electronics, 2014, 29(2): 1006-1017.
[23] Liu Yonglu, Sun Yao, Su Mei. A control method for bridgeless Cuk/Sepic PFC rectifier to achieve power decoupling[J]. IEEE Transactions on Industrial Electronics, 2017, 64(9): 7272-7276.
[24] Song Kejian, Konstantinou G, Li Jing, et al. High performance control strategy for single-phase three- level neutral-point-clamped traction four-quadrant converters[J]. IET Power Electronics, 2017, 10(8): 884-893.
Control Strategy for Single-Phase Unified Power Quality Conditioner of Parallel Converter Based on Specific Order Harmonics Compensation
Abstract There is a pulsating power difference between the parallel and series converter of the single-phase unified power quality conditioner (UPQC). The pulsating power generates low-frequency voltage ripple on the dc-link capacitor and affects the compensation performance of the UPQC. This paper analyzes the reasons for the low-frequency voltage ripple of the dc-link and its influence on the compensation performance. In order to suppress the influence on the compensation current, a notch filter is added to the outer voltage loop to reduce the voltage ripple and the harmonic reference current is generated. The specific order harmonic current compensation of the grid is introduced into the inner current loop to further suppress the influence on the modulation signal. Simulation and experiment verify the low-frequency ripple analysis. The proposed control strategy is feasible and effective.
keywords：Single-phase unified power quality conditioner (UPQC), low-frequency voltage ripple, voltage ripple influence suppress， specific order harmonics compensation
DOI: 10.19595/j.cnki.1000-6753.tces.191397
中图分类号：TM714.2
孟令辉 男，1992年生，博士研究生，研究方向为电力电子变换器控制与调制策略。E-mail: mlh_menglinghui@163.com
舒泽亮 男，1979年生，教授，博士生导师，主要研究电力电子技术及应用，包括多电平变换装置、电力电子变压器、同相供电系统及电力电子应用中的数字信号处理技术等。E-mail: shuzeliang@swjtu.edu.cn（通信作者）
收稿日期 2019-10-23
改稿日期 2020-03-16
国家轨道交通电气化与自动化工程技术研究中心（NEEC-2019-A04）和四川省科技厅重点研发（2018GZ0066）资助项目。
（编辑 崔文静）