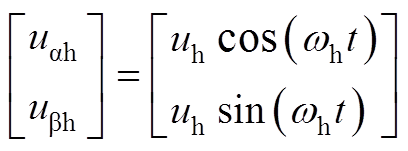（1）
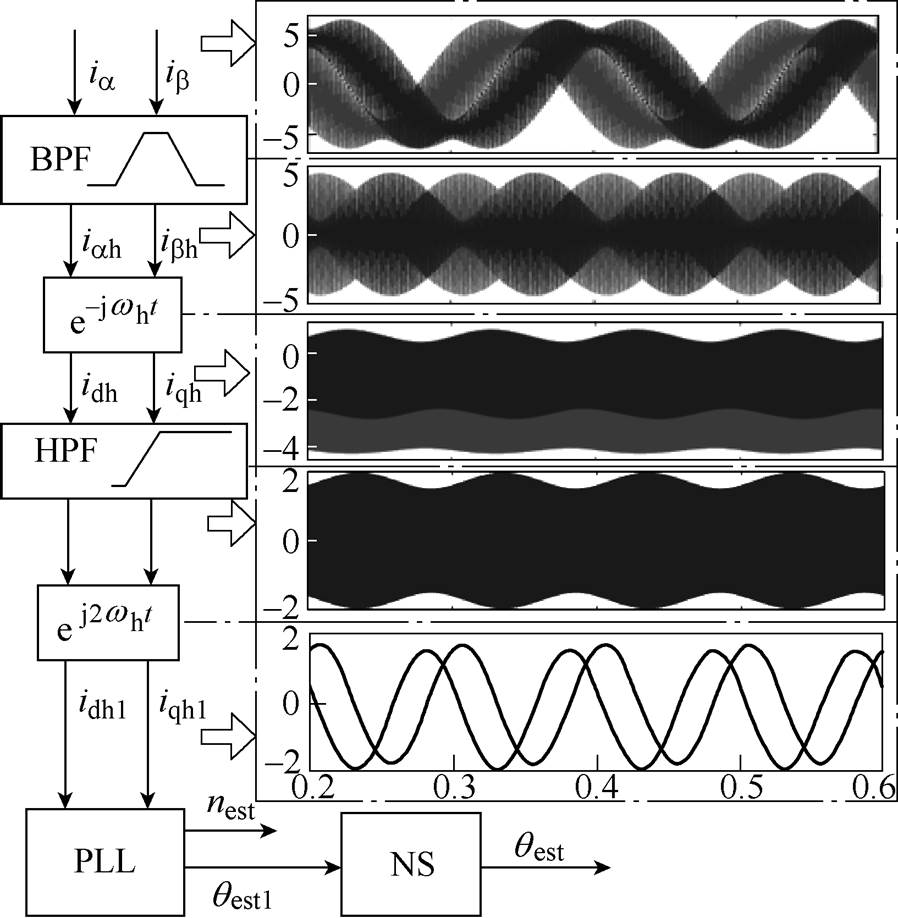
图1 高频响应信号解调原理
Fig.1 Demodulation diagram of high frequency response signal
摘要 旋转高频注入法能够估算永磁同步电机零速和低速下的转子磁极位置，但在转子磁极位置解调过程中使用滤波器会带来估算误差。该文提出一种利用正序电流分量对转子估算误差进行在线补偿的方法，阐述了该方法在电机零速、低速运行过程中的补偿机理，理论推导在解调过程中正序电流和负序电流相位变化的关系，分析在考虑定子电阻影响时利用正序电流对滤波器导致误差的补偿效果。针对外差法求得的误差补偿量和转子位置存在多个收敛点的问题进行改进，增加收敛点检测环节，可排除部分错误收敛点。仿真和实验验证了所提方法对于转子位置误差补偿的效果。
关键词：旋转高频注入法 转子位置估算误差 正序电流分量 在线误差补偿
永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）的高精度控制需要电机实时转子位置，为了解决旋转变压器和光电编码器等传统位置传感器在成本和可靠性方面的问题，以及适应一些不便于安装位置传感器的应用场合，永磁同步电机无位置传感器控制得到了广泛研究。而零速和低速时电机反电动势低，采用基于反电动势的观测器方法难以准确估算转子位置，所以通常采用高频注入法。高频注入法是给电机施加频率介于电机基波频率和开关频率的合适高频电压，利用电机的凸极效应来检测转子位置。高频注入法不依赖电机参数，能很好地解决零速和低速下的转子位置估计问题。
高频注入法通常分为旋转高频注入[1-2]和脉振高频注入[3]。旋转高频注入法主要用于凸极率较大的内埋式永磁同步电机，而脉振高频注入法适用于凸极率很小甚至是表贴式电机。但旋转高频注入法易于工程实现[4]，得到了广泛研究。
传统高频注入法对电机高频模型进行了简化，且转子位置解调过程中用到带通滤波器（Band Pass Filter, BPF）和高通滤波器（High Pass Filter, HPF），都会带来估算误差。电机零转速时滤波器对转子位置估算误差影响不明显，但随着电机转速升高，负序电流频率偏离带通中心频率越远，带通滤波器导致的误差越大。为了进一步提升高频注入法检测精度，目前对高频注入法的研究集中到转子估算位置的误差分析和补偿方法上。
文献[5]分析了电机运行时参数变化导致的脉振高频注入法估算转子位置误差，总结出控制器频率、逆变器直流母线电压及脉振高频信号电压幅值对转子位置估算误差的影响规律。而文献[6]则分析交叉饱和、采样量化误差以及滤波器相位延时和多重凸极效应等带来的转子位置估算误差，总结了通过优化控制算法和电机本体设计减小误差的措施。刘兵等利用全通滤波器构成自适应滤波器来提取高频分量，并消除脉振高频注入法因为电机参数不对称及检测电流误差等导致的位置检测误差[7]。吕晓源等在传统脉振高频注入法的基础上加入虚拟高频旋转坐标解决传统脉振高频注入法的过零点问题[8]。
文献[9]针对传统高频旋转注入法带通滤波器和带阻滤波器会带来相位延时导致估算误差这一问题，在多个高频同步旋转坐标系下，利用高通滤波器提取各个高频同步旋转坐标系下的有用高频分量并滤掉无用的低频分量，从而取代带通滤波器和带阻滤波器。文献[10]用全通滤波器代替带通滤波器和低通滤波器，从而减小相位延时带来的误差。采用正交方波注入法代替旋转高频波注入，可以减小滤波器带来的误差[11]。文献[12]研究了注入旋转电压的频率、幅值等对电机无位置传感器矢量控制性能的影响。S. Kim等通过把注入电压的频率提高到开关频率来改善电机无位置控制的动态响应特性并降低噪声[13-15]。但在逆变器开关频率较高时，电流的准确检测较为困难。
刘景林等通过对高频电流正、负序分量的相位差进行最小二乘估计，来提高转子初始位置的准确 度[16]。杨键、李浩源等提出了利用正序电流的偏差量来补偿转子初始位置估算误差[17-18]的思想，但尚未对正序电流补偿初始位置的原理以及适用条件进行深入研究。尤其是在电机运行过程中，带通滤波器对高频响应电流相位延时作用受转速变化影响明显，电机运行过程中的补偿更为复杂。
除上述新方法外，目前常用的方法是先算出简化模型和滤波器的误差，再通过查表补偿。这种补偿前期工作量大，在电机状态发生改变后精确度难以保证。
除了滤波器带来的误差外，简化高频模型、数字控制延时以及电力电子器件的非线性[19]等，都会对估算结果带来影响。
本文提出一种能在电机不同运行状态时，利用负序电流分量估算转子位置，通过正序电流在线补偿位置误差的方法，并对滤波器和忽略定子绕组导致的误差进行了在线补偿及分析，最后，搭建永磁同步电机矢量控制仿真模型进行仿真与实验验证。
旋转高频注入法是在ab 坐标系下，给永磁同步电机注入一个频率远高于电机基波频率但低于开关频率的旋转电压，通过带通滤波器、高通滤波器以及坐标变换对含有转子位置信息的负序分量进行解调，得到转子位置。高频响应信号解调原理如图1所示。
假设在ab 坐标系下注入的高频电压为
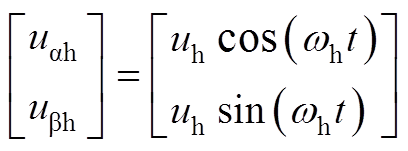（1）
图1 高频响应信号解调原理
Fig.1 Demodulation diagram of high frequency response signal
式中，wh为注入高频电压的角速度；uh为注入高频电压幅值。在低速条件下通常将电机看作纯电感模型并忽略交直轴的耦合量，简化后ab坐标系下的高频模型为
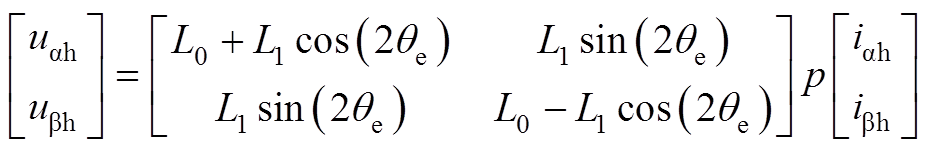（2）其中
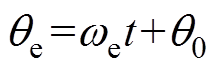
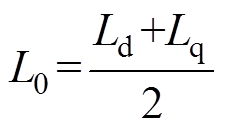
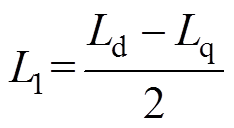
式中，iah、ibh为ab 坐标系下高频响应电流；p为微分算子；we为基波电角速度；qe为电机转子位置；q0为电机初始位置；Ld、Lq分别为d、q轴电感。
采样电流通过带通、高通滤波和同步轴系滤波后得到电流为
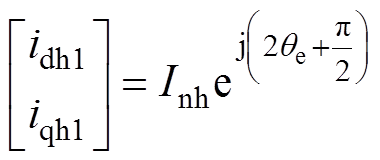（3）式中，Inh为负序高频响应电流幅值。idh1、iqh1通过锁相环和转子磁极判断可以得到估算的转速nest和转子位置qest。而极性判断通常在电机静止时进行，且已有较多方法[8, 17]，这里不做详细介绍。
简化后的高频电流响应模型忽略了交叉耦合和绕组电阻的影响，而高通滤波器和带通滤波器也会对电流相位有所影响，这都会导致估算的转子位置出现误差。
为了实时补偿转子误差，提出一种基于正序分量在线转子估算位置补偿的方法，对现有的旋转高频注入法进行改进，改进后转子位置估算方法如图2所示。
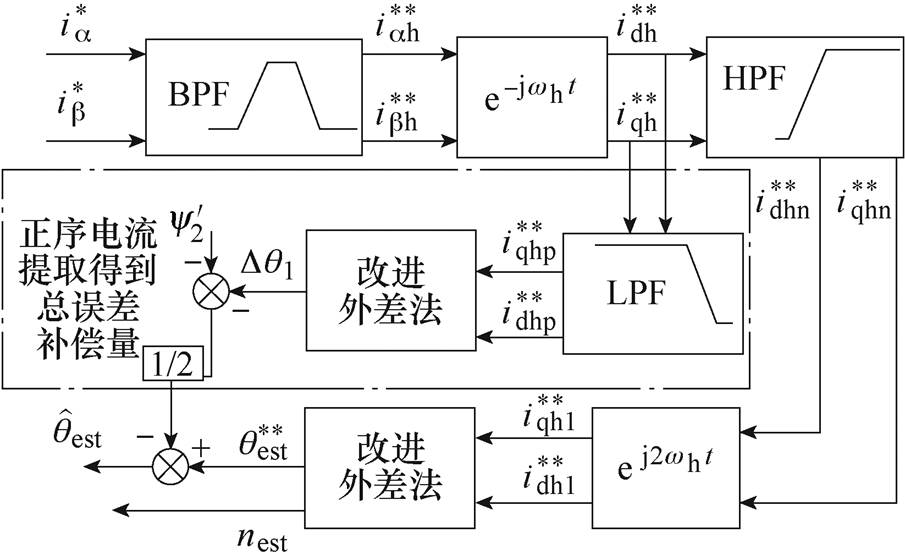
图2 改进后的转子位置估算方法
Fig.2 The improved rotor position estimation method
基波旋转坐标系下忽略交直轴的耦合，考虑定子电阻的影响，将电机看成电感加电阻模型。电机的高频激励模型可写为
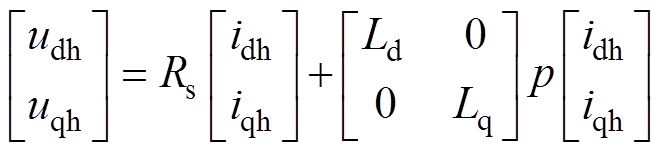（4）式中，Rs为电机定子相绕组电阻；idh、iqh为dq坐标系下高频响应电流。而在基波旋转坐标系下，注入的高频电压频率是wh-we，注入电压可写成
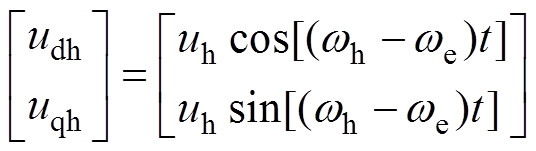（5）
将式（5）代入式（4）可以求得旋转坐标系下高频电流响应表达式为
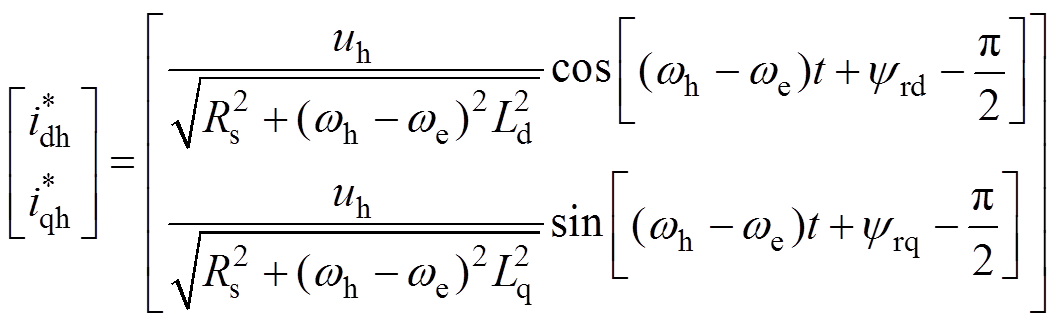（6）其中
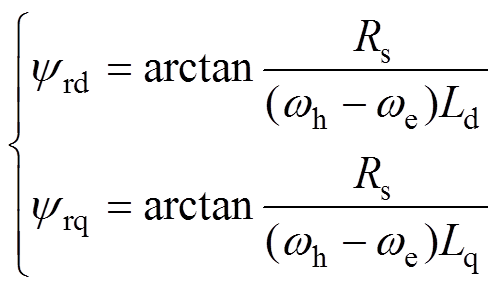
变换到静止坐标系下为
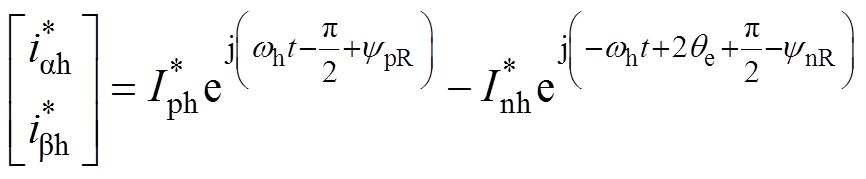（7）式中，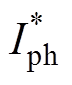
、
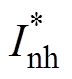分别为正序、负序高频响应电流幅值；ynR、ypR分别为忽略电阻导致的正、负序电流相位偏差。
在对高频电流信号解调过程中，需要用到滤波器。相比于电流采样和微处理器计算导致的延时，滤波器延时是解调过程误差的主要来源[20]。在电机处于稳态下，高频响应电流的正序分量角频率为wh，负序分量的角频率大小为wh-2we。假设使用的带通滤波器对于wh、wh-2we两个频率点处的幅值衰减为K0倍和K1倍，相位滞后分别为y0和y1，滤波器两个截止频率分别为Fc1、Fc2，则结合式（7）可知高频响应电流经过带通滤波器后变为
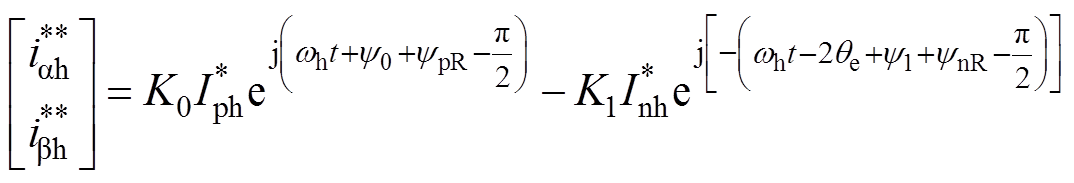（8）考虑定子电阻和滤波器影响，高频响应电流变换到角速度为wh的旋转坐标系下，可得电机正序分量为直流量，有
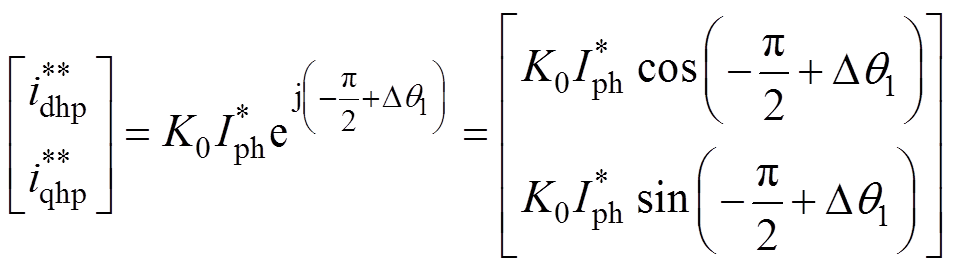（9）
其中
Dq1=y0+ypR
传统外差法会有多个收敛点，利用改进的外差法增加了收敛点检测，计算补偿量Dq1原理框图如图3所示。正序分量由于变成直流量，通过低通滤波器后相位不会发生改变，而幅值衰减为原来的K2倍。构造的sin(-p/2+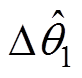
)和cos(-p/2+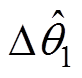)分别与正序直交轴电流相乘后作差得
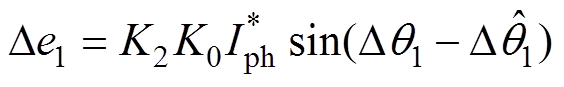（10）
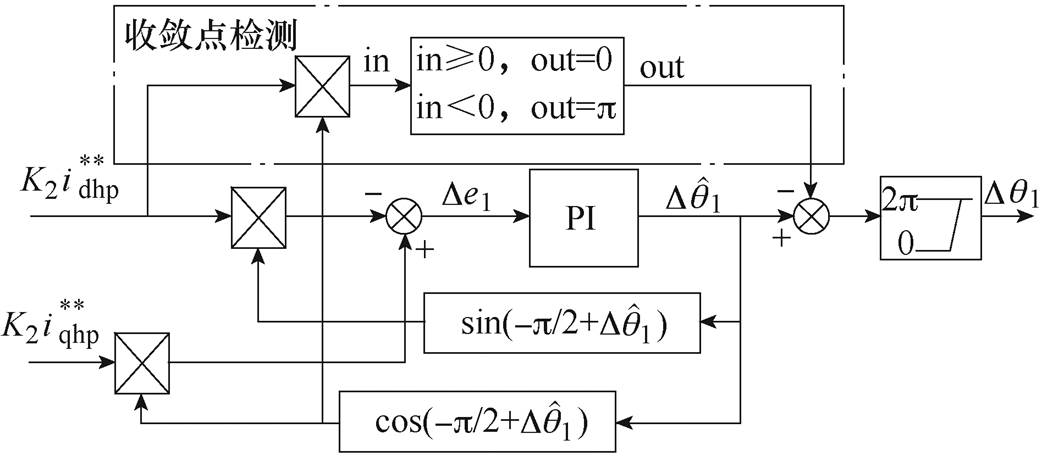
图3 改进的外差法提取误差补偿量
Fig.3 Improved heterodyne method for extracting error compensation
通过PI调节器使得De1为零，此时的收敛点可能为Dq1或Dq1+p。收敛点检测通过其输入的正负可以确定唯一的Dq1。若为正，说明收敛在Dq1；若为负，说明收敛在Dq1+p，对PI调节器的输出量减去p 可得到Dq1。电流的幅值仅仅起到标称作用，此过程中引入低通滤波器导致的正序电流幅值变化不会对检测产生影响。
通过高通滤波器滤除提取负序分量，高通滤波器对于角频率大小为2wh-2we的电流相位延迟为y2，幅值衰减为K3，再变换到-2wh角速度旋转坐标系下，得到2we角速度的低频交流量为
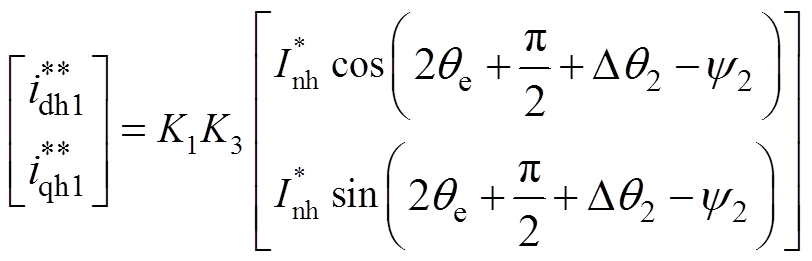（11）其中
Dq2=-y1-ynR
利用改进的外差法提取负序电流转子位置信息原理框图如图4所示。
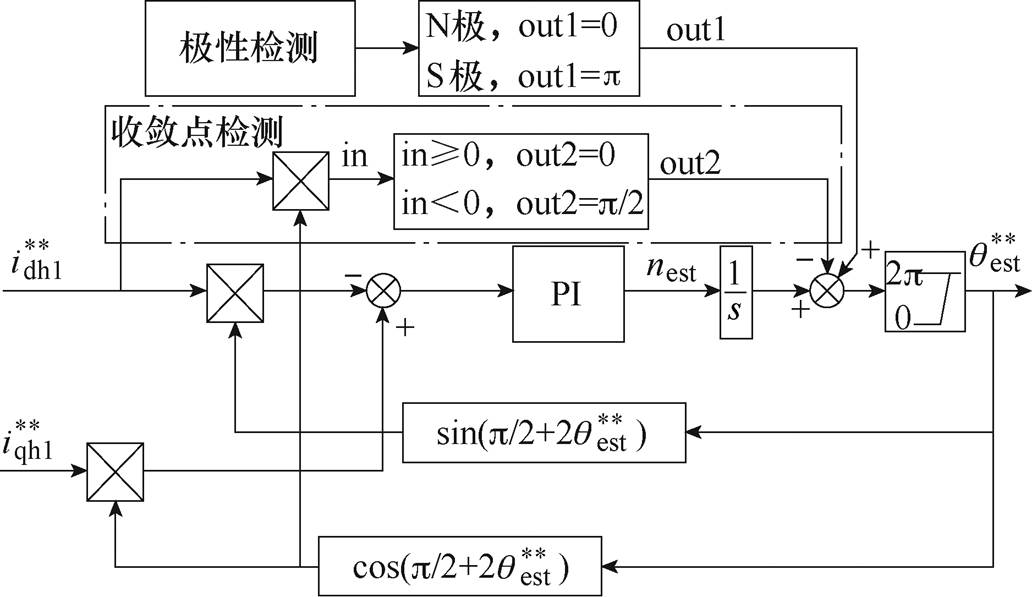
图4 改进的外差法提取转子位置
Fig.4 The improved heterodyne method for extracting rotor position
通过PI调节器的转速积分后得到转子磁极位置可能收敛在qest或qest+p/2或qest+p。通过初始位置极性检测[9]判别是否收敛在qest+p，通过收敛点检测确定是收敛在qest还是qest+p/2。
若不做补偿，求得的转子位置为
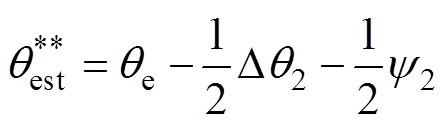
按照图2，利用正序分量求得的Dq1对由模型简化和忽略滤波器影响导致的转子位置进行补偿，用定量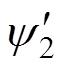
补偿高通滤波器后得到的转子位置为
（12）
带通滤波器是解调得到转子位置的关键环节，带通滤波器的幅频特性影响对高频响应电流的提取效果，决定了估算转子位置的抖动幅度甚至位置估算的成败。高频电流相对基波通常较小，而高频电流正负序电流幅值之比为Iph/Inh=(Ld+Lq)/(Lq-Ld)，包含转子位置信息的负序电流比正序电流小。要能检测到高频响应电流，则滤波器对高频响应电流的衰减要小，而对基频电流和开关频率电流的衰减应足够大，以保证解调过程不受干扰，否则会导致估算的转子位置出现明显波动。
但滤波器的幅频特性和相频特性往往无法兼顾，滤波器设计时过分追求幅频特性，又会导致相频特性变差，加大滤波器带来的相位延迟。带通滤波器相位延迟带来的估算转子误差为y1/2。
高频响应电流正序分量和负序分量的角频率大小分别为wh、wh-2we，但如果将滤波器的中心频率（截止频率中点）设置在wh-we处，以注入频率为500Hz、基波频率为5Hz、Fc1=475Hz、Fc2=515Hz为例，高通滤波器在角频率wh、wh-2we处的相位延迟关于中心频率处反向对称，如图5所示。
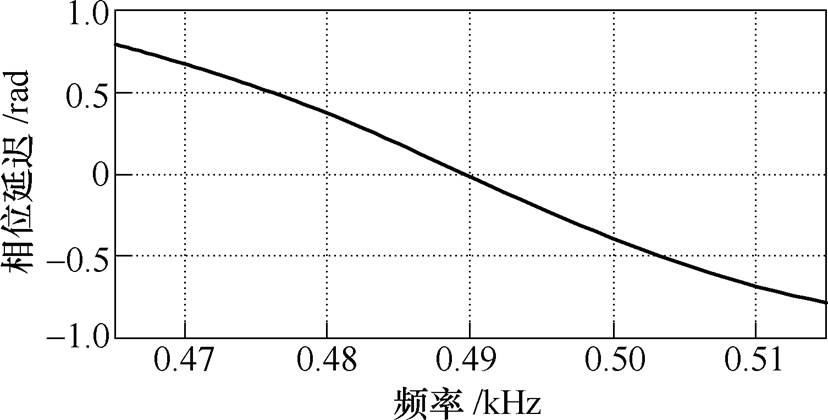
图5 带通滤波器相频特性局部图
Fig.5 Band-pass filter phase-frequency characteristic
故可以认为y1=-y0，采用所提补偿方法后由带通滤波器引起的误差接近于0。
电机转速改变时要实现上述效果，带通滤波器的中心频率要随转速进行调整。用xn、yn分别表示输入和输出状态量，二阶带通滤波器可离散化为
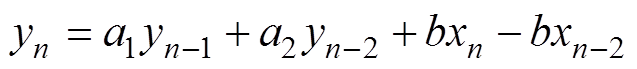（13）通过分析，拟合出系数a1、a2、b随带通滤波器中心频率变化的表达式。在电机实际运行过程中，根据估算的电角速度west确定带通滤波器中心频率，再结合拟合的表达式可以确定带通滤波器参数，保证带通滤波器中心频率为wh-west。
在对负序电流进行提取的过程中还用到了高通滤波器，高通滤波器对于角频率大小为2wh-2we的电流相位延迟为y2，而高通滤波器对于负序电流的相位延时在负序分量频率点附近基本不变。故可用固定值来补偿高通滤波器导致的误差。
考虑电机定子绕组作用时，参考文献[21]得到忽略电阻会导致的正、负序电流相位偏差为
（14）
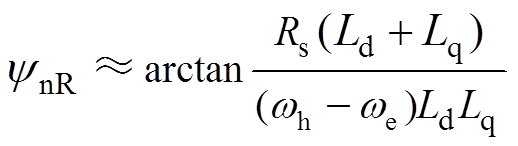（15）
用Dq1对由模型简化和忽略滤波器影响导致的转子位置进行补偿，由转子导致的位置误差变量为ypR/2+ynR/2，ypR和ynR均为正，这样补偿会导致忽略电阻引起的误差变大。
ypR和ynR均较小，可以认为
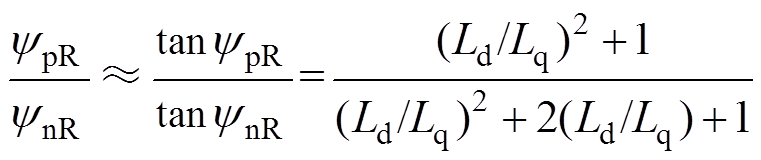（16）当Ld=Lq时，式（16）取最小，ypR≈ynR/2，而电机凸极率较高时，ypR≈ynR，所以ynR/2＜ypR＜ynR，所提补偿方法会导致由忽略电阻引起的误差增大50%～100%。但由于忽略电阻引起的误差远小于滤波器带来的误差，采用所提补偿方法仍能取得明显效果。
为了验证所提出的转子位置估算误差补偿法的正确性和有效性，搭建了一套永磁同步电机的矢量控制仿真模型，电机和变频器部分参数见表1。
表1 三相永磁同步电机控制平台参数
Tab.1 The parameters of three-phase PMSM drive systerm
参 数数 值 电机极对数4 电机额定转速/(r/min)1 000 电机额定电流/A4.5 转子交轴电感/mH16.46 直流母线电压/V330 注入电压频率/Hz500 电机额定功率/kW1 电机额定转矩/(N·m)9.5 电机额定电压/V220 转子直轴电感/mH7.92 开关频率/Hz10 000 注入电压幅值/V20
通过Matlab里面fdatool分析，电机基波频率为零时，截止频率为500Hz的一阶巴特沃斯高通滤波器导致的相位延迟量y2=0.46rad，而电机基波频率为25Hz时相位延迟量0.45rad，相差很小，说明电机运行在低速区间用固定值就能较好补偿高频滤波器引起的误差。
电机空载起动，指令转速分别为50r/min、150r/min时在0.6s处突加额定负载转矩，电机相电流波形、估算转速和补偿前后估算转子位置如图6和图7所示。从图6和图7可以看出，电机150r/min未补偿时误差比50r/min大，这是因为转速高时对应基波频率大，正、负序电流离带通滤波器中心频率远，滤波前后相位变化大，而高通滤波器对正、负序电流相位的偏移几乎为定值，故总体上，转速越高滤波器导致的相位误差会越大。在转速为50r/min和150r/min时，采用本文提出的方法补偿后估算的转子位置误差都得到了明显减小。补偿后转子位置误差在0.1rad以内，且电机在突加负载转矩时，该补偿方法仍能起到明显作用。
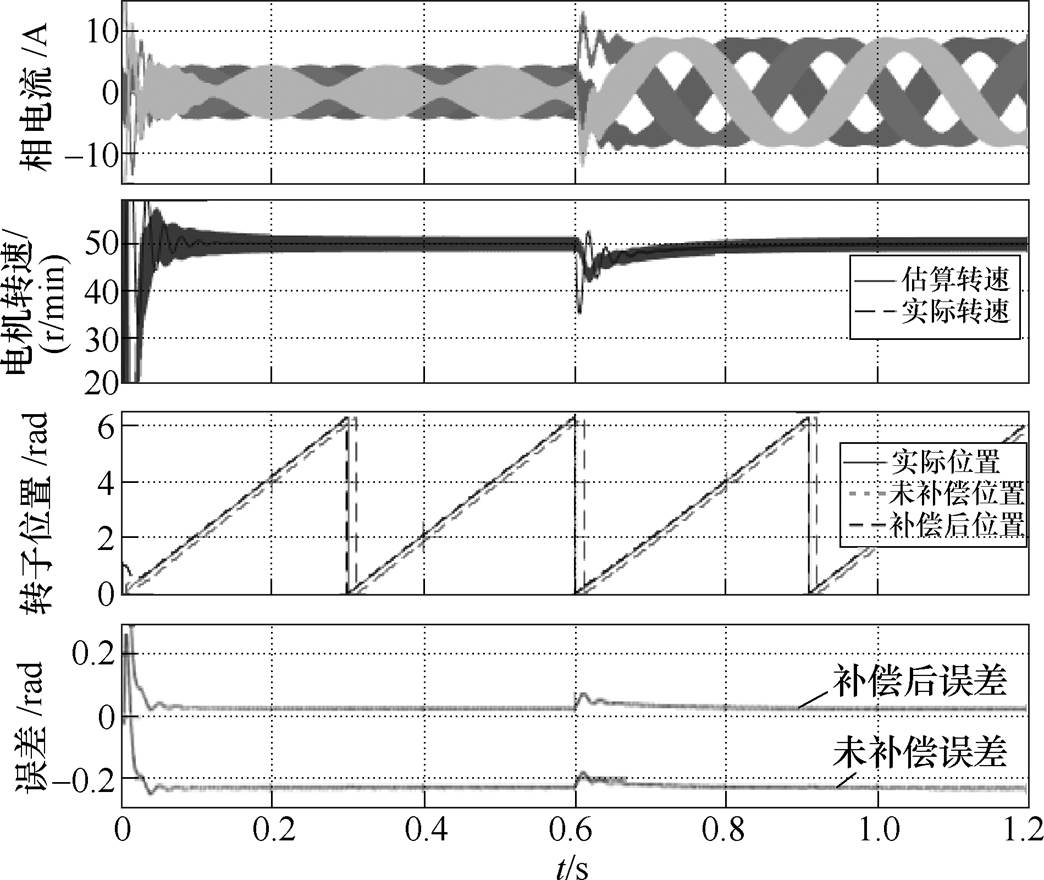
图6 转速50r/min突加负载仿真波形
Fig.6 Simulation waveforms at 50r/min with sudden load
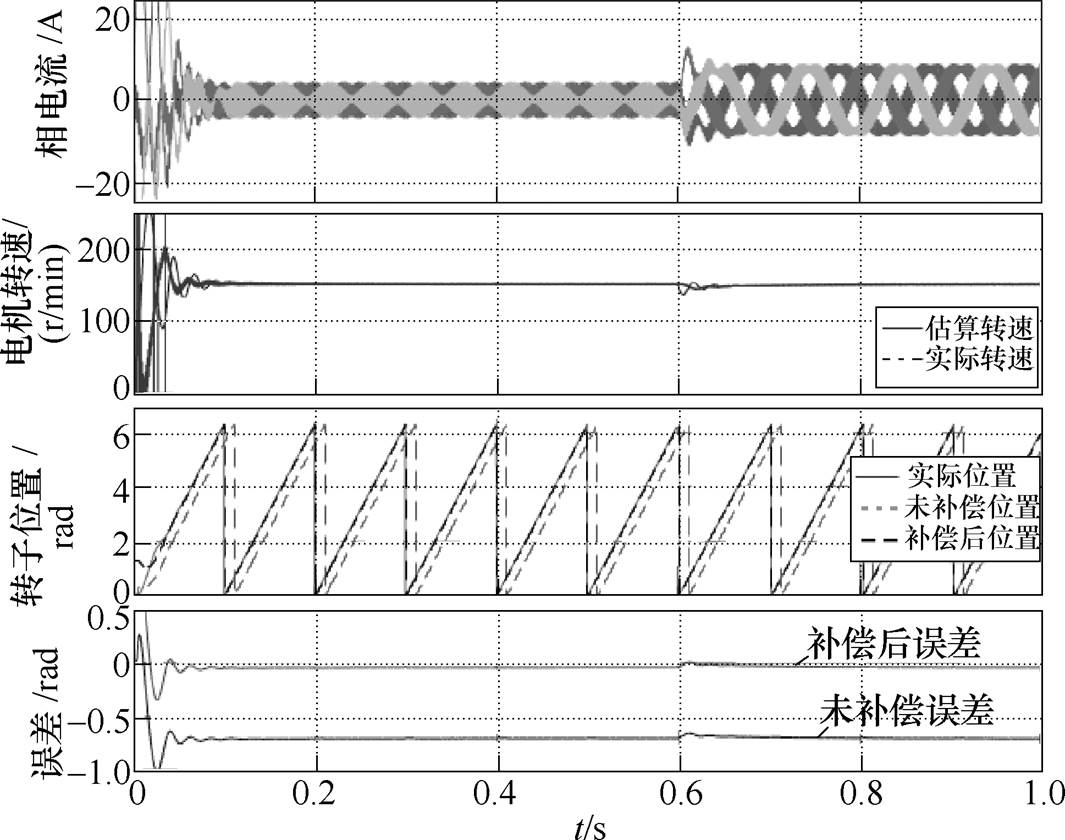
图7 转速150r/min突加负载仿真波形
Fig.7 Simulation waveforms at 150r/min with sudden load
为进一步验证所提出的方法，搭建了如图8所示的永磁同步电机对拖实验平台，两台永磁同步电机参数相同，永磁同步电机参数和变频器参数见 表1。DSP28335内部变量信息通过串口发送给计算机显示，电机转子位置以及补偿前后的转子位置等信息由3路DA转换后通过示波器探头采集。
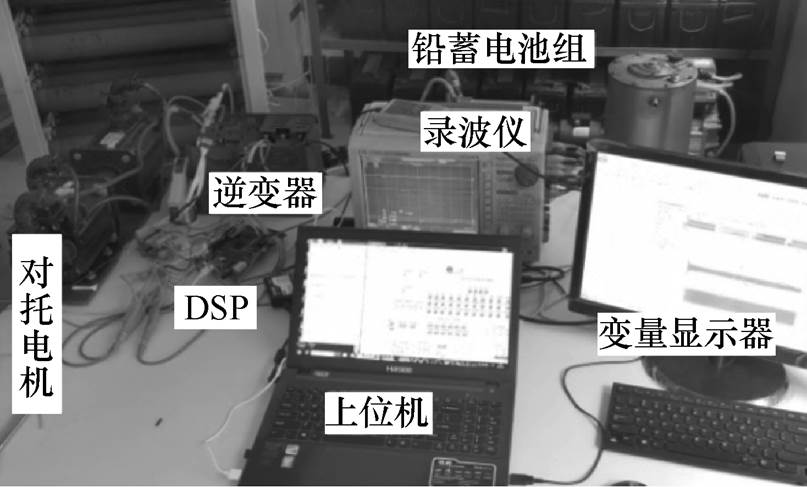
图8 实验平台
Fig.8 Experiment platform
由于以下原因：①解调过程用到了高通滤波器和带通滤波器，估算的转速总是滞后于实际转速；②估算的转子位置存在多个收敛点。实际控制中电机增速过快时，加速过程中估算的转速就越低于电机实际转速，由估算转速与指令转速偏差量得到的q轴指令电流也会偏大，如果此时转速环和电流环PI参数调得较大，电机实际转速又迅速增加，会进一步加大估算转速、转子位置与实际值的偏差，最终导致估算的转子位置收敛在错误点，电机控制失败。突加重载时也与之类似。
所以相比有位置传感器矢量控制，基于旋转高频注入法的矢量控制的转速环PI、电流环PI参数和指令转速调整斜率取值相对较小，导致实验中电机突加负载和突增目标转速时电机调整速度相对有位置传感器矢量控制较慢。
电机转速分别为50r/min、150r/min时突加负载，相电流、实际转子位置、补偿前后的转子位置及误差量分别如图9和图10所示。从图9和图10可以看出，采用基于旋转高频注入法的矢量控制时电机空载电流小，电机突加负载时，通过增大电流来增加转矩达到新的转矩平衡。突加负载瞬间估算的转子位置与真实位置的误差会出现明显波动，但当电机再次达到稳定后转子误差量能保持稳定，且补偿后转子估算位置误差相比未补偿时明显减小。
在电机以转速50r/min空载运行时突增转速到150r/min，电机转速、实际转子位置和补偿后估算转子位置通过3路DA转换后进行采集，电机相电流、转速、转子位置和补偿后位置误差等相关波形如图11所示。空载突增转速，电机负载增加不大，相电流幅值变化不明显。在转速变化的过程中，补偿后估算转子位置与实际位置偏差量变化不大，且均保持在0.1rad以内，说明采用的补偿方法在电机转速变化时能实现实时补偿。
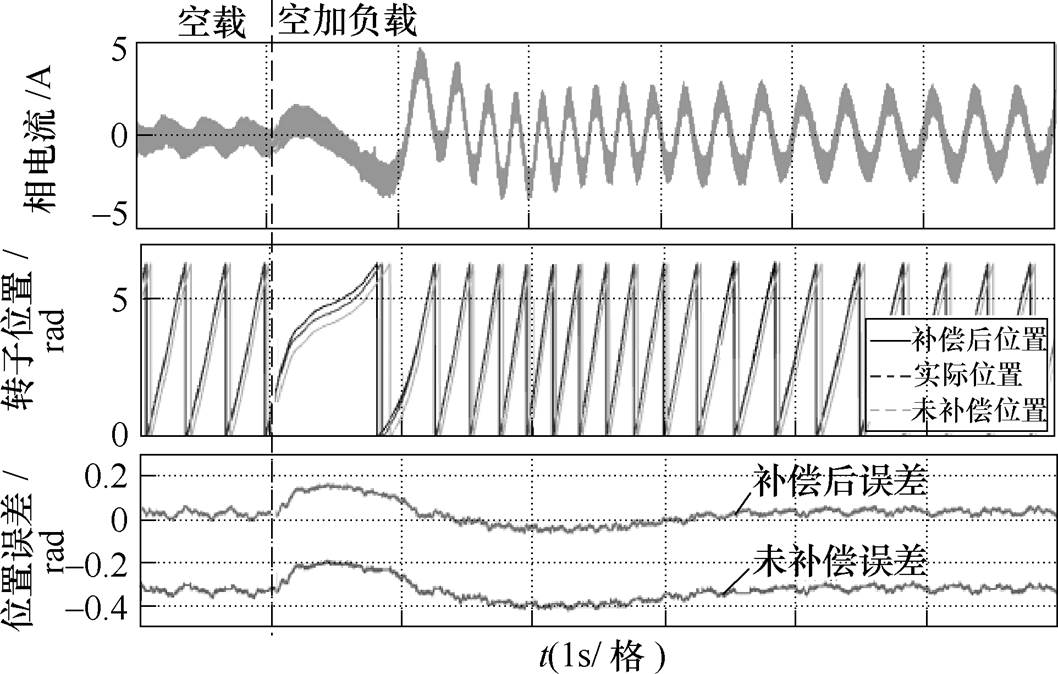
图9 转速50r/min突加负载实验波形
Fig.9 Experimental waveforms at 50r/min with sudden load
图10 转速150r/min突加负载实验波形
Fig.10 Experimental waveforms at 150r/min with sudden load
为减小旋转高频注入法使用滤波器导致的电机在低速下的转子位置估算误差，本文提出了基于正序电流分量的在线误差补偿方法，给出了用正序电流补偿位置误差的理论依据，利用仿真和实验平台对提出的补偿方法进行验证。结果表明，电机运行在不同转速及负载工况下，该方法对转子估算误差实时补偿效果明显，补偿后平均误差在0.1rad以内。
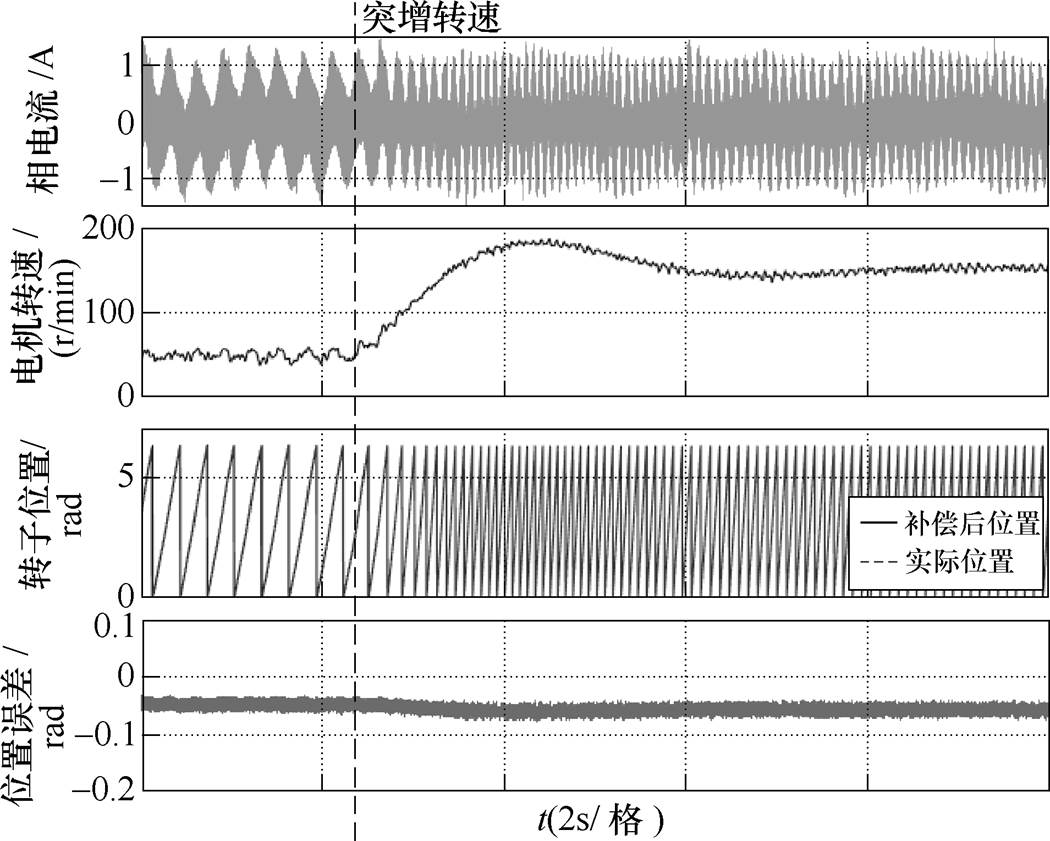
图11 转速50r/min突增到150r/min实验波形
Fig.11 Experimental waveforms when speed increases from 50r/min to 150r/min
参考文献
[1] 刘毅, 贺益康, 秦峰, 等. 基于转子凸极跟踪的无位置传感器永磁同步电机矢量控制研究[J]. 中国电机工程学报, 2005, 25(17): 121-126.
Liu Yi, He Yikang, Qin Feng, et al. Investigation of rotor saliency tracking based sensorless vector control drive for PMSM[J]. Proceedings of the CSEE, 2005, 25(17): 121-126.
[2] 陈书锦, 李华德, 李擎, 等. 永磁同步电动机起动过程控制[J]. 电工技术学报, 2008, 23(7): 39-44.
Chen Shujin, Li Huade, Li Qing, et al. Start process control of permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2008, 23(7): 39-44.
[3] 王高林, 杨荣峰, 李刚, 等. 基于高频信号注入的IPMSM无位置传感器控制策略[J]. 电工技术学报, 2012, 27(11): 62-68.
Wang Gaolin, Yang Rongfeng, Li Gang, et al. Position sensorless control strategy of IPMSM based on high frequency signal injection[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 62-68.
[4] 秦峰, 贺益康, 刘毅, 等. 两种高频信号注入法的无传感器运行研究[J]. 中国电机工程学报, 2005, 25(5): 116-121.
Qin Feng, He Yikang, Liu Yi, et al. Comparative investigation of sensorless control with two high- frequency signal injection schemes[J]. Proceedings of the CSEE, 2005, 25(5): 116-121.
[5] 刘海东, 周波, 郭鸿浩, 等. 脉振高频信号注入法误差分析[J]. 电工技术学报, 2015, 30(6): 38-44.
Liu Haidong, Zhou Bo, Guo Honghao, et al. Error analysis of high frequency pulsating signal injection method[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 38-44.
[6] 李华阳, 王涛, 林环城, 等. 基于高频注入的PMSM无传感器控制的误差分析[J]. 微特电机, 2013, 41(11): 64-70.
Li Huayang, Wang Tao, Lin Huancheng, et al. Analysis of position errors in high-frequency carrier signal injection based sensorless control of PMSM[J]. Small & Special Electrical Machines, 2013, 41(11): 64-70.
[7] 刘兵, 周波. 脉振高频电压注入SPMSM无位置传感器控制的估计误差分析与抑制方法[J]. 中国电机工程学报, 2018, 38(14): 4232-4241.
Liu Bing, Zhou Bo. Analysis and compensation of position estimation error in SPMSM sensor-less control based on high frequency pulsating voltage injection[J]. Proceedings of the CSEE, 2018, 38(14): 4232-4241.
[8] 吕晓源, 刘刚, 毛琨, 等. 基于虚拟脉振高频注入法的永磁电机初始位置检测[J]. 电工技术学报, 2017, 33(23): 34-40.
Lü Xiaoyuan, Liu Gang, Mao Kun, et al. Initial position detection of permanent magnet motor based on virtual pulsating high-frequency injection method[J]. Transactions of China Electrotechnical Society, 2017, 33(23): 34-40.
[9] 廖军, 张兴, 杨淑英, 等. 改进高频信号注入法的IPMSM转子位置检测研究[J]. 合肥工业大学学报(自然科学版), 2010, 33(8): 1161-1165.
Liao Jun, Zhang Xing, Yang Shuying, et al. Research on the IPMSM rotor position estimation based on improved high frequency injection method[J]. Journal of Hefei University of Technology (Natural Science, 2010), 33(8): 1161-1165.
[10] Kim S I, Im J H, Song E Y, et al. A new rotor position estimation method of IPMSM using all-pass filter on high-frequency rotating voltage signal injection[J]. IEEE Transactions on Industrial Elec- tronics, 2016, 63(10): 6499-6509.
[11] Wang Gaolin, Xiao Dianxun, Zhang Guoqiang, et al. Sensorless control scheme of IPMSMs using high- frequency orthogonal square-wave voltage injection into stationary reference frame[J]. IEEE Transactions on Power Electronics, 2018, 34(3): 2573-2584.
[12] Gabriel F, De Belie F, Neyt X, et al. High-frequency issues using rotating voltage injections intended for position self-sensing[J]. IEEE Transactions on Indu- strial Electronics, 2013, 60(12): 5447-5457.
[13] Kim S, Ha J I, Sul S K. PWM switching frequency signal injection sensorless method in IPMSM[J]. IEEE Transactions on Industry Applications, 2012, 48(5): 1576-1587.
[14] Kim S, Kwon Y C, Sul S K, et al. Position sensorless operation of IPMSM with near PWM switching frequency signal injection[C]//IEEE International Conference on Power Electronics & ECCE Asia, Jeju, 2011: 1660-1665.
[15] Ji Xinhai, Ni Ronggang, Chen Wei. High frequency voltage injection methods and observer design for initial position detection of permanent magnet synchronous machines[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 7971-7979.
[16] 刘景林, 鲁家栋. 基于相电流正负序分量相角差的高精度内置式永磁同步电机转子初始位置检测方法[J]. 电工技术学报, 2016, 31(23): 63-69.
Liu Jinglin, Lu Jiadong. High-precision estimation method of initial rotor position for IPMSM based on phase difference of positive and negative sequence current component[J]. Transactions of China Electro- technical Society, 2016, 31(23): 63-69.
[17] 杨健, 杨淑英, 李浩源, 等. 基于旋转高频电压注入的永磁同步电机转子初始位置辨识方法[J]. 电工技术学报, 2018, 33(15): 3547-3555.
Yang Jian, Yang Shuying, Li Haoyuan, et al. Initial rotor position estimation for IPMSM based on high frequency rotating voltage injection[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3547-3555.
[18] 李浩源, 张兴, 杨淑英, 等. 基于旋转高频注入的内置式永磁同步电机初始位置检测算法[J]. 电工技术学报, 2018, 33(8): 1723-1731.
Li Haoyuan, Zhang Xing, Yang Shuying, et al. A detecting algorithm for initial position of interior permanent magnet synchronous motor based on rotating high frequency injection[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1723- 1731.
[19] Wang Tianhao, Shi Bowen, Xu J, et al. Accuracy improvement of carrier signal injection sensorless control for IPMSM in consideration of inverter nonlinearity[C]//IEEE Conference of the IEEE Indu- strial Electronics Society, Yokohama, Japan, 2016: 273-278.
[20] 刘家曦. 无传感器内嵌式永磁同步电机转子磁极位置检测技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.
[21] 高健伟. 基于高频注入法的永磁同步电机转子位置估计误差的分析[D]. 济南: 山东大学, 2012.
An Online Position Error Compensation Method of Rotating High-Frequency Injection Based on Positive Sequence Components
Abstract The rotating high-frequency injection method can estimate the rotor position of permanent magnet synchronous motor at zero speed and low speed, but the use of the filter may bring estimation errors during the demodulation process of the rotor position. The paper presents a method for online compensation of rotor estimation error using positive sequence current component. The mechanism of the compensation method was described when the motor was in zero speed and low speed. The phase delay of positive and negative sequence current in demodulation process was theoretically derived. The compensation effect of the positive sequence current was analyzed considering the influence of the stator resistance. The error compensation amount and rotor position obtained by the heterodyne method have multiple convergence points. Hence, a convergence point detection was added to eliminate some error convergence points. Simulation and experiments verified the effect of the proposed method on rotor position error compensation.
keywords：Rotating high-frequency injection, rotor position estimation error, positive sequence current, online error compensation
DOI: 10.19595/j.cnki.1000-6753.tces.191568
中图分类号：TM921.51
彭 威 男，1992年生，博士研究生，研究方向为电力电子与舰船电力推进。E-mail: 1530911613@qq.com
乔鸣忠 男，1971年生，教授，博士生导师，研究方向为电力自动化和舰船电力推进。E-mail: qiaomingzhong@126.com（通信作者）
收稿日期2019-11-19
改稿日期 2020-05-12
国家自然科学基金资助项目（51877212，51807197）。
（编辑 崔文静）