
图1 CFETR超导磁体系统
Fig.1 Superconducting magnet system of CFETR
摘要 针对中国聚变工程实验堆(CFETR)高参数等离子体约束要求,其纵场(TF)混合磁体的设计方案为采用三种不同性能的超导导体绕制,峰值磁场可达14.43T,最大应力超过700MPa。该文结合CFETR纵场磁体面临的稳态以及瞬态热负荷条件,系统分析混合磁体中高性能Nb3Sn四饼线圈在不同扰动长度及扰动时间工况下的稳定性温度裕度和能量裕度,并对背景场强度及有效应变等因素对稳定性裕度的影响进行讨论。结果表明,高性能Nb3Sn CICC导体在峰值磁场及-0.7%~-0.5%有效应变预计区间内拥有2.0K以上的温度裕度;但极端条件(B=14.43T, e=-0.7%)下的电磁扰动(Lp=10m, tp=100ms)对应导体能量裕度仅有11.41mJ/cc,局部恶劣工况下导体能量裕度下降严重的问题亟待解决。针对高场区单饼线圈在典型扰动下行为的计算表明,典型机械扰动(Lp=0.1m, tp=1ms)引起的失超能够在5s内使导体热点温度升高至接近120K,这对磁体失超保护系统提出了较高的要求。
关键词:中国聚变工程试验堆 纵场超导磁体 高性能Nb3Sn 稳定性裕度
超导磁体系统是磁约束聚变装置中最重要的子系统之一。在托卡马克装置中,磁体系统通过产生具有特定位形的强磁场对高参数等离子体进行约束,使其能够安全稳定地进行聚变反应。高磁场约束性能是获得高参数等离子体的必备条件[1-2],具有高临界特性的大型超导磁体对提高等离子体参数具有重要意义。同时,高载流超导电缆也在大功率输电、储能等领域具有广泛的应用[3-6]。于2015年完成工程概念设计的“中国聚变工程试验堆(China Fusion Engineering Testing Reactor, CFETR)”计划是我国发展可控核聚变的一个重要里程碑项目。CFETR的超导磁体系统主要由16组纵场(Toroidal Field, TF)磁体、8组中心螺管(Central Solenoid, CS)磁体以及6组平衡场(Poloidal Field, PF)磁体等组成,如图1所示[7-8]。

图1 CFETR超导磁体系统
Fig.1 Superconducting magnet system of CFETR
聚变堆正常态或故障态时,超导磁体可能面临的瞬态热负荷主要来自于[9-12]:①作用距离较长的机械扰动,包括正常态或故障态下真空室、杜瓦冷屏的瞬态热辐射,以及主机结构件到超导磁体的局部热传导,个别工况下可以达到较高的瞬时功率;②聚变中子核热效应,尤其在靠近等离子体的绕组内侧,表现为空间和时间不连续的点热源,强度较低,可以归为广义的机械扰动;③作用距离较长的电磁扰动,包括线圈自身局部热负荷,如接头电阻发热,以及等离子体位形变化或故障态工况下的局部交流损耗热沉积等,热负荷功率高低不等。这些影响范围、持续时间各不相同的热负荷带来的能量输入耦合沉积在磁体系统上,就会导致局部临界电流密度、分流温度等参数下降,一旦超过稳定性裕度,将会引起局部失超等影响磁体系统安全运行的工况。由于聚变堆超导磁体储能达到数个GJ,超导磁体发生失超会给聚变堆带来灾难性的后果。因此,充足的稳定性裕度是磁体设计时需要优先考虑的因素之一[13]。
本文针对CFETR纵场磁体工作条件下的不同热负载带来的典型扰动特性,建立混合磁体高场区高性能Nb3Sn管内电缆导体(Cable-In-Conduit-Conductor, CICC)导体的一维有限元模型,针对不同扰动长度和扰动时间,分别计算出高性能Nb3Sn CICC导体的最小失超能,并系统分析了背景场强度、平均有效应变等因素对稳定性裕度的影响。此外,针对两种典型的扰动工况:①扰动长度Lp=10m,扰动时间tp=100ms的电磁扰动;②扰动长度Lp=0.1m,扰动时间tp=1ms的机械扰动,着重进行了导体的稳定性及失超行为分析。为CFETR纵场磁体电磁设计以及未来实验测试提供参考。
CFETR的纵场磁体系统由16组高约17m,宽约12m的D形线圈组成[14]。为了实现对10~12MA等离子体长约束以得到合适的磁位型,其中一种方案是采用三种不同性能的超导材料组成混合磁体。混合磁体方案每组D形线圈包括:①由两个六饼线圈和一个四饼线圈组成的高性能Nb3Sn高场区绕组,最高磁场强度为14.43T;②由4个四饼线圈组成的ITER Nb3Sn中场区绕组,最高磁场强度为11.09T;③由两个六饼线圈组成的NbTi低场区绕组,最高磁场强度约为6T。此方案的优势在于可以充分发挥不同参数导体的性能,节约成本,但绕线、接头布置以及氦回路布置存在困难。TF磁体D形线圈结构如图2所示。
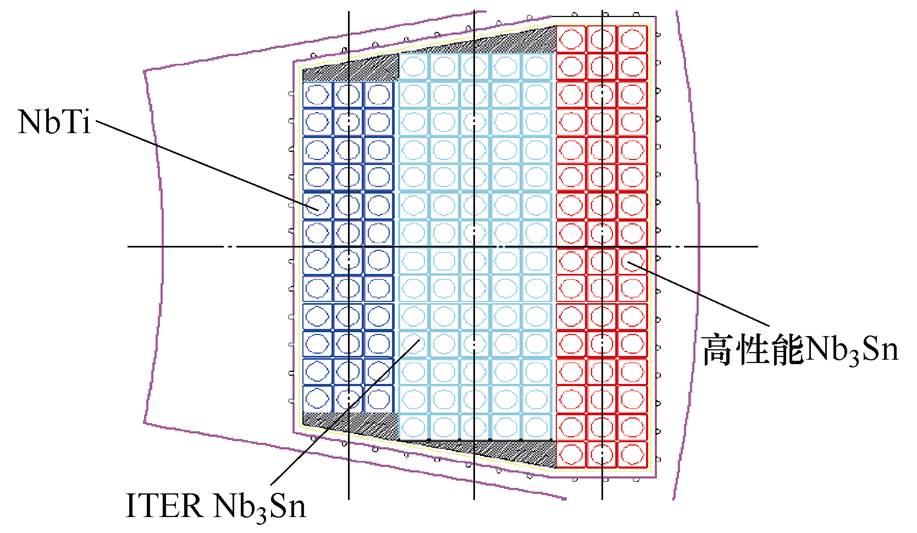
图2 TF磁体D形线圈结构示意图
Fig.2 Structure of TF magnet D-coil
绕制CFETR纵场磁体的CICC导体的铜缆与超导缆比例接近1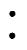 1,导体直径48mm,经不锈钢带花包后穿入不锈钢制铠甲内,为导体提供机械支撑与防护。经过压方与包绝缘,最终制成CICC导体。单根导体横截面示意图如图3所示,结构参数见表1。
1,导体直径48mm,经不锈钢带花包后穿入不锈钢制铠甲内,为导体提供机械支撑与防护。经过压方与包绝缘,最终制成CICC导体。单根导体横截面示意图如图3所示,结构参数见表1。
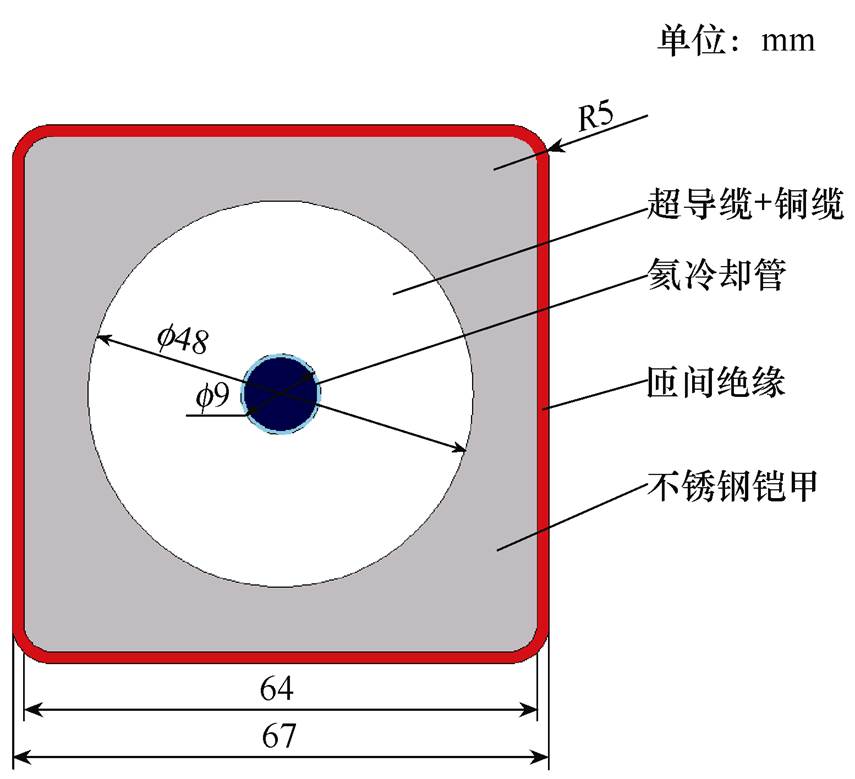
图3 高性能Nb3Sn CICC导体示意图
Fig.3 Sketch of high-performance Nb3Sn CICC conductor
建立导体一维有限元模型用于计算电磁及热工水利参数的方法,已广泛用于国际热核聚变实验堆(International Thermonuclear Experimental Reactor, ITER)计划超导磁体系统设计及校核过程[15-18]。通过分别对超导导体在热、电、磁、力多物理场耦合条件下的性能参数,对接头、管道、热交换器、阀门等组件的热工水力参数,以及对电阻、电感、电源等元件的电学参数进行计算,可以得到导体在复杂条件和工况下的稳定性裕度和参数变化等信息。
表1 高性能Nb3Sn CICC导体结构参数
Tab.1 Parameters of high-performance Nb3Sn CICC conductor

参 数数 值 导体横截面尺寸/64×64 导体长度(六饼/四饼)/m775/515 不锈钢铠甲截面积/mm22 275.928 匝间绝缘层面积/mm2382.055 铜丝数量900 Nb3Sn超导丝数量899 铜丝/超导丝直径/mm0.9 空隙率(%)33.2 运行电流/kA95.6 峰值磁场强度/T14.43 有效应变(%)-0.7~-0.5 E0/(V/m)1.03310-4 n20 中心冷却孔内径/mm9.0 中心冷却孔截面积/mm263.617 电缆束冷却流道截面积/mm2586.544 中心冷却孔湿周长/mm28.274 电缆束冷却流道湿周长/mm4 417.863
临界温度、上临界磁场和临界电流密度是超导材料最重要的3个临界参数。Nb3Sn超导导体的临
界参数与温度、磁场和应变有关,国内外学者针对其开发了多种计算方法和经验公式。在本文中,临界参数数学模型选用ITER组织推荐的Nb3Sn临界关系定标率公式[19],有
临界电流密度
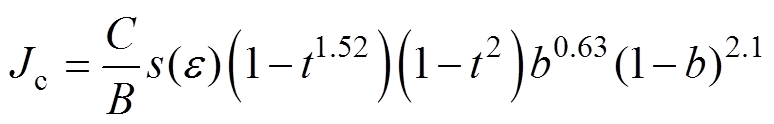 (1)
(1)临界温度
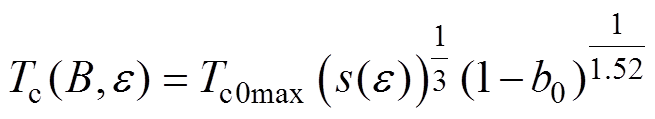 (2)
(2)
临界磁场
 (3)
(3)应变函数
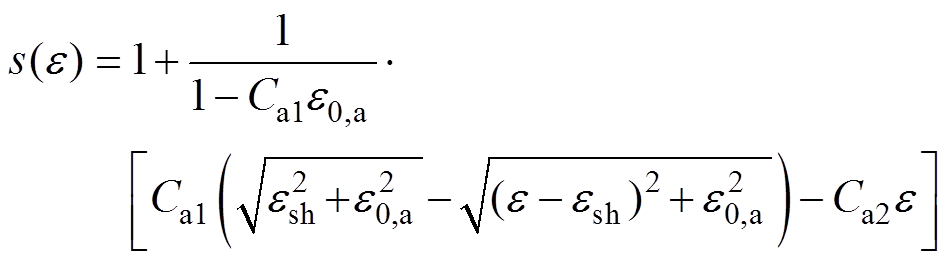 (4)
(4)
其中
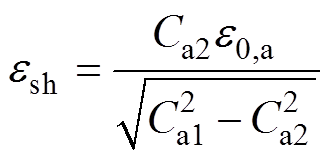 (5)
(5)约化磁场
 (6)
(6)
零温下约化磁场
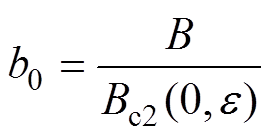 (7)
(7)约化温度
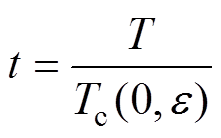 (8)
(8)
式中,B为磁场强度;T为温度;e 为有效应变;Bc20max、Tc0max、e0,a分别为磁场强度常量、温度常量和应变常量;Ca1、Ca2为经验参数。
图4以TF磁体高场区绕组四饼线圈为例,给出了以氦进口处为零点,背景磁场强度沿导体长度方向的分布,以及D形磁体磁场强度分布云图。图中,相邻两虚线间的部分代表单匝导体范围(42m)内的磁场强度变化,以位于D形线圈底部的氦进出口位置为起点,磁场强度峰值出现在D形磁体竖直段,由竖直段向外侧磁场强度逐渐降低;从磁场分布云图中可以看出,高性能Nb3Sn导体所处的内侧绕组磁场显著高于外侧绕组,即D形线圈竖直段内侧绕组所处工况为整个磁体最不利工况。
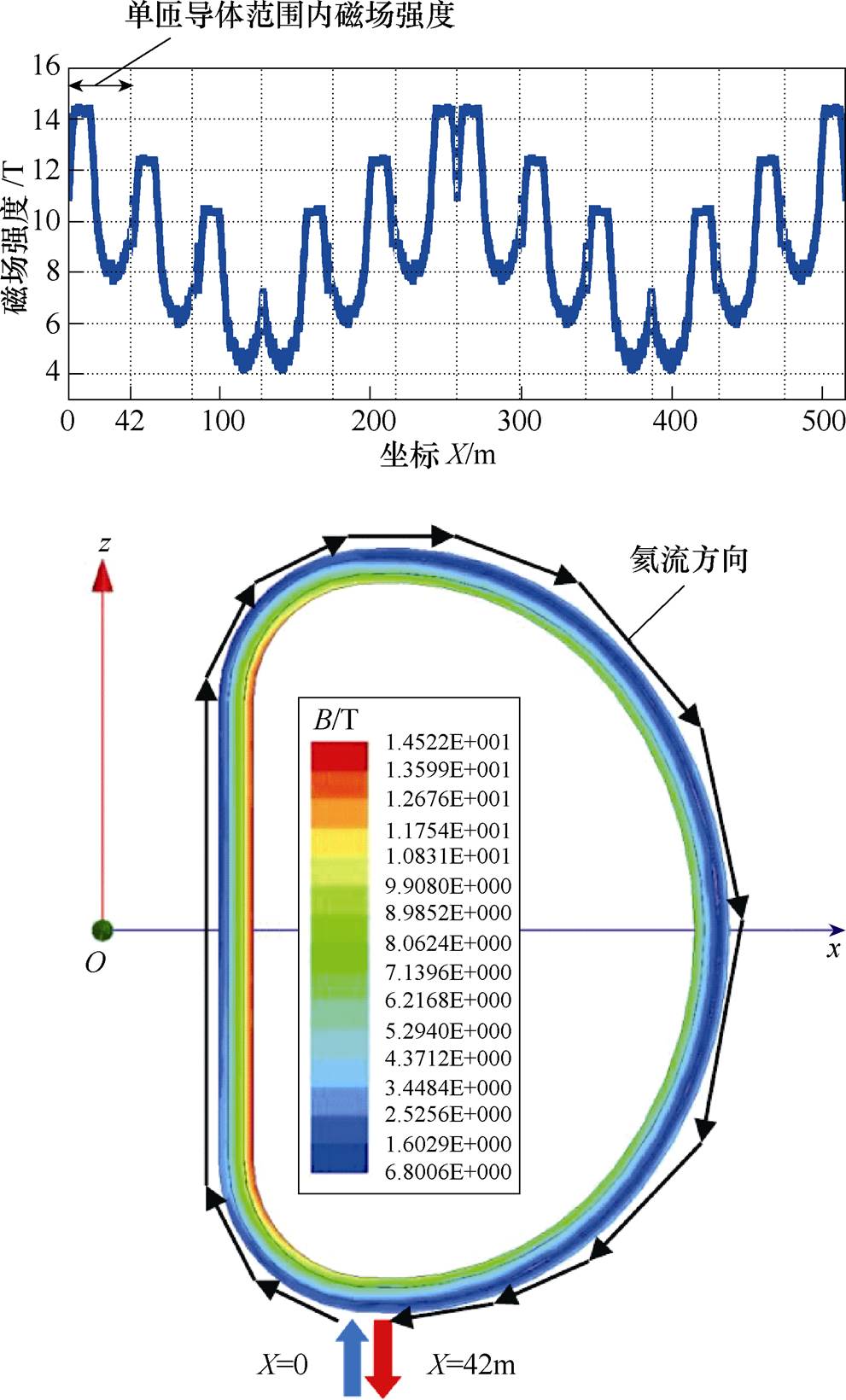
图4 TF磁体D形线圈耦合磁场强度分布
Fig.4 Distribution of coupled magnetic field of TF magnet D-coil
超导磁体低温系统可以简化为具有一定体积的节点(junction)以及具有一定长度的流道(pipe)相连接的循环系统。而对单匝CICC导体来说,其水力特性从构造上可以由3个简单流动[20-21]组成:①电缆束内子缆之间的空隙中流动;②中心冷却孔内的流动;③电缆束内与中心冷却孔之间的流体质量交换。图5是CFETR纵场磁体冷却系统单回路简化后示意图。工作介质为加压的超临界氦,以避免回路内发生局部相变。简化后的回路由以下元件组成:5个连接节点,包括导体进口节点以及出口节点;一个冷源换热器(heat exchanger),以及一个泄压池(relief pool);两个导体内流道,包括中心冷却孔(hole helium)流道以及电缆束内(bundle helium)流道;两个连接管,一个控制阀,一个氦流泵(pump),以及一个泄压阀(relief value)。回路内初始压力为6.03105Pa,初始温度为4.5K,泄压阀泄放压差为1.03105Pa。
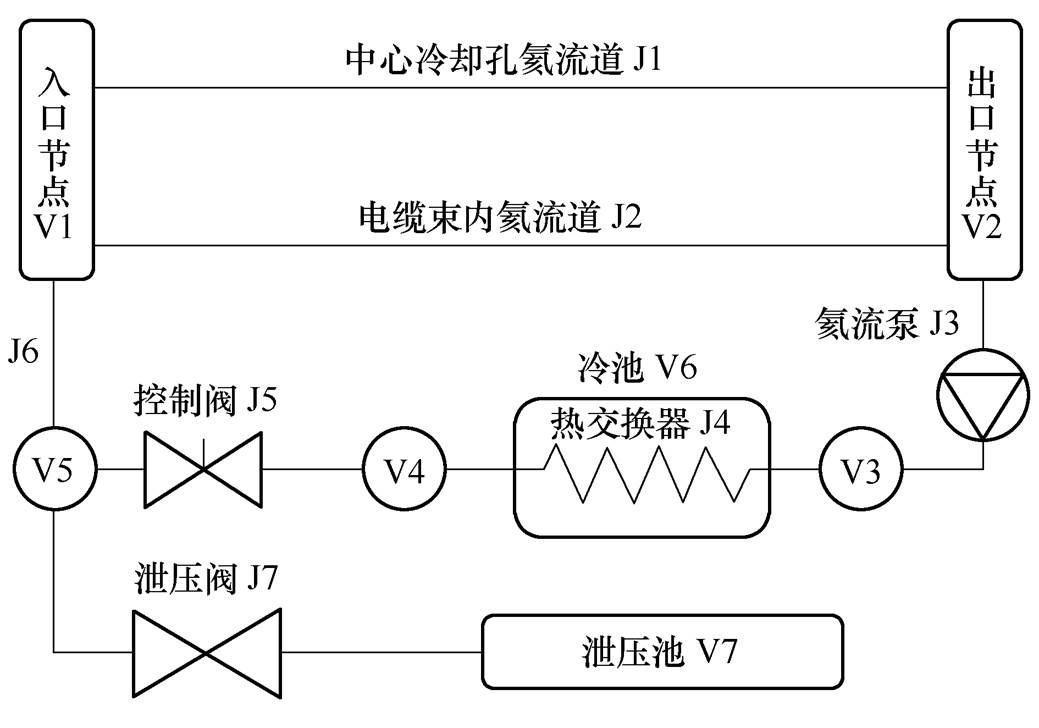
图5 超导磁体低温系统简化回路示意图
Fig.5 Sketch of Simplified loop of superconducting magnet cryogenic system
本文中低温系统通过中心冷却孔氦流道J1与电缆束内氦流道J2分别与CICC导体各组件间的热交换,与一维导体稳定性模型建立耦合;J1流道与J2流道内的流动分别遵从Blasius条件和Katheder条件。
针对导体电流网络进行的简化与归类可以将所有超导与非超导元器件分为四种类型:电阻、电感,电压源与电流源。导体相关电学参数可以通过求解基尔霍夫定律以及关于该网络的微分方程式得到,有
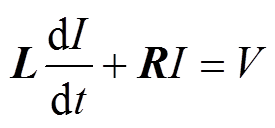 (9)
(9)式中,L和R分别为导体的电感与电阻矩阵;I为网络电流;V为网络端电压。
在本文的一维有限元模型中,单匝超导CICC导体超导态下的电学特性等效于一个包含并联电流源、电感与电阻的网格;而发生失超时,超导电缆等效于电感与可变电阻串联。电物理模型通过电流在CICC导体超导层、铜导体层的流动,与本文一维导体稳定性模型建立耦合。
衡量超导导体稳定性裕度的指标通常包括能量裕度和温度裕度。在局部受到一定能量的扰动时,如果能量恰好能够引起导体失超且无法恢复,这一扰动能量水平被称为导体的最小失超能(Minimum Quench Energy, MQE)(mJ/cc),即稳定性能量裕度。MQE[22]表达式为
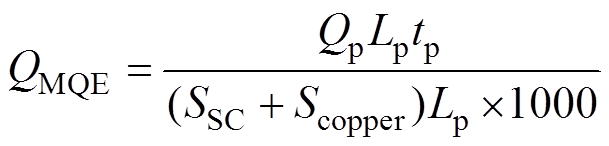 (10)
(10)式中,Qp为输入的单位长度扰动功率(W/m);Lp为扰动长度(m);tp为扰动时间(s);SSC和Scopper分别为超导丝和铜丝的截面积(m2)。超导导体的稳定性温度裕度通常指导体分流温度与工作温度的差值[23],有
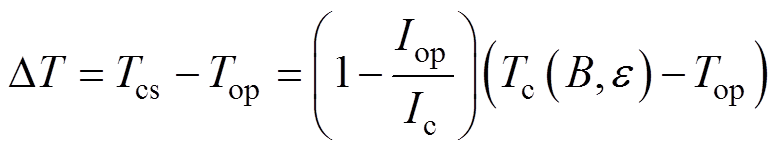 (11)
(11)
式中,Tcs为超导体分流温度;Top为工作温度;Tc(B, e )为磁场B和应变e 对应的临界温度;Iop和Ic分别为工作电流和临界电流。
CFETR纵场磁体在运行过程中,由于受到等离子体放电、局部机械应变、中子核热效应、交流损耗等多种因素影响,超导电缆局部会发生临界性能衰退,这些影响因素被称为扰动[24]。在工程实际中,按照扰动空间尺度的长短,通常可以分为电磁扰动(扰动长度10-3~1m,扰动时间较短,如等离子体破裂、局部中子核热效应等)和机械扰动(扰动长度1~10m,扰动时间较长,如热应力循环、局部交流损耗等)。
高性能Nb3Sn CICC导体在不同扰动长度与扰动时间下的稳定性能量裕度见表2。为了反映最不利条件下导体的稳定性裕度,计算条件取峰值磁场强度14.43T,有效应变在预计区间内取最大值-0.7%,考虑到对导体低温系统的要求,氦质量流量取12g/s。采用逼近法确定临界值,控制误差在1‰以下。值得注意的是,在14.43T磁场以及-0.7%有效应变的最极端工况下,扰动长度和时间都较长的电磁扰动对应的能量裕度较小,最低仅有11.41mJ/cc,这意味着较小的输入能量即有可能引起导体局部失超。如何改善恶劣工况下高性能Nb3Sn CICC导体局部能量裕度下降严重的问题,是CFETR纵场磁体亟待解决的。
表2 不同扰动时间与扰动长度下导体的能量裕度(@B=14.43T, e =-0.7%)
Tab.2 Energy margin of the conductor under different duration and perturbation length (@B=14.43T, e =-0.7%)

扰动长度/m扰动时间/ ms扰动功率/ (W/m)能量/J能量裕度/ (mJ/cc) 101145 2941 452.9130.96 101016 5831 658.3144.91 10100130.6130.611.41 1100374.137.4131.53 0.11001 198.711.987104.72
图6展示了导体平均有效应变对稳定性裕度的影响。在CFETR纵场磁体峰值磁场(@14.43T)以及有效应变预计区间(e =-0.7%~-0.5%)条件下,电磁扰动(Lp=10m, t =100ms)对应的温度裕度最低为2.969K,高于2.0K的温度裕度要求。在纵场磁体有效应变预计区间内,电磁扰动对应的能量裕度分别下降了40.39mJ/cc(@14.43T)以及151.34mJ/cc(@10T)。图7是不同扰动时间下氦流量对最小失超能的影响(扰动时间tp=1ms, 5ms, 50ms)。当高性能Nb3Sn CICC导体超临界氦质量流量由14.0g/s下降至8.0g/s时,对应的稳定性能量裕度由480.21mJ/cc下降至476.45mJ/cc(Lp=10m, tp=100ms),计算结果表明,一定范围内氦流量对超导体能量裕度的影响不大。
由于混合磁体高场区绕组峰值磁场出现在D形线圈最内侧绕组处,因此出于减少有限元数量,简化计算的考虑,取纵场磁体最危险段45m长单匝线圈计算结果作为高性能Nb3Sn CICC导体在典型扰动下的行为代表。图8为CICC导体在典型电磁扰动(Lp=10m, tp=100ms)下的恢复与失超时超导股线温度分布变化情况。图9展示了导体在电磁扰动下恢复与失超时电压、热点温度、进出口压力以及氦质量流量等参数。为了考察最极端情况下导体的稳定性与失超特性,本文中针对高性能Nb3Sn CICC导体在典型扰动下的行为均未考虑失超保护系统的影响。

图6 平均有效应变对温度裕度与能量裕度的影响
Fig.6 Temperature margin and energy margin of conductor in different effective strain
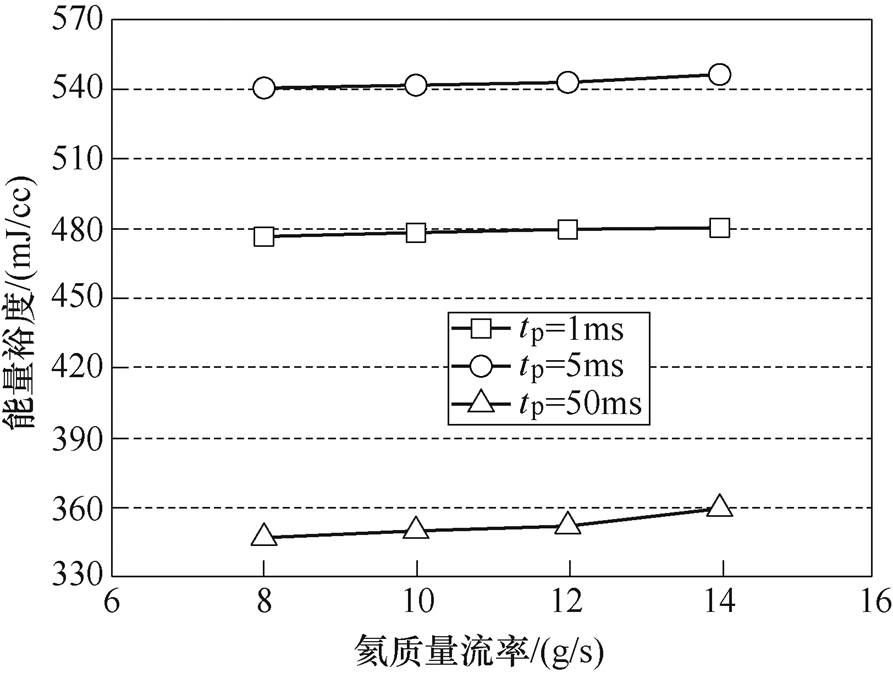
图7 不同扰动时间下氦流量对最小失超能的影响(扰动时间tp=1ms, 5ms, 50ms)
Fig.7 Effect of helium mass flow on minimum quench energy of conductor in different duration (tp=1ms, 5ms, 50ms)
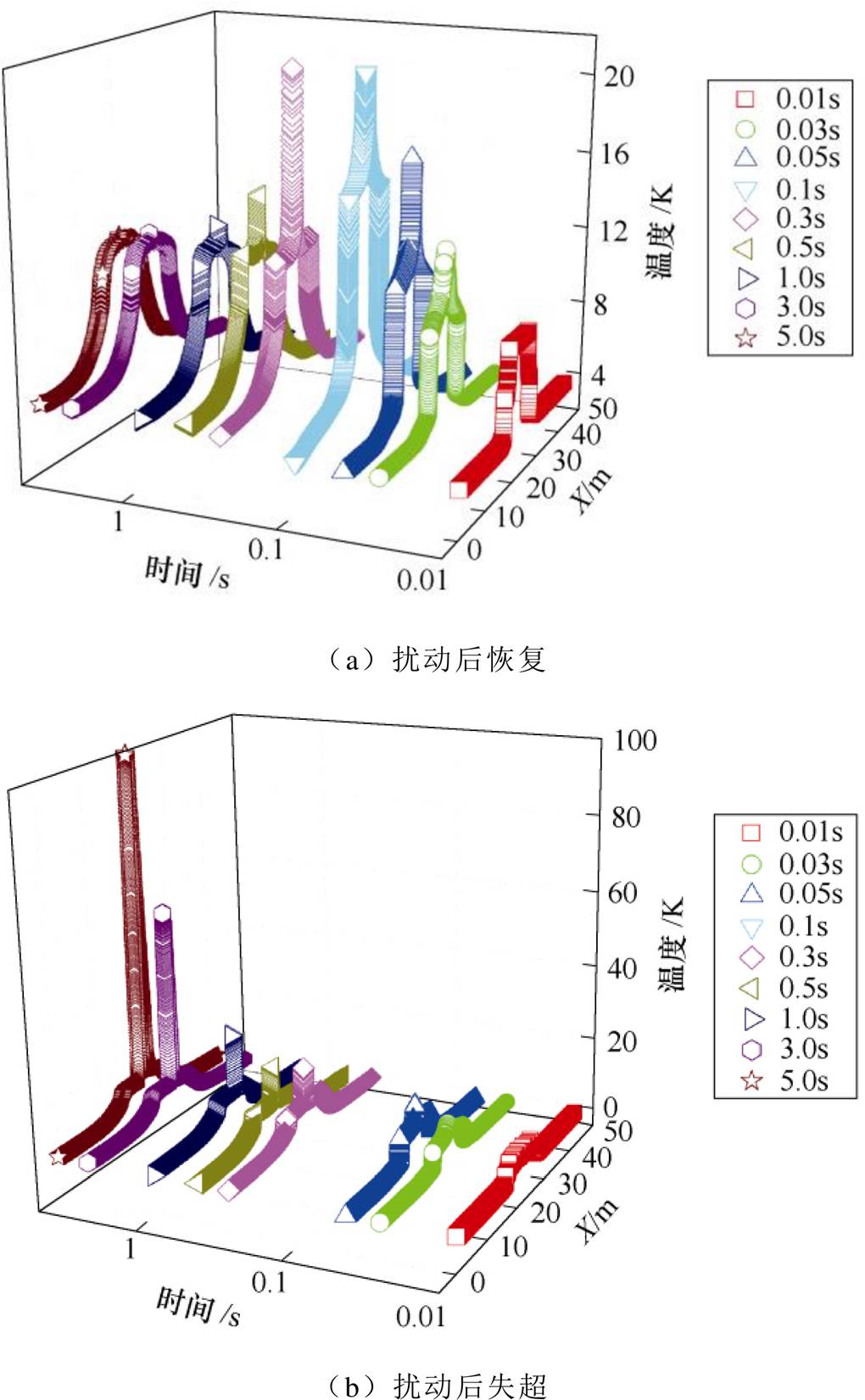
图8 电磁扰动(Lp=10m, tp=100ms)下导体温度分布随时间变化
Fig.8 Temperature distribution of conductor for electromagnetic perturbation (Lp=10m, tp=100ms)
当扰动能量小于对应的MQE时,超临界氦冷却剂能够带走导体因为扰动和局部失超而产生的额外能量,在扰动长度较长的电磁扰动下,扰动中心会出现10~20K的温度峰值,局部温度裕度甚至会下降至零。虽然这一峰值最终不会导致超导磁体出现大范围的失超,但仍然存在被失超保护系统检测到,引起保护系统误动作的可能性,从而影响聚变堆正常运行。当扰动能量超过导体稳定性能量裕度而引起失超时,在失超保护系统未动作的情况下,导体最大热点温度出现在扰动的中段,由于氦冷却剂流过热点后温度上升,且由于出口压力增大导致冷却循环恶化,失超沿氦流动方向的扩散速度比相反方向的扩散更快。
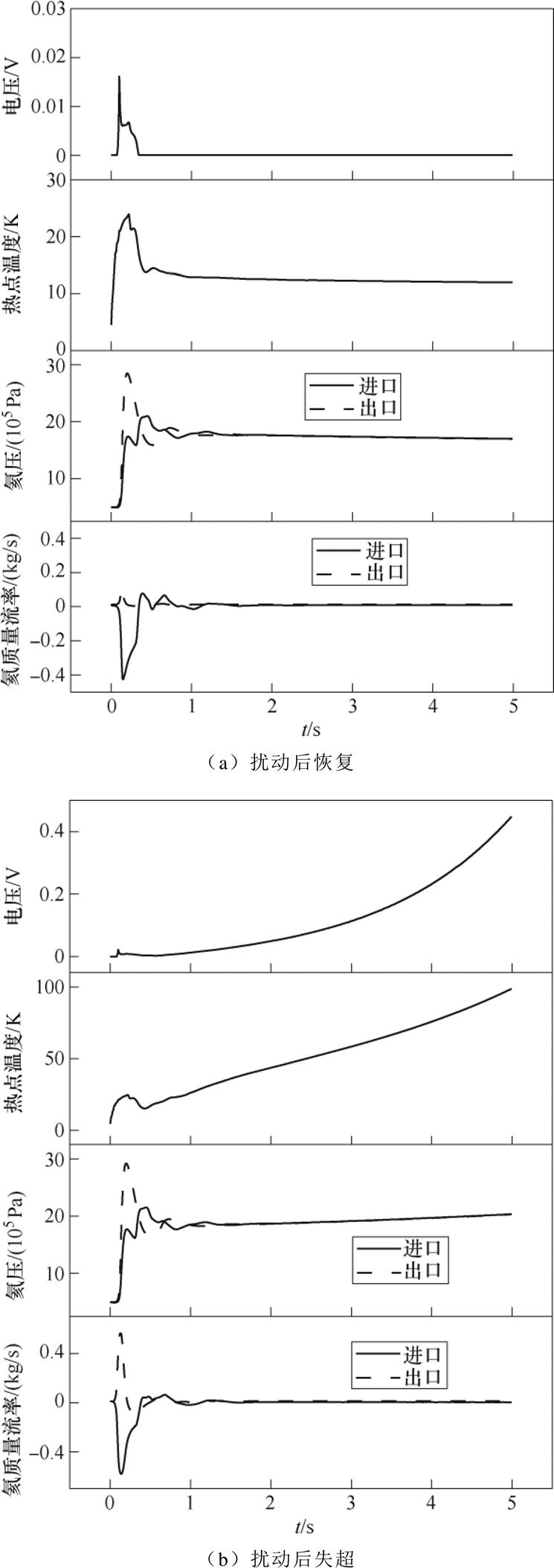
图9 电磁扰动(Lp=10m, tp=100ms)下导体端电压、热点温度、进出口氦压以及总质量流量随时间变化
Fig.9 Voltage/hot spot temperature/inlet & outlet pressure and helium mass flow of conductor for electromagnetic perturbation (Lp=10m, tp=100ms)
图10为CICC导体在典型机械扰动(Lp=0.1m, tp=1ms)下的失超与恢复时超导股线温度分布变化情况。除扰动有关参数外,导体其余条件与前述电磁扰动保持一致,以针对性研究不同典型扰动对导体稳定参数变化的影响。与电磁扰动相比,机械扰动由于扰动长度较短,导体温度上升更为迅速,且受超临界氦流动的影响更大。由于氦流过热点区后温度升高,导致沿流动方向之后的区域冷却效率下降,表现在股线温度上则是热点区域沿氦流动方向扩散更为迅速,恢复时最大热点温度出现在扰动区域的后方。

图10 机械扰动(Lp=0.1m, tp=1ms)下导体温度分布随时间变化
Fig.10 Temperature distribution of conductor for mechanical perturbation (Lp=0.1m, tp=1ms)
图11展示了导体在机械扰动下恢复和失超时端电压等参数的变化情况。虽然机械扰动稳定性裕度更高,较难引起失超,但由其引发的局部失超能量集中,最大热点温度上升十分迅速,5s内最高温度即可接近120K。由于失超段导体对低温系统的加热,在达到泄放压力之前,氦回路内的压力会持续升高,出口流量升高,进口流量骤减,进一步恶化失超导体的冷却情况。如果失超保护系统不能够及时探测到失超信号并迅速动作,将超导线圈储能导出至泄能回路,局部高温短时间内即有可能对导体造成不可逆损害,这对超导磁体系统甚至整个聚变堆都是十分危险的。

图11 机械扰动(Lp=0.1m, tp=1ms)下导体端电压、热点温度、进出口氦压以及总质量流量随时间变化
Fig.11 Voltage/hot spot temperature/inlet & outlet pressure and Helium mass flow of conductor for mechanical perturbation (Lp=0.1m, tp=1ms)
本文从CFETR纵场磁体所面临的多耦合磁场、高载流、复杂热负荷工况,针对混合磁体中工作环境最为恶劣的高场区绕组——高性能Nb3Sn CICC导体建立一维有限元模型,计算其在不同扰动下的稳定性裕度。从结果可以看出,温度裕度随背景磁场升高以及平均应变的增加明显减小,但在纵场磁体峰值磁场强度(B=14.43T)以及常规工况应变(e = -0.7%~-0.5%)下,导体分流温度仍能超过工作温度2.0K以上。计算中最不利工况下电磁扰动对应的导体稳定性能量裕度仅为11.41mJ/cc,极端恶劣工况下导体局部能量裕度下降严重的问题亟待解决。
此外,分别针对典型电磁扰动以及典型机械扰动,计算了高性能Nb3Sn CICC导体在不考虑失超保护系统的极端条件下,受到典型扰动时恢复以及失超两种情况下的参数。扰动能量低于最小失超能时,电磁扰动的峰值温度较高,恢复时间较短,而机械扰动导致的氦压及流量波动都较为显著;机械扰动的能量裕度一般高于电磁扰动,而一旦因机械扰动引起导体失超,由欧姆加热与冷却剂流量下降双重因素作用,热点温度上升尤为迅速,对失超保护系统检测及动作时间的要求更加严格。
参考文献
[1] Wesche R, Sarasola X, Sedlak K, et al. DEMO central solenoid design based on the use of HTS sections at highest magnetic field[J]. IEEE Transa- ctions on Applied Superconductivity, 2018, 28(3): 1-5.
[2] Maksoud W A, Genini L, Ciazynski D, et al. Progress of the JT-60 SA toroidal field coils tests in the cold test facility[J]. IEEE Transactions on Applied Super- conductivity, 2018, 28(3): 1-4.
[3] 张立晖, 石晶, 严思念, 等. 磁通约束型超导限流开关系统应用[J]. 电工技术学报, 2018, 33(22): 152-159.
Zhang Lihui, Shi Jing, Yan Sinian, et al. System application of flux-coupling superconducting fault current limiting switch[J]. Transactions of China Electrotechnical Society, 2018, 33(22): 152-159.
[4] 刘晟源, 林振智, 李金城, 等. 电力系统态势感知技术研究综述与展望[J]. 电力系统自动化, 2020, 44(3): 229-239.
Liu Shengyuan, Lin Zhenzhi, Li Jincheng, et al. Review and prospect of situation awareness techno- logies of power system[J]. Automation of Electric Power Systems, 2020, 44(3): 229-239.
[5] 李万杰, 张国民, 王新文, 等. 飞轮储能系统用超导电磁混合磁悬浮轴承设计[J]. 电工技术学报, 2020, 35(增刊1): 10-18.
Li Wanjie, Zhang Guomin, Wang Xinwen, et al. Integration design of high-temperature supercon- ducting bearing and electromagnetic thrust bearing for flywheel energy storage system[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 10-18.
[6] 许周, 孙永辉, 谢东亮, 等. 计及电/热柔性负荷的区域综合能源系统储能优化配置[J]. 电力系统自动化, 2020, 44(2): 53-63.
Xu Zhou, Sun Yonghui, Xie Dongliang, et al. Optimal configuration of energy storage for integr- ated region energy system considering power/thermal flexible load[J]. Automation of Electric Power Systems, 2020, 44(2): 53-63.
[7] Zheng Jinxing, Song Yuntao, Liu Xufeng, et al. Overview of the design status of superconducting magnet system of CFETR[J]. IEEE Transactions on Applied Superconductivity, 2018, 28(3): 1-5.
[8] Yun Taosong, Song Taowu, Jian Gangli, et al. Concept design of CFETR tokamak machine[J]. IEEE Transa- ctions on Plasma Science, 2014, 42(3): 503-509.
[9] Bessette D, Zapretilina E, Shatil N. Nuclear heat, disruption loads and other AC losses and their impact on the ITER toroidal field coils conductor design[J]. IEEE Transactions on Appiled Superconductivity, 2000, 10(1): 1074-1077.
[10] Bonifetto R, Buonora F, Richard L S, et al. 4C code simulation and benchmark of ITER TF magnet cool-down from 300K to 80K[J]. IEEE Transactions on Applied Superconductivity, 2012, 22(3): 4902604.
[11] Nijhuis A, Lanen E P A V, Rolando G. Optimization of ITER Nb3Sn CICCs for coupling loss, transverse electromagnetic load and axial thermal contraction[J]. Superconductor Science & Technology, 2012, 25(1): 24.
[12] 滕玉平, 戴少涛, 魏周荣, 等. ITER装置超导磁体线圈导体用超导电缆的绞制[J]. 电工技术学报, 2013, 28(4): 7-12.
Teng Yuping, Dai Shaotao, Wei Zhourong, et al. Cabling for the superconducting cable of magnet coils for ITER[J]. Transactions of China Electro- technical Society, 2013, 28(4): 7-12.
[13] Kessel C E, Blanchard J P, Davis A, et al. Overview of the fusion nuclear science facility, a credible break-in step on the path to fusion energy[J]. Fusion Engineering and Design, 2018, 135: 236-270.
[14] Liu Xufeng, Zheng Jinxing, Wu Huan, et al. Con- ceptual design and analysis of CFETR TF coil[J]. Journal of Fusion Energy, 2015, 34(5): 1027-1032.
[15] Bagni T, Duchateau J L, Breschi M, et al. Analysis of ITER NbTi and Nb3Sn CICCs experimental minimum quench energy with JackPot, MCM and THEA models[J]. Superconductor Science and Technology, 2017, 30(9): 095003.
[16] Sedlak K, Bruzzone P. Results and analysis of the hot-spot temperature experiment for a cable-in- conduit conductor with thick conduit[J]. Cryogenics, 2015, 72: 9-13.
[17] Bermudez S I, Bajas H, Bottura L. Quench modeling in high-field Nb3Sn accelerator magnets[J]. Physics Procedia, 2015, 67: 840-846.
[18] 何欣, 郑金星, 宋云涛, 等. CFETR极向场磁体CICC导体稳定性与交流损耗分析[J]. 电工技术学报, 2016, 31(19): 224-231.
He Xin, Zheng Jinxing, Song Yuntao, et al. Stability and AC loss analysis of the CICC for CFETR poloidal field coils[J]. Transactions of China Electro- technical Society, 2016, 31(19): 224-231.
[19] Devred A. ITER Nb3Sn critical surface parameteri- zation[R]. ITER Organization: Cadarache, 2008.
[20] 彭楠. ITER纵向场超导磁体系统降温过程热力学分析[D]. 北京: 中国科学院研究生院(理化技术研究所), 2009.
[21] Zanino R, Giors S, Richard L S. CFD model of ITER CICC. part VI: heat and mass transfer between cable region and central channel[J]. Cryogenics, 2010, 50(3): 158-166.
[22] 蒋华伟, 李国平, 赵玉娟, 等. 基于稳定性CICC设计模型[J]. 电工技术学报, 2011, 26(1): 14-26.
Jiang Huawei, Li Guoping, Zhao Yujuan, et al. Model to design for CICC based on stability[J]. Transactions of China Electrotechnical Society, 2011, 26(1): 14-26.
[23] Jiang Huawei, Wu Songtao. Research of simulation design for CICC based on energy margin and temperature margin[J]. IEEE Transactions on Applied Superconductivity, 2010, 20(3): 1436-1439.
[24] Bruzzone P, Fuchs A, Stepanov B, et al. Transient stability results for Nb3Sn cable-in-conduit con- ductors[J]. IEEE Transactions on Applied Super- conductivity, 2002, 12(1): 512-515.
Stability Analysis of High-Performance Nb3Sn CICC Conductor in China Fusion Engineering Testing Reactor Toroidal Field Superconducting Magnets
Abstract In order to obtain the high-parameter confined plasma in China fusion engineering testing reactor (CFETR), the hybrid magnets of CFETR toroidal field (TF) magnetic system is to use three kinds of superconductors with different properties. The peak magnetic field can reach 14.43T and the maximum stress exceeds 700MPa. In this paper, the temperature margin and energy margin of the high-performance Nb3Sn pancake coils of hybrid magnets are analyzed under different perturbation lengths and durations based on steady-state and transient thermal load conditions of CFETR TF magnets. The results show that the high-performance Nb3Sn CICC conductors have a temperature margin of 2.0K and above under the peak field and -0.7%--0.5% effective strain. However, the energy margin for electromagnetic disturbance (Lp=10m, tp=100ms) under extreme conditions (B=14.43T, e =-0.7%) is only 11.41mJ/cc. The decline of energy margin under severe local conditions is a serious problem. The quench caused by typical mechanical perturbation (Lp=0.1m, tp=1ms) can raise the hot spot temperature of the conductor to above 100K within 5 seconds, which puts forward a high demand on the magnet quench protection system.
keywords:China fusion engineering testing reactor, toroidal field superconducting magnets, high-performance Nb3Sn, stability margin
DOI: 10.19595/j.cnki.1000-6753.tces.191369
中图分类号:TM249.7
张正硕 男,1998年生,硕士,研究方向为超导磁体稳定性分析。E-mail: zhengshuo.zhang@ipp.ac.cn
郑金星 男,1987年生,副研究员,研究方向为聚变堆高场超导磁体设计。E-mail: jxzheng@ipp.ac.cn(通信作者)
收稿日期2019-10-22
改稿日期 2020-03-16
安徽省杰出青年基金(2008085J28)、国家自然科学基金杰出青年基金(51525703)、国家重点研发专项(2017YFE030050,2017YFE0123400)和中国科学院青年创新促进会优秀会员(Y201979)资助项目。
(编辑 崔文静)