图1 气隙缺陷示意图
Fig.1 Schematic diagram of air gap defects
摘要 对运行工况下的XLPE电缆气隙放电发展阶段进行准确识别，有利于将电缆故障扼杀在萌芽状态，保障电力系统正常运行。该文首先介绍了模拟XLPE电缆气隙放电的试验平台搭建、缺陷模型制作和特征量提取及降维的方法及步骤，基于试验观察和对大量数据样本进行聚类分析，将XLPE电缆气隙放电发展过程分为四个阶段，针对以往XLPE电缆气隙放电阶段识别模型的训练周期长、计算复杂度高和收敛速度慢等问题，该文提出一种经高斯函数加权的改进K-近邻（KNN）分类算法应用于XLPE电缆气隙放电阶段识别。对气隙放电的随机测试样本采用基于二叉树的核函数支持向量机、未改进的K-近邻算法和改进后的K-近邻算法三种算法分别进行了阶段识别。试验结果表明，改进后的K-近邻算法识别正确率高、速度快，处理含噪信号鲁棒性好，相比另两种算法更优。
关键词：XLPE 气隙放电 特征参量 改进K-邻近算法 支持向量机
XLPE电缆被广泛应用于中高压电力电缆中，一旦电缆绝缘存在可能危及电缆安全运行寿命的缺陷，常在局部放电上有所体现[1]。XLPE电缆在生产过程中可能会出现绝缘偏心、绝缘掺有杂质、电缆受潮、交联度不均匀等绝缘问题；在施工过程中，电缆绝缘表面可能会留下细小划痕，因这些划痕长期暴露在空气中，存在吸入水分等现象，这些问题可能会导致电力电缆在竣工试验中或投运后出现故障，对电缆长期安全运行造成严重隐患。其中，比较典型的局部放电现象是电缆本体或接头处的气隙放电[2]。因此，对电力电缆气隙放电发展特性分析并建立专家比对库，通过识别算法进行判断分析，可以为局部放电风险程度评估提供有效的参考。
气隙放电是一个复杂的随机放电现象，气隙放电会受气隙中的电场、温度和气压等不确定因素的影响。国内外学者通过在实验室中制作各种局部放电模型来模拟其放电发展过程，对局部放电的机理和特性进行了大量的研究，加拿大学者R. Bartnikas将局部放电分为火花放电、辉光放电、亚辉光放电等类型[3]。南非金山大学C. Nyamupangedengu等通过大量局部放电试验，研究了局部放电频谱对电源电压频率变化的响应，得出气隙缺陷两端的电压会受到空间电荷的影响，间接导致气隙缺陷中的放电相位与其他缺陷放电类型有所不同[4]。
在放电特征量提取方面，常见的特征提取法包括局部放电脉冲相位分布模式（Phase Resolved Partial Discharge, PRPD）、局部放电时间分布模式（Time Resolved Partial Discharge, TRPD）、放电时差Δt模式和脉冲序列相位分布分析模式（Phase Resolved Pulse Sequence Analysis, PRPSA）谱图。目前用于表征局部放电的特征参量主要有基本特征、统计特征、波形特征、三维q-φ-n谱图、图像矩特征、分形特征参量以及小波特征参量等[5]。文献[6]将分形理论和小波分析相结合，利用核判别分析分形维数进行特征提取；文献[7]提取局部放电灰度图像的数学形态谱作为特征参量，对局部放电类型进行识别；文献[8]提出了基于灰度-共生梯度共生矩阵特征提取方法，通过计算共生矩阵的15个参数作为特征参量，应用于故障电弧的识别；文献[9]提出了基于小波包分解后的能量变化分布规律，并以能量变化特征作为局部放电发展特性的新特征量；文献[10]提出一种基于二维经验小波变换（2 Dimension Little wood-Paley Empirical Wavelet Transform, 2D-LPEWT）的特征提取方法，可实现电缆局部放电不同缺陷类型的准确识别。综上所述，局部放电特征参量较多且信息分散，计算复杂度高。
在识别分类器方面，目前模式识别分类器的方法主要有支持向量机、神经网络、贝叶斯分类器、模糊逻辑等，支持向量机模型需要考虑二次凸优化的问题，这导致支持向量机对于求解大样本数据，计算复杂度高；文献[11]运用支持向量机结合分形理论对气体绝缘组合电器局部放电类型识别；神经网络算法虽然得到了广泛的应用，但学习效率固定，收敛速度较慢；文献[12]利用反向传播神经网络算法对局部放电类型进行识别，但也存在所需训练时间过长，局部最小值等问题；文献[13]利用概率神经网络对变压器局部放电类型进行识别，具有训练快速、不易产生局部最优等特点，但对输入的特征量要求高，未能广泛使用。总体而言，当前模式识别算法主要存在收敛速度较慢、训练周期较长、易陷于局部最小和训练样本需求量大等问题。
针对上述模式识别分类器所存在的不足，本文提出一种基于高斯核函数加权改进的K-近邻（K-Nearest Neighbor, KNN）分类算法应用于XLPE电缆气隙放电发展阶段识别。再运用聚类分析法将降维处理后的特征参量进行气隙放电阶段划分，并形成数据样本集，在此基础上，随机产生训练集与测试集。通过添加高斯核函数进行属性加权，高斯核函数可以有效避免为近邻分配很大的权重、稍远一点的权重会衰减很快的现象，因此改进后的K-近邻算法克服了传统K-近邻识别算法识别效率低的缺点，通过基于高斯核函数加权后的K-近邻算法进行XLPE电缆气隙放电阶段识别，该方法不仅具有结构较简单、容错率高的特点，而且在处理含噪信号时鲁棒性较好。
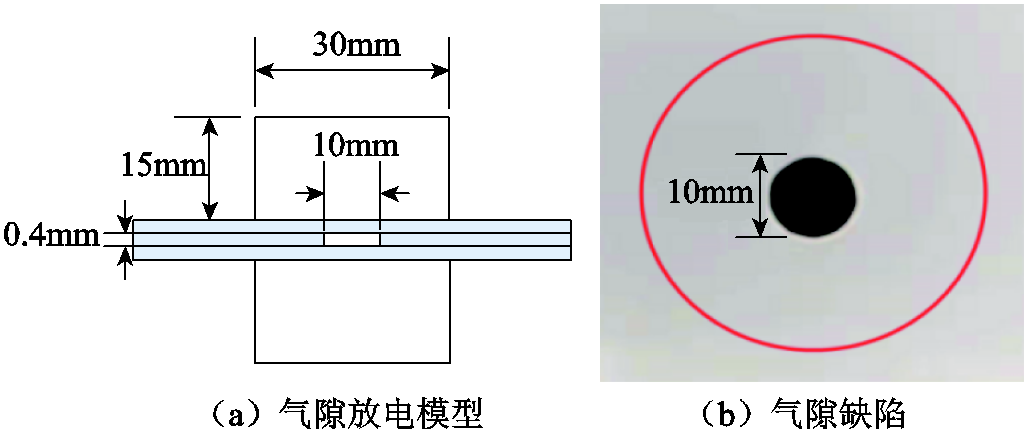
参照CIGRÉ Method II和ASTM D149—09的推荐方法[14]，制作圆柱形气隙模型，模拟XLPE电缆绝缘内部气隙放电，气隙缺陷示意图如图1所示。在图1a中，气隙放电模型上、下两端分别为高压、接地电极，电极直径为30mm、高为15mm，电极表面进行抛光处理，防止电极表面出现尖端现象，影响气隙放电试验效果。气隙缺陷模型采用“三明治”结构，试验样品由直径为80mm、厚度为0.4mm的三层XLPE绝缘片经绝缘胶粘合而成，试品的中间层为模拟气隙缺陷层，该圆柱形气隙缺陷的直径为10mm、高为0.4mm，如图1b所示，所有缺陷样本为防止出现毛刺，将XLPE绝缘片进行打磨处理工作，然后通过干燥箱进行24h干燥处理。
图1 气隙缺陷示意图
Fig.1 Schematic diagram of air gap defects
本文设计长140mm、宽120mm、高80mm环氧树脂绝缘装置，内充填绝缘油，将制作的气隙缺陷模型放置其中。利用型号为HRKZT(T)-200kV/ 250mA的无局放工频试验变压器提供试验电压，通过FRC型交直流电容式分压器连接到数字示波器（TDS5052B）进行测量，该分压器的分压比为1:1 000；采用阻值为10Ω的精密电阻，采样频率为12.5MHz。按照GB/T 7354—2018搭建了局部放电测试回路并开展试验，试验测量系统接线如图2所示。
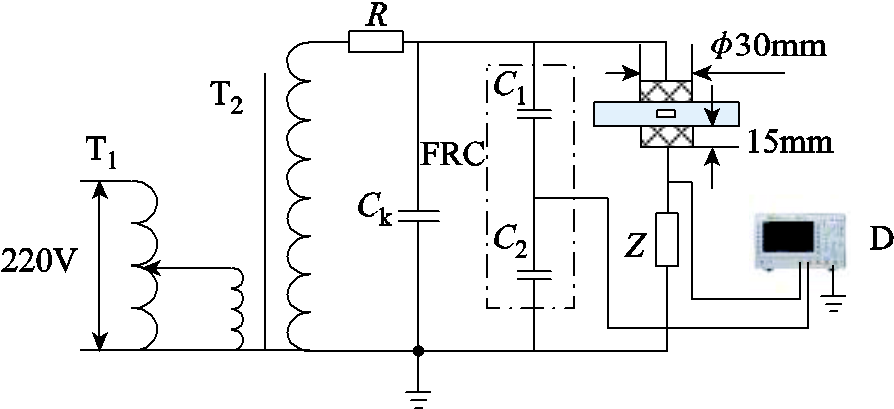
图2 气隙放电试验测量系统
T1—调压器 T2—无局放试验变压器 R—保护电阻 Ck—耦合电容 FRC—分压器 D—数字示波器 Z—检测阻抗
Fig.2 Air gap discharge test measuring system
国际标准IEC 61294提出，可将局部放电量超过100pC时的电压值作为起始放电电压，采用该方法得到的起始放电电压相对准确[15]。试验采用逐步升压法进行气隙放电试验，以0.5kV为升压步长，每次升压后停留2min，观察示波器显示的脉冲幅值，确定没有发生气隙放电后再继续升高外加电压，当放电脉冲幅值达到或超过2倍的噪声幅值时，此时施加的电压即为起始放电电压。当出现脉冲电压信号时，以0.5kV为升压步长，每次升压停留10min，待放电稳定后进行数据采集。
本文将工频相位φ在一个工频周期内划分256个统计区间，统计500组放电信号在工频周期内的放电次数n、视在放电量q、以及放电相位φ，构建q-φ-n三维图谱。通过多次反复试验，得到气隙起始放电电压约为9.7kV，击穿电压约为30.7kV，典型不同发展阶段的放电图谱如图3所示。图3a为外施电压为9.7kV时，负半周期的放电相位分布在260°~320°左右，正半周期的放电相位分布在80°左右；随着放电通道的扩展和积累，自由电子数目累增，正半周期放电相位逐步向0°方向扩散，负半周期放电相位逐步向180°方向扩散，如图3b和图3c所示。放电相位会因气隙通道中累积的自由电子数目增加而扩宽，增加逃离气隙缺陷通道的概率，XLPE绝缘板表面的电导率增加，从而使气隙放电的相位前移[16]。
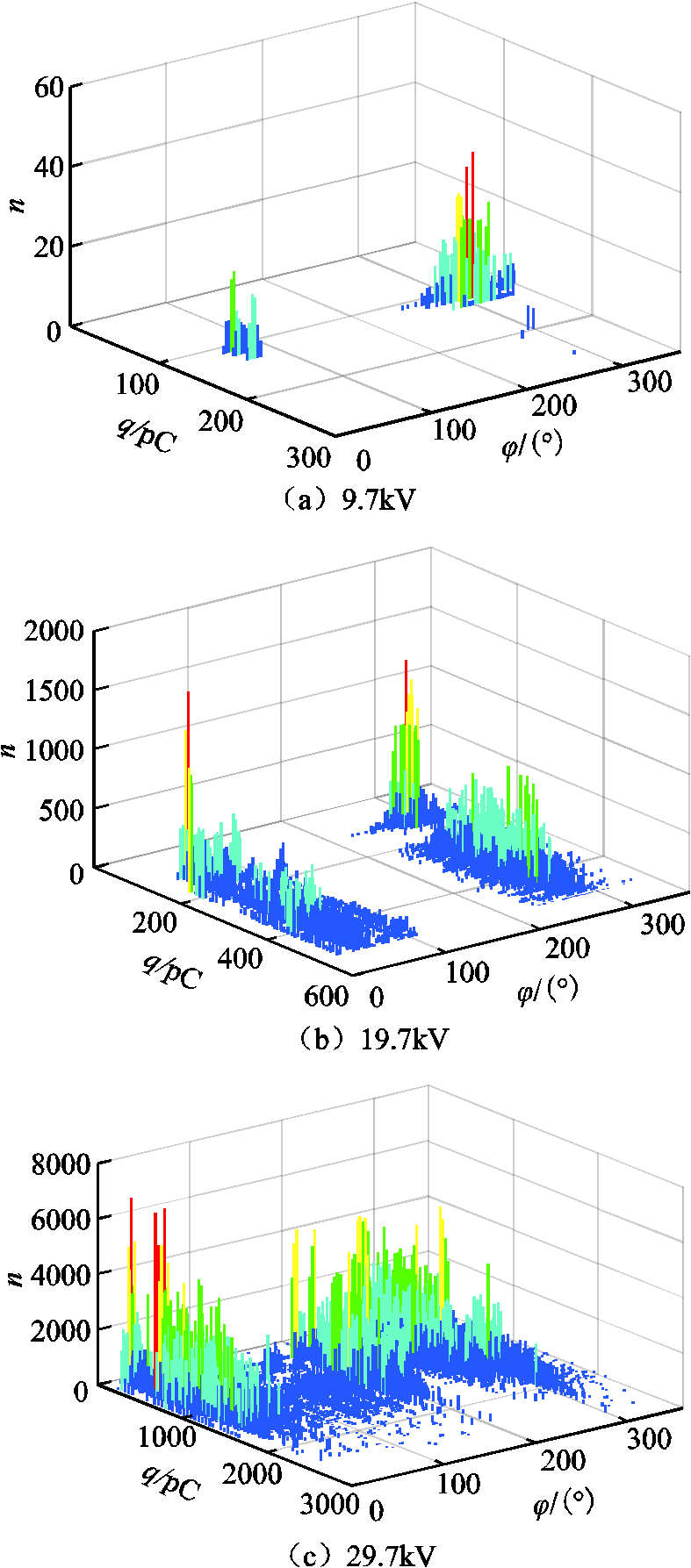
图3 q-φ-n三维图
Fig.3 The three-dimensional figure of q-φ-n
根据q-φ-n三维图谱进行二维投影并处理，得到XLPE电缆气隙放电最大放电幅值相位分布Hqmax(φ)、放电次数幅值分布Hn(q)、放电次数相位分布Hn(φ)。根据上述图谱可得平均放电量相位分布Hqn(φ)。从以上四种图谱得出特征参数[18]，并按照工频周期分为正半周期和负半周期统计算子，见表1。
表1 特征参数统计算子
Tab.1 Statistical operators of characteristic parameters
名称参数 Hqmax(φ)Sk-Sk+Ku-Ku+Pe-Pe+Asycc Hqn(φ)Sk-Sk+Ku-Ku+Pe-Pe+Asycc Hn(φ)Sk-Sk+Ku-Ku+Pe-Pe+Asycc Hn(q)SkKuPeαβ
本文采用核主元分析（Kernel Principal Component Analysis，KPCA）方法进行特征降维处理。该方法是通过一个非线性映射将数据从输入空间映射到特征空间，在特征空间中进行PCA，其中的内积运算采用一个核函数来替代。文献[19]中详细地介绍了该方法的计算过程，处理结果见表2。
表2 KPCA计算结果
Tab.2 The calculation results of KPCA
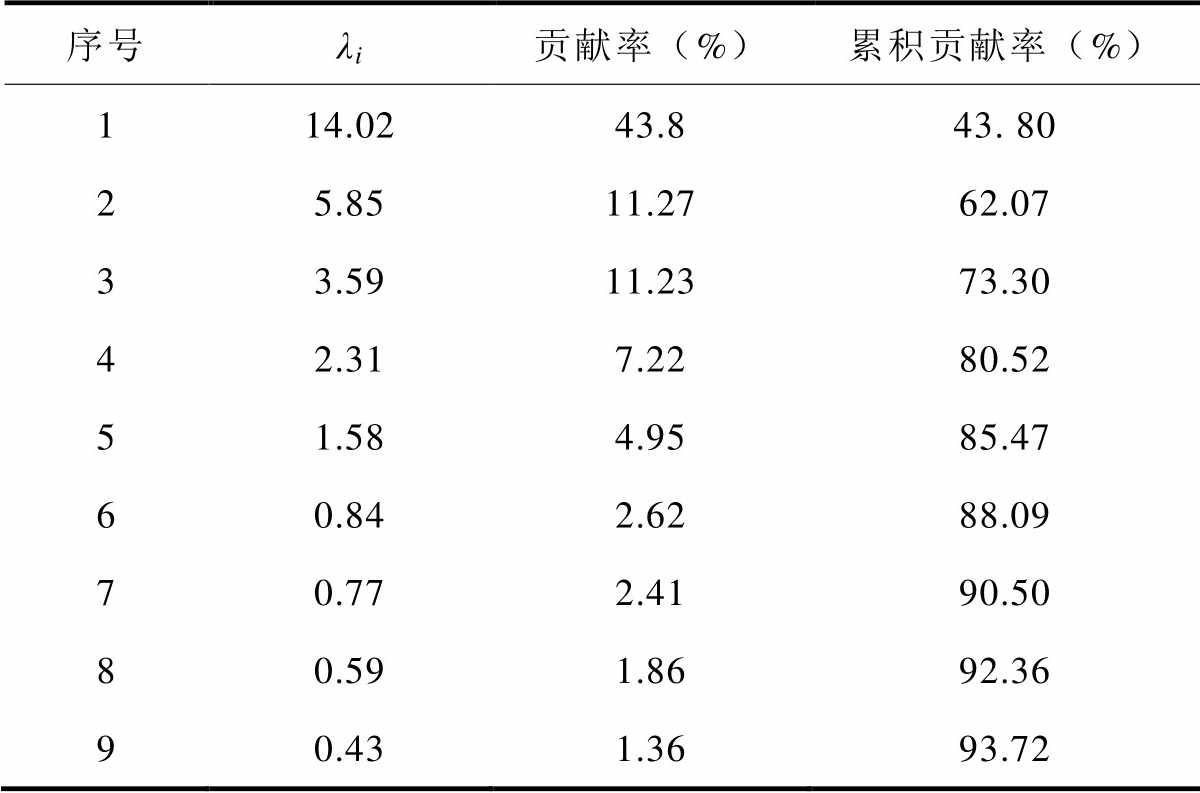
序号λi贡献率（%）累积贡献率（%） 114.0243.843. 80 25.8511.2762.07 33.5911.2373.30 42.317.2280.52 51.584.9585.47 60.842.6288.09 70.772.4190.50 80.591.8692.36 90.431.3693.72
由表2可知，核主元分析后第一主元的贡献率为43.80%，经降维处理后的9个新特征参量累积贡献率已达93.72%，说明降维后的新特征量能够表征原始特征量的主要信息[19]，因此将放电信号经KPCA降维后的9个特征参数作为新的统计特征参数，降低特征参量维数，减少计算复杂程度。
聚类是将数据分类到不同的类或者簇的一个过程，因此同一个簇中的对象有很大相似性，而不同簇间的对象有很大差异性[20]。
将经核主元分析提取的9维特征量用于聚类分析，采用系统聚类法对整个XLPE电缆气隙放电发展过程进行阶段划分。文献[20]详细阐明了聚类分析的原理与步骤，本文采用欧式距离计算各特征值元素之间的距离，序号1~43表示以起始放电电压（9.7kV）、步长为0.5kV，击穿电压（30.7kV）的试验电压等级对应的放电特征参量样本，其系统聚类结果如图4所示。图中纵坐标表示距离，横坐标表示样本序号。当距离为8时，43个样本被划分为4个阶段，样本1、3~12对应为阶段一，样本2、13~22对应为阶段二，样本23~35对应为阶段三，样本36~43为阶段四，除样本2因气隙放电随机性被划分至阶段二外，其余样本数据的聚类结果与外施电压和放电时长具有一致的对应关系。试验观察发现，放电波形随着外施电压和放电时长的累积呈明显变化的趋势。放电相位随着气隙缺陷通道中的自由电子数目增加而变宽，由于逃离气隙缺陷通道的概率增加，使绝缘板表面的电导率增加，导致相位前移；视在放电量和放电重复率呈现出增加，减小，再急剧增加的趋势。综上，基于试验观察和系统聚类方法将气隙放电发展过程划分为四个阶段，依次为放电起始、放电发展、放电爆发、放电预击穿阶段。
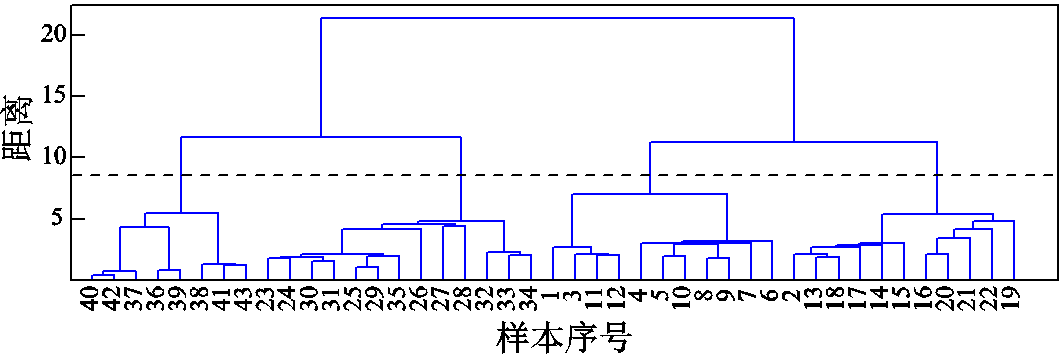
图4 聚类谱图
Fig.4 Cluster spectrum
T. Cover和P. Hart在1968年提出了K-近邻方法，该方法主要思想是将输入项x分配给相邻标记中最频繁的标记，KNN方法主要包含以下两个步骤。
（1）样本相似性度量。样本相似度量也称为距离度量，相似性一般用空间内两个点的欧式距离来度量，距离越大，表示两个点越不相似。常用的度量方法有欧几里得距离、余弦值（cos）、相关度（correlation）、曼哈顿距离（Manhattan distance）。本文采用欧式距离进行度量，假设在二维空间中，存在两点，坐标分别为A（x1, y1），B（x2, y2），则A、B两点的欧式距离dAB公式为
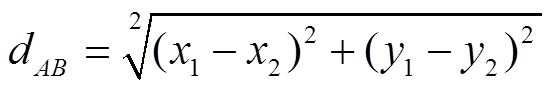（1）（2）K值设定。K值大小将影响最终分类结果，使用交叉验证方法检验分类器的误差率[21]。重复上述过程，每次检验K增值1，直至选取产生最小误差率的K值。
传统K-近邻算法结构比较简单，对于类内距离小、类间距离大的样本集分类效果比较好，对训练含噪声数据具有鲁棒性。但传统K-近邻算法依赖K的取值和计算时间来计算一个新的测试元素和所有类元素之间的距离，对于随机分布的数据集分类效果不佳。XLPE电缆气隙放电发展过程统计特征参量维数较多，且各放电发展阶段之间的类间距离比较小，传统KNN算法对气隙放电发展阶段划分效果不佳。
因此在原有KNN算法基础上加以改进，通过属性加权来改变分类策略，以提高XLPE电缆气隙放电发展过程划分效果。
改进后的KNN算法对降维后的9维特征值进行属性加权处理，主要思想是增加相邻区域的权值对待测样本进行分类。
改进KNN算法的实现步骤：
（1）数据集分类，将数据集聚类成相似的组，由聚类分析方法将整个气隙放电阶段划分为四个类别，将所有数据分为训练样本集和测试样本集，假设每个训练样本的所属类别已知。因此训练数据集合为D={(Si, Ni) | i=1, 2, 3 ,…, n}；n为训练样本数；Si为训练样本；Ni为类别标识，Ni∈{ Lj | j=1, 2, 3, …, r}，r为类别数，Lj为类别。假设测试样本集合为B={(Yt, Nt) | t=1, 2, 3, …, m}，m为测试样本数；Yt为测试样本，它的类别Nt待测。
（2）类中的每个样本项都依赖该样本与每个样本的训练数据中心点之间的距离，将输入的训练样本求出所属的类中心[22]，可根据式（2）求出。
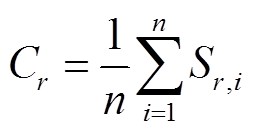（2）式中，Cr为类r的中心；n为该类训练样本个数；Sr,i为第r类中的第i样本。
本文所提取的放电特征量为9维向量，因此将训练样本中的同类别分成a组，同类别中每组的类中心按照式（2）进行计算，并重新构成训练样本集合Yi。
（3）对于测试样本Yt的类别判断
计算测试样本到每个训练样本的距离可由式（3）求出。
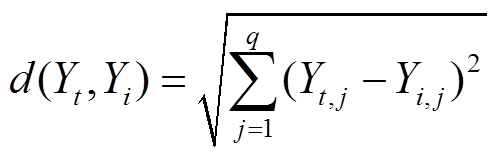（3）式中，d(Yt, Yi)为测试样本与每个训练样本之间的距离；q为该特征值维数总和。
（4）设置K值，根据测试样本与每个训练样本间距离的大小排序，以此确定K+1个近邻样本，即Yt,1, Yt,2, Yt,3, …, Yt,K+1，并按式（4）将距离进行标准化处理。
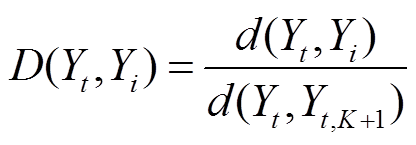（4）式中，D(Yt,Yi)为标准化处理的距离；d(Yt, Yt, K+1)为从K+1个近邻样本中与Yt的最大距离。
（5）进行属性加权，其权重表示该特征参量的重要性，本文通过添加高斯核函数进行距离加权[23]。
高斯核函数（Gaussian Kernel），也称径向基（Radial Basis Function, RBF）函数，通过高斯核函数进行距离加权后，距离越近的点权重越大，距离越远的点权重越小，高斯核函数的定义为
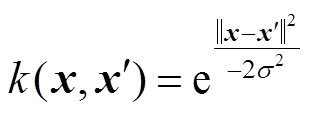（5）式中，x、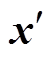
为假设的两个向量；
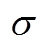为带宽，控制径向作用范围。
将标准化后的距离D(Yt,Yi)代入式（5）中得到同类别概率函数[24]，即
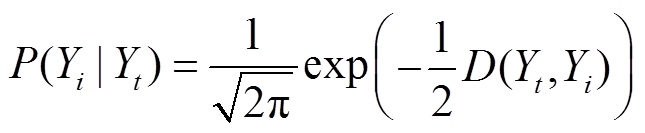（6）式中，P(Yi | Yt)为同类别概率。
（6）根据测试样本与K个近邻同类别概率，求出Yt为类别Ni(i=1,2,3,…,r)的后验概率为
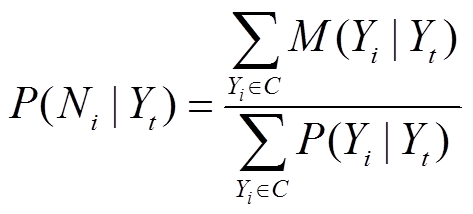（7）其中
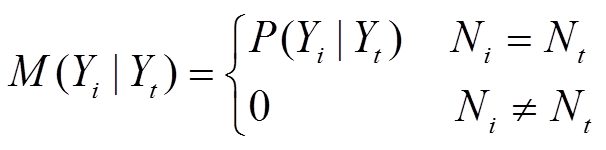
式中，P(Ni |Yt)为后验概率；Ni为训练样本i对应的类别；Nt为测试样本t对应的类别。
根据后验概率最大值所对应的类别被判定为Yt所对应的类别。
改进的K-近邻算法流程如图5所示。
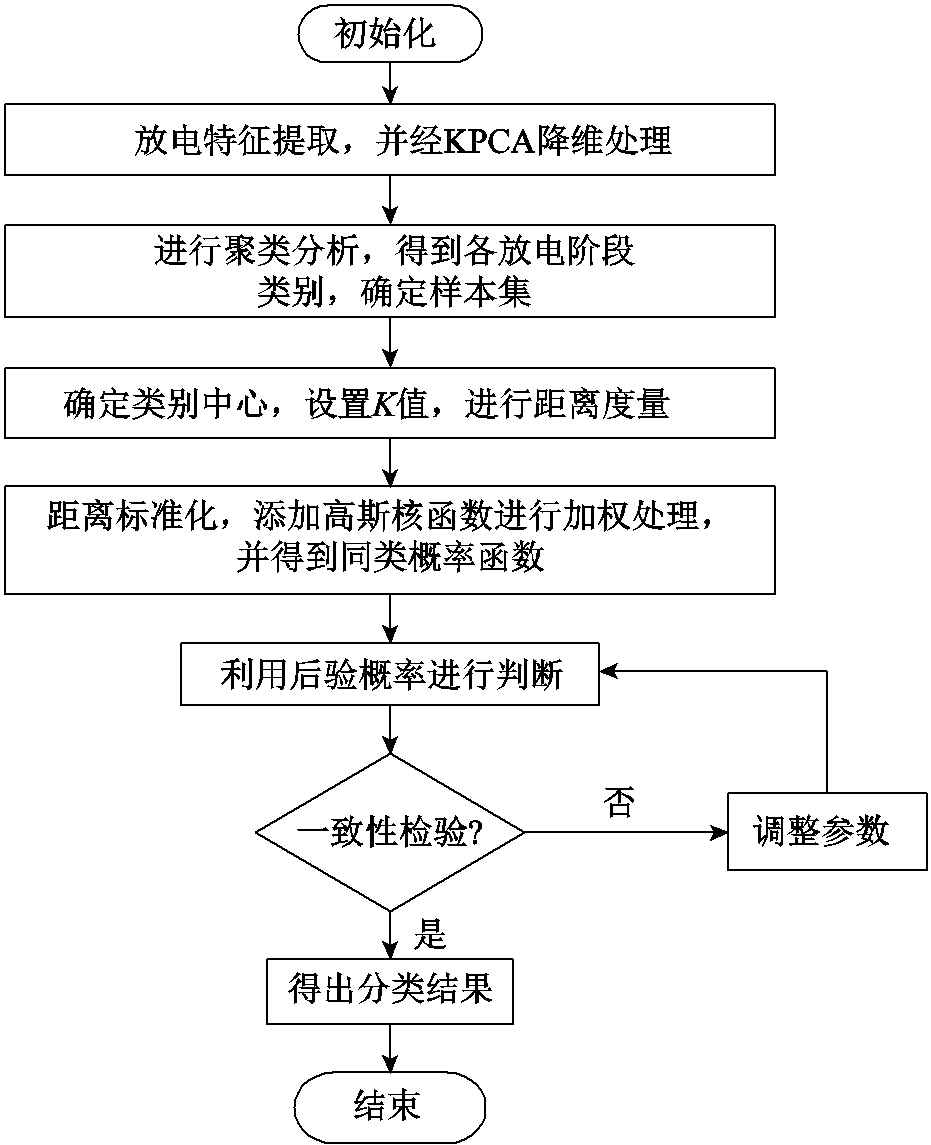
图5 改进K-近邻算法实现流程
Fig.5 Implementation process of improved KNN algorithm
系统聚类将XLPE气隙放电发展阶段分为四个阶段，因此将四个阶段按起始、发展、爆发、预击穿依次定义为类别A、B、C、D，选取放电样本数据共计600组，每类数据150组，在各类中随机抽取80%作为训练样本，剩余20%作为测试样本。
不同识别算法原理存在差异，识别率也会因训练样本、测试样本的数量存在一定差异而受影响。为了更好地分析说明改进KNN算法的识别效果，本文选取了支持向量机、传统KNN、改进KNN三种算法分别对XLPE电缆气隙放电发展阶段进行识别。
（1）支持向量机。采用基于二叉树的核函数支持向量机（Support Vector Machine, SVM）算法进行XLPE电缆气隙放电阶段识别。将所有训练样本进行集合，先分成类别A和类别B、C、D两大类，输出期望值；然后对B、C、D样本进行集合训练，分为类别B和类别C、D两大类，输出期望值，重复上述步骤，直至输出类别D的期望值。
（2）传统KNN与改进KNN算法。KNN算法是一种较为简单的分类方法；而改进后的KNN算法利用高斯核函数进行加权，优化分类策略，将每类各120组数据作为最初训练集，以4组为单位，分别求出每4组的类中心，并将其组合成30组新的训练样本。按照3.1节、3.2节步骤进行传统KNN、改进KNN识别，此处不再赘述。
4.2.1 识别率
改进KNN算法采用交叉验证确定K值大小，取值方法已在前面阐述，多次仿真确定当K值取7时，识别率最高，第一、二、三主元的分类效果如图6所示。
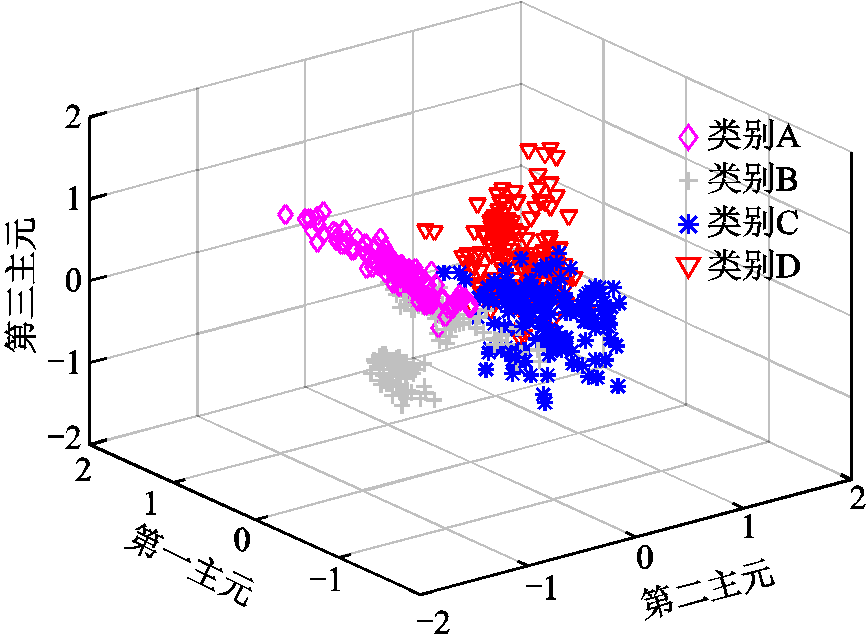
图6 改进KNN算法分类效果图
Fig.6 Improved KNN algorithm classification effect diagram
将支持向量机、传统KNN、改进KNN三种算法按照上述步骤对XLPE电缆气隙放电发展阶段进行识别，识别率如图7所示。
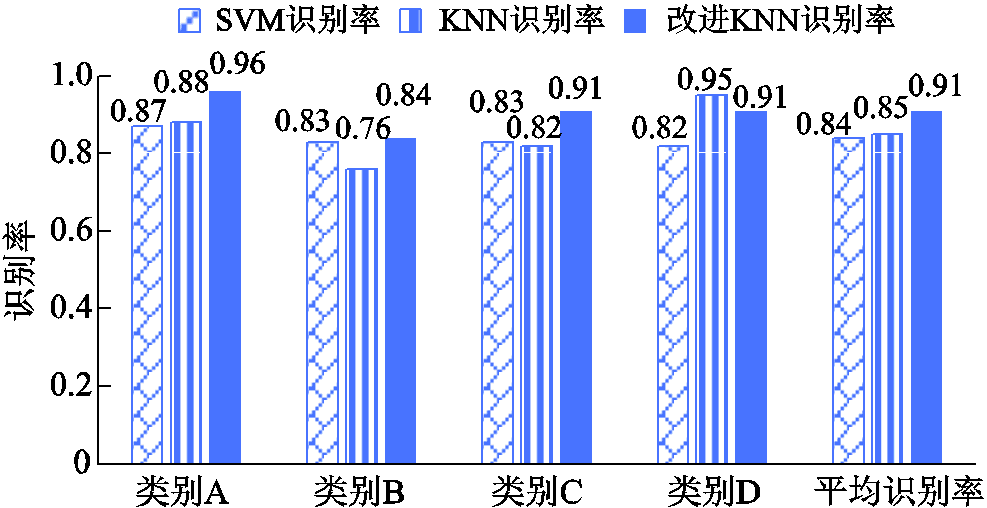
图7 三种算法识别率
Fig.7 Recognition rates of three algorithms
结果表明，改进后的KNN识别算法平均识别率达到了0.91，高于SVM及传统KNN算法。
4.2.2 识别速度
基于三种算法的放电发展阶段识别在FL8000UN华硕电脑（CPUi7-8550u，内存8G）的64位Win10操作系统上运行完成，不同算法的识别速度结果见表3。从表3可以看出，传统KNN及改进后的KNN算法的识别速度明显高于基于二叉树核函数的SVM算法；改进后的KNN算法识别速度略高于传统KNN算法，识别时间仅需8.38s。
表3 三种算法识别速度
Tab.3 Three algorithms identify speed comparison
识别算法SVM传统KNN算法改进KNN算法 识别时间/s21.639.068.38
综上，改进KNN算法中由于增加了高斯核函数对样本距离进行加权处理，克服了传统KNN算法赋予所有类别间特征参量权重相同的缺点；使得测试样本的结果与训练样本更相似，从而优化了分类策略，提高了识别率和识别速度。
在XLPE电缆的实际运行工况下，现场局放测试通常受到环境噪声干扰从而导致测量不准确，进而影响局部放电的分析和识别效果。为了进一步探究噪声干扰对所提出的改进KNN算法识别效果的影响，本节将讨论不同程度背景噪声水平以及经去噪处理后的气隙放电阶段识别结果。
4.3.1 背景噪声干扰对识别效果的影响
分别按照信噪比为40dB、30dB、20dB、10dB对不同阶段共600组气隙放电信号添加背景噪声，信噪比数值越低，背景噪声干扰越大。10dB对应的背景噪声水平约为脉冲电压幅值的32%。未加噪声与信噪比10dB的典型气隙放电周波数据如图8所示。
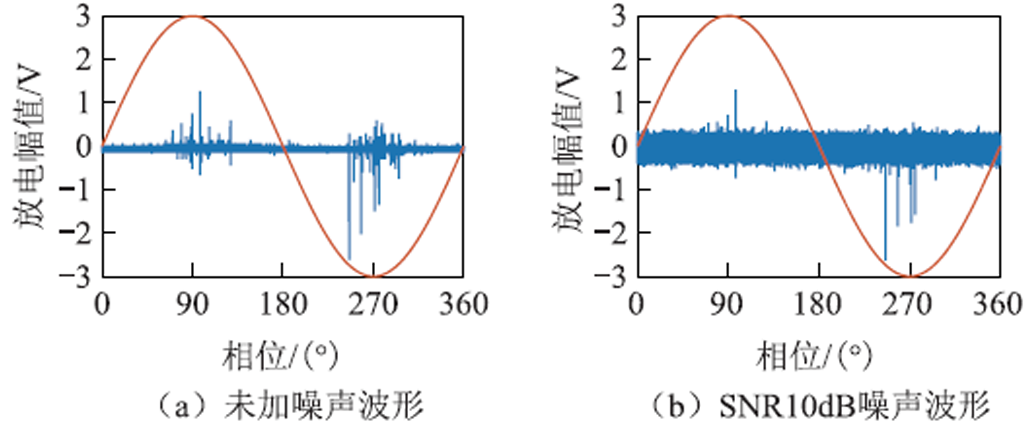
图8 典型气隙放电周波
Fig.8 Typical PD signal
按照4.1节步骤分别利用三种算法对不同信噪比的气隙放电信号进行阶段识别，结果如图9所示。
从图9得出，背景噪声水平越高，含噪数据的平均识别率越低，远低于理想试验数据。造成此现象的原因是：由于含噪信号会影响其放电特征值的提取，导致各算法的识别精度均有所降低，但噪声干扰对改进后KNN算法识别精度的影响低于另两种识别算法，在信噪比为10dB时，平均识别率可达到0.81。
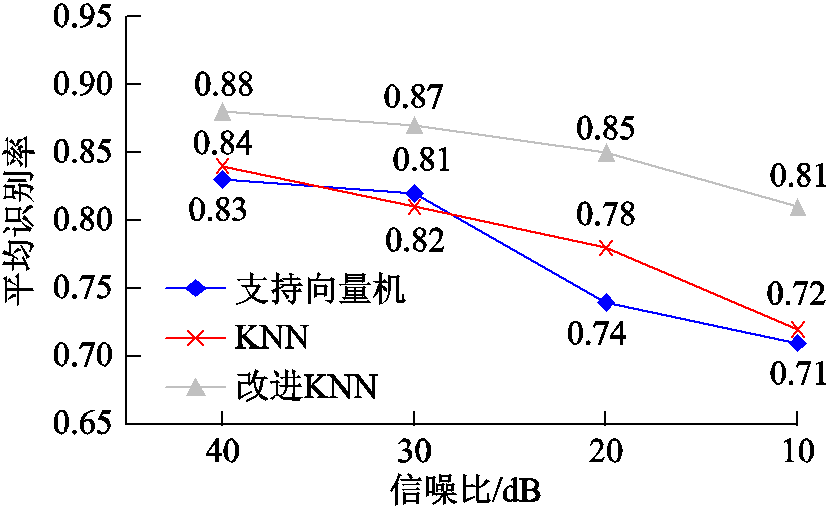
图9 含噪信号的识别率分析结果
Fig.9 The recognition rate results of the noise signal
不同背景噪声信号对三种算法识别速度的影响见表4。与表3相比，随着背景噪声值提高，三种算法的识别速度均有不同程度的下降。其中基于二叉树的支持向量机识别速度下降幅度最大，改进KNN识别速度下降幅度最小。可以看出，背景噪声干扰对改进KNN的识别速度影响最小。
表4 不同背景噪声对三种算法识别速度影响
Tab.4 The influence of different background noise on the recognition speed of the three algorithms
SNR/dB识别速度/s SVM传统KNN算法改进KNN算法 4021.689.118.39 3022.719.148.68 2024.6910.138.89 1024.7211.129.28
综上，受不同背景噪声干扰影响，三种识别算法的识别率和识别速度均有所下降，但是改进KNN算法的识别率和识别速度相较另两种方法更优，识别效果更好。说明该方法对背景噪声干扰下的气隙放电数据进行识别处理时，具有鲁棒性。
4.3.2 经小波去噪处理后的识别精度
虽然GB/T 7354—2018和IEC62478—2016等标准推荐在实际工程测量中采用干扰源移除或屏蔽、单点接地、滤波、校准等方式，能够在一定程度上降低干扰信号对实测局部放电信号的影响，使背景干扰低于许可的局部放电水平。但为更有效地对局部放电信号进行分析诊断，众多学者提出对含噪声的局部放电信号采用不同的软件去噪方法进行数据预处理。
基于文献[25]所述小波阈值去噪原理，对信噪比为10dB的含噪信号经db4小波分解，分解层数为4层，根据ddencmp函数自动生成小波去噪的阈值，利用每一层小波分解的噪声水平估计阈值进行处理，对修正后的小波分解结构进行重构。去噪处理前后信噪比10dB的典型放电周波数据如图10所示。
按照前述章节的识别步骤，将经小波阈值去噪处理后的不同阶段气隙放电数据采用三种算法进行阶段识别，结果见表5。
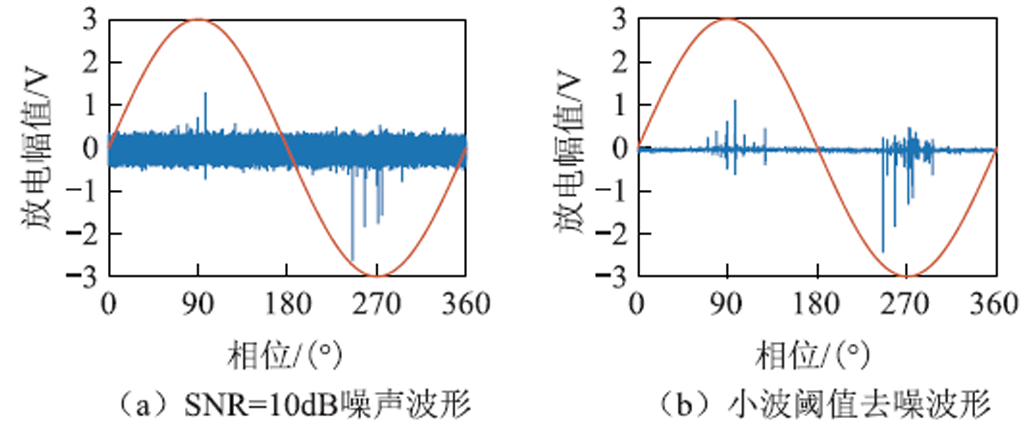
图10 去噪前后气隙放电信号对比
Fig.10 Comparison of PD signals before and after denoising
表5 三种算法对去噪信号的识别结果
Tab.5 Three algorithms identify the results of denoising signal
识别类平均识别率识别速度/s A类B类C类D类 SVM0.810.780.770.710.7722.95 KNN0.790.810.790.780.7910.21 改进KNN0.870.820.850.830.848.86
从表5可知，改进KNN算法较另两种方法识别率更高，识别速度更快。实验结果验证了基于改进KNN的XLPE电缆气隙放电阶段识别方法的有效性。
本文通过搭建XLPE电缆气隙放电试验平台，并制作气隙缺陷模型，开展多次重复性放电试验。试验分析表明：XLPE电缆气隙放电发展过程分为放电起始、放电发展、放电爆发、放电预击穿四个阶段。本文提出一种经高斯核函数加权的改进KNN分类算法，并将其应用于XLPE电缆气隙放电发展阶段识别。主要结论如下：
1）改进KNN相较传统KNN和基于二叉树的核函数支持向量机两种方法，具有更高的识别率和更快的识别速度，在XLPE电缆气隙放电阶段识别应用中体现出更优的识别效果。
2）噪声干扰对改进后KNN算法识别精度的影响低于另两种分类识别器识别算法，在噪声干扰的情况下鲁棒性较好；对高含噪信号进行去噪处理后，改进KNN算法整体识别效果更优。
参考文献
[1] 周远翔, 赵健康, 刘睿, 等. 高压/超高压电力电缆关键技术分析及展望[J]. 高电压技术, 2014, 40(9): 2593-2612. Zhou Yuanxiang, Zhao Jiankang, Liu Rui, et al. Key technical analysis and prospect of high voltage and extra-high voltage power cable[J]. High Voltage Engineering, 2014, 40(9): 2593-2612.
[2] 杨帆, 杨旗, 程鹏, 等. 电缆接头内部气隙放电缺陷下的绝缘劣化程度表征方法[J]. 电工技术学报, 2017, 32(2): 24-32. Yang Fan, Yang Qi, Cheng Peng, et al. Study of cracking extent for gap discharge in insulating material of power cable joint[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 24-32.
[3] Bartnikas R. Partial discharges. their mechanism, detection and measurement[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2002, 9(5): 763-808.
[4] Nyamupangedengu C, Jandrell I R. Partial discharge spectral response to variations in the supply voltage frequency[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2012, 19(2): 521-532.
[5] 谢波. 油纸绝缘气隙放电产气和能量变化特性及信号能量熵特征研究[D]. 重庆: 重庆大学, 2016.
[6] 肖迎群, 冯良贵, 何怡刚. 基于小波分形和核判别分析的模拟电路故障诊断[J]. 电工技术学报, 2012, 27(8): 230-238. Xiao Yingqun, Feng Lianggui, He Yigang. A fault diagnosis approach of analog circuit using wavelet-based fractal analysis and kernel LDA[J]. Transactions of China Electrotechnical Society, 2012, 27(8): 230-238.
[7] 刘云鹏, 律方成, 李成榕. 局部放电灰度图象数学形态谱的研究[J]. 中国电机工程学报, 2004, 24(5): 179-183. Liu Yunpeng, Lü Fangcheng, Li Chengrong. Study on pattern spectrum of patial discharge grayscale image[J]. Proceedings of the CSEE, 2004, 24(5): 179-183.
[8] 郭凤仪, 邓勇, 王智勇, 等. 基于灰度-梯度共生矩阵的串联故障电弧特征[J]. 电工技术学报, 2018, 33(1): 71-81. Guo Fengyi, Deng Yong, Wang Zhiyong, et al. Series arc fault characteristics based on gray level-gradient co-occurrence matrix[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 71-81.
[9] 陈伟根, 谢波, 龙震泽, 等. 基于小波包能量熵的油纸绝缘气隙放电阶段识别[J]. 中国电机工程学报, 2016, 36(2): 563-569. Chen Weigen, Xie Bo, Long Zhenze, et al. Stage identification in air-gap discharge of oil-impregnated paper insulation based on wavelet packet energy entropy[J]. Proceedings of the CSEE, 2016, 36(2): 563-569.
[10] 秦雪, 钱勇, 许永鹏, 等. 基于2D-LPEWT的特征提取方法在电缆局部放电分析中的应用[J]. 电工技术学报, 2019, 34(1): 170-178. Qin Xue, Qian Yong, Xu Yongpeng, et al. Application of feature extraction method based on 2D-LPEWT in cable partial discharge analysis[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 170-178.
[11] 弓艳朋, 刘有为, 吴立远. 采用分形和支持向量机的气体绝缘组合电器局部放电类型识别[J]. 电网技术, 2011, 35(3): 135-139.Gong Yanpeng, Liu Youwei, Wu Liyuan. Identification of partial discharge in gas insulated switchgears with fractal theory and support vector machine[J]. Power System Technology, 2011, 35(3): 135-139.
[12] 汤会增, 韩湘, 毛建坤, 等. 基于BP网络的GIS局部放电声电联合检测故障定位方法[J]. 工业仪表与自动化装置, 2016(4): 57-60. Tang Huizeng, Han Xiang, Mao Jiankun, et al. The fault location method of acoustic electric joint partial discharge detection based on BP network in GIS[J]. Industrial Instrumentation & Automation, 2016(4): 57-60.
[13] 李正明, 钱露先, 李加彬. 基于统计特征与概率神经网络的变压器局部放电类型识别[J]. 电力系统保护与控制, 2018, 46(13): 55-60. Li Zhengming, Qian Luxian, Li jiabin. Type recognition of partial discharge in power transformer based on statistical characteristics and PNN[J]. Power System Proteceion and Control, 2018, 46(13): 55-60.
[14] D149—09 Standard Test method for dielectric breakdown voltage and dielectric strength of solid electrical insulating materials at commercial power frequencies[S]. 2013.
[15] 崔鲁, 陈伟根, 杜劲超, 等. 植物油-纸绝缘气隙放电形态及发展特征[J]. 电工技术学报, 2018, 33(3): 618-626. Cui Lu, Chen Weigen, Du Jinchao, et al. Investigation on air-gap discharge patterns and development characteristics of vegetable oil-paper insulation[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 618-626.
[16] 陈伟根, 龙震泽, 谢波, 等. 不同气隙尺寸的油纸绝缘气隙放电特征及发展阶段识别[J]. 电工技术学报, 2016, 31(10): 49-58. Chen Weigen, Long Zhenze, Xie Bo, et al. Characteristics and development stage recognition of air-gap discharge within oil-paper insulation considering effect of cavity size[J]. Transactions of China Electrotechnical Society, 2016, 31(10): 49-58.
[17] 谢波, 陈伟根, 崔鲁, 等. 油纸绝缘气隙放电发展能量熵特征研究[J]. 电工技术学报, 2016, 31(12): 58-64. Xie Bo, Chen Weigen, Cui Lu, et al. Energy entropy feature research in air-gap discharge development process of oil-immersed paper insulation[J]. Transactions of China Electrotechnical Society, 2016, 31(12): 58-64.
[18] 周凯, 吴广宁, 吴建东, 等. 基于局部放电统计参量的脉冲电压下绝缘老化分析[J]. 电工技术学报, 2008, 23(4): 6-12. Zhou Kai, Wu Guangning, Wu Jiandong, et al. Analysis of aging properties for insulation based on statistical parameters of partial discharge under pulse voltage[J]. Transactions of China Electrotechnical Society, 2008, 23(4): 6-12.
[19] 唐炬, 谢颜斌, 周倩, 等. 基于最优小波包变换与核主分量分析的局部放电信号特征提取[J]. 电工技术学报, 2010, 25(9): 35-40. Tang Ju, Xie Yanbin, Zhou Qian, et al. Feature extraction for partial discharge signals based on the optimal wavelet packet basis transform and kernel principal component analysis[J]. Transactions of China Electrotechnical Society, 2010, 25(9): 35-40.
[20] 辛焕平. MATlAB R2017a模式识别与智能计算[M]. 北京: 电子工业出版社, 2018.
[21] Kohavi R. A study of cross-validation and bootstrap for accuracy estimation and model selection[C]//Proc eedings of the 14th Int ernational Joint Conference on Artificial Intelligence(IJCAI), Montréal, Morgan Kaufmann, 1995: 1137-1143.
[22] 陈法法, 汤宝平, 苏祖强. 基于等距映射与加权KNN的旋转机械故障诊断[J]. 仪器仪表学报, 2013, 34(1): 215-220. Chen Fafa, Tang Baoping, Su Zuqiang. Rotating machinery fault diagnosis based on isometric mapping and weighted KNN[J]. Chinese Journal of Scientific Instrument, 2013, 34(1): 215-220.
[23] Sarah M A, Ahmed I S, Labib M L. Gene expression cancer classification using modified K-Nearest neighbors technique[J]. Biosystems, 2019, 176: 41-51.
[24] 朱明旱, 罗大庸, 易励群. 一种序列的加权KNN分类方法[J]. 电子学报, 2009, 37(11):2584-2588. Zhu Minghan, Luo Dayong, Yi Liqun. A sequential weighted K-nearest neighbor classification method[J]. Acta Electronica Sinica, 2009, 37(11): 2584-2588.
[25] 王维博, 董蕊莹, 曾文入, 等. 基于改进阈值和阈值函数的电能质量小波去噪方法[J]. 电工技术学报, 2019, 34(2): 409-418. Wang Weibo, Dong Ruiying, Zeng Wenru, et al. A wavelet de-noising method for power quality based on an improved threshold and threshold function[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 409-418.
Development Stage Identification of XLPE Cable Air-Gap Discharge Based on Improved K-Nearest Neighbor Algorithm
Abstract It is essential to identify development stages of air-gap discharge in XLPE cable accurately under operation. It will not only help to prevent the cable fault, but to safeguard operation of power system. In this paper, the test platform and artificial defect sample manufacture method were introduced firstly. Then feature extraction and dimension reduction steps on a large number of experimental samples were described. Based on experimental observation and cluster analysis, the development process of air-gap discharge was classified into four stages accordingly. Aiming at the problems such as long training cycle, high computational complexity and slow convergence rate, this paper proposes an improved K-nearest neighbor (KNN) r classification algorithm weighted by Gaussian function to identify the air-gap discharge stage of XLPE cable. Three kinds of algorithms, namely kernel support vector machine (SVM) based on binary tree, unimproved KNN and improved KNN, were used to identify the random test samples of air gap discharge. Results show that improved KNN algorithm has high recognition accuracy, fast recognition speed and good robustness in processing noisy signals, which is better than the other two algorithms.
Keywords：XLPE, air-gap discharge, characteristic parameter, improved K-nearest neighbor (KNN), support vector machine
中图分类号：TM85
DOI：10.19595/j.cnki.1000-6753.tces.191400
重庆市基础研究与前沿探索项目（重庆市自然科学基金）（cstc2018jcyjAX0295）、重庆市教委科学技术研究项目（KJQN202001146）和国家自然科学基金（51607019）资助项目。
收稿日期2019-11-01
改稿日期 2020-05-26
陈 曦 男，1986年生，博士，讲师，研究方向为电力设备在线监测与智能诊断技术、能源互联网、能源经济与市场等。E-mail：chenxi1986@cqut.edu.cn
骆高超 男，1994年生，硕士研究生，研究方向为电力设备在线监测与智能诊断技术。E-mail：472473953@qq.com（通信作者）
（编辑 郭丽军）