温度和老化意识融合驱动的电动车辆锂离子动力电池电量和容量协同估计
王 榘1 熊 瑞1 穆 浩1,2
(1.电动车辆国家工程实验室(北京理工大学) 北京 100081 2. 北京空间飞行器总体设计部 北京 100094)
摘要 作为电动车辆的技术瓶颈,动力电池具有强时变非线性特性且可测量有限,使用时易受温度和老化的影响,全寿命周期和宽温度下精确状态估计一直是行业的技术难题。为此,该文首先使用不同温度和不同老化阶段的数据,建立了具有温度和老化意识的多阶段模型;然后利用概率密度函数计算单一模型的权值,提出了多阶段模型融合驱动的动力电池荷电状态(SOC)和容量协同估计方法;最后考虑不确定老化和温度因素的验证结果表明,提出的方法具有较高的SOC和容量估计精度,且对初值误差不敏感,-10%~50%初始误差时SOC估计误差小于2%,收敛速度快。
关键词:动力电池 全寿命周期 协同估计 荷电状态 容量估计
0 引言
发展节能与新能源汽车是国际共识,是中国的战略性新兴产业和“中国制造2025”确立的重点领域。显然,新能源汽车迎来了前所未有的发展机遇,与此同时带动了电池产业的迅猛发展。但是,动力电池作为燃油的替代品,循环寿命较低,衰减程度难以预测,环境适应性差,老化和温度变化显著影响其充放电性能;当动力电池的荷电状态(State-of-Charge, SOC)不准确时,极易引发过充放电,加剧寿命衰减,甚至引发安全问题。因此全生命周期和宽温度范围内状态精准估计至关重要[1]。
电池老化时会出现容量下降、内阻上升、开路电压(Open Circuit Voltage, OCV)收缩、极化效应加剧等表现。针对上述现象,国内外学者开展了一系列研究,M.Galeotti等利用阻抗谱测试建立了交流阻抗和老化的映射关系,该方法具有较好的估计精度[2],但实车应用受制于电池系统和车载设备。马泽宇等探究了不同老化下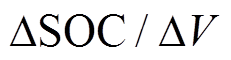 曲线,发现该曲线的峰值与老化状态有关,利用该值可实现老化状态的估计[3]。另外老化过程中SOC-OCV曲线会发生改变,熊瑞等通过构建OCV-SOC-容量的三维响应面实现了容量的准确估计[4],但对于曲率较小的电池,适用性有待深入探讨。电池内阻是老化的直观表现之一,Chen Lin等采用在线辨识算法实现了内阻的实时估计,利用内阻增长和容量衰退率之间的关系对电池的老化状态进行估计[5]。但在电池系统实际运行中,内阻易受温度、线束压降等因素的影响,导致估计结果出现较大误差[6]。针对锂离子动力电池恒压充电段中电流的变化趋势,A.Eddahech等发现电流变化的时间常数与容量衰退率之间存在较强的线性关系[7],该方法可用于单体电芯的老化状态识别,对于系统而言,有一定的局限性。受开路电压和内阻等因素影响,电池在老化后端电压会出现明显的变化,因此G.W.You等利用电池端电压、电流、温度作为输入,以SOC-健康状态作为输出,训练神经网络模型,并采用电池管理系统对结果进行验证[8],但该方法受限于训练集数据的完备性。
曲线,发现该曲线的峰值与老化状态有关,利用该值可实现老化状态的估计[3]。另外老化过程中SOC-OCV曲线会发生改变,熊瑞等通过构建OCV-SOC-容量的三维响应面实现了容量的准确估计[4],但对于曲率较小的电池,适用性有待深入探讨。电池内阻是老化的直观表现之一,Chen Lin等采用在线辨识算法实现了内阻的实时估计,利用内阻增长和容量衰退率之间的关系对电池的老化状态进行估计[5]。但在电池系统实际运行中,内阻易受温度、线束压降等因素的影响,导致估计结果出现较大误差[6]。针对锂离子动力电池恒压充电段中电流的变化趋势,A.Eddahech等发现电流变化的时间常数与容量衰退率之间存在较强的线性关系[7],该方法可用于单体电芯的老化状态识别,对于系统而言,有一定的局限性。受开路电压和内阻等因素影响,电池在老化后端电压会出现明显的变化,因此G.W.You等利用电池端电压、电流、温度作为输入,以SOC-健康状态作为输出,训练神经网络模型,并采用电池管理系统对结果进行验证[8],但该方法受限于训练集数据的完备性。
尽管电池使用工况、温度存在随机不确定性,但电池老化后常表现为极化电压增大,开路电压曲线变形,而温度对极化和开路电压也有相似的影响,故电池的端电压中耦合了温度和老化的因素。本文通过建立温度和老化意识参数融合驱动的电池模型,解耦了温度和老化。在此基础上,结合滤波算法实现了动力电池电量和容量的协同估计。
1 电池建模及参数标定
1.1 电池温变模型
由于Thevenin模型拟合精度高,且具有计算量小、实时性高的特点[9]。本文以该模型为基础,建立了含有温度输入的温变模型。第i个老化阶段模型的离散控制方程为[10]
式中,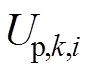 为第i个老化阶段下k时刻极化电压;
为第i个老化阶段下k时刻极化电压;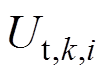 为k时刻端电压;
为k时刻端电压;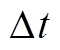 为采样间隔;iL,k为流经电池的电流,充电为负,放电为正;
为采样间隔;iL,k为流经电池的电流,充电为负,放电为正;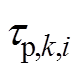 为第i个老化阶段下k时刻模型的极化常数,该值可表述为
为第i个老化阶段下k时刻模型的极化常数,该值可表述为
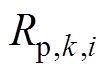 为第i个老化阶段下第k时刻模型的极化电阻,该值可表述为
为第i个老化阶段下第k时刻模型的极化电阻,该值可表述为
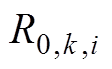 为第i个老化阶段下k时刻模型的欧姆内阻,该值可表述为
为第i个老化阶段下k时刻模型的欧姆内阻,该值可表述为
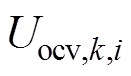 为第i个老化阶段下k时刻模型的开路电压,该值表述为
为第i个老化阶段下k时刻模型的开路电压,该值表述为
式中,Tk为实测温度;zk为SOC;q、f、h、p四个参数取决于电池特性数据中温度测试的数量。m、g、j、l取决于每个老化点下电池模型的变化轨迹;Ac,i、Bc,i、Cc,i、Dc,i四个矩阵为老化阶段i待辨识参数。
1.2 动力电池试验测试
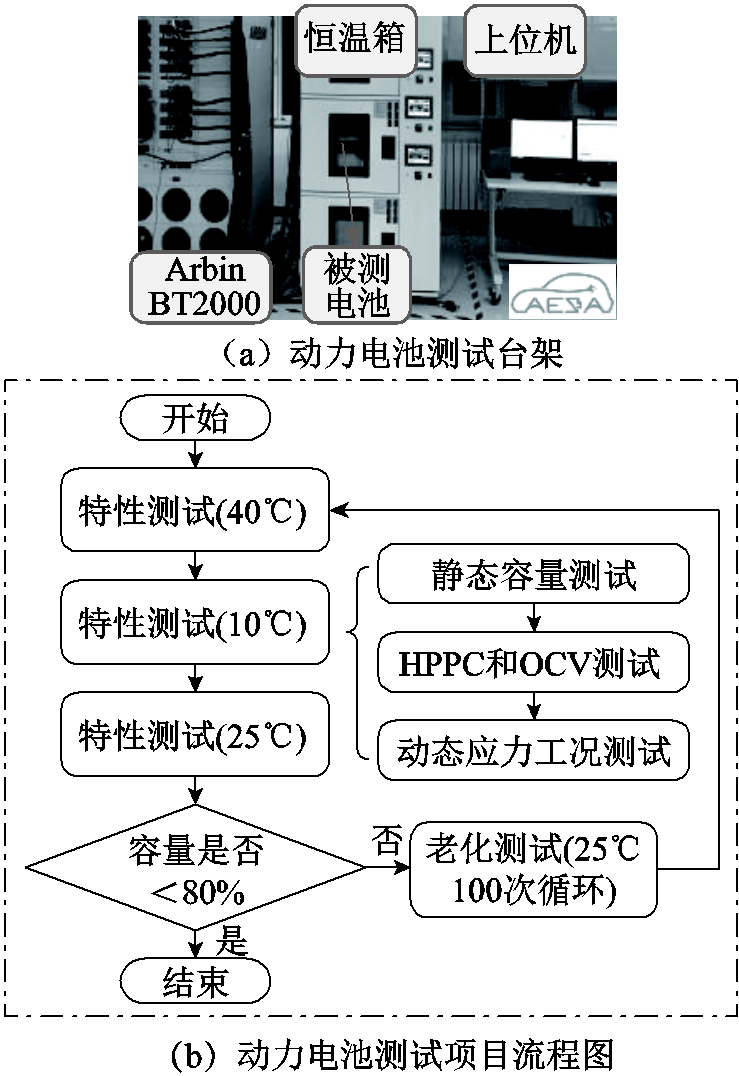
以某车用锂离子动力电池作为研究对象,电池基本参数见表1,搭建的测试台架如图1a,包括电池充放电测试设备、恒温箱、上位机、被测电池,其中电池测试设备用于控制动力电池充放电,恒温箱为电池提供稳定的环境温度,上位机用于控制恒温箱的工作温度和充放电设备的输出信号,同时记录测试数据。本文采用的试验流程如图1b所示,选择10℃、25℃、40℃三个温度开展特性试验,包括静态容量测试、混合脉冲功率测试(Hybrid Pulse Power Characteristic, HPPC)、开路电压测试及动态应力测试工况(Dynamic Stress Test, DST)。以动力电池最大可用容量是否小于其额定容量的80%作为老化试验截至条件。其中,老化过程采用1C的恒流恒压充电和恒流放电[9]。
1.3 参数辨识及模型验证
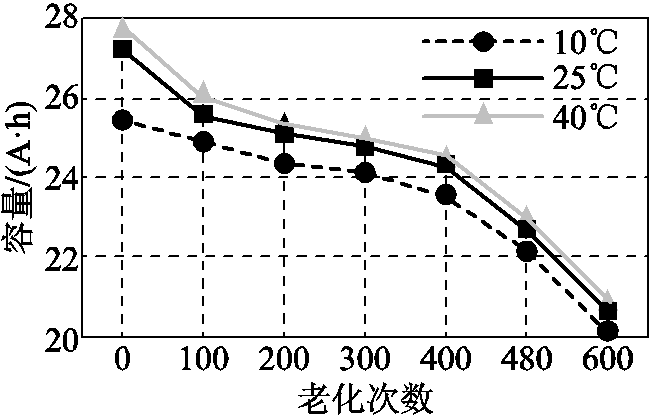
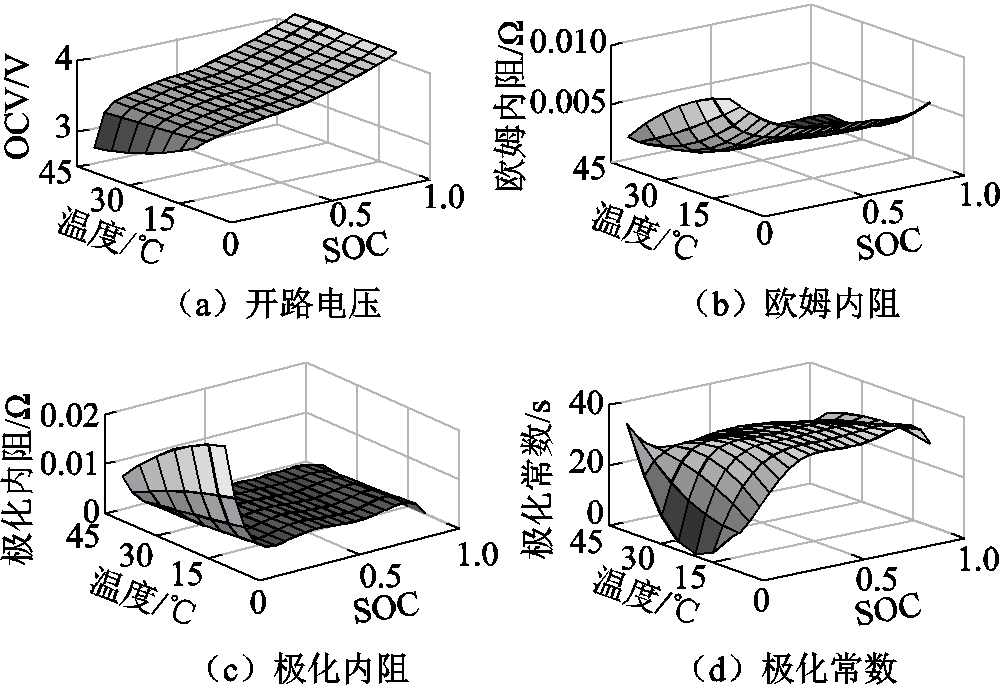
本文以容量表征电池的老化状态[11],为有效估计动力电池的容量,老化意识驱动的模型参数应能够覆盖电池的整个生命周期。图2为电池在25℃下循环老化后的容量衰退曲线,以100次老化循环点为例,图中对应的三个温度点的容量为电池特性试验中的测试值,结果表明:各温度下电池容量随老化次数逐渐降低,老化初期容量衰退明显,中期衰退呈线性趋势,末期加速衰退,这是由于老化过程是在25℃时开展,老化后测试出不同温度下的容量值,因此温度越低容量也越小。本文以0次、300次、600次老化后的电池数据进行模型的训练。
以0次老化循环为例,利用特性测试数据,基于上述变温度模型进行参数辨识,确定Ac,1、Bc,1、Cc,1、Dc,1矩阵的值。采用的参数辨识方法以及矩阵计算方法可参考文献[12-15],首先利用HPPC测试数据,提取不同温度不同SOC点下的模型参数,采用拟合的方法,建立参数随电量变化曲线,然后利用回归优化方法拟合上述四个矩阵的参数,构建当前老化条件下的模型参数随温度和电量的变化规律,辨识结果如图3所示。同理,依此辨识出300次、600次老化后的模型参数,模型精度的测试结果见表2,最大误差为84.91mV,最大的方均根误差(Root Mean Square Error, RMSE)为68.63mV。
表1 电池基本参数
Tab.1 The basic parameters of tested battery

正极材料额定容量/(A·h)最高电压/V最低电压/ V 镍钴锰254.22.8
表2 电池温变模型误差
Tab.2 The voltage error of temperature-varied model

老化次数温度/℃最大误差/mVRMSE/mV 01072.0144.01 2564.1143.34 4051.0949.18 3001050.1225.95 2536.633.9 4084.9168.63 6001052.4733.48 2552.6746.55 4074.963.68
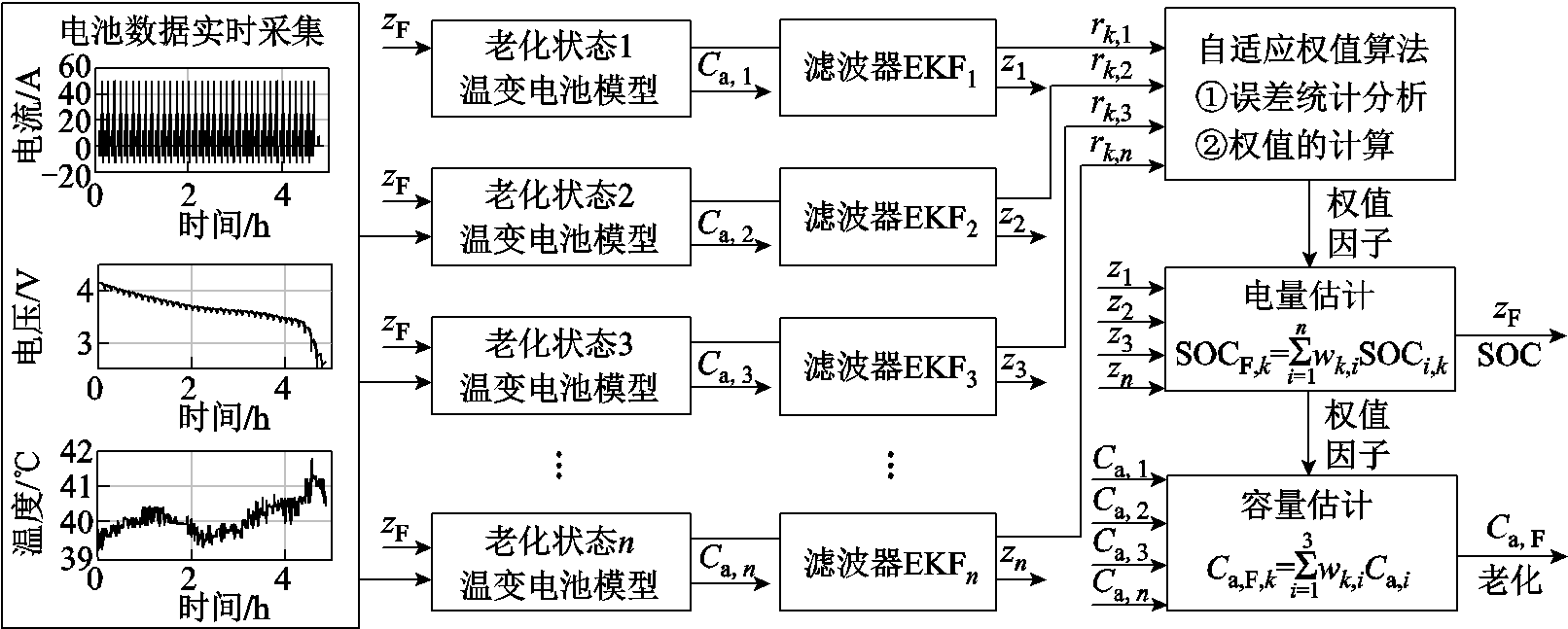
2 电量-容量融合估计方法
2.1 电量估计方法
扩展卡尔曼滤波器(Extended Kalman Filter, EKF)因其能应用于非线性模型,且可有效抑制白噪声,估计结果具有较好的稳定性和精度,常用于动力电池电量估计中[16-17]。设电池Thevenin模型的线性离散状态方程为
其中
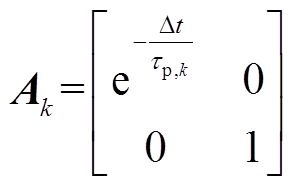
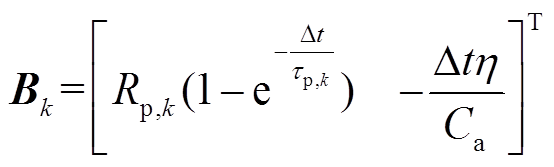
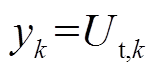
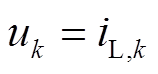
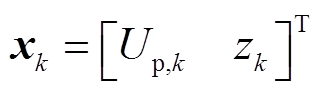
式中,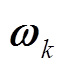 为均值为0、协方差为Q的白噪声;
为均值为0、协方差为Q的白噪声; 为量测白噪声,均值为0,方差为R;
为量测白噪声,均值为0,方差为R;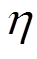 为充放电效率;
为充放电效率;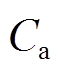 为最大可用容量,由静态容量测试获得。
为最大可用容量,由静态容量测试获得。
EKF算法是一种加权滤波方法,权值卡尔曼增益K的更新由先验估计的协方差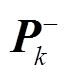 和量测噪声方差Q确定,流程如下。
和量测噪声方差Q确定,流程如下。
时间更新
状态更新
式中,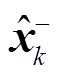 为k时刻的状态先验估计;
为k时刻的状态先验估计;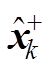 为k时刻的后验估计;
为k时刻的后验估计;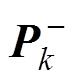 、
、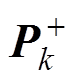 分别为k时刻状态前验估计和后验估计协方差矩阵;
分别为k时刻状态前验估计和后验估计协方差矩阵;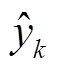 为量测量的预测值,在算法中指端电压预测值
为量测量的预测值,在算法中指端电压预测值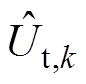 。
。
2.2 融合方法
电池模型的端电压残差能够对模型的精度进行较好的评价[18]。假设残差服从正太分布,通过统计一段时间窗口长度内的残差均值和方差,建立实时计算概率密度,计算出各个模型的融合权值。过程如下。
1)设置窗口长度m,计算第i个模型的端电压估计的残差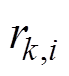 ,均值
,均值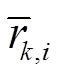 及方差
及方差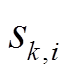 。
。
2)计算第i个模型k时刻下条件概率密度函数[16]即
3)计算第i个模型在k时刻的权值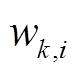
式中,n为老化阶段的数量。
采用步骤3)计算出的权值进行状态的加权计算,获取当前电池的SOC和容量的估计值分别为
2.3 电量-容量融合估计算法
本文提出的动力电池SOC和容量协同估计算法框架如图4所示。基于建立的与工作温度和老化状态相关联的动力电池模型族,依据动力电池电流和电压逐一采用扩展卡尔曼滤波算法建立状态估计器,通过融合模块加权、融合具有不同特性的状态估计结果,实现动力电池SOC和容量的联合估计。算法执行流程见表3。
表3 协同估计算法执行流程
Tab.3 The execution flow of co-estimation algorithm

初始化算法参数: ,,,,m,, 算法迭代过程:k = 1,2,(1)读取当前实时测量的电流,,电压,温度 (2)状态和端电压的更新:模型迭代i=1,2,3先验估计:后验估计:端电压残差计算: (3)权值计算:模型迭代i=1,2,3如果k>m,更新均值和残差方差:否则,残差不更新:计算概率密度值: 计算权值: (4)电量和容量的融合更新:
算法的主要配置参数包括状态初值、协方差初值、噪声先验值、残差统计步长窗口及初始方差和均值,具体见表4所示,该方法有三大特点:
1)算法具有抗动力电池老化和温度意识。通过不同老化状态和温度因素下参数化融合建模可以获得能够适应不同老化和温度变化的预测模,具有稳定使用边界和精度约束。
2)权值实时更新机制。模型的跟踪误差用于确定融合权值,实现了权值的动态更新。
3)估计结果的解耦性。由于模型输入为SOC,是前端融合结果,输入的容量是当前老化阶段下的最大可用容量,可以实现SOC和容量解耦,提升估计性能。
表4 算法参数
Tab.4 Parameters of the proposed algorithm

算法参数(i=1,2,3)配置值 状态初值[0,0.5]T 协方差初值[100,0;0,100] 过程噪声[0.0001,0;0,0.000001] 量测噪声0.01 窗口长度m500 方差初值1 均值初值1
3 验证及讨论
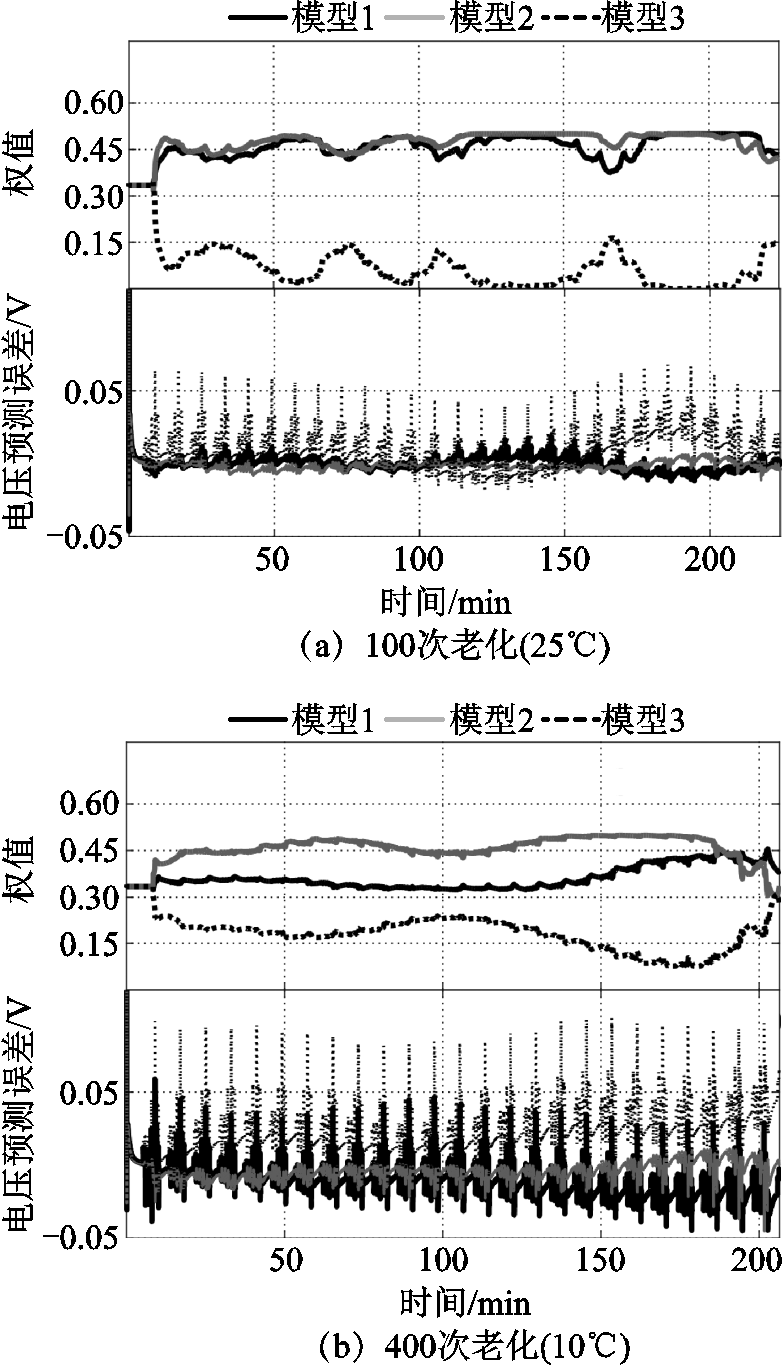
为验证算法的有效性,采用不同老化状态和不同环境温度的实验数据进行分析,图5a为100次老化下(25℃)的动态权值及端电压预测结果。图中模型1指基于0次老化阶段(新电池)的温变模型,模型2指基于300次老化阶段下的温变模型,模型3指基于600次老化阶段下的温变模型。
由图5a可见,25℃时模型1和2输出的端电压误差相近,计算权值在0.45左右,而模型3的权值为0.1左右。这说明动力电池经历100次老化后,充放电特性处于模型1和模型2之间。经历400次循环的老化后,10℃时的权值计算结果如图5b所示,结果表明,该温度下,动力电池的电流-电压响应特性与模型2较为接近,而与模型3的差异较大。
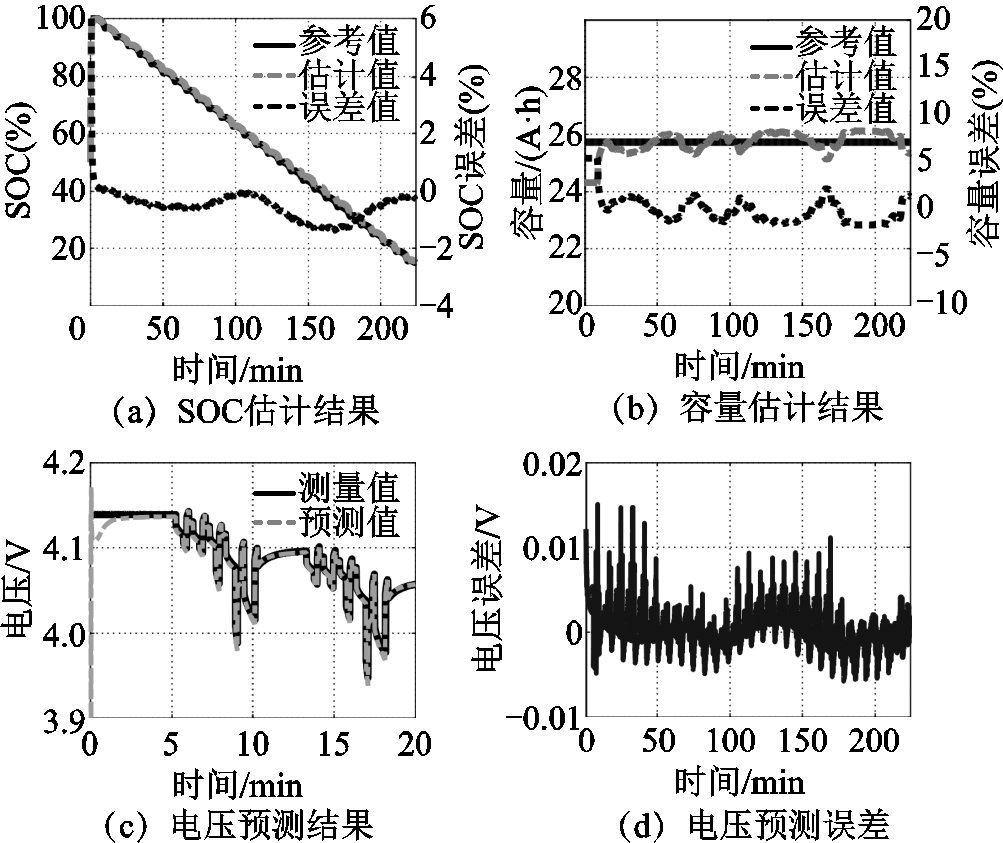
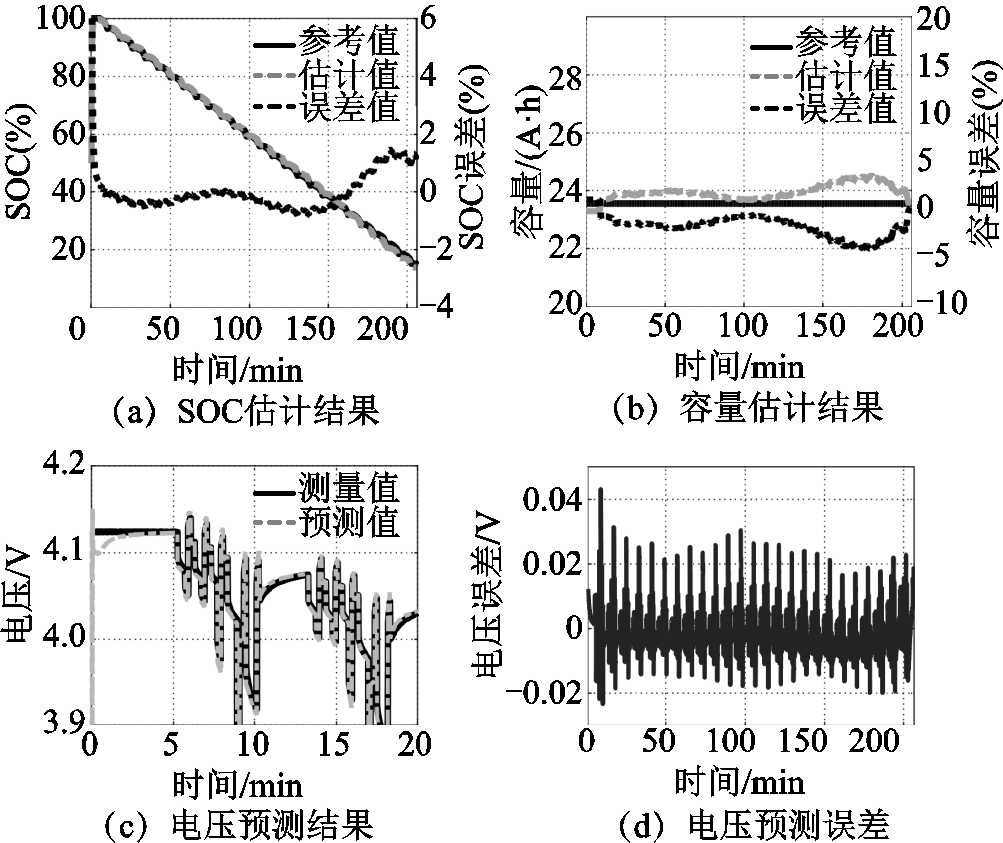
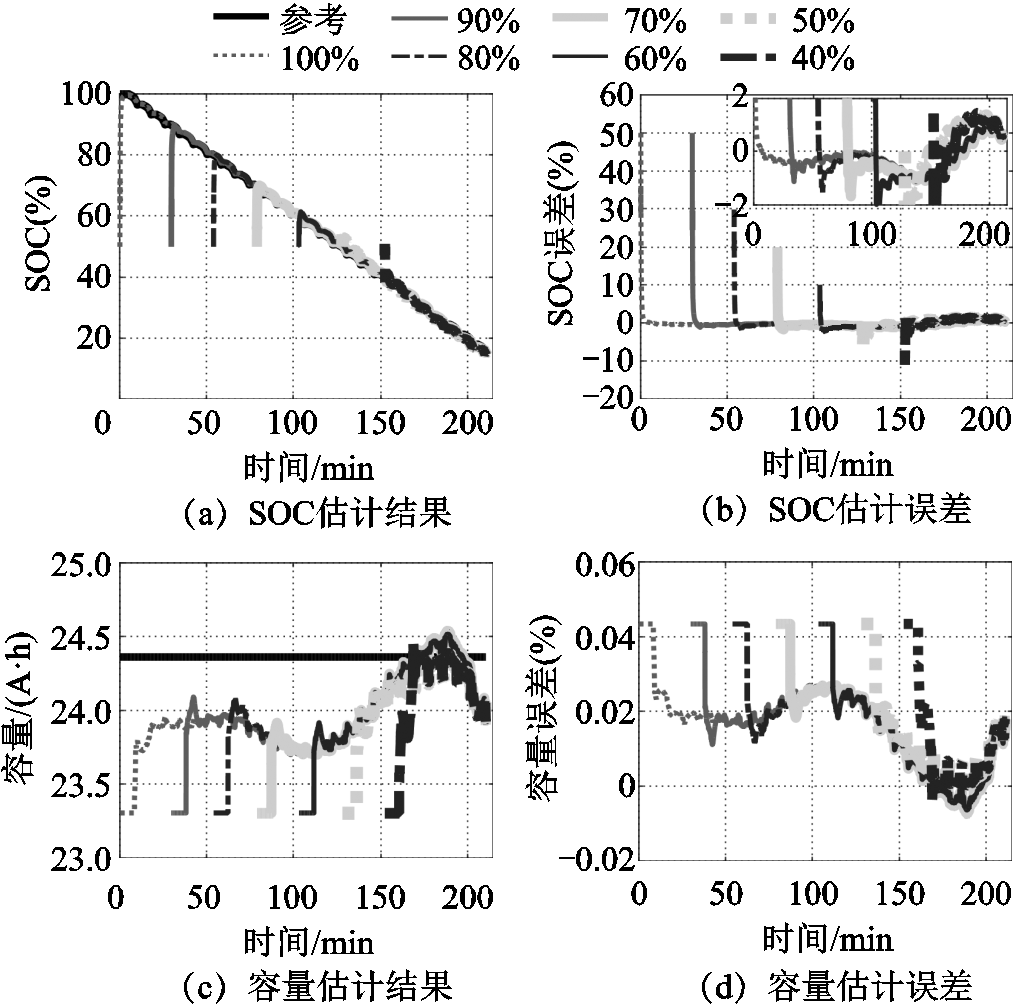
图6和图7分别为循环次数为100次和400次以及不同温度下SOC和容量的估计结果。
可见,老化状态为100次循环且环境温度为25℃时,动力电池SOC和容量的估计误差分别在2%和4%以内;端电压预测结果如图6c~图6d所示。结果表明最大预测误差在15mV以内。老化状态为400次循环且环境温度为10℃时,动力电池SOC和容量的估计误差分别在2%和4.5%以内,端电压最大预测误差在40mV以内(小于1%的上截止电压–4.2V)。
精确的模型是开展基于模型状态估计的前提,而准确的SOC是模型高精度预测的基础,不准确的SOC会引起开路电压的偏差从而引起模型误差增大,最终使得估计结果愈发偏离实际甚至发散。可见,SOC和开路电压的关系是促使端电压误差闭环修正SOC估计的桥梁,而温度和老化是影响这一关系的关键,因此,开展具有温度和老化意识驱动的状态估计必要且实用。为分析初始误差对估计结果的影响,以200循环次数的老化状态和50%的SOC初值为例,分析100%、90%、80%、70%、60%、50%、40%等不同SOC设定初值下算法的收敛性,估计结果如图8所示。可见,算法在不同初始偏差下,SOC和容量都能够在60个步长内快速收敛至真实值附近,具有稳定和精确的收敛性能,对不精确的初值不敏感。
4 结论
本文提出了一种温度和老化意识参数融合驱动的锂离子动力电池SOC和容量协同估计方法,通过实时更新动态权值实现融合估计,主要结论如下:
1)模型的温度和老化意识:通过建立动力电池温变模型,实现了老化状态和环境温度与动力电池端电压的解耦;结合端电压预测误差方差特性,实时动态更新多阶段模型的融合权值,实现了对不确定老化状态和环境温度下的电量SOC和容量的融合估计。
2)算法的估计精度:经过不同老化状态和环境温度数据的验证表明,该融合方法下动力电池SOC估计误差均小于2%,同时具有准确的容量和端电压预测性能。
3)算法的收敛性能:当状态初值具有不确定性偏差扰动时,算法能够在60个计算步长内将动力电池SOC和容量估计结果准确收敛至参考值。
参考文献
[1] 熊瑞. 动力电池管理系统核心算法[M]. 北京: 机械工业出版社, 2018.
[2] Galeotti M, Cinà L, Giammanco C, et al. Performance analysis and SOH (state of health) evaluation of lithium polymer batteries through electrochemical impedance spectroscopy[J]. Energy, 2015, 89: 678-686.
[3] 马泽宇, 姜久春, 王占国, 等. 基于容量增量分析的石墨负极磷酸铁锂电池 SOC 估算方法研究[J]. 汽车工程, 2014, 36(12): 1439-1444. Ma Zeyu, Jiang Jiuchun, Wang Zhanguo, et al. A research on SOC estimation for LiFePO4 battery with graphite negative electrode based on incremental capacity analysis[J]. Automotive Engineering, 2014, 36(12): 1439-1444.
[4] Xiong Rui, Sun Fengchun, Chen Zheng, et al. A data-driven multi-scale extended Kalman filtering based parameter and state estimation approach of lithium-ion polymer battery in electric vehicles[J]. Applied Energy, 2014, 113: 463-476.
[5] Chen Lin , Lü Zhiqiang, Lin W, et al. A new state-of-health estimation method for lithium-ion batteries through the intrinsic relationship between ohmic internal resistance and capacity[J]. Measurement, 2018, 116: 586-595..
[6] 范兴明, 王超, 张鑫, 等. 基于增量学习相关向量机的锂离子电池SOC预测方法[J]. 电工技术学报, 2019, 34(13): 2700-2708. Fan Xingming, Wang Chao, Zhang Xin, et al. A prediction method of li-ion batteries SOC based on incremental learning relevance vector machine[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2700-2708.
[7] Eddahech A, Briat O, Vinassa J M. Determination of lithium-ion battery state-of-health based on constant-voltage charge phase[J]. Journal of Power Sources, 2014, 258: 218-227.
[8] You G W, Park S, Oh D. Real-time state-of-health estimation for electric vehicle batteries: a data-driven approach[J]. Applied Energy, 2016, 176: 92-103,
[9] Wang Ju, Xiong Rui, Li Linlin, et al. A comparative analysis and validation for double-filters-based state of charge estimators using battery-in-the-loop approach[J]. Applied Energy, 2018, 229: 648-659.
[10] Xiong Rui, Zhang Yongzhi, He Hongwen, et al. A double-scale particle-filtering energy state prediction algorithm for lithium-ion batteries[J]. IEEE Transactions on Industrial Electronics, 2017, 65(2): 1526-1538.
[11] 连湛伟, 石欣, 克潇, 等. 电动汽车充换电站动力电池全寿命周期在线检测管理系统[J]. 电力系统保护与控制, 2014, 42(12): 137-142. Lan Zhanwei, Shi Xin,Ke Xiao, et al.The whole life cycle on-line detection and management system of power battery in the electric vehicle charging and exchanging station[J]. Power System Protection and Control, 2014, 42(12): 137-142.
[12] 黄凯, 郭永芳, 李志刚. 基于信息反馈粒子群的高精度锂离子电池模型参数辨识[J]. 电工技术学报, 2019, 34(增刊1): 378-387. Huang Kai, Guo Yongfang, Li Zhigang.High precision parameter identification of lithium-ion battery model based on feedback particle swarm optimization algorithm[J]. Transactions of China Electrotechnical Society,2019, 34(S1): 378-387.
[13] 余波, 梁锐, 蒲亦非, 等. 超级电容器恒流充电的时域分数阶电路模型[J]. 电工技术学报, 2019, 34(17): 3533-3541. Yu Bo, Liang Rui, Pu Yifei, et al. Time-domain fractional circuit model for constant current charging of supercapacitor[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3533-3541.
[14] Chaoui H, El Mejdoubi A, Gualous H. Online parameter identification of lithium-ion batteries with surface temperature variations[J]. IEEE Transactions on Vehicular Technology, 2017, 66(3): 2000-2009.
[15] 谢长君, 费亚龙, 曾春年, 等. 基于无迹粒子滤波的车载锂离子电池状态估计[J]. 电工技术学报, 2018, 33(17): 3958-3964. Xie Changjun, Fei Yalong, Zeng Chunnian, et al. State-of-charge estimation of lithium-ion battery using unscented particle filter in vehicle[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 3958-3964.
[16] Plett G L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs - part 2. Modeling and identification[J]. Journal of Power Sources, 2004, 134(2): 262-276.
[17] 谷苗, 夏超英, 田聪颖. 基于综合型卡尔曼滤波的锂离子电池荷电状态估算[J]. 电工技术学报, 2019, 34(2): 419-426. Gu Miao, Xia Chaoying, Tian Congying. Li-ion battery state of charge estimation based on comprehensive Kalman filter[J]. Transactions of China Electro technical Society, 2019, 34(2): 419-426.
[18] Lin Cheng, Mu Hao, Xiong Rui, et al. Multi-model probabilities based state fusion estimation method of lithium-ion battery for electric vehicles: state-of-energy[J]. Applied Energy, 2017, 194: 560-568.
Co-Estimation of Lithium-Ion Battery State-of-Charge and Capacity Through the Temperature and Aging Awareness Model for Electric Vehicles
Wang Ju1 Xiong Rui1 Mu Hao1,2
(1. National Engineering Laboratory for Electric Vehicles Beijing Institute of Technology Beijing 100081 China 2. Beijing Institute of Spacecraft System Engineering Beijing 100094 China)
Abstract As the technical bottleneck of electric vehicles, batteries have strong time-varying nonlinear characteristics and limited measurability. They are easily affected by temperature and aging during use. Accurate state estimation under the full life cycle and the wide temperature has always been a technical problem in the industry. Therefore, this paper first uses the data of different temperatures and different aging stages to establish a multi-stage model with temperature and aging awareness; then uses the probability density function to calculate the weight of the single models and proposes a multi-stage model fusion-driven battery state of charge (SOC) and capacity estimation method. Finally, the verification results considering uncertainty of aging and temperature factors show that the proposed method has high SOC and capacity estimation accuracy and is not sensitive to the initial error. The SOC estimation error is less than 2% with the -10% to 50% of the initial SOC errors, and the convergence is fast.
keywords: Powerlithium-ion battery, full life, joint estimation, state of charge, capacity estimation
中图分类号:TM912.9
DOI:10.19595/j.cnki.1000-6753.tces.191598
国家自然科学基金资助项目(51707011, 51877009)。
收稿日期2019-11-22
改稿日期 2020-07-02
作者简介
王 榘 男,1991年生,博士研究生,研究方向为新能源汽车动力电池系统管理。E-mail:wang_ju@bit.edu.cn
熊 瑞 男,1985年生,教授,博士生导师,IET Fellow,研究方向为电动载运装备动力系统、动力电池系统和人工智能。E-mail:rxiong@bit.edu.cn(通信作者)
(编辑 赫蕾)
 曲线,发现该曲线的峰值与老化状态有关,利用该值可实现老化状态的估计[3]。另外老化过程中SOC-OCV曲线会发生改变,熊瑞等通过构建OCV-SOC-容量的三维响应面实现了容量的准确估计[4],但对于曲率较小的电池,适用性有待深入探讨。电池内阻是老化的直观表现之一,Chen Lin等采用在线辨识算法实现了内阻的实时估计,利用内阻增长和容量衰退率之间的关系对电池的老化状态进行估计[5]。但在电池系统实际运行中,内阻易受温度、线束压降等因素的影响,导致估计结果出现较大误差[6]。针对锂离子动力电池恒压充电段中电流的变化趋势,A.Eddahech等发现电流变化的时间常数与容量衰退率之间存在较强的线性关系[7],该方法可用于单体电芯的老化状态识别,对于系统而言,有一定的局限性。受开路电压和内阻等因素影响,电池在老化后端电压会出现明显的变化,因此G.W.You等利用电池端电压、电流、温度作为输入,以SOC-健康状态作为输出,训练神经网络模型,并采用电池管理系统对结果进行验证[8],但该方法受限于训练集数据的完备性。
曲线,发现该曲线的峰值与老化状态有关,利用该值可实现老化状态的估计[3]。另外老化过程中SOC-OCV曲线会发生改变,熊瑞等通过构建OCV-SOC-容量的三维响应面实现了容量的准确估计[4],但对于曲率较小的电池,适用性有待深入探讨。电池内阻是老化的直观表现之一,Chen Lin等采用在线辨识算法实现了内阻的实时估计,利用内阻增长和容量衰退率之间的关系对电池的老化状态进行估计[5]。但在电池系统实际运行中,内阻易受温度、线束压降等因素的影响,导致估计结果出现较大误差[6]。针对锂离子动力电池恒压充电段中电流的变化趋势,A.Eddahech等发现电流变化的时间常数与容量衰退率之间存在较强的线性关系[7],该方法可用于单体电芯的老化状态识别,对于系统而言,有一定的局限性。受开路电压和内阻等因素影响,电池在老化后端电压会出现明显的变化,因此G.W.You等利用电池端电压、电流、温度作为输入,以SOC-健康状态作为输出,训练神经网络模型,并采用电池管理系统对结果进行验证[8],但该方法受限于训练集数据的完备性。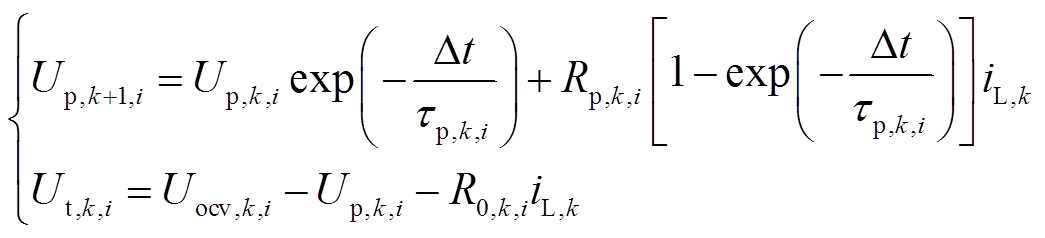 (1)
(1)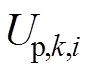 为第i个老化阶段下k时刻极化电压;
为第i个老化阶段下k时刻极化电压;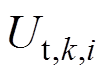 为k时刻端电压;
为k时刻端电压;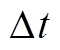 为采样间隔;i
为采样间隔;i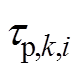 为第i个老化阶段下k时刻模型的极化常数,该值可表述为
为第i个老化阶段下k时刻模型的极化常数,该值可表述为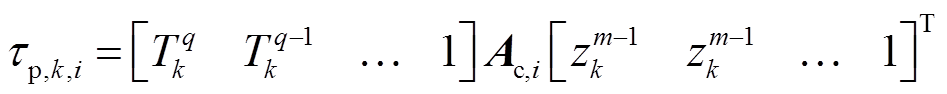 (2)
(2)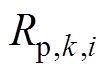 为第i个老化阶段下第k时刻模型的极化电阻,该值可表述为
为第i个老化阶段下第k时刻模型的极化电阻,该值可表述为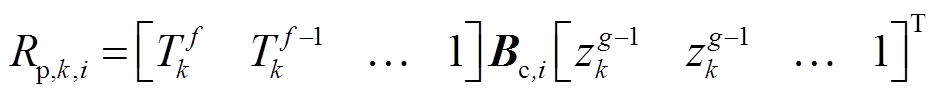 (3)
(3)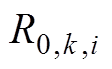 为第i个老化阶段下k时刻模型的欧姆内阻,该值可表述为
为第i个老化阶段下k时刻模型的欧姆内阻,该值可表述为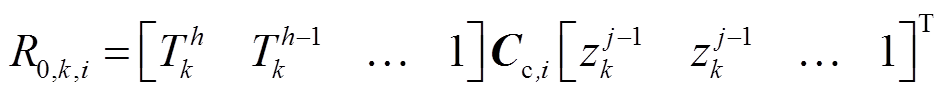 (4)
(4)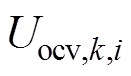 为第i个老化阶段下k时刻模型的开路电压,该值表述为
为第i个老化阶段下k时刻模型的开路电压,该值表述为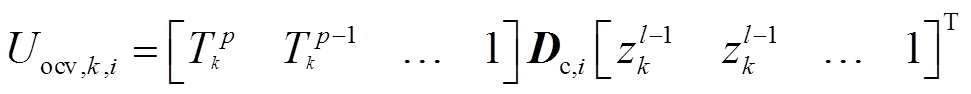 (5)
(5)


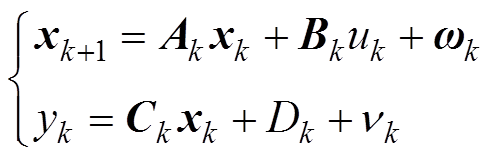 (6)
(6)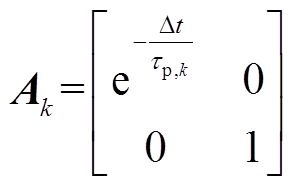
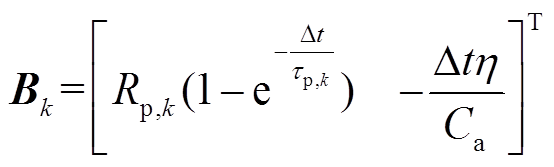
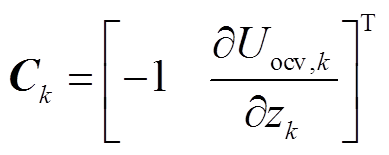
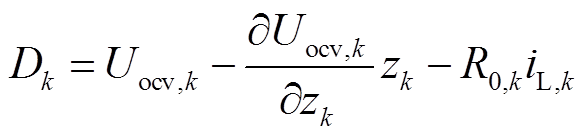
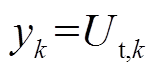
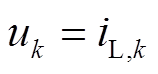
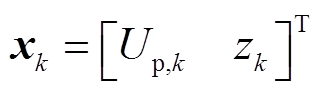
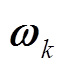 为均值为0、协方差为Q的白噪声;
为均值为0、协方差为Q的白噪声;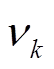 为量测白噪声,均值为0,方差为R;
为量测白噪声,均值为0,方差为R;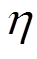 为充放电效率;
为充放电效率;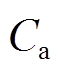 为最大可用容量,由静态容量测试获得。
为最大可用容量,由静态容量测试获得。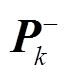 和量测噪声方差Q确定,流程如下。
和量测噪声方差Q确定,流程如下。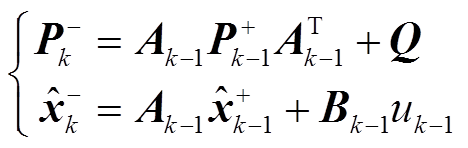 (7)
(7)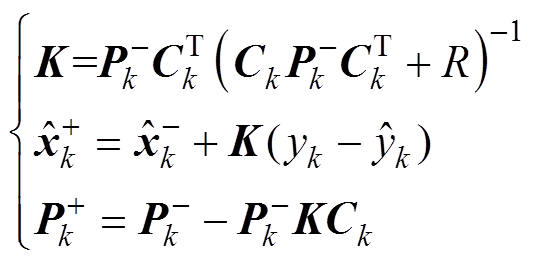 (8)
(8)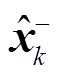 为k时刻的状态先验估计;
为k时刻的状态先验估计;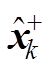 为k时刻的后验估计;
为k时刻的后验估计;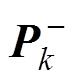 、
、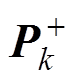 分别为k时刻状态前验估计和后验估计协方差矩阵;
分别为k时刻状态前验估计和后验估计协方差矩阵;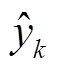 为量测量的预测值,在算法中指端电压预测值
为量测量的预测值,在算法中指端电压预测值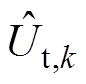 。
。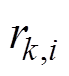 ,均值
,均值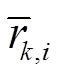 及方差
及方差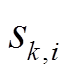 。
。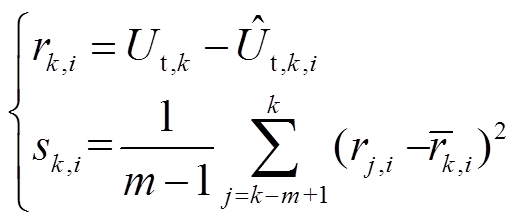 (9)
(9)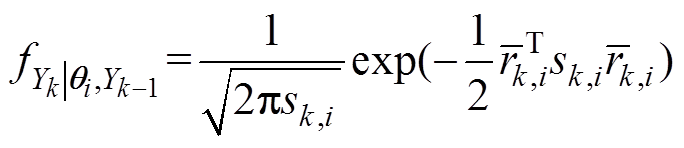 (10)
(10)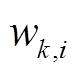
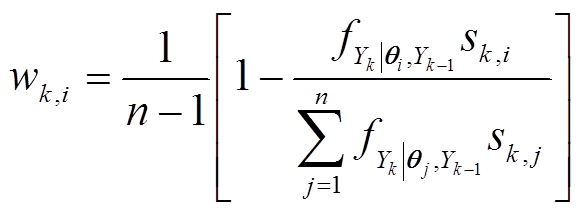 (11)
(11)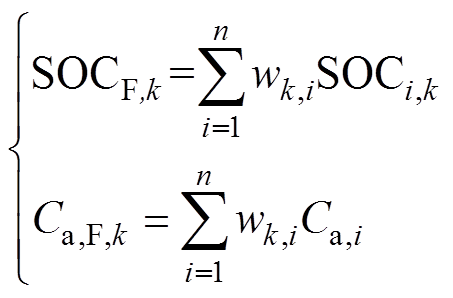 (12)
(12)