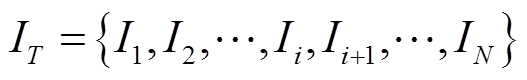，电流的精度为
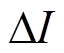。摘要 为了提升居民用户参与需求响应的积极性，考虑居民用户的舒适度和使用习惯是非常重要的。该文提出一种基于负荷状态集关联分析的居民用户可平移负荷辨识。首先提出了滑动均值负荷状态提取法，通过负荷的电流值提取负荷的工作状态，形成负荷状态集。然后建立负荷状态集关联分析模型，并利用FP-Growth算法求解，得到负荷的强关联性和时间关联性。最后对于需要进行可平移负荷辨识的日用电负荷状态集进行强关联状态集合划分，并根据负荷状态集的时间关联性确定其是否可平移以及平移可接受时段，从而完成可平移负荷辨识，为居民需求响应的分布式控制、家庭用能管理优化提供数据基础。
关键词：可平移负荷辨识 负荷状态提取 关联分析 负荷状态时间关联性 需求响应
近年来，以电力系统为核心的能源互联网高速发展，逐渐实现能源背景下的万物互联。依托物联网的底层架构，可以自动化、互动化、信息化、数字化地解决能源高效、安全、可持续利用等问题。物联网中，除了重视电力系统一次设备通过输配电网的物理互联，更应该着眼于广域内海量分布式设备之间的信息交互与协调[1]。高级量测体系（Advanced Metering Infrastructure, AMI）作为物联网中重要的信息采集系统，丰富了配电网用户侧信息[2]。通过对用户侧信息的多维度分析，能挖掘出潜藏的用户偏好、用电习惯、用电设备特性等大量有价值的信息，为用户能量精细化管理、电网智能化业务分析与决策提供支撑[3-4]。
可控负荷是电力系统中重要的分布式设备，其反应时间快，地域分布广，可作为电网优化运行调控、可再生能源间歇性平抑、电网故障紧急处理等多种场景下，维持系统功率平衡的有效手段[5-6]。目前，对负荷的控制常常以牺牲用户体验为代价，导致用户参与负荷调控的积极性不高。文献[7]指出，负荷控制应具有非破坏性（non-disruptive）的特征，即在满足电力系统调控需求的同时，不能对用户产生明显的负面影响。因此，合理分析用户侧数据，考虑用户的舒适度、便捷度评估用户的可调控负荷资源具有重要意义。
居民用电在全社会用电量中占比大，是重要的可控负荷资源。并且，随着工商业电价交叉补贴居民电价的政策逐步取消，居民电价上涨，居民参与负荷调控从而节约成本、获取收益的热情会被激发[8]。对于居民用户来说，可控负荷可以分为可平移负荷、可削减负荷、可转移负荷三类[9]。居民用电设备多为中小型电器，对其能量分段拆解效益不明显；且其用电行为往往具有连贯性，可转移负荷的应用范围有限。另外，负荷直接削减会带来比较大的用户体验损失，不满足负荷控制的“非破坏性”原则，属于用户满意度较低的负荷控制手段[10]。因此，可平移负荷是居民侧最重要的可控负荷资源，需要对其深入研究。
目前，可平移负荷的相关研究主要聚焦于可平移负荷的数学模型搭建与参与需求响应的策略。文献[11]将家庭负荷分为基荷、空调类、可转移类（Ⅰ、Ⅱ）、可中断类，对每类负荷分别建模，提出了考虑用户满意度的两阶段DR资源调控模型。文献[12]将家庭用电负荷分为刚性负荷、简单可调负荷、电池、HVAC系统，并提出混合能源协同控制的家庭用能优化控制模型，用户舒适性、经济性都有所提高。文献[13]提出了可平移负荷的实用化等效模型，将具有较多变量的离散优化问题转换为具有较少变量的连续优化问题。上述研究中，普遍会选择洗衣机、洗碗机、烘干机、电视等负荷作为可平移负荷，而冰箱、空调等负荷作为不可平移负荷[11-13]。对于可平移负荷与平移可接受时段的判定也多为研究者主观意识，缺少对用户用电行为的考虑，也缺少可平移负荷的通用判断标准。而用户的用电行为受其心理因素影响大，只有当用户认为电价收益足以弥补因改变用电习惯造成的舒适度损失时，用户才会参与负荷调控[14-15]。显然，人为主观判定可平移负荷无法为居民参与负荷调控提供参考。研究者需要从用户用电行为数据出发，考虑用户的用电习惯，提出更有参考意义的可平移负荷辨识方法。并且，随着居民生活质量提升，家电更加“多元化”与“智能化”。一方面，家电的“多元化”增加了可平移负荷的种类与数量，使人主观判断负荷是否可平移的门槛提升，更加需要可平移负荷辨识方法；另一方面，家电的“智能化”意味着降低了用户的负荷平移实现成本，成熟的可平移负荷辨识算法可以植入电器的控制终端，通过与用户“建议式”的交互形式，实现保证用户体验的负荷平移。
传统用电信息采集仪表获取的测量信息单位最小只能到一个用户，而可平移负荷辨识需要具体到每个设备的用电信息。因此，针对可平移负荷辨识的研究尚少。但是，近些年来兴起的非侵入式负荷辨识（Non–Intrusive Load Monitoring, NILM）研究，可以将智能电表采集的总用电曲线，分解为每个设备的用电曲线，为可平移负荷辨识的研究与落地提供数据支持[16-19]。
本文提出了一种基于电器状态关联分析的居民可平移负荷辨识方法。本文的主要贡献在于：
（1）提出了一种滑动均值负荷状态提取方法，将负荷的电流值转换为电器工作状态。
（2）提出了负荷状态关联性、负荷时间关联性的概念，建立了负荷状态集的关联性分析模型，并利用FP-Growth算法求解。
（3）提出了可平移负荷的计算方法，利用负荷状态关联性对需要进行辨识的日负荷状态集进行强关联集合划分，并依据负荷状态时间关联性判断强关联集合是否可平移，以及平移可接受的时段。
算例分析表明，本文所提负荷状态提取方法解决了现有负荷状态提取法普适性差、抗噪能力差等问题，可为可平移负荷辨识提供基础数据。所获得的负荷状态关联性、负荷状态时间关联性可以基本揭示用户的用电习惯，描述用户组合使用不同电器的关系及时间对用户用电的影响。本文所提可平移负荷辨识方法的结果，较其他方法更贴合用户的用电习惯，可为负荷调控提供更有效的资源。
负荷状态提取是将负荷用电数据还原为负荷的工作状态，负荷的每个工作状态的功率可认为是服从均值为m，方差为s2的正态分布[19]。
在平移负荷的过程中，用户可以控制电器所处状态，但不能控制电器状态消耗的功率。因此，负荷状态提取是可平移负荷辨识的前序关键步骤。
本文利用负荷电流为特征值进行计算，避免了电压不稳定带来的功率波动影响，计算流程如下。
（1）某电器在一段时间T内的电流采样数据形成的集合为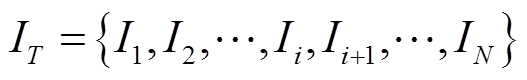 ，电流的精度为。
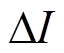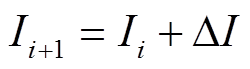（1）统计所有电流值的出现频数，记为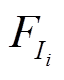
，并依据电流值排序。
（2）求取电流频数滑动均值：利用窗口w进行滑动，对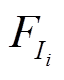求取滑动平均值
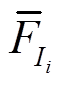，小于噪声过滤阈值
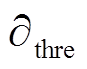的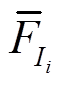用0代替。电流频数滑动均值公式为
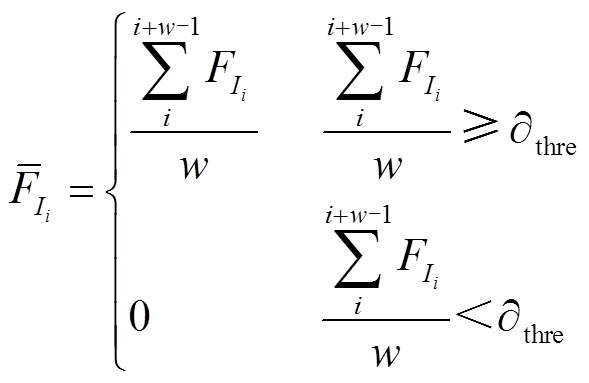（2）其中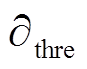，的计算式为
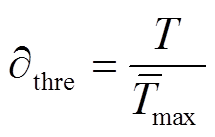（3）式中，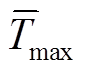
为负荷功率的最长平均出现周期，即至少每隔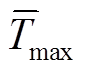要出现一次。经过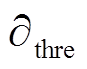过滤，将T时间内平均出现周期高于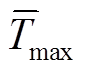的负荷功率过滤掉。
（3）找到所有频数滑动平均值的局部峰值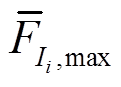
，并找到该平均值对应窗口的电流值中出现频数最高的电流值
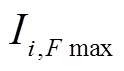，对所有求得的
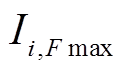进行去重、排序。
（4）找到各个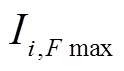之间的频数滑动平均值的最小值
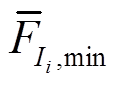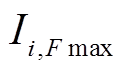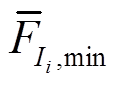。若存在多个最小值，则取位置远离边界的。取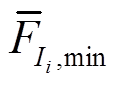对应窗口的电流值中靠近中间位置的电流值
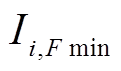，并以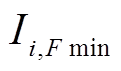为间隔依据，对IT进行状态划分，将电流采样数据转换为状态序列ET。
由于样本的数量会直接影响负荷状态提取结果的准确性，为保证算法准确性，需要根据采样频率选择采样周期。当采样频率较高的时候，所需的采样周期较短；反之，当采样频率较低的时候，所需采样周期较长。
负荷特性辨识包括负荷状态关联性辨识与负荷状态时间关联性辨识。负荷状态关联性辨识是挖掘不同负荷状态之间的关联性，将用户组合使用不同负荷状态的习惯转换为负荷状态的强关联集合。强关联集合不可拆分，平移时需整体考虑。负荷状态时间关联性辨识是挖掘负荷状态集与时间的关联性，并将其转换为用户是否要在特定时间使用特定负荷的概率。
在某一时间尺度内频繁同时出现的负荷状态具有负荷状态关联性，需要以负荷状态为最小单位，进行负荷状态关联性辨识，找到负荷状态间的强关联规则。
负荷状态关联性包括两种：
（1）不同负荷状态间的关联性。比如在家庭用电的场景下，使用完热水器后（洗澡），再使用电吹风（吹干头发），这一行为在数据上会表现为热水器负荷的某些状态和电吹风负荷的某些状态频繁相继出现，并且出现的间隔时间较短。
（2）同一负荷不同状态间的关联性。比如，在家庭用电的场景下，用户在烹饪过程中会多次开启、关闭电磁炉且其工作状态发生频繁变化。这一行为在数据上会表现为电磁炉的某些状态频繁相继出现。
根据有负荷状态关联性的定义，建立负荷状态关联性分析模型如下：
（1）项e：负荷的非零状态为项，例如：电磁炉-状态1。项的集合为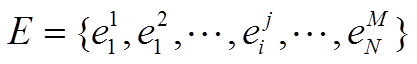
，其中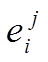
为第i个负荷的状态j，j＞0。
（2）事务s：给定时段内，所有负荷的非零状态集合称为一个事务st，st为E的子集。例如：给定2h，对状态序列ET进行划分，12:00~14:00的负荷非零状态集 {电磁炉-状态1，电磁炉-状态2，洗碗机-状态1} 可以称为一个事务。
（3）关联规则：A, B为两组项集，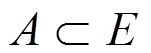
, 
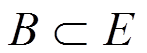，且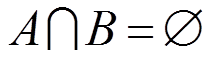
，定义关联规则形式如
。
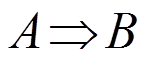一般情况下，一个关联规则有两个主要参数：支持度（support）和置信度（confidence）。对于规则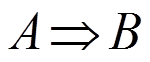
，两个参数的描述见表1。支持度描述了关联规则的重要性，用于定义频繁项集，即支持度大于某个阈值的项集叫作频繁项集。置信度描述了关联规则的准确性，置信度与支持度的共同约束定义了强关联规则，即大于或等于最小支持度阈值和最小置信度阈值的规则叫作强关联规则。
表1 关联规则主要参数
Tab.1 Key parameters in association rules
名称指标特性概率公式强关联规则的条件 支持度关联规则的重要性＞最小支持度 置信度关联规则的准确性＞最小置信度
负荷关联性辨识的目的就是找到负荷状态项集间的强关联规则。若{电磁炉-状态1，电磁炉-状态2}→{洗碗机-状态1}为强关联规则，则表示如果{洗碗机-状态1}出现，那么{电磁炉-状态1，电磁炉-状态2}有极大的概率出现。两个具有强关联规则的集合的负荷状态组合起来，用户才能实现某种行为目的。
因为用户的生活工作行为具有一定的周期性，所以其用电数据也应具有周期性规律。用户很有可能在某一种周期规律的某一个时间点上高频重复某一种用电行为，如每周末利用洗衣机、烘干机做家务（周期为星期）、每天晚上看电视收看新闻（周期为日）。定义具有上述特性的负荷状态为具有时间关联性特性的负荷状态。通过负荷状态时间关联性辨识，可以得出频繁出现在某一时间点上的负荷状态，这些负荷状态在可平移负荷辨识中为不可平移的负荷状态。
负荷状态时间关联性辨识步骤如下：
（1）建立关联规则，并求解频繁项。整理负荷i每日非零状态的时刻数据，将状态序列ET以日为单位进行分隔，每日采样的时刻点记为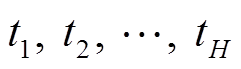
。负荷i的非零状态采样时刻点为项，每日的非零状态采样时刻点集为负荷i当日的事务
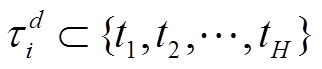，d为第d天。
（2）频繁项连接成频繁时间区间，如图1所示（H=8）。将步骤（1）所得的频繁项集（图1中灰色部分）取并集，并按升序排列。然后连接成时刻区间，规则为，若相邻的两个时刻数据相差小于等于ng，则属于同一时刻区间，并对中间空缺的时间值进行补全；否则，新增一个时间区间。ng表示家庭用户完成一组用电行为过程中间断的最长时间点数，其大小与采样频率f相关，即ngf为固定时间长度，对于大多数家庭可取15min。
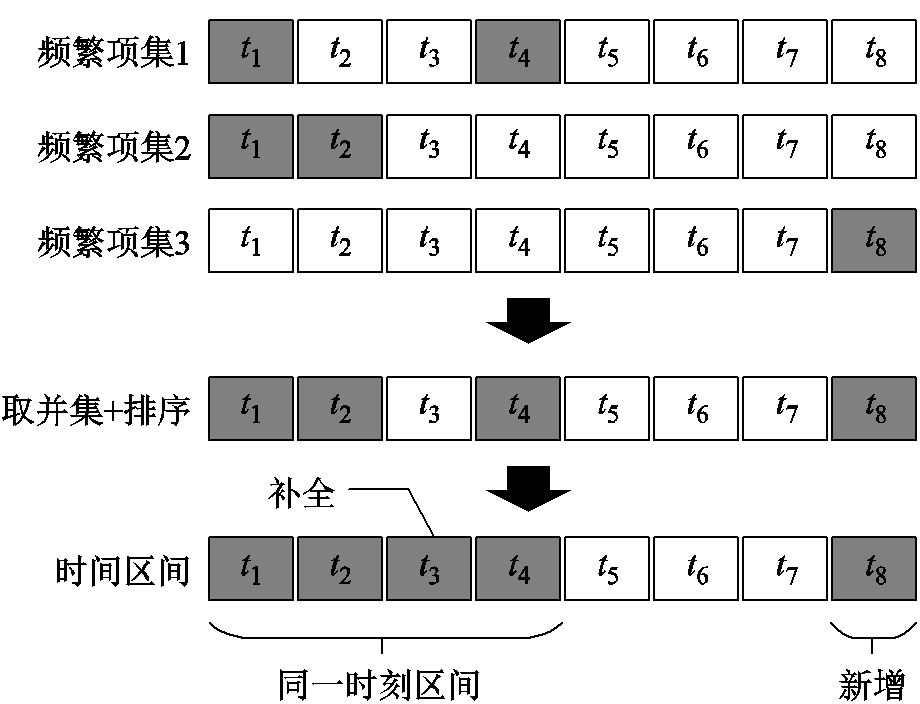
图1 频繁时间区间生成示意图（ng=3）
Fig.1 Schematic diagram of frequent time interval (ng=3)
（3）计算负荷i非零状态对应的时间数据每隔一定周期Ts（如：1日、2日、1周等）与频繁项集的某个时段[ts, te]存在交集的概率。若在某种周期Ts下，负荷i的非零状态对应的时间数据与频繁项的某一时段[ts, te]存在交集的占比高于负荷状态时间关联性阈值bthre（如80%），则可认为该负荷在周期Ts下，负荷i与[ts, te]具有强时间关联性，每日[ts, te]的负荷i不可平移。
（4）循环步骤（1）~步骤（3）直至所有负荷完成时间关联性辨识。
同时，若某负荷的某些状态从不出现在某个特定时段内，则这些负荷状态具有反时间关联性。在考虑将可平移负荷进行平移时，应该回避其反时间关联性对应的时段。
本文的关联规则挖掘，主要依靠FP-Growth算法实现，其计算速度快，存储空间需求小[20]。其主要流程为构造FP-Tree和利用FP-Tree挖掘[21]。
2.3.1 构造FP-Tree
FP-Tree的构造，输入为负荷状态事务数据库S，S中存储了所有事务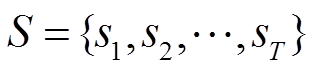
，输出为该数据库的FP-Tree，主要包括三个步骤：
（1）遍历S，记录每一个项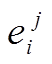
出现的频数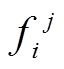
，并按照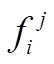
降序排列，去除小于最小支持度阈值fthre的元素项，形成头指针表head。
（2）再次遍历S，对S的每一个事务中的项根据head进行筛选和排序，形成新的数据集S′。
（3）利用S′构建FP-Tree。以空集作为根节点，将S′中的各事务si依次添加到树中。首先判断现有树中是否存在与si相同的前缀分支：若存在，则共同前缀分支包含的节点项计数值加1；若不存在，则在共同前缀分支的最后一个节点的子节点处建立新的分支，新的分支所包含节点项赋值为1。直至所有事务处理完成，FP-Tree构建成功。
2.3.2 利用FP-Tree挖掘
基于FP-Tree的频繁项集挖掘的核心过程为各项的条件模式基的生成与条件FP-Tree的构建。某项的条件模式基为：以该项为终端节点的路径集合，路径包含根节点、该项节点、以及之间的所有项节点。某项的条件FP-Tree为：以该项的条件模式基为数据结构的FP-Tree。通过把每一项的条件FP-Tree中的满足支持度阈值的元素项加入到频繁项集列表中，完成数据集频繁项的挖掘。
图2所示为可平移负荷的辨识流程，首先对负荷进行状态提取，将负荷电流/功率转换为负荷状态。然后，对历史负荷状态进行关联性分析，求得该用户的负荷状态关联性与负荷状态时间关联性。接着，根据负荷特性的辨识结果对待分析日的可平移负荷进行计算，最后输出当日的可平移负荷集合以及对应的平移接受时段。
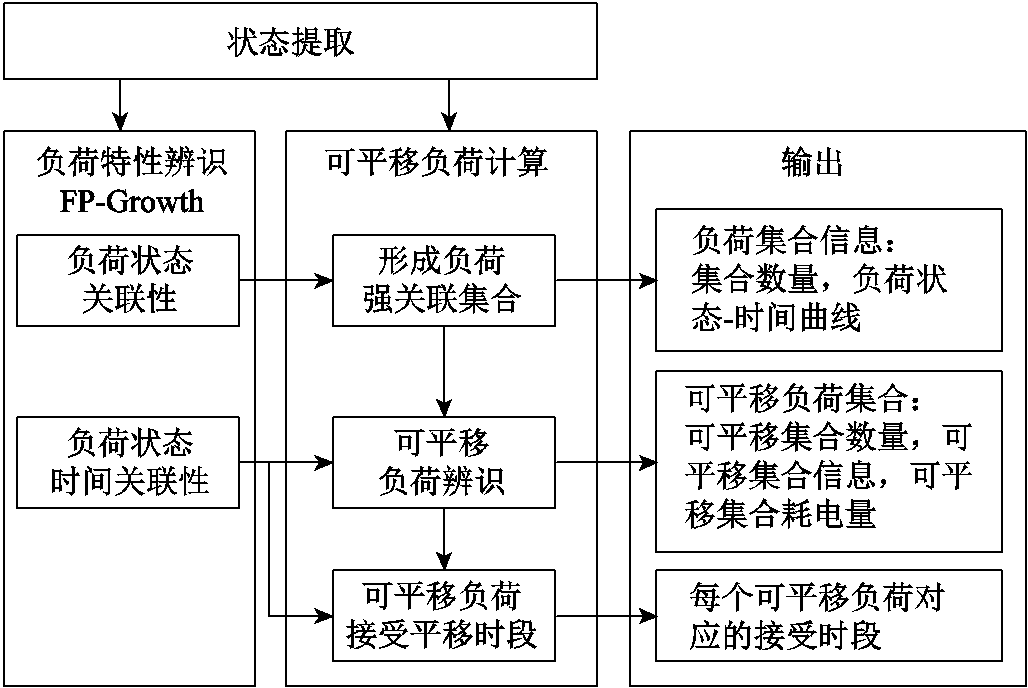
图2 可平移负荷的辨识流程
Fig.2 Flow diagram of shiftable load calculation
图2中，可平移负荷计算的主要步骤包括形成负荷强关联集合、可平移负荷辨识、可平移负荷接受平移时段计算。
形成负荷强关联集合，包括两个步骤：
（1）形成同一负荷的连续非零状态集合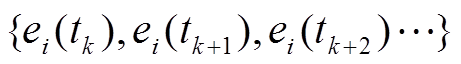
为包容测量误差或采样产生的负荷零状态，应设定裕度值，即允许连续非零状态中出现长度
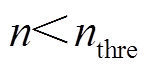点的零状态，记为
。
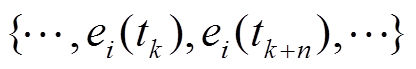（2）根据负荷状态关联性，将步骤（1）所得集合进行组合，形成负荷强关联集合。若两负荷集合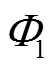
和
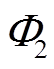，存在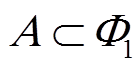
，
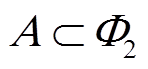，且存在强关联规则
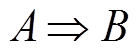或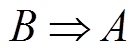
，则形成负荷强关联集合
。
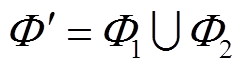将负荷集合划分为可平移负荷集合和不可平移负荷集合，划分规则为：包含具有时间关联性负荷状态的集合为不可平移负荷集合，其他集合为可平移负荷集合。
对于每个可平移负荷集合，需计算其可接受平移时段。计算集合中每个负荷状态的反时间关联性时间区间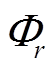
。一天的时间
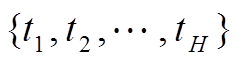除去反时间关联性区间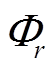，形成
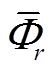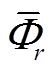。的形式为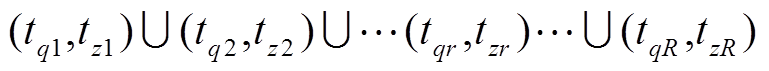
。设可平移负荷集合
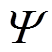的长度为
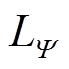，若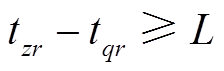
，则时间区间
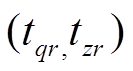可作为可平移负荷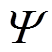的可接受平移时段。
本文利用负荷辨识开放数据集AMPds中4~8月的洗衣机、烘干机、洗碗机、娱乐设备（电视、音响等）、办公设备（台灯、计算机等）五种负荷的电流数据进行验证。本文选择不同功率等级电器进行算例分析是为说明算法的适用性，实际进行负荷管理时可只针对大功率电器，暂不考虑小功率电器，减小问题的复杂程度。
AMPds数据集包括一个典型家庭11个常见负荷每分钟间隔采样的一年的用电数据，包括负荷的电流、电压、有功功率等[22]。它较其他开放数据集建立日期更新，负荷相关数据采集更完整，满足文章的数据需求[23-24]。
首先，对其电流数据进行了5min降采样。然后，通过对比滑动均值算法与增加冗余类中心消除判据的迭代k-means聚类算法的状态提取结果，证明了滑动均值算法的有效性、数据兼容性和计算效率上的优势[19]。接着，通过对用户4个月负荷状态数据的分析，求得该用户的负荷状态强关联集合和负荷的时间关联性，并选取负荷较多的一天进行可平移负荷辨识。通过与其他可平移负荷辨识方法进行对比，最终验证了本文算法的可行性与有效性。
本文选取文献[19]中增加冗余类中心消除判据的迭代k-means算法作为对比算法（以下统称为聚类状态划分），对本文的滑动均值状态划分算法的效果进行说明。聚类算法中给定方差阈值sthre对计算结果影响较大，经试验取0.1效果较好。小电流标准取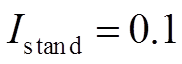
。本文提出的滑动均值状态划分算法中，滑动窗口w= 5，¶thre=17(
)。
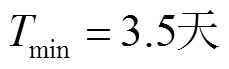两种算法划分结果如图3所示，其横坐标为测量的电流值，纵坐标对应其电流值的出现频数，不同颜色代表划分成不同状态。为了能清晰展示出每个负荷状态的位置，没有对所有状态出现的频数进行完全展示。
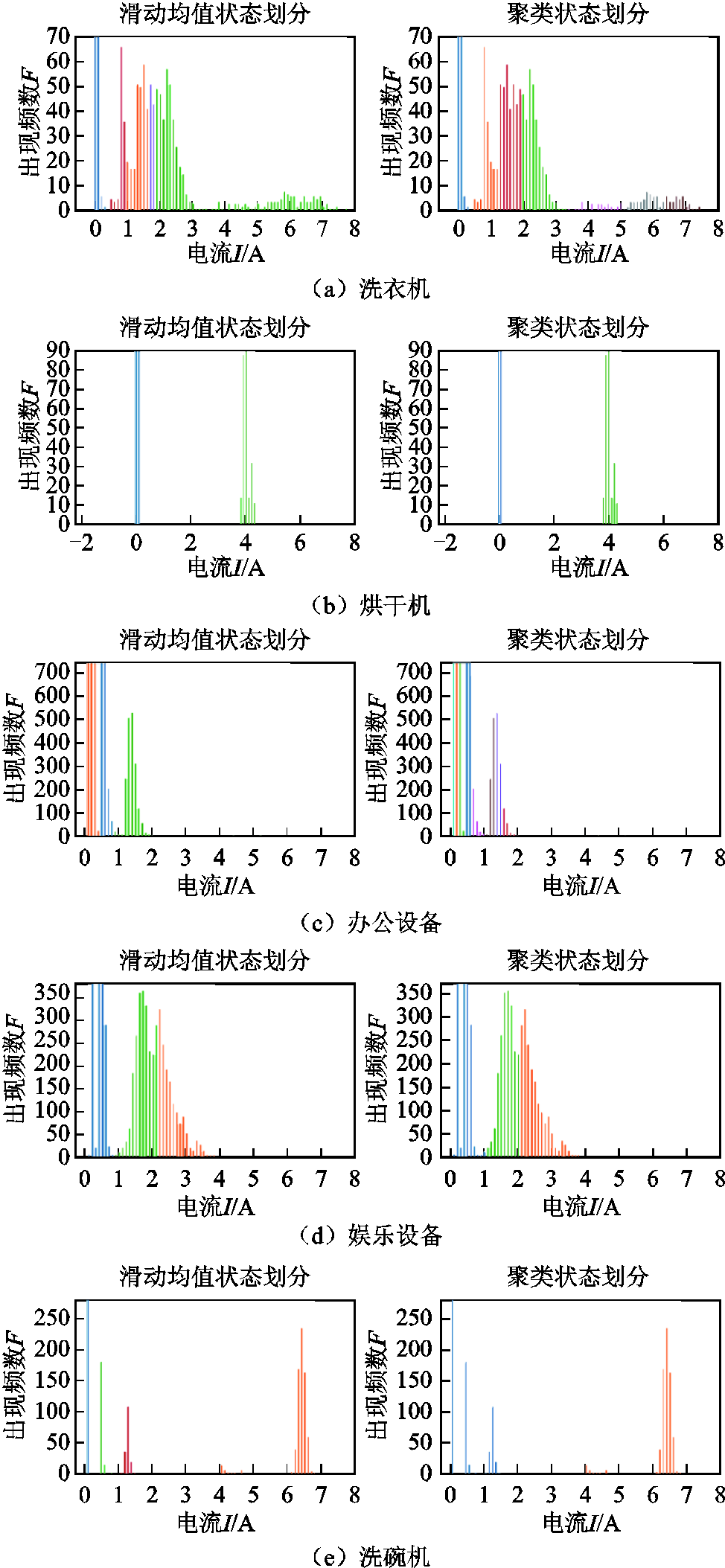
图3 负荷状态划分结果
Fig.3 The partition of load states
如图3所示，对于烘干机和娱乐设备，两种电流波动小、噪声小的负荷，滑动均值算法与聚类算法得出的状态划分结果相同。而对于洗衣机、办公设备、洗碗机三种负荷的状态划分，分别体现出滑动均值算法较聚类算法的三种优势：
（1）滑动均值算法的抗噪能力强。洗衣机负荷产生了很多大数值、低频次的电流值，这些电流在4个月的4 000余个采样点中仅出现了不到10次，说明其并不是稳定负荷状态下的电流值，将其单独分类是不合理的，而聚类算法无法识别数据是否为噪声数据，将其单独分为三类。对于本文算法，将其归入正常负荷类中电流值最大的一类，根据“误差的正态分布”原则具有合理性。虽然会对高电流负荷状态的分类产生一定影响，但由于其频数远远小于正常负荷状态电流出现的频数，影响暂可忽略。
（2）滑动均值算法在功率波动较大的情况下不会出现误增分类、漏分类。对于办公设备，其每个负荷状态的功率波动没有呈现出均匀对称的正态分布，此时聚类算法因为基于正态分布的方差进行类数增减，因此错把3类负荷分为8类负荷；同样，对于洗碗机数据，聚类算法并没有将明显分隔开的0、1、2状态划分出来，而是作为一类数据。
（3）滑动均值算法的参数设置对数据不敏感，适应性强。对于5种功率波动不同、分布不同的负荷，滑动均值算法均可以进行有效的识别，不需要针对不同负荷设置参数；而如果想让聚类算法表现更佳，则需要对每一种负荷通过试验单独设定方差阈值sthre。
另外，由于滑动均值算法复杂度低，计算效率远远高于聚类算法，速度平均提升了100倍以上。可以应用到负荷数量更多的场景下，其计算时间见表2。
表2 状态划分算法计算时间对比
Tab.2 Calculation time for partitioning load states
负荷名称聚类算法计算时间/s滑动均值算法计算时间/s本文算法提速(倍) 洗衣机1.740.001 11582 烘干机0.250.003 571 娱乐设备0.270.002 5108 洗碗机0.110.004 028 办公设备1.720.006 0287 平均值0.8180.003 4415
对负荷状态进行关联性分析，需要选取关联周期、支持度阈值、置信度阈值三个参数。其中，关联周期决定多长时间内出现的负荷是可能有关联性的，关联周期越短，对负荷状态的关联性要求越高，也对用户体验越不友好。对于居民用户来说，选择在0.5~3h之间比较适宜。支持度阈值的选择考虑了用户的行为规律：支持度阈值过高，会忽略掉用户的一些低频电器使用习惯；支持度阈值过低，会导致误把一些偶然事件当成用户习惯，缩减可平移负荷资源。对于居民用户，可以根据对可平移资源和用户体验的权衡，在1~5次/月内进行选择。置信度阈值决定了关联规则的准确度，置信度越高，则对负荷间关联性要求越高，可根据需求在65%~95%间进行选择。这三个参数选取的本质是在可平移资源的丰富性和用户体验之间做权衡，本文对所用数据集进行了测试，关联周期为2h，支持度阈值为10，置信度阈值为75%时，可平移负荷资源量较为合适。
FP-Growth计算所得强关联规则见表3。
表3 强关联规则
Tab.3 Patterns of strong correlation
强关联规则置信度（%） {洗衣机4}→{洗衣机1}92.3 {洗碗机3}→{洗碗机2}78.6 {烘干机1}→{烘干机2}100 {洗碗机3}→{洗碗机1}83.3 {娱乐设备1}→{娱乐设备2，办公设备2}90.9 {娱乐设备2}→{娱乐设备1，办公设备2}100 {娱乐设备1}→{娱乐设备2，办公设备1}75 {娱乐设备2}→{娱乐设备1，办公设备1}100 {娱乐设备1}→{娱乐设备2}86.9 {娱乐设备2}→{娱乐设备1}88.3
表3中同一负荷不同状态产生的强关联规则，如{洗衣机4}→{洗衣机1}，置信度92.3%，可理解为用户在使用洗衣机状态1后，有92.3%的可能性会在2h内使用洗衣机状态4。因此在计算可平移负荷时，若出现相隔2h内的洗衣机状态1与状态4，则必须要联合考虑，不可单独平移其中任一负荷。
表3中多挡电器较多，同一负荷的不同状态间存在关联性，如洗碗机、烘干机、洗衣机、娱乐设备。不同负荷的状态间也存在强关联性，如该用户娱乐设备和办公设备同时使用的频率非常高，可以猜测用户存在办公娱乐交叉进行或同时进行的习惯，所以两个负荷在平移时也需要同时考虑。
取时间关联性阈值bthre=80%进行负荷的时间关联性分析，采样周期取1~7天，可发现该用户有85%的概率在每天11:30~14:30使用娱乐设备。因此为了尽量减少用户体验的牺牲，涉及11:30~14:30的娱乐设备负荷不作为可平移负荷。
由于8月10日负荷使用较多，本文取该日进行可平移负荷计算，该日负荷状态曲线见附录。取连续裕度值nthre=3，形成负荷集合，见表4。
表4 连续负荷集合划分结果
Tab.4 Set partition of continuous load
集合序号负荷所属电器开始时间结束时间包含状态消耗功率/ (kW×h) 1洗衣机08:109:10[1,2,3,4]0.19 2烘干机10:3010:55[1,2]2.61 3烘干机13:0013:50[1,2]1.61 4娱乐设备11:4513:45[1,2]0.41 5办公设备5:107:35[1,2]0.38 6办公设备9:1010:25[2]0.27 7办公设备10:4021:50[1,2]0.96
根据表3的强关联规则，将表4中集合4~7合并为集合4，完成强关联集合划分。根据负荷的时间关联性，娱乐设备在11:30~14:30区间内使用为固定性行为；而集合4包含具有时间关联性的负荷状态，为不可平移集合。集合1、2、3不包含具有时间关联性的负荷状态，为可平移集合。
对集合1~3，根据本文提出的算法，利用近一个月数据分别计算可接受平移时间段。同时，对比主观选择的可平移负荷与按照文献[14]计算的可平移负荷，结果见表5。
表5 负荷可平移时段结果
Tab.5 Results of shiftable load monitoring
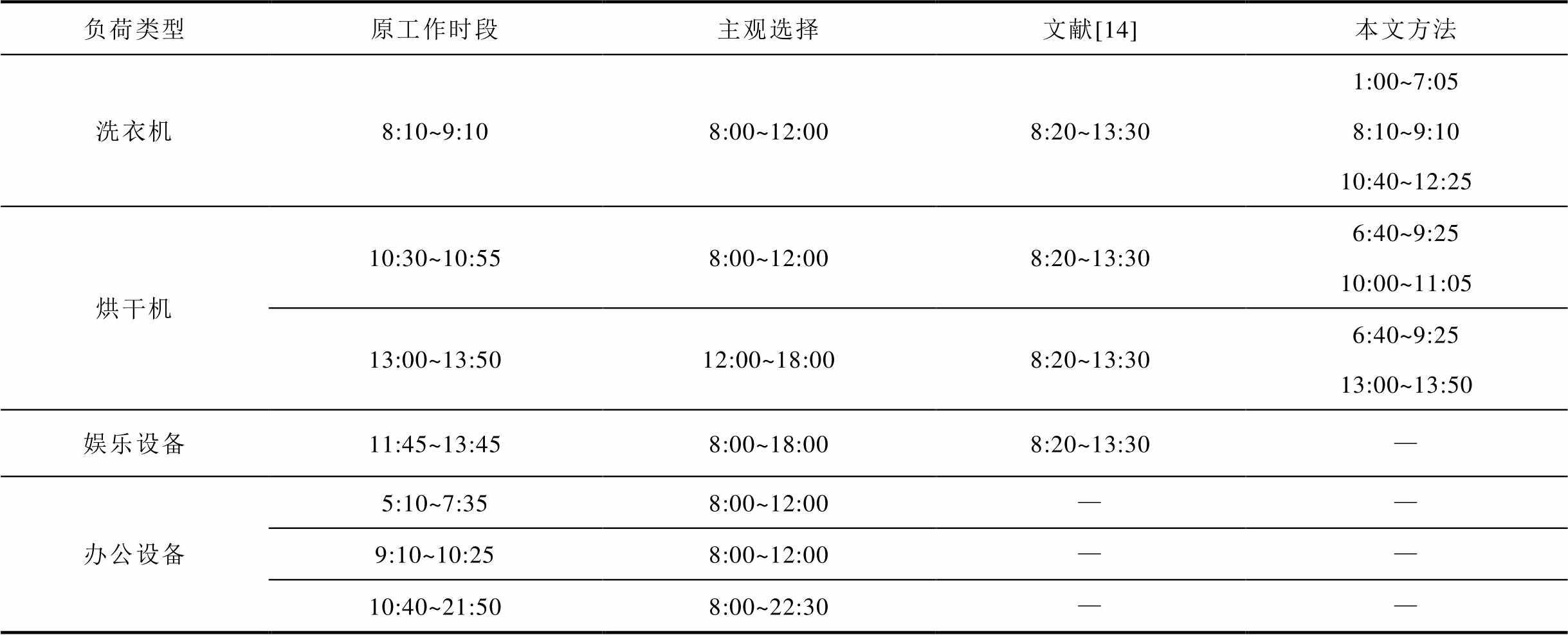
负荷类型原工作时段主观选择文献[14] 本文方法 洗衣机8:10~9:108:00~12:008:20~13:301:00~7:058:10~9:1010:40~12:25 烘干机10:30~10:558:00~12:008:20~13:306:40~9:2510:00~11:05 13:00~13:5012:00~18:008:20~13:306:40~9:2513:00~13:50 娱乐设备11:45~13:458:00~18:008:20~13:30— 办公设备5:10~7:358:00~12:00—— 9:10~10:258:00~12:00—— 10:40~21:508:00~22:30——
若根据主观意识判断，会直接选择洗衣机、烘干机、洗碗机和娱乐设备的所有负荷作为可平移负荷，选取全天或者同一半天的某个连续时段作为平移可接受时间段。然而，对于该用户来说，其娱乐设备的使用与办公设备的使用存在很强的关联性。在办公设备的用电负荷不做平移的前提下，平移娱乐设备的用电负荷，不符合用户的使用习惯，用户很难接受。另一方面，通过负荷状态时间关联性分析可知，该用户有85%的概率在每天11:30~14:30会使用娱乐设备，说明用户在使用娱乐设备上有非常规律的使用行为。打破这种长期规律，对用户体验牺牲很大。
文献[14]的可平移负荷计算结果和本文计算结果有部分重合。但与本文方法相比，其对洗衣机、烘干机的可平移时段计算结果粗略，缺乏精细化考量。与主观意识判断相同，文献[14]也把娱乐设备归为可平移的范畴，与事实不符。
本文算法所求得的可平移负荷考虑了办公设备和娱乐设备的关联性，并认为包含11:30~14:30的娱乐设备使用时段是不可平移的。另外，在可接受平移时段的选择上，本文算法给出的结果排除了用户从来没有使用过相应负荷的时间段，考虑了用户因为上班、休息等不可抗拒因素无法进行负荷平移的影响。
本文提出了一种基于电器状态集关联分析的居民用户可平移负荷辨识方法。该方法利用滑动均值法提取负荷状态，并建立负荷状态集关联分析模型，用FP-Growth算法求解，得到负荷状态集关联性与负荷状态时间关联性，最后计算可接受平移时段。在上述理论基础上，本文用开放数据集AMPds进行算例验证，算例结果表明，本文所提方法具备如下优点：
1）提出的滑动均值负荷状态提取法较现有效果较好的增加冗余类中心消除判据的迭代k-means算法，更能准确地还原电器的工作状态，并且计算效率提升了100倍以上。
2）所提算法能有效地进行可平移负荷辨识，较主观判定和已有文献的辨识结果较好。本算法在进行可平移负荷辨识的过程中充分考虑了用户使用电器的习惯，在尽量减小牺牲用户体验的前提下，辨识用户参与需求响应的可平移负荷资源。
3）本文算法涉及的参数易于获得，一类用户只需要进行一次参数设置，减轻了落地时的参数调试压力。
综上所述，本文所提的可平移负荷辨识结果较已有方法更贴合用户用电习惯，并具有可行性。
本文的研究工作未能考虑环境因素对可平移负荷的影响，而很多负荷的工作状态都与环境因素相关，如空调、照明等。同时，本文算法仅可支持采样频率高于15min每点的可平移负荷辨识。进一步研究可以在可平移负荷辨识中考虑负荷状态的环境因素关联性，并兼顾算法在低频采样数据中的适用性，更加合理地评估可控负荷资源。
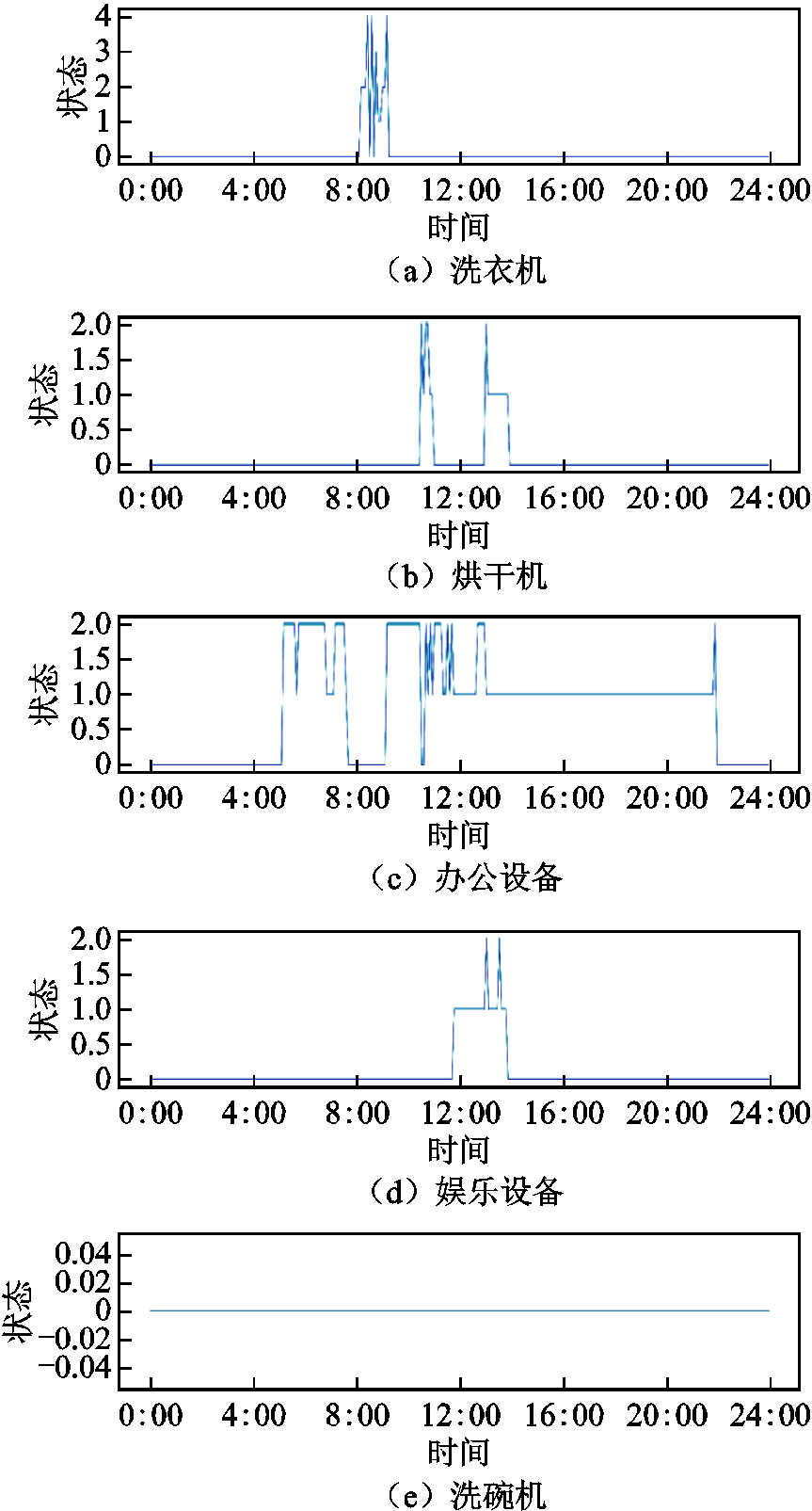
附图1 负荷情况曲线（8月10日）
App.Fig.1 The load curves (Aug.10)
参考文献
[1] 董朝阳, 赵俊华, 文福拴, 等. 从智能电网到能源互联网:基本概念与研究框架[J]. 电力系统自动化, 2014, 38(15): 1-11. Dong Zhaoyang, Zhao Junhua, Wen Fushuang, et al. From smart grid to energy internet:basic concept and research framework[J]. Automation of Electric Power Systems, 2014, 38(15): 1-11.
[2] 胡江溢, 祝恩国, 杜新纲, 等. 用电信息采集系统应用现状及发展趋势[J]. 电力系统自动化, 2014, 38(2): 131-135. Hu Juangyi, Zhu Enguo, Du Xingang, et al. Application status and development trend of power consumption information collection system[J]. Automation of Electric Power Systems, 2014, 38(2): 131-135.
[3] 宋亚奇, 周国亮, 朱永利. 智能电网大数据处理技术现状与挑战[J]. 电网技术, 2013, 37(4):927-935. Song Yaqi, Zhou Guoliang, Zhu Yongli. Present status and challenges of big data processing in smart grid[J]. Power System Technology, 2013, 37(4): 927-935.
[4] 陆俊, 朱炎平, 彭文昊, 等. 智能用电用户行为分析特征优选策略[J]. 电力系统自动化, 2017, 41(5): 58-63, 83. Lu Jun, Zhu Ynping, Peng Wenhao, et al. Feature selection strategy for electricity consumption behavior analysis in smart grid[J]. Automation of Electric Power Systems, 2017, 41(5): 58-63, 83.
[5] 王珂, 姚建国, 姚良忠, 等. 电力柔性负荷调度研究综述[J]. 电力系统自动化, 2014, 38(20): 127-135.Wang Ke, Yao Jianguo, Yao Liangzhong, et al. Survey of research on flexible loads scheduling technologies[J]. Automation of Electric Power Systems, 2014, 38(20): 127-135.
[6] 徐青山, 刘梦佳, 戴蔚莺, 等. 计及用户响应不确定性的可中断负荷储蓄机制[J]. 电工技术学报, 2019, 34(15): 3198-3208. Xu Qingshan, Liu Mengjia, Dai Weiying, et al. Interruptible load based on deposit mechanism considering uncertainty of customer behavior[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3198-3208.
[7] Callaway D S, Hiskens I A. Achieving controllability of electric loads[J]. Proceedings of the IEEE, 2011, 99(1): 184-199.
[8] 李童佳, 张晶, 祁兵. 居民用户需求响应业务模型研究[J]. 电网技术, 2015, 39(10): 2719-2724. Li Tongjia, Zhang Jing, Qi Bing. Studies on business model of demand response for residential users[J]. Power System Technology, 2015, 39(10): 2719-2724.
[9] 孙川, 汪隆君, 许海林. 用户互动负荷模型及其微电网日前经济调度的应用[J]. 电网技术, 2016, 40(7): 2009-2015. Sun Chuan, Wang Longjun, Xu Hailin. An interaction load model and its application in microgrid day-ahead economic scheduling[J]. Power System Technology, 2016, 40(7): 2009-2015.
[10] 阳小丹, 李扬. 家庭用电响应模式研究[J]. 电力系统保护与控制, 2014, 42(12): 51-56. Yang Xiaodan, Li Yang. Research on household electricity response mode[J]. Power System Protection and Control, 2014, 42(12): 51-56.
[11] 曾鸣, 武赓, 王昊婧, 等. 智能用电背景下考虑用户满意度的居民需求侧响应调控策略[J]. 电网技术, 2016, 40(10): 2917-2923. Zeng Ming, Wu Geng, Wang Haojing, et al. Regulation strategies of demand response considering user satisfaction under smart power background[J]. Power System Technology, 2016, 40(10): 2917-2923.
[12] 徐建军, 王保娥, 闫丽梅, 等. 混合能源协同控制的智能家庭能源优化控制策略[J]. 电工技术学报, 2017, 32(12): 214-223. Xu Jianjun, Wang Baoe, Yan Limei, et al. The strategy of the smart home energy optimization control of the hybrid energy coordinated control[J]. Transactions of China Electrotechnical Society, 2017, 32(12): 214-223.
[13] 马丽. 基于博弈论的智能配用电系统优化运行方法[D]. 北京: 华北电力大学, 2017.
[14] 孙毅, 刘迪, 李彬, 等. 基于家庭用电负荷关联度的实时优化策略[J]. 电网技术, 2016, 40(10): 1825-1829. Sun Yi, Liu Di, Li Bin, et al. Research on real-time optimization strategy based on correlation of household electrical load[J]. Power System Technology, 2016, 40(10): 1825-1829.
[15] 范龙, 李献梅, 陈跃辉, 等. 激励CCHP参与需求侧管理双向峰谷定价模型[J]. 电力系统保护与控制, 2016, 44(17): 45-51. Fan Long, Li Xianmei, Chen Yuehui, et al. Pricing model of bidirectional peak-valley for motivating CCHP to participate in DSM[J]. Power System Protection and Control, 2016, 44(17): 45-51.
[16] 程祥, 李林芝, 吴浩, 等. 非侵入式负荷监测与分解研究综述[J]. 电网技术, 2016, 40(10): 3108-3117. Cheng Xiang, Li Linzhi, Wu Hao, et al. A survey of the research on non-intrusive load monitoring and disaggregation[J]. Power System Technology, 2016, 40(10): 3108-3117.
[17] 陈思运, 高峰, 刘烃, 等. 基于因子隐马尔可夫模型的负荷分解方法及灵敏度分析[J]. 电力系统自动化, 2016, 40(21): 128-136. Chen Siyuan, Gao Feng, Liu Ting, et al. Load disaggregation method based on factorial hidden markov model and its sensitivity analysis[J]. Automation of Electric Power Systems, 2016, 40(21): 128-136.
[18] 徐青山, 娄藕蝶, 郑爱霞, 等. 基于近邻传播聚类和遗传优化的非侵入式负荷分解方法[J]. 电工技术学报, 2018, 33(16): 212-222. Xu Qingshan, Lou Oudie, Zheng Aixia, et al. A non-intrusive load decomposition method based on affinity propagation and genetic algorithm optimization[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 212-222.
[19] 燕续峰, 翟少鹏, 王治华, 等. 深度神经网络在非侵入式负荷分解中的应用[J]. 电力系统自动化, 2019, 43(1): 126-132, 167. Yan Xufeng, Zhai Shaopeng, Wang Zhihua, et al. Application of deep neutral network in non-intrusive load disaggregation[J]. Automation of Electric Power System, 2019, 43(1): 126-132, 167.
[20] 晏杰, 亓文娟. 基于Aprior & FP-growth 算法的研究[J]. 计算机系统应用, 2013, 22(5):122-125. Yan Jie, Qi Wenjuan. Research based on aprior & FP-growth algorithm[J]. Computer Systems & Applications, 2013, 22(5): 122-125.
[21] 王新宇, 杜孝平, 谢昆青. FP-growth算法的实现方法研究[J]. 计算机工程与应用, 2004, 40(9): 174-176. Wang Xxinyu, Du Xiaopig, Xie Kunqing. Research on implementation of the FP-growth algorithm[J]. Computer Engineering and Applications, 2004, 40(9): 174-176.
[22] Makonin S, Popowich F, Bartram L, et al. AMPds: A public dataset for load disaggregation and eco-feedback research[C]// 2013 IEEE Electrical Power & Energy Conference, Halifax, NS, Canada, 2014, DOI: 10.1109/EPEC.2013.6802949.
[23] Anderson K, Ocneanu A, Benitez D, et al. Blued:a fully labeled public dataset for event-based non-intrusive load monitoring research [C]//Proceedings of the 2nd KDD Workshop on Data Mining Applications in Sustainability, Beijing, China: 2012: 1-5.
[24] Kolter J Z, Johnson M J. REDD: A public data set for energy disaggregation research[J]. Sustkdd, 2011, 25.
Resident Shiftable Loads Monitoring Based on Load States Set Correlation Analysis
Abstract To guide residents to participate demand response, a shiftable load monitoring algorithm was proposed based on the analysis of load states set correlation. Firstly, a sliding average method was introduced to extract the load states, which extracts load’s working states from its current value and form the load states set. Then load states set correlation analysis model was established, load states correlation and load characteristic time could be obtained by using FP-Growth solver. The former leads to a strong-correlated loads set from the data of daily electricity demand, while the latter determines whether the loads set is shiftable and the time period of being shiftable. The daily shiftable loads monitoring was achieved from both results, which can provide necessary data to distributed control of resident demand response and optimization of household energy management.
keywords：Shiftable load monitoring, load states extracting, load correlation, load characteristic time, demand response
中图分类号：TM73
DOI：10.19595/j.cnki.1000-6753.tces.191809
国家重点研发计划资助项目（2016YFB0901300）。
收稿日期 2019-12-29
改稿日期 2020-03-05
王孝慈 女，1994年生，硕士研究生，研究方向为智能用电与需求响应。E-mail：982128684@qq.com
董树锋 男，1982年生，博士，副教授，研究方向为状态估计和有源配电网分析。E-mail：dongshufeng@zju.edu.cn（通信作者）
（编辑 郭丽军）