
图1 VSC换流站等效电路
Fig.1 The equivalent circuit of the VSC converter station
摘要 目前配电网中配置的量测装置种类简单且数量有限,分布式电源(DG)出力和用户负荷通常具有非高斯分布的不确定性,加剧了交直流配电网状态估计的不确定性和误差。针对这些问题的研究严重滞后于对交直流系统进行灵活调度的发展目标,因此需要研究更有效的交直流配电网状态估计方法来支撑调度系统。该文采用计及电压源换流器(VSC)损耗的模型,基于高斯混合模型(GMM)对非高斯不确定性进行伪量测建模,充分考虑交流和直流配电网间不确定性的耦合计算,提出一种交直流配电网两阶段概率状态估计算法。采用IEEE 33节点修改算例进行交直流配电网仿真,结果表明,所提两阶段算法适用于实时量测少、数据冗余度低的情况;对已有交流状态估计算法继承性好,具有实用性,未来可扩展到三相不平衡交直流配电网状态估计中。
关键词:伪量测建模 交直流配电网 概率状态估计 分布式电源 高斯混合模型
随着新能源技术的大力发展,越来越多的分布式电源(Distributed Generation, DG)以多种形式接入电力系统[1]。由于直流配电系统供电容量较高,网损较低,更易于DG的渗入及直流负荷的接入,从而减少大量换流器,节省投资费用[2-3]。同时交直流配电网还可以更好地利用DG、储能装置等电力电子设备,为交流配电网提供有效的控制方式[4]。因此在已有交流电网中,引入多端柔性直流技术,形成更灵活的交直流配电网以满足更多分布式电源入网需求是目前研究的一个热点[5-6]。
灵活的交直流配电网的安全运行[6]和系统调度控制[7]需要状态估计来为其提供实时工况和更加精确、完整的电力系统状态值。目前关于交直流配电网状态估计的研究较少,交直流混联系统的状态估计研究多集中在交直流输电网的研究上,算法上主要分为两类:统一迭代法[8-9]和交替迭代法[10-12]。统一迭代法需要将交流直流所有量测方程联立求解,收敛性好,但是不能很好地继承原有交流状态估计程序;交替迭代法依次求解交流直流状态估计,能较好地利用已有交流状态估计程序,因此得到了更多关注[12]。
而对于交直流配电网来说,其交流部分一般呈辐射状,运行方式改变时可能出现少量环网且支路的R/X比很大;直流部分可接入大量电力电子设备如DG和储能设备,连同交流部分接入的设备使得电网中不确定性更大,需要对这些电力电子设备进行更加精准的建模;同时节点众多,实时量测装置较输电网相对不足,数据冗余度不足[13-15]。以上特点使得现有状态估计算法不能直接应用在交直流配电网上:交流部分的辐射网等问题使得交直流配电网采用统一迭代法时可能会面临雅可比阵病态、迭代不收敛等问题;节点众多的问题使得统一迭代法和交替迭代法计算时间较长[16],分布式方法将是较好的选择[17]。为了解决量测数据不足和含不确定性的问题,在不改变现有量测装置的基础上,交直流配电网状态估计需要更加精确的伪量测建模方法来提高数据冗余度,同时准确地模拟配电网中的非高斯不确定性以提高状态估计的精度。
配电网中的伪量测数据如DG出力数据一般是单一地采用历史数据或出力预测数据得到的,不够精确,容易引入误差。为了有效地计入不确定性,配电网中常采用的不确定性的建模方法有区间数模型[18-19]和概率模型[20-22]。文献[18]提出了用区间数的方法来描述量测的不确定性。文献[19]进一步将其应用在含DG的主动配电网,采用基于迭代运算的线性规划算法进行求解。文献[20]通过历史统计数据建立了DG出力和负荷功率的概率密度函数(Probability Density Function, PDF)来描述其不确定性。文献[21]采用高斯混合模型(Gaussian Mixture Model, GMM)描述DG和负荷的出力的概率密度函数,基于加权最小二乘(Weighted Least Square, WLS)算法进行状态估计。与区间模型相比,概率模型不仅能够得到状态变量的分布范围,还能得到其可能的概率分布,为状态变量的后续趋势提供参考意见。但在交直流配电网中,与概率状态估计相关的研究还较少,文献[20-22]均未考虑交流配电网和直流配电网不确定性间的耦合,且统一迭代的方法计算量大。
另外,已有的交直流混联系统状态估计研究中通常会简化电压源换流器(Voltage Source Converter, VSC)模型,忽略换流站的有功损耗[9]。随着交直流配电网规模的增大,VSC个数的增多和传输功率的提高,换流站损耗对于交直流系统的影响不容忽视[23]。在量测冗余度不足的交直流配电网中,计及VSC损耗将会提高伪量测数据的精度和状态估计效果。
综上所述,本文在分布式算法的基础上,针对交直流配电网量测数据冗余度低的问题,提出了一种基于高斯混合模型的交直流配电网两阶段概率状态估计方法。该方法可以有效地考虑交流配电网和直流配电网之间非高斯不确定性的耦合,且在接口处考虑完整的VSC损耗模型,提高了伪量测数据的精度。另外,本文算法采取两阶段计算框架:第一阶段采取局部交流配电网和直流配电网并行的概率状态估计,通过交互模块计算得到边界注入功率为量测数据和相应不确定度;在第二阶段中,利用新的伪量测数据和实时量测数据再一次并行直流和交流配电网的概率状态估计。两阶段算法采用交直流并行计算,减少计算时间。最后,在经改进的IEEE 33节点交直流配电网算例中验证了所提算法的精确度和可行性。
VSC是连接交流配电网和直流配电网之间的重要控制元件,需要对其进行合理建模。文献[24]采用了不计损耗的换流器模型。文献[25]采用等效电阻来描述VSC内部损耗和换流变压器损耗。文献[26]采用了损耗模拟系数来描述VSC工作损耗。为保证更高计算精度且简化计算,本文采用计及损耗的VSC模型,其等效电路如图1所示。

图1 VSC换流站等效电路
Fig.1 The equivalent circuit of the VSC converter station
图1给出了第i个VSC换流站的等效电路,交直流系统稳态运行时,可忽略换流器谐波分量。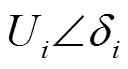 为交流子系统母线公共连接点的电压相量。交流母线经电压比为
为交流子系统母线公共连接点的电压相量。交流母线经电压比为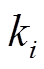 的换流变压器
的换流变压器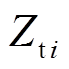 、滤波器
、滤波器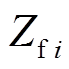 和换相电抗器
和换相电抗器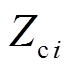 与VSC母线
与VSC母线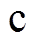 连接。VSC母线c的输出基波电压相量为
连接。VSC母线c的输出基波电压相量为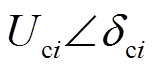 。VSC直流侧采用双极接线连接到直流母线,直流侧电压为
。VSC直流侧采用双极接线连接到直流母线,直流侧电压为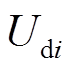 。采用
。采用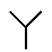 -△变换可消去滤波器支路节点
-△变换可消去滤波器支路节点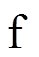 ,得到交流电网注入换流站有功功率
,得到交流电网注入换流站有功功率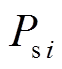 、无功功率
、无功功率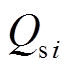 及注入VSC母线处有功功率
及注入VSC母线处有功功率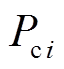 和无功功率
和无功功率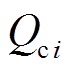 分别为
分别为
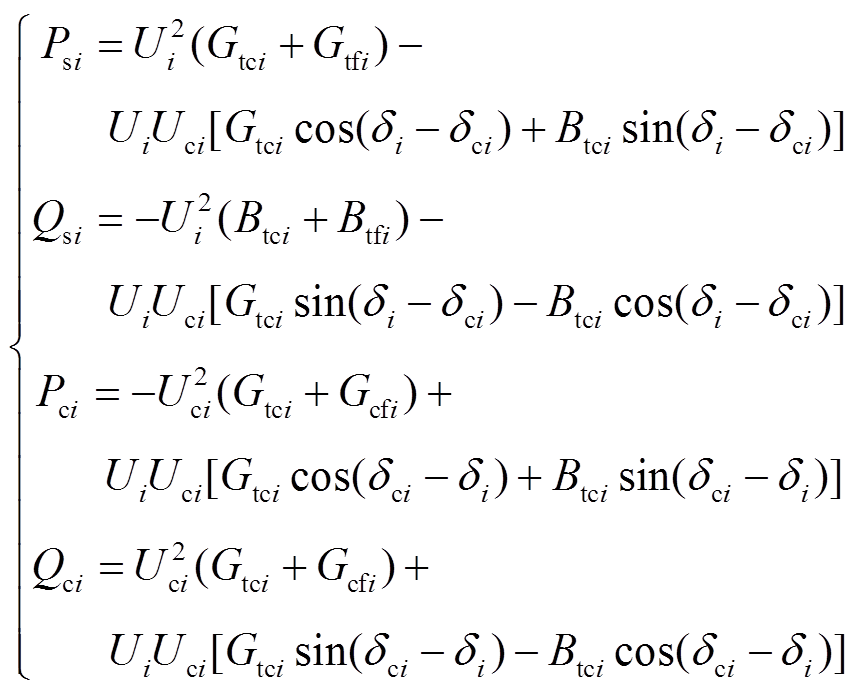 (1)
(1)式中,Ytci、Ycfi、Ytfi分别为由换流变压器、滤波器、换向电抗器导纳 -△变换而得的等效导纳,
-△变换而得的等效导纳,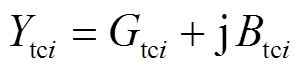 ,
,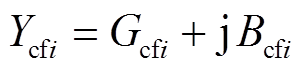 ,
,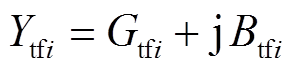 ,具体定义可参见文献[26]。
,具体定义可参见文献[26]。
此外VSC换流器需满足电压约束[27]
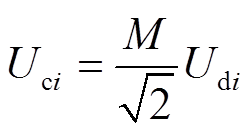 (2)
(2)式中,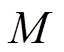 为VSC的调制比。
为VSC的调制比。
选取图1中功率方向为正,则功率平衡关系为
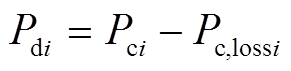 (3)
(3)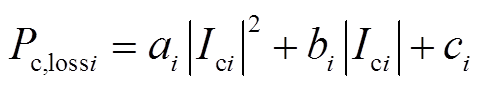 (4)
(4)式中,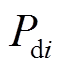 为VSC注入直流电网功率;
为VSC注入直流电网功率;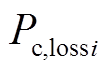 为换流器损耗[28];
为换流器损耗[28];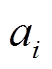 模拟与
模拟与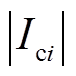 2成正比的损耗;
2成正比的损耗;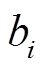 模拟与
模拟与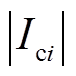 成正比的损耗;
成正比的损耗;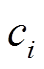 模拟固定损耗;
模拟固定损耗;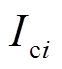 为VSC交流支路电流,其幅值满足
为VSC交流支路电流,其幅值满足
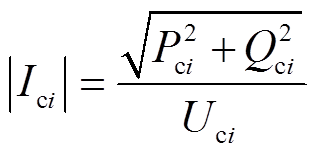 (5)
(5)交流配电网中,量测量主要采用传统的节点电压幅值、节点注入有功功率、节点注入无功功率、交流支路潮流有功功率和交流支路潮流无功功率。交流配电网中,采用节点电压幅值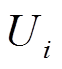 和电压相角
和电压相角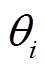 作为状态变量,因而量测方程为
作为状态变量,因而量测方程为
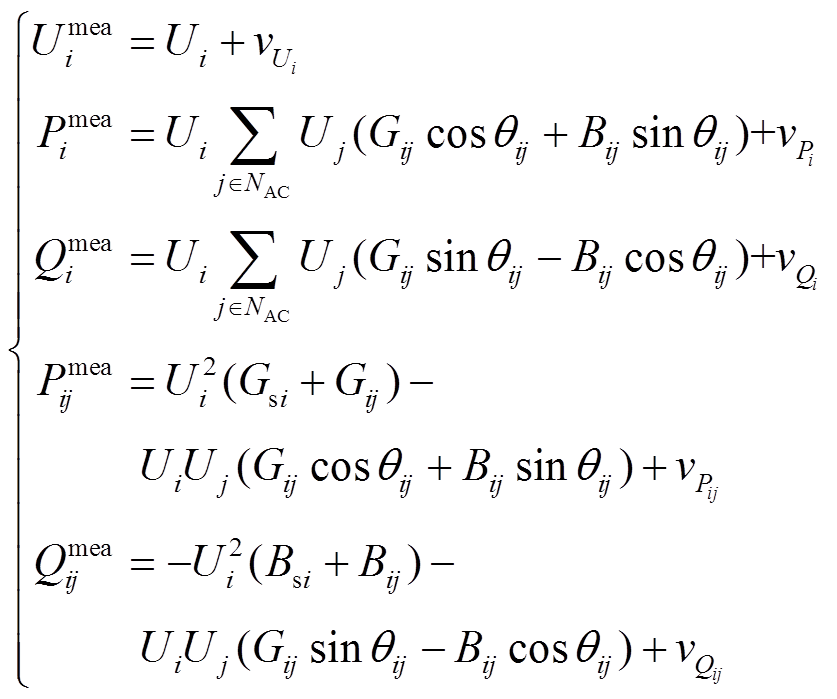 (6)
(6)式中,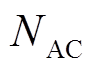 为交流配电网节点集合;
为交流配电网节点集合;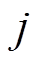 为直接和节点
为直接和节点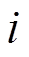 相连的节点;
相连的节点;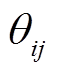 为节点
为节点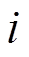 和节点
和节点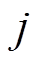 间的相位差;Yij为节点
间的相位差;Yij为节点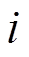 和节点
和节点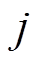 间的导纳,
间的导纳,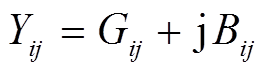 ;Ysi为节点
;Ysi为节点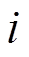 的对地导纳,
的对地导纳,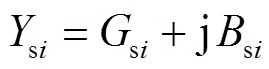 ;
;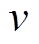 为量测误差,其下标表示量测误差的类型。
为量测误差,其下标表示量测误差的类型。
与交流配电网相似,直流配电网中量测方程为
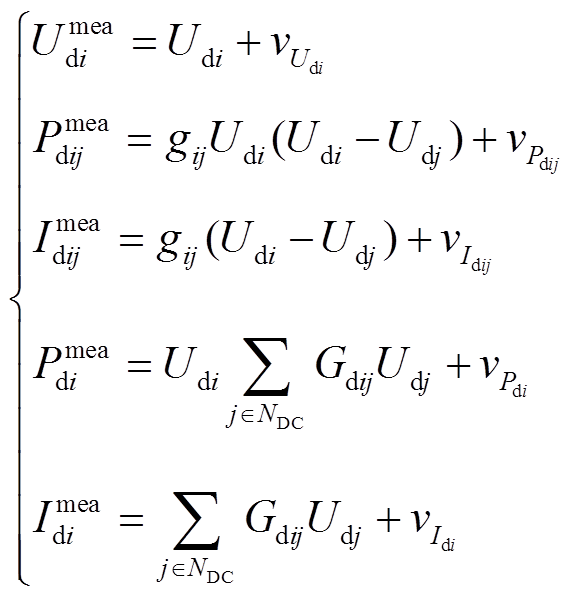 (7)
(7)式中,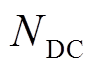 为直流配电网节点集合;
为直流配电网节点集合;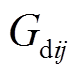 为直流网络电导矩阵中的元素;
为直流网络电导矩阵中的元素;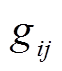 为直流支路
为直流支路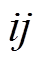 的电导。
的电导。
本文所提算法框架如图2所示,其中将交直流配电网状态估计问题描述为一个两阶段状态估计问题。
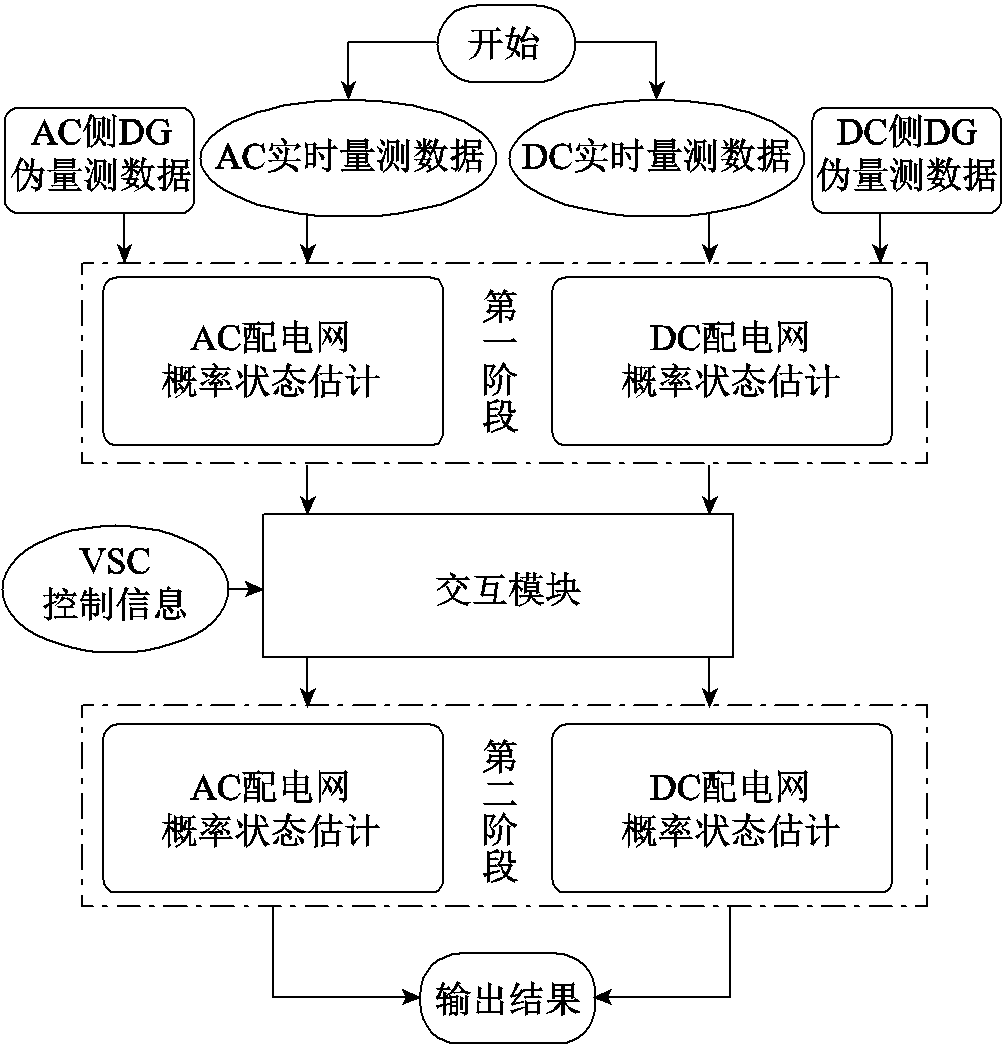
图2 交直流配电网两阶段概率状态估计框架
Fig.2 The framework of two-stage probabilistic state estimation in AC-DC distribution network
如图2所示,连接VSC的节点构成了边界点的集合。在第一阶段中,实施并行的交流配电网和直流配电网概率状态估计,初步得到各自系统边界的值和不确定度。边界值和不确定度通过交互模块进行VSC损耗的计算和不确定度的耦合交互,得到可以运用在另一个子系统的伪量测数据。第二阶段中,新获得的伪量测数据和各自子系统的原有量测数据相结合进行第二次概率状态估计,更新上一次状态估计的结果。
与传统单一的交流配电网或直流配电网算法相比,本文所提算法考虑两个电网之间的交互,精确计入VSC的损耗和各自电网非高斯不确定性的耦合,在避免交互误差的同时可以增加子系统配电网的数据冗余度,提高状态估计精度。其中,交互协调环节总是采用各子系统最新的状态估计结果来交互协调,这有助于各子系统采用非同步的量测数据,始终为配电网提供最新的估计结果,因此适用于各子系统状态估计算法完成时间不一致的情况。与传统交直流配电网算法相比,本文所提算法可保证交流直流各自状态估计的完整性(可分别采用适用于不同子系统特性的状态估计算法),便于应用。下面将具体介绍算法。
在两阶段概率状态估计中,交流配电网和直流配电网的概率状态估计是并行计算的。这里采取基于GMM的概率状态估计(Gaussian Mixture Model based Probabilistic State Estimation, GMM-PSE)算法来进行含有非高斯不确定性的概率状态估计。
2.1.1 非高斯不确定性的建模
随着DG、储能系统、微电网、电动汽车等在电网中的渗透率的提高,电力系统面临的随机性和不确定性也日益增加。这些不确定性往往不服从正态分布,呈现出非高斯不确定性。本文以DG为例进行讨论。DG可以通过VSC接入交流子系统,也可以通过VSC接入直流子系统。本文采用GMM将一个不规则的出力曲线等效为一个正态分布函数从而求取其均值和标准差[29]。在GMM里,DG的出力y的概率密度函数可被等效为几个不同的正态分布函数[29],即
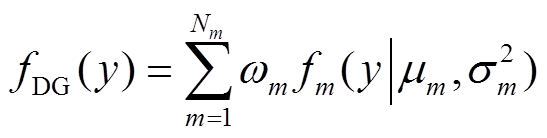 (8)
(8)式中,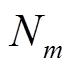 为子高斯函数的个数;
为子高斯函数的个数;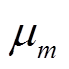 、
、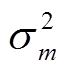 分别为第
分别为第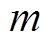 个子高斯函数的均值和方差;
个子高斯函数的均值和方差;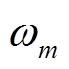 为第
为第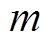 个子高斯函数的权重值。
个子高斯函数的权重值。
这些子高斯函数的权重满足
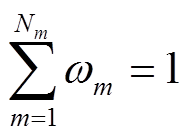 (9)
(9)子高斯函数的参数可采用最大期望(Expectation Maximization, EM)算法[29]求解。由高斯子函数等效的DG出力高斯函数的均值和方差求解分别为
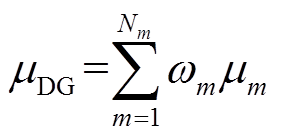 (10)
(10)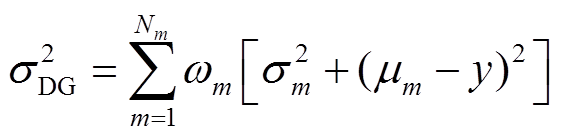 (11)
(11)不同于一些传统的特定分布(例如威布尔分布、beta分布),GMM能够模拟任何分布的概率密度函数,因此可以很好地刻画非高斯不确定性。GMM的子函数越多,所模拟的分布也就更加逼近原分布。
2.1.2 GMM-PSE估计器
基于GMM采用子函数的组合模拟任何PDF的特性,概率状态估计问题可以转换为一个求解多次子函数组合的WLS估计问题[21]。假设系统中具有非高斯不确定性的DG总数为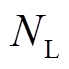 ,则总的高斯子函数组合有
,则总的高斯子函数组合有
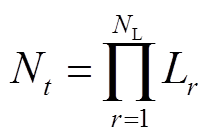 (12)
(12)式中,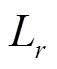 为第
为第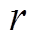 个DG的高斯子函数个数。
个DG的高斯子函数个数。
每一次WLS求解,选取一种对应的高斯子函数组合作为伪量测数据进行求解。WLS问题可采用式(13)进行求解[30]。
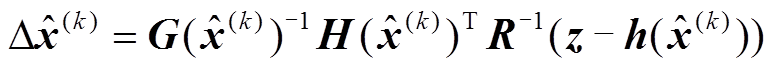 (13)
(13)式中,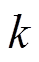 为迭代次数;
为迭代次数;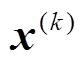 为第
为第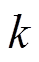 次迭代的状态向量;
次迭代的状态向量;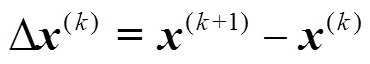 ;
;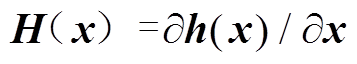 为雅可比阵;
为雅可比阵;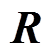 为协方差矩阵,通常被假设为对角矩阵,对角元素为各量测数据方差
为协方差矩阵,通常被假设为对角矩阵,对角元素为各量测数据方差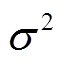 ;
;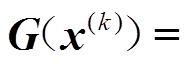
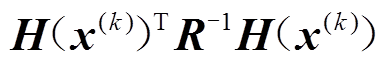 为增益矩阵,对其求逆可得状态变量的协方差矩阵为
为增益矩阵,对其求逆可得状态变量的协方差矩阵为
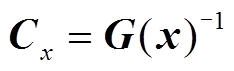 (14)
(14)计算完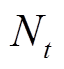 次WLS后,状态变量的PDF和估计值为
次WLS后,状态变量的PDF和估计值为
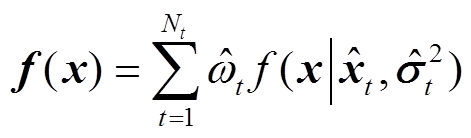 (15)
(15)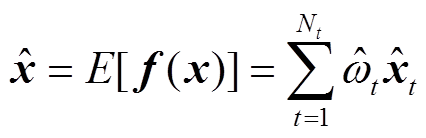 (16)
(16)式中,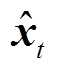 为第
为第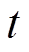 次WLS状态估计值;
次WLS状态估计值;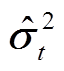 为第
为第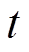 次WLS中式(14)所得协方差阵的对角元素构成的向量;
次WLS中式(14)所得协方差阵的对角元素构成的向量;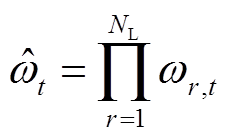 ,
,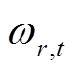 为第
为第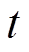 次WLS下第
次WLS下第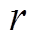 个DG对应的高斯子函数权重值,且满足
个DG对应的高斯子函数权重值,且满足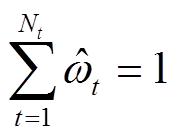 。
。
第一阶段完成后,局部AC配电网和DC配电网相应得到其状态估计值,该结果将进入到交互模块,为第二阶段的局部AC-DC并行概率状态估计提供带有高斯不确定性的伪量测数据。这一过程通过边界交互模块算法得到。为了避免引入交互误差,交互模块采用基于控制信息的分层计算确保AC侧向DC侧传递的计算和DC侧向AC侧传递的计算相互独立。交互模块算法框架如图3所示。
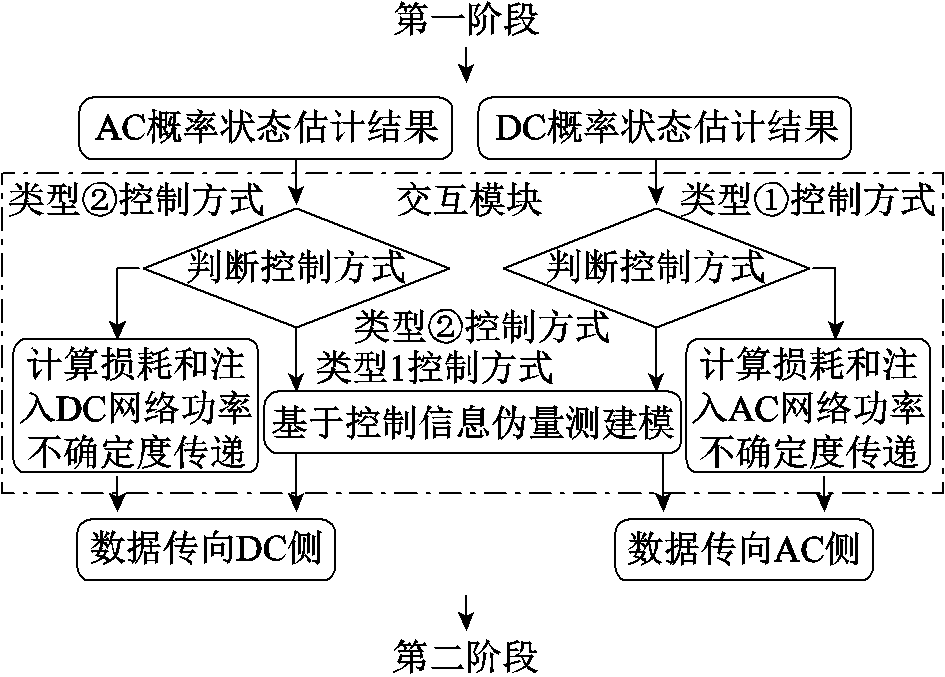
图3 交互模块算法框架
Fig.3 The framework of the algorithm for the interaction module
从图3可得,交互模块按照控制方式分类进行计算。由于VSC采用全控型开关器件,每个换流器可以同时控制直流侧某一状态变量(直流电压、直流功率或直流电流)和交流侧某一状态变量(交流侧电压或交流侧无功功率),因而分为如下两种控制类型:①定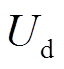 定
定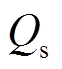 控制和定
控制和定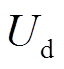 定
定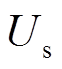 控制;②定
控制;②定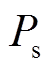 定
定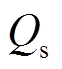 控制和定
控制和定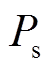 定
定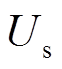 控制。
控制。
接下来阐述不同控制方式下的边界量和不确定度的交互计算。
2.2.1 边界量的交互计算
1)AC向DC侧传递估计值
AC向DC侧传递的边界量应遵循从交流量到直流量的原则。对采用类型①控制方式的VSC边界节点来说,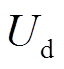 为已知的直流控制信息。由于VSC控制的目标值接近于实际运行值,可认为由此添加的伪量测值较为精确,并且能反映当前时间断面或一段时间内的系统运行状况,因而可给定较高权值,并直接将
为已知的直流控制信息。由于VSC控制的目标值接近于实际运行值,可认为由此添加的伪量测值较为精确,并且能反映当前时间断面或一段时间内的系统运行状况,因而可给定较高权值,并直接将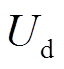 控制信息送往DC侧作为伪量测信息。
控制信息送往DC侧作为伪量测信息。
对采用类型②控制方式的VSC边界节点来说,根据简单潮流计算公式,可以得到VSC交流母线侧电压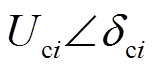 ,从而可由式(2)~式(5)得到损耗
,从而可由式(2)~式(5)得到损耗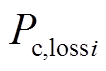 ,进而得到注入直流网络节点的功率
,进而得到注入直流网络节点的功率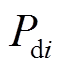 。
。
2)DC向AC侧传递估计值
DC向AC侧传递的边界量同样应遵循直流量到交流量的原则。对采用类型②控制方式的VSC边界节点来说,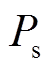 、
、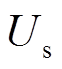 、
、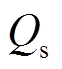 均为已知的交流侧控制信息,可根据控制信息精度较高的原则,直接送往AC侧作为伪量测控制信息。
均为已知的交流侧控制信息,可根据控制信息精度较高的原则,直接送往AC侧作为伪量测控制信息。
对采用类型①控制方式的VSC边界节点,VSC损耗与目前未知的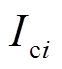 有关,因此注入AC网络的边界注入量测量
有关,因此注入AC网络的边界注入量测量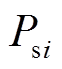 需要通过迭代的方式计算。为表述方便,以下省略VSC节点下标
需要通过迭代的方式计算。为表述方便,以下省略VSC节点下标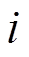 ,并标明第
,并标明第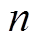 次迭代和第
次迭代和第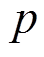 次内迭代。迭代中,类型①控制方式的控制信息
次内迭代。迭代中,类型①控制方式的控制信息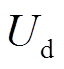 、
、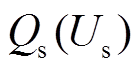 保持恒定。
保持恒定。
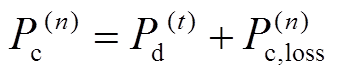 (17)
(17)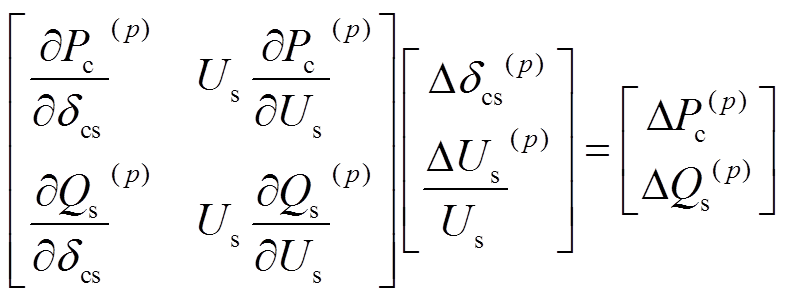 (18)
(18)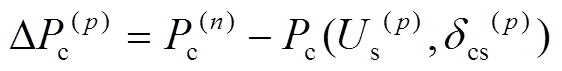 (19)
(19) (20)
(20)式中,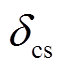 为VSC母线电压和交流母线电压的相位差。
为VSC母线电压和交流母线电压的相位差。
图4为DC侧向AC侧传递的边界量计算流程,图中描述了类型①控制方式中已知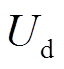 、
、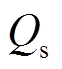 的情况,若已知
的情况,若已知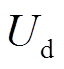 、
、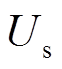 ,则可直接采用式(2)~ 式(5)取代框图中点画线部分的内循环,进行
,则可直接采用式(2)~ 式(5)取代框图中点画线部分的内循环,进行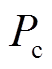 的迭代循环。
的迭代循环。
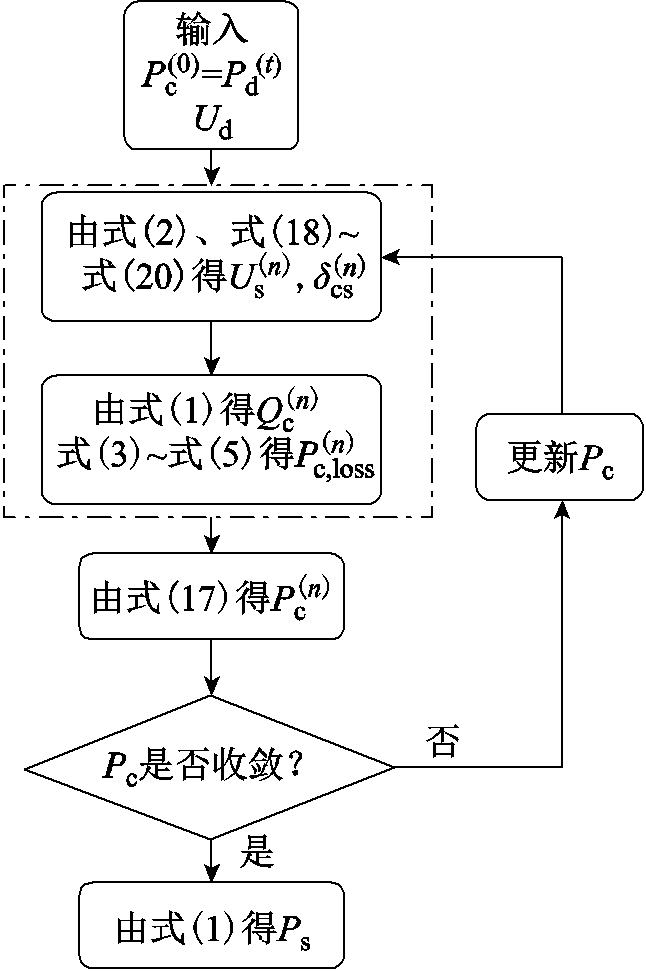
图4 DC侧向AC侧传递的边界量计算流程
Fig.4 The flow chart for the equivalent injection into the AC network
2.2.2 不确定度的交互计算
在GMM-PSE算法和交互模块中的计算中,状态变量到边界值、边界值计算损耗后到转换为可用的伪量测数据都需要计算交互的不确定度[31]。式(14)中的状态变量的协方差矩阵可以被用来计算由状态变量转换到其他电气量的不确定度。
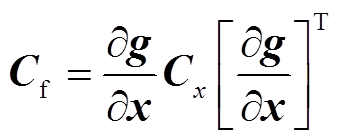 (21)
(21)式中,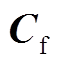 为其他电气量如边界注入功率的协方差矩阵;
为其他电气量如边界注入功率的协方差矩阵;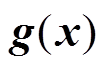 为其他电气量关于状态变量
为其他电气量关于状态变量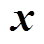 的函数关系式。
的函数关系式。
为验证本文所提算法的实际效果,本文采用的交直流配电网系统如图5所示。交流配电网采用IEEE 33节点系统[32],交流基准电压为12.66kV,基准容量为10MV∙A;直流配电网选取文献[32]中结构,基准电压为10kV,基准容量为10MV∙A。采用三个VSC与直流配电网相连,其中直流节点负荷参数、直流线路参数和VSC参数见附表1~附表3。DG出力不确定性参数根据历史数据、天气情况所得出力预测曲线经高斯混合模型分解出的子高斯函数参数[21]得到,见附表4。量测配置方案见附表5。
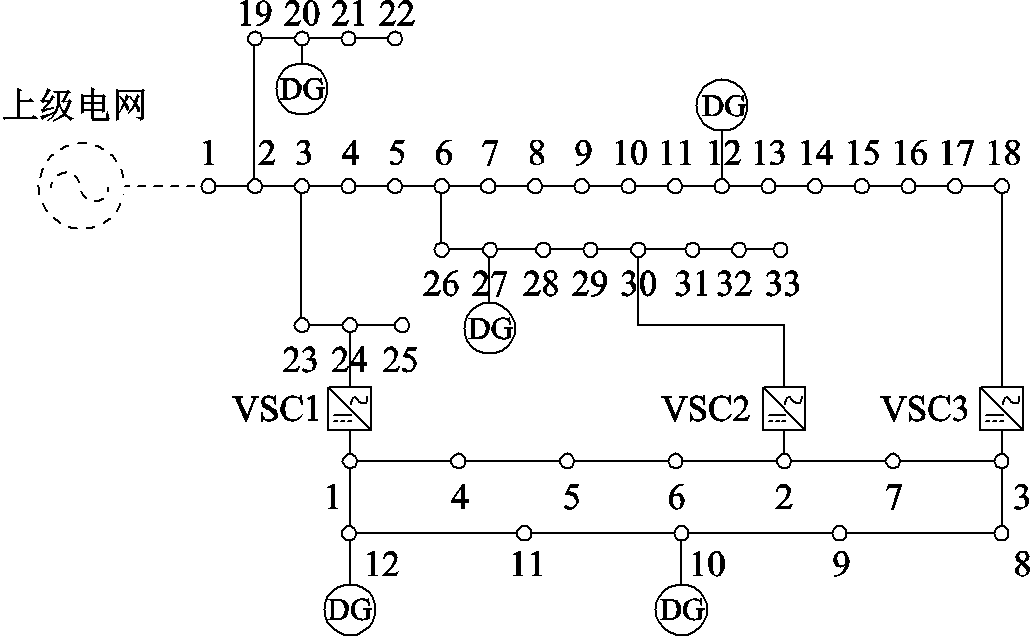
图5 交直流配电网系统
Fig.5 The AC/DC distribution network
本文采用绝对误差的平均值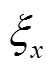 和最大值
和最大值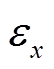 作为状态估计的性能指标[32];采用方均根误差(Root Mean Squared Error, RMSE)[33]衡量观测值与真值之间的偏差,公式分别为
作为状态估计的性能指标[32];采用方均根误差(Root Mean Squared Error, RMSE)[33]衡量观测值与真值之间的偏差,公式分别为
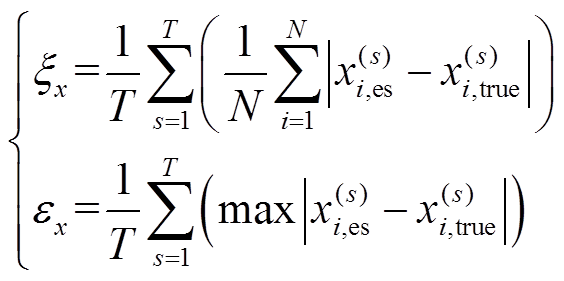 (22)
(22)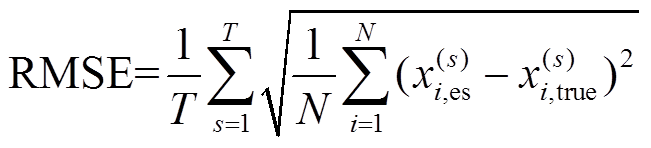 (23)
(23)式中,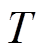 为估计总次数;
为估计总次数;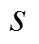 为状态估计次数;
为状态估计次数;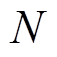 为系统节点数;
为系统节点数;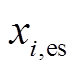 和
和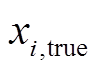 分别为节点
分别为节点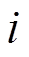 状态变量
状态变量 的状态估计值和真值。
的状态估计值和真值。
为排除DG出力不确定性干扰,先不考虑DG对交直流配电网的影响,观察在同一个时间断面下,交互计算中是否考虑损耗对状态估计精度的影响。考虑方法如下:①交直流子网分别局部估计;②采用本文所提两阶段分布式状态估计框架,交互计算不计VSC损耗;③在方法②的基础上计入VSC损耗。
状态真值来自于交直流配电网潮流计算[34],并在其之上叠加相应不确定度[35]得到量测数据,为排除量测数据不确定度的随机影响,采用蒙特卡洛仿真(Monte Carlo Simulation, MCS)进行分析,重复MCS实验25 000次,取平均值作为状态估计结果,前250次状态估计结果如图6和图7所示。
由图6可得,在直流配电网数据冗余度最小(由假设量测配置决定)时,方法②和方法③由于采用了来自交流侧的伪量测数据,可以使得RMSE相较于方法①有效减少;方法③由于精确计入了VSC损耗,伪量测数据精度最高,因此在三种方法中直流电压幅值平均误差和RMSE均最低,有效地提高了状态估计精度。
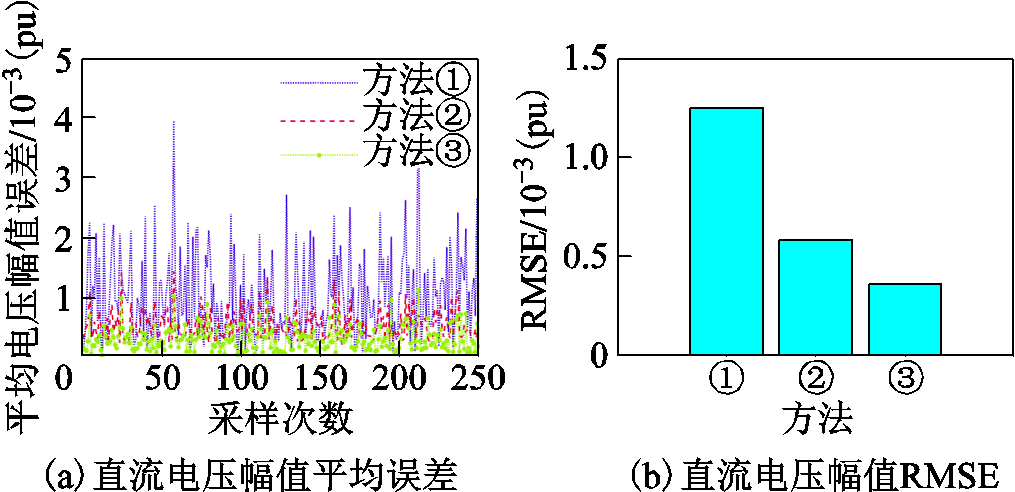
图6 直流状态变量估计结果
Fig.6 The DC state estimation results
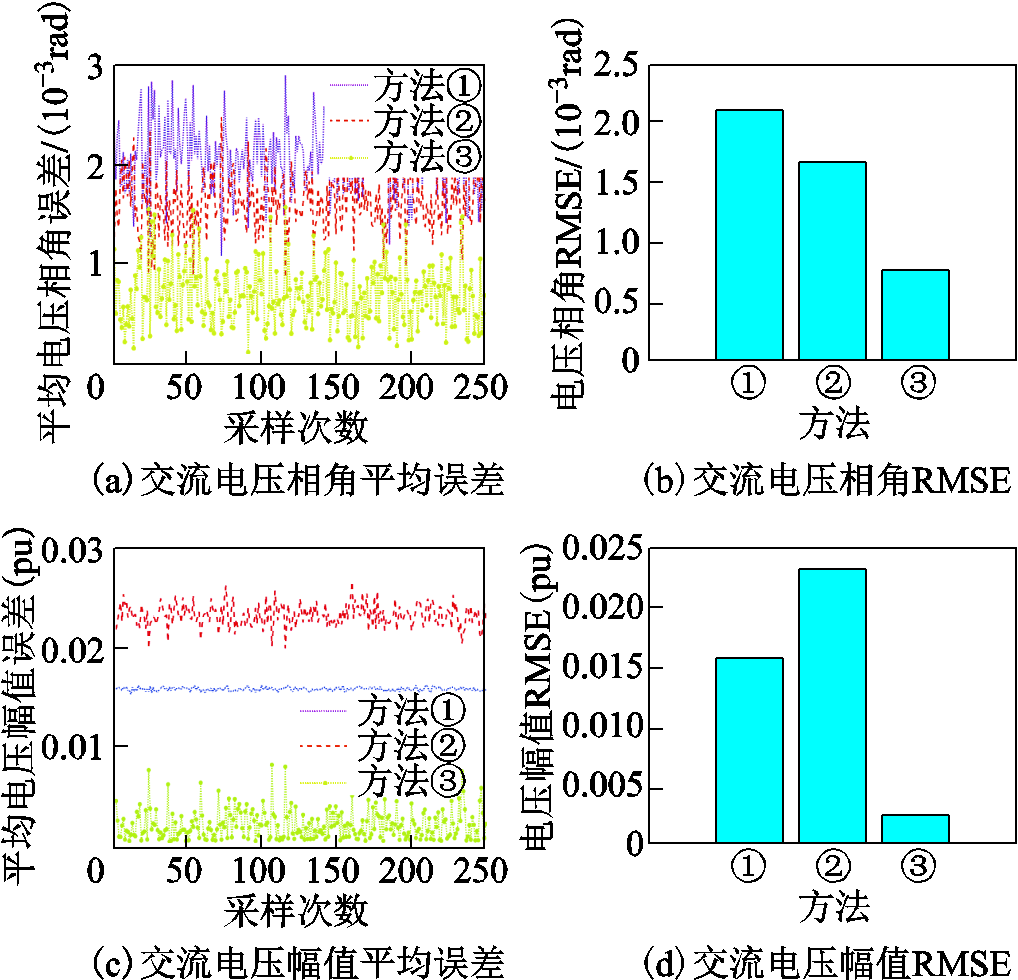
图7 交流状态变量估计结果
Fig.7 The AC state estimation results
由图7可得,由于AC子系统采用了来自DC子系统交互环节得到的伪量测数据,即边界注入有功功率和交流电压幅值,对交流系统而言,相角精度的提升依赖于有功功率伪量测的增多,而幅值精度的提升也得益于电压幅值伪量测的增多,因此方法③在电压相角和电压幅值两方面估计精度较方法①和方法②均有所提升。根据不确定度交互原则,交互环节计算所得伪量测不确定度为DC子系统状态变量的叠加,因此方法②和方法③的误差波动范围均较方法①增加。但由于本文所提算法已考虑不确定度交互原则,因此方法③的误差波动范围增大,总体误差较方法①仍有所下降。
为验证本文所提算法的有效性,接下来考虑不同量测配置下算法的估计性能,见表1和表2。
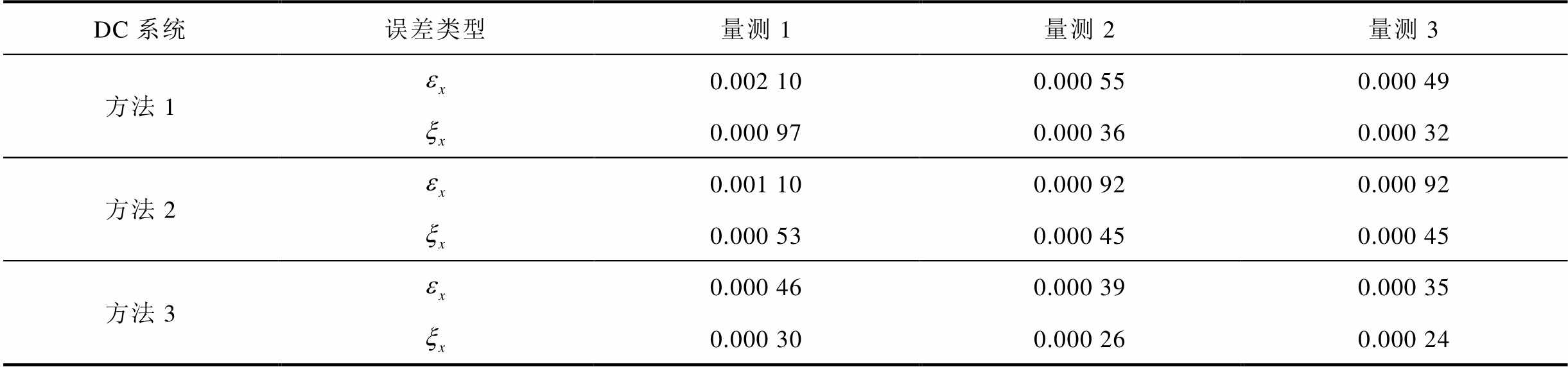
表1 不同量测配置下直流状态变量估计结果
Tab.1 The DC state estimation results with three measurement configurations
DC系统误差类型量测1量测2量测3 方法10.002 100.000 550.000 49 0.000 970.000 360.000 32 方法20.001 100.000 920.000 92 0.000 530.000 450.000 45 方法30.000 460.000 390.000 35 0.000 300.000 260.000 24
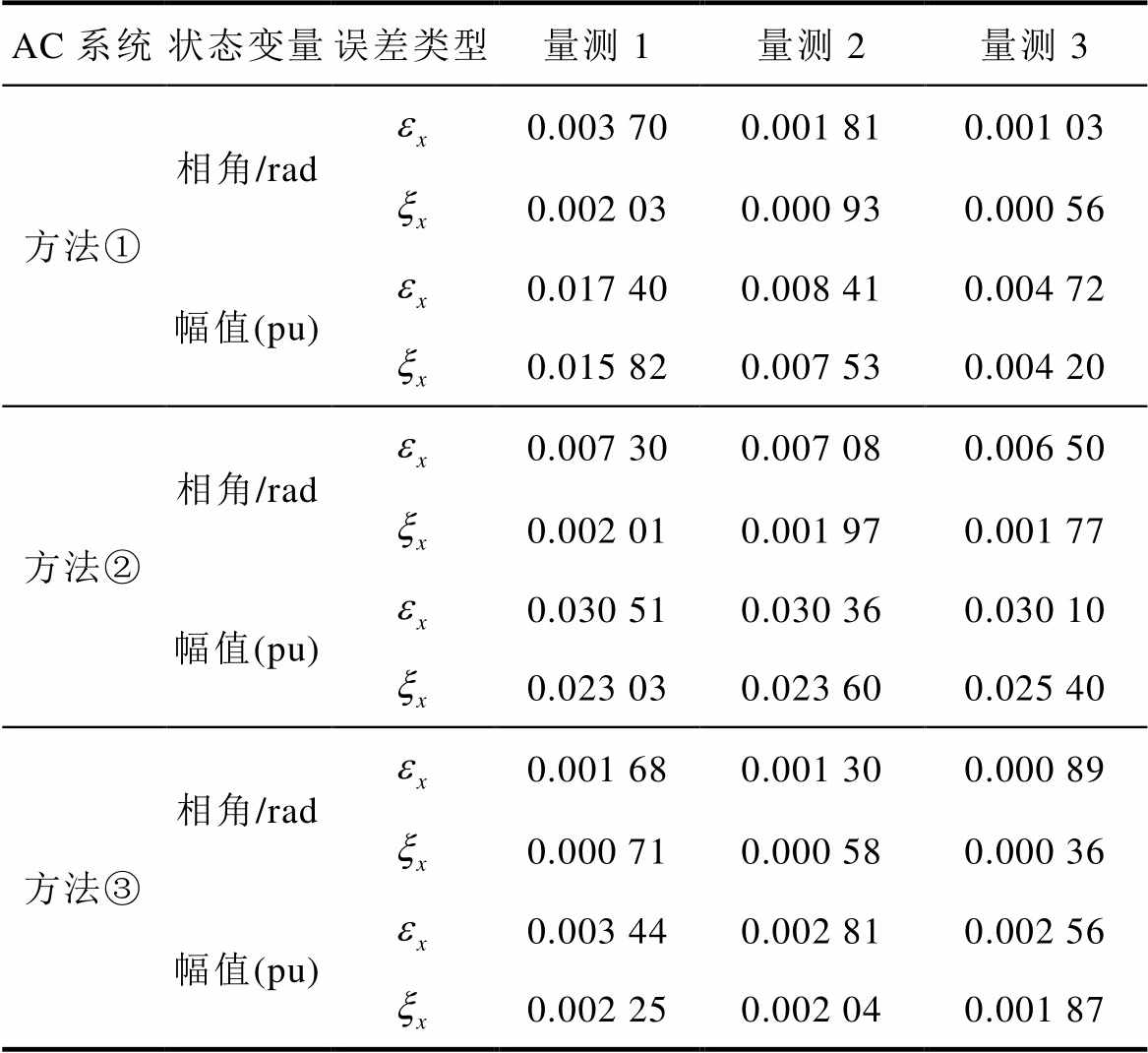
表2 不同量测配置下交流状态变量估计结果
Tab.2 The AC state estimation results with three measurement configurations
AC系统状态变量误差类型量测1量测2量测3 方法①相角/rad0.003 700.001 810.001 03 0.002 030.000 930.000 56 幅值(pu)0.017 400.008 410.004 72 0.015 820.007 530.004 20 方法②相角/rad0.007 300.007 080.006 50 0.002 010.001 970.001 77 幅值(pu)0.030 510.030 360.030 10 0.023 030.023 600.025 40 方法③相角/rad0.001 680.001 300.000 89 0.000 710.000 580.000 36 幅值(pu)0.003 440.002 810.002 56 0.002 250.002 040.001 87
从表1和表2可以得到,在实时量测依次增多的情况下,三种方法的精度均有所提高,但量测配置对每种方法提高幅度不一。其中方法①和方法②在实时量测较多的情况下(量测3),DC子系统的平均误差均大于或接近于在实时量测较少的情况(量测1)的方法③。这说明严格计入了VSC损耗的较高精度的伪量测在实时量测较少的配电网中具有重要的作用。
为验证本文所提算法的实时性,接下来在量测配置最多(量测3)情况下比较所提算法和交替迭代法的计算时间。重复MCS实验1 000次,取平均计算时间作为指标,结果见表3。
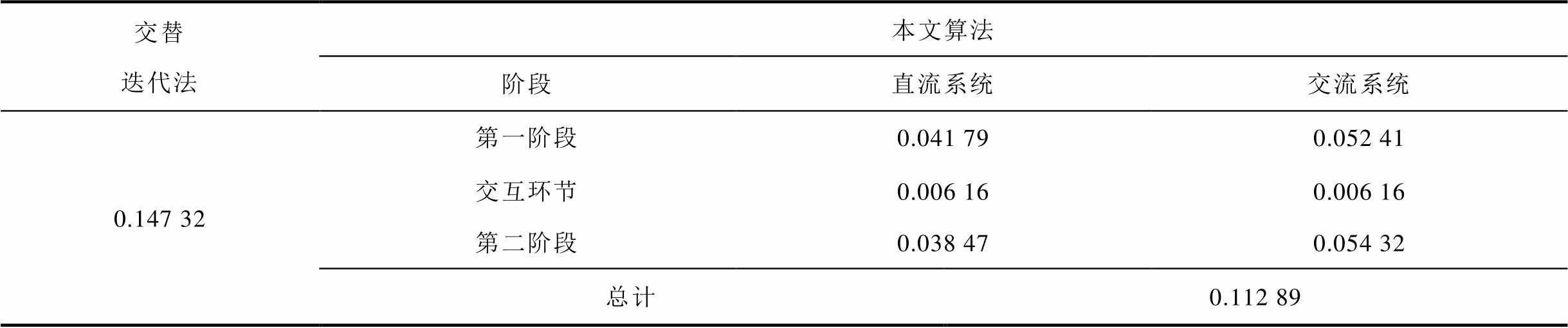
对比表3结果可知,本文所提算法平均计算时间比交替迭代法更少,表明所提模型的收敛速度及计算时间能满足交直流配电网实时状态估计结果的要求。此外,在实际交直流配电网中量测数目更少,其计算时间会相应减少。从表3还可以发现,对于各子系统状态估计算法完成时间不一所引起的各子系统第一阶段与第二阶段存在时间差的情况,总计时间选取两个阶段的最长时间的和。但在实时运行时,交互协调环节总是采用各自系统最新的状态估计结果,因此运算速度更快的直流子系统在第一阶段运算完成后,将调用交流系统最近一次运算结果进入第二阶段,减少等待时间,加快估计进程。
表3 不同方法的平均计算时间统计结果
Tab.3 Statistical results of average calculating time of different methods (单位:s)
交替迭代法本文算法 阶段直流系统交流系统 0.147 32第一阶段0.041 790.052 41 交互环节0.006 160.006 16 第二阶段0.038 470.054 32 总计0.112 89
接下来考虑DG接入交直流配电网后带来的非高斯不确定性对状态估计的影响。采用MCS模仿不同DG出力时的潮流情景,非高斯不确定性由DG出力体现。为了模拟真实量测情况,量测值是在潮流计算所得真值的基础上叠加高斯分布噪声,设置同上。直流配电网量测配置采用直流量测1,交流配电网量测配置采用交流量测1。
采用两阶段状态估计算法框架,考虑以下三种估计器的性能:①WLS;②加权最小绝对值(Weighted Least Absolute Value,WLAV)估计器[36];③GMM-PSE。
仿真结果如如图8、图9所示。由图8和图9可得,在直流系统和交流系统中,采用GMM-PSE能得到更为精确的概率密度函数曲线,集中在估计值附近,所得估计值相较于WLS法波动性更小。同时,GMM-PSE估计值相较于WLS法更加接近于真值。因此,采用GMM能够有效地对伪量测进行拟合,将非高斯不确定性精确考虑进状态估计之中,提高估计精度。这说明为了弥补实时量测不足的情况,GMM-PSE可以充分利用伪量测的概率分布来应对在量测不足情况下的高不确定性问题。概率状态估计的结果可以为电力系统安全分析和运行等提供参考意见。
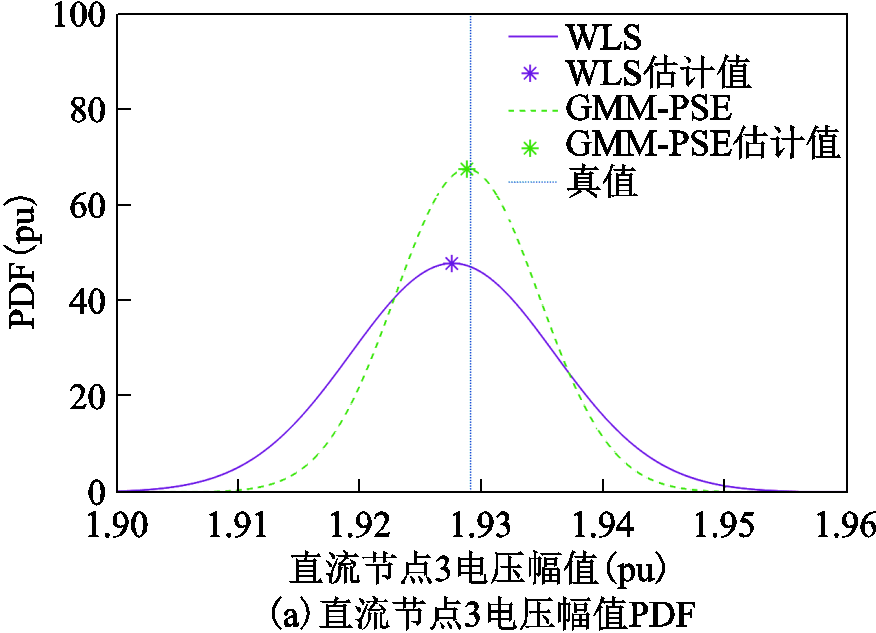
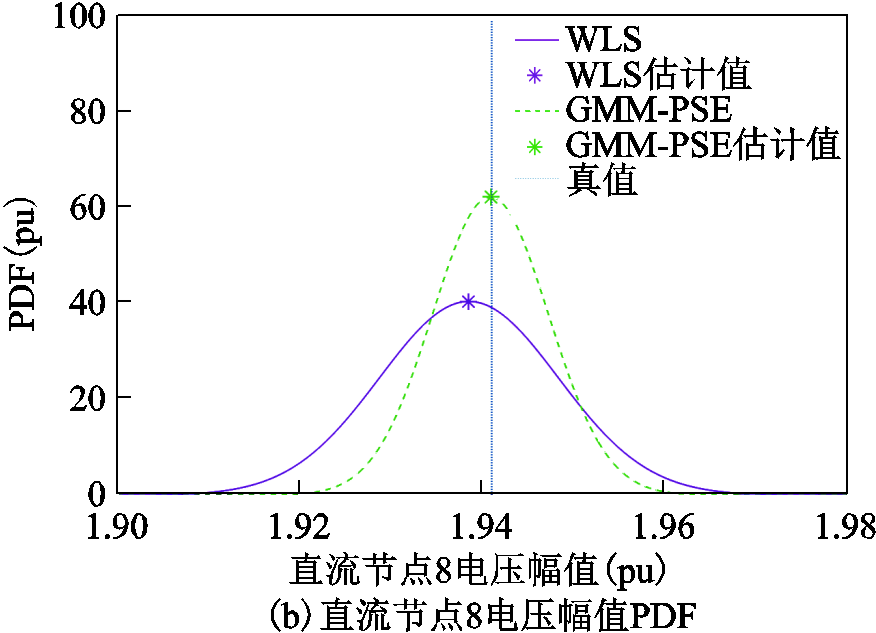
图8 直流状态变量概率估计结果
Fig.8 The DC probabilistic state estimation results
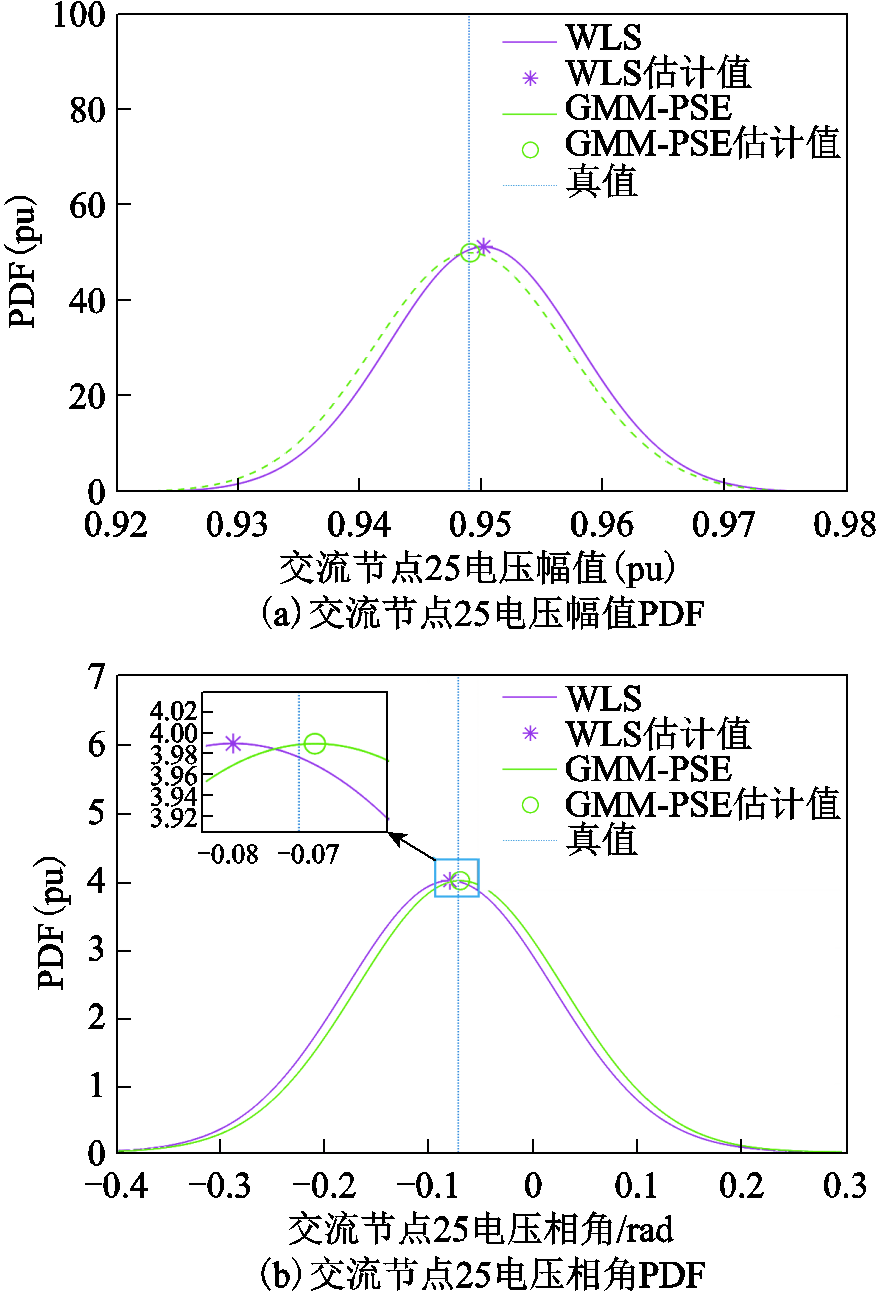
图9 交流状态变量概率估计结果
Fig.9 The AC probabilistic state estimation results
除了能额外提供概率信息之外,由于精确计入了DG的非高斯分布,伪量测更加精确,因此精度也有相应提高。进一步对本文GMM-PSE估计器、WLS估计器和WLAV估计器[36]做比较,前50次MCS仿真结果如图10和图11所示。
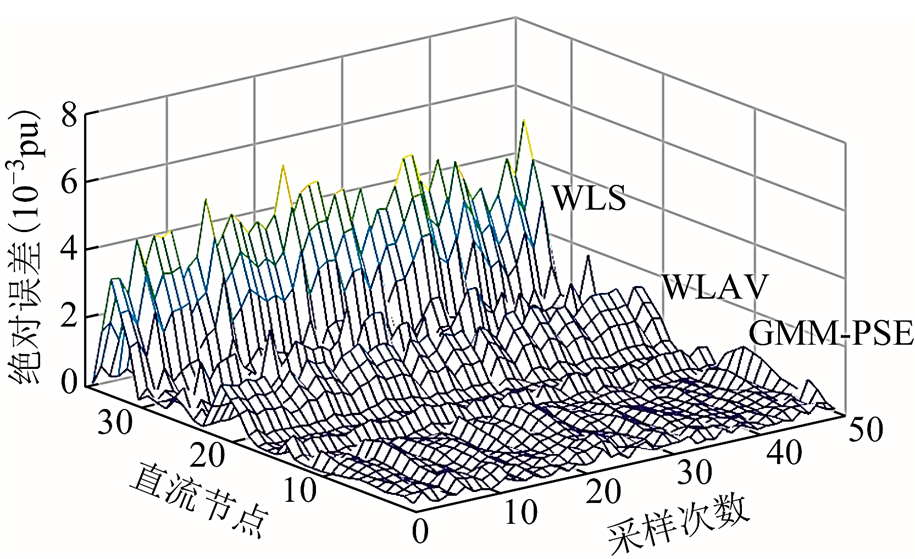
图10 直流节点电压幅值绝对误差
Fig.10 The absolute error in DC state estimation results
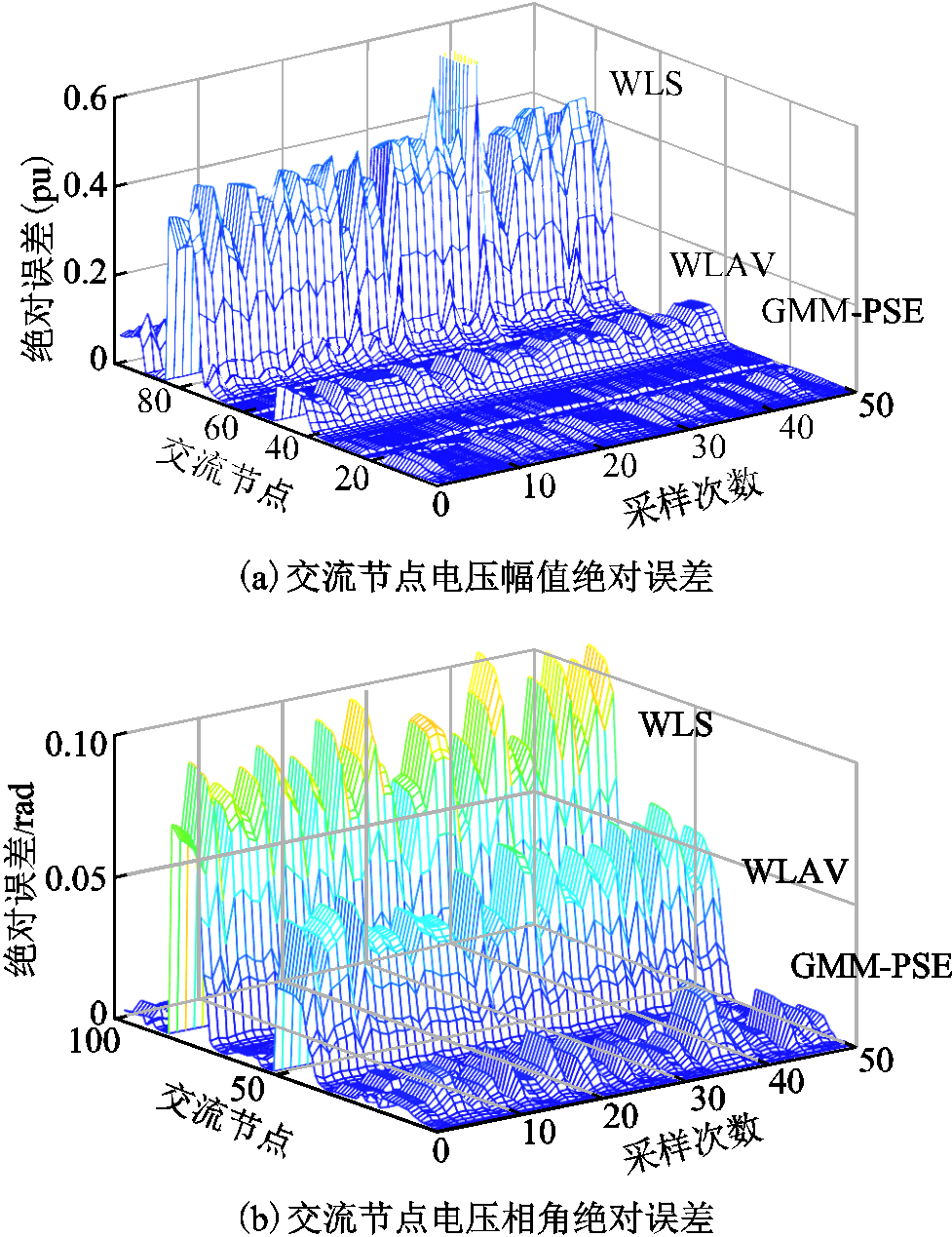
图11 交流节点状态变量绝对误差
Fig.11 The absolute error in AC state estimation results
由图10和图11可以看出,各节点误差随着时间序列的变化呈现波动性。总体来说,采用GMM-PSE估计器的估计结果比另外两种估计器更为精确。在DG出力具有非高斯不确定性的场景下,传统WLS方法将其简单拟合为一个等效正态分布作为伪量测,因而估计结果在不同时间序列里有较大误差。WLAV估计器虽然无法精确计入DG的非高斯不确定性,但由于WLAV估计器作为一种鲁棒估计器对坏数据具有抗差性[36],因此相比于WLS,其估计精度有所提高。而GMM-PSE可以考虑具有非高斯不确定性的误差数据,因而对抗差性有所改善,在三种估计器中估计精度最高。此外,可将GMM-PSE在未知分布情况下误差数据对状态估计的影响作为未来研究方向。
本文提出了一种考虑非高斯耦合不确定性的交直流配电网两阶段概率状态估计,主要有以下创新点:
1)考虑VSC损耗,所需VSC信息仅为控制信息,无需获取VSC内部量测数据。实现两侧损耗独立计算,避免交互误差,实现两阶段算法,并行减少计算时间。
2)计入非高斯不确定性,增加伪量测精度,同时考虑交流配电网和直流配电网间的不确定性耦合计算。
3)完全保证交流直流各自状态估计的完整性(便于采用适用于不同子系统特性的状态估计算法),无需修改已有交流状态算法,只需添加交互模块程序,应用性较好。
算例仿真充分说明本文所提算法考虑VSC损耗,在较低的量测配置下具有较高精度,适用于交直流配电网数据冗余度低的场景;能有效利用VSC控制信息增加伪量测数据,提高系统经济性和灵活性;能较好地计及DG出力的不确定性,可适用于未来新能源渗透率不断提高的未来交直流配电网;带有概率密度的估计结果,可以为未来系统的安全运行提供参考意见。
附表1 直流节点负荷参数
App.Tab.1 The parameters of the DC loads
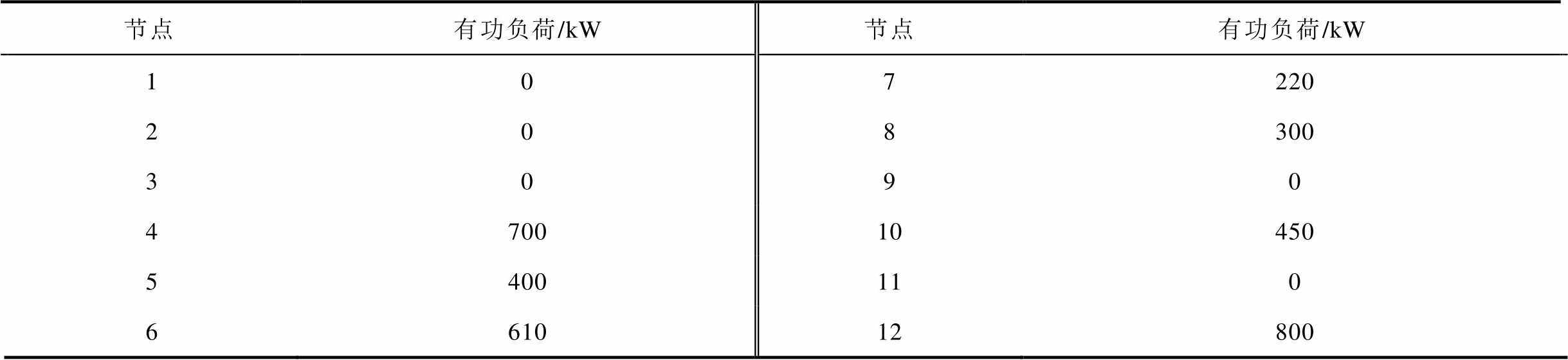
节点有功负荷/kW节点有功负荷/kW 107220 208300 3090 470010450 5400110 661012800
附表2 直流线路参数
APP.Tab.2 The parameters of the DC lines
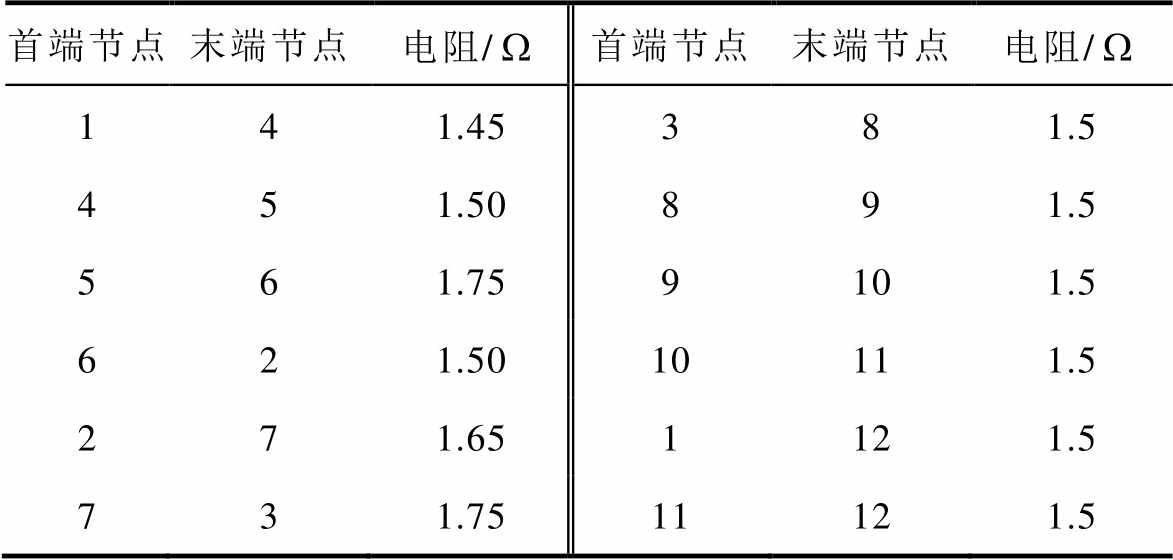
首端节点末端节点电阻/首端节点末端节点电阻/ 141.45381.5 451.50891.5 561.759101.5 621.5010111.5 271.651121.5 731.7511121.5
附表3 VSC换流器参数
APP.Tab.3 The parameters of the VSC converters

VSC 1230 0 0 VSC控制策略(pu) 10.120.002 90.0031=2,=-0.2 20.120.002 90.0031=-0.10,=-0.2 30.120.002 90.0031=-0.15,=-0.2
附表4 DG的GMM子函数参数
APP.Tab.4 The parameters of DGs using GMM theory
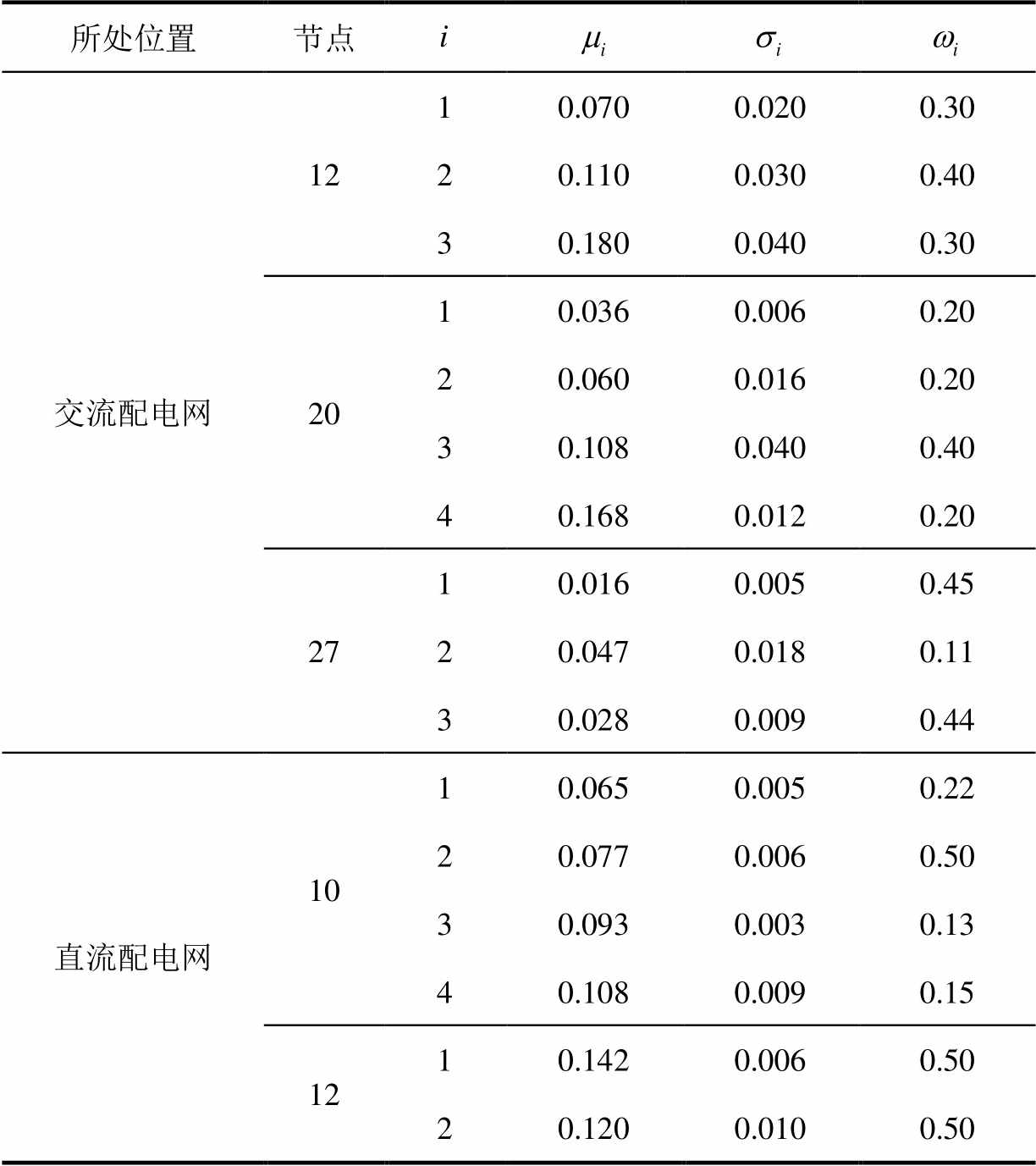
所处位置节点 交流配电网1210.0700.0200.30 20.1100.0300.40 30.1800.0400.30 2010.0360.0060.20 20.0600.0160.20 30.1080.0400.40 40.1680.0120.20 2710.0160.0050.45 20.0470.0180.11 30.0280.0090.44 直流配电网1010.0650.0050.22 20.0770.0060.50 30.0930.0030.13 40.1080.0090.15 1210.1420.0060.50 20.1200.0100.50
附表5 三种量测配置方案
APP.Tab.5 Three measurment configurations in this paper

系统量测类型量测配置 123 交流配电网支路有功013 支路无功013 直流配电网支路功率133 支路电流003
参考文献
[1] 方治, 宋绍剑, 林予彰, 等. 含光伏电站和蓄电池储能系统的主动配电系统状态估计[J]. 电力系统自动化, 2019, 43(13): 71-83. Fang Zhi, Song Shaojian, Lin Yuzhang, et al. State estimation for active distribution systems incorporating photovoltaic plant and battery energy storage system[J]. Automation of Electric Power Systems, 2019, 43(13): 71-83.
[2] Zhang Xing, Wang Mingda, Zhao Tao, et al. Topological comparison and analysis of medium-voltage and high-power direct-linked PV inverter[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(4): 327-334.
[3] 崔学深, 张恒, 刘其辉, 等. 直流并网型双馈风力发电系统限转子功率运行控制方法[J]. 电机与控制学报, 2019, 23(12): 8-15. Cui Xueshen, Zhang Heng, Liu Qihui, et al. Limited rotor power control method of double-fed wind power generation system connected to DC grid[J]. Electric Machines and Control, 2019, 23(12): 8-15.
[4] 张释中, 裴玮, 杨艳红, 等. 基于柔性直流互联的多微网集成聚合运行优化及分析[J]. 电工技术学报, 2019, 34(5): 1025-1037. Zhang Shizhong, Pei Wei, Yang Yanhong, et al. Optimization and analysis of multi-microgrids integration and operation based on flexible DC interconnection[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1025-1037.
[5] 罗志刚, 韦钢, 袁洪涛, 等. 基于区间直觉模糊理论的直流配网规划方案综合决策[J]. 电工技术学报, 2019, 34(10): 2011-2021. Luo Zhigang, Wei Gang, Yuan Hongtao, et al. Comprehensive decision of DC distribution network planning based on interval intuitionistic fuzzy theory[J]. Transactions of China Electrotechnical Society, 2019,34(10): 2011-2021.
[6] 曹文远, 韩民晓, 谢文强, 等. 交直流配电网逆变器并联控制技术研究现状分析[J]. 电工技术学报, 2019, 34(20): 4226-4241. Cao Wenyuan, Han Minxiao, Xie Wenqiang, et al. Analysis on research status of parallel inverters control technologies for AC/DC distribution Network[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4226-4241.
[7] 颜宁, 潘霄, 张明理, 等. 基于多时间尺度的微电网群阶梯控制方法研究[J]. 电机与控制学报, 2019, 23(9): 26-34.Yan Ning, Pan Xiao, Zhang Mingli, et al. Step control method of multi-microgrids based on different time levels[J]. Electric Machines and Control, 2019, 23(9): 26-34.
[8] 郑伟业, 吴文传, 张伯明, 等. 基于内点法的交直流混联系统抗差状态估计[J]. 电力系统保护与控制, 2014, 42(21): 1-8. Zheng Weiye, Wu Wenchuan, Zhang Boming, et al. Robust state estimator for AC/DC hybrid power system based on an interior point method[J]. Power System Protection and Control, 2014, 42(21): 1-8.
[9] 孙国强, 李育燕, 卫志农, 等. 含VSC-HVDC的交直流混合系统状态估计[J]. 电力自动化设备, 2010, 30(9): 6-12.Sun Guoqiang, Li Yuyan, Wei Zhinong, et al. State estimation of power system with VSC-HVDC[J]. Electric Power Automation Equipment, 2010, 30(9): 6-12.
[10] Ding Qifeng, Chung T S, Zhang Boming. An improved sequential method for AC/MTDC power system state estimation[J]. IEEE Transactions on Power Systems, 2001, 16(3): 506-512.
[11] 孙宏斌, 李大志, 刘崇茹, 等. 基于主从分裂法的交直流混合状态估计[J]. 中国电机工程学报, 2007, 27(31): 27-32. Sun Hongbin, Li Dazhi, Liu Chongru, et al. Master-slave splitting method based state estimation for AC/DC hybrid power system[J]. Proceedings of the CSEE, 2007, 27(31): 27-32.
[12] 张潼, 王毅, 翟明玉, 等. 含电压源换流器的交直流混联电网状态估计快速解耦法[J]. 电力系统自动化, 2018, 42(21): 70-78. Zhang Tong, Wang Yi, Zhai Mingyu, et al. Fast decoupling algorithm of state estimation for hybrid AC/DC power systems with voltage source converters[J]. Automation of Electric Power Systems, 2018, 42(21): 70-78.
[13] 许寅, 和敬涵, 王颖, 等. 韧性背景下的配网故障恢复研究综述及展望[J]. 电工技术学报, 2019, 34(16): 3416-3429. Xu Yin, He Jinghan, Wang Ying, et al. A review on distribution system restoration for resilience enhancement[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3416-3429.
[14] 孙江山, 刘敏, 邓磊, 等. 基于自适应无迹卡尔曼滤波的配电网状态估计[J]. 电力系统保护与控制, 2018, 46(11): 1-7.Sun Jiangshan, Liu Min, Deng Lei, et al. State estimation of distribution network based on AKUF[J]. Power System Protection and Control, 2018, 46(11): 1-7.
[15] 怀全, 候小虎, 何良策, 等. 一种含分布式电源的中低压配电网状态估计方法研究[J]. 电力系统保护与控制, 2018, 46(21): 69-77. Huai Quan, Hou Xiaohu, He Liangce, et al. A method of state estimation for middle voltage and low voltage distribution network with distributed generations[J]. Power System Protection and Control, 2018, 46(21): 69-77.
[16] 王家融, 艾欣, 王坤宇, 等. 基于增广雅可比矩阵的交直流解耦潮流新算法[J]. 电工技术学报, 2018, 33(6): 1382-1389.Wang Jiarong, Ai Xin, Wang Kunyu, et al. A novel AC-DC decoupled power flow calculation method based on the augmented Jacobian matrix[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1382-1389.
[17] 张佳楠, 袁启海, 余建明, 等. 基于联络线扩展区域分解协调的分布式并行状态估计[J]. 电力系统自动化, 2019, 43(4): 166-178. Zhang Jianan, Yuan Qihai, Yu Jianming, et al. Distributed parallel state estimation based on decomposition and coordination of tie-line extended area[J]. Automation of Electric Power Systems, 2019, 43(4): 166-178.
[18] 徐俊俊, 吴在军, 胡秦然, 等. 考虑多类型分布式电源和负荷不确定性的主动配电网区间状态估计[J]. 中国电机工程学报, 2018, 38(11): 3255-3266. Xu Junjun, Wu Zaijun, Hu Qinran, et al. Interval state estimation for active distribution networks considering uncertainties of multiple types of DGs and Loads[J]. Proceedings of the CSEE, 2018, 38(11): 3255-3266.
[19] Al-Othman A K, Irving M R. A comparative study of two methods for uncertainty analysis in power system State estimation[J]. IEEE Transactions on Power Systems, 2005, 20(2): 1181-1182.
[20] Woolley N C, Milanovic J V. Statistical estimation of the source and level of voltage unbalance in distribution network[J]. IEEE Transactions on Power Delivery, 2012, 27(3): 1450-1460.
[21] Valverde G, Saric A T, Terzija V. Stochastic monitoring of distribution networks including correlated input variables[J]. IEEE Transactions on Power Systems, 2013, 28(1): 246-255.
[22] Huang Yu, Xu Qingshan, Hu Cheng, et al. Probabilistic State estimation approach for AC/MTDC distribution system using deep belief network with non-Gaussian uncertainties[J]. IEEE Sensors Journal, 2019, 19(20): 9422-9430.
[23] 和敬涵, 李智诚, 王小君, 等. 计及换流器损耗与电压下垂控制的交直流系统最优潮流算法[J]. 电力系统自动化, 2017, 41(22): 48-55. He Jinghan, Li Zhicheng, Wang Xiaojun, et al. Optimal power flow algorithm for hybrid AC/DC power systems considering power loss of converter and voltage-droop control[J]. Automation of Electric Power Systems, 2017, 41(22): 48-55.
[24] Jegatheesan R, Duraiswamy K. AC/multiterminal DC power system state estimation-a sequential approach[J]. Electric Machines and Power Systems,1987, 12(1): 27-42.
[25] 王紫瑶, 廖进贤, 杨家豪, 等. 计及功率控制模式的VSC-MTDC交直流并列运行系统概率潮流计算[J]. 电气技术, 2019, 20(2): 12-17. Wang Ziyao, Liao Jinxian, Yang Jiahao, et al. Probabilistic load flow calculation of VSC-MTDC AC/DC parallel operation system considering power control mode[J]. Electrical Engineering, 2019, 20(2): 12-17.
[26] 柴润泽, 窦竟铭, 张保会. 含电压源换流器的交直流混合电网潮流统一表达与可行解求取[J]. 中国电机工程学报, 2016, 36(5): 1260-1268. Chai Runze, Dou Jingming, Zhang Baohui. Unified power flow expressions and algorithm to obtain feasible solution for hybrid AC/DC grids incorporating VSCs[J]. Proceedings of the CSEE, 2016, 36(5): 1260-1268.
[27] 雷婧婷, 安婷, 杜正春, 等. 含直流配电网的交直流潮流计算[J]. 中国电机工程学报, 2016, 36(4): 911-918. Lei Jingting, An Ting, Du Zhengchun, et al. A united AC/DC power flow algorithm with DC distribution[J]. Proceedings of the CSEE, 2016, 36(4): 911-918.
[28] Daelemans G. VSC HVDC in meshed networks[D]. Leuven, Belgium: Katholieke Universiteit Leuven, 2008.
[29] Singh R, Pal B C, Jabr R A. Statistical representation of distribution system loads using Gaussian mixture model[J]. IEEE Transactions on Power Systems, 2010, 25(1): 29-37.
[30] Abur A, Exposito A G. Power system state estimation: theory and implementation[M]. Boca Raton, FL, USA: CRC Press, 2004.
[31] Pau M, Sadu A, Pillai S, et al. A state estimation algorithm for hybrid AC/DC networks with multi-terminal DC grid[C]//2016 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Ljubljana, 2016: 1-6.
[32] 马鑫. 交直流配电网状态估计及日前调度模型研究[D]. 杭州: 浙江大学, 2019.
[33] 张越, 单连飞, 余建明, 等. 基于ε-模糊树方法的电力系统状态估计[J]. 电力系统保护与控制, 2019, 47(5): 138-144. Zhang Yue, Shan Lianfei, Yu Jianming, et al. Power system state estimation based on ε-fuzzy tree method[J]. Power System Protection and Control, 2019, 47(5): 138-144.
[34] Beerten J, Cole S, Belmans R. Generalized steady-state VSC MTDC model for sequential AC/DC power flow algorithms[J]. IEEE Transactions on Power Systems, 2012, 27(2): 821-829.
[35] Muscas C, Sulis S, Angioni A, et al. Impact of different uncertainty sources on a three-phase state estimator for distribution networks[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(9): 2200-2209.
[36] Gol M, Abur A. LAV based robust state estimation for systems measured by PMUs[J]. IEEE Transactions on Smart Grid, 2014, 5(4): 1808-1814.
Two-Stage Probabilistic State Estimation for AC/DC Distribution Network Considering Non-Gaussian Coupling Uncertainties
Abstract At present, real-time measurements implemented in distribution networks only have simple structures and limited quantities. The randomness from DGs (Distributed Generations) and loads are usually non-Gaussian, which exacerbate the uncertainties and errors of state estimations in hybrid AC-DC distribution network. These problems seriously inhibit the development of flexible management in AC-DC distribution networks. Therefore, it is necessary to develop more effective methods for AC-DC distribution network state estimations to support hybrid distribution network management. This paper proposes a two-stage probabilistic estimation for AC-DC distribution network. The proposed method is based on voltage source converter (VSC) loss model and Gaussian mixture model (GMM). It gives full consideration of the coupling uncertainties between AC and DC distribution subnetworks. Simulations conducted based on the modified IEEE-33 node AC-DC distribution network show that the proposed two-stage estimation method is suitable for situations with limited real-time measurements and low data redundancy. The method can be practically implemented in existing AC state estimation modules. It can also be extended to consider three-phase unbalanced AC subnetwork in the future.
keywords:Pseudo measurement modeling, AC-DC distribution network, probabilistic state estimation, distributed generation, Gaussian mixture model
中图分类号:TM734
DOI:10.19595/j.cnki.1000-6753.tces.191590
国家自然科学基金资助项目(51877133)。
收稿日期2019-11-21
改稿日期 2020-03-19
李幸芝 女,1996年生,博士研究生,研究方向为电力系统状态估计。E-mail:xz.li531@sjtu.edu.cn
韩 蓓 女,1984年生,博士,讲师,研究方向为含微网的配电网模型。E-mail:han_bei@sjtu.edu.cn(通信作者)
(编辑 赫蕾)