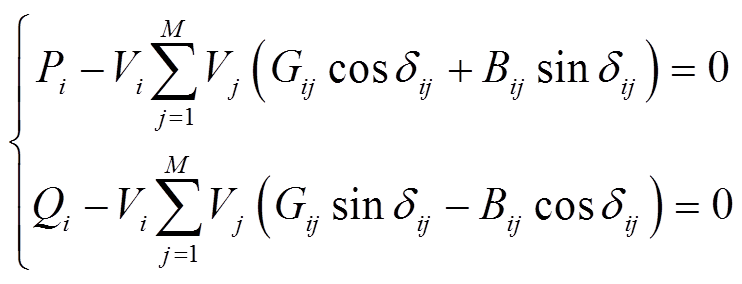 (1)
(1)摘要 随机潮流针对电网不确定因素建模,快速准确的计算结果对于系统运行控制非常重要。该文提出了基于聚类抽样的随机潮流计算方法。首先,基于历史数据,采用蒙特卡洛算法产生大量随机变量样本;其次,采用误差二次方和与平均轮廓系数确定样本聚类簇数,并采用K-means算法进行样本聚类;然后,依据聚类中心和簇内样本的平均概率密度,将簇内样本均值带入潮流方程中进行确定性潮流计算;最后,对潮流计算结果和对应的平均概率密度信息进行数据统计,得到状态变量的概率密度函数。以修改后IEEE 39系统和某实际区域电网为算例,进行计算精度和计算效率分析。结果表明,所提方法兼顾了计算速度和计算精度,在大系统中更具优势,可为电网调度计划的制定和运行分析提供决策依据。
关键词:随机潮流 不确定性 聚类 抽样
随机潮流(Stochastic Load Flow, SLF)[1]针对不确定因素构建概率模型,得到系统状态变量概率分布,计算结果可为运行控制决策提供依据。
可再生能源出力的随机性和波动性,给电网安全运行带来了挑战[2]。考虑高渗透率光伏、风电的不确定性对电力系统运行的影响时,随机潮流计算中通常将可再生能源的出力预测误差作为随机变量。随机潮流的计算方法可分为近似法、解析法和模拟法。近似法将预测误差假定为已知的分布模型简化计算,得到状态变量的概率分布函数[3-4]。但文献[5]指出,预测误差的分布特性不能由单一已知分布函数表示。近似法的简化计算虽然提高了计算效率,但是计算精度较低。解析法是在线性化潮流方程的基础上,通过随机变量分布函数的卷积运算得到状态变量的分布函数[6]。但卷积运算在复杂系统中计算量大。解析法的改进算法如半不变量法,将卷积运算化简为半不变量的代数运算[7-8],降低了求解难度,提高了计算效率。但是在处理波动范围较大的随机变量时,都会因为潮流方程的线性化处理,出现随机潮流计算结果误差较大的问题[9],而且其计算速度受网络规模的影响较大[10]。模拟法根据随机变量的概率分布产生大量样本,对每个样本进行确定性潮流计算,统计得出状态变量的分布函数[11-12]。模拟法可用于处理复杂分布的随机量,但求解精度需要足够的抽样次数来保证。蒙特卡洛法是模拟法中普遍应用的算法,需要大量的样本才能够涵盖随机变量的全分布特征,这将导致随机潮流计算精度和速度无法同时满足实时调度需求。针对蒙特卡洛模拟法用时较长的缺陷[13],国内外学者提出了若干改进方法,如重要抽样法(Importance Sampling, IS)[14]依据对系统状态影响的大小来确定相应区域的抽样次数,提高随机潮流的计算效率。此方法以随机变量概率分布函数为基础,但往往随机变量分布特性复杂,其准确的分布函数表达式不易求得。拉丁超立方抽样法(Latin Hypercube Sampling, LHS)[15-16]是基于累计密度函数等概率区间的分层抽样法,有效地减小了抽样次数,但是在低概率密度区间,分布函数拟合精度较低;等间距抽样(Equal Spacing Sampling, ESS)[17]是在随机变量取值范围内等区间的分层抽样,此方法也具有抽样次数少的优点。但是在概率密度变化率较大的区间,分布函数拟合精度较低。
本文综合考虑随机潮流计算的精度和速度,提出基于聚类抽样的随机潮流计算方法。该方法的核心思想是对基于历史数据采用蒙特卡洛法产生的大量样本进行聚类,然后抽样进行确定性潮流计算。对计算结果进行统计处理,可得到状态变量概率分布。这种方法可兼顾实时调度对计算精度和效率的要求。
在给定运行方式下,电力系统必须时刻保证功率平衡,满足潮流方程,即
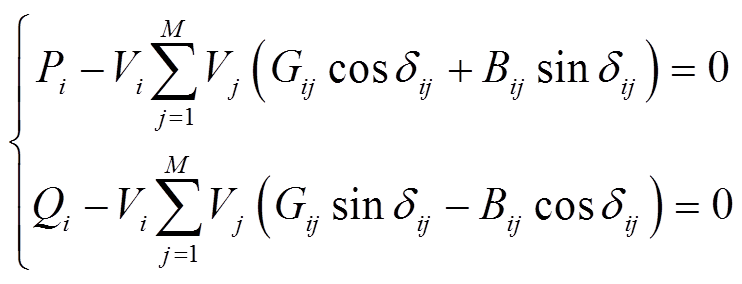 (1)
(1)式中,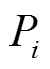 和
和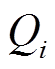 分别为节点
分别为节点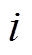 的注入有功功率和无功功率;
的注入有功功率和无功功率;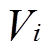 和
和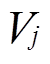 分别为节点
分别为节点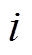 与相邻节点
与相邻节点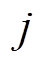 的电压幅值;
的电压幅值;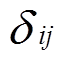 为节点
为节点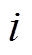 与相邻节点
与相邻节点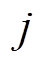 间的相位差,
间的相位差,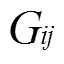 和
和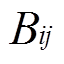 分别为系统导纳矩阵元素的实部和虚部;
分别为系统导纳矩阵元素的实部和虚部;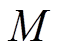 为系统总节点数。
为系统总节点数。
可再生能源和负荷会给电网带来不确定性。下面以并网风电的随机性为例来构建随机潮流模型。
可再生能源出力的预测误差具有随机性,可设为系统的随机变量。
预测误差的历史数据可基于风电出力历史数据与相应的预测值得到。对于系统接入的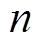 个风电场预测误差历史数据拟合得到具有相关性的联合概率分布。采用蒙特卡洛法,生成
个风电场预测误差历史数据拟合得到具有相关性的联合概率分布。采用蒙特卡洛法,生成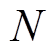 组随机变量样本,每组含
组随机变量样本,每组含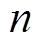 个随机变量。定义样本空间为
个随机变量。定义样本空间为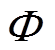 ,构成随机变量矩阵
,构成随机变量矩阵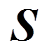 为
为
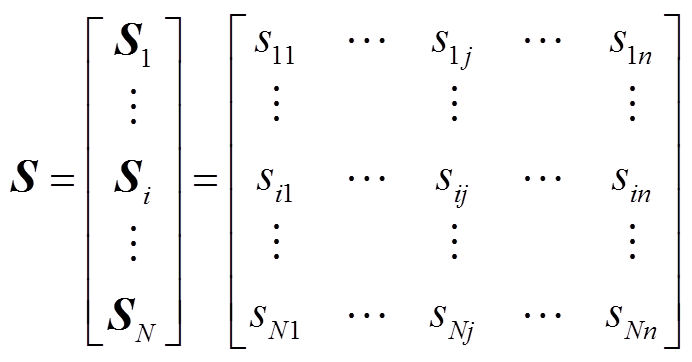 (2)
(2)式中,sij为第i个样本中第j个随机变量值。
对于含风电接入的电力系统,式(1)中节点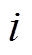 的注入功率
的注入功率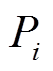 和
和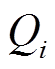 由发电机注入功率
由发电机注入功率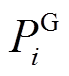 和
和 、风电并网功率
、风电并网功率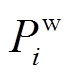 和
和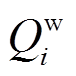 、负荷消耗功率
、负荷消耗功率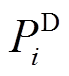 和
和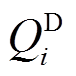 等值求得,即
等值求得,即
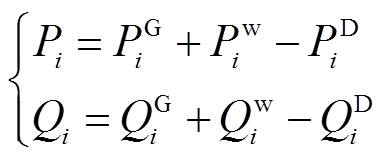 (3)
(3)风电并网功率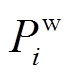 和
和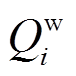 可由预测值和预测误差表示,即
可由预测值和预测误差表示,即
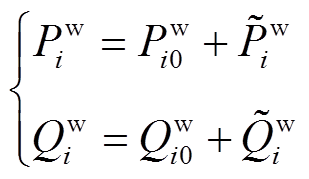 (4)
(4)式中,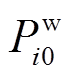 和
和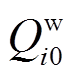 分别为风电场的有功和无功的预测值;
分别为风电场的有功和无功的预测值;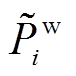 和
和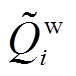 分别为风电场的有功和无功的预测误差。
分别为风电场的有功和无功的预测误差。
对某区域两个风电场进行了为期一年的出力监测,风电出力预测误差原数据分布及采用正态分布和t分布对数据进行拟合得到的曲线如图1所示。
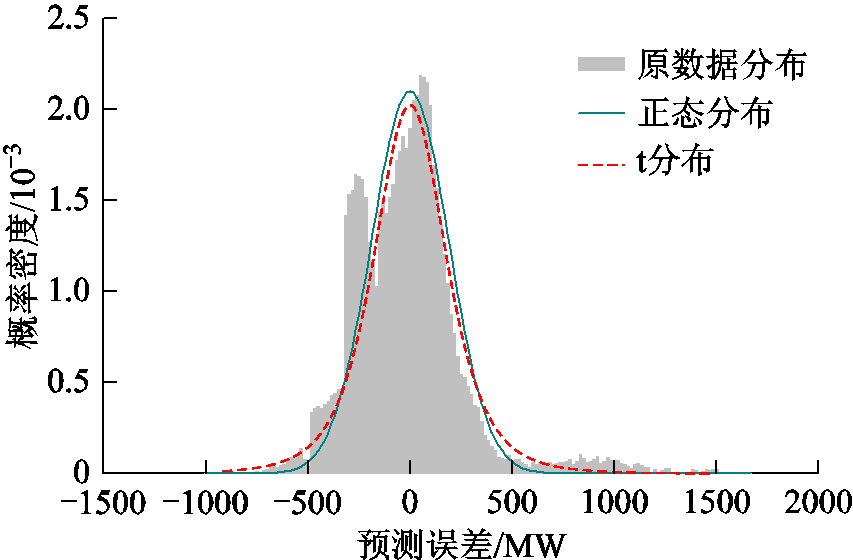
图1 风电预测误差概率密度函数
Fig.1 PDF of wind power prediction error
由图1可得,该风电出力预测误差波动范围较大,采用正态分布[18-19]和t分布[20-21]拟合存在较大偏差。如果采用近似法计算随机潮流,会因为输入偏差使得计算结果可信度不高。而使用解析法计算随机潮流,计算结果将会在预测误差较大的地方产生线性化误差,影响计算精度。模拟法虽然原理上可弥补近似法和解析法的缺陷,但是传统的模拟法基于抽样的大量样本的确定性潮流计算次数过多,将使其计算效率下降,从而无法满足实时调度需求。本文将采用基于聚类抽样的方法,在保留随机变量矩阵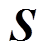 全样本特性的前提下,减少确定性潮流计算次数,从而提高计算效率。
全样本特性的前提下,减少确定性潮流计算次数,从而提高计算效率。
聚类抽样方法能够将大量样本中属性相似的样本聚集为簇,以簇为单位开展样本属性近似代替,大大减少样本数量,有效提高计算效率。
在矩阵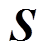 中,功率是本文随机样本的唯一属性。对于这种单一属性但大量的高维数据聚类,在此采用“基于划分”的K-means算法[22]。该算法实现简单,计算效率高。
中,功率是本文随机样本的唯一属性。对于这种单一属性但大量的高维数据聚类,在此采用“基于划分”的K-means算法[22]。该算法实现简单,计算效率高。
为了准确地衡量聚类效果,引入误差二次方和(Sum of Squared Error, SSE)指标,即
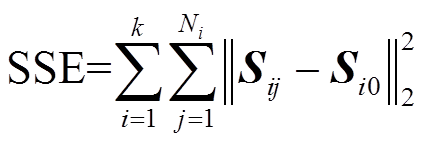 (5)
(5)式中,k为聚类簇数;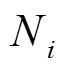 为簇
为簇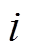 内样本数量;Sij为簇i内第j个样本;Si0为簇
内样本数量;Sij为簇i内第j个样本;Si0为簇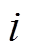 内样本的均值。SSE越小,表示每簇样本越接近其质心,聚类效果越好。
内样本的均值。SSE越小,表示每簇样本越接近其质心,聚类效果越好。
明显地,聚类簇数越多,SSE越小。但过多的聚类簇数会影响随机潮流的计算速度。所以应合理确定样本聚类簇数,使随机潮流计算精度和速度达到最优状态下的平衡。从数据样本属性和分布情况出发,寻找能够适应该类样本的最佳聚类簇数,使得簇内样本要具备尽可能大的相似性以及簇间样本具备尽可能大的差异性。
定义样本Sa与其所在簇内其他样本的平均欧氏距离为
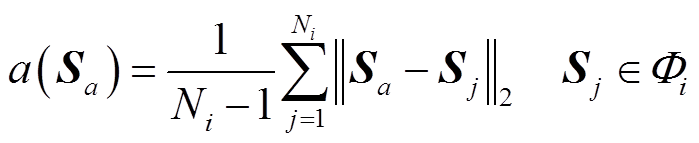 (6)
(6)式中,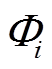 为簇
为簇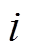 的样本空间,
的样本空间,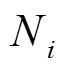 为簇
为簇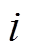 内样本数量;Sj为簇
内样本数量;Sj为簇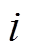 内任意样本。
内任意样本。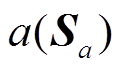 数值越小,则表示该样本与簇心之间的相似性越高。
数值越小,则表示该样本与簇心之间的相似性越高。
定义样本Sa距离最近的簇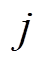 内样本的平均欧氏距离为
内样本的平均欧氏距离为
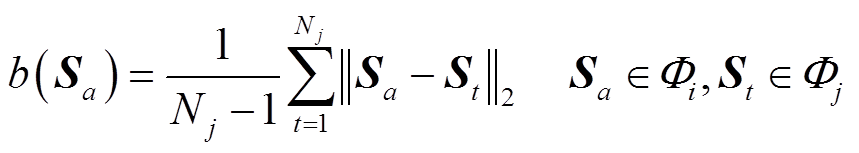 (7)
(7)式中,Φj为与样本Sa距离最近的簇空间;St为簇j内任意样本;Nj为簇j内样本数量。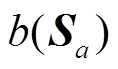 数值越大,表示该样本聚类的差异性越大。
数值越大,表示该样本聚类的差异性越大。
为评定整体数据的聚类可信度,以样本聚类的相似度和差异度为基础,定义平均轮廓系数(Average Silhouette Coefficient, ASC)为[23]
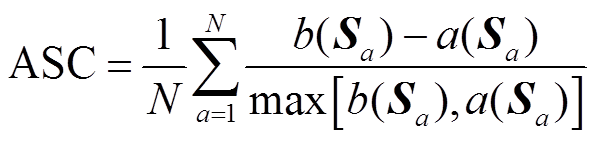 (8)
(8)式中,N为整体样本数据数量。ASC数值越大,则聚类效果越好。
综合考虑SSE和ASC两个指标,当SSE取值较小且ASC取值较大时,对应的聚类簇数即为最佳聚类簇数,记为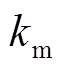 。
。
在确定最佳聚类簇数之后,采用K-means算法,将样本聚类为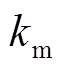 个簇。
个簇。
簇i的空间收敛于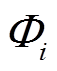 ,簇心为Sc,i,簇内样本数为Ni。依据簇空间大小和簇内样本数量,可确定簇i平均密度
,簇心为Sc,i,簇内样本数为Ni。依据簇空间大小和簇内样本数量,可确定簇i平均密度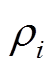 为
为
 (9)
(9)式中,Nξa为某样本Sa邻域空间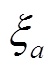 内所包含的样本个数;Aξa为簇内样本邻域
内所包含的样本个数;Aξa为簇内样本邻域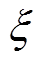 空间体积,是预先设定值。
空间体积,是预先设定值。
考虑采用K-means算法进行样本聚类,可能出现某簇内样本数太少的情况,从而导致簇样本平均密度信息失准。在此,设置限定簇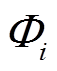 内的
内的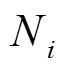 满足
满足
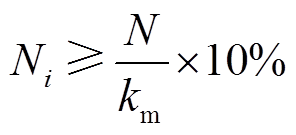 (10)
(10)当某簇内样本数不满足式(10),将该簇内样本选取与之欧式距离最近的邻簇进行归类,聚类簇数相应减小1,即簇数为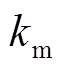 -1,保证所有簇内样本数均满足该条件。
-1,保证所有簇内样本数均满足该条件。
选取簇心Sc,i和簇平均密度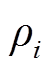 ,构建聚类中心向量Sc和簇密度向量
,构建聚类中心向量Sc和簇密度向量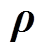 作为抽样样本。簇心的位置对应原分布函数抽样位置,簇平均密度近似等于抽样点处的概率密度。因此簇心和簇平均概率密度组成的向量能够近似表示原样本的分布特性。
作为抽样样本。簇心的位置对应原分布函数抽样位置,簇平均密度近似等于抽样点处的概率密度。因此簇心和簇平均概率密度组成的向量能够近似表示原样本的分布特性。
随机潮流计算的输出结果会因为抽样样本不具有代表性而产生误差。为了验证上述方法的有效性,在算例中将与拉丁超立方抽样方法、等间距抽样方法对比抽样效果和潮流计算结果的精度。
定义加权平均半径(Weighted Average Radius, WAR)作为抽样精度的指标评价,WAR为
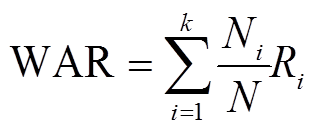 (11)
(11)式中,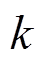 为簇的数量;
为簇的数量;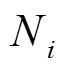 /
/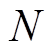 反映了该簇在所有簇中的重要程度,比值越大,该簇对随机潮流计算结果影响越大,要求计算结果的精度也就越高;
反映了该簇在所有簇中的重要程度,比值越大,该簇对随机潮流计算结果影响越大,要求计算结果的精度也就越高;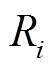 为该簇中所有样本到聚类中心的平均欧氏距离,反映了簇内样本和簇心之间的平均误差。加权平均半径
为该簇中所有样本到聚类中心的平均欧氏距离,反映了簇内样本和簇心之间的平均误差。加权平均半径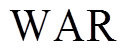 能够综合评价不同重要程度下的抽样精度,
能够综合评价不同重要程度下的抽样精度,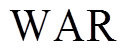 越小,说明抽样精度越高。
越小,说明抽样精度越高。
以蒙特卡洛法随机潮流计算结果作为参考标准,定义输出随机变量的期望和方差的误差作为潮流计算结果精度的评价指标,即
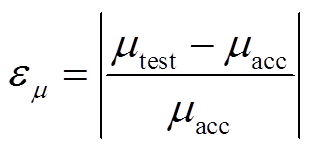 (12)
(12) (13)
(13)式中,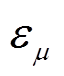 和
和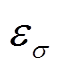 分别为测试方法与蒙特卡洛法之间的期望误差和方差误差;
分别为测试方法与蒙特卡洛法之间的期望误差和方差误差; 和
和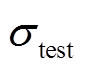 分别为测试方法的期望及方差;
分别为测试方法的期望及方差;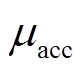 和
和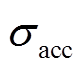 分别为蒙特卡洛法得到的期望和方差。
分别为蒙特卡洛法得到的期望和方差。
本文提出的基于聚类抽样的随机潮流计算方法的具体流程如图2所示,计算过程包括样本聚类抽样和潮流计算两部分。

图2 随机潮流计算流程
Fig. 2 Stochastic load flow calculation flowchart
样本聚类抽样是通过样本的相似性来缩减确定性潮流计算样本。首先,依据随机变量的分布特性,采用蒙特卡洛抽样法生成能够准确表示随机变量的全分布特征的大量样本。然后,基于K-means算法,综合采用SSE和ASC指标来确定最佳聚类簇数,依据样本间的欧式距离进行样本归类。最后在该聚类方案下,将簇心和簇内样本的平均概率密度作为随机变量的抽样样本。
潮流计算模型是基于前述抽样样本形成的系统注入功率,然后开展确定性潮流计算。在获取簇心和簇内样本的平均概率密度后,对各簇心的潮流计算结果进行加权统计,可得到状态变量的概率分布计算结果。
以修改的IEEE 39系统和某实际区域电网为算例,验证本文算法的有效性和优越性。
以风电出力预测误差历史数据为基础,将其中的风电场1和风电场2的实时出力数据按容量成比例注入IEEE 39系统的节点2和节点5,形成修改IEEE 39系统。区域电网由8 039个节点和10 135条支路构成。风电场配置见表1。
表1 风电场配置
Tab.1 Configuration of wind farms

系统风电场节点编号风电场总容量/MW 修改IEEE 39系统2,51 000 区域电网5,37711 300
在风电预测误差样本空间内,随机变量的SSE随聚类簇数变化如图3所示,ASC随聚类簇数变化如图4所示。
由图3和图4可知,SSE随着聚类簇数的增加而减小;ASC随着聚类簇数的增加先减小后增大。综合SSE和ASC,当聚类簇数为25时,SSE的变化率为0.004 9,ASC的变化率小于0.001。考虑到过多的聚类簇数会影响随机潮流的计算速度,同时,核查所有聚类簇的簇内样本数均满足式(10)的限定,在此将算例样本聚类簇数取为25。
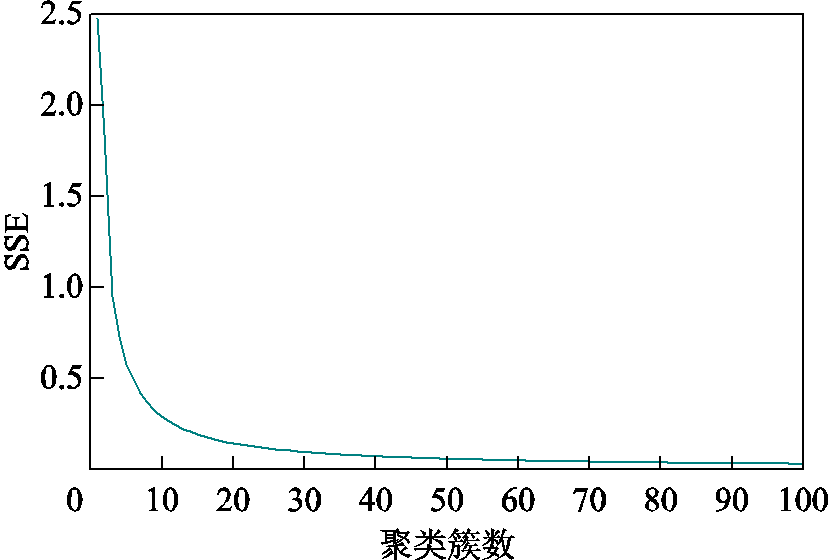
图3 SSE曲线
Fig.3 SSE curve
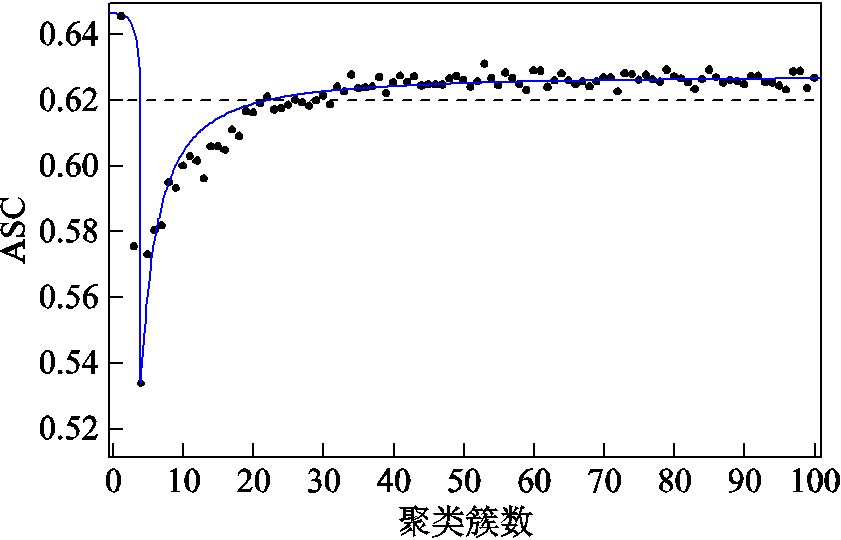
图4 平均轮廓系数曲线
Fig.4 Average silhouette coefficient curve
将风电预测误差历史数据按25簇进行聚类,聚类结果如图5所示,其中不同的簇用不同符号区分,并给出了簇心标记。
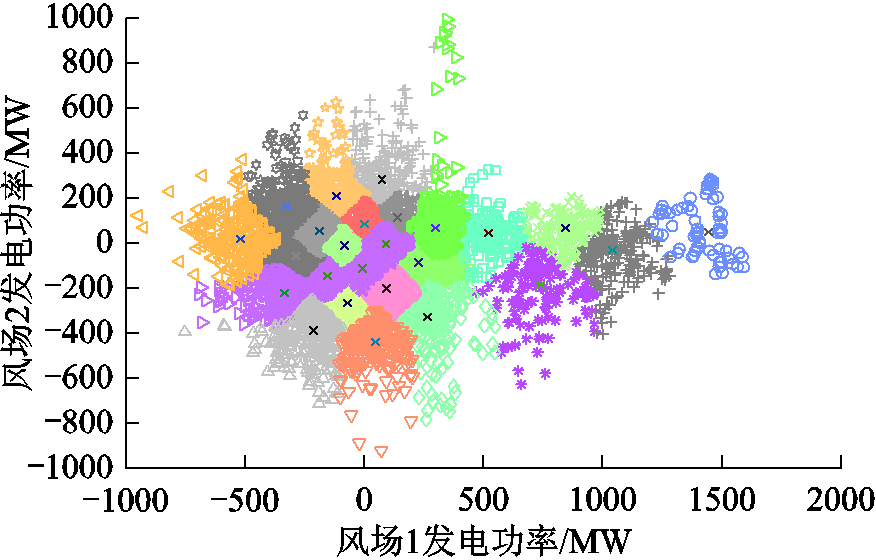
图5 K-means聚类分组示意图
Fig.5 K-means clustering diagram
分别采用本文的聚类抽样法、等间距抽样法、拉丁超立方抽样法进行抽样,抽样精度结果如图6所示。
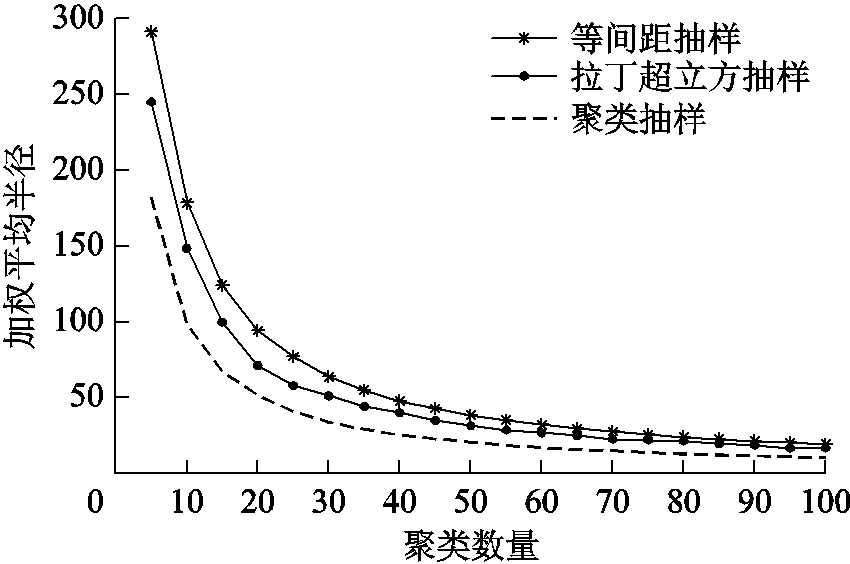
图6 不同抽样方法加权平均半径曲线
Fig.6 WAR of different sampling methods
由图6可知,三种方法的抽样精度指标随着抽样次数增多而增大。在相同的抽样次数下,本文的聚类抽样方法的抽样精度最高。
图7给出了风电场1的历史数据在等间距抽样法、拉丁超立方抽样法、聚类抽样法和蒙特卡洛抽样法下的概率密度函数拟合曲线。
依据图7计算结果可知,等间距抽样法对概率密度变化反应敏感,在概率密度变化大的区域拟合度较差,而在低概率密度区域拟合效果较好;拉丁超立方抽样法对概率密度的大小反应敏感,在高概率密度区域拟合效果最好,但在低概率密度区域缺失较多信息,拟合效果欠佳;聚类抽样法的抽样效果综合了拉丁超立方抽样和等间距抽样的优点,能够描述高概率密度和低概率密度分布的局部细节,涵盖了随机变量所有取值范围的概率分布的信息。
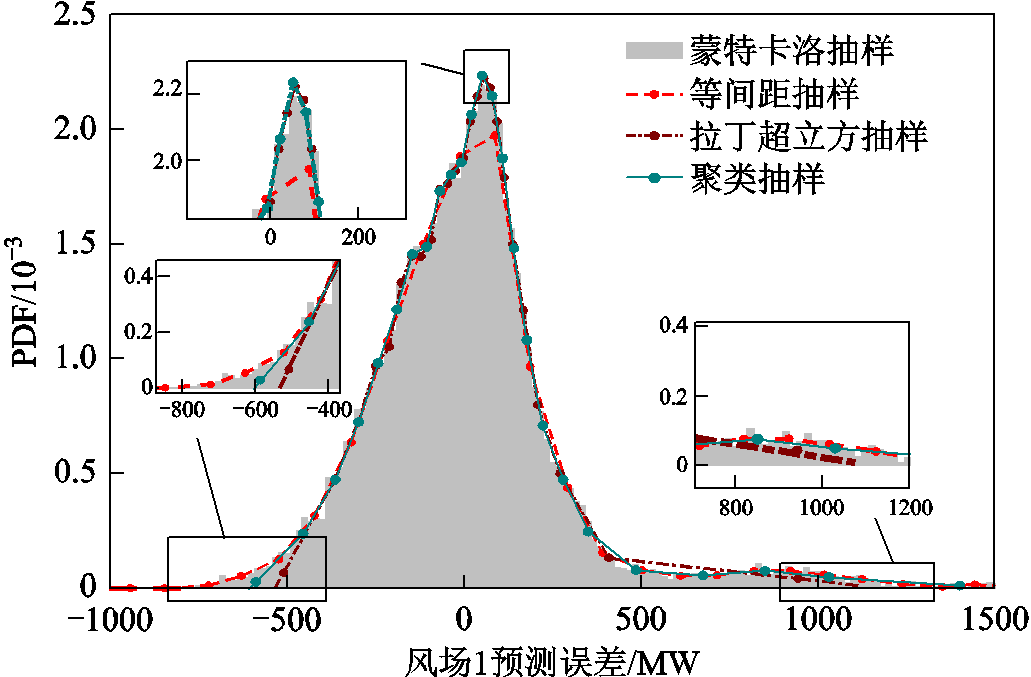
图7 不同抽样法的概率密度拟合效果
Fig.7 PDF fitting curves of different sampling methods
分别使用蒙特卡洛模拟法、拉丁超立方抽样法、等间距抽样法和聚类抽样法的抽样样本计算系统潮流。由于功率注入对注入点的电压相位和平衡节点的功率影响最大,计算结果更具代表性。在此选取修改IEEE 39系统的节点1的有功功率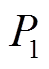 和节点2(风场1所在节点)的电压相位
和节点2(风场1所在节点)的电压相位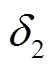 进行监测。
进行监测。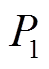 和
和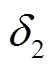 的概率密度函数分别如图8、图9所示。
的概率密度函数分别如图8、图9所示。
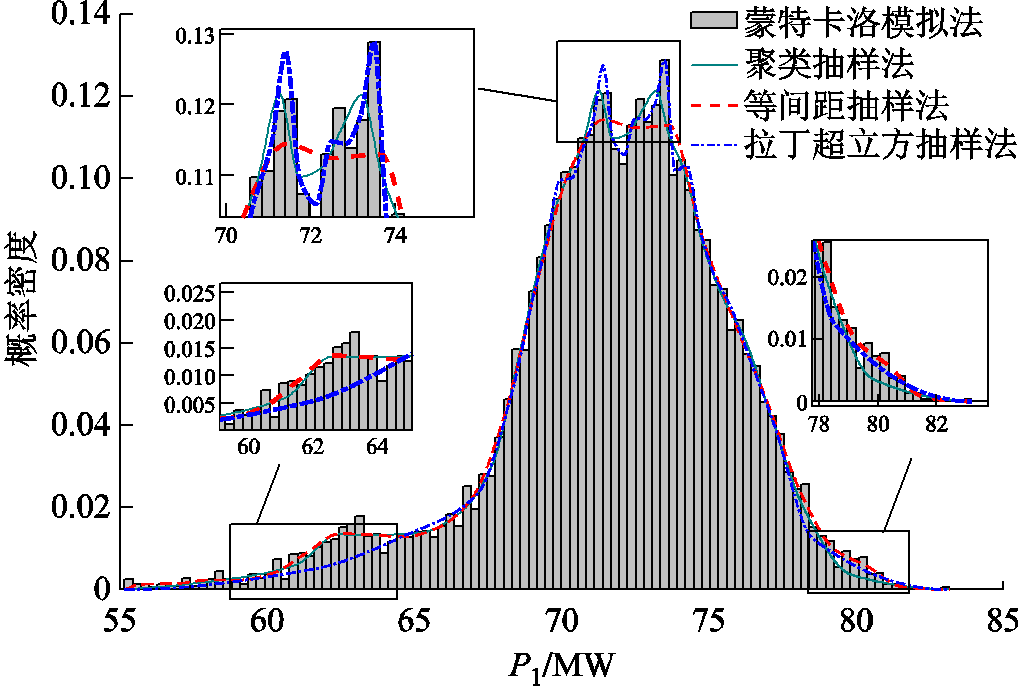
图8 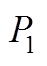 概率密度函数
概率密度函数
Fig.8 PDF of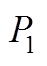
由图8和图9可知,在高概率密度区域,等间距抽样的结果误差最大,拉丁超立方抽样和聚类抽样的结果误差较小并且相似;在低概率密度区域,拉丁超立方抽样的结果误差最大,等间距抽样的结果误差最小,聚类抽样的结果误差略大于等间距抽样。由误差分布可以看出,本文提出的基于聚类抽样的随机潮流计算方法能够更准确地描述状态变量的全分布特性。
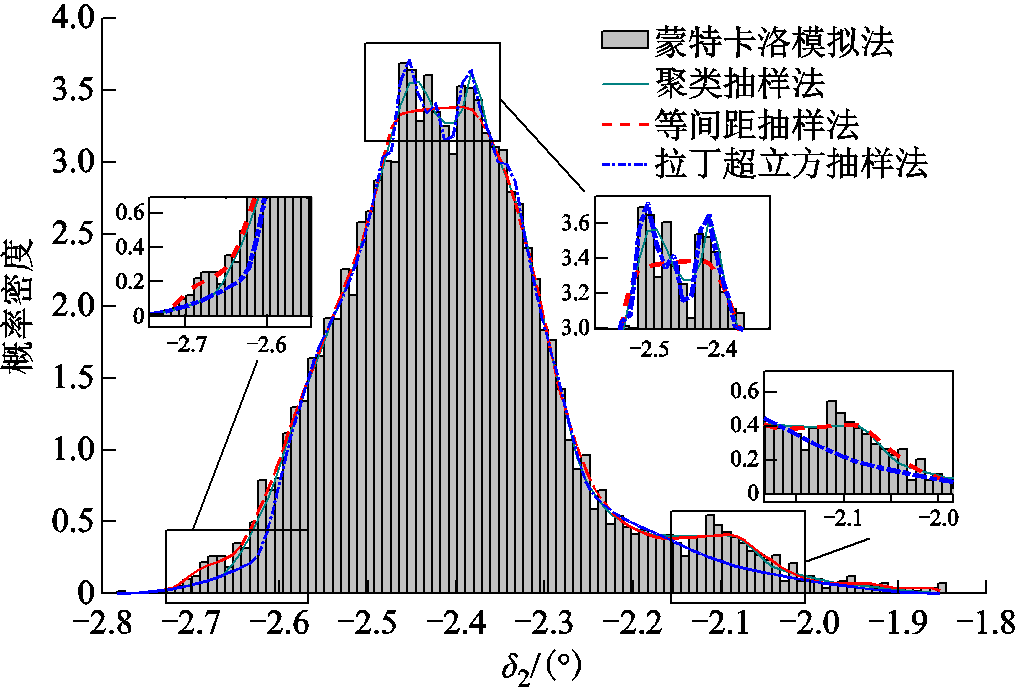
图9 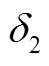 概率密度函数
概率密度函数
Fig.9 PDF of 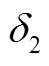
计算修改IEEE 39节点系统和区域电力系统随机潮流,以蒙特卡洛法得到的结果作为基准值,等间距抽样法、拉丁超立方抽样法和本文的聚类抽样法三种方法得到的潮流计算期望误差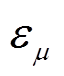 和方差误差
和方差误差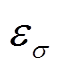 见表2。
见表2。
表2 随机潮流计算误差测试
Tab.2 SLF calculate error test (%)

状态变量误差聚类抽样法拉丁超立方法等间距抽样法 修改IEEE 39系统期望误差0.8002.060.023 2 方差误差0.4930.3652.955 期望误差0.9452.170.028 9 方差误差0.5220.4044.101 区域电网期望误差1.2113.2280.037 方差误差0.7230.6114.775 期望误差1.0912.740.031 9 方差误差0.6440.5223.305
由表2可得,随机潮流结果的计算误差与选用的抽样方法相关。以蒙特卡洛法随机潮流计算结果的期望和方差作为评价标准,可以发现,等间距法的期望误差最小,但方差误差最大;拉丁超立方法的方差误差最小,但期望误差最大;聚类抽样法的期望误差和方差误差介于等间距法和拉丁超立方法之间。
本文算例在表3所示的运行环境中求解。
在上述硬件配置下,聚类抽样法通过聚类再抽取25个簇心用于开展确定性潮流计算。以其相应的抽样精度为基准,采用拉丁超立方抽样法和等间距抽样法进行确定性潮流计算,分别为38次和47次。对于修改IEEE 39系统和区域电网开展随机潮流计算,计算时间统计结果见表4。
表3 随机潮流运行环境参数
Tab.3 SLF operating environment parameters

环境参数配置 CPU内存Intel core i5-6300U 2.4GHz8GB 显卡Intel HD Graphics 520 软件平台PSD-BPA Matlab 2017R
表4 随机潮流计算时间统计
Tab.4 SLF calculation time (单位:s)
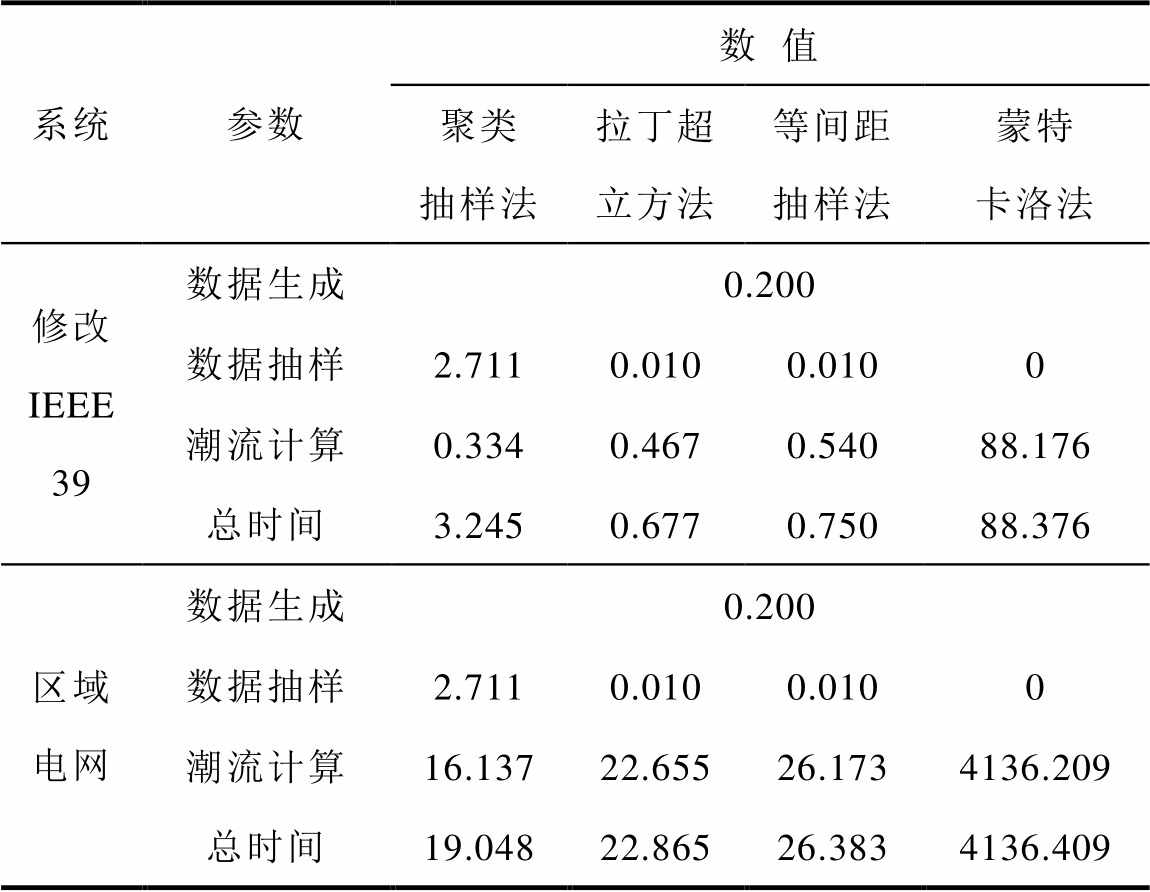
系统参数数值 聚类抽样法拉丁超立方法等间距抽样法蒙特卡洛法 修改IEEE39数据生成0.200 数据抽样2.7110.0100.0100 潮流计算0.3340.4670.54088.176 总时间3.2450.6770.75088.376 区域电网数据生成0.200 数据抽样2.7110.0100.0100 潮流计算16.13722.65526.1734136.209 总时间19.04822.86526.3834136.409
由表4可知,三种方法相比于传统蒙特卡洛法,大大缩短了随机潮流计算时间。其中,聚类抽样在抽样阶段耗费的时间较长,随机潮流计算时间短;而拉丁超立方法和等间距抽样法的抽样时间非常短,但是随机潮流计算时间较长。在修改的IEEE 39系统中聚类抽样法的计算速度低于拉丁超立方法和等间距抽样法;在区域系统中,聚类抽样法的性能优于拉丁超立方法和等间距抽样法。这表明本文提出的基于聚类抽样的随机潮流计算方法在大系统中更具优势。
本文提出了基于聚类抽样的随机潮流计算方法。此方法采用SSE和ASC来确定最佳聚类簇数,将簇心和簇内样本的平均概率密度作为随机变量的抽样样本,然后进行确定性潮流计算,对所有样本计算结果进行统计得到状态变量的概率密度分布。本文方法以预测误差历史数据构建随机变量样本空间,兼顾计算精度和计算效率要求,可用于电力系统调度计划的制定和运行分析。
在相同样本数下,本文方法抽样精度高于拉丁超立方抽样法和等间距抽样法;与传统的蒙特卡洛模拟法相比,本文方法计算效率有较大提升。以蒙特卡洛法计算结果为基准,在相同的精度下,聚类抽样法的计算效率高于拉丁超立方法和等间距法;系统规模越大,本文方法的计算效率优势更明显。本文是以并网风电预测误差为例进行方法的说明,此方法可扩展到其他类型的可再生能源出力不确定性和负荷不确定性建模中。
参考文献
[1] Dopazo J F, Klitin O A, Sasson A M. Stochastic load flows[J]. IEEE Transactions on Power Apparatus and Systems, 1975, 94(2): 299-309.
[2] 邵振国, 黄伟达. 考虑出力不确定性的分布式电源谐波传播计算[J]. 电工技术学报, 2019, 34(增刊2): 674-683. Shao Zhenguo, Huang Weida. A calculation method of harmonic propagation considering the uncertainty of distributed generation[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 674-683.
[3] 韩佶, 苗世洪, 李超, 等. 计及相关性的电-气-热综合能源系统概率最优能量流[J]. 电工技术学报, 2019, 34(5): 1055-1067. Han Ji, Miao Shihong, Li Chao, et al. Probabilistic optimal energy flow of electricity-gas-heat integrated energy system considering correlation[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1055-1067.
[4] 刘宇, 高山, 杨胜春, 等. 电力系统概率潮流算法综述[J]. 电力系统自动化, 2014, 38(23): 127-135. Liu Yu, Gao Shan, Yang Shenchun, et al. Review on algorithms for probabilistic load flow in power system[J]. Automation of Electric Power Systems, 2014, 38(23): 127-135.
[5] 赵书强, 李志伟. 考虑可再生能源出力不确定性的多能源电力系统日前调度[J]. 华北电力大学学报:自然科学版, 2018, 45(5): 1-10.Zhao Shuqiang, Li Zhiwei. Day-ahead scheduling of multi-energy power system considering renewable energy uncertain output[J]. Journal of North China Electric Power University, 2018, 45(5): 1-10.
[6] 朱星阳, 刘文霞, 张建华, 等. 电力系统随机潮流及其安全评估应用研究综述[J]. 电工技术学报, 2013, 28(10): 257-270. Zhu Xingyang, Liu Wenxia, Zhang Jianhua, et al. Reviews on power system stochastic load flow and its applications in safety evaluation[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 257-270.
[7] Amid P, Crawford C. Cumulant-based probabilistic load flow analysis of wind power and electric vehicles[C]//2016 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), IEEE, Beijing, China, 2016: 1-6.
[8] 孙玲玲, 赵美超, 王宁, 等. 基于电压偏差机会约束的分布式光伏发电准入容量研究[J]. 电工技术学报, 2018, 33(7): 1560-1569. Sun Lingling, Zhao Meichao, Wang Ning, et al. Research of permitted capacity of distributed photovoltaic generation based on voltage deviation chance constrained[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1560-1569.
[9] 李振坤, 崔静, 路群, 等. 基于时序动态约束的主动配电网滚动优化调度[J]. 电力系统自动化, 2019, 43(16): 17-29. Li Zhenkun, Cui Jing, Lu Qun, et al. Rolling optimal scheduling of active distribution network based on series dynamic constraints[J]. Automation of Electric Power Systems, 2019, 43(16): 17-29.
[10] 石飞, 杨胜春, 冯树海, 等. 适用于超大规模电网的在线概率潮流算法[J]. 电力系统自动化, 2018, 42(21): 84-92. Shi Fei, Yang Shengchun, Feng Shuhai, et al. Online probabilistic power flow algorithm for super-large-scale power grid[J]. Automation of Electric Power Systems, 2018, 42(21): 84-92.
[11] Cao Jia, Yan Zheng. Probabilistic optimal power flow considering dependences of wind speed among wind farms by pair-copula method[J]. International Journal of Electrical Power & Energy Systems, 2017, 84: 296-307.
[12] Zhang H, Li P. Probabilistic analysis for optimal power flow under uncertainty[J]. IET Generation, Transmission & Distribution, 2010, 4(5): 553-561.
[13] 韦鹏飞, 徐永海, 王金浩, 等. 基于拉丁超立方采样的节点敏感设备暂降免疫水平评估[J]. 电工技术学报, 2018, 33(15): 3415-3425. Wei Pengfei, Xu Yonghai, Wang Jinhao, et al. Sag immunity level evaluation of sensitive equipment at node based on Latin hypercube sampling[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3415-3425.
[14] Huang Jie, Xue Yusheng, Dong Z Y, et al. An adaptive importance sampling method for probabilistic optimal power flow[C]//2011 IEEE Power and Energy Society General Meeting, IEEE, Detroit, MI, USA, 2011: 1-6.
[15] Xu Xiaoyuan, Yan Z heng. Probabilistic load flow evaluation with hybrid Latin hypercube sampling and multiple linear regression[C]//2015 IEEE Power & Energy Society General Meeting, IEEE, Denver, CO, USA, 2015: 1-5.
[16] Xu Qingshan, Yang Yang, Liu Yujun, et al. An improved Latin hypercube sampling method to enhance numerical stability considering the correlation of input variables[J]. IEEE Access, 2017, 5: 15197-15205.
[17] 黄江宁, 郭瑞鹏, 赵舫, 等. 电力系统可靠性评估中的分层均匀抽样法[J]. 电力系统自动化, 2012, 36(20): 19-24. Huang Jiangning, Guo Ruipeng, Zhao Fang, et al. Stratified uniform sampling method for power system reliability evaluation[J]. Automation of Electric Power Systems, 2012, 36(20): 19-24.
[18] Wang Jianhui, Shahidehpour M, Li Zuyi. Security-constrained unit commitment with volatile wind power generation[J]. IEEE Transactions on Power Systems, 2008, 23(3): 1319-1327.
[19] 丁华杰, 宋永华, 胡泽春, 等. 基于风电场功率特性的日前风电预测误差概率分布研究[J]. 中国电机工程学报, 2013, 33(34): 136-144. Ding Huajie, Song Yonghua, Hu Zechun, et al. Probability density function of day-ahead wind power forecast errors based on power curves of wind farms[J]. Proceedings of the CSEE, 2013, 33(34): 136-144.
[20] Bae K Y, Jang H S, Sung D K. Hourly solar irradiance prediction based on support vector machine and its error analysis[J]. IEEE Transactions on Power Systems, 2017, 32(2): 935-945.
[21] 刘立阳, 吴军基, 孟绍良. 短期风电功率预测误差分布研究[J]. 电力系统保护与控制, 2013, 41(12): 65-70. Liu Liyang, Wu Junji, Meng Shaoliang. Research on error distribution of short-term wind power prediction[J]. Power System Protection and Control, 2013, 41(12): 65-70.
[22] 隋心怡, 王瑞刚, 张鸿翔. 一种改进的K-均值聚类算法[J]. 计算机与数字工程, 2018, 46(4): 682-685. Sui Xinyi, Wang Ruigang, Zhang Hongxiang. An improved K-means clustering algorithm[J]. Computer & Digital Engineering, 2018, 46(4): 682-685.
[23] 朱连江, 马炳先, 赵学泉. 基于轮廓系数的聚类有效性分析[J]. 计算机应用, 2010, 30(2): 139-141. Zhu Lianjiang, Ma Bingxian, Zhao Xuequan. Clusting validity analysis based on silhouette coefficient[J]. Journal of Computer Application, 2010, 32(2): 139-141.
Stochastic Load Flow Calculation Method Based on Clustering and Sampling
Abstract Stochastic load flow is designed for power systems with uncertainties, whose fast and accurate calculation results are very important for grid operational control. In this paper, a stochastic load flow calculation method was proposed on basis of clustering and sampling. Firstly, according to history data, Monte Carlo simulation method was used to generate a large number of random variable samples. Secondly, the optimal cluster number was determined for samples by the average silhouette coefficient and sum of squared error, and the samples were clustered by using K-means. Thirdly, according to the clustering center and the average probability density of the sample in the cluster, load flow was calculated with the mean values of each cluster. Finally, the power flow calculation results and the corresponding average probability density were statistically analyzed, and the probability density function of the state variables was obtained. The modified IEEE39 system and a real regional power grid were taken as examples to analyze the calculation accuracy and calculation efficiency. The results show that the method proposed in this paper can balance calculation accuracy and calculation speed, and there are more advantageous in large systems. It provides decision basis for grid dispatching plan and operation analysis.
keywords:Stochastic load flow, uncertainty, clustering, sampling
中图分类号:TM711
DOI: 10.19595/j.cnki.1000-6753.tces.191618
国家电网有限公司总部科技项目“新一代能源发展战略评估推演关键技术及应用研究”资助(SGXJJY00GHJS1900031)。
收稿日期 2019-11-26
改稿日期 2020-02-28
谢 桦 女,1970年生,博士,副教授,研究方向为储能规划与控制、综合能源系统优化运行。E-mail:hxie@bjtu.edu.cn
任超宇 男,1994年生,硕士研究生,研究方向为电力系统分析。E-mail:494192416@qq.com
(编辑 赫蕾)