

图1 风电场结构示意图
Fig.1 Wind farm structure diagram
摘要 针对风电场集电线路因短路故障造成的弃风窝电问题,提出采用全相位快速傅里叶变换(apFFT)频谱校正和极限梯度提升(XGBoost)的风电场集电线路单相接地故障测距方法。首先,搭建双馈风电场多分支混合线路的仿真模型,并通过apFFT频谱校正法获取故障电压和电流的基波相量,以构建原始特征集;然后,采用XGBoost算法建立单端故障测距的回归模型,并计算获取故障特征的重要度及排序,直观地挖掘特征量与故障距离之间的关系;最后,应用XGBoost故障定位器根据现存模态完成对新输入模态的定位,获得故障点精确位置。PSCAD/EMTDC实验证明,该方法对风电场多分支、混合短线路测距具有明显优势,定位性能优于随机森林(RF)方法,且不受故障位置、过渡电阻的影响,可满足风电场对测距精度的需求。
关键词:风电场集电线路 apFFT频谱校正 极限梯度提升 单相接地故障 单端故障测距 特征重要度
随着风电场规模的不断扩大和风力机组容量的不断增加,风电场的安全可靠运行变得越来越重要。风电场多处于地形复杂的荒山草原,受气候条件和地理环境的影响,极易发生雷击、绝缘雾闪、绝缘子风偏和线路金具损坏而引起的短路故障,其中单相接地故障约占系统故障的80%[1]。因此,有效的故障定位技术能够帮助风电场运行人员减小排查范围,查找故障迅速、可靠;显著减少风机窝电时间,对于提高风电场的经济效益和满足电网对风电场的运行考核指标具有重要意义。
风电场是典型的多端电源供电系统,网络拓扑结构特殊,尚缺乏有效的故障检测和分析手段。目前测距方法主要有行波法[2-10]、故障分析法[11-16]和人工智能算法[17-23]。行波法测距精度高,但配电网和风电场内存在分支线和混合线,使行波易发生折反射,加之线路较短,导致波头检测和波速确定困难。文献[9]采用等效思想对配电线路归一化处理以解决混合线路的行波波速不一致问题,但需在每个分支线末端装设同步测量装置,且海量故障数据处理要求系统硬件具有较高的性能,算法实现成本高。文献[10]提出基于行波固有频率的双端输电线路故障定位方法,技术的关键在于准确提取自然频率,但对于拓扑结构复杂的配电网和风电场,特征频率混叠导致提取失败,无法完成故障定位。故障分析法受制于过渡电阻和模型准确度使其测距精度有限,且计算量大。文献[15]分析沿线电压分布规律,由切线交叉原理迭代求解故障点。文献[16]适用于T接线路,利用测距函数判断故障分支,进而求解故障距离,但难以向多分支、混合短线路的故障定位拓展。
国务院印发的《新一代人工智能发展规划》已将人工智能上升到国家战略层面。人工智能技术的快速发展,使智能算法用于多分支、混合短线路的故障定位已成为趋势。文献[22]通过测量光伏阵列输出电压和电流,应用高斯过程回归进行光伏阵列故障定位,性能优于BP神经网络。文献[23]采用离散傅里叶变换对线路一端三相电压信号提取谐波分量的幅值作为特征量,并基于K最邻近回归模型实现单相接地故障的准确测距。
根据风电场集电线路分支多、混合且短的特点,本文提出采用全相位快速傅里叶变换(all-phase Fast Fourier Transform, apFFT)频谱校正和极限梯度提升(eXtreme Gradient Boosting, XGBoost)的风电场集电线路故障测距方法。搭建了双馈风电场仿真模型,且通过apFFT频谱校正法从单端测点数据提取电压和电流的基波特征量。目前,尚未见XGBoost集成算法在风电场集电线路故障定位的应用研究,该方法采用多线程并行计算和二阶泰勒展开,具有较高的运算效率和预测精度。因此,引入人工智能技术XGBoost回归模型,根据特征被选择用来划分的次数情况对特征重要度进行量化分析及排序,完成故障点的准确定位。PSCAD/EMTDC实验证明,本文方法适用于风电场复杂网络的故障测距,定位精度高于随机森林(Random Forest, RF)集成树方法,对不同故障位置和过渡电阻的单相接地短路均能够有效测距。
风电场结构如图1所示。其中,图1a为风电场网络拓扑结构,本文风机均采用双馈异步风力发电机,图1b为双馈风力发电系统结构。
风电场模型的结构特点为:
1)风电场为多风电机组分支,电缆线和架空线混合,相邻风电机组间的距离较短。
2)集电线路接线采用链型结构,是典型的辐射网。对于单条集电线路,总长一般不超过20km。
3)虽然风电场电压等级为35kV,但为确保其安全性与可靠性,通常采用Z型接地变压器,作为风电场的人为中性点。


图1 风电场结构示意图
Fig.1 Wind farm structure diagram
apFFT[24-27]是一种新型的频谱分析方法,与传统FFT相比,具有优良的频谱泄露抑制性、抗噪性以及“相位不变性”。选择单频复指数信号作为输入,以展示apFFT的优越性。
 (1)
(1)式中,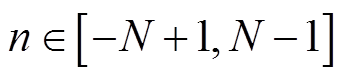 ;A0为幅值;ω0为角频率;φ0为初相位;2πβ/N为角频率倍数形式。
;A0为幅值;ω0为角频率;φ0为初相位;2πβ/N为角频率倍数形式。
传统FFT分析的幅频表达式为
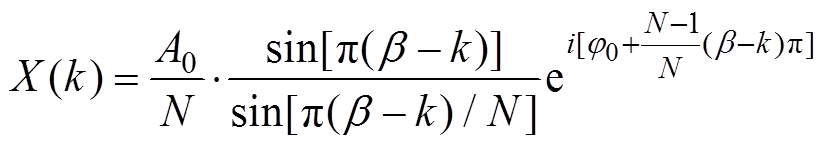 (2)
(2)apFFT分析求得归一化频谱表达式为
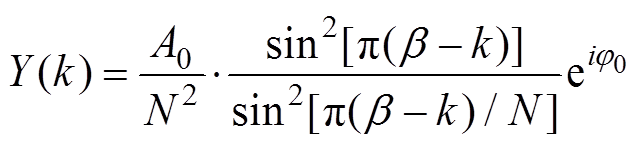 (3)
(3)式中,k为0~N-1内的整数。由式(2)、式(3)可知,apFFT谱幅值具有二次方变化特性,旁瓣衰减更快,则主瓣更突出,频谱泄露更小;其相位始终为φ0,同频率偏移量β-k无关,具有“相位不变性”。
利用apFFT相位差校正法[24]将FFT与apFFT相结合,实现对风电场集电线路故障信号的分析。角频率ω0、幅值A0、初相位φ0的校正流程如图2所示。
由图2可知,风电场集电线路故障信号的基波相位则直接由汉宁卷积窗apFFT获得,而幅值校正式为
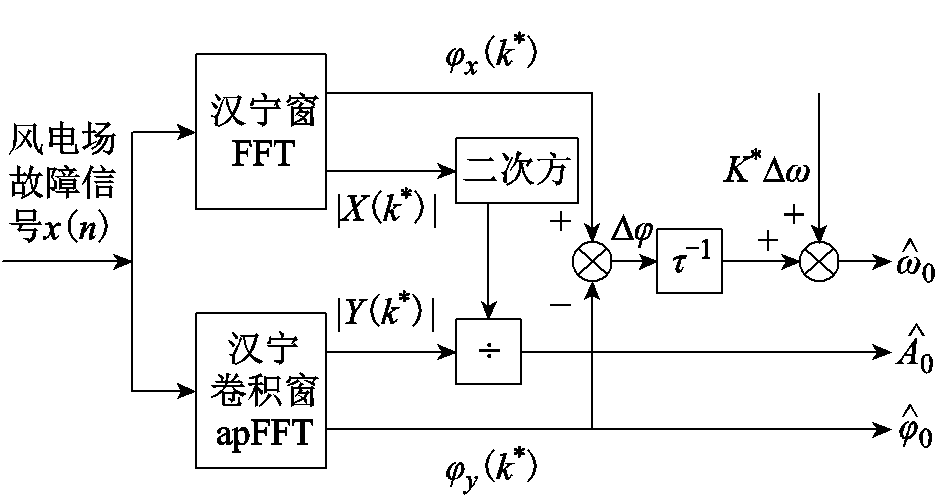
图2 apFFT相位差频谱校正流程
Fig.2 Spectrum correction procedure for apFFT phase difference method
 (4)
(4)式中,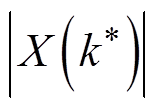 和
和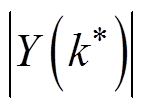 分别为汉宁窗FFT与汉宁卷积窗apFFT的幅值。经相位补偿后的角频率为
分别为汉宁窗FFT与汉宁卷积窗apFFT的幅值。经相位补偿后的角频率为
 (5)
(5)式中,τ为群延时;Dj为两种谱分析的主谱线相位差,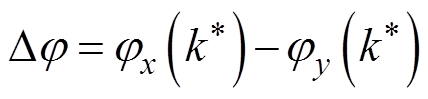 ;Dω为频率分辨率。
;Dω为频率分辨率。
数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已。因此,特征工程十分重要,特征选取的好坏将直接影响故障回归定位器的性能。构建故障特征量时应遵循如下原则:特征量的选取能比较好地反映故障位置;特征量的计算满足高效性;特征量与风电场规模大小无关。
故障特征提取参考文献[1,22]设计,其均采用电压和电流作为故障特征量,分别完成了对风电和光伏系统的故障定位。此外,基于XGBoost的特征重要度分析表明,电压和电流基波特征量能够体现故障信息,并有效完成风电场集电线路的故障测距。搭建如图1a所示的双馈风电场拓扑模型,仅在35kV侧出口集电线路首端安装一个测点,应用apFFT相位差校正法对单相接地故障时测点测量的数据提取三相电压、电流及零序网络电压、电流基波相量,用于构成特征值1(F1)~特征值16(F16),具体见表1。
本文算法思想如下:首先,将风电场集电线路单相接地故障测距问题建模为回归问题;然后,进行风电场历史故障数据采样,用于训练XGBoost回归故障定位器;最后,将当前的采样数据输入XGBoost回归故障定位器中,以实现风电场集电线路的单端故障测距。
表1 风电场集电线路单相接地故障特征
Tab.1 The features of single phase grounding fault for wind farm power line

特征特征描述特征特征描述 F1A相电压有效值F9A相电压相位 F2B相电压有效值F10B相电压相位 F3C相电压有效值F11C相电压相位 F4零序电压有效值F12零序电压相位 F5A相电流有效值F13A相电流相位 F6B相电流有效值F14B相电流相位 F7C相电流有效值F15C相电流相位 F8零序电流有效值F16零序电流相位
XGBoost[28]是一种基于Boosting的监督式集成学习模型,其基学习器选择分类回归树(Classification And Regression Tree, CART)。采用apFFT频谱校正法获取风电场集电线路单端测点的电压和电流特征量后,可得用于故障测距的数据集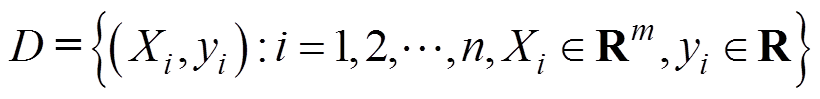 ,其中,共有n个训练样本Xi,每个样本有m个故障特征,且对应一个目标值即真实故障距离yi,则K棵CART构成的集成树模型为
,其中,共有n个训练样本Xi,每个样本有m个故障特征,且对应一个目标值即真实故障距离yi,则K棵CART构成的集成树模型为
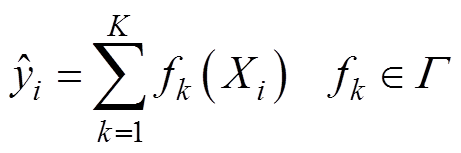 (6)
(6)式中, 为预测故障距离;fk对应第k棵独立树的结构q和叶子权重ω;
为预测故障距离;fk对应第k棵独立树的结构q和叶子权重ω;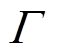 为CART构成的集合空间。XGBoost模型的目标函数为
为CART构成的集合空间。XGBoost模型的目标函数为
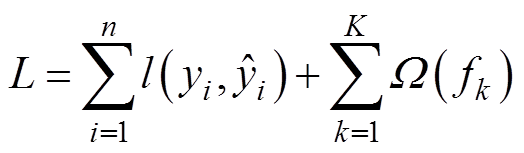 (7)
(7)式中,l为训练误差函数,即损失函数,体现拟合数据的程度,对于回归问题常采用方均误差,则有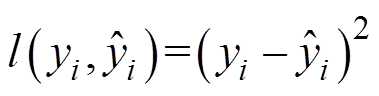 。为防止模型过拟合,定义用于控制复杂度的正则项为
。为防止模型过拟合,定义用于控制复杂度的正则项为
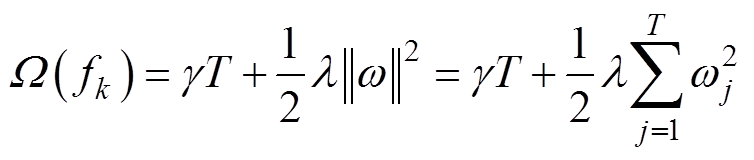 (8)
(8)式中,γ和λ为模型的惩罚系数;T为叶子节点数;ωj为叶子节点j的权重。
采用前向分步加法算法,即在每一轮迭代中添加增量函数ft(Xi)来最优化目标函数。
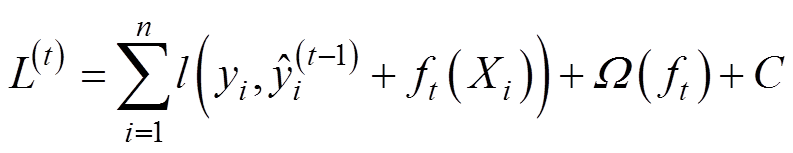 (9)
(9)对式(9)的损失函数进行二阶泰勒展开,并移除常数项C,定义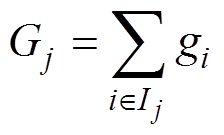 ,
,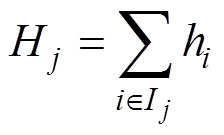 ,得
,得
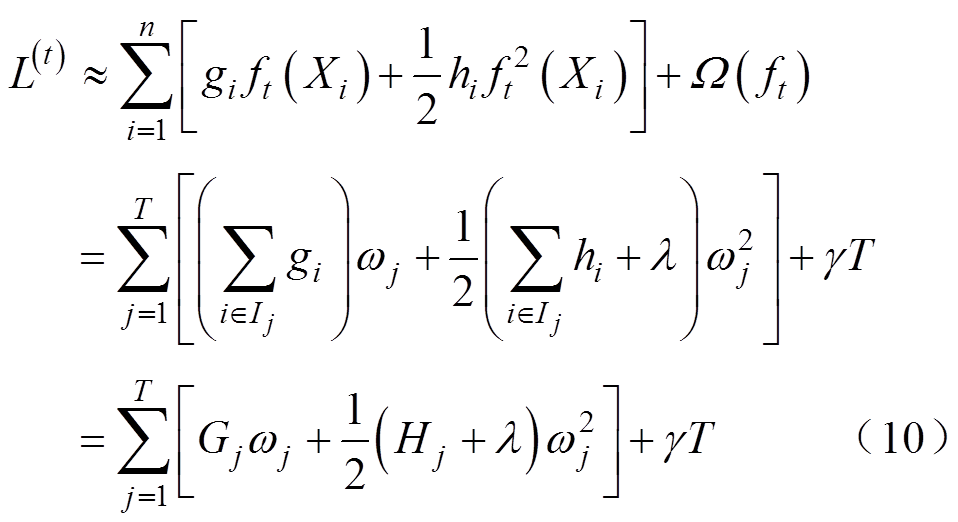
式中,gi、hi分别为损失函数的一阶、二阶导数,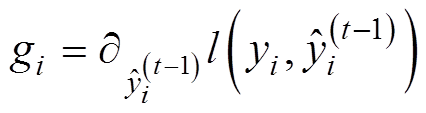 ,
, ;Ij为叶子节点j的样本集,
;Ij为叶子节点j的样本集,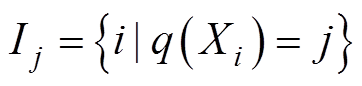 。
。
由此,目标函数简化为关于ωj的一元二次方程,求最小值问题。设树结构q确定,对ωj求偏导得叶子节点j的最优权重,即
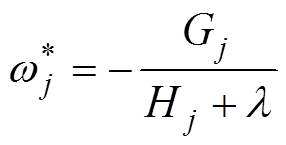 (11)
(11)将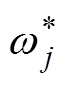 代入式(10)可得最优目标函数值为
代入式(10)可得最优目标函数值为
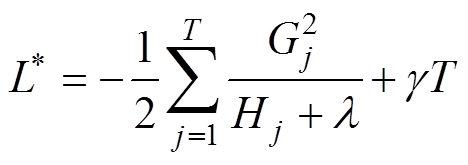 (12)
(12)因不可能枚举所有可能的树结构,故采用贪心算法对子树进行划分,选择目标函数值最小,增益最大的划分,增益表达式为
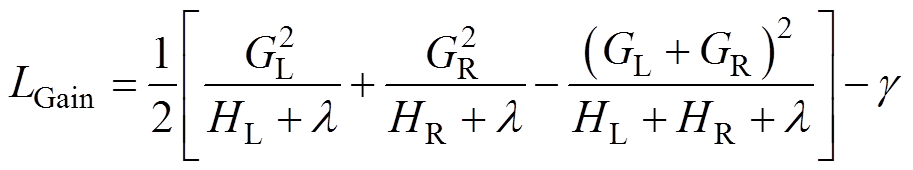 (13)
(13)apFFT频谱校正能够抑制频谱泄露,同时可提高风电场故障分析与特征提取的准确度。XGBoost集成树算法在解决风电场集电线路故障距离预测问题上具有如下优势:①自动多线程并行计算,运算速度快,适于处理大规模电力数据;②增加了控制模型复杂度的正则化项,防止发生过拟合;③对损失函数进行二阶泰勒展开,预测精度高。因此,本文apFFT频谱校正和XGBoost技术适合风电场集电线路的故障测距。采用apFFT相位差校正和XGBoost的风电场单相接地故障测距流程如图3所示。
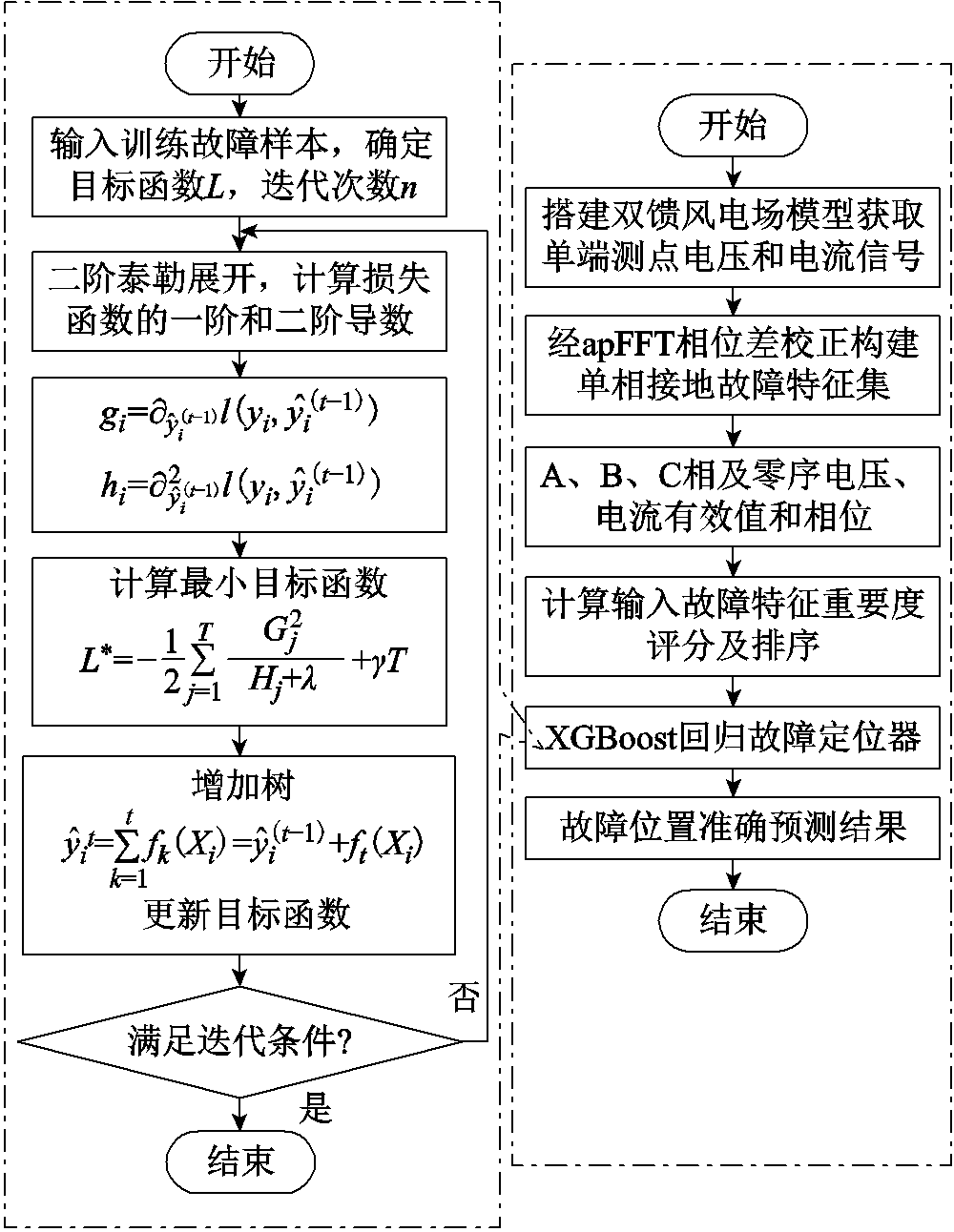
图3 风电场故障测距算法流程
Fig.3 Fault location flow of wind farm
步骤如下:
1)数据预处理。读取双馈风电场集电线路单端测点数据,应用Matlab R2 015b环境下apFFT频谱校正法构建表1中的16个原始特征。
2)故障特征重要度分析。应用Python3.7环境下人工智能技术XGBoost算法计算输入特征重要度评分及排序。
3)最优回归模型构建。将故障样本输入到XGBoost定位器中训练,并使用测试样本对故障距离进行评估。
为验证本文方法在风电场故障测距中的适用性,采用电磁暂态PSCAD/EMTDC软件搭建如图4所示的两条集电线路风电场模型进行故障仿真研究。
风电场统一设置在0.3s时刻发生单相接地故障,采样频率设为1 600Hz。集电线路电缆型号为YJLV23-26/35kV-3×240(2表示钢带铠装、3表示聚乙烯外护套在钢带外、额定电压26/35kV、3芯×截面积240mm2),长度为100m,架空线型号为LGJ240,且相邻风机间架空线长度为2km。风力发电机组类型为双馈异步风电机组,单机最大输出功率为2MW。风电场集电线路参数见表2。
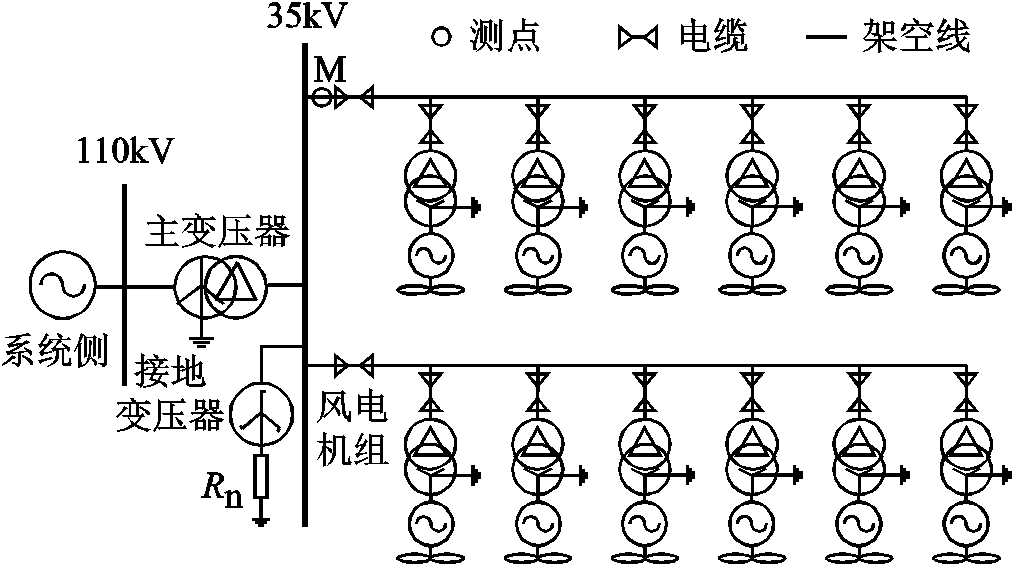
图4 风电场仿真模型
Fig.4 Wind farm simulation model
表2 风电场集电线路参数
Tab.2 The parameters of wind farm power line

集电线型号序分量电阻/(Ω/km)电抗/(Ω/km)电纳/(10-6S/km) YJLV23-26/35kV-3×240正序0.125 00.113 091.000 0 零序1.250 00.395 557.000 0 LGJ240正序0.131 00.372 04.050 6 零序0.281 01.116 02.794 6
风电场仿真分别从apFFT频谱校正的单相接地故障特征值构建,使用XGBoost算法对输入特征重要度进行分析,不同故障位置和不同过渡电阻的故障测距,XGBoost和RF集成树算法预测结果对比分析五个方面验证所提测距方法的准确性。
读取风电场单端测点M单相接地短路下的波形数据后,需借助apFFT相位差校正法计算各相电压、电流及零序分量的基波相量,进而获取原始特征集。当集电线路上距首端35kV母线2 200m处经100Ω过渡电阻发生A相接地故障时,以测点M测量的A相电压为例,采用apFFT相位差频谱校正法处理的结果如图5所示。
由图5可知,经apFFT频谱校正法分别获得A相故障电压幅值谱和相位谱后便可计算出其电压基波相量,即图5b和图5c中采样点4对应的幅值除以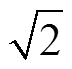 和相位,有效值为3.104 3kV,相位为240.647 3°。因此,采用apFFT频谱校正法对测点M所有数据处理后,能够有效完成故障特征集的构建。
和相位,有效值为3.104 3kV,相位为240.647 3°。因此,采用apFFT频谱校正法对测点M所有数据处理后,能够有效完成故障特征集的构建。
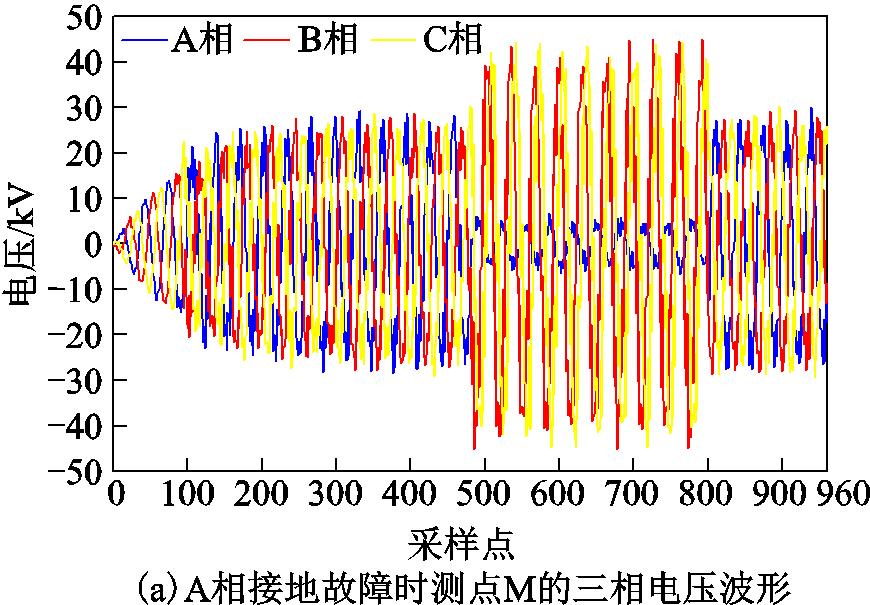
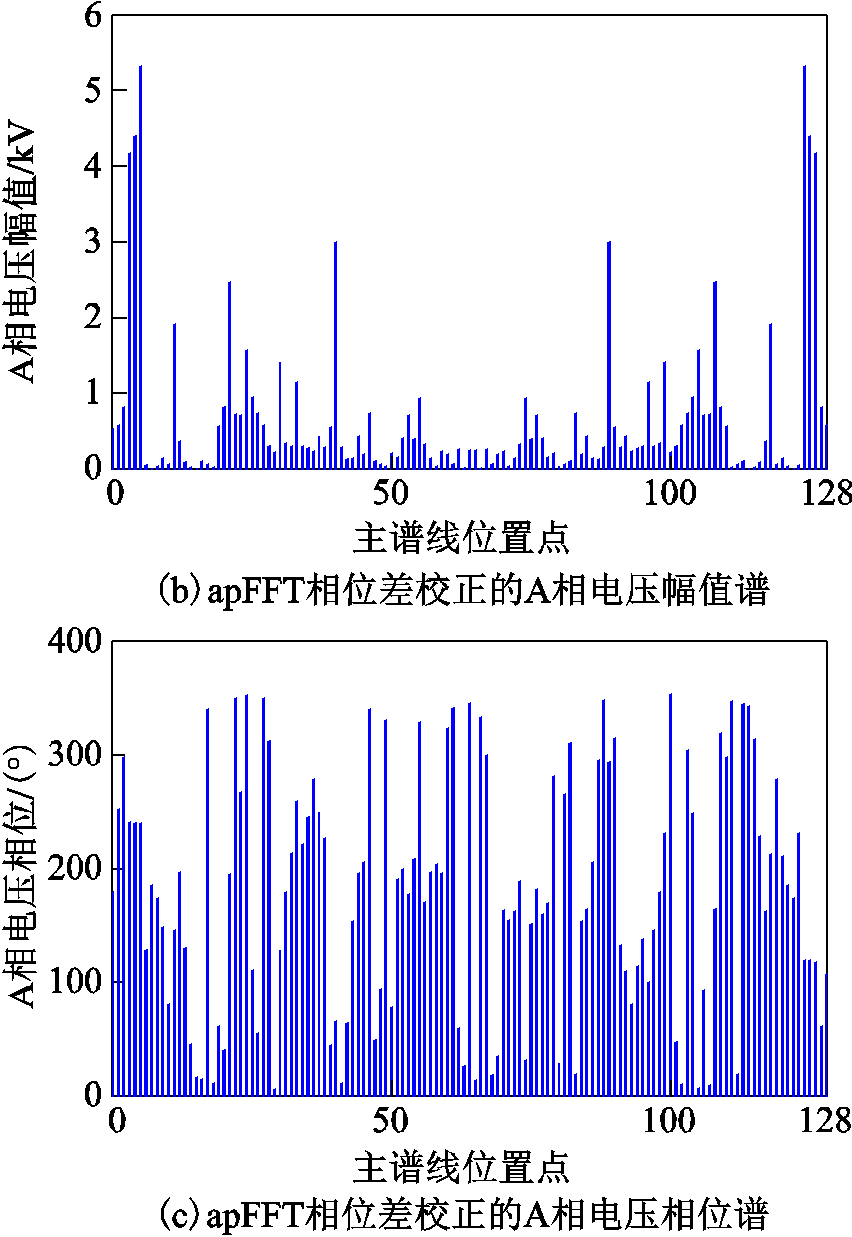
图5 在2 200m处经100Ω过渡电阻发生A相接地故障时测点M的电压仿真波形及apFFT相位差校正结果
Fig.5 Voltage simulation waveform and apFFT phase difference correction results of measuring point M when A phase-to-ground fault occurs via 100Ω at 2 200m
训练故障样本对生成XGBoost回归模型至关重要。本文沿风电场集电线路每隔200m设置一个单相接地故障点,且在每个故障点分别设置过渡电阻0Ω、30Ω、50Ω、70Ω、100Ω共5种阻值,用于训练XGBoost回归故障定位器,由此计算的输入特征重要度及排序如图6所示。特征重要度与各故障特征在模型训练过程中的利用率直接相关,表示特征分裂的总次数。特征重要度评分越高意味着该特征越重要。由图6可知,发生A相接地故障时,F1重要度评分最高,F9次之,因此,其最能体现故障信息,在回归定位中起到的作用较大,与实际相吻合。此外,F4重要度评分较低,由于3倍的零序分量是测点对应时刻的三相分量相加,对于模型来说,属于相关的冗余特征,但在模型训练中也起到一定作用,且从实际角度分析,接地故障时风机因所连箱式变压器35kV侧绕组为三角形联结,故不会注入零序电流,零序网络不受风机影响,可靠性高。综上分析,本文XGBoost回归模型考虑所有特征量建立故障定位器。

图6 故障特征重要度评分及排序
Fig.6 Fault feature importance score and sequence
为了验证本文人工智能技术XGBoost的预测定位效果,测试样本集的选择应覆盖各种故障信息,且与训练样本存在差异性。由此,在风电场集电线路上距首端升压站35kV母线测点M的距离分别为650m、2 650m、4 700m、8 650m、9 500m处设置故障点,故障类型为A相接地短路,短路过渡电阻为30Ω。采用本文方案对故障点进行定位,不同故障位置的仿真实验测距结果见表3。
表3 风电场集电线路不同故障位置测距结果
Tab.3 Fault location results under different fault locations of wind farm power line

故障位置/m过渡电阻/Ω故障预测结果/m故障预测误差/m 65030794.70144.70 2 650302 360.26-289.74 4 700304 569.08-130.92 8 650308 768.48118.48 9 500309 779.03279.03
由表3可知,无论在风电场集电线路上何处发生故障,本文方法均能够进行有效故障点定位,故障的预测值与故障的真实值接近,最大预测误差出现在2 650m处发生故障时,其故障距离预测误差值为-289.74m。因此,本文人工智能算法均能以较小的预测误差实现故障点的精确查找,可满足含多分支、混合短线路的风电场网络对故障测距准确度的要求。
电力系统实际短路故障在短路点常存在过渡电阻,一般为非金属性短路。因此,本文还需要进一步验证该方案对非金属性故障下含不同过渡电阻的测试样本集是否适用。在不同位置经不同过渡电阻发生A相接地短路故障时,本方案的仿真验证预测结果见表4。
表4 风电场集电线路不同过渡电阻测距结果
Tab.4 Fault location results under different transition resistances of wind farm power line
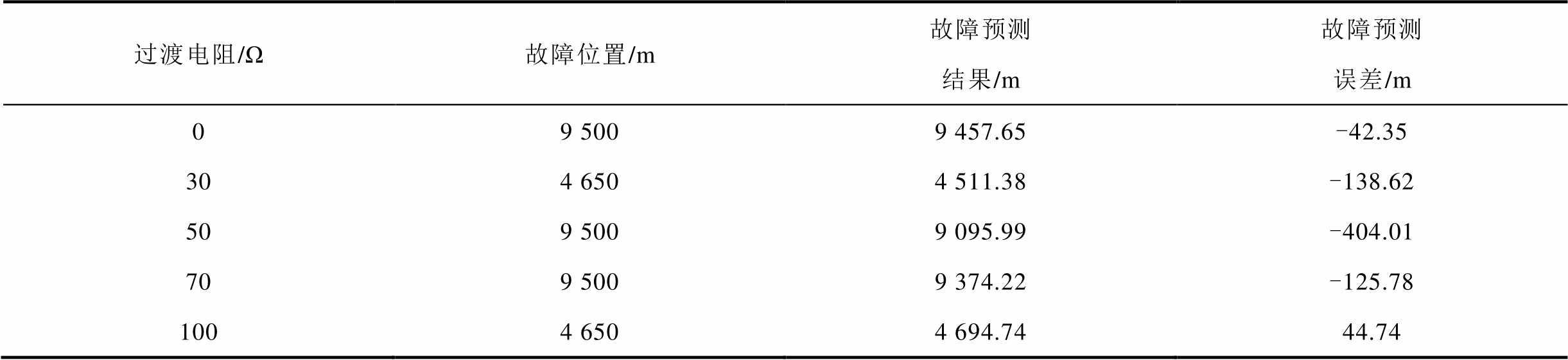
过渡电阻/Ω故障位置/m故障预测结果/m故障预测误差/m 09 5009 457.65-42.35 304 6504 511.38-138.62 509 5009 095.99-404.01 709 5009 374.22-125.78 1004 6504 694.7444.74
由表4可知,故障预测误差对于较高的过渡电阻值仍然能够保持在可接受的范围内,可有效地避免传统单端阻抗法随着过渡电阻的增加而无法正确定位及存在伪根的问题。因此,本文方案对过渡电阻的变化不敏感,通过XGBoost回归模型能完成复杂风电场网络故障点的可靠定位。
在由apFFT频谱校正法提取故障特征量相同的前提下,将基于Boosting的XGBoost与基于Bagging的RF进行比较分析,两者均为集成树算法,对测试样本的故障距离预测结果见表5。
表5 风电场集电线路不同回归算法的测距对比结果
Tab.5 Fault location comparison results under different regression algorithms of wind farm power line

故障位置/m过渡电阻/ΩXGBoost回归RF回归 预测结果/m预测误差/m预测结果/m预测误差/m 65030794.70144.701 324.35674.35 2 650302 360.26-289.742 321.63-328.37 4 700304 569.08-130.925 341.49641.49 8 650308 768.48118.488 256.24-393.76 9 500309 779.03279.039 190.94-309.06 9 50009 457.65-42.359 852.19352.19 4 650304 511.38-138.623 654.47-995.53 9 500509 095.99-404.019 108.68-391.32 9 500709 374.22-125.789 617.51117.51 4 6501004 694.7444.744 935.73285.73 平均预测误差/m171.84448.93
由表5可知,采用RF算法进行故障距离预测时,各故障的预测值与真实值之间偏差较大,且平均预测误差为448.93m;而本文XGBoost故障定位器获得的预测值与真实值较接近,平均预测误差只有171.84m。因此,XGBoost回归算法比RF回归算法具有更优的预测准确度,平均提高277.09m。此外,证明了XGBoost算法用于预测风电场集电线路故障距离的有效性。
本文针对风电场集电线路因短路故障导致的弃风窝电问题,提出一种基于apFFT频谱校正和XGBoost的单相接地故障测距思路,主要工作和结论如下:
1)读取单端测点故障后波形数据,利用apFFT相位差校正法获得相应电气基波相量,无需通信,且可有效抑制频谱泄露,具备一定的抗噪性。
2)设计了特征重要度量化分析方法,充分挖掘特征与故障距离之间的关系,同时也验证了本文特征选取的有效性。
3)建立了基于XGBoost回归的故障定位器,避免了以解析法为基础的故障测距需要求解复杂方程问题,不存在伪根,不受过渡电阻的影响,故障定位简单,且同RF算法相比预测定位精度高。
4)搭建了PSCAD/EMTDC双馈风电场仿真模型,单相接地故障实验证明了本文方法对多分支、混合短线路的适用性。
参考文献
[1] 张科, 孙立志, 朱永利, 等. 基于矢量偏离度的风电场集电线路故障定位方法[J]. 电力系统自动化, 2019, 43(10): 127-134. Zhang Ke, Sun Lizhi, Zhu Yongli, et al. Fault location method of wind farm collection line based on vector deviation degree[J]. Automation of Electric Power Systems, 2019, 43(10): 127-134.
[2] 熊列彬, 吴高华, 王志洋. 基于IHHT的多测点行波法故障测距在全并联AT牵引网中的研究[J]. 电工技术学报, 2019, 34(15): 3244-3252. Xiong Liebin, Wu Gaohua, Wang Zhiyang. Study on fault location of multi measuring points traveling wave method based on IHHT in all parallel AT traction network[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3244-3252.
[3] 徐铭铭, 肖立业, 林良真. 基于零模行波衰减特性的配电线路单相接地故障测距方法[J]. 电工技术学报, 2015, 30(14): 397-404. Xu Mingming, Xiao Liye, Lin Liangzhen. A fault location method for the single-phase-to-earth fault in distribution system based on the attenuation characteristic of zero-mode traveling wave[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 397-404.
[4] Benato R, Sessa S D, Poli M, et al. An online travelling wave fault location method for unearthed-operated high-voltage overhead line grids[J]. IEEE Transactions on Power Delivery, 2018, 33(6): 2776-2785.
[5] 邓丰, 李欣然, 曾祥君. 基于全波形信息的混联线路单端行波定位方法[J]. 电工技术学报, 2018, 33(15): 3471-3485. Deng Feng, Li Xinran, Zeng Xiangjun. Single-ended traveling-wave-based fault location algorithm for hybrid transmission line based on the full-waveform[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3471-3485.
[6] 刘顺桂, 李勋, 张宏钊, 等. 一种采用时间判别法的混合线路故障行波定位方法[J]. 电力系统保护与控制, 2017, 45(1): 41-46. Liu Shungui, Li Xun, Zhang Hongzhao, et al. A traveling wave fault location method of hybrid line using time discrimination[J]. Power System Protection and Control, 2017, 45(1): 41-46.
[7] 张艳霞, 王海东, 李婷, 等. LCC-VSC混合直流输电线路的组合型单端故障定位方法[J]. 电力系统自动化, 2019, 43(21): 187-194. Zhang Yanxia, Wang Haidong, Li Ting, et al. Combined single-end fault location method for LCC-VSC hybrid HVDC transmission line[J]. Automation of Electric Power Systems, 2019, 43(21): 187-194.
[8] 彭楠, 杨智, 梁睿, 等. 一种半波长输电线路的分布式行波测距方法[J]. 电机与控制学报, 2019, 23(8): 35-42. Peng Nan, Yang Zhi, Liang Rui, et al. Distributed traveling wave fault location scheme for half-wavelength transmission lines[J]. Electric Machines and Control, 2019, 23(8): 35-42.
[9] 刘晓琴, 王大志, 江雪晨, 等. 利用行波到达时差关系的配电网故障定位算法[J]. 中国电机工程学报, 2017, 37(14): 4109-4115. Liu Xiaoqin, Wang Dazhi, Jiang Xuechen, et al. Fault location algorithm for distribution power network based on relationship in time difference of arrival of traveling wave[J]. Proceedings of the CSEE, 2017, 37(14): 4109-4115.
[10] 于华楠, 马聪聪, 王鹤. 基于压缩感知估计行波自然频率的输电线路故障定位方法研究[J]. 电工技术学报, 2017, 32(23): 140-148. Yu Huanan, Ma Congcong, Wang He. Transmission line fault location method based on compressed sensing estimation of traveling wave natural frequencies[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 140-148.
[11] 宋国兵, 蔡新雷, 高淑萍, 等. 高压直流输电线路故障定位研究综述[J]. 电力系统保护与控制, 2012, 40(5): 133-137, 147. Song Guobing, Cai Xinlei, Gao Shuping, et al. Survey of fault location research for HVDC transmission lines[J]. Power System Protection and Control, 2012, 40(5): 133-137, 147.
[12] Jia Ke, Bi Tianshu, Ren Zhefeng, et al. High frequency impedance based fault location in distribution system with DGs[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 807-816.
[13] 马伟, 裘愉涛, 丁冬, 等. 基于阻尼最小二乘法的单相接地故障定位方案[J]. 电网技术, 2018, 42(9): 3049-3054. Ma Wei, Qiu Yutao, Ding Dong, et al. Single-phase grounding fault location scheme based on levenberg-marquarat algorithm[J]. Power System Technology, 2018, 42(9): 3049-3054.
[14] 贾科, 冯涛, 赵其娟, 等. 基于故障高频电压稀疏量测的直流配电网双极短路故障定位[J]. 电力系统自动化, 2020, 44(1): 142-151. Jia Ke, Feng Tao, Zhao Qijuan, et al. Bipolar short-circuit fault location for DC distribution network based on sparse measurement of fault high-frequency voltage[J]. Automation of Electric Power Systems, 2020, 44(1): 142-151.
[15] 李振兴, 王新, 田斌, 等. 基于沿线电压分布规律的快速故障测距[J]. 电工技术学报, 2018, 33(1): 112-120. Li Zhenxing, Wang Xin, Tian Bin, et al. A fast fault location method based on distribution voltage regularities along transmission line[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 112-120.
[16] 陈旭, 朱永利, 高艳丰, 等. 基于故障分支快速辨识的T型高压输电线路故障定位新算法[J]. 电力系统自动化, 2016, 40(4): 105-110. Chen Xu, Zhu Yongli, Gao Yanfeng, et al. A new fault location algorithm for high-voltage three-terminal transmission lines based on fault branch fast identification[J]. Automation of Electric Power Systems, 2016, 40(4): 105-110.
[17] 张嫣, 林涌艺, 邵振国. 电压暂降可观约束下的定位监测点多目标优化配置[J]. 电工技术学报, 2019, 34(11): 2375-2383.Zhang Yan, Lin Yongyi, Shao Zhenguo. Multi-objective optimal allocation of monitors for voltage sag location under observability constraint[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2375-2383.
[18] 陈婷. 基于模拟退火粒子群算法的含分布式电源配电网故障定位[J]. 电气技术, 2019, 20(8): 59-63. Chen Ting. Fault location of distribution network with distributed power supply based on simulated annealing particle swarm optimization[J]. Electrical Engineering, 2019, 20(8): 59-63.
[19] 刘文轩, 严凤, 田霖, 等. 基于LVQ神经网络的配电网故障定位方法[J]. 电力系统保护与控制, 2012, 40(5): 90-95. Liu Wenxuan, Yan Feng, Tian Lin, et al. LVQ neural network approach for fault location of distribution network[J]. Power System Protection and Control, 2012, 40(5): 90-95.
[20] 王秋杰, 金涛, 谭洪, 等. 基于分层模型和智能校验算法的配电网故障定位技术[J]. 电工技术学报, 2018, 33(22): 5327-5337. Wang Qiujie, Jin Tao, Tan Hong, et al. The technology on fault location of distribution network based on hierarchical model and intelligent checking algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(22): 5327-5337.
[21] Peng Nan, Cheng Menghan, Liang Rui, et al. Asynchronous fault location scheme for half-wavelength transmission lines based on propagation characteristics of voltage travelling waves[J]. IET Generation, Transmission & Distribution, 2019, 13(4): 502-510.
[22] 徐瑞东, 陈昊, 胡义华, 等. 基于高斯过程的光伏阵列故障定位[J]. 电工技术学报, 2013, 28(6): 249-256. Xu Ruidong, Chen Hao, Hu Yihua, et al. Fault location of photovoltaic array based on gaussian process[J]. Transactions of China Electrotechnical Society, 2013, 28(6): 249-256.
[23] Farshad M, Sadeh J. Accurate single-phase fault-location method for transmission lines based on k-nearest neighbor algorithm using one-end voltage[J]. IEEE Transactions on Power Delivery, 2012, 27(4): 2360-2367.
[24] 黄翔东, 王兆华. 基于全相位频谱分析的相位差频谱校正法[J]. 电子与信息学报, 2008, 30(2): 293-297. Huang Xiangdong, Wang Zhaohua. Phase difference correcting spectrum method based on all-phase spectrum analysis[J]. Journal of Electronics & Information Technology, 2008, 30(2): 293-297.
[25] 邱伟, 唐求, 唐璐, 等. 基于准同步序列重构的非稳态电力谐波分析[J]. 中国电机工程学报, 2018, 38(2): 456-464. Qiu Wei, Tang Qiu, Tang Lu, et al. Power system harmonic analysis under non-stationary situations based on quasi-synchronous and sequence reconstruction[J]. Proceedings of the CSEE, 2018, 38(2): 456-464.
[26] Liu Sujuan, Lyu N, Cui Jiashuai, et al. Improved blind timing skew estimation based on spectrum sparsity and ApFFT in time-interleaved ADCs[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68(1): 73-86.
[27] 王尧, 李奎, 任伯飞, 等. 基于全相位傅里叶变换的磁调制交直流漏电电流检测方法[J]. 电工技术学报, 2015, 30(18): 254-260. Wang Yao, Li Kui, Ren Bofei, et al. Study of fluxgate current detecting method for AC-DC earth leakage current based on apFFT[J]. Transactions of China Electrotechnical Society, 2015, 30(18): 254-260.
[28] 赵洪山, 闫西慧, 王桂兰, 等. 应用深度自编码网络和XGBoost的风电机组发电机故障诊断[J]. 电力系统自动化, 2019, 43(1): 81-90. Zhao Hongshan, Yan Xihui, Wang Guilan, et al. Fault diagnosis of wind turbine generator based on deep autoencoder network and XGBoost[J]. Automation of Electric Power Systems, 2019, 43(1): 81-90.
Single Phase Grounding Fault Location for Power Lines of Wind Farm Based on apFFT Spectrum Correction and XGBoost Algorithm
Abstract Aiming at the problem relating to electricity transmission stopping and wind power abandonment caused by any short circuit in a power line of a wind farm, a single phase grounding fault location method based on all phase fast fourier transform (apFFT) spectrum correction and extreme gradient boosting (XGBoost) for the measured signals of the faulted line is proposed. During the research, the simulation models of doubly fed generators with multi branch hybrid power lines in a wind farm is firstly constructed, and the fundamental phasors of relating voltages and currents during a fault period are obtained by apFFT spectrum correction method to build an original feature set. Then the regression model on single terminal fault location is established by an algorithm called as XGBoost, and the model contains the feature importance and sorting of the fault and can be used to discover the relationship between the features and the fault distance. Finally the fault location can be estimated using the model based on the current input pattern. The experimental results by PSCAD/EMTDC show that the proposed method has distinct advantages in the fault location of a short overhead/cable hybrid line with multi-branches in a wind farm. Its fault location performance is better than random forest (RF) algorithm, and not affected by fault location and grounding resistance. It can meet the fault location accuracy requirement of a wind farm.
keywords:Wind farm power line, all-phase fast Fourier transform (apFFT) spectrum correction, extreme gradient boosting (XGBoost), single phase grounding fault, single terminal fault location, feature importance
中图分类号:TM77
DOI:10.19595/j.cnki.1000-6753.tces.191584
国家自然科学基金资助项目(51677072)。
收稿日期 2019-11-21
改稿日期 2020-02-06
彭 华 男,1989年生,博士研究生,研究方向为风电场集电线路故障定位。E-mail:penghua890415@126.com
朱永利 男,1963年生,教授,博士生导师,研究方向为电力设备状态监测和分析、电力系统分析与控制、电力系统网络化监控和智能信息处理。E-mail:yonglipw@163.com(通信作者)
(编辑 赫蕾)