图1 基于PMU的配电网网络接线
Fig.1 Connection Diagram of Distribution Network Based on PMU
摘要 分布式电源大量接入、网络拓扑结构和运行方式复杂多变，使得有源配电网故障诊断与定位面临新的挑战。同步相量测量单元（PMU）在配电网中的应用为故障处理提供了新的信息支撑。该文首先利用开关变位和PMU实时通信状态等信息，提出一种基于邻接子阵法的同步测量区段实时更新方案，可考虑配电网拓扑结构变化和PMU通信中断等场景；进而利用三相电压/电流同步相量数据，提出基于时空特征矩阵Frobenius范数的自适应短路故障区段定位算法；最后利用PSCAD软件搭建含分布式电源的IEEE 34节点系统，仿真验证所提出算法有效性。
关键词：智能配电网 同步相量测量 网络拓扑 区段定位 短路故障
配电网在接纳可再生能源、保障电网安全高效运行中发挥着重要作用[1]。配电网发生短路故障时，迅速、准确地进行故障区段定位是隔离故障区段并恢复非故障区域供电的前提[2-3]。随着分布式电源（Distributed Generator, DG）大规模接入，逆变器型DG因控制器限流环节使得DG侧短路电流容量变小，故障电流幅值变化不明显，传统利用电流幅值为特征量的方法难以准确定位短路故障[4]。
目前，含DG配电网短路故障区段定位方法从原理上主要分为矩阵法[5-9]、人工智能算法[10-12]和特征量比较法[13]等。其中，矩阵法容错能力较弱，易发生误判、漏判，且不能考虑配电网拓扑变化问题；基于人工智能的区段定位方法虽然容错性较好，但普遍存在模型构建相对复杂、模型不完善、定位效率低等问题；特征量比较法由于物理意义明确，具有绝对的选择性，近年来得到广泛关注。文献[13-14]提出基于故障电流幅值特征的充分式保护方案。文献[15]分析了短路故障时区段两端电流相位差变化情况，提出使用正序电流相位突变量的方向进行定位。文献[16]利用两端克拉克电流的相位差进行区段定位。文献[17]进一步考虑了线路电容的影响并提出自适应整定判据。文献[18]考虑逆变类DG特性，提出一种基于正序分量的电流差动保护方案。文献[19]提出一种基于扩展卡尔曼滤波算法的MMC换流器故障诊断策略，通过评判系统内部状态变量的观测量与其实际反馈量收敛情况来确定系统是否处于故障状态。由于配电网分支线众多，当量测装置不完全配置或区段内含有负荷时，上述算法仍存在以下问题：①对DG接入水平有一定限制，多考虑DG渗透率25%以内的场景，无法满足DG高渗透率接入[20]下的故障定位需求；②未考虑区段内负荷投切及DG时变性等扰动的影响，无法区分负荷电流变化与故障电流的区别。
基于广域同步相量数据为解决上述问题提供新的信息支撑。目前基于数据采集与监视控制（Supervisory Control and Data Acquisition, SCADA）系统的故障诊断仅能利用非同步的电压/电流幅值特征，而高精度同步相量测量单元（Phasor Measurement Units, PMU）可以实现同步相量信息的快速提取和实时传输，在配电网中得到越来越多的关注[21-22]。PMU将各测点电压/电流的幅值、相位等信息传入主站，利用全局同步电压/电流相量，对电网运行特征进行实时监测、分析，为DG高渗透率下的故障特征辨识和故障区段定位提供了新的思路[23]。
实时、准确地获取网络拓扑是配电网故障区段定位的前提。传统配电网通常根据分段开关将馈线分段，应用PMU后，同步测量区段则以PMU为划分的依据。由于配电网开关操作频繁、拓扑结构多变及普遍存在T接线，故障定位算法对区段信息的实时更新提出更高要求；PMU装置的通信异常也将导致同步量测区段发生变化，进而影响量测量使用。因此，需实时更新同步测量区段的划分方式。
结合PMU在有源配电网中的应用，本文提出考虑实时网络拓扑和馈线负荷波动的短路故障区段定位方法，适用于配电网DG高渗透率下的短路故障检测和区段定位。首先，利用配电自动化系统的开关变位信息、PMU通信状态等生成配电网动态全局拓扑边集矩阵，并基于Dijkstra算法和邻接子阵法识别并实时更新多端同步量测区段；然后，考虑负荷对短路电流的影响，利用同步相量信息构造时空特征矩阵，通过比较各同步量测区段特征矩阵的Frobenius范数确定故障区段；最后通过仿真验证算法的有效性。
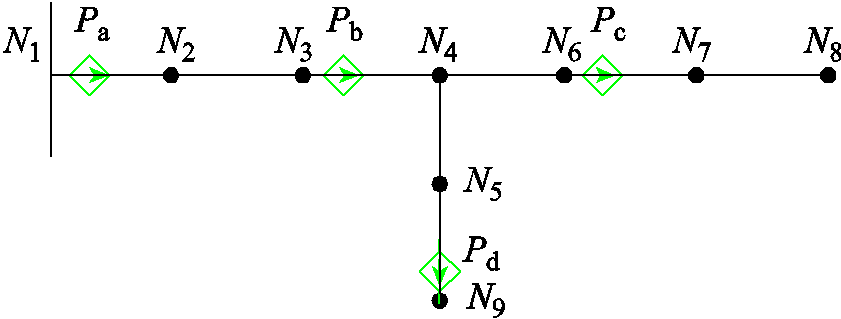
利用配电自动化系统的拓扑信息和开关变位信息，并结合PMU配置和通信状态，可为故障诊断提供网络拓扑结构和同步测量区段信息。以图1含PMU的配电网网络接线为例，对同步测量区段辨识过程进行详细说明。
图1 基于PMU的配电网网络接线
Fig.1 Connection Diagram of Distribution Network Based on PMU
图1中N1~N9为配电网节点，其中N3、N6、N9为开关节点；Pa~Pd为PMU测点。为提高拓扑辨识效率，网络拓扑和PMU安装位置均使用以节点表示的边集表达：网络基础边集矩阵中各支路以节点[Nx, Ny]表示，维数为p×2，其中p为支路数；PMU边集矩阵储存PMU所处支路的信息，由于PMU均安装于各支路之间，则任意PMU装置Pi的安装位置以2阶矩阵[Nx, Pi; Pi, Ny]表示，矩阵维数为2q×2，其中q为PMU个数。实时开关状态矩阵储存当前断开状态下的开关节点编号，维数为r×1，其中r为当前处于断开状态下的开关节点个数。
由图1导出网络拓扑信息的过程如图2所示。由于同步测量区段以PMU为划分依据，获取的网络基础边集矩阵应与PMU边集矩阵整合为考虑PMU的静态全局拓扑边集矩阵。此外，PMU边集矩阵的加入会造成冗余环路，故采用深度优先搜索算法遍历全网拓扑，删除冗余连接关系（如图实线区域标注）。分析实时开关状态矩阵，假设开关节点N6断开，则将全局拓扑矩阵中含有N6节点及受N6节点影响无法与主网连通的连接关系置0（如图中虚线区域标注），其他连接关系置1。删除标志位为0的连接关系，则可得到配电网动态全局拓扑边集矩阵。
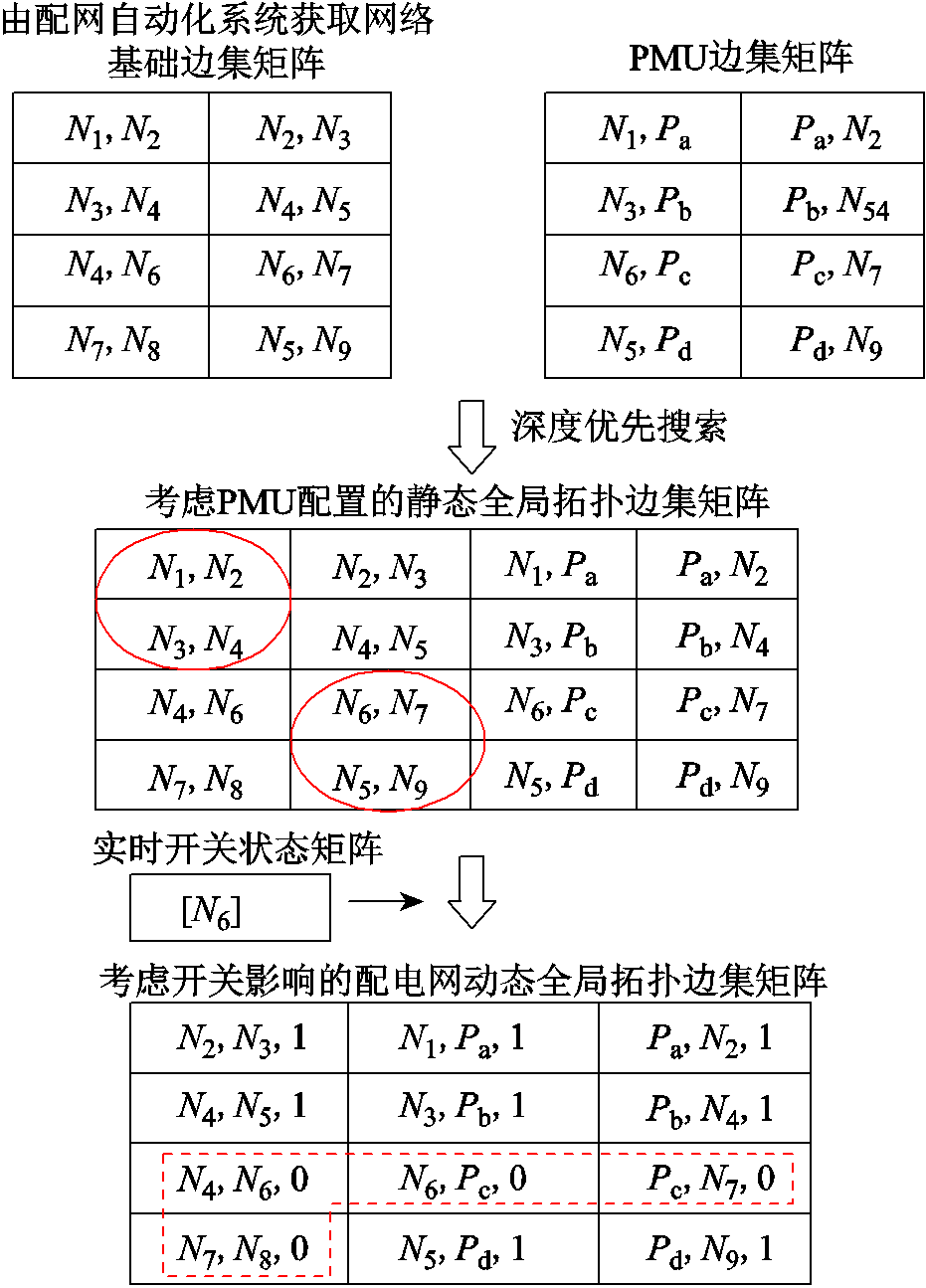
图2 考虑开关影响的拓扑矩阵生成流程
Fig.2 Flow chart of topology matrix generation considering switching effect
利用所形成的配电网动态全局拓扑边集矩阵构造两端同步量测区段矩阵。图1中4个PMU经排列组合可得任意两个PMU之间含有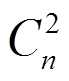
即6种组合方式，n为处于通信状态中的PMU个数。由图1中Pa和Pc位置关系可知，非相邻PMU不能作为两段区段形式使用。Dijkstra算法作为解决单源最短路径的经典方法[24]，可以对任意两PMU的最短路径进行遍历，进而删除非相邻PMU的区段，得出图1中两端区段配置矩阵为[Pa, Pb; Pb, Pc; Pb, Pd; Pc, Pd]。
各PMU作为独立节点，它们之间的连接关系可以通过0-1邻接矩阵直观表示。将两端区段配置矩阵转变为0-1邻接矩阵，且将矩阵对角线全部置1，则多端区段的邻接子阵必为三角阵结构。假设当前运算节点为Pb（位置如图1所示），遍历邻接矩阵中Pb所在行，可得与Pb生成两端区段的为Pa、Pc、Pd，即3个PMU。提取上述PMU编号所对应的邻接子阵Aa~d，若为N+1维三角矩阵且非零元素全为1，则确定上述PMU为N+1端区段形式。若不满足三角矩阵结构，则将剩余PMU进行两两组合并与Pb组合成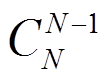
种N端区段假设，分别验证各假设构造的邻接子阵是否为三角矩阵结构，若符合要求，则输出此N端区段形式，同时将当前运算节点Pb与剩余PMU组成两端区段形式。迭代上述过程，直到所有相连PMU均与Pb组成区段。若所有邻接子阵均不为三角矩阵，则输出
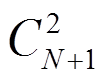个两端区段形式。具体步骤如图3所示，最终可得三端区段[Pb, Pc, Pd]与两端区段[Pa, Pb]。此外，基于Dijkstra算法对各末端节点到主网接入点需经过的最近PMU路径，可得单端区段[Pc]。
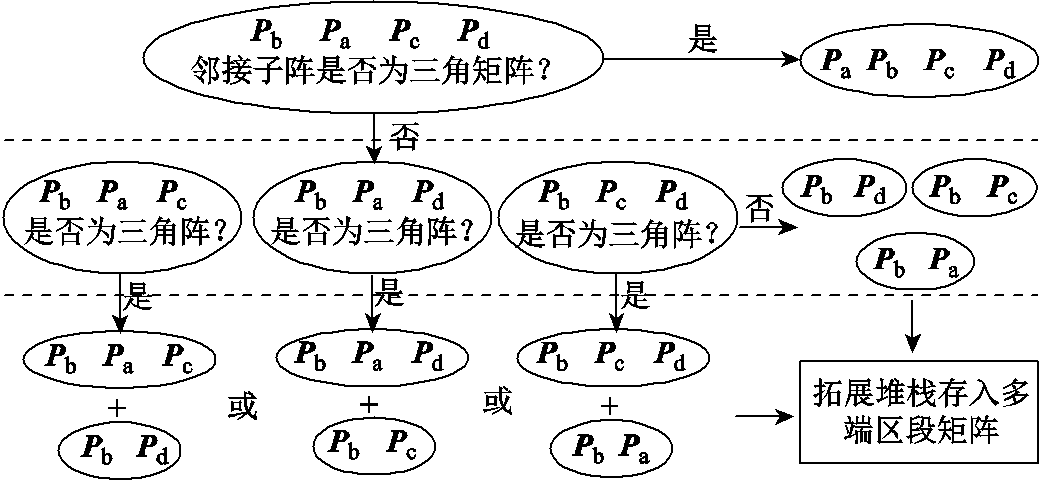
图3 邻接子阵法示例
Fig.3 Example of method based on constructing sub matrices of adjacency matrix
最后，由于多数故障诊断算法要求获取区段各端点的上、下游情况，因此基于Dijkstra算法计算各PMU到主网接入点（定义为初始节点）的最短路径长度，将距离初始节点最短的PMU编号放置于该区段第一位，以保证所生成区段可以表征上、下游顺序。在形成的PMU多端区段信息中加入区段类型和区段编号，若区段信息中最大端口数为k，区段数量为m，则最终形成m×(k+2)的多端区段配置矩阵。图1中配电网所形成的多端区段配置矩阵为
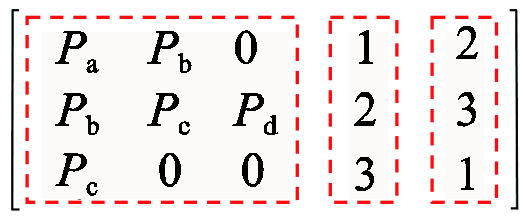（1）式（1）中，第一个矩形区域储存多端区段的端点，第二个矩形区域储存各区段的编号，第三个矩形区域储存各区段类型信息。多端区段配置矩阵可供故障定位等功能模块进行调用，并随配电网动态全局拓扑边集矩阵更新而实时更新。此外，当PMU装置损坏或由于通信异常等导致数据丢失时，也会发生PMU装置离线的问题[25]。同步测量区段以PMU为划分界点，网络中某PMU的数据丢包或通信中断后，将导致此PMU无法提供同步相量数据，进而导致同步测量区段的变化。假定图1中Pb通信异常，将Pb位置信息剔除，可得多端区段配置矩阵为
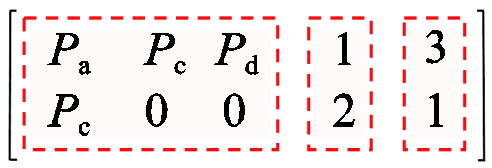（2）图4为算法的流程图。所提出区段实时更新算法以0-1邻接矩阵子阵的结构形式为基础，利用邻接矩阵表达多节点连通性，实时对网络拓扑结构及区段信息进行更新，从而保证后续故障定位算法的自适应性，并可根据上传的开关变位信息和PMU通信状态信息进行实时更新。此外，算法对于PMU配置需求较低，仅需保证馈线含有一定数量的PMU以完成配电网分段即可。实际应用中，PMU一般可以安装在含有PT、CT的开关上以节约成本，且同步测量区段辨识所需数据源和基本步骤如图5所示。
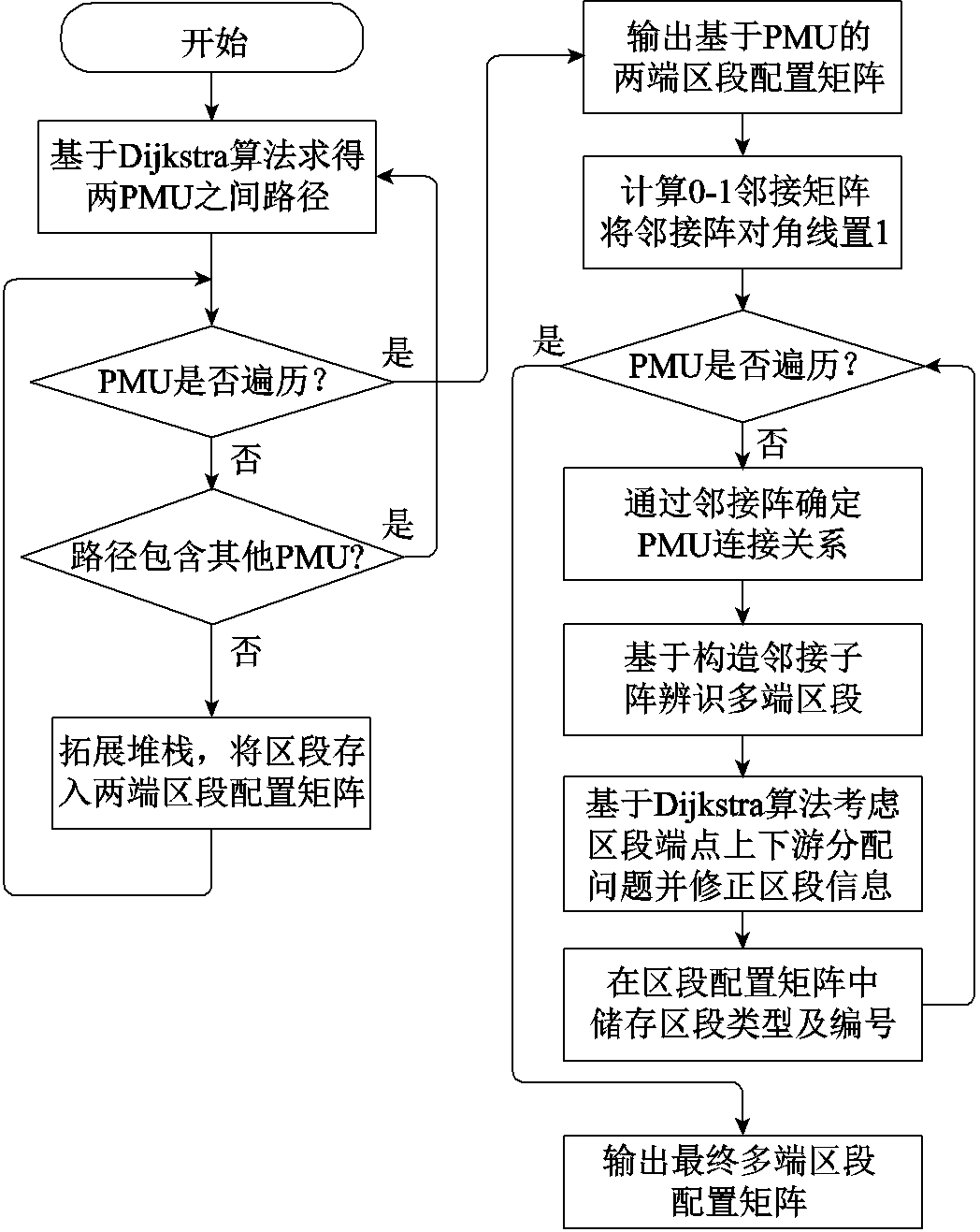
图4 区段实时更新算法流程
Fig.4 Flow chart of section real-time update algorithm
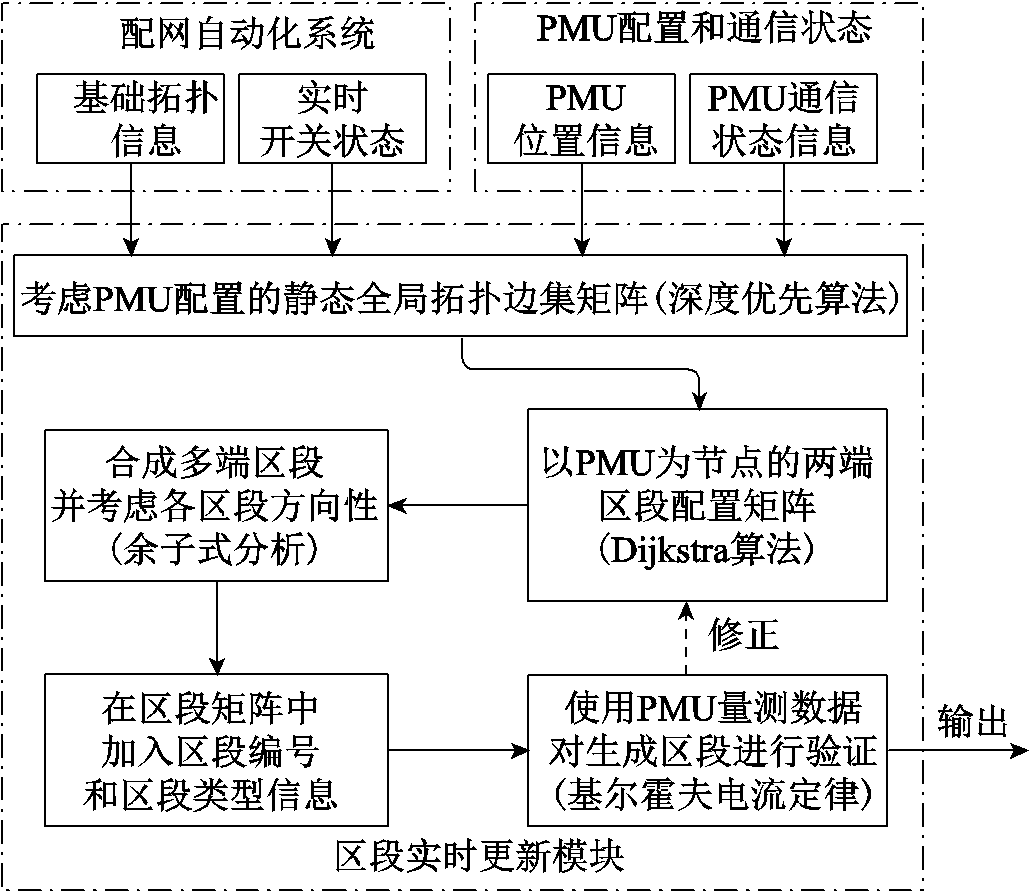
图5 同步测量区段实时辨识基本步骤
Fig.5 Schematic diagram of real-time synchronous measurement section
假设PMU将配电网分为多个多端区段，DG并网点处均装置PMU，部分区段内含有负荷或无源分支线。定义PMU量测量方向为由主网接入点指向末端负荷方向。由于配电网中T接线较多，所分区段可分为二端及多端区段。如图6所示，在区段ABC中，节点处含有多条负荷出线或无源分支线。
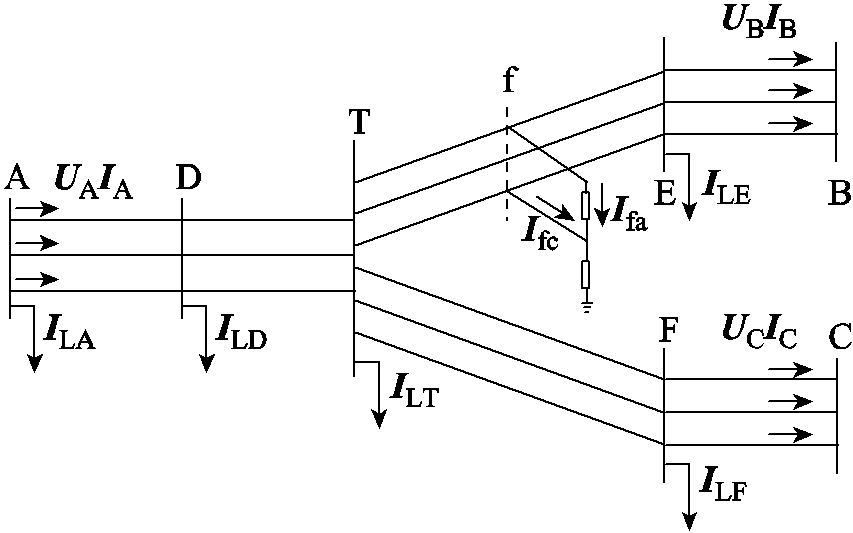
图6 含有负荷和无源分支线的三端区段图
Fig.6 Three-end section diagram with load and branch line
正常运行时，因区段主馈线各处电压相量近似一致，可通过简化处理近似计算区段内负荷的等值阻抗为
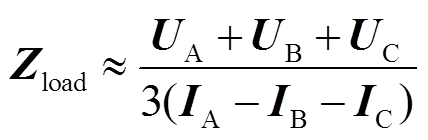（3）式中，UA、UB、UC、IA、IB、IC为三维列向量，分别表征区段ABC三端相电压、相电流矢量；Zload为等效阻抗，可表征正常情况下区段内各相负荷水平。同时，利用三端电压、电流矢量近似求得各相负荷电流Iload为
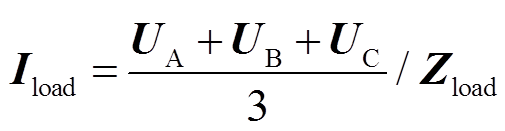（4）当正常运行或发生区外故障时，区段内旁路电流主要为负荷电流，区段ABC内相电流矢量关系为
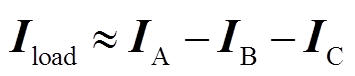（5）当区段内部发生短路故障时（如图6所示f点发生两相接地故障），区段内的旁路电流由负荷电流和故障分量电流共同组成，可得区段相电流矢量应满足
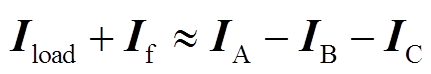（6）综上可知，使用故障电流分量、负荷电流分量与区段端点各相电流进行矢量运算，可以明确分辨故障和非故障区段，且短路故障过渡电阻阻值越小，故障电流越大，判断结果越精确。
设PMU将配电网划分为m个多端区段，其中区段i为n端区段，区段某一端点j的同步三相电压和三相电流矢量分别为Uij和Iij，即
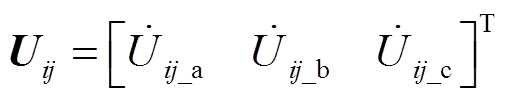（7）
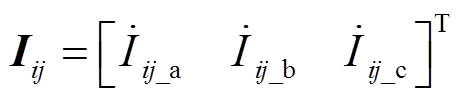（8）故障发生后，调取故障前区段i各端的同步电流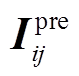数据
和电压数据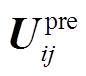
，求得多端区段i内各相负荷情况Zload_i。为避免区段内不含负荷时造成算法求解困难，实际运算时求解Zload_i的倒数，即
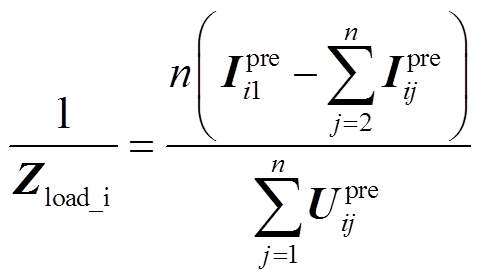（9）利用故障后区段两端同步电压数据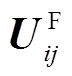
和故障前负荷情况Zload_i，以
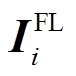近似估算故障发生时多端区段i内部负荷的电流水平，为
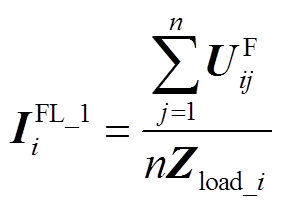（10）上述算法基于恒阻抗负荷模型进行计算。基于恒功率负荷模型的计算结果为
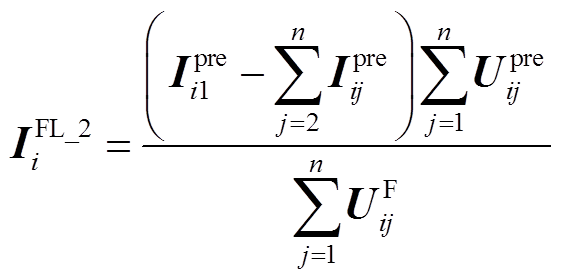（11）综合负荷模型按40%恒功率和60%恒阻抗计算，则可知上述故障发生时区内负荷电流水平为
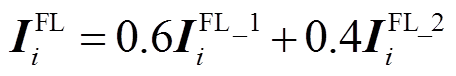（12）同时，设配电网内主网和DG电源共k个，依据安装在主网和DG接入点处的PMU同步量测数据，可以得出故障时配电网内多电源所提供的综合短路电流ΔIF为
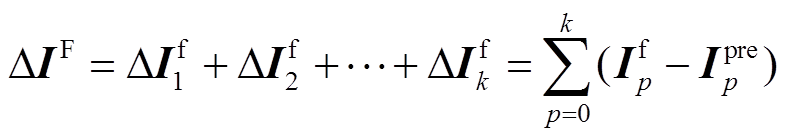（13）式中，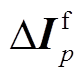
为电源p对短路电流的贡献值；
、
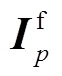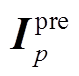分别为故障前、后电源p提供的电流矢量。
分别假设故障发生在每一个区段，通过各区段多端同步电流矢量Iij、故障时负荷电流水平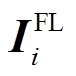、多电源共同提供的短路电流
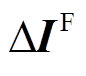计算各区段故障时电流矢量特征量
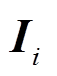为
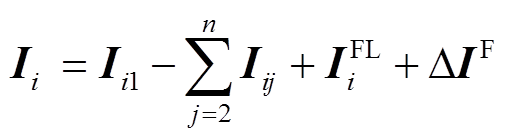（14）构造智能配电网电流时空特征矩阵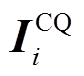
，在一个时间段内统计故障特征量。
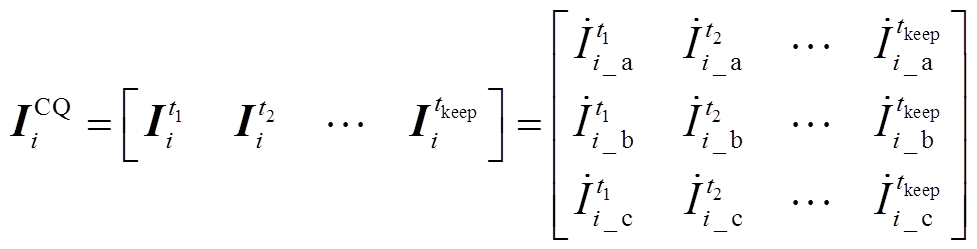（15）式中，tkeep为获取特征量需要电网正常运行态的时间，一般为几个周波。电流时空特征矩阵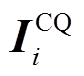的行矢量表征不同测点的各相电流，列矢量表征所获取的不同时序电气量。
此外，若为单端量测区段，则将区段末端节点定义为电流矢量为0、电压矢量与该区段PMU节点一致的虚拟节点，按照两端区段进行计算。
计算各区段电流时空特征矩阵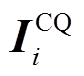，并分别求解其Frobenius范数（F-范数）为
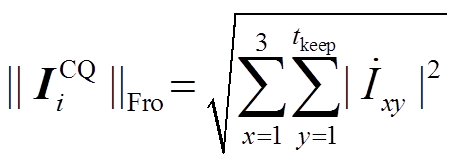（16）最小范数值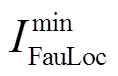
对应的区段即为故障区段为
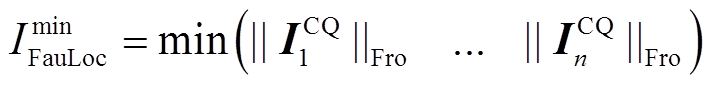（17）上述判据在适应过渡电阻的灵敏性和算法本身精确性之间存在矛盾。启动判据的阈值设置得越低，算法可以检测到过渡电阻越大的短路故障，但受DG、电动汽车等扰动影响，易发生误判。为兼顾定位算法的可靠性和准确性，增加一步验证环节。将故障时配电网内多电源共同提供的短路电流ΔIF按时空特征矩阵形式整合为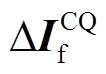
并求解其F-范数
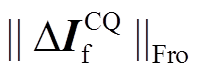为
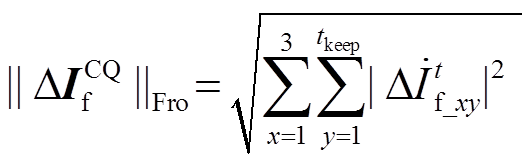（18）设置验证判据为
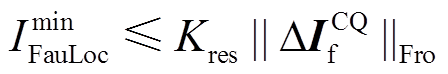（19）式中，Kres为可靠性系数。将所得故障区段F-范数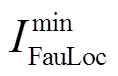与短路电流范数进行比较。理论上，若发生短路故障，基于基尔霍夫电流定律，故障区段各端电流矢量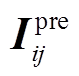、负荷电流Zload_i以及短路电流ΔIF的向量和为0，则有
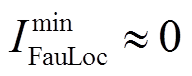，因此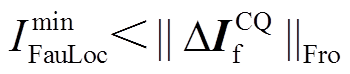
；反之，非故障状态下始终有
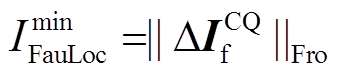。为保证判据可靠性，Kres取值一般为0.5~0.8。
算法的具体执行过程如图7所示。
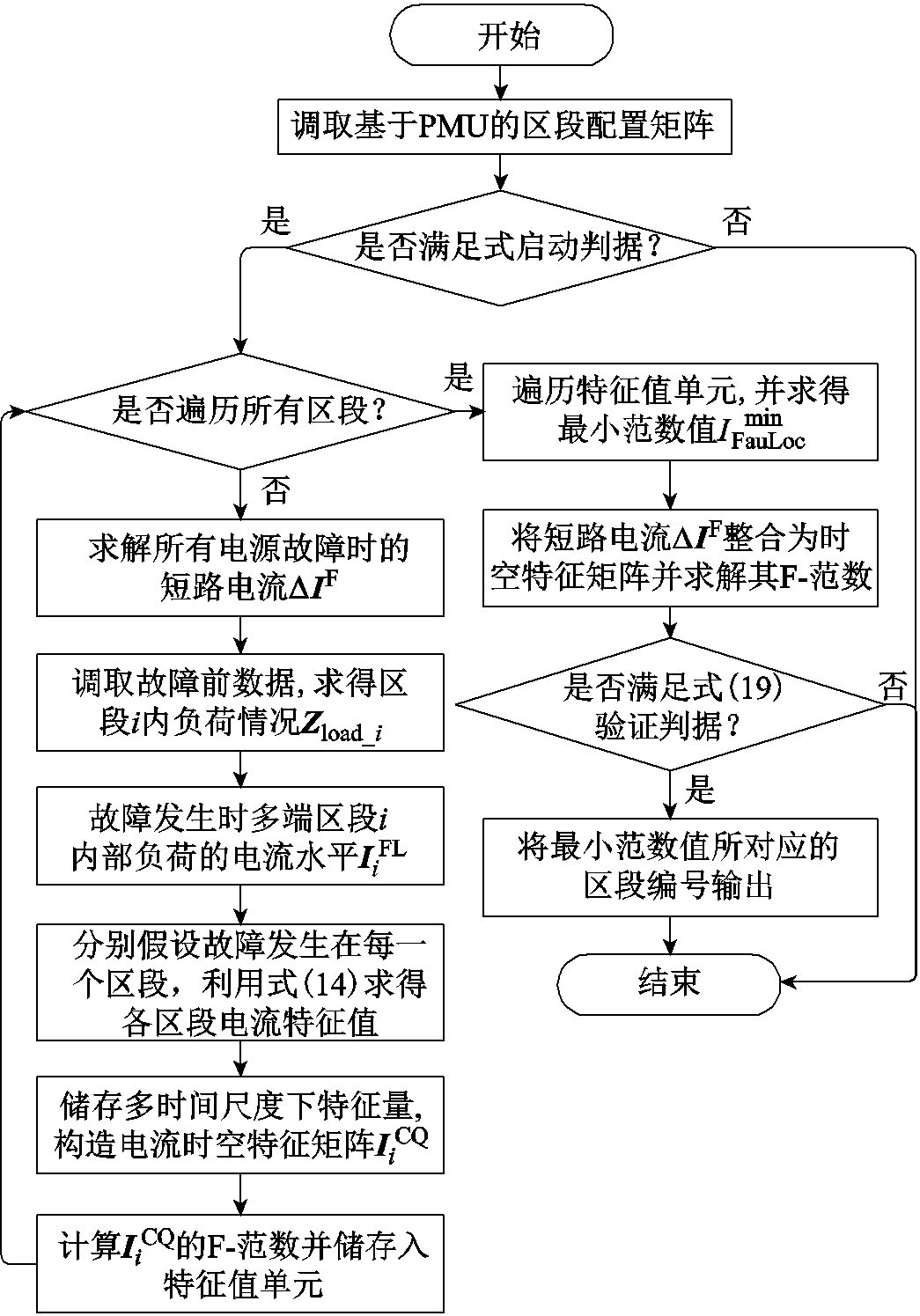
图7 故障定位算法流程
Fig.7 Flow chart of fault location algorithm
算法采用电流幅值突变量/零序电压/负序电压的逻辑或作为启动判据特征值。其中，零序/负序电压阈值均为0.1~0.15倍的额定相电压，且考虑DG接入影响，电流幅值突变量阈值设为1.5~2倍的额定电流。首先获取基于PMU的区段配置矩阵，并判断当前是否满足启动判据。若满足启动判据，则通过由式（13）计算得到的短路电流ΔIF、由式（10）~式（12）计算得到的区段内部负荷电流水平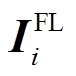及区段各端口量测数据，计算各区段故障时电流矢量特征量Ii，构造电流时空特征矩阵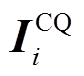并求解其F-范数
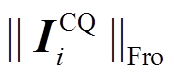。若已遍历全部区段，则找出最小范数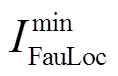，将短路电流ΔIF按时空特征矩阵形式整合为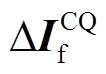并求解其F-范数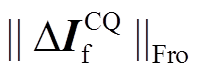，判断是否满足式（19）的验证判据。若是，则以最小范数对应的区段编号为故障区段输出；否则，认为当前没有发生短路故障。
ZIP模型可以较好地模拟各区段的负荷情况，但仍有可能造成一定的负荷电流估算误差。考虑极端情况，即区段内负荷为单一恒功率负荷时，负荷电流误差最大为
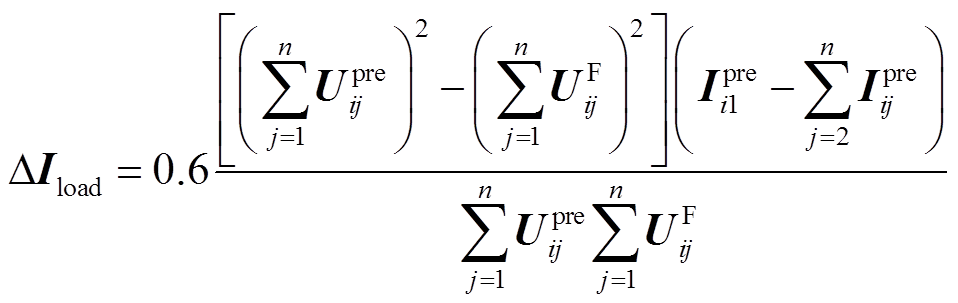（20）式中，ΔIload为区段内全为恒功率负荷时ZIP模型的误差。假设故障后各相平均电压降低为故障前的α倍，即
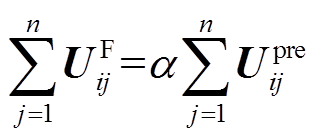（21）则可将式（6）化简为
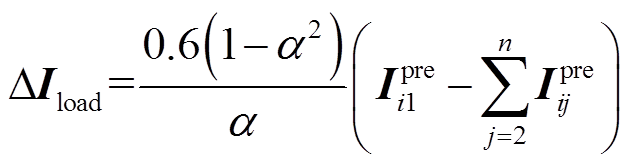（22）由式（22）易知，ZIP模型的误差ΔIload随α单调递减，ΔIload在负荷保持恒功率特性的最小电压值（0.8倍的额定电压）处取得误差最大值，ΔIload最大为0.27倍的稳态负荷电流，远小于故障电流，误差可忽略不计。
综上所述，短路故障区段定位算法在各电源处取故障时电流突变量并估算短路电流ΔIF，方法不受DG时变性影响，并可适用于任意DG渗透率下的配电网短路故障定位。如配电网中第i测点处DG出力为0时，其对短路电流的贡献值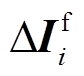
也为0，故不会影响算法的准确性。此外，本文所使用的特征量为相电流的相位、幅值及其突变量，参数和负荷三相不平衡现象对算法影响较小。
为验证本文所提出的方法，在PSCAD软件中搭建如图8所示IEEE 34节点系统模型，并加入5个DG，网络节点标号取值为800~890；PMU标号取值为1~14，并以PMU划分同步量测区段。负荷模型为综合负荷模型，按40%恒功率、60%恒阻抗的进行配置；额定负荷总量为2.49MW，负荷波动取±10%。DG1为双馈风机，额定出力0.2MW；DG2为直驱风机，额定出力0.2MW；DG3、DG4和DG5均为光伏发电电压，额定出力均为0.45MW。额定状态下DG渗透率为70.3%。仿真过程中风速和光照设置为随机模式，以模拟实际运行中DG出力时变性特征。
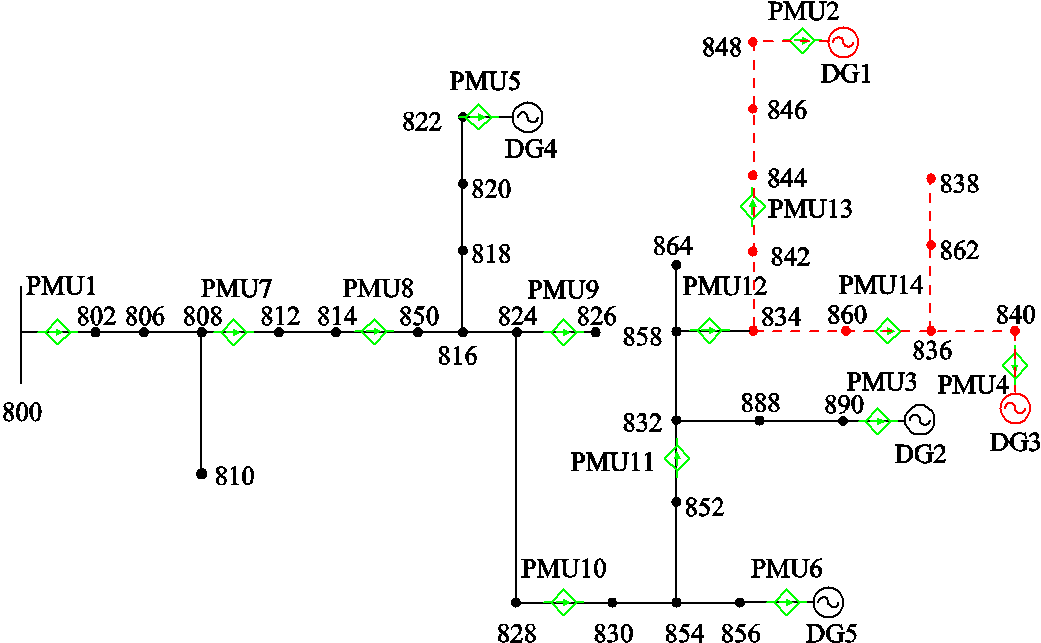
图8 智能配电网典型仿真模型拓扑
Fig.8 Topology diagram of typical simulation model for intelligent distribution network
基于邻接子阵法，区段信息实时更新为
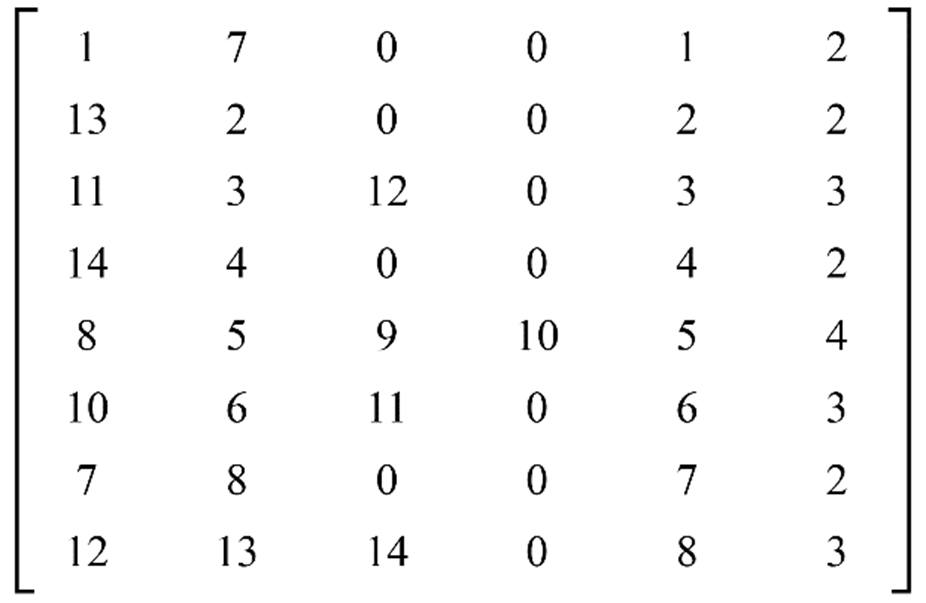
仿真验证所提出方法对开关变位及PMU通信异常情况下的性能。假定如图8所示834节点处联络开关未变位，但PMU13通信中断，则同步测量区段实时更新算法模块进行运算，将区段信息实时更新为
通过在PMU通信状态改变情况下对同步测量区段的实时更新，保证了故障定位算法对相量数据的正确使用，避免因PMU通信影响而造成故障误判、漏判。
假设在运行过程中834节点处联络开关断开，此时由配电网自动化系统提供的实时开关状态矩阵将由空矩阵变为[834]，则同步测量区段实时更新算法将图8中834节点及右侧所连接网络移除，同步测量区段更新为
分别于联络开关状态改变前后在854节点处设置短路故障，故障类型为AB相接地故障，过渡电阻为10W，故障持续时间0.6s。设Kres为0.75，则联络开关状态改变前后，各区段电流时空特征矩阵所计算的F-范数如图9所示。
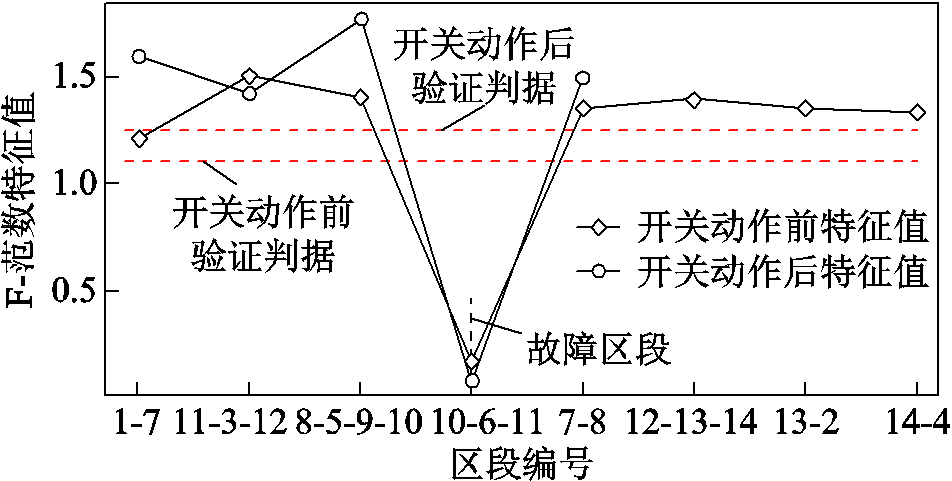
图9 开关变位前后算法的表现情况
Fig.9 Performance of algorithm before and after switching action
由图9可知，834节点处联络开关变位后，区段实时更新算法可以根据实时开关状态矩阵的变化进行区段更新。此外，开关断开前后在同一点处设置短路故障，故障区段的区段电流时空特征矩阵F-范数较非故障区段具有明显的差异性。
仿真验证所提出算法对不同DG渗透率的适应性。如图8所示，分别在节点806（第1~11组）、812（第12~22组）、824（第23~33组）、854（第34~44组）、858（第45~55组）、834（第56~66组）、840（第67~77组）和846（第78~88组）八处故障点设置过渡电阻为20Ω的三相短路接地故障，按照DG渗透率为0%,10%,
,100%分别对八处故障点各仿真11次，分析不同DG渗透率、不同位置故障场景下的算法性能。由于所提出算法取最小值作为故障区段特征值，为凸显曲线效果，取各区段F-范数特征值的倒数进行对比分析（图10所示），x-y坐标系投影如图11所示。由图易知，所提出算法不受DG渗透率影响，在各区段故障时均能生成明确的故障判据结果，实现对故障区段的精确判断。
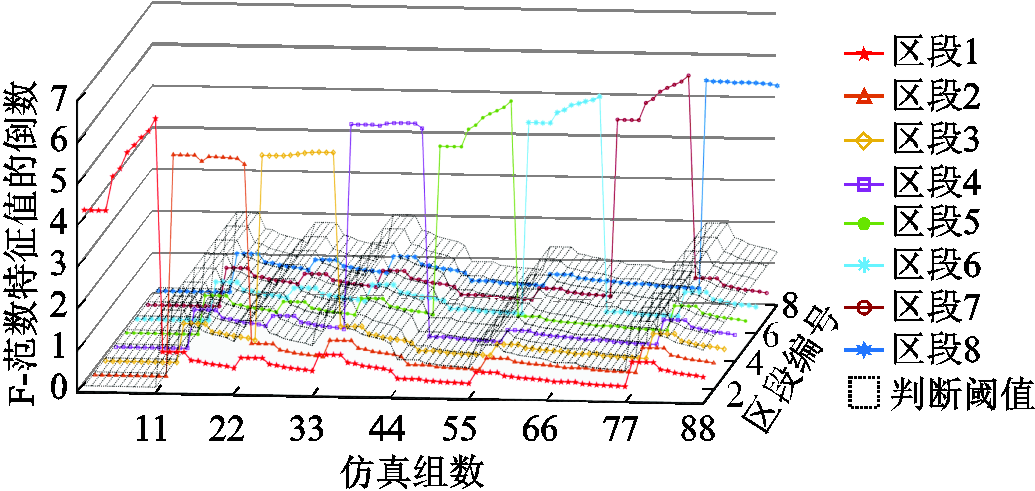
图10 不同DG渗透率下算法的表现情况
Fig.10 Performance of the algorithm under different DG permeability
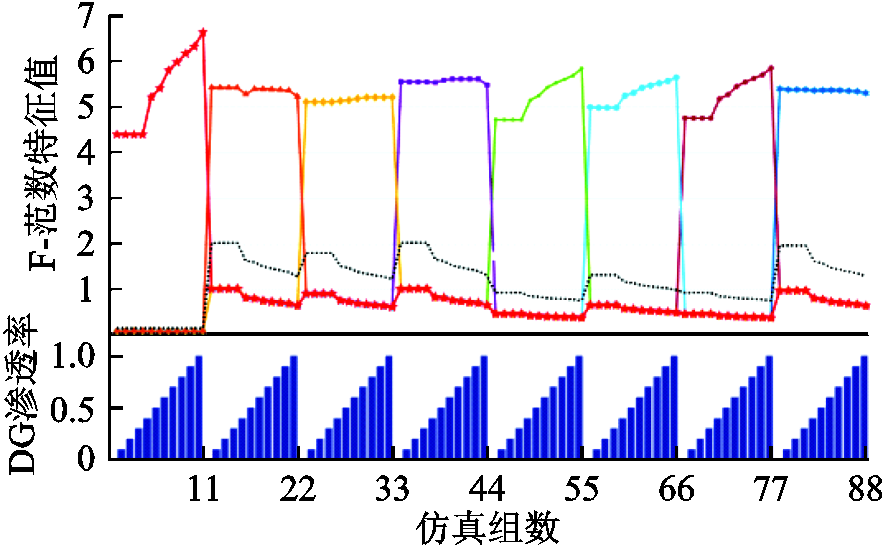
图11 不同DG渗透率下算法的表现情况(x-y坐标系)
Fig.11 Performance of the algorithm under different DG permeability(the x-y coordinate system)
仿真验证所提出算法对不同过渡电阻阻值的适应性。选择四端区段8-5-9-10中的816节点设置两相短路接地故障，过渡电阻范围为0~1 500Ω，仿真结果见表1。由表1数据可知，所提算法依托PMU提供的同步量测相量数据，可以对故障发生后各区段的电流关系进行更加精确的矢量运算，从而保证算法在高阻状态下仍然能够精确地定位故障区段。
表1 不同过渡电阻条件下的仿真验证结果
Tab.1 Validation results of results of different transition resistances
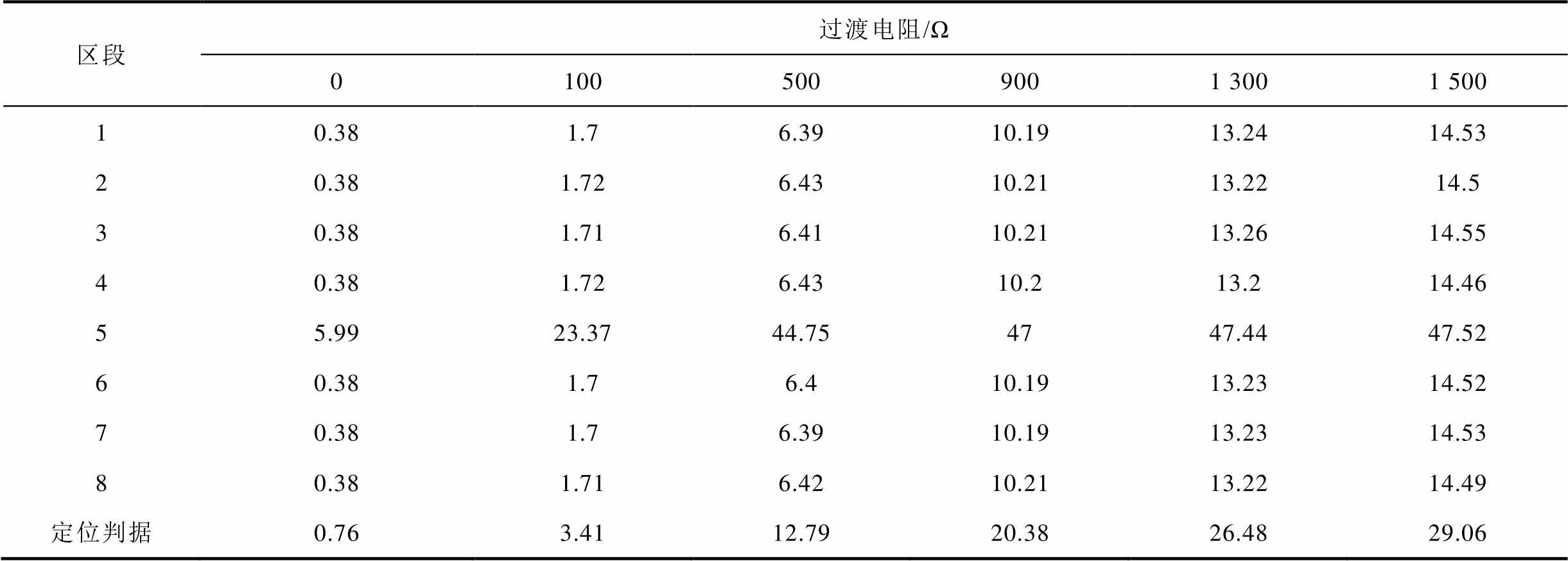
区段过渡电阻/Ω 01005009001 3001 500 10.381.76.3910.1913.2414.53 20.381.726.4310.2113.2214.5 30.381.716.4110.2113.2614.55 40.381.726.4310.213.214.46 55.9923.3744.754747.4447.52 60.381.76.410.1913.2314.52 70.381.76.3910.1913.2314.53 80.381.716.4210.2113.2214.49 定位判据0.763.4112.7920.3826.4829.06
传统差动保护对于保护区段内无负荷情况时具有较高的灵敏性和可靠性，但由于配电网中负荷分布较广、开关动作频繁，为兼顾经济性和可靠性指标，差动保护无法保证区段内无负荷分布。当图8所示配电网中双馈风机DG1处自然条件为每0.5s改变风速，且风速在6~15m/s随机取值时，区段13-2处电流相位差与差动保护判据阈值结果如图12所示。
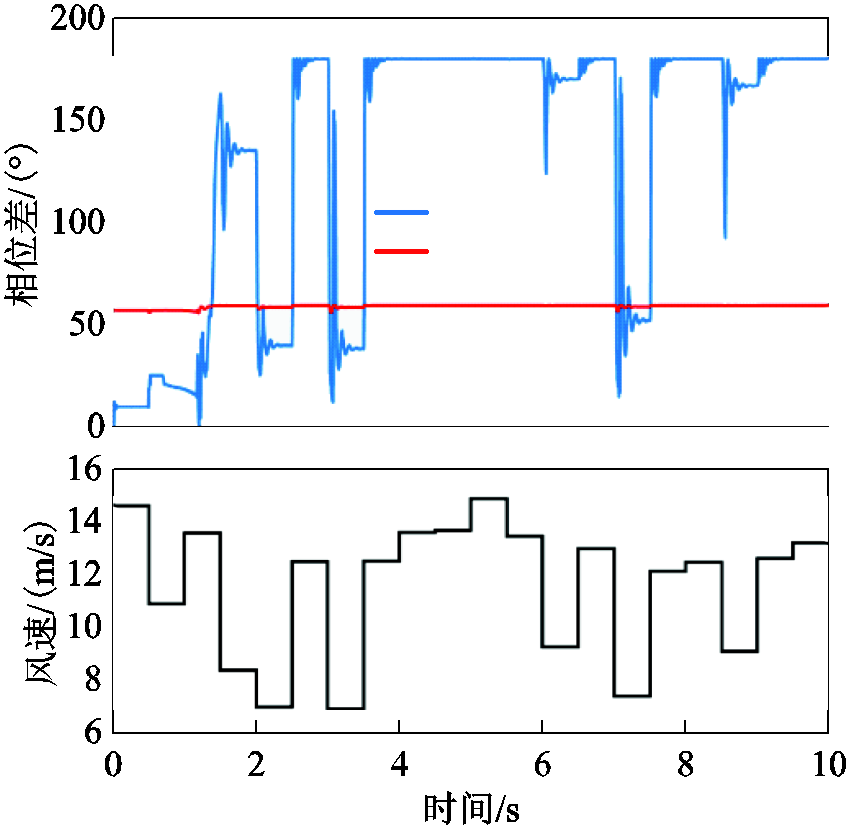
图12 风速随机波动对差动算法的影响
Fig.12 Influence of wind speed random fluctuation on differential protection
如图12仿真情况所示，系统稳定运行时差动保护易受DG波动影响而发生误判。当区段中含有负荷及无源分支线时，智能配电网作为多电源系统，必然会出现一个或多个两端向其供电的负荷节点，此时该区段稳定运行时相位差大于90°，且随着DG出力的时变性及负荷的波动性，这类区段在整个系统中移动，极易造成各类算法误判情况的发生。本文所提算法对PMU配置要求低，经济性较好，利用三相电流相量运算并考虑了负荷分流的影响，在DG出力变化时可以保证特征值无相应波动，有效地避免了算法误判的情况。
利用有源配电网故障诊断模块开发与自动测试平台[26]仿真验证算法在不同故障场景下的性能。该平台基于Python和PSCAD接口工具实现故障场景的批量仿真，实现故障数据获取、诊断模块测试和标准化报告生成的自动化测试过程。利用图8所示配电网，改变配点网中性点接地方式、短路故障类型、过渡电阻阻值及DG渗透率，共获取仿真数据780组，验证短路故障区段定位方法的正确性，具体结果见表2。
表2 短路故障批量仿真验证结果
Tab.2 Validation results of batch simulation for short-circuit faults
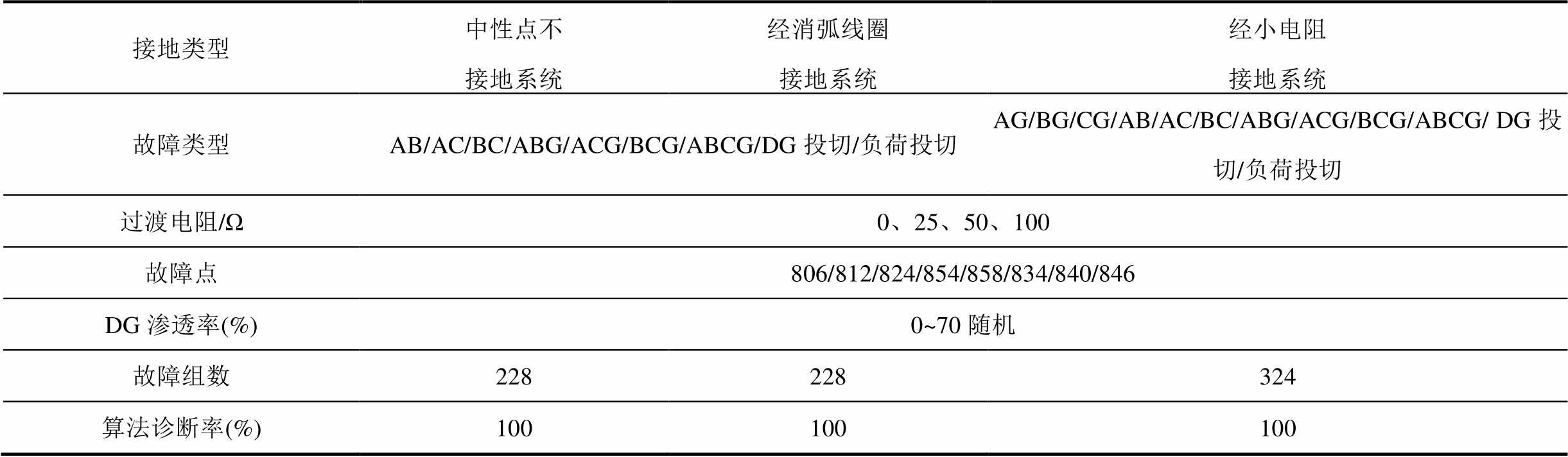
接地类型中性点不接地系统经消弧线圈接地系统经小电阻接地系统 故障类型AB/AC/BC/ABG/ACG/BCG/ABCG/DG投切/负荷投切AG/BG/CG/AB/AC/BC/ABG/ACG/BCG/ABCG/ DG投切/负荷投切 过渡电阻/Ω0、25、50、100 故障点806/812/824/854/858/834/840/846 DG渗透率(%)0~70随机 故障组数228228324 算法诊断率(%)100100100
由表2可知，测试平台从接地方式、过渡电阻等多角度模拟了配电网的各类运行方式（DG投切及负荷投切）和故障场景。测试结果证明，本文算法适应于各类有源配电网下不同场景的短路故障检测，均可准确地定位故障区段。
结合配电网PMU技术发展与应用，提出基于邻接子阵法的同步测量区段实时更新方案和基于时空特征阵F-范数的自适应故障区段定位算法。区段实时更新算法基于Dijkstra算法和邻接子阵法对多端区段进行识别，得到实时更新的多端同步量测区段配置矩阵；短路故障定位算法考虑负荷变化场景，基于同步量测数据的相量运算构造电流时空特征矩阵，通过比较各区段电流时空特征矩阵的F-范数确定故障区段。通过典型配电网的多故障场景仿真对算法进行验证，结果表明，所提出的算法可以规避拓扑结构改变造成的区段信息改变的问题，能够自适应运行方式的变化（包括DG和负荷投切），具备较高的灵敏性和可靠性，适用于有源配电网DG高渗透率下的短路故障区段定位。
参考文献
[1] 徐丙垠, 李天友, 薛永端. 配电网继电保护与自动化[M]. 北京: 中国电力出版社, 2017.
[2] 刘鑫, 滕欢, 梁梦可, 等. 基于电流偏差2-范数的有源配电网故障距离定位[J]. 电工技术学报, 2019, 34(增刊2): 720-728. Liu Xin, Teng Huan, Liang Mengke. Fault distance location of active distribution network based on 2-norm current deviation[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 720-728.
[3] 文娟, 谭阳红, 何怡刚, 等. 含分布式电源的复杂配电网多阶段故障恢复方法[J]. 电工技术学报, 2018, 33(14): 3332-3341. Wen Juan, Tan Yanghong, He Yigang, et al. A multi-stage service restoration method for complex distribution networks with distributed generators[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3332-3341.
[4] 徐彪, 尹项根, 张哲, 等. 电网故障诊断的分阶段解析模型[J]. 电工技术学报, 2018, 33(1): 4113-4122. Xu Biao, Yin Xianggen, Zhang Zhe, et al. A staged analytical model for power system fault diagnosis[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 4113-4122.
[5] Wu Leping, Huang Chun, Qi Yong, et al. A new adaptive matrix algorithm for fault location in distribution network with distributed generation[C]//International Conference on Electrical and Control Engineering, Yichang, 2011: 499-504.
[6] 黄佳乐, 杨冠鲁. 配电网故障区间定位的改进矩阵算法[J]. 电力系统保护与控制, 2014, 42(11): 41-45. Huang Jiale, Yang Guanlu. Modified matrix algorithm for fault section location of distribution network[J]. Power System Protection and Control, 2014, 42(11): 41-45.
[7] Majidi M , Etezadi-Amoli M. A new fault location technique in smart distribution networks using sync- hronized/nonsynchronized measurements[J]. IEEE Tr- ansactions on Power Delivery, 2018, 33(3): 1358-1368.
[8] 徐彪, 尹项根, 张哲, 等. 基于拓扑图元信息融合的电网故障诊断模型[J]. 电工技术学报, 2018, 33(3): 50-60. Xu Biao, Yin Xianggen, Zhang Zhe, et al. Power grid fault diagnosis model based on information fusion of topological graph element[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 50-60.
[9] 康忠健, 田爱娜, 冯艳艳, 等. 基于零序阻抗模型故障特征的含分布式电源配电网故障区间定位方法[J]. 电工技术学报, 2016, 31(10): 214-221. Kang Zhongjian, Tian Aina, Feng Yanyan, et al. Fault section locating method based on zero sequence impedance model fault feature in distribution network with distributed generatorss[J]. Transactions of China Electrotechnical Society, 2016, 31(10): 214-221.
[10] Rafinia A, Moshtagh J. A new approach to fault location in three-phase underground distribution system using combination of wavelet analysis with ANN and FLS[J]. International Journal of Electrical Power & Energy Systems, 2014, 55(2): 261-274.
[11] 蒋海峰, 张曼, 赵斌炎, 等. 基于改进Hilbert-Huang变换的电网故障诊断[J]. 电工技术学报, 2019, 34(增刊1): 336-342. Jiang Haifeng, Zhang Man, Zhao Binyan, et al. Fault diagnosis of power grid based on improved Hilbert-Huang transform[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 336-342.
[12] 张艳霞, 尹佳鑫, 蒙高鹏, 等. 基于错误逻辑区域检测的配电网容错故障定位[J]. 电机与控制学报, 2017, 21(11): 1-8. Zhang Yanxia, Yin Jiaxin, Meng Gaopeng, et al. False-tolearnt fault location method for distribution networks based on wrong-logic region detecting[J]. Electric Machines and Control, 2017, 21(11): 1-8.
[13] 许偲轩, 陆于平, 章桢, 等. 分布式发电配电网新型充分式保护原理及方案[J]. 电网技术, 2014, 38(9): 2532-2537. Xu Sixuan, Lu Yuping, Zhang Zhen, et al. Principle and implementation of a novel sufficient criterion protection for distribution network with distributed generation[J]. Power System Technology, 2014, 38(9): 2532-2537.
[14] Li Hanlin, Lu Yuoing. A novel sufficient differential protection for distribution network with DGs based on fault synchronous information[C]//International Con- ference on Electric Utility Deregulation and Restructuring and Power Technologies, Changsha, 2016: 858-863.
[15] 司新跃, 陈青, 高湛军, 等. 基于电流相角突变量方向的有源配电网保护[J]. 电力系统自动化, 2014, 38(11): 97-103. Si Xinyue, Chen Qing, Gao Zhanjun, et al. Protection scheme for active distribution system based on directions of current phase angle variation[J]. Auto- mation of Electric Power Systems, 2014, 38(11): 97-103.
[16] 牛耕, 周龙, 裴玮, 等. 基于克拉克电流相角差值的低压有源配电网故障定位方法[J]. 中国电机工程学报, 2015, 35(增刊1): 15-24. Niu Geng，Zhou Long，Pei Wei，et al. Fault location method for low voltage active distribution network based on phase-angle differences of the clark currents[J]. Proceedings of the CSEE, 2015, 35(S1): 15-24.
[17] 牛耕, 周龙, 裴玮, 等. 低压有源配电网在线故障区间定位与识别方法[J]. 中国电机工程学报, 2017, 37(9): 2525-2538. Niu Geng, Zhou Long, Pei Wei, et al. On-line fault section location and classification technique for low voltage active distribution network[J]. Proceedings of the CSEE, 2017, 37 (9): 2525-2538.
[18] 李娟, 高厚磊, 朱国防. 考虑逆变类分布式电源特性的有源配电网反时限电流差动保护[J]. 电工技术学报, 2016, 31(17): 74-83. Li Juan, Gao Houlei, Zhu Guofang. Inverse-time current differential protection in active distribution network considering characteristics of inverter- interfaced distributed generations[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 74-83.
[19] 殷实, 谭国俊. 一种基于扩展卡尔曼滤波算法的MMC系统故障诊断策略[J]. 电工技术学报, 2016, 31(19): 74-84. Yin Shi, Tan Guojun. A novel fault diagnosis strategy of mmc system based on EKFA[J]. Transactions of China Electrotechnical Society, 2016, 31(19): 74-84.
[20] 彭克, 张聪, 徐丙垠,等. 含高密度分布式电源的配电网故障分析关键问题[J]. 电力系统自动化, 2017, 41(24): 184-192. Peng Ke, Zhang Cong, Xu Bingyin, et al. Key issues of fault analysis on distribution system with high-density distributed generations[J]. Automation of Electric Power Systems, 2017, 41(24): 184-192.
[21] Von Meier A, Stewart E, Mceachern A, et al. Precision micro-synchrophasors for distribution syst- ems: a summary of applications[J]. IEEE Transactions on Smart Grid, 2017, 8(6): 2926-2936.
[22] 张恒旭, 靳宗帅, 刘玉田. 轻型广域测量系统及其在中国的应用[J]. 电力系统自动化, 2014, 38(22): 85-90. Zhang Hengxu, Jin Zongshuai, Liu Yutian. Wide-area measurement system light and its application in china[J]. Automation of Electric Power Systems, 2014, 38(22): 85-90.
[23] Yu Wenpeng, Yao Wenxuan, Liu Yilu. Definition of system angle reference for distribution level synchronized angle measurement application[J]. IEEE Transactions on Power Systems, 2018, 34(1): 818-820.
[24] Yang Yue. An efficient implementation of shortest path algorithm based on dijkstra algorithm[J]. Journal of Wuhan Technical University of Surveying & Mapping, 1999, 3(4): 199-212.
[25] 杨博, 魏路平, 占震滨, 等. 基于概率分布的广域测量系统时延特性分析[J]. 电力系统自动化, 2015, 39(12): 38-43. Yang Bo, Wei Luping, Zhan Zhenbin, et al. Power system short-term load forecasting based on improved random forest with grey relation projection[J]. Automation of Electric Power Systems, 2015, 39(12): 38-43.
[26] Liu Jinsong, Xu Tangyun, Sun Baicong, et al. Testing platform for fault diagnosis and location algorithm in the active distribution network[C]//International Conference on Energy Internet and Energy System Integration, Beijing, 2018: 1-5.
Adaptive Section Location Method for Active Distribution Network Based on Synchronized Phasor Measurement
Abstract Due to the large number of distributed power access, complex network topology and changeable operation mode, fault diagnosis and location of active distribution network is facing new challenges. The application of phasor measurement units (PMU) in distribution network provides new information for fault diagnosis. In this paper, a real-time updating scheme of synchronous measurement section based on adjacency submatrix is proposed by using the information of the switch position and real-time communication status of PMU, which considers the change of distribution network topology and PMU communication failures. Meanwhile, based on the three-phase voltage and current synchronous phasor data, an adaptive short-circuit fault location algorithm based on the Frobenius norm of time-space characteristic matrix is proposed. Finally, the IEEE 34 node system with distributed generators is built in PSCAD, simulation result verifies the effectiveness of the proposed algorithm.
keywords：Smart distribution network, synchronous phasor measurement, network topology, section location, short circuit fault
中图分类号：TM771
DOI:10.19595/j.cnki.1000-6753.tces.191556
国家重点研究发展计划项目（2017YFB0902800, 2017YFB0902802）和国家电网有限公司科技项目（52094017003D）资助。
收稿日期2019-11-20
改稿日期 2020-03-18
邢晓东 男，1995年生，硕士研究生，研究方向为电力系统故障检测与诊断技术。E-mail：xingxd_sdu@163.com
石 访 男，1982年生，博士，副教授，研究方向为电力系统稳定分析与控制、配电网PMU技术与应用。E-mail：shifang@sdu.edu.cn（通信作者）
（编辑 赫蕾）