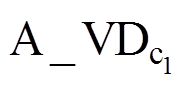 表示A桥臂第一个钳位二极管,
表示A桥臂第一个钳位二极管,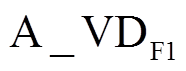 表示A桥臂第一个IGBT模块的反并联二极管,以此类推。
表示A桥臂第一个IGBT模块的反并联二极管,以此类推。摘要 为实现单相中点钳位(NPC)型H桥级联逆变器性能优化设计,分析基于脉冲跳变空间矢量脉宽调制(SVPWM)均压调制的开关损耗计算方法。针对开关管有效动作频率与控制频率不同、开关动作分散且无规律的问题,提出基于整体的开关损耗计算方法,直接计算得到所有开关的暂态损耗之和;针对均压冗余矢量动作不确定的问题,提出最值估算法对开关暂态损耗进行理论估算。仿真结果表明,推导的开关损耗解析式计算值与实际值的单个周期最大误差为9.55 %,最小误差为1.29 %,实验得到的损耗结果与理论值最大误差均在10%以内,表明该损耗解析式较为准确。
关键词:开关损耗 单相中点钳位型H桥级联逆变器 脉冲跳变空间矢量脉宽调制 有效开关频率
与传统的多电平逆变器相比,级联型多电平逆变器具有便于扩容、容错性好等优点[1-3],广泛应用于轨道交通、武器发射和新能源发电等领域[4-6]。单相中点钳位型H桥级联逆变器(Neutral Point Clamped, H-Bridge Cascaded, CHB-NPC)是一种典型的级联多电平逆变器,同时兼具NPC型逆变器耐压高、级联单元直流电源数量少等优势,在高压大功率场合具有很好的应用前景[7]。
虽然单相CHB-NPC逆变器有很多优势,但是存在直流侧电容电压不均的固有问题[8]。目前较多文献给出了各种有效的均压控制策略[9-14],但忽视了逆变器自身参数设计对电容电压不均的影响。理论上开关频率越大,电容电压不均程度越小,但同时也会导致开关损耗增大,因此开关频率存在一定的取值范围。需要同时考虑开关损耗与直流侧电容电压不均的折中最优解,建立系统性能优化模型,首先要明确开关频率与开关损耗的解析关系。
本文在文献[9-10]所提出的脉冲跳变空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)滞环均压控制的基础上展开研究,对单相CHB-NPC逆变器的开关频率与开关损耗解析关系进行分析。目前关于开关损耗的求解主要分为两类:一类是从器件物理特性出发,利用开关的物理模型对损耗进行仿真求解。文献[15]分析了器件本体参数对开关损耗的影响,但对逆变器调制策略影响开关损耗的分析不足。文献[16]基于开关器件实验测量值,建立了开关过程线性化模型,但是采用在线的方法对开关损耗进行计算,没有提出开关频率与开关损耗的解析表达式。虽然基于物理特性的损耗求解考虑了器件的本体特性,但得到的损耗模型不便于解析建模。另一类是从数学建模的角度解析计算开关损耗,文献[17]采用不连续SVPWM减小开关损耗,但对改进算法的损耗评估是通过软件仿真进行的,未对开关损耗进行定量分析。文献[18]对载波移相正弦波脉宽调制(Sinusoidal PWM, SPWM)的多电平逆变器开关损耗进行了定量分析,但其有效开关频率与载波频率为简单的正比关系。文献[19-20]对基于SPWM调制的NPC型H桥逆变器损耗的解析计算进行了详细分析,但SPWM调制算法的开关频率与控制频率相等,有效开关频率的确定比较简单。而基于脉冲跳变SVPWM的有效开关动作及次数与电压不均有关,每个基波周期选用的均压冗余矢量各不相同,不能直接采用类似的解析方法进行计算。
基于脉冲跳变SVPWM调制算法,本文求解单相CHB-NPC逆变器开关损耗解析表达式。首先,对桥臂状态电流路径进行分析,明确了逆变器各开关器件的有效动作区域,得到开关器件作用的一般规律。针对每个调制周期内均压冗余矢量随电压不均变化的问题,基于整体的分析方法提出对有效开关频率最大值和最小值进行定量分析,结合电压不均稳态特点,对开关损耗的解析表达式进行推导。最后通过仿真和实验验证了理论分析的正确性,结果表明,IGBT的开关损耗理论值与实际值的最大误差和最小误差分别为7.79%和1.90%,钳位二极管的最大误差和最小误差分别为9.55%和1.29%,理论计算结果较准确,得到的开关频率与开关损耗解析式可以作为分析均压优化的损耗模型。
单相CHB-NPC逆变器拓扑结构如图1所示。它由两个NPC型H桥CH1和CH2级联构成,直流侧由恒压源UH1和UH2供电,母线电容为C1、C2、C3、C4,对应电压分别为UC1、UC2、UC3、UC4,输出端与R、L负载相连,iL为负载电流。规定流出逆变器的方向为正方向,逆变器的4个桥臂分别定义为A、B、C、D,每个桥臂由4个IGBT功率模块和2个钳位二极管构成。图中,A_VT1表示A桥臂第一个IGBT,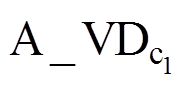 表示A桥臂第一个钳位二极管,
表示A桥臂第一个钳位二极管,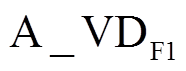 表示A桥臂第一个IGBT模块的反并联二极管,以此类推。
表示A桥臂第一个IGBT模块的反并联二极管,以此类推。
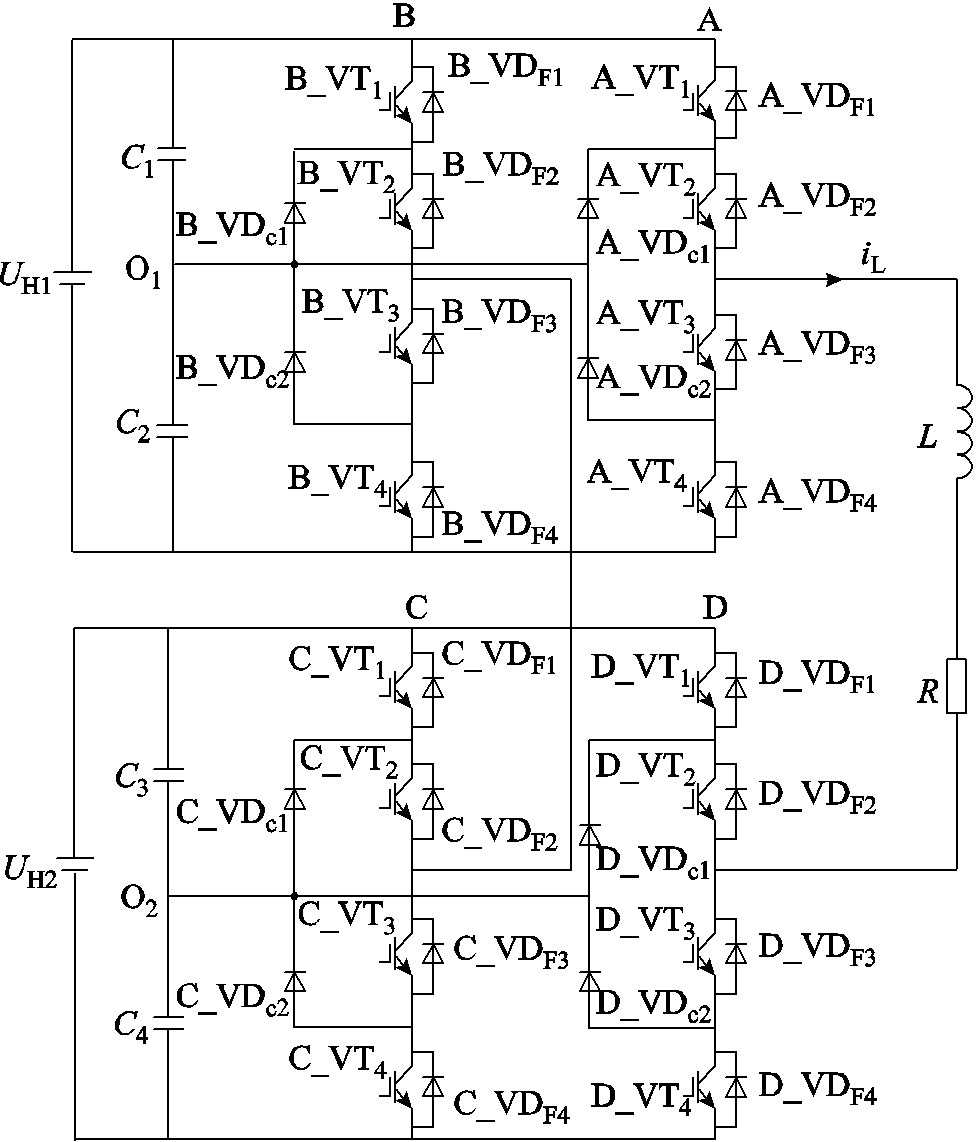
图1 单相NPC型H桥级联逆变器
Fig.1 Single-phase NPC H-bridge cascaded inverter
假设桥臂X的第i个IGBT状态SXi开通和关断分别用1和0表示,桥臂状态SX定义为
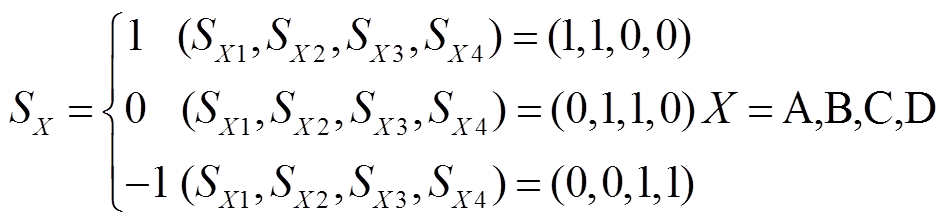 (1)
(1)文献[9-10]对脉冲跳变SVPWM进行了详细分析,根据参考矢量Ur与上一个控制周期终止矢量Vend的位置关系,将脉冲跳变类型分为三种:不跳变、单跳变和双跳变。在此基础上本文分析了该算法调制波与跳变类型的关系,设调制波的表达式为Ur = msin(ωrt),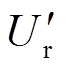 为
为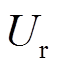 的一阶导数,Vend为上一个控制周期结束的终止矢量,调制波与跳变类型的关系如图2所示,二者之间的关系为:
的一阶导数,Vend为上一个控制周期结束的终止矢量,调制波与跳变类型的关系如图2所示,二者之间的关系为:
(1)在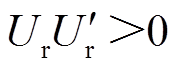 的区间内,始终有|Ur|>|Vend|,根据脉冲跳变规则,这些区间内的脉冲类型只有双跳变;在
的区间内,始终有|Ur|>|Vend|,根据脉冲跳变规则,这些区间内的脉冲类型只有双跳变;在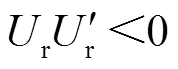 的区间内,会出现|Ur|<|Vend|的情况,因此双跳变和单跳变类型同时存在,但是在t1 ~ t2和t3 ~ t4区间,由于Ur仍然满足|Ur|>|Vend|,所以这两个区间的跳变类型为双跳变。
的区间内,会出现|Ur|<|Vend|的情况,因此双跳变和单跳变类型同时存在,但是在t1 ~ t2和t3 ~ t4区间,由于Ur仍然满足|Ur|>|Vend|,所以这两个区间的跳变类型为双跳变。
(2)当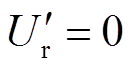 且调制比大小恰好等于基本矢量大小时,会出现不跳变类型。可以看出,在
且调制比大小恰好等于基本矢量大小时,会出现不跳变类型。可以看出,在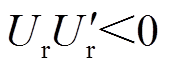 的区间内,脉冲跳变类型有单跳变和不跳变,通过将当前周期的初始矢量与上一周期的终止矢量重合,减小了开关切换次数,开关损耗更小。
的区间内,脉冲跳变类型有单跳变和不跳变,通过将当前周期的初始矢量与上一周期的终止矢量重合,减小了开关切换次数,开关损耗更小。
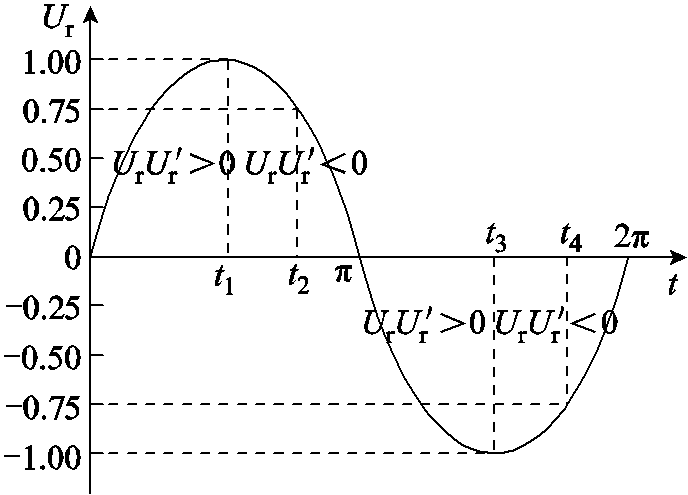
图2 调制波与跳变类型关系分析
Fig.2 Analysis of the relation between modulation wave and shift type
设电容C1=C2=C3=C4=C,合法的开关矢量对电容电压的影响见表1,表中“0”表示电容电压没有变化,“-1”表示电容电压变化量为-iLΔt/C,“1”表示电容电压变化量为iLΔt/C。
可以看到±E,±2E和±3E各有4个冗余矢量可实现电压不均调节。由于每个调制周期电容电压不均且随时间变化,而且没有周期性,所以冗余矢量的不确定性给开关损耗的直接分析计算带来困难。
表1 开关矢量与电容电压的关系
Tab.1 The relation between switching vector and capacitor voltage

作用电平作用矢量(SA,SB,SC,SD)iL>0(ΔU1, ΔU2,ΔU3, ΔU 4)iL<0(ΔU1, ΔU2,ΔU3, ΔU4) +4E(1,-1,1,-1)(-1, -1, -1, -1)(1, 1, 1, 1) +3E(1,-1,0,-1)(1,0,1,-1)(0,-1,1,-1)(1,-1,1,0)(-1,-1,0,-1)(-1,0,-1,-1)(0,-1,-1,-1)(-1,-1,-1,0)(1,1,0,1)(1,0,1,1)(0,1,1,1)(1,1,1,0) +2E(1,0,0,-1)(1,0,1,0)(0,-1,0,-1)(0,-1,1,0)(-1,0,0,-1)(-1,0,-1,0)(0,-1,0,-1)(0,-1,-1,0)(1,0,0,1)(1,0,1,0)(0,1,0,1)(0,1,1,0) +E(0,0,0,-1)(1,0,0,0)(0,-1,0,0)(0,0,1,0)(0,0,0,-1)(-1,0,0,0)(0,-1,0,0)(0,0,-1,0)(0,0,0,1)(1,0,0,0)(0,1,0,0)(0,0,1,0) 0(0,0,0,0)(0,0,0,0)(0,0,0,0) -E(-1,0,0,0)(0,0,0,1)(0,-1,0,0)(0,1,0,0)(0,1,0,0)(0,0,1,0)(0,0,0,1)(1,0,0,0)(0,-1,0,0)(0,0,-1,0)(0,0,0,-1)(-1,0,0,0) -2E(-1,0,0,1)(1,0,0,1)(-1,0,-1,0)(0,1,-1,0)(0,1,1,0)(1,0,1,0)(0,1,0,1)(1,0,0,1)(0,-1,-1,0)(-1,0,-1,0)(0,-1,0,-1)(-1,0,0,-1) -3E(-1,0,-1,1)(-1,1,0,1)(-1,1,-1,0)(0,1,-1,1)(0,1,1,1)(1,1,1,0)(1,1,0,1)(1,0,1,1)(0,-1,-1,-1)(-1,-1,-1,0)(-1,-1,0,-1)(-1,0,-1,-1) -4E(-1,1,-1,1)(1,1,1,1)(-1,-1, -1,-1)
根据开关管的开关过程,可以将开关管的损耗分为导通损耗、阻断损耗、开通损耗和关断损耗,其中开通损耗和关断损耗统称为开关暂态损耗。开关频率的变化主要影响开关暂态损耗,因此本文只分析开关暂态损耗的解析计算。
开关暂态损耗产生的条件是开关管有电压脉冲,并且有电流流过开关管,即电压和电流存在切换重叠区。文献[20]给出稳态情况下的IGBT和二极管开关暂态损耗计算公式分别为
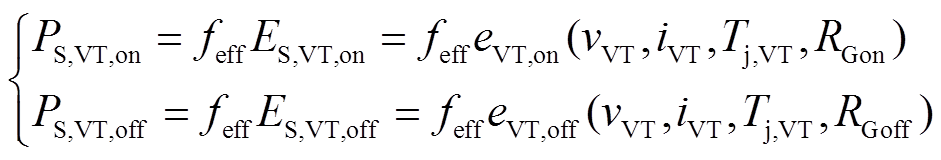 (2)
(2)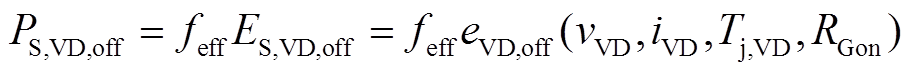 (3)
(3)式中,feff为有效开关频率;VT为IGBT,VD为二极管;on、off分别表示开通和关断,RGon与RGoff分别为IGBT的开通与关断电阻,vX和iX分别为开关管阻断电压和导通电流;ES,X为开关能量;Tj,X为工作结温。上述参数可通过查阅器件手册获取。在逆变器运行过程中,虽然有的开关管存在导通脉冲,但没有电流流过,也不会产生开关暂态损耗,因此根据开关暂态损耗产生的条件,将一个周期内能产生开关暂态损耗的开关动作称为有效开关动作,对应的频率feff为有效开关频率,求解开关损耗的关键是确定有效开关频率。
为确定有效开关频率,首先明确有效开关动作发生的区段。图3为A桥臂和B桥臂在1、0、-1三种状态下的电流导通路径。当A桥臂的电流iL>0或B桥臂的电流iL<0时,1状态导通的开关管为SVT1和SVT2,0状态导通的开关管为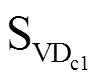 和
和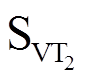 ,-1状态导通的开关管为
,-1状态导通的开关管为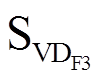 和
和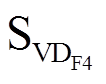 ;当A桥臂的电流iL<0或B桥臂的电流iL>0时,1状态导通的开关管为
;当A桥臂的电流iL<0或B桥臂的电流iL>0时,1状态导通的开关管为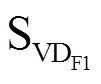 和
和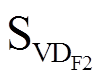 ,0状态导通的开关管为
,0状态导通的开关管为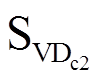 和
和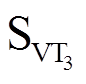 ,-1状态导通的开关管为
,-1状态导通的开关管为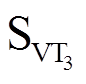 和
和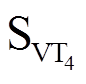 ,可以看出导通状态与电流方向、桥臂状态有关。
,可以看出导通状态与电流方向、桥臂状态有关。
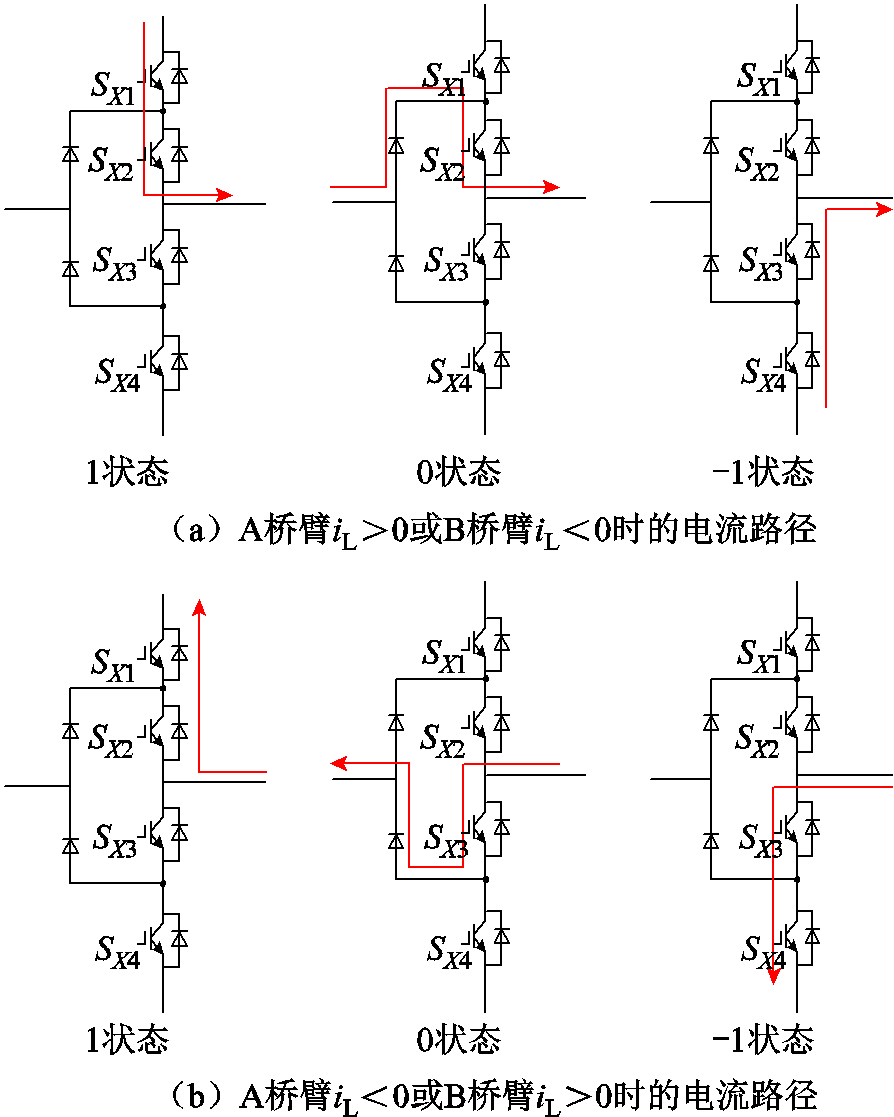
图3 单桥臂不同状态下的电流路径
Fig.3 Current path of single bridge arm under different conditions
图4为一个调制波周期内,参考矢量在矢量空间的旋转过程。以CH1为例对一个调制波周期内的开关管有效开关动作发生过程进行如下分析。
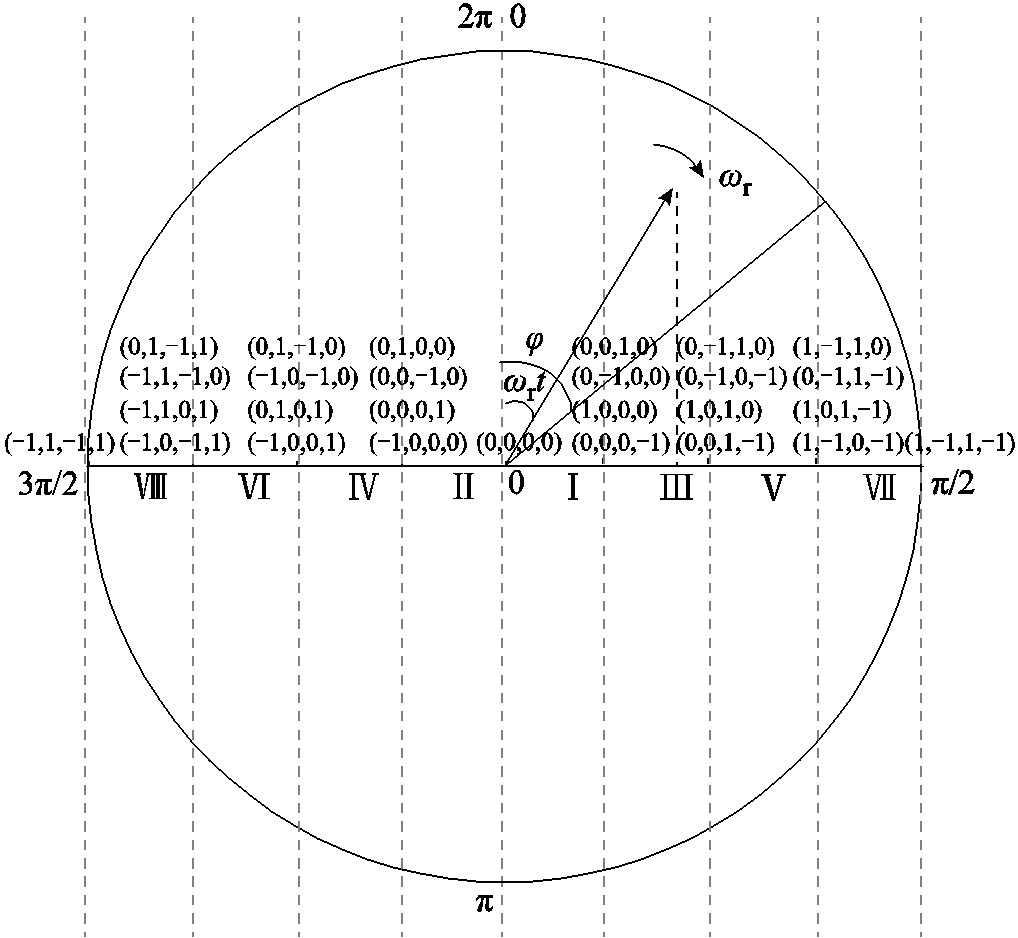
图4 一个调制波周期内参考矢量作用过程
Fig.4 The action process of reference vector in a modulation wave period
A桥臂:根据图4的参考矢量作用过程,在0~p中,A桥臂只在0状态和1状态之间切换。根据调制波与负载电流相位关系,当0<ωrt<φ时,负载电流iL<0,结合图3中的电流导通路径,分两种情况对开关管导通状态进行讨论:SA=0时,A_VT3和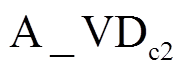 导通,SA=1时,
导通,SA=1时,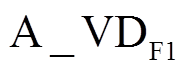 和
和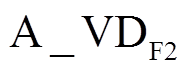 导通。当φ<ωrt<p时,负载电流iL>0,开关管导通状态为:SA=0时,A_VT2和
导通。当φ<ωrt<p时,负载电流iL>0,开关管导通状态为:SA=0时,A_VT2和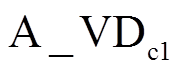 导通,SA=1时,A_VT1和A_VT2导通。当SA在0状态和1状态之间切换时,相应的开关组合会产生有效开关动作,由于同一时刻SA只存在一种状态,所以A_VT2和
导通,SA=1时,A_VT1和A_VT2导通。当SA在0状态和1状态之间切换时,相应的开关组合会产生有效开关动作,由于同一时刻SA只存在一种状态,所以A_VT2和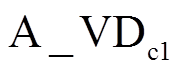 、A_VT1和A_VT2两个组合的导通时间互补,值得注意的是,在φ<ωrt<p时间段内,不论SA在0和1之间如何切换,A_VT2始终导通,因此不产生有效开关动作。
、A_VT1和A_VT2两个组合的导通时间互补,值得注意的是,在φ<ωrt<p时间段内,不论SA在0和1之间如何切换,A_VT2始终导通,因此不产生有效开关动作。
同理,对CH 1区间p ~ 2p内和CH 2区间0~2p内的有效开关动作进行分析,得到有效开关动作分布区间见表2,表中“0”代表开关管始终关断,“1”代表始终导通,0↔1代表存在有效开关动作。
通过表2可以得到有效开关动作的分布规律:
(1)一个基波周期内对于每个开关管仅在两个区间内存在有效开关动作。
(2)在(φ, p)和(p+φ, 2p)区间内,由于电流方向和调制波方向相同,使得中间管始终保持开通或关断,不产生有效开关动作。
表2 一个调制周期内有效开关动作区间分布
Tab.2 Distribution of effective switching action in a modulation wave period

桥臂开关(0, φ)(φ, p)(p, p+φ)(p+φ, 2p) A桥臂1VDF:0↔1VT:0↔100 2VDF:0↔1VT:1VT:0↔10 3VT:0↔10VDF:0↔1VT:1 400VDF:0↔1VT:0↔1 B桥臂100VDF:0↔1VT:0↔1 2VT:0↔10VDF:0↔1VT:1 3VDF:0↔1VT:1VT:0↔10 4VDF:0↔1VT:0↔100 C桥臂1VDF:0↔1VT:0↔100 2VDF:0↔1 0VT:0↔10 3VT:0↔10VDF:0↔10 400VDF:0↔1VT:0↔1 D桥臂100VDF:0↔1VT:0↔1 2VT:0↔10VDF:0↔10 3VDF:0↔1 0VT:0↔10 4VDF:0↔1VT:0↔100 A桥臂VDc10VD:0↔1VD:0↔10 VDc2VD:0↔100VD:0↔1 B桥臂VDc1VD:0↔100VD:0↔1 VDc20VD:0↔1VD:0↔10 C桥臂VDc10VD:0↔1VD:0↔10 VDc2VD:0↔100VD:0↔1 D桥臂VDc1VD:0↔100VD:0↔1 VDc20VD:0↔1VD:0↔10
(3)A桥臂和B桥臂、C桥臂和D桥臂的有效开关动作具有对称性。例如,一个调制波周期内B桥臂的1,2,3,4, VDc1, VDc2有效开关动作区间分别与A桥臂的4,3,2,1, VDc2, VDc1有效开关动作区间相同,产生这种现象的原因是同一时刻桥臂A和B的电流方向相反。
首先分析IGBT功率模块的开关损耗,根据器件手册,VDFx的单次关断损耗Eoff,VDF最大值不足IGBT单次开关损耗Esw,VT最大值的10%。而且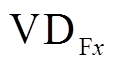 仅在续流过程中导通,关断次数与功率因数角φr有关,当φr较小时,VDFx的关断损耗远小于IGBT的开关损耗。因此本文中IGBT功率模块的开关损耗以IGBT功率单元的开关损耗为主,忽略了VDFx的开关损耗。
仅在续流过程中导通,关断次数与功率因数角φr有关,当φr较小时,VDFx的关断损耗远小于IGBT的开关损耗。因此本文中IGBT功率模块的开关损耗以IGBT功率单元的开关损耗为主,忽略了VDFx的开关损耗。
基于脉冲跳变SVPWM调制算法的有效开关动作与SPWM有效开关动作作用规律不同,作用矢量是根据直流侧电容电压不均实时确定的。每个调制波周期内电平切换时间与参考矢量有关,开关管的切换次数与均压冗余矢量的选取有关,导致有效开关动作存在不确定区。直接针对每个开关管的有效开关频率确定比较复杂,而且建立的模型是含有直流侧电容电压不均的递推表达式,很难找到直观的数学解析表达式。
为简化IGBT开关有效频率的求解过程,提出基于整体的有效开关频率确定方法,直接对整个逆变器中所有IGBT的有效开关次数进行确定。对脉冲跳变SVPWM算法而言,负载电压电平跳变的实质是开关管的切换,因此负载电压电平切换的时刻与开关管切换的时刻相对应。在电压电平跳变的时刻,级联H桥中至少有一个桥臂存在有效开关动作,可以通过负载电压电平跳变频率来确定逆变器有效开关频率。
采用的脉冲跳变SVPWM算法在选取合法矢量的过程中,已经剔除了状态越级变化的矢量,每一个桥臂的状态切换只在相邻状态之间进行。结合图3的不同电流导通路径,可以看出一个桥臂的不同状态切换只有一个IGBT动作。例如:A桥臂iL>0的情况,从1状态到0状态切换,只有SA1关断;从0状态到-1状态切换,只有SA2关断,因此每个桥臂的状态变化只能在相邻状态之间进行,而且只对应一个IGBT切换动作。
分析图4参考矢量在旋转过程中的合成矢量可知,±4E电平到±3E电平、±E电平到零电平的切换只有一个桥臂状态出现变化。±3E到±2E、±2E再到±E的电平切换由于存在均压冗余矢量,桥臂状态变化与电容电压不均有关,最多可能出现四个桥臂状态同时变化,也可能出现三个桥臂、两个桥臂和一个桥臂状态的变化情况。当±3E、±2E和±E六种电平在相邻两个电平之间切换时,会出现一个IGBT有效动作或三个IGBT有效动作,当出现电平越级跳变时会出现两个或四个IBGT有效动作。图5为调制波和电流单位化后的相位关系图,根据不同电平对应的时间长度,将一个调制周期分为14段。根据表2的分析,标明了每一个区间内可能动作的IGBT,由于负载电压电平跳变与IGBT动作时刻相对应,因此不需要确定具体是哪个IGBT动作,图中加粗部分为开关动作不确定区。
由于每个作用电平之间是等间隔的,可以根据调制波计算出各个电平的作用时间,表3给出了开关频率为fs的每个电平对应的开关周期数量,ωr为调制波角频率,m为调制比。
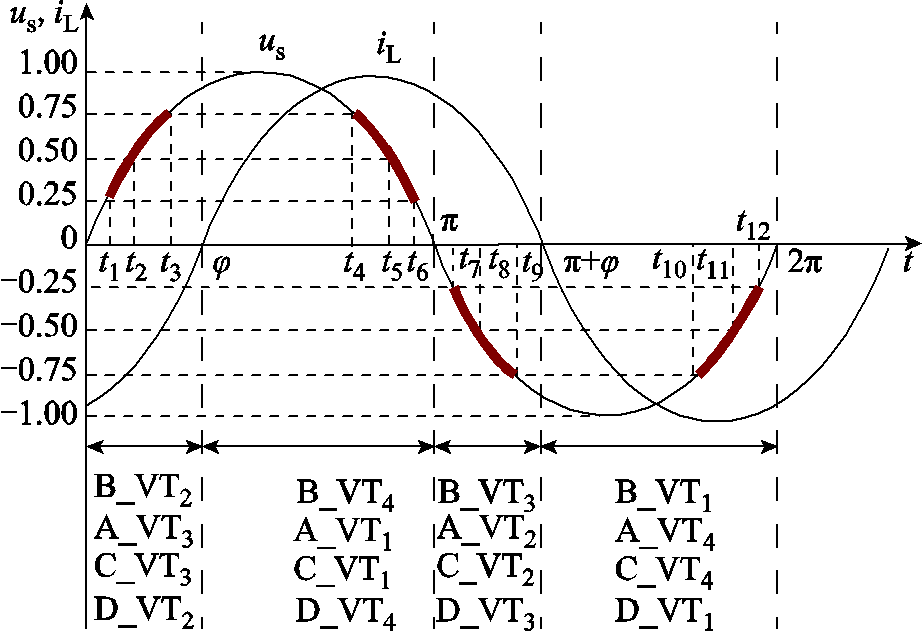
图5 一个调制波周期内IGBT动作分布
Fig.5 Distribution of IGBT action interval in a modulation wave period
表3 各电平区段内的开关周期数量
Tab.3 Number of switching cycles in each level section

分段作用电平作用时间开关周期数量 (0,t1),(t6,p),(p,t7),(t12,2p)0, ±Earcsin(0.25/m)/ωrarcsin(0.25/m) fs/ωr (t1,t2),(t5, t6),(t7,t8),(t11,t12)±E, ±2E[arcsin(0.5/m)-arcsin(0.25/m)]/ωr[arcsin(0.5/m)-arcsin(0.25/m)] fs/ωr (t2,t3), (t4,t5),(t8,t9),(t10,t11)±2E, ±3E[arcsin(0.75/m)-arcsin(0.5/m)]/ωr[arcsin(0.75/m)-arcsin(0.5/m)] fs/ωr (t3,t4), (t9,t10)±3E, ±4E2[p/2-arcsin(0.75/m)]/ωr2[p/2-arcsin(0.75/m)] fs/ωr
在0~t4和p~t10区间内,脉冲跳变类型为双跳变,在电平切换的开关周期,电平切换方式为越级切换;在t4 ~ p和t10 ~ 2p区间内,脉冲跳变类型为双跳变与单跳变交替的组合方式,在电平切换的开关周期,电平切换方式为相邻电平切换;不跳变类型出现的次数较少,而且不存在有效开关动作,可忽略不计。
为简化求解,采用最值法对不确定区内的有效开关次数范围进行估计,得到一个调制波周期内有效开关次数最大值和最小值见表4。表中N1~N4的分别为表3中对应区段的开关周期数量,如果N1 ~ N4的计算结果不是整数,进行四舍五入近似处理。fVT_min(i)为有效开关次数最小,L为相邻电平切换,Y为越级电平切换。根据图4的分析,L取值为1或3,Y取值为2或4,L1和L3分别表示有效开关次数为1和3的相邻电平切换,Y2和Y4分别表示有效开关次数为2和4的越级电平切换,2表示电平跳变类型为双跳变,1表示单跳变,2+1表示双跳变和单跳变交替出现。
表4 各电平区段内IGBT有效开关次数范围
Tab.4 The effective switching frequency range of IGBT in each level section
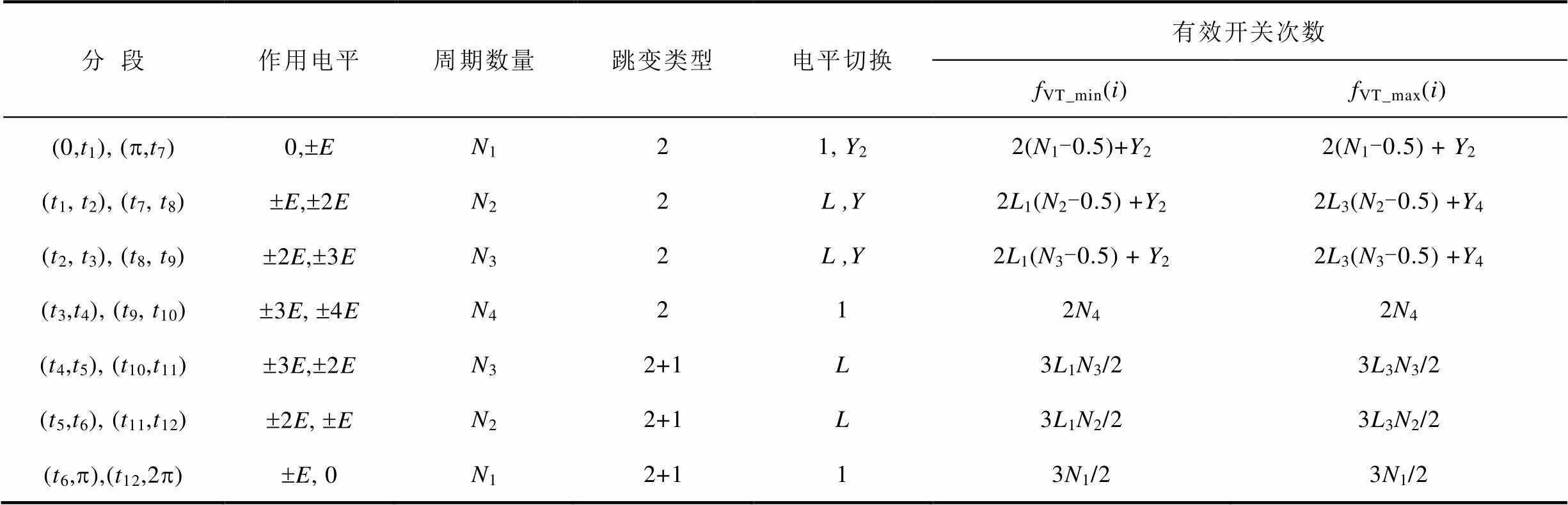
分段作用电平周期数量跳变类型电平切换有效开关次数 fVT_min(i)fVT_max(i) (0,t1), (p,t7)0,±EN121, Y22(N1-0.5)+Y22(N1-0.5) + Y2 (t1, t2), (t7, t8)±E,±2EN22L ,Y2L1(N2-0.5) +Y22L3(N2-0.5) +Y4 (t2, t3), (t8, t9)±2E,±3EN32L ,Y2L1(N3-0.5) + Y22L3(N3-0.5) +Y4 (t3,t4), (t9, t10)±3E, ±4EN4212N42N4 (t4,t5), (t10,t11)±3E,±2EN32+1L3L1N3/23L3N3/2 (t5,t6), (t11,t12)±2E, ±EN22+1L3L1N2/23L3N2/2 (t6,p),(t12,2p)±E, 0N12+113N1/23N1/2
图6为一个调制波周期内钳位二极管的有效动作区间分布。由于钳位二级管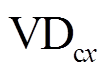 的反向恢复损耗仅出现在桥臂0状态向1状态或-1状态切换的时刻,定义等效跳变类型为桥臂从0状态向其他状态变换的有效切换。如(0,t1)区间为双跳变类型,但
的反向恢复损耗仅出现在桥臂0状态向1状态或-1状态切换的时刻,定义等效跳变类型为桥臂从0状态向其他状态变换的有效切换。如(0,t1)区间为双跳变类型,但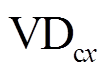 的关断损耗仅出现在0状态向1状态或-1状态切换的时刻,因此等效跳变类型为单跳变。仿照IGBT有效开关动作的分析过程可以得到一个调制波周期内
的关断损耗仅出现在0状态向1状态或-1状态切换的时刻,因此等效跳变类型为单跳变。仿照IGBT有效开关动作的分析过程可以得到一个调制波周期内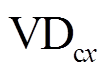 的有效开关动作见表5,与IGBT有效开关动作分析相比,
的有效开关动作见表5,与IGBT有效开关动作分析相比,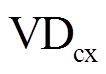 增加了在冗余矢量的区域等效脉冲跳变类型的不确定性,双跳变类型的等效跳变为2或1,单跳变类型的等效跳变为1或0,表中N表示开关周期数量,相邻电平切换L的取值可能为1或2,越级电平切换Y的取值可能为2或3。
增加了在冗余矢量的区域等效脉冲跳变类型的不确定性,双跳变类型的等效跳变为2或1,单跳变类型的等效跳变为1或0,表中N表示开关周期数量,相邻电平切换L的取值可能为1或2,越级电平切换Y的取值可能为2或3。
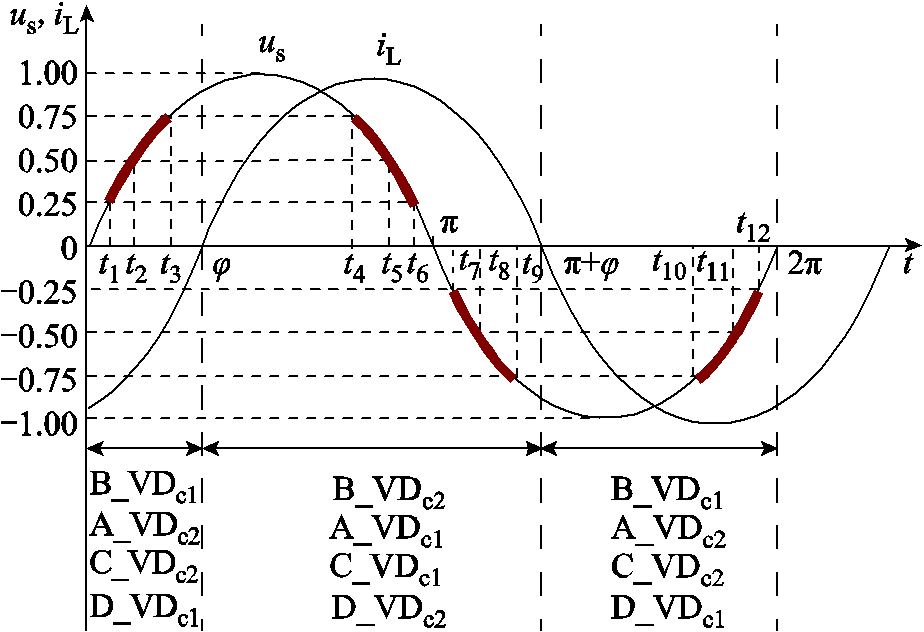
图6 一个调制波周期内钳位二极管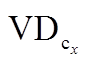 动作分布
动作分布
Fig.6 Action distribution of clamp diode in a modulation wave period
表5 各电平区段内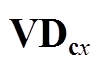 有效开关次数范围
有效开关次数范围
Tab.5 The effective switching frequency range of 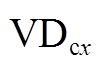 in each level section
in each level section
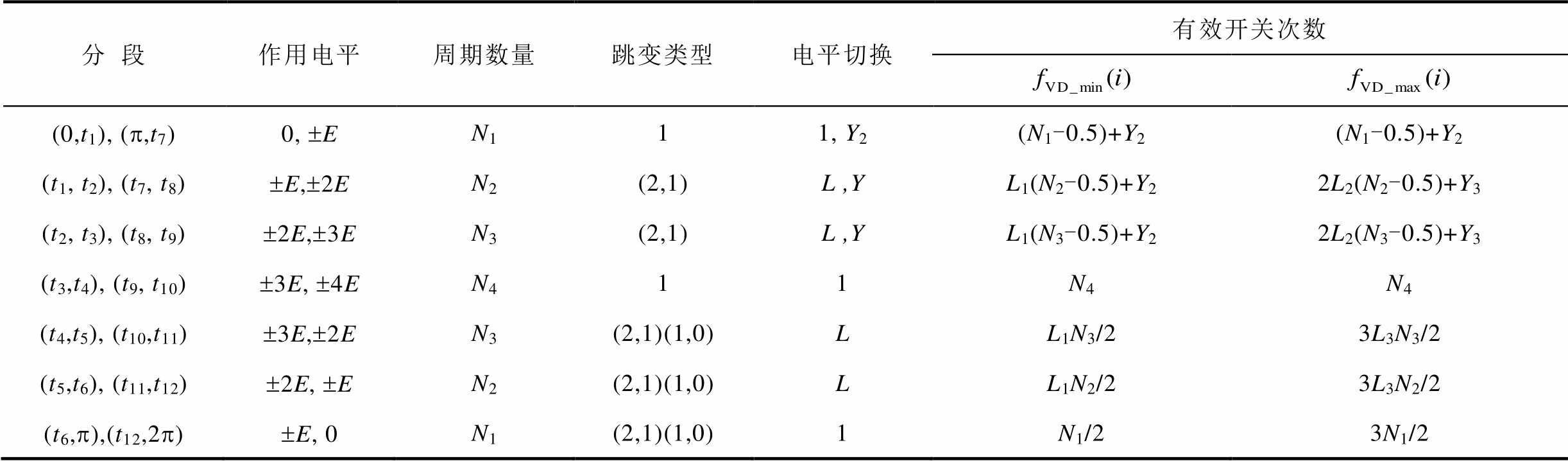
分段作用电平周期数量跳变类型电平切换有效开关次数 (0,t1), (p,t7)0, ±EN111, Y2(N1-0.5)+Y2(N1-0.5)+Y2 (t1, t2), (t7, t8)±E,±2EN2(2,1)L ,YL1(N2-0.5)+Y22L2(N2-0.5)+Y3 (t2, t3), (t8, t9)±2E,±3EN3(2,1)L ,YL1(N3-0.5)+Y22L2(N3-0.5)+Y3 (t3,t4), (t9, t10)±3E, ±4EN411N4N4 (t4,t5), (t10,t11)±3E,±2EN3(2,1)(1,0)LL1N3/23L3N3/2 (t5,t6), (t11,t12)±2E, ±EN2(2,1)(1,0)LL1N2/23L3N2/2 (t6,p),(t12,2p)±E, 0N1(2,1)(1,0)1N1/23N1/2
结合式(2)及表4可得,一个调制波周期内IGBT开关损耗的最小值PS,VT_min和最大值PS,VT_max可分别表示为
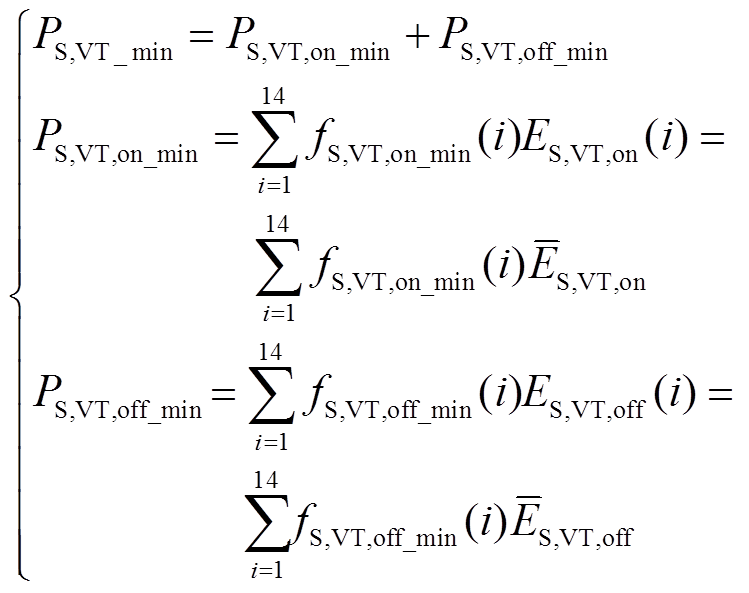 (4)
(4)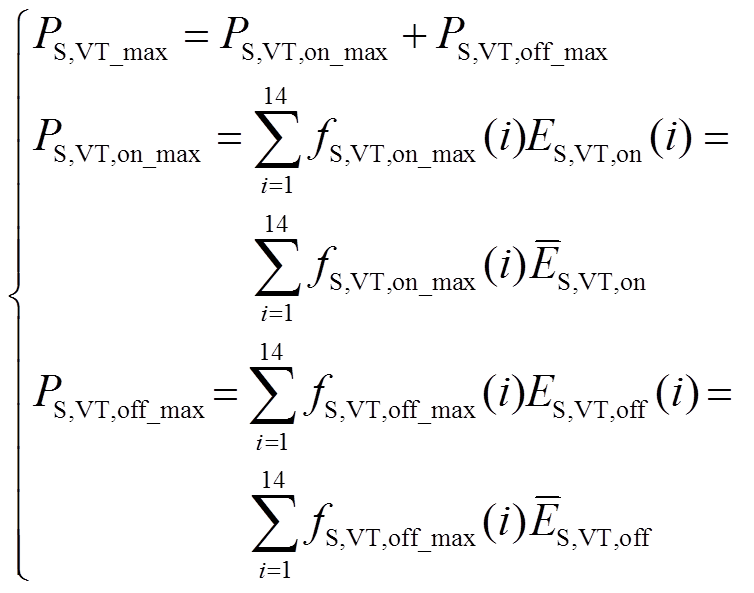 (5)
(5)式中,fS,VT,on、fS,VT,off分别为一个调制波周期内IGBT有效开通次数和有效关断次数,fS,VT,on=fS,VT,off= fS,VT/2;ES,VT,on(i)、ES,VT,off(i)分别为第i区段IGBT开通一次能量损耗和关断一次能量损耗;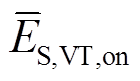 、
、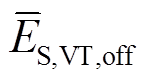 分别为IGBT平均开通能量和平均关断能量。
分别为IGBT平均开通能量和平均关断能量。
结合式(3)和表5可得,一个调制波周期内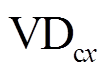 关断损耗的最小值和最大值分别为
关断损耗的最小值和最大值分别为
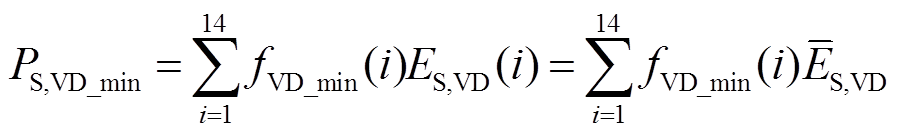 (6)
(6)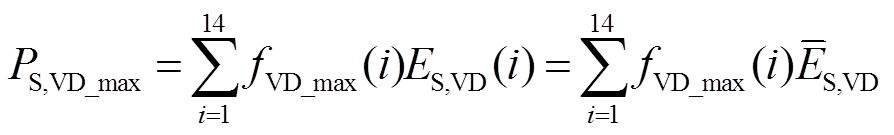 (7)
(7)式中,fVD_min、fVD_max分别为二极管VD有效关断最小、最大次数;ES,VD(i)为第i个区段二极管VD关断一次的能量损耗;`ES,VD为平均关断能量。当驱动电阻和结温一定时,开关器件X的开关能量ES,X(i)为[20]
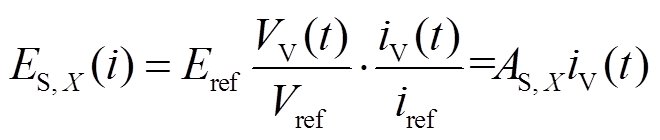 (8)
(8)式中,Eref为Vref和iref时对应的器件开通或关断能量;VV(t)和iV(t)分别为实际电压和实际电流。忽略电容电压波动时,每个IGBT的实际电压VV=VH/2,AS,X为器件X的能量拟合系数。假设电流表达式为iV(t)=Imsin(ωrt+φ),结合表4和表5中各区段有效开关频率表达式,可得到IGBT的解析表达式为
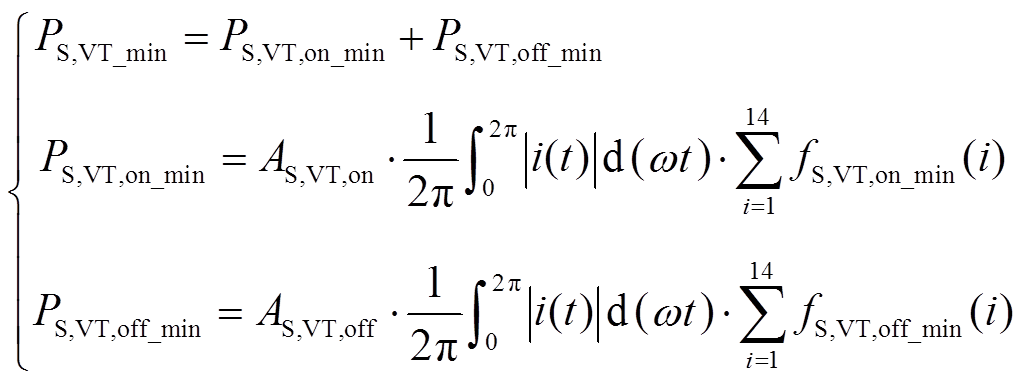 (9)
(9)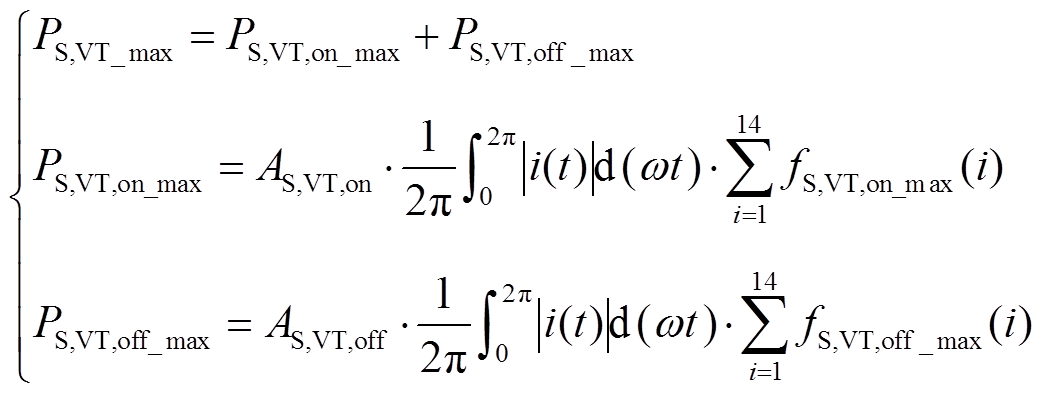 (10)
(10)由于VDc的导通区间只有半个调制波周期,所以|i(t)|的积分区间为(0,p),有效开关频率区间i的取值为1~7,钳位二极管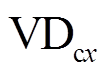 表达式为
表达式为
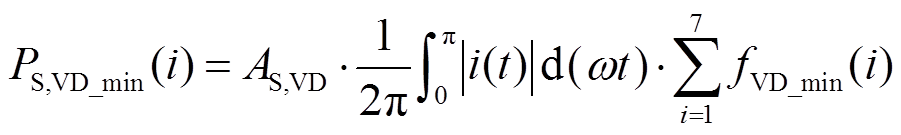 (11)
(11)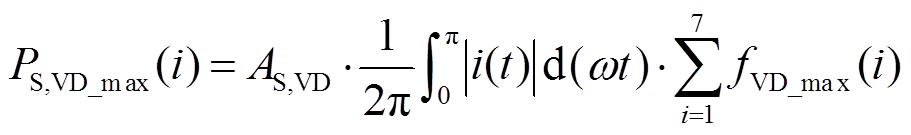 (12)
(12)虽然均压冗余矢量造成了不确定区,每个调制波周期内的开关损耗各不相同,但是当电容电压不均达到周期稳态时,开关损耗分布在平均损耗附近。结合式(9)~式(12),得到一个周期Tr内IGBT和VDc的开关损耗功率与开关频率的关系为
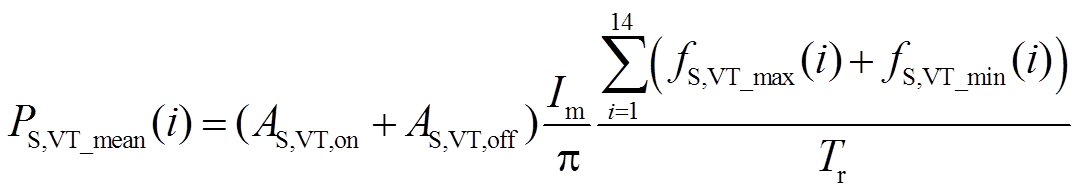 (13)
(13)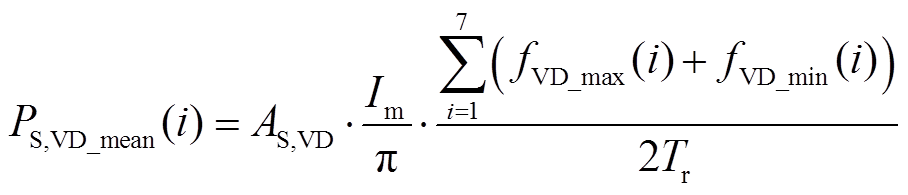 (14)
(14)为验证开关暂态损耗分析的正确性,在Simulink/PLECS仿真环境下对IGBT和钳位二极管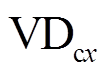 的相关结论进行仿真验证。仿真条件见表6。IGBT型号为FZ3600R17KE3_B2,
的相关结论进行仿真验证。仿真条件见表6。IGBT型号为FZ3600R17KE3_B2,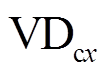 型号为DZ3600S17K3_B2。
型号为DZ3600S17K3_B2。
表6 开关损耗仿真条件
Tab.6 Switch loss simulation conditions

参数数值 调制波/Hz50 功率因数0.83 开关频率/kHz2 负载阻抗/Ω0.071 电容大小/mF98 调制比0.909 输入电压UH1/V2 200 输出电压/V4 400
首先对开关器件的有效开关作用区域进行仿真验证,图7a给出0.04~0.08s两个调制波周期的A桥臂IGBT电流。可以看出,A_VT1、A_VT2、A_VT3、A_VT4的有效开关动作区间分别是(φ, p)、(p, p+φ)、(0, φ)、(p+φ, 2p)。图7b为流过A桥臂两个钳位二极管A_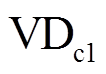 和A_
和A_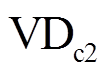 的电流示意图,A_
的电流示意图,A_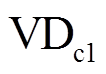 和A_
和A_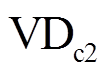 有效作用区间分别是(φ,p+φ)和(p+φ,2p+φ),IGBT和
有效作用区间分别是(φ,p+φ)和(p+φ,2p+φ),IGBT和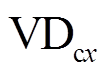 的有效开关动作区间与表2分析结果一致,其余三个桥臂中的开关器件有效开关动作分布区域仿真结果与分析结果均一致,此处不再赘述。
的有效开关动作区间与表2分析结果一致,其余三个桥臂中的开关器件有效开关动作分布区域仿真结果与分析结果均一致,此处不再赘述。
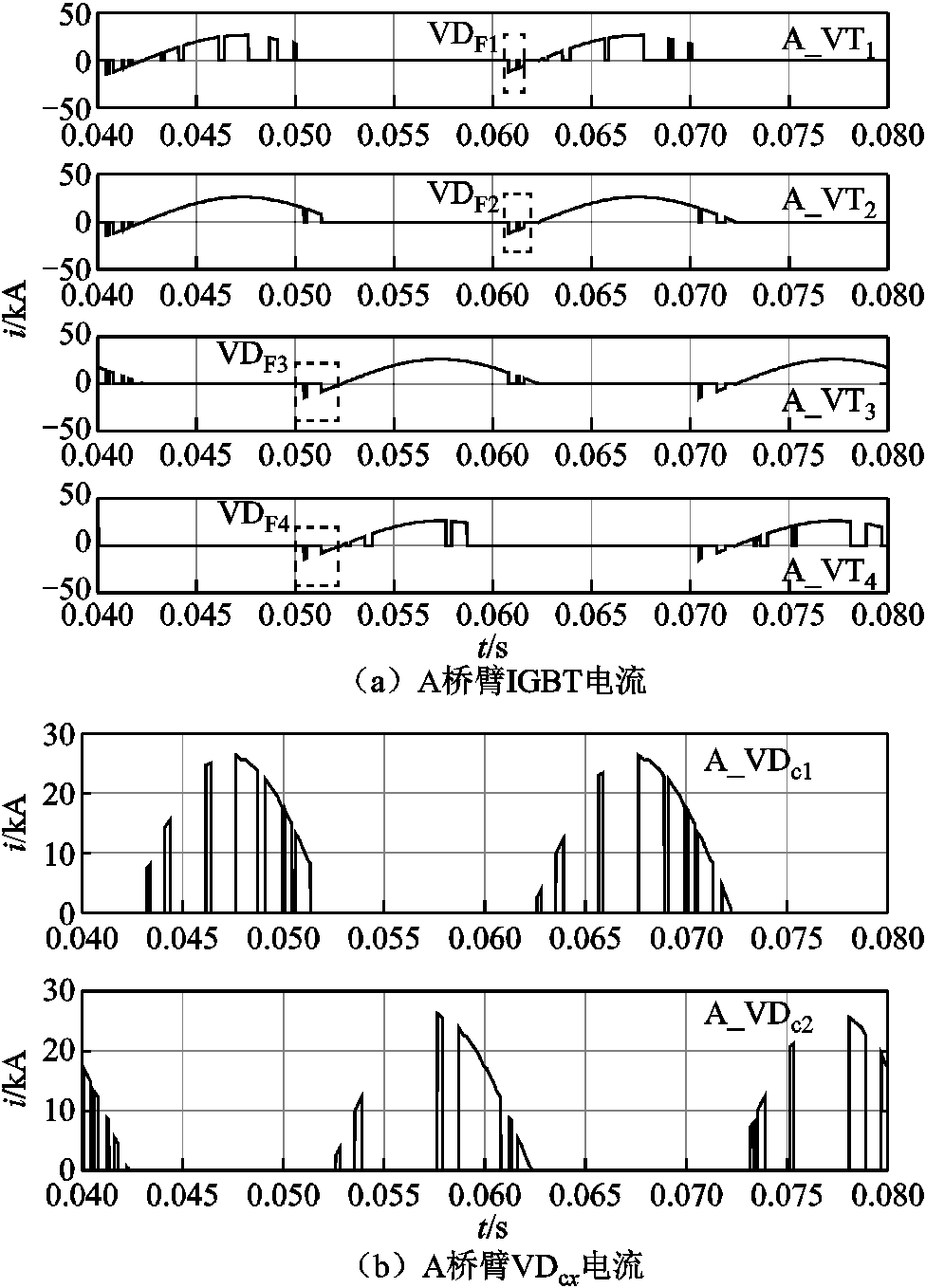
图7 开关管有效动作区间分布
Fig.7 Distribution of effective action interval of switch tube
为验证开关损耗理论分析的正确性,采用PLECS仿真软件对IGBT和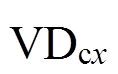 的开关损耗进行仿真分析。利用脉冲平均模块对一个周期内的开关损耗求平均值,初值损耗为0,周期1~5的平均损耗如图8所示,由于每个周期的冗余矢量随电容电压不均随时变化,作用的矢量不相同,因此对应的开关损耗也不相同。
的开关损耗进行仿真分析。利用脉冲平均模块对一个周期内的开关损耗求平均值,初值损耗为0,周期1~5的平均损耗如图8所示,由于每个周期的冗余矢量随电容电压不均随时变化,作用的矢量不相同,因此对应的开关损耗也不相同。
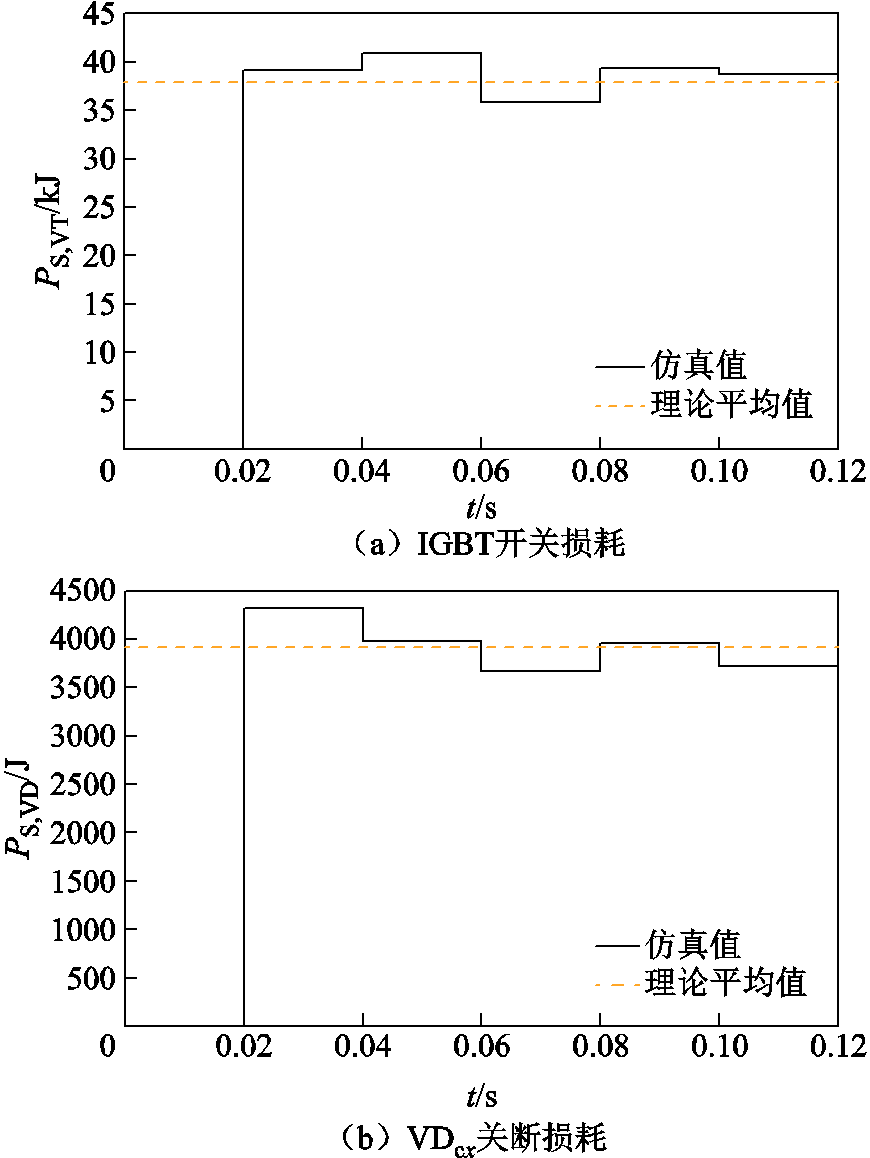
图8 5个调制波周期内IGBT和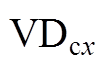 开关损耗
开关损耗
Fig.8 IGBT and 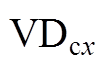 switching losses in five modulation wave cycles
switching losses in five modulation wave cycles
IGBT和钳位二极管VDc的开关损耗参数可从器件手册上获得,结合式(9)~式(14),得到理论计算值与仿真值的结果对比见表7。
表7 开关损耗仿真值与理论值对比
Tab.7 Comparison between simulation and theoretical values of switching losses
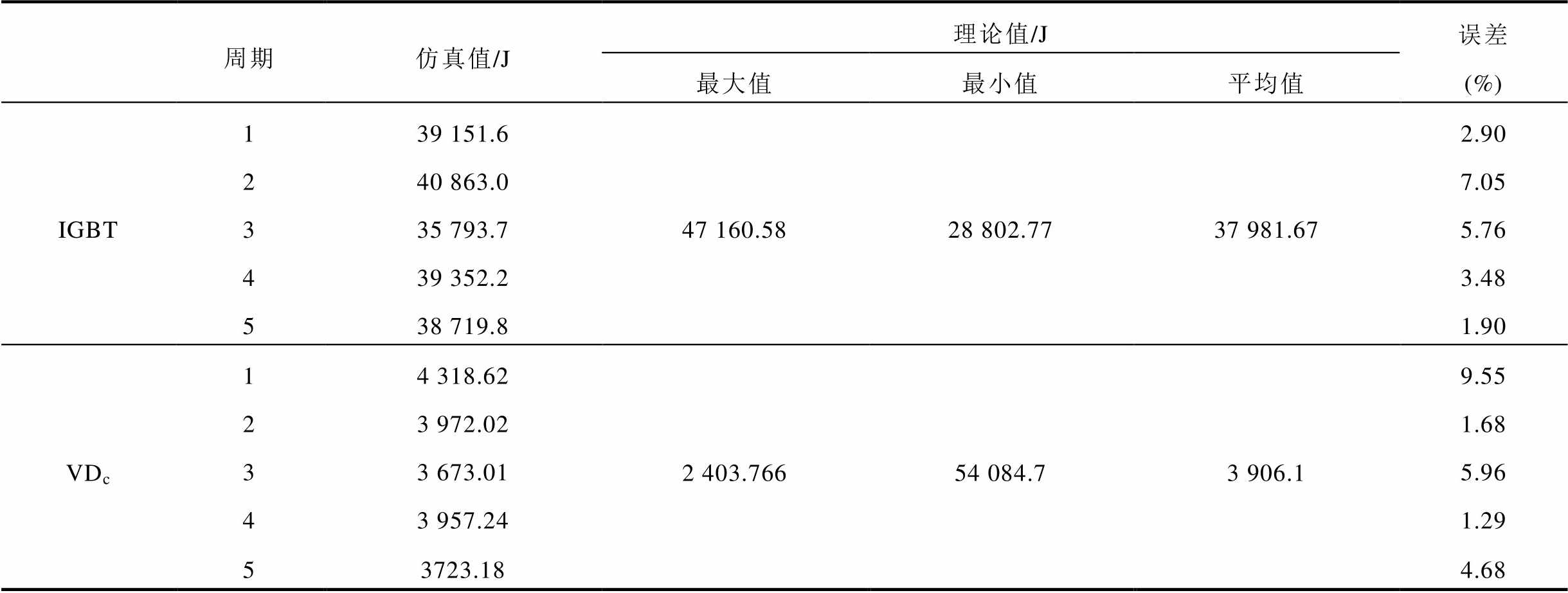
周期仿真值/J理论值/J误差 (%) 最大值最小值平均值 IGBT139 151.647 160.5828 802.7737 981.672.90 240 863.07.05 335 793.75.76 439 352.23.48 538 719.81.90 VDc14 318.622 403.76654 084.73 906.19.55 23 972.021.68 33 673.015.96 43 957.241.29 53723.184.68
可以看出,仿真值分布在理论最值的范围内,且5个周期内IGBT开关损耗与理论计算平均值的最大误差为7.05%,最小误差为1.90%,VDc关断损耗与理论计算平均值的最大误差为9.55%,最小误差为1.29%,最大误差控制在10%以内,说明开关损耗与开关频率的模型比较准确,式(13)和式(14)可用来解析计算开关损耗大小。
为进一步验证理论分析的正确性,搭建了实验样机平台,首先对IGBT(FZ3600R17KE3_B2)进行关断电压尖峰测试,以验证器件的可靠性。测试结果如图9所示,关断电压尖峰为1 400 V,在额定峰值电压范围之内。在此基础上进行CHB-NPC测试实验,调制波频率50Hz,开关频率2kHz,输出电压电流波形如图10所示,可以看到清晰的九电平电压波形。
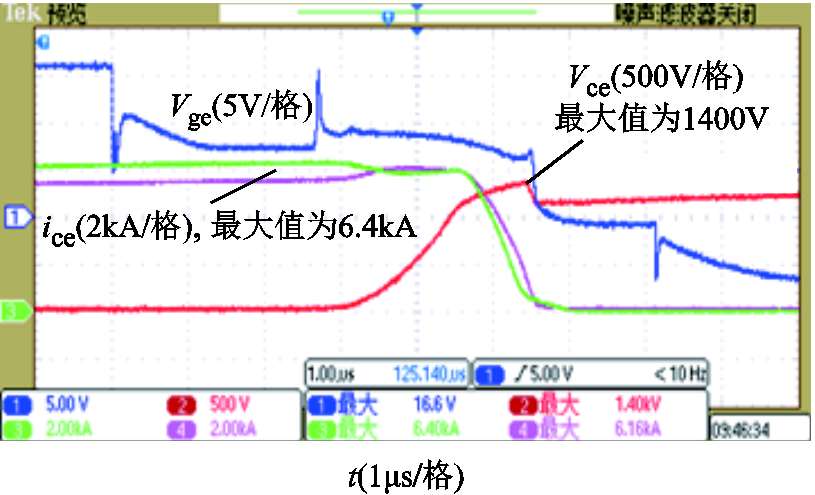
图9 IGBT关断尖峰测试
Fig.9 IGBT turn-off peak test
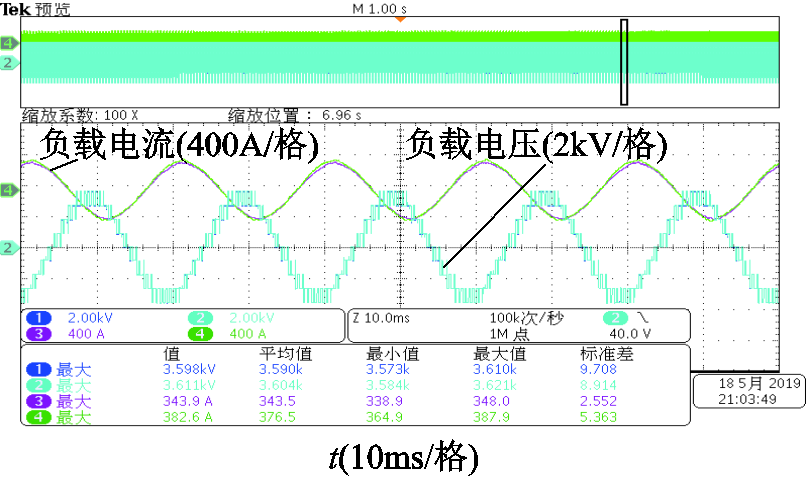
图10 单相CHB-NPC逆变器输出电压波形
Fig.10 Output voltage waveforms of single-phase CHB-NPC inverter
开关损耗的计算采用了英飞凌的相关规定,把开关管电压与电流的乘积作为开关暂态损耗[21]。计算得到的理论值与实验开关损耗值比较见表8,实验数据的具体分析方法与仿真部分数据分析相同,不再赘述。测量得到5个周期内IGBT与VDc的实验值与理论计算的误差均在10%以内,说明建立的开关频率与开关损耗解析关系式能较好地反映二者之间的定量关系。
表8 开关损耗实验值与理论值对比
Tab.8 Comparison between experimental and theoretical values of switching losses

周期实验值/J理论值/J误差(%) 最大值最小值平均值 IGBT139 765.147 160.5828 802.7737 981.674.69 238 815.92.91 339 812.44.82 435 020.87.79 536 494.13.92 VDc14 077.572 403.76654 084.73 906.14.38 23 615.517.44 34 152.186.30 43 866.251.02 53 818.992.23
针对单相CHB-NPC逆变器采用脉冲跳变SVPWM均压调制算法的开关频率与开关损耗的定量关系进行分析,主要结论和创新点如下:
1)针对单个开关管开关频率与控制频率不同,有效开关动作分散且与直流侧均压耦合的特点,提出采用基于整体的开关损耗计算思路。明确一个调制周期内各个开关管可能发生有效动作的区间,但不用明确具体动作的开关器件即可直接计算出所有器件的开关损耗之和。
2)针对均压冗余矢量导致的开关动作不确定问题,采用最值法对开关有效动作进行估计,结合电压不均多周期稳态时的均压冗余矢量均衡作用的特点,最终确定平均开关损耗作为理论估算的开关损耗。
3)提出的基于整体损耗分析方法和最值估算法适用于其他类似的SVPWM调制方法,基于有效开关频率的分析过程同样适用于一般的SPWM调制。
参考文献
[1] 马伟明, 肖飞, 聂世雄. 电磁发射系统中电力电子技术的应用与发展[J]. 电工技术学报, 2016, 31(19): 1-10. Ma Weiming, Xiao Fei, Nie Shixiong.Applications and development of power electronics in electromagnetic launch system[J]. Transactions of China Electrotechnical Society, 2016, 31(19): 1-10.
[2] 张琦, 李江江, 孙向东, 等. 单相级联七电平逆变器拓扑结构及其控制方法[J].电工技术学报, 2019, 34(18): 3843-3853. Zhang Qi, Li Jiangjiang, Sun Xiangdong, et al.Topology and control method of single-phase cascaded seven-level inverter[J].Transactions of China Electrotechnical Society,2019, 34(18): 3843-3853.
[3] 陈仲, 孙健博, 章修齐, 等. 级联型逆变器载波周期脉冲调整的功率均衡方法及特性分析[J]. 电工技术学报, 2019, 34(22): 4761-4771.Chen Zhong, Sun Jianbo, Zhang Xiuqi, et al.Power balance method and characteristic analysis based on carrier period pulse adjustment for cascaded inverter[J]. Transactions of China Electrotechnical Society,2019, 34(22): 4761-4771.
[4] Tolbert L M, Peng F Z, Habetler T G. Multilevel converters for large electric drives[J]. IEEE Transactions on Industry Applications, 2002, 35(1): 36-44.
[5] Zhu Junjie, Sun Xingfa, Nie Ziling, et al. Synchronous control strategy of dual five-level converters based on the improved SVPWM[J]. IET Power Electronics, 2018, 11(14): 2311-2318.
[6] 陈息坤, 李婷娜. 基于控制自由度组合的简化多电平空间矢量脉宽调制控制策略[J]. 电工技术学报, 2019, 34(22): 4781-4794. Chen Xikun, Li Tingna. A kind of simplified multilevel space vector pulse width modulation control strategy based on control degrees of freedom combination[J]. Transactions of China Electrote-chnical Society, 2019, 34(22): 4781-4794.
[7] Panagiotis K, Konstantinos P, Antonios K, et al. A single-phase nine-level inverter for renewable energy systems employing model predictive control[J]. Energy Conversion and Management, 2015, 89: 427-437.
[8] Cui Dongdong, Ge Qiongxuan. A novel hybrid voltage balance method for five-level diode-clamped converters[J]. IEEE Transactions on Industrial Electronics, 2018, 65(8): 6020-6031.
[9] 李卫超, 马伟明, 汪光森. 中点钳位型H桥级联单相逆变器新型空间矢量脉宽调制方法[J]. 中国电机工程学报, 2014, 34(30): 5313-5319. Li Weichao, Ma Weiming, Wang Guangsen, et al. A novel SVPWM method for single phase casecaded NPC H-bridge inverter[J]. Proceedings of the CSEE,2014, 34(30): 5313-5319.
[10] 林城美, 王公宝, 汪光森. 基于脉冲跳变的空间矢量脉冲宽度调制策略[J]. 电机与控制学报, 2016, 20(1): 43-51.Lin Chengmei, Wang Gongbao, Wang Guangsen, et al. Novel spacevector pulse width modulation based on pulse shifting[J]. Electric Machinesand Control, 2016, 20(1): 43-51.
[11] 舒泽亮, 马伟天, 柳明. 中点钳位型H桥级联单相变换器均压SVPWM最优工作点转移路径研究[J]. 中国电机工程学报, 2016, 36(13): 3565-3572. Shu Zeliang, Ma Weitian, Liu Ming. An optimal SVPWM transition path for voltage equalization in NPC cascade H-bridge single-phase inverters[J]. Proceedings of the CSEE,2016, 36(13): 3565-3572.
[12] Lin Hongjian, Zhu Leilei, Yin Tao, et al. An optimal-path SVPWM algorithm with mutual DC voltages balancing capacity for three-module cascaded multilevel converter[C]// 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, 2018: 1-5.
[13] 柳明. 单相三电平H桥多模块级联变换器SVPWM算法研究[D]. 成都: 西南交通大学, 2017.
[14] Lin Hongjian, Shu Zeliang, He Xiaoqiong, et al. N-D SVPWM with DC voltage balancing and vector smooth transition algorithm for cascaded multilevel converter[J]. IEEE Transactions on Industrial Electronics, 2017, 65(5):3837-3847.
[15] Mirizadeh A, Baroogh F A, Gheydi M, et al. Evaluation of conduction and switching losses in cascaded multilevel inverters[C]//2017 10th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, 2017: 124-127.
[16] Andler D, Kouro S, Perez M, et al. Switching loss analysis of modulation methods used in neutral point clamped converters[C]//2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, 2009: 2565-2571.
[17] 胡锐, 陈权, 胡存刚. 基于动态DSVPWM的三电平逆变器热可靠性研究[J]. 电力电子技术, 2019, 53(6): 87-89, 107. Hu Rui, Chen Quan, Hu Cungang. Study on thermal reliability of three-level inverter based on dynamic DSVPWM[J]. Power Electronics, 2019, 53(6): 87-89, 107.
[18] Alemi P, Lee D, Analysis of semiconductor power losses in M-level NPC inverters[C]//2013 International Conference on Electrical Machines and Systems (ICEMS), Busan, 2013: 1513-1519.
[19] 景巍, 谭国俊, 叶宗彬. 大功率三电平变频器损耗计算及散热分析[J].电工技术学报, 2011, 26(2): 134-140. Jing Wei, Tan Guojun, Ye Zongbin. Losses calculation and heat dissipation analysis of high-power three-level converters[J]. Transactions of China Electrot-echnical Society,2011, 26(2):134-140.
[20] 孟庆云. 大容量NPC若干关键问题研究[D]. 武汉: 海军工程大学, 2010.
[21] Dieckerhoff S, Bernet S, Krug D. Power loss-oriented evaluation of high voltage IGBTs and multilevel converters in transformerless traction applications[J].IEEE Transactions on Power Electronics, 2005, 20(6): 1328-1336.
Analytical Calculation of Switching Loss of Single-Phase Neutral Point Clamped H-Bridge Cascaded Inverters Based on SVPWM
Abstract In order to optimize the performance of single-phase neutral point clamped (NPC) H-bridge cascaded inverter, the calculation method of switching loss based on pulse-shifting space vector pulse width modulation (SVPWM) voltage-sharing modulation is analyzed. To solve the problem that the effective switching frequency and control frequency are different, and the switching action is scattered and irregular, a new method based on the pulse-shifting SVPWM voltage-sharing modulation is proposed. The total switching loss calculation method directly calculates the sum of all switching transient losses. Aiming at the uncertainty of balancing voltage redundancy vector action, a maximum estimation method is proposed to estimate the switching transient losses. The simulation results show that the maximum and minimum errors of the calculated and actual switching losses are 9.55% and 1.29% respectively. The maximum errors of the experimental results and the theoretical values are less than 10%, which shows that the analytical expressions are more accurate.
keywords:Switch loss, single-phase neutral point clamped (NPC) H-bridge cascaded inverter, pulse-shifting space vector pulse width modulation (SVPWM), effective switching frequency
中图分类号:TM76
DOI: 10.19595/j.cnki.1000-6753.tces.191646
国家自然科学基金资助项目(51977218)。
收稿日期 2019-11-26
改稿日期 2020-02-04
原景鑫 男,1995年生,博士研究生,研究方向为电力电子与电力传动。E-mail:2199123844@qq.com
聂子玲 男,1975年生,教授,博士生导师,研究方向为电力电子与电力传动。E-mail:nieziling@163.com(通信作者)
(编辑 郭丽军)