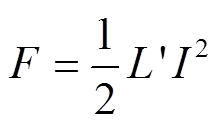（1）摘要 电感梯度是电磁轨道发射装置的重要参数，对于推力及发射效率有着重要影响。现有文献对电感梯度的研究主要存在两点不足：一是常规的解析计算方法在考虑导轨尺寸对电感梯度的影响时，未考虑电流扩散的影响，因而无法描述其动态特性；二是有限元方法能够对电流扩散的影响加以分析，但计算效率较低。为此，该文基于趋肤深度和磁能等效原则提出一种综合考虑导轨尺寸和电流扩散影响的电感梯度解析计算方法，采用所提方法与参考文献的计算结果进行了对比，呈现出较好的一致性。该方法能够为电磁轨道发射装置的优化设计和性能分析提供行之有效的理论指导。
关键词：电磁轨道发射装置 趋肤深度 电感梯度 解析法
电磁轨道发射装置可以在ms级的时间内将弹丸加速至每秒数千米的速度，突破了传统化学能武器的速度限制[1-4]。电感梯度作为电磁轨道发射装置最重要的参数之一，对于推力及发射效率有着重要影响。电磁轨道发射装置的基本形式如图1所示，它由两根平行导轨、电枢及脉冲电源组成。发射过程的推力F为[3]
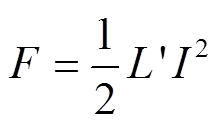（1）式中，
为单位长度的电感值（H/m），即电感梯度；I为驱动电流（A）；F为电枢受到的推力（N）。在早期的研究中，电感梯度通常被当作常数处理，如文献[5]中F. W. Grover等提出了电流在导轨中完全扩散时的电感梯度计算方法，也被称为低频电感梯度；文献[6-7]中研究了电流集中在表面时的高频电感梯度。上述方法求解得到的电感梯度都是一个定值，而实际电磁发射为瞬态过程，不同时刻电流和磁场在导轨中的扩散程度不同，因此导轨的电感梯度实际上是动态变化的。
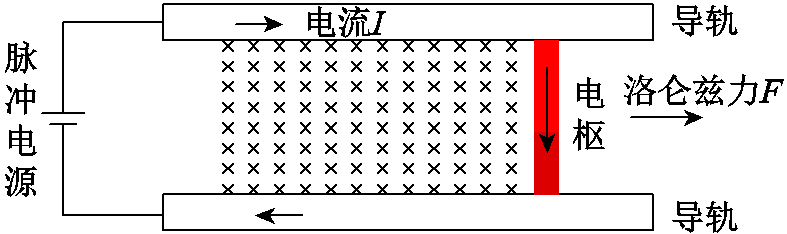
图1 电磁轨道发射装置示意图
Fig.1 The schematics of the electromagnetic rail launcher
如果不能准确计算导轨电感梯度，则无法实现对电枢出口速度的精准控制。目前国内外已经有不少学者对电感梯度的动态变化过程进行了研究：F. J. Deadrick等[8]考虑到导轨在受到外扩力之后其间距会发生变化，基于间距的变化建立了电感梯度的时变模型，但是该方法没有考虑电流扩散对电感梯度的影响；M. Ghassemi等[9]通过瞬态场仿真得到了给定电流下的电感梯度随时间变化曲线；文献[10-11]利用时频分析的方法先求得不同时刻的电流瞬时频率，再利用有限元仿真得到不同频率下的电感梯度。上述有限元仿真的方法都考虑了电流扩散的影响，缺点是计算过程较为耗时。
本文重点论述了矩形导轨电感梯度的解析计算方法，基于趋肤深度和磁能等效的概念，对文献[7]中的方法进行了适当的推广和改进，使所提出的方法能够同时计及导轨尺寸和电流扩散的影响。
先以最常见的圆形导体为例进行说明：当圆形导体中通入高频电流时，由于存在趋肤效应，导致导体中的电流密度从导体表面到中心按指数规律下降，因此导轨的有效通流面积也会减少。不同频率下圆形导体的趋肤深度
为
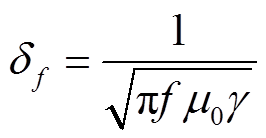（2）式中，f为频率；m0为真空磁导率；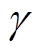
为导体电导率。
根据式（2）求得当频率f分别为100Hz、1kHz、10kHz时，铜导体的趋肤深度分别为6.6mm、2.1mm、0.66mm。在Maxwell软件中建立直径为20mm的单位长度实心圆导体的二维模型，然后基于趋肤深度等效原则建立了宽度分别为6.6mm、2.1mm、0.66mm的圆环作为等效几何模型，如图2所示。实心圆导体采用涡流场求解不同频率下的电感梯度，而作为等效模型的圆环则采用静磁场求解电感梯度，计算结果见表1。
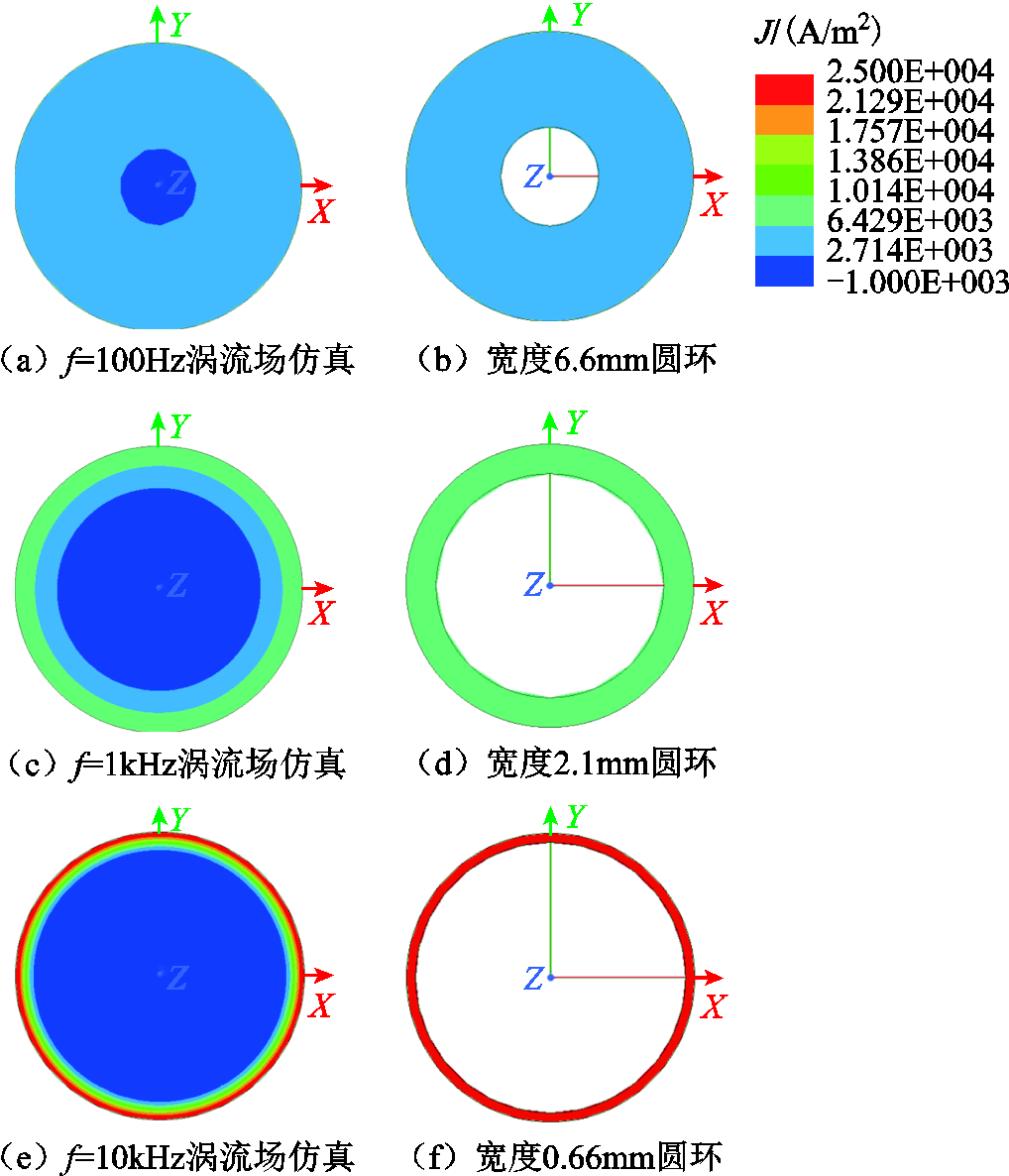
图2 基于趋肤深度的等效几何模型仿真结果
Fig.2 Simulation results of equivalent geometric model based on skin depth
表1 圆形导体原始模型和趋肤深度等效几何模型计算结果对比
Tab.1 Comparison between original model and skin-depth equivalent geometric model of the circular conductor
频率/ Hz趋肤深度/ mm原始模型电感梯度/(μH/m)等效几何模型电感梯度/(μH/m)误差 (%) 1006.60.808 30.801 1-0.89 1 0002.10.781 50.774 7-0.87 10 0000.660.767 30.765 1-0.29
表1中，等效几何模型的电感梯度和原始模型电感梯度的误差在1%以内。该结果表明，基于趋肤深度构建等效几何模型计算电感梯度是可行的，经过等效，涡流场问题简化为静磁场问题。
针对两根单位长度的矩形导轨，基于趋肤深度建立导轨截面的等效几何模型如图3所示。图3中，s为两导轨间距，w为导轨宽度，h为导轨高度，d 为趋肤深度。
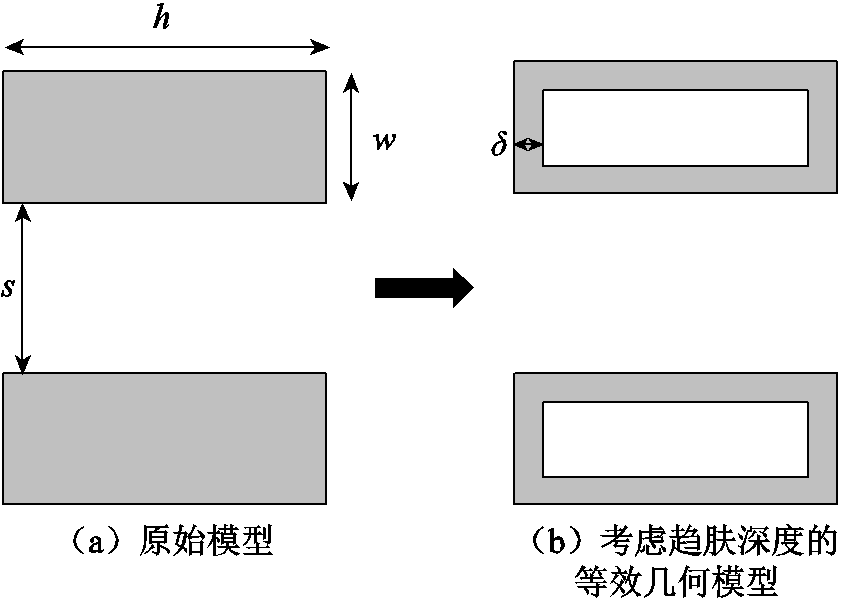
图3 基于趋肤深度的矩形导轨等效几何模型
Fig.3 Equivalent geometry model of rectangular rail based on skin depth
图4所示为高频下矩形导轨的电密分布情况[12-14]，可以看到，电流主要集中在两导轨内表面、左右两侧及尖角部位。
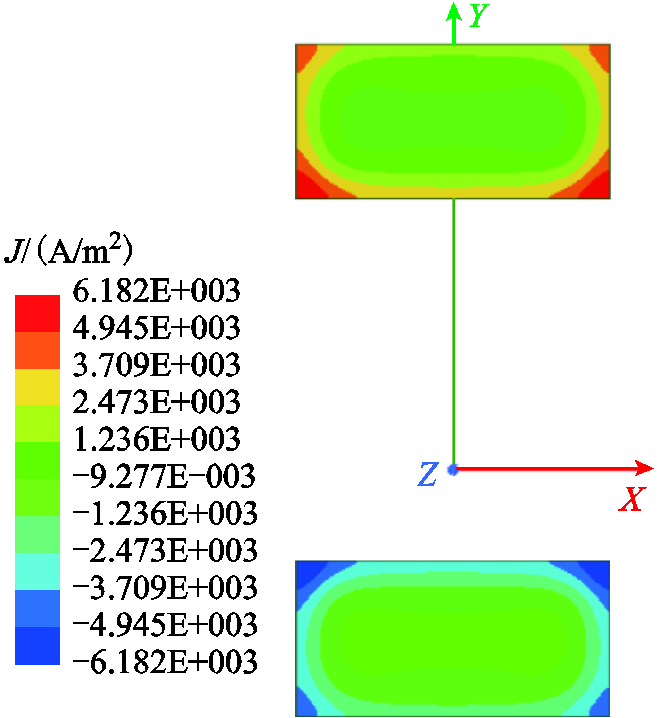
图4 矩形导轨截面电密分布情况（f=500Hz）
Fig.4 Current density distribution of rectangular rail (f=500Hz)
考虑不同位置处趋肤深度的差异，为图3中等效几何模型的各边赋予不同的折算因子w1、w2、w3（由于导轨具有对称性，因此左右两侧的趋肤深度折算因子均为w3），如图5所示。根据文献[3]，可取w1、w2、w3分别为1、0.4、0.8，由折算因子可知：最内侧导轨表面电流密度更高，其次是左右两侧，最外侧导轨电密最低。
导轨几何尺寸取为s=70mm, h=40mm, w=20mm，建立有限元模型如图6a所示；同时，根据频率100Hz、1kHz、10kHz时的趋肤深度建立考虑折算因子后的等效几何模型如图6b~图6d所示。
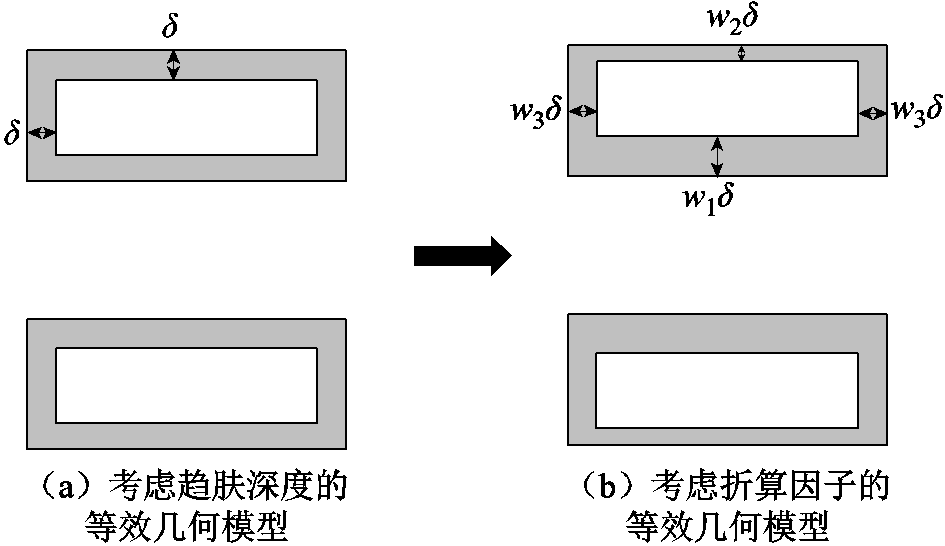
图5 考虑趋肤深度折算因子的等效几何模型
Fig.5 Equivalent geometric model considering skin depth weight factor
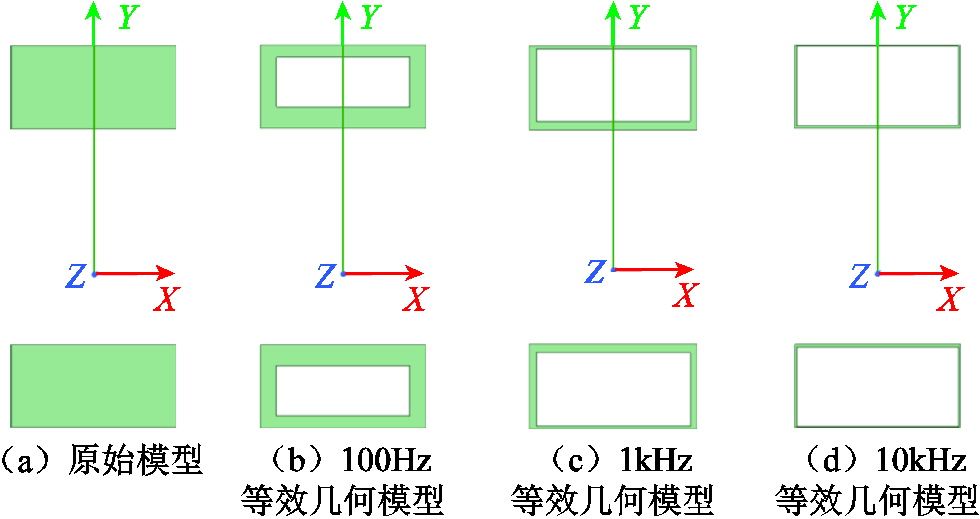
图6 不同频率下矩形导轨等效几何模型
Fig.6 Equivalent geometric model of rectangular rail at different frequencies
矩形导轨的电感梯度计算结果见表2。可以看到，三种不同频率工况下采用等效几何模型计算的误差均在3%以内。
表2 矩形导轨原始模型和趋肤深度等效几何模型计算结果对比
Tab.2 Comparison between original model and equivalent geometric mode of the rectangular rail
f/Hz原始模型电感梯度/(mH/m)等效几何模型电感梯度/(mH/m)误差 (%) 1000.736 180.71489-2.89 1 0000.682 180.67847-0.54 10 0000.662 720.66626+0.53
下面将依据导轨的等效几何模型对电感梯度的解析计算公式进行推导。对等效几何模型进行拆分如图7所示。
将图7中矩形导轨的等效几何模型拆分成四组，拆分后各组导轨如图8所示。图8中s11~s33、w11~w33、h11~h33分别为拆分后各组导轨的间距、厚度和高度，具体表达式见式（3）。其中，导轨3-3′和导轨4-4′具有相同的尺寸。可以看到，式（3）中的部分尺寸是关于趋肤深度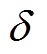
的表达式。当电流扩散情况不同时，由于趋肤深度发生变化，拆分后的各导轨的尺寸也会发生变化。
图7 对等效几何模型进行拆分
Fig.7 Split equivalent geometry model
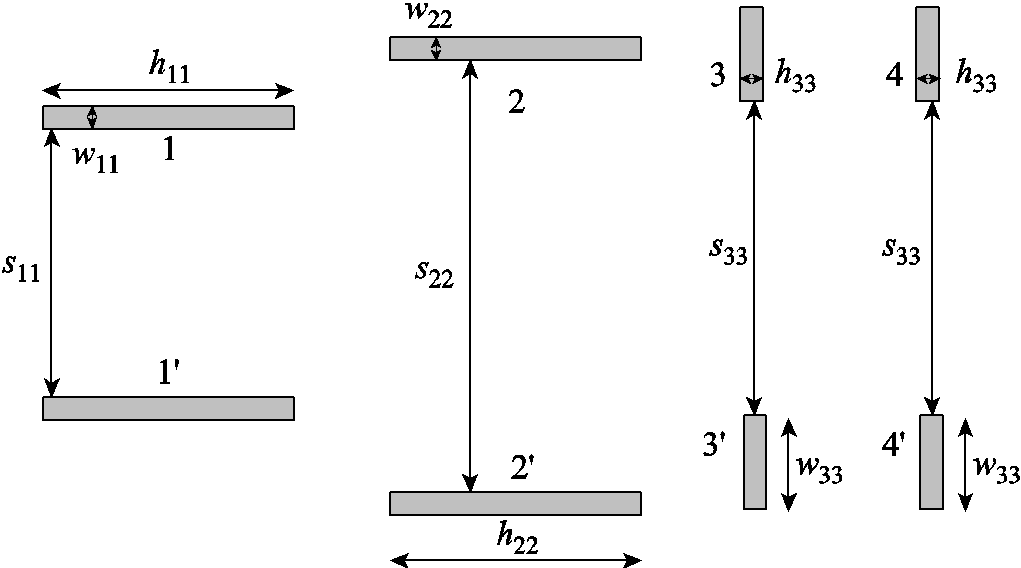
图8 拆分后四组导轨的结构尺寸
Fig.8 Dimensions of four sets of split rails
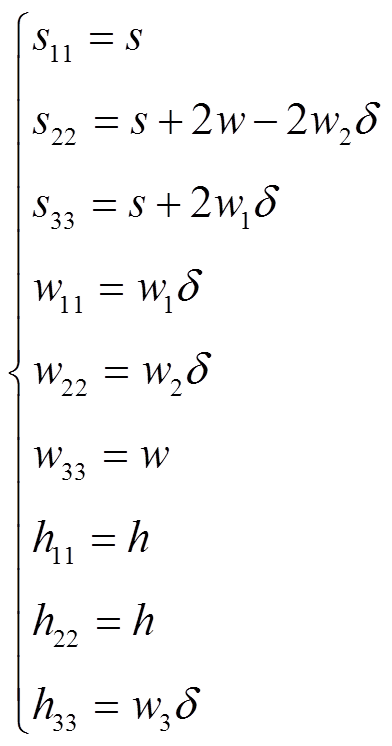（3）四组导轨分别构成四个独立的回路，得到电感梯度矩阵为
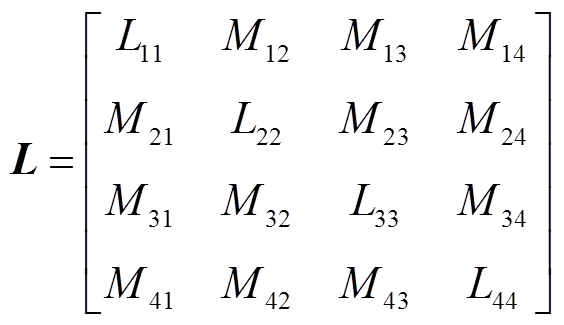（4）式中，Lii为回路i的自感梯度；Mij为回路i和回路j的互感梯度。如果能求得式（4）中各回路的自感梯度和互感梯度，则可以依据总磁场能等效的原则求出等效电感梯度。
2.1.1 自感梯度
依据Grover提出的电感梯度计算方法[5]可以得到四组导轨的自感梯度分别为
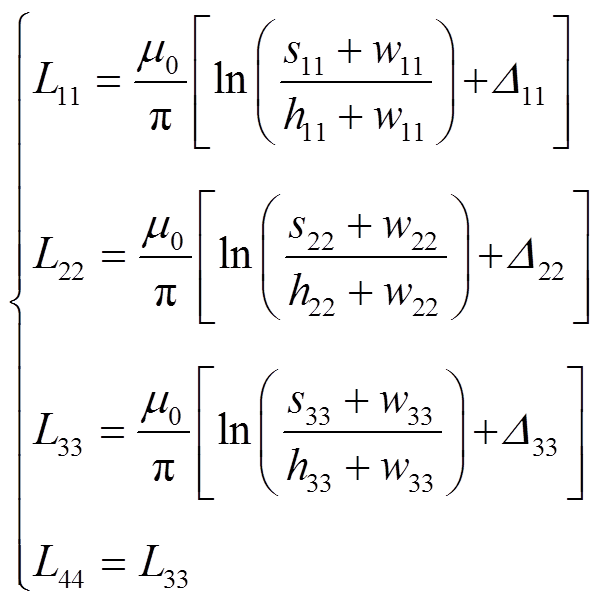（5）
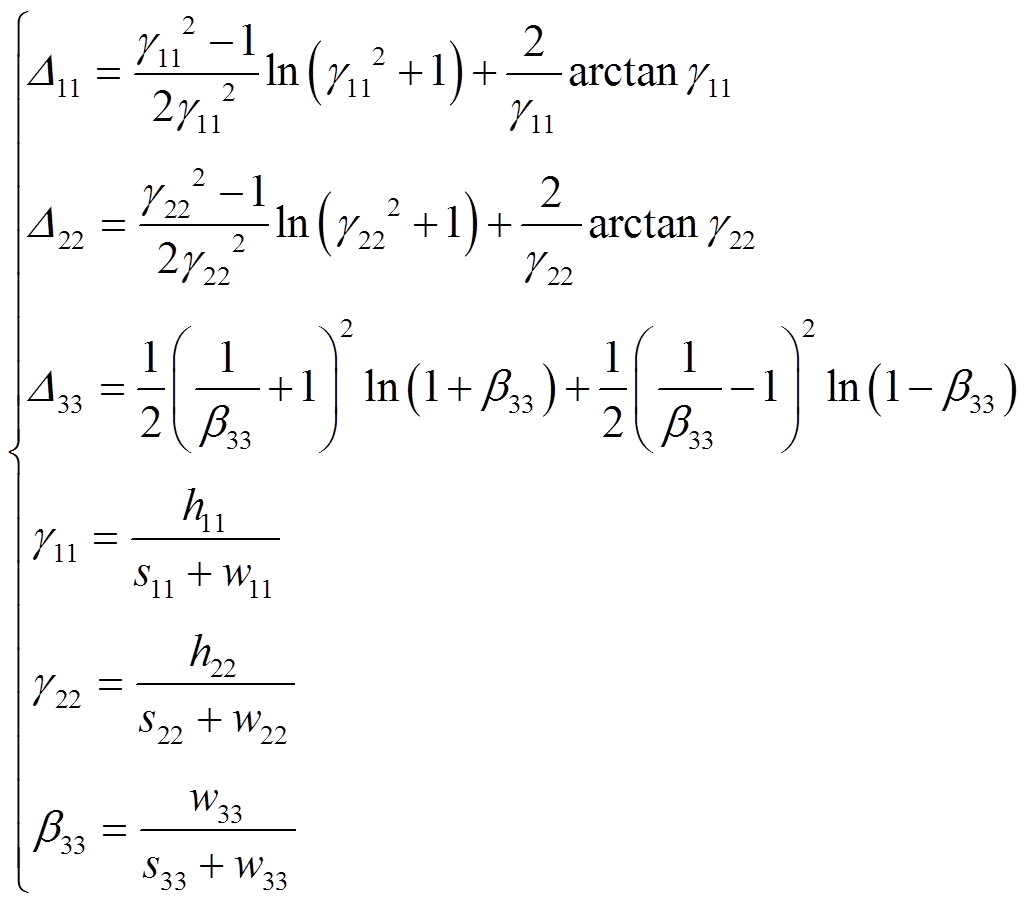（6）式中，由于3-3′导轨和4-4′导轨尺寸相同、位置对称，因此有L44=L33； D11~D33为考虑了几何平均距离的修正项。
由式（5）、式（6）可计算得到如图9所示的各导轨自感梯度随趋肤深度变化的规律。从图9可知，随着趋肤深度增加，L33和L44迅速增加，而L11和L22则缓慢减小。L33和L44之所以会增加，主要是由于趋肤深度增加时，图8所示L33和L44的导轨间距s33=s+2w1d 会增加，使得导轨间包围的面积增大，同样电流下产生的磁链增大（
），从而电感梯度增大；反之，L11和L22之所以会随着趋肤深度增加而减小，主要是由于导轨宽度w11=w1d 和w22=w2d 随着趋肤深度的增加而增加，导致两导轨所包围的面积减小，同样电流下产生的磁链减小，从而电感梯度减小。
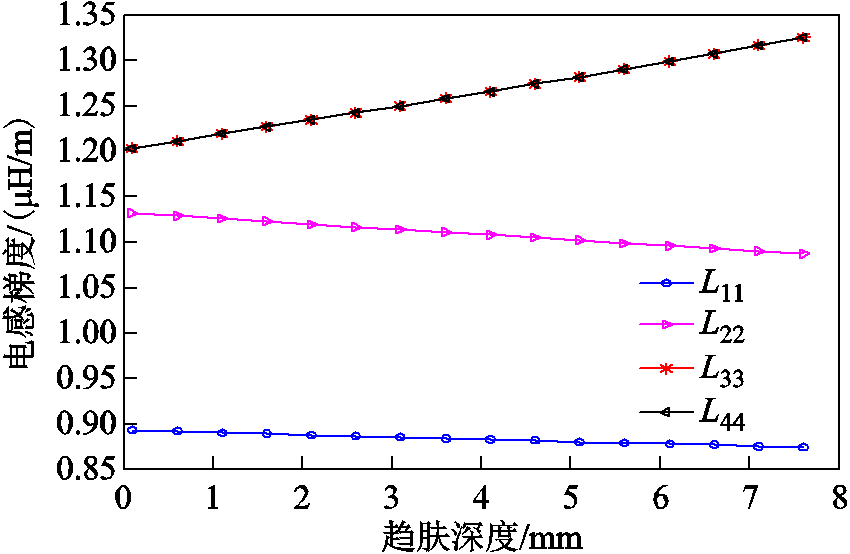
图9 各组导轨自感梯度随趋肤深度变化规律
Fig.9 Variation of self-inductance gradient with skin depth
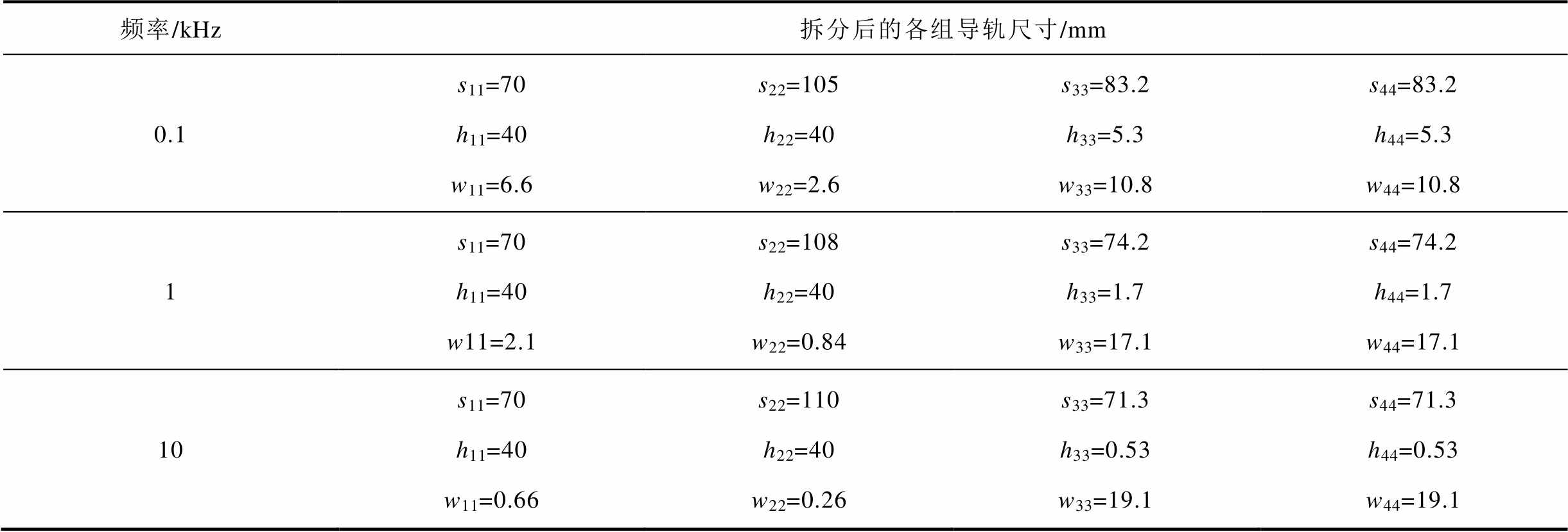
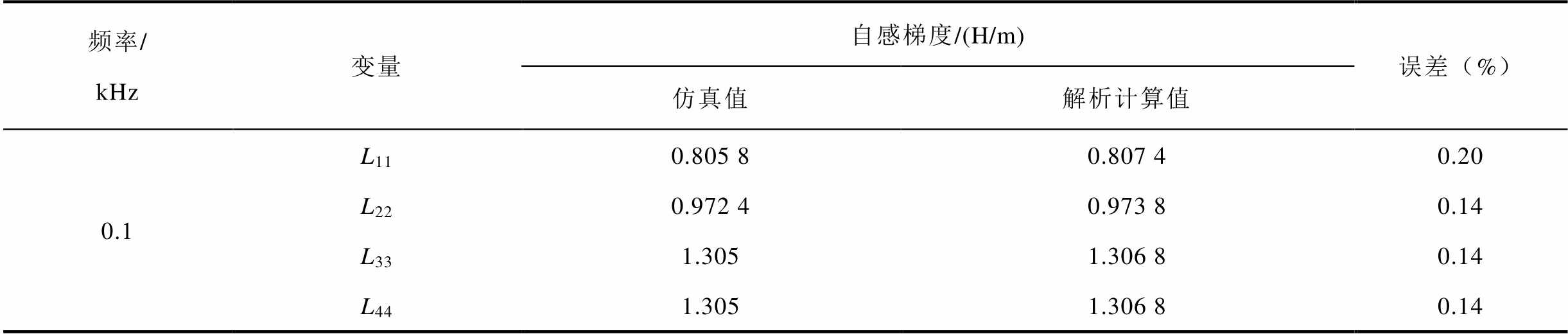
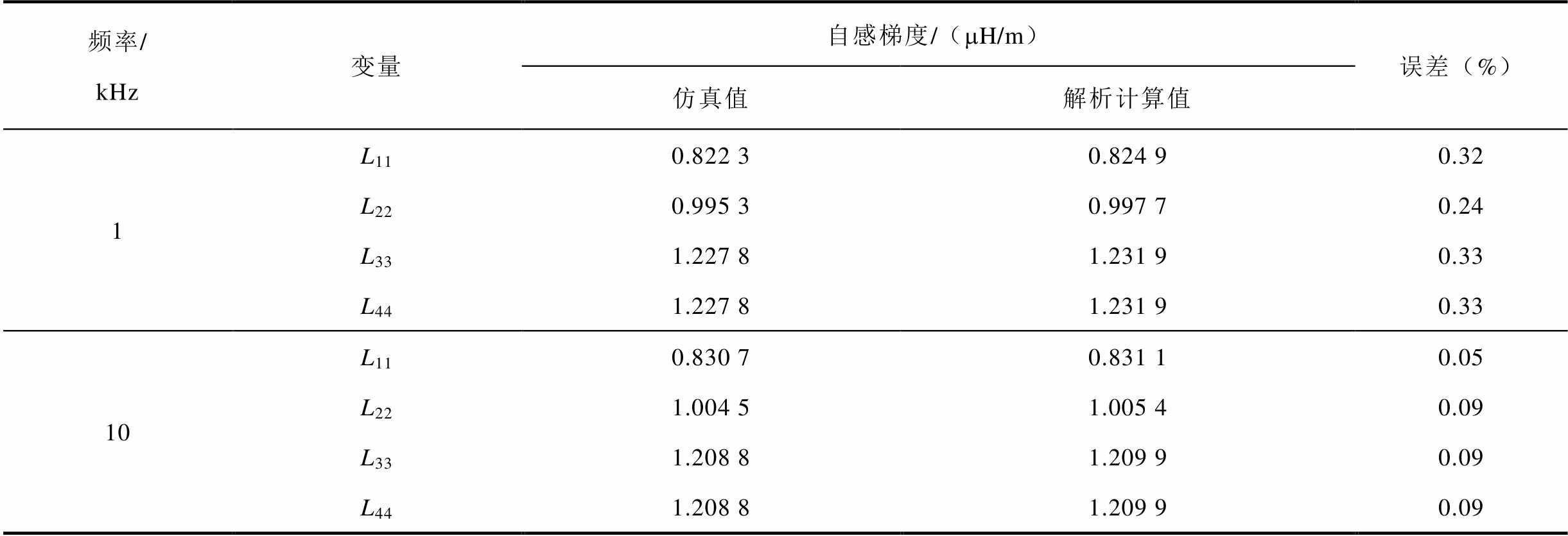
针对导轨尺寸为s=70mm、h=40mm、w=20mm的原始模型，根据式（2）和式（3）可以得到表3所示的f=100Hz、1kHz、10kHz时经等效拆分后的各组导轨的尺寸参数。依据表3的数据和式（5）、式（6），计算得到各组导轨的自感梯度计算结果见表4，可以看到各组导轨自感梯度的解析计算值与仿真值的误差在1%以内。
表3 不同频率下拆分后各组导轨的尺寸
Tab.3 Dimensions of each set of split rails at different frequencies
频率/kHz拆分后的各组导轨尺寸/mm 0.1s11=70h11=40w11=6.6s22=105h22=40w22=2.6s33=83.2h33=5.3w33=10.8s44=83.2h44=5.3w44=10.8 1s11=70h11=40w11=2.1s22=108h22=40w22=0.84s33=74.2h33=1.7w33=17.1s44=74.2h44=1.7w44=17.1 10s11=70h11=40w11=0.66s22=110h22=40w22=0.26s33=71.3h33=0.53w33=19.1s44=71.3h44=0.53w44=19.1
表4 不同频率下的自感梯度计算结果
Tab.4 Calculation results of self-inductance gradient at different frequencies
频率/ kHz变量自感梯度/(H/m)误差（%） 仿真值解析计算值 0.1L110.805 80.807 40.20 L220.972 40.973 80.14 L331.3051.306 80.14 L441.3051.306 80.14
（续）
频率/ kHz变量自感梯度/（mH/m）误差（%） 仿真值解析计算值 1L110.822 30.824 90.32 L220.995 30.997 70.24 L331.227 81.231 90.33 L441.227 81.231 90.33 10L110.830 70.831 10.05 L221.004 51.005 40.09 L331.208 81.209 90.09 L441.208 81.209 90.09
2.1.2 互感梯度
求得各组导轨的自感梯度后，接下来还需求出各导轨间的互感梯度。
先以平行长直导线为例进行说明：对于如图10所示的两对平行长直导线1-2和3-4（忽略线径），互感梯度为[5,15-16]。
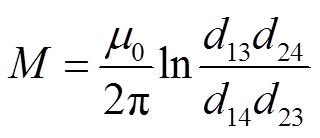（7）式中，dij为i导线和j导线中心间的距离，i, j=1~4。
图10 两对平行的长直导线
Fig.10 Two equal parallel straight wires
然而，区别于长直导线，不同截面形状的矩形导体之间的互感梯度计算更为复杂，需要求出不同截面惯量中心之间的距离，涉及复杂的积分运算[5]。为了简化计算，这里将拆分后的每根导轨用三根电流丝元来等效，即图11所示的Pij和Nij。
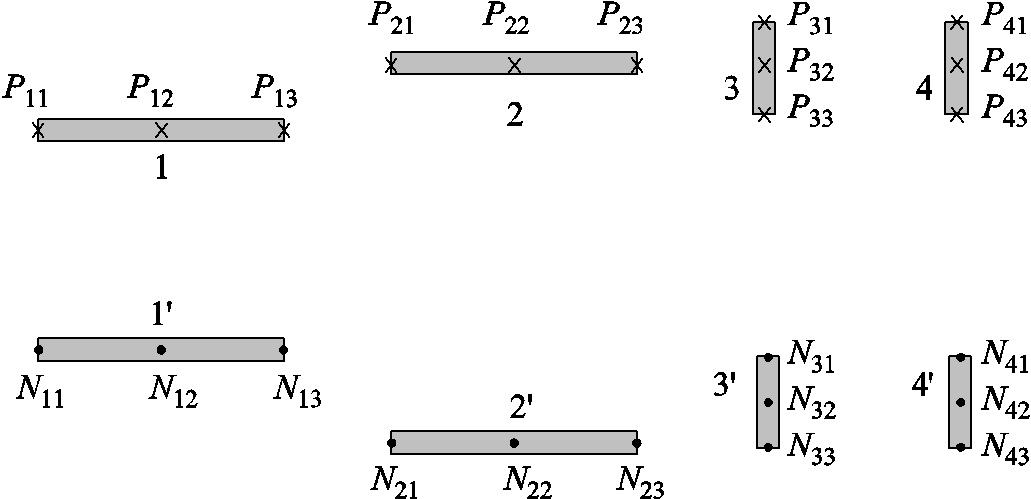
图11 等效电流丝模型
Fig.11 Equivalent filaments model
各组导轨间的互感梯度可取为每组导轨电流丝回路的互感梯度平均值，则导轨i-i′和导轨j-j′的互感梯度Mij为
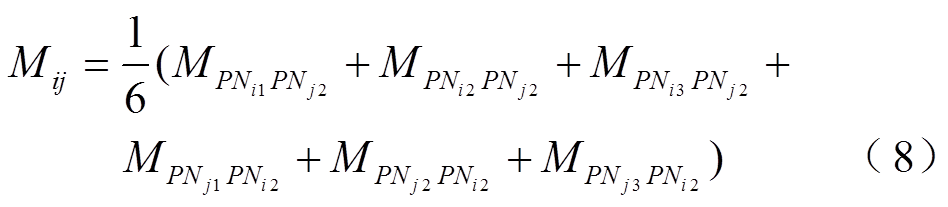
式中，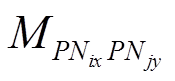
为回路Pix-Nix与回路Pjy-Njy之间的互感梯度。
以导轨1-1′和导轨1-3′为例，其互感梯度M13为
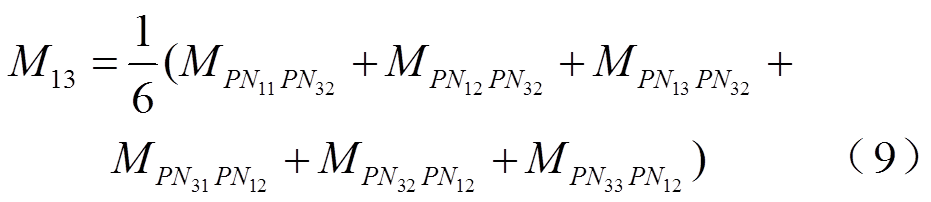
式中，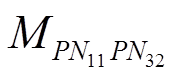
为回路P11-N11与回路P32-N32的互感梯度；
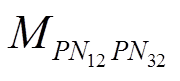为回路P12-N12与回路P32-N32的互感梯度；其他项目以此类推。
当趋肤深度不同时，各组导轨的尺寸和间距会发生变化，因而互感梯度也会随着变化。由式（8）可以计算得到如图12所示的各导轨互感梯度随趋肤深度变化的曲线。由图12可知，各组导轨的互感梯度都随着趋肤深度增加而增加。
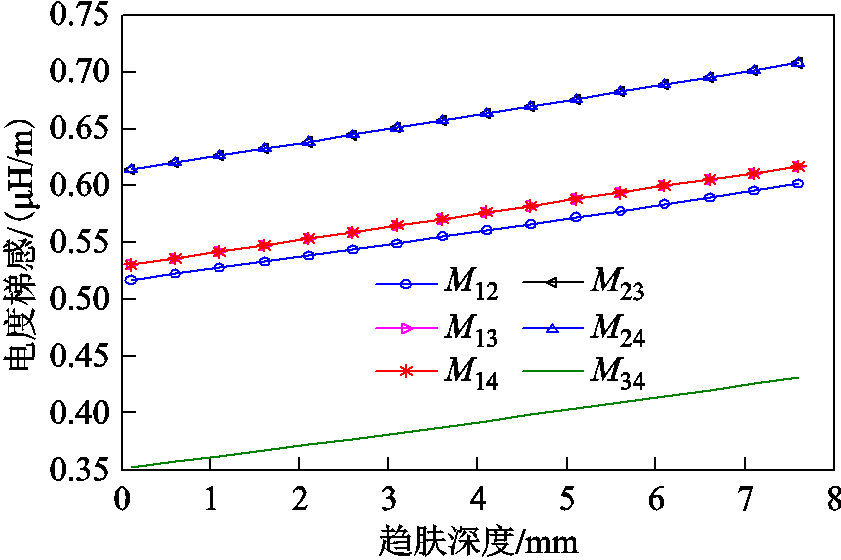
图12 各组导轨互感梯度随趋肤深度变化规律
s=70 mm, h=40mm, w=20 mm
Fig.12 Variation of mutual-inductance gradient with skin depth
依据表3的数据和式（8），计算得到表5所示的不同频率下的互感梯度。可以看到互感梯度的解析计算值与仿真值的误差在5%以内。
表5 不同频率下的互感梯度计算结果
Tab.5 Calculation results of mutual-inductance gradient at different frequencies
频率/ kHz变量互感梯度/（H/m）误差（%） 仿真值解析计算值 0.1M120.602 40.589 7-2.11 M130.629 50.605 4-3.83 M140.629 50.605 4-3.83 M230.726 20.695 1-4.28 M240.726 20.695 1-4.28 M340.420 70.420 5-0.05
（续）
频率/ kHz变量互感梯度/（H/m）误差（%） 仿真值解析计算值 1M120.546 40.538 2-1.50 M130.549 80.553 40.65 M140.549 80.553 40.65 M230.633 80.638 50.74 M240.633 80.638 50.74 M340.344 40.344 70.08 10M120.530 70.522 7-1.51 M130.558 90.536 8-3.95 M140.558 90.536 8-3.95 M230.643 40.621 2-3.45 M240.643 40.621 2-3.45 M340.357 50.357 90.11
得到各导轨自感梯度和互感梯度之后，即可根据总磁场能求出等效电感梯度。
假设原始模型中导轨通入电流为I，则根据有效通流面积之比可求得拆分后四组导轨的电流分别为
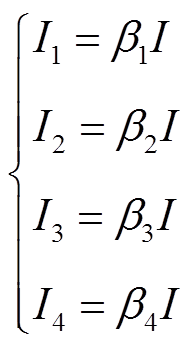（10）
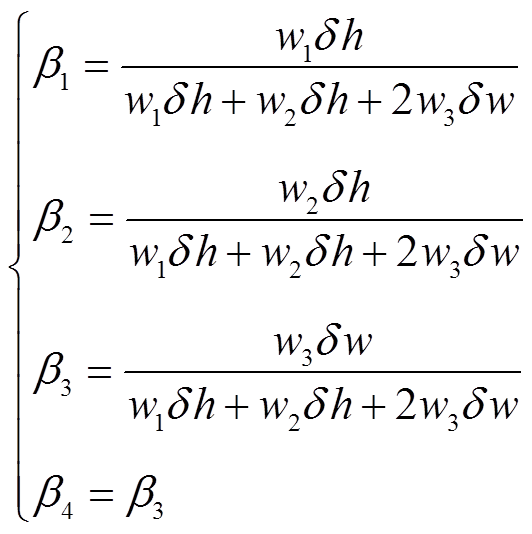（11）式中，I1~I4分别为四组导轨中通入的电流；b1~ b4分别为四组导轨的电流占总电流I的比例。
依据电感和磁场能的关系，可以推导出单位长度导轨总磁场能为
基于总磁场能等效的原则，即可得到导轨的等效电感梯度为
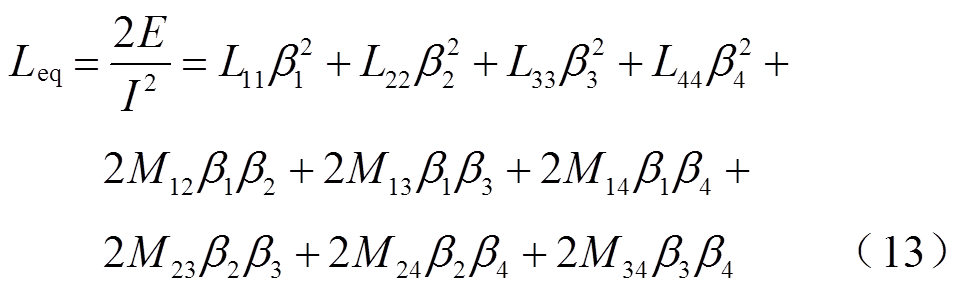
保持导轨尺寸不变（s=70mm，h=40mm，w=20mm），利用式（2）和式（13）即可求出不同频率下的电感梯度值。图13、图14所示为不同计算方法得到的电感梯度随频率变化的情况。图13中，由于Kerrisk方法（高频电感梯度）假设电流完全趋于表面，而Grover方法（低频电感梯度）假设电流均匀分布于整个导轨，因此这两种方法的计算结果都是不随频率变化的定值[17]。而本文方法与有限元方法计算结果则处于Kerrisk电感梯度与Grover电感梯度之间，从图中可以看到，随着频率提高，电感梯度逐渐减小。由图14可知，本文方法与有限元方法的误差在5%以内。
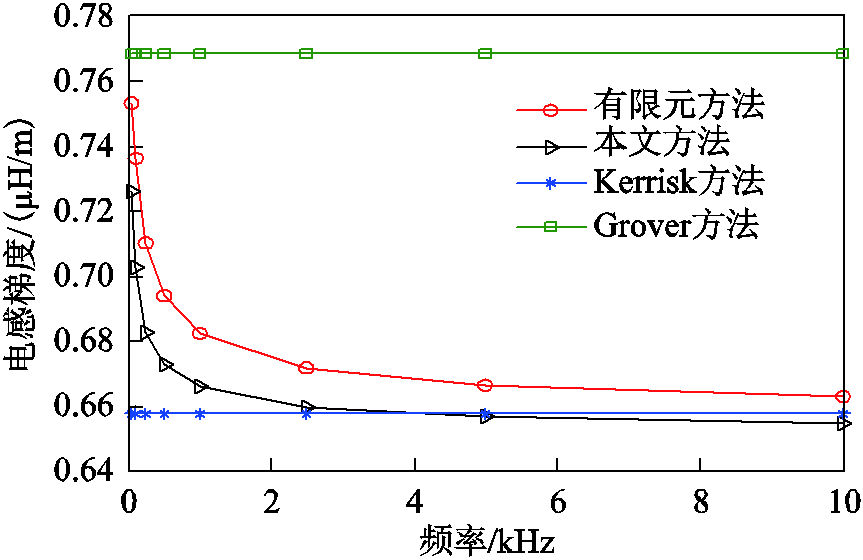
图13 不同计算方法对比
Fig.13 Comparison of different calculation methods
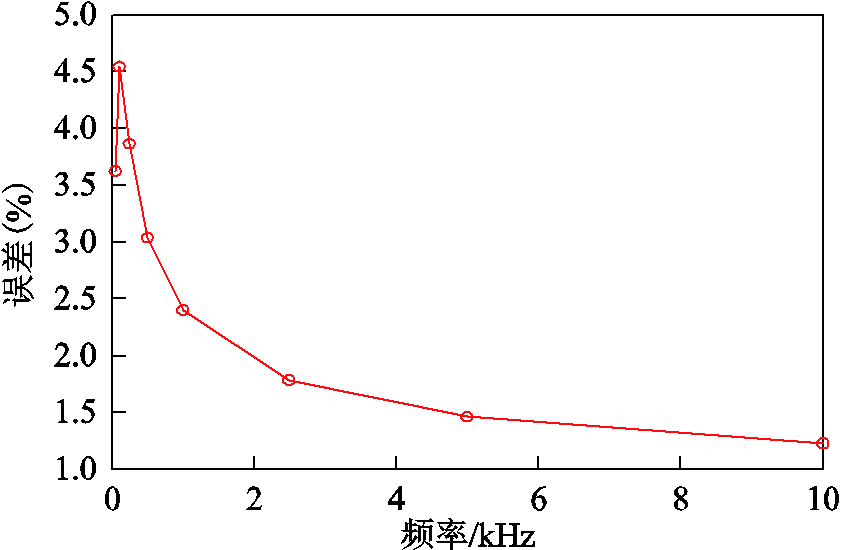
图14 本文方法与有限元方法的误差情况
Fig.14 The error between the proposed method and the finite element method
利用式（13）还可以求出导轨几何参数对电感梯度的影响。以文献[18]中的导轨作为算例，分别考虑s、h、w对电感梯度的影响。在分析单个因素变化时，其余参数保持不变。计算结果如图15所示。
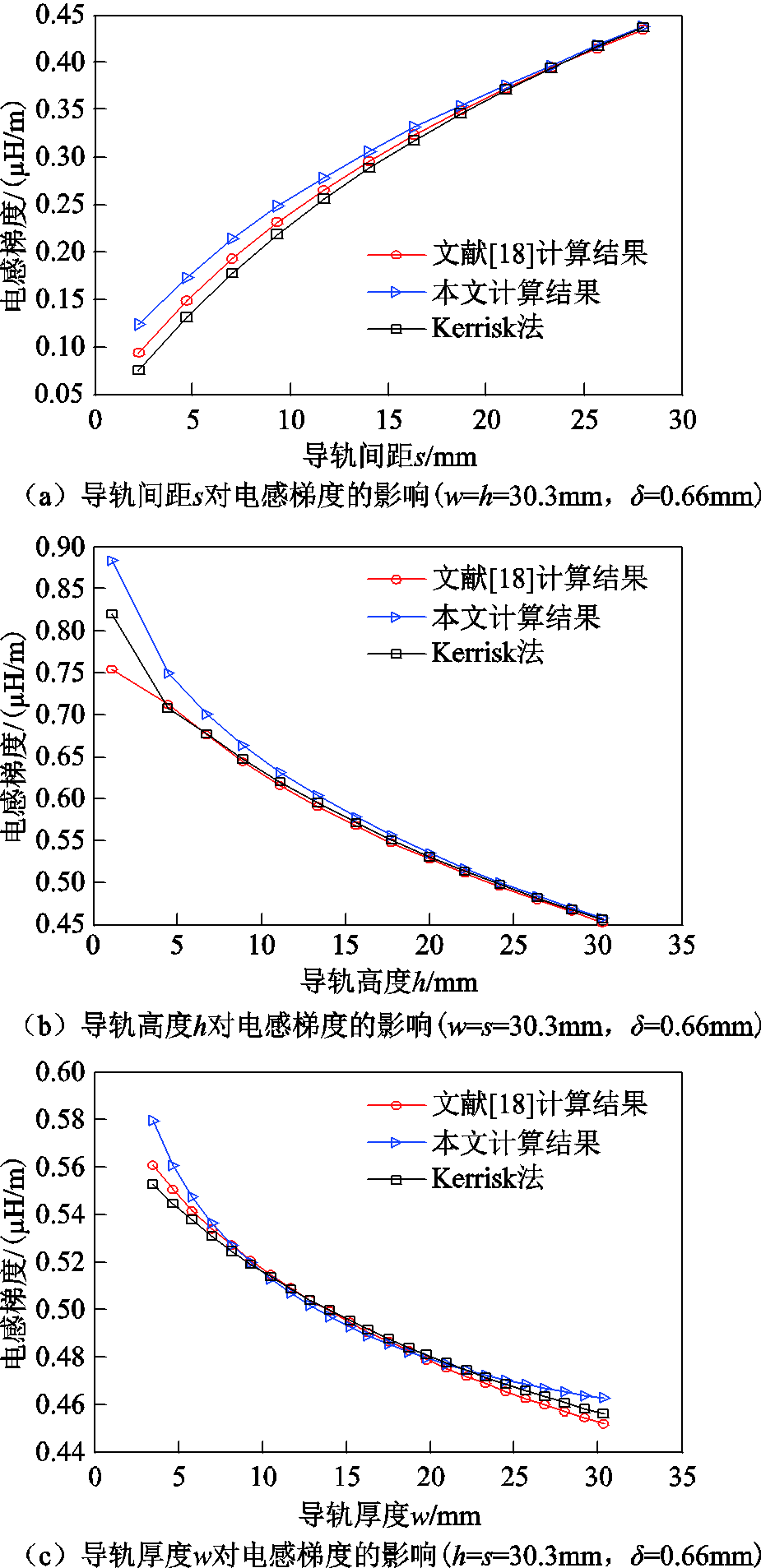
图15 导轨几何参数对电感梯度的影响
Fig.15 The influence of geometric parameters of rail on inductance gradient
图15中，三种方法计算出的电感梯度均体现了相同的规律：①导轨间距s越大，电感梯度越高；②导轨厚度w越小，电感梯度越高；③导轨高度h越小，电感梯度越高。
要获得瞬态情况下导轨电感梯度的变化，必须获知电流在导轨中的扩散情况[13-14]，国内的杨玉东[10]、王志增[19]等均对此进行了较为充分的研究。为了验证本文方法的正确性，以文献[19]中的导轨作为研究对象，并选取相同的电流波形，将本文计算结果与文献中的结果进行对比。其中，导轨尺寸为h=20mm，w=10mm，s=12mm，电流波形如图16所示。
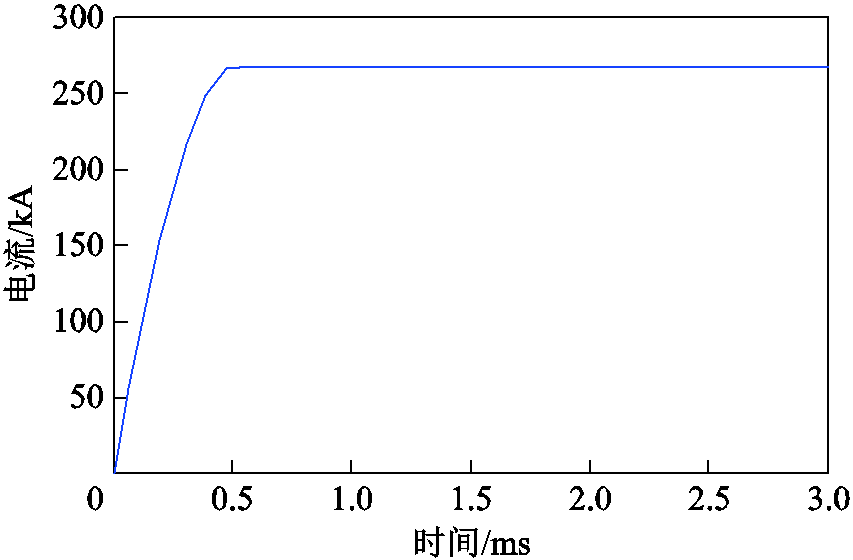
图16 电流随时间变化曲线
Fig.16 Time-varying curve of current
对于如图16所示的电流波形，可采用阶跃电流激励下的趋肤深度公式进行近似计算[12]，即
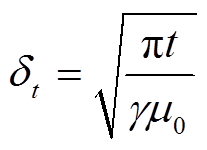（14）式中，
为趋肤深度；m0为真空磁导率；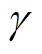
为导体电导率；t为通流时间。由式（14）可知，趋肤深度是关于通流时间t的函数，通流时间越短，则电流越趋近于导轨表面。
根据趋肤深度和导轨尺寸即可求出导轨的电感梯度，结果如图17所示。
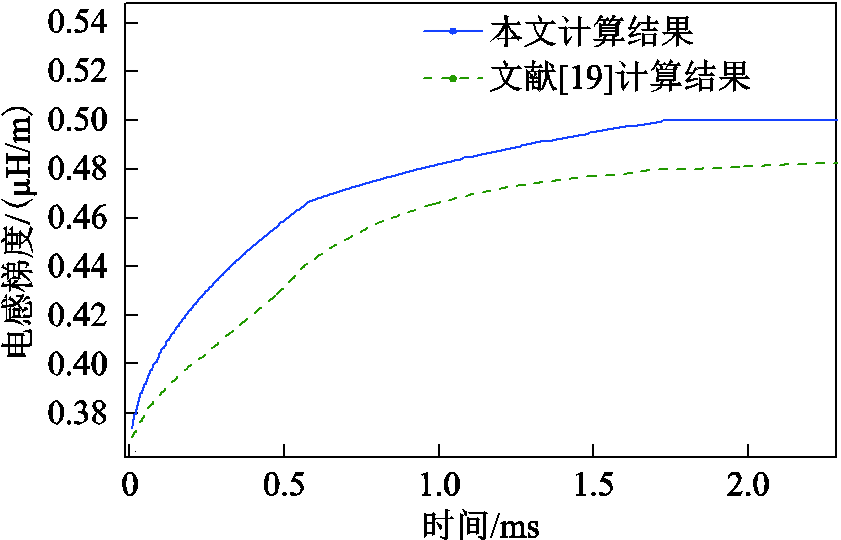
图17 电感梯度随时间变化曲线
Fig.17 Time-varying curve of inductance gradient
从图17可以看到，本文计算结果与文献[19]计算结果较为吻合，电感梯度随着时间逐渐增大，最后趋于稳定。
本文基于趋肤深度构建了矩形导轨的等效几何模型，并且由磁能等效的原则推导了电感梯度的解析表达式，所提出的方法能够综合考虑导轨尺寸和电流扩散对电感梯度的影响。通过与不同参考文献的计算结果进行对比，本文方法的正确性得到了验证。
应注意，实际发射过程中电流趋肤深度的变化过程较为复杂，需结合具体情况进行推导和计算。但以导轨尺寸及趋肤深度作为核心参数来求取时变电感梯度的计算方法仍然适用。
参考文献
[1] 李军, 严萍, 袁伟群. 电磁轨道发射技术的发展与现状[J]. 高电压技术, 2014, 40(4): 1052-1064. Li Jun, Yan Ping, Yuan Weiqun. Electromagnetic gun technology and its development[J]. High Voltage Engineering, 2014, 40(4): 1052-1064.
[2] 鲍晓华, 刘佶炜, 孙跃, 等. 低速大转矩永磁直驱电机研究综述与展望[J]. 电工技术学报, 2019, 34(6): 1148-1160. Bao Xiaohua, Liu Jiwei, Sun Yue, et al. Review and prospect of low-speed high-torque permanent magnet machines[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1148-1160.
[3] 王莹, 肖峰. 电炮原理[M]. 北京: 国防工业出版社, 1995.
[4] 吕亚军, 程思为, 王东, 等. 表贴式永磁电机在电枢磁场作用下的定子受力计算模型[J]. 电工技术学报, 2019, 34(15): 3124-3135. Lü Yajun, Cheng Siwei, Wang Dong, et al. The stator force calculation model for surface mounted permanent magnet motor under the action of armature magnetic field[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3124-3135.
[5] Grover F W. Inductance calculations: working formulas and tables[M]. New York: Dover Publications, 1962.
[6] Kerrisk J F. Current distribution and inductance calculations for rail-gun conductors[R]. Los Alamos, NM, USA: Los Alamos National Laboratory, 1981.
[7] Keshtkar A, Bayati S. Derivation of a formula for inductance gradient using intelligent estimation method[J]. IEEE Transactions on Magnetics, 2009, 45(1): 305-308.
[8] Deadrick F, Hawke R, Scudder J. MAGRAC-a electromagnetic rail launcher simulation program[J]. IEEE Transactions on Magnetics, 2003, 18(1): 94-104.
[9] Ghassemi M, Barsi Y M, Hamedi M H. Analysis of force distribution acting upon the rails and the armature and prediction of velocity with time in an electromagnetic launcher with new method[J]. IEEE Transactions on Magnetics, 2006, 43(1): 132-136.
[10] 杨玉东, 王建新, 薛文. 轨道炮动态负载特性的分析与仿真[J]. 兵工学报, 2010, 31(8): 1026-1031.Yang Yudong, Wang Jianxin, Xue Wen. Simulation and analysis for dynamic load characteristic of electromagnetic rail-gun[J]. Acta Armamentarii, 2010, 31(8): 1026-1031.
[11] 李湘平, 鲁军勇, 李玉, 等. 基于解析法的电磁发射弹丸内膛磁场分布特性分析[J]. 兵工学报, 2016, 37(12): 2205-2211. Li XiangPing, Lu Junyong, Li Yu. Analysis of distribution characteristics of in-bore magnetic field of electromagnetically launched projectile based on analytical method[J]. Acta Armamentarii, 2016, 37(12): 2205-2211.
[12] Marshall R A, Ying W. Electromagnetic rail launchers: their science and technology[M]. Beijing: China Machine Press, 2004.
[13] Lü Qingao, Xiang Hongjun, Lei Bin, et al. Physical principle and relevant restraining methods about velocity skin effect[J]. IEEE Transactions on Plasma Science, 2015, 43(5): 1523-1530.
[14] 苏子舟, 国伟, 张涛. 电磁轨道发射装置技术[M]. 北京: 国防工业出版社, 2019.
[15] 刘治鑫, 王东, 余中军, 等. 基于磁性槽楔修正模型的感应电动机气隙磁场的分布磁路法[J]. 电工技术学报, 2019, 34(15): 3112-3123. Liu Zhixin, Wang Dong, Yu Zhongjun, et al. Distributed magnetic circuit method for calculating air-gap magnetic field of induction motor based on modified model considering the effect of magnetic slot wedges[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3112-3123.
[16] 彭飞, 杨文英, 翟国富. 基于优化的传输线法的并行静磁场有限元方法[J]. 电工技术学报, 2019, 34(13): 2716-2725. Peng Fei, Yang WenYing, Zhai Guofu. An optimized parallel transmission line iteration for parallel finite element analysis in magnetostatic field[J]. Transactions of China Electrotechnical Society, 2019, 34(13): 2716-2725.
[17] Kohlberg I, Coburn W O A. solution for the three dimensional rail gun current distribution and electromagnetic fields of a rail launcher[J]. IEEE Transactions on Magnetics, 1995, 31(1): 413-416.
[18] Keshtkar A. Effect of rail dimension on current distribution and inductance gradient[J]. IEEE Transactions on Magnetics, 2005, 41(1): 383-386.
[19] 王志增, 袁伟群, 严萍. 瞬态情况下电磁轨道发射器的电感梯度[J]. 高电压技术, 2017, 43(12): 4039-4044. Wang Zhizeng, Yuan Weiqun, Yan Ping. Inductance gradient for rail-type electromagnetic launcher under transient conditions[J]. High Voltage Engineering, 2017, 43(12): 4039-4044.
Modeling and Analysis of Time-Varying Inductance Gradient for Electromagnetic Rail Launcher
Abstract Inductance gradient, an important parameter of electromagnetic rail launcher, weighs strongly on propulsive force and efficiency. There are two main weaknesses in the previous research of inductance gradient: 1) The general analytical method take the rail dimensions into account regardless of the influence of current diffusion, thus the dynamic characteristics cannot be described; 2) Though the finite element method can analyze the influence of the current diffusion, the calculation process is lack of efficiency. Therefore, considering the influence of both rail dimensions and current diffusion, this paper proposes an analytical method to calculate the inductance gradient, which is based on the skin depth and the principle of magnetic energy equivalence. The results calculated by this method were compared with those from different references, and good agreements were obtained. The proposed method can provide an effective theoretical guidance for the optimization design and performance analysis of electromagnetic rail launcher.
keywords：Electromagnetic rail launcher, skin depth, inductance gradient, analytical method
中图分类号：TM153+.2
DOI: 10.19595/j.cnki.1000-6753.tces.191611
收稿日期2019-11-25
改稿日期2020-03-19
彭之然 男，1992年生，博士研究生，研究方向为电磁发射技术。E-mail：zhiranpeng@qq.com
汪光森 男，1969年生，教授，博士生导师，研究方向为电力电子技术。E-mail：guangsenwang@sina.com（通信作者）
（编辑 赫蕾）