 (1)
(1)摘要 电磁发射装置是一种依靠电磁能将弹丸以极快的速度推射出膛的电气设备。该文针对弹丸弹道姿态测量问题,提出一种基于高速摄像技术以及图像增强与边缘提取后处理技术的弹丸姿态测量方法。由于弹丸运动速度极快,采用高速摄像技术对飞行中的弹丸进行拍摄,同时鉴于摄像设备硬件以及拍摄条件限制,提出一种基于伽马变换以及二型模糊集的图像增强算法以改善图像对比度及清晰度。进一步基于SUSAN算法与形态学操作对图像边缘进行提取并利用基于最小二乘原理的多项式拟合迭代方法实现了对弹丸边缘的拟合和姿态的提取,最后通过实验验证该文方法的有效性。
关键词:电磁发射 弹丸姿态 二型模糊集 SUSAN算法
电磁发射不同于传统发射技术,其可将电磁能转换为被发射物的动能[1],具有弹丸出膛速度精确可控的优势,在防空、反导以及对地支援方面具有极其广阔的应用前景[2-3]。随着对电磁发射装置的研究从理论化向工程化不断迈进,针对电磁发射装置及其发射物的相关测试技术逐渐成为研究热点。电磁轨道发射装置的中间弹道是指弹丸出膛后,弹拖、电枢与弹丸分离的过程,中间弹道飞行姿态作为超高声速弹丸设计参考的重要实验指标,对提升电磁发射装置打击精确度具有重要意义。由于电磁发射装置刚由理论阶段过渡到工程阶段,对于弹丸中间弹道姿态的测量基本属于空白。与传统火炮不同的是,电磁发射装置弹丸发射速度更高,可达2 000m/s[4-5],同时其射程远大于传统火炮,这使得弹丸的姿态变化不断在距离上进行累积,影响最终的打击精度。由于没有类似于传统发射装置内的膛线设计,弹丸出膛后不存在自旋,导致弹丸姿态可能有较大变化,同时弹丸体积相对较小,因此需要测量精度更高。
在弹丸上搭载传感器在一定程度上会改变弹丸重心等物理特性,因此一般采用高速摄像的非接触方法对弹丸中间弹道姿态进行测量。高速摄像作为一种非接触式光学测量手段,具有测量结果直观,测量数据后处理方式灵活多样的优点,被广泛应用于电磁轨道发射装置膛内关于固体电枢的观察与测量[6]。由于发射弹丸速度快,弹丸体积较小,受高速摄像设备及实验成本限制,拍摄得到的弹丸图像分辨率有限,同时受到发射过程中的弧光干扰,很难得到清晰的弹丸图像,给进一步分析弹丸的姿态造成了很大障碍。数字图像增强技术为提升图像清晰度与对比度提供了有力工具,一般来讲,可以将数字图像增强技术分为空间域增强与变换域增量两种处理方法。与空间域增强技术相比,例如傅里叶变换、小波变换等变换域增强技术可以有效地提升图像质量,但同时也存在计算量较大的缺点[7]。针对以上问题,基于模糊理论的图像增强算法得到了快速发展。J. M. S. Prewitt[8]首次提出将图像子集看作模糊集的观点,基于这种观点,S. A. Pal等[9]提出了基于模糊集合理论的图像增强算法,此算法将图像像素点灰度通过非线性变换映射到模糊域中,基于灰度特征确定像素点相对应的隶属度,进一步通过设定适当的阈值对像素隶属度进行迭代变换,最终反变换到灰度场,实现图像增强的效果。针对Pal算法中出现的灰度截断舍去的缺陷,诸多学者对非线性映射函数以及阈值确定方法进行了改进。但没有发生改变的是,无论使用何种映射方式,数字图像中的像素灰度值都对应一个确定的隶属度,而这会降低算法的鲁棒性。为此L. A. Zadeh在模糊集(一型模糊集)的基础上引入二型模糊集[10],其隶属度不再是一个确定的值,而处于在一个区间内,将模糊理论从二维空间提升到了三维空间。关于二型模糊集图像增强算法的研究目前还比较少,H. R. Tizoosh等[11]基于两级隶属度函数创建了一种新的隶属度函数,并将其运用到二型模糊集图像增强中。T. Chair等[12]提出利用Hamcher T余模集合算子,基于二型模糊集隶属度函数上界与下界构建新的隶属度函数,从而实现图像增强,取得了较好的增强效果。
本文首先对中间弹道测试系统以及二型模糊集基础理论进行介绍;然后提出一种基于T余模变换的二型模糊集图像增强算法,对拍摄的弹丸图像进行增强,同时基于改进SUSAN边缘检测算子,对图像中目标弹丸进行边缘检测,并基于检测边缘结果提出边缘曲线函数拟合方法,实现弹丸姿态的提取;最终仿真结果显示本文所提算法具有较高的测量精度。
由于弹丸飞行速度极快,要求高速摄像机的拍摄频率也较高,本文采用Phantom高速摄像机,其可以提供超过40 000帧的拍摄频率。由于拍摄频率很高,较长时间的拍摄需要大量内存空间,因此无法对整个实验过程进行全程拍摄。若要精确捕捉飞行过程中的弹丸进行姿态,需在弹丸发射的瞬间提供给高速摄像机精确的触发信号。
由于单一拍摄位置只能获取目标弹丸的二维空间信息,因此采用两台同步触发的高速摄像机在距炮口相同距离处进行正交布设。一台高速摄像机位于炮口水平中心平面,对弹丸进行正侧视拍摄,用于获取弹丸在垂直平面内的姿态;另一台高速摄像机位于炮口垂直中心平面上,对弹丸进行正俯视拍摄,用于获取弹丸在水平平面上的姿态。现实中,摄像机成像会产生径向畸变、离心畸变、薄棱镜畸变的镜头畸变[13]。高速摄像机成像可以使用4个坐标系进行描述,分别为世界坐标系、摄像机坐标系、镜头成像坐标系及图像像素坐标系。一般在短焦距光学镜头中,径向畸变起主要作用。镜头畸变矫正可以表示为
 (1)
(1)式中,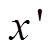 和
和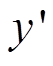 分别为在图像像素坐标系中坐标(x, y)矫正后的坐标;k1和k2为非线性畸变系数,可以通过实验的方法获取。一般而言k1和k2大小接近,可近似认为在x方向与y方向畸变程度近似,因此相机的畸变对成像图像中的姿态角度影响很小,可忽略其对弹丸姿态的影响,从而简化实验流程与坐标系变换解算过程的计算量。
分别为在图像像素坐标系中坐标(x, y)矫正后的坐标;k1和k2为非线性畸变系数,可以通过实验的方法获取。一般而言k1和k2大小接近,可近似认为在x方向与y方向畸变程度近似,因此相机的畸变对成像图像中的姿态角度影响很小,可忽略其对弹丸姿态的影响,从而简化实验流程与坐标系变换解算过程的计算量。
一型模糊集图像增强算法中的非线性映射函数,即像素点对应的隶属度函数一般由专家根据其经验或实验获得。二型模糊集理论消除了映射函数的主观影响,并因为其隶属度函数具有不确定性得到广泛的应用[14]。如图1所示,以高斯次隶属度函数为例进行说明,其在一型模糊集的基础上引入隶属度函数的不确定区域,而非一型模糊集针对某一元素的固定的隶属度函数,进一步提升了该集合针对不确定性描述的自由度以及鲁棒性。二型模糊集定义如下。
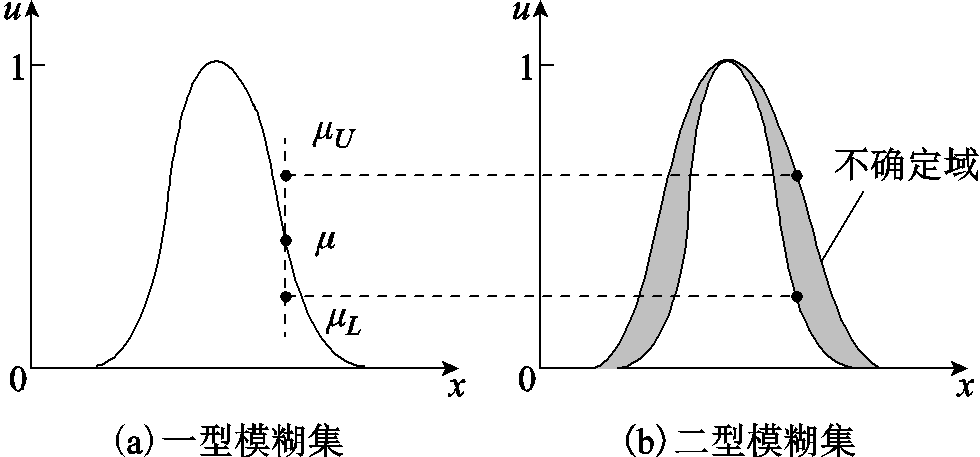
图1 一型模糊集与二型模糊集示意图
Fig.1 Schematic diagram of type I and type II fuzzy sets
定义1 二型模糊集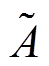 ,其隶属度函数可以定义为
,其隶属度函数可以定义为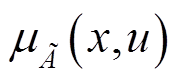 ,其中
,其中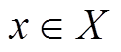 ,
,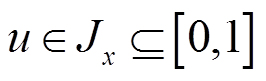 ,则二型模糊集可以表示为
,则二型模糊集可以表示为
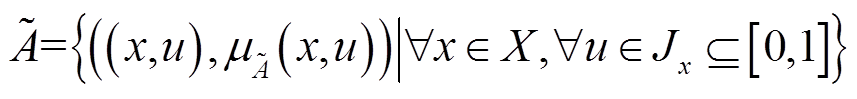 (2)
(2)其中,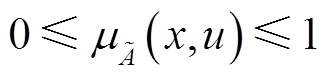 。二型模糊集
。二型模糊集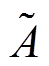 可以表示为积分形式,即
可以表示为积分形式,即
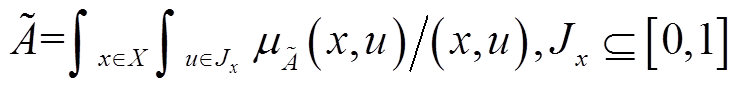 (3)
(3)式中,二重积分表示关于所有x和u的并集;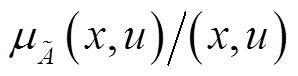 表示对模糊集元素x及其对应隶属度u的二重隶属度。为了得到实用性更强的二型模糊集,可以规定其隶属度函数不确定区域的上、下界,进一步则二型模糊集可以表示为
表示对模糊集元素x及其对应隶属度u的二重隶属度。为了得到实用性更强的二型模糊集,可以规定其隶属度函数不确定区域的上、下界,进一步则二型模糊集可以表示为

式中,隶属度的上、下界分别定义为
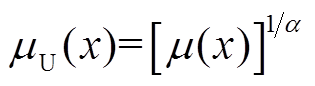 (5)
(5)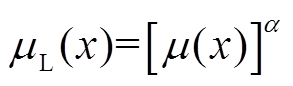 (6)
(6)基于实验得出,当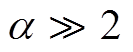 时,通常对于图像数据而言是没有意义的,因此一般其取值范围为[0, 2]。
时,通常对于图像数据而言是没有意义的,因此一般其取值范围为[0, 2]。
由于弹丸飞行速度极快,基于高速摄像机成像原理,其拍摄时所设定的频率越高,拍摄分辨率就会越低,同时弹丸体积较小,这就导致在实际拍摄过程中很难获取清晰的弹丸图像。在发射过程中拍摄会受到强弧光的干扰,使得背景光强变化较大,很难精确把控摄像机的曝光设置。同时弧光会导致图像中灰度偏移现象的产生,一般认为灰度偏移场是在真实图像上叠加的一个缓慢变化的灰度变化场,因此拍摄图像可能会在局部方向上出现对比度较差的情况。无论基于何种方法实现对弹丸姿态的提取,其获取精度均与图像质量直接相关,因此提升图像清晰度与对比度以获取较为清晰的弹丸边缘信息成为提升测试精度的关键环节。
与一般图像增强算法相比,模糊图像增强算法具有更高的像素灰度自由度,更适用于图像中像素隶属不明确的情况。二型模糊集作为普通集合的一种拓展,同样存在与普通集合中如并集、交集等相似的集合操作,在模糊集理论中,这些操作被称为T模和T余模。T模和T余模存在多种表现形式[15-16],可以根据其运算类型将其分为两类:一类为仅包含有纯代数运算的变换运算,如Hamacher所提出的T模和T余模运算;另一类为包含有最大或最小运算的条件运算。
T模运算为
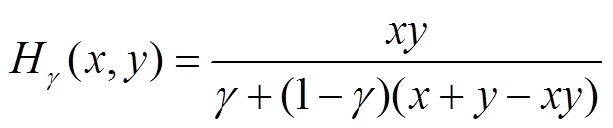 (7)
(7)其中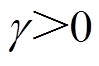 ,衰减因子可以表示为
,衰减因子可以表示为
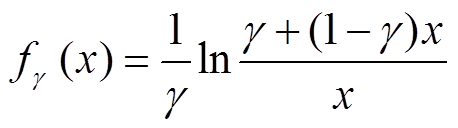 (8)
(8)
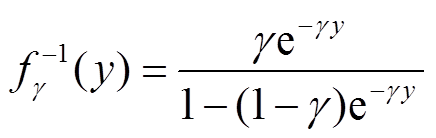 (9)
(9)T余模运算为
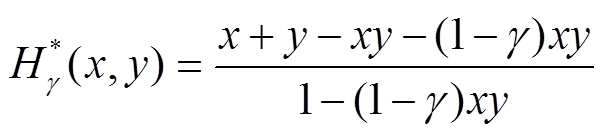 (10)
(10)增长因子可以表示为
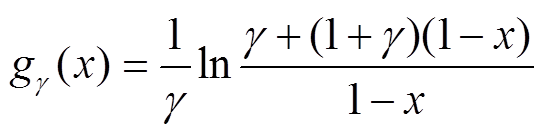 (11)
(11)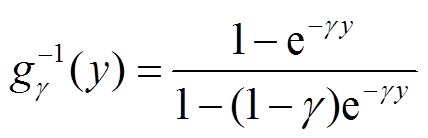 (12)
(12)Yager提出的T模运算可以表示为
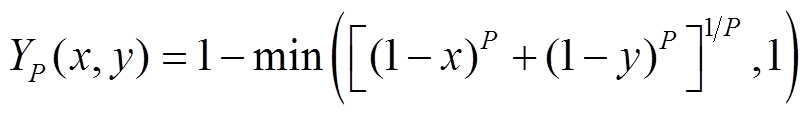 (13)
(13)式中,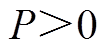 。衰减因子为
。衰减因子为
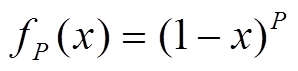
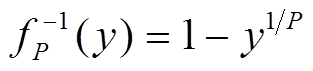
T余模运算可以表示为
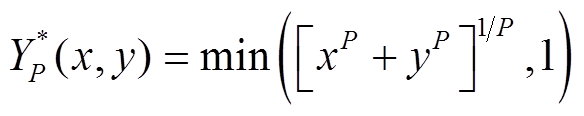 (14)
(14)其中,增长因子为
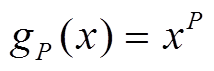
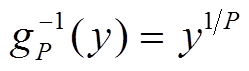
虽然包括最大值与最小值运算的条件操作更加简单,但其对图像的最终增强效果比不包括最值运算的T模和T余模运算差,因此本文采用Hamacher所提出的T模和T余模运算来实现图像增强。
假设所拍摄的图像大小为M×N,首先需要通过映射变换的方式将其变换到模糊域,即将像素的灰度转变为其相对应的隶属度函数。由于二型模糊集隶属度处于一个不确定区域内,因此不需要像一型模糊图像增强算法那样使用非常复杂的映射函数,一般使用式(15)进行变换。
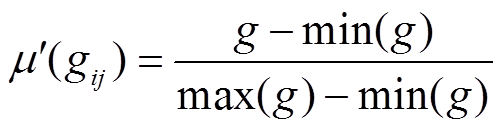 (15)
(15)式中,g为像素的灰度值,max(g)和min(g)分别表示图像中的最大灰度值和最小灰度值。由于拍摄图像受炮口弧光的影响,不均匀的曝光导致的灰度偏移场使图像中一部分灰度总体偏大,而另一部分灰度总体较小,因此本文在隶属度映射函数中引入伽马变换,伽马变换基本形式为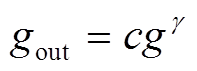 ,其中c和g为正常数,对于不同的g 值,
,其中c和g为正常数,对于不同的g 值,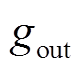 与g有着不同的输出变化范围,如图2所示。
与g有着不同的输出变化范围,如图2所示。
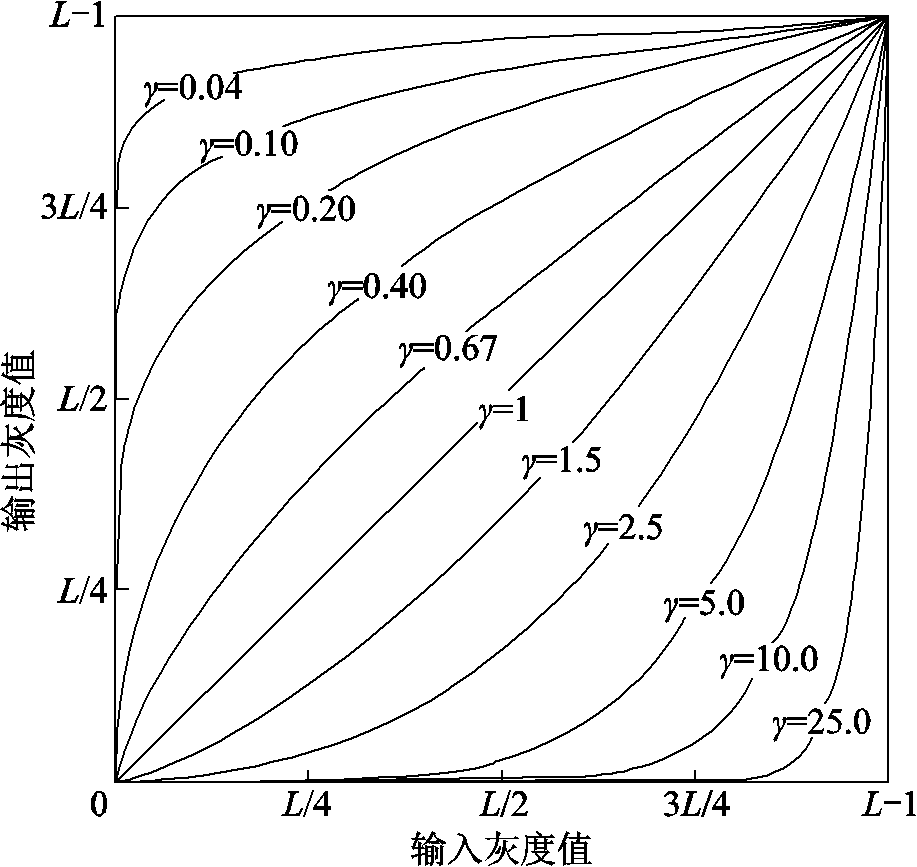
图2 Gamma灰度变换示意图
Fig.2 Gamma gray level transform diagram
隶属度映射函数变为
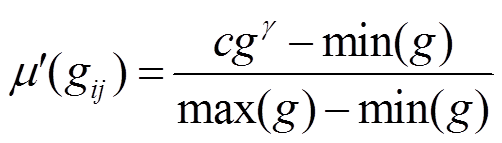 (16)
(16)进一步,在考虑不确定域上、下界的条件下,对隶属度函数进行Hamacher T余模变换,可以得到
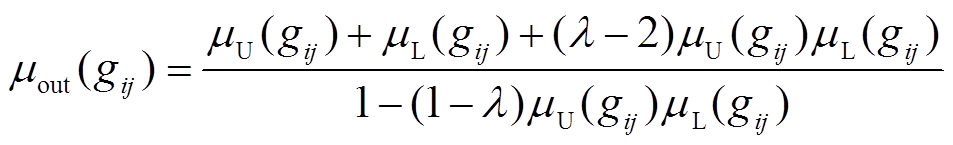 (17)
(17)式中,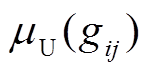 和
和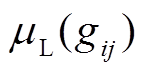 分别为隶属度函数在对应像素位置的上界和下界,隶属度不确定区域的上下界由
分别为隶属度函数在对应像素位置的上界和下界,隶属度不确定区域的上下界由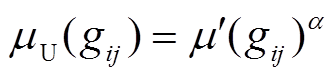 ,
,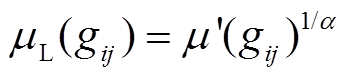 确定,式中的参数
确定,式中的参数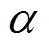 、c及
、c及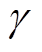 需要通过试错实验进行确定,本文取
需要通过试错实验进行确定,本文取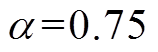 ,
,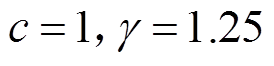 ,
,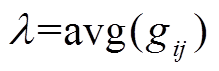 即
即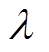 取图像中的像素灰度均值。为进一步解决由于弧光干扰而产生的灰度不均匀现象,本文将图像数据分为较小的子集即图像子集,分别对每一个小图像块进行图像增强,再将图像子集进行拼接,实现对图像不同对比度的局部增强。在拼接过程中,图像子集拼接处会出现较为严重的伪影,因此在划分图像子集时,可使每个相邻子集间有部分重叠区域进行依次拼接,以此实现图像子集拼接边界处灰度平滑的效果,消除由此产生的伪影,本文采用的图像子集大小为
取图像中的像素灰度均值。为进一步解决由于弧光干扰而产生的灰度不均匀现象,本文将图像数据分为较小的子集即图像子集,分别对每一个小图像块进行图像增强,再将图像子集进行拼接,实现对图像不同对比度的局部增强。在拼接过程中,图像子集拼接处会出现较为严重的伪影,因此在划分图像子集时,可使每个相邻子集间有部分重叠区域进行依次拼接,以此实现图像子集拼接边界处灰度平滑的效果,消除由此产生的伪影,本文采用的图像子集大小为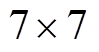 ,重叠区域的大小为
,重叠区域的大小为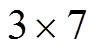 、
、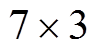 或大小为33个像素点的不规则形状,如图3所示。
或大小为33个像素点的不规则形状,如图3所示。
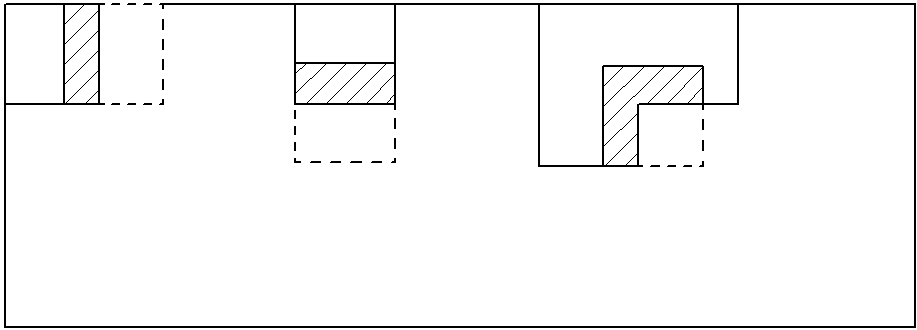
图3 图像子集拼接示意图
Fig.3 Sub image mosaic schematic
所拍摄的水平侧面视角弹丸图片如图4所示,通过二型模糊图像增强算法后的弹丸图片如图5所示。

图4 原始图像
Fig.4 Initial image

图5 增强变换后图像
Fig.5 Image after enhancement
通过图5可以看出,该算法克服了由于弧光干扰导致的局部对比度较差的现象,弹丸与背景的对比度大幅提升,增强后图像细节更加丰富,弹丸的边缘更加清晰,与非增强图像相比可以较为清晰地看到由于弹丸高速运动在尾部产生的空气激波。
经过对拍摄图像进行增强,图像的对比度及清晰度大幅提升,为获取弹丸姿态需要准确的检测出弹丸的边界,弹丸边界的检测及提取直接影响到最终的测量准确性。本文引入SUSAN(small univalve segment assimilating nucleus)方法对增强后的图像进行边缘提取,从而最终获取弹丸的中间弹道姿态。
SUSAN算子是一种不依赖计算图像梯度的快速边缘检测技术[17],具有定位精确及抗噪声能力强等优点,其使用圆形探测模板在目标图像中移动,以逐个对比圆形模板内部图像像素点灰度与模板中心像素点灰度的差异,计算出与中心像素灰度值近似的像素数量,进一步通过判别函数判断,从而实现边缘、角点提取的目的[18]。一般SUSAN算法采用37像素近似圆形模板进行移动掩膜。
由灰度值与中心像素灰度值之差在阈值范围内的模板内像素点组成的集合称为核值相似区域(USAN),判别函数为
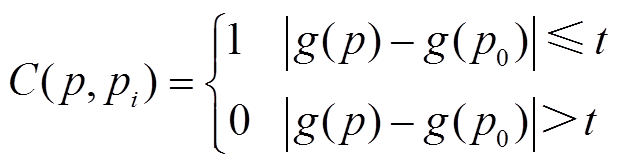 (18)
(18)式中,p和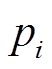 分别为模板中心像素点与模板上其余像素点;
分别为模板中心像素点与模板上其余像素点;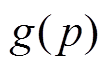 和
和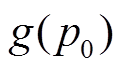 分别为其对应的灰度值。本文采用更加稳定的核值相似区域判别函数。
分别为其对应的灰度值。本文采用更加稳定的核值相似区域判别函数。
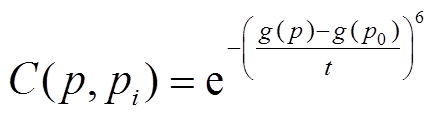 (19)
(19)式中,t为设定阈值,可以基于图像像素灰度统计特征获取。
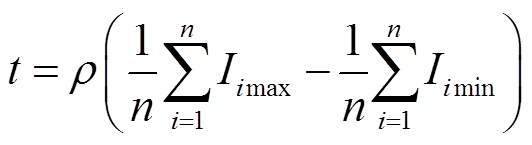 (20)
(20)式中,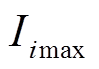 、
、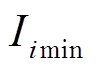 分别为图像中灰度值最大和最小的i个像素灰度。进而图像中每个像素点的USAN区域为
分别为图像中灰度值最大和最小的i个像素灰度。进而图像中每个像素点的USAN区域为
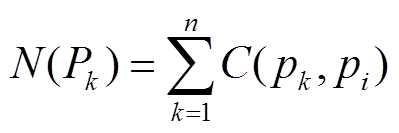 (21)
(21)式中,n为图像中像素点总数。当近似圆形模板在图像上移动时,USAN会随着模板处于图像不同部分而发生变化,其区域示意图如图6所示。
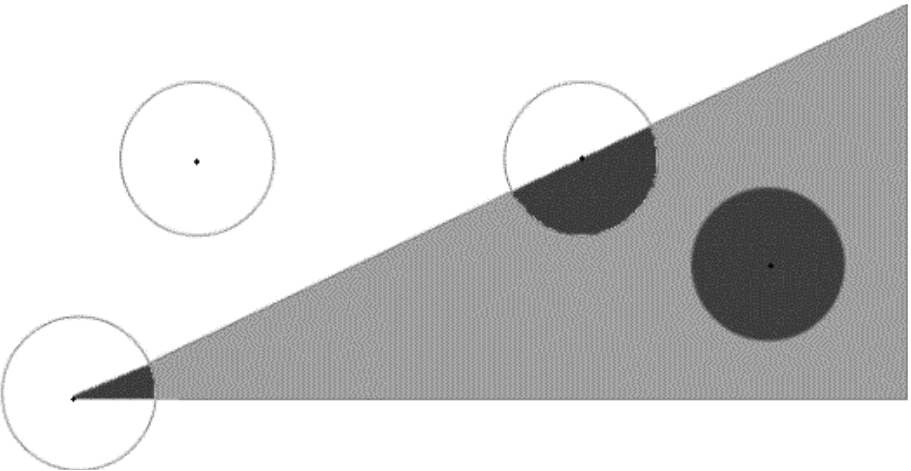
图6 USAN区域示意图
Fig.6 USAN area diagram
当模板中心像素点处于图像目标物边缘但非角点时,USAN区域约占模板面积的一半;当模板完全处于图像目标物内或完全置于图像目标物外时,USAN区域为模板面积区域;当模板中心像素点处于图像目标物角点上时,USAN区域最小。根据USAN的大小,通过判别函数来判断模板中心像素是否处于图像中目标物边缘以实现图像边缘提取的目的,判别函数为
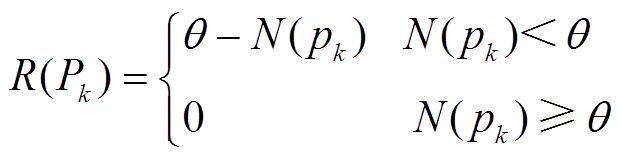 (22)
(22)式中,![]() 为通过试错实验设定的几何门限值,综合考虑计算速度与图像分割精度需要,设定为模板大小的0.75倍。利用SUSAN算子对增强图像进行边缘提取,提取结果如图7所示。
为通过试错实验设定的几何门限值,综合考虑计算速度与图像分割精度需要,设定为模板大小的0.75倍。利用SUSAN算子对增强图像进行边缘提取,提取结果如图7所示。
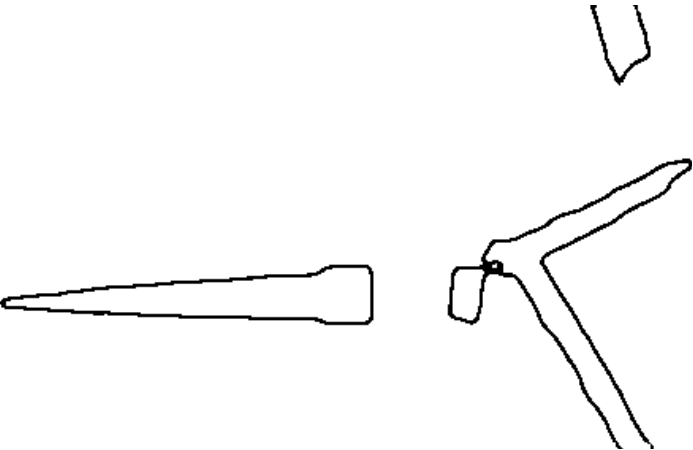
图7 SUSAN算子边缘提取结果
Fig.7 Edge extraction results by SUSAN operator
可以看出弹丸、电枢及蛋托的边缘被清晰地提取出来。为充分提取边缘,USAN阈值设置较大,因此边缘较粗。为提升弹丸姿态的精度,进一步对边缘图像采用形态学操作以细化边缘,结果如图8所示。
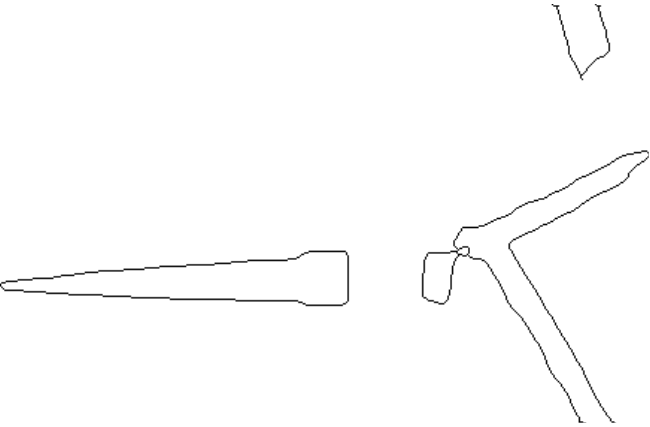
图8 形态学细化后边缘结果
Fig.8 Edge results after morphological refinement
设弹丸头部为锥体且参数未知,关于水平顺时针旋转偏转角度为正。获取其姿态偏角有两种方法。一种是获取弹丸头部像素点坐标和弹丸尾部中心像素点坐标,从而得到弹丸中心线,进而得到弹丸的姿态角。但由于弹丸头部选取单一像素点误差较大,本文采用另外一种方法来获取弹丸的姿态。分别采集弹丸上、下边缘的像素坐标信息,并对其坐标信息进行多项式函数拟合,得到上、下边缘在图像坐标系中的函数表达式。通过函数表达式来确定上、下边缘对于水平方向的角度即其斜率,最终得到弹丸的偏转角度。从微观角度来看,除绝对水平与垂直线段外,曲线与其余线段在数字图像中均由一系列矩形像素子集相互连接构成,像素子集大小的方差及连接方式将会影响对边缘拟合的精度,而在水平或垂直直线中并不存在这种情况,因此采用迭代的方式将待求线段旋转至绝对水平以减小误差。
令第n次获取的弹丸偏转角度为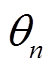 ,则将图像关于水平旋转
,则将图像关于水平旋转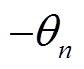 ,再次对弹丸偏转角度进行计算并记为
,再次对弹丸偏转角度进行计算并记为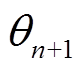 ,当
,当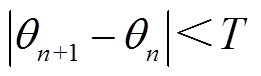 或达到最大迭代次数N时停止迭代,最终的偏转角度为
或达到最大迭代次数N时停止迭代,最终的偏转角度为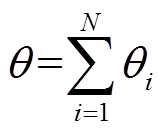 。
。
首先对其上边缘像素坐标进行提取,并使用基于最小二乘法原理的多项式拟合出其在图像坐标系中对应的表达式。分别采用线性拟合和二次多项式进行拟合,线性函数表达式为
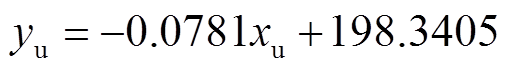 (23)
(23)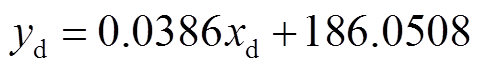 (24)
(24)式中,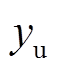 和
和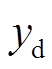 分别为上边缘与下边缘的线性函数。则弹丸关于水平的偏转角度
分别为上边缘与下边缘的线性函数。则弹丸关于水平的偏转角度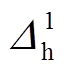 可以表示为
可以表示为
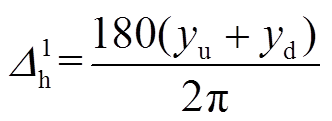 (25)
(25)求得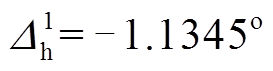 ,二次多项式拟合函数表达式为
,二次多项式拟合函数表达式为
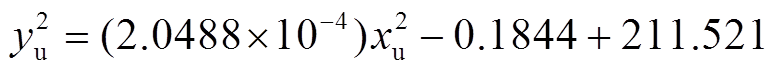 (26)
(26)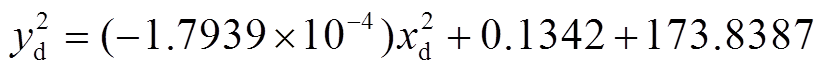 (27)
(27)式中,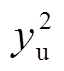 和
和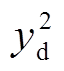 分别为上边缘与下边缘的二次函数。分别对
分别为上边缘与下边缘的二次函数。分别对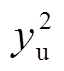 和
和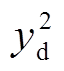 求一阶导数,并在边缘像素坐标范围内求其一阶导数的平均值,并认为该均值即为边缘关于水平方向的偏角,则弹丸关于水平的偏转角度
求一阶导数,并在边缘像素坐标范围内求其一阶导数的平均值,并认为该均值即为边缘关于水平方向的偏角,则弹丸关于水平的偏转角度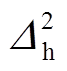 为
为
 (28)
(28)可以求得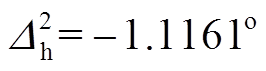 。
。
为了进一步说明实验测试方法的有效性,进行仿真验证。在不同图像分辨率的情况下合成近似形状的弹丸图像,弹头部分为标准三角形,并设定其水平偏转角度,对其使用上述算法进行姿态提取,最终得出其偏转角度并与设置角度进行对比。使用弹丸偏转角度为15°的图像进行说明,使用本文算法进行边缘提取后结果如图9所示。
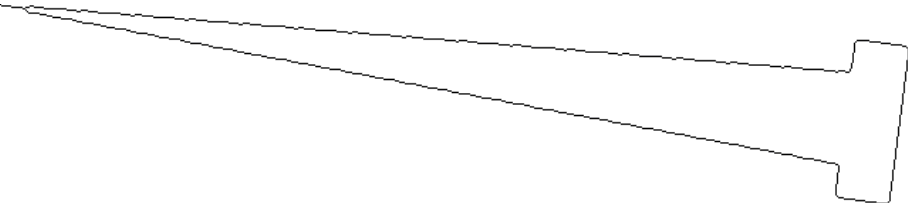
图9 仿真图像边缘结果
Fig.9 Simulated image edge results
使用线性拟合计算出其水平的偏转角度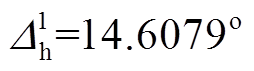 ,使用二次多项式拟合计算得出其水平的偏转角度
,使用二次多项式拟合计算得出其水平的偏转角度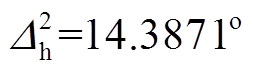 。
。
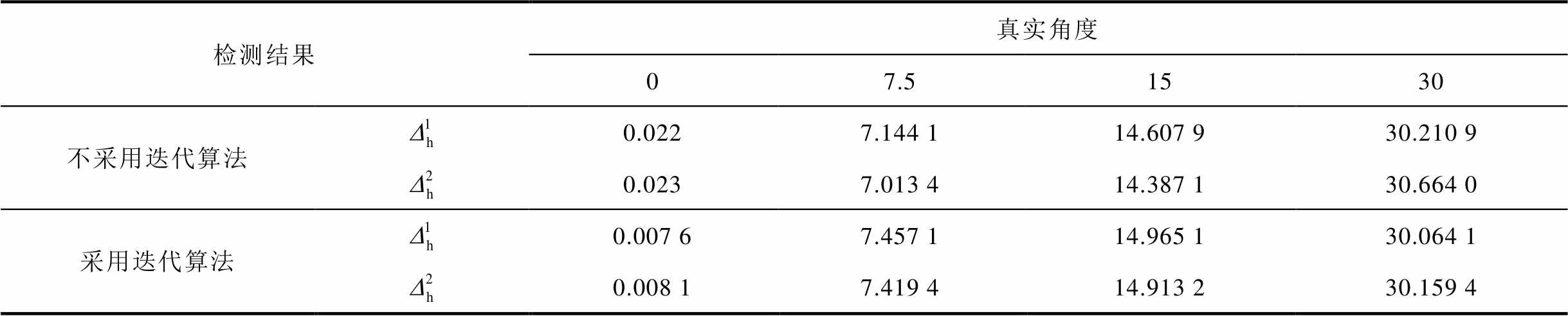
改变弹丸的偏转角度,真实水平偏角与边缘检测得出的水平偏角见表1。
表1 不同水平偏角实验结果
Tab.1 Experimental results of different horizontal deflection angles(单位:°)
检测结果真实角度 07.51530 不采用迭代算法0.0227.144 114.607 930.210 9 0.0237.013 414.387 130.664 0 采用迭代算法0.007 67.457 114.965 130.064 1 0.008 17.419 414.913 230.159 4
由于弹头部分为标准三角形,采用迭代算法精度高于不采用迭代算法,该算法可以在一定程度上对斜线在数字图像中的表示误差进行纠正。线性拟合方法所得结果较二次拟合测量方法相比精度更高,并非是多项式拟合次数越高,结果精度就越高,还需要依据弹丸外形进行相应选择。
本文阐述了电磁发射中弹丸姿态测量的需求以及涉及的主要障碍,提出了一种基于高速摄像技术及数字图像后处理技术的弹丸姿态测量方法。首先对实验所用测量平台以及二型模糊集基本理论进行了概述,进一步结合二型模糊集处理模糊图像的优势,提出了基于Gamma变换的二型模糊集增强算法,采用划分图像子集分区增强的方法克服图像中的灰度不均匀现象,并将其应用于低对比度实验图像中,取得了良好效果。基于图像增强结果,运用SUSAN算子对增强后图像进行边缘提取,利用形态学操作对提取的边缘进行细化,并利用基于最小二乘原理的多项式函数进行拟合,得到弹丸边缘在图像坐标系中的函数表达式,据此得出弹丸的水平姿态角度。最后,通过设计仿真进一步验证本文所提算法的有效性,仿真结果显示本文算法具有较高精确度,可基本测试需求。
参考文献
[1] 马伟明, 肖飞, 聂世雄. 电磁发射系统中电力电子技术的应用于发展[J]. 电工技术学报, 2016, 31(19): 1-10. Ma Weiming, Xiao Fei, Nie Shixiong. Applications and development of power electronics in electromagnetic launch system[J]. Transactions of China Electrotechnical Society, 2016, 31(19): 1-10.
[2] Fair H D. Electromagnetic launch science and technology in the United States enters a new era[J]. IEEE Transactions on Magnetics, 2005, 41(1): 158-164.
[3] 刘旭堃, 于歆杰, 刘秀成, 等. 电磁轨道炮运行阶段系统发射效率和电枢出膛动能研究[J]. 电工技术学报, 2017, 32(2): 210-217. Liu Xukun, Yu Xinjie, Liu Xiucheng, et al. Researchers on the system launch efficiency and the armature muzzle kinetic energy of a constructed electromagnetic railgun[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 210-217.
[4] Ma Weiming, Lu Junyong. Thinking and study of electromagnetic launch technology[J]. IEEE Transactions on Plasma Science, 2017, 45(7): 1071-1077.
[5] 常馨月, 于歆杰, 刘旭堃. 一种实现电枢出膛速度控制的电磁轨道炮脉冲电源触发策略[J]. 电工技术学报, 2018, 33(10): 2261-2267. Chang Xinyue, Yu Xinjie, Liu Xukun. A velocity-controlling triggering strategy of capacitive pulsed power supply electromagnetic railgun system[J]. Transactions of China Electrotechnical Society, 2018, 33(10): 2261-2267.
[6] Chakravarthy K M, Watt T J, Bourell D L. The use of high-speed video as an in-bore diagnostic for electromagnetic launchers[J]. IEEE Transactions on Plasma Science, 2011, 39(2): 809-814.
[7] Gonzalez R C, Woods R E. Digital image processing[M]. 2nd ed. Upper Saddle River: Prentice Hall, 2002.
[8] Prewitt J M S. Interactive decision-making for picture processing[C]//IEEE Conference on Decision and Control including the 16th Symposium on Adaptive Processes and A Special Symposium on Fuzzy Set Theory and Applications, IEEE, 1978.
[9] Pal S A, King R A. Image enhancement using smoothing with fuzzy sets[J]. IEEE Transactions on Systems Man & Cybernetics, 1981, 11(7): 494-501.
[10] Zadeh L A. A fuzzy-set-theoretic interpretation of linguistic hedges[J]. Journal of Cybernetics, 1972, 2(3): 4-34.
[11] Ensafi P, Tizhoosh H R. Type-2 fuzzy image enhancement[C]//International Conference Image Analysis and Recognition, Springer, Berlin, Heidelberg, 2005.
[12] Chaira T. An improved medical image enhancement scheme using type II fuzzy set[J]. Applied Soft Computing, 2014, 25: 293-308.
[13] 田原嫄, 黄合成, 谭庆昌, 等. 摄像机镜头畸变的研究[J]. 计算机工程与应用, 2009, 45(26): 49-52. Tian Yuanyuan, Huang Hecheng, Tan Qingchang, et al. Reacher on camera lens distortion[J]. Computer Engineering and Applications, 2009, 45(26): 49-52.
[14] Mendel J M , John R I B . Type-2 fuzzy sets made simple[J]. IEEE Transactions on Fuzzy Systems, 2002, 10(2): 117-127.
[15] Weber S. A general concept of fuzzy connectives, negations and implications based on t-norms and t-conorms[J]. Fuzzy Sets and Systems, 1983, 11(1-3): 103-113.
[16] Yager R R. On a general class of fuzzy connectives[J]. Fuzzy Sets and Systems, 1980, 4(3): 235-242.
[17] 王兆文, 李浩, 黄都, 等. 基于Matlab/GUI的汽油机缸内直接喷雾图像处理方法[J]. 农业机械学报, 2013, 44(9): 19-23. Wang Zhaowen, Li Hao, Huang Du, et al. Digital image processing method of gasoline direct injection spray based on Matlab/GUI[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(9): 19-23.
[18] 夏凯. 基于改进的SUSAN算法的火焰图像边缘检测研究[J]. 现代电子技术, 2015, 38(5): 58-61. Xia Kai. Research on flame image edge detection base on improved SUSAN algorithm[J]. Modern Electronics Technique, 2015, 38(5): 58-61.
Research on Ballistic Attitude Measurement of Projectile in Electromagnetic Launcher
Abstract Electromagnetic launcher is a new type of electrical equipment, which relies on electromagnetic energy to push projectiles out of the chamber at a very fast speed. Aiming at the problem of ballistic attitude measurement of projectile, a method of attitude measurement based on high-speed camera technology and image enhancement and edge extraction post-processing technology is proposed. Because the projectile moves very fast, this paper uses high-speed camera technology to shoot the projectile in flight. At the same time, considering the limitations of camera hardware and shooting conditions, this paper proposes an image enhancement algorithm based on gamma transform and two-type fuzzy sets to improve image contrast and clarity. Further, this paper extracts image edge based on SUSAN algorithm and morphological operation, and uses iterative polynomial fitting method based on least square principle to extract projectile attitude. Finally, the credibility of this method is verified by experiments
keywords:Electromagnetic launch, attitude measurement of projectile, type-2 fuzzy set, SUSAN algorithm
中图分类号:TM930
DOI:10.19595/j.cnki.1000-6753.tces.191506
国家自然科学基金(51877214,51607187)和国家重点基础研究发展计划(613262)资助。
收稿日期 2019-11-18
改稿日期 2019-12-20
李松乘 男,1993年生,博士研究生,研究方向为电磁发射及其测试。E-mail:1453150687@qq.com
鲁军勇 男,1978年生,教授,博士生导师, 研究方向为电磁发射。E-mail:jylu2019@163.com(通信作者)
(编辑 赫蕾)