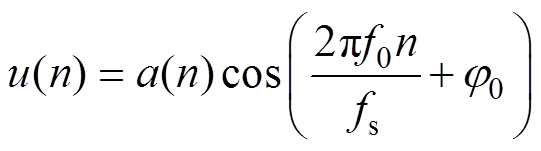 (1)
(1)摘要 该文提出一种基于泰勒-傅里叶滤波器(TFF)的动态电压闪变测量方法。首先使用TFF提取闪变信号包络,运用各阶泰勒系数表征包络参数,实现了调制深度和频率的快速估计以及包络突变时刻的检测;然后对所提取的包络进行二次TFF运算,估计闪变频率成分的时频信息;最后根据IEC相关标准,结合所估计的包络参数实现闪变值的准确测量。与基于能量算子的S变换方法相比,该文所提方法具有更高准确度和更小计算量,实现了闪变成分的时频特征提取。实测结果验证了该方法的准确性和有效性。
关键词:电压闪变 泰勒-傅里叶滤波器(TFF) 泰勒展开 动态向量 最小二乘法
电压闪变是电压波动的类型之一,它被定义为波动幅度在工频电压10%内的低频电压波动。电压闪变测量主要是计算闪变值,瞬时闪变值Put、短时间闪变值Pst和长时间闪变值Plt是国际电工委员会(International Electrotechnical Commission, IEC)推荐的用于衡量电压闪变刺激程度的主要指标。闪变值的计算依赖于调制深度与调制频率的计算。此外在闪变测量中,通过跟踪调制深度的变化,可以获得闪变实时波动分量,从而实现闪变源定位[1]。检测闪变信号包络的突变,可以判断负荷是否波动,从而在负荷接入电力系统前判断负荷运行是否会产生闪变[2]。本文方法将实现上述的电压闪变测量分析。
IEC61000-4-15:2010标准给出了闪变测试系统的原理框图[3]。传统方法使用平方检波法进行包络提取,但其无法满足低频段闪变测试需求。本文方法遵循文献[4]的数字闪变仪设计思路,即先提取闪变信号包络,然后求取包络参数。常用的信号解调方法有改进能量算子(Improved Teager Energy Operator, ITEO)[5-6]和Hilbert变换。ITEO是对TEO进行的改进,减少了算法的计算误差偶然性,但未彻底消除对噪声和电压突变敏感的缺点;而Hilbert变换运算量大且提取的包络存在严重边沿飞翼的缺点。此外两种算法都无法隔离谐波,在含谐波情况下提取的基波包络会受到谐波的严重影响。能用于计算包络参数的算法有离散傅里叶变换(Discrete Fourier Transform, DFT)、扩展Kalman滤波(Extended Kalman Filter, EKF)、S变换(S Transform, ST)[7-8]、小波变换(Wavelet Transform, WT)等。基于DFT的算法由于快速傅里叶变换(Fast Fourier Transform, FFT)的简化改进,而被广泛运用。然而DFT本身不能反映信号的动态变化,因此利用基于DFT的算法[9]处理动态信号如时变电压闪变信号时,会产生很大误差,类似的还有旋转因子变换插值法[10],此外DFT本身受栅栏效应和频谱泄漏影响。EKF能估算包络参数但需要预知处理信号的具体模型。ST和WT具有对信号进行时频分析的能力,但WT的小波基不易被选择,而ST需要反复调整才能获得具有合适形状的高斯窗函数。此外,两种算法的动态响应能力不足且计算量大。
泰勒-傅里叶滤波器(Taylor-Fourier Filter, TFF)最早在文献[11]中提出,文献[12]将TFF的应用范围扩展到处理基波含谐波信号。文献[13-16]对TFF的特性作了补充与改进。传统TFF并不完全满足电压闪变测量分析的要求。本文将TFF与闪变测量中的时变单多频正弦调制信号、矩形调制信号结合分析,总结了TFF在闪变测量中的优点,如隔离谐波[17]、检测基波频偏、提取基波包络、快速估算调制深度与调制频率、检测包络突变现象和计算包络参数。最后通过实验验证了该方法的准确性和有效性。
对于230V、60W电力系统,闪变觉察频率范围为1~25Hz。根据IEC61000-4-15:2010标准,电压闪变信号表示为
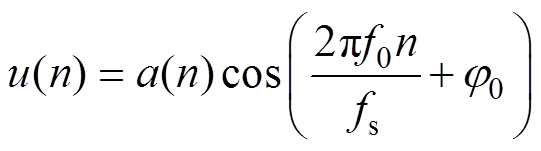 (1)
(1)式中,n=-∞,…, -1, 0, 1, …,+∞;a(n)=Um[1+mcos(2pfn/fs)]为待提取的电压闪变包络,m、f和fs分别为调制深度、调制频率和采样频率;Um、f0和j 分别为工频电压幅值、频率和相位。令Um=1(pu),利用欧拉公式,改写式(1)为
 (2)
(2)
式中,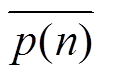 为p(n)的共轭复数;p(n)为复包络,表示为
为p(n)的共轭复数;p(n)为复包络,表示为
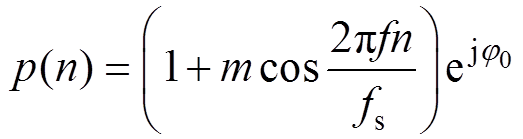 (3)
(3)设一次TFF运算使用输入信号的采样点数为N,令N为奇数,第l次TFF运算的输入信号u(i)为
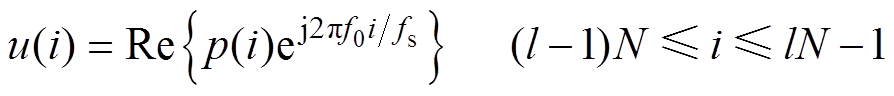 (4)
(4)
在第Nl个采样点处,将式(4)进行二阶泰勒展开,得到近似输入信号为
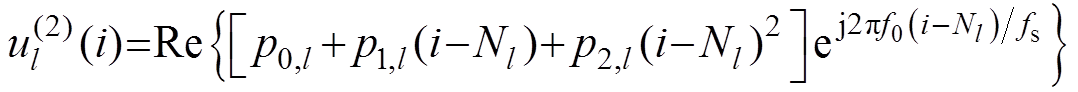 (5)
(5)式中,(2)表示二阶泰勒展开;Nl为TFF运算窗口中点,Nl=(2l-1)N/2;在中点处,p0,l=p(0),p1,l=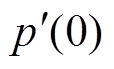 ,p2,l=
,p2,l=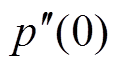 /2。
/2。
将式(5)表示成矩阵运算的形式为
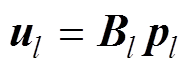 (6)
(6)其中
 (7)
(7)
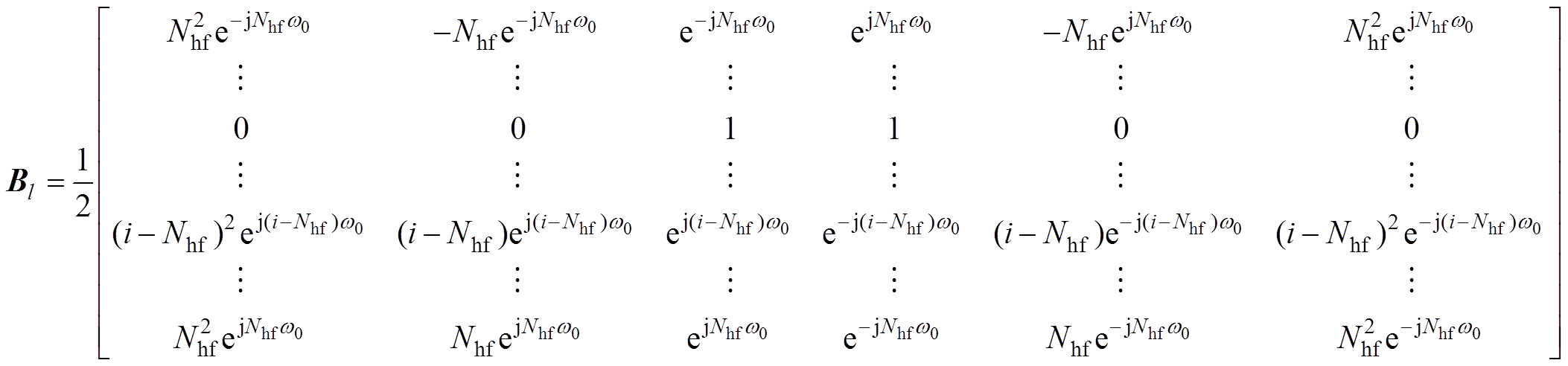 (8)
(8)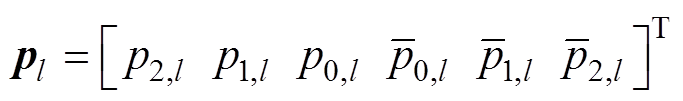 (9)
(9)
式中,w0=2pf0/fs;Nhf 为每个TFF运算窗口的中间点左右两侧的采样点数,Nhf =(N-1)/2。
输入信号与其二阶泰勒近似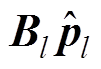 的残差为
的残差为
 (10)
(10)当残差二次方和最小时,得到pl的最佳估计为
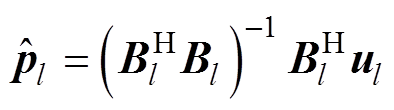 (11)
(11)
式中,H表示Hermitian运算符。计算出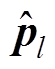 后,各阶复包络系数、幅值系数和相位系数的关系分别为
后,各阶复包络系数、幅值系数和相位系数的关系分别为
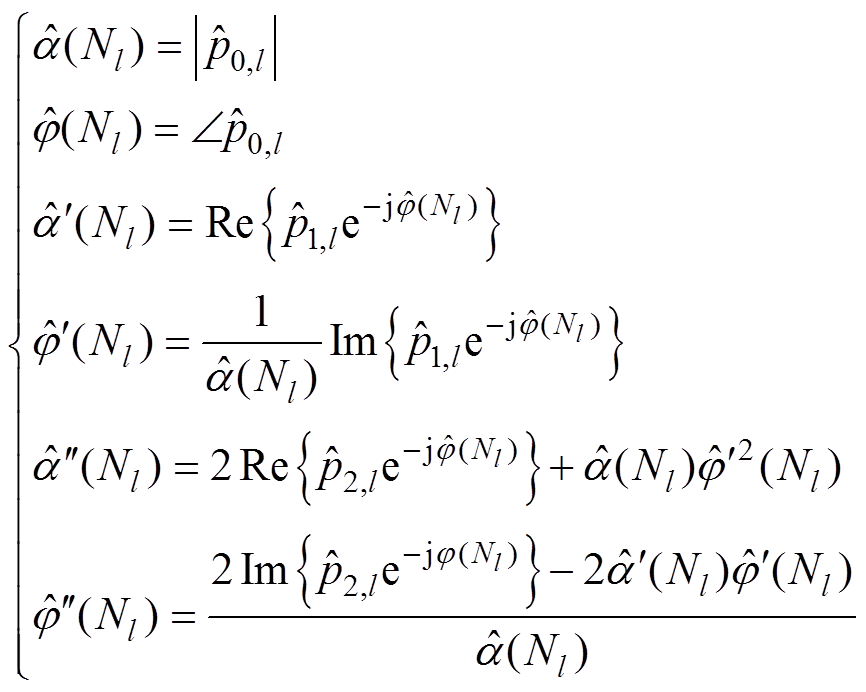 (12)
(12)利用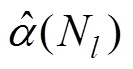 、
、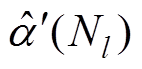 和
和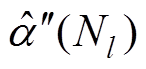 ,得到每次TFF运算提取的包络为
,得到每次TFF运算提取的包络为
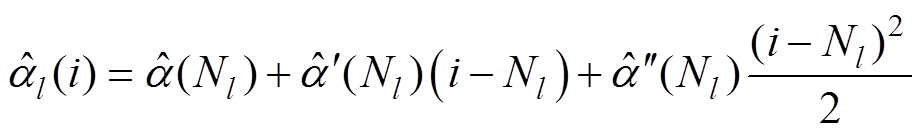 (13)
(13)
通常情况下实际频率freal与TFF设置的中心频率fcenter存在偏差,设置频率偏差为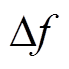 =freal-fcenter,利用一阶相位系数
=freal-fcenter,利用一阶相位系数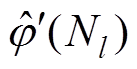 得到
得到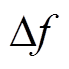 为
为
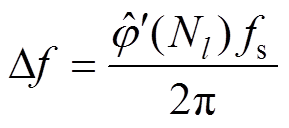 (14)
(14)本文利用当前TFF运算得到的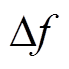 去修正下一次TFF运算的fcenter,使TFF的平顶增益频带以实际频率为中心频率分布,它们的关系为
去修正下一次TFF运算的fcenter,使TFF的平顶增益频带以实际频率为中心频率分布,它们的关系为
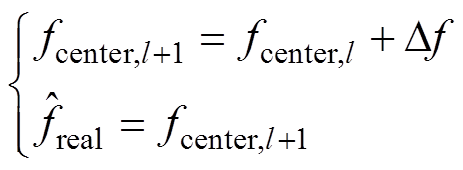 (15)
(15)
多个中心频率的情况下,输入信号可表示为
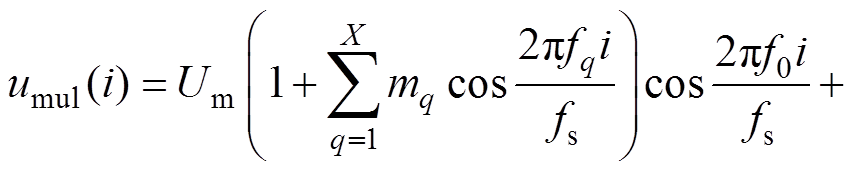
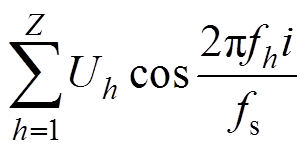 (16)
(16)
式中,X为调制频率个数;mq和fq分别为各个调制频率成分的调制深度和频率;Z为谐波频率个数;Uh和fh分别是各谐波成分的幅值和频率。本文考虑谐波不受调制的闪变信号,并利用谐波频率偏差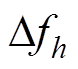 计算基波频率偏差
计算基波频率偏差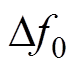 ,即
,即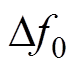 =
=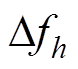 /h。
/h。
利用欧拉公式和K阶泰勒展开,得到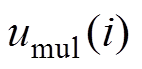 的估计值为
的估计值为
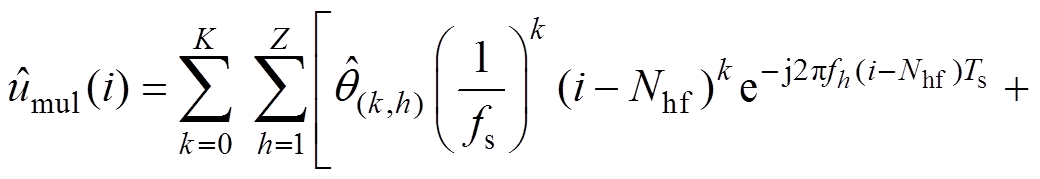
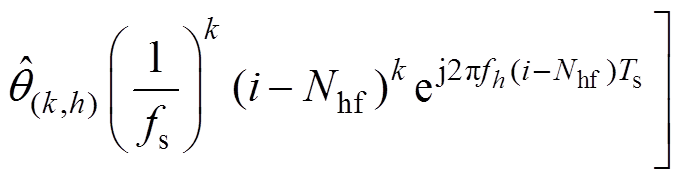 (17)
(17)
式中,Ts=1/fs。将式(17)改写成线性变换形式为
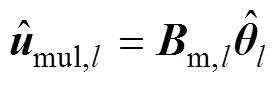 (18)
(18)式中,列向量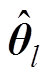 由各中心频率的各阶复包络系数以及它们的共轭复数组成,
由各中心频率的各阶复包络系数以及它们的共轭复数组成,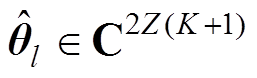 ,
,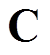 为复数集合,上标2Z(k+1)为向量维数,各元素为
为复数集合,上标2Z(k+1)为向量维数,各元素为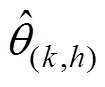 ;Bm,l为Hermitian矩阵,Bm,l
;Bm,l为Hermitian矩阵,Bm,l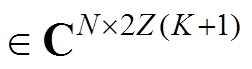 ;列向量
;列向量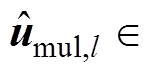
 为输入信号。使用最小二乘法求解式(18)中的
为输入信号。使用最小二乘法求解式(18)中的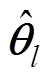 ,然后利用式(12)~式(14)计算各中心频率的幅值和频率。
,然后利用式(12)~式(14)计算各中心频率的幅值和频率。
对于矩形调制,由于矩形调幅波只含高低电平两种状态,所以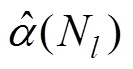 即可表示为m。对于正弦调制,本文给出m的近似计算。由于TFF提取的包络为二次函数,因此本文利用式(13)中二次函数的极值近似表示调制深度m。将式(13)写为顶点式,有
即可表示为m。对于正弦调制,本文给出m的近似计算。由于TFF提取的包络为二次函数,因此本文利用式(13)中二次函数的极值近似表示调制深度m。将式(13)写为顶点式,有
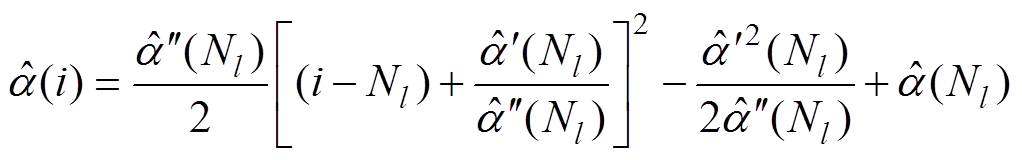 (19)
(19)式中,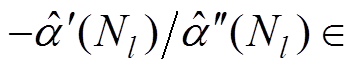 [-N/2, N/2]。由式(19)可知,TFF运算得到的包络的极值可以在采样点i=Nl-
[-N/2, N/2]。由式(19)可知,TFF运算得到的包络的极值可以在采样点i=Nl- 处获得。
处获得。
调制深度的近似值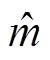 可用极值表示为
可用极值表示为
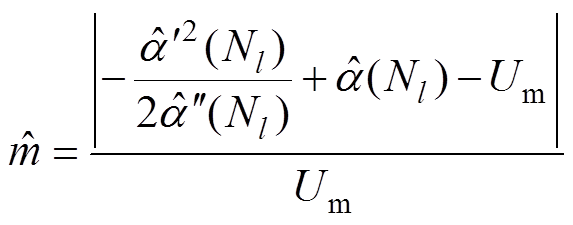 (20)
(20)利用式(20)可以在每个TFF运算窗口中得到一个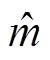 。根据泰勒展开的性质,幅值包络在TFF窗口的中间点处误差最小,往两边延伸误差逐渐增大,在端点处达到最大。当i=Nl即
。根据泰勒展开的性质,幅值包络在TFF窗口的中间点处误差最小,往两边延伸误差逐渐增大,在端点处达到最大。当i=Nl即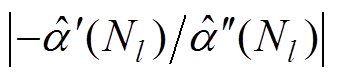 = 0时
= 0时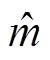 的准确度最高。本文将
的准确度最高。本文将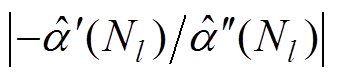 <N/2对应的
<N/2对应的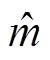 序列作为m的快速估计序列,将最小
序列作为m的快速估计序列,将最小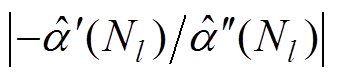 对应得到的
对应得到的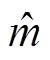 作为快速估计值。
作为快速估计值。
将理想幅值包络a(n)=Um[1+mcos(2πfn/fs)]在第l个窗口的中间点 处进行二阶泰勒展开为
处进行二阶泰勒展开为
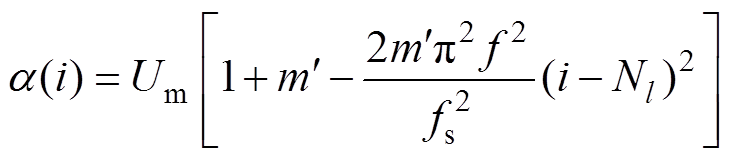 (21)
(21)当取得的 为最小,即i最接近
为最小,即i最接近 时,在i=Nl-
时,在i=Nl- 处,利用式(20)得到的调制深度最佳估计
处,利用式(20)得到的调制深度最佳估计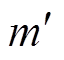 为
为
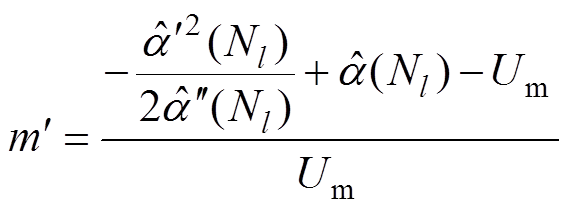 (22)
(22)
结合式(13)和式(21),得到估算调制频率的等式为
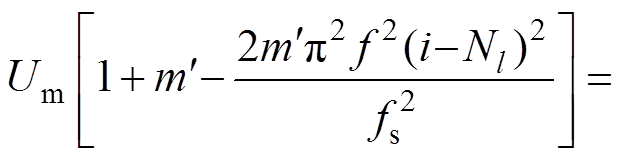
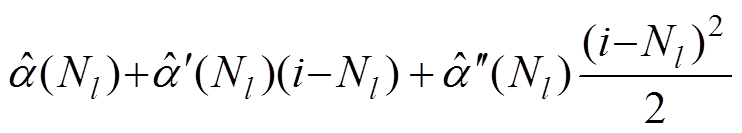 (23)
(23)
将式(22)代入式(23)得到
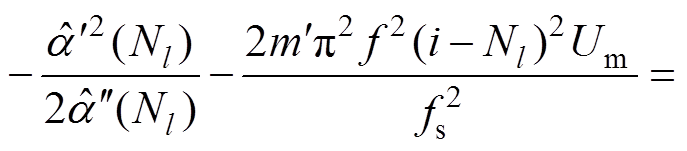
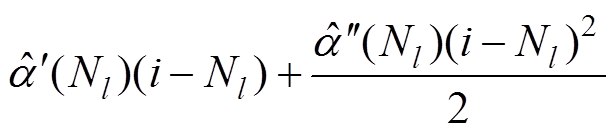 (24)
(24)
由于 ≈0且i≈Nl,得到
≈0且i≈Nl,得到
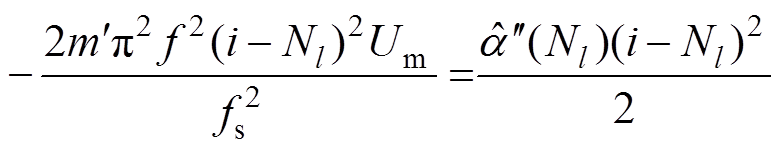 (25)
(25)由式(25)得到调制频率f的估算值为
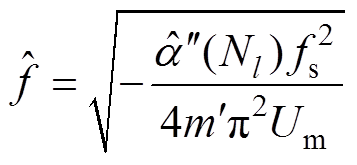 (26)
(26)
由于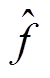 的准确度会受各阶幅值包络系数和
的准确度会受各阶幅值包络系数和 的影响,因此本文将式(26)中得到的
的影响,因此本文将式(26)中得到的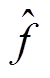 作为第二个TFF的中心频率,并利用第二个TFF中式(14)的频率修正能力对
作为第二个TFF的中心频率,并利用第二个TFF中式(14)的频率修正能力对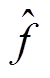 进行逐次修正。设定N0=fs/fcenter,当TFF窗口长度N=4N0时,能够修正偏离实际频率±20%以上的fcenter;当N=2N0时,能够修正偏离±40%以上的fcenter。
进行逐次修正。设定N0=fs/fcenter,当TFF窗口长度N=4N0时,能够修正偏离实际频率±20%以上的fcenter;当N=2N0时,能够修正偏离±40%以上的fcenter。
此外,多频调制下利用FFT估算各个调制频率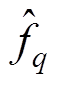 的具体操作如下:
的具体操作如下:
(1)利用长度为NFFT的FFT得到包络v(k)的傅里叶变换序列V(k/(NFFTTs))。
(2)判断包络的各个频率成分,判断条件为
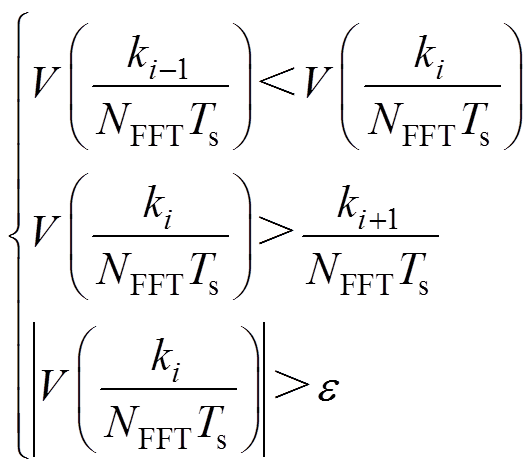 (27)
(27)式中,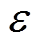 为防止由于FFT频谱泄漏造成频率成分误判而设定的阈值。
为防止由于FFT频谱泄漏造成频率成分误判而设定的阈值。
文献[18]提出利用ST的幅值突变检测能力检测闪变发生与停止时刻。本文提出的基于输入信号u与重构信号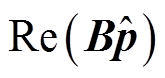 形成的绝对误差序列E(i)的包络突变检测方法,不仅可以检测闪变起止时刻,还可以检测矩形调制中的包络突变。首先计算E(i)为
形成的绝对误差序列E(i)的包络突变检测方法,不仅可以检测闪变起止时刻,还可以检测矩形调制中的包络突变。首先计算E(i)为
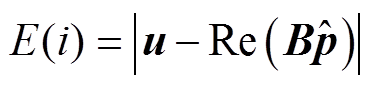 (28)
(28)当运算窗口中存在唯一突变时,突变发生时刻的E(i)会远大于该窗口中其他时刻的E(i)。TFF使用的N可调且较短,因此可以实现一个窗口中只含一次包络突变。本文通过设置后验阈值的方式去判断并得到包络突变时刻。设E(j)标准差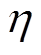 为
为
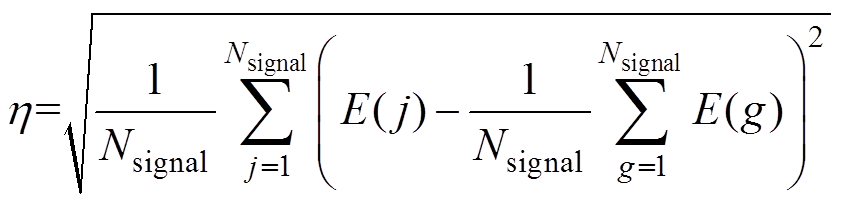 (29)
(29)
式中, 为输入信号总长度。
为输入信号总长度。
E(j)与其均值的绝对偏差序列Q(j)为
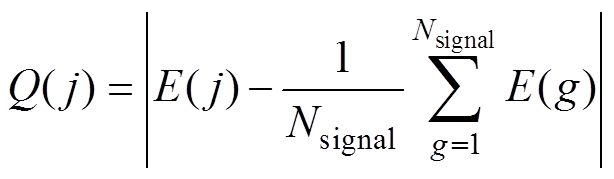 (30)
(30)Q(j)按照运算窗口划分成数段Ql(s),其中(l-1)N≤s≤lN-1。判断第l次TFF运算是否含有包络突变的条件为
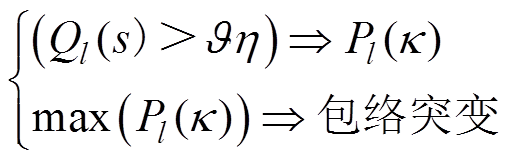 (31)
(31)
式中,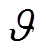 为后验阈值。
为后验阈值。
考虑矩形调制情况,设置m=10%,信噪比SNR= 40dB,f =10Hz,fs =12.8kHz,f0=50Hz和N=N0。此外,输入信号长度为1s,即包络发生20次突变。矩形调制包络的突变检测如图1所示,从仿真结果可以清楚地观察到发生突变的时刻,此时后验阈值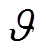 设置为1.2。
设置为1.2。
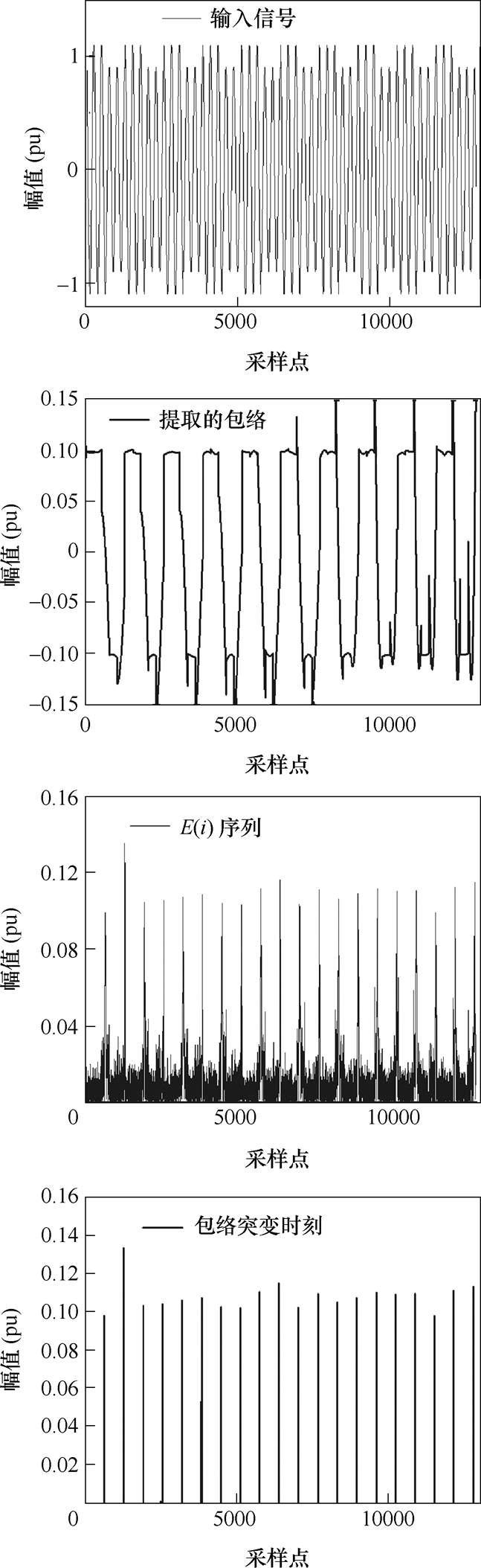
图1 矩形调制包络的突变检测
Fig.1 The detection of the envelope changes of the rectangular modulation
文献[19]证明TEO提取的包络比二次方检波和整流检测的准确度高。此外,由文献[19]的结论可得,对TEO提取的包络进行时频分析时,使用ST的准确度高于使用HHT、EKF、WT和FFT。因此本文采用TEO+ST作为对比方法。
本文方法的基本运算次数主要来自TFF中伪逆矩阵求解。利用奇异值分解计算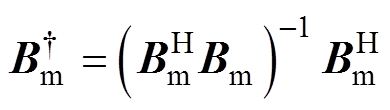 的时间复杂度为O(
的时间复杂度为O(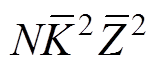 )。由于本文使用二阶泰勒模型,所以
)。由于本文使用二阶泰勒模型,所以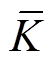 =3,第一和第二个TFF的
=3,第一和第二个TFF的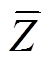 分别为2Z和2X。此外用作频率粗估计的FFT的时间复杂度为O(Nlog2N)。对TEO+ST,TEO需要2N次乘法运算和N次加法运算,而ST的时间复杂度为O(N2log2N)。表1给出了本文方法与TEO+ST的时间复杂度对比,其中,Z
分别为2Z和2X。此外用作频率粗估计的FFT的时间复杂度为O(Nlog2N)。对TEO+ST,TEO需要2N次乘法运算和N次加法运算,而ST的时间复杂度为O(N2log2N)。表1给出了本文方法与TEO+ST的时间复杂度对比,其中,Z N,X
N,X N。从表1可知,本文方法的计算量远小于TEO+ST。此外,在单频情况下1.3节模型可以替代FFT实现第二个TFF中心频率的粗估计,进一步减小算法运算量。
N。从表1可知,本文方法的计算量远小于TEO+ST。此外,在单频情况下1.3节模型可以替代FFT实现第二个TFF中心频率的粗估计,进一步减小算法运算量。
表1 时间复杂度的对比分析
Tab.1 The comparisons of time complexities

时间复杂度本文方法TEO+ST FFT 单频调制O(36NZ)—O(36N)O(N2log2N) 多频调制O(36NZ)O(Nlog2N)O(36NX)O(N2log2N)
Matlab中实现的运算量对比仿真如下,设置输入信号的调制频率为4Hz、8.8Hz、15Hz和20Hz,fs=12.8kHz。此外设置第一个TFF的运算窗口长度NTFF1=0.5N0,第二个TFF的NTFF2=2N0。当输入信号长度Nsignal=0.6s时,本文方法与TEO+ST的运算时间分别为0.344s和4.175s;当Nsignal=1s时,运算时间分别为0.452s和20.589s。
二阶TFF模型的频率响应特性如图2所示,频率落入带宽范围内的窄带信号可以通过式(14)进行频率修正,运算窗口长度N越短的TFF具有越宽的平顶增益带宽。第一个TFF需要考虑(50-25)Hz~(50+25)Hz的宽带信号,要求N较短,第二个TFF只需考虑中心频率处的窄带信号,可选用较长的N。
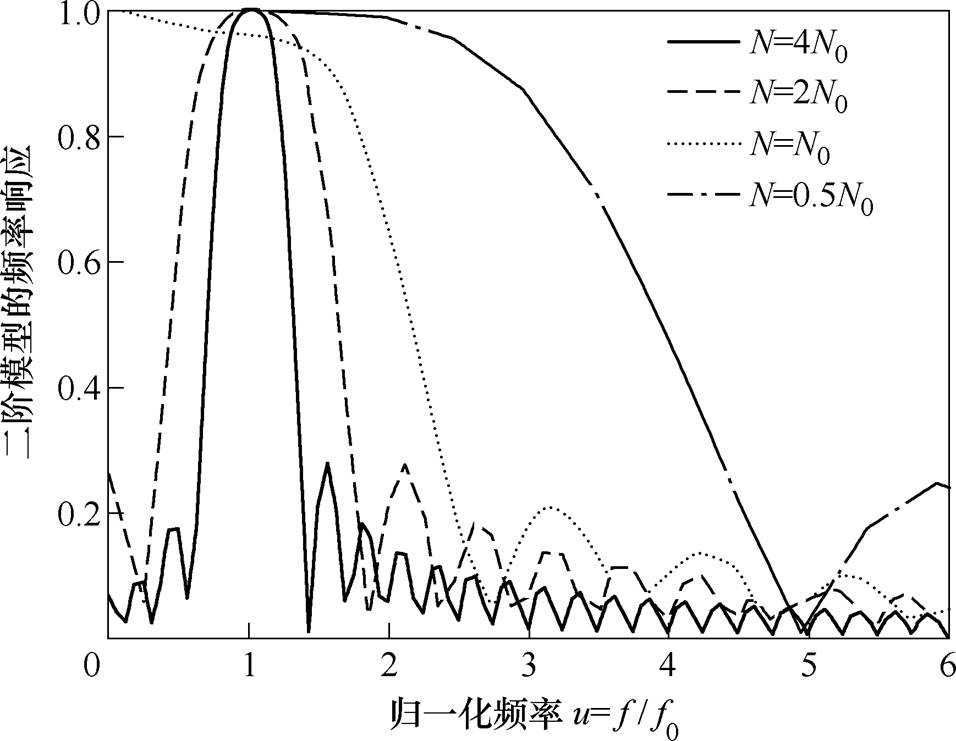
图2 二阶TFF模型的频率响应特性
Fig.2 The frequency response of the 2nd order model TFF
IEC 61000-4-15:2010标准第15页表1b给出了230V/50Hz的正弦电压波动情况下的闪变仪测试调制频点,本文对其中各频点进行测试。设置fs= 6.4kHz,f0=50Hz,总长Nsignal=16 000,即2.5s,NTFF1= 0.4N0,NTFF2=4N0。此外将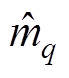 序列的均值作为得到的调制深度。利用1.3节模型确定fcenter后,fcenter逐次修正效果如图3所示。随着调制频率上升,估算的初始中心频率误差增大。低频部分,估算频率的准确度高,且由于提取的包络准确度高,所以能实现数个数量级的相对误差修正。高频部分估算的频率误差相对较大且不稳定,但第二个TFF的频率修正能力弥补了这一缺点。高频部分频率修正幅度大且同样能实现量级上的相对误差修正。当达到一定修正次数后,fcenter围绕freal波动变化,如图3虚线圈所示。不同方法计算的TFF的闪变包络参数如图4所示,调制频率计算选用4次修正的结果。本文方法计算的调制深度与频率远比TEO+ST的准确。
序列的均值作为得到的调制深度。利用1.3节模型确定fcenter后,fcenter逐次修正效果如图3所示。随着调制频率上升,估算的初始中心频率误差增大。低频部分,估算频率的准确度高,且由于提取的包络准确度高,所以能实现数个数量级的相对误差修正。高频部分估算的频率误差相对较大且不稳定,但第二个TFF的频率修正能力弥补了这一缺点。高频部分频率修正幅度大且同样能实现量级上的相对误差修正。当达到一定修正次数后,fcenter围绕freal波动变化,如图3虚线圈所示。不同方法计算的TFF的闪变包络参数如图4所示,调制频率计算选用4次修正的结果。本文方法计算的调制深度与频率远比TEO+ST的准确。
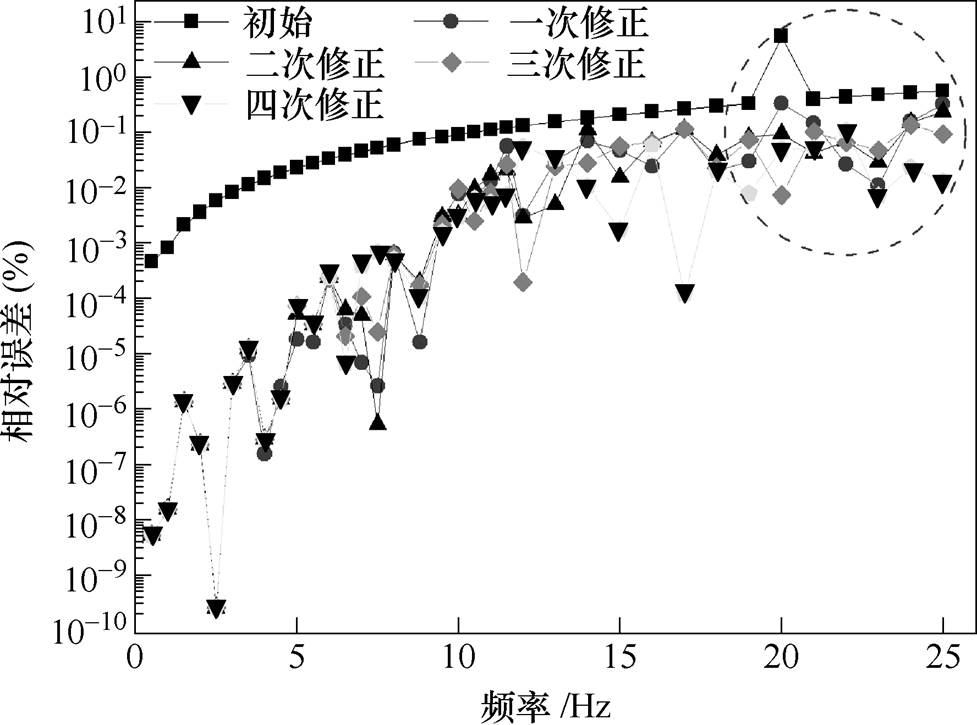
图3 TFF对本文方法估算的初始中心频率的修正效果
Fig.3 The corrections of the initial center frequency estimated by using the frequency calculation model
当包络幅值时变时,较短的N能提高第二个TFF跟踪包络幅值变化的能力。设置f=8.8Hz,NTFF1= 0.4N0,NTFF2=2N0,m的变化为

图4 不同方法计算的m、f的相对误差
Fig.4 Relative errors of m, f calculated by different methods
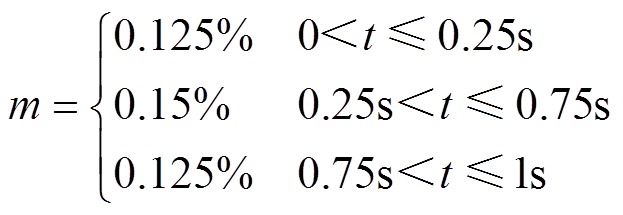 (32)
(32)时变调制下不同方法提取的包络与计算的包络参数如图5所示。从图5a可以看出,ITEO和TFF提取的包络在包络幅值突变处都会畸变。本文方法和TEO+ST计算的调制深度的平均相对误差分别为1.7%和4.7%,前者小于后者。从图5b也可以看出,与TEO+ST相比,本文方法计算的调制深度更接近设定。此外受到提取包络的畸变的影响,在各时间段的调制深度计算上,利用1.2节模型比利用TFF准确度更高。
考虑式(16)的时变多频调制闪变信号。设置基频为49.8Hz,fs=12.8kHz,第一个TFF的中心频率为50Hz,3次谐波含量为10%,5次谐波含量为5%。调制频率设置为1Hz、8.8Hz、15Hz和25Hz,调制深度分别为0.03(pu)、0.05(pu)、0.07(pu)和0.1(pu)。此外,Nsignal=64 000,利用FFT进行调制频率成分粗估算的长度为NFFT=6 400,NTFF1=0.4N0,NTFF2=2N0。本文方法提取的基频包络如图6所示,TFF实现了谐波成分的隔离,并准确地跟踪基波包络的变化。利用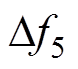 得到修正后的f0为50-(1.0112/5)= 49.797 8Hz。设置
得到修正后的f0为50-(1.0112/5)= 49.797 8Hz。设置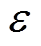 =0.01(pu),利用FFT得到第二个TFF各初始中心频率为2Hz、8Hz、16Hz和26Hz,选取最小频率f0为2Hz计算NTFF2。4次修正后,各中心频率绝对误差分别为9.246 3×10-4Hz、5.913 0× 10-4Hz、4.022 9×10-5Hz和-2.774×10-5Hz。各闪变成分的调制深度动态变化如图7所示。
=0.01(pu),利用FFT得到第二个TFF各初始中心频率为2Hz、8Hz、16Hz和26Hz,选取最小频率f0为2Hz计算NTFF2。4次修正后,各中心频率绝对误差分别为9.246 3×10-4Hz、5.913 0× 10-4Hz、4.022 9×10-5Hz和-2.774×10-5Hz。各闪变成分的调制深度动态变化如图7所示。
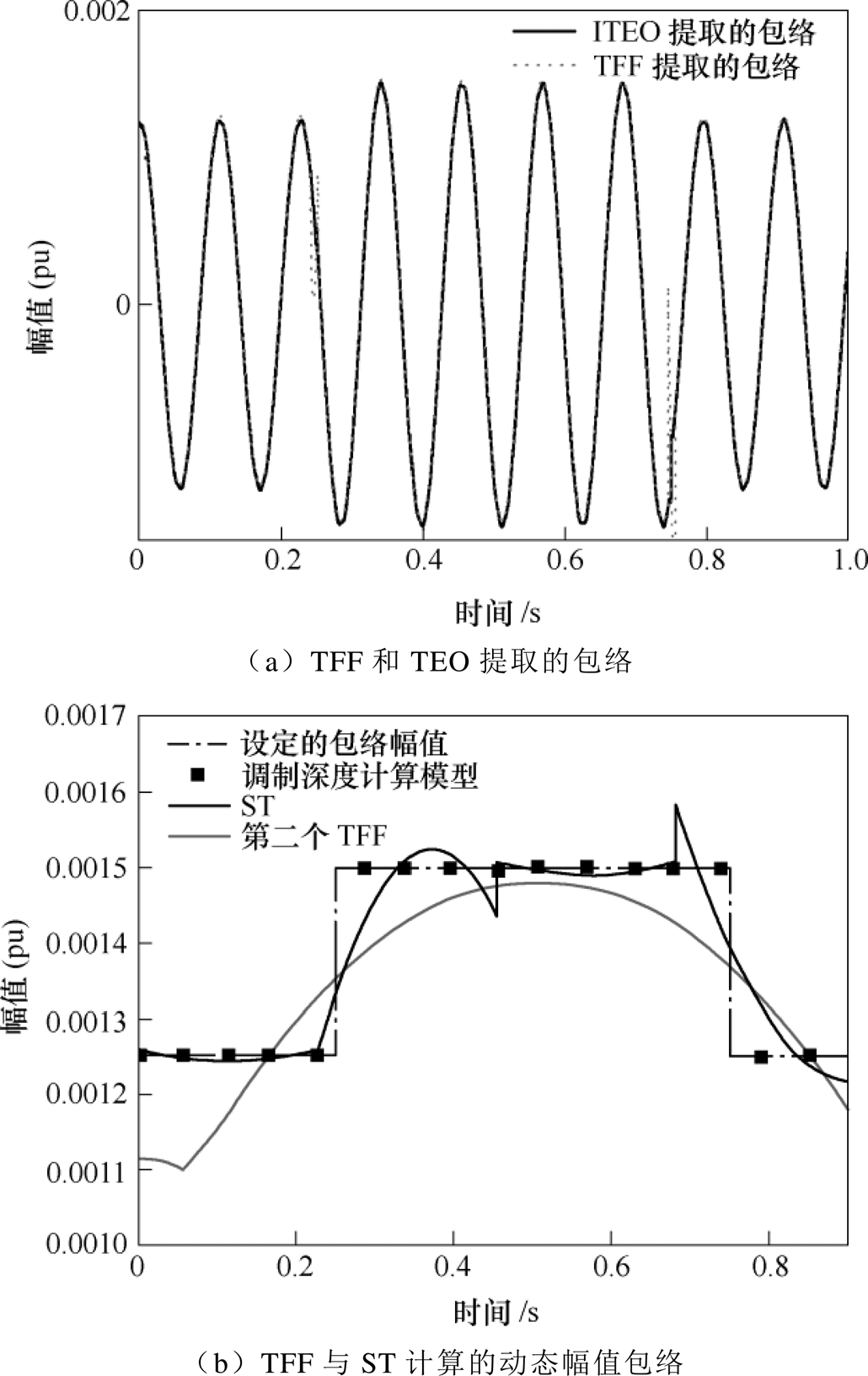
图5 时变调制下不同方法提取的包络与计算的包络参数
Fig.5 The envelopes and their parameters of the input signal calculated by different methods in thecase of time-varying sinusoidal modulation
当输入信号的某个调制频率成分的幅值是线性变化时,设定8.8Hz调制频率成分的动态幅值为
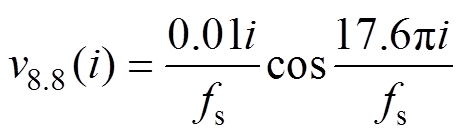 (33)
(33)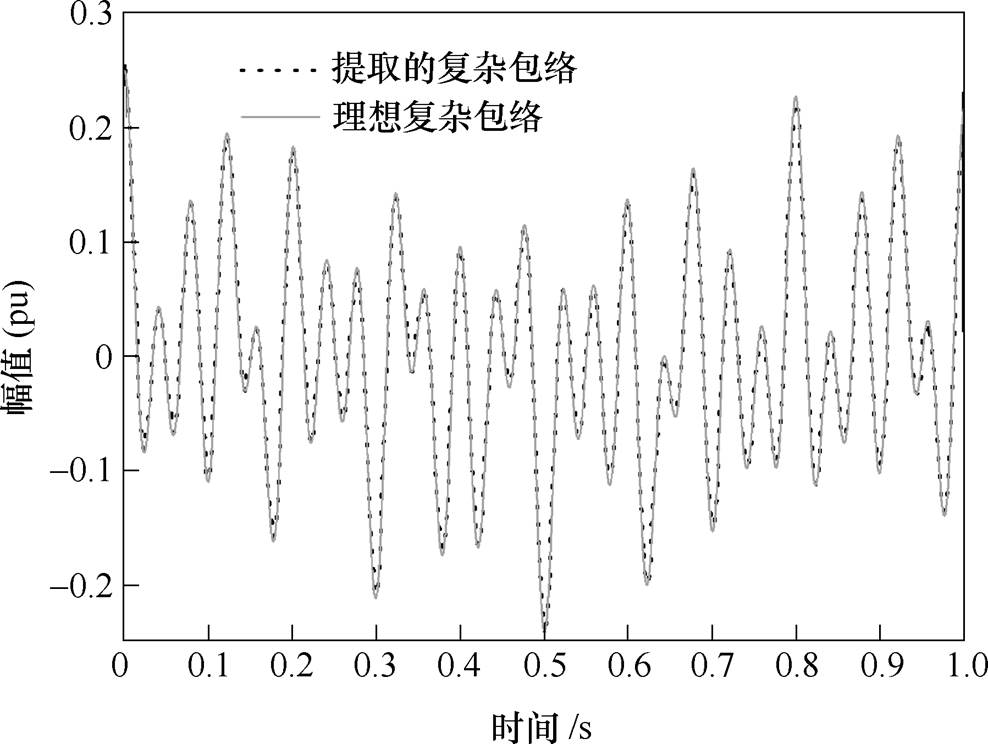
图6 本文方法提取的基频包络
Fig.6 The extracted envelope of fundamental frequency
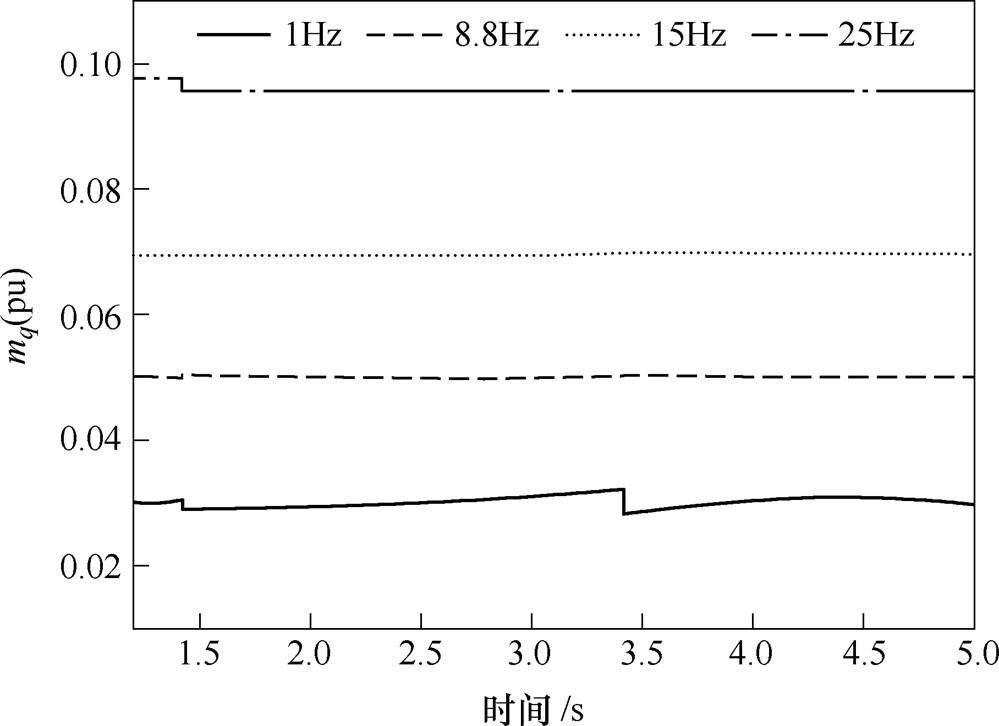
图7 本文方法计算的不同调制频率成分的调制深度
Fig.7 The estimated mq of different frequencies
估算的不同调制频率成分的动态调制深度如图8所示,8.8Hz频率成分的幅值呈线性变化。对其幅值序列进行最小二乘线性拟合得到斜率为0.009 993,与设定的m8.8=0.01i/fs吻合。
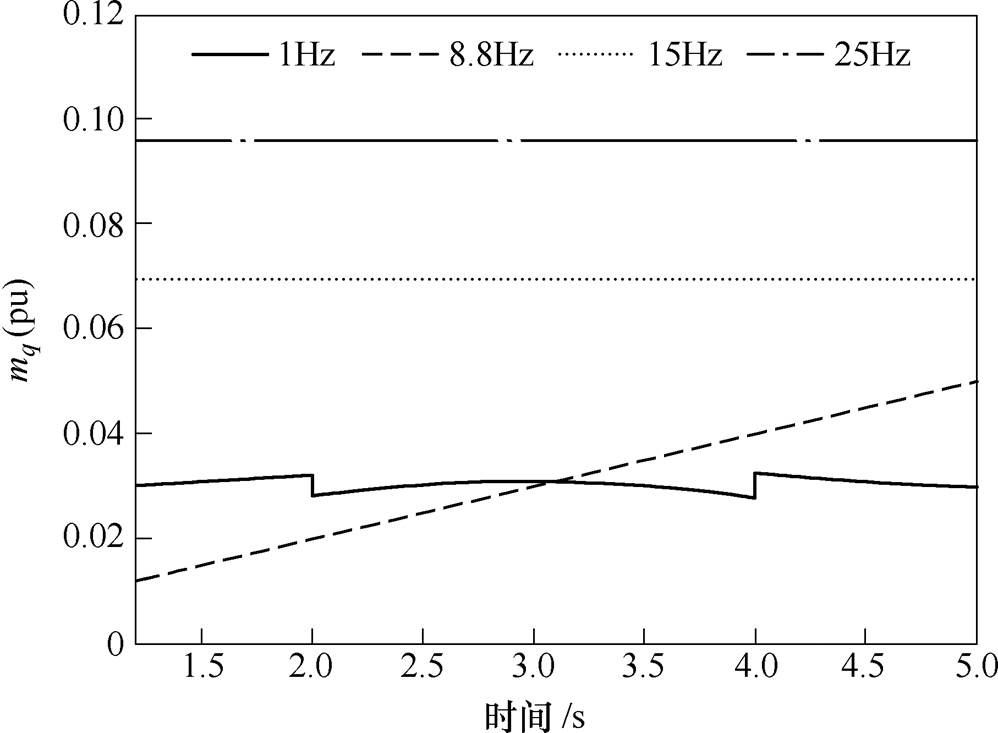
图8 估算的不同调制频率成分的动态调制深度
Fig.8 The estimated dynamic mq of different frequencies
本文利用Fluke 6100B信号源产生的闪变信号进行测试。整个测试系统的结构为Fluke 6100B+信号采集模块+计算机。其中信号采集模块为NI DAQ- USB 6210。测试系统的完整框架结构原理如图9所示。
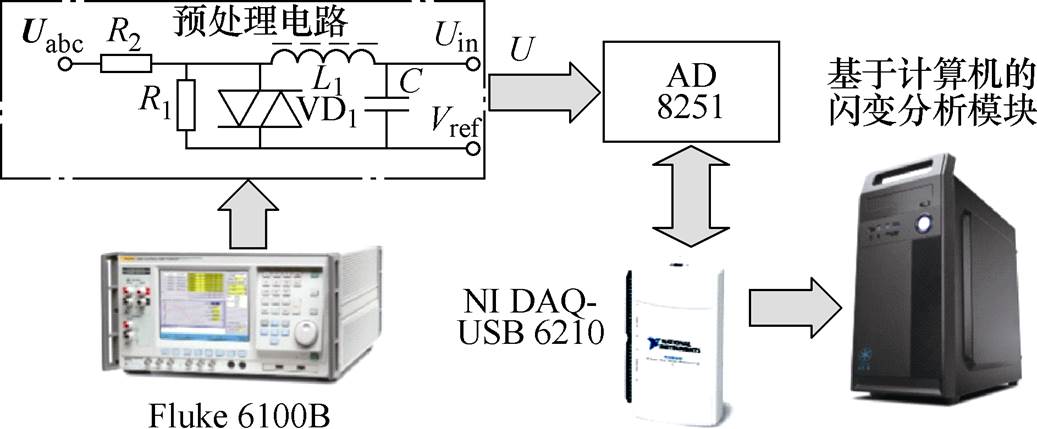
图9 测试系统的框架结构原理
Fig.9 The schematic diagram of the measuring system
单频调制下本文方法得到的不同闪变成分的参数实测结果见表2。表2中,dv=2m,表示电压波动值;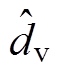 为dv的测量值;Ddv/dv为对dv的测量相对误差。由于TFF的运算窗口长度会影响其频率响应特性,因此对5Hz使用NTFF1=2N0,对8.8Hz、18Hz和20Hz使用NTFF1=0.7N0,对25Hz使用NTFF1= 0.5N0。其余设置与3.1节相同。
为dv的测量值;Ddv/dv为对dv的测量相对误差。由于TFF的运算窗口长度会影响其频率响应特性,因此对5Hz使用NTFF1=2N0,对8.8Hz、18Hz和20Hz使用NTFF1=0.7N0,对25Hz使用NTFF1= 0.5N0。其余设置与3.1节相同。
表2 本文方法在单频调制下的实测结果
Tab.2 Application tests of the proposed method in the case of sinusoidal modulation
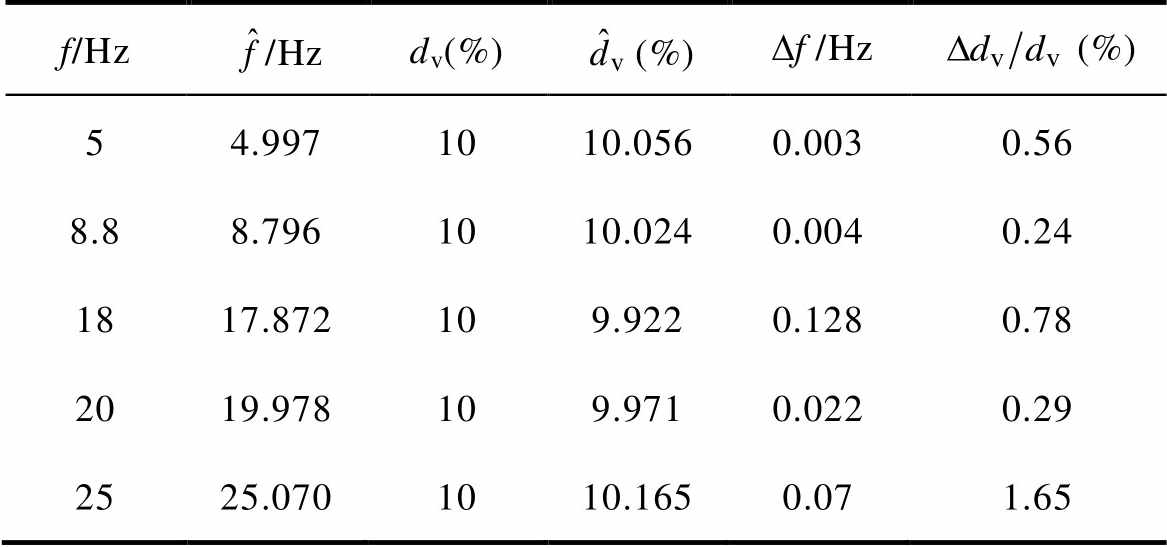
f/Hz/Hzdv(%)(%)/Hz(%) 54.9971010.0560.0030.56 8.88.7961010.0240.0040.24 1817.872109.9220.1280.78 2019.978109.9710.0220.29 2525.0701010.1650.071.65
本文提出了一种基于TFF的电压闪变测量方法,适用于分析调制深度时变的单频、多频正弦调制和矩形调制闪变信号。通过使用基于TFF的方法,提取了闪变信号包络并动态测量了包络参数,实现了闪变值的计算。本文方法还实现了基波频偏、谐波和幅值突变定位的计算分析。此外,结合本文的调制深度和调制频率估算模型可以提高测量准确度和进一步减小单频调制情况下的计算量。
参考文献
[1] 倪良华, 肖李俊, 历馨, 等. 基于HHT与闪变功率流向法的闪变源定位识别[J]. 电网与清洁能源, 2018, 34(1): 26-31.
Ni Lianghua, Xiao Lijun, Li Xin, et al. Flicker source tracing based on HHT and flicker power flow direction method[J]. Power System and Clean Energy, 2018, 34(1): 26-31.
[2] Albistur C F, Aravena P A, Morán L A, et al. A simple predictive method to estimate flicker[J]. IEEE Transactions on Industry Applications, 2014, 50(3): 2150-2155.
[3] IEC 61000-4-15 Testing and measurement tech- niques: flickermeter-functional and design specifica- tions[S]. 2010.
[4] Gary W Chang, Cheng -I Chen, Huang Yalun. A digital implementation of flickermeter in the hybrid time and frequency domains[J]. IEEE Transactions on Power Delivery, 2009, 24(3): 1475-1482.
[5] 李林, 高云鹏, 张韵琦, 等. 基于改进k值能量算子改进Chirp-Z变换的闪变包络参数提取[J]. 电工技术学报, 2018, 33(11): 2636-2646.
Li Lin, Gao Yunpeng, Zhang Yunqi, et al. Voltage flicker envelope tracking based on improved k-value energy operator and improved Chirp-Z transform[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2636-2646.
[6] 高云鹏, 李峰, 陈婧, 等. 基于Teager-Kaiser能量算子Rife-Vincent窗频谱校正的电压闪变测量[J]. 电工技术学报, 2014, 29(6): 248-256.
Gao Yunpeng, Li Feng, Chen Jing, et al. Voltage flicker measurement using the Teager-Kaiser energy operator based on Rife-Vincent window spectral correction[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 248-256.
[7] 李建闽, 林海军, 梁成斌, 等. 基于双分辨率S变换和学习向量量化神经网络的电能质量扰动检测方法[J]. 电工技术学报, 2019, 34(16): 3453-3463.
Li Jianmin, Lin Haijun, Liang Chengbin, et al. Detection method of power quality disturbances based on double resolution S transform and learning vector quantization neural network[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3453-3463.
[8] 易吉良, 周曼, 李中启, 等. 采用不完全S变换的复杂谐波参数估计[J]. 电工技术学报, 2018, 33(增刊1): 112-120.
Yi Jiliang, Zhou Man, Li Zhongqi, et al. Complex harmonic parameters estimation using incomplete S transform[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 112-120.
[9] 牛胜锁, 梁志瑞, 张建华, 等. 基于三谱线插值FFT的电力谐波分析算法[J]. 中国电机工程学报, 2012, 32(16): 130-136.
Niu Shengsuo, Liang Zhirui, Zhang Jianhua, et al. An algorithm for electrical harmonic analysis based on triple-spectrum-line interpolation FFT[J]. Proceedings of the CSEE, 2012, 32(16): 130-136.
[10] 李兰芳, 马明, 盛超, 等. 基于旋转因子变换插值的电压闪变检测算法[J]. 电工技术学报, 2016, 31(22): 178-185.
Li Lanfang, Ma Ming, Sheng Chao, et al. The voltage flicker detection algorithm based on rotation factor transforming interpolation[J]. Transactions of China Electrotechnical Society, 2016, 31(22): 178-185.
[11] de la O Serna J A. Dynamic phasor estimates for power system oscillations[J]. IEEE Transactions on Instrumentation & Measurement, 2007, 56(5): 1648- 1657.
[12] Platas-Garza M A, de la O Serna J A. Dynamic harmonic analysis through Taylor-Fourier trans- form[J]. IEEE Transactions on Instrumentation & Measurement, 2011, 60(3): 804-813.
[13] Belega D, Fontanelli D, Petri D. Low-complexity least-squares dynamic synchrophasor estimation based on the discrete Fourier transform[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(12): 3284-3296.
[14] José Antonio de la O Serna, Miguel Angel Platas- Garza. Maximally flat differentiators through WLS Taylor decomposition[J]. Elsevier Digital Signal Processing, 2011, 21(2): 183-194.
[15] de la O Serna J A. Synchrophasor measurement with polynomial phase-locked-loop Taylor-Fourier filters[J]. IEEE Transactions on Instrumentation & Measurement, 2015, 64(2): 328-337.
[16] 刘洁波, 黄纯, 江亚群, 等. 基于强跟踪泰勒-卡尔曼滤波器的动态相量估计算法[J]. 电工技术学报, 2018, 33(2): 433-441.
Liu Jiebo, Huang Chun, Jiang Yaqun, et al. Dynamic phasor estimator based on strong tracking Taylor- Kalman filter[J]. Transactions of China Electro- technical Society, 2018, 33(2): 433-441.
[17] 雍静, 晏小龙, 曾礼强. 电压间谐波对紧凑型荧光灯光闪变效应的实验研究[J]. 电工技术学报, 2015, 30(8): 273-281.
Yong Jing, Yan Xiaolong, Zeng Liqiang. Experi- mental study for flicker of compact fluorescent lamp caused by interharmonics[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 273-281.
[18] 唐求, 滕召胜, 高云鹏. 基于S变换的平方检测法测量电压闪变[J]. 中国电机工程学报, 2012, 32(7): 60-67.
Tang Qiu, Teng Zhaosheng, Gao Yunpeng. Voltage flicker measurement using square demodulation method based on S-transform[J]. Proceedings of the CSEE, 2012, 32(7): 60-67.
[19] Yao Wenxuan, Tang Qiu, Teng Zhaosheng, et al. Fast S-transform for time-varying voltage flicker analysis[J]. IEEE Transactions on Instrumentation & Measurement, 2013, 63(1): 72-79.
Voltage Flicker Measurement Based on Taylor-Fourier Transform
Abstract This paper proposes a method for dynamic voltage flicker measurement based on Taylor-Fourier filter (TFF). Firstly, the envelope of voltage flicker is extracted by TFF, and the envelope parameters can be expressed by the Taylor coefficients. The estimation of the modulation depth, modulation frequency and detection of the envelope transients can thus be achieved. Secondly, the TFF of the extracted envelop is performed to estimate the time and frequency domain information of each flicker component. Finally, based on the estimated envelope parameters, the flicker values are calculated according to the definitions of IEC (international electrotechnical commission). Compared with the S-transform method based on Teager energy operator, the proposed method has higher accuracy and smaller calculation amount. The proposed method can achieve the measurement of time-varying voltage flicker. The measured results verify the accuracy and usefulness of the proposed method.
keywords:Voltage flicker, Taylor-Fourier filter, Taylor expansion, dynamic phasor, least squares method
中图分类号:TM930.1
DOI: 10.19595/j.cnki.1000-6753.tces.191136
国家自然科学基金项目(61771190)和湖南省自然科学基金项目(2009JJ20001)资助。
收稿日期 2019-09-03
改稿日期 2019-10-21
邝昊云 男,1994年生,硕士研究生,研究方向为智能检测、电气参数测量新方法与应用、频谱分析理论与应用等。E-mail: kuanghaoyun@126.com
温 和 男,1982年生,教授,博士生导师,研究方向为智能检测、电气参数测量新方法与应用、频谱分析理论与应用等。E-mail: he_wen82@126.com(通信作者)
(编辑 陈 诚)