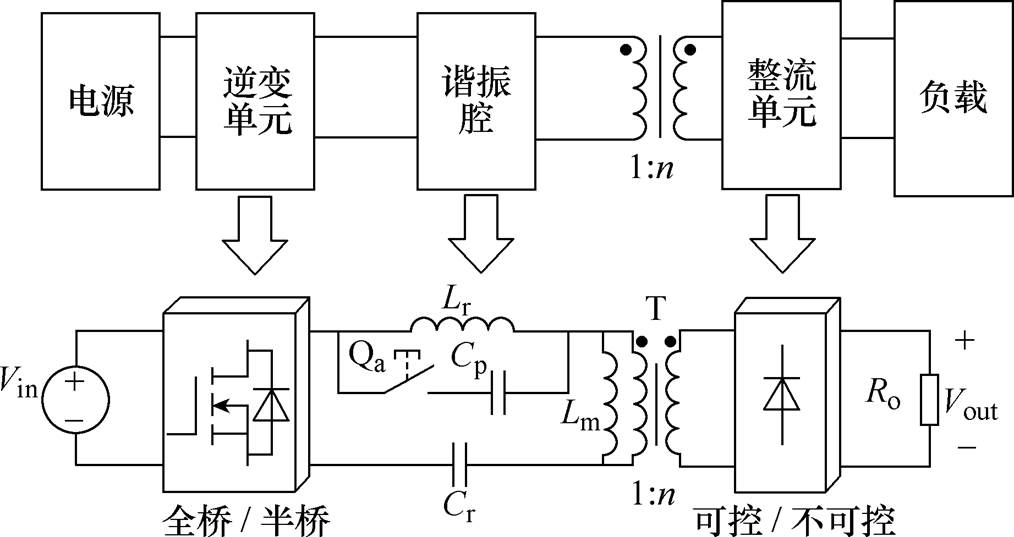
图1 所提变换器拓扑
Fig.1 Topology of the proposed converter
摘要 该文提出一种具有两模式切换运行特性的软开关谐振型直流变换器,通过控制辅助开关管的通断,来改变谐振腔结构进而决定变换器的运行模式。该变换器共有两种工作模式:LLC模式和LLCC模式。结合LLC谐振变换器的参数设计方法及所提变换器的特点,设计出可以同时满足两种运行模式要求的参数。通过对模式切换点进行优化选择,变换器可以在较窄的频率范围内同时实现高效率和宽增益范围的目标。另外,在不增加拓扑复杂度的基础上引入额外的谐振零点,实现了内在的过电流保护功能。最后,搭建一台1kW的实验样机来验证上述理论分析的正确性。实验结果表明:所提变换器具有优良的性能,当输入电压从150~400V变化时,输出电压一直稳定在400V,所测最高效率值为97.3%。
关键词:模式切换 软开关 谐振型直流变换器 高转换效率 宽输入电压范围
伴随着化石能源的紧缺及生态环境保护的迫切需要,可再生能源的开发和利用为解决世界性能源和环境问题开辟了新途径。由于新能源的输出电压随着外界环境的改变会有较大的波动,因此常常需要将新能源发出来的电经直流变换器转换至合适的电压等级后再利用逆变技术供给用户使用。相应地,研究具有良好性能且适用于宽输入电压范围应用场景的直流变换器对于新能源发电技术的发展具有十分重要的推动作用[1-3]。
谐振型直流变换器因具有高频、高效、高功率密度的特点,得到了学术界的广泛关注。最基本的谐振变换器为两元件谐振变换器,即串联谐振变换器(Series Resonant Converter, SRC)和并联谐振变换器(Parallel Resonant Converter, PRC)。当以上两种变换器的开关频率大于其谐振频率时,工作在零电压开通(Zero Voltage Switching, ZVS)区域,可以降低开关损耗,提升效率,但是它们也有各自的局限性。具体来说,SRC的电压增益恒小于或等于1,不能升压,且在轻载情况下,调压能力较差。而PRC电路中由于负载和谐振元件并联,导致电路中环流较大,转换效率受到影响。
作为上述两种变换器的结合,三元件谐振变换器——LLC很好地综合了它们的优点,可以在实现ZVS的前提下,进一步拓宽电压增益范围。但是LLC的高频特性与SRC类似,即在轻载条件下,其转换效率和电压增益特性互相限制,彼此矛盾。因此,为了改善这两方面的问题,很多研究就此展开。
在效率优化方面,一些文献基于经典的LLC拓扑围绕谐振参数优化[4-6]和器件优化[7-8]进行了细致研究。文献[4]提出一种基波分析结合时域仿真的改进型谐振参数设计方法,可以准确地反映变换器的电压增益特性,从而对谐振参数进行更合理的设计。在器件优化方面,文献[7]采用一种改进的磁性元件设计方法,变换器的轻载效率提高了6%。
在改善电压增益特性方面,一些基于LLC拓扑的衍生变换器取得了良好的效果[9-13]。文献[9]中提出的变换器增加了额外的LC谐振结构,在不同的开关频率下,该结构表现出可变电感的特性,使得变换器适用于宽输入电压范围的场景。文献[11]提出了一种采用电阻压缩网络(Resistance Com- pression Network, RCN)的新型变换器,可以在较宽的输入电压范围内实现软开关。文献[12-13]将陷波器结构引入到LLC拓扑中,形成了一系列含等效陷波器结构的四元件谐振变换器。该类变换器的电压增益曲线上含有独特的电压增益零点,因此获得了从零可调的电压增益范围,电压调节能力得以增强。但该类变换器又引入了高次谐波问题,导致无功环流增加,转换效率下降。因此,仍需对该类变换器做出改进以提升其性能。
以上研究分别对LLC变换器的效率和电压增益特性有了不同程度的提升,但是它们的拓扑都采用固定结构,且仅对变换器在特定场合下的某一性能有所改善,变换器的灵活性由此受到限制。针对这一问题,一系列拓扑切换型的多模式变换器应运而生[14-17]。文献[14]提出了一种具有双变压器串联结构的改进型LLC变换器,它共有四个运行模式,通过模式切换,其最大输入电压是最小输入电压的4倍,这进一步拓宽了变换器的电压增益范围。文献[15]讨论了一类带有辅助开关的LLC变换器,通过引入辅助开关来增加额外的充电路径从而提高电压增益,维持输出电压的稳定。在文献[16]中,其变换器中的逆变单元可在全桥结构和半桥结构之间灵活切换。而全桥电路的电压增益是半桥电路的两倍,因此变换器可以在较窄的工作频率范围内获得较宽的电压增益。这种拓扑变换的思想还可以应用在其他应用场景中[17]。
为此,本文以LLC变换器为基础,提出一种两模式切换运行的谐振型软开关直流变换器。该变换器将两个相对简单的电路(LLC电路和LLCC电路)进行结合并利用辅助开关管来控制变换器的工作模式。经合理的参数设计,变换器可以同时满足两种工作模式的运行条件。通过对切换点的选择进行详细的分析,变换器能够在较窄的频率范围内实现较宽范围的电压调节,同时保持高转换效率。另外,拓扑本身引入了特殊的谐振零点,不需要增加额外的辅助保护电路,就可以获得内在的过电流保护功能。最后,本文针对一台1kW的实验样机进行实验验证,最高的转换效率为97.3%。
所提变换器为一种两模式切换运行的谐振型软开关直流变换器,通过辅助开关管的通断来控制谐振电容的接入与断开,谐振腔可以在传统的三元件谐振电路(LLC电路)以及四元件谐振电路(LLCC电路)之间灵活切换,从而优化变换器的性能。
所提直流变换器的拓扑如图1所示,它由逆变单元、谐振腔、变压器以及整流单元四部分构成。在变换器工作时,逆变单元将直流输入电压转变为方波电压;此后,经谐振腔的作用将电能转换为正弦形式的电能;再利用变压器实现交流变压并提供前后级的隔离;最后,经整流单元的整流作用,电能再次变换成直流形式供给后侧的负载使用。

图1 所提变换器拓扑
Fig.1 Topology of the proposed converter
谐振腔内共包含四个谐振元件:串联谐振电容Cr、并联谐振电容Cp、串联谐振电感Lr以及励磁电感Lm。高频变压器T的电压比为1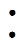 n。
n。
由于所提变换器为一种两模式切换运行的直流变换器,为了方便读者理解,本文先对LLC电路和LLCC电路的特性进行对比分析。
所提变换器的逆变单元采用全桥结构(Q1~Q4),整流单元为二极管整流桥(VD1~VD4)。其中,谐振腔为可变单元,其等效电路由辅助开关管Qa来控制。当辅助开关管Qa关断时,变换器以LLC模式运行;当其闭合时,并联电容Cp接入谐振腔参与谐振,变换器转换成LLCC工作模式。不同运行模式下的等效结构如图2所示。
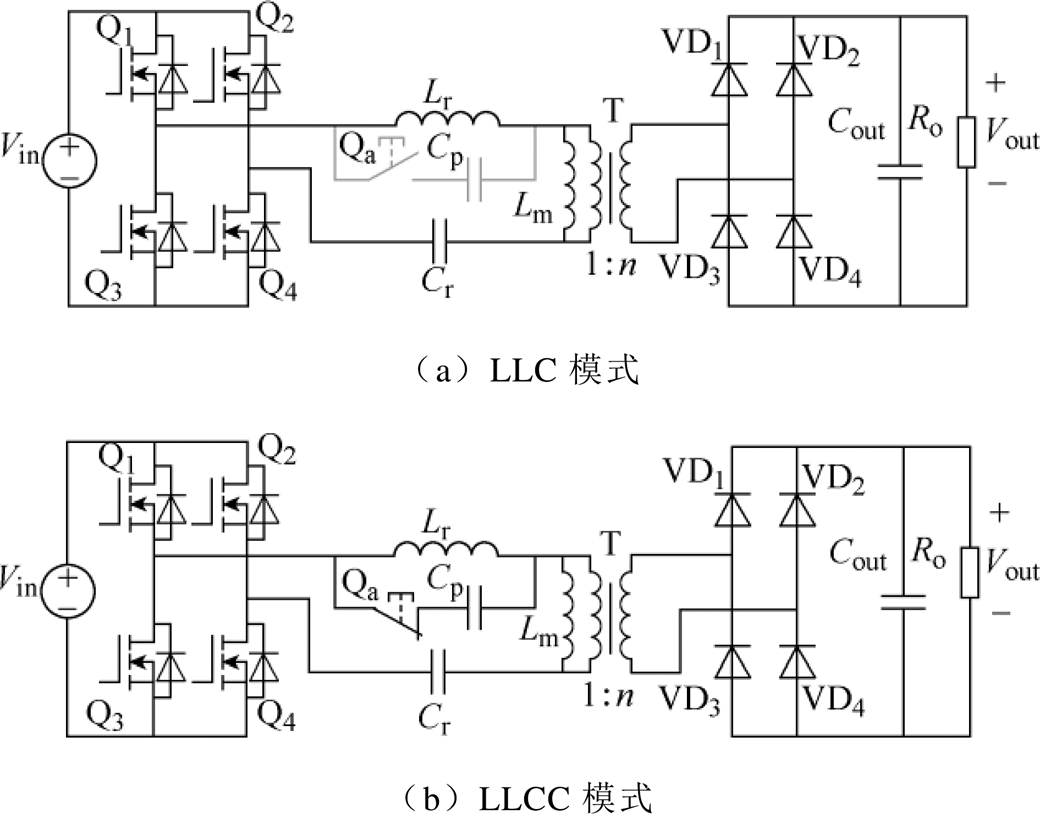
图2 所提变换器的不同运行模式
Fig.2 Different operating modes of the proposed converter
在谐振变换器工作时,励磁电感只参与开关周期中一段时间内的谐振,在其余时间其两端电压被输出电压所钳位。因此无论是LLC电路还是LLCC电路,其工作特性主要由回路中的其他谐振元件所决定。图3给出了输出端短路时的不同模式下的等效输入阻抗电路。
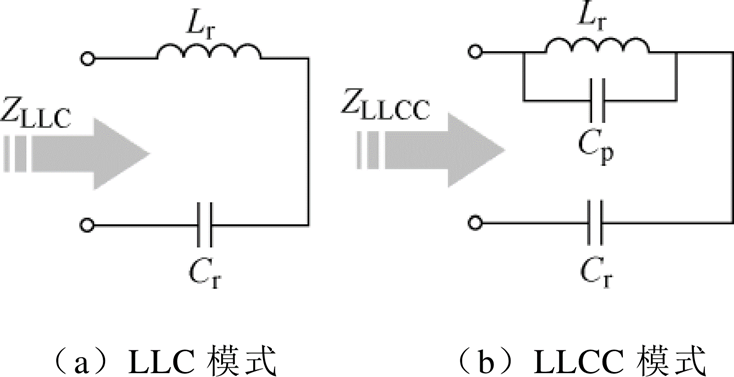
图3 输出端短路时的等效输入阻抗电路
Fig.3 Equivalent input circuit at output short
为便于理解,将LLC电路的输入阻抗ZLLC和LLCC电路的输入阻抗ZLLCC以及特征阻抗Zr分别定义为
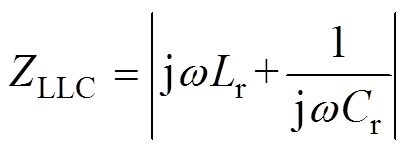 (1)
(1)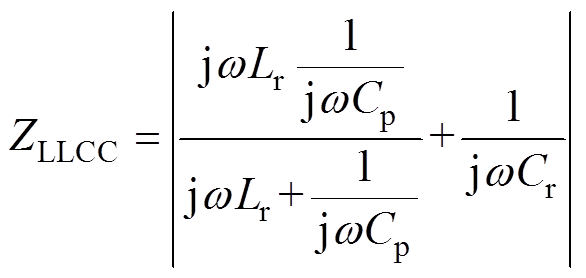 (2)
(2)
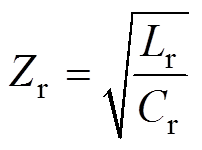 (3)
(3)
令ZLLC的值为零,可以得到LLC电路的谐振频率f0为
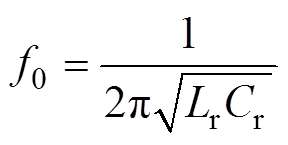 (4)
(4)同理,可推得LLCC电路的谐振频率f1和f2分别为
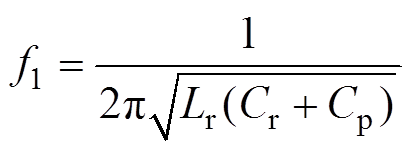 (5)
(5)
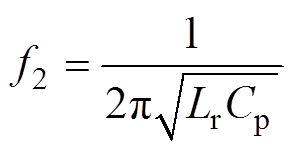 (6)
(6)基于式(1)~式(3),可以绘制出LLC电路及LLCC电路的归一化阻抗ZLLC/Zr、ZLLCC/Zr与归一化频率fn之间的关系,如图4所示。fn为开关频率fs与谐振频率f0的比值。可以看出,在谐振频率f0处(即横坐标为1时),LLC的阻抗为零,基波能量几乎可以全部通过LLC变换器传递到负载侧,即此时LLC可视为一个带通滤波器。当fs<f0(即横坐标小于1)时,ZLLC随着开关频率的增加而快速下降;当fs>f0(即横坐标大于1)时,ZLLC随开关频率的增加而缓慢上升,这种缓慢的上升趋势将带来两方面的影响:①变换器的输出电压调节能力受限。也就是说,运行在该区间内,为了满足宽范围的电压调节需求,频率必须提升到足够高;②变换器的过电流保护仍然很难实现。如文献[18]所述,在过载或短路情况发生时,需要限制流经器件的电流值来维持电路的稳定运行。这都需要变换器提高开关频率以增加谐振腔阻抗从而抑制谐振腔电流。尽管开关频率的提升可以在一定程度上解决上述问题,但也会带来一些新问题:一是会造成开关管产生较大的功率损耗,影响转换效率;二是磁性元件的应力不平衡,导致磁性元件的设计变得困难[18]。
然而,四元件LLCC谐振电路的特性和LLC电路有很大的不同。从图4可知,LLCC电路有两个谐振频率f1和f2。当fs<f1时,ZLLCC的大小随开关频率的增加而迅速下降,在该范围内LLCC表现出和LLC类似的特性。而当f1<fs<f2时,ZLLCC的值随开关频率的增加而快速增加,代表着此时的电压增益变化很快。在fs=f2时,ZLLCC为无穷大,谐振腔的电流被谐振腔本身所吸收,而不会传递至负载侧,变换器的输出电压降为零。输出端和输入端可被视为完全没有电气连接,此时的LLCC更像是一个带阻滤波器。因此,通过调节开关频率可以使变换器工作在f2处来实现过电流保护。当fs>f2时,ZLLCC再次减小,变换器在此区间内的特性和fs<f1时类似。
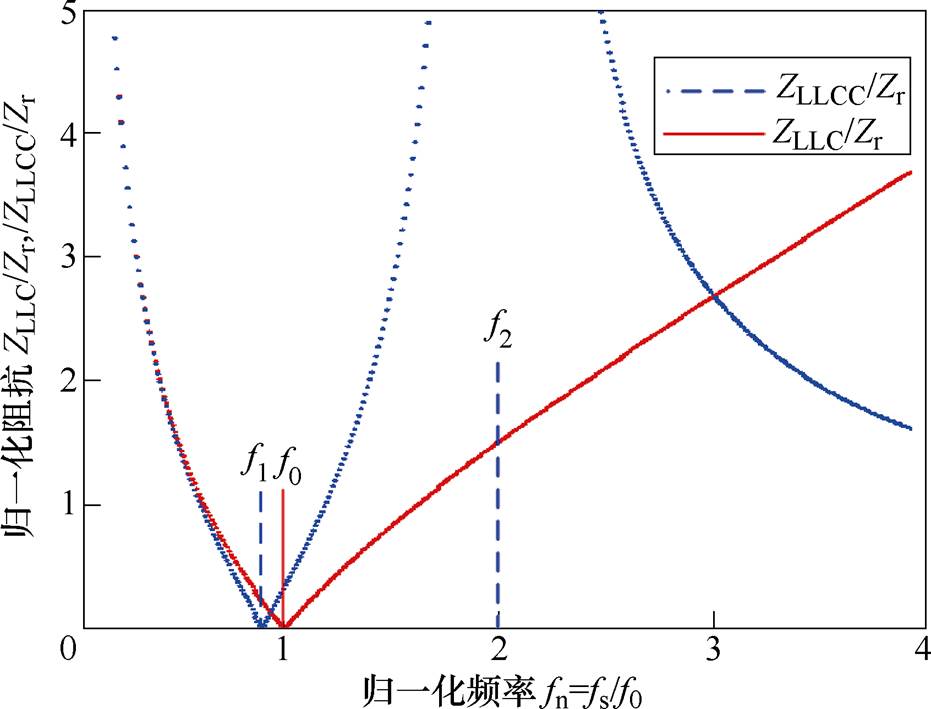
图4 归一化阻抗ZLLC/Zr、ZLLCC/Zr与归一化频率fn的关系
Fig.4 Relationship between normalized impedanceZLLC/Zr, ZLLCC/Zr and normalized frequency fn
电压增益曲线可直观反映变换器的性能,因此本文采用基波等效(First-order Harmonic Appro- ximation, FHA)法[19]来进一步分析所提变换器的特性。LLC模式和LLCC模式下的电压增益曲线如图5所示。

图5 不同运行模式下的电压增益曲线
Fig.5 Voltage gain curves under different operation modes
两种电路在电压增益方面表现出不同的特性,相较而言,LLCC电路具有更宽的电压增益范围。从图5b可以看出,当fs<f1时,LLCC电路的增益特性和LLC相似;当f1<fs<f2时,LLCC电路的增益曲线变得陡峭,且获得了从零可调的增益范围。当输入电压快速变化时,LLCC可以保证在相对狭窄的频率范围内进行电压调节,这得益于并联谐振电容Cp和串联谐振电感Lr构造了特殊的陷波器结构,创建了谐振零点f2。比较来说,如图5a所示,LLC电路没有谐振零点,在fs>f0时电压增益曲线较平缓,电压调节能力受限。
除电压增益外,效率是衡量变换器性能的另一个重要指标,接下来对两种电路的效率特性进行对比。
首先分析额定工作条件下的效率。结合图5可知,两种变换器在额定工作点(谐振频率点)处均能传递高次谐波。对LLCC电路来说,无论在轻载还是重载条件下,其高次谐波分量对应的电压增益值均较高。而LLC电路在较高的开关频率范围内,其电压增益明显低于LLCC电路。下面将对此现象进行数学验证。
为了简化分析,先定义如下的物理量:定义N为谐波次数,而N次谐波对应的频率和角频率分别为Nfs和Nw。结合基波等效法,可以得到LLC电路N次谐波对应的电压增益VLLCN为
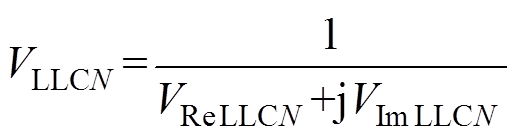 (7)
(7)其中
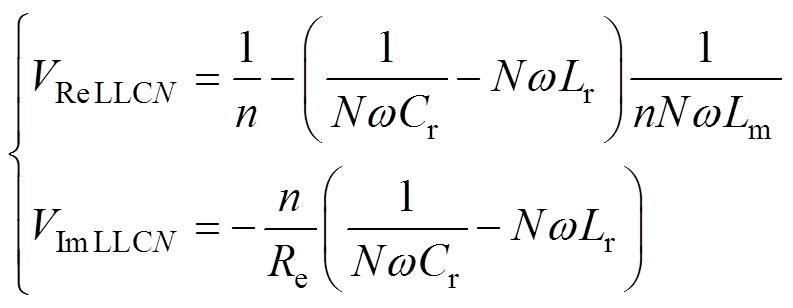
式中,VReLLCN和VImLLCN分别为VLLCN的实部和虚部。经计算可得,VReLLCN、VImLLCN均不为零,即运行在额定点附近时,LLC电路会传递一定量的高次谐波。
类似的方法可以用来分析LLCC电路的高次谐波情况,其相应的电压增益VLLCCN推导为
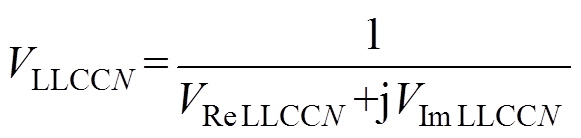 (8)
(8)其中
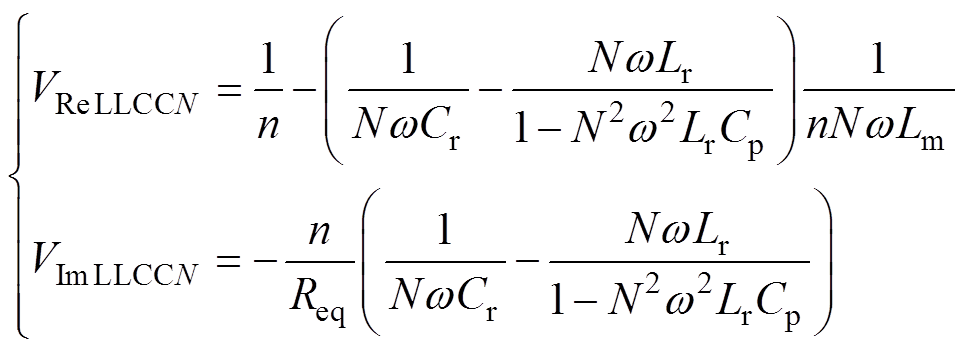
式中,VReLLCCN和VImLLCCN分别为VLLCCN的实部和虚部,且均不为零,代表着在LLCC电路内也含有一定程度的高次谐波。分析可知,高开关频率范围内较高的电压增益值代表着变换器的高次谐波含量较多。而高次谐波会导致电流畸变,带来额外的损耗从而影响效率。相较LLC电路来说,LLCC电路增加了辅助开关管和并联谐振电容,也会引入器件损耗。因此,在相同电压和功率等级下,在额定工作点附近,LLC的效率会高于LLCC的效率。
而当开关频率大于谐振频率时,两种电路效率的变化情况也会有所不同。如文献[20]所述,就LLC而言,当开关频率高于谐振频率时,其会失去零电流软开关(Zero Current Switching, ZCS)特性。此外,该运行区间内开关管的关断电流Iturnoff也会增加,而突增的关断电流和开关频率fs的提升将导致关断损耗Pturnoff迅速增加,相应的数学表达式为
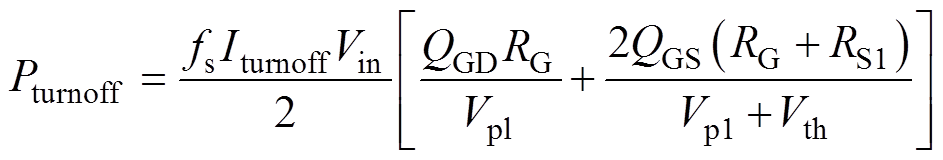 (9)
(9)式中,QGD、QGS分别为开关管栅极和漏极,栅极和源极间存储的电荷;Vpl、Vth分别为米勒平台电压和导通阈值电压;RG、RS1分别为栅极回路电阻和源极等效电阻。这些物理量均可查阅相关技术手册得到。
此外,开关频率的提升也会带来额外的高频损耗,这些因素都会导致LLC电路的效率进一步降低。因此,变换器运行在LLC模式时,其工作频率不能无限增加,但根据上述分析,对工作频率的限制也意味着变换器的电压调节能力受到制约。
结合图5b可知,由于LLCC电路独特的谐振零点的存在,当开关频率大于谐振频率时,其对应的电压增益曲线较LLC电路的电压增益曲线更为陡峭。因此,在相同电压增益时,LLCC电路的工作频率低于LLC电路。因此,运行在LLCC模式下可避免过高的工作频率引入的高频损耗。理论分析认为,在该频率范围内,LLCC电路的效率会更占优势。
结合两种电路在不同运行频率区间内的优势以及两者结构上的相似性,便形成了本文所提的两模式切换运行的谐振型软开关直流变换器。综合考虑效率和电压增益特性,在额定工作点附近,所提变换器以LLC模式运行,这是为了保证较高的转换效率。而随着输入电压的增加,辅助开关管Qa闭合,谐振电容Cp参与谐振工作,变换器切换为LLCC模式来获得较宽的电压增益范围和良好的过电流保护能力。
针对所提变换器,共有5个参数需要确定,分别为变压器电压比n、串联谐振电容Cr、串联谐振电感Lr、励磁电感Lm和并联谐振电容Cp。根据上述分析,变换器首先工作在LLC模式,然后随着输入电压的升高再切换到LLCC模式。因此,参数设计首先应满足LLC电路的运行要求。为了对该变换器进行定量分析和研究,必须对电路的各部分参数进行设计,下面阐述参数选择的具体过程。
LLC电路的设计主要围绕变压器电压比n、励磁电感Lm与谐振电感Lr的比值k以及品质因数Q三个参数进行。品质因数Q为等效阻抗Zr与等效到一次侧的负载电阻Req的比值,相关的公式为
 (10)
(10)本例中,变换器的额定功率为1kW,额定的输入电压Vin和输出电压Vout分别为160V和400V,额定开关频率fr=100kHz,最小工作频率fmin=80kHz。此外,变换器应满足新能源发电的要求,适用于宽输入电压范围的应用场景。因此将输入电压的变化范围设为150~400V。
在参数计算过程中,首先要确定变压器的电压比。把额定工作点设置在谐振频率点处以优化变换器性能,结合变换器的电压增益Vgain为
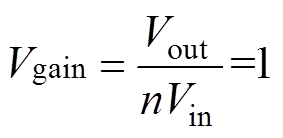 (11)
(11)求解得到电压比n=2.5。
为了保证变换器在全频率范围内性能的最优,工作在最小工作频率时,变换器也应满足ZVS条件。根据文献[4]分析,将最小开关频率对应的工作点设置为ZVS和ZCS的分界点,则在该频率点处应达到最大电压增益,从而可推得k的限制条件为
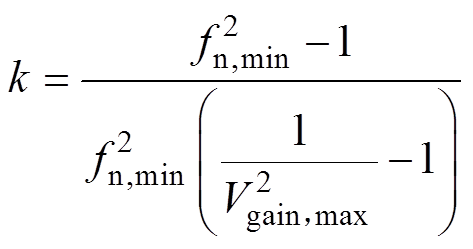 (12)
(12)式中,fn,min为归一化开关频率的最小值,它可通过公式fn,min=fmin/fs得到。当谐振电感固定时,k值越大,励磁电感值越大,电路中的环流越小,效率越高。根据工程经验,一般k值的选取范围为3~6,结合计算得到的k值,最终本文选取的k值为4。
接下来要对最后一个变量Q进行选择。
在其他参数不变的条件下,Q值越小,励磁电感越小,相应地,电路中的环流越大,这将引入额外的损耗。而Q值越大,电压增益曲线越平缓,电压调节特性越差。所提变换器的工作频率区间为大于谐振频率的范围,对效率的要求较高,而电压调节特性可以通过模式切换来改善,因此选择较大的Q值更能满足本文的设计要求。同时,在满足其他要求的前提下应使谐振电容的电压应力尽可能小,该因素会直接影响到谐振腔的体积大小和元件成本,以及电路运行的安全性。结合电路仿真结果,最终确定的Q值为0.95。
根据计算结果n=2.5,k=4,Q=0.95并结合实际实验条件下的电感电容参数,最终确定的LLC变换器的谐振参数为Cr=80nF,Lr=32mH,Lm=128mH。
至此,只剩下LLCC模式下的并联电容Cp的取值尚未确定。根据式(6)可知,谐振频率f2与Cp的取值密切相关,因此可以通过确定谐振频率f2的位置来计算出Cp。如图5b所示,f2的位置决定了LLCC电路电压增益的变化趋势。分析来说,f2不应离额定谐振频率点f1太近也不应太远。如果太远的话,电压增益曲线在(f1, f2)范围内比较平缓,变换器无法在相对狭窄的频率范围内获得较宽的增益范围,电压调节特性没有得到改善。如果太近的话,陷波器将会影响额定谐振频率的传输,能量将会在陷波器中循环。此外,根据傅里叶变换,将谐振腔的输入电压进行傅里叶展开后仅包含奇次谐波,所以f2应设置为f1的偶数倍来避免额定条件下的无功环流[21]。综合考虑上述因素,将f2设为200kHz,计算得到Cp=20nF。
根据上述分析,可以获得一组合理的谐振参数。因为所提变换器有LLC和LLCC两种工作模式,相应的设计过程也包括这两部分,参数设计流程如图6所示。由于两种电路在结构上具有相似性,它们共用了Cr、Lr、Lm等谐振元件,所以该设计方法可以很好地满足两种模式的运行要求。
综合上述分析,变换器在不同的运行模式下各有优势,而模式切换的目的是使之在相对狭窄的频率范围内同时保证高转换效率和宽增益范围,因此,切换点的选择成为了本文另一重点关注的因素。
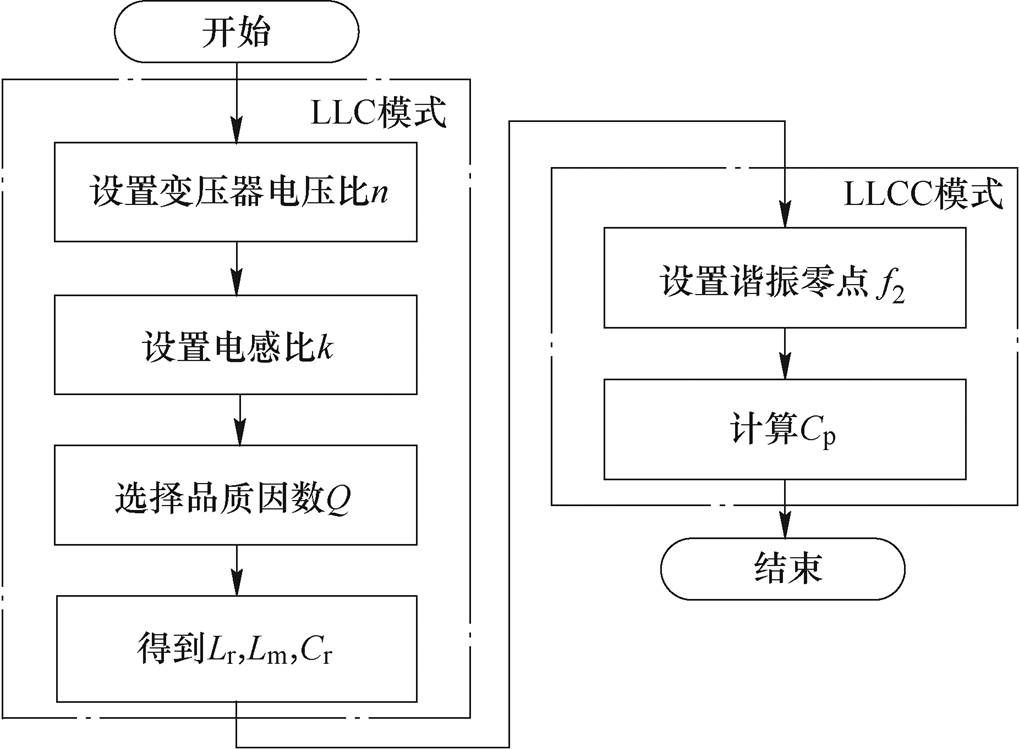
图6 参数设计流程
Fig.6 Flow chart of parameter design process
基于1.3节中关于效率的分析,在额定工作点附近,LLC的效率比LLCC的效率高;而当输入电压增高即电压增益减小时,LLCC的效率比LLC更具优势。所以,在开关频率大于谐振频率的频率区间内,LLC和LLCC会有一个效率重合点,可以选择此相交点作为切换点以保证变换器的效率最优。为准确把握该效率相交点的位置,需要分别对两种模式进行不同频率下的损耗计算。就谐振型直流变换器而言,损耗主要来源于五个方面,分别为变压器损耗、开关管损耗、二极管损耗、电容损耗以及电感损耗[22-23]。
但通过损耗计算确定两种模式的效率相交点作为切换点的方式存在一些固有缺陷。首先,通过损耗计算可得到两种模式下的效率重合点,依此可确定相应的开关频率并使之作为模式之间的切换频率。这可能会出现切换频率偏离额定频率过多的情况。虽然此时仍可以保证正常的切换,但变换器的工作频率范围过宽,其性能受到限制,失去了模式切换的意义。此外,以效率为优化目标的情况下,切换过程中的输出电压难免会存在波动,影响变换器的安全稳定运行。其次,对两种模式分别进行效率估算的过程较为复杂,实验参数和器件型号稍有变动,就得重新进行损耗计算,计算量较大,无法建立一个通用模型,方法的适用性有待提高。另外,受实验条件的影响,理论计算效率和实测效率会存在一定的偏差。尽管这种误差可以通过提高损耗计算的精度来减小,但是仍然无法完全消除。为了解决上述问题,本文提出一种以相同电压增益点作为切换点的方法,可以满足在狭窄频率范围内获得较宽的电压增益,同时保证变换器的稳定运行,下面将对这一方法进行详细阐述。
根据第2节得到的谐振参数,可以绘制出所提变换器两种模式下的电压增益曲线,将它们整合到一个图中,便得到了如图7所示的复合电压增益曲线,同时4个特殊点(a点,b点,c点,d点)也均在图中标出。为了叙述方便,将LLC模式称为模式Ⅰ,将LLCC模式称为模式Ⅱ。a点为模式Ⅰ的额定工作点,当开关频率超过此点之后,模式Ⅰ的电压增益曲线变得平缓。为了在较窄的频率范围内拓宽电压增益范围,本文将模式Ⅰ中200kHz对应的电压增益点(b点)选择为模式切换点。为了保证模式间的平滑切换,在模式Ⅱ中与b点电压增益相同的点(c点),被选作另一模式切换点。而d点则为模式Ⅱ中的谐振零点。
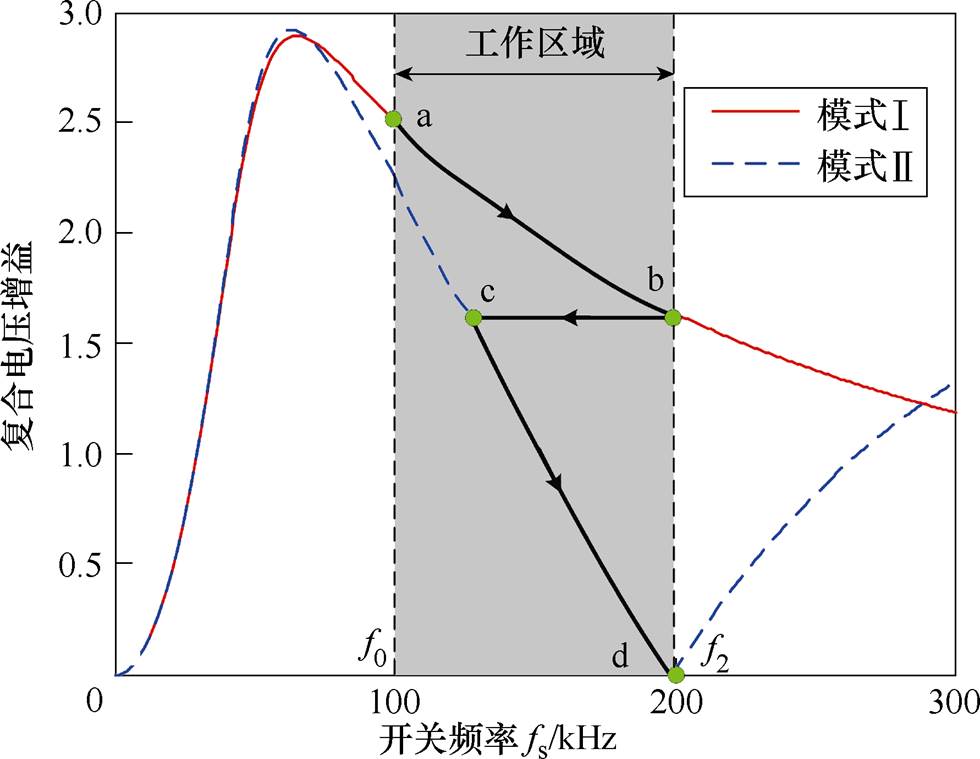
图7 所提变换器复合电压增益曲线
Fig.7 Compound voltage gain curves of the proposed converter
在两种模式下各截取一段曲线,组成所提变换器的复合增益曲线,切换过程按照箭头方向所示。即从a点到b点,变换器先运行在模式Ⅰ下,而随着输入电压的升高,当开关频率达到200kHz(b点),变换器从模式Ⅰ切换到模式Ⅱ(c点)。在超过c点之后,变换器便一直运行在模式Ⅱ下。总结来说,在狭窄的频率范围(f0, f2)内,变换器的电压调节能力得到提升,同时效率也得到保证。
为了验证所提的两模式切换运行的谐振型软开关直流变换器结构的合理性,本文基于一台1kW的样机进行了实验测试,图8给出了实验样机。
接下来将对各个特殊点的运行情况进行验证,为了更清晰地展示变换器优良的软开关特性,给出了相应的软开关细节图。a点为模式Ⅰ中的额定工作点,图9给出了变换器在该点的实验波形。VGS为开关管驱动信号,VQ1和iQ1分别表示开关管Q1的电压和电流,相应地,VVD1和iVD1则表示二极管VD1的电压和电流,VCr为谐振电容Cr两端电压。在额定条件下,开关频率fs=100kHz,输入电压Vin=160V,输出电压Vout=398.8V,计算得到的电压增益为2.49,与额定点的设计值接近。由图9可以看出,开关管电流滞后电压一个角度,即开关管实现了ZVS开通,也实现了ZCS关断。iVD1在开通和关断时刻近似为零,即二极管也实现了理想的ZCS特性。该点的实测效率为97.3%,在额定点处变换器实现了较高的转换效率。

图8 所提变换器的实验样机
Fig.8 Experimental prototype of the proposed converter
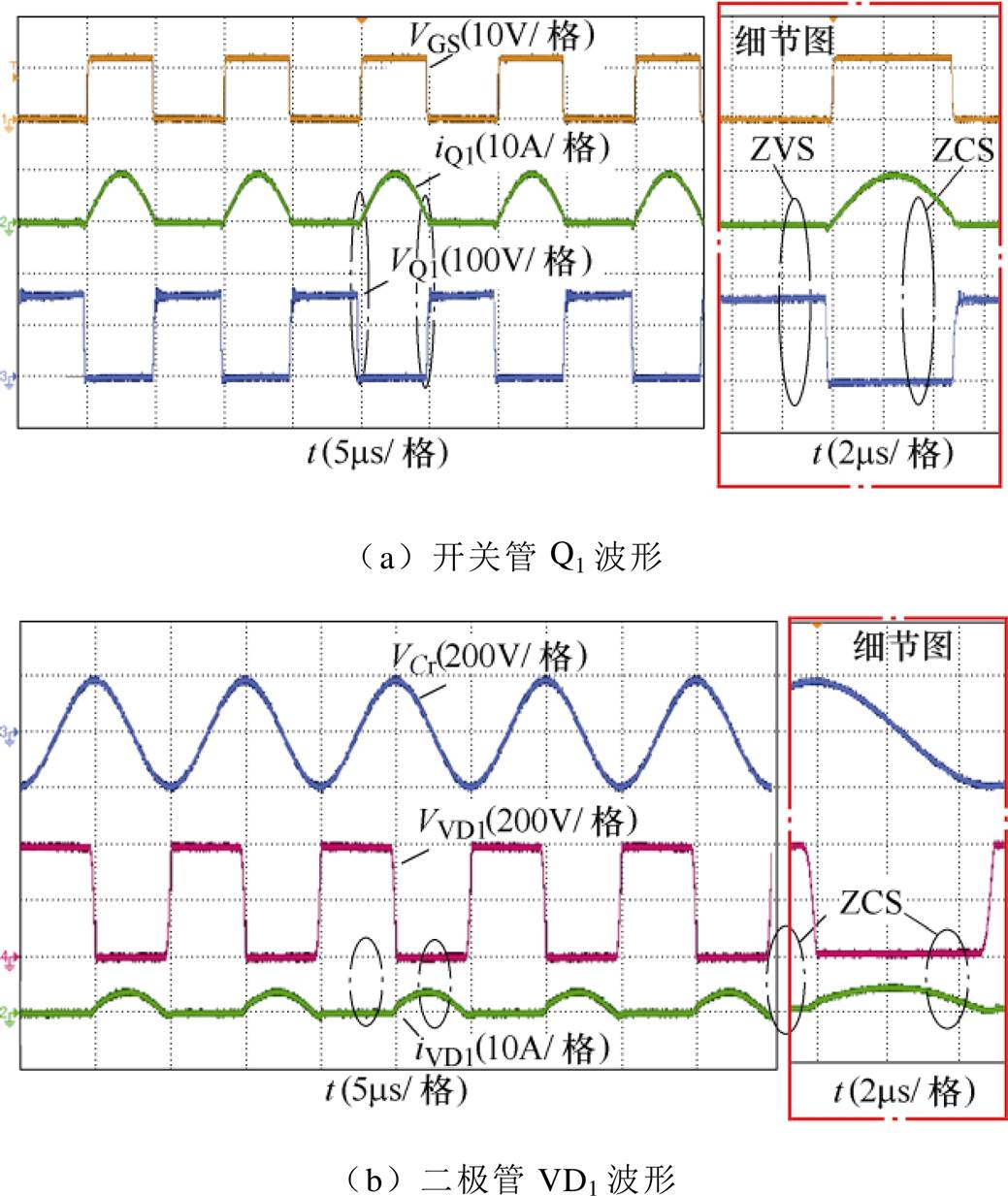
图9 额定条件下的实验波形
Fig.9 Experimental waveforms at rated condition
图10给出了模式Ⅰ中切换点b点的实验波形。此时的输入电压Vin=239.6V,Vout=400V,电压增益为1.67。由实验波形可知,开关管电流滞后电压的角度变大,代表着开关管此时仍可以实现ZVS开通,但是却失去了ZCS特性。表现为在关断过程中,开关管的关断电流值变大。另外,对二极管来说,其电流在开关时刻从零开始变化,实现了准ZCS(Q-ZCS)特性。综合来说,变换器的效率会降低,实测该点的效率值为96.0%。
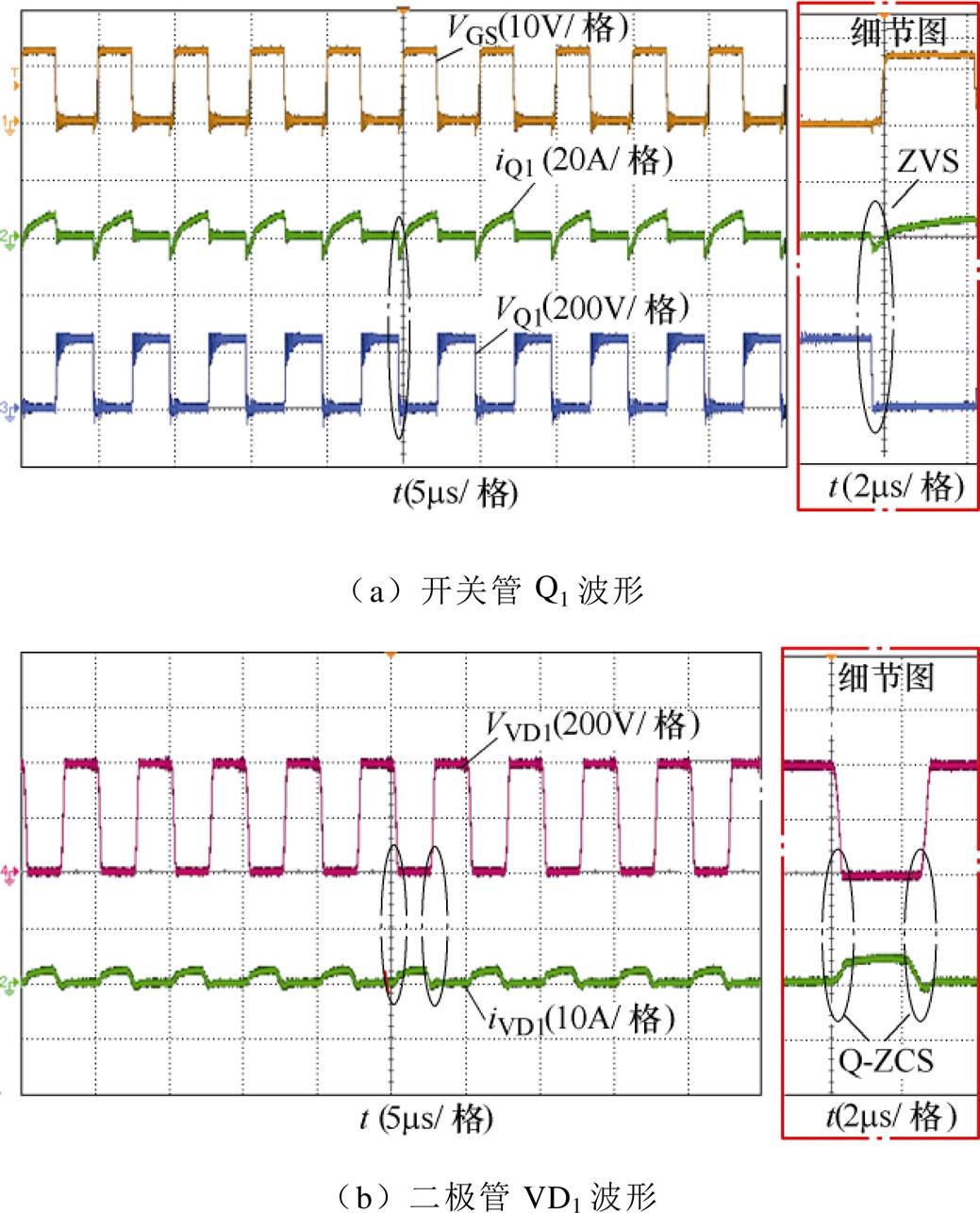
图10 b点的实验波形
Fig.10 Experimental waveforms of point b
为了变换器效率和电压增益性能的优化,随着输入电压的增加,辅助开关管Qa闭合,变换器从模式Ⅰ切换到模式Ⅱ。图11给出了运行在c点的实验波形,此点的电压增益和b点的电压增益相同,因此变换器可以在两个模式之间平滑切换。由图11可知,此时的开关管仍实现了ZVS。变压器一次和二次电流均含有高次谐波,一定程度上影响了转换效率。但在相同增益的情况下,c点的开关频率低于b点,缓解了由于工作频率过高而带来的高频损耗,实验测得该点的效率为95.2%。
之后,变换器一直运行在模式Ⅱ下,图12给出工作在d点的实验波形。当输入电压Vin=400V时,输出电压Vout只有3V左右,输出电流被限制在很小的数值。这意味着,输入功率被谐振腔内部结构所吸收。因此,相较其他变换器,不需要增加额外的辅助保护电路,所提变换器工作在该点便可以实现过电流保护,可靠性得到提升。
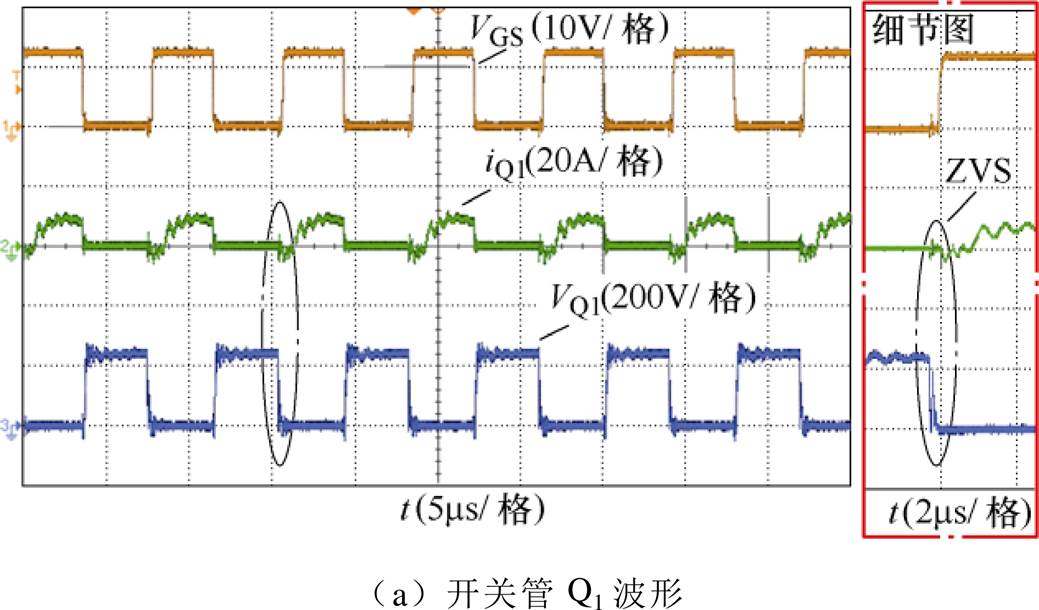

图11 c点的实验波形
Fig.11 Experimental waveforms of point c
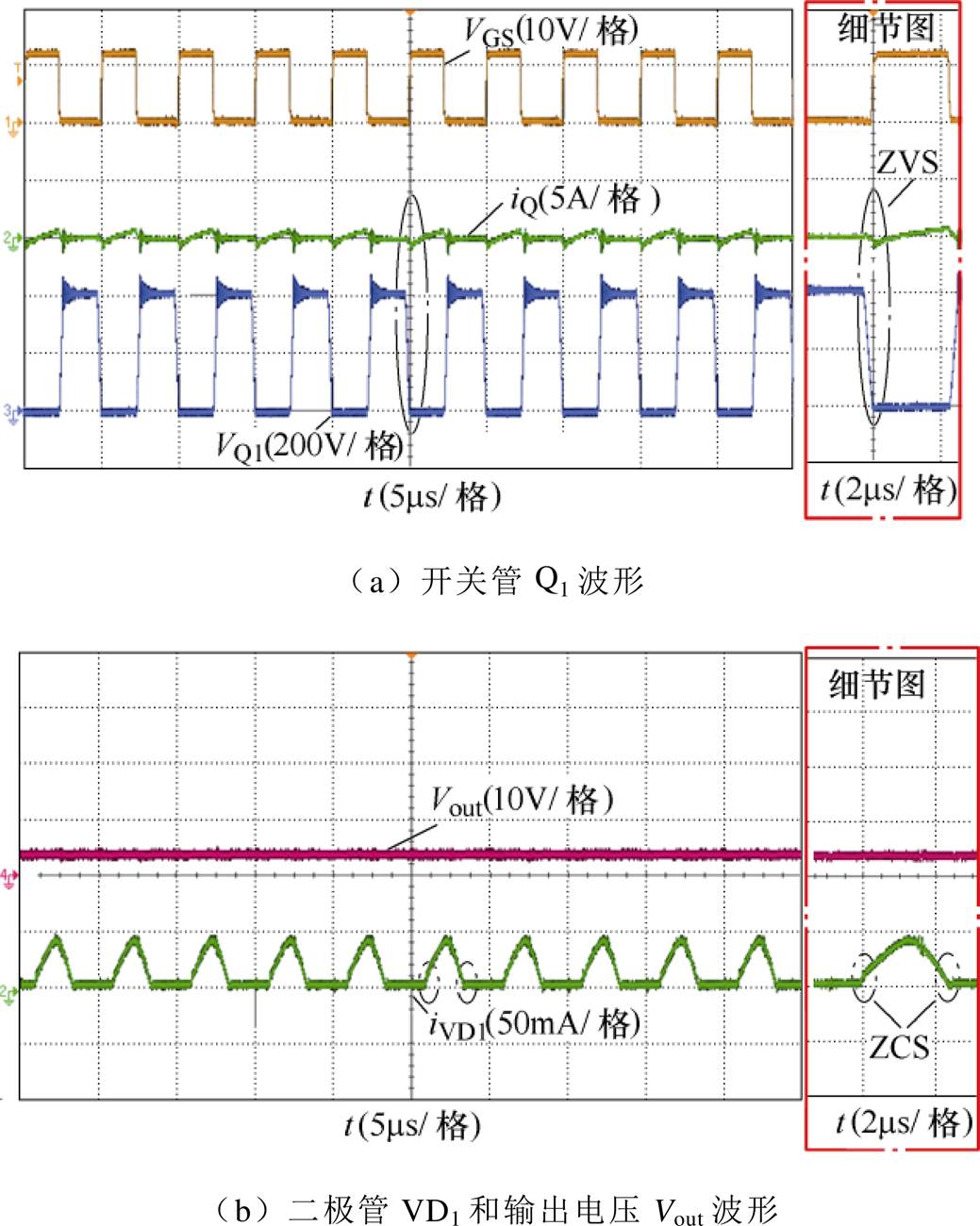
图12 d点的实验波形
Fig.12 Experimental waveforms of point d
变换器在不同模式下效率的测试结果如图13所示。效率曲线总共包括两段,因为输出电压固定在400V,效率点与不同的输入电压有关。如图13所示,变换器在模式Ⅰ达到了最高效率97.3%。由于模式Ⅱ中高次谐波的存在,模式Ⅱ下的效率值均低于模式Ⅰ的效率值,即便如此,变换器在整个增益范围内仍保持较高的转换效率(92%以上)。

图13 所提变换器的效率曲线
Fig.13 Efficiency curves of the proposed converter
进一步地,为了测试所提变换器模式切换的可行性,图14给出了模式切换的实验波形。其中,dQa为辅助开关管Qa的驱动信号;iCr为流经谐振电容Cr的电流,即谐振腔电流。起初,输入电压数值较低,此时没有触发dQa,并联电容Cp没有参与电路谐振,变换器运行在模式Ⅰ下。随着输入电压的升高,当输入电压达到240V左右,达到了最佳切换点,触发驱动信号dQa使Cp参与谐振,变换器切换到模式Ⅱ。随后,输入电压进一步上升,变换器仍然运行在模式Ⅱ下。谐振腔电流iCr随着变换器运行在不同的模式而发生相应的变化。

图14 模式切换的实验波形
Fig.14 Experimental waveforms of mode transition
在整个切换过程中,当输入电压从150V上升到400V,输出电压始终维持在400V,再次证明了所提变换器具备良好的电压调节能力。
本文提出了一种两模式切换运行的谐振型软开关直流变换器。它将两种相对简单的电路结合,利用辅助开关管来控制变换器的工作模式。在额定条件下,变换器运行在LLC模式,而随着输入电压的升高,变换器工作在LLCC模式,从而获得在相对狭窄的频率范围内效率和电压增益性能最优。所提变换器适用于宽输入电压范围和高效率的应用场景下,具有以下特点:
1)拓扑结构和控制相对简单。变换器的拓扑结构不复杂,制作成本相对较低;根据输入电压的大小来决定辅助开关管的通断,控制方法简单。
2)较宽的电压增益范围。通过两种工作模式的切换,可以实现较宽范围内的电压调节功能。
3)良好的软开关特性。变换器始终工作在ZVS区域,功率开关管实现ZVS,二极管实现ZCS,良好的软开关特性使得变换器在全增益范围内保持较高的效率。
4)内在的过电流保护功能。拓扑本身引入了特殊的谐振零点,可以实现过电流保护,不需要增加额外的辅助电路就可以确保变换器的可靠运行。
最后,本文对一台额定功率为1kW的样机进行测试,验证了理论的正确性和可行性。变换器的最高效率为97.3%。高效率和宽增益范围的特点使得该变换器非常适用于新能源发电系统。因此,相关研究具有一定的价值,在未来的研究中,可通过高频化磁集成技术和平面化磁件的方式制作变换器,并采用更为先进的高频功率器件,进一步实现高频化、小型化、轻量化的设计目标。同时,需开发一种具有双向功率流动的直流变换器,以实现功率的高效、双向传递,由此提高变换器的应用普及程度。
参考文献
[1] 高珊珊, 王懿杰, 徐殿国. 一种高频高升压比改进型Sepic变换器[J]. 电工技术学报, 2019, 34(16): 3366-3372.
Gao Shanshan, Wang Yijie, Xu Dianguo. A high frequency high voltage gain modified Sepic converter[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3366-3372.
[2] 周强, 汪宁渤, 何世恩, 等. 高弃风弃光背景下中国新能源发展总结及前景探究[J]. 电力系统保护与控制, 2017, 45(10): 147-154.
Zhou Qiang, Wang Ningbo, He Shien, et al. Summary and prospect of China’s new energy development under the background of high abandoned new energy power[J]. Power System Protection and Control, 2017, 45(10): 147-154.
[3] 郭灵瑜, 姚钢, 周荔丹. 全直流海上风电场高升压比DC/DC变换技术综述[J]. 电力系统保护与控制, 2018, 46(12): 159-169.
Guo Lingyu, Yao Gang, Zhou Lidan. Research review on high step-up ratio DC/DC converter for offshore DC wind farm[J]. Power System Protection and Control, 2018, 46(12): 159-169.
[4] 马皓, 祁丰. 一种改进的LLC变换器谐振网络参数设计方法[J]. 中国电机工程学报, 2008, 28(33): 6-11.
Ma Hao, Qi Feng. An improved design method for resonant tank parameters of LLC resonant con- verter[J]. Proceedings of the CSEE, 2008, 28(33): 6-11.
[5] Fang Xiang, Hu Haibin, Shen Z J, et al. Operation mode analysis and peak gain approximation of the LLC resonant converter[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1985-1995.
[6] 辛德锋, 安昱, 郜亚秋, 等. 适用于ISOS拓扑的高压DC/DC变换器研究[J]. 电力系统保护与控制, 2017, 45(13): 65-70.
Xin Defeng, An Yu, Gao Yaqiu, et al. Study on high voltage DC/DC converter based on ISOS topology[J]. Power System Protection and Control, 2017, 45(13): 65-70.
[7] Kundu U, Yenduri K, Sensarma P. Accurate ZVS analysis for magnetic design and efficiency improve- ment of full-bridge LLC resonant converter[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 1703-1706.
[8] Lee JaeBum, Kim JaeKuk, Kim JaeHyun, et al. A high-efficiency PFM half-bridge converter utilizing a half-bridge LLC converter under light load con- ditions[J]. IEEE Transactions on Power Electronics, 2015, 30(9): 4931-4942.
[9] Kim Dong-Kwan, Moon Sang Cheol, Yeon Cheol-O, et al. High-efficiency LLC resonant converter with high voltage gain using an auxiliary LC resonant circuit[J]. IEEE Transactions on Power Electronics, 2016, 3(1): 6901-6909.
[10] Inam W, Khurram K A, Perreault D J, et al. High efficiency resonant DC/DC converter utilizing a resistance compression network[J]. IEEE Transa- ctions on Power Electronics, 2014, 29(8): 4126-4135.
[11] Wang Yifeng, Han Fuqiang, Yang Liang, et al. A novel D-CLT multiresonant DC-DC converter with reduced voltage stresses for wide frequency variation applications[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(5): 4509-4523.
[12] Huang Daocheng, Fred C L, Fu Dianbo. Classi- fication and selection methodology for multi-element resonant converters[C]//2011 Twenty-Sixth Annual IEEE Applied Power Electronics Conference and Exposition, Fort Worth, USA, 2011: 558-565.
[13] Batarseh I. Resonant converter topologies with three and four energy storage elements[J]. IEEE Transa- ctions on Power Electronics, 1994, 9(1): 64-73.
[14] Hu Haibing, Fang Xiang, Chen Frank, et al. A modified high efficiency LLC converter with two transformers for wide input-voltage range applica- tions[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1946-1960.
[15] Wang Hongliang, Chen Yang, Fang Peng, et al. An LLC converter family with auxiliary switch for hold-up mode operation[J]. IEEE Transactions on Industry Applications, 2017, 32(6): 4291-4306.
[16] Jovanovic M M, Irving B T. On-the-fly topo- logymorphing control-efficiency optimization method for LLC resonant converters operating in wide input and/or output-voltage range[J]. IEEE Transactions on Industry Applications, 2016, 31(3): 2596-2608.
[17] Liang Zhigang, Guo Rong, Li Jun, et al. A high efficiency PV module-integrated DC/DC converter for PV energy harvest in FREEDM systems[J]. IEEE Transactions on Power Electronics, 2011, 26(3): 897- 909.
[18] Yang Bo, Lee F C, Concannon M. Over current protection methods for LLC resonant converter[C]// IEEE Applied Power Electronics Conference and Exposition, Rhodes, Greece, 2003: 605-609.
[19] Simone S D, Adragna C, Spini C, et al. Design- oriented steady state analysis of LLC resonant converters based on FHA[C]//IEEE International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Taormina, Italy, 2006: 16-23.
[20] Chen Bo, Wang Ping, Wang Yifeng, et al. Com- parative analysis and optimization of power loss based on the isolated series/multi resonant three-port bidirectional DC-DC converter[J]. Energies, 2017, 10(10): 1565.
[21] Fu Dianbo, Fred C L, Ya Liu, et al. Novel multi- element resonant converters for front-end DC/DC converters[C]//IEEE Power Electronics Specialists Conference, Rhodes, Greece, 2008: 250-256.
[22] 陈斌, 李琳, 赵志斌. 双向全桥DC-DC变换器中大容量高频变压器绕组与磁心损耗计算[J]. 电工技术学报, 2017, 32(22): 123-133.
Chen Bin, Li Lin, Zhao Zhibin. Calculation of high- power high-frequency transformer’s copper loss and magnetic core loss in dual-active-bridge DC-DC converter[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 123-133.
[23] 李梦柏, 谢竹君, 林卫星, 等. 一种适用于新能源并网的高增益单向直流变压器[J]. 电工技术学报, 2018, 33(2): 301-309.
Li Mengbo, Xie Zhujun, Lin Weixing, et al. Cascaded LC-AC transformer unidirectional DC-DC converter with high stepping ratio[J]. Transactions of China Electrotechnical Society, 2017, 33(2): 301-309.
A Two-Mode Soft-Switching Resonant DC-DC Converter for Wide Input Voltage Range Applications
Abstract A two-mode soft-switching resonant DC-DC converter is proposed in this paper. The resonant structure is changed by controlling the auxiliary switch, and thus the operating modes are determined. There are two working modes in total, namely LLC mode and LLCC mode. Combining the traditional parameter design of the LLC converter and the characteristics of the proposed converter, a novel parameter process that can meet the requirements of the two modes is designed. Moreover, by optimizing the switching point, the converter can achieve high efficiency and wide gain range within a narrow frequency range. In addition, an extra resonant zero point is introduced without increasing the complexity of the topology. As a result, the inherent over-current protection is guaranteed. Finally, a 1kW prototype is built to verify the correctness of the above theoretical analysis. The experimental results show that the proposed converter has excellent performance. When the input voltage varies from 150V to 400V, the output voltage remains constant at 400V and the maximum efficiency is 97.3%.
keywords:Mode transition, soft-switching, resonant DC-DC converter, high conversion efficiency, wide input voltage range
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.191330
国家重点研发计划资助项目(2018YFB0904700)。
收稿日期 2019-10-14
改稿日期 2020-04-29
刘瑞欣 女,1995年生,硕士研究生,研究方向为谐振型软开关直流变换器。E-mail: rxliu1210@tju.edu.cn
王议锋 男,1981年生,博士,副教授,研究方向为高频电能变换技术、磁集成技术、软开关技术及交直流微电网中的电力电子技术等。E-mail: wayif@tju.edu.cn(通信作者)
(编辑 崔文静)