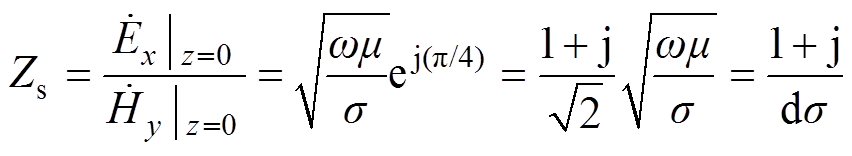 (1)
(1)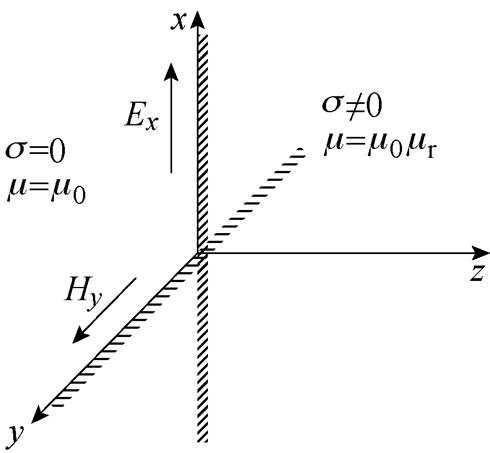
图1 模型分界面示意图
Fig.1 Diagram of model interface
摘要 该文基于表面阻抗理论对表面阻抗法在电力变压器导磁钢结构件(如油箱、铁心拉板等)杂散损耗计算中的实际应用展开研究。针对变压器杂散损耗工程计算中面临的多尺度、小透入深度问题带来的计算精度和计算效率不易兼顾的难题,综合考虑导磁钢构件的趋肤效应和三维杂散场分布特征,提出一种对趋肤深度区域和场量衰减区域分别进行边界条件处理的局部表面阻抗建模分析方法,实现了杂散损耗的有效计算;并以国际TEAM杂散损耗基准模型P21-B为研究对象搭建变压器杂散损耗测试系统,通过相应的实验研究和仿真分析发现,局部表面阻抗方法与常规有限元方法具有相当的计算精度,但从计算规模和计算时间角度分析,前者在保证计算精度的前提下可以显著节省计算资源,提高计算效率,具有较高的工程实用价值。
关键词:表面阻抗法 杂散损耗 漏磁场 计算规模
电气工程中的杂散损耗问题,对实验研究和数值仿真而言都是一个复杂的经典难题。以大型电力变压器为例,杂散损耗是变压器漏磁场在金属构件中感应产生的,虽然变压器基本理论和产品设计、制造已有百余年的历史,但是如何精准、快速地计算杂散损耗问题仍未解决[1]。
电力变压器作为特高压输电工程的关键电磁装备,其单台容量和电压等级在不断提升,使得变压器的结构越来越复杂,由杂散损耗引起的金属构件的局部过热问题越来越突出[2]。近年来,国内外曾多次发生由于变压器局部过热导致的运行故障,如大电流套管升高座连接螺栓过热故障、大电流套管引起的空气侧结构件过热故障、低压侧升高座法兰过热故障等[3]。因此,对变压器漏磁场的分析以及杂散损耗的计算是电力变压器产品设计和开发中的重要环节。
油箱、铁心拉板等是变压器功能及结构支撑的重要组成部件[4],主要制造材料为导磁钢板,其结构尺寸一般具有长度、宽度远大于厚度的特点并且具有明显的趋肤效应。因此在对该类多尺度、小透入深度问题进行电磁场分析和杂散损耗计算时经常会面临计算精度和计算效率无法兼顾的难题。
本文基于国际TEAM P21-B基准模型,对电力变压器工程中的杂散损耗问题展开研究[5]。目前该问题的主要解决方法是基于矢量位和标量位的有限元法[6-9],该类方法在对具有小透入深度现象的三维非线性涡流场问题进行处理时,为保证一定的计算精度,需要对仿真模型进行细致的实体剖分,从而导致有限元离散化方程组中的未知数个数增多,计算规模庞大[10-11]。为解决细致剖分引起的过多单元和节点问题,国内外很多学者对表面阻抗法进行了相关研究。文献[12]通过对换流变压器油箱材料的分析给出了基于表面阻抗的谐波涡流损耗求解方法,利用该方法对大型换流变压器的涡流损耗进行了计算和验证。文献[13]采用表面阻抗法对变压器夹件、油箱和电磁屏蔽进行建模,计算了变压器油箱表面的涡流及其损耗分布,分析了不同屏蔽结构对变压器油箱涡流损耗的影响。文献[14]通过对一维表面阻抗理论的推导,建立了二维和三维表面阻抗仿真模型,计算了三相三柱变压器箱壳的漏磁场分布和涡流损耗。文献[15]利用传统有限元法和表面阻抗法对变压器铁心夹件上的涡流损耗进行计算,获得了两种建模方法对应的涡流密度分布并进行了对比分析,验证了表面阻抗法计算导体表面涡流分布的准确性。需要指出的是,虽然上述文献都涉及表面阻抗法在处理含铁磁材料的三维涡流场计算中的应用,但大多仅针对涡流损耗进行计算,同时也未考虑材料的磁滞损耗计算问题,而变压器箱壳及其钢构件大多为导磁材料制作,这显然是不够合理的。
综上所述,虽然表面阻抗法可以较好地解决含铁磁材料的涡流场数值计算问题,对于材料表面的磁场分布和涡流分布也获得了较好的计算结果,但其对于关乎磁损耗求解的材料内部区域的电磁场量和相应边界条件的处理,以及基于场量计算结果的杂散损耗计算方法,还有待进一步研究。针对上述问题,本文基于考虑边角区的表面阻抗边界条件提出了一种有限元仿真模型的局部表面阻抗建模方法,并实现了杂散损耗的准确计算和实验验证。该方法克服了常规有限元法由于网格疏密过渡而导致的单元过多的困难,考虑了导体边角区对阻抗边界条件的影响,并解决了涡流损耗和磁滞损耗的有效计算问题,在不失计算精度的前提下大幅降低了计算成本。
表面阻抗概念最早由S. A. Schelkunoff针对电磁场在导体表面的一维渗透问题提出,近年来在处理含铁磁材料的涡流场数值计算中得到广泛应 用[16]。表面阻抗指的是正弦交变磁场作用下的导体,其表面电场强度与磁场强度切向分量的比值为一常数,称为表面阻抗。假设一个半无限大导体,处于电角频率为w 的正弦交变磁场中,如图1所示。导体内电场强度只有x轴分量,磁场强度只有y轴分量,Ex和Hy只随z轴变化,导体电导率s,磁导率m 均为线性、各向同性。根据麦克斯韦方程组,推导出一维表面阻抗边界条件[16]为
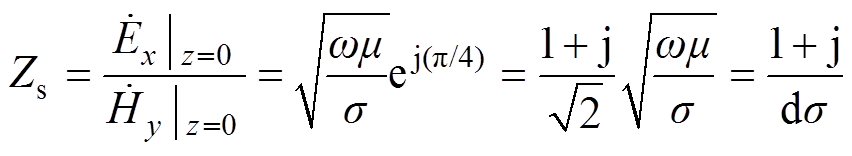 (1)
(1)
图1 模型分界面示意图
Fig.1 Diagram of model interface
在导体表面的非边界区域,假设电磁量只有切向分量,对计算结果的影响较小;但是在导体边界区,导体表面上的磁场并非只有切向分量,其法向分量对计算结果的影响较大,因此,一维表面阻抗边界条件在导体边界区域将不再适用。
针对一维表面阻抗边界条件的局限性,考虑边角区的表面阻抗边界条件可以有效弥补其缺陷,图2为靠近导体侧一条棱边处的横向磁场(横向磁场的方向与z轴方向垂直),磁场随时间按照正弦规律变化,x轴和y轴方向的边界磁场强度的切向分量分别记为Hx0和Hy0。
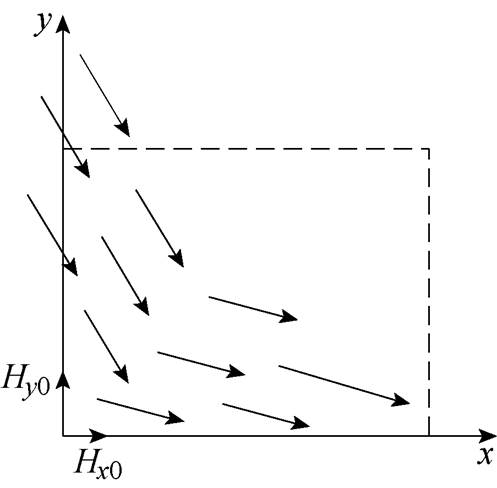
图2 二维边界磁场
Fig.2 Two-dimensional boundary magnetic field
此时电场分量为Ez表示只有z轴分量,因此磁场满足涡流方程的复数形式分别为
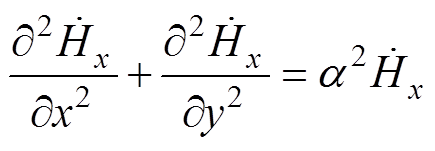 (2)
(2)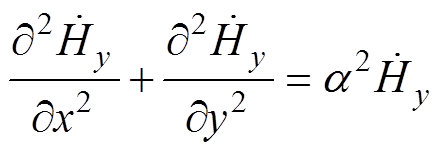 (3)
(3)
其中
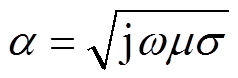
通常在小透入深度的情况下,随着与拐角距离的增加,边界上的法向磁通逐渐减少,切向磁场则逐渐增加到一个大体上的常值,因此在靠近矩形角处方程的近似解表示为
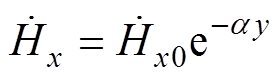 (4)
(4)
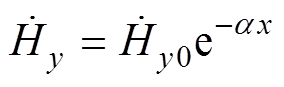 (5)
(5)利用麦克斯韦第一方程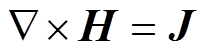 和
和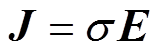 可以求出电场强度
可以求出电场强度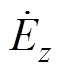 ,其表示为
,其表示为
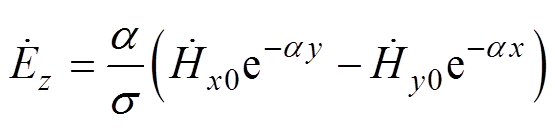 (6)
(6)
因此,在拐角区周围沿x轴和y轴方向边界上的表面阻抗可以分别表示为
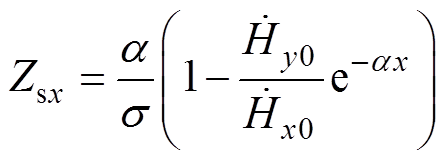 (7)
(7)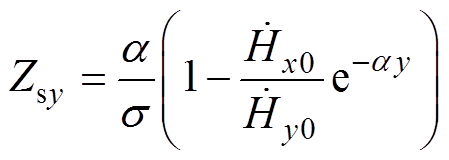 (8)
(8)
进一步地,将二维表面阻抗边界条件推广到三维涡流计算中,导体中三个平面交相构成的棱边与拐角区如图3所示[17]。
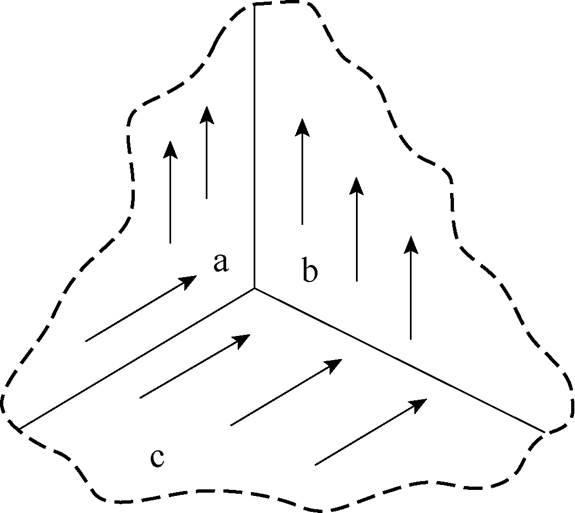
图3 三维边界磁场
Fig.3 Three-dimensional boundary magnetic field
对于磁场强度的处理与二维表面阻抗边界条件相同,将其分解为切向分量和法向分量,并引入表面阻抗条件的修正函数,具体定义表示为
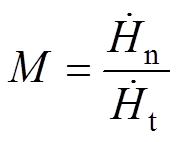 (9)
(9)式中,M为修正函数;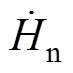 和
和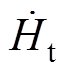 分别为平面上磁场强度的法向分量和切向分量。将修正函数引入到表面阻抗条件中表示为
分别为平面上磁场强度的法向分量和切向分量。将修正函数引入到表面阻抗条件中表示为
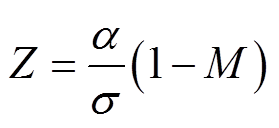 (10)
(10)
因此,在边角区各个面(a、b、c)的表面阻抗条件的近似表达式可以分别表示为
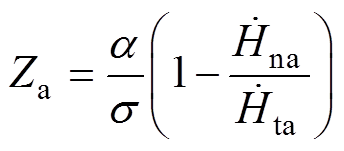 (11)
(11)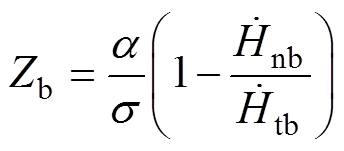 (12)
(12)
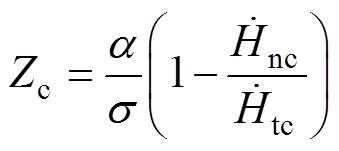 (13)
(13)
式中, 、
、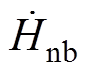 、
、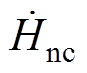 分别为a、b、c平面上H的法向分量;
分别为a、b、c平面上H的法向分量;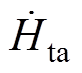 、
、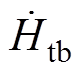 、
、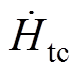 分别为a、b、c平面上H的切向分量。
分别为a、b、c平面上H的切向分量。
考虑到变压器导磁钢构件多为薄板材料,其长度和宽度往往可达数米,而厚度仅仅只有几毫米到十几毫米,故在导磁钢板的边角区基于半无限大导体假设条件下的一维表面阻抗边界条件将不再适用,因此在使用表面阻抗法进行数值计算时必须考虑边角区对阻抗值的影响。本文以TEAM P21-B基准模型为研究对象,分别使用一维表面阻抗条件和考虑边角区的表面阻抗条件进行数值计算,并以常规有限元仿真结果为依据进行对比分析。P21-B几何模型及导磁钢板边角区示意图如图4所示。
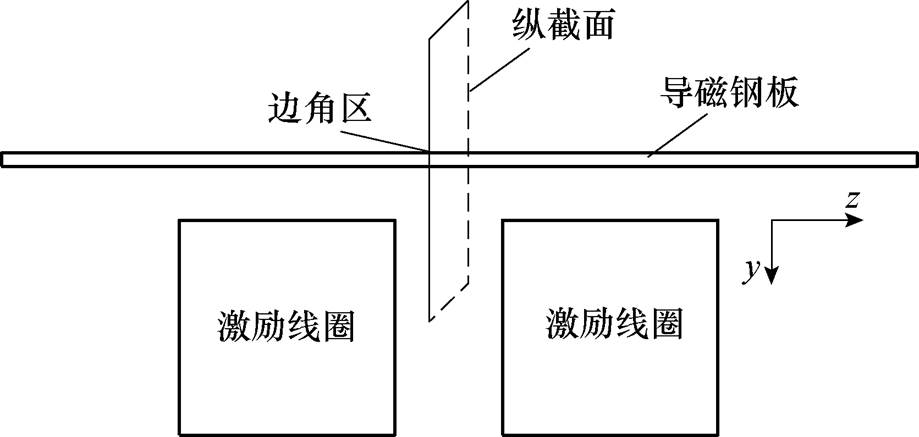
图4 P21-B模型示意图
Fig.4 The diagram of P21-B model
对于频率为50Hz、电流有效值为25A激励条件(激励线圈为300匝),采用考虑边角区的表面阻抗法,一维表面阻抗法和常规有限元法计算所得(y-z截面)磁通密度的矢量分布如图5所示。将图5a、图5b计算结果与图5c常规有限元算法计算结果进行对照[18]:从磁通密度幅值角度分析,应用考虑边角区的表面阻抗边界条件所得结果的准确度比采用一维表面阻抗边界条件更高;从磁通密度分布来看,与一维表面阻抗法相比,考虑边角区的表面阻抗法在导磁钢的边角区磁通密度具有明显的法向分量,这与常规有限元算法所得结果基本相符,而一维表面阻抗法仅有切向分量,与常规有限元算法所得结果有相当大的偏差。因此,综合以上两方面可以看出,对于图4所示三维涡流场计算问题,考虑边角区的表面阻抗法计算结果更加合理、准确。
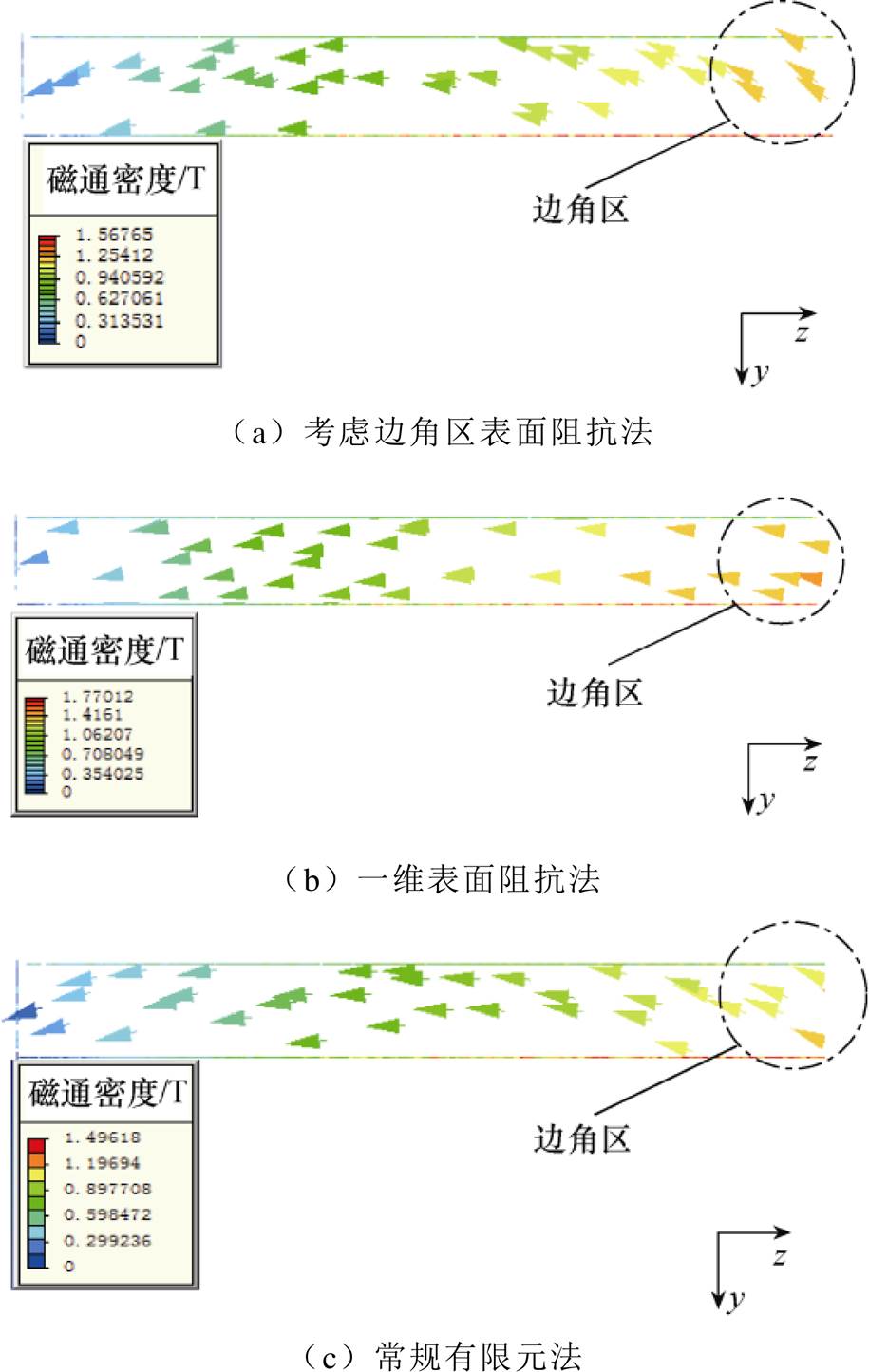
图5 磁通密度矢量分布
Fig.5 Magnetic density vector diagram
2.1.1 常规有限元法
常规有限元法(Finite Element Method, FEM)在解决多尺度、小透入深度问题时,为保证计算精度的要求,需要对大型薄板材料进行分层剖分,因此考虑趋肤效应的有限元模型按照电流密度等梯度下降原则进行,具体实施如下:当Je=0.8J0时,y1=ln(1.25)d,则y1≈0.22d;同理可知Je=0.6J0、Je=0.4J0、Je=0.2J0、Je≈0J0时的剖分厚度依次为y2=0.51d、y3=0.92d、y4=1.61d、y5=5.00d[19],其中,电流密度Je可以表示为
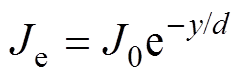 (14)
(14)式中,J0为导体表面电流密度;y为剖分厚度;d为趋肤深度。以激励频率250Hz为例,有限元剖分数据见表1。
表1 有限元剖分
Tab.1 Finite element mesh

频率/ Hz第一层/ mm第二层/ mm第三层/ mm第四层/ mm第五层/ mm第六层/ mm第七层/ mm 2500.10.20.40.77.60.70.3
相应的有限元剖分模型如图6所示,由图6可以发现,常规有限元方法在考虑趋肤效应进行分层剖分时会产生大量的剖分单元和节点,导致计算规模庞大、计算效率降低等问题。
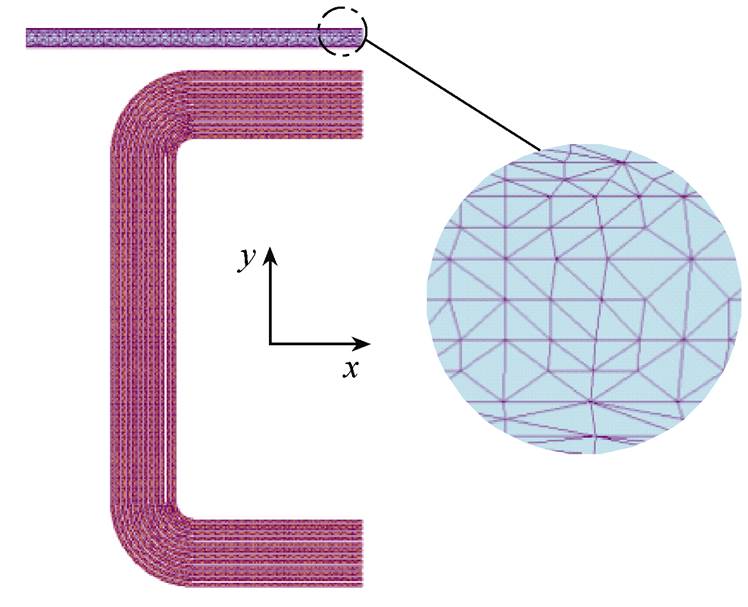
图6 有限元剖分模型
Fig.6 Finite element mesh model
2.1.2 全局表面阻抗法
对于求解域中含实心铁磁材料的三维涡流场计算,很难实现合理的网格剖分,常规有限元法会出现求解规模庞大、计算效率低的问题。全局表面阻抗法(Impedance Boundary, IB)是解决这一问题的方法之一,其将铁磁材料排除到求解域之外,对材料内部不剖分、不计算,而仅需对材料表面阻抗进行计算[20-21]。表面阻抗法求解区域如图7所示,外部边界分成SB和SH两部分,在SB上给定磁感应强度的法向分量,在SH上给定磁场强度的切向分量;V1表示非涡流区;V2表示导体区域,阴影表示V2在求解区之外,不考虑V2区内的电磁量;在S12上施加表面阻抗边界条件。表面阻抗针对非导磁材料而言,仅需考虑导体的涡流效应时,可以保证一定的计算精度[16],但是对于导磁材料而言,其无法考虑材料内部的磁滞效应,因此在计算杂散损耗时,若以牺牲内部电磁量数据为代价提高计算效率,则会大大降低计算杂散损耗精度。
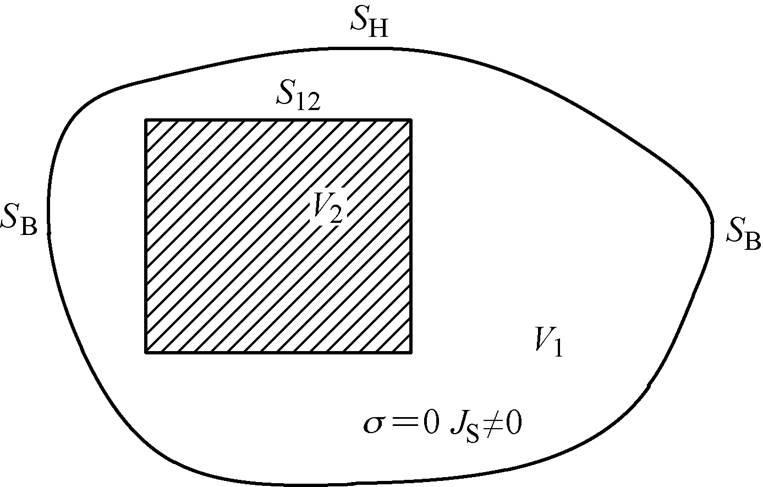
图7 表面阻抗法
Fig.7 Surface impedance method
2.1.3 局部表面阻抗法
针对小透入深度涡流场计算中,有限元法和表面阻抗法遇到的计算精度和计算效率难以兼顾的问题,本文提出一种局部表面阻抗建模方法。
为了初步考察正弦交变磁场作用下导磁钢内部磁通密度分布,采用有限元法对P21-B模型,在激励电流有效值25A、频率50Hz激励条件进行数值计算,纵截面(见图4)处导磁钢内部磁通密度分布如图8所示。可以看出,导磁钢磁通密度分布由表面向内部逐渐衰减,根据导体内磁场和涡流密度的幅值均按e指数衰减的分布特点可知,其主要分布在距离0~3d的导体区域内,当距导磁钢板表面深度为5d时,电磁场量的幅值已经降为表面场的e-5(0.67%),与表面场相比,可以认为已经近乎为零。

图8 导磁钢内部磁通密度分布
Fig.8 Magnetic density distribution inside steel
综上所述,本文提出采用局部表面阻抗建模方法对铁磁材料内部的电磁量以及磁损耗进行数值计算。即对小透入深度导体区进行有限元数值建模,对场量衰减区进行局部表面阻抗数值建模,建模方法如图9所示。
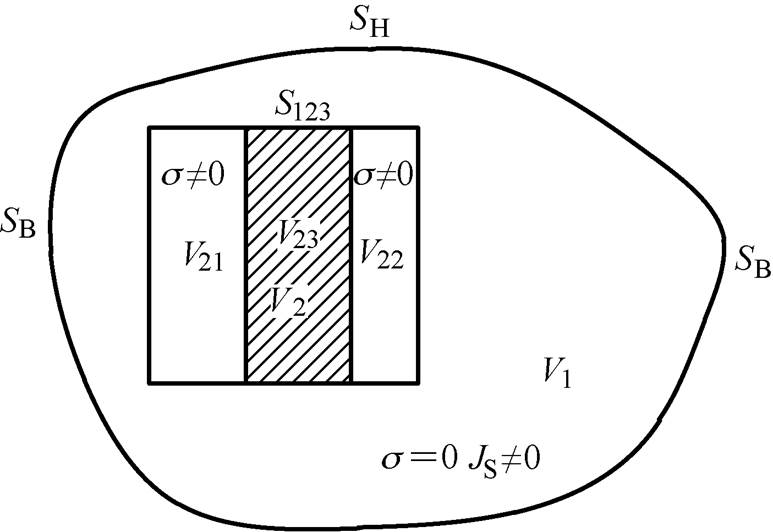
图9 局部表面阻抗法
Fig.9 Local surface impedance method
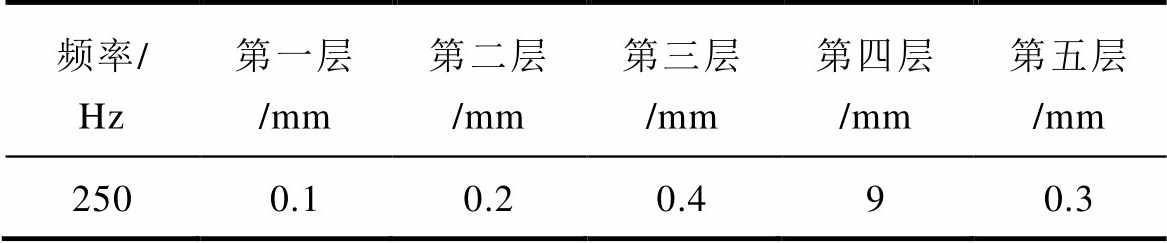
图9中,V1表示非涡流区;V2表示导体区域,将V2分成V21、V22和V23,V21和V22表示小透入深度导体区,V23表示内部导体区(电磁场量几乎衰减为零);S123表示V23与V1、V21、V22的交界面,给定考虑边角区的表面阻抗边界条件;V的外部边界分成SB和SH,在SB上给定磁感应强度的法向分量;在SH上给定磁场强度的切向分量。以频率250Hz为例,采用上述局部表面阻抗建模方法(Local Impedance Boundary, LIB),P-21B基准模型的剖分数据见表2,剖分模型如图10所示。
表2 局部表面阻抗剖分
Tab.2 Local surface impedance mesh
频率/ Hz第一层/mm第二层/mm第三层/mm第四层/mm第五层/mm 2500.10.20.490.3
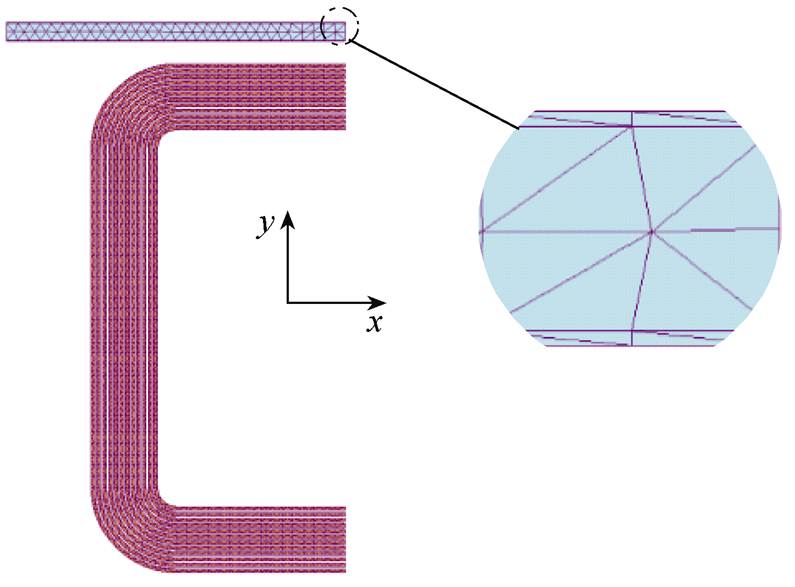
图10 局部表面阻抗模型
Fig.10 Local surface impedance model
可以看出,局部表面阻抗建模方法既可以考虑导磁钢内部的电磁量分布规律,又可以较大限度地减少计算规模,提高计算效率。
2.2.1 杂散损耗计算方法
采用表面阻抗边界条件对导磁钢涡流损耗进行计算时[20],有
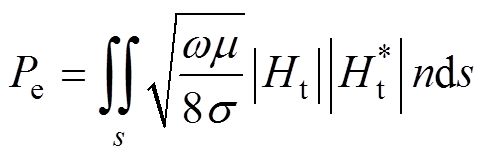 (15)
(15)式中,Pe为涡流损耗;s为包含涡流部分的面积,方向为表面法向;Ht为磁场切向分量;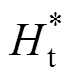 为Ht的共轭。利用麦克斯韦第一方程
为Ht的共轭。利用麦克斯韦第一方程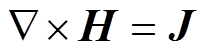 和趋肤深度公式
和趋肤深度公式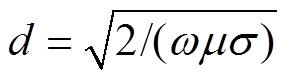 ,经过离散后得到涡流损耗,有
,经过离散后得到涡流损耗,有
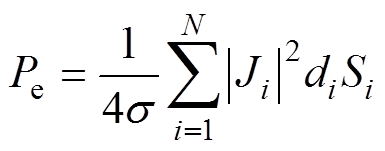 (16)
(16)
式中,Ji为导磁钢板表面涡流密度;di为对应透入深度;Si为单元的表面积;N为单元的个数。
磁滞损耗计算方法[22]是利用磁滞损耗Wh与磁通密度幅值Bm函数关系进行计算,使用磁滞损耗曲线进行插值得到每个单元的磁滞损耗,通过求和的方式得到整体的磁滞损耗。每个单元的磁滞损耗采用Steinmetz经验公式进行计算,表示为
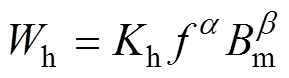 (17)
(17)式中,Wh为单位质量磁滞损耗(W/kg);f为激励频率(Hz);Bm为磁通密度幅值(T);Kh、a、b 为与铁心材料磁性能有关的磁滞损耗系数,可通过对材料磁特性数据拟合确定。
采用局部表面阻抗方法对导磁钢磁滞损耗进行计算时,有
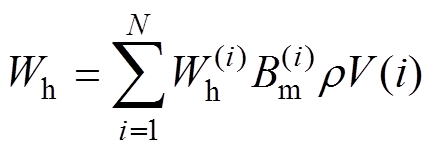 (18)
(18)式中,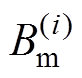 为单元的磁通密度幅值(T);
为单元的磁通密度幅值(T);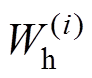 为单位磁通密度幅值对应单元的磁滞损耗(W/kg);r 为材料密度(kg/m3);V(i)为体积(m3)。
为单位磁通密度幅值对应单元的磁滞损耗(W/kg);r 为材料密度(kg/m3);V(i)为体积(m3)。
2.2.2 杂散损耗分布
为初步考察导磁钢内部损耗分布,采用常规有限元法(网格划分见表1)计算电流为3A、频率为250Hz激励条件时导磁钢板内部损耗,其分布见表3。
表3 导磁钢损耗分布(FEM)
Tab.3 Distribution of loss of magnetic steel (FEM)
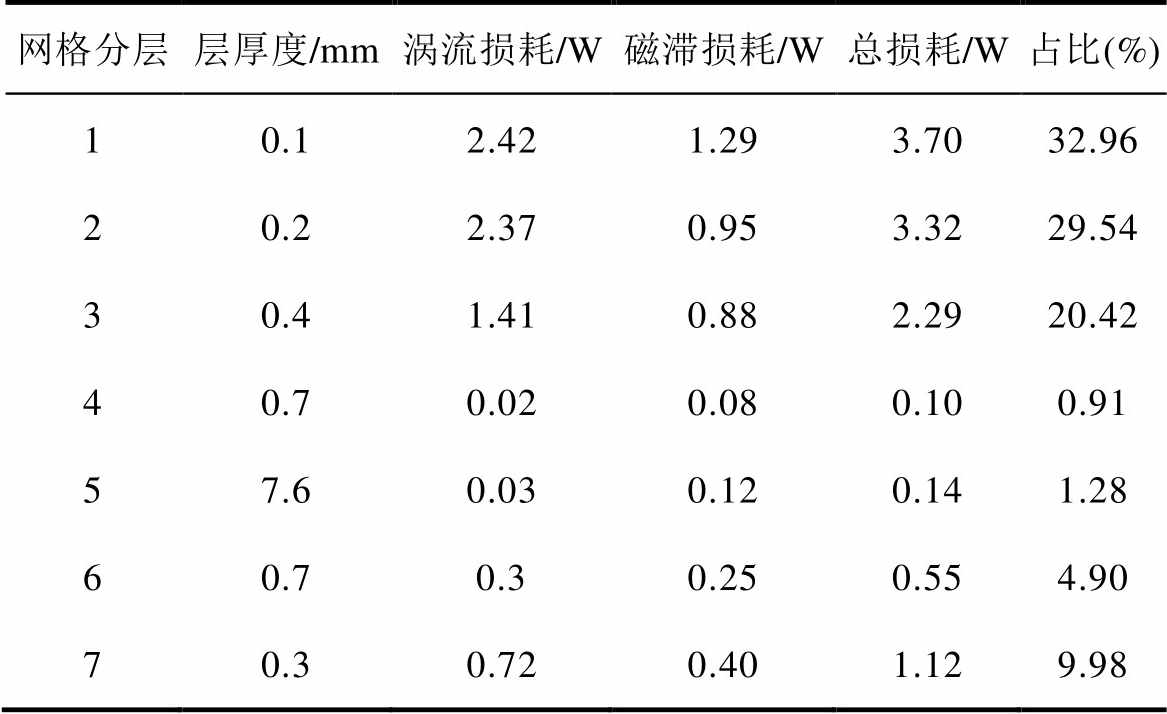
网格分层层厚度/mm涡流损耗/W磁滞损耗/W总损耗/W占比(%) 10.12.421.293.7032.96 20.22.370.953.3229.54 30.41.410.882.2920.42 40.70.020.080.100.91 57.60.030.120.141.28 60.70.30.250.554.90 70.30.720.401.129.98
由表3导磁钢损耗分布规律可以看出,采用常规有限元计算时,导磁钢内部大量剖分单元的损耗仅占总损耗的很少一部分,因此使用该方法的计算效率较低。若采用全局表面阻抗计算仅能考虑涡流损耗,而无法计算磁滞损耗,因此必然会造成较大误差。
针对上述问题,按照2.1.3节给出的局部表面阻抗建模方法进行求解时(网格划分见表2),对V21和V22区域使用有限元法进行计算;而对V23区域给定表面阻抗边界条件进行计算。常规有限元法、全局表面阻抗法和局部表面阻抗法在电流有效值3A、频率250Hz条件下P21-B模型杂散损耗计算结果对比见表4。
表4 I=3A,f =250Hz杂散损耗计算
Tab.4 I=3A, f =250Hz calculated value of stray loss
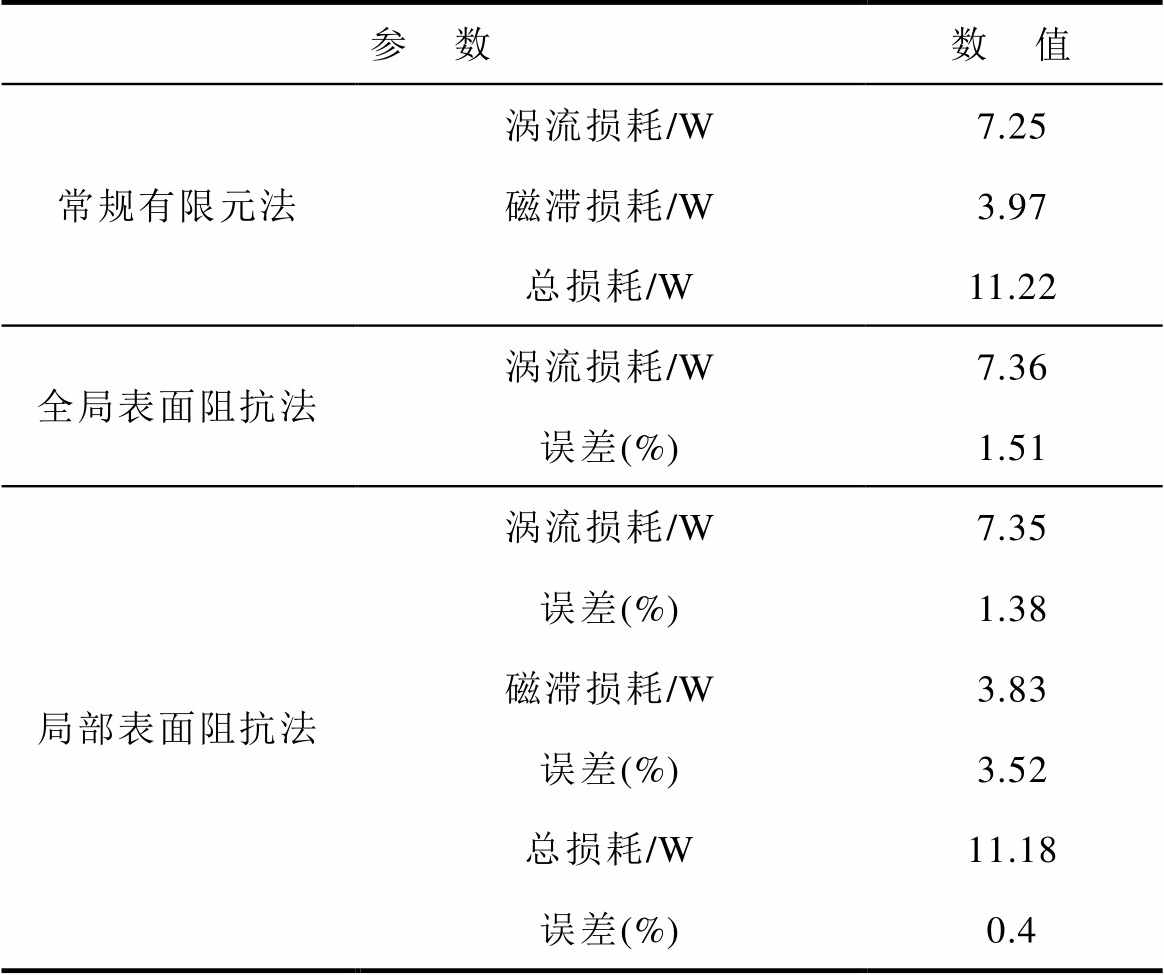
参 数数 值 常规有限元法涡流损耗/W7.25 磁滞损耗/W3.97 总损耗/W11.22 全局表面阻抗法涡流损耗/W7.36 误差(%)1.51 局部表面阻抗法涡流损耗/W7.35 误差(%)1.38 磁滞损耗/W3.83 误差(%)3.52 总损耗/W11.18 误差(%)0.4
由表4分析可知,与常规有限元法相比,局部表面阻抗法计算杂散损耗时具有相当的计算精度,全局表面阻抗法仅能保证涡流损耗的计算精度。
为了对比有限元法和局部表面阻抗法的计算规模,现给出电流有效值3A,不同频率激励条件下的计算时间,其结果见表5、表6和如图11所示。
表5 求解时间
Tab.5 Calculation time
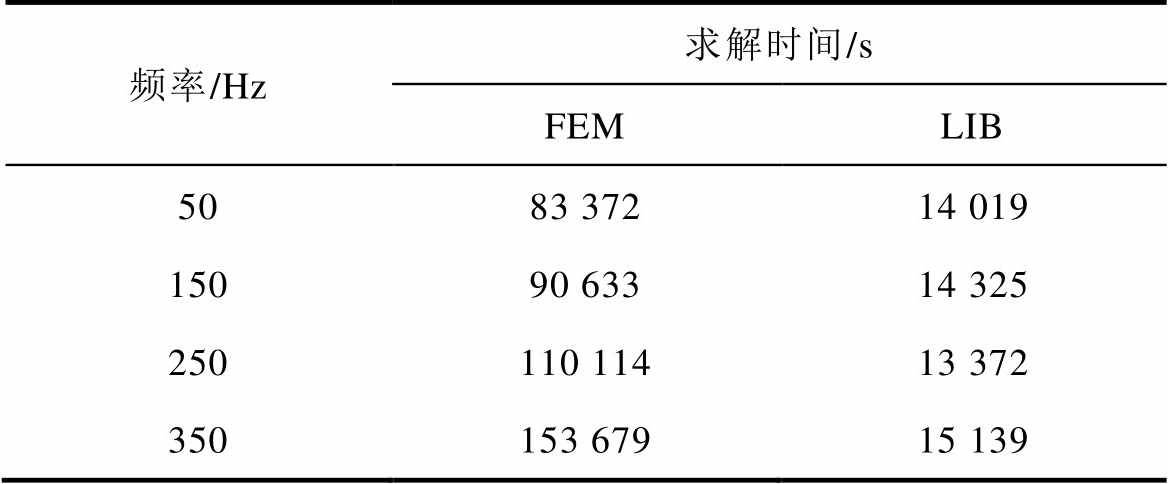
频率/Hz求解时间/s FEMLIB 5083 37214 019 15090 63314 325 250110 11413 372 350153 67915 139
表6 网格划分
Tab.6 Meshes

方法单元数节点数非零元素 FEM6 091 6151 018 565193 488 901 LIB1 605 727272 70653 755 803 工作站参数为: Intel (R) Xeon (R) CPU E5-2690 v3@ 2.60GHz RAM 64GB
由表5、表6和图11分析可知,局部表面阻抗的剖分单元节点个数明显少于有限元;与有限元法相比,局部表面阻抗法计算时间减少了80%左右。
为从实验角度验证局部表面阻抗法计算杂散损耗的准确性,基于产品级变压器的设计标准和制造工艺制作了TEAM P21基准模型,进行导磁钢杂散损耗实验研究。P21-B模型中包含激励线圈和导磁钢板,其中激励线圈用来精确模拟变压器绕组产生的漏磁场,本文为增加进入导磁钢的漏磁场强度,在实验时中采用反向激励模式。在P21-B模型的基础之上搭建如图12所示的变压器杂散损耗实验系统,该系统由TEAM P21-B模型、信号发生器(NF WF1974)、功率放大器(NF 4520A)和功率分析仪(LMG500)组成。通过功率分析仪分别测量P21-B模型的空载和负载损耗,得到导磁钢杂散损耗[23-24]。
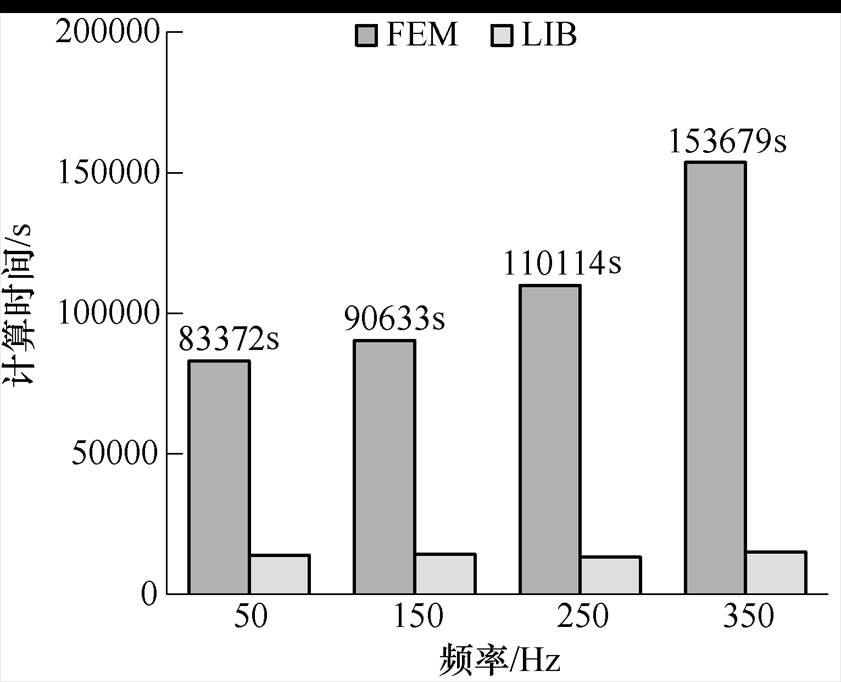
图11 计算时间
Fig.11 Calculating time

图12 杂散损耗测试系统
Fig.12 Stray loss measurement system
现采用F. W. Bell公司的高斯计(Model 8010 Gauss meter)对激励电流有效值3A、频率250Hz工况下靠近线圈导侧和远离线圈侧导磁钢表面(空气中)的法向漏磁通密度进行测量,并与计算结果进行对比。磁通密度分布测量点如图13所示,沿线圈轴向在导磁钢板表面各设有25个测量点,高斯计探头厚度为1.52mm,霍尔元件中心0.76mm,测量点位于导磁钢板表面0.76mm处。比较远离线圈侧导磁钢表面(y=157.76mm)和靠近线圈侧导磁钢表面(y= 146.24mm)图示位置处磁通密度的计算值(FEM和LIB)和测量值(Measure, MEA),结果如图14所示。
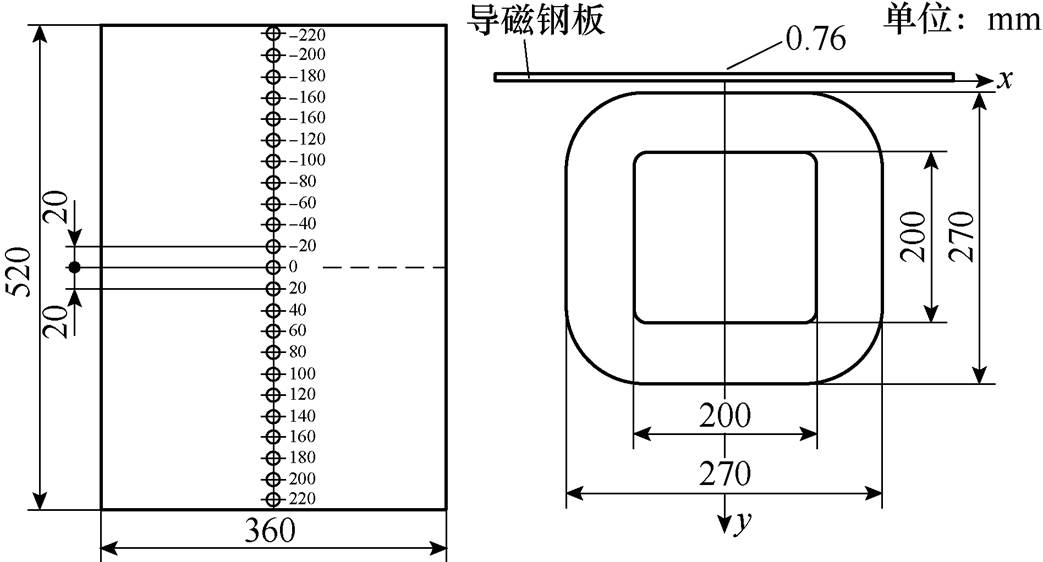
图13 磁通密度分布测量点
Fig.13 Measuring point of magnetic distribution
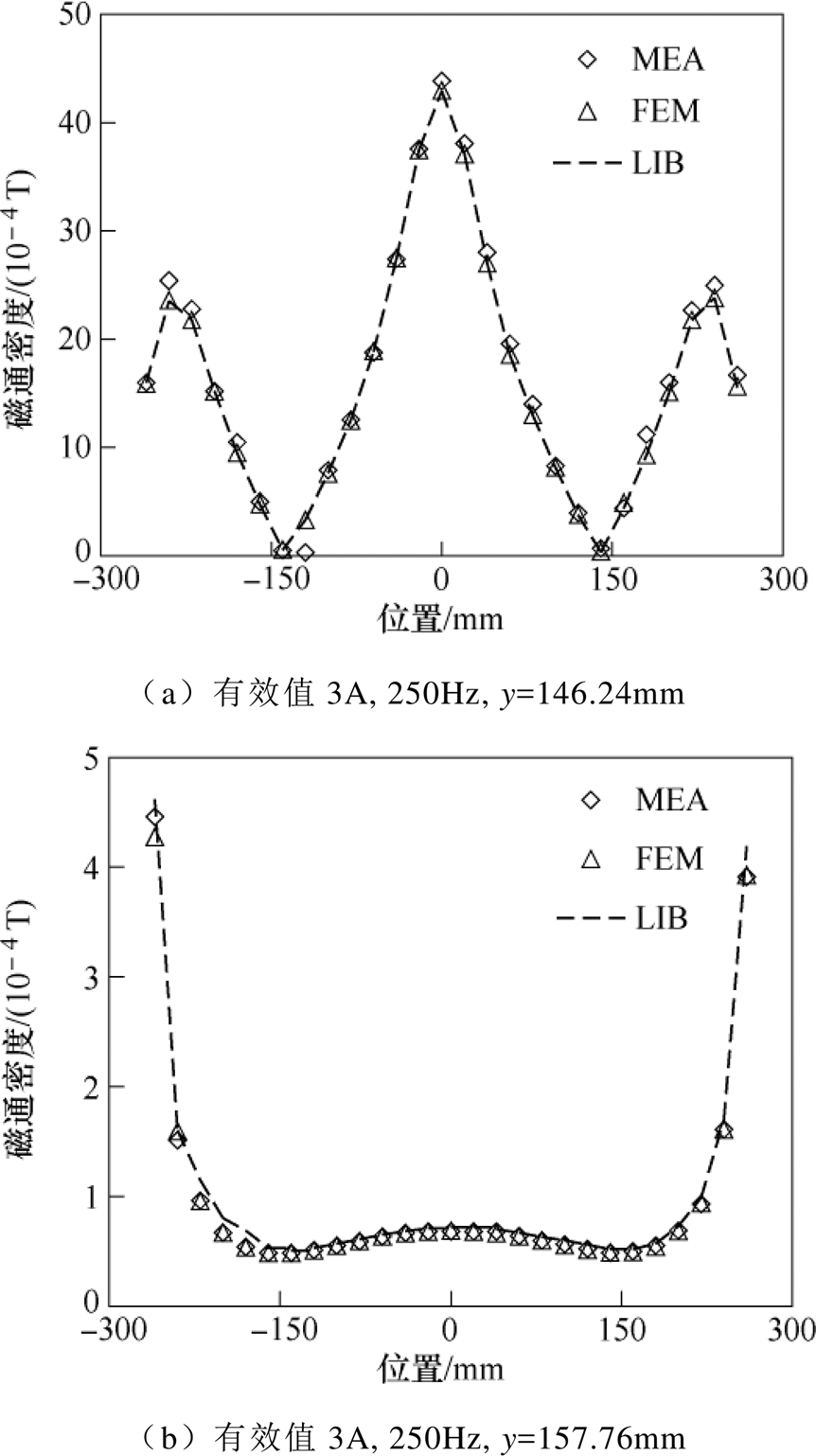
图14 磁通密度分布
Fig.14 Magnetic density distribution
由图14分析可知,两种方法得到的磁通密度分布规律与实验值相同。因此从实验角度验证了FEM和LIB对空间漏磁场分布求解的准确性。
进一步地,为验证局部表面阻抗法计算杂散损耗的准确性,现比较电流有效值3A、不同频率条件下导磁钢板杂散损耗实验值与计算值,结果见表7。由表7分析可知,与有限元法相比,使用局部表面阻抗法具有与有限元相当的计算精度,当频率为350Hz时,误差仅为1.31%。局部表面阻抗法的计算精度随频率增大而提高,其原因是导磁钢的趋肤效应随频率增大而明显,更加满足局部表面阻抗法的适用条件。
表7 变压器导磁钢板杂散损耗验证
Tab.7 Stray loss verification

频率/Hz实验值/W计算值 FEM/W误差(%)LIB/W误差(%) 501.751.712.271.606.43 1506.266.073.115.955.02 25011.6111.223.3911.183.73 35016.7816.810.1816.561.31
本文针对变压器杂散损耗工程计算中面临的多尺度、小透入深度问题带来的计算精度和计算效率不易兼顾的难题,提出了一种对趋肤深度区域和场量衰减区域分别进行边界条件处理的局部表面阻抗建模分析方法,得到如下结论:
1)针对一维表面阻抗边界条件无法计算边角区法向磁通密度的问题,给出了在导磁钢边角区引入修正函数的表面阻抗边界条件,并进行电磁场数值计算,所得结果与常规有限元法基本一致,相较于一维表面阻抗边界条件,其能更准确地反映电磁场量的分布。
2)综合考虑铁磁材料的小透入深度现象和三维杂散场分布特征,提出一种适用于处理含铁磁材料的三维正弦涡流场问题的局部表面阻抗建模方法。与有限元法相比,该方法既能实现合理的网格剖分,又可以兼顾考虑导体趋肤深度区和场量衰减区的磁场分布,进而较好地解决了全局表面阻抗边界难以对磁滞损耗进行有效计算的问题。
3)基于产品级变压器的设计标准和制造工艺制作了TEAM P21基准模型并建立了杂散损耗测试系统,通过详细的实验研究和分析,验证了本文局部表面阻抗建模方法,在进行铁磁材料杂散损耗求解时,相对于常规的有限元方法,其不但具有相当的计算精度,还具有更高的计算效率。
参考文献
[1] 潘超, 王格万, 蔡国伟, 等. 交直流混杂模式下变压器励磁电流谐波与箱体损耗映射研究[J]. 电工技术学报, 2019, 34(13): 2830-2838.
Pan Chao, Wang Gewan, Cai Guowei, et al. Study on the mapping between the excitation current harmonic of transformer and the box loss under the AC-DC hybrid mode[J]. Transactions of China Electro- technical Society, 2019, 34 (13): 2830-2838.
[2] 张荣伦, 王帅, 穆海宝, 等. 大型电力变压器损耗带电测试技术研究[J]. 电工技术学报, 2019, 34(4): 51-60.
Zhang Ronglun, Wang Shuai, Mu Haibao, et al. Research on live loss measurement technology of large power transformers[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 51-60.
[3] 刘振亚, 张启平, 董存, 等. 通过特高压直流实现大型能源基地风、光、火电力大规模高效率安全外送研究[J]. 中国电机工程学报, 2014, 34(16): 2513- 2522.
Liu Zhenya, Zhang Qiping, Dong Cun, et al. Research on large-scale, efficient and safe delivery of wind, light and thermal power to large-scale energy bases through UHVDC[J]. Proceedings of the CSEE, 2014, 34(16): 2513-2522.
[4] 王建民, 单志英, 韩莹, 等. 换流变压器两种屏蔽结构对漏磁及附加损耗影响的仿真研究[J]. 变压器, 2018, 55(4): 15-19.
Wang Jianmin, Shan Zhiying, Han Ying, et al. Simulation study on the effect of two shielding structures of converter transformer on magnetic flux leakage and additional loss[J]. Transformer, 2018, 55(4): 15-19.
[5] 程志光, 刘涛, 范亚娜, 等. 基于TEAM P21三维杂散场问题建模仿真与验证[J]. 电工技术学报, 2014, 29(9): 194-203.
Cheng Zhiguang, Liu Tao, Fan Yana, et al. Modeling, simulation and validation of three-dimensional stray field problem based on TEAM P21[J]. Transactions of China Electrotechnical Society, 2014, 29(9): 194- 203.
[6] 张宁, 李琳, 魏晓光. 非正弦激励下磁心损耗的计算方法及实验验证[J]. 电工技术学报, 2016, 31(17): 224-232.
Zhang Ning, Li Lin, Wei Xiaoguang. Calculating method and experimental verification of core loss under non-sinusoidal excitation[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 224- 232.
[7] 王晓远, 高鹏. 等效热网络法和有限元法在轮毂电机温度场计算中的应用[J]. 电工技术学报, 2016, 31(16): 26-33.
Wang Xiaoyuan, Gao Peng. Application of equivalent thermal network method and finite element method in temperature field calculation of hub motor[J]. Transactions of China Electrotechnical Society, 2016, 31(16): 26-33.
[8] 李亚丽, 凌跃胜, 刘宏勋, 等. 高频变压器涡流损耗公式的推导及有限元方法的验证[J]. 电工技术学报, 2015, 30(增刊2): 82-87.
Li Yali, Ling Yuesheng, Liu Hongxun, et al. Derivation of eddy current loss formula for high frequency transformer and verification of finite element method[J]. Transactions of China Electro- technical Society, 2015, 30(S2): 82-87.
[9] 周剑明. 电磁场有限元综合模拟方法及大刑变压器漏磁场的研究[D]. 武汉: 华中理工大学, 1990.
[10] 刘刚, 孙立鹏, 王雪刚, 等. 正弦及谐波激励下的铁心损耗计算方法改进及仿真应用[J]. 电工技术学报, 2018, 33(21): 4909-4918.
Liu Gang, Sun Lipeng, Wang Xuegang, et al. Improvement and simulation application of core loss calculation method under sinusoidal and harmonic excitation[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4909-4918.
[11] 鲍晓华, 张程, 胡云鹏. 空心电抗器的复合被动屏蔽结构的电磁性能分析[J]. 电工技术学报, 2016, 31(增刊1): 68-75.
Bao Xiaohua, Zhang Cheng, Hu Yunpeng. Electro- magnetic performance analysis of compound passive shielding structure of hollow reactor[J]. Transactions of China Electrotechnical Society, 2016, 31(S1): 68-75.
[12] 刘华, 刘锐, 付洋洋, 等. 基于阻抗边界法的换流变压器箱壳谐波损耗计算[J]. 高电压技术, 2015, 41(9): 3171-3176.
Liu Hua, Liu Rui, Fu Yangyang, et al. Harmonic loss calculation of converter transformer case based on impedance boundary method[J]. High Voltage Engin- eering, 2015, 41(9): 3171-3176.
[13] Milagre A M, Ferreira da Luz M V, Cangane G M, et al. 3D calculation and modeling of eddy current losses in a large power transformer[C]//IEEE Inter- national Conference on Electrical Machines, Marseille,France, 2012, DOI: 10.1109/ICElMach.2012.6350200.
[14] Li Mo, Shen Zejun, Zou Jun, et al. Applicability of the standard impedance boundary condition in the calculation of 3D eddy current loss in condu- ctors[C]//IEEE Sixth International Conference on Electromagnetic Field Problems and Applications, Dalian, China, 2012, DOI: 10.1109/ICEF.2012.6310417.
[15] 姜宇琦, 林育艺. 电力变压器铁芯夹件涡流损耗计算[J]. 电工技术, 2017(8): 25-26.
Jiang Yuqi, Lin Yuyi. Calculation of eddy current loss of iron core sandwich of power transformer[J]. Electrical Engineering, 2017(8): 25-26.
[16] Schelkunoff S A. The impedance concept and its application to problems of reflection, shielding and power absorption[J]. Bell System Technical Journal, 1938, 17(1): 17-48.
[17] Deeley E M. Surface impedance near edges and corners in three-dimensional media[J]. IEEE Transa- ctions on Magnetics, 1990, 26(2): 712-714.
[18] 谢德馨. 三维涡流场的有限元分析[M]. 北京: 机械工业出版社, 2007.
[19] Li Yan, Eerhemubayaer, Sun Xin, et al. Calculation and analysis of 3-D nonlinear eddy current field and structure losses in transformer[C]//International Conference on Electrical Machines and Systems, Beijing, China, 2011: 1-5.
[20] Guerin C, Meunier G, Tanneau G. Surface impedance for 3D nonlinear eddy current problems-application to loss computation in transformers[J]. IEEE Transa- ctions on Magnetics, 1996, 32(3): 808-811.
[21] Schelkunoff S A. The impedance concept and its application to problems of reflection, refraction, shielding and power absorption[J]. Bell Labs Technical Journal, 2013, 17(1): 17-48.
[22] 李龙女, 李岩, 井永腾, 等. 电力变压器漏磁场与杂散损耗计算的研究[J]. 电工技术学报, 2013, 28(增刊2): 122-127.
Li Longnu, Li Yan, Jing Yongteng, et al. Study on calculation of leakage magnetic field and stray loss of power transformer[J]. Transactions of China Electro- technical Society, 2013, 28(S2): 122-127.
[23] 孟凡辉. 多谐波激励条件下构件损耗的模拟与验证[D]. 保定: 华北电力大学, 2017.
[24] 刘涛, 刘兰荣, 张俊杰, 等. 基于TEAM P21基准模型的杂散损耗测量方法研究与验证[J]. 电力科学与工程, 2017, 33(12): 61-66.
Liu Tao, Liu Lanrong, Zhang Junjie, et al. Research and verification of stray loss measurement method based on TEAM P21 benchmark model[J]. Electric Power Science and Engineering, 2017, 33(12): 61- 66.
Calculation Method of Stray Loss Based on Local Surface Impedance Boundary Modeling Method
Abstract This paper studies the practical application of surface impedance method in stray loss calculation of magnetic conductive steel components of power transformer, such as oil tank, core pull plate, etc. Due to the problems of multi-scale and small penetration depth in the calculation of stray loss of transformer, it is difficult to consider both calculation accuracy and calculation efficiency. In this paper, considering the skin effect and three-dimensional stray field distribution characteristics of the magnetic steel, a local surface impedance modeling and analysis method is proposed to deal with the boundary conditions of the skin depth region and the field attenuation region respectively, which realizes the effective calculation of stray loss. Taking the international TEAM P21-B model as the research object, the stray loss measurement system of transformer is built. The experiment and simulation show that the local surface impedance method has the same calculation accuracy as the finite element method, but from the perspective of calculation scale and time, the former can greatly save computing resources and improve calculation efficiency while guaranteeing the calculation accuracy, which has high engineering practical value.
keywords:Surface impedance, stray loss, leakage magnetic field, computation scale
中图分类号:TM41
DOI: 10.19595/j.cnki.1000-6753.tces.191296
国家自然科学基金项目(51677052)、省部共建电工装备可靠性与智能化国家重点实验室自主研究课题重点项目(ERIZZ2018002)资助。
收稿日期2019-10-08
改稿日期 2020-02-13
赵志刚 男,1981年生,博士,博士生导师,主要研究方向为电工磁材料磁性能模拟与工程电磁场数值仿真及应用。E-mail: zhaozhigang@hebut.edu.cn(通信作者)
温 涛 男,1993年生,硕士,主要研究方向为电工磁材料磁性能模拟与工程电磁场数值仿真及应用。E-mail: 401362719@qq.com
(编辑 崔文静)