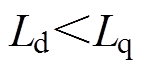 ,为了充分利用磁阻转矩,一般采用最大转矩电流比(Maximum Torque Per Ampere, MTPA)控制[13],因此输出的电磁转矩还包含dq轴电流乘积项的分量,使得IPMSM的动态模型的线性化处理比较复杂。经典的MPC算法通常基于数学模型相对简单的dq轴电感相等的PMSM,或者采用
,为了充分利用磁阻转矩,一般采用最大转矩电流比(Maximum Torque Per Ampere, MTPA)控制[13],因此输出的电磁转矩还包含dq轴电流乘积项的分量,使得IPMSM的动态模型的线性化处理比较复杂。经典的MPC算法通常基于数学模型相对简单的dq轴电感相等的PMSM,或者采用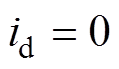 的控制策略使得模型易于线性化,但会使得描述输出转矩中占相当大比例的磁阻转矩部分缺失。
的控制策略使得模型易于线性化,但会使得描述输出转矩中占相当大比例的磁阻转矩部分缺失。摘要 为了提高内置式永磁同步电机(IPMSM)的转速控制性能,该文提出一种线性变参数模型预测控制(LVP-MPC)算法,利用扩展卡尔曼滤波器(EKF)对负载转矩等未知参数进行估计来提高鲁棒性,通过将IPMSM的动态模型在稳态运行点处线性化,把得到的线性状态方程等效为增量形式,并设计增量形式的预测模型以及代价函数实现了转速与电流的最优调节,从而克服了因模型参数不匹配以及外部扰动引起的稳态误差。同时,用多面体约束来近似驱动系统的电压、电流的二次型约束条件,最终将所提出的模型预测控制(MPC)最优化问题转化为标准形式的二次规划(QP)而求解。仿真及实验结果表明,所提算法具有良好的转速动态性能和无偏差的转速指令跟踪能力。
关键词:转速控制 内置式永磁同步电机 模型预测控制 观测器
内置式永磁同步电机(Interior Permanent Magnet Synchronous Motor, IPMSM)因其高效率、高扭矩/功率密度、高可靠性等优点被广泛地应用于电动汽车驱动系统中[1]。磁场定向控制(Field Oriented Control, FOC)通过矢量变换将定子电流中的励磁分量和转矩分量实现解耦,分别独立进行控制,可获得良好的控制性能,在经典的FOC控制结构中,使用若干个比例积分(Proportional-Integral, PI)调节器构成电流、转速的闭环回路,通常能够提供较为理想的控制性能[2-3]。在电动汽车驱动系统中要特别考虑诸如定子电流幅值和电压源逆变器最大输出能力等物理约束条件得到明确、强制的执行,以保证可靠性和安全性。然而采用这种方案时,各个回路的控制器的运行是相对独立的,而且在其设计和运行过程中不能以系统、明确的方式处理约束条件,从而限制了驱动系统在多变量约束条件下的总体性能优化。
模型预测控制(Model Predictive Control, MPC),也称为滚动时域优化控制,具有内在的显式处理输入和状态约束的特性,提供多输入多输出控制能力,它通过在每一时刻的滚动优化过程中解决受约束系统的有限时域的最优控制问题来实现优化控制[4-8]。近十年来,微控制器计算能力的巨大提升使得MPC在电机驱动领域取得快速发展。文献[9]提出一种级联结构的MPC实现永磁同步电机的转速控制,内环提供快速的电流控制,外环实现转速参考跟踪,将电流传感器偏移误差引起的干扰归结到外环MPC的设计中,包括起动过程以及转速纹波消除的相关处理,但该算法仅将内环的q轴电流信号作为调速的手段,缺少对d轴电流的控制。文献[10]提出了转速电流一体化的显式MPC算法,采用非级联方式进行设计,对于转矩与q轴电流构成线性关系PMSM,通过将转速相关项视为测量扰动,并将该扰动扩张到状态向量中,由此获得线性的预测模型,该算法可以在控制器中强制执行电流和电压限制,通过代价函数中对dq轴电流以及转速偏差的惩罚来实现调速。在此基础上,文献[11]优化了预测模型和约束条件的线性化方法,对非线性项的处理方式允许其对磁通量进行控制,由此设计的MPC控制器实现了一定的弱磁运行的能力,该算法需要增加状态向量的维度,维数的增加会引起参数解复杂性并导致对微处理器存储空间的需求增加。文献[12]针对IPMSM转矩方程的非线性特点设计了非线性模型预测控制算法,它包含两个非线性模型预测控制器分别实现对转速和电流的控制,利用泰勒级数展开的方法预测有限范围内的系统响应,利用扰观测器来估计由参数不确定性和负载转矩变化引起的偏移,来增强系统鲁棒性,但级联的结构难以系统地处理约束并实现总体控制目标最优。通常IPMSM设计为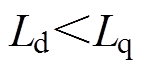 ,为了充分利用磁阻转矩,一般采用最大转矩电流比(Maximum Torque Per Ampere, MTPA)控制[13],因此输出的电磁转矩还包含dq轴电流乘积项的分量,使得IPMSM的动态模型的线性化处理比较复杂。经典的MPC算法通常基于数学模型相对简单的dq轴电感相等的PMSM,或者采用
,为了充分利用磁阻转矩,一般采用最大转矩电流比(Maximum Torque Per Ampere, MTPA)控制[13],因此输出的电磁转矩还包含dq轴电流乘积项的分量,使得IPMSM的动态模型的线性化处理比较复杂。经典的MPC算法通常基于数学模型相对简单的dq轴电感相等的PMSM,或者采用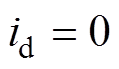 的控制策略使得模型易于线性化,但会使得描述输出转矩中占相当大比例的磁阻转矩部分缺失。
的控制策略使得模型易于线性化,但会使得描述输出转矩中占相当大比例的磁阻转矩部分缺失。
针对以上问题,本文以状态空间模型线性化为基础,提出了一种基于线性变参数MPC(Linear Parameter-Varying, LPV-MPC)的IPMSM转速控制算法,采用了增量式MPC概念,设计了多输入多输出、转速和电流一体化设计的控制器,将电流、电压的物理约束条件纳入控制器设计过程,在满足约束条件的同时实现高动态性能的IPMSM的转速控制,同时,为了应对模型参数失配和外部扰动引起的控制偏差,设计了基于扩展卡尔曼滤波器(Extended Kalman Filter, EKF)的负载扰动观测器来观测未知负载等参数,以增强其鲁棒性。
预测控制算法需要一个描述系统动态行为的模型来预测系统未来的动态,通常选取系统的离散时间状态空间模型作为预测模型。考虑线性时不变状态空间方程为
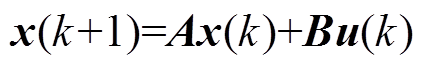 (1)
(1)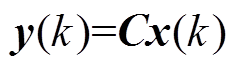 (2)
(2)
式中,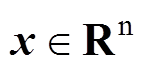 为系统状态向量;
为系统状态向量;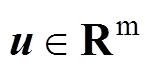 为系统的输入向量;
为系统的输入向量;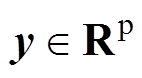 为输出向量;A、B、C为状态矩阵、输入矩阵、输出矩阵。通常控制性能指标定义二次型代价函数为
为输出向量;A、B、C为状态矩阵、输入矩阵、输出矩阵。通常控制性能指标定义二次型代价函数为
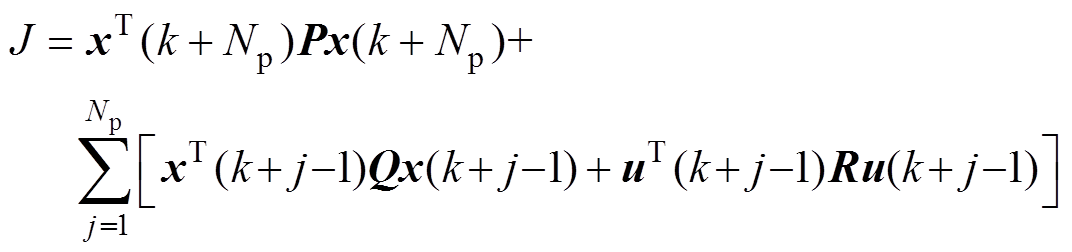 (3)
(3)式中,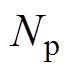 为预测时域;
为预测时域; 、
、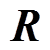 分别为对称、正定的加权矩阵用于惩罚当前状态和控制行为;
分别为对称、正定的加权矩阵用于惩罚当前状态和控制行为;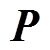 为保证闭环系统的稳定性增加的终端状态约束惩罚矩阵。
为保证闭环系统的稳定性增加的终端状态约束惩罚矩阵。
代价函数的使用允许处理各种或可能冲突的控制目标,具有在一个控制器中合并多个控制模式的能力,使得MPC具备多变量控制能力,应用在多输入多输出的系统上十分理想。代价函数式(3)用于评估和比较不同的控制输入序列对系统预测的影响。系统模型矩阵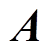 、
、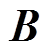 能够在预测时域
能够在预测时域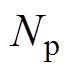 内根据初始状态
内根据初始状态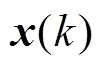 和输入变量
和输入变量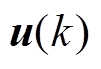 来预测系统未来的状态,求解以下具有约束的最优化问题
来预测系统未来的状态,求解以下具有约束的最优化问题
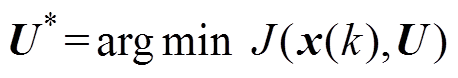 (4)
(4)并服从于以下约束条件
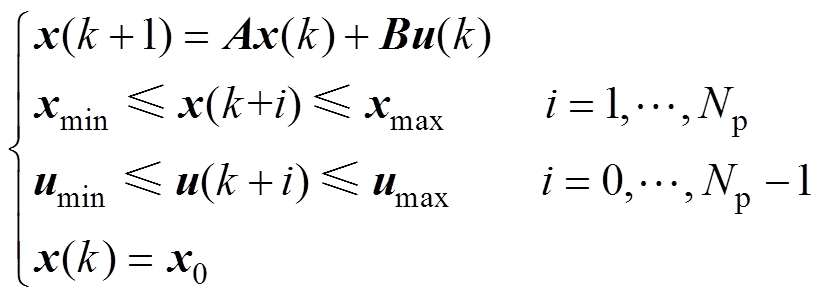 (5)
(5)
式中,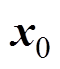 为k时刻系统状态的初始值,
为k时刻系统状态的初始值,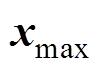 、
、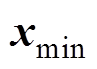 为系统状态的上、下边界值;
为系统状态的上、下边界值;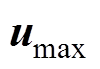 、
、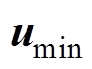 为系统输入的上、下边界值;
为系统输入的上、下边界值;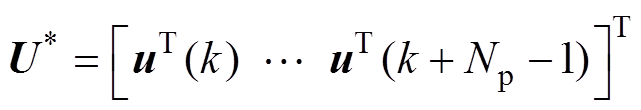 为
为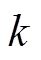 时刻的优化问题式(4)、式(5)的解,将
时刻的优化问题式(4)、式(5)的解,将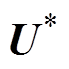 中的第一个分量作用于系统,在
中的第一个分量作用于系统,在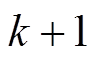 时刻以测量得到状态更新值x(k+1)为初始条件,利用系统动态模型式(1)和式(2)重新预测系统未来的输出并求解该优化问题,由于x(k+1)是用传感器测量或者是用测量值计算得到的,在预测控制过程中起到了反馈修正的作用。尽管这种有限时域优化目标通常得到的是全局的次优解,但是MPC采用时间向前滚动式的优化策略能够顾及由于模型参数失配、外部干扰等引起的不确定性,在闭环控制过程中及时进行弥补,因此MPC结合了开环约束最优化和时域滚动准则来提供状态反馈,实现系统的闭环控制的最优性[14]。预测过程中每个时刻的状态变量和控制输入的关系为
时刻以测量得到状态更新值x(k+1)为初始条件,利用系统动态模型式(1)和式(2)重新预测系统未来的输出并求解该优化问题,由于x(k+1)是用传感器测量或者是用测量值计算得到的,在预测控制过程中起到了反馈修正的作用。尽管这种有限时域优化目标通常得到的是全局的次优解,但是MPC采用时间向前滚动式的优化策略能够顾及由于模型参数失配、外部干扰等引起的不确定性,在闭环控制过程中及时进行弥补,因此MPC结合了开环约束最优化和时域滚动准则来提供状态反馈,实现系统的闭环控制的最优性[14]。预测过程中每个时刻的状态变量和控制输入的关系为
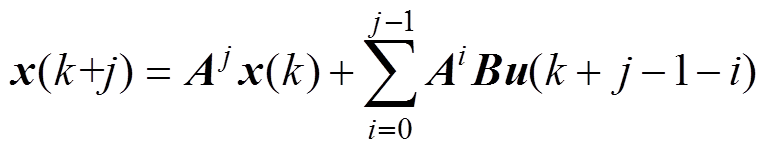 (6)
(6)把式(5)代入式(3)中,遵循相应的约束条件并考虑关系式(6),式(3)可重写为关于初始状态和控制输入的函数,有
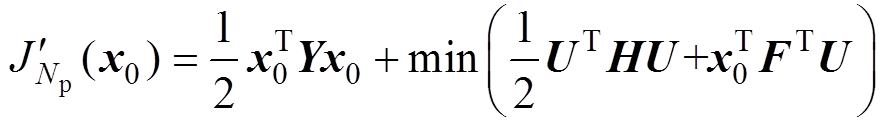 (7)
(7)
满足约束条件
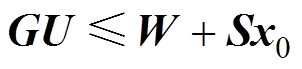 (8)
(8)式中,矩阵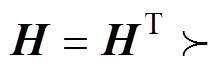 0;矩阵
0;矩阵 、
、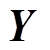 、
、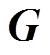 、
、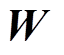 和
和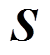 可从原始加权矩阵
可从原始加权矩阵 、
、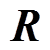 、
、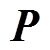 和约束条件式(5)中的上、下边界
和约束条件式(5)中的上、下边界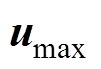 ,
,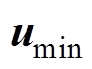 、
、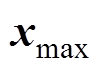 ,
,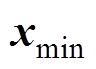 以及系统的模型矩阵
以及系统的模型矩阵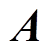 、
、 、
、 中计算得到[15]。MPC的最优化问题转化为式(7)和式(8)描述的标准的二次规划(Quadratic Programming, QP)问题。QP问题可采用积极集法[16](active-set method)、内点法[17](interior-point method)等数值方法来求解,或者采用专为嵌入式控制应用设计的通用QP求解器如ODYS QP Solver[18]等。
中计算得到[15]。MPC的最优化问题转化为式(7)和式(8)描述的标准的二次规划(Quadratic Programming, QP)问题。QP问题可采用积极集法[16](active-set method)、内点法[17](interior-point method)等数值方法来求解,或者采用专为嵌入式控制应用设计的通用QP求解器如ODYS QP Solver[18]等。
在转子磁场定向的同步旋转坐标系(dq坐标系)中,星形联结三相永磁同步电机非线性状态方程可以描述为
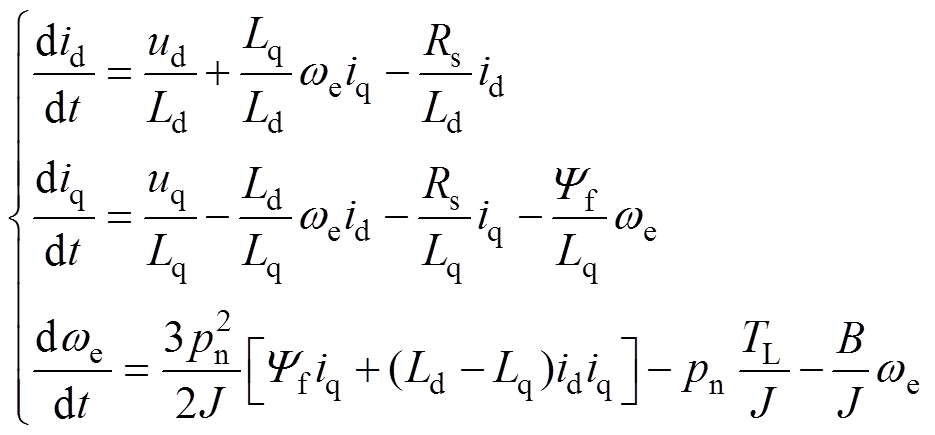 (9)
(9)式中,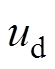 、
、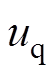 为定子电压d、q轴分量;
为定子电压d、q轴分量;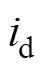 、
、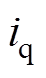 定子电流d、q轴分量;
定子电流d、q轴分量;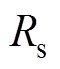 定子电阻;
定子电阻;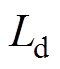 、
、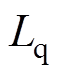 为定子电感分量;
为定子电感分量;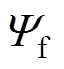 永磁体磁链;
永磁体磁链;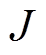 为转动惯量;
为转动惯量;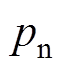 为极对数;
为极对数;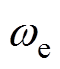 为转子电角速度;
为转子电角速度;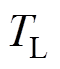 为负载转矩;
为负载转矩;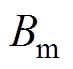 为摩擦因数,通常为一很小的值,在本文中忽略摩擦系数的影响,取
为摩擦因数,通常为一很小的值,在本文中忽略摩擦系数的影响,取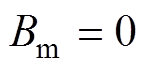 。令
。令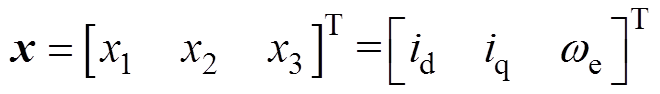 为状态变量,
为状态变量,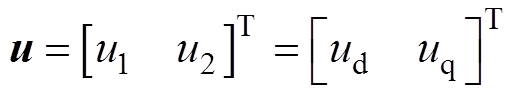 为输入变量,可得连续时间IPMSM的状态空间模型为
为输入变量,可得连续时间IPMSM的状态空间模型为
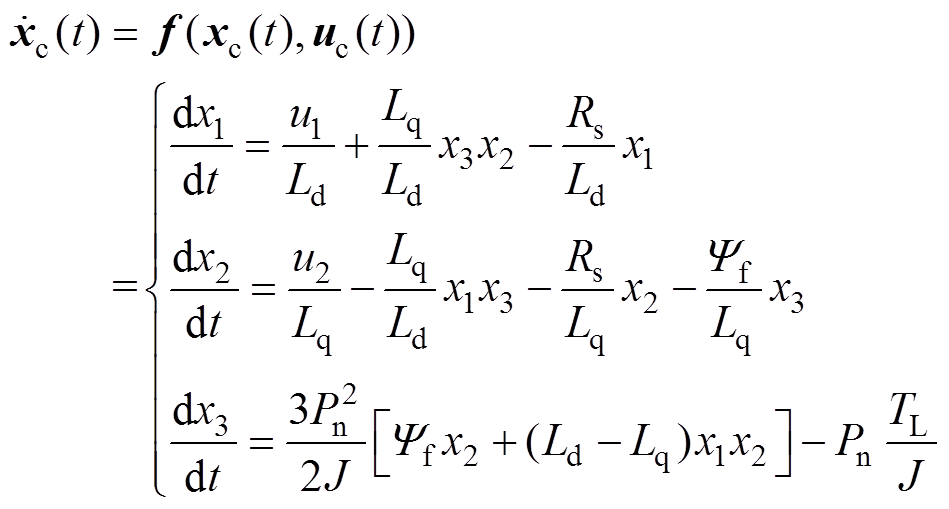 (10)
(10)
该状态空间模型每个方程中都包含两个状态的乘积项,是一个非线性模型。不妨用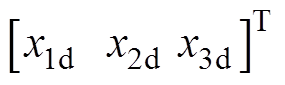 表示状态x的目标值,对于某一给定的目标角速度
表示状态x的目标值,对于某一给定的目标角速度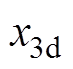 ,根据MTPA定子电流最优策略,在满足输出的电磁转矩的同时,电流幅值
,根据MTPA定子电流最优策略,在满足输出的电磁转矩的同时,电流幅值 最小的dq轴电流组合会使铜损
最小的dq轴电流组合会使铜损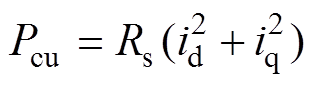 最小,对于某一个给定的
最小,对于某一个给定的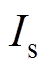 求得目标电流与输出转矩为
求得目标电流与输出转矩为
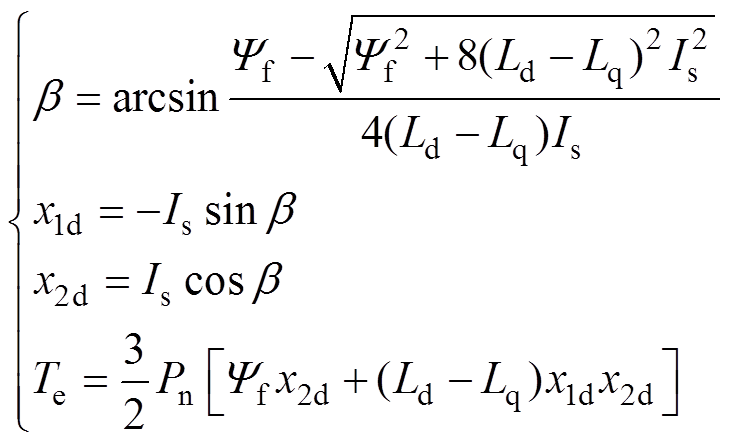 (11)
(11)式中,b 为MTPA控制的电流相位。
在获得负载转矩的估计值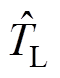 之后,再通过如图1所示的算法经过简单的迭代求得d、q轴目标电流
之后,再通过如图1所示的算法经过简单的迭代求得d、q轴目标电流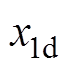 、
、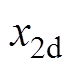 ,则对应的稳态目标输入电压为
,则对应的稳态目标输入电压为
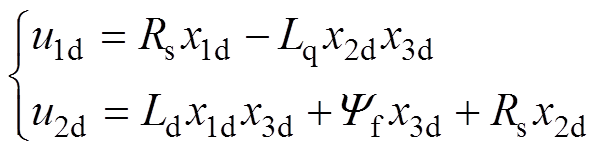 (12)
(12)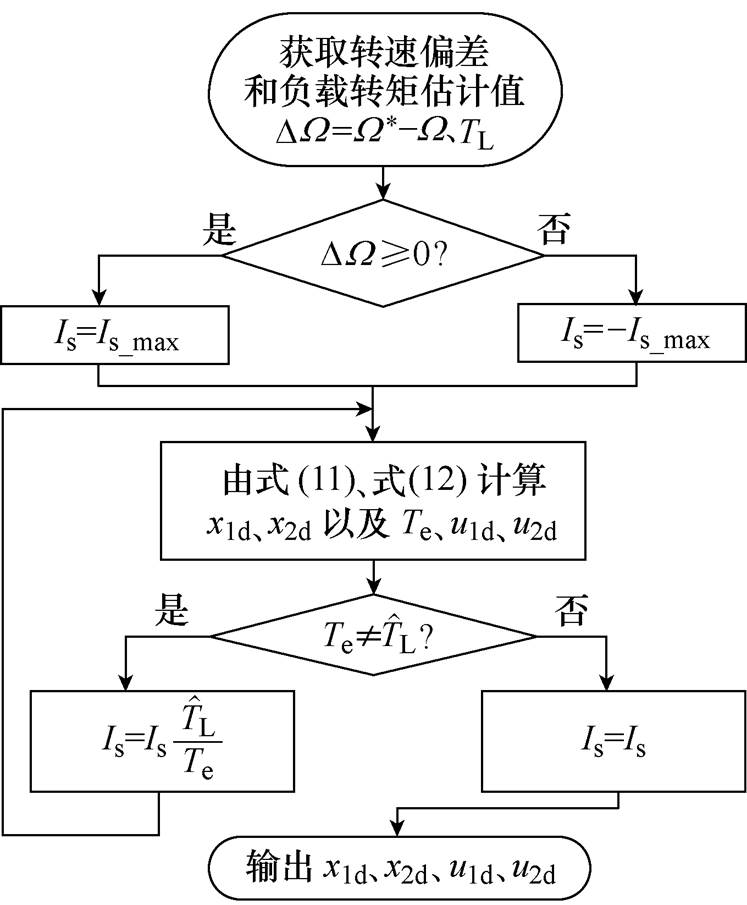
图1 目标获取算法流程
Fig.1 Flowchart of target acquisition algorithm
负载转矩观测器的设计将在2.4节中介绍。在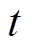 时刻将式(10)描述的IPMSM非线性动态模型在MTPA上任意的稳态运行点
时刻将式(10)描述的IPMSM非线性动态模型在MTPA上任意的稳态运行点 ,
,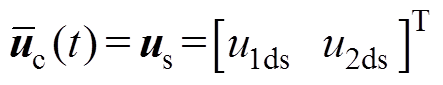 处进行线性化,有
处进行线性化,有
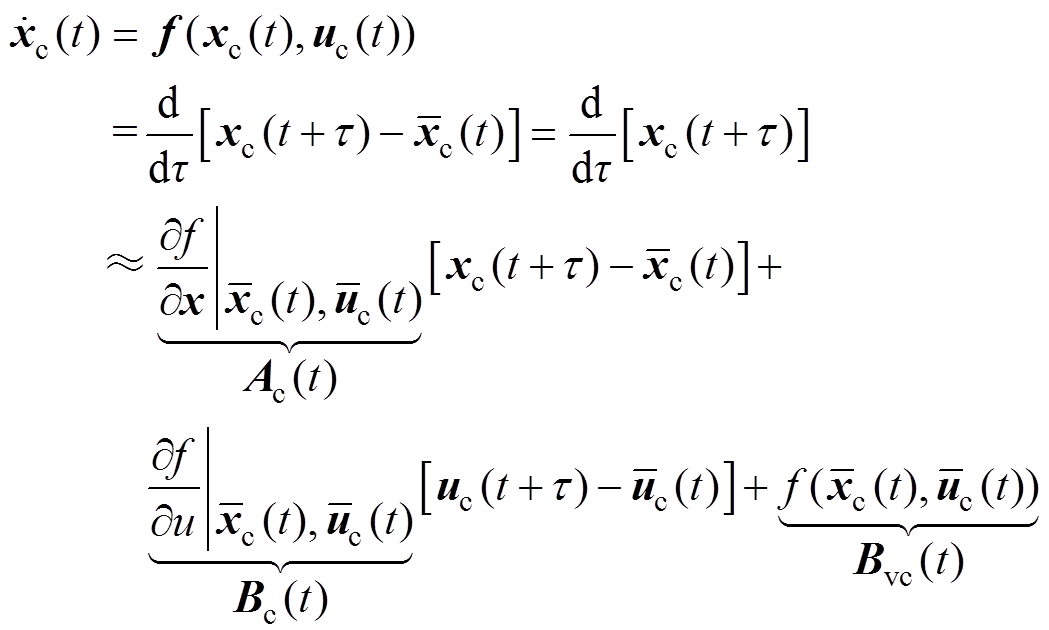 (13)
(13)由于IPMSM在稳态工作点附近具有近似的线性特性且有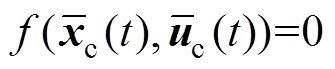 ,可根据上述线性化方法对非线性的IPMSM动态模型在
,可根据上述线性化方法对非线性的IPMSM动态模型在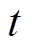 时刻线性化处理得到近似的LPV模型。定义状态增量和控制输入增量为
时刻线性化处理得到近似的LPV模型。定义状态增量和控制输入增量为
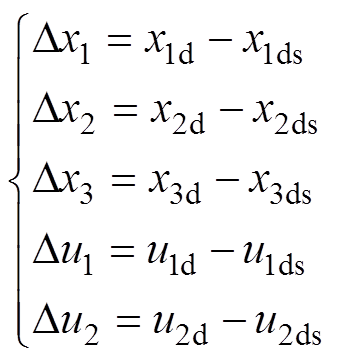 (14)
(14)
定义目标状态向量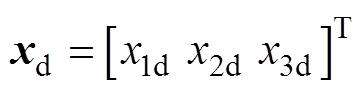 ,状态增量向量
,状态增量向量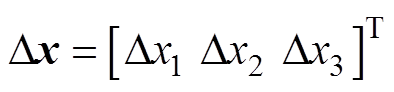 ,目标控制输入向量
,目标控制输入向量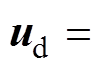
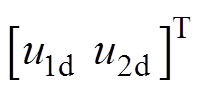 ,控制增量向量
,控制增量向量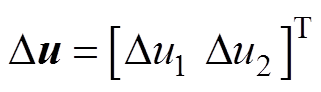 。将式(10)按照式(13)的方法在稳态运行点处展开,并将式(14)代入可得
。将式(10)按照式(13)的方法在稳态运行点处展开,并将式(14)代入可得
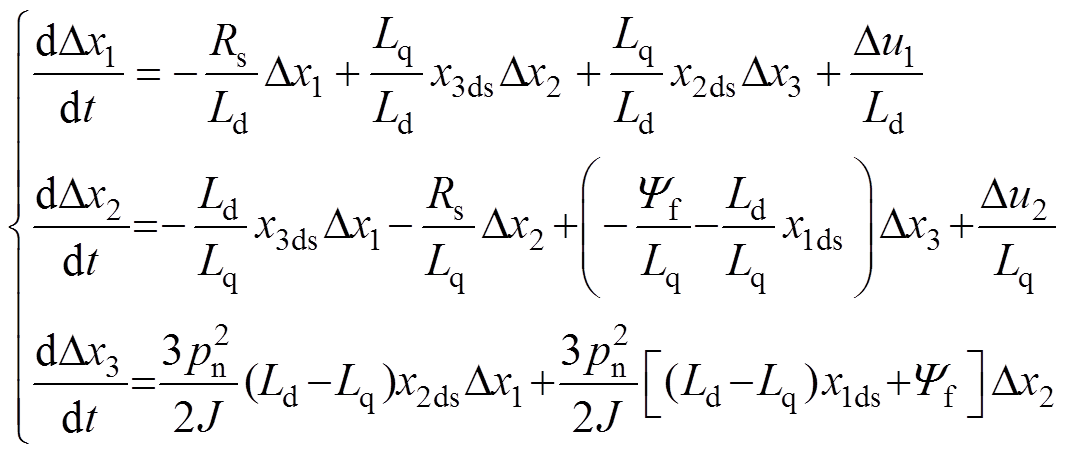 (15)
(15)若以常数时间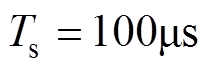 作为采样间隔,对
作为采样间隔,对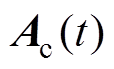 、
、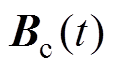 采用前向欧拉进行离散化处理可得:
采用前向欧拉进行离散化处理可得: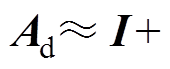
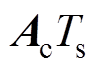 ,
, 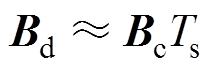 ,由于采样时间很小,该离散化方法可获得足够精度的状态增量模型,将式(15)按此方法离散化处理后得到
,由于采样时间很小,该离散化方法可获得足够精度的状态增量模型,将式(15)按此方法离散化处理后得到
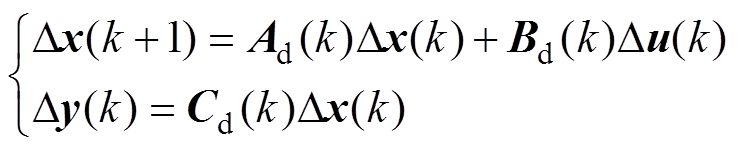 (16)
(16)
其中
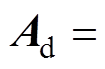
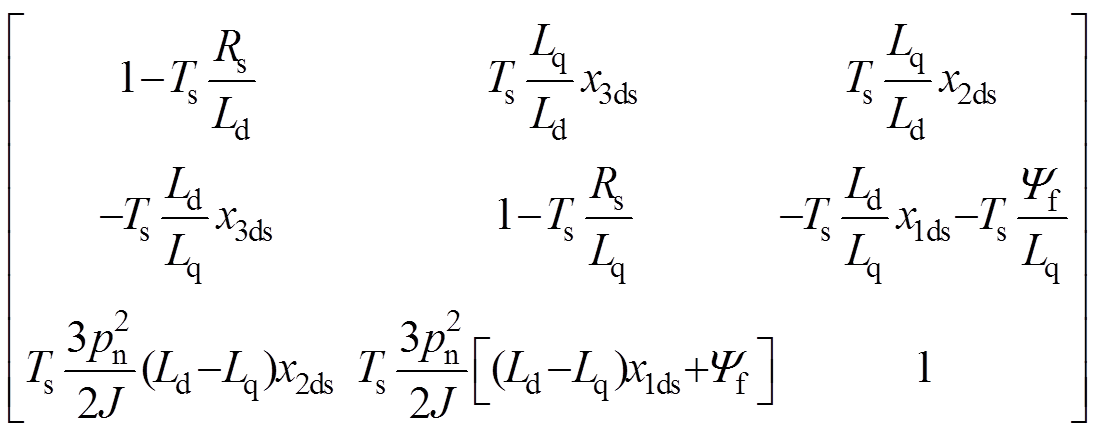
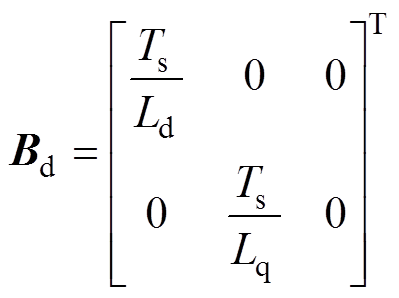
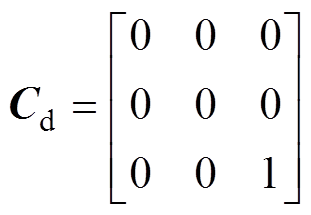
IPMSM驱动系统的两个主要的约束条件是电流和电压的二次不等式约束,对应于dq平面上的两个圆形的约束条件描述为
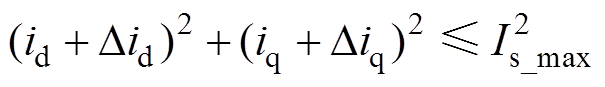 (17)
(17)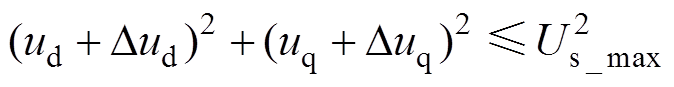 (18)
(18)
式中,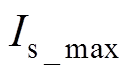 为IPMSM或逆变器最大允许输出的电流;
为IPMSM或逆变器最大允许输出的电流;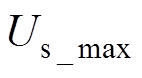 为逆变器能够输出最大相电压,本文采用SVPWM线性调制,所以
为逆变器能够输出最大相电压,本文采用SVPWM线性调制,所以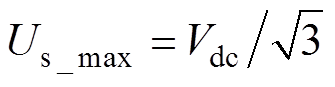 ,其中,
,其中,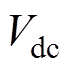 是逆变器母线电压,由式(17)和式(18)描述的圆形约束可以用多面体来近似,如图2所示,且多面体的阶数越大,则可获得的近似程度越高,但计算越复杂。
是逆变器母线电压,由式(17)和式(18)描述的圆形约束可以用多面体来近似,如图2所示,且多面体的阶数越大,则可获得的近似程度越高,但计算越复杂。
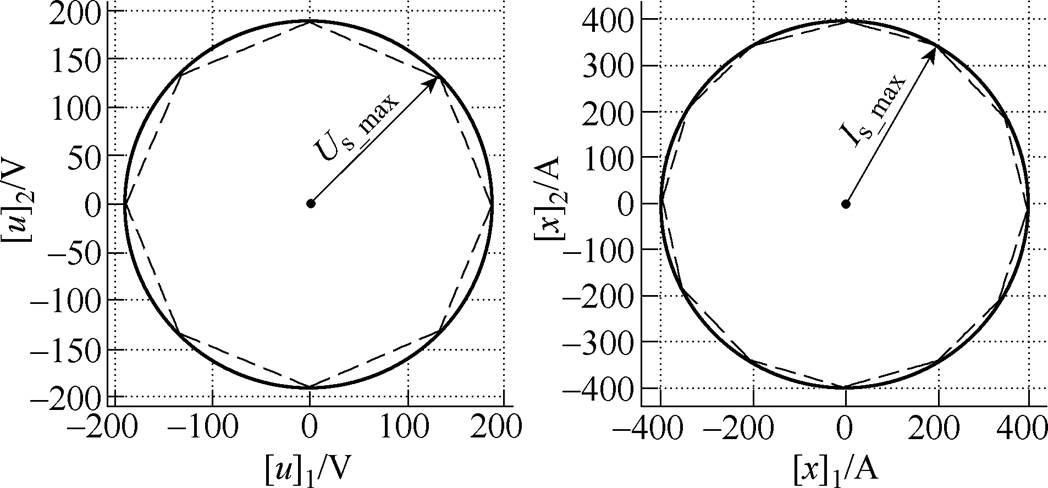
图2 电压和电流的约束条件
Fig.2 Current and voltage constraints
本文中取多面体的阶数为8,把控制量、状态量相关的二次约束条件转化为两组不等式描述的线性约束来近似,得到控制量的线性约束为
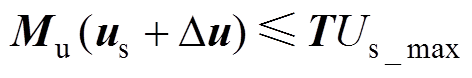 (19)
(19)状态量的线性约束为
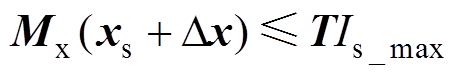 (20)
(20)
其中
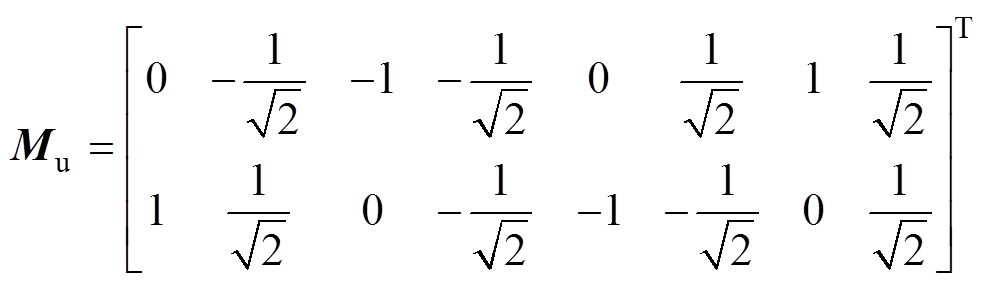
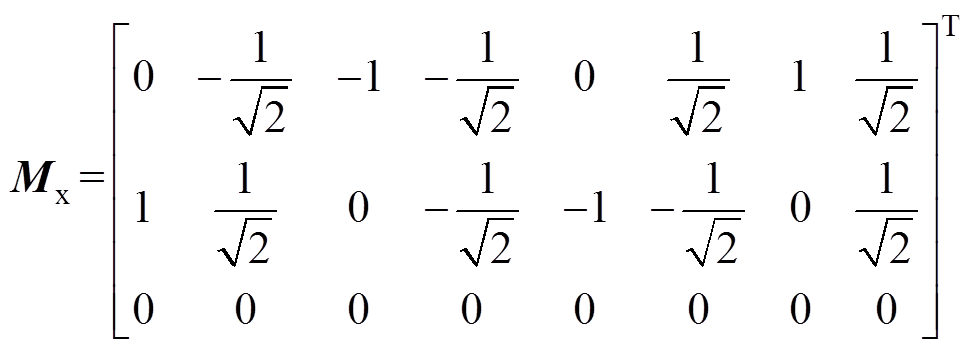
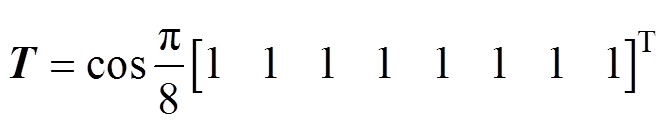
利用式(16)作为预测模型,状态向量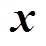 中的
中的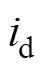 、
、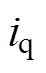 以及
以及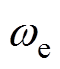 在每个采样时刻由传感器测量采样,把
在每个采样时刻由传感器测量采样,把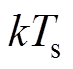 时刻的状态增量向量的初始值记为
时刻的状态增量向量的初始值记为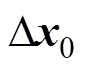 。由于采用了增量形式的预测模型,设计代价函数为
。由于采用了增量形式的预测模型,设计代价函数为
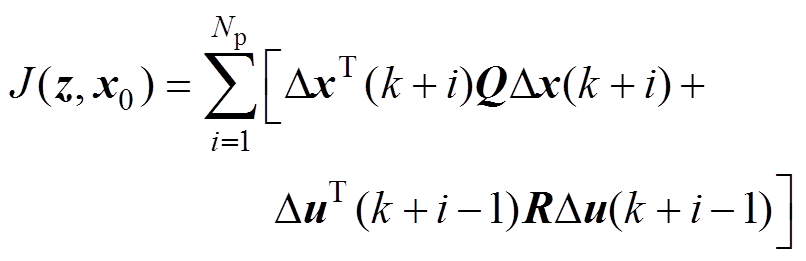 (21)
(21)
式中,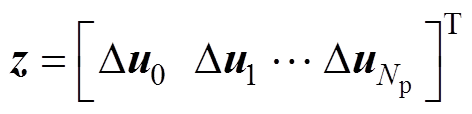 为在代价函数式(21)取得最小值时得到的最优控制输入增量序列。在预测时域
为在代价函数式(21)取得最小值时得到的最优控制输入增量序列。在预测时域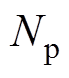 步内,由式(16)计算可得状态增量与输入增量、偏差初始值
步内,由式(16)计算可得状态增量与输入增量、偏差初始值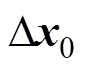 的关系为
的关系为
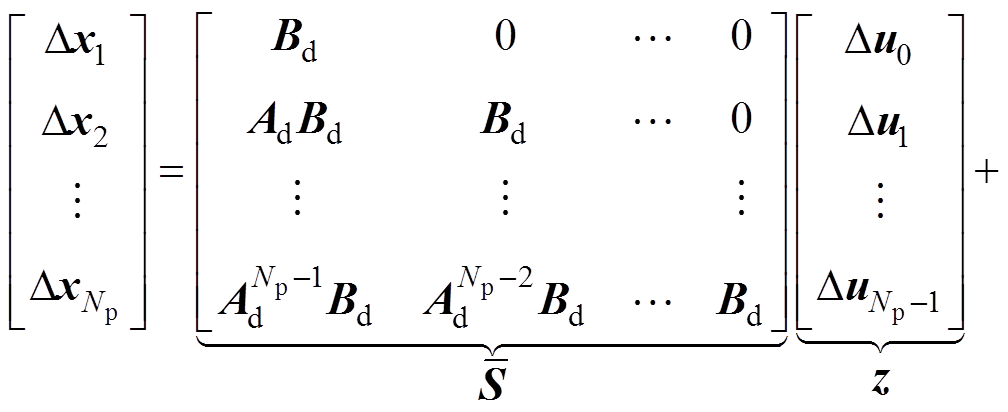
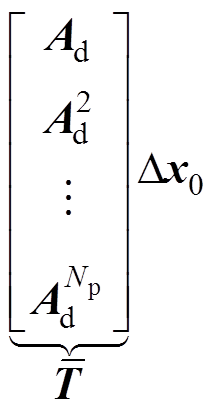 (22)
(22)
把式(22)代入代价函数式(21),有
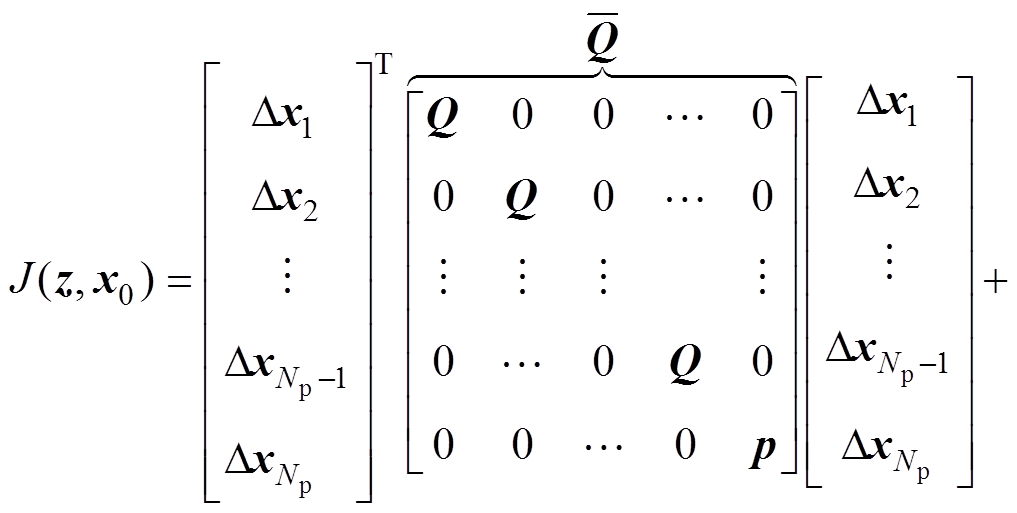
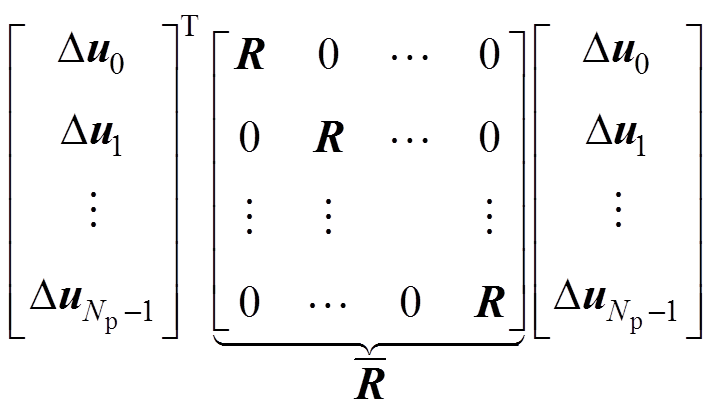 (23)
(23)
根据式(22)和式(23),则代价函数式(21)可重写为
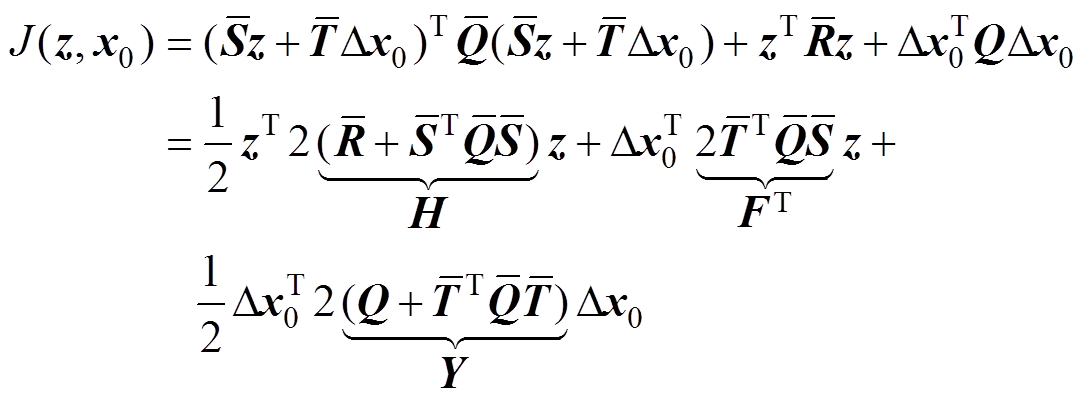
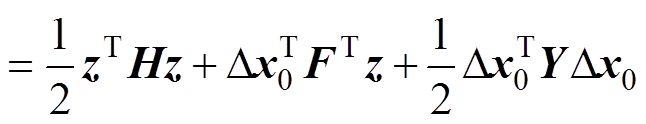 (24)
(24)
这样代价函数转化为如式(7)所示的标准的QP问题需要的形式。同时需要将预测时域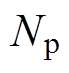 步内的约束条件转化为如式(8)描述的标准QP问题需要的形式。首先,把输入增量约束条件式(19)重写为
步内的约束条件转化为如式(8)描述的标准QP问题需要的形式。首先,把输入增量约束条件式(19)重写为
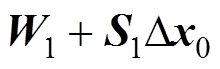 的形式,有
的形式,有
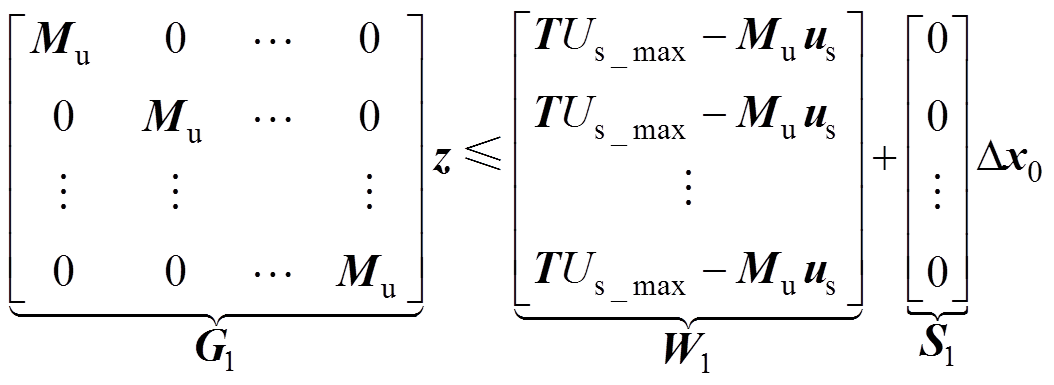 (25)
(25)接下来将状态增量约束矩阵式(20)重写为关于输入增量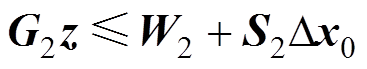 的形式,由状态增量与输入增量的关系式(22)以及状态约束条件式(20),可得
的形式,由状态增量与输入增量的关系式(22)以及状态约束条件式(20),可得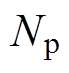 步内状态约束为
步内状态约束为
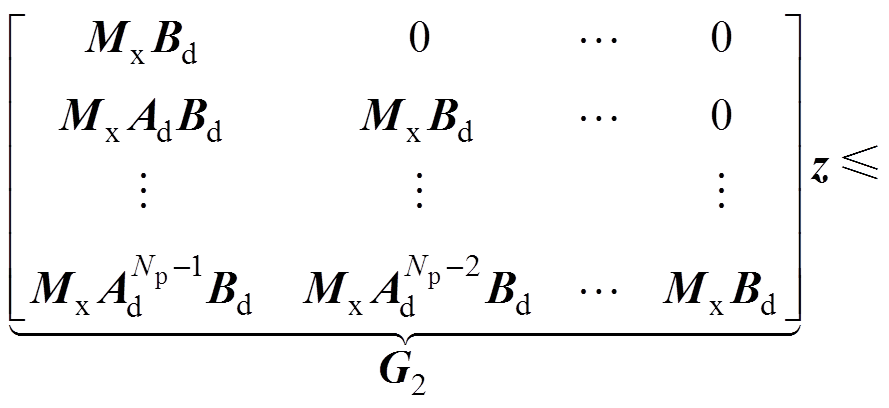
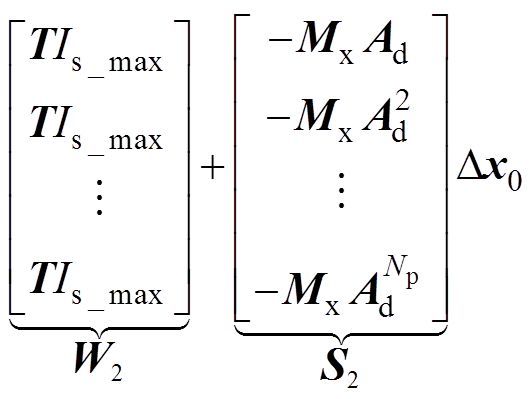 (26)
(26)由式(25)和式(26)可知,状态和控制输入的约束可以整理为标准QP形式,有
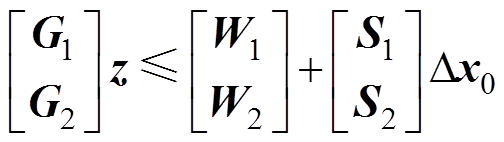 (27)
(27)
由状态空间增量模型式(16)约束条件式(27)以及代价函数式(24)构成的LPV-MPC的约束最优化问题已经转化为标准QP问题,在每个采样周期中利用嵌入式的解算器求解,在求得的最优控制增量序列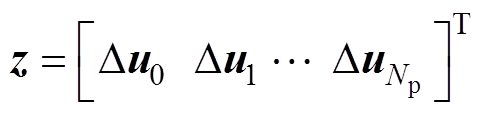 中取第一个分量
中取第一个分量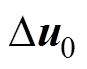 ,最终得到本周期作用于系统的控制电压,有
,最终得到本周期作用于系统的控制电压,有
 (28)
(28)得到的控制电压将驱动状态向量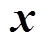 从当前采样时刻的稳态运行点沿着最优状态轨线向目标状态移动。
从当前采样时刻的稳态运行点沿着最优状态轨线向目标状态移动。
负载转矩观测器是根据IPMSM数学模型及卡尔曼滤波算法构建的,观测器不但能够提供负载转矩的估计值,还能提供dq轴电流采样值滤波后的结果作为系统的反馈来提高对测量噪声的抗干扰能力。假设负载转矩在相邻两次采样时间内保持不变,有
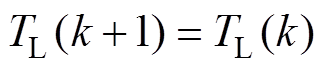 (29)
(29)用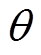 表示转子电角度,考虑到
表示转子电角度,考虑到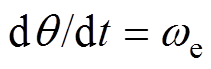 ,令
,令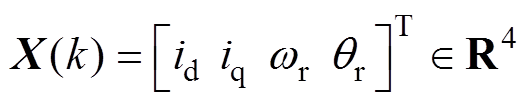 为状态向量,取静止坐标系下的定子电压
为状态向量,取静止坐标系下的定子电压 为输入向量、电流
为输入向量、电流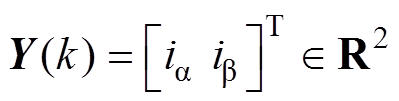 为输出向量,用
为输出向量,用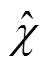 表示未知的负载转矩
表示未知的负载转矩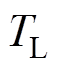 ,可把系统描述为如下状态方程
,可把系统描述为如下状态方程
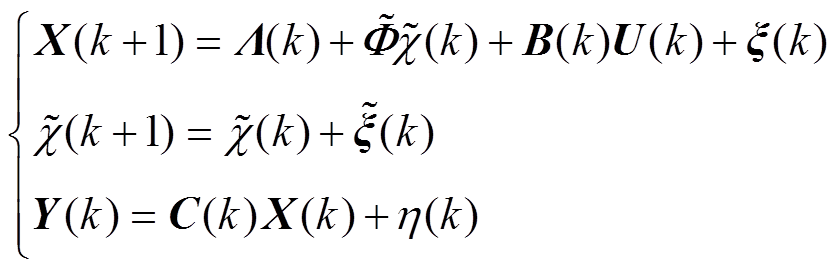 (30)
(30)
其中
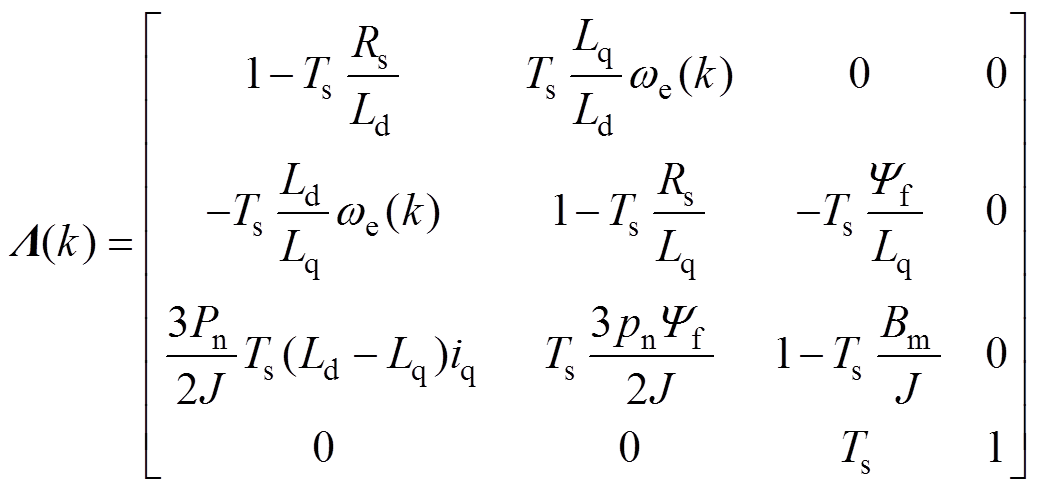
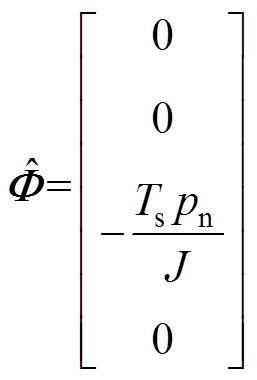
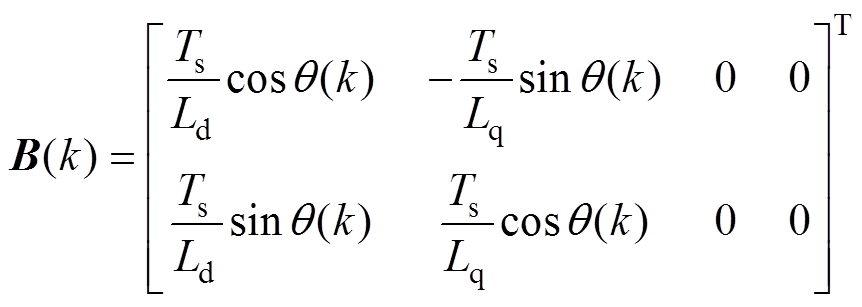
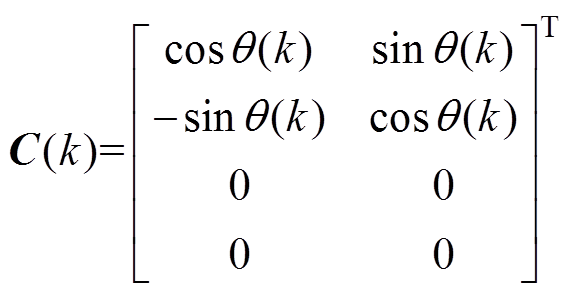
向量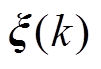 代表系统参数误差及未建模的非线性部分的影响,
代表系统参数误差及未建模的非线性部分的影响,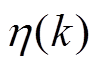 表示测量噪声的影响,并假设两者不相关。将所有和未知转矩
表示测量噪声的影响,并假设两者不相关。将所有和未知转矩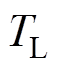 相关的参数都用上标“
相关的参数都用上标“ ”来表示;与系统状态
”来表示;与系统状态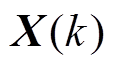 以及未知转矩
以及未知转矩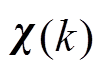 同时相关的参数用上标“
同时相关的参数用上标“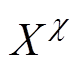 ”表示。同时认为
”表示。同时认为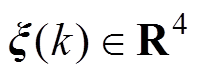 、
、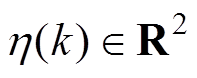 和
和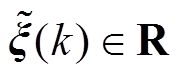 为均值为0的高斯白噪声,其相应的协方差矩阵定义为
为均值为0的高斯白噪声,其相应的协方差矩阵定义为
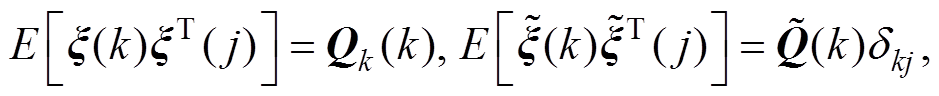
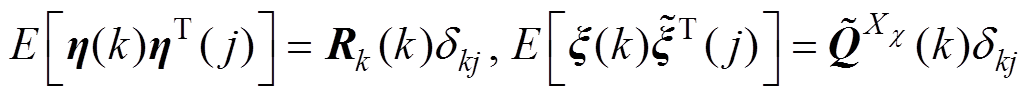
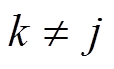
其中,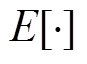 表示数字期望;当
表示数字期望;当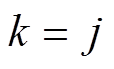 时
时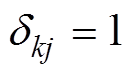 ,当
,当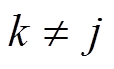 则
则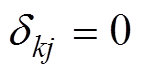 。定义增广向量
。定义增广向量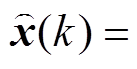
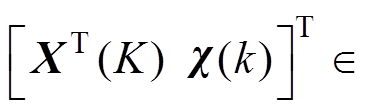
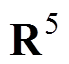 ,把式(30)改写为增广形式,有
,把式(30)改写为增广形式,有
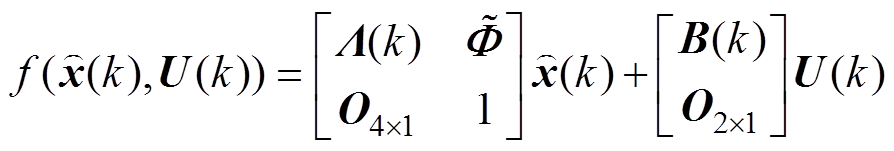 (31)
(31)其扩展卡尔曼滤波算法设计为
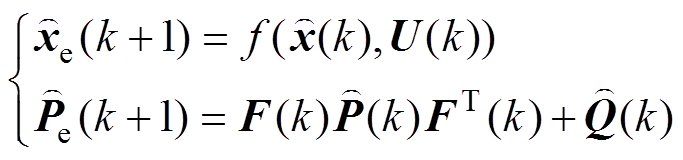 (32)
(32)
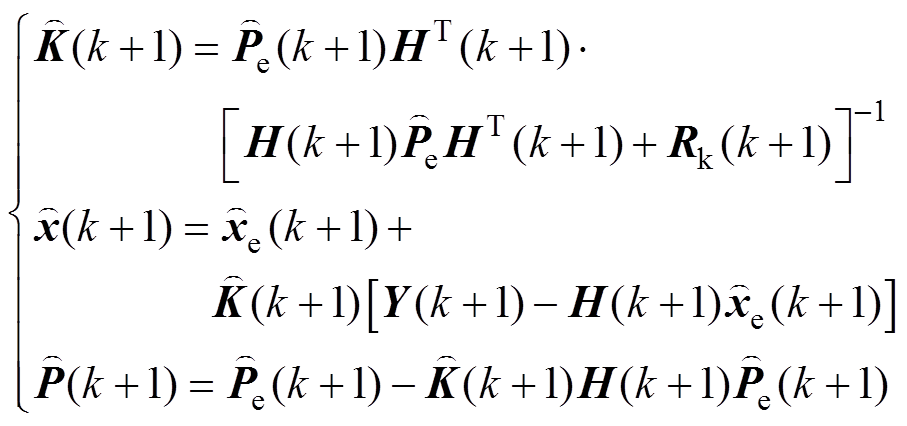 (33)
(33)式中,下标“ ”表示在测量值更新之前获得的先验估计值;
”表示在测量值更新之前获得的先验估计值;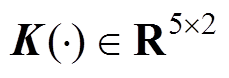 为卡尔曼增益矩阵;
为卡尔曼增益矩阵;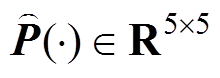 状态估计误差的协方差矩阵;
状态估计误差的协方差矩阵;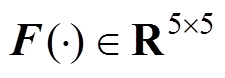 和
和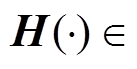
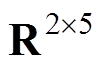 为雅可比矩阵。
为雅可比矩阵。
图3给出了所提控制方案的系统框图,使用旋转变压器测量实际转子位置并通过计算得到实际转速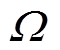 ;使用霍尔电流传感器测量相电流并最终得到经过EKF滤波后的
;使用霍尔电流传感器测量相电流并最终得到经过EKF滤波后的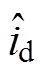 、
、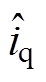 ;连同负载转矩器观测的
;连同负载转矩器观测的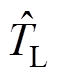 一同作为反馈参与到所提算法中的目标向量获取、模型线性化以及MPC滚动优化计算中,将得到最优控制输入电压经调制后作用于电机。
一同作为反馈参与到所提算法中的目标向量获取、模型线性化以及MPC滚动优化计算中,将得到最优控制输入电压经调制后作用于电机。
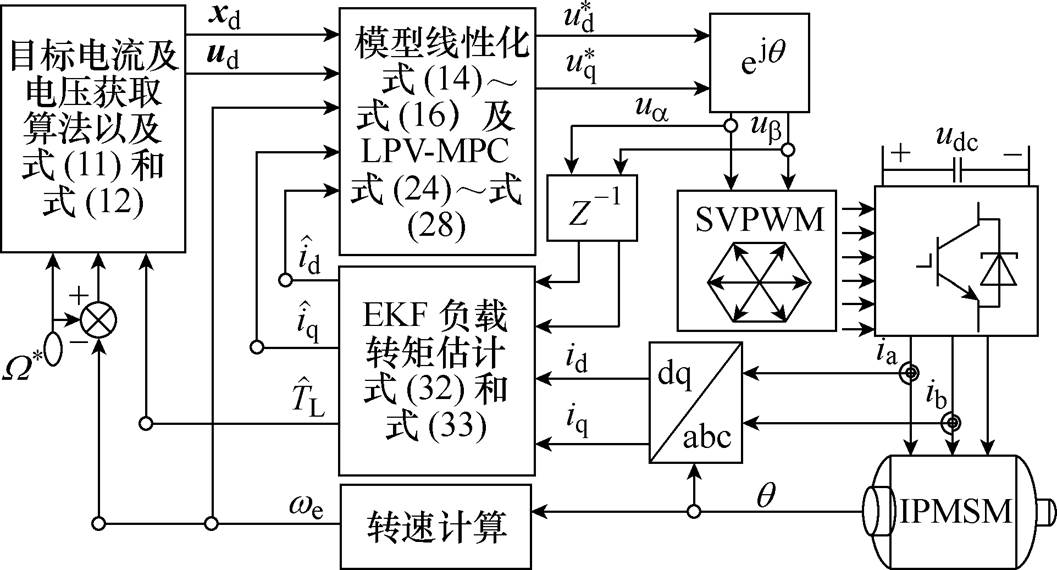
图3 控制系统结构框图
Fig.3 Block diagram of the control structure
为了验证所提算法的有效性和正确性,使用Matlab/Simulink软件进行了仿真验证,同时搭建了以英飞凌处理器Tricore TC1782为控制核心的电压源型逆变器实验平台开展实验研究,实验装置如图4所示。

图4 实验装置
Fig.4 Experimental setup
仿真及实验中使用的电机参数见表1。考虑到在采样时刻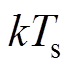 求得的最优控制电压作用于系统后,在
求得的最优控制电压作用于系统后,在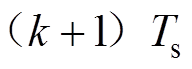 时刻dq轴电流才会发生变化,这意味着控制预测时域需要满足
时刻dq轴电流才会发生变化,这意味着控制预测时域需要满足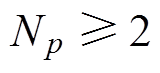 才会获得比较理想的效果,本文取
才会获得比较理想的效果,本文取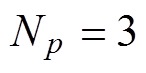 。代价函数中的惩罚矩阵
。代价函数中的惩罚矩阵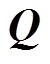 和
和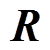 之间的比率权衡系统快速性和灵敏度性,另外对不同状态的相对重要性选择单个权重以确定目标的优先级,为了实现转速跟踪参考的目的,惩罚矩阵
之间的比率权衡系统快速性和灵敏度性,另外对不同状态的相对重要性选择单个权重以确定目标的优先级,为了实现转速跟踪参考的目的,惩罚矩阵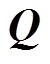 的取值应侧重于对转速偏差项的惩罚,仿真和实验中设置为
的取值应侧重于对转速偏差项的惩罚,仿真和实验中设置为 ,对输入增量的惩罚设置为
,对输入增量的惩罚设置为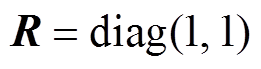 。影响观测器增益一个关键的参数为预测协方差矩阵,初始值设定为
。影响观测器增益一个关键的参数为预测协方差矩阵,初始值设定为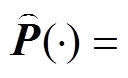
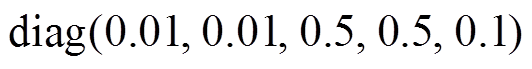 ,由于噪声向量不相关,所以
,由于噪声向量不相关,所以 、
、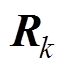 矩阵都为对角阵,增加
矩阵都为对角阵,增加 就是加大了数学模型的不确定性,与此同时,滤波器增益矩阵的元素也会增大,即加大了测量反馈的加权作用,增加
就是加大了数学模型的不确定性,与此同时,滤波器增益矩阵的元素也会增大,即加大了测量反馈的加权作用,增加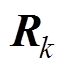 则意味着测量噪声大,即减弱电流滤波的权重。基于上述考虑以及实验测试,初始值确定为
则意味着测量噪声大,即减弱电流滤波的权重。基于上述考虑以及实验测试,初始值确定为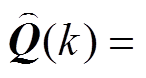
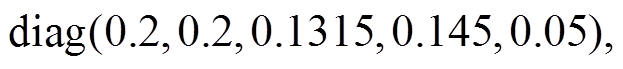
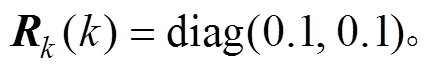
表1 IPMSM电机参数
Tab.1 IPMSM Specifications
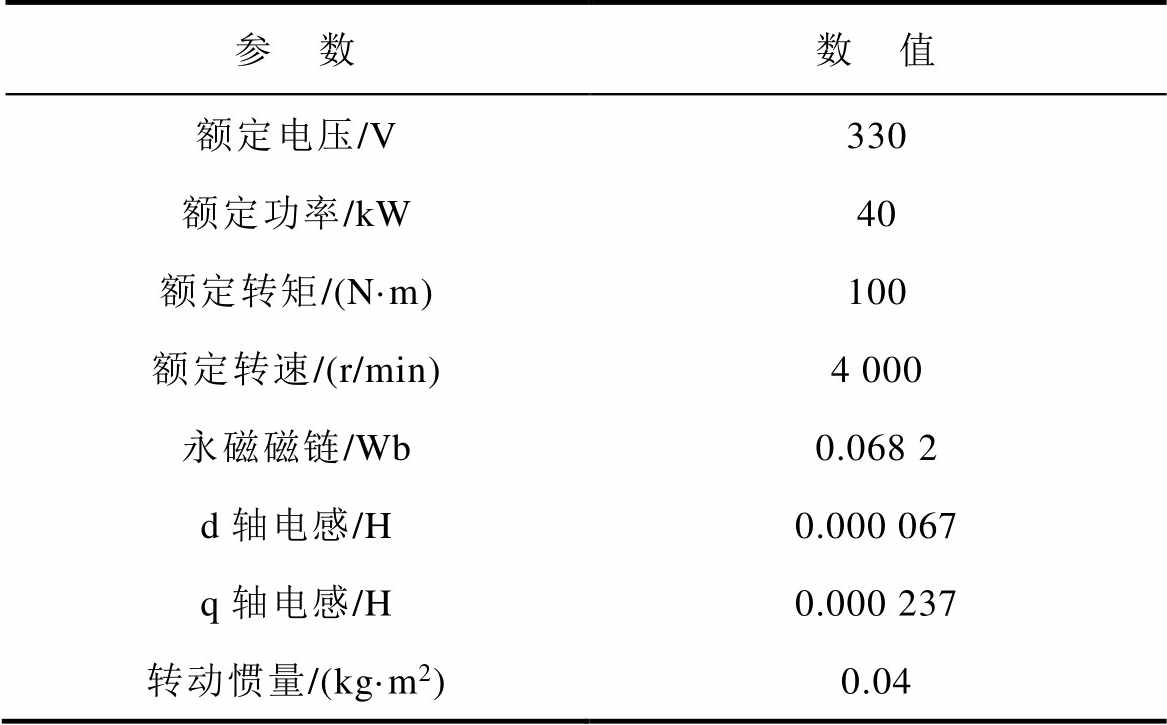
参 数数 值 额定电压/V330 额定功率/kW40 额定转矩/(N·m)100 额定转速/(r/min)4 000 永磁磁链/Wb0.068 2 d轴电感/H0.000 067 q轴电感/H0.000 237 转动惯量/(kg·m2)0.04
设定电流约束条件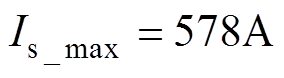 ,电机空载,在第0s、0.15s和0.3s时刻,分别以阶跃的形式给定目标转速2 000r/min、4 000r/min和2 000r/min,图5为动态响应过程中电机转速、转矩、dq轴电流、电压及其矢量幅值的波形。可见转速的动态响应非常快,其原因是在每次加速、减速过程中,MPC控制器都能提供快速的最优控制电压(见图5c)作用于定子,激发出定子dq轴电流(见图5b)继而产生电磁转矩(见图5a)。由图5a和图5b可知,在每次转速动态响应过程,都能以最大电流来生成转矩完成加减速动作。由图5b和图5c可知,在0.15s及0.3s的转速阶跃响应过程中电压矢量幅值
,电机空载,在第0s、0.15s和0.3s时刻,分别以阶跃的形式给定目标转速2 000r/min、4 000r/min和2 000r/min,图5为动态响应过程中电机转速、转矩、dq轴电流、电压及其矢量幅值的波形。可见转速的动态响应非常快,其原因是在每次加速、减速过程中,MPC控制器都能提供快速的最优控制电压(见图5c)作用于定子,激发出定子dq轴电流(见图5b)继而产生电磁转矩(见图5a)。由图5a和图5b可知,在每次转速动态响应过程,都能以最大电流来生成转矩完成加减速动作。由图5b和图5c可知,在0.15s及0.3s的转速阶跃响应过程中电压矢量幅值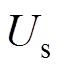 、电流矢量幅值
、电流矢量幅值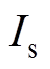 存在同时触发最大幅值的约束条件的动态过程,证明了本文所提出的转速控制算法能够在充分利用最大可输出母线电压的同时严格遵守电流约束条件,提供尽可能大的输出转矩,以达到快速的转速动态响应,即在满足多变量约束条件下提供最优控制性能。当电机在不同转速稳态运行时,转速波动极小且无稳态误差。由于所提出的转速预测控制算法具有前馈-反馈的结构,并能够提供最优控制电压,因此实现了快速的转速动态响应,且动态过程无超调。
存在同时触发最大幅值的约束条件的动态过程,证明了本文所提出的转速控制算法能够在充分利用最大可输出母线电压的同时严格遵守电流约束条件,提供尽可能大的输出转矩,以达到快速的转速动态响应,即在满足多变量约束条件下提供最优控制性能。当电机在不同转速稳态运行时,转速波动极小且无稳态误差。由于所提出的转速预测控制算法具有前馈-反馈的结构,并能够提供最优控制电压,因此实现了快速的转速动态响应,且动态过程无超调。
考虑到IPMSM的电感参数对铁心的饱和程度很敏感,其饱和程度随着dq轴电流幅值的变化而变化,为验证所提算法的参数鲁棒性在电机运行过程中,将IPMSM的交、直轴电感在0.05s时刻突变为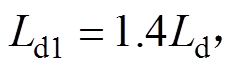
 ,且算法中的其他参数保持不变,重复3.1节的实验工况得到参数失配条件下的转速阶跃响应仿真结果如图6所示。从图6a可知,在预测模型参数失配的情况下,仍然能够实现动态响应无超调且无稳态误差的参考转速跟踪效果,但是在后两次动态过程中输出转矩的波动变大,不能够在加、减速过程始终维持最大转矩输出,导致调速时间变长,这是因为预测模型与被控对象模型参数失配,导致预测的状态与实际系统状态出现偏差,电流、电压输出波形在0.05s时出现明显的瞬态波动,如图6b和图6d所示,但是在滚动优化闭环控制过程中,代价函数中惩罚转速偏差的惩罚因子远远大于惩罚电流增量的因子,而输出电压是如式(28)的增量形式,所以通过代价函数的最小化的迭代过程,得到的控制电压增量仍然能够动态调节来维持目标转速跟踪,并最终进入稳态。这里应该指出,稳态时的工况应为不会同时触发电压、电流约束条件的运行点。模型参数失配引起目标电流和目标电压与实际不符,导致动态过程中的电压、电流约束条件同时触发的时间变长如图6c和图6e所示,但MPC处理约束条件是其固有的优势,即便约束条件同时触发的时间变长的条件下仍然不会失控。结果表明,尽管参数变化的范围非常大,导致动态过程相比于正常条件下的结果出现一定程度的输出转矩下降,但仍然能够获得无稳态误差跟踪目标转速的控制效果。
,且算法中的其他参数保持不变,重复3.1节的实验工况得到参数失配条件下的转速阶跃响应仿真结果如图6所示。从图6a可知,在预测模型参数失配的情况下,仍然能够实现动态响应无超调且无稳态误差的参考转速跟踪效果,但是在后两次动态过程中输出转矩的波动变大,不能够在加、减速过程始终维持最大转矩输出,导致调速时间变长,这是因为预测模型与被控对象模型参数失配,导致预测的状态与实际系统状态出现偏差,电流、电压输出波形在0.05s时出现明显的瞬态波动,如图6b和图6d所示,但是在滚动优化闭环控制过程中,代价函数中惩罚转速偏差的惩罚因子远远大于惩罚电流增量的因子,而输出电压是如式(28)的增量形式,所以通过代价函数的最小化的迭代过程,得到的控制电压增量仍然能够动态调节来维持目标转速跟踪,并最终进入稳态。这里应该指出,稳态时的工况应为不会同时触发电压、电流约束条件的运行点。模型参数失配引起目标电流和目标电压与实际不符,导致动态过程中的电压、电流约束条件同时触发的时间变长如图6c和图6e所示,但MPC处理约束条件是其固有的优势,即便约束条件同时触发的时间变长的条件下仍然不会失控。结果表明,尽管参数变化的范围非常大,导致动态过程相比于正常条件下的结果出现一定程度的输出转矩下降,但仍然能够获得无稳态误差跟踪目标转速的控制效果。
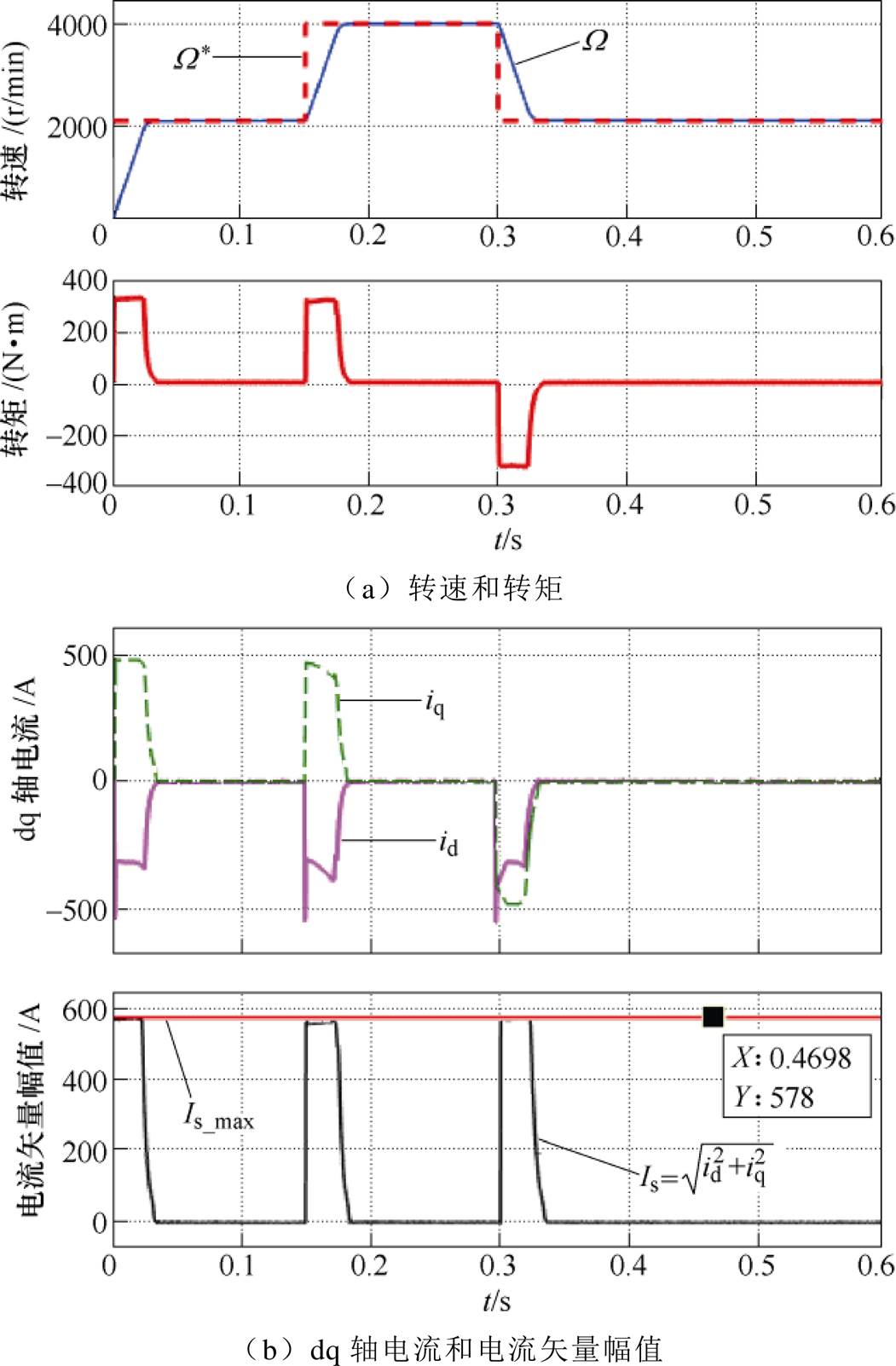
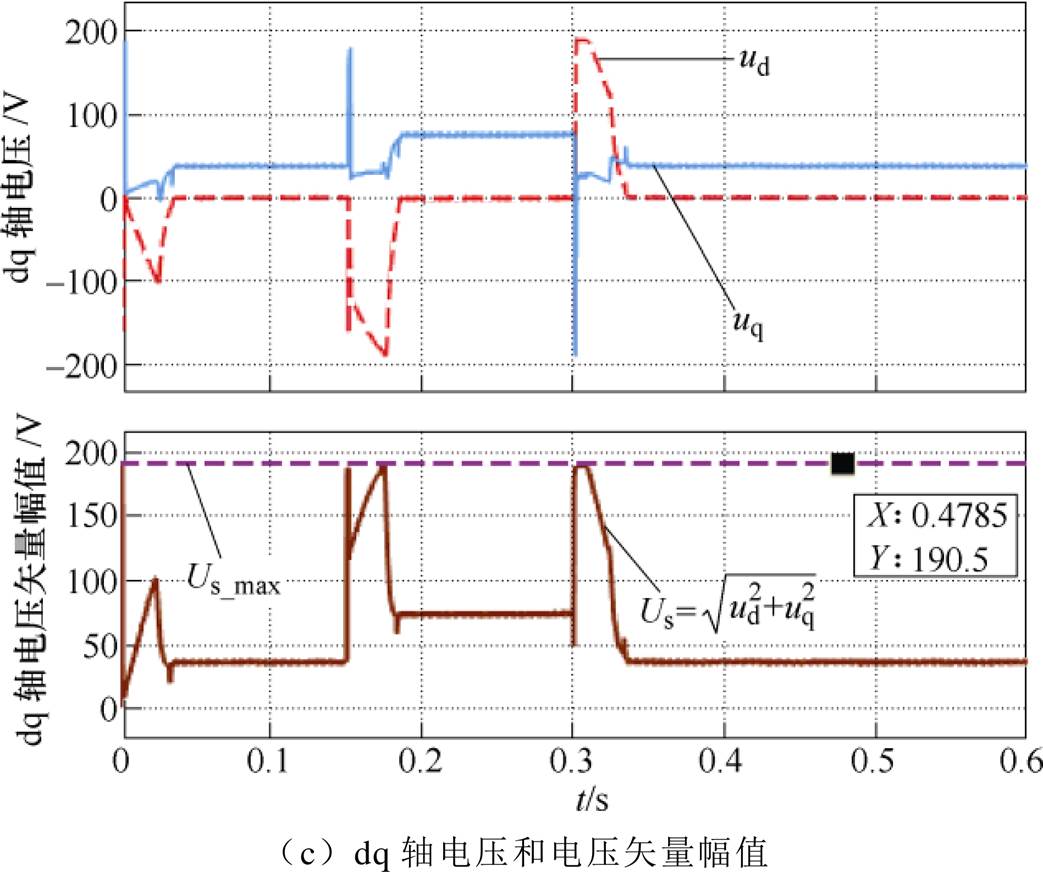
图5 转速阶跃响应仿真结果
Fig.5 Simulation results of speed step response
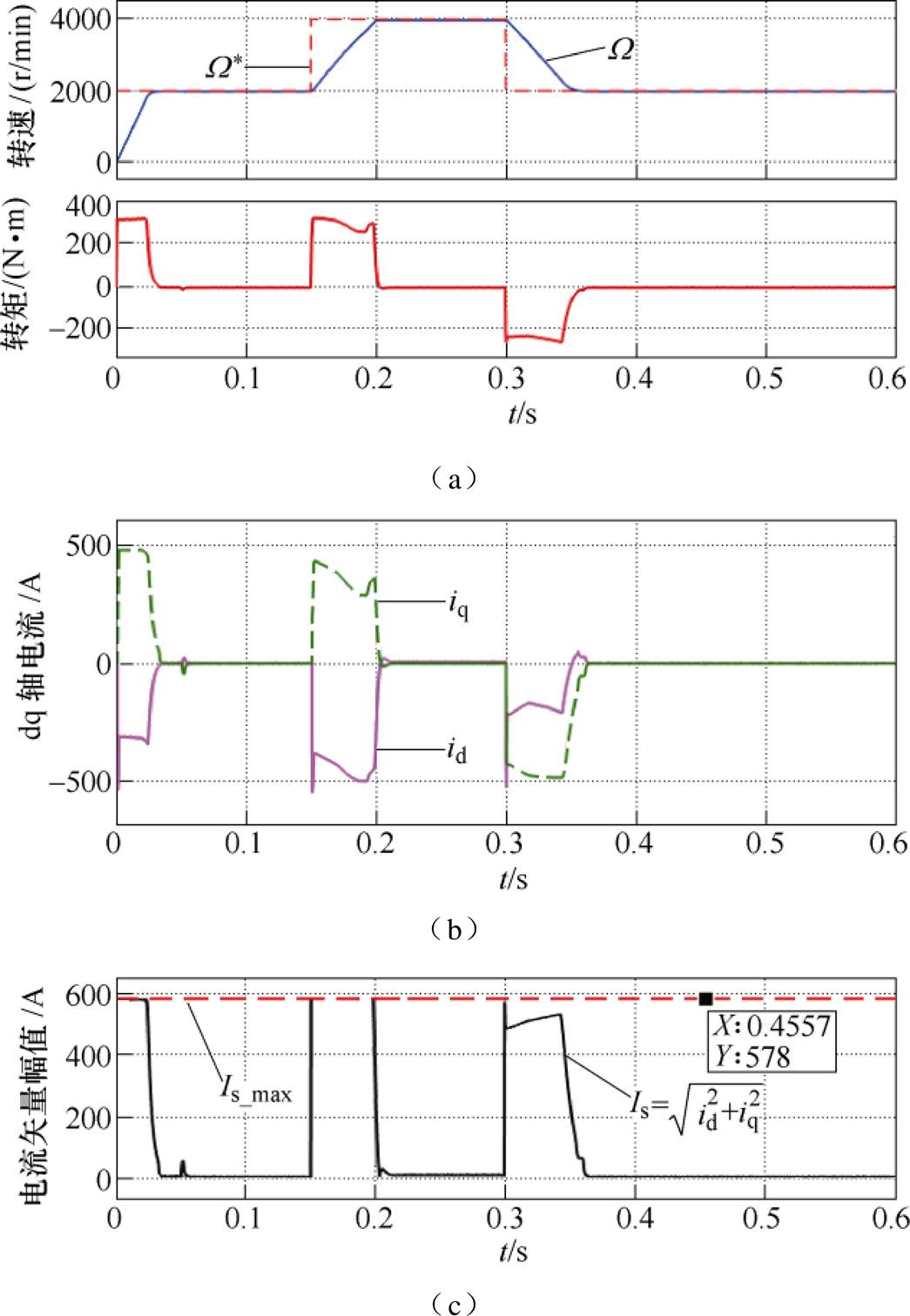
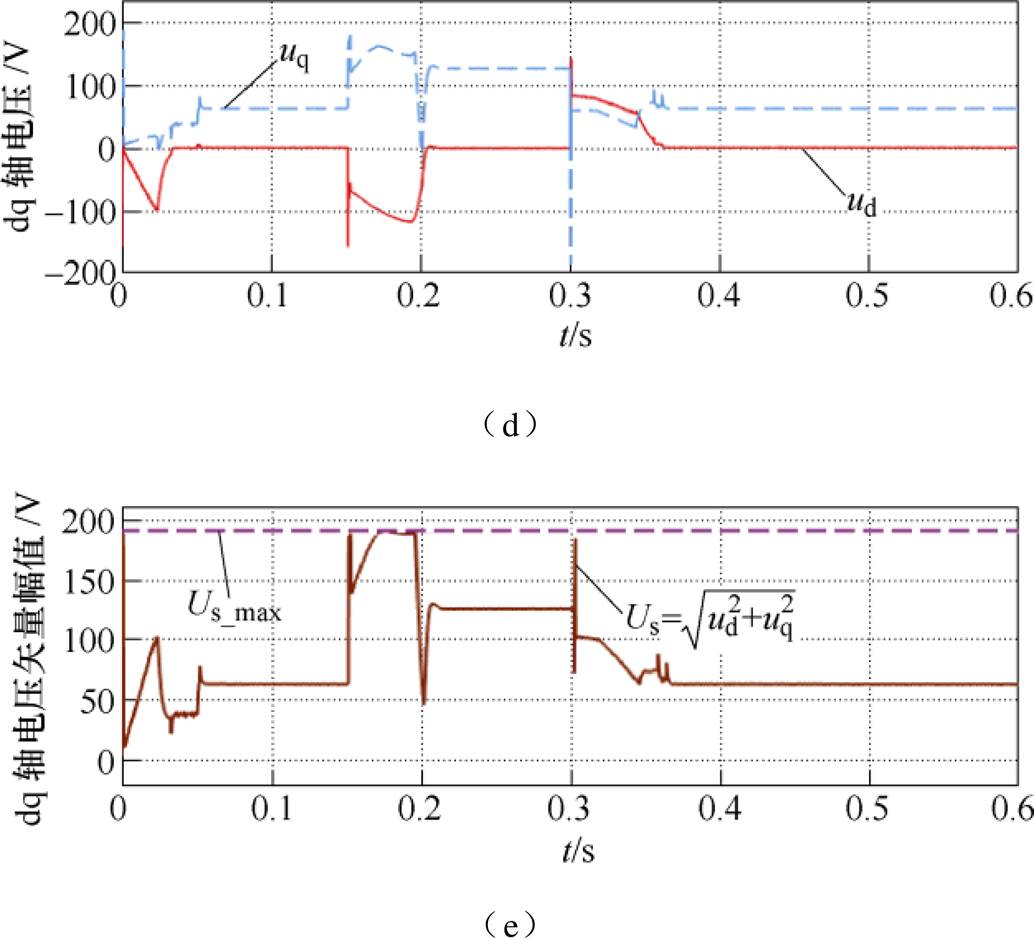
图6 参数失配条件下的转速阶跃响应仿真结果
Fig.6 Simulation results under speed step change command with model parameter variations
用机械法兰连接IPMSM与作为负载的电力测功机,用本文所提算法控制IPMSM运行在额定转速4 000r/min,测功机运行在转矩模式作为负载。在0.25s时刻负载转矩从0N·m阶跃到额定转矩100N·m,此时运行在额定工况;0.75s时刻负载转矩以阶跃的形式增大到120N·m;在1.0s时刻从120N·m减少到50N·m,在负载扰动下的转速控制效果以及观测到的负载转矩如图7所示。从图7a由测量得到的转速波形可知,在加载和卸载的过程中,尽管负载转矩不断地以阶跃形式快速变化,但电机的实际转速在负载的冲击下没有出现明显的波动。从图7b的负载转矩观测结果可知,无论负载增加还是减少,所观测到的负载转矩都能够快速、准确地收敛到实际值。
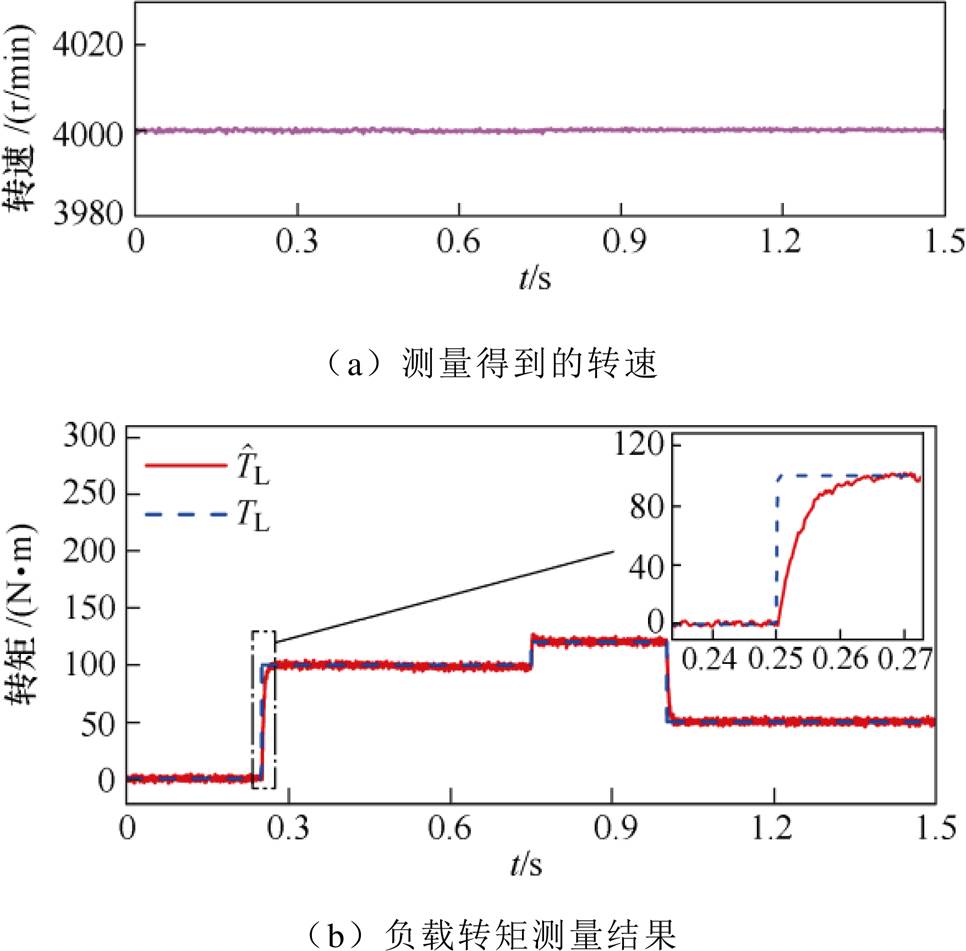
图7 负载转矩阶跃下的实验结果
Fig.7 Experimental results under load torque step change
图8为负载转矩阶跃变化下,相应的dq轴电压、电流以及MTPA电流相位b 的波形,可见在负载阶跃过程中电压的动态响应很快,并且稳态时控制电压的波动较小,因此保证了在转速控制时对负载转矩扰动的良好的动态、稳态性能。以上结果证明了所提出的转速控制算法具有良好的带负载的能力和抗负载扰动的性能。
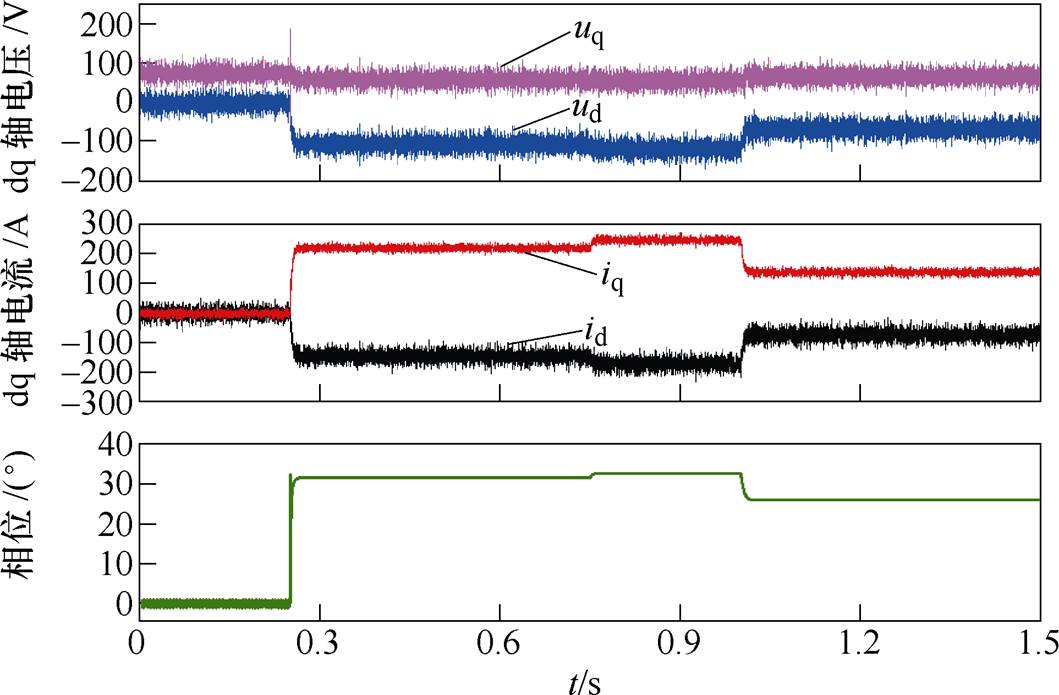
图8 负载转矩阶跃下dq轴电压、电流及电流相位
Fig.8 Waveforms of dq-axis voltage, current and phase angle under load torque step change
在对比实验中选择与传统的级联PI方法进行比较研究,因为传统的PI控制方法在工业中得到广泛应用,另外所提出的LPV-MPC方案具有非级联结构,与传统的级联PI控制方法进行比较分析,以便评估控制性能的改进。传统级联PI控制器是基于文献[19]来设计的。实验过程为:额定负载100N·m下,0~4 000r/min的阶跃响应。设置最大允许电流幅值为490A,图9给出了用级联PI算法和本文所提算法的调速实验结果波形。从图9a可知,两种算法均获得了较好的转速动态响应,并且均无稳态误差,但是LPV-MPC控制得到了更快的转速响应,LPV-MPC控制器的输出转矩在动态响应过程中得到了更好的控制,恒转矩输出的时间更长,因为目标参考纳入了控制算法中也会影响到当前的控制动作,能够充分预测的未来信息遇见未来发生的违背约束的可能性,提前必要的控制动作主动控制约束的触发。如图9b上部分为dq轴电流波形,下部分为对应的电流矢量幅值,可见所提算法能够很好地处理多变量约束条件下的优化控制,完成动态响应,并在到达目标转速后快速地从最大输出调整到满足稳态工况的平稳输出。然而基于级联结构的PI控制不能以明确的方式执行约束条件,而是以限幅和抗饱和(anti-windup)的形式实现对边界条件的约束,所以表现出不同于LPV-MPC算法的输出转矩的特性,在起动初始阶段,目标转速和实际转速的差值较大,所以转速外环PI会输出最大转矩(饱和/限幅)给电流内环,据此计算出电流参考。由图9c可知,随着转速的快速增加会使得内环电流PI调节器进入饱和状态,为了避免电流环PI调节器失控,抗饱和机制迫使其退出饱和状态,导致电流幅值减小,所以不再能够维持最大输出能力,因此转矩出现一定程度的下降。综合图9b和图9c可知,相比于LPV- MPC算法,级联PI算法在转速接近额定转速时,会使得电压矢量幅值触发最大允许约束条件(线性SVPWM调制的最大输出电压),在退出饱和进入稳态的调节过程中导致输出转矩下降,因此本文所提算法获得了更好的动态响应性能。
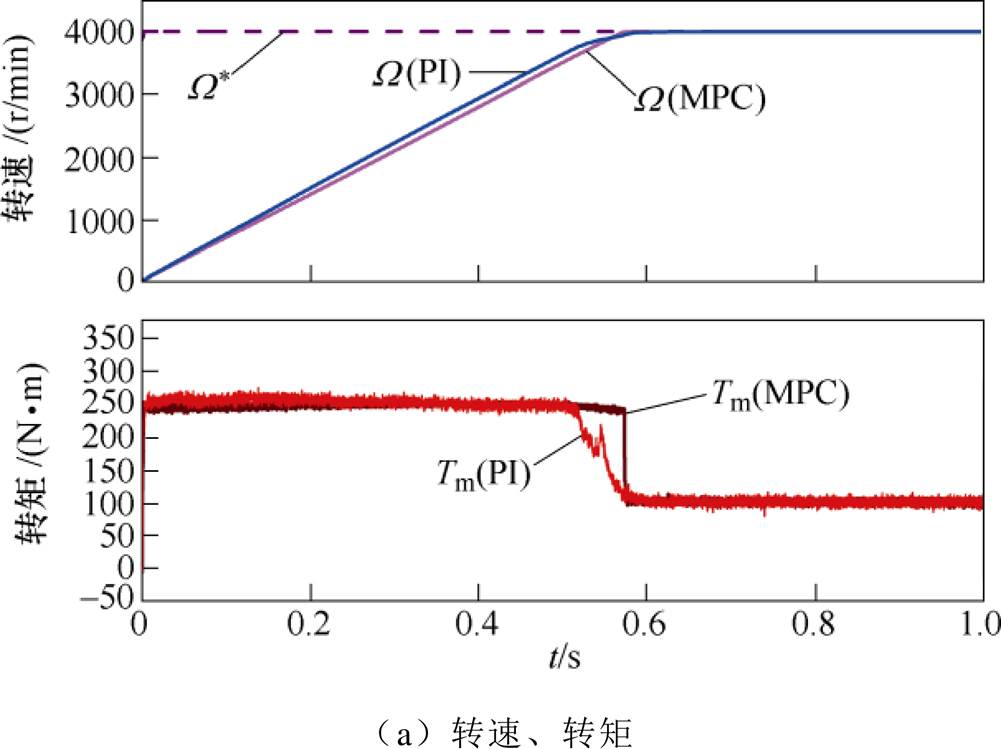
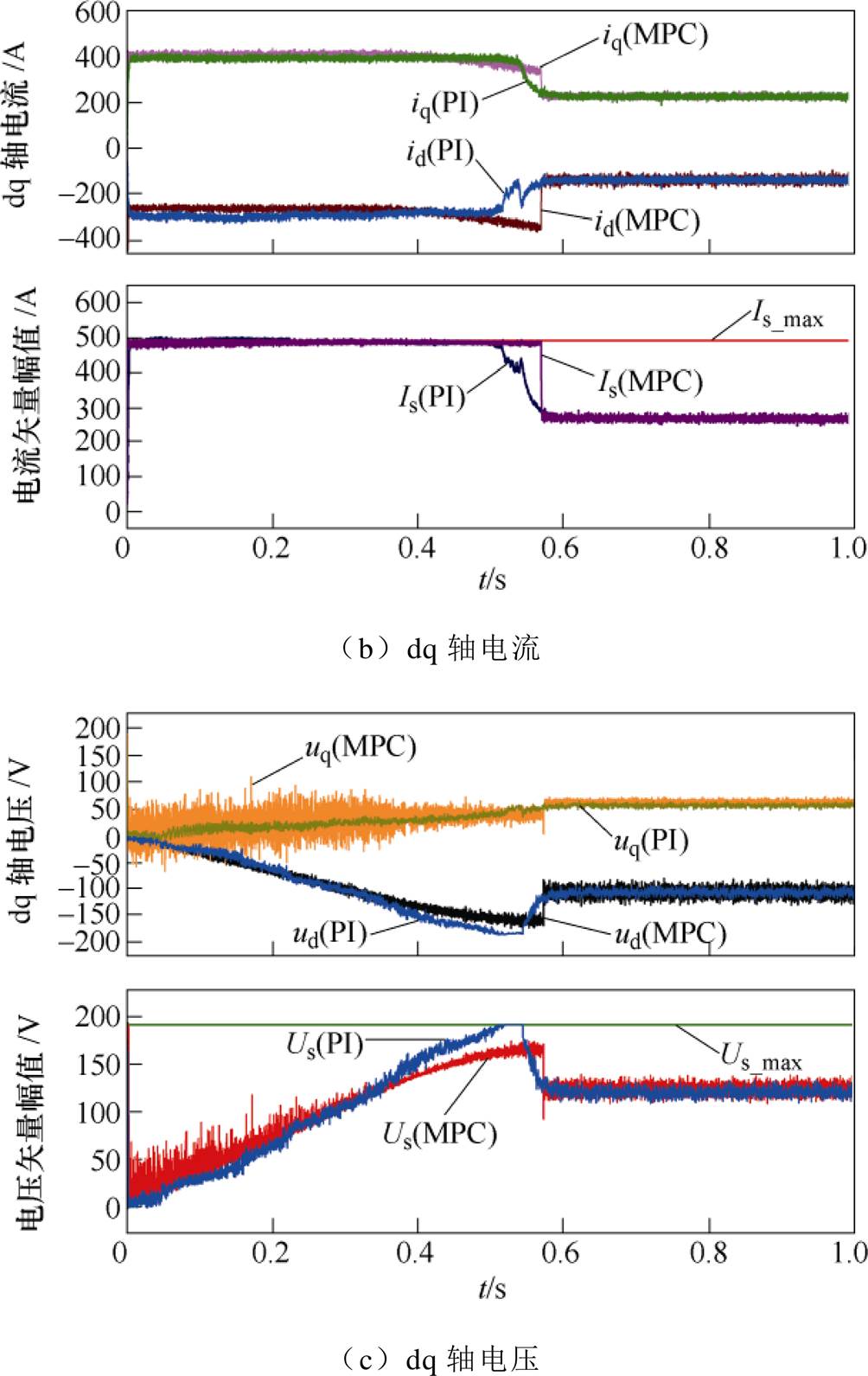
图9 调速实验结果对比
Fig.9 Dynamics comparison between LPV-MPC and PI
本文提出了一种非级联结构的IPMSM转速控制策略LPV-MPC,利用稳态工作点将系统的动态模型线性化,将二次型的电压、电流约束条件近似为线性矩阵不等式,由此设计增量形式的模型预测算法,进而将该模型预测的约束最优化问题转化为标准的QP问题而求解,利用EKF设计了负载转矩观测器对负载转矩等未知参数进行观测,通过仿真分析和实验验证得到以下结论:
1)所提出的LPV-MPC转速控制器提供了良好的动态性能和稳态时无偏差的目标转速跟踪效果。
2)该算法具有前馈-反馈的结构、增量形式的控制输入,与负载转矩观测器构成的转速闭环控制系统,具有一定的鲁棒性。
3)与传统的级联PI控制算法相比较,具有更好的多变量约束处理能力。
参考文献
[1] Finken T, Felden M, Hameyer K. Comparison and design of different electrical machine types regarding their applicability in hybrid electrical vehicles[C]//In 18th International Conference on Electrical Machines, Vilamoura, Portugal, 2008: 1-5.
[2] 李永东. 交流电机数字控制系统[M]. 北京: 机械工业出版社, 2002.
[3] 麦志勤, 肖飞, 刘计龙, 等. 基于准比例谐振级联PI的双三相永磁同步电机谐波电流抑制策略[J]. 电工技术学报, 2018, 33(24): 5751-5759.
Mai Zhiqin, Xiao Fei, Liu Jilong, et al. Harmonic current suppression strategy of dual three-phase permanent magnet synchronous motor based on quasi proportional resonant cascading-PI[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5751-5759.
[4] 陈卓易, 邱建琪, 金孟加. 内置式永磁同步电机无位置传感器自适应集总电动势模型预测控制[J]. 电工技术学报, 2018, 33(24): 25-35.
Chen Zhuoyi, Qiu Jianqi, Jin Mengjia. Sensorless adaptive lumped electromotive-force model predi- ctive control of interior permanent magnet syn- chronous motors[J]. Transactions of China Electro- technical Society, 2018, 33(24): 25-35.
[5] Jia Chengyu, Wang Xudong, Liang Yafei, et al. Robust current controller for ipmsm drives based on explicit model predictive control with online disturbance observer[J]. IEEE Access, 2019, 7(1): 45898-45910.
[6] 康劲松, 李旭东, 王硕. 计及参数误差的永磁同步电机最优虚拟矢量预测电流控制[J]. 电工技术学报, 2018, 33(24): 5731-5740.
Kang Jinsong, Li Xudong, Wang Shuo. Optimal virtual vector predictive current control for per- manent magnet synchronous motor considering parameter errors[J]. Transactions of China Electro- technical Society, 2018, 33(24): 5731-5740.
[7] 周湛清, 夏长亮, 陈炜, 等. 具有参数鲁棒性的永磁同步电机改进型预测转矩控制[J]. 电工技术学报, 2018, 33(5): 965-972.
Zhou Zhanqing, Xia Changliang, Chen Wei, et al. Modified predictive torque control for PMSM drives with parameter robustness[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 965-972.
[8] 张永昌, 杨海涛, 魏香龙, 等. 基于快速矢量选择的永磁同步电机模型预测控制[J]. 电工技术学报, 2016, 31(6): 66-73.
Zhang Yongchang, Yang Haitao, Wei Xianglong, et al. Model predictive control of permanent magnet synchronous motors based on fast vector selection[J]. Transactions of China Electrotechnical Society, 2016, 31(6): 66-73.
[9] Chai Shan, Wang Liuping, Rogers E. A cascade MPC control structure for a PMSM with speed ripple minimization[J]. IEEE Transactions on Industrial Electronics, 2013, 60(8): 2978-2987.
[10] Bolognani S, Bolognani S, Peretti L, et al. Design and implementation of model predictive control for electrical motor drives[J]. IEEE Transactions on Industrial Electronics, 2009, 56: 1925-1936.
[11] Mynar Z, Vesely L, Vaclavek P. PMSM model predictive control with field weakening imple- mentation[J]. IEEE Transactions on Industrial Electronics, 2016, 63(8): 5156-5166.
[12] Errouissi R, Ouhrouche M A, Chen Wenhua, et al. Robust cascaded nonlinear predictive control of a PMSM with anti-windup compensator[J]. IEEE Transactions on industrial Electronics, 2012, 59(8): 3184-3189.
[13] 李峰, 夏超英. 考虑磁路饱和的IPMSM电感辨识算法及变参数MTPA控制策略[J]. 电工技术学报, 2017, 32(11): 136-144.
Li Feng, Xia Chaoying. Inductance identification algorithm and variable-parameters MTPA control strategy for IPMSM considering magnetic circuit saturation[J]. Transactions of China Electrotechnical Society, 2017, 32(11): 136-144.
[14] 席裕庚, 李德伟. 模型预测控制—现状与挑战[J]. 自动化学报, 2012, 38(9): 1-15.
Xi Yugeng, Li Dewei. Model predictive control status and challenges[J]. Acta Automatica Sinica, 2012, 38(9): 1-15.
[15] Mayne D Q, Rawlings J B, Rao C V, et al. Con- strained model predictive control: stability and optimality[J]. Automatica, 2000, 36(6): 789-814.
[16] Bartlett R A, Wachter A, Biegler L T. Active set vs. interior point strategies for model predictive control[C]//Proceedings of the 2000 American Control Conference, Chicago, IL, USA, 2000: 4229-4233.
[17] Rao C V, Wright S J, Rawlings J B. Application of interior-point methods to model predictive control[J]. Journal of Optimization Theory and Applications, 1998, 99(3): 723-757.
[18] Cimini G, Bemporad A, Bernardini D. ODYS QP Solver[Z]. 2017.
[19] Morimoto S, Sanada M, Takeda Y. Wide-speed operation of interior permanent magnet synchronous motors with high-performance current regulator[J]. IEEE Transactions on Industry Applications, 1994, 30(4): 920-926.
Design of Interior Permanent Magnet Synchronous Motor Speed Controller Based on Linear Parameter-Varying Model Predictive Control
Abstract In order to improve the speed control performance of interior permanent magnet synchronous motor (IPMSM), a linear variable parameter model predictive control (LVP-MPC) algorithm is proposed. Herein, the extended Kalman filter (EKF) is used for estimating unknown parameters such as load torque to enhance the robustness. By linearizing the dynamic model of IPMSM at the steady-state operating point, the obtained linear state equation is equivalent to an incremental form, and the predictive model and cost function of the incremental form are designed to achieve the optimal adjustment of the speed and current. Hence, the steady-state error caused by model parameter mismatch and external disturbance is overcome. In addition, polyhedron constraints are used to approximate the quadratic constraints of the drive system. Finally, the MPC optimization problem of the speed control proposed is transformed into a standard form of quadratic programming (QP). The simulation and experimental results show that the proposed architecture has high dynamic performance and zero-offset reference tracking ability.
keywords:Speed control, interior permanent magnet synchronous motor, model predictive control (MPC), observer
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.191162
黑龙江省普通本科高等学校青年创新人才培养计划资助项目(UNPYSCT-2017099)。
收稿日期2019-09-08
改稿日期 2019-12-30
贾成禹 男,1983年生,博士研究生,研究方向为永磁同步电机驱动技术。E-mail: chengyujia@163.com(通信作者)
王旭东 男,1958年生,教授,博士生导师,研究方向为电力电子与电力传动、新能源汽车及电机驱动技术。E-mail: wxd6158@163.com
(编辑 崔文静)