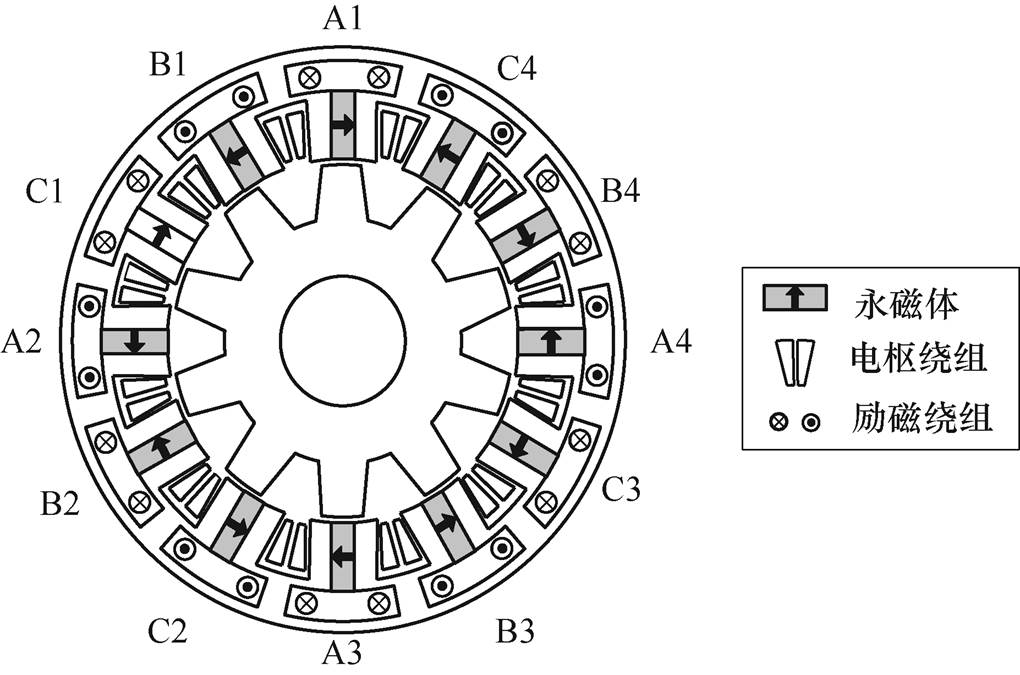
图1 HESFPM电机的拓扑结构
Fig.1 Topology of HESFPM machine
摘要 由于混合励磁电机在传统建模时很少考虑电机运行中的损耗，导致电机实时模型仿真与实验存在较大误差。为了解决这一问题，该文提出一种计及铁耗、铜耗以及永磁体损耗的混合励磁电机建模方法。应用神经网络建立混合励磁电机模型，并在此基础上加入损耗计算，从而得到一种计及损耗的混合励磁电机实时仿真模型。以12槽10极混合励磁开关磁链永磁电机为例，在dSPACE中搭建电机与逆变器模型，从而构成硬件在环仿真平台。实验结果表明，与未计及损耗的混合励磁电机模型相比，计及损耗的混合励磁电机相电流幅值的仿真精度在轻载与重载时，分别最大提高了5.7%和12.5%。
关键词：混合励磁电机 神经网络 损耗模型 硬件在环仿真
硬件在环（Hardware-In-Loop, HIL）电机仿真模型因实时性好、成本低，常被用于验证电机控制算法。硬件在环仿真是半实物仿真的一种，它将实际电机以等效模型描述，替代真实电机。不仅缩短了开发周期，降低了开发成本，而且具有较高的安全性，可有效地对开发对象进行各种条件特别是极限、故障条件下的测试[1]，因此主要用于新算法的开发和故障容错的研究[2-3]。
混合励磁开关磁链永磁（Hybrid-Excited Switched Flux Permanent Magnet, HESFPM）电机的永磁体、电枢绕组和励磁绕组都置于定子内，转子结构简单、可靠[4-9]。然而，在传统的电机控制模型中很少考虑电机运行过程中的损耗，与实验相比存在一定的误差[10]，因此建立较为精确的数学模型需要在电机控制模型中考虑铁耗、铜耗及永磁体损耗。文献[11]建立了考虑损耗的混合励磁发电机空载模型，没有考虑到负载时的损耗，因此存在误差。文献[12]分析并建立了考虑损耗的永磁同步电机模型，但该模型只考虑了基波下的损耗，与真实的电机仍有偏差。
由于HESFPM电机存在较大的磁链谐波，因此电机中的谐波损耗不容忽视。文献[11-12]中的电机模型只考虑了空载以及基波的损耗，因此与真实电机存在误差。本文通过有限元仿真获得不同负载下的各次谐波电流产生的损耗，通过该数据训练神经网络得到电机损耗模型，从而更精确地实现HESFPM电机建模，减小了电机模型与实际样机之间的误差。文献[13]建立了考虑耦合、谐波、涡流损耗和磁滞损耗等因素的永磁同步电机模型，但该模型复杂，无法用于实时仿真模型。
在文献[14-15]中通过神经网络建立了开关磁阻电机的非线性磁链模型，得到了电机非线性模型。在此基础上，本文通过神经网络建模加入了损耗模型，实现负载和转速变化时计及损耗的混合励磁电机建模。
建立HESFPM电机数学模型的关键之处在于精确地建立反映电机损耗的模型。上述研究普遍存在两个问题：一是计算的损耗电阻不准确，降低了模型的精确性；二是模型建立较为复杂，不适用于实时仿真模型。针对以上问题，本文提出了一种计及损耗的HESFPM电机实时仿真模型，并给出了电机的等效电路，包含由等效可变电阻表示的损耗。通过神经网络建立损耗模型，并将损耗模型应用到电机的模型中，与未计及损耗的HESFPM电机模型进行仿真对比。最后将以上两种模型分别应用于12槽10极HESFPM电机HIL系统建模中进行实验对比。
图1为12槽10极HESFPM电机的拓扑结构。在dq同步旋转坐标系中，HESFPM电机的等效电路如图2所示[16-17]。直流励磁绕组的主要作用是调节磁链，因此在d轴的等效电路模型中考虑了直流励磁绕组的磁链[18]。
图1 HESFPM电机的拓扑结构
Fig.1 Topology of HESFPM machine
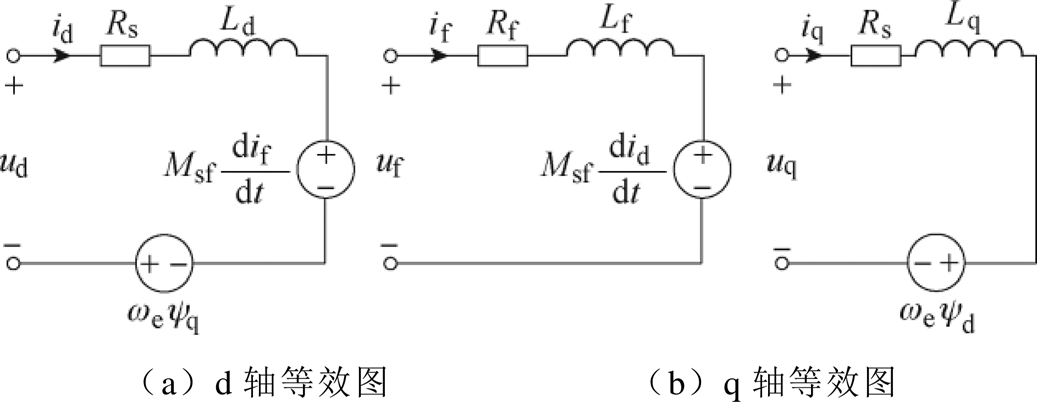
图2 HESFPM电机的等效电路
Fig.2 Equivalent circuit of HESFPM machine
由于电机磁链受转子位置角、电枢电流、励磁电流影响，因此可将磁链表示为
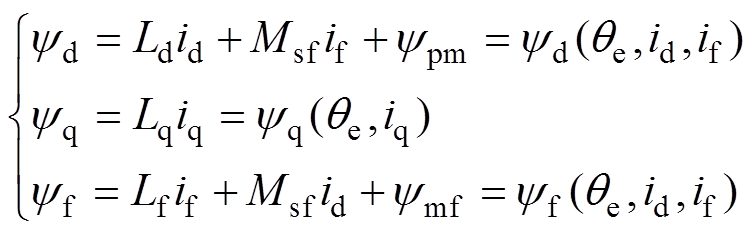（1）电压、转矩方程为
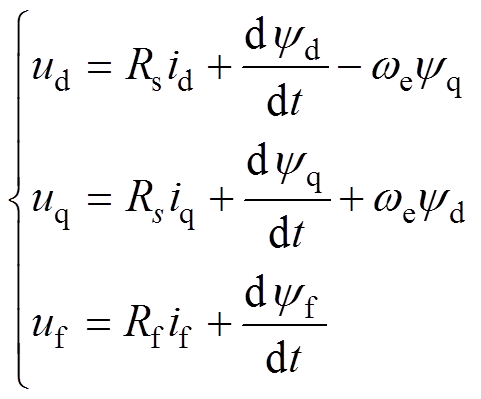（2）
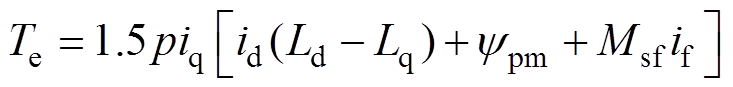（3）式中，ud、uq、id、iq、yd、yq、Ld、Lq分别为d轴和q轴上的电压、电流、磁链和电感；Lf、Msf分别为励磁绕组的自感、励磁绕组与电枢绕组的互感；yf为直流励磁绕组的磁链；ypm、ymf 分别为永磁磁链和励磁磁链；uf、if分别为励磁绕组电压和电流；Rs、Rf分别为电枢绕组电阻和励磁绕组电阻；we、p、Te分别为转子电角速度、极对数和电磁转矩。
通过反向传播（Back Propagation, BP）神经网络来建立电机的磁链模型[19-22]。磁链模型结构如图3所示，通过有限元仿真磁链数据训练得到电机磁链模型，并运用到HESFPM电机仿真系统中。
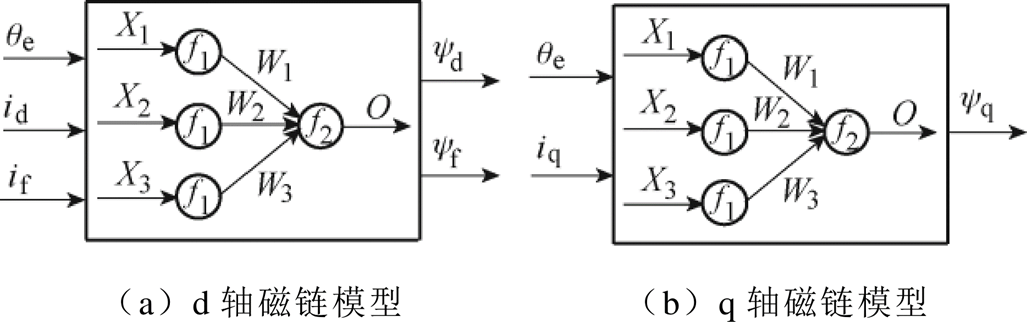
图3 基于BP神经网络的磁链模型
Fig.3 Flux-linkage model based on BP neural network
采用10 633组数据训练神经网络，d轴电流、励磁电流均为-6～0A，q轴电流为0～6A，电流间隔为1A，转子电角度qe为0°～360°，间隔为12°。图4为通过有限元仿真获得的HESFPM电机磁链样本数据，通过该数据训练得到电机磁链模型。可以看出，磁链随电流增大呈非线性饱和状态，随转子位置角呈周期性波动。
图2中的等效电路模型仅体现了铜耗的影响，即电压方程的Rsid和Rsiq项。而在电机实际运行中，铁耗与永磁体损耗也会对电机定子电流产生影响，尤其是对于转速较高的工况。损耗对电机运行状态影响很大，忽略损耗会导致电机模型与真实电机状态差别较大。因此，本文通过在电机dq轴等效电路中并联损耗等效电阻的方式来体现损耗对电机运行状态的影响。
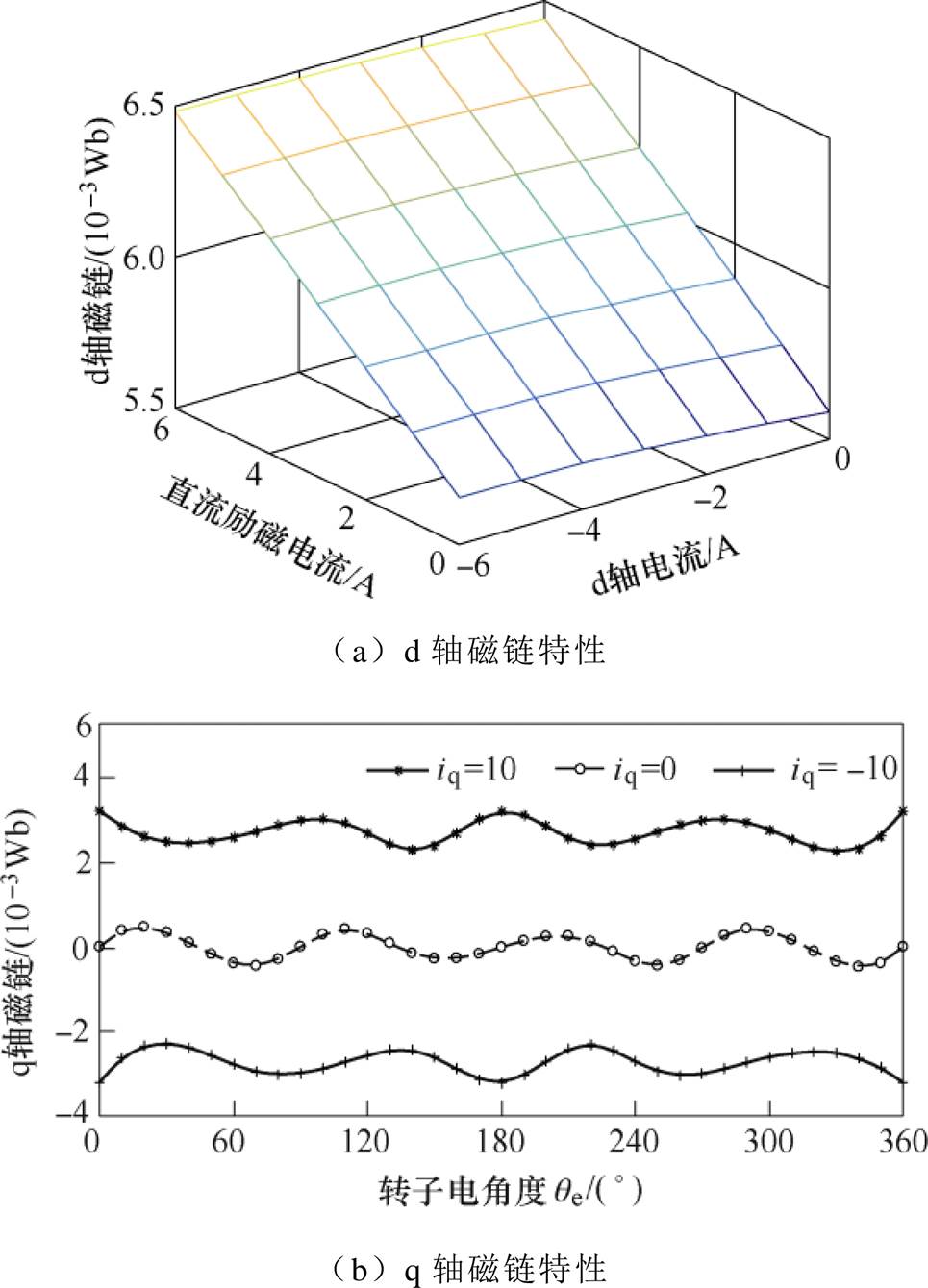
图4 HESFPM电机磁链特性
Fig.4 Flux-linkage characteristics of HESFPM machine
图5所示为计及损耗的HESFPM电机dq轴并联损耗电阻等效电路。将Rc看作与频率、电流相关的函数，即可在等效电路中体现损耗的影响。
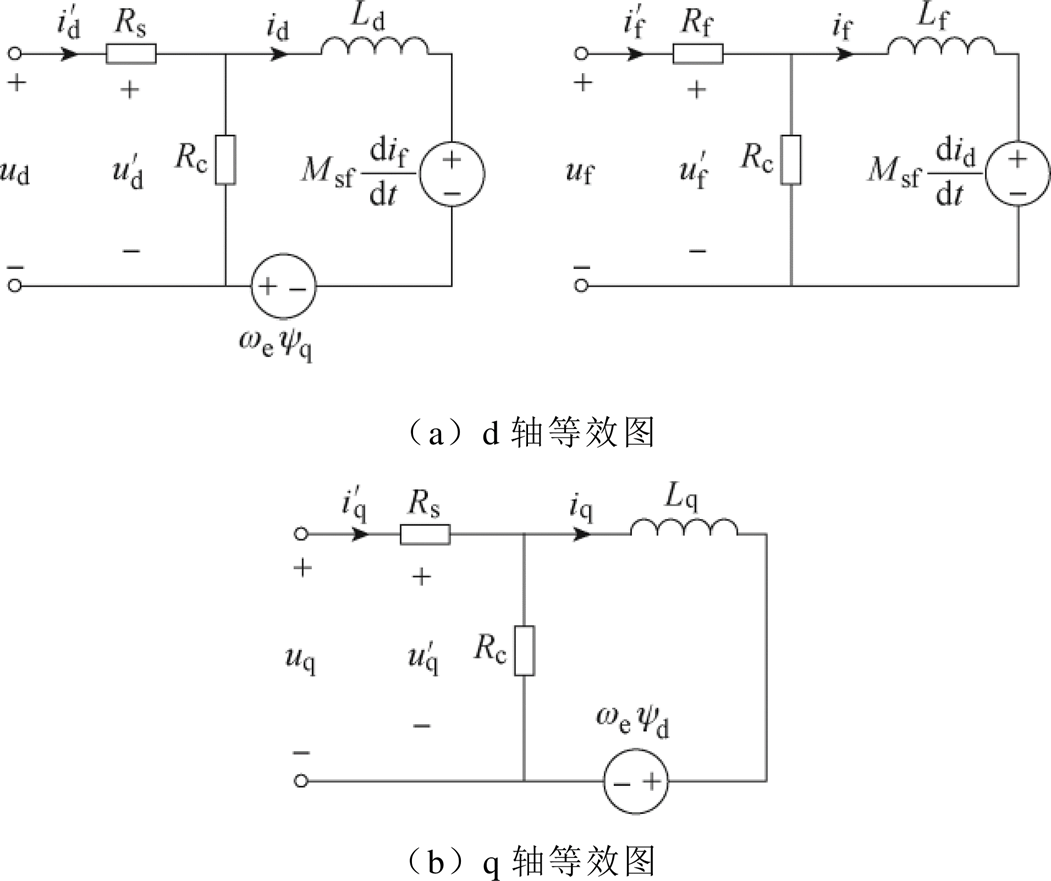
图5 计及损耗的HESFPM电机dq模型
Fig.5 dq model of HESFPM machine considering losses
由图5可得到电压方程为
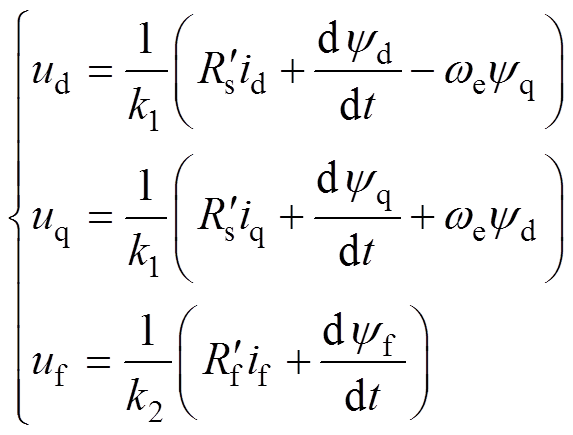（4）其中
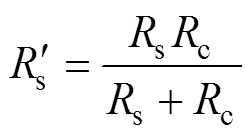
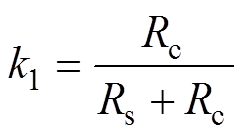
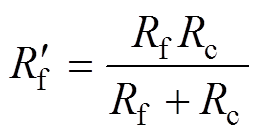
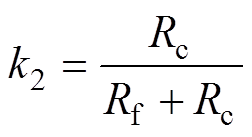
式中，yd、yq、yf均由图3中的神经网络训练得到；Rc为等效损耗电阻，随着电机的转速而变化，即
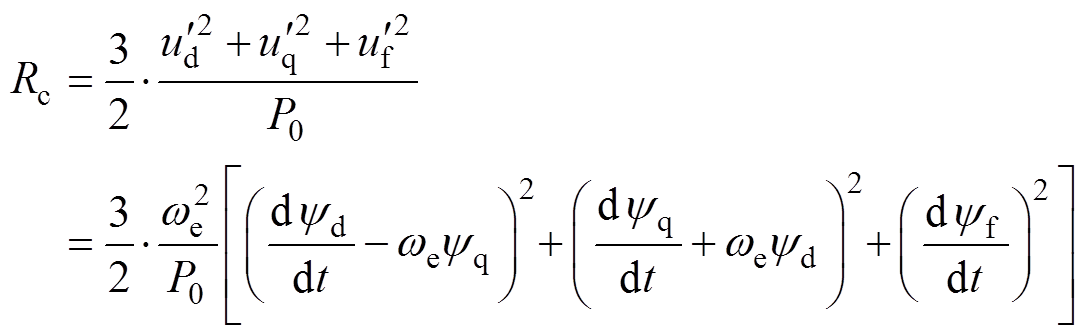（5）式中，P0为电机运行过程中的损耗，包含铁耗、永磁体损耗，其中铁耗占大部分，铁耗包括磁滞损耗、涡流损耗和附加损耗。考虑损耗后，电流方程为
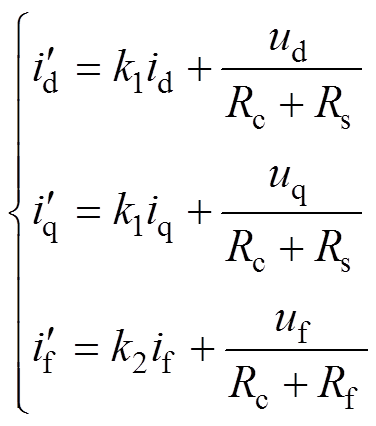（6）
电磁转矩为
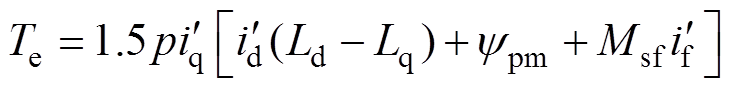（7）损耗等效转矩为
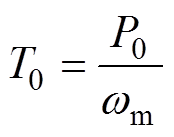（8）
运动方程为
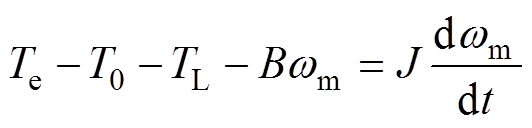（9）式中，TL、J、B和wm分别为负载转矩、转动惯量、阻尼系数和机械角速度。可见考虑损耗后，在损耗等效电阻上消耗的电流使得电机的输出转矩下降，转矩下降的大小为T0。
本文采用有限元法计算得到了HESFPM电机在不同转速、电流运行状态下的电机损耗，以考虑不同转速、负载对电机损耗的影响。通过有限元仿真得到电机损耗，根据式（5）可计算出损耗等效电阻。因此，基于BP神经网络建立如图6所示的损耗模型。
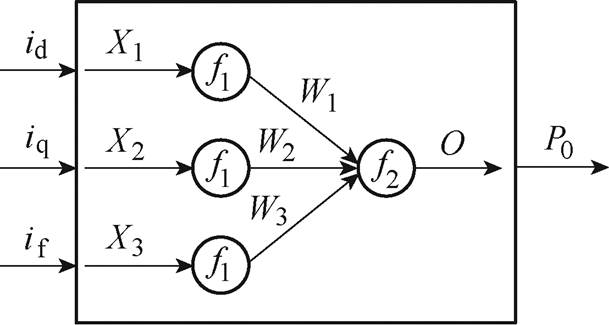
图6 基于BP神经网络的损耗模型
Fig.6 Loss model based on BP neural network
HESFPM电机损耗特性如图7所示。图7a为空载情况下，电机损耗与转速的关系，图7b和图7c为转速n=1 500r/min的情况下，电机损耗分别与励磁电流和电枢电流的关系。采用138 229组数据训练神经网络，d轴电流、励磁电流均为-6～0A，q轴电流为0～6A，电流间隔为1A，转速为0～6 000r/min，转速间隔为500r/min，转子电角度qe为0°～360°，间隔为12°。将训练好的损耗模型应用到HESFPM电机的精确建模中。
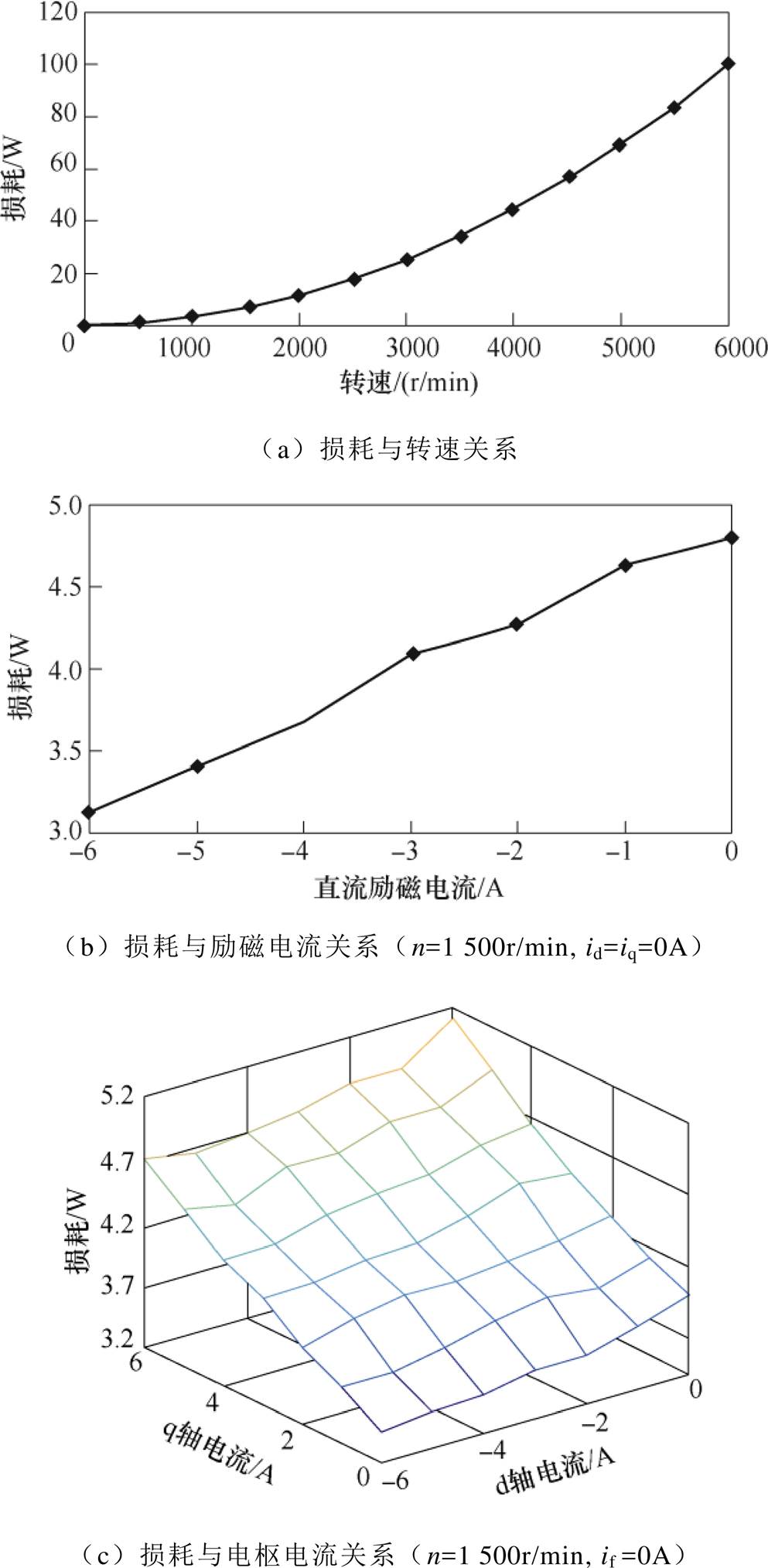
图7 HESFPM电机损耗特性
Fig.7 Loss characteristics of HESFPM machine
为了提高运算速度，通过占空比和频率直接计算出电枢绕组相电压和直流励磁电压，再输入到电机模型中，这简化了开关过程，从而提高了运算速度。同时在建模过程中考虑逆变器死区时间的影响，将死区时间设置为500ns。以A相为例，有
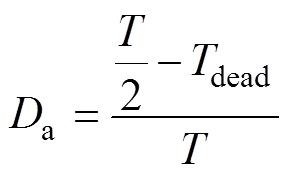（10）式中，Da为A相控制信号的占空比；T为脉宽调制（Pulse Width Modulation, PWM）波周期；Tdead为死区时间。
根据占空比计算的三相交流电压为
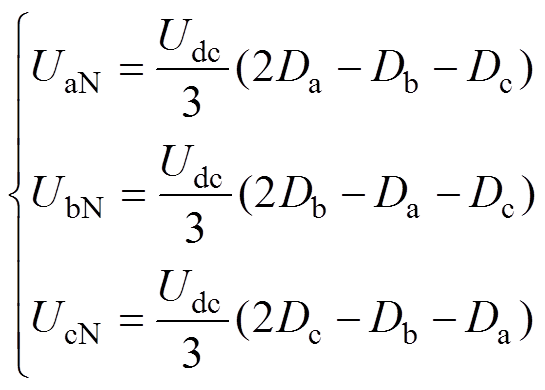（11）直流励磁电压为
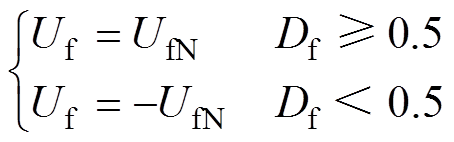（12）
式中，UaN、UbN、UcN、Uf分别为电机三相交流相电压和直流励磁电压；Udc、UfN分别为电枢绕组母线电压和直流励磁绕组母线电压；Da、Db、Dc、Df为4路控制信号的占空比。
通过对逆变器驱动桥的建模，在输出特性相同的基础上简化了模型，提高了运算速度。与使用Matlab/ Simulink中自带的逆变器模块相比，减小了运算步长。在保证仿真准确性的基础上，提高了运算实时性，同时建模也更加简单快速，具有更好的通用性。
为了验证本文建立的损耗模型的输出特性，在dSPACE平台上搭建电机与逆变器模型。与此同时，在相同条件下与12槽10极HESFPM样机的实验结果进行对比。
HIL仿真系统由DSP和dSPACE联合建立，其中，dSPACE作为HIL仿真平台中虚拟电机的载体，将HESFPM电机模型和逆变器模型编译并导入到dSPACE中，再通过接口与DSP相连接，组成HIL系统。使用dSPACE中的数字I/O以及DAC模块，DSP作为电机的控制器，选用型号为TMS320F28335。DSP中输出的PWM波频率为20kHz，通过采集dSPACE中电机模型的输出电流和转子位置信号，通过矢量控制，将PWM控制信号输入给dSPACE中的逆变器模型，进而驱动电机模型，完成闭环控制。图8为HIL仿真平台实物图，8路PWM中的6路用来控制电机ABC三相电压，2路控制直流励磁电压。
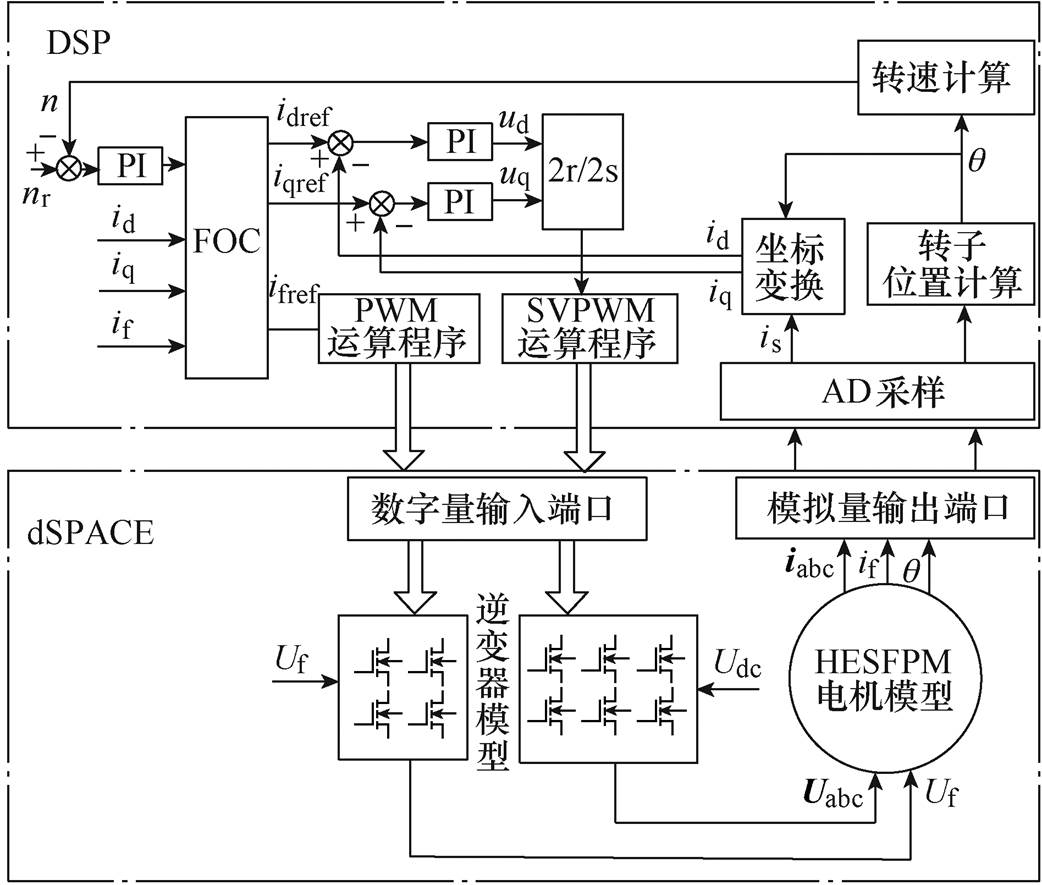
图8 HIL仿真平台组成关系
Fig.8 Composition of HIL simulation platform
电机实验平台主要由HESFPM样机、测功机、DSP和逆变器驱动板组成。DSP作为电机的控制器，使用与HIL仿真平台相同的程序驱动HESFPM样机，使样机在测功机的加载下运行。实验平台实物如图9所示。
图9 HESFPM电机实验平台实物图
Fig.9 Photo of HESFPM machine platform
12槽10极HESFPM样机参数见表1。其中，nN为电机额定转速，TN为额定负载转矩。
表1 HESFPM电机的主要参数
Tab.1 Main parameters of HESFPM machine
参 数数 值参 数数 值 p10Rs/W0.41 ypm/Wb6.3×10-3Rf /W0.77 Udc/V48Ld/mH0.261 Uf/V60Lq/mH0.270 TN/(N·m)1.2Lf /mH0.47 nN/(r/min)400Msf /mH0.054
在上述的实验平台上完成关于HESFPM电机的仿真和实验时，采用相同的控制策略，并且分别控制未计及损耗、计及损耗的电机模型以及实验样机在相同的负载、转速下运行，对实验结果进行比较。
本文在仿真和实验时，电机负载转矩分别为0.3N·m、0.6N·m、0.9N·m，每种负载情况下给定转速为500～1 500r/min。图10～图12分别是未计及损耗的HESFPM电机模型、计及损耗的HESFPM电机模型和实验样机输出的A相电流波形、电流幅值对比以及误差。
表2、表3分别是未计及损耗的HESFPM电机模型、计及损耗的HESFPM电机模型和实验样机输出的A相电流幅值以及误差。表中，De为两种模型误差的差值。误差计算公式为
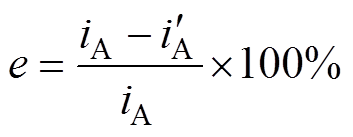（13）式中，iA、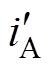
分别为实验样机与电机硬件在环仿真模型的电流幅值。
在高速或负载较大的运行情况下，采用SVPWM时，由于HESFPM电机的磁链谐波较大，电机中的谐波电流很难避免。由图12可以看出，与未计及损耗的电机实时模型相比，计及损耗的电机实时模型准确度明显提高，从表2和表3可以得出，在轻载、重载条件下相电流幅值的仿真精度分别最大提高了5.7%和12.5%。
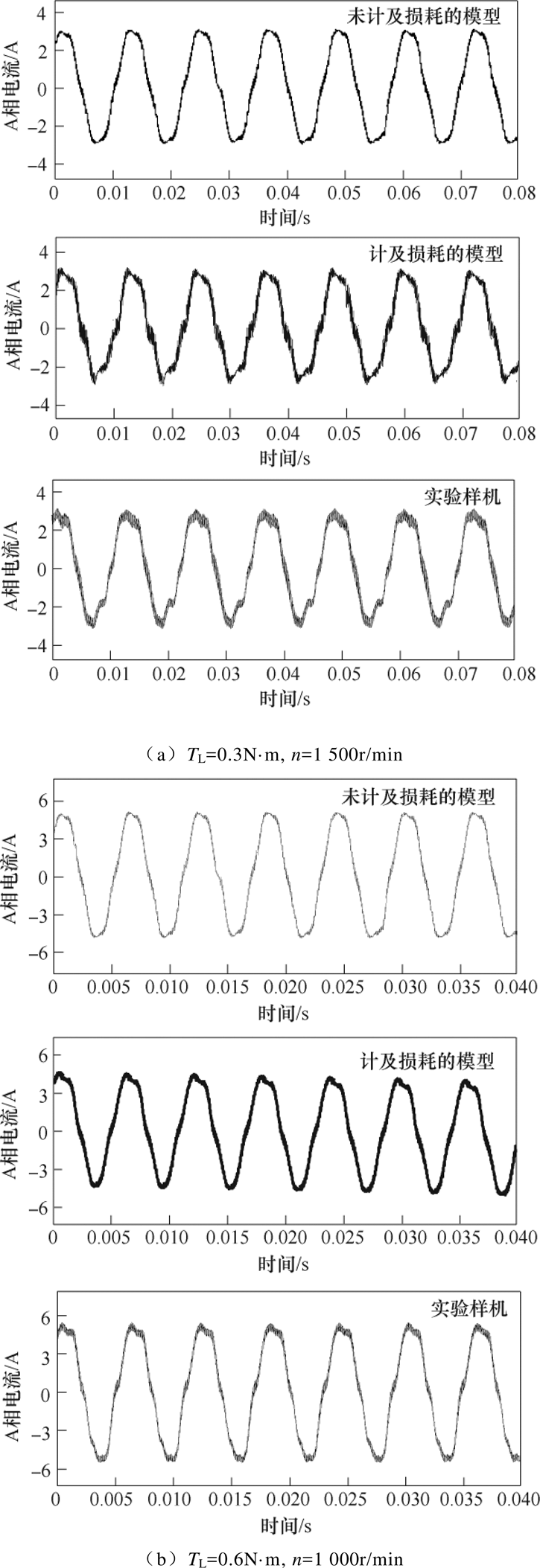
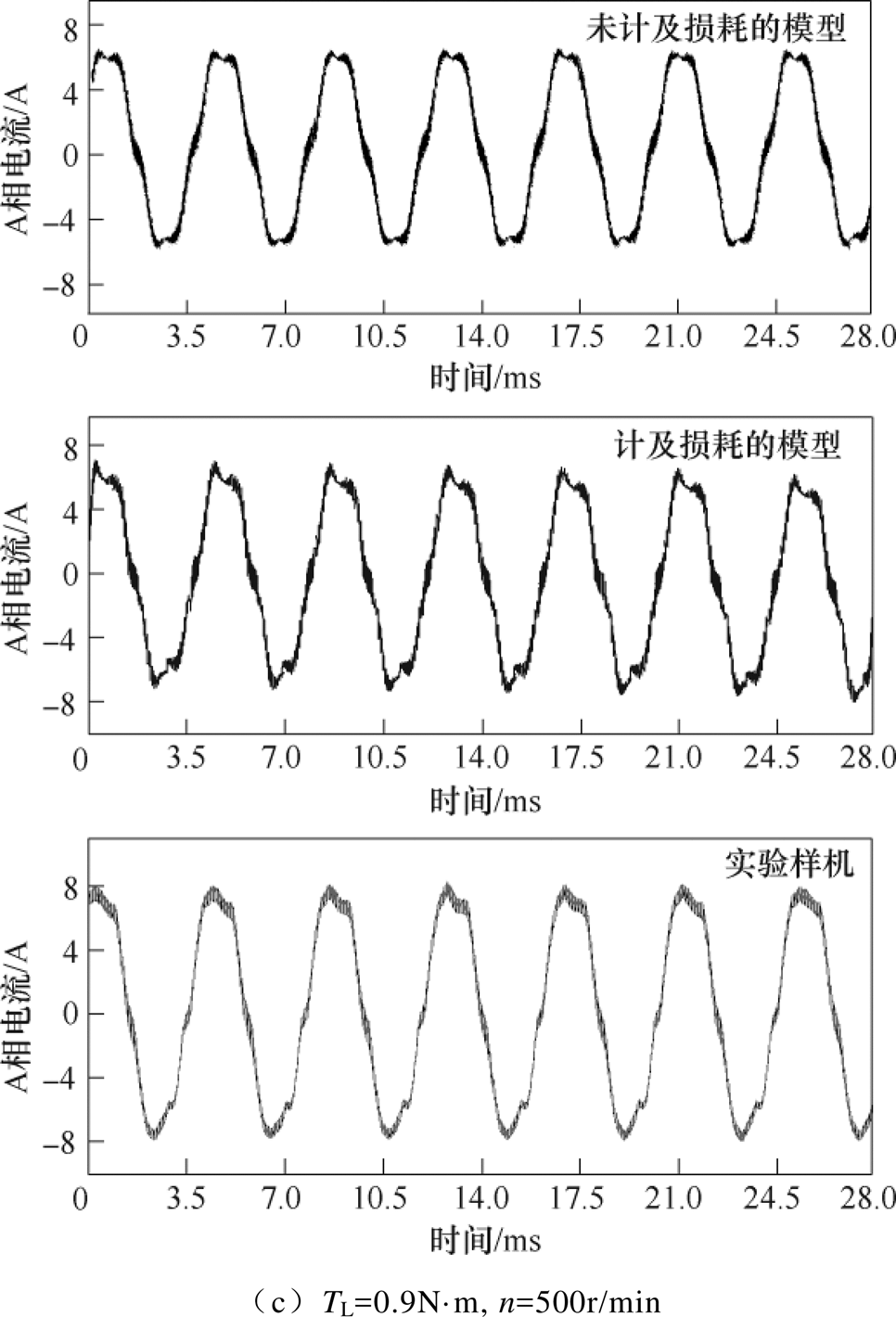
图10 不同电机模型的A相电流波形
Fig.10 Comparison of A-phase current waveforms using different machine models
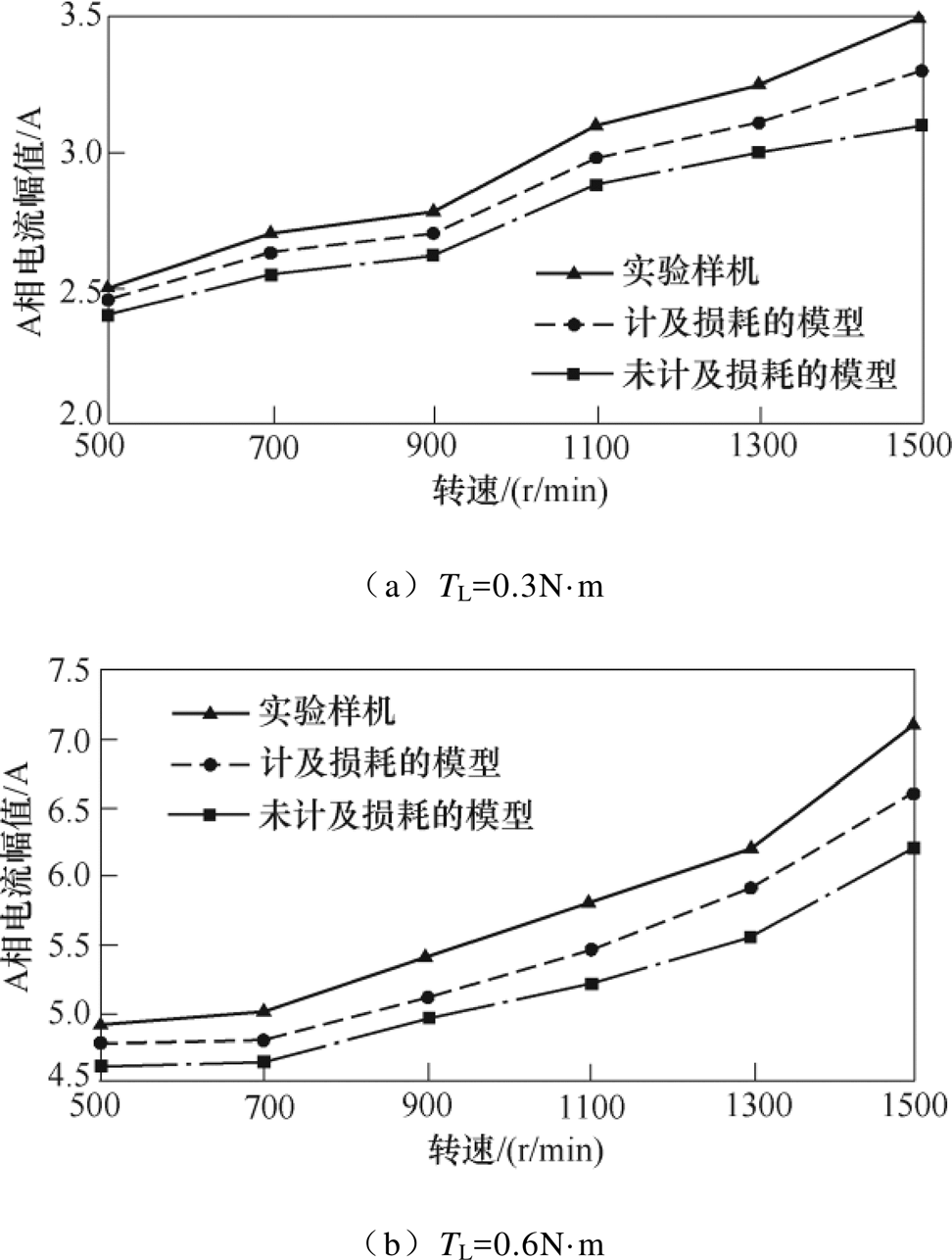
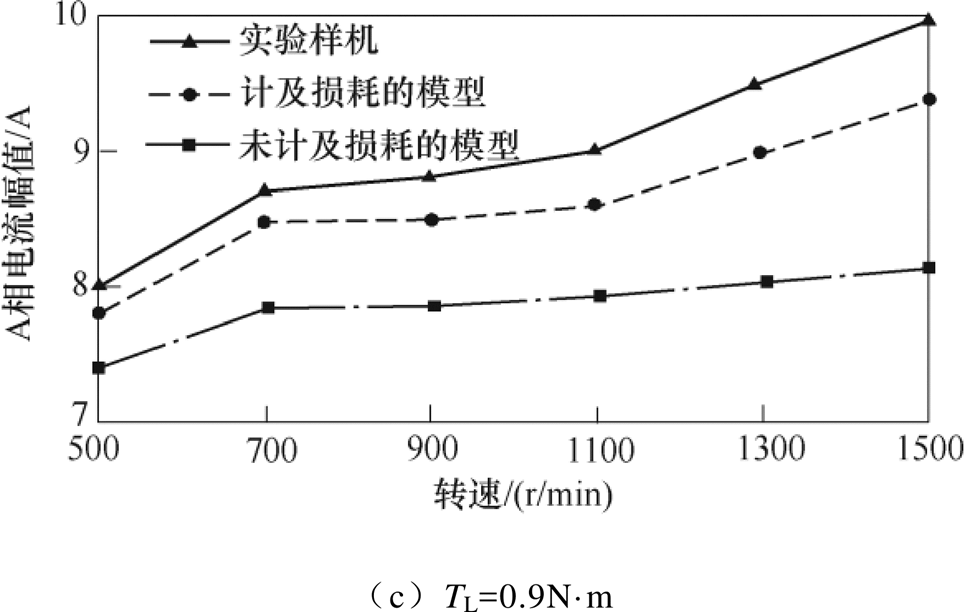
图11 不同电机模型的A相电流幅值对比
Fig.11 Comparison of A-phase current amplitude against speed at different loads
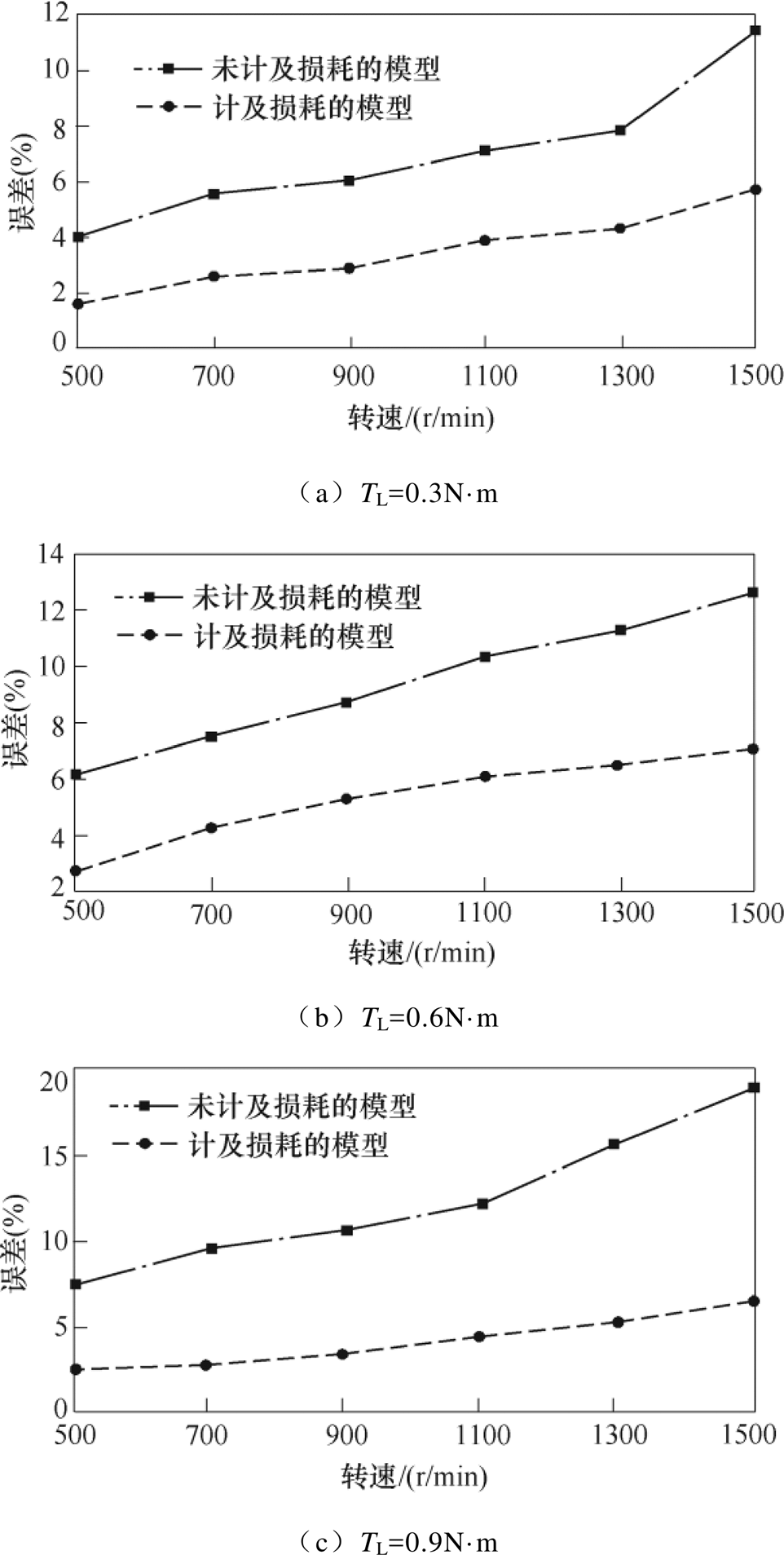
图12 不同电机模型A相电流幅值误差
Fig.12 Comparison of A-phase current amplitude error against speed at different loads
表2 A相电流幅值以及误差（TL=0.3N·m）
Tab.2 A-phase current amplitude and error (TL=0.3N·m)
转速/ (r/min)A相电流幅值/A误差(%)De(%) 未计及损耗计及损耗实验样机未计及损耗计及损耗 5002.402.462.504.01.72.3 7002.562.642.715.52.53.0 9002.642.732.816.12.93.2 1 1002.882.983.107.13.83.3 1 3002.993.113.258.04.23.8 1 5003.103.303.4911.25.55.7
表3 A相电流幅值以及误差（TL=0.9N·m）
Tab.3 A-phase current amplitude and error (TL=0.9N·m)
转速/ (r/min)A相电流幅值/A误差(%)De(%) 未计及损耗计及损耗实验样机未计及损耗计及损耗 5007.407.808.007.52.55.0 7007.818.428.649.62.67.0 9007.858.518.8010.83.27.6 1 1007.928.609.0012.14.27.9 1 3008.038.999.4815.35.210.1 1 5008.139.389.9818.56.012.5
由于传统混合励磁电机建模中忽略了损耗，导致仿真结果与实验样机相比存在较大误差，针对该问题，本文提出了一种计及损耗的混合励磁电机的建模方法，建立了计及损耗的HESFPM电机模型。搭建了基于dSPACE的电机与逆变器模型，DSP作为控制器的HIL仿真平台。通过与实验样机的对比，计及损耗的电机模型相电流仿真结果更接近实验样机，与未计及损耗的HESFPM电机模型相比，相电流幅值的仿真精度在轻载与重载时，分别最大提高了5.7%和12.5%。
参考文献
[1] Ingalalli A, Satheesh H, Kande M. Platform for hardware in loop simulation[C]//2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Anacapri, 2016: 41-46.
[2] 郝琦, 葛兴来, 宋文胜, 等. 电力牵引传动系统微秒级硬件在环实时仿真[J]. 电工技术学报, 2016, 31(8): 189-198.
Hao Qi, Ge Xinglai, Song Wensheng, et al. Micro- second hardware-in-the-loop real-time simulation of electrical traction drive system[J]. Transactions of China Electrotechnical Society, 2016, 31(8): 189- 198.
[3] 王宇, 刘崇茹, 李庚银. 基于FPGA的模块化多电平换流器实时仿真建模与硬件在环实验[J]. 中国电机工程学报, 2018, 38(13): 3912-3920, 4033.
Wang Yu, Liu Chongru, Li Gengyin. FPGA-based real-time modeling of modular multilevel converters and hardware-in-loop simulation[J]. Proceedings of the CSEE, 2018, 38(13): 3912-3920, 4033.
[4] 林楠, 王东, 魏锟, 等. 新型混合励磁同步电机的数学模型与等效分析[J]. 电工技术学报, 2017, 32(3): 149-156.
Lin Nan, Wang Dong, Wei Kun, et al. Mathematical model and equivalent analysis of a novel hybrid excitation synchronous machine[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 149- 156.
[5] Zhu Ziqiang, Cai Shun. Overview of hybrid excited machines for electric vehicles[C]//2019 Fourteenth Inter- national Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 2019: 1-14.
[6] 刘旭, 邢栋, 牛大强, 等. 考虑磁链谐波的混合励磁电机硬件在环系统[J]. 微电机, 2019, 52(8): 66-70, 82.
Liu Xu, Xing Dong, Niu Daqiang, et al. Hardware- in-loop platform for hybrid excited machine accounting for flux-linkage harmonics[J]. Micro- motors, 2019, 52(8): 66-70, 82.
[7] 余俊月, 曹煜, 朱姝姝, 等. 一种双端混合励磁的无刷直流发电机运行特性分析[J]. 电工技术学报, 2019, 34(22): 4634-4641.
Yu Junyue, Cao Yu, Zhu Shushu, et al. Analysis of operation characteristics for dual-direction hybrid excitation brushless DC generator[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4634- 4641.
[8] 张晓祥, 张卓然, 刘业, 等. 双端励磁内置转子磁分路混合励磁电机设计与转子强度分析[J]. 电工技术学报, 2018, 33(2): 245-254.
Zhang Xiaoxiang, Zhang Zhuoran, Liu Ye, et al. Design and rotor strength analysis of a hybrid excitation synchronous machine with dual-direction built-in field windings[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 245-254.
[9] 李生民, 张泽灵, 郭思语, 等. 混合励磁同步电机反馈线性化控制[J]. 电工技术学报, 2019, 34(增刊1): 39-51.
Li Shengmin, Zhang Zeling, Guo Siyu, et al. Feedback linearization control of hybrid excitation synchronous motor[J]. Transactions of China Elec- trotechnical Society, 2019, 34(S1): 39-51.
[10] Zhang Dongdong, Liu Tianhao, Zhao Haisen, et al. An analytical iron loss calculation model of inverter- fed induction motors considering supply and slot harmonics[J]. IEEE Transactions on Industrial Elec- tronics, 2019, 66(12): 9194-9204.
[11] Mbayed R, Vido L, Salloum G, et al. Effect of iron losses on the model and control of a hybrid excitation synchronous generator[C]//2011 IEEE International Electric Machines & Drives Conference (IEMDC), Niagara Falls, 2011: 971-976.
[12] 高瑾, 殷桂来, 霍锋伟, 等. 考虑损耗的内置式永磁同步电机标幺化系统硬件在环实时仿真与测试[J]. 电工技术学报, 2016, 31(19): 147-154.
Gao Jin, Yin Guilai, Huo Fengwei, et al. The real-time simulation and test of IPMSM per-unit HIL system considering loss[J]. Transactions of China Electrotechnical Society, 2016, 31(19): 147-154.
[13] Luo Guangzhao, Zhang Rong, Chen Zhe, et al. A novel nonlinear modeling method for permanent- magnet synchronous motors[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6490-6498.
[14] 饶哲宇, 王进华. 基于BP神经网络的开关磁阻电机建模及仿真[J]. 电气开关, 2019, 57(1): 37-40, 44.
Rao Zheyu, Wang Jinhua. Modeling and simulation of switched reluctance motor based on BP neural network[J]. Electric Switchgear, 2019, 57(1): 37-40, 44.
[15] 高宇, 戴跃洪, 宋林. 基于BP神经网络的开关磁阻电机建模[J]. 电力电子技术, 2017, 51(2): 72-74.
Gao Yu, Dai Yuehong, Song Lin. Modeling of switched reluctance motor based on BP neural network[J]. Power Electronics, 2017, 51(2): 72-74.
[16] Zhang Jian, Wen Xuhui, Wang Youlong, et al. Modeling and analysis of nonlinear interior permanent magnet synchronous motors considering saturation and cross-magnetization effects[C]//2016 IEEE Trans- portation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Busan, 2016: 611- 615.
[17] Patin N, Vido L, Monmasson E, et al. Control of a hybrid excitation synchronous generator for aircraft applications[J]. IEEE Transactions on Industrial Electronics, 2008, 55(10): 3772-3783.
[18] 许泽刚, 谢少军. 磁桥式磁通切换型混合励磁电机电感特性分析与建模[J]. 微特电机, 2015, 43(12): 31-36.
Xu Zegang, Xie Shaojun. Inductances analysis and modeling method of flux-switching hybrid excitation machine with magnetic bridge[J]. Small and Special Electrical Machines, 2015, 43(12): 31-36.
[19] Lü Chen, Xing Yang, Zhang Junzhi, et al. Levenberg- marquardt backpropagation training of multilayer neural networks for state estimation of a safety critical cyberphysical system[J]. IEEE Transactions on Industrial Informatics, 2018, 14(8): 3436-3446.
[20] 王捷, 艾红. 基于自适应模糊神经网络的异步电动机SVM-DTC控制[J]. 电气技术, 2017, 18(9): 40-45.
Wang Jie, Ai Hong. SVM-DTC control of induction motor based on adaptive fuzzy neural network[J]. Electrical Technology, 2017, 18(9): 40-45.
[21] 赵希梅, 原浩, 朱文彬. 基于小波神经网络和非线性扰动观测器的直线伺服系统控制[J]. 电工技术学报, 2019, 34(19): 3989-3996.
Zhao Ximei, Yuan Hao, Zhu Wenbin. Control of linear servo system based on wavelet neural network and nonlinear disturbance observer[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 3989-3996.
[22] 张立伟, 张鹏, 刘曰锋, 等. 基于变步长Adaline神经网络的永磁同步电机参数辨识[J]. 电工技术学报, 2018, 33(增刊2): 377-384.
Zhang Liwei, Zhang Peng, Liu Yuefeng, et al. Parameter identification of permanent magnet synchronous motor based on variable step-size adaline neural network[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 377-384.
Modeling Method for Hybrid-Excited Machine and Hardware-in-Loop Real-Time Simulation System with Accounting for Loss Calculation
Abstract Since the loss is rarely considered in the modelling of the hybrid-excited machine, the simulation results have large error compared with the experimental results. Therefore, taking into account iron loss, copper loss and PM loss, this paper proposes a modeling method for the hybrid-excited machine. Based on the model obtained by the neural network, the loss calculation is added in the real-time simulation model of hybrid-excited machine. By establishing the machine and inverter models in dSPACE, the Hardware-in-Loop (HIL) platform was built. A prototype of 12-slot 10-pole hybrid-excited switched flux permanent magnet machine is used to evaluate the accuracy of machine model considering the losses. The results show that compared with the model without the losses, the simulation accuracy of phase current amplitude of the model considering the losses is increased by 5.7% and 12.5% at light load and heavy load, respectively.
keywords：Hybrid-excited machine, neural network, loss model, hardware-in-loop simulation
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.191341
国家自然科学基金（51507045）、天津市自然科学基金（16JCYBJC42100）、河北省自然科学基金（E2018202252）、河北省人社厅（E2016100004）资助项目。
收稿日期2019-10-15
改稿日期 2019-12-22
曹 阳 女，1993年生，博士研究生，研究方向为电机及其控制。E-mail: caoyang_hebut@163.com
刘 旭 男，1984年生，教授，博士生导师，研究方向为电机及其控制。E-mail: liuxu@hebut.edu.cn（通信作者）
（编辑 崔文静）