图1 硅钢片磁特性测试设备
Fig.1 The test insulation for magnetic characteristic of silicon steel sheet
摘要 为研究变频电机在不同温度、不同谐波下的电磁性能及考虑硅钢片磁致伸缩影响的振动特性，该文首先对变频电机铁心硅钢片在不同温度及谐波下的磁性能展开研究，给出硅钢片在不同温度及谐波下的B-H曲线、B-P曲线及磁导率曲线。其次对硅钢片的磁致伸缩特性展开了测试与分析，给出硅钢片的蝴蝶曲线及磁致伸缩单值曲线。基于硅钢片磁特性及磁致伸缩特性的测试结果，对1 140V/75kW变频电机的电磁性能及振动展开仿真分析，在仿真过程中考虑了温度、谐波及磁致伸缩对变频电机铁心硅钢片性能的影响。最后对1 140V/75kW变频电机展开振动实验，为变频电机的电磁-振动分析提供了一个新的思路。
关键词：变频电机 硅钢片 电磁特性 振动 仿真及实验
近年来，交流变频调速系统以其卓越的调速性能、显著的节电效果以及在世界经济各个领域的广泛适用性，在逐步取代直流调速系统的同时，成为最有前景的调速方式之一[1]，但其自身的稳定性问题也不可忽视。在对电机的设计与分析过程中需要考虑多种因素，如电磁设计过程中定子铁心硅钢片的磁化特性、振动及噪声分析过程中定子铁心硅钢片的磁致伸缩特性等。但直到目前为止，以电磁装备制造为主的高校、科研院所以及各大企业在对电磁装置进行设计与研究过程中对于硅钢片特性参数的应用主要集中在采用室温下的磁感应强度曲线及损耗曲线，通常不考虑实际工作温度对电机的影响；同时，在分析电机的振动及噪声时，大都没有考虑硅钢片磁致伸缩对其的影响，这些作用累加起来，将有可能放大电机设计、性能计算与分析时的误差。
目前，国内外学者对电磁装置用硅钢片展开了广泛的研究工作。文献[2]对取向硅钢片在不同温度、谐波条件下的磁性能展开测试分析。文献[3]对取向硅钢片在不同直流偏磁下的磁致伸缩特性展开研究工作。文献[4]针对无取向硅钢片磁致伸缩对应力的敏感性进行研究。文献[5]对PWM供电下的无取向硅钢片的磁致伸缩及振动特性展开研究。文献[6]在理论上研究了取向硅钢片的特性，建立了定量描述磁致伸缩和磁感应强度以及应力之间关系的数学模型，并且得到了磁致伸缩的变化趋势。文献[7]研究了含硅量分别为3.25%～6%取向硅钢的磁特性以及磁致伸缩特性，认为提高硅钢片的含硅量可以使其磁导率提高到磁化曲线的拐点位置，同时降低样片的损耗，其磁致伸缩特性也得到了很大的改善，提高含硅量可以很大程度上抑制磁致伸缩引起的振动。文献[8]研究了冷轧硅钢片直流各向异性磁致伸缩特性，通常认为轧制方向和横向上磁致伸缩特性的差异最大，但研究表明，55°方向和轧制方向之间的磁致伸缩特性差异最大，矫顽力也表现出相同的趋势；同时指出磁致伸缩的各向异性是由样片本身的晶粒结构以及纹理度决定的。文献[9-10]搭建了旋转单片测试系统，并对取向硅钢的磁致伸缩特性进行了研究，结果表明，样片的损耗和磁致伸缩都随着磁感应强度或者磁化方向和轧制方向间的夹角增大而增大。当磁感应强度按椭圆形、菱形变化时，磁致伸缩表现出相似的特性。文献[11]对变压器铁心硅钢片的磁致伸缩在不同退火温度、机械应力等条件下的变化趋势进行了实验研究。具体如下：为了考察退火温度对磁致伸缩应变的影响，实验分别对加工后的取向硅钢片采用不同的退火工艺进行处理，并对取向硅钢片进行了直流磁化，得到磁致伸缩应变与磁感应强度的关系，随着退火温度的增加，磁致伸缩应变逐渐由正值变为负值，且磁致伸缩曲线的单调性发生变化。
针对电机的分析方法主要有经验法、解析法及有限元法。现阶段普遍采用有限元法对电机的电磁-机械等特性展开分析工作[12-20]。文献[12]应用二维有限元法对一台高速永磁同步电动机的磁场展开研究。文献[13-15]采用多物理场有限元法对永磁同步电动机的损耗、温度及应力展开研究。文献[16]分析了永磁同步电动机电磁力波特征参数和各个阶力波的谐波来源，建立了多物理场永磁同步电动机振动及噪声分析模型，但没有考虑磁致伸缩对永磁同步电动机振动及噪声的影响。文献[17]在不考虑逆变器谐波的情况下研究了0阶力波对永磁同步电动机振动的影响。文献[18-21]分析了硅钢片磁致伸缩对电机振动及噪声的影响，但没有综合考虑温度、谐波对电机磁性能及振动特性的影响。
基于此，本文首先对无取向硅钢片在不同温度、谐波、磁致伸缩下的特性展开测试与分析，给出了B-H、B-P及磁致伸缩等数据；其次以不同温度、谐波、磁致伸缩下的特性数据为基础，基于COMSOL有限元分析软件对一台1 140/75kW变频电机的电磁特性、振动特性展开仿真分析；最后对其进行振动实验研究，验证了所提方案的正确性。
变频电机通常工作在温度高、供电质量差、负载工况多变的条件下。而硅钢片生产厂商通常情况下仅给出室温及工频下硅钢片的磁特性数据曲线，与变频电机的实际运行工况不符。因此，研究不同温度、谐波引起的变频电机定子铁心材料的磁特性具有重要意义。
基于此，本文对1 140V/75kW煤矿用变频电机定子铁心硅钢片在不同温度、不同谐波下的电磁特性进行分析，给出了不同温度及谐波条件下的硅钢片磁性能数据。
图1所示为硅钢片磁特性测量装置，该装置主要用于测量各类软磁材料的磁特性，该系统符合IEC（IEC 60404和IEC 60205）和ASTM标准。实验中通过温度控制系统调节硅钢片的工作温度，通过激励电源调节硅钢片的输入波形。通过数据采集系统获得硅钢片的B-H数据、B-P数据及磁导率数据。
图1 硅钢片磁特性测试设备
Fig.1 The test insulation for magnetic characteristic of silicon steel sheet
图2所示为硅钢片磁特性测量装置的剖面图，实验采用单片测量原理测量硅钢片在不同温度及谐波条件下的磁性能。样片被放置在线圈骨架的中央，并与铁轭构成闭合磁路，铁轭由硅钢片叠积而成。为了使施加在样件上的磁场均匀分布，样件与铁轭之间应有足够的接触面积。其中，B线圈表示磁感应强度测量线圈，H线圈表示磁场强度测量线圈；B线圈和励磁线圈分内外两层均匀缠绕在线圈骨架上。H线圈均匀缠绕在由非导磁绝缘材料制成的板形支架上，并尽可能地与样件靠近。
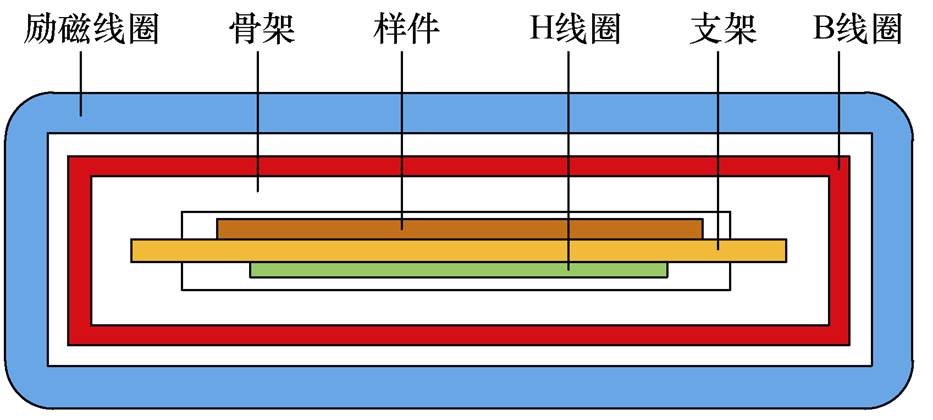
图2 单片测量装置剖面图
Fig.2 Single sheet tester section plan
进一步分析，硅钢片磁特性测试系统数据采集部分通过励磁线圈、H线圈、B线圈采集到的电压转换为磁场强度，有
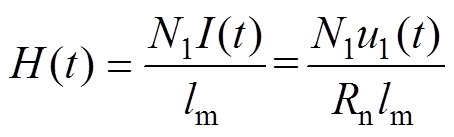（1）同时，通过采集到的B线圈电压求取磁感应强度，有
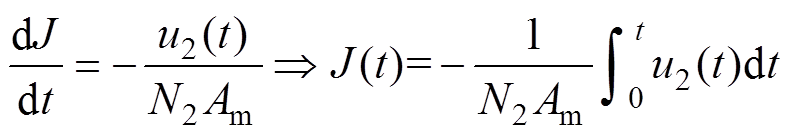（2）
式中，H(t)为磁场强度；N1为初级绕组的数量；I(t)为初级电流；lm为磁路长度；u1(t)为一次电压；Rn为等效电阻；u2(t)为二次电压；N2为次级绕组的数量；Am为等效面积；J(t)为磁感应强度。
单片硅钢片测量装置的性能参数见表1。
表1 单片硅钢片测量装置的性能参数
Tab.1 Performance parameters of single-piece silicon steel sheet measuring device
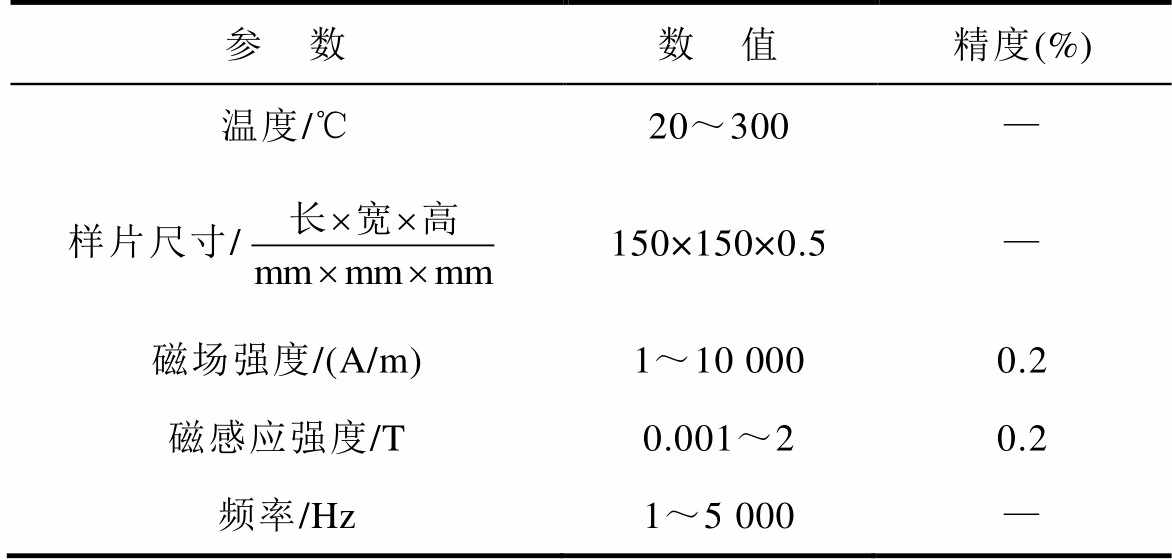
参 数数 值精度(%) 温度/℃20～300— 样片尺寸/150×150×0.5— 磁场强度/(A/m)1～10 0000.2 磁感应强度/T0.001～20.2 频率/Hz1～5 000—
1.2.1 不同温度无取向硅钢片磁特性测试与分析
图3所示为无取向硅钢片在不同温度下的B-H曲线、B-P曲线及磁导率曲线。
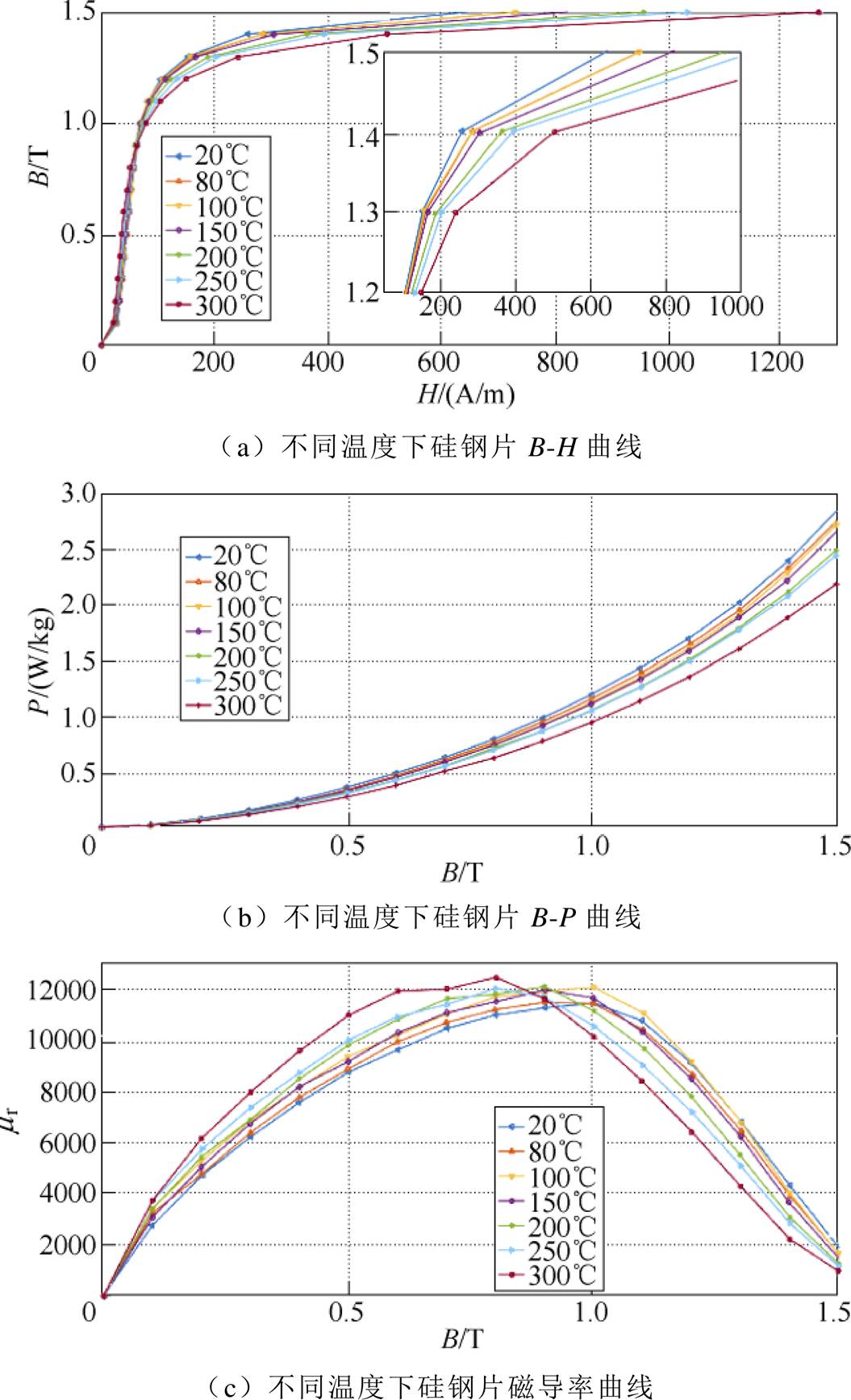
图3 不同温度下硅钢片B-H曲线、B-P曲线及磁导率曲线
Fig.3 B-H curves, B-P curves and magnetic permeability curves of silicon steel sheets at different temperatures
从图3a中可以看出，随着温度的升高，无取向硅钢片工作点向右偏移，饱和磁感应强度下降；从图3b中可以看出，随着温度的升高，同一个磁感应强度下硅钢片的损耗下降；从图3c中可以看出，随着温度的升高，硅钢片磁导率升高。
图3的结果说明，温度升高使硅钢片的磁畴变化活跃程度提高，其磁滞特性下降，进而使磁感应强度下降，损耗下降，磁导率增强。表明温度对硅钢片的磁性能具有一定的影响，在应用硅钢片进行电磁产品设计时，应考虑工作温度的影响。
1.2.2 不同谐波下无取向硅钢片磁特性测试与分析
图4所示为硅钢片在不同谐波下的B-H曲线、B-P曲线及磁导率曲线。
从图4a中可以看出，随着频率的升高，硅钢片磁感应强度工作点向右偏移，饱和磁感应强度下降；从图4b中可以看出，随着频率的升高，硅钢片损耗增加；从图4c中可以看出，随着频率的升高，硅钢片磁导率下降，说明在非工频状态下，频率越高，硅钢片的磁性能越差。
图4 不同谐波下硅钢片B-H曲线、B-P曲线及磁导率曲线
Fig.4 B-H curves, B-P curves and magnetic permeability curves of silicon steel sheets under different harmonics
在磁场的作用下，硅钢片不仅电磁特性会发生变化，还会出现周期性的伸张和收缩现象（硅钢片的磁致伸缩效应）。硅钢片的伸张和收缩，将引起电磁装置的振动和噪声。基于此，本文对无取向硅钢片的磁致伸缩特性进行测试与分析。图5所示为硅钢片磁致伸缩测量装置，硅钢片磁致伸缩测量装置性能参数[15]见表2。
图5 硅钢片磁致伸缩测量装置
Fig.5 Silicon steel sheet magnetostrictive measuring device
表2 硅钢片磁致伸缩测量装置性能参数
Tab.2 Silicon steel sheet magnetostrictive measuring device performance parameters
项 目参 数 硅钢片型号DW315-50 交流励磁参数50Hz, Bpeak=0.5～1.7T
图6所示为硅钢片B-H磁滞回线族，图7所示为硅钢片磁致伸缩蝴蝶曲线，其中，图6、图7显示的数值从内向外磁感应强度依次增大，图8所示为硅钢片磁致伸缩单值曲线。
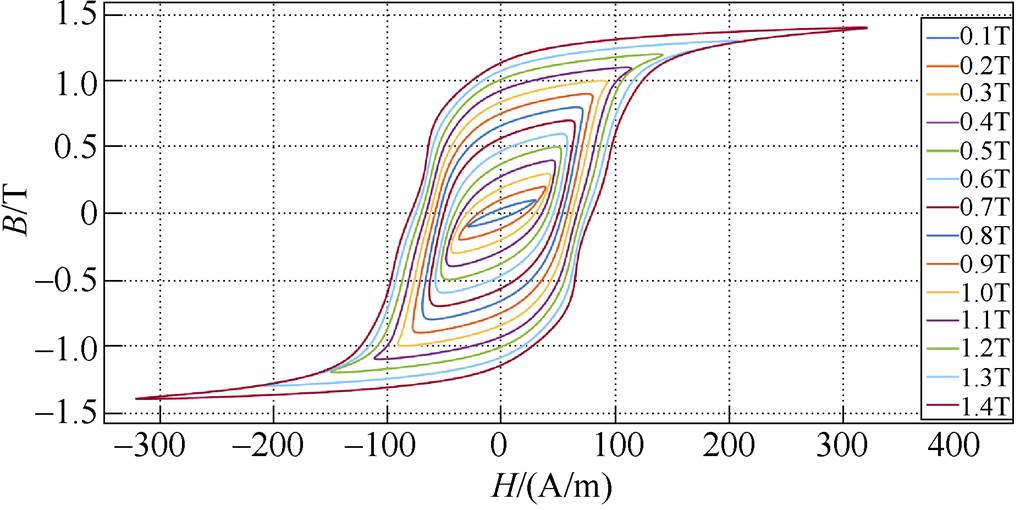
图6 硅钢片B-H磁滞回线族
Fig.6 Silicon steel sheet B-H hysteresis loop family
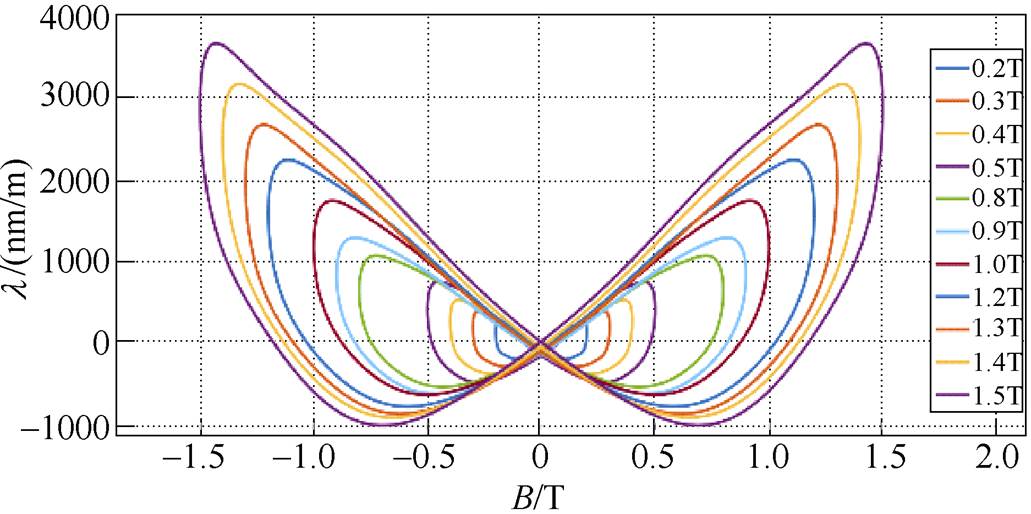
图7 硅钢片磁致伸缩蝴蝶曲线
Fig.7 Siliconsteel sheet magnetostrictive butterfly curves
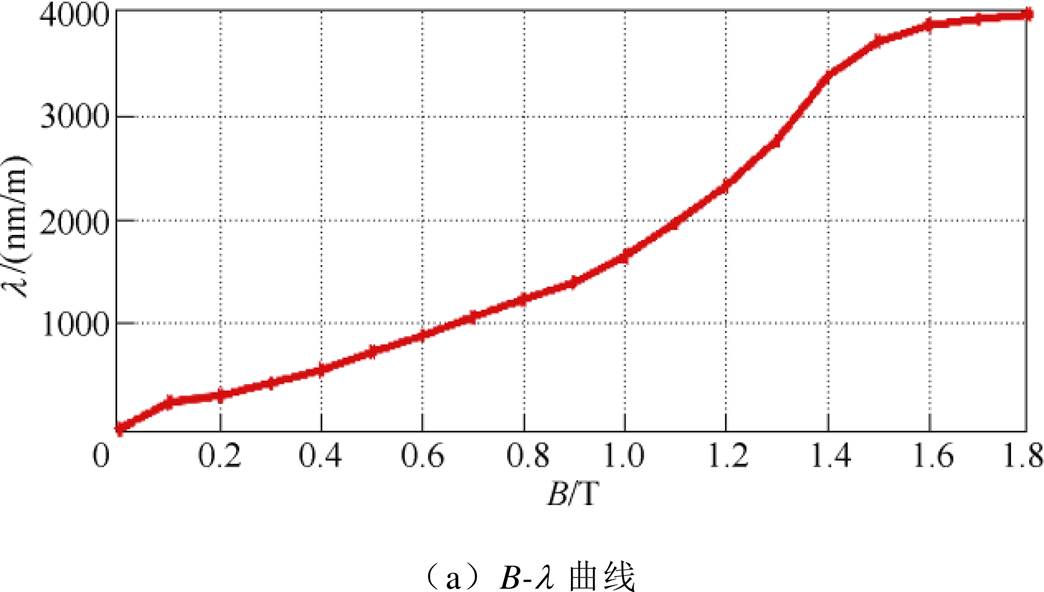
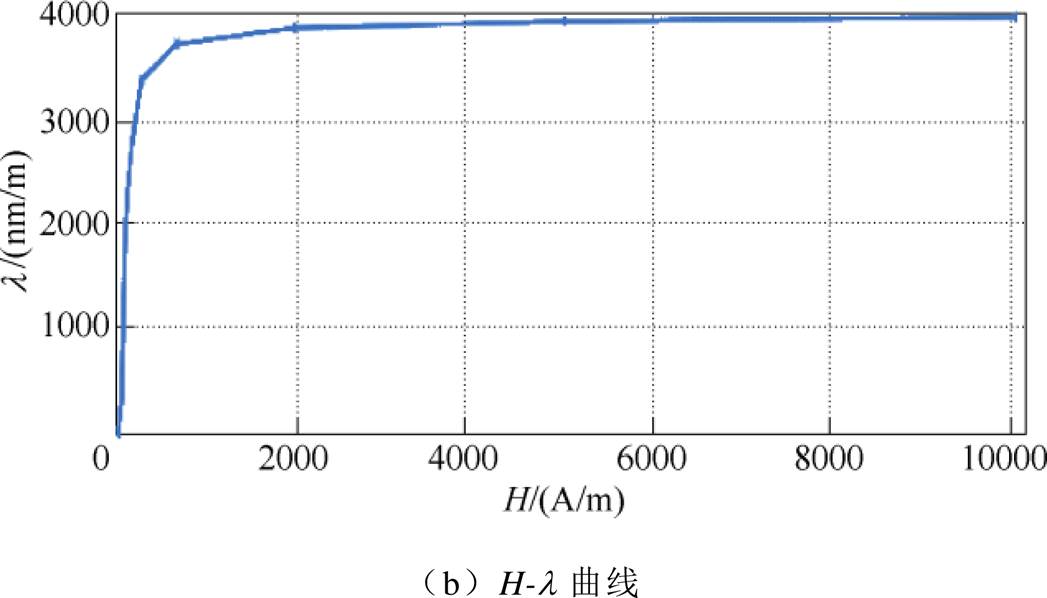
图8 硅钢片磁致伸缩单值曲线
Fig.8 Siliconsteel sheet magnetostrictive single value curves
从图7中可以看出，随着磁感应强度的增加，磁致伸缩蝴蝶曲线面积增加，表明随着磁感应强度的增加，硅钢片的振动加剧。从图8中可以看出，当达到饱和时，硅钢片磁致伸缩量稳定在4 000nm/m。
基于COMSOL有限元软件对1 140V/75kW变频电机在不同温度、不同谐波及考虑磁致伸缩特性下的电磁-振动特性展开仿真分析，变频电机基本参数见表3。
图9所示为变频电机电磁-振动有限元分析的流程。首先建立变频电机有限元模型；其次分别将不同温度、不同谐波及磁致伸缩单值曲线代入到有限元模型中，对变频电机的磁感应强度、振动等进行仿真与分析；最后将仿真与实验进行对比分析。
表3 变频电机基本参数
Tab.3 Variable frequency motor basic parameters
参 数数 值 额定功率/kW75 额定电压/V1 140 额定电流/A48.32 极对数2 额定转速/(r/min)1 478
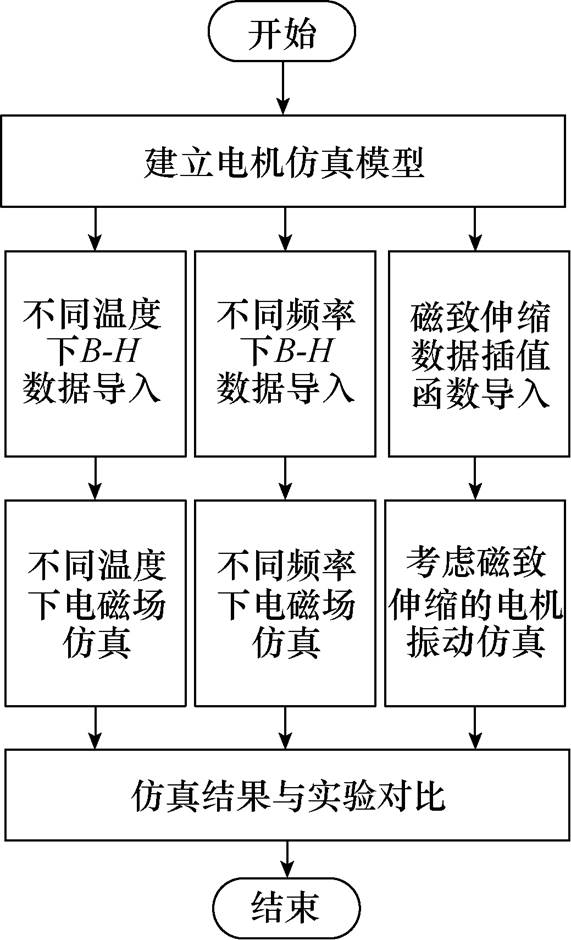
图9 有限元分析流程
Fig.9 Finite element analysis flowchart
按照图9所示的有限元分析流程，对不同温度及谐波下的变频电机电磁特性展开仿真分析，图10所示为不同温度下变频电机磁感应强度分布。图11所示为不同谐波下变频电机磁感应强度分布。
从图10中可以看出，随着硅钢片测试温度的增加，电机内部磁感应强度在一定程度上降低，而在电机设计与性能研究过程中，一般使用室温下测量得到的磁感应强度数据，因此在进行电机分析与设计时应该考虑硅钢片测试温度对电机性能的影响。
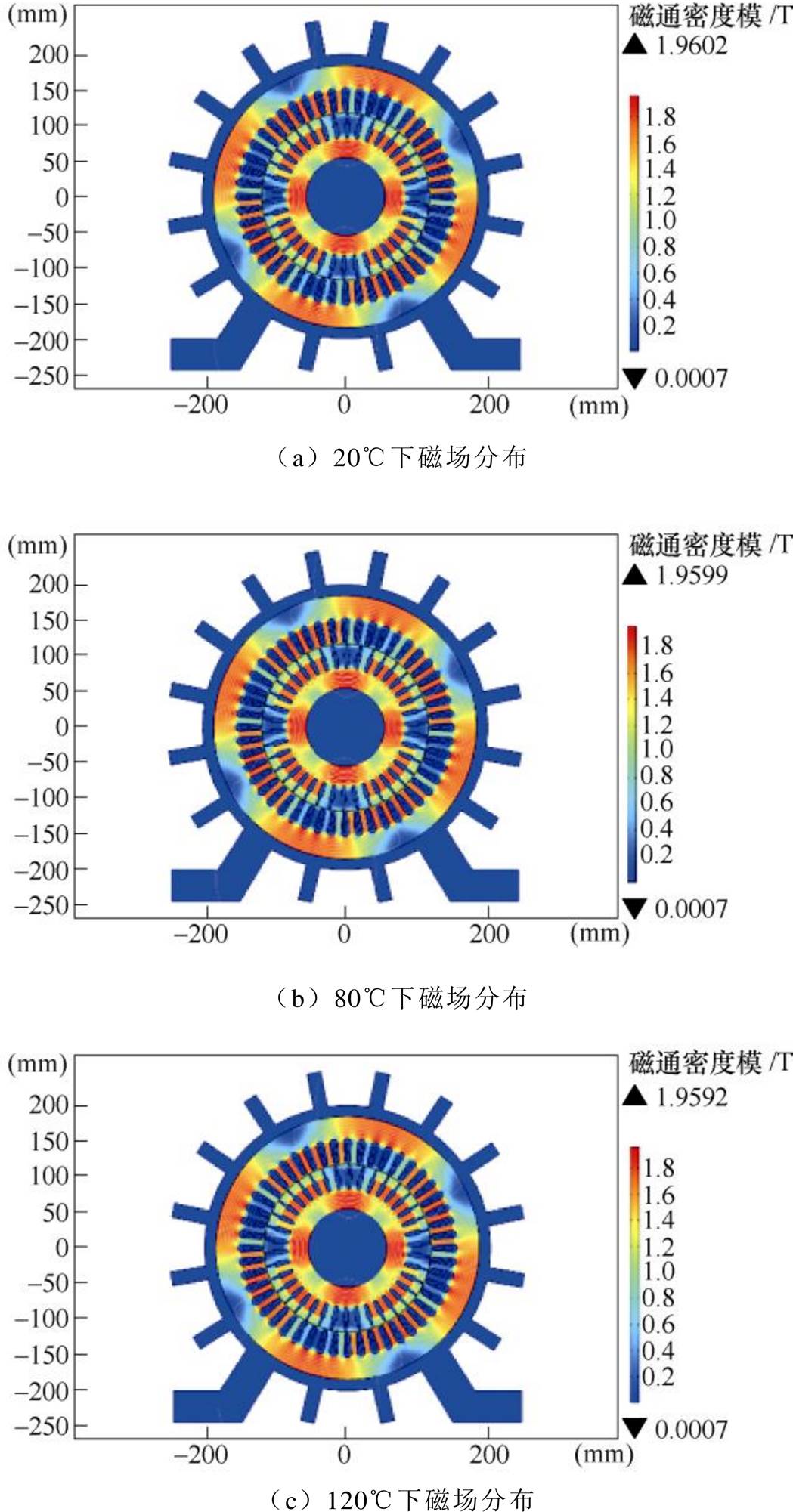
图10 不同温度下电机磁场分布
Fig.10 Magnetic field distribution of motor at different temperatures
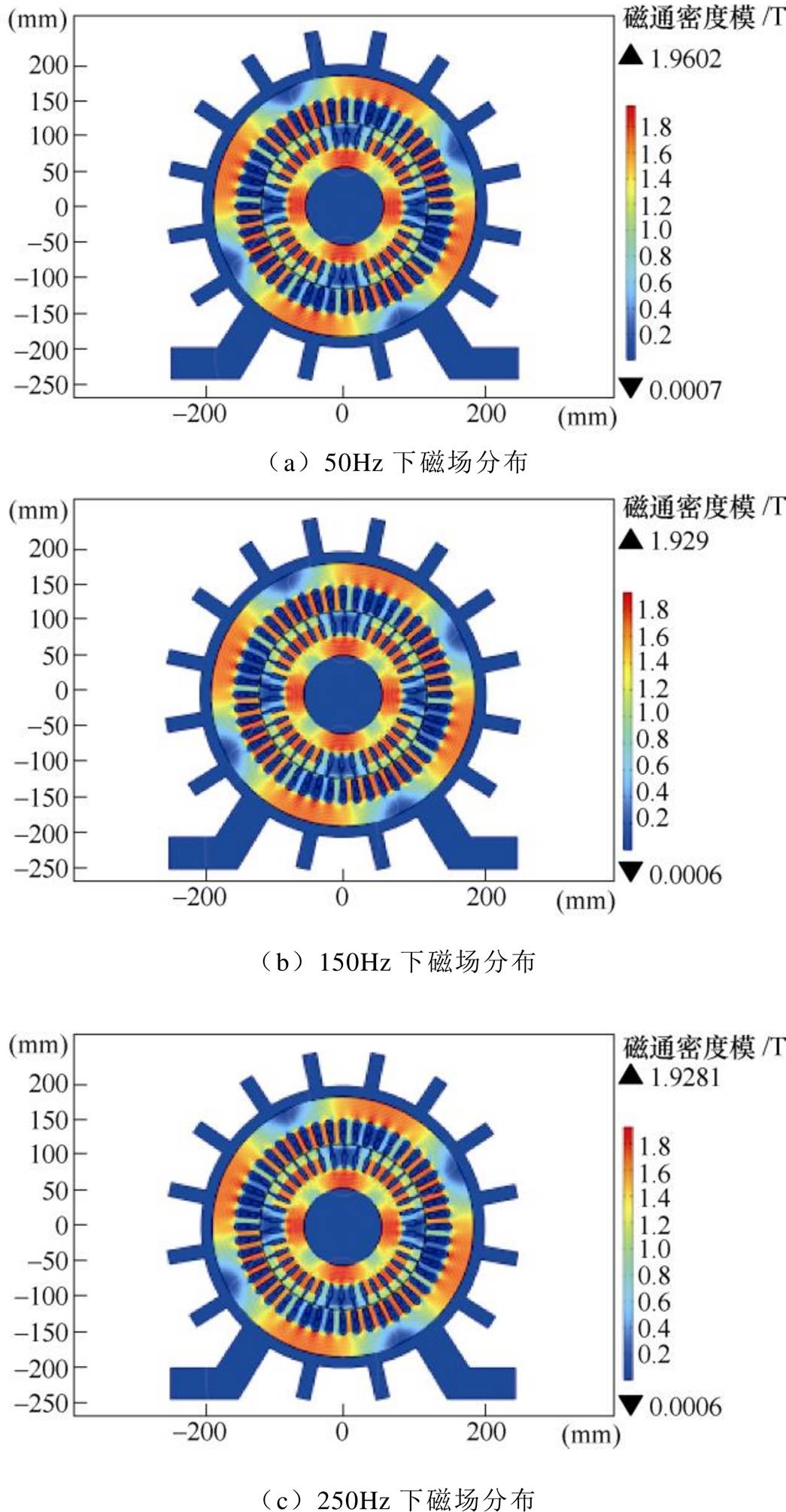
图11 不同谐波下电机磁场分布
Fig.11 Magnetic field distribution of motor at different frequencies
从图11中可以看出，随着硅钢片测试频率的增加，电机内部磁感应强度下降，将导致电机的损耗、温度等参数发生变化，尤其是在变频供电下的电机性能变化更明显。
为了研究硅钢片磁致伸缩对变频电机振动的影响，基于COMSOL有限元分析软件，建立了考虑硅钢片磁致伸缩影响的电机振动有限元分析模型，图12所示为1 140V/75kW变频电机振动计算流程。图13所示为考虑磁致伸缩影响的变频电机应力场分布，图14所示为考虑磁致伸缩影响的变频电机振动形变。
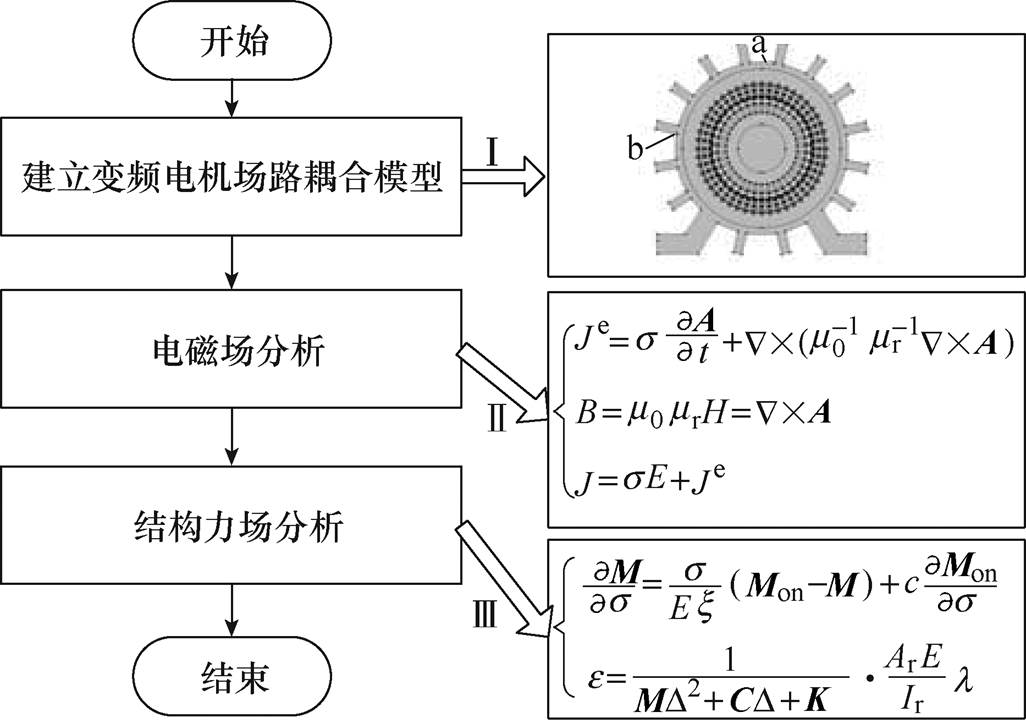
图12 变频电机振动计算流程
Fig.12 Calculation process of the vibration for variable frequency motor
图12中，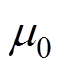
为真空磁导率；
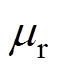为相对磁导率；A为矢量磁位；J为电流密度；E为电场强度；M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；x 为阻尼比；D 为位移对时间的偏导；l 为形变量；s 为应力；e 为应变；Ir为能量泛函。
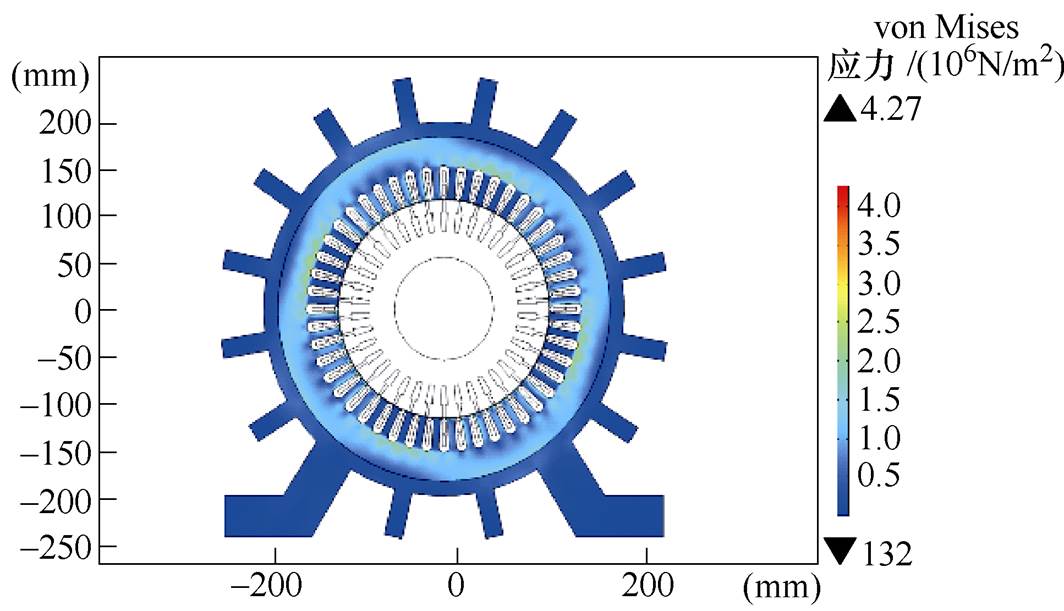
图13 电机应力场分布
Fig.13 Motor stress field distribution
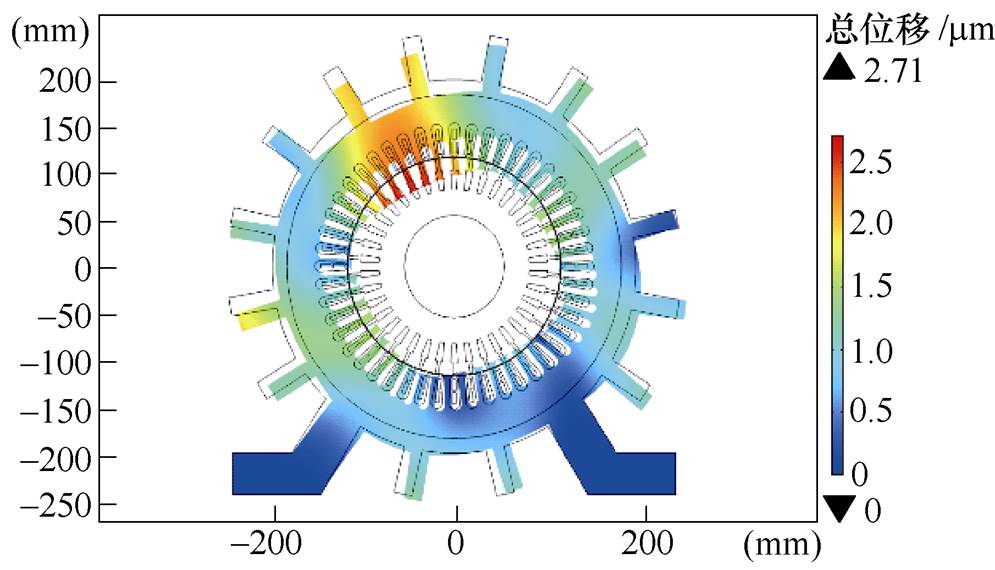
图14 考虑磁致伸缩的电机振动形变
Fig.14 Vibration distortion of a motor considering magnetostriction
从图13中可以看出，变频电机绕组槽底部所受应力最大，最大应力处可达到4.27×106N/m2。从图14中可以看出，考虑磁致伸缩影响时，最大位移量为2.71mm。
图15所示为选取变频电机两个测点（见图12）的振动位移曲线。从图15中可以看出，a点振动位移在(-2～2)mm之间；b点振动位移在(-0.4～2.2)mm 之间。
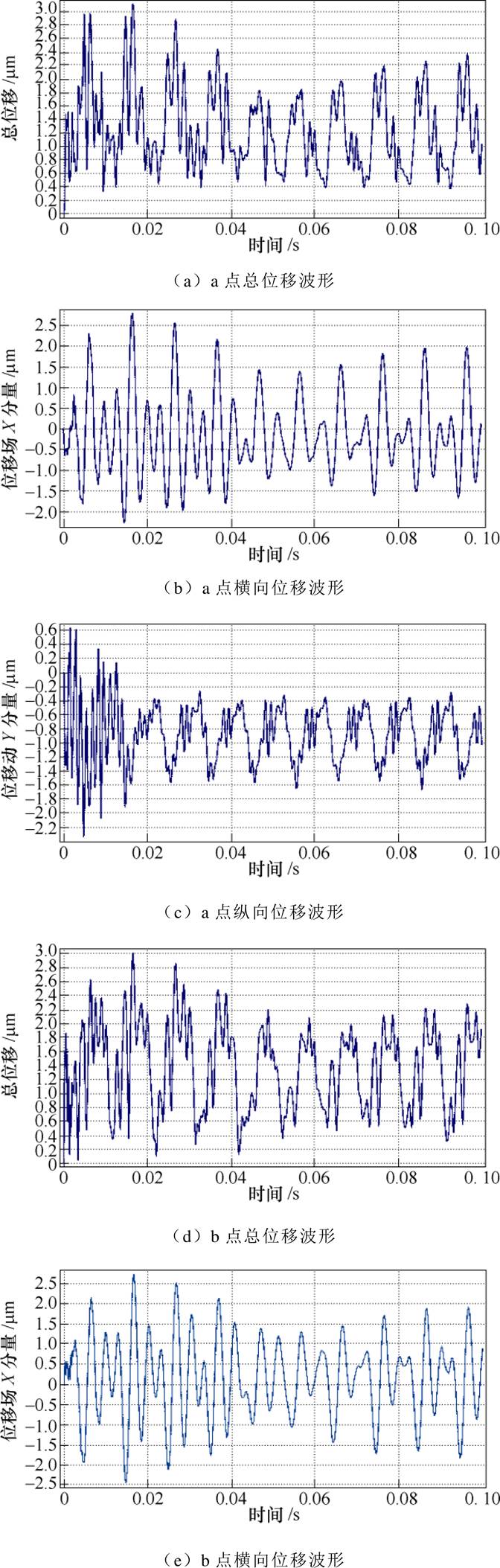
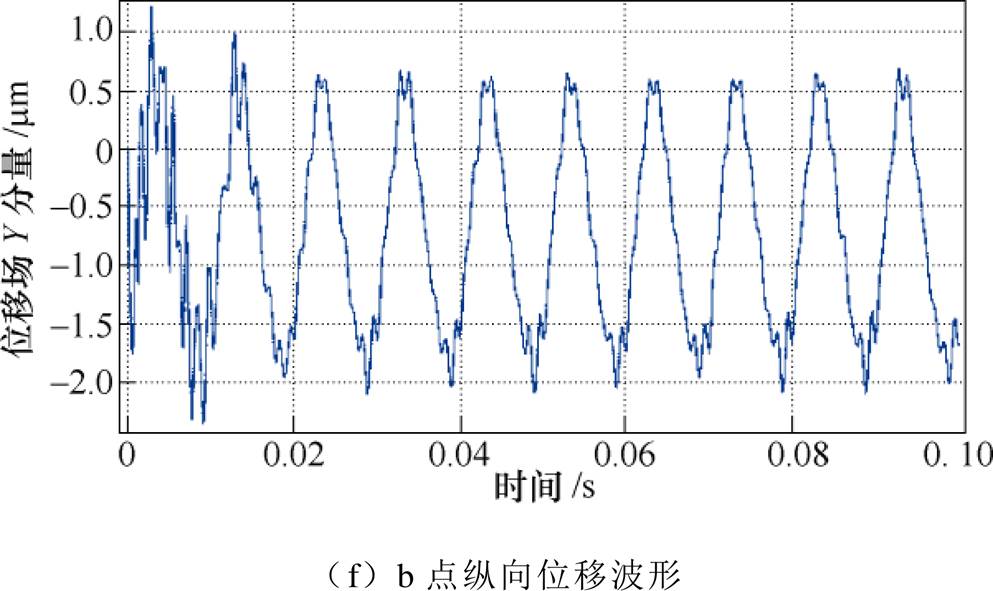
图15 变频电机振动位移波形曲线
Fig.15 Variable frequency motor vibration displacement curves
考虑磁致伸缩影响前后的a点与b点振动位移对比见表4。
表4 振动位移对比
Tab.4 Comparison of vibration displacement
项目a点振动位移/mmb点振动位移/mm 考虑磁致伸缩-2～2-0.4～2.2 未考虑磁致伸缩-1.4～1.7-0.2～1.8
从表4中可以看出，无论是a点还是b点，考虑磁致伸缩影响下，变频电机的振动位移要比未考虑磁致伸缩影响的振动位移大。
为验证本文所提方案的正确性，对1 140V/75kW变频电机的振动展开了实验研究，图16所示为变频电机实验系统。
图16 变频电机实验系统
Fig.16 Experimental system of variable frequency motor
如图16a所示，测试平台主要包括变频电机、负载、检测与控制系统、变频器、负载等。图16b所示为变频电机振动测试点，a点在距离电机轴侧的端部，b点集中在电机中间部位。图16c所示为变频电机振动测试仪器，主机采用HBM公司MX410B，振动加速度传感器采用BK公司4525-B。
图17所示为变频电机5Hz下a、b点振动加速度及位移曲线。图18所示为变频电机25Hz下a、b点振动加速度及位移曲线。图19所示为变频电机50Hz下a、b点振动加速度及位移曲线。
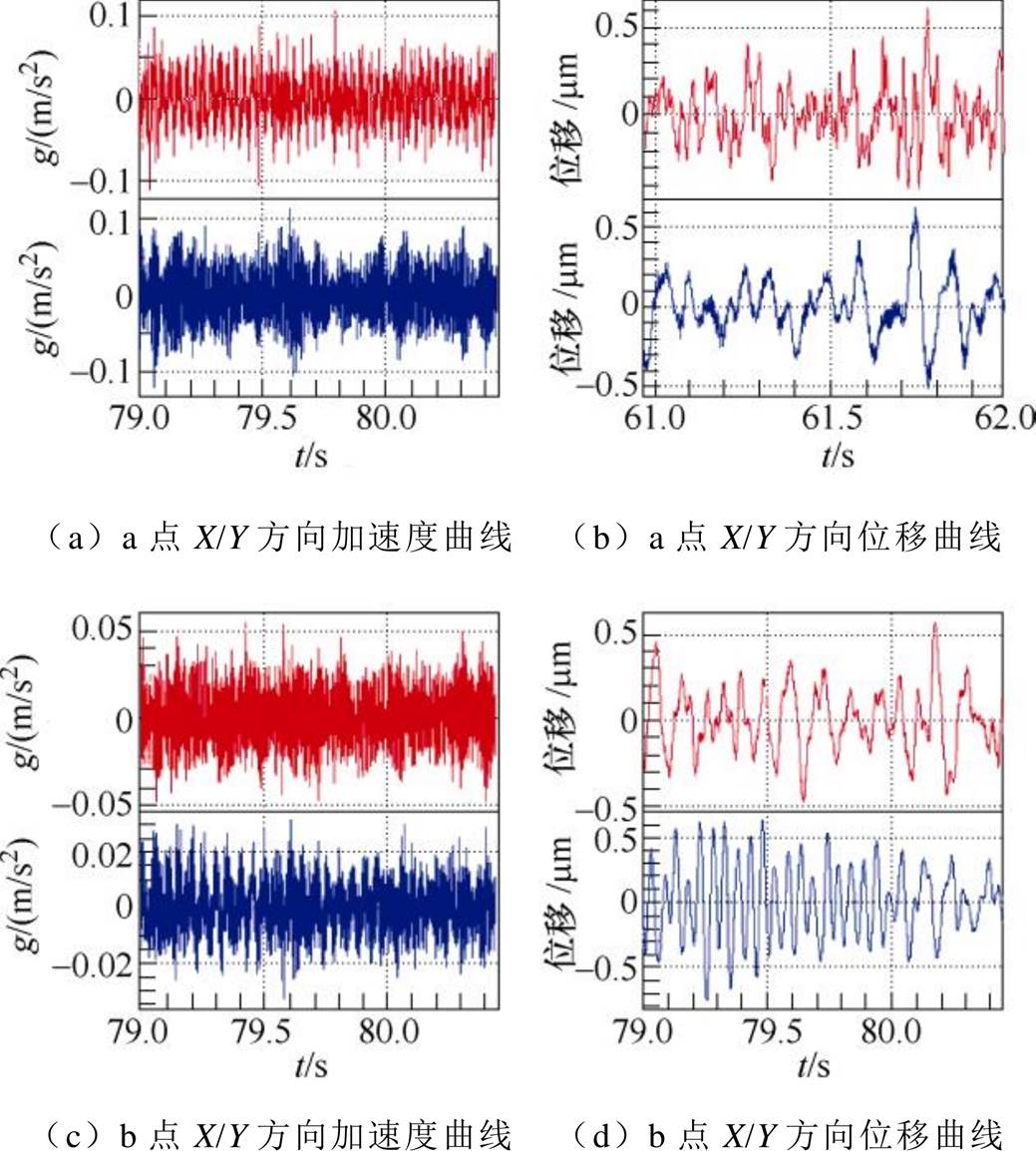
图17 5Hz下a、b点振动加速度及位移曲线
Fig.17 Vibration acceleration and displacement curves of points a and b at 5Hz
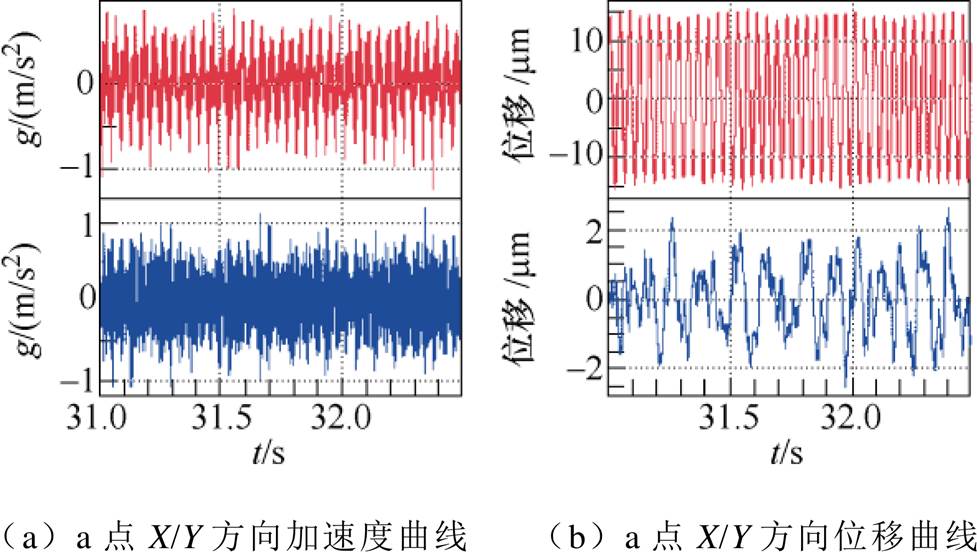
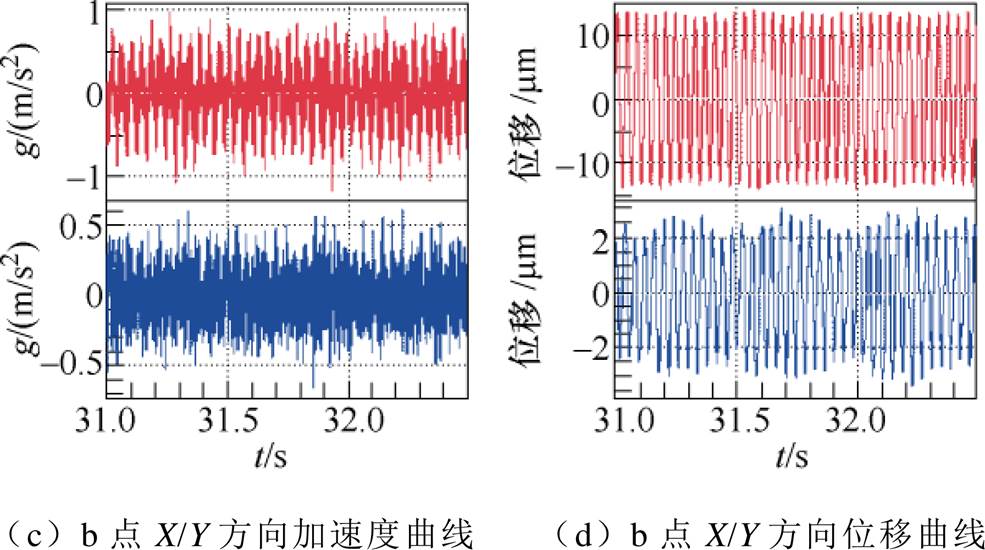
图18 25Hz下a、b点振动加速度及位移曲线
Fig.18 Vibration acceleration and displacement curves of points a and b at 25Hz
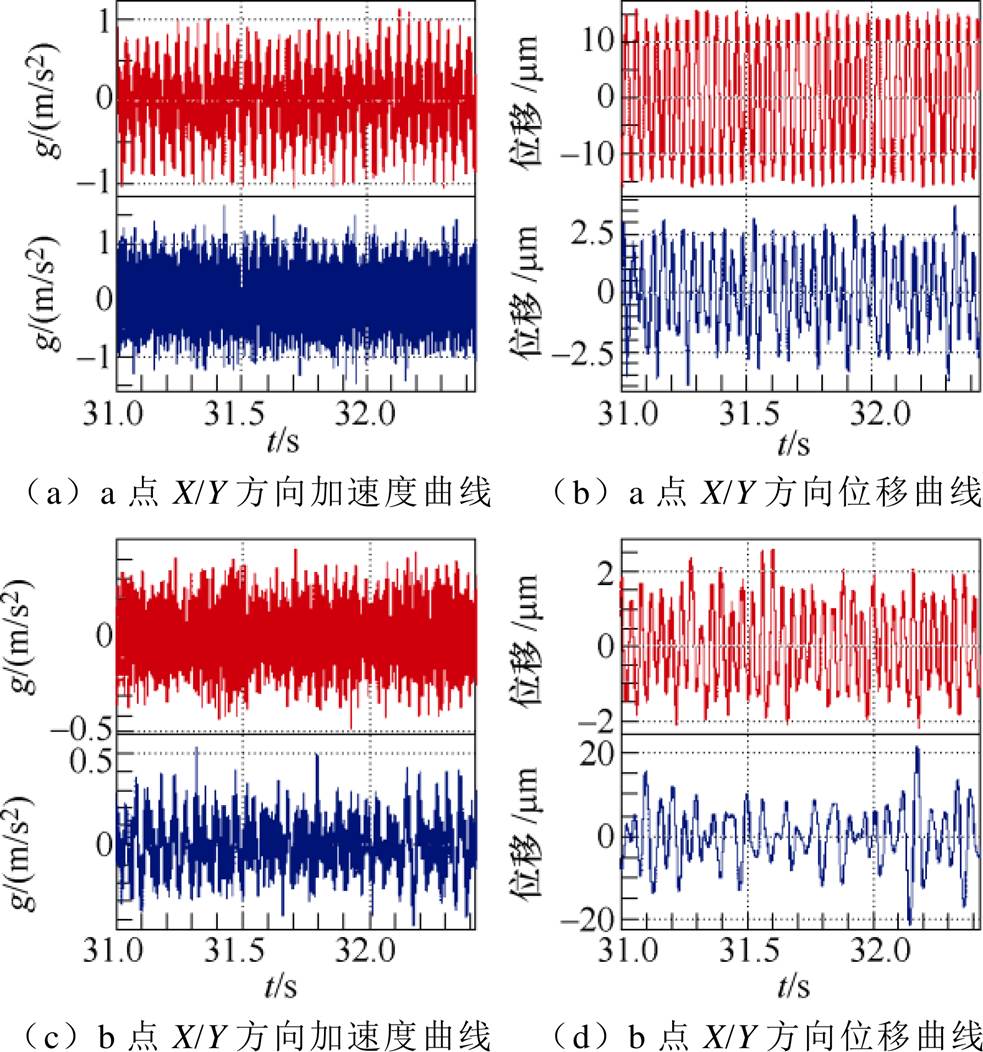
图19 50Hz下a点、b点振动加速度及位移曲线
Fig.19 Vibration acceleration and displacement curves of points a and b at 50Hz
从图17～图19中可以看出，测量得到的变频电机振动位移数据与仿真得到的振动位移曲线误差在一个数量级上，趋势保持一致，可以定性分析变频电机的振动趋势。分析误差原因：①仿真过程中变频电机为理想模型，而实验中变频电机为底部约束，且通过柔性联轴器与陪试电机连接，增加了误差；②测量仪器存在测量误差。
本文针对1 140V/75kW变频电机的电磁特性及振动特性展开的分析与研究，得到如下结论：
1）测量了不同温度下无取向硅钢片的磁性能，测试结果表明：在磁感应强度1.4T下，20℃时磁场强度为270A/m，80℃时磁场强度为300A/m，300℃时磁场强度为500A/m；20℃时相对磁导率为2 000，80℃时磁导率为1 800，300℃时相对磁导率为1 500；在磁感应强度1.5T下，20℃时单位铁损为2.7W/kg，80℃时单位铁损为2.5W/kg，300℃时单位铁损为2.2W/kg。说明温度对无取向硅钢片的磁性能有一定的影响，在分析与设计电磁装置的过程中，应该考虑温度的影响。
2）测量了不同谐波下的无取向硅钢片的磁性能，测试结果表明，随着频率的升高，磁感应强度的拐点向右偏移。
3）利用不同温度及谐波下的无取向硅钢片的磁性能数据，对变频电机进行了电磁特性仿真，利用20℃时测得的硅钢片磁特性曲线与120℃时测得的硅钢片磁特性曲线变频电机的磁感应强度相差0.001T。利用50Hz时测得的硅钢片磁特性曲线与250Hz测得的硅钢片磁特性曲线变频电机的磁感应强度相差0.032 1T。
4）利用测量得到的无取向硅钢片单值磁致伸缩曲线，对变频电机进行了振动仿真，考虑磁致伸缩影响下变频电机的振动位移要比未考虑磁致伸缩影响的振动位移大，其中a点大0.3mm，b点大0.4mm。
5）搭建了1 140V/75kW变频电机在变频供电下的振动实验平台，并进行了振动实验研究。实验结果表明，振动位移的仿真及实验在一个数量级内，其理论分析可以指导电机的分析与设计。
参考文献
[1] 白保东, 陈德志, 王鑫博. 逆变器IGBT损耗计算及冷却装置设计[J]. 电工技术学报, 2013, 28(8): 97-106.
Bai Baodong, Chen Dezhi, Wang Xinbo. IGBT loss calculation and cooling device design of inverters[J]. Journal of Electrical Technology, 2013, 28(8): 97-106.
[2] Chen Dezhi, Fang Liwei, Kwon B I, et al. Measure- ment research on magnetic properties of electrical sheet steel under different temperature, harmonic and DC bias[J]. AIP Advances, 2017, 7(5): 056682.
[3] Chen Dezhi, Feng Zhiyu, Wang Qingpeng, et al. Study of analysis and experiment for ability to withstand DC bias in power transformers[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-5.
[4] Anderson P I，Moses A J，Stanbury H J. Assessment of the stress sensitivity of magnetostriction in grain- oriented silicon steel[J]. IEEE Transactions on Magnetics, 2007, 43(8): 3467-3476.
[5] Somkun S, Moses A J, Anderson P I. Mechanical resonance in nonoriented electrical steels induced by magnetostriction under PWM voltage excitation[J]. IEEE Transactions on Magnetics, 2008, 44(11): 4062- 4065.
[6] Allia P, Ferro-Milone A, Montalenti G, et al. Theory of negative magnetostriction in grainoriented 3% SiFe for various inductions and applied stresses magnetics[J]. IEEE Transactions on Magnetics, 1978, 14(5): 362-364.
[7] Houze G L, Ames S L, Bitler W R. The effect of magnetic annealing on the properties and domain structure of oriented Si steel containing 3.25-6 percent Si[J]. IEEE Transactions on Magnetics, 1970, 6(3): 708-711.
[8] Marian S. Anisotropy of DC magnetostriction in cold-rolled electrical sheets of goss texture[J]. IEEE Transactions on Magnetics, 1989, 25(4): 3166-3168.
[9] Shilyashki G, Pfützner H, Ange J, et al. Magneto- striction of transformer core steel considering rotational magnetization[J]. IEEE Transactions on Magnetics, 2014, 50(1): 8400115.
[10] Masayuki Y, Daisuke W, Masato E. Vector magnetic properties and 2-D magnetostriction of variouse- lectrical steel sheets under rotating flux condition[J]. IEEE Transactions on Magnetics, 2014, 50(4): 6100404.
[11] Foster S L, Reiplinger E. Characteristics and control of transformer sound[J]. IEEE Transactions on Power Apparatus and Systems, 1981, 100(3): 1072-1077.
[12] 佟文明, 王云学, 贾建国, 等. 变频器供电内置式永磁同步电机转子损耗计算与试验[J]. 电工技术学报, 2018, 33(24): 177-186.
Tong Wenming, Wang Yunxue, Jia Jianguo, et al. Calculation and test of rotor loss of built-in permanent magnet synchronous motor powered by inverter[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 177-186.
[13] Ko H S, Kim K J. Characterization of noise and vibration sources in interior permanent-magnet brushless DC motors[J]. IEEE Transactions on Magnetics, 2004, 40(6): 3482-3489.
[14] Islam R, Husain I. Analytical model for predicting noise and vibration in permanent-magnet synchronous motors[J]. IEEE Transactions on Industry Appli- cations, 2011, 46(6): 2346-2354.
[15] Zuo Shuguang, Fu Lin, Wu Xudong. Noise analysis, calculation and reduction of external rotor permanent magnet synchronous motor[J]. IEEE Transactions on Industrial Electronics, 2015, 62(10): 6204-6212.
[16] 赵文峰, 赵博, 徐永向. 磁场干涉对永磁电机电磁力特性影响研究[J]. 电机与控制学报, 2018, 22(2): 33-40.
Zhao Wenfeng, Zhao Bo, Xu Yongxiang. Research of permanent magnet motors cogging force affected by interferential magnetic field[J]. Electric Machines and Control, 2018, 22(2): 33-40.
[17] Boesing, Doncker D. Exploring a vibration synthesis process for the acoustic characterization of electric drives[J]. IEEE Transactions on Industry Applications, 2012, 48(1): 70-78.
[18] 张鹏宁, 李琳, 聂京凯, 等. 考虑铁心磁致伸缩与绕组受力的高压并联电抗器振动研究[J]. 电工技术学报, 2018, 33(13): 3130-3139.
Zhang Pengning, Li Lin, Nie Jingkai, et al. Study on the vibration of high voltage shunt reactor con- sidering of magnetostriction and winding force[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 3130-3139.
[19] 朱健, 曹君慈, 刘瑞芳, 等. 电动汽车用永磁同步电机铁心采用非晶合金与硅钢的性能比较[J]. 电工技术学报, 2018, 33(增刊2): 102-108.
Zhu Jian, Cao Junci, Liu Ruifang, et al. Performance comparison of amorphous alloy and silicon steel used in permanent magnetic synchronous motor core of electric vehicle[J]. Transactions of China Electro- technical Society, 2018, 33(S2): 102-108.
[20] Zhang Wenjuan, Gao Jian, Dai Litao, et al. Analysis of magnetic field and torque for all-harmonic-torque motor with surface-mounted permanent magnets[J]. CES Transactions on Electrical Machines and Systems, 2018, 2(1), 175-180.
[21] 吴胜男, 于慎波，佟文明，等. 磁致伸缩引起的径向磁通电机定子铁心振动精确解析模型[J]. 电工技术学报, 2019, 34(2): 28-37.
Wu Shengnan, Yu Shenbo, Tong Wenming, et al. Accurate analytical model of stator core vibration of radial flux motor caused by magnetostriction[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 28-37.
Electromagnetic-Forceand Vibrationof Silicon Steel Sheetand Variable Frequency Motor under Different Temperature and Harmonic
Abstract In order to study the electromagnetic properties of the variable frequency motor at different temperatures and harmonics as well as the vibration characteristics considering the magnetostriction effect of silicon steel sheet, the magnetic properties of the silicon steel sheet in the core of the variable frequency motor at different temperatures and harmonics are first studied. The B-H curve, B-P curve and permeability curve of the silicon steel sheet are given. Secondly, the magnetostrictive characteristics of the silicon steel sheet are tested and analyzed to obtain the butterfly curve and the magnetostrictive single value curve. Based on the above test results, the electromagnetic performance and vibration of 1 140V/75kW variable frequency motor are simulated. The influence of temperature, harmonics and magnetostriction on the performance of silicon steel sheet isconsidered in the simulation process. Finally, avibration experiment of 1 140V/75kW variable frequency motor is carried out, which provides a new idea for electromagnetic-vibration analysis of the variable frequency motor.
keywords：Variable frequency motor, electrical steel sheet, electromagnetic characteristics, vibration, simulation and experiment
中图分类号：TM343
DOI: 10.19595/j.cnki.1000-6753.tces.191228
辽宁省科技厅（220180550037）和辽宁省教育厅（LFGD2019002）资助项目。
收稿日期 2019-09-25
改稿日期 2020-04-18
陈德志 男，1982年生，副教授，博士生导师，研究方向为特种电机及其控制系统、变压器、电抗器设计与分析等。E-mail: chendezhi@sut.edu.cn（通信作者）
张玉庸 1995年生，硕士研究生，研究方向为特种电机及其控制系统。E-mail: zyy1136737582@163.com
（编辑 崔文静）