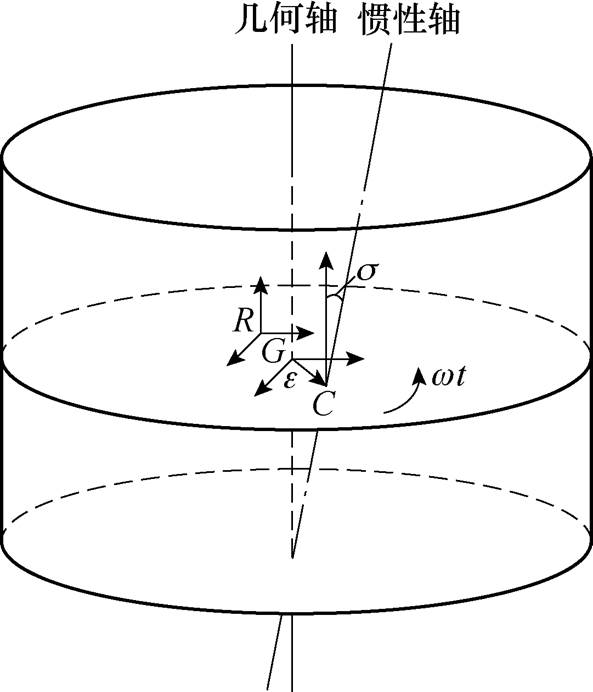
图1 刚性转子几何轴与惯性轴空间示意图
Fig.1 Spatial schematic diagram of geometric axis and inertia axis of rigid rotor
摘要 该文提出一种基于扩张状态观测器的磁悬浮轴承支承刚性转子的现场动平衡方法。根据磁悬浮转子的运动方程,设计扩张状态观测器,由对象系统的输入输出信息即可估算旋转时系统所受的扰动力,并给出离散状态下观测器的收敛条件。为了去除系统倍频扰动和噪声信号对估测结果的影响,设计开关电容滤波器,用于提取扰动中的转速同频分量。针对系统中存在的误差,采用系数矩阵迭代优化方法克服开环观测的不足以提高动平衡精度。该方法在实际使用中仅需试重一次即可得到优化系数矩阵,再经过两次配重,转子不平衡质量显著降低。在机组长期运行时,该方法可部署于微处理器中,实时监测转子不平衡量,起到预警、指导动平衡的作用。
关键词:磁悬浮轴承 现场动平衡 刚性转子 扩张状态观测器
磁悬浮轴承因无接触、无摩擦、无需润滑等特点,在透平机械、分子泵、飞轮储能等高速场合得到了广泛的应用[1-3]。在高速旋转机械中,转子质量不平衡是80%以上的系统振动的来源[4]。过大的系统振动会导致转子悬浮精度差,功放长期工作在饱和区,同时振动还会传递至机壳。若机组长期工作在振动情况严重的场合,出现机械故障的概率将大幅提高[5]。
目前磁悬浮转子的振动抑制有两个实现思路:
(1)主动振动控制。其基本原则是尽可能使得转子绕惯性轴而非几何轴旋转,以消除不平衡质量旋转时产生的扰动力对转子运动带来的影响。对此,国内外专家学者进行了大量的探索和研究[6-8],并在工程领域进行了广泛的应用。但主动控制方法有以下几点不足:①系统长期运行时,主动振动控制无法兼顾高悬浮精度与低振动力;②主动振动控制需要将振动抑制算法嵌入至闭环控制系统,可能对系统闭环稳定性产生影响。
(2)转子动平衡。动平衡分为离线动平衡和现场动平衡两种。无论是离线或现场动平衡,基本思路都是通过物理去重或者增重,使得转子的惯性轴和几何轴尽可能重合。相比于离线动平衡,现场动平衡又有如下优势:①无需拆机,采用磁悬浮轴承的系统中,机械结构一般较为复杂,拆装一次代价高昂;②相比于离线动平衡方法需要在动平衡机上实现,进行现场动平衡时,转子运行于实际的支承状态,有更好的动平衡效果;③成本低,无需相关配套仪器设备,磁轴承自身即具备传感器系统与动平衡算法实现条件。
传统现场动平衡方法主要有影响系数法[9-10]、模态平衡法[11]等。但这些方法想要达到理想效果往往需要反复试重,动平衡效率很低。文献[12]在实现零位移控制的基础上,根据力与电流的线性关系解算校正质量。但该方法需首先设计凹陷滤波器并嵌入闭环系统,系统的稳定性调节较为复杂。文献[13]对转子实现力自由控制,使其旋转轴尽可能靠近惯性轴,通过辨识转子的位移,去解算惯性轴与几何轴之间的相对位置从而获得扰动力关系。但想要完全实现转子绕惯性轴旋转十分困难,最终的解算精度难以保证。文献[14]通过对系统进行精确建模,无需试重便可解算不平衡质量。但实际系统的精确数学模型一般难以获得,因此工程应用难度较大。
而对于系统中存在的未知扰动,自抗扰控制器中的核心部分——扩张状态观测器,是一种高效、高精度的观测手段[15-16]。扩张状态观测器根据系统的状态方程即可构建观测器模型,由系统的输入输出即可完成对扰动的估测。该方法具有精度高、算法简单、配置参数少、易于实现等特点,在工业控制领域已经得到了一定的应用[17]。
因此,为了准确获取磁悬浮刚性转子旋转时所受的扰动力(矩),本文提出了一种基于扩张状态观测器的现场动平衡方法。该方法将扰动作为系统扩张状态变量对其进行估测,并设计了开关电容滤波器用于提取结果中的同频有效信号。同时考虑实际应用时的各种误差,采用优化系数矩阵方法以克服开环观测的不足,进一步提高动平衡精度。
本文研究对象为一台磁悬浮高速离心压缩机。转子设计一阶弯曲频率为1 589Hz,电机额定工作频率为833Hz,在全转速范围均可认为是刚性转子。
实际转子系统中,由于加工误差、材料不均匀等因素,转子上会不可避免地存在不平衡质量。不平衡质量会引起转子质心的偏移。刚性转子几何轴与惯性轴空间示意图如图1所示,R、G、C分别代表旋转中心、几何中心和质心,w 为转子绕Z方向转动的角速度。惯性主轴相对于几何轴的偏心量e与倾角s 分别反映了该转子的静不平衡量与动不平衡量。下面分别分析静不平衡与动不平衡对转子运动的影响。

图1 刚性转子几何轴与惯性轴空间示意图
Fig.1 Spatial schematic diagram of geometric axis and inertia axis of rigid rotor
静不平衡与惯性轴与几何轴之间的偏心量ε相关。静不平衡如图2所示,以旋转中心R为坐标原点建立R-X-Y坐标系。以转子几何中心G建立旋转坐标系G-H-V,设偏心矢量与H坐标轴之间的夹角为g。
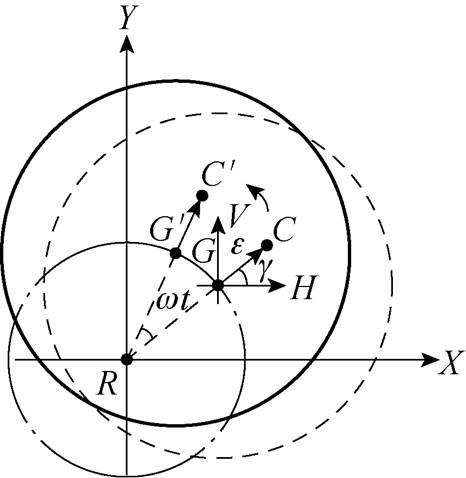
图2 静不平衡
Fig.2 Static imbalance
在该坐标系中,根据转子的旋转方向,同时考虑质心坐标与几何中心坐标关系的情况下,由牛顿第二定律即可写出质心C的运动方程,化简后有
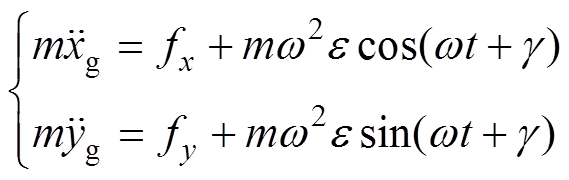 (1)
(1)式中,m为转子的质量;xg、yg为几何中心在平动坐标系中的坐标;fx、fy分别为在X和Y方向上施加的力;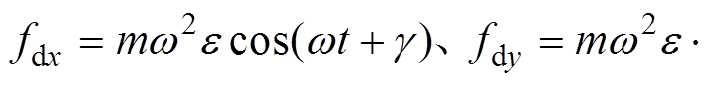
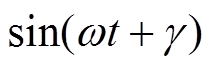 即为由于几何轴与惯性轴之间存在偏心距,旋转时产生的扰动力。
即为由于几何轴与惯性轴之间存在偏心距,旋转时产生的扰动力。
动不平衡与几何轴和惯性轴之间偏离的角度s相关。定义图3坐标系中绕Z、X、Y轴转动的角速度分别为w、a 和b,以逆时针为转动正方向。
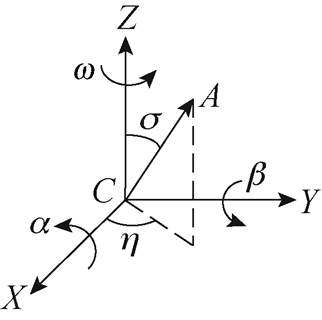
图3 平动与转动坐标系正方向定义
Fig.3 The definition of the positive direction in the plane of motion and rotating coordinate system
将惯性轴CA分别投影至X-C-Z平面与Y-C-Z平面,如图4所示。
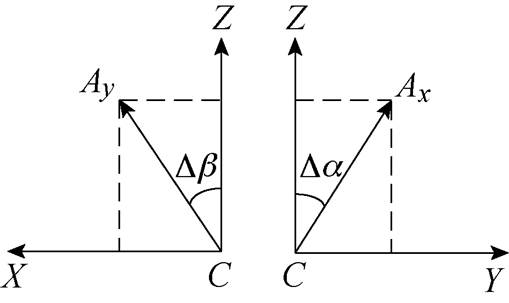
图4 X-C-Z和Y-C-Z平面上惯性轴的投影
Fig.4 Projection of the inertia axis on the X-C-Z and Y-C-Z planes
根据图3和图4坐标系中的几何关系,在几何轴与惯性轴之间偏离角度很小的情况下,考虑它们之间近似的角度关系,由欧拉动力学即可写出质心C的角运动方程,化简后有
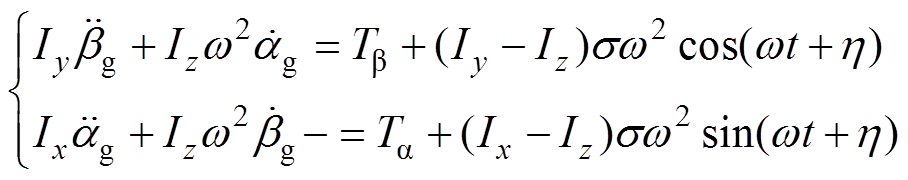 (2)
(2)式中,ag、bg为几何轴在转动坐标系中的坐标;Ix和Iy分别为转子径向X和Y方向的转动惯量;Iz为转子轴向Z方向的转动惯量;h 为惯性轴投影至X-C-Y平面中后与CX之间的夹角;s 为惯性轴CA与CZ的夹角;Tb、Ta 分别为在b、a 方向施加的力矩。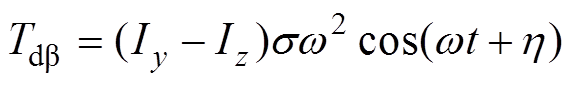 、
、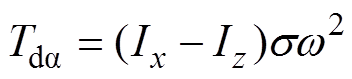
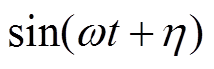 为由于惯性轴和几何轴存在倾角,旋转时产生的扰动力矩。
为由于惯性轴和几何轴存在倾角,旋转时产生的扰动力矩。
由1.1节中建立的坐标系,可将转子分别投影至X-R-Z平面和Y-R-Z平面,如图5所示。
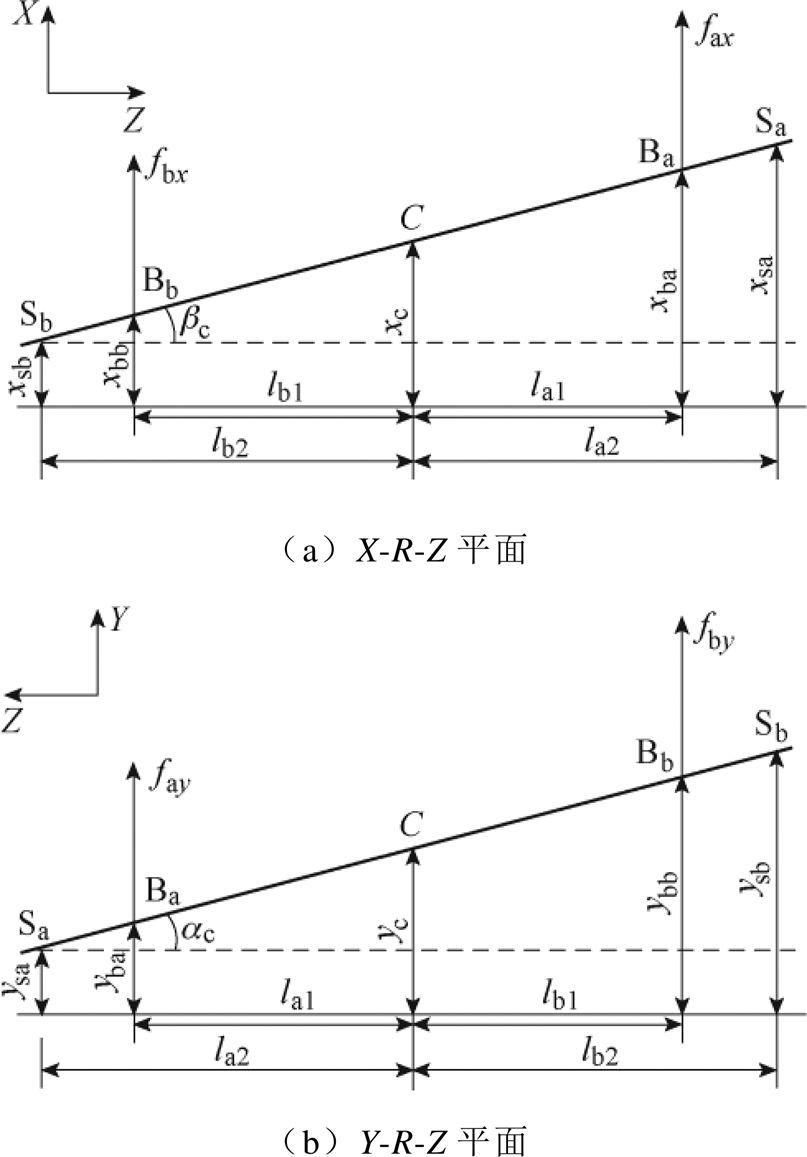
图5 X-R-Z平面和Y-R-Z平面转子的投影
Fig.5 Projection of the rotor on the X-R-Z and Y-R-Z planes
图5中,C为质心位置,Sa和Sb为A端和B端传感器位置,Ba和Bb为A端和B端磁轴承位置,la1、lb1、la2、lb2分别为质心到A、B端磁轴承以及传感器的距离。
结合图5与1.1节、1.2节中的分析,可以写出转子在广义坐标系下的运动方程为
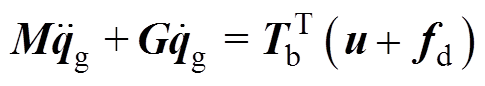 (3)
(3)式中,qg=[bg xg -ag yg]T为几何轴在平动坐标系和转动坐标系下的坐标;u=[ fax fbx fay fby]T为转子四自由度所受悬浮力;fd=[ fdax fdbx fday fdby]T为等效至磁轴承坐标系下的各自由度扰动力;M为转子的质量特性信息矩阵;G为陀螺矩阵;Tb为质心到磁轴承坐标的坐标变换关系矩阵。表达式分别为
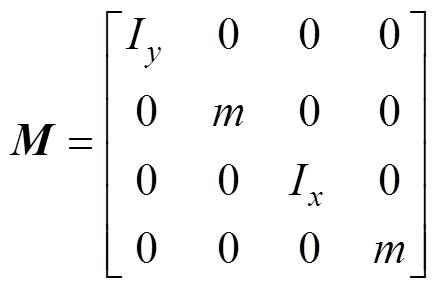 (4)
(4)
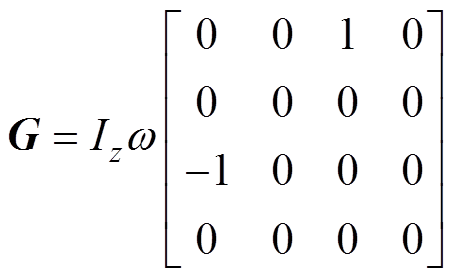 (5)
(5)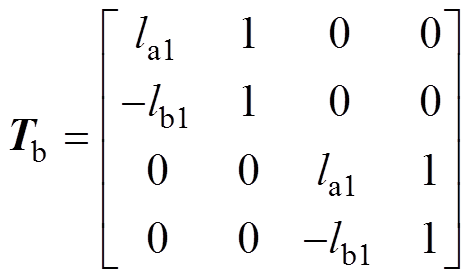 (6)
(6)
各自由度悬浮力可根据静态下测得的位移刚度ks以及电流刚度ki计算[18]得到,有
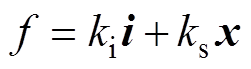 (7)
(7)式中,i为转子各自由度电流,分别为iax、iay、ibx以及iby;x为传感器坐标系下转子位移xsa、xsb、ysa、ysb。
根据图5,可以得到几何轴在磁轴承坐标系以及传感器坐标系下的坐标分别为qb=[xba xbb yba ybb]T,qs=[xsa xsb ysa ysb]T。由于几何轴和惯性轴之间的偏离比较小,当转子在角坐标系中做较小运动时,几何轴在广义坐标系下的坐标qg与qb、qs之间的坐标变换关系可近似写为
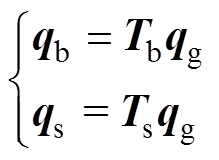 (8)
(8)式中,Ts为质心到传感器坐标的坐标变换关系矩阵,表达式为
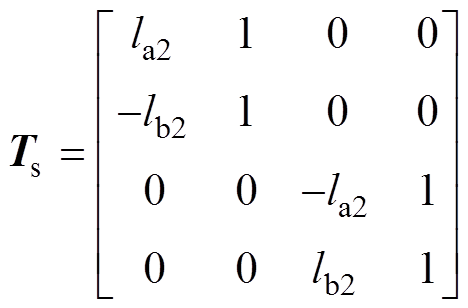 (9)
(9)
将式(8)中qb与qg的关系代入式(3)中,在转速较低且转子较为细长的情况下,忽略陀螺耦合项,轴承坐标系下的运动方程为
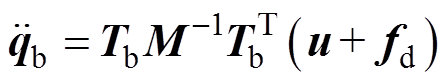 (10)
(10)将式(10)展开,并将由转子动力学仿真软件中得到的转子的质量、尺寸等信息代入,有
 (11)
(11)
从式(11)可以得出两个结论:
(1)在磁轴承坐标系下,转子一端X(Y)方向的运动受转子另外一端X(Y)方向力的影响很小,基本可以忽略不计。
(2)在磁轴承坐标系下,转子在X(Y)方向的运动与其在Y(X)方向的受力无关。
因此对于刚性转子,近似认为转子在磁轴承坐标系下双端四个自由度上的运动是解耦的,可以对转子四个自由度的运动进行分散控制。
本文提出的现场动平衡方法原理框图如图6所示,下文将对图中各个部分进行理论推导。
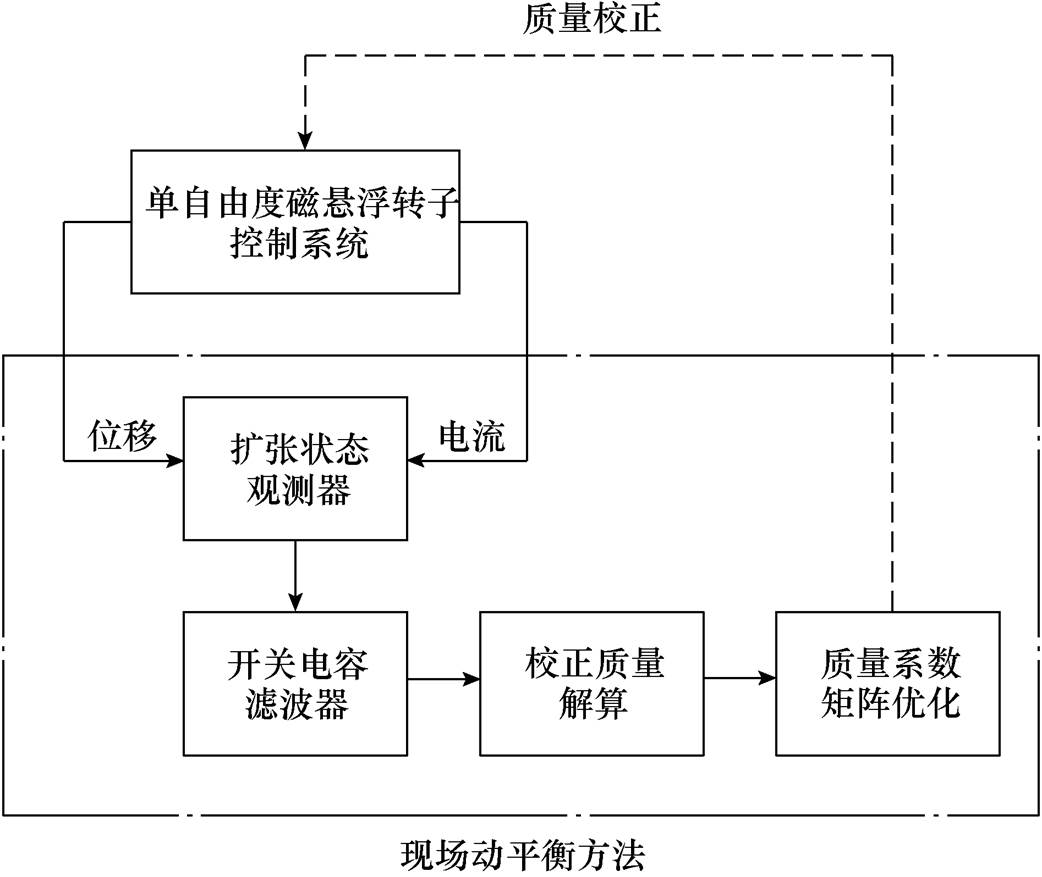
图6 现场动平衡方法原理框图
Fig.6 Block diagram of field dynamic balancing method
在研究单端磁轴承某个自由度的运动时,根据1.3节的分析,可认为不同自由度之间的运动是解耦的,因此各自由度的独立运动方程可以写为
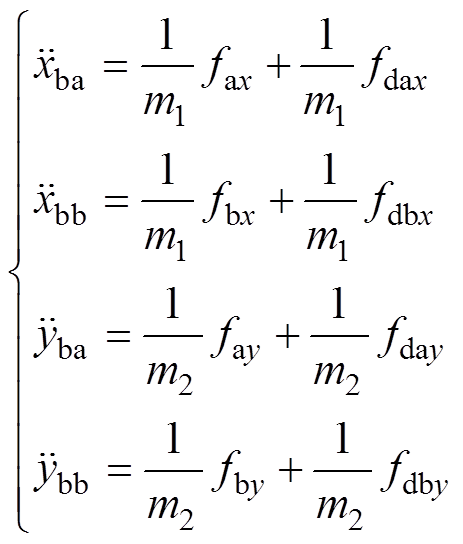 (12)
(12)式中,m1、m2分别为转子在A端磁轴承和B端磁轴承的等效质量,有
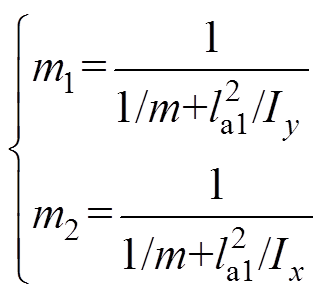
以A端磁轴承X自由度为例,可根据其状态方程设计扩张状态观测器来估测该自由度的扰动力fdax。其他三个自由度可以通过同样的方法获得相应的扰动力。根据式(12)中A端X自由度的运动方程,并将未知扰动fdax/m1拓展为一个系统状态变量x3,可以写出系统的扩张状态方程为
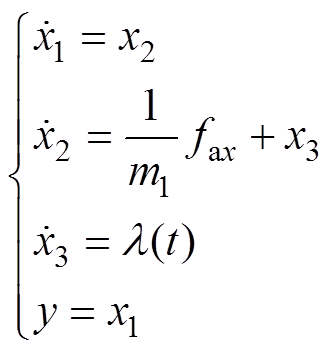 (13)
(13)其中
x1=xba
x3=fdax/m1
由以上述线性系统的输入和输出量,设计扩张状态观测器为
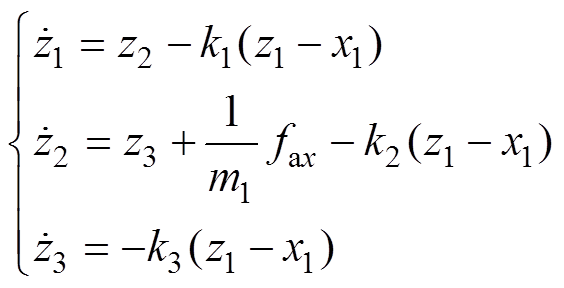 (14)
(14)式中,z1、z2、z3为构造的扩张状态观测器中的状态变量。
则误差状态方程可以写为
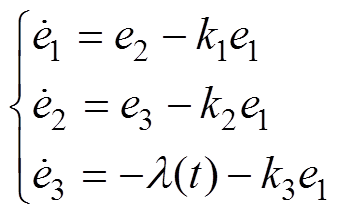 (15)
(15)式中,e1、e2、e3分别为构造的扩张状态观测器中的状态变量z1、z2、z3与式(13)系统状态方程中的状态变量x1、x2、x3的差。
对于该扩张状态观测器需要选取合适的增益使得观测结果收敛,因此下文将对离散状态下的该观测器的参数收敛范围进行推导。
首先根据式(15)将误差方程组写为差分方程形式,由于采样频率很高,可近似地认为相邻采样周期内系统所受扰动加速度不发生变化,有
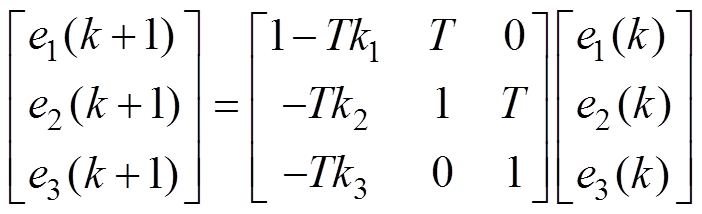 (16)
(16)式中,T为系统计算周期。
由离散系统的稳定性条件可知,特征矩阵的特征值均在单位圆内,观测器稳定。而根据文献[19],当增益系数满足
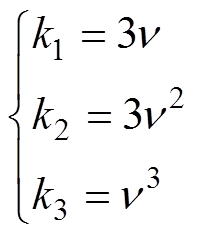 (17)
(17)系统稳定性较好且过渡过程较平稳。因此,该离散系统的稳定参数域为
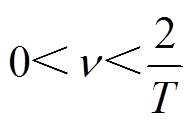 (18)
(18)
当观测器增益满足式(18)时,误差方程结果收敛且满足
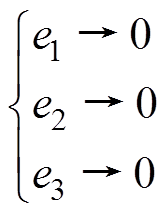 (19)
(19)即该扩张状态观测器能够实现对如下原扩张系统三个状态量的准确估测,有
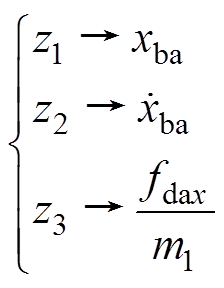 (20)
(20)
由于传感器检测面圆度误差、转子材料不均匀等非线性因素的影响,实际系统中采集到的转子的位移信息中会包含转速倍频信号。倍频信号及噪声均会对观测结果准确性产生影响,因此需要滤除转子位移以及线圈电流信息中的非转速同频分量。
本文采用开关电容滤波器进行滤波处理,其本质是一种带通滤波器,频域表达式为
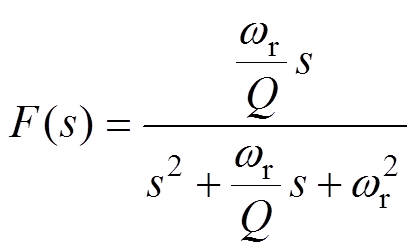 (21)
(21)式中,wr为滤波器中心频率;Q为品质因数。在中心频率选取为250Hz情况下,不同品质因数下的带通滤波器幅频相频特性如图7所示。
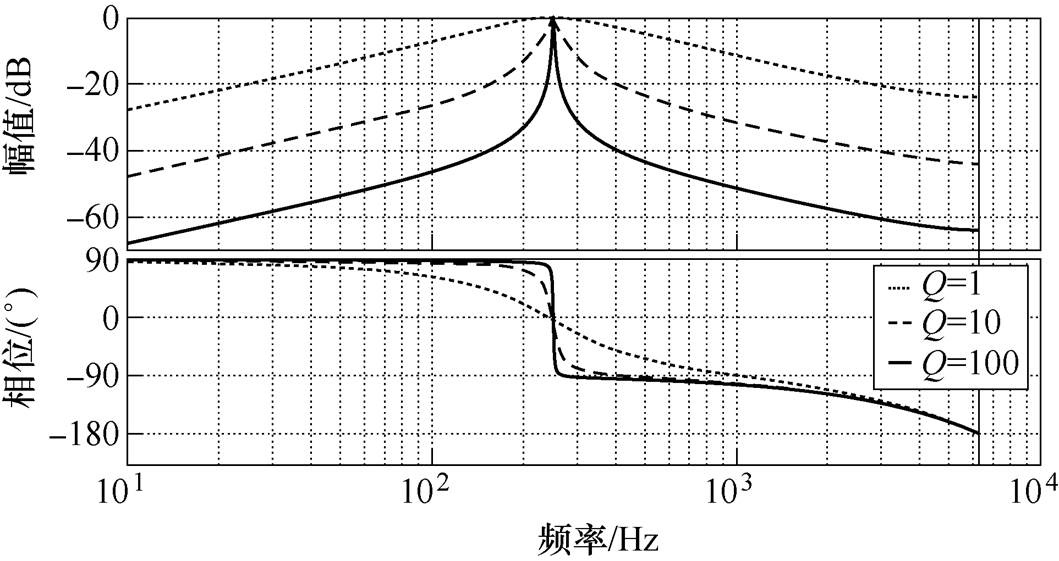
图7 不同品质因数下带通滤波器的伯德图
Fig.7 Bode diagram of bandpass filter with different quality factors
可以看出,随着品质因数的提高,带通滤波器的通带会变窄,滤波能力增强,但同时收敛速度也会变慢。尽管采用较大的品质因数能获得更好的滤波效果,但在数字实现时,由于计算精度的限制,带通滤波器的中心频率会发生一定的偏移,当通带过窄时,即品质因数过大时,可能会造成有效信号的衰减,因此该值需权衡选取。
上述扩张观测器观测出的扰动力为磁轴承坐标系下的扰动力,实际配重位置是在转子两端的配重盘上,因此想要解算出校正质量需要将磁轴承坐标系下的扰动力等效至两侧配重盘处,如图8所示。
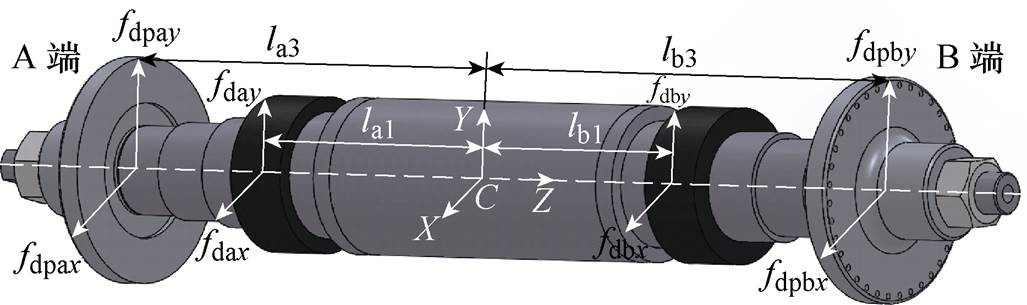
图8 等效至双端配重盘的扰动力
Fig.8 Disturbance equivalent to the counterweight plates in both ends
等效的原则是要使配重盘处施加在质心的力和力矩与磁轴承处施加在质心的力和力矩分别相等。则有
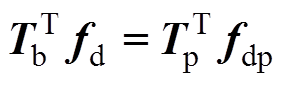 (22)
(22)式中,fdp=[ fdpax fdpay fdpbx fdpby]T为等效至配重盘处A端和B端在X、Y方向的扰动力;la3和lb3分别为双端配重盘到质心的距离;Tp为质心到双端配重盘处的坐标变换关系矩阵,表达式为
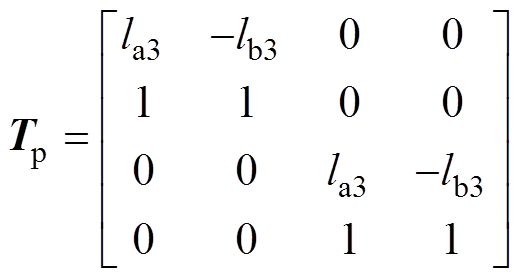 (23)
(23)
选取配重面上转角槽运动至转角传感器处为基准位置,以旋转方向作为角度正方向。假设转角传感器与X正方向的夹角为q,在A端配重盘上在距转角槽ja角度处增加校正质量为ma的螺钉,如图9所示。将该质量分别投影至X正方向和Y正方向就可以得到max和may一组正交质量。
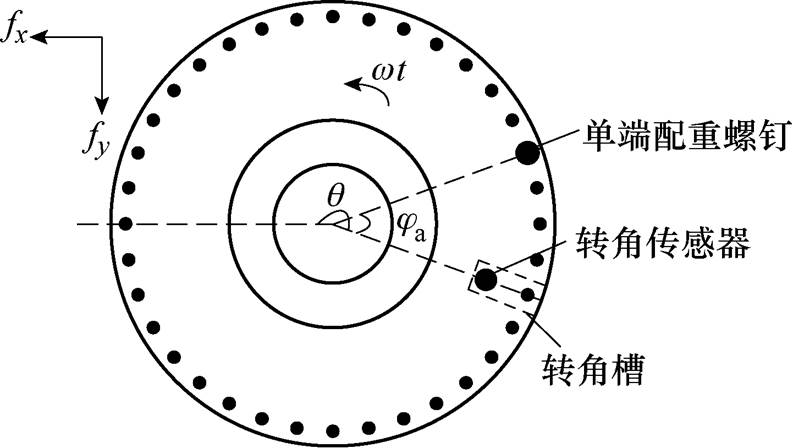
图9 校正质量示意图
Fig.9 The diagram of correction mass
则旋转时该正交质量的时域表达式为
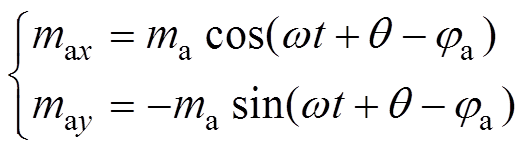 (24)
(24)配重的目的是使得校正质量在配重盘处X和Y方向产生的校正力与扰动力相抵消,因此有
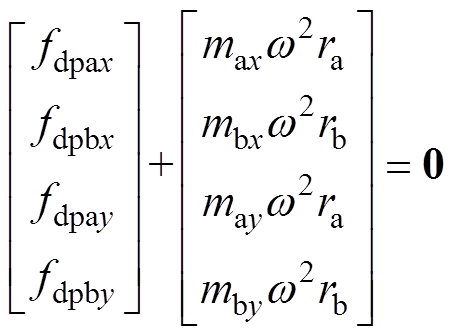 (25)
(25)
式中,ra和rb分别为A端和B端配重盘半径。根据最终解算出的校正质量的幅值和相位以及转角槽基准信号即可确认配重质量的大小和位置。
在实际系统中,以下几个因素会对估算去重质量的准确性产生影响:
(1)扩张状态观测器自身的幅频相频特性产生的估测幅值衰减和相位滞后。
(2)材料特性、加工、装配引起的模型参数的误差。
(3)在涡流的作用下,旋转时的实际电流刚度和位移刚度与静态测量值之间存在的误差。
(4)初始转角槽基准信号标定误差。
(5)离散动平衡算法计算周期的限制导致对估测角度存在的固有误差。
因此,只进行一次动平衡一般来说不能获得完全满意的效果。本文采用一种系数矩阵迭代优化方法,对各环节误差进行修正。
假设配重盘处的真实校正质量Mc=[max mbxmay mby]T和计算校正质量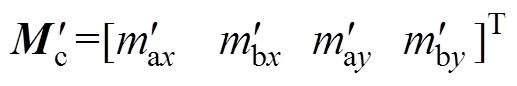 之间关系为
之间关系为
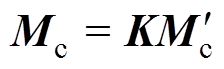 (26)
(26)第一次动平衡之后有
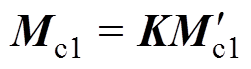 (27)
(27)
式中,系数矩阵K默认在初始动平衡时为单位矩阵。根据第一次计算出的校正质量Mc1,在配重盘对应位置加重,并再进行一次升速可以得到优化系数矩阵与真实校正质量的关系为
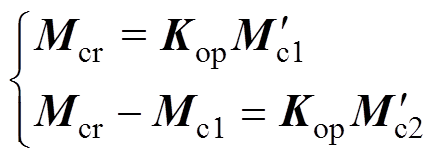 (28)
(28)式中,Mcr为第一次动平衡时真实的校正质量;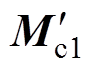 和
和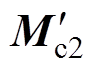 分别为第一次和第二次动平衡计算出的校正质量矩阵;Kop为优化后的系数矩阵。根据式(28)即可得到优化系数矩阵的表达式为
分别为第一次和第二次动平衡计算出的校正质量矩阵;Kop为优化后的系数矩阵。根据式(28)即可得到优化系数矩阵的表达式为
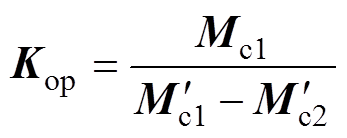 (29)
(29)
将优化后的系数矩阵代入式(28)则可以得到在初始条件下优化后的新的校正质量,取下第一次的增重螺钉,根据新的校正质量即可进行重新配重。
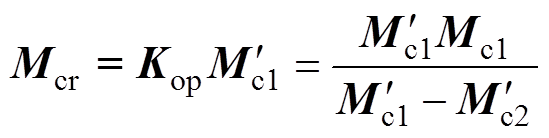 (30)
(30)该方法克服了开环观测的弊端,通过增加一次配重完成“闭环”,在动平衡过程中可根据实际情况反复迭代以获得更好的效果。
为验证扩张状态观测器对系统状态变量估测的准确性,在Matlab/Simulink环境中分别搭建控制系统模型、刚性转子A端X方向单自由度运动模型以及离散观测器模型。仿真参数见表1。
观测器输出的观测值——转子位移、速度和扰动力分别与实际值对比的仿真结果如图10所示。由仿真结果可以看出,扩张状态观测器根据对象系统的输入和输出可以准确地对系统状态变量——转子单自由度位移、转子单自由度速度以及系统的扩张状态变量——转子单自由度所受扰动力进行准确地估测。同时由于观测器自身的幅频相频特性,对扰动力的观测存在微小的幅值和相位误差。
表1 仿真参数
Tab.1 Simulation parameters setting

参 数数 值 A端等效质量m1/kg2.02 A端电流刚度kiax, kiay/(N/A)54.0 A端位移刚度ksax, ksay/(N/m)191 322 计算周期T/ms80 动平衡转速w/(r/min)15 000 观测器增益Kob15 000
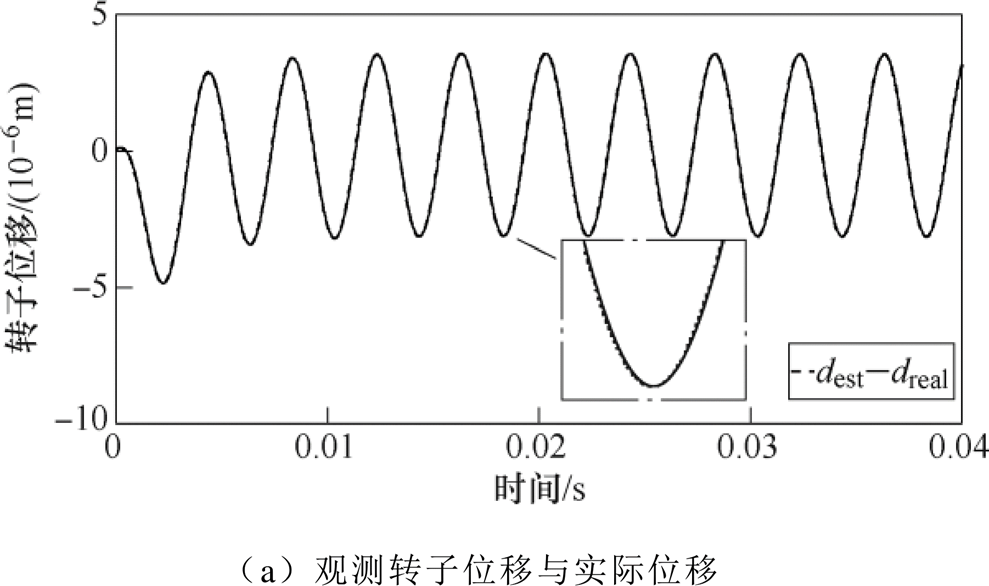
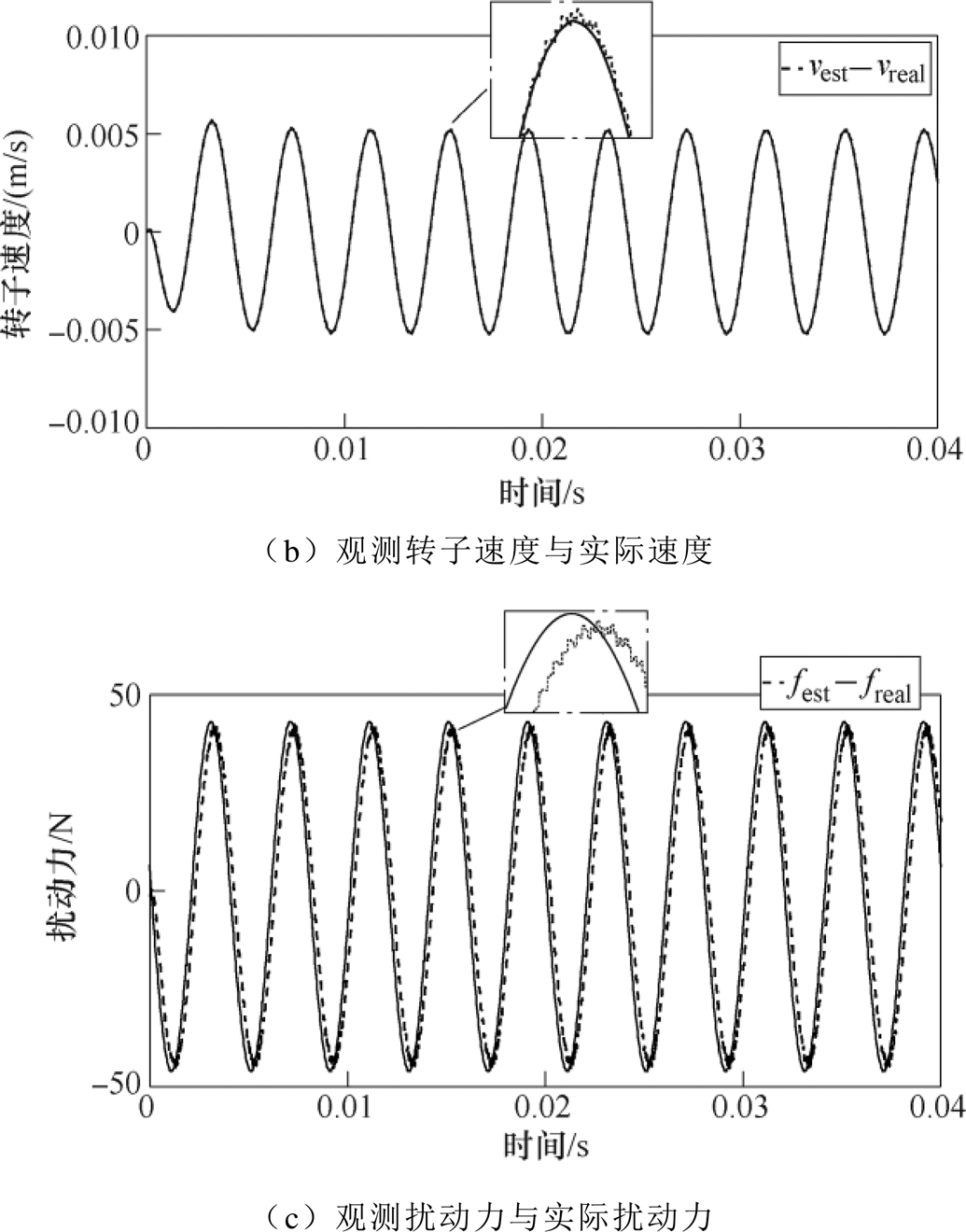
图10 观测器输出与实际状态变量对比
Fig.10 Comparison between the output of the observer and actual state variables
在一台磁悬浮高速离心压缩机上进行实验验证,转子两端各有一个三自由度混合励磁磁轴承支承。在磁轴承两端外侧的转子上安装两个配重盘,其中配重盘圆周上,每10°相邻共加工了36个M2螺纹孔用于安装配重螺钉,其实验平台如图11所示。控制器部分采用先进精简指令集机器(Advanced RISC Machine, ARM)+现场可编程逻辑门阵列(Field Programmable Gate Array, FPGA)作为运算单元,模数转换器(Analog to Digital Converter, ADC)采样速率400kHz,动平衡算法计算周期为80ms,观测器增益为6 400,动平衡转速为15 000r/min。磁悬浮轴承及转子的结构特性参数见表2。

图11 实验平台示意图
Fig.11 The diagram of test rig
表2 磁悬浮轴承及转子的结构特性参数
Tab.2 Structural characteristic parameters of magnetic bearings and rotor

参 数数 值 转子质量m/kg3.84 轴向转动惯量Iz/(kg·m2)0.001 236 径向转动惯量Ix, Iy/(kg·m2)0.030 32 A端磁轴承到质心距离la1/m0.083 96 B端磁轴承到质心距离lb1/m0.084 04 A端传感器到质心距离la2/m0.121 11 B端传感器到质心距离lb2/m0.121 19 A端配重盘到质心距离la3/m0.155 66 B端配重盘到质心距离lb3/m0.155 74 A端电流刚度kiax, kiay/(N/A)54.0 B端电流刚度kibx, kiby/(N/A)65.6 A端位移刚度ksax, ksay/(N/m)191 322 B端位移刚度ksbx, ksby/(N/m)292 248 A、B端配重盘半径ra, rb/m0.037 5
首先在转子未进行动平衡时,由变频器驱动至动平衡转速15 000r/min,此时各自由度磁轴承转子位移和线圈电流如图12所示。可以看出,未进行动平衡时转子自身不平衡量很大,转子位移波动剧烈,电流变化明显。
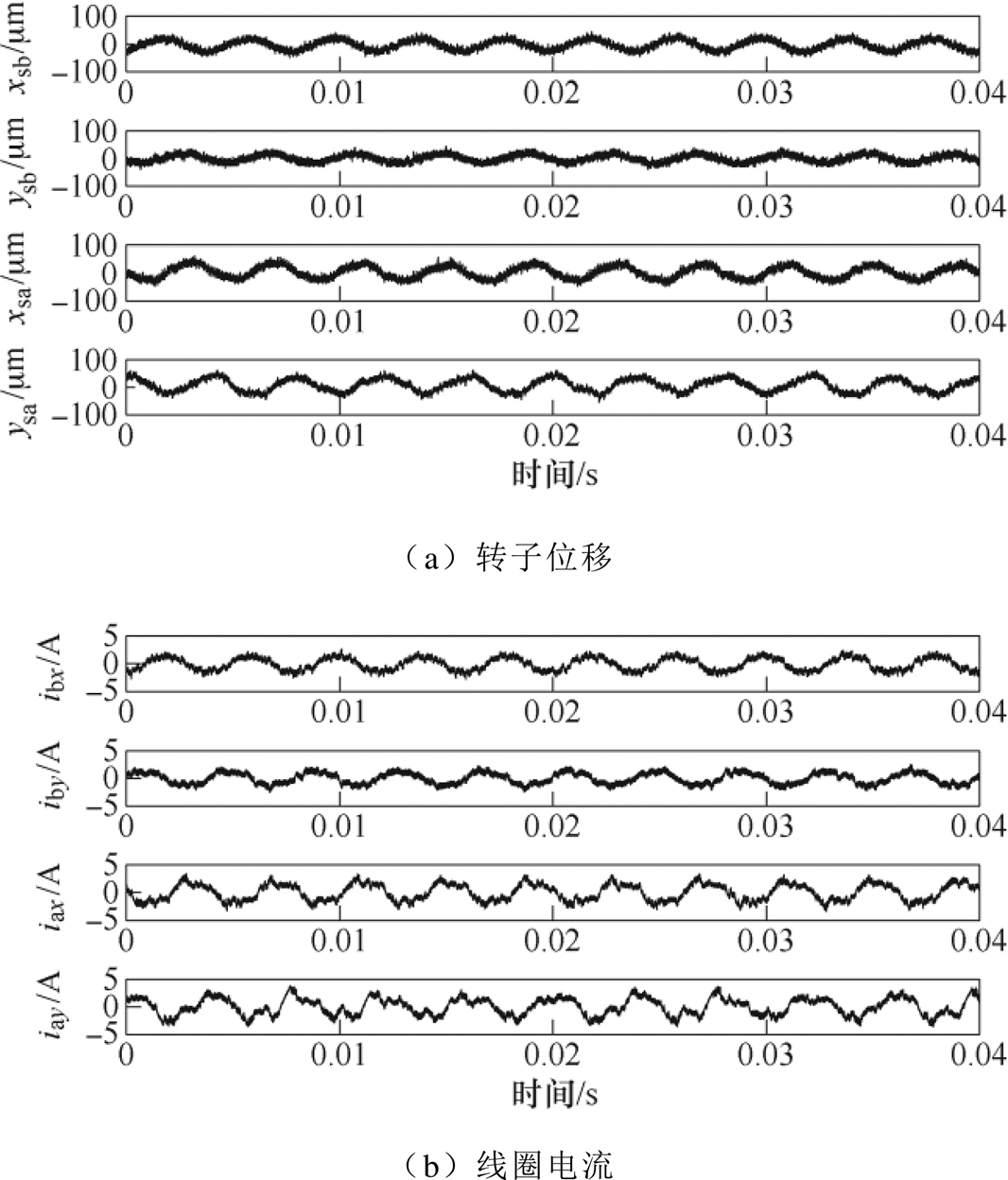
图12 未进行动平衡时15 000r/min转子位移和线圈电流
Fig.12 Rotor displacement and coil current at 15 000r/min before dynamic balancing
根据本文提出的现场动平衡方法,首先进行两次升速并做一次增重操作,记录相关数据并计算出优化系数矩阵为
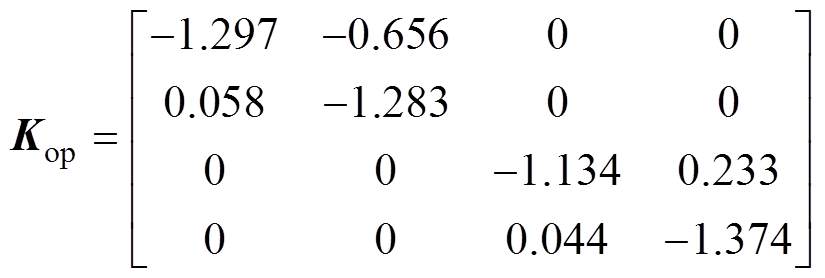 (31)
(31)利用式(30)即可得到第一次优化后转子两端配重盘上的增重质量矢量分别为
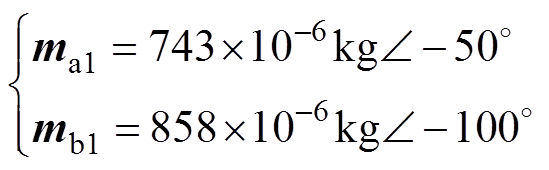 (32)
(32)
但由于配重螺钉质量误差,安装角度误差等原因,在经过上述增重后,又进行了一次升速实验进行残余不平衡质量修正,根据第二次升速得到的增重质量矢量在配重盘上加重,其增重矢量为
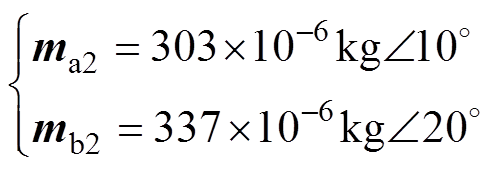 (33)
(33)A端和B端前后两次配重情况如图13所示。
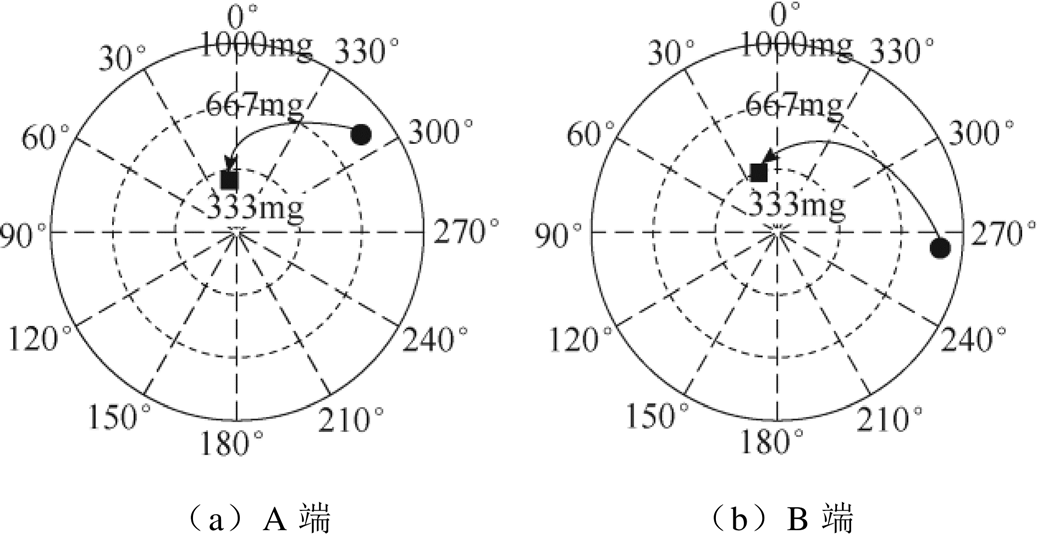
图13 A端和B端两次校正质量示意图
Fig.13 Diagram of correction mass at end A and B
在经过两次动平衡后,转子重新稳定运行在15 000r/min时,磁轴承转子位移和线圈电流如图14所示。
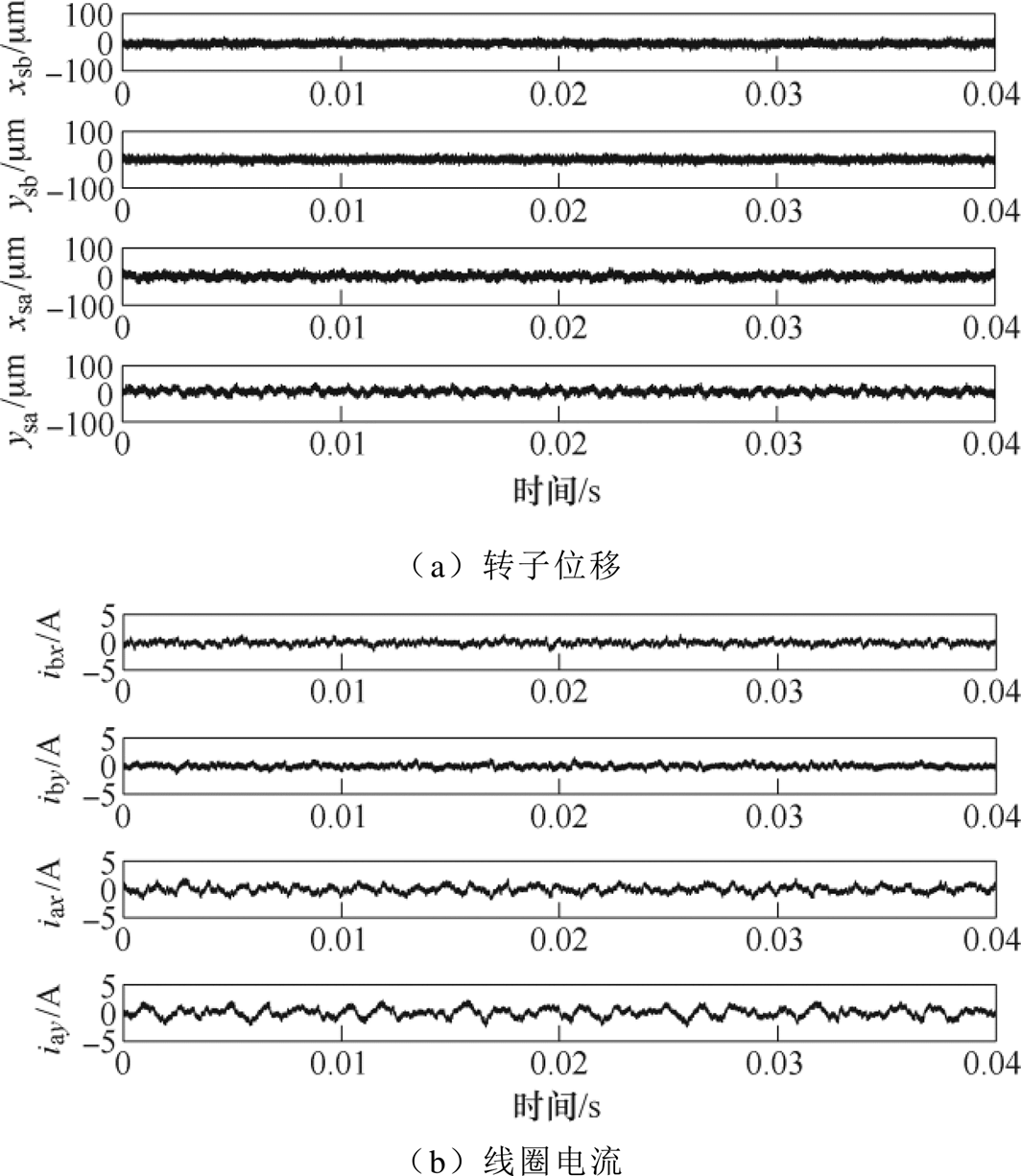
图14 动平衡后15 000r/min转子位移和线圈电流
Fig.14 Rotor displacement and coil current at 15 000r/min after dynamic balancing
对比图12与图14的位移和电流的实验波形可以看出,采用本文提出的现场动平衡方法后,转子位移和线圈电流中的波动幅值明显减小,磁轴承的悬浮控制精度明显提高,线圈电流幅值下降也使得功放不再处于接近饱和的状态。
将动平衡前后的转子各自由度位移和电流分别进行快速傅里叶变换(Fast Fourier Transformation, FFT)分析。一般来说,由于单个磁轴承两个自由度的位移幅值和线圈电流基本一致,相位相差约90°,为方便分析,选取A端和B端X方向位移、电流进行分析,其结果如图15所示。FFT波形表明,校正后转子位移和线圈电流中的转速同频分量均有明显下降,不平衡质量显著减小。
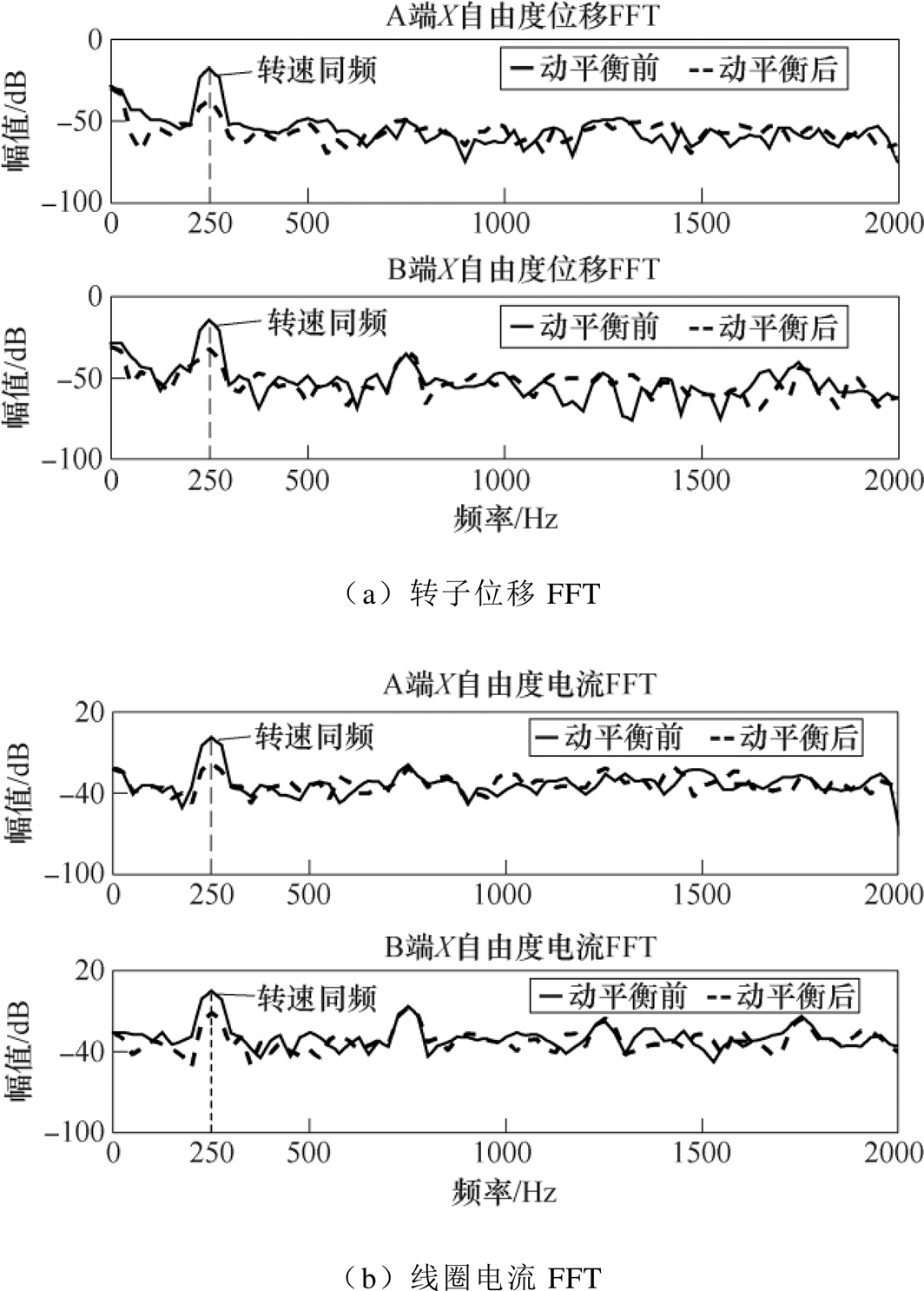
图15 校正前后转子位移和线圈电流FFT
Fig.15 FFT of rotor displacement and coil current before and after correction
动平衡前后双端位移和电流的FFT结果见表3。根据FFT分析中的波形和数据,可以看出,动平衡后,转子A端和B端位移波动显著下降,其中位移同频分量分别下降了85.5%和88.5%。而由于不平衡质量的大幅降低,磁轴承线圈中的同频电流分别下降了83.8%和87.4%。与此同时,直流电源输出功率也由125W降低至85W,损耗显著降低。
表3 校正前后双端位移和电流FFT幅值
Tab.3 The FFT amplitude of displacement and current in both ends before and after correction

条件(同频)电流位移 A端B端A端B端 动平衡前/dB2.450-16.04-18.01 动平衡后/dB-13.34-17.96-32.80-36.80 下降百分比(%)83.887.485.588.5
针对转子质量不平衡问题,提出一种利用扩张状态观测器观测转子单自由度扰动力的方法,并通过开关电容带通滤波器提取结果中有效同频分量。采用系数矩阵迭代方法修正校正质量以提高该方法精度。相比于传统方法,本文提出的基于扩张状态观测器的现场动平衡方法具有试重次数少、运行效率高、不影响系统稳定性、可软件部署实时监测等优点。实验结果显示,在获得优化系数矩阵后,经过两次配重,转子不平衡质量显著降低,可以在高旋转精度以及低振动力水平下稳定运行。
参考文献
[1] 张维煜, 朱熀秋, 袁野. 磁悬浮轴承应用发展及关键技术综述[J]. 电工技术学报, 2015, 30(12): 12- 20.
Zhang Weiyu, Zhu Huangqiu, Yuan Ye. Study on key technologies and applications of magnetic bearings[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 12-20.
[2] 陈亮亮, 祝长生, 王忠博. 基于逆系统解耦的电磁轴承飞轮转子系统二自由度控制[J]. 电工技术学报, 2017, 32(23): 100-114.
Chen Liangliang, Zhu Changsheng, Wang Zhongbo. Two-degree-of-freedom control for active magnetic bearing flywheel rotor system based on inverse system decoupling[J]. Transactions of China Electro- technical Society, 2017, 32(23): 100-114.
[3] 赵旭升, 邓智泉, 王晓琳, 等. 永磁偏置磁轴承的研究现状及其发展[J]. 电工技术学报, 2009, 24(9): 9-20.
Zhao Xusheng, Deng Zhiquan, Wang Xiaolin, et al. Research status and development of permanent magnet biased magnetic bearings[J]. Transactions of China Electrotechnical Society, 2009, 24(9): 9-20.
[4] Addabbo T, Fort A, Biondi R, et al. Measurement of angular vibrations in rotating shafts: effects of the measurement setup nonidealities[J]. IEEE Transa- ctions on Instrumentation and Measurement, 2013, 62(3): 532-543.
[5] 张凤阁, 杜光辉, 王天煜, 等. 高速电机发展与设计综述[J]. 电工技术学报, 2016, 31(7): 1-18.
Zhang Fengge, Du Guanghui, Wang Tianyu, et al. Review on development and design of high speed machines[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 1-18.
[6] Herzog R, Buhler P, Gahler C, et al. Unbalance compensation using generalized notch filters in the multivariable feedback of magnetic bearings[J]. IEEE Transactions on Control Systems Technology, 1996, 4(5): 580-586.
[7] Cui Peiling, Sheng Li, Wang Qirui, et al. Harmonic current suppression of AMB rotor system at variable rotation speed based on multiple phase-shift notch filters[J]. IEEE Transactions on Industrial Electronics, 2016, 63(11): 6962-6969.
[8] Zheng Shiqiang, Han Bangcheng, Rui Feng, et al. Vibration suppression control for AMB supported motor driveline system using synchronous rotating frame transformation[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5700-5708.
[9] 徐宾刚, 屈梁生, 孙瑞祥. 基于影响系数法的柔性转子无试重平衡法研究[J]. 西安交通大学学报, 2000, 34(7): 63-67.
Xu Bingang, Qu Liangsheng, Sun Ruixiang. Balancing of flexible rotors without test weights[J]. Journal of Xi’an Jiaotong University, 2000, 34(7): 63-67.
[10] Liu Zhengshi, Lu Yiming, Wang Yu, et al. Relative coefficient method for rotor balancing and its performing with dynamic signal analyzer[J]. Key Engineering Materials, 2004, 259-260: 751-755.
[11] Foiles W C, Allaire P E, Gunter E J. Review: rotor balancing[J]. Shock and Vibration, 1998, 5(5-6): 325- 336.
[12] Fang Jiancheng, Wang Yingguang, Han Bangcheng, et al. Field balancing of magnetically levitated rotors without trial weights[J]. Sensors, 2013, 13(12): 16000- 16022.
[13] Xu Xiangbo, Chen Shao. Field balancing and harmonic vibration suppression in rigid AMB-rotor systems with rotor imbalances and sensor runout[J]. Sensors, 2015, 15(9): 21876-21897.
[14] 韩辅君, 房建成. 磁悬浮飞轮转子系统的现场动平衡方法[J]. 航空学报, 2010, 31(1): 184-190.
Han Fujun, Fang Jiancheng. Field balancing method for rotor system of a magnetic suspending fly- wheel[J]. Acta Aeronautica Et Astronautica Sinica, 2010, 31(1): 184-190.
[15] 韩京清. 一类不确定对象的扩张状态观测器[J]. 控制与决策, 1995, 10(1): 85-88.
Han Jingqing. The “extended state observer” of a class of uncertain systems[J]. Control and Decision, 1995, 10(1): 85-88.
[16] 林飞, 张春朋, 宋文超, 等. 基于扩张状态观测器的感应电机转子磁链观测[J]. 中国电机工程学报, 2003, 23(4): 145-147.
Lin Fei, Zhang Chunpeng, Song Wenchao, et al. Flux observer of induction motor based on extended state observer[J]. Proceeding of the CSEE, 2003, 23(4): 145-147.
[17] 毛海杰, 李炜, 蒋栋年, 等. 基于线性扩张状态观测器的永磁同步电机状态估计与性能分析[J]. 电工技术学报, 2019, 34(10): 2155-2165.
Mao Haijie, Li Wei, Jiang Dongnian, et al. State estimation and performance analysis based on linear extended state observer for permanent magnet synchronous motor[J]. Transactions of China Electro- technical Society, 2019, 34(10): 2155-2165.
[18] Schweitzer G, Maslen E H. Magnetic bearings: theory, design, and application to rotating machinery[M]. Berlin: Springer, 2009.
[19] Gao Zhiqiang. Active disturbance rejection control: a paradigm shift in feedback control system design[C]// IEEE American Control Conference, Minneapolis, MN, USA, 2006: 2399-2405.
A Filed Dynamic Balancing Method for Rigid Rotor Supported by Magnetic Bearings
Abstract In this paper, a filed dynamic balancing method based on an extended state observer for magnetic bearing supporting rigid rotor is proposed. According to the equation of motion of the rotor supported by magnetic bearings, the extended state observer is designed. The dynamic disturbance of the system can be estimated by the input and output information of the target system. And the convergence conditions of the observer in discrete state are given. In order to remove the influence of multiple frequency disturbance and noise signals on the estimation results, a switched capacitor filter is designed to extract the synchronous component in the disturbance. For the errors existing in the system, the coefficient matrix iterative optimization method is used to improve the dynamic balance accuracy. In the actual use, this method can calculate the matrix of the optimization coefficient only through once trial weighting. And after balancing twice, the unbalanced mass of the rotor is significantly reduced. When the unit is in long-term operation, this method can be deployed in the microprocessor to monitor the rotor unbalance, which plays the role of early warning and guidance of the dynamic balancing.
keywords:Magnetic bearings, field dynamic balancing, rigid rotor, extended state observer
中图分类号:TH133.3
DOI: 10.19595/j.cnki.1000-6753.tces.191289
国家自然科学基金资助项目(51577087)。
收稿日期2019-10-08
改稿日期 2019-12-10
黄 威 男,1995年生,硕士,研究方向为磁悬浮轴承控制。E-mail: hw@nuaa.edu.cn
邓智泉 男,1969年生,教授,博士生导师,研究方向为无轴承电机、高速电机、交流电机控制等。E-mail: dzq@nuaa.edu.cn(通信作者)
(编辑 崔文静)