0 引言
绝缘材料的介电响应特性蕴含了丰富的绝缘状态信息[1]。基于介电响应理论的回复电压法[2]（Recovery Voltage Method, RVM）、极化去极化电流法[3-4]（Polarization And Depolarization Current,PDC）和频域介电谱法[5-6]（Frequency Domain Spectroscopy, FDS）具有对绝缘无损伤、携带丰富绝缘信息以及方便实施等优点，广泛用于电气设备的绝缘状态，尤其是油浸式电力变压器的状态诊断和评估中。
相比于PDC 和RVM，FDS 测量技术由于具有相对较强的抗干扰能力，而且测试结果对油纸绝缘性能变化反映更为灵敏，得到了较为广泛的理论和应用研究。大量研究结果表明，FDS 的介质损耗频域谱曲线在低频段（f＜0.1Hz）的变化能够有效地表征油纸绝缘的水分含量，可利用该频段的tanδ -f 特性定量表征绝缘的水分含量[7]。基于该原理，目前也有商用仪器问世，用于对变压器的受潮状态进行诊断，具有代表性的是美国Megger 公司的IDAX和奥地利Omicron 公司的Dirana 绝缘介质诊断仪。然而，准确获取低频段的介质响应特性需要较长时间，不利于在现场有限的停电时间下进行测试。提高低频段FDS 的测试效率，缩短测量时间逐渐成为研究的热点。
目前，缩短FDS 测量时间最为常用的方法是时-频等效转换法，即利用绝缘在直流激励下的时域响应电流（即PDC 测试结果），经过数学计算推导交流激励下的不同频率的介电响应频谱。常用的有两种方法：扩展Debye 电路模型等效法[8-10]和全电流Fourier 变换法[7]。Omicron 公司的Dirana 绝缘诊断仪在测试时提供了“PDC+FDS”的测量模式，即是利用时-频等效变换的方法，缩短测量时间至传统扫频模式的55%～75%。
然而，扩展Debye 模型本质上是将油纸绝缘等效为一系列具有线性特性的电阻、电容串并联电路，当绝缘介质处于非线性区域时该模型将不再适用；同样，Fourier 时-频转换方法也仅适用于线性响应系统。当待分析的绝缘介质表现出非线性响应特性时，基于扩展Debye 模型支路电阻Ri、电容Ci 及时间常数 iτ 等特征参量的绝缘评估方法不再有效，同样，基于扩展Debye 模型和Fourier 变换的时-频转换结果也不再适用或将造成较大误差。
众所周知，随着激励电场强度的增加，油纸绝缘会表现出一定的非线性特性[11-12]。该特性会导致在FDS 的扫频测试中响应电流产生3 次和5 次谐波，其严重程度取决于激励电压的幅值大小和频率高低[13]；在PDC 测量中施加较高的直流电压时，响应电流会逐渐偏移相应线性系统电流，整体低于预期线性响应电流。因此，在获取以油浸式电力变压器为代表的高压设备绝缘介电响应特性时，通常要求在保证测试信号信噪比的前提下，尽量施加较低的激励电压，以避免激发出介质的非线性特性。例如，RVM 和 PDC 测量的激励电压通常不超过2 000V，而FDS 激励电压峰值不超过200V[14]。然而，除了测量电压外，油纸绝缘的非线性特性还受到其他诸多因素影响，如测试温度和油纸绝缘的自身绝缘状态。文献[15]指出，绝缘受潮和老化等都会导致绝缘的非线性特性。如何对介质响应测试过程中绝缘介质的非线性特性进行表征，相关的研究工作目前还少见报导。文献[16]提出在扩展 Debye模型电路中增加一个电流控电压源（Current Controlled Voltage Source, CCVS），以模拟PDC 测试中非线性绝缘的极化电流，但仿真结果与实测极化电流仍存在较大误差，并且未给出CCVS 的参数确定方法。在本课题组前期研究成果中，曾提出通过Hammerstein- Wiener（简称H-W）数学模型来等效油纸绝缘介电响应特性以达到缩短低频介电响应测量时间的目的[17]，研究中发现，H-W 模型中包括了线性环节和两个非线性环节，可以对介质中的非线性行为进行等效；然而，并未深入研究油纸绝缘材料非线性特性的影响因素，以及H-W 模型对材料非线性特性的等效效果。
本文进一步通过试验研究受潮程度对油纸绝缘非线性响应特性的影响，采用H-W 模型作为油纸绝缘的等效模型，并对比分析采用扩展Debye 模型、Fourier 变换及H-W 模型对不同受潮状态下绝缘介质响应的时频转换结果的有效性。
1 传统时频转换方法
1.1 基于扩展Debye 模型的转换方法
变压器油纸绝缘可以用一系列串并联的电阻、电容组成的等效电路模拟其电气特性，由R 和C 组成的电路称为扩展Debye 模型，如图1 所示。其中，R0 和C0 分别为绝缘电阻和几何电容，Ri 和Ci 的串联支路为不同时间常数的松弛极化过程[18]。
图1 扩展Debye 模型
Fig.1 Extended Debye model
对等效电路施加幅值为U0 的阶跃电压时，流过介质内部的极化电流ipol 和去极化电流idepol 可分别表示为
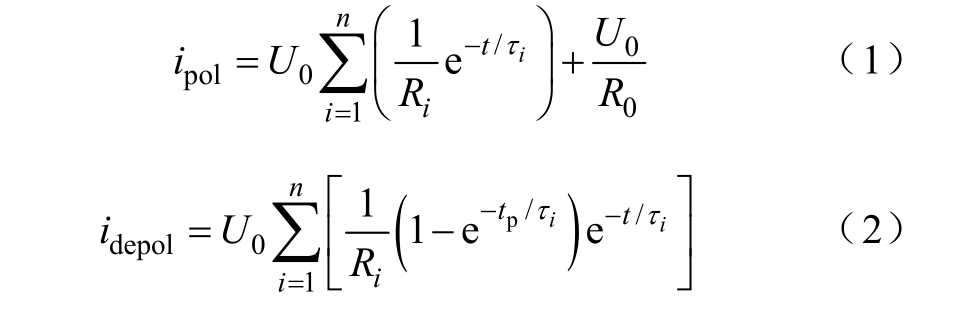
式中，i 为极化支路序数；n 为极化支路总数；tp 为极化时间；t 为测试时间。
当对扩展Debye 模型等效电路施加正弦激励电压U(ω)时，流过电路的总电流I(ω)为
进一步将复电容实部 C′(ω)和虚部 C′(ω)及介质损耗因数表示为
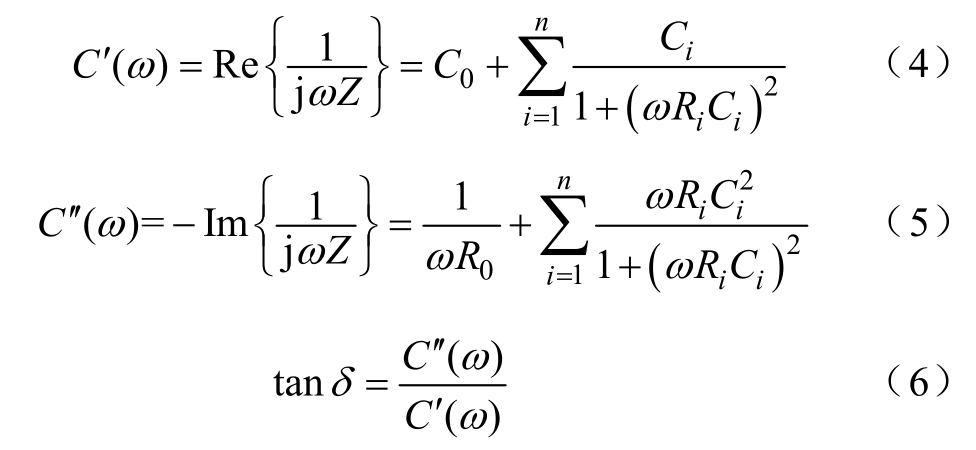
式中，C′(ω)、C′(ω)分别为复电容实部、虚部；tanδ为介质损耗；ω 为角频率；Z 为复阻抗。
由此，已知时域PDC 数据时，可根据式（1）和式（2）拟合，得到扩展Debye 模型中的RC 参数值，再根据式（4）～式（6）计算得到频域介电谱，实现时域到频域的转换；反之，当频域数据已知时，求解时域数据的方法类似。
1.2 基于Fourier 变换的转换方法
式中， ε0 为真空介电常数；ε∞为光频介电常数； σ0为材料的体积电导率；δ (t ) 为单位脉冲函数；f ( t) 为材料的时域介电响应函数。
当在Tc 时刻撤去阶跃电压后，去极化电流可表示为
当充电时间Tc 足够长时，f (t -Tc)≈0，则介电响应函数可分别用极化电流和去极化电流表示为
若对介质施加电压激励U(ω)，则流过电介质的频域电流可以对式（7）进行Fourier 变换得
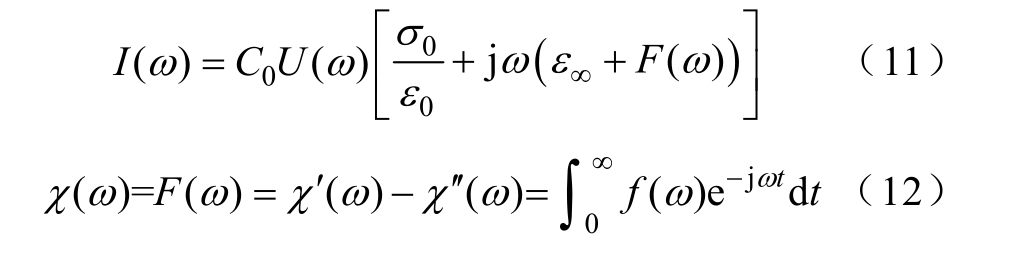
相应地，可将时域介电响应函数用复极化率虚部 χ′(ω)表示为
而复相对介电常数的实部ε ′(ω)和虚部ε ′(ω)可分别用时域电流表示为
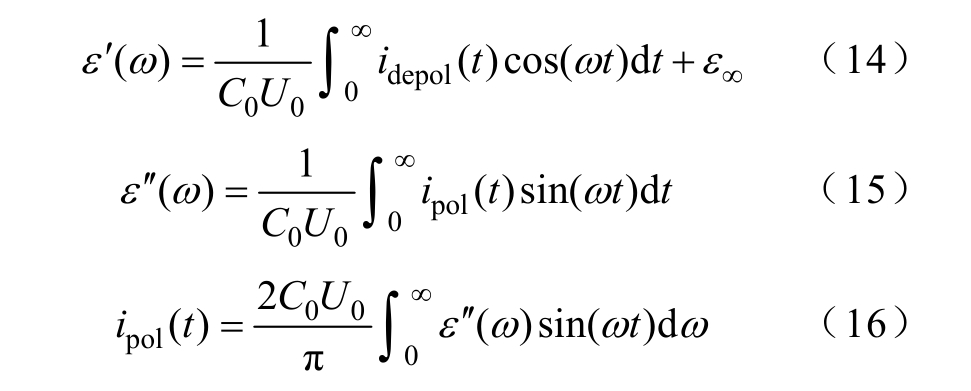
因此，可以利用Fourier 变换实现时域和频域测试数据的相互转换。
2 基于H-W 等效模型的时频转换方法
2.1 H-W 模型的基本结构
绝缘介质是一个受诸多因素影响的复杂系统，无法依据简单原理进行等效，但其动态响应特性其实包含于测试所得的输入和输出信号中，因此可将绝缘介质视作灰盒，不考虑内部的极化过程，根据实际测试的激励电压和响应电流，选择具有一定物理意义的等效数学模型，通过求解其各项系数获得绝缘介质的唯一等效。在前期研究工作中，考虑油纸绝缘系统的弛豫极化特性，提出采用如图2 所示的H-W 模型作为绝缘介质响应的等效数学模型[17]。u(t)和y(t)为系统的输入和输出，x1(t)和x2(t)为虚拟的中间变量。
图2 H-W 模型的基本结构
Fig.2 Basic block diagram of H-W model
H-W 模型包括线性动态环节G(z)、非线性输入环节(f)和输出环节(g)。各环节的数学表达式为
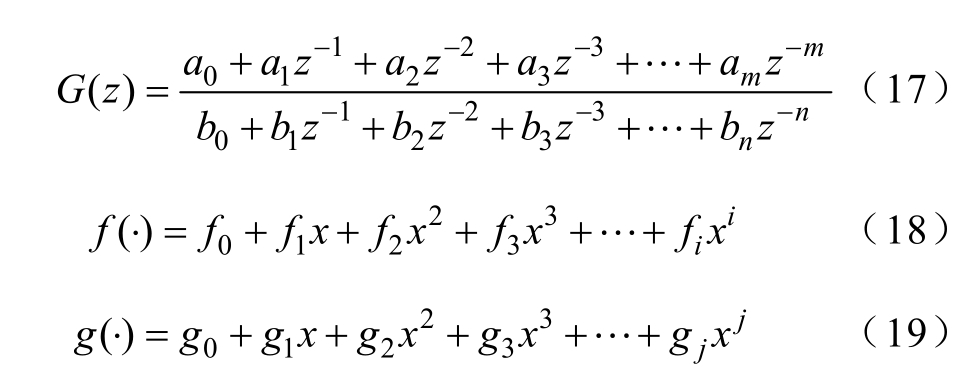
式中，z 为Z 变换算子；a0, a1,…, am 和b0, b1,…, bn 为线性环节的待辨识参数；f0, f1,…, fi 和 g0, g1,…, gj分别为输入和输出环节的待辨识参数。
实际上，线性动态环节G(z)的数学表达式与扩展Debye 模型的传递函数相似，主要用于表征绝缘系统的线性响应特性。当 f(⋅)= g (⋅)=1 时，H-W 模型中只包含中间的动态线性环节，即等效为扩展Debye 模型。
绝缘介质大多表现为容性系统，在宏观上可用RC 串联或RC 并联模型表征。H-W 模型在线性环节基础上增加了输入和输出非线性环节，可以表达绝缘介质的动态极化特性，能够同时表征线性和非线性绝缘系统，适用于多种绝缘介质的等效，比传统电介质模型具有更加广泛的适用范围。对于不同绝缘介质而言，其对应的H-W 模型的数学结构是一致的，也就是说，模型的整体框架是固定的，只需要调整模型阶次和各项系数便可获得绝缘介质的唯一等效。
2.2 H-W 模型参数的获取方法
为了能够表征油纸绝缘系统的线性和非线性特性，输入系统的激励信号需要确保能够激励出油纸绝缘系统的动态特性，即弛豫极化特性[19-20]。根据前期研究成果，白噪声信号是具有脉冲形式的自相关函数，功率谱密度在一定频率范围内不为零，符合最优输入信号的要求[21-22]。对于容性绝缘介质而言，随测试频率降低其阻抗增大，且目标频率范围为0.001Hz～0.04Hz，因此，最终变换得到如图3所示625s 输入激励电压信号[23]。
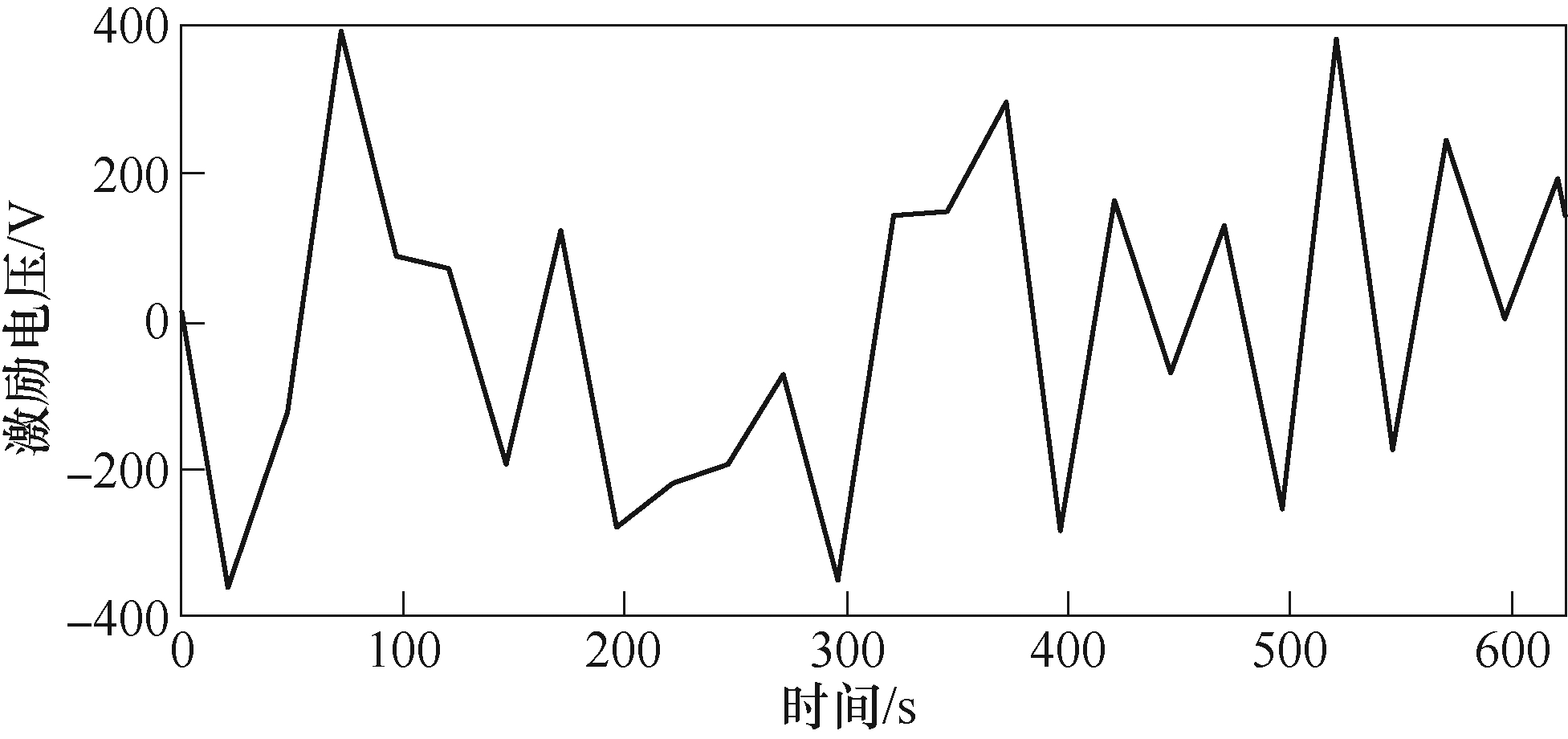
图3 输入激励电压信号波形
Fig.3 Input excitation voltage signal waveform
将激励电压施加到绝缘介质后获得的响应电流中便包含了绝缘的弛豫极化特性，通过激励电压和响应电流便可确定H-W 模型的输入和输出信号。残差二次方和函数 r (θ)为
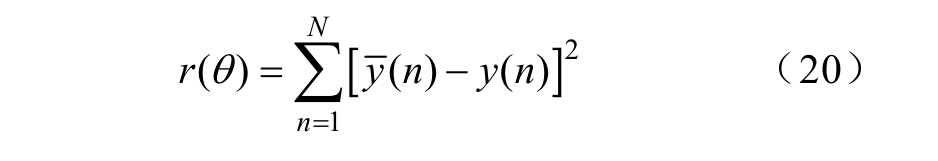
式中，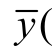
n )为当前辨识参数下数学模型输出信号；y(n)为实际测量油纸绝缘系统的输出信号；N 为采样点数。当 r (θ )取得极小值时，认为数学模型与实际测量油纸绝缘系统等效。
根据Gauss-Newton 迭代算法，通过有限次迭代计算，寻找未知参数θ 的最优解，从而使得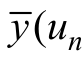
,θ )能够实现对于实际测试输入输出(un, yn)的最优拟合[24-25]，再将得到的参数最优解代入数学模型，从而确定待测油纸绝缘的唯一等效H-W 模型。
所获得H-W 等效数学模型的拟合精度与测试信号的信噪比、选取的非线性输入输出环节和线性环节的阶次以及迭代计算的次数有关。提升测试装置的屏蔽性能可保证测试信噪比，使测试信号中有效成分不受噪声影响，提高H-W 模型对绝缘拟合的准确性。而增加各个环节阶次和计算迭代次数亦有助于获得更为准确的等效模型，但阶次过高或迭代次数较多会增加冗余的计算量，导致拟合时间过长，对于油纸绝缘而言，不需要太高的环节阶次和迭代次数即可达到理想的时频转换精度。
2.3 频域介电谱的获取方法
基于H-W 模型的频域介电谱获取如图4 所示，在Matlab 中用不同频率离散正弦序列u 激励所确定的H-W 等效数学模型，得到响应电流的正弦序列i，并利用快速傅里叶变换（Fast Fourier Transform,FFT）算法将输入输出序列变换到频域提取相应的幅值和相位信息。
图4 基于H-W 模型的频域介电谱获取
Fig.4 Frequency domain spectroscopy acquisition based on H-W model
计算油纸绝缘系统的频域介电响应数据，有
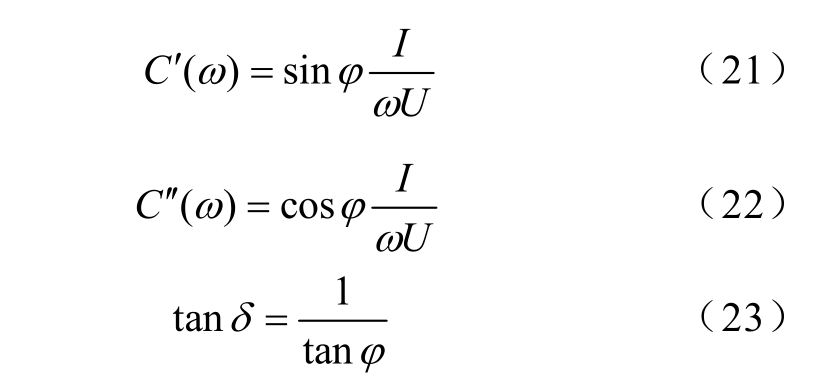
式中，ω =2π f 为激励信号的角频率；U 为施加正弦激励幅值；I 为响应电流幅值；φ 为功率因数角。
3 受潮对油纸绝缘非线性特性的影响
3.1 u-i 特性曲线
为研究水分含量对油纸绝缘系统非线性的影响，制备不同水分含量的油纸绝缘样品以测量其伏安特性。将厚度为1mm、直径为160mm 的圆形干燥普通牛皮绝缘纸板放入干燥、脱气的25 号环烷基变压器矿物绝缘油中，真空浸渍48h 得到干燥的油浸绝缘纸板样品，随后通过控制自然吸潮时间的方法制备出不同水分含量的油浸绝缘纸板，利用瑞士万通卡尔费休水分仪885+851 测得其水分含量m.c.分别为1.03%、3.45%、5.43%的（简称PB1、PB2 和PB3），分别为干燥、中等受潮和严重受潮三种受潮程度。
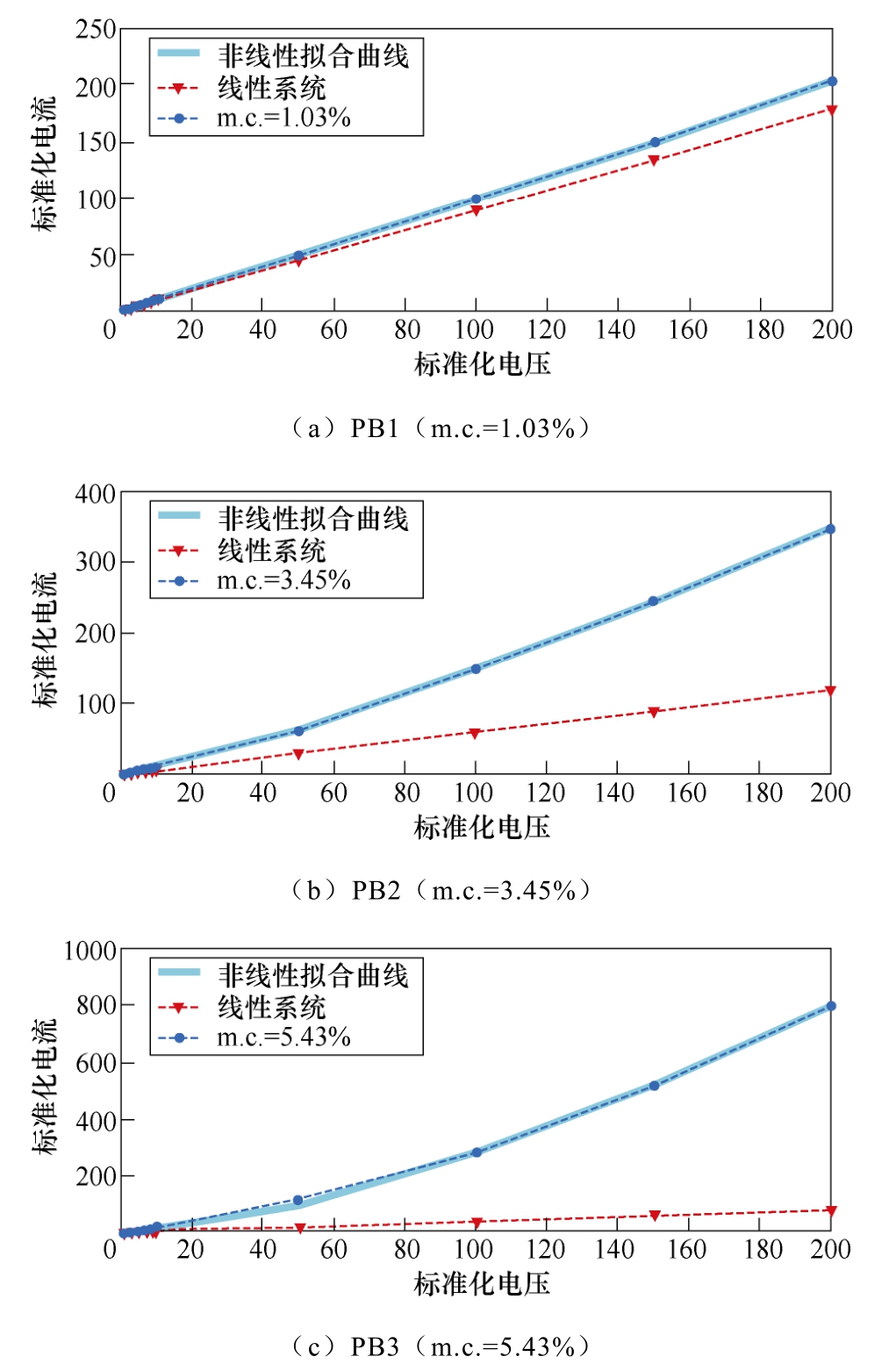
图5 不同水分含量油浸绝缘纸板u-i 特性曲线
Fig.5 u-i characteristic curves of oil-immersed pressboard with different moisture content
为了得到三类油浸绝缘纸板的u-i 特性曲线，对样品施加电压幅值为1～200 V、频率为0.001 Hz的正弦激励电压，测试不同电压幅值下的响应电流幅值。为方便绘图和拟合需要，以1V 的激励电压和对应的响应电流值为基准值，对电压电流进行线性标准化处理，得到u-i 特性曲线，如图5 所示。图5 中，响应电流幅值随受潮程度严重而增加，这是由于水分含量增加会导致油纸绝缘电导率增大，同时u-i 特性曲线逐渐呈现非线性特性。固体绝缘介质的电导特性可分为低电场电导区和高电场电导区，u-i 特性曲线在这两个区域中分别呈现欧姆特性（即i 随u 线性变化）和指数关系，油纸绝缘中水分含量的增加会导致导电离子的增加，电流与电压将不再成正比例关系，通常采用指数函数[26]或幂函数[27]来描述固体绝缘u-i 特性曲线的非线性特性。其中，幂函数关系为
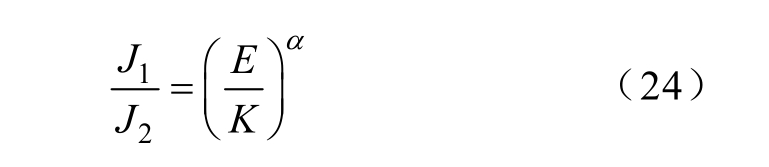
式中，J1 和J2 为施加于固体介质电场强度E 时对应的体电流密度；K 为一常数；α 为曲线的非线性系数。当α =1 时，J 与E 呈线性关系，对应的K 值即为固体绝缘的电阻率；当α ＞1 时，曲线的非线性程度随α 的增加而增加。
类似地，拟合三种油纸绝缘样品的u-i 特性曲线，有
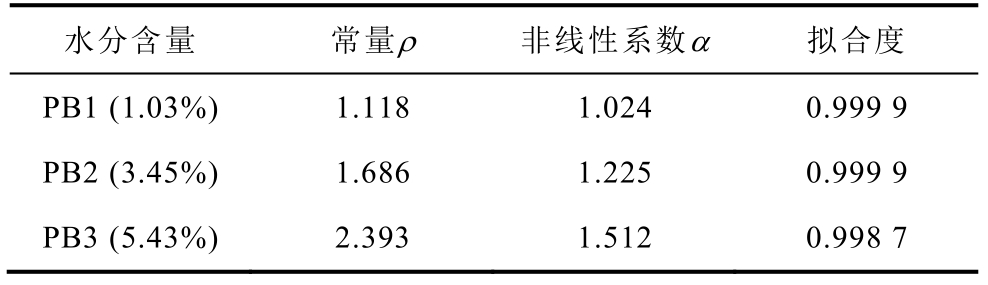
式中，I 为响应电流幅值；U 为激励电压幅值；ρ为与绝缘自身相关的常数。拟合结果见表1，可以看出，随着绝缘纸板受潮程度的增加，其非线性系数α 增大，非线性程度增加。拟合曲线亦绘制于图5，根据拟合度和图示曲线可知，拟合有效。
表1 不同水分含量油浸绝缘纸板的非线性拟合参数
Tab.1 The fitting parameters of nonlinearity of oil-immersed pressboard with different moisture content
?
当非线性系数α =1 时，即为绝缘的等效线性系统，如图5 所示，干燥的绝缘纸板PB1 的u-i 特性曲线仍然呈线性关系，而PB2 和PB3 的u-i 特性曲线偏离线性系统，表现出明显的非线性特性。
3.2 u-i 迟滞圆曲线
电压幅值和绝缘纸板受潮程度的增加会导致响应电流信号中高次谐波的产生，影响测量结果的准确性。本文测量了频率为1kHz 和0.001Hz，幅值为1～200V 的标准正弦电压下不同水分含量油浸绝缘纸板的响应电流，得到u-i 迟滞圆曲线如图6所示。
当响应电流中不存在谐波时，激励电压和响应电流的迟滞圆曲线应为一个闭合的椭圆环；而当谐波出现时，椭圆环则会发生畸变，并且随谐波成分的增加，畸变更加严重。从图6 中可以看出，三种受潮程度的绝缘纸板的迟滞圆曲线在高频下均为标准的椭圆环，而在低频下由于受潮程度的增加导致响应电流中高次谐波的出现，PB2 的迟滞圆曲线在激励电压等级较高时，可以看出椭圆环的畸变现象，而PB3 受潮程度最为严重，即使是在较低的激励电压下，椭圆环的畸变也十分明显。因此，随着绝缘纸板受潮程度的增加，响应电流中会产生高次谐波导致非线性现象，影响测量的准确性。
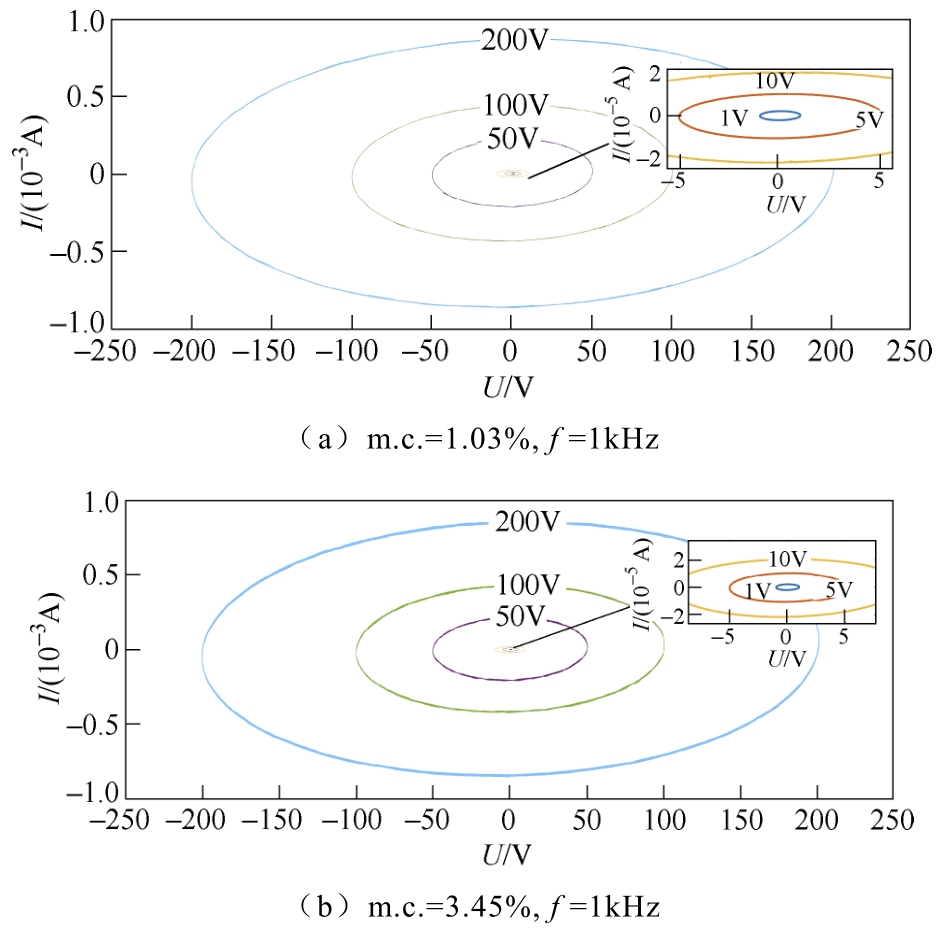
图6 不同水分含量油浸绝缘纸板u-i 迟滞圆曲线
Fig.6 u-i hysteresis curves of oil-immersed pressboard with different moisture content
3.3 tanδ 随激励电压U 的变化
介质损耗角正切值 tanδ 常用于表征交流电压下电介质内部的功率损耗大小，工程上常采用R、C并联电路模型对电介质进行等效，tanδ 的值由激励电压角频率ω、电介质的等效电阻R 和等效电容C共同决定，数值上等于1/(ω RC)，不随激励电压幅值变化而变化。图7 给出频率为0.001Hz 的正弦激励电压下三种受潮程度样品的 tanδ 随激励电压幅值的变化关系。
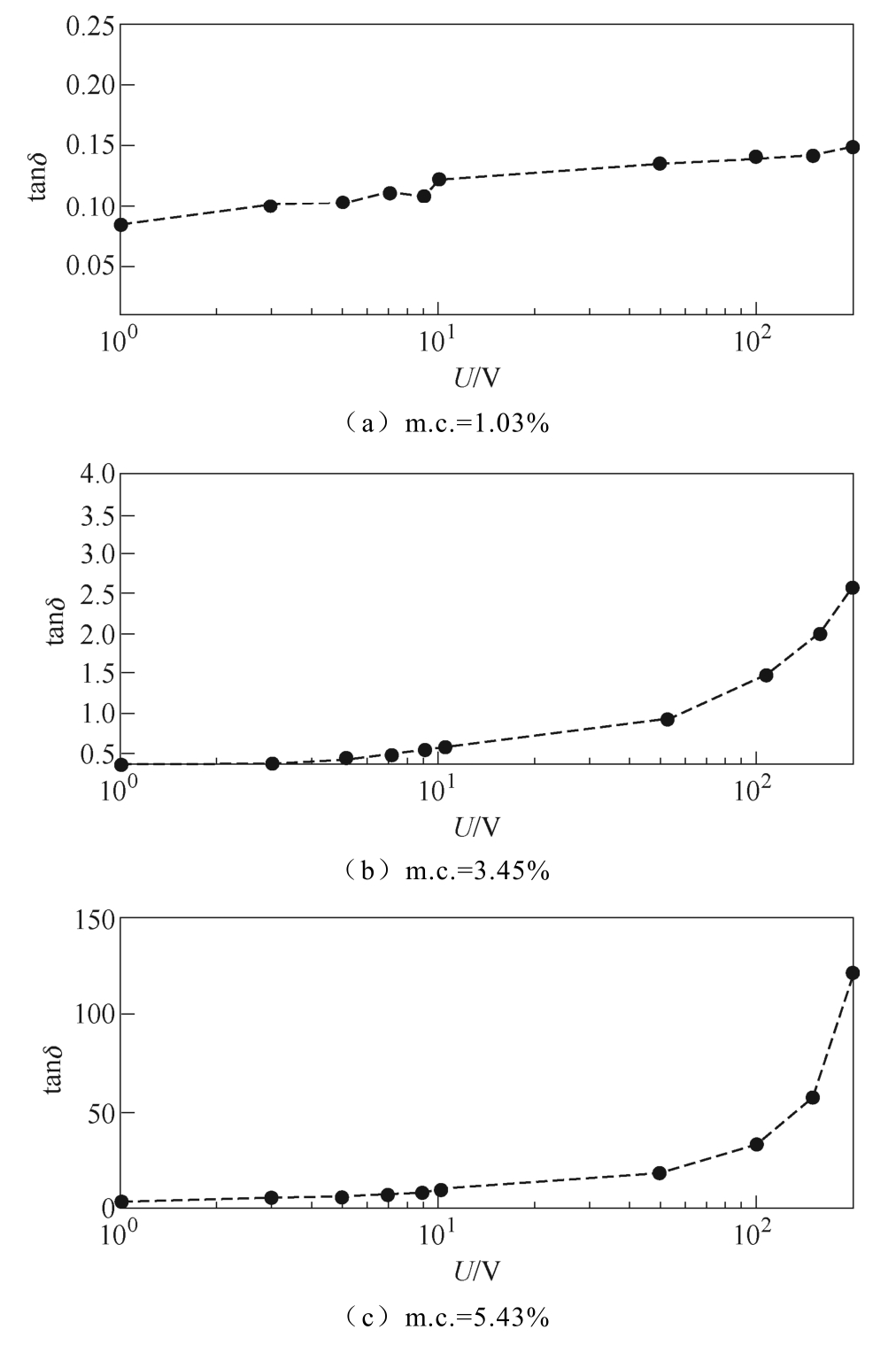
图7 不同水分含量油浸绝缘纸板tanδ -U 曲线
Fig.7 tanδ -U curves of oil-immersed pressboard with different moisture content
可以看出，激励电压幅值对不同受潮程度的绝缘纸板的 tanδ 值均会产生影响，随激励电压幅值的增加，tanδ 值增大。相比而言，水分含量最低的PB1 在1～200V 的测量电压变化范围内tanδ 值变化很小，约为0.1；而PB2 的tanδ 值则从U=1V 时的0.35 增加到U=200V 时的2.71；对于严重受潮的PB3，tanδ 值随激励电压幅值的增加呈现出更为明显的增长趋势。水分含量的增加导致 tanδ 受激励电压幅值影响的现象也是油纸绝缘非线性特性的一种表现形式。
4 不同时频转换方法的介电响应结果
首先采用标准扫频方法获取油纸绝缘样品的FDS 曲线，测试电压U=200V，测试频率范围f =0.001Hz～1kHz，测试温度T=25℃，不同水分含量油浸绝缘纸板的频域介电谱测试结果如图8 所示。
图8 不同水分含量油浸绝缘纸板的频域介电谱
Fig.8 FDS curves of oil-immersed pressboard with different moisture content
从扫频方法得到的FDS 结果中可以看出，在整个测试频率范围内，油纸绝缘的介质损耗tanδ 均随受潮程度的增加而增大，并呈现出不同的损耗峰形状，这与已有的研究成果吻合。
4.1 基于扩展Debye 模型和Fourier 变换的时频转换结果
通过扫频方法测量时，由于需要对每个所关心频率点进行完整的正弦波测量，在低频测量中需要耗费大量时间。因此，如引言中所提到的，可以选择采用时域的PDC 测试结果，计算扩展Debye 模型中的各阶R 和C 参量，进一步计算低频范围的频域介电谱结果。类似地，也可以通过Fourier 变换对极化去极化电流进行时频域转换，获取频域测试结果。
在200V 的直流电压下，对PB1～PB3 进行极化电流测量，极化时间为3 000s。利用1.1 节中式（1）～式（6）对所测的极化电流计算得到对应的扩展Debye 模型的R 和C 参量，见表2。
根据拟合得到的R 和C 参量，对PB1～PB3 的极化电流进行了拟合，并与实测极化电流进行对比，不同水分含量油浸绝缘纸板极化电流曲线如图9 所示，拟合极化电流和实测极化电流基本重合，说明通过极化电流所确定的扩展Debye 模型有效。
在确定扩展Debye 模型中的R 和C 参量后，利用相应的等效电路模型对PB1～PB3 进行频域数据计算。类似地，根据1.2 节提到的Fourier 变换方法对测量的时域极化电流作时频转换，将通过扩展Debye 模型和Fourier 变换得到的介损频谱结果同扫频方法得到的结果进行对比，不同受潮程度油纸绝缘通过传统时频转换得到介损频谱如图10 所示。
表2 不同水分含量油浸绝缘纸板的扩展Debye 模型参量
Tab.2 The parameters of extended Debye model of oil-immersed pressboard with different moisture content
?
图9 不同水分含量油浸绝缘纸板极化电流曲线
Fig.9 Polarization current curves of oil-immersed pressboard with different moisture content
从图10 可以看出，对于PB1 和PB2，由于其受潮程度较低，纸板不表现非线性特性或仅表现出轻微的非线性特性，通过扩展Debye 模型和Fourier变换对极化电流进行时频转换得到的介损 tanδ 频域转换结果在0.001Hz～0.04Hz，与通过扫频方法测量得到的介损结果十分接近。其中，扩展Debye模型的转换结果与扫频测试结果在高频误差较大是由于油纸绝缘在高频和低频极化特性不同，对应扩展Debye 模型也有所差异，而根据极化电流得到的扩展Debye 模型主要反映低频极化特性。而对于严重受潮的绝缘纸板PB3，通过两种时频转换方法得到的介损结果均高于扫频测试结果。这是由于油浸绝缘纸板在受潮严重时表现出强烈的非线性特性，转换结果有较大误差。
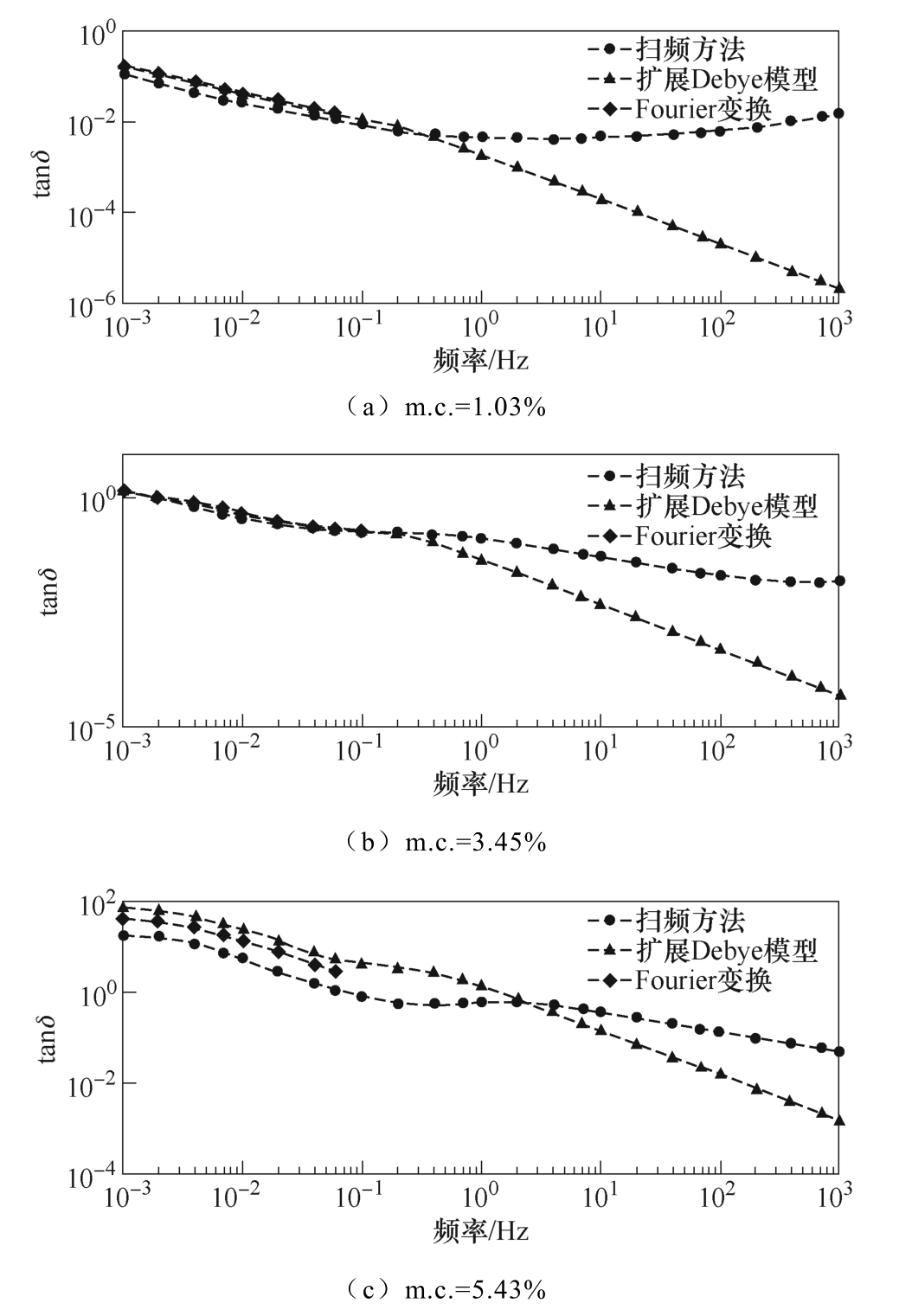
图10 不同水分含量油浸绝缘纸板传统时频转换方法介损频谱
Fig.10 FDS curves of oil-immersed pressboard with different moisture content by conventional time-frequency conversion method
不难想象，对于现场需要测试设备的油纸绝缘系统来说，事先并不知道其受潮程度，为了在较短时间内获得低频段的FDS 特性曲线，无论采用扩展Debye 模型或是Fourier 变换的转换方法，均有可能由于油纸绝缘的非线性特性而造成较大的误差。
4.2 基于H-W 模型的时频转换结果
按照2.2 节介绍的方法分别获取三种受潮程度绝缘样品的H-W 等效模型。在根据响应电流和激励电压信号拟合H-W 模型参数时，对线性环节分子、分母阶次以及非线性环节多项式阶次均设定为 9阶，即式（17）～式（19）中，m=n=i=j=9。采用Matlab 实现H-W 模型参数的辨识，获得H-W 模型的参数后，给模型输入不同频率的正弦电压信号，结合模型输出的响应电流信号以计算FDS 曲线。
为了验证H-W 等效数学模型的有效性，以PB3为例，采用频率为1mHz、幅值为200V 的正弦序列激励PB3 对应的H-W 模型，对比输出等效电流信号和实测电流信号在整个周期的时域波形。如图11所示，等效电流与实测电流重合，标准方均根误差（NRMSE）为
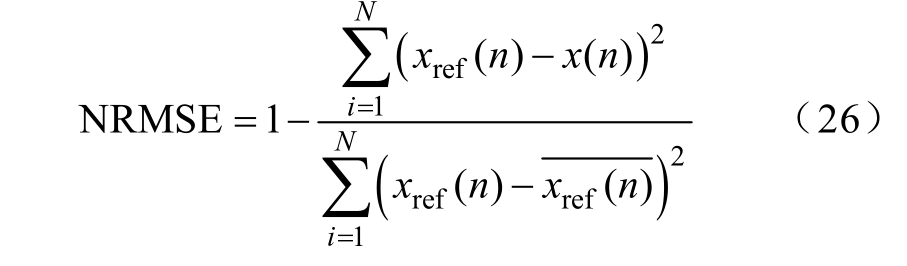
式中，xref (n)为参考数组；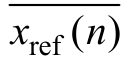
为参考数组平均值；x(n)为计算数组。计算拟合度为99.51%，表明H-W模型能准确表达油纸绝缘的低频特性。
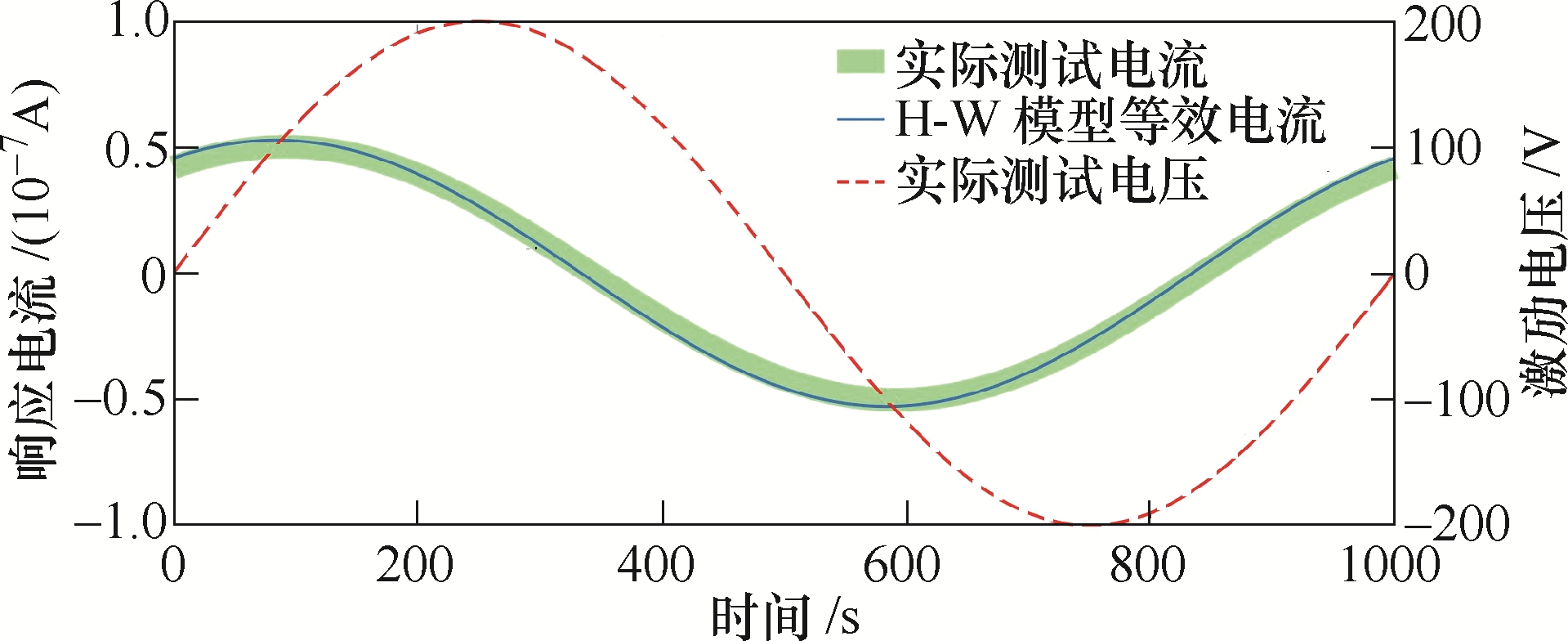
图11 频率1mHz、幅值200V 正弦电压下PB3 拟合电流与实测电流对比
Fig.11 Comparison of fitted current and measured current at 1mHz and 200V sinusoidal voltage of PB3
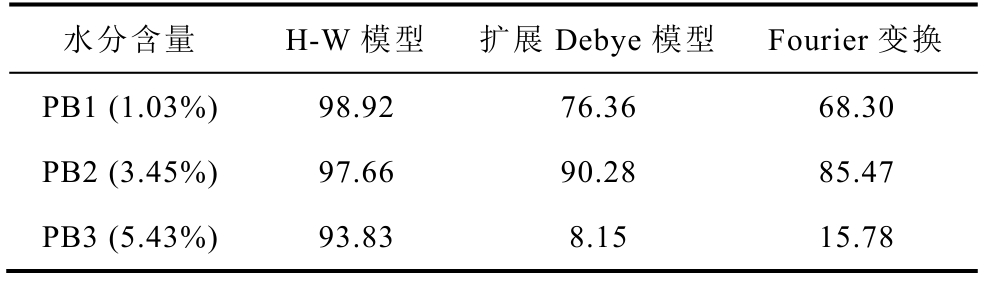
获得PB1～PB3 对应的H-W 模型后，根据2.3节中的方法得到目标频域范围的介电响应参数。图12 为1mHz～0.04Hz 频域范围内，H-W 模型转换所得tanδ 与扫频方法测试得到tanδ 的对比结果。如图12 所示，由于H-W 模型中包含了输入和输出非线性环节，兼具线性和非线性特性。无论油浸绝缘纸板的受潮情况如何，通过H-W 模型进行时频转换得到的介损都能与扫频测试结果很好地吻合。为了更清晰对比三种时频转换方法对不同水分含量油浸绝缘纸板介质损耗的转换效果，采用式（26）计算NRMSE 评估介损的拟合度，最终计算结果见表3。
图12 不同水分含量油浸绝缘纸板H-W 模型转换介损频谱
Fig.12 FDS curves of oil-immersed pressboard with different moisture content by H-W model conversion method
表3 不同时频转换方法的介损转换拟合度
Tab.3 Fitting degree of converted dielectric loss by different time-frequency conversion methods（%）
?
从表3 的拟合结果中可以看出，H-W 模型对于不同水分含量的介质损耗转换结果与扫频方法的拟合度都达到了90%以上，且明显高于扩展Debye 模型和Fourier 变换方法得到的结果，证明了H-W 模型可用作线性和非线性系统的时频转换桥梁，并保证了转换结果的准确性。
5 结论
本文测试了不同受潮程度的油纸绝缘系统的非线性特性，证明了传统时频转换方法的局限性，为等效油纸绝缘的非线性特性，提出采用H-W 模型表征油纸绝缘，实现时频域介电响应数据转换，得到了以下结论：
1）受潮会导致油纸绝缘的非线性特性逐渐显现，随受潮程度的增加，油纸绝缘的非线性程度增强，响应电流中的谐波成分增大，影响频域介电谱的扫频测试结果。
2）基于扩展Debye 模型和Fourier 变换的时频转换方法由于其线性特性，仅适用于受潮程度较低的油纸绝缘系统；当油纸绝缘由于受潮表现出非线性特性，时频转换结果会出现误差，导致受潮状态评估时产生不客观的评价。
3）采用H-W 等效数学模型实现油纸绝缘介电响应的时频转换，其包含了输入和输出非线性环节，可以同时等效线性和非线性绝缘系统，具有更广泛的适用范围。通过H-W 模型得到不同受潮程度的油纸绝缘的时频转换结果具有较高精度。
[1] 杨丽君, 王松华, 郑含博, 等. 多频正弦电压激励的快速频域介质响应测试及波形参数优化方法[J].电工技术学报, 2018, 33(1): 175-184.Yang Lijun, Wang Songhua, Zheng Hanbo, et al. A fast frequency domain dielectric spectroscopy method under multisine voltage excitation and waveform parameters optimization[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 175-184.
[2] 蔡金锭, 叶荣, 陈汉城. 回复电压多元参数回归分析的油纸绝缘老化诊断方法[J]. 电工技术学报,2018, 33(21): 5080-5089.Cai Jinding, Ye Rong, Chen Hancheng. Aging diagnosis method of oil-paper insulation based on multiple parameter regression analysis of recovery voltage[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 5080-5089.
[3] Saha T K. Review of time-domain polarization measurements for assessing insulation condition in aged transformers[J]. IEEE Transactions on Power Delivery, 2003, 18(4): 1293-1301.
[4] 高竣, 廖瑞金, 王有元, 等. 基于扩展 Debye 模型的变压器油纸绝缘老化特征量研究[J]. 电工技术学报, 2016, 31(4): 211-217.Gao Jun, Liao Ruijin, Wang Youyuan, et al. Ageing characteristic quantities of oil-paper insulation for transformers based on extended Debye model[J].Transactions of China Electrotechnical Society, 2016,31(4): 211-217.
[5] 杨丽君, 彭攀, 高竣, 等. 基于频域介电响应特征指纹的油纸绝缘受潮及老化状态区间识别[J]. 电工技术学报, 2018, 33(9): 2105-2114.Yang Lijun, Peng Pan, Gao Jun, et al. The range recognition of moisture and aging status of oil-paper insulation based on frequency domain dielectric response characteristic fingerprint[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 2105-2114.
[6] 张明泽, 刘骥, 齐朋帅, 等. 基于介电响应技术的变压器油纸绝缘含水率数值评估方法[J]. 电工技术学报, 2018, 33(18): 4397-4407.Zhang Mingze, Liu Ji, Qi Pengshuai, et al. Numerical evaluation method for moisture content of transformer oil-paper insulation based on dielectric response technique[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4397-4407.
[7] 高竣. 基于介电指纹特征识别的变压器主绝缘老化与受潮状态评估研究[D]. 重庆: 重庆大学, 2017.
[8] 张涛, 左倩, 任乔林, 等. 油纸绝缘非标准极化谱的中心时间常数提取[J]. 电机与控制学报, 2018,22(8): 82-88.Zhang Tao, Zuo Qian, Ren Qiaolin, et al. Central time constant of nonstandard polarization spectrum of oil-paper insulation[J]. Electric Machines and Control,2018, 22(8): 82-88.
[9] Saha T K, Purkait P. Investigation of polarization and depolarization current measurements for the assessment of oil-paper insulation of aged transformers[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2004, 11(1): 144-154.
[10] 贺德华, 蔡金锭, 黄云程. 基于等效电路参数特征量的油纸绝缘老化状态评估[J]. 电机与控制学报,2017, 21(6): 44-49.He Dehua, Cai Jinding, Huang Yuncheng. Study on insulation condition of power transformer based on the equivalent circuit characteristic parameters[J].Electric Machines and Control, 2017, 21(6): 44-49.
[11] Zhao Haoxiang, Yang Li, Wen Jiaye, et al. Diagnosis of moisture content in oil-immersed paper based on dielectric loss with variable voltage at power frequency[C]//International Conference on Dielectric Liquids,Roma, 2019: 1-4.
[12] Sha Yanchao, Zhou Yuanxiang, Nie Dexin, et al. A study on electric conduction of transformer oil[J].IEEE Transactions on Dielectrics and Electrical Insulation, 2014, 21(3): 1061-1069.
[13] Yang Xu, Nielsen S, Ledwich G. Investigations of dielectric monitoring on an energised transformer oilpaper insulation system[J]. IET Science, Measurement& Technology, 2015, 9(1): 102-112.
[14] 董明, 王丽, 吴雪舟, 等. 油纸绝缘介电响应检测技术研究现状与发展[J]. 高电压技术, 2016, 42(4):1179-1189.Dong Ming, Wang Li, Wu Xuezhou, et al. Status and progress in study of dielectric response technology for oil-paper insulation[J]. High Voltage Engineering,2016, 42(4): 1179-1189.
[15] Koch M, Feser K, Reliability and influences on dielectric diagnostic methods to evaluate the aging state of oil-paper insulations[C]//International Conference on Advances in Processing, Testing and Application of Dielectric Materials, Wrocław, 2004: 1-7.
[16] Ashkezari A D, Ma H, Saha T K, et al. Investigation of non-linearity in dielectric response measurements for transformer insulation diagnosis[C]//IEEE PES Innovative Smart Grid Technologies, Perth, 2011: 1-7.
[17] Yang Lijun, Chen Junru, Wang Songhua, et al.Dielectric response measurement of oil-paper insulation based on system identification and its timefrequency-domain conversion method[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2018, 25(5): 1688-1698.
[18] 杜林, 冉鹂蔓, 蔚超, 等. 基于扩展德拜模型的油纸绝缘受潮频域特征量研究[J]. 电工技术学报,2018, 33(13): 3051-3058.Du Lin, Ran Liman, Yu Chao, et al. Study on frequency domain characteristics of moisture in oilpaper insulation based on extended Debye model[J].Transactions of China Electrotechnical Society, 2018,33(13): 3051-3058.
[19] 陈晶. 一类非线性系统的参数辨识方法研究[D].江苏: 江南大学, 2013.
[20] Godfrey K R. Introduction to non-binary signals in system identification[C]//International Conference on Control, Edinburgh, 1991: 161-166.
[21] 艾余雄, 寇艳红. 一种基于FPGA 的高斯白噪声发生器的设计与实现[J]. 遥测遥控, 2009, 30(6): 36-40.Ai Yuxiong, Kou Yanhong. Design and implementation of a gaussian white noise generator based on FPGA[J]. Journal of Telemetry, Tracking and Command, 2009, 30(6): 36-40.
[22] 谭建国. 泊松白噪声激励下的随机时滞系统的数值解及应用研究[D]. 天津: 天津大学, 2010.
[23] Yang Lijun, Chen Junru, Jun Gao, et al. Accelerating frequency domain dielectric spectroscopy measurements on insulation of transformers through system identification[J]. IET Science, Measurement & Technology,2018, 12(2): 247-254.
[24] Chittora P, Singh A, Singh M. Gauss-Newton-based fast and simple recursive algorithm for compensation using shunt active power filter[J]. IET Generation,Transmission & Distribution, 2017, 11(6): 1521-1530.
[25] 何昆鹏, 王晨阳, 王晓雪. 基于高斯牛顿迭代的MIMU 误差参数辨识[J]. 沈阳工业大学学报, 2015,37(3): 318-323.He Kunpeng, Wang Chenyang, Wang Xiaoxue. Error parameter identification of MIMU based on Gauss-Newton iteration[J]. Journal of Shenyang University of Technology, 2015, 37(3): 318-323.
[26] 朱德恒, 严璋. 高电压绝缘[M]. 北京: 清华大学出版社, 1992.
[27] Levinson L M, Philipp H R. The physics of metal oxide varistors[J]. Journal of Applied Physics, 1975,46(3): 1332-1341.