0 引言
油纸绝缘系统是油浸式变压器、油浸式高压套管、油浸式互感器等电气设备内绝缘的主要形式。油纸绝缘类设备在电网设备中占据了很大比例，其在输变电过程的各个环节中承担着能量转换、绝缘保护、电能计量等重要作用。由于长时间受机械压力、化学腐蚀、表面污秽、运行电压及潮湿等多因素的联合作用，电气设备的绝缘性能将逐渐下降，并可能最终导致绝缘击穿而引发设备故障[1]。其中，因水分会使绝缘纸受潮而被视作油纸绝缘系统的“头号威胁”[2]。因此，准确评估油纸绝缘受潮状态成为保障设备安全乃至电力系统运行可靠性的关键问题之一。
近年来，基于电介质弛豫理论的介电响应类方法[3]——回复电压（Return/Recovery Voltage Measurement,RVM ） [4-5] 、 极 化 去 极 化 电 流（ Polarization/Depolarization Current, PDC）[6]以及频域介电谱[7-8]（Frequency Domain Spectroscopy, FDS）作为新型无损绝缘状态检测手段而逐渐成为国内外研究热点。随之产生的问题则是如何准确解读各种介电响应曲线所反映出的绝缘受潮信息。目前主要有以下三种基本思路：①对比实测与标准样本的曲线，通过两者之间的相对位置关系对受潮程度做出定性评估[9]；②直接提取曲线本身的特征点或其他几何、统计特征作为特征量，建立这类特征量与微水含量之间的关系式，以对水分含量进行反推计算[10-11]；③参照曲线反解绝缘介质某一介电响应模型的全部参数，并从参数变化模式的角度寻找对水分含量变化敏感的特征参量[12-13]。其中，通过建模分析受潮状态的途径，因其基于电介质的微观介电行为，所以模型参数具有清晰的物理含义且能够建立与微观行为之间的数学联系，有助于直接确定绝缘受潮状态与水分含量之间的数值关系。
目前，有关学者对油纸绝缘等效模型的状态特征量进行了大量研究。例如，林燕桢等基于回复电压曲线结合带压缩因子的改进离子群算法识别扩展德拜模型参数，指出模型大时间常数支路参数对油纸绝缘微水含量较敏感[14]；刘捷丰等利用去极化电流曲线通过分步拟合法求解扩展德拜模型（extended Debye model）参数，并基于去极化电流理论提取极化电量的斜率和稳定极化电量作为受潮状态特征参数[15]。这类研究所采用的等效模型大多为扩展德拜模型，且用于模型参数计算的参考源数据大多采用RVM 和PDC 两种时域介电谱。但由于测量仪器的最高采样频率限制，时域介电谱的高频段测量精度通常较低，导致时域谱图携带的高频信息不准确，加之时域小信号测量的噪声敏感性问题，时域介电响应的总体测量误差相对较大。因此，作为参数辨识的源数据，时域介电谱的这种误差特性将直接传递至由其计算出的模型参数上，并将直接影响最终受潮诊断的准确性。相比之下，FDS 测量频带宽泛，同时抗干扰能力强，目前已被更加广泛地应用于前期定性评判电气设备的绝缘水分含量上。理论上而言，直接采用FDS 曲线辨识的模型将具有良好的宽频精度，是有效利用FDS 宽频介电信息提取特征量的模型基础。然而，采用FDS 辨识扩展德拜模型却鲜有研究。
针对这一问题，本文基于油纸绝缘介电响应等效模型——扩展德拜模型，通过分析模型参数变化规律提取介电特征参量：首先针对油纸电容式试验套管开展不同温度下的频域介电谱测试，基于频域介电谱试验数据，提出油纸绝缘宽频等效电路模型参数的计算方法；然后，基于参数化的油纸绝缘扩展德拜模型，分别研究了温度、绝缘微水含量对电路模型参数的影响规律，并在此基础上提取表征绝缘介质受潮特性的特征参量，实现了套管油浸纸芯体受潮程度的定量判断。
1 基于FDS 的油纸绝缘扩展德拜模型参数辨识
1.1 扩展德拜模型
变压器油为弱极性分子，而绝缘纸为极性分子。绝缘纸由纤维素组成，纤维素分子自身的偶极矩使得分子在外加电场下形成分子极化。水分子中的氧原子与两个氢原子的空间位置不共线，三个原子呈三角形排布，水分子内部不重合的正负电荷中心使得水分子具有较大的偶极矩。而绝缘纸的吸水性很强，绝缘材料中的水分会显著影响介质总体的介电特性，改变介质的弛豫时间。在外电场的作用下，受潮的绝缘介质内部会由束缚态和自由态的水分子发生弛豫过程引起偶极子极化。同时，油浸纸绝缘是两种电介质的组合绝缘形式，其极化过程同单一介质的情况存在差异，由于电导率、介电常数不同，在电场作用下，电荷会累积于两种材料的交界面，形成界面极化。
偶极子极化与界面极化均属于弛豫极化，而原始的德拜模型采用单一的RC 结构模拟弛豫极化过程。但油浸纸绝缘系统的微观介电过程十分复杂，其内部同时存在具有多弛豫时间的有损极化过程，介质的总极化电流则为具有不同弛豫时间的极化电流分量共同组成，因此可将单条RC 支路扩展为多条电阻电容串联后的并联结构以对油纸绝缘系统整体的介电响应进行更为准确的等效，此即为扩展德拜模型[16]，如图1 所示。在该模型中，C0 表征具有一定结构的绝缘主体以及无损极化所体现出的总体电容量，R0 为绝缘电阻，表征介质的电导特性，多条Ri-Ci 串联支路则代表具有各自松弛时间的多种弛豫极化行为。
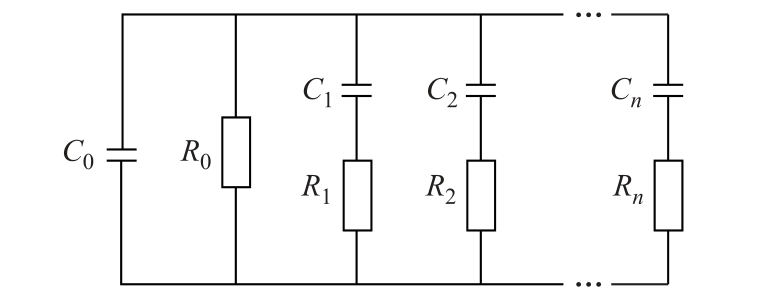
图1 扩展德拜模型
Fig.1 Extended Debye model
复电容实部、虚部及介质损耗因数是频域介电谱的几种常用谱参量，式（1）～式（3）给出了在扩展德拜模型的电路结构下，这些谱参数同等效电路元件值之间的关系。
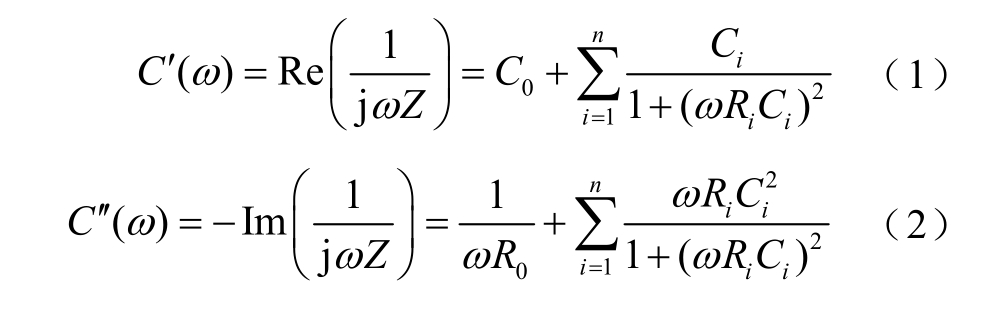
式中，C′(ω)、C"(ω)分别为复电容的实部和虚部，介质损耗因数定义为复电容虚部与实部的比值，即
1.2 扩展德拜模型参数的求解
除用于在理论上定性解释电介质的介电过程外，为使该模型具有实用意义，需要进一步根据实测的介电响应进行模型参数估计，以便借助模型参数值充分反映介电响应结果所携带的水分信息。等效电路参量估计的目的是计算出模型中所有支路的元件参数值，使得依据式（1）～式（3）得出的计算谱图同实测谱图之间的总体误差达到最小。由于复电容实部、虚部以及介质损耗因数这三个参量仅两两独立，因此此处仅选取复电容实部C′(ω)和虚部C″(ω)作为参数估计的参照数据。
针对电介质介电谱这一具体的物理问题，应注意到，复电容虚部在全频段跨越的量级差异十分显著。若直接使用基于最小二乘的绝对误差控制项将可能导致算法进入病态，即数值较小的谱图数据点无法得以精确匹配，因而首先对实部及虚部误差项分别进行加权，权值设为实测值倒数的二次方，因而复电容实部和虚部两部分的单独的优化目标可合并为如式（4）所示的加权最小二乘单目标优化模型。
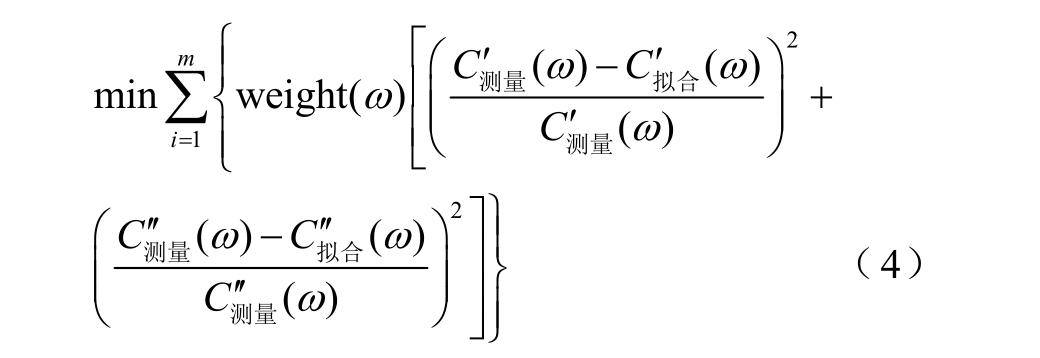
式中，weight(ω)为引入的与频率点相关的另一权值函数。由于扩展德拜模型参数估计的结果是绝缘含水量诊断的数值基础，因此，模型参数辨识并非纯数学问题，而更应关注模型参数对介电特征的反应程度和契合度，使参数辨识具有更强的物理意义而不仅是数值逼近。因此，本文通过权值函数weight(ω)对FDS 的低频（对绝缘受潮敏感的特征频带）数据进行赋权处理，以提升频带范围内的拟合精度，以便将低频段所携带的受潮信息更加突出地体现在扩展德拜模型的参数上。而另一方面，从实际测量的角度而言，测试频率越低，则流过介质的总电流越小，因而低频段数据的测量精度又相对较低。平衡考虑受潮诊断及源数据准确性两方面，选取权值函数具体表达式为
本文采用一种遗传算法（Genetic Algorithm, GA）与LMA 算法（Levenberg-Marquardt Algorithm）的融合方法（GA-LMA）进行扩展德拜电路的元件参数计算[17]。首先，调用遗传算法开始最优化模型的全局求解；第二步，将遗传算法结束后给出的粗略解作为L-M 算法的初始值进行局部优化，直至满足最终的收敛精度要求从而得出匹配实测谱图的电容与电阻值。此外，扩展德拜模型实际是一系列具有相似结构的电路集合，仅当极化支路数n 被给定后模型结构及参数辨识目标函数才能唯一确定。一般意义下，该电路的串联RC 数量越多则越符合介质内部极化过程的多样性及真实微观行为，但RC 串联结构数量过多会同时增加待求未知量的数量。由于多参数非线性拟合问题本身的复杂性，待优化参数的增多会显著增加计算量。同时，实测样本数据点有限，过多的参数将造成模型过拟合及泛化性能变差。因此，参考目前的相关文献研究结果[18-19]，并综合考虑逼近效果、计算复杂度及模型性能等多方面的因素，在后文分析中均将该电路模型的RC串联支路数默认为6 条而不再单独另行说明。最后，采用拟合优度R 作为评价指标用以衡量扩展德拜模型对源数据的逼近效果，即
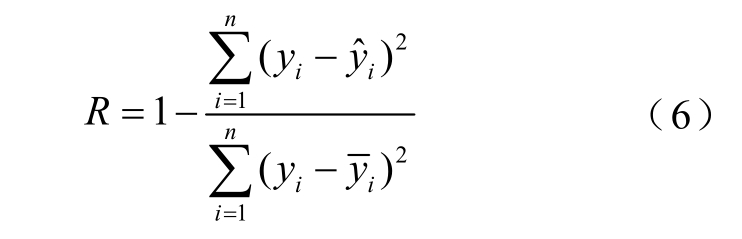
式中， y i为在FDS 测量频点上的某一介电谱参数，此处为复电容值；
为对应频点的计算值，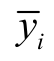
为所有频点测量数据的均值。R 的取值范围为(0, 1)，其值越趋近于1 则表示模型对目标数据集的逼近效果越理想。
2 油纸电容式套管人工受潮模拟试验
2.1 试验套管
油纸电容式套管是电网中较具代表性的一类油纸绝缘设备，其主要功能是实现设备引出线与设备外壳之间的电气绝缘及机械固定作用。若以变压器油纸电容式套管为油纸绝缘设备的代表性研究对象，则需以测量自含有受潮故障的套管介电谱图为数据来源进行分析。因此，首先对套管进行了人工受潮模拟实验。
为避免使用真型套管进行实验存在的体积、质量大、试验操作困难、试验周期长、试验条件难以精确控制等缺点，设计了一种小型油纸电容式套管试验模型用于受潮模拟，兼顾了试验对象的真实性和可操作性。该模型的内、外绝缘结构设计和商用套管保持基本一致，并考虑到模型套管主要用于开展介电响应测试，其测试激励电压较低（＜500V），可对应降低对电容芯子的电气强度要求，以达到减少电容屏层数，从而显著缩小试验套管体积的目的。和真型套管相对应，模型套管仍然由油浸纸卷制而成的主芯体、中心导管、外瓷瓶以及安装法兰组成。其中，电容芯子承受套管导杆对地的运行电压，为套管内绝缘的主要部分。在电容芯子等电容设计原则之下，并考虑其电气强度满足介电响应及直阻测试电压的基础上，将该套管模型的电容芯子设计为六层极板、三级台阶式的结构，套管模型结构示意图及实物图分别如图2 和图3 所示。
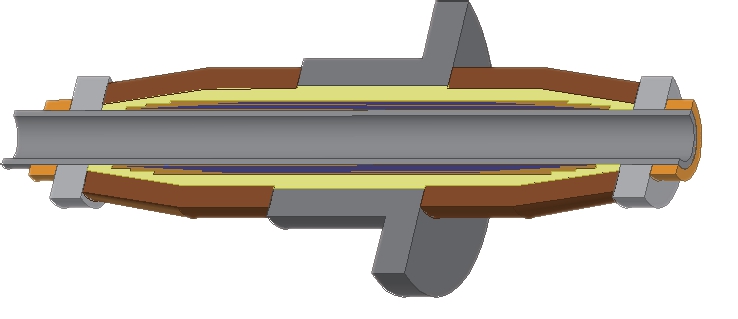
图2 试验套管剖面结构示意图
Fig.2 Section view of the test bushing
图3 电容芯子及试验套管实物图
Fig.3 Photographs of the test bushings and their condenser bodies
2.2 受潮电容芯子的制备
不同含水量的电容芯子采用人工吸潮的方式进行制备，因此第一步是按照真实套管的生产工艺流程制备出正常干燥的套管芯子。首先，将卷制完成的电容芯子和用于浸润芯子的绝缘油分别置于特制的真空罐中进行干燥预处理，并将真空罐抽真空后放入温度箱中（干燥温度设定为90℃）进行真空干燥48h。真空干燥结束后，将电容芯子置于60℃真空环境下浸油48h，最后向真空罐中充入氮气浸油24h，以使套管芯子油纸间隙充分浸油，上述预处理过程同真实套管的生产工艺流程保持一致。
预处理过程完成后，将充分浸油的电容芯子置于空气中进行吸潮，并通过称重法制备了具有一定预期含水量的样本芯子。本文共计进行了前后两阶段的受潮模拟试验，第一阶段主要采用受潮芯子进行变温试验，则分别制备了含水量为0.71%、1.78%、2.62%的三个电容芯子样本；第二阶段对样本芯子的水分含量阶梯进行了更为精细的划分，分别制备了预期含水量为0.79%、0.93%、1.12%、1.27%、1.35%、1.54%、1.66%、2.71%、2.86%、3.12%的10 组样本用于在恒温50℃下进行介电响应试验。为便于区分，下文将第一阶段制备的三个电容芯子称为1～3 号电容芯子，而将与第二阶段10 组不同水分含量相关的数据称为“不同含水量下”的样本芯子数据。
受潮处理完毕后，需将芯子同套管模型的其余部件进行整体组装。组装完成后，对套管抽真空静置24h，然后打开注油阀，绝缘油被缓慢吸入套管，完成一次完整的制备过程，试验套管的整体制备流程如图4 所示。
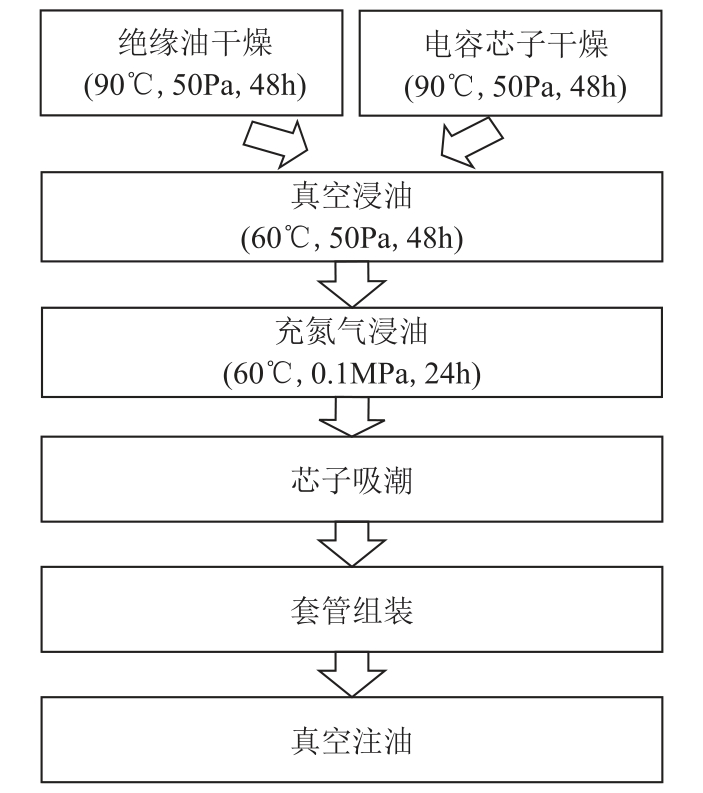
图4 受潮套管的制备流程
Fig.4 Preparation process of the moistened bushings
2.3 试验流程
在完成受潮套管的制备后，将样本套管放入温度箱中进行控温条件下的介电响应测量，测量仪器采用Dirana 介电响应分析测试仪。测试的接线方式选择为带屏蔽的UST (Ungrounded Specimen Test)方式，其同现场对真实套管主绝缘进行FDS 及工频介损测试的接线方式完全一致。在此连接方式下，响应电流信号直接取自末屏，主要反映绝缘芯子本体的介电响应，套管腔体中绝缘油隙的影响可忽略不计。同时，屏蔽端子能去除套管瓷套表面泄漏电流对频域介电谱结果的影响，介电响应试验装置如图5 所示。
图5 介电响应试验装置图
Fig.5 Photographs of the dielectric response test setup
第一阶段变温试验的操作步骤为：①以 30℃为起始测量温度点，以10℃为变温步长，每次升温并保温至下一温度测点持续 6h，直到温度达到最后一个测点 80℃；在每一测试温度下开展样本套管的频域介电谱测量及绝缘油温度的实时监测；②在完成频域介电谱测量后，通过Keithley6517B 高阻计测量该温度下套管的绝缘电阻。特别地，绝缘电阻描述了电介质在直流电压下的电导行为，也属于基本介电参量之一，在第4 节中将同时使用FDS及绝缘电阻值两类实测源数据开展模型参数辨识。第二阶段恒温试验的10 组样本依次在50℃的恒定温度下完成全程测量，其测量方法和参量与第一阶段相同。
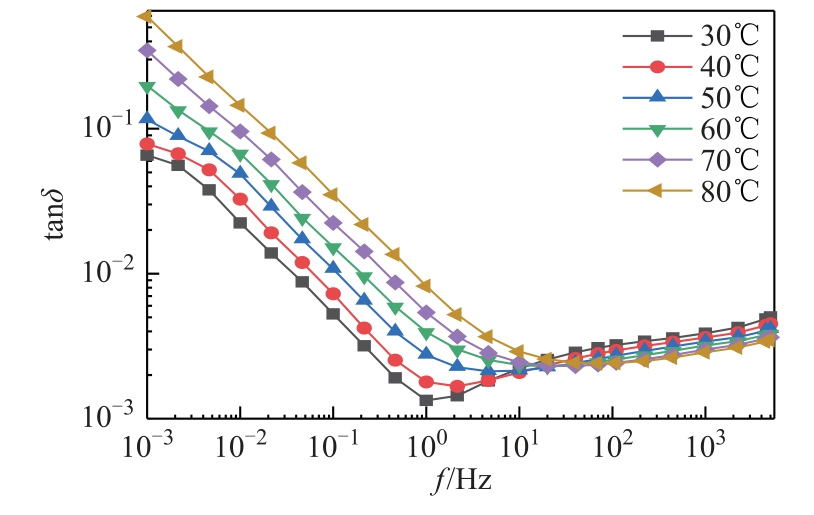
图6 1 号样本芯子介损曲线
Fig.6 The tanδ-f curves of 1# condenser body
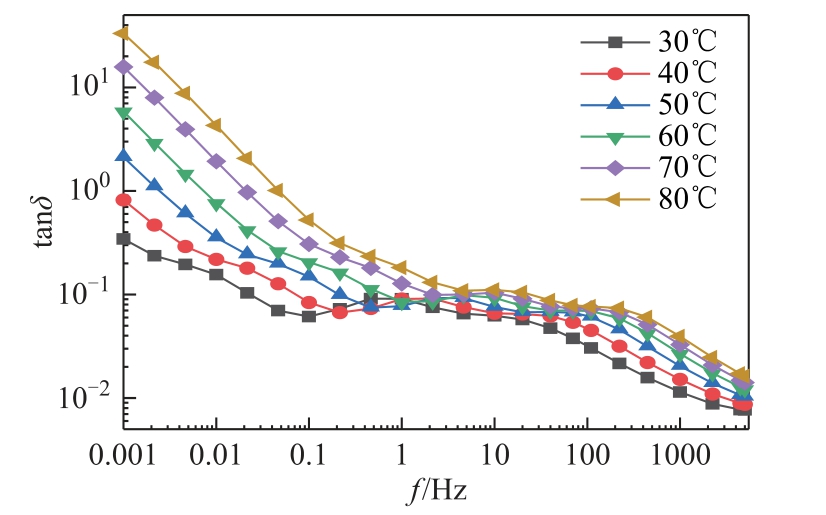
图7 2 号样本芯子介损曲线
Fig.7 The tanδ-f curves of 2# condenser body
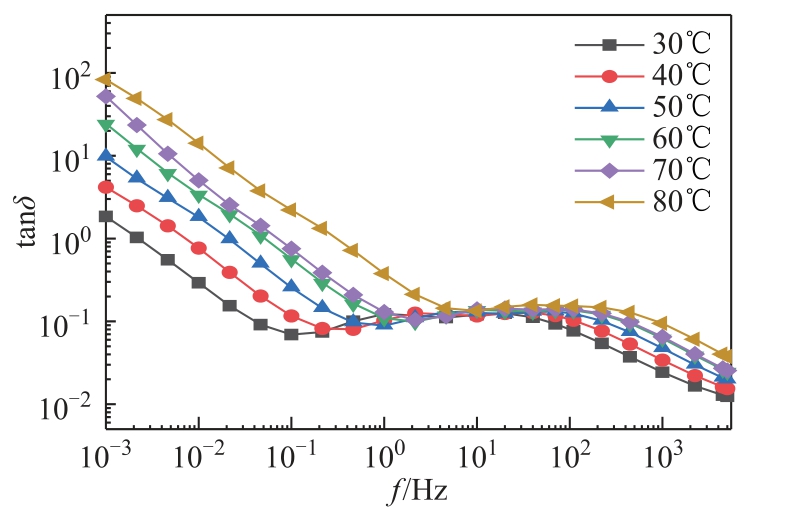
图8 3 号样本芯子介损曲线
Fig.8 The tanδ-f curves of 3# condenser body
3 温度对FDS 的影响规律及其校正方法
图6～图8 给出了1～3 号样本芯子在30 ～80℃范围内共计6 个温度测点下的复电容实测曲线。温度对频域介电谱介损曲线的影响主要体现在1 Hz以下的低频部分。对于水分含量不同的三个样本芯子，随着温度的升高，每组样本曲线均沿频率轴向右平移，同时曲线形状不发生明显变化，表明温度对油纸绝缘介电谱具有较为显著的影响。
在介电谱的实际应用中，温度是不可避免的环境因素之一，不同于水分含量为未知因素，在现场进行介电谱测试时，通常是将设备切除运行，并等待其充分降温至室温再行测量，即此时设备绝缘的温度通常已知，可采用一定的方法对温度的影响进行消除，以使介电谱图的变化仅体现受潮状态的信息而不至于被温度的影响所淹没。目前，国内外学者主要运用“频温叠加”方法消除温度对介电谱的影响[20]。该方法的基本思想是：在理想情况下，温度的不同仅改变介电谱的水平位置，而不影响其形状。反之，将不同温度下的实测介电谱曲线沿着标准温度的方向水平移动一定距离则可方便地对应到该温度下的介电谱曲线，而不必在此温度下进行真实的测量，已被平移至标准温度下的曲线被称为“主曲线”。将该主曲线同标准温度下状态已知的标样曲线进行对比，即可推知目标绝缘体的相关绝缘状态。平移系数 Tα 定义为
式中， 1f 为目标频率； f0 为参考频率点；Ea 为活化能（kJ/mol）；R 为气体常数，R=8.314 5J/mol/K；T 为温度（K）。对1～3 号三个套管样本芯子在30℃、40℃、50℃三个测试温度下的曲线以50℃为标准温度进行平移即可构建出频域介电谱主曲线，如图9 所示。
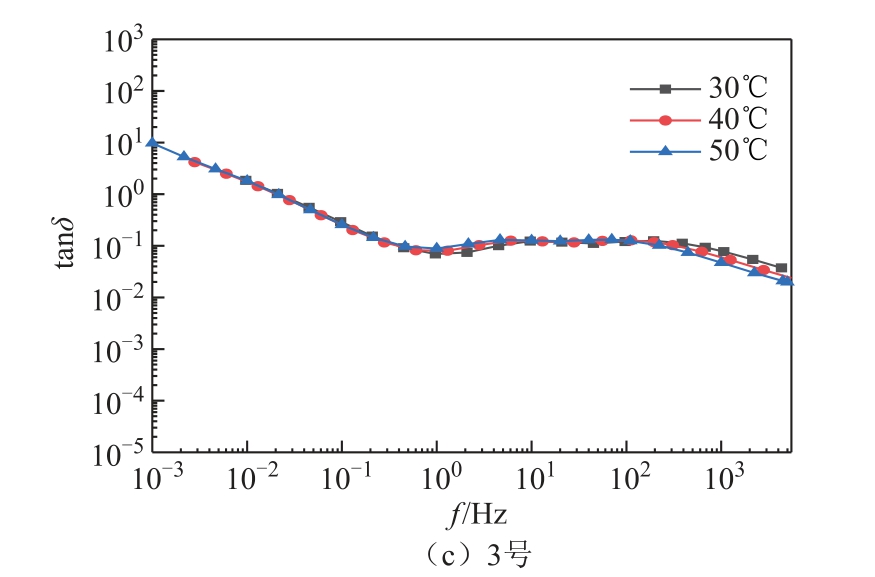
图9 1～3 号套管芯子介电谱主曲线
Fig.9 The principal FDS curves of 1#～3# condenser bodies
在对应于三组样本的不同受潮梯度下，各温度下的FDS 曲线均符合频温叠加的移动方法，且构造出的FDS 主曲线重合度较高。表1 给出了样本芯子在不同受潮程度和温度下的频温移动因子。
表1 1～3 号套管芯子的频温移动系数 Tα
Tab.1 The Tα of 1#～3# condenser bodies
绝缘状态 30℃ 40℃ 50℃1 号套管 0.71% 0.391 5 0.651 2 1 2 号套管 1.78% 0.377 3 0.613 6 1 3 号套管 2.62% 0.380 9 0.626 9 1
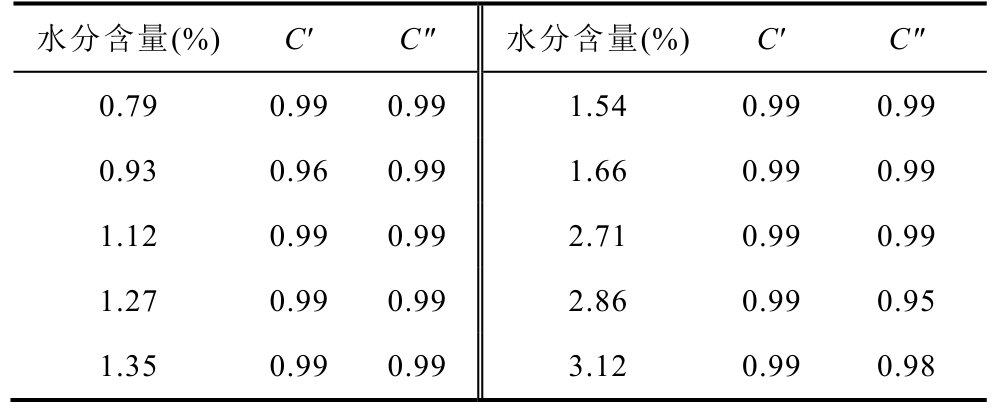
三个套管芯子样品的 Tα 随着测试温度的增加而迅速增大，且每个测试温度下的 Tα 相差不大。这表明，油纸绝缘水分含量的增加对 Tα 的影响不大。此处进一步将表1 中不同水分含量及不同温度下的Tα 与热力学温度进行拟合，结果见表2。由表2可知，平移系数 Tα 与热力学温度之间遵循较为显著的指数关系，拟合优度高达0.99以上。
表2 频温平移因子 Tα 与热力学温度T 的拟合方程
Tab.2 The fitting equations between Tα and absolute temperature T
绝缘状态 Tα 与测试温度T 的关系 拟合优度1 号套管0.71% Tα =3.93314×10-7exp(0.04565T) 0.996 2 号套管1.78% Tα =1.43047×10-7exp(0.04877T) 0.999 3 号套管2.62% Tα =1.98417×10-7exp(0.04776T) 0.999
温度对介电谱的影响规律较为一致，完全可通过曲线平移的方式将温度的影响消除而不必在标样研究过程中考虑温度维度，从而达到简化样本数据库而仅需重点关注状态因素的目的。因此，第二阶段的精细化受潮试验不再将温度作为变量而全程采用恒温50℃进行测量。
4 等效模型参数辨识及分析
4.1 参数辨识结果
本节基于10 组不同水分含量的电容芯子实测FDS 曲线采用上述的GA-LMA 融合优化算法进行了参数辨识，得出不同水分含量下的模型参数值，并通过模型重构频域介电谱图，实测曲线和重构曲线的对比如图10 所示，各组数据的拟合优度见表3。
图10 不同含水量下的电容芯子复电容拟合曲线
Fig.10 The fitted curves of the complex capacitance of the condenser bodies with different moisture contents
表3 不同水分含量的套管参数辨识结果对实测FDS 曲线的拟合优度
Tab.3 The fitting goodness of reconstructed vs. measured FDS curves of the bushings with different moisture contents
?
将各极化支路按照支路时间常数大小降序排列，将1 和2、3 和4、5 和6 支路分别定义为大时间、中时间及小时间常数支路，并将与几何尺寸相关的C0、R0 支路统称为几何支路。图10 显示，根据模型参数得出的计算谱图的拟合精度较测量谱图高。表3 显示，不同温度及不同水分含量条件下的FDS 拟合优度值均超过了0.90，表明所采用的GA-LMA 融合优化算法对于模型参数辨识具有充分的有效性。
模型辨识得出的阻容参量数值范围与文献中采用时域介电谱计算出且被广泛接受的参数范围完全一致，为（109Ω、10-9F）[21]，表明本模型不仅对FDS建模精度高，且各参量物理意义明确、合理，证实了扩展德拜模型对FDS 在宽频范围内（10-3～103Hz）的理论适用性，解决了该模型目前仅能匹配时域介电谱，而对FDS 重构效果较差的难题，为使用扩展德拜模型解读FDS 携带的绝缘状态信息提供了重要的模型基础。
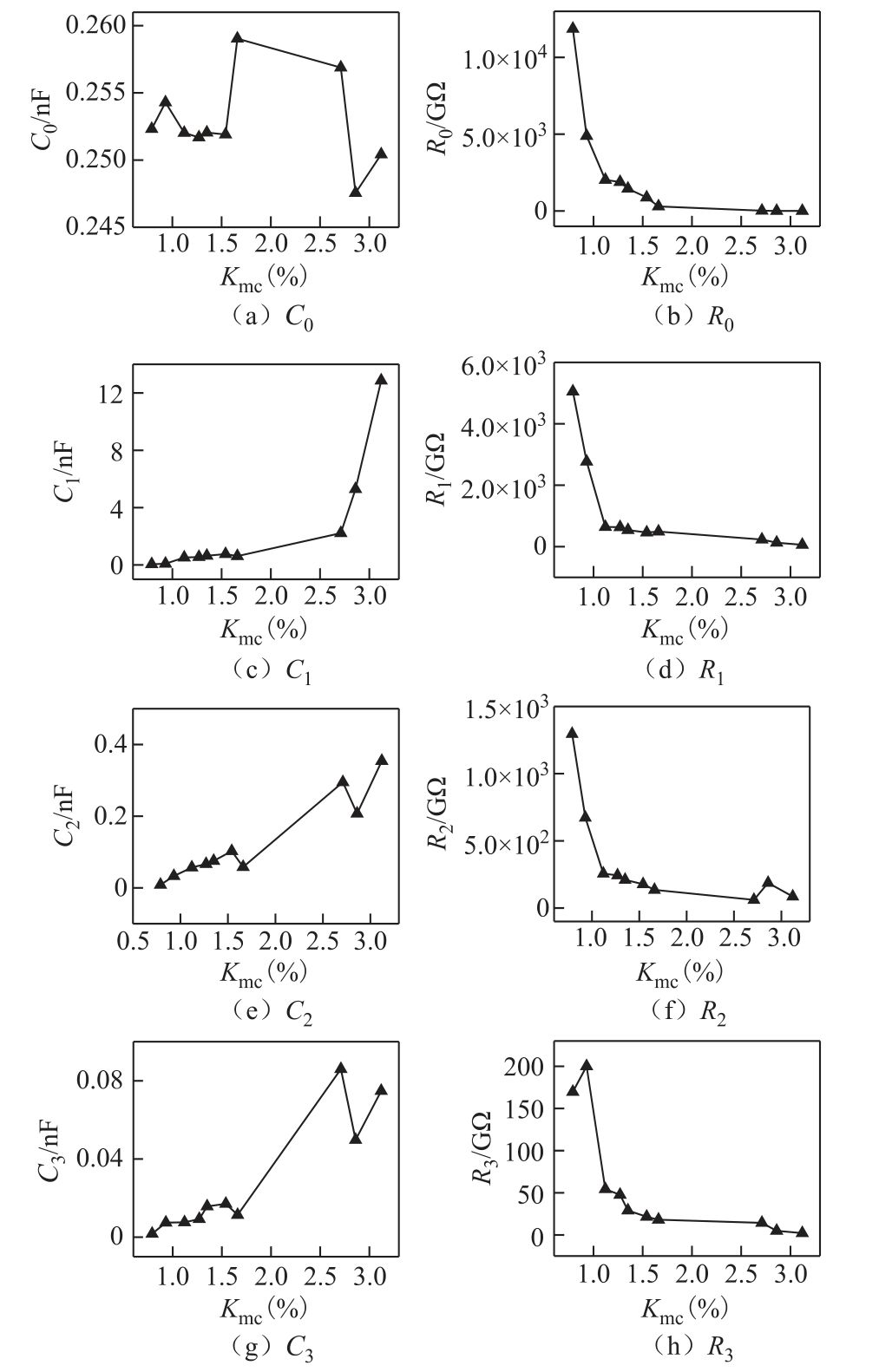
图11 部分模型支路参数随微水含量的变化
Fig.11 The variations of partial model parameters regarding moisture contents
4.2 绝缘微水含量对扩展德拜模型参数的影响规律
扩展德拜模型的部分支路参数随微水含量的变化如图11 所示。不同微水含量下模型中的几何电容C0 基本不变，因为油纸绝缘系统结构和尺寸并不受微水含量的影响。绝缘电阻R0 随微水含量增加而单调减小，其对微水含量的变化十分敏感。这是由于含杂质的水分本身导电性较高，且还能作为催化剂加快杂质的分解，进一步导致绝缘体内部载流子数增加，从而显著提高套管绝缘介质的电导率，对应的绝缘电阻明显下降。对于各极化支路，极化电容值随着微水含量的增大基本呈增大的趋势，而极化电阻则呈现出与极化电容相反的趋势，即随着微水含量增加而单调减小，这是因为由于水分增加而引入的杂质使得绝缘介质夹层极化增强，因而宏观上表现为系统相对介电常数和极化电容的增大。
图12 给出了在相同温度下电容芯子各支路时间常数随微水含量的变化曲线。C0、R0 支路的时间常数τ0 随微水含量的增加显著减小，而第1 极化支路的最大时间常数 τ1 随微水含量的增加呈现增加趋势。
图12 几何支路时间常数及最大时间常数随微水含量的变化
Fig.12 The variations of the time constants of the geometry branch and the largest-time-constant branch regarding moisture contents
5 油纸绝缘系统受潮状态特征量提取
频域介电谱是电介质介电响应特性在宽频范围内的宏观体现形式。介质在微观层面的电导及极化行为的改变直观地反映为频域介电谱曲线特征的改变，进而使绝缘介电响应等效模型的参数发生相应的变化。因此，介电等效模型参数和绝缘状态之间存在定量关联。目前在国内外相关研究中取得广泛认可的一点是，油纸绝缘的介损正切tanδ 与复电容虚部曲线的低频段对微水含量十分敏感。作者的前期研究表明，复电容虚部曲线的低频部分由R0 支路以及低频C1R1、C2R2、C3R3 支路主导，其他极化支路对复电容虚部的贡献由于数量级差异太大可忽略不计[22]。
为便于叙述，将第C1R1、C2R2、C3R3 极化支路统称为低频支路，而文献[22]中的支路介电谱分解分析表明，绝缘电阻支路及低频支路的参数：R0、R1、R2、R3、C1、C2、C3 为介质受潮状态的敏感参数范围。结合图11 和图12 的样本数据分析结果，本节选取对油纸绝缘含水量具有一致性变化规律的绝缘电阻R0、低频支路极化电阻R1、R2 及最大时间常数τ1四个指标作为油纸绝缘系统受潮的特征量，并将上述参量同绝缘含水量进行拟合，如图13 所示。进而建立了上述参量与油纸绝缘水分含量之间的关系式，见表4。
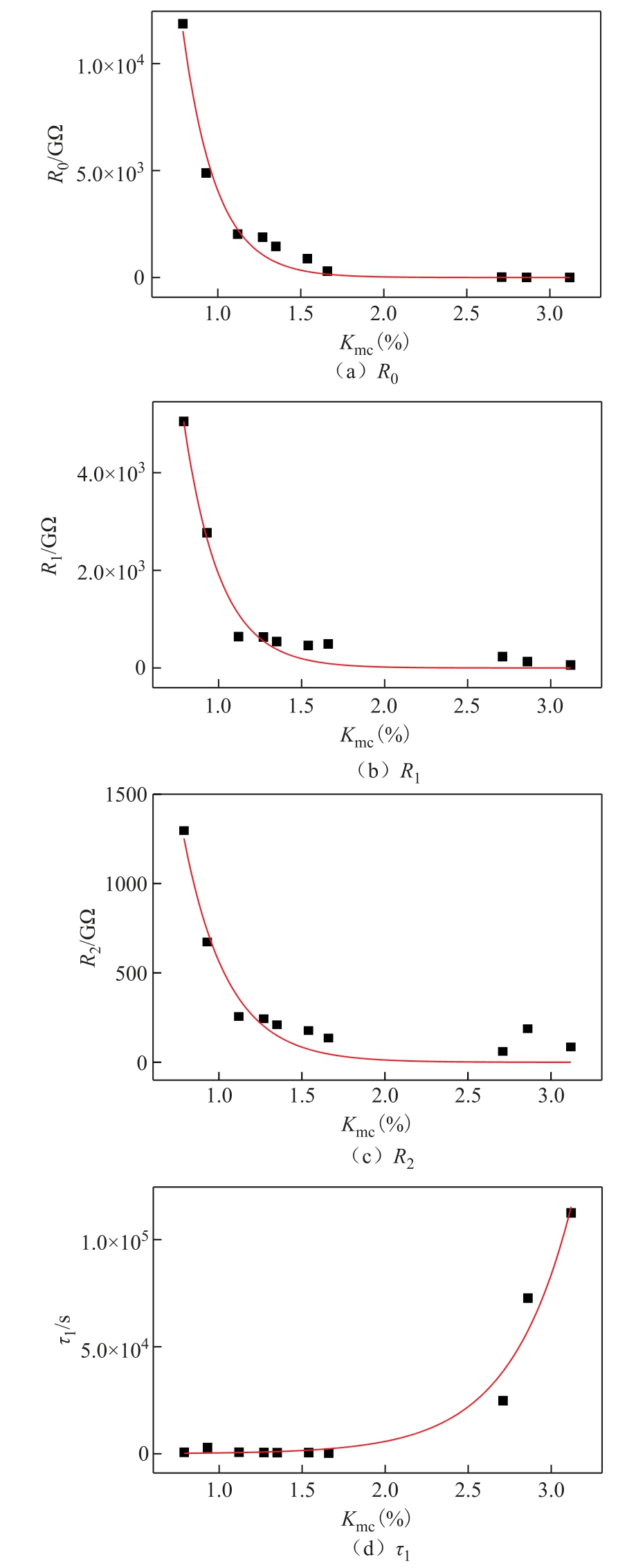
图13 受潮状态特征量与绝缘水分含量的拟合曲线
Fig.13 The fitted curves between the characteristic quantities for moisture state and moisture contents
为验证水分评估方法的有效性，此处仍然使用相同的模型套管芯子及人工受潮方法另行制备了三组不同水分含量的电容芯子样品，其真实水分含量分别为0.72%、1.18%、1.57%，并将其分别编号为1～3 号验证样本。首先对这三组验证样本进行频域介电谱测量，其测量结果如图14 所示，并按照上文完全相同的思路进行参数辨识，并提取出4 个特征参量（R0、R1、R2、τ1），见表5。
表4 受潮状态特征量与水分含量的回归关系式
Tab.4 The fitting equations between the characteristic quantities for moisture state and moisture contents
?
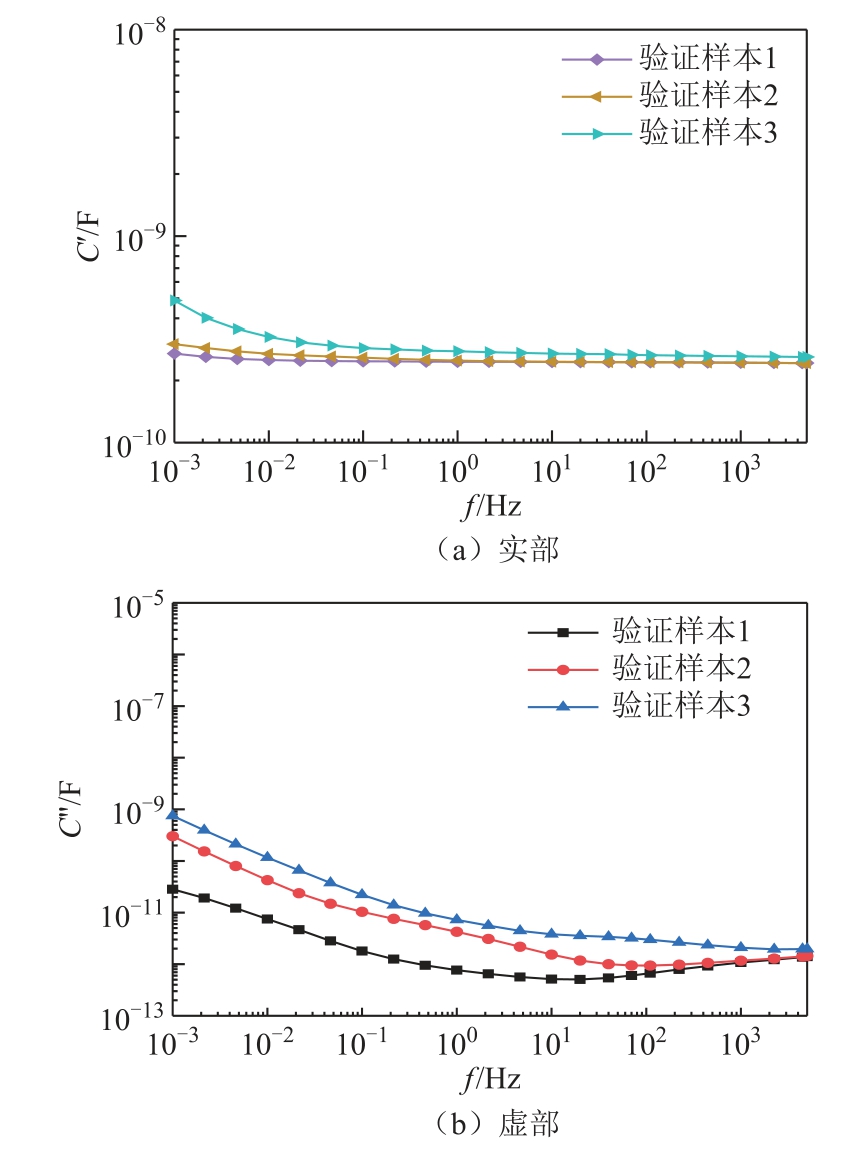
图14 验证样本的复电容测量结果
Fig.14 The measured complex capacitance of the bushing samples for verification
表5 验证样本的受潮特征参量及受潮评估结果
Tab.5 The characteristic parameters of the bushing samples for verification and the evaluation results of their moisture state
?
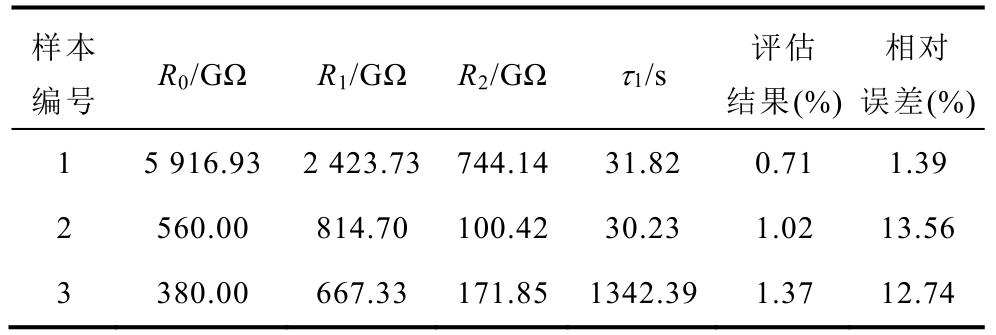
在计算得出了特征参量后，针对三个验证样本各自对应的四个特征参量值，通过已确定出的定量关系式反解出水分含量，并由四种特征量分别确定出的水分含量数值求取算数平均值作为该样本的最终水分含量评判结果。和实际水分含量对比表明，当水分含量较低时，本方法的评判误差较小，随着绝缘水分含量的增加，评判误差有所增大。
6 结论
本文以油纸电容式套管模型为典型研究对象，以频域介电响应为理论基础研究了基于扩展德拜模型的油纸绝缘系统受潮状态分析方法，得出以下结论：
1）提出了一种采用FDS 曲线进行油纸绝缘宽频等效模型参数辨识的GA-LMA 融合优化算法。辨识结果对13 组实测FDS 谱图的拟合优度均达到了0.90 以上，证实了扩展德拜模型对FDS 在宽频范围内（10-3～103Hz）的理论适用性，解决了该模型目前仅能匹配时域介电谱，而对FDS 重构效果较差的难题，为使用扩展德拜模型解读FDS 携带的绝缘状态信息提供了重要的模型基础。
2）得出了扩展德拜模型低频关键支路参数随绝缘微水含量的变化规律：随着绝缘微水含量的增加，极化支路电容Ci 及最大时间常数τ1 呈一致性增大趋势，而支路电阻Ri 及几何支路时间常数τ0 呈一致性减小趋势。
3）提取了对绝缘水分含量敏感的扩展德拜模型低频支路特征参量：绝缘电阻R0、第一极化电阻R1、第二极化电阻R2 以及最大时间常数 1τ ，分别建立了各特征量与微水含量的定量关系式并进行了验证，可实现对油纸绝缘系统受潮状态的定量评估。
[1] 杜伯学, 朱闻博, 李进, 等. 换流变压器阀侧套管油纸绝缘研究现状[J]. 电工技术学报, 2019, 34(6):1300-1309.Du Boxue, Zhu Wenbo, Li Jin, et al. Research status of oil-paper insulation for valve side bushing of converter transformer[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1300-1309.
[2] 王伟, 董文妍, 李芳义, 等. 升温过程中水在矿物油和纤维素界面扩散和聚集行为的分子模拟[J].电工技术学报, 2019, 34(17): 3696-3704.Wang Wei, Dong Wenyan, Li Fangyi, et al. Molecular simulation of the diffusion and aggregation of water at the interface between mineral oil and cellulose during temperature rising[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3696-3704.
[3] Islam M M, Lee G, Hettiwatte S N. A review of condition monitoring techniques and diagnostic tests for lifetime estimation of power transformers[J].Electrical Engineering, 2018, 100(2): 581-605.
[4] 林智勇, 张达敏, 黄国泰, 等. 采用回复电压曲线分解法的变压器等效电路研究[J]. 电力系统保护与控制, 2019, 47(13): 18-23.Lin Zhiyong, Zhang Damin, Huang Guotai, et al.Research on equivalent circuit of transformer by decomposing return voltage curve[J]. Power System Protection and Control, 2019, 47(13): 18-23.
[5] 蔡金锭, 叶荣, 陈汉城. 回复电压多元参数回归分析的油纸绝缘老化诊断方法[J]. 电工技术学报,2018, 33(21): 5080-5089.Cai Jinding, Ye Rong, Chen Hancheng. Aging diagnosis method of oil-paper insulation based on multiple parameter regression analysis of recovery voltage[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 5080-5089.
[6] Yang Lijun, Chen Junru, Wang Songhua, et al.Dielectric response measurement of oil-paper insulation based on system identification and its timefrequency-domain conversion method[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2018, 25(5): 1688-1698.
[7] Yang Lijun, Zou Tiantian, Deng Bangfei, et al.Assessment of oil-paper insulation aging using frequency domain spectroscopy and moisture equilibrium curves[J]. IEEE Access, 2019, 7: 45670-45678.
[8] Liu Jun, Zhou Lijun, Luo Yang, et al. Dielectric frequency response of oil-paper composite insulation with transient moisture distribution[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2013, 20(4): 1380-1387.
[9] Gao Jun, Yang Lijun, Wang Youyuan, et al. Condition diagnosis of transformer oil-paper insulation using dielectric response fingerprint characteristics[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2016, 23(2): 1207-1218.
[10] 林燕桢, 蔡金锭. 回复电压极化谱特征量与油纸绝缘变压器微水含量关系分析[J]. 电力系统保护与控制, 2014, 42(5): 148-153.Lin Yanzhen, Cai Jinding. Analysis of the relationship between the characteristics of the return voltage polarization spectrum and micro water content of oilpaper insulation transformer[J]. Power System Protection and Control, 2014, 42(5): 148-153.
[11] Liao Ruijin, Hao Jian, Chen G, et al. Quantitative analysis of insulation condition of oil-paper insulation based on frequency domain spectroscopy[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2015, 22(1): 322-334.
[12] 杜林, 冉鹂蔓, 蔚超, 等. 基于扩展德拜模型的油纸绝缘受潮频域特征量研究[J]. 电工技术学报,2018, 33(13): 3051-3058.Du Lin, Ran Liman, Wei Chao, et al. Study on frequency domain characteristics of moisture in oilpaper insulation based on extended Debye model[J].Transactions of China Electrotechnical Society, 2018,33(13): 3051-3058.
[13] Fofana I, Hemmatjou H, Meghnefi F, et al. On the frequency domain dielectric response of oil-paper insulation at low temperatures[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2010, 17(3):799-807.
[14] 林燕桢. 基于等效电路分析法的油纸绝缘变压器微水含量分析与研究[D]. 福州：福州大学, 2014.
[15] 刘捷丰, 廖瑞金, 吕彦冬, 等. 电力变压器油纸绝缘含水量定量评估的时域介电特征量[J]. 电工技术学报, 2015, 30(2): 196-203.Liu Jiefeng, Liao Ruijin, Lü Yandong, et al. Time domain dielectric characteristics for quantitative assessment of moisture content in transformer oilpaper insulation[J]. Transactions of China Electrotechnical Society, 2015, 30(2): 196-203.
[16] Saha T K, Purkait P, Muller F. Deriving an equivalent circuit of transformers insulation for understanding the dielectric response measurements[J]. IEEE Transactions on Power Delivery, 2005, 20(1): 149-157.
[17] 杜林, 杨峰, 蔚超, 等. 基于频域介电谱的油纸绝缘宽频等效模型参数辨识研究[J]. 电工技术学报,2018, 33(5): 1158-1166.Du Lin, Yang Feng, Wei Chao, et al. Parameter identification of the wide-band model of oilimpregnated paper insulation using frequency domain spectroscopy[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1158-1166.
[18] Saha T K, Purkait P, Muller F. Deriving an equivalent circuit of transformers insulation for understanding the dielectric response measurements[J]. IEEE Transactions on Power Delivery, 2005, 20(1): 149-157.
[19] Ma H, Saha T K, Ekanayake C. Interpretation of dielectric response measurements of transformer insulation under temperature variations and transient effects[C]//IEEE, Power & Energy Society General Meeting, San Diego, CA, USA, 2012, DOI: 10.1109/PESGM.2012.6344903.
[20] 张明泽, 刘骥, 齐朋帅, 等. 基于介电响应技术的变压器油纸绝缘含水率数值评估方法[J]. 电工技术学报, 2018, 33(18): 4397-4407.Zhang Mingze, Liu Ji, Qi Pengshuai, et al. Numerical evaluation method for moisture content of transformer oil-paper insulation based on dielectric response technique[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4397-4407.
[21] 郑君亮, 江修波, 蔡金锭, 等. 去极化电流解谱分析油纸绝缘等效电路参数研究[J]. 电力系统保护与控制, 2014, 42(21): 54-58.Zhen Junliang, Jiang Xiubo, Cai Jinding, et al.Research on spectrum analysis of the depolarization current to identify the parameter of oil/paper insulation equivalent circuit[J]. Power System Protection and Control, 2014, 42(21): 54-58.
[22] 冉鹂蔓. 基于等效电路模型的油纸绝缘设备受潮状态评估研究[D]. 重庆: 重庆大学, 2018.