0 引言
中性点经消弧线圈接地或不接地配电网单相接地故障后可持续运行1~2h,但不利于人员及设备的安全;中性点经小电阻接地方式可降低接地故障暂态过电压,提高低过渡电阻故障的接地电流,利于馈线零序保护的故障检测,适用于电缆为主的配电网,若应用于架空配电线路,则会出现跳闸率激增的问题,影响供电可靠性。近年来电网企业拟利用不同接地方式的优势[1-6],通过多种接地方式灵活、适时地投入,配合选线与线路保护快速处置配电网单相接地故障,如中性点经消弧线圈并联小电阻接地方式。但在架空配电线路的实际应用中,由于瞬时性接地故障跳闸激增,导致系统的供电可靠性大幅下降[7]。目前实际的工程应用中,普遍基于工程经验确定固定延时,以区分瞬时和永久故障,往往存在瞬时性故障跳闸增多或永久性故障切除滞后的问题。因此,快速辨识接地故障瞬时或永久性质的发展趋势,有利于适时地改变中性点接地方式,对提升配电网单相接地故障的自愈能力和保护自适应性具有重要的意义[8]。
配电网的单相接地故障从过渡电阻的性质方面可分为金属性故障、低阻故障、高阻故障[9-12];若为电弧性故障,从电弧的稳定燃烧特性可分为间歇性故障[13]及弧光故障[14-16];从线路重合闸的角度出发,若故障跳闸后重合成功,则为瞬时故障,重合失败,则为永久故障。在输电网中,也有利用正序无功与负序无功极性跃变[17]、二次电弧[18-20]及拍频[21-22]等特征判定故障的瞬时永久特性。配电网的故障特性及运行方式与输电网有所不同,首先,小电流接地的配电网发生单相接地故障时可以继续运行一段时间,不会立即跳闸;其次,配电网的电压等级相比输电网较低,相间耦合微弱,所产生的潜供电流几乎可以忽略。若将馈线与大地之间的绝缘电阻整体等效为过渡电阻,则配电网正常运行时,过渡电阻近似为无穷大;若发生单相接地故障,过渡电阻将发生变化。因此可利用故障的稳态电气量,构造反映过渡电阻实时变化规律的判据,若过渡电阻为有限值且不变或是变小,则预判为永久故障;若快速变大,则预判为瞬时故障。
本文提出利用故障后的稳态零序电流和零序电压构造伏安曲线,通过计算和比较连续多个周期伏安曲线的面积,实现故障性质的预判,进而适时改变随调式消弧线圈及小电阻的投入时机,并进一步利用中性点设备主动投入所导致的零序电流相位及幅值的变化完成单相接地故障性质的判别。
1 中性点不同接地方式下的故障特征分析
1.1 零序分量与过渡电阻的关联性分析
假设A 相发生单相接地故障,考虑中性点的不同接地方式,配电网单相接地故障的零序等效电路如图1 所示[23-24]。R 为三相线路的泄漏电阻以及消弧线圈的阻尼电阻,Rd 为接地故障的过渡电阻,C为三相线路的对地电容之和,L 为消弧线圈的等效电感,Rn 为中性点的小电阻。
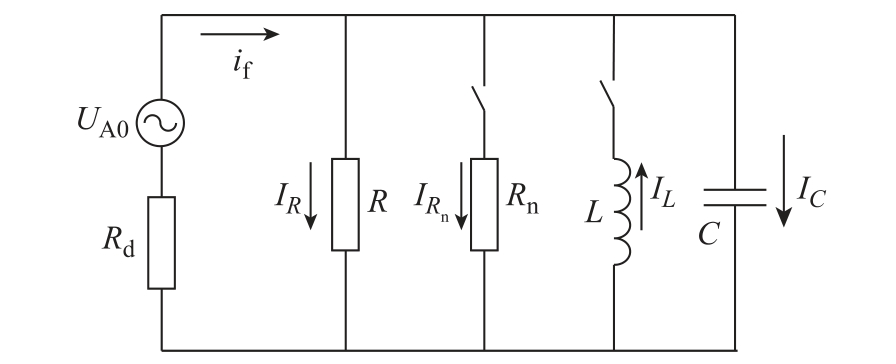
图1 不同接地方式下单相接地故障等效电路
Fig.1 Single phase ground fault equivalent circuit under different grounding modes
依据上述等效电路,不接地、经消弧线圈接地和小电阻接地方式,其零序电压分别为
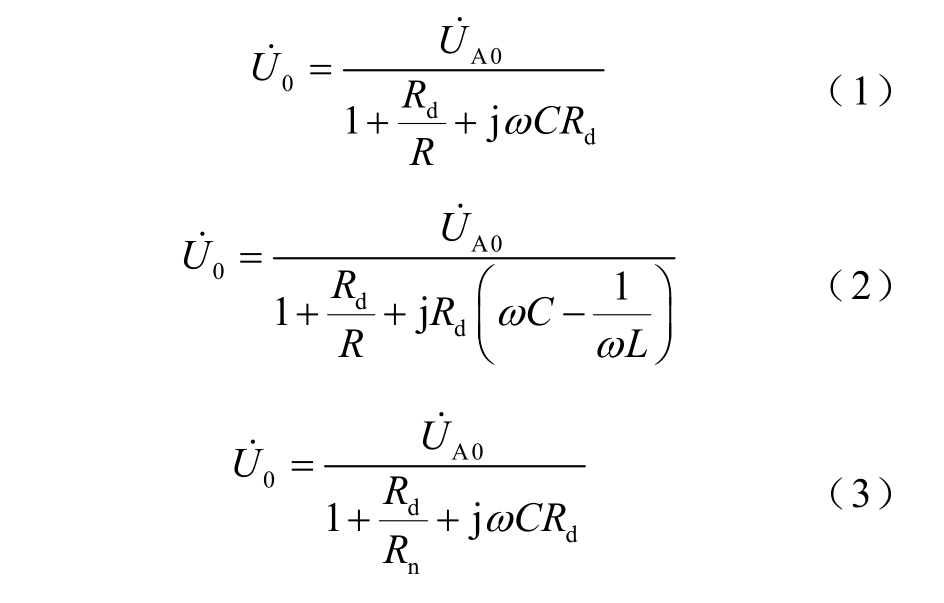
相应的故障点电流和零序电流分别为
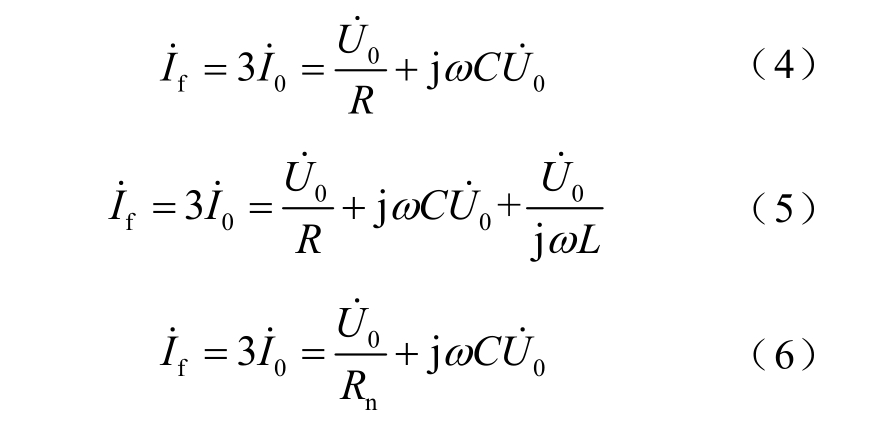
由式(1)~式(3)可知,中性点在不接地、经消弧线圈接地或经小电阻接地的情况下,零序电压与故障电阻成反比关系,即

由式(3)~式(5)可知,故障电流与零序电压成正比关系,即

在不同的接地方式下,当故障过渡电阻增加时,零序视在功率将减小;反之,故障过渡电阻减小时,零序视在功率将随之增大[25]。假设配电网发生单相接地故障,过渡电阻从金属性接地变化至3 000Ω,其零序电压及零序电流如图2a 和图2b 所示。
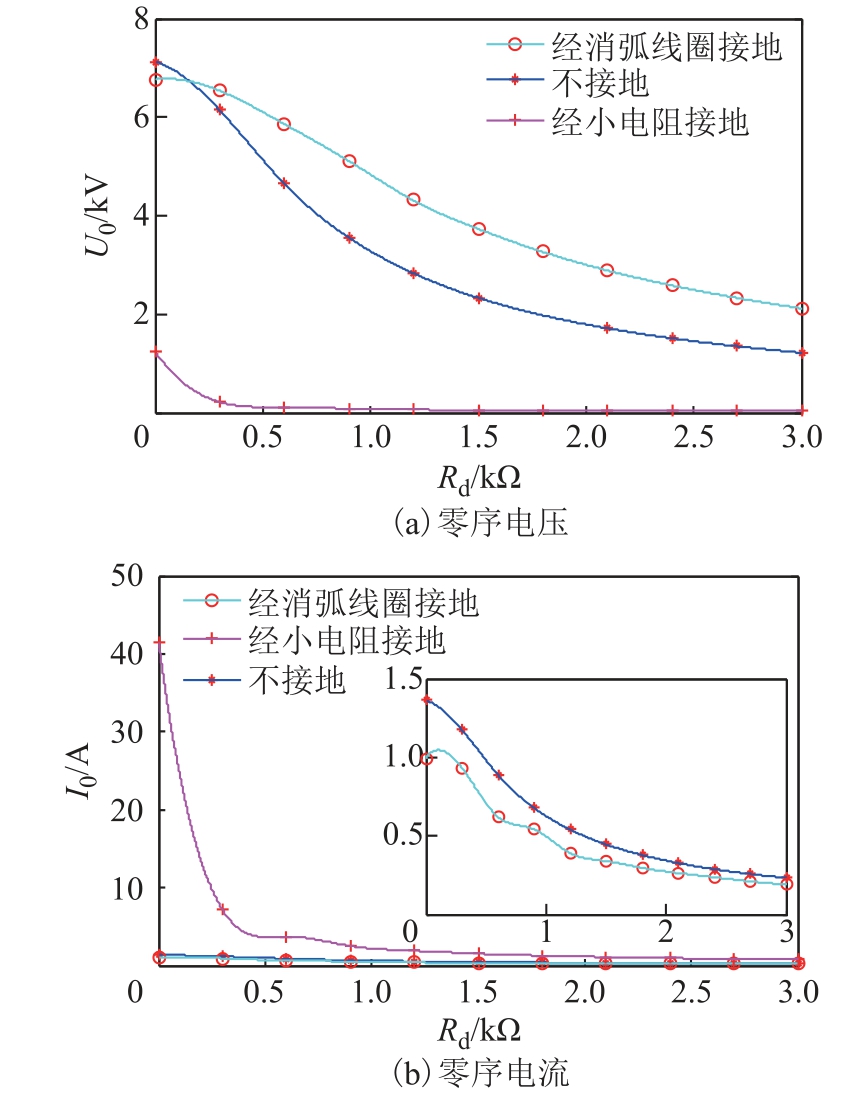
图2 零序分量与过渡电阻的关系
Fig.2 Relationship between zero sequence component and transition resistance
因此,保护安装处测量的零序有功和零序无功会随着过渡电阻的变化而变化,可利用零序有功功率或无功功率构造反映过渡电阻变化的时域判据。
1.2 零序伏安曲线面积的物理意义
用稳态零序电压和零序电流的瞬时采样值做伏安特性曲线,该曲线的参数方程为
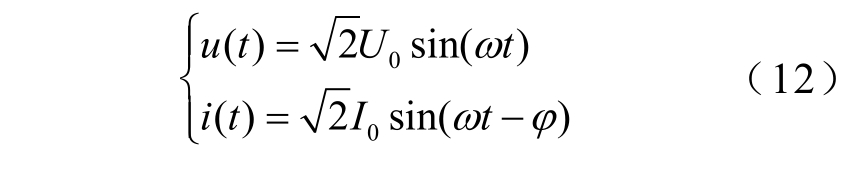
式中,φ 为功率因数角。
在i、u 为横、纵坐标的笛卡尔坐标系中,一个工频周期的伏安曲线为一条围绕坐标原点的封闭曲线。
将式(12)转换为极坐标方程,即

式中,T 为一个工频周期的时间,将式(13)代入式(14)并计算化简可得

因此,接地故障零序伏安曲线的面积与一个工频周期的无功能量成正比。当发生接地故障时,若系统无相关操作,则可认为系统参数不变,伏安曲线面积的变化将直接反映过渡电阻变化对系统无功功率产生的影响。
图3a 为不接地方式下零序伏安曲线随过渡电阻的变化,图3b 为消弧线圈接地方式下零序伏安曲线随过渡电阻的变化。
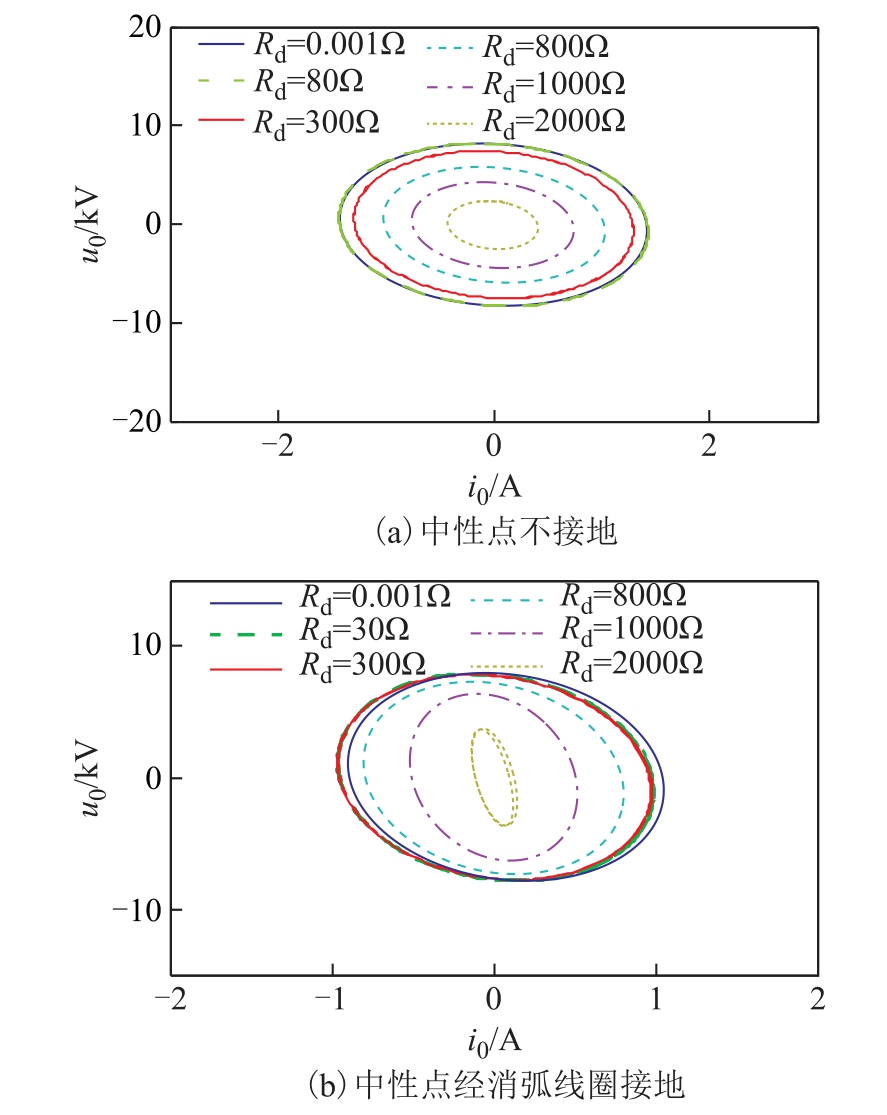
图3 不同接地方式下零序伏安曲线
Fig.3 Zero sequence volt-ampere curve under different grounding modes
由图3 可以看出,接地故障过渡电阻增大时,零序伏安曲线形成的曲面在不断缩小;过渡电阻减小时,零序伏安曲线所形成的曲面则不断增大;过渡电阻不变时,零序伏安曲线形成的曲面不会发生变化。
1.3 基于零序伏安曲线面积的故障性质预判
配电网正常运行时,馈线与大地之间绝缘,过渡电阻近似于无穷大,而配电网发生单相接地故障后,线路与大地之间的绝缘被破坏,过渡电阻发生变化。故障过渡电阻可能变大,也可能变小,若过渡电阻持续变大,则线路与大地之间绝缘趋于逐步恢复;若过渡电阻变小,则线路与大地之间的绝缘趋于持续减弱;若过渡电阻为稳定的有限值,则线路与大地之间有稳定的衔接点。
无论配电网采用何种中性点接地方式,接地故障的零序电压和零序电流随过渡电阻的变化规律相同。因此,可利用零序伏安曲线面积的变化来反映故障过渡电阻的变化,依据过渡电阻的变化趋势实现故障性质的预判。如果配电网的故障是永久性故障,故障的过渡电阻会变小或几乎不变,则零序伏安曲线的面积会增大或保持不变;若为瞬时故障,过渡电阻会逐渐增大至无穷大,则零序伏安曲线的面积将会减小。
1.4 基于中性点变动的单相接地故障性质检测
通过中性点的主动变动,可形成零序电流相位和幅值的确定性变化,利用新的特征信息作为故障性质判别的确定性判据。
在中性点不接地方式下,对于三相负荷平衡的配电网络,如果配电网的故障依旧存在,中性点投入消弧线圈之后,则故障馈线的零序电流会出现“倒相”现象[24],消弧线圈投入之前与投入之后的零序电流相位差为180°;若继续投入小电阻,则系统零序阻抗将减小,零序故障电流的幅值将增大,即投入小电阻之后与投入之前的零序电流幅值比将大于1。如果在故障消失后投入消弧线圈,中性点的电压会稍有偏移,产生较小的不平衡电流,但基本为零;若故障消失后投入小电阻,零序电流基本上也接近于零。
在中性点经消弧线圈接地方式下,若在故障消失前投入小电阻,则如上文所述,投入小电阻之后与投入之前的零序电流幅值比将大于1;若在故障消失后投入小电阻,零序电流基本为零。
通过中性点变动前后零序电流的相位和幅值变化,可以形成单相接地故障性质辨识的依据:
(1)对于中性点不接地系统,在消弧线圈投入的前后,如果故障一直存在,则故障馈线的零序电流在动作前后其相位差为180°,若继续投入小电阻,投入后与投入前的零序电流幅值比大于1。
(2)对于中性点经消弧线圈接地系统,如果故障存在,小电阻投入后与投入前的零序电流幅值比大于1。
2 基于故障性质预判的中性点主动变动策略
中性点的变动也会影响单相接地故障的性质。消弧线圈投入,因为补偿作用,有利于故障电流的减小和故障消失;小电阻的投入会增大零序电流,利于保护动作,及时切除故障部分,避免长时间过电压导致的发展性故障;在中性点经消弧线圈接地的情况下,故障消失可使相电压及时恢复正常,抑制电压的偏移。而配电网的瞬时故障时间大都小于1s,为了便于研究分析,并结合配电网现场实际情况,则按照以下原则相继投入消弧线圈及小电阻:
(1)若预判为永久故障,无论采用何种中性点的接地方式,都在故障后0.2s 投入小电阻,及时增大零序电流,利于保护动作,切除故障部分,保证无故障部分的正常运行。
(2)若预判为瞬时故障,并且中性点为不接地方式,则在故障后0.2s 投入消弧线圈,减小故障电流,促使故障消失,有利于配电网的自愈。如果消弧线圈投入后故障并没有消失,则在消弧线圈投入后的0.6s投入小电阻,使保护动作,避免长时间的过电压。
(3)若预判为瞬时故障,并且中性点是经消弧线圈接地,则在故障后0.6s 投入小电阻。即使故障在小电阻投入之前消失,小电阻的投入也可使得电压快速恢复;如果故障没有消失,则保护动作,避免长时间的过电压。
3 单相接地故障性质的辨识流程
首先计算故障后5 个周期的零序伏安曲线面积,对曲面面积做一次拟合,求取直线的斜率,基于斜率大小预判故障性质;然后基于故障性质的预判投入相应的中性点设备,根据消弧线圈或小电阻投入所引起的零序电流相位及幅值变化检验故障是否消失,从而完成故障性质的辨识。具体步骤如下:
(1)截取故障后20~120ms 的零序电压及零序电流,分解为5 个周期,构造各周期的零序伏安曲线。
(2)计算各周期零序伏安曲线的面积,并对曲面面积作一次拟合,计算拟合直线的斜率。
(3)若拟合直线的斜率小于零,则预判为瞬时性故障,中性点不接地系统转入步骤(4),中性点经消弧线圈接地系统转入步骤(5);若拟合直线的斜率大于或等于零,则预判为永久性故障,转入步骤(6);为保留一定的裕度,此阈值设定为-0.01,也可根据实际电网进行调整。
(4)延时0.2s 投入消弧线圈,计算投入前后零序电流的相位差θL,若θL 接近180°,则故障存在,转入步骤(5)继续判别,否则判定为瞬时性故障。
式中,θ0 为不接地时零序电流的相位;θ0L 为经消弧线圈接地时零序电流的相位。
(5)延时0.6s 投入小电阻,根据小电阻投入之后与投入之前零序电流的幅值比KLR 判断故障性质
式中,I0R 为小电阻接地时的零序电流;I0L 为消弧线圈接地时的零序电流。如果KLR>1,则确定为永久故障;如果KLR 接近于0,则确定为瞬时故障。
(6)延时0.2s 投入小电阻,根据小电阻投入之后与投入之前零序电流的幅值比KCR判断故障性质, KCR 为
式中,I0C 为中性点不接地的零序电流。如果KCR>1,则确定为永久故障;如果KCR 接近于0,则确定为瞬时故障。
单相接地故障性质辨识流程如图4 所示。
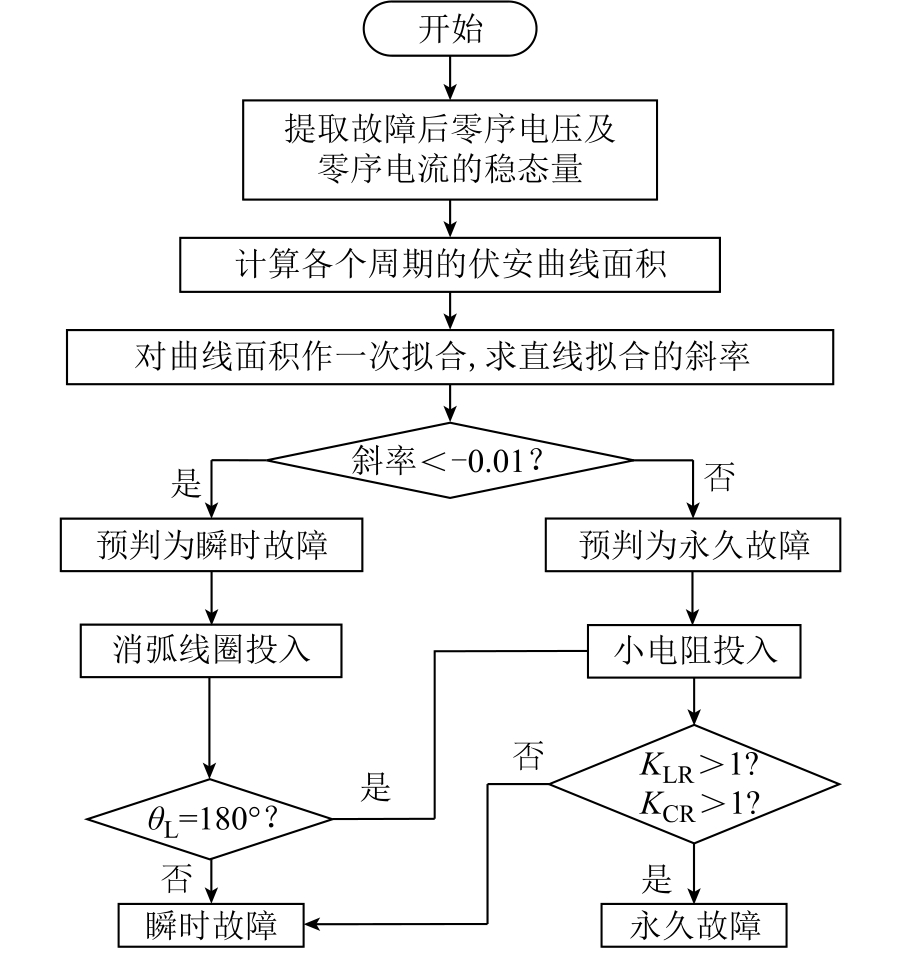
图4 故障性质辨识流程
Fig.4 Identification process of single phase ground fault property
4 仿真分析及实测数据验证
4.1 仿真模型
利用PSCAD/EMTDC 建立如图5 所示的配电网仿真模型,110kV/10kV 的变电所共有六回出线,馈线L1、L2、L4、L6 为架空线路,馈线L3 和L5 是纯电缆线路。其中,架空馈线的正序阻抗为

当开关S1 断开时,为不接地系统,开关S1、S2动作时,可将消弧线圈及小电阻投入;当开关S1 闭合时,该系统的中性点经消弧线圈接地,开关S2 动作时,可将小电阻投入。该配电系统的中性点从母线的Z 字形接地变压器引出,经消弧线圈L 并联小电阻Rn 接地,rL 为消弧线圈的阻尼电阻,消弧线圈的补偿方式为过补偿,系统采样频率为10kHz。
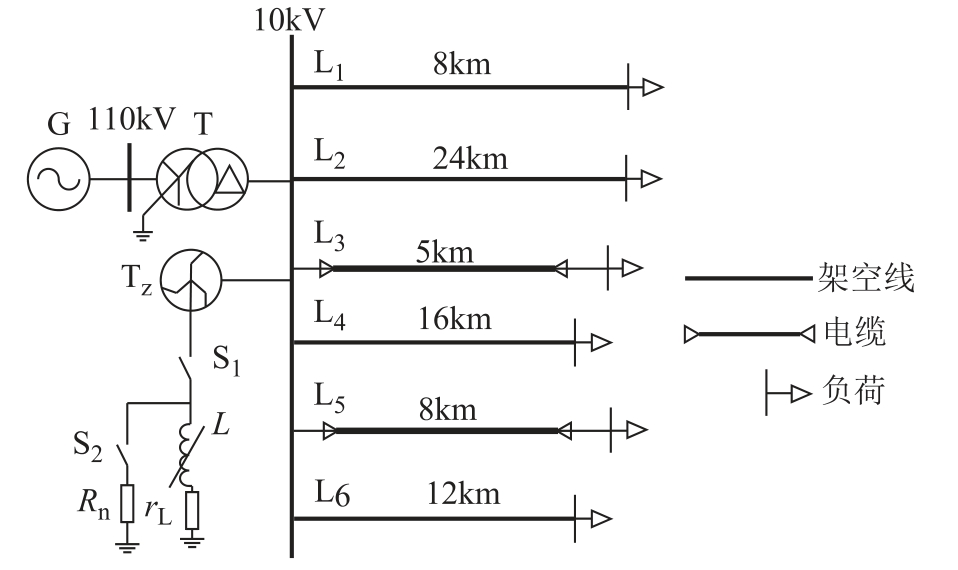
图5 配电网仿真模型
Fig.5 Simulation model of distribution network
4.2 仿真算例分析
4.2.1 算例1
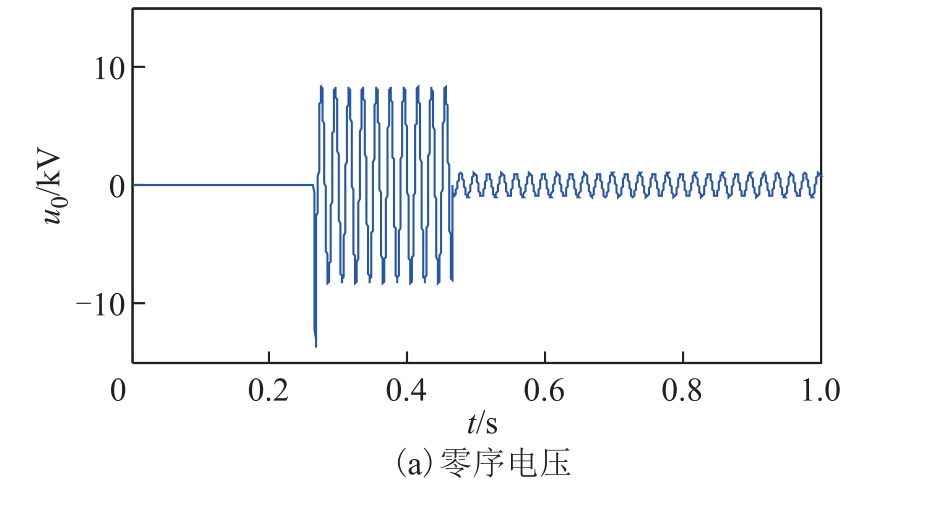
假设在中性点不接地系统中,距离母线7km 处的线路L2 上发生过渡电阻不变的永久性故障,其零序电压及零序电流分别如图6a 和图6b 所示。
截取故障后20~120ms 构造零序伏安曲线,如图7a所示,各曲面面积及其一次拟合如图7b 所示。
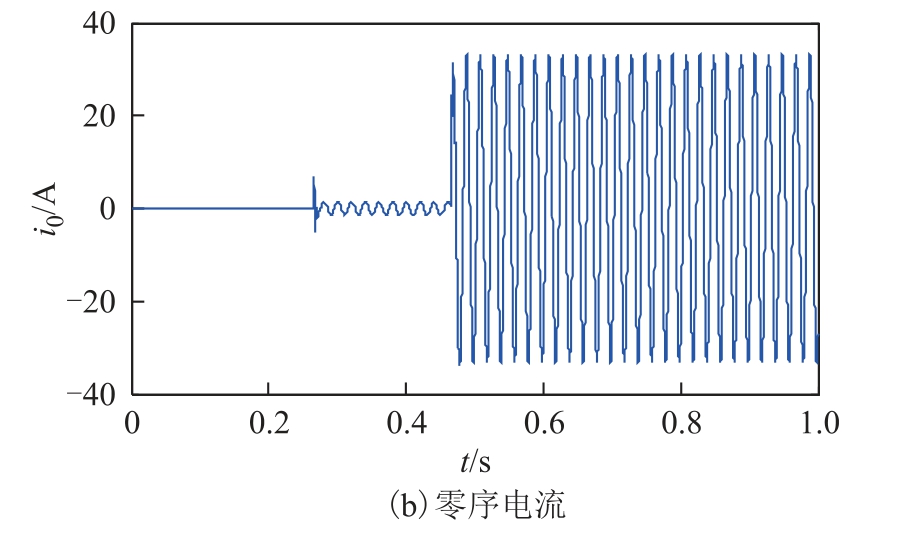
图6 算例1 的零序电压及零序电流
Fig.6 Zero sequence voltage and current of example 1

图7 算例1 的零序伏安曲线及其面积
Fig.7 Zero sequence voltammetric curve and its area of example 1
曲面面积分别为37.806 8、37.802 2、37.801 7、37.801 8 和37.802 1,直线拟合的斜率为-0.000 68,大于-0.01,故预判为永久故障;中性点在故障后0.2s 投入小电阻,小电阻投入后与投入前的零序电流幅值比为22.934 0,故将此次单相接地故障判断为永久故障。
4.2.2 算例2
假设在中性点不接地系统中,距离母线10km 处的线路L4 上发生瞬时性故障,其零序电压及零序电流分别如图8a 和图8b 所示。
截取故障后20~120ms 构造零序伏安曲线,如图9a 所示,各曲面面积及其一次拟合如图9b 所示。
曲面面积分别为34.335 5、29.772 8、21.790 6、12.154 6 和5.026 0,直线拟合的斜率为-0.381 2,小于-0.01,故预判为瞬时故障;中性点在故障后0.2s 投入消弧线圈,投入前、后的零序电流相位差为32.157 3°,不为180°,故将此次单相接地故障判断为瞬时故障。
4.2.3 算例3
假设在中性点经消弧线圈接地系统中,距离母线3km 处的线路L5 上发生瞬时性故障,其零序电压及零序电流分别如图10a 和图10b 所示。
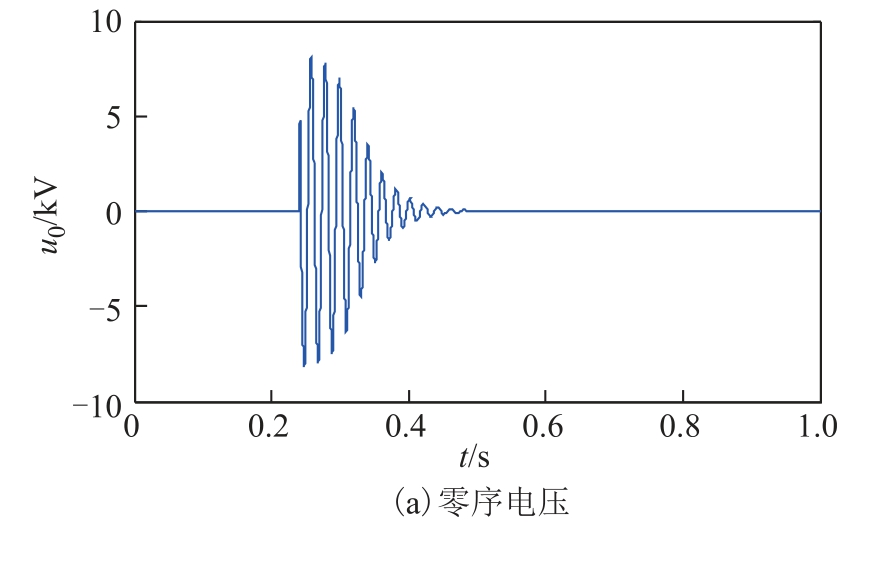
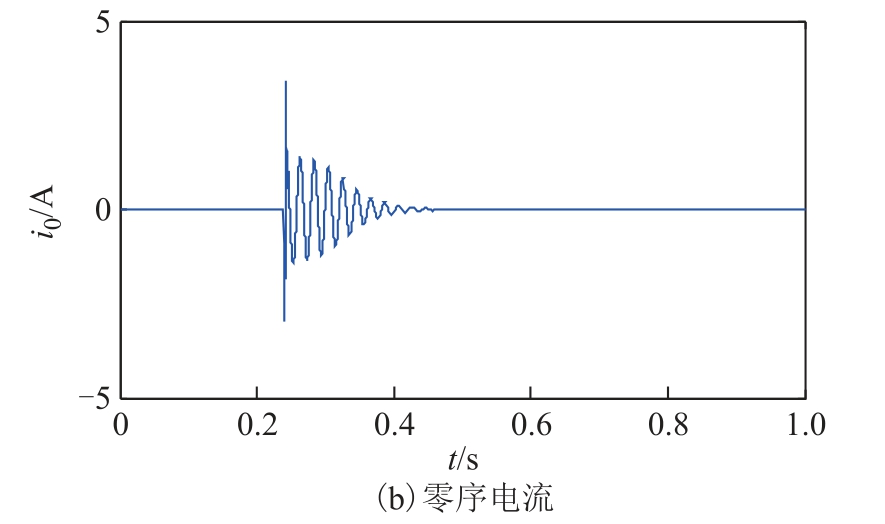
图8 算例2 的零序电压及零序电流
Fig.8 Zero sequence voltage and current of example 2

图9 算例2 的零序伏安曲线及其面积
Fig.9 Zero sequence voltammetric curve and its area of example 2
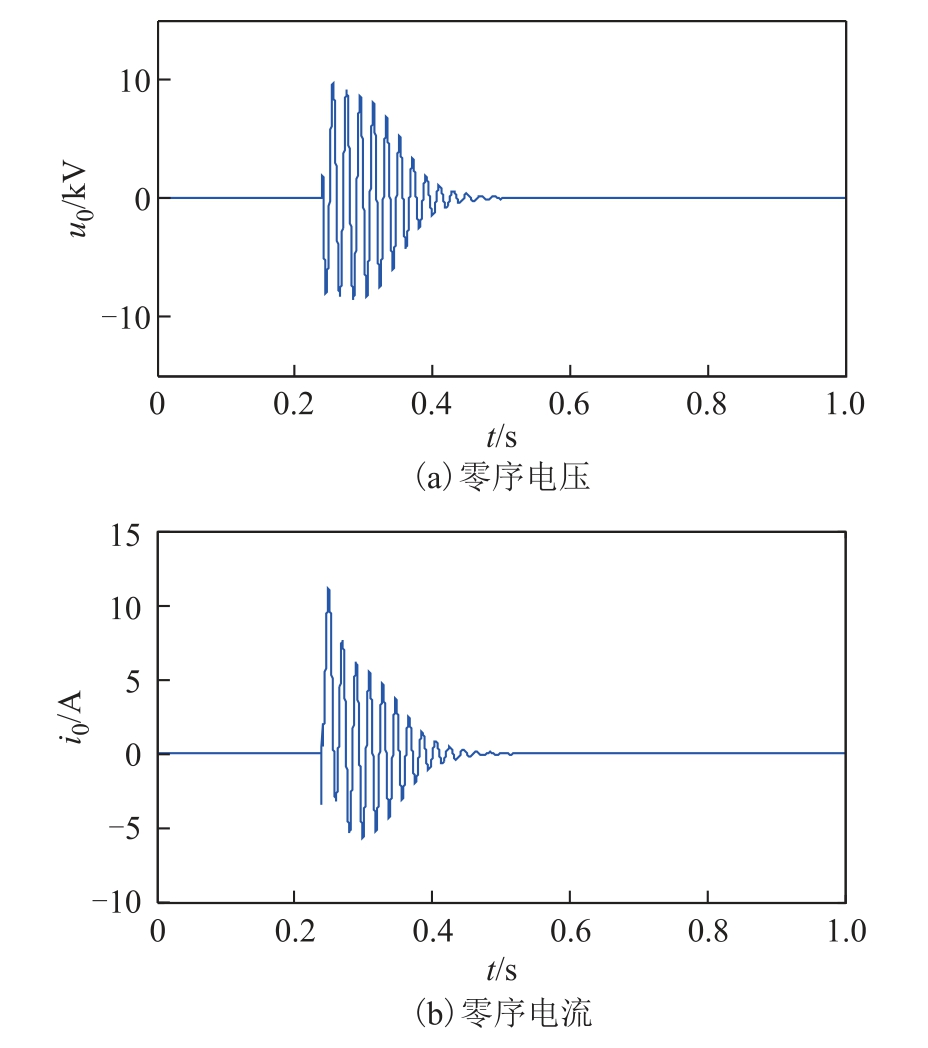
图10 算例3 的零序电压及零序电流
Fig.10 Zero sequence voltage and current of example 3
截取故障后20~120ms 构造零序伏安曲线,如图11a 所示,各曲面面积及其一次拟合如图11b 所示。
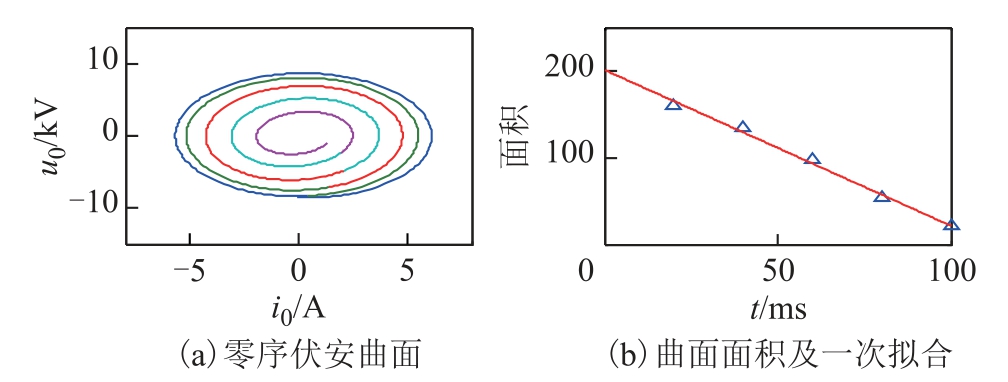
图11 算例3 的零序伏安曲线及其面积
Fig.11 Zero sequence voltammetric curve and its area of example 3
曲面面积分别为160.215 3、135.218 9、97.843 9、53.784 6 和21.401 8,直线拟合的斜率为-1.795 3,小于-0.01,故预判为瞬时故障;中性点在故障后0.6s投入小电阻,投入后前的零序电流幅值比为0.021 7,故将此次单相接地故障判断为瞬时故障。
4.2.4 算例4
假设在中性点经消弧线圈接地系统中,距离母线5km 处的线路L6 上发生永久性故障,其零序电压及零序电流分别如图12a 和图12b 所示。
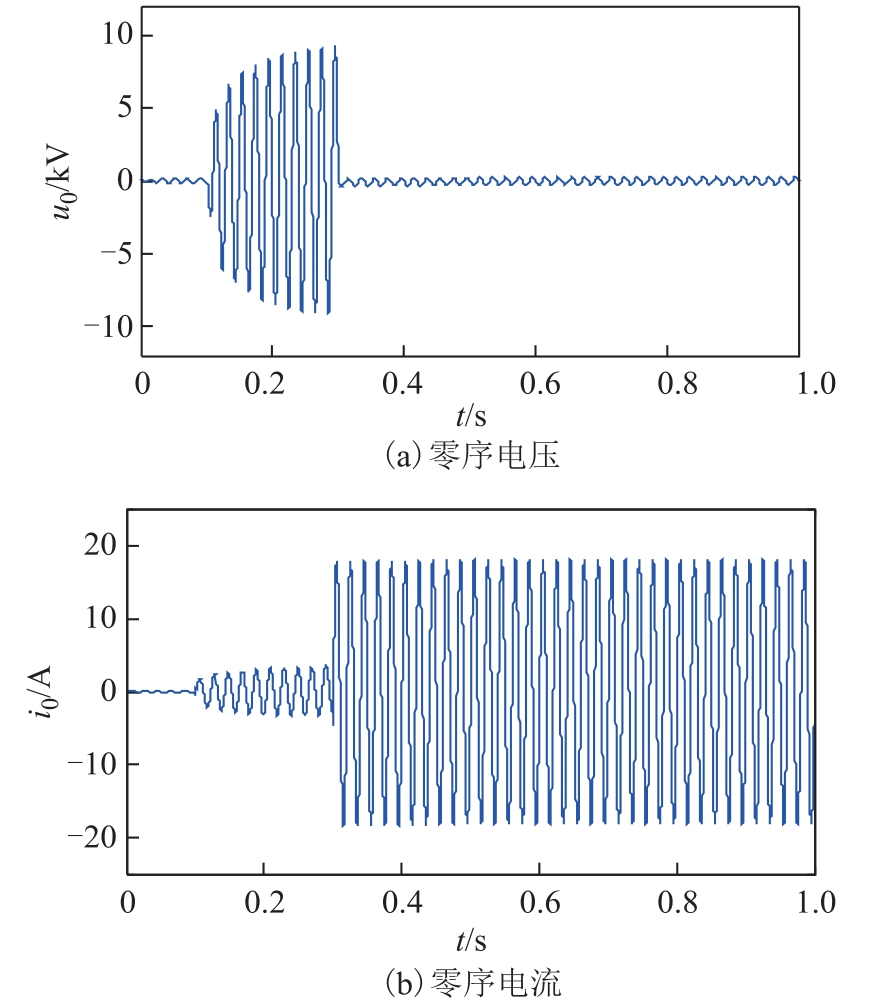
图12 算例4 的零序电压及零序电流
Fig.12 Zero sequence voltage and current of example 4
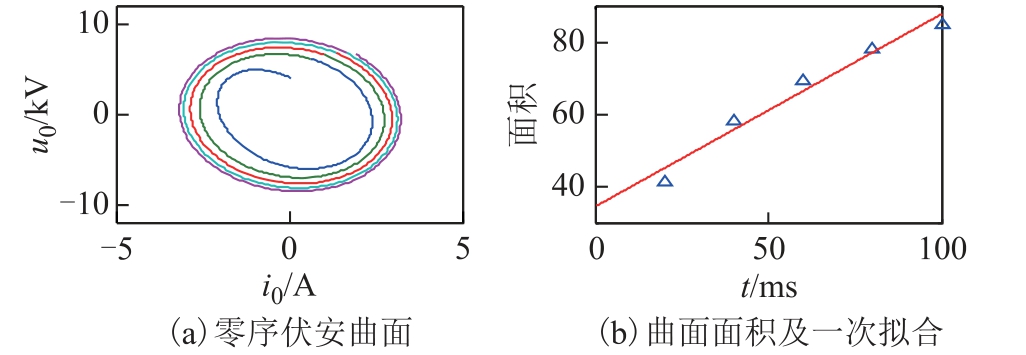
图13 算例4 的零序伏安曲线及其面积
Fig.13 Zero sequence voltammetric curve and its area of example 4
截取故障后20~120ms 构造零序伏安曲线,如图13a所示,各曲面面积及其一次拟合如图13b 所示。
曲面面积分别为41.509 8、58.227 4、69.445 9、78.393 1 和84.995 0,直线拟合的斜率为0.535 7,大于-0.01,预判为永久故障;中性点在故障后0.6s 投入小电阻,投入前、后的零序电流的幅值比为5.113 7,故将此次单相接地故障判断为永久故障。
4.3 故障性质预判的实测数据验证
该方法还未应用至实际工程现场,暂无法考虑中性点变动的实际测量数据情况,故只验证中性点变动之前的故障性质预判方法。下述实测数据均取自某110kV 变电站的Ⅰ段母线,该母线有5 条10kV线路,主干均为架空线路,无纯电缆线路,但有部分分支采用电缆。
实测数据1:过渡电阻不变的永久性接地故障。其零序电压及零序电流分别如图14a 及图14b 所示,零序伏安曲线及其面积分别如图14c 及图14d 所示。
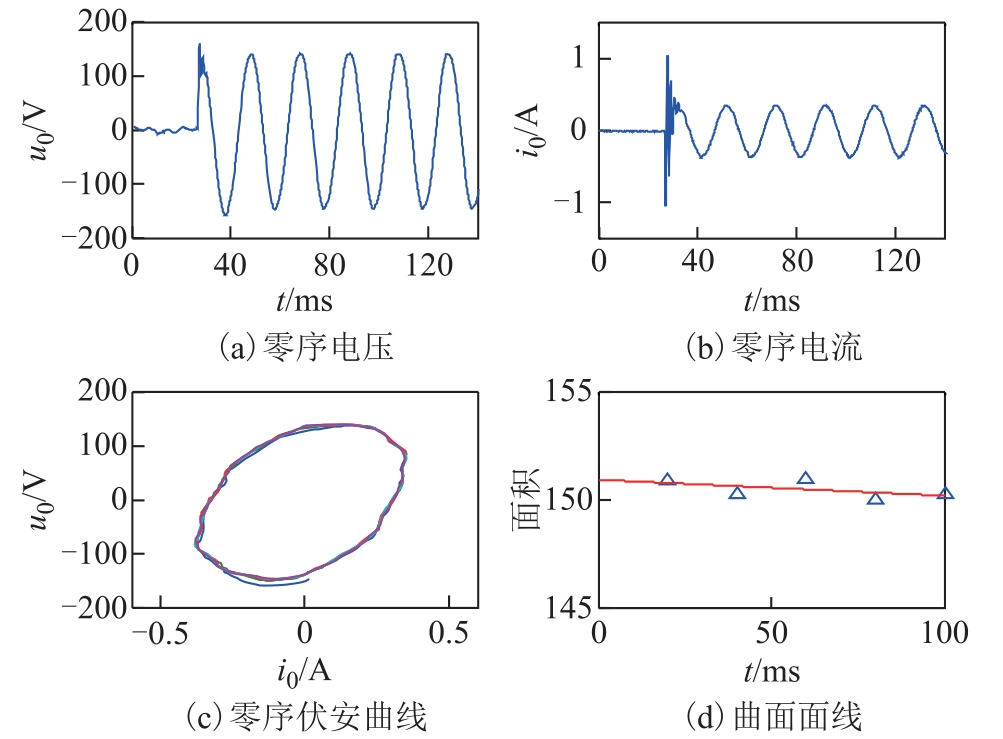
图14 过渡电阻不变的永久故障
Fig.14 Permanent fault with constant transition resistance
由图14 可知,过渡电阻不变的单相接地故障其零序电压及零序电流的稳态量也基本不变,取故障后20~120ms 的5 个周期,其零序伏安曲线面积分别为150.870 2、150.256 5、150.968 4、150.012 4、150.250 1,基本没有发生变化,直线拟合的斜率为-0.007 4,故预判为永久性故障。该故障巡检结果为某配电变压器高压线夹断裂导致的接地故障。
实测数据2:过渡电阻变小的永久性接地故障。其零序电压及零序电流分别如图15a 及图15b 所示,零序伏安曲线及其面积分别如图15c 及图15d 所示。
由图15 可知,过渡电阻变小的单相接地故障其零序电压及零序电流的稳态量逐渐增大,取故障后20~120ms 的5 个周期,其零序伏安曲线面积分别为29.432 5、53.789 2、78.748 4、110.782 4、147.685 2,伏安曲线的面积逐渐增大,直线拟合的斜率为1.467 5,故预判为永久性故障。该故障巡检结果为某线路的避雷器老化导致的接地故障。
实测数据3:瞬时性接地故障。其零序电压及零序电流分别如图16a 及图16b 所示,线路的零序伏安曲线及其面积分别如图16c 及图16d 所示。

图15 过渡电阻变小的永久故障
Fig.15 Permanent fault of transition resistance becomes small
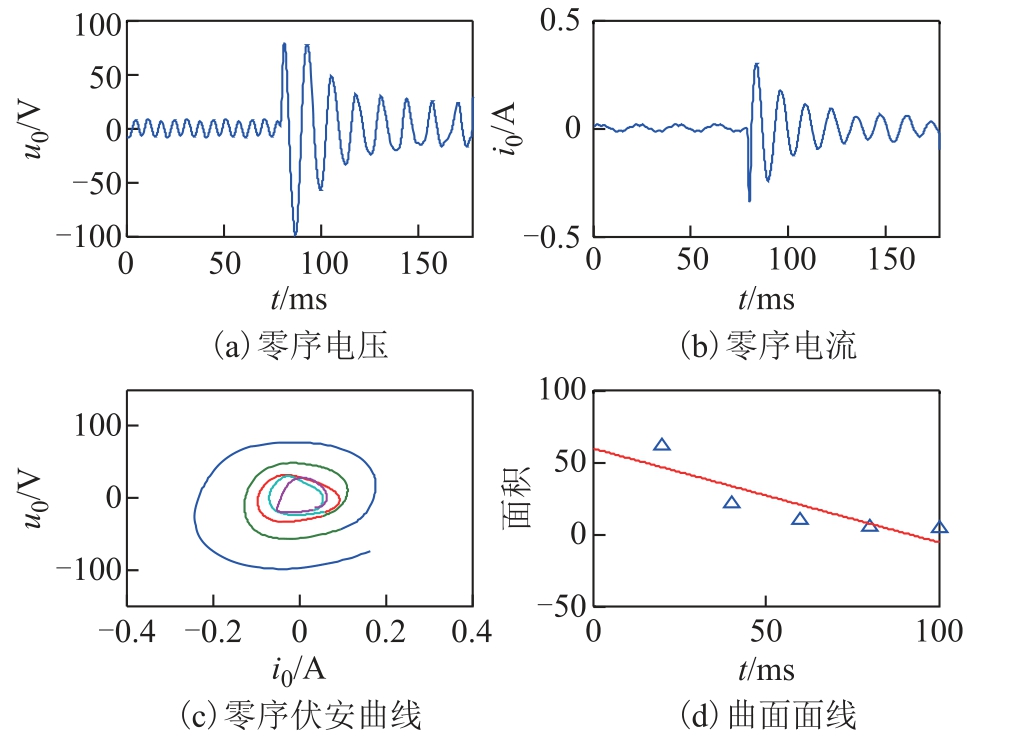
图16 过渡电阻变大的瞬时故障
Fig.16 Instantaneous fault with transition resistance becomes large
由图16 中可知,在过渡电阻逐渐变大的情况下,其零序电压及零序电流的稳态量逐渐地减小,取故障后20~120ms 的5 个周期,其零序伏安曲线面积分别为61.514 5、20.791 5、9.252 2、5.208 0、4.119 6,伏安曲线的面积也逐渐减小,直线拟合的斜率为-0.651 9,故预判为瞬时性故障。该故障巡检结果为不明原因故障,未找到故障点。
实测数据4:稳定的电弧接地故障,其零序电压及零序电流工频分量分别如图17a 及图17b 所示,经傅里叶变换后提取工频分量并构造零序伏安曲线,如图17c 所示,其面积如图17d 所示。

图17 稳定电弧故障
Fig.17 Stable arc fault
由图17 可知,稳定电弧故障的工频零序电压及零序电流基本不变,其5 个周期的零序伏安曲线面积分别为78.604 3、78.564 9、78.561 6、78.409 6、78.526 8,基本没有发生变化,直线拟合的斜率为-0.001 6,故预判该故障为永久性故障。该故障巡检结果为某线路的电缆分支箱电缆接头故障。
通过仿真实验分析及实测故障数据验证,基于零序分量伏安曲线面积的变化可推测过渡电阻的变化,进而预判此次的故障性质;结合故障性质的预判结果调整中性点的投入设备,并根据中性点设备的投入形成检验性判据,进而对故障性质进行联合辨识,这对配电网的故障性质辨识具有一定的适用性。
5 结论
将线路与大地之间等效为绝缘电阻,根据故障时过渡电阻的变化推测故障性质,中性点根据故障性质的预判投入相应的设备,以提高配电网的可靠性及自愈能力。
1)通过理论分析及仿真表明,利用故障线路零序分量构造伏安曲线,其面积变化可推测过渡电阻的变化趋势,进而预判此次单相接地故障的性质。
2)根据故障性质的预判结果,中性点投入相应的设备可提高配电网发生单相接地故障后的自愈能力及故障的快速处置能力。
3)利用中性点设备主动投入形成的零序电流相位及幅值变化规律,对故障性质进行检验判断,提高了故障性质辨识的可靠性。
中性点设备的投入时间可根据过渡电阻变化的剧烈程度进行调整,以增强配电网的单相接地故障处置的选择性和可靠性。本方法目前只考虑了故障的过渡电阻,对于间歇性故障还有一定的局限性,其他故障类型及特性还在继续的研究当中。
[1] 刘健, 芮骏, 张志华,等. 智能接地配电系统[J]. 电力系统保护与控制, 2018, 46(8): 130-134.Liu Jian, Rui Jun, Zhang Zhihua, et al. Smart grounding power distribution systems[J]. Power System Protection and Control, 2018, 46(8): 130-134.
[2] 刘健, 王玉庆, 芮骏, 等. 智能接地配电系统关键参数设计[J]. 电力系统自动化, 2018, 42 (16): 186-192.Liu Jian, Wang Yuqing, Rui Jun, et al. Key parameter design of smart grounding distribution systems[J].Automation of Electric Power Systems, 2018, 42 (16):186-192.
[3] 要焕年, 曹雪月. 电力系统谐振接地[M]. 2 版. 北京:中国电力出版社, 2009.
[4] 陈维江, 蔡国雄, 蔡雅萍, 等. 10kV 配电网中性点经消弧线圈并联电阻接地方式[J]. 电网技术, 2004,28(24): 56-60.Chen Weijiang, Cai Guoxiong, Cai Yaping, et al.Neutral grounding mode in 10kV distribution network via peterson coil with parallel resistance[J]. Power System Technology, 2004, 28(24): 56-60.
[5] 付晓奇, 徐粮珍, 赵宝丽. 10kV 配网中性点小电阻接地技术与应用[J]. 电力系统保护与控制, 2010,38(23): 227-230.Fu Xiaoqi, Xu Liangzhen, Zhao Baoli. Discussion on the technology and of 10kV distribution network neutral grounding through small resistance[J]. Power System Protection and Control, 2010, 38(23): 227-230.
[6] 刘明岩. 配电网中性点接地方式的选择[J]. 电网技术, 2004, 28(16): 86-89.Liu Mingyan. Selection of neutral grounding modes in power distribution network[J]. Power System Technology, 2004, 28(16): 86-89.
[7] 徐丙垠, 薛永端, 冯光, 等. 配电网接地故障保护若干问题的探讨[J]. 电力系统自动化, 2019, 43(20):1-7.Xu Bingyin, Xue Yongduan, Feng Guang, et al.Discussion on several problems of earthing fault protection in distribution network[J]. Automation of Electric Power Systems, 2019, 43(20): 1-7.
[8] 许寅, 和敬涵, 王颖, 等. 韧性背景下的配网故障恢复研究综述及展望[J]. 电工技术学报, 2019,36(16): 3416-3429.Xu Yin, He Jinghan, Wang Ying, et al. A review on distribution system restoration for resilience enhancement[J]. Transactions of China Electrotechnical Society, 2019, 36(16): 3416-3429.
[9] 李政洋, 李景禄, 苏盛, 等. 基于配电网单相接地故障分区的中性点智能电阻接地方法[J]. 电力系统自动化, 2019, 43(6): 145-150, 170.Li Zhengyang, Li Jinglu, Su Sheng, et al. Intelligent resistance grounding method of neutral point based on single-phase grounding fault zone of distrbution network[J]. Automation of Electric Power Systems,2019, 43(6): 145-150, 170.
[10] 王宾, 耿建昭, 董新洲. 配网高阻接地故障伏安特性分析及检测[J]. 中国电机工程学报, 2014, 34(22):3815-3823.Wang Bin, Geng Jianzhao, Dong Xinzhou. Analysis and detection of volt-ampere characteristics for high impedance faults in distribution systems[J].Proceedings of the CSEE, 2014, 34(22): 3815-3823.
[11] 耿建昭, 王宾, 董新洲, 等. 中性点有效接地配电网高阻接地故障特征分析及检测[J]. 电力系统自动化, 2013, 37(16): 85-91.Geng Jianzhao, Wang Bin, Dong Xinzhou, et al.Analysis and detection of high impedance grounding fault in neutral point effectively grounding distribution network[J]. Automation of Electric Power Systems, 2013, 37(16): 85-91.
[12] 丁芃, 朱珂, 朱裕庆, 等. 基于模型辨识的配电线路永久性故障判定方法[J]. 电工技术学报, 2019,34(5): 1004-1012.Ding Peng, Zhu Ke, Zhu Yuqing, et al. Determining the permanent fault in distribution lines based on model recognition[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1004-1012.
[13] 顾荣斌, 蔡旭, 陈海昆, 等. 非有效接地电网单相电弧接地故障的建模及仿真[J]. 电力系统自动化,2009, 33(13): 63-67.Gu Rongbin, Cai Xu, Chen Haikun, et al. Modeling and simulating of single-phase arc grounding fault in non-effective earthed networks[J]. Automation of Electric Power Systems, 2009, 33(13): 63-67.
[14] 任万滨, 金建炳, 郭继峰, 等. 碳电极交流电弧伏安特性的实验研究[J]. 电工技术学报, 2014, 29(1): 18-22.Ren Wanbin, Jin Jianbing, Guo Jifeng, et al.Experimental research on voltage-current characteristics of carbon AC arc[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 18-22.
[15] 许晔, 郭谋发, 陈彬, 等. 配电网单相接地电弧建模及仿真分析研究[J]. 电力系统保护与控制, 2015,43(7): 57-64.Xu Ye, Guo Moufa, Chen Bin, et al. Modeling and simulation analysis of arc in distribution network[J].Power System Protection and Control, 2015, 43(7): 57-64.
[16] 陈奎, 陈博博. 基于改进暂态相关分析和支持向量机的电弧故障选线研究[J]. 电力系统保护与控制,2016, 44(24): 66-73.Chen Kui, Chen Bobo. Research on arc fault line selection based on improved transient correlation analysis and support vector machine[J]. Power System Protection and Control, 2016, 44(24): 66-73.
[17] 罗勋华, 黄纯, 潘志敏, 等. 基于序分量无功功率的单相自适应重合闸[J]. 电工技术学报, 2016,31(11): 149-156.Luo Xunhua, Huang Chun, Pan Zhimin, et al. Singlephase adaptive reclosure based on reactive power of sequence components[J]. Transactions of China Electrotechnical Society, 2016, 31(11): 149-156.
[18] 陈诚, 江亚群, 黄纯. 输电线路单相瞬时性故障熄弧判定方法[J]. 电力系统及其自动化学报, 2015,27(11): 21-25.Chen Cheng, Jiang Yaqun, Huang Chun. An approach to judge extinction arc of single-phase transient fault in transmission lines[J]. Proceedings of the CSUEPSA, 2015, 27(11): 21-25.
[19] 梁林, 江亚群, 黄纯. 带并联电抗器的超高压输电线路单相故障识别[J]. 电力系统及其自动化学报,2016, 28(8): 32-37.Liang Lin, Jiang Yaqun, Huang Chun. Identification of single-phase fault for UHV transmission lines with shunt reactor[J]. Proceedings of the CSU-EPSA, 2016,28(8): 32-37.
[20] 罗薇, 黄纯, 罗勋华, 等. 改进ACUSUM 算法的自适应重合闸判据[J]. 电力系统及其自动化学报,2017, 29(9): 136-142.Luo Wei, Huang Chun, Luo Xunhua, et al. Adaptive reclosure criterion based on improved ACUSUM algorithm[J]. Proceedings of the CSU-EPSA, 2017,29(9): 136-142.
[21] 王庆庆, 王慧芳, 林达, 等. 基于并联电抗器差模电流波形特征的三相自适应重合闸永久性故障识别[J]. 电网技术, 2015, 39(4): 1127-1132.Wang Qingqing, Wang Huifang, Lin Da, et al.Identification of permanent faults for three-phase adaptive reclosure based on waveform characteristics of differential mode currents in shunt reactors[J].Power System Technology, 2015, 39(4): 1127-1132.
[22] 索南加乐, 邵文权, 宋国兵. 基于参数识别的单相自适应重合闸研究[J]. 中国电机工程学报, 2009,29(1): 48-54.Suonan Jiale, Shao Wenquan, Song Guobing. Study on single-phase adaptive reclosure scheme based on parameter identification[J]. Proceedings of the CSEE,2009, 29(1): 48-54.
[23] 骆仁意. 10kV 配电网中性点复合接地方式研究[D].重庆: 重庆大学, 2016.
[24] 束洪春. 配网选线保护与故障定位[M]. 北京: 科学出版社, 2016.
[25] 龙毅, 欧阳金鑫, 熊小伏, 等. 基于零序功率变化量的配电网单相高阻接地保护[J]. 电工技术学报,2019, 34(17): 3687-3695.Long Yi, Ouyang Jinxin, Xiong Xiaofu, et al.Protection principle of single-phase high resistance fault for distribution network based on zero-sequence power variation[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3687-3695.