0 引言
随着智能电网技术的发展，电力用户与电网之间的友好互动成为了目前主要研究的热点[1-3]，其中，负荷监测是实现这一技术最为关键的一步。近年来随着研究人员对负荷监测技术的深入研究[4-6]，传统的负荷检测方法[7-8]逐步向智能化方向发展，形成了以非侵入式负荷监测（Non-Intrusive Load Monitoring,NILM）为主的测量方式，它不再依赖每个用电设备上加装监测装置，而仅需通过对电力负荷入口处的电压、电流及功率等信息的实时测量和分析，便可得到负荷内部的负荷种类以及不同用电设备实时能源消耗比例[9]。在技术成本、设备维护及用户接受度方面[10]非侵入式监测方式明显优于其他监测方案。另外，非侵入式技术与智能电表的结合，可进一步推动分项能耗计量工作，同时激励电网公司与用户友好互动，实现负荷移峰和削峰填谷，提高电力系统运行的经济性与可靠性[11-13]。
在整个非侵入式负荷监测中，负荷事件检测是实现NILM 的第一步，其负责检测负荷投/切状态，为后续的负荷特征提取以及负荷辨识奠定基础。通常，负荷事件反映在功率曲线的变化上，文献[14]采用对相邻时间段负荷印记进行阶跃检测，当变化超过阈值则认为有负荷设备进行投切。文献[15]采用平均值窗进行事件检测，当滑动窗内的均值发生较大改变时，即认为有负荷事件发生，然而对于电气量缓慢变化的情况检测效果并不理想。文献[16]采用广义似然比检验的方法, 通过突变点检测的方法进行事件检测。文献[17-20]采用拟合优度检验的方法进行NILM 事件检测，根据总功率曲线中两个窗口内的样本比较，获取负荷事件，该方法相较于文献[16]方法准确率稍高。文献[21]等对排列熵算法进行改进，检测电流信号的变化，以实现精确地检测负荷事件。文献[22-23]采用累积和（Cumulative Sum,CUSUM）控制图进行变点检测，然而该方法过度依赖时域信息，特别对时间相近的事件容易漏检。文献[24]提出了基于贝叶斯信息准则的负荷事件检测算法，以解决常规CUSUM 算法中的漏检问题。然而，在现有的这些负荷事件检测方法中，大多是对电气量直接进行变点检测，缺少对状态特征的分析。而且，采用孤立的采样点进行监测，特别是在暂态过程比较长的事件中，经常发生误检或漏检，使得负荷事件检测准确率降低。
为了避免负荷事件的误检或漏检，提高负荷事件检测准确率，本文提出了一种基于状态聚类的非侵入式负荷事件检测方法。该方法通过规定数据块长度以及对数据块进行分析，利用滑动窗初步确定负荷可能发生的状态改变时刻，然后针对这些时间点数据，采用均值漂移（Mean-shift）聚类方法确定每一个状态的质心，并依据状态域内数据点的时域信息确定负荷事件发生点，实现可靠的负荷事件检测。最后，本文在实测数据样本集上验证了所提方法对于负荷事件检测的准确性和有效性。
1 状态聚类
1.1 数据块内状态域分布特点
在非侵入式负荷监测中，通常将原始的电压、电流信息转换为有功、无功、谐波等信息，并通过监测负荷事件所引起的这些信息的变化来感知负荷事件。
令NILM 系统监测到的有功、无功、谐波等d维特征的非零数据集Ω={ω1, ω2, ω3,…, ωn}包含n个元素，其中ωi∈Rd，从而构成多维特征空间。在负荷事件未发生时，数据点通常会保持在一个稳定范围内，表现为一个簇，称为稳定域。当存在负荷事件时，状态域会发生迁移，通常将其定义为暂态过程，迁移过程记录的数据点所属区域称为过渡域。一般而言，根据有功功率的变化情况，可以将电器的完整运行过程分为若干过渡区段和稳定区段，稳定区段表示负荷平稳，功率不发生突变。总负荷的过渡区段包括一个或多个电器的过渡区段，而稳定区段不包括任何电器的过渡区段，过渡区段与稳态区段在时间上通常交替出现[25-26]。由于电气特征众多，根据文献[27-28]的分析，本文采用特征最为显著的有功、无功以及对小负荷区分度较高的电流3次谐波幅值开展进一步研究。
图1 展示了某空调投切时有功、无功和3 次谐波的特征变化情况。当空调起动时，由于压缩机工作，有功功率、无功功率、3 次谐波缓慢上升。传统负荷事件检测方法常在类似暂态过程存在时出现漏检和多检的情况，增加了后续负荷特征可靠提取及辨识的难度。因此，本文将数据点投影到特征空间进行分析，以便负荷事件的准确检测。
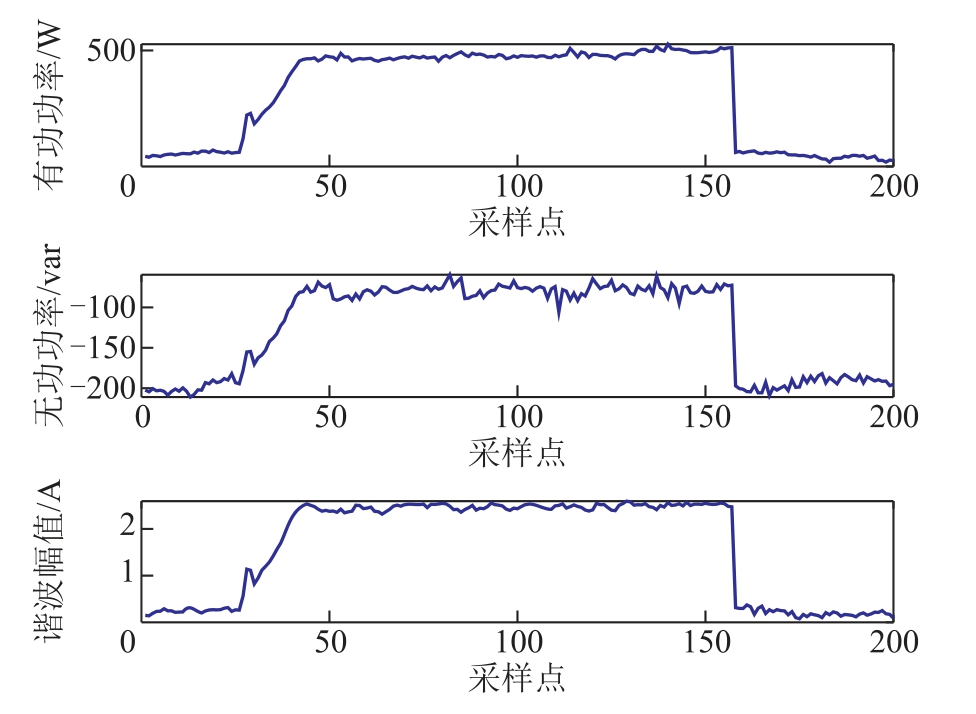
图1 某空调起停过程的P-Q-H 波形
Fig.1 P-Q-H feature of an air conditioner from its start to stop process
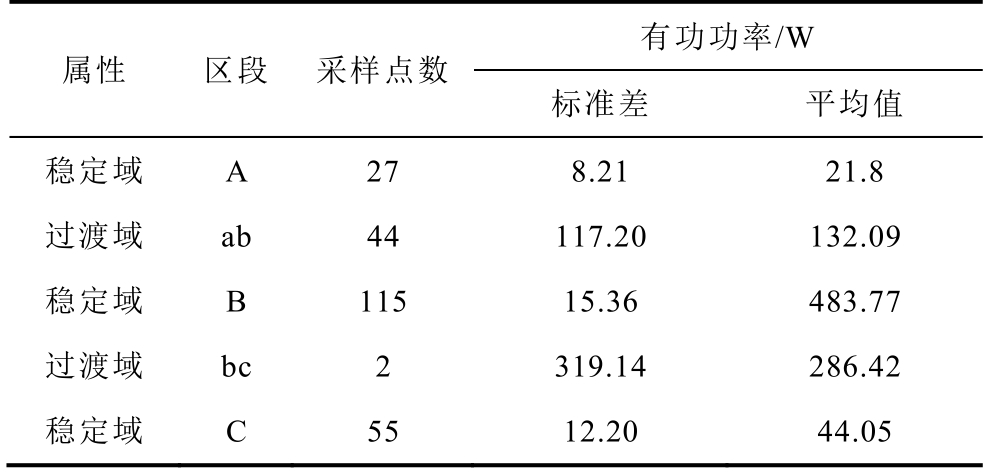
图2 展示出空调的起-停事件过程的P-Q-H 三维特征的状态域。令ΦA，ΦB，ΦC 分别为空调投入前、稳定运行和空调关闭后的稳定状态域，特征空间上数据点的集合满足 ΩA={ω|ω∈ΦA}, ΩB={ω|ω∈ΦB}, ΩC={ω|ω∈ΦC}。显然，状态域中各特征分布在有限区域内，但是稀疏程度有所不同。表1 列出了稳定域和过渡域的相关特征。不难发现，过渡域的标准差较高，即稳态域数据聚类相对集中，而稳定域标准差较低。由此，可通过相邻两个稳定域聚类中心改变作为负荷事件的依据。
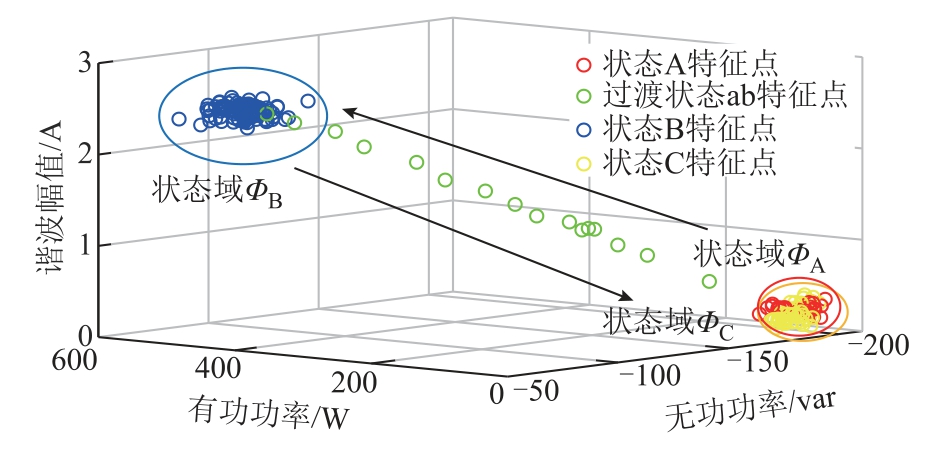
图2 某空调起停过程的P-Q-H 三维特征状态转换过程
Fig.2 P-Q-H 3-dimensional feature of an air conditioner during start and stop process
表1 某型号空调起停过程数据点分布统计
Tab.1 Statistics data point distribution statistics of a certain type of air conditioner start and stop process
?
1.2 聚类机理
对于一个电器设备的完整运行过程而言，其负荷投切之前和之后都存在一个稳定的区域，这个稳定的区域包括具有相同特性的数据，而过渡阶段则认为是类区分的一个分界，即为负荷事件发生的依据。为了准确找到负荷事件，由1.1 节描述可知，通过对负荷数据进行聚类可检测出潜在的负荷事件。
均值漂移（Mean-shift）算法作为一种基于密度的聚类方法，具有对相似数据点自适应迭代聚类[29-30]等优势，最终收敛到概率密度最大的地方，收敛到同一点的被称为一类。基于此，本文将其应用于负荷特征数据聚类，实现负荷事件检测的目的，其主要过程如下。
1）构建目标函数
非零数据集Ω 中，Bh 是一个固定带宽为h 的高维球区域
式中，x 为球心；y 为高维球区域内任意一点；h 为球的带宽，其决定了在稳定域内对极大值密度点的搜索范围。通常，h 越大，识别小负荷的能力越弱，对电气特征波动的检测能力越强；反之识别小负荷的能力越强，对于电气特征波动越敏感。
在高维球区域Bh 中，Mean-shift 算法的优化目标函数为
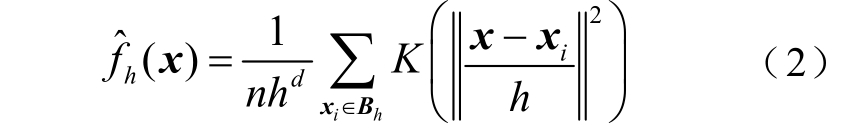
式中，n 为高维球内数据点数量；d 为特征维数；xi为第i 个数据点；K(x)为镜像对称核函数，表示为
式中，ck,d 为归一化常数；k(x)为K(x)的剖面函数。出于对最小方均误差的考虑， 本文采用Epanechnikov 核函数。
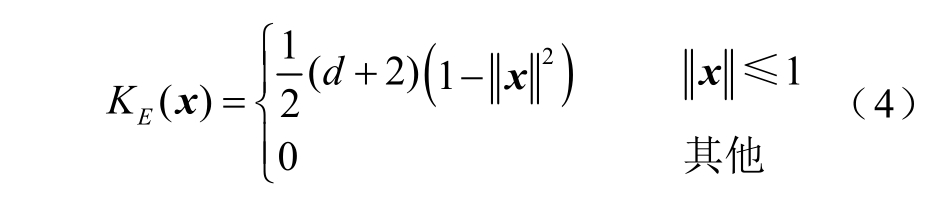
2）获取高维球Bh 及球心x 的更新方向
令
x)=0，并对目标函数进行求导可得
mh,g(x)即为球心更新的方向。
3）对高维球Bh 及其球心x 进行更新迭代
经过反复迭代，均值会朝着数据样本密集的方向移动，最终得到概率密度函数的峰值点xp 及其高维球区域Bh(x)，分别代表当前总负荷稳态密度中心及其稳定区域。
2 滑动窗差值搜索的Mean-shift 聚类算法
在Mean-shift 聚类过程中，当负荷运行在过渡域时，初始中心的选择会影响聚类范围，从而对后续负荷事件检测产生影响。因此，为了合理地选取初始聚类中心点，本文利用负荷采集得到时间序列信息，首先对某一特征量采用滑动窗差值搜索方法确定初始聚类中心，对特征量选取方法如下。
采集常用电器设备从开启到稳定运行时段的d维特征信号，并对稳定域和过渡域的数据点进行标识，为衡量不同特征对过渡状态和稳定状态的表征效果，本文参照轮廓系数的概念[31]，定义电器设备状态轮廓系数SCE(q)来衡量第E 个电器设备在稳定状态和过渡状态时数据点q 维特征下的分离程度，即
式中，nE 为当前电器设备稳定状态内的数据点数量；a(q)(i)为第q 维特征中第i 个稳定状态内的数据点到稳定状态内其他数据点的平均距离；b(q)(i)为第q 维特征中第i 个稳定状态内的数据点到过渡状态的每个点的平均距离。
考虑到状态轮廓系数可表征不同特征下各电器设备的分离程度，为了衡量特定场景中不同特征对电气设备的区分效果，定义第q 维特征下平均状态轮廓系数SC(q)，令实验环境内包含电器数量为L，可通过式（10）计算SC(q)。
为提高计算效率，滑动窗选取单一特征量进行差值搜索，所以应选择该场景最具状态变化代表性的特征。因此，对式（10）得到的d 维特征量的SC(q)进行排名，取排名第一的特征作为滑动窗差值搜索的特征量，以确定初始聚类点。
设第p 维特征的SC(p)排名第一，定义宽度为m的滑动窗Yi 为
式中，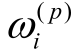 
为在i 数据点的特征p 的数值。于是，可求得滑动窗Yi 内数据点特征量p 的平均值为
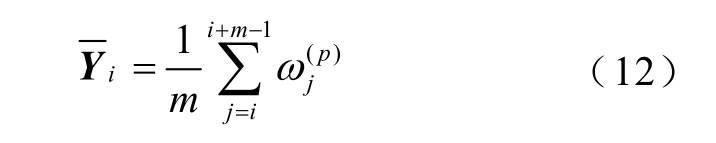
由于滑动窗内部差值旨在搜寻稳定域，若窗内数据点差值均小于阈值θ，可认为该滑动窗处于稳定域内，极差可表示数据变化的最大范围，定义为
式中，ω(p)为滑动窗Yi 内数据点的p 维特征值；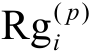
为Yi 内数据点p 维特征的极差。
规定稳定点的波动范围在一定限度内，则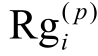 
应满足
式中，θ 为无电器投入时所选取特征量下的极差，以得到各稳定状态点。
若将式（14）确定的稳定状态点设置为初始聚类点，则初始聚类点过多，聚类算法运行时间过长。为了避免这一现象，本文过滤稳定状态点得到初始聚类点。首先记录满足式（14）的稳定状态点，将首个稳定状态点记录为第一个初始聚类点，同时定义滑动窗Yi 与前一初始聚类点s 所代表的滑动窗Ys之间p 维特征的差量为
式中，γ为负荷事件的最小检出量。通常，该值可根据实际场景中检出负荷大小来设置。
由此，通过滑动窗差值搜索可以得到每个状态域至少一个数据点作为初始聚类点。然后根据该数据点所包含的该状态域的相关信息，即可进一步对状态域分布展开研究。滑动窗宽度m 是一个影响负荷事件检测的重要参数，它决定了能够检出的连续两个开关事件的最小时间间隔。设定两电器开关最小间隔长度为Ts，采样周期为Δt，可定义窗宽度m 为
式中，[·]表示取整。
图3 给出了寻找初始聚类中心的整个流程。
图3 滑动窗差值搜索流程
Fig.3 Flow chart of sliding window difference search
为了在Mean-shift 聚类时避免特征分量量纲不同，在聚类之前数值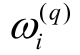
需要归一化为
。
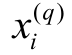式中， q∈ [1, d]；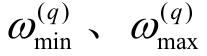
分别为当前测量环境预计承载的负载最小时和负载最大时采集数据点特征q 的最小值和最大值。
另外，由于高维球半径选取与电气测量环境的噪声有关，为了便于参数选取，这里给出高维球半径h 的参考计算方法。假定在没有电器设备投入运行的情况下，采集N 个采样点，记录其d 维特征，经过式（18）归一化后，可估算半径h 的取值为
式中， x i =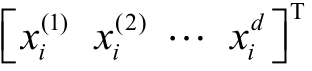
为第i 个数据点的d 维特征的取值；Ωd 为本次采样数据构建的d 维空间；
为空间内数据点取均值得到的密度中心。
进一步地，当数据量较大时，为了提升本文方法的处理速度，采用分块方法对采样信息进行处理，每隔w 个采样点分析一次；对w 个采样点的电力数据进行Mean-shift 聚类，得到每个数据块的电气量稳定状态数量和各自的稳态特征。
为了可靠地实现负荷投切检测，将除去最后一个稳定域之外，其他每个稳定域高维球内的最大时间序列点视为当前状态的结束点，因此可视为下个状态的起始点，即为事件发生点。最后，输出负荷事件的发生时刻。其整个流程如图4 所示。
图4 算法流程
Fig. 4 The flow chart of algorithm
3 案例分析及探讨
为了验证文中负荷事件检测的效果，选用一个家庭内空调、电饭煲、微波炉、电磁炉、电水壶、电视机、电冰箱、电冰柜、电风扇、台式计算机10个典型家用电器。在实验中，将上述各个用电设备运行的有功功率、无功功率及谐波等进行间隔Δt =2s 的数据采集，然后与现有算法进行对比，通过三个典型场景，验证对负荷事件发生情况的检测性能。表2 给出了各电器的有功、无功、谐波的状态轮廓系数，可见有功功率轮廓系数最高，因此实验中选取滑动窗差值搜索的特征量为有功功率。另外，本实验场景开启电器均由人工操作，两两电器起动时间有一定的间隔，设定Ts=5s，计算得m=3。
表2 电器设备状态的轮廓系数
Tab.2 Silhouette coefficient of equipment state
电器设备电器设备状态轮廓系数有功功率 无功功率 谐波幅值空调 0.95 0.92 0.96电饭煲 0.99 0.32 0.15微波炉 0.99 0.84 0.96电磁炉 0.97 0.63 0.52电水壶 0.99 0.54 0.7电视机 0.93 0.38 0.43电冰箱 0.98 0.98 0.6电冰柜 0.88 0.74 0.15电风扇 0.98 0.85 0.41计算机 0.97 0.96 0.96均值 0.96 0.72 0.58
3.1 场景1
本场景对空调进行起动操作，分别采用阈值触发法[14]、双边CUSUM 滑动窗算法[22]和本文算法进行事件检测。文献[14]的方法，设置阈值触发事件检测的有功功率阈值为70；CUSUM 事件检测中，按照文献[22]中提出的参数值最优选取方法选取参数和计算阈值，根据待监测电器设置最小突变量Δmin 为200，噪声大小为30。经过稳定状态下的实际测量，稳定状态有功功率波动均小于30，最小检出对象有功功率为 70，可根据参数选取条件设置θ=30， γ=70，迭代收敛阈值e 为0.01，搜索半径h设置为0.05。
图5 给出了空调起动过程有功、无功和谐波的变化情况。在起动阶段，起动事件前后有功功率最终变化为450W 左右，期间有功功率呈持续增加的爬升状态。图中*代表通过有功特征进行本文滑动窗差值搜索后得到的初始聚类点，然后进行 Meanshift 聚类，结果如图6 所示。不难发现，状态聚类得到两个状态域（图6 圆圈范围内），对应稳定状态1和状态2。特别地，第一个状态域内时间序列末尾的数据点即为过渡域起始点，即为事件发生点。
图5 场景1 的P-Q-H 波形曲线
Fig. 5 The P-Q-H curve in Scene 1
图6 场景1 状态聚类结果
Fig.6 Clustering results of state feature in Scene 1
表3 给出了负荷事件检测对比结果。该场景中，空调在73 时刻附近发生投入事件。阈值触发的方法未能有效检测到事件发生时刻，形成漏检；而CUSUM 算法在80 时刻和85 时刻分别检测到有暂态事件发生，产生多检。相比之下，本文方法由于状态聚类分析特性，从稳定状态进行状态分析，可避免因暂态过程中的负荷变化过程较长引起的持续性误检，因此能够准确检测到该负荷事件。
表3 场景1 事件检测结果对比
Tab.3 Comparison results of event detection in Scene 1
?
3.2 场景2
为了检验大功率电器运行对小功率电器投切事件检测能力的影响，本场景在第10 时刻点开启电磁炉，作为大功率电器的代表，电磁炉运行功率约2 000W，其运行过程中产生约70W 左右的功率波动，然后在26 时刻起动以台式计算机为代表的小功率电器，其运行功率约为70～90W，此时投切事件容易与电磁炉的波动相混淆。
对比测试中，同样采用场景1 所提及的三种算法。由于最小待检测功率在70～90W，CUSUM 算法中，除最小突变量Δmin 设置为可变之外，其他设置均与场景1 相同，本场景算法中，除了设置数据块大小w 为150 之外，其他参数与场景1 相同。图7展示了场景2 的特征曲线变化情况，其中*代表本文滑动窗差值搜索后得到的初始聚类时刻点。由此，根据初始聚类点通过Mean-shift 聚类，得到图8 所示的特征聚类结果，其中稳定状态由图7 有功功率曲线图中标示数字1～5，图8 圆圈代表高维球在特定维度的边界范围。
图7 场景2 的P-Q-H 曲线
Fig.7 The P-Q-H curve in Scene 2
图8 场景2 状态特征聚类结果
Fig.8 Clustering results of state feature in Scene 2
从图7 和图8 可知，场景2 中各个稳定状态1～5，经过滑动窗差值搜索后，状态3 存在四个初始聚类中心，状态5 存在两个初始聚类中心，其他的各状态对应一个初始聚类中心，详见图8 圆圈。多个初始聚类中心经过Mean-shift 聚类，状态3 中的四个初始聚类中心合并为一个聚类中心，同理状态5 的两个初始聚类中心也被合并为一个聚类中心，其他各状态保持原有的单一聚类中心。由此，最终得到五个聚类中心，分别对应五个稳定状态，可因此确定存在四次投切事件。
考虑到各个算法中参数取值对算法的负荷事件检测的影响，表4～表6 分别给出了阈值触发法、CUSUM 算法和本文算法中参数选择对事件检测的实验结果。这里采用机器学习中分类器的评价方法，其中真阳性（True Positive, TP）表示正确地检测到负荷事件发生；真阴性（True Negative, TN）表示结果显示没有负荷事件发生，实际上也没有负荷事件发生；假阳性（False Positive, FP）表示判定有负荷事件发生，实际上没有负荷事件发生；假阴性（False Negative, FN）表示有负荷事件发生，但是并没有检测出事件。另外，由于绝大多数时刻点都是负荷稳定运行状态，因此真阴性值高且难以统计，故TN 通常忽略，而采用H. Altrabal 等提出的F-Measur 评价标准[32]。FM 越高，说明检测性能越好。由表4～表6 可以看出，阈值法中，参数设置80～90 较为合理；CUSUM 中，最小突变量Δmin 设置为90 左右比较合理；而本文方法中，半径h 设置为0.02～0.05 范围都具有较高的检测性能。
表4 阈值触发法中阈值变化的检测结果
Tab.4 Detection results of threshold change in threshold triggering method
阈值 TP FP FN FM 60 4 9 0 0.46 70 4 5 0 0.61 80 4 3 0 0.72 90 4 3 0 0.72 100 3 2 1 0.66 110 2 1 2 0.57
表5 CUSUM 算法中最小突变量变化的检测结果
Tab.5 Detection results of minimum mutation change in CUSUM algorithm
?
表6 本文算法中高维球半径h 变化的检测结果
Tab.6 Detection results of high-dimensional spherical radius h change in this algorithm
?
另外，由表4 可以看出，依靠单点来判断的阈值触发法易将小功率电器投切事件与噪声相混淆；CUSUM 算法的最优参数区间较小，需要对电器功率有准确统计；而本文算法的关键参数h 的取值在一定程度上是对聚类范围的划分，特别是小负荷，设置0.02～0.05 的效果较优，超过0.05 则会出现检测失效，因此对于小负荷事件检测，可设置h≤0.05。
3.3 场景3
本场景在实验过程中将空调、电饭煲、微波炉、电磁炉、电水壶、电视机、电冰箱、电冰柜、电风扇、台式计算机10 个电器无顺序起停100 次，取其中4 000 个采样点，各算法关键参数取值选取场景2 表现最为理想的参数。图9 展示了有功功率和无功功率的波形曲线，图10 展示了整体状态的分布情况。本文算法将该场景数据分为10 个数据块，每个数据块内有400 个采样点，状态特征分布如图10 所示。最终的结果见表7。
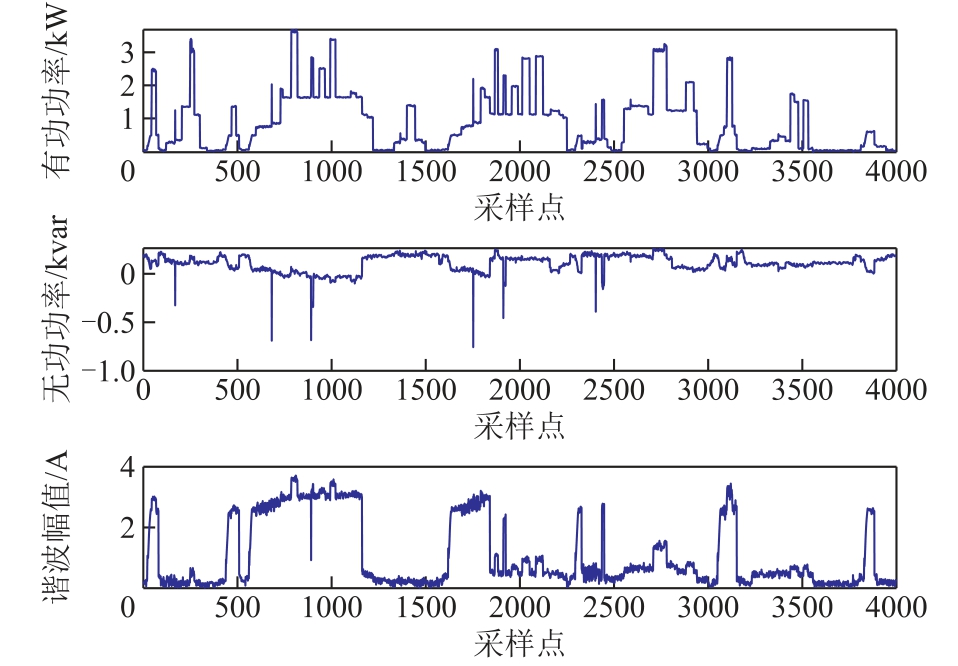
图9 场景3 的P-Q-H 曲线
Fig.9 The P-Q-H curve in scene 3
表7 给出了各个算法的负荷事件检测结果。从整体上来讲，阈值触发法FN 较低，原因在于阈值设置为最小投切负荷的功率大小，当功率差值超过阈值时，会记录为事件信息。然而当功率波动较大或负荷缓慢上升时，也会存在将单一负荷事件误检为多个负荷事件的现象，因此FP 较高。CUSUM 算法受窗口宽度限制，对缓慢变化的事件容易误检为多个事件发生，因此FP 也会较高，且较大的噪声易与小功率投切相混淆，使得FN 也偏高。而本文算法通过状态聚类的方式，极大程度地避免了对缓慢变化的事件和小功率负荷等影响，使得FP 和FN 均较低。但是需要注意的是，当事件发生在数据块边界时，新的稳定状态无法被检测到，则需要进一步对边界进行处理。
此外，为验证本文所提算法的适用性，图11 给出了阈值触发法的阈值、CUSUM 算法的最小突变量、状态聚类算法的高维球半径变化后的检测效果绘制P-R 曲线，该曲线是根据精准率（precision）和召回率（recall）两个变量绘制而成。通常当一个算法的P-R 曲线可以覆盖另一个算法的曲线，那么可判定其性能较后者更优；当无法完全覆盖时，可分别计算精确率等于召回率时的平衡点，值更大的算法性能较好[33]。不难发现，本文算法较其他两个算法性能更佳。
图10 场景3 状态特征分布情况
Fig.10 The distribution of state feature in scene 3
表7 检测效果比较
Tab.7 Comparison of test results
算法 TP FP FN FM阈值触发法 99 28 1 0.87 CUSUM 算法 90 20 10 0.85本文算法 98 5 2 0.97
图11 算法的P-R 曲线
Fig.11 The P-R curve of the algorithm
4 滑动窗参数性能评价
滑动窗差值搜索的算法是确定初始聚类中心的关键技术，因此，本节对相关参数进行测试与评价。
4.1 参数m 和θ 性能评估
为了验证参数m 和θ 的设置对状态域检测的有效性，在其他参数一定的情况下，对θ 的选取范围为5～60 间隔为5 的值，以及m 以1 为单位，取值范围为2～10，采用网格搜索算法[34]进行参数效果的验证，并定义滑动窗差值搜索的算法性能度量指标为
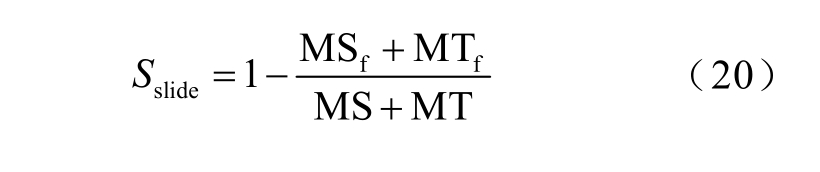
式中，MS 为场景中实际总稳定状态数量；MSf 为通过滑动窗差值搜索后未标记有稳定点的稳定状态的数量；MT 为过渡时长超过采样间隔的过渡区域数量；MTf 为通过滑动窗差值搜索后标记有稳定点的过渡区域数量。显然，Sslide 分数越大，表示参数选取的效果越佳。特别地，当滑动窗差值搜索得到的初始聚类点在每一个稳定域均有分布，而且在过渡域没有分布的时候，即MSf=0 且MTf =0 时，Sslide=1，此时滑动窗差值搜索的性能最优。
表8 给出了m 和θ 参数设置的结果。不难发现，随着滑动窗长度的增加，评价分数先上升后下降。这表明在m 较小时，窗内极差小于阈值θ 的条件容易满足，而过渡时间较长的事件容易将该过渡域误判为稳定域，使得MTf 较大，Sslide 分数较低。随着滑动窗宽度m 的增加，MTf 降低，因此Sslide 分数升高。而当滑动窗的宽度m 过宽时，出现对投切间隔较近的稳定域的漏检，MSf 增加，Sslide 分数降低，θ 参数同理。因此，一般可选取m为3，阈值θ 为30 较为合理，例如场景3，Sslide 值为0.98。
4.2 参数γ 性能评估
参数γ 作为控制初始聚类中心个数的参数，本节对场景3 中γ 以10 为单位，范围为0～100 测试，定义CMean 表示每个稳定域平均初始聚类点数量，以反映计算量变化，见表9。可以发现，γ 越大，Sslide有变小的趋势，而且平均初始聚类点的数量也在减少。为此，根据最小检出量设置γ 为70，保证了Sslide较高，同时也具有较低的CMean，即算法在精准覆盖所有稳定区域的同时，也具有较低的计算量。
表8 m,θ 参数各取值下的Sslide 分布
Tab.8 The Sslide distribution under the values of m and θ parameters
m θ=5 θ=10 θ=15 θ=20 θ=25 θ=30 θ=35 θ=40 θ=45 θ=50 θ=55 θ=60 2 0.93 0.93 0.92 0.92 0.92 0.92 0.92 0.91 0.91 0.91 0.91 0.9 3 0.79 0.97 0.98 0.98 0.98 0.98 0.94 0.92 0.92 0.92 0.92 0.92 4 0.51 0.82 0.94 0.98 0.98 0.98 0.98 0.97 0.95 0.95 0.95 0.93 5 0.31 0.64 0.9 0.97 0.98 0.97 0.98 0.98 0.98 0.98 0.97 0.96 6 0.23 0.51 0.76 0.9 0.95 0.95 0.97 0.97 0.97 0.98 0.98 0.97 7 0.22 0.4 0.66 0.82 0.92 0.93 0.94 0.98 0.98 0.98 0.98 0.97 8 0.21 0.36 0.57 0.77 0.89 0.91 0.94 0.97 0.97 0.98 0.98 0.98 9 0.2 0.3 0.5 0.67 0.82 0.88 0.93 0.96 0.97 0.97 0.97 0.98 10 0.2 0.27 0.44 0.6 0.75 0.84 0.88 0.93 0.94 0.94 0.94 0.95
表9 γ 取值对Sslide 及CMean 的影响
Tab.9 Influence of the value of γ on Sslide and CMean
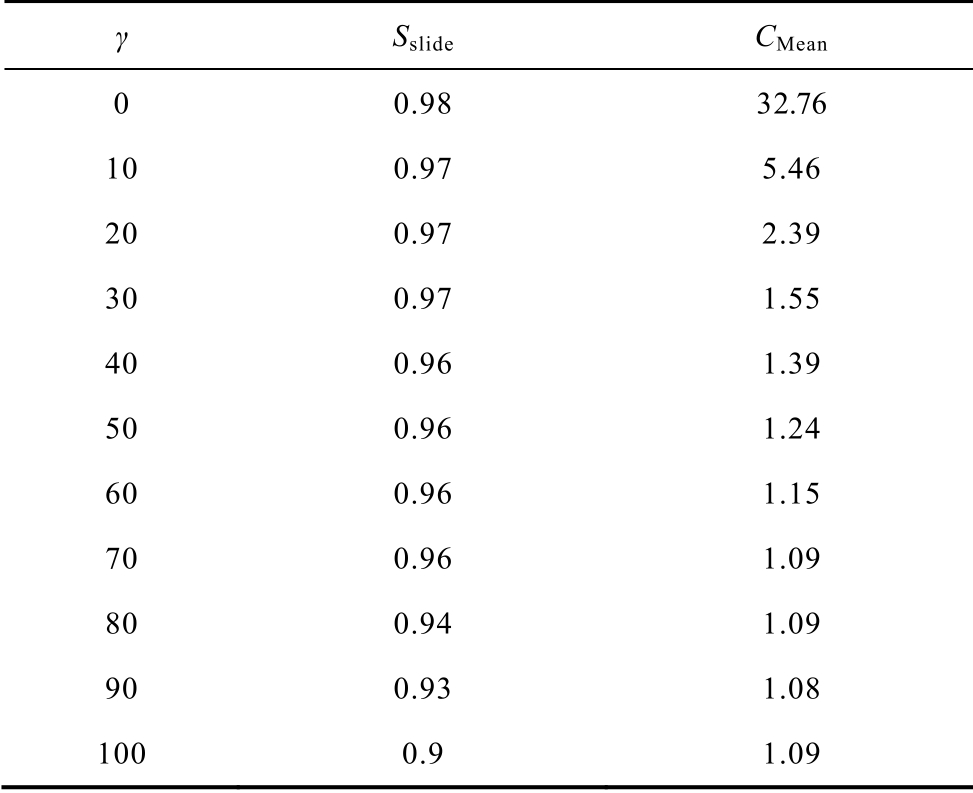
γ Sslide CMean 0 0.98 32.76 10 0.97 5.46 20 0.97 2.39 30 0.97 1.55 40 0.96 1.39 50 0.96 1.24 60 0.96 1.15 70 0.96 1.09 80 0.94 1.09 90 0.93 1.08 100 0.9 1.09
5 结论
本文提出一种基于状态特征聚类的负荷事件检测方法，不仅采用有功功率、无功功率、3 次谐波特征，而且以一定时间长度的数据块为单位开展分析，拓展了监测负荷状态变化的信息量，有助于事件检测准确率的提升。同时，本文通过轮廓系数对多种特征进行特定环境下负荷状态变化响应程度的评估，从而进行特征选择，有助于提高算法性能的稳定性。然后，本文对十种电器随机起停进行实验，采用精确率、召回率、ROC 曲线等指标对结果进行评价，并与另外两种事件检测算法进行比较，结果表明本文算法性能较优。最后，本文对关键参数的选取依据进行分析说明，提升所提方法的实用性。
然而，当多种电器起停间隔小于采样频率时，可视为负荷同时起停，本文算法失效。因此未来将进一步挖掘多维特征隐藏的信息，并开展负荷辨识与分解的研究。
[1] Farhangi H. The path of the smart grid[J]. IEEE Power& Energy Magazine, 2009, 8(1): 18-28.
[2] 张超, 江贤康, 任建文, 等. 基于高级量测体系的用电器分类测量终端的设计[J]. 电气技术, 2010,11(8): 117-120.Zhang Chao, Jiang Xiankang, Ren Jianwen, et al. A design of classification electrical metering terminal based on AMI[J]. Electrical Engineering, 2010, 11(8):117-120.
[3] 张虹, 侯宁, 葛得初, 等. 供需互动分布式发电系统收益-风险组合优化建模及其可靠性分析[J]. 电工技术学报, 2020, 35(3): 623-635.Zhang Hong, Hou Ning, Ge Dechu, et al. Modeling and reliability analysis of benefit-risk portfolio optimization for supply and demand interactive distributed generation system[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 623-635.
[4] 黄伟, 熊伟鹏, 华亮亮, 等. 基于动态调度优先级的主动配电网多目标优化调度[J]. 电工技术学报,2018, 33(1): 3486-3498.Huang Wei, Xiong Weipeng, Hua Liangliang, et al.Multi-objective optimization dispatch of active distribution network based on dynamic schedule priority[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 3486-3498.
[5] 吴润泽, 包正睿, 王文韬, 等. Hadoop 架构下基于模式匹配的短期电力负荷预测方法[J]. 电工技术学报, 2018, 33(7): 1542-1551.Wu Runze, Bao Zhengrui, Wang Wentao, et al. Shortterm power load forecasting method based on pattern matching in hadoop framework[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1542-1551.
[6] 汤波, 林顺富, 陈光, 等. 居民配电网负荷谐波电流发射水平评估方法[J]. 电工技术学报, 2018,33(3): 533-542.Tang Bo, Lin Shunfu, Chen Guang, et al. The harmonic current emission level of the residential loads in the distribution network[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 533-542.
[7] 余贻鑫. 智能电网的技术组成和实现顺序[J]. 南方电网技术, 2009, 3(2): 1-5.Yu Yixin. Technical composition of smart grid and its implementation sequence[J]. Southern Power System Technology, 2009, 3(2): 1-5.
[8] 徐青山, 娄藕蝶, 郑爱霞, 等. 基于近邻传播聚类和遗传优化的非侵入式负荷分解方法[J]. 电工技术学报, 2018, 33(16): 3868-3878.Xu Qingshan, Lou Oudie, Zheng Aixia, et al. A nonintrusive load decomposition method based on affinity propagation and genetic algorithm optimization[J].Transactions of China Electrotechnical Society, 2018,33(16): 3868-3878.
[9] 李如意, 黄明山, 周东国, 等. 基于粒子群算法搜索的非侵入式电力负荷分解方法[J]. 电力系统保护与控制, 2016, 44(8): 30-36.Li Ruyi, Huang Mingshan, Zhou Dongguo, et al.Optimized nonintrusive load disaggregation method using particle swarm optimization algorithm[J].Power System Protection & Control, 2016, 44(8): 30-36.
[10] 李如意, 王晓换, 胡美璇, 等. RPROP 神经网络在非侵入式负荷分解中的应用[J]. 电力系统保护与控制, 2016, 44(7): 55-61.Li Ruyi, Wang Xiaohuan, Hu Meixuan, et al.Application of RPROP neural network in nonintrusive load decomposition[J]. Power System Protection &Control, 2016, 44(7): 55-61.
[11] 崔亮节, 孙毅, 刘耀先, 等. 考虑分时段状态行为的非侵入式负荷分解方法[J]. 电力系统自动化,2020, 44(5): 215-222.Cui Liangjie, Sun yi, Liu Yaoxian, et al. Non-intrusive load disaggregation method considering time-phased state behavior[J]. Automation of Electric Power Systems, 2020, 44(5): 215-222.
[12] 武昕, 焦点, 高宇辰. 基于非侵入式用电数据分解的自适应特征库构建与负荷辨识[J]. 电力系统自动化, 2020, 44(4): 101-114.Wu Xi, Jiao Dian, Gao Yuchen. Construction of adaptive feature library and load identification based on decomposition of non-intrusive power consumption data[J]. Automation of Electric Power Systems, 2020,44(4): 101-114.
[13] 刘兴杰, 曹美晗, 许月娟. 基于改进鸡群算法的非侵入式负荷监测[J]. 电力自动化设备, 2018, 38(5):235-240.Liu Xingjie, Cao Meihan, Xu Yuejuan. Non-intrusive load monitoring based on improved chicken swarm optimization algorithm[J]. Electric Power Automation Equipment, 2018, 38(5): 235-240.
[14] Liang J, Ng S K, Kendall G, et al. Load signature study—part I: basic concept, structure, and methodology[J]. IEEE Transactions on Power Delivery, 2010, 25(2): 551-560.
[15] Tsai M, Lin Y. Modern development of an adaptive non-intrusive appliance load monitoring system in electricity energy conservation[J]. Applied Energy,2012, 96: 55-73．
[16] Anderson K D, Berges M E, Ocneanu A, et al. Event detection for non-intrusive load monitoring[C]//38th Annual Conference on IEEE Industrial Electronics Society, Montreal, 2012: 3312-3317.
[17] Jin Y, Tebekaemi E, Berges M, et al. A time-frequency approach for event detection in non-intrusive load monitoring[C]//Conference on Signal Processing,Sensor Fusion, and Target Recognition XX, Orlando,2011: 1-13.
[18] Jin Y, Tebekaemi E, Berges M, et al. Robust adaptive event detection in non-intrusive load monitoring for energy aware smart facilities[C]//Proceedings of the 2011 IEEE International Conference on Acoustics,Speech and Signal Processing, Prague, 2011: 4340-4343.
[19] Yang C C, Soh C S, Yap V V. A systematic approach to ON-OFF event detection and clustering analysis of non-intrusive appliance load monitoring[J]. Frontiers in Energy, 2015, 9(2): 231-237.
[20] 谢政艳. 非侵入式负荷监测的事件检测方法研究[D]. 北京: 华北电力大学(北京), 2018.
[21] Gao Haohan, Zhang Li, Qiao Liang, et al. An improved permutation entropy algorithm for nonintrusive load state change detection[C]//2018 IEEE Innovative Smart Grid Technologies-Asia, Singapore,2018: 886-890.
[22] 牛卢璐, 贾宏杰. 一种适用于非侵入式负荷监测的暂态事件检测算法[J]. 电力系统自动化, 2011,35(9): 30-35.Niu Lulu, Jia Hongjie. Transient event detection algorithm for non-intrusive load monitoring[J].Automation of Electric Power Systems, 2011, 35(9):30-35.
[23] Lin Shanfu, Zhao Lunjia, Li Fangxing, et al. A nonintrusive load identification method for residential applications based on quadratic programming[J].Electric Power Systems Research, 2016, 133: 241-248.
[24] 肖江, Auger F , 荆朝霞, 等. 基于贝叶斯信息准则的非侵入式负荷事件检测算法[J]. 电力系统保护与控制, 2018, 46(22): 8-14.Xiao Jiang, Auger F, Jing Zhaoxia, et al. Nonintrusive load event detection algorithm based on Bayesian information criterion[J]. Power System Protection & Control, 2018, 46(22): 8-14.
[25] Hart G W. Nonintrusive appliance load monitoring[J].Proceedings of the IEEE, 1992, 80(12): 1870-1891.
[26] 余贻鑫, 刘博, 栾文鹏. 非侵入式居民电力负荷监测与分解技术[J]. 南方电网技术, 2013, 7(4): 1-5.Yu Yixin, Liu Bo, Luan Wenpeng. Nonintrusive residential load monitoring and decomposition technology[J]. Southern Power System Technology,2013, 7(4): 1-5.
[27] 李秋硕, 肖勇, 李鹏, 等. 用于 NILM 的电器设备谐波特征研究[J]. 南方电网技术, 2016, 10(10): 73-78.Li Qiushuo, Xiao Yong, Li Peng, et al. Research on harmonic characteristics of electric devices for nonintrusive load monitoring[J]. Southern Power System Technology, 2016, 10(10): 73-78.
[28] 孙毅, 崔灿, 陆俊, 等. 基于差量特征提取与模糊聚类的非侵入式负荷监测方法[J]. 电力系统自动化, 2017, 41(4): 86-91.Sun Yi, Cui Can, Lu Jun, et al. Non-intrusive load monitoring method based on delta feature extraction and fuzzy clustering[J]. Automation of Electric Power Systems, 2017, 41(4): 86-91.
[29] Fukunaga K, Hostetler L. The estimation of the gradient of a density function, with applications in pattern recognition[J]. IEEE Transactions on Information Theory, 1975, 21(1): 32-40.
[30] Cheng Y. Mean shift, mode seeking, and clustering[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995, 17(8): 790-799.
[31] 朱连江, 马炳先, 赵学泉. 基于轮廓系数的聚类有效性分析[J]. 计算机应用, 2010(12): 139-141.Zhu Lianjiang, Ma Bingxian, Zhao Xuequan.Clustering validity analysis based on silhouette coefficient[J]. Journal of Computer Applications,2010(12): 139-141.
[32] Altrabalsi H, Liao J, Stankovic L, et al. A lowcomplexity energy disaggregation method: Performance and robustness[C]//2014 IEEE Symposium on Computational Intelligence Applications in Smart Grid (CIASG), Orlando, FL, 2014: 1-8.
[33] 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016.
[34] 王宁, 谢敏, 邓佳梁, 等. 基于支持向量机回归组合模型的中长期降温负荷预测[J]. 电力系统保护与控制, 2016, 44(3): 92-97.Wang Ning, Xie Min, Deng Jialiang, et al. Mid-long term temperature-lowering load forecasting based on combination of support vector machine and multiple regression[J]. Power System Protection and Control,2016, 44(3): 92-97.