0 引言
近年来，随着城镇化建设和用电需求的增长，配电网一直在不断地改造和扩建，其规模也不断扩大，配电网处于电力系统的末端，具有地域分布广、电网规模大、设备种类多、网络连接多样、运行方式多变等鲜明特点。国网系统内大多数县级以上配电网的规模都已达到百条馈线以上，一些中、大型城市的中压馈线已达到或超过千条[1]。随着配电自动化、用电信息采集等系统的推广应用，对于有千条馈线的大规模配电网，配电网中会产生指数级增长的海量异构、多态的数据。对配电网中的电能质量数据进行高效的采集与分析对配电网负荷预测、运行状态评估与预警、电能质量监测和评估、确保电网有效运行以及配电网规划具有重要意义[2-4]。
如果对电能质量数据进行采样时仍遵循奈奎斯特-香农采样定理，伴随着采集—压缩—存储—传输—检测-识别这一过程，就势必会造成海量的采样数据，而且随着数据量的增多，其处理时间也过长，大大增加了存储和传输的代价[5-6]。基于傅里叶变换的电能质量数据采集和分析方法[7]的优势主要体现在对信号的频域分析上，缺少时域的分析能力，因此其压缩性能并不是很好。文献[8]提出了一种基于单类支持向量机（One Class Support Vector Machine, OCSVM）与归一化距离测度的电能质量信号压缩方法，其对各类信号的压缩性能差异较大，且压缩比较低。文献[9]对电能质量数据采用基于多小波阈值变换和有损、无损相结合的压缩方式，对小波系数矩阵的高频部分采用SPIHT 有损压缩算法，低频部分采用基于hash 函数的LZ77 无损压缩算法，不过小波变换存在小波基选取困难的问题[10]，算法的自适应性较差。文献[11]提出了一种基于相似度分段及重采样的自适应波形数据压缩方法。通过自相关系数自动分段得到稳态和暂态，对稳态数据重采样后用快速傅里叶变换（Fast Fourier Transform,FFT）和ZLIB 级联压缩，对暂态数据采用ZLIB 无损压缩，并提出综合压缩系数评价指标。这些方法虽各具特色，但其共同点均建立在奈奎斯特采样定理的基础上，给电力系统数据传输和存储带来巨大压力。文献[12]采用感知压缩的电能质量数据采集技术，通过稀疏、测量和重构三个过程实现了仅需要少量的测量值便可以对原始信号进行精确重构，对电网量测与控制的智能化具有重要意义。文献[13]提出用压缩传感理论来解决三相电能质量数据的压缩，实现了三相电能质量扰动信号同时处理，且精确地检测出多项性能指标。
然而当对多个结构存在相关性的信号同时进行压缩采集时，压缩感知技术又未能利用信号间的这种相关性来更好地提升数据的压缩率[14]。鉴于此，本文提出一种基于分布式压缩感知和边缘计算的配电网电能质量数据压缩存储方法。该方法首先以分布式压缩感知算法为边缘算法对整个配电网中的电能质量数据进行压缩采集，然后将产生的测量值和稀疏字典原子上传至云端。在云端，一方面对上传的字典原子进行整合形成完备字典，对上传数据的可恢复性进行验证；另一方面通过分析各节点电能质量数据在完备字典下稀疏系数的互相关度对配电网进行分区，便于对配电网中的谐波进行分析和调控。
1 基于分布式压缩感知的边缘算法
分布式压缩感知（Distributed Compressed Sensing,DCS）是D. Baron 提出的一种利用原始数据之间的相关性，对原始数据进行高效压缩观测、合理稀疏表示的数据融合方法，其可以理解为压缩感知和分布式信源编码的结合[15]，主要包括四个过程：联合稀疏模型的建立，稀疏冗余字典的设计，测量矩阵的选取，联合重构算法的设计。其实现过程如图1所示。
图1 分布式压缩所感知的实现过程
Fig.1 Implementation process perceived by distributed compression
1.1 联合稀疏模型
由于配电网中电能质量数据在时域上不具有稀疏性，因此在通过分布式压缩感知对配电网中各节点电能质量数据进行压缩采集时，首先需要通过稀疏基将其稀疏分解。考虑电能质量信号的频率成分中仅含基波和少量各次谐波，因此本文采用傅里叶正变换矩阵为初始稀疏基，构建第二联合稀疏模型JSM-2，对电能质量数据进行压缩采集。在该模型中，信号的共同部分为零，新息部分用同一个稀疏基进行稀疏表示为
式中， xj 为原始信号； zc 为信号的共同部分； zj为信号的新息部分；Ψ 为稀疏矩阵；θ j 为对应稀疏系数。
1.2 稀疏字典的设计
在电能质量数据的处理中，信号的稀疏表示可以理解为采用较少的原子数对原始信号进行线性组合的表示，如图2 所示。
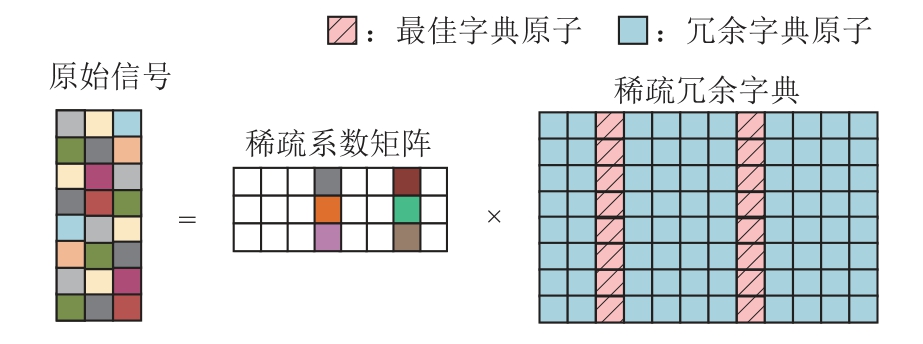
图2 稀疏分解示意图
Fig.2 Sparse decomposition diagram
信号稀疏性越好则使用字典原子个数越少，向云端上传的数据量也就越小。由于设计型字典的原子通常是由与信号特征匹配的数学函数转换定义得到的[16]，其原子的类型较为简略单一，不能和原始信号进行自适应的匹配，对于复杂含噪声的信号稀疏效果不是很好。因此本文采用基于K-SVD 字典学习算法[17]的学习型稀疏字典，通过多次字典更新来降低重构信号与原始信号间的误差，不仅可以提高原始信号的稀疏效果，还能使信号重构的信噪比有显著的提升。其主要包括稀疏分解和字典更新两个部分。
1）稀疏分解阶段
选择一个初始稀疏字典D，通过正交匹配追踪（Orthogonal Matching Pursuit，OMP）算法求解稀疏表示，获得稀疏表示系数xˆj 为
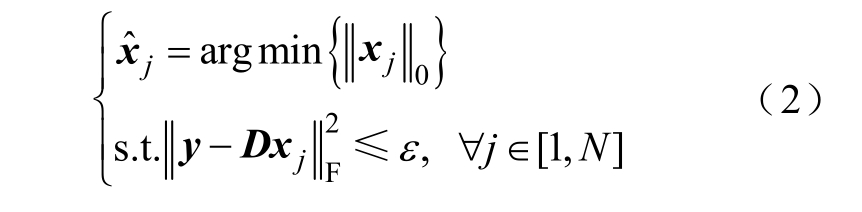
2）字典更新阶段
K-SVD 算法在每次迭代过程中仅更新一个原子，若更新第k 个原子 dk ，则有
式中，
为稀疏系数矩阵X 的第j 行。令 E k为除第k 个原子以外的所有原子产生的误差，则式（3）变为
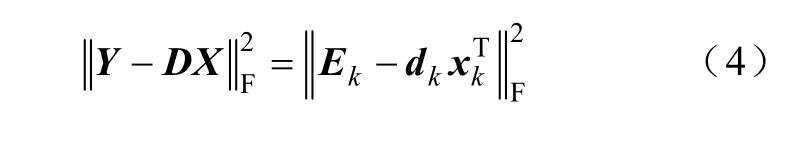
令ωk = {i |1 ≤ i ≤ K ,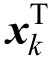 
( i )≠0}表示使用原子的d k样本信号Y 的索引，以防止结果发散，定义 Ωk 为N × ωk的矩阵，其中(ω k (i ), i )为非零值，其余都是零值，则式（5）可以表示为
式中，U 和V 为两个相互正交的矩阵；Δ 为对角矩阵，通过分解得到的U 的第一列来更新初始字典中的 dk 。同时以矩阵V 的第一列与 Δ(1,1)的乘积来更新替换稀疏表示系数 xj ，从而完成稀疏字典的更新。
1.3 测量矩阵的选取
测量矩阵的作用是对基于稀疏矩阵表示的信号进行降维映射[18]。其构造方法主要分为两类，一类为随机观测矩阵，如高斯观测矩阵、贝努利观测矩阵、局部傅里叶观测矩阵等；另一类为确定性观测矩阵，在构造此类矩阵的时候，系统和构造的参数一旦确定，矩阵也随之确定。对于高斯矩阵来说，当观测值的数目满足 M ＞μ K lg( K / N)（μ 为一个很小的常数）时便可以对原始信号进行重构，相比于其他测量矩阵，其所需的测量值数目是最少的。因此本文选用高斯矩阵为测量矩阵。其在满足约束等距条件时方可保证重构信号的准确性，即存在一个0≤ δ≤ 1常数δk，使得测量矩阵Φ 对所有的稀疏向量X 都有
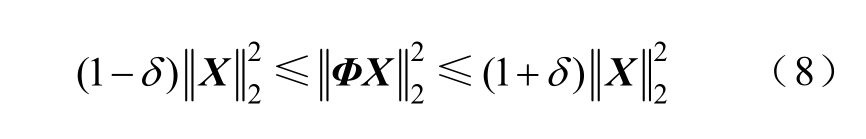
1.4 DCS-SOMP 联合重构算法
本文基于K-SVD 字典学习算法和同步正交匹配追踪算法（Synchronous OMP, SOMP）[19]，提出了一种改进的DCS-SOMP 联合重构算法。首先通过SOMP 算法对采集到的电能质量数据进行重构，然后由K-SVD 算法不断更新稀疏字典来降低重构误差，直至重构信号的信噪比满足所设定的阈值。该方法可以利用较少的字典原子和测量值表示多个节点的电能质量信号，其主要实现步骤为：
（1）进行参数初始化，令初始残差为 r j= y j ,j∈[ 1, s]，s 为节点的个数，索引值ξ = 0，索引集Λ 0 =
，选用字典原子个数τ 。
（2）输入原始信号矩阵X n×s，初始字典 Ψ n×n，测量值矩阵 Φ m×n及最低重构信噪比 SNR def ，其中n为数据的长度，m 为测量值的数量。
（3）构建传感矩阵 Am × n =Ψ m× n Φ n × n。
（4）计算每一行残差与传感矩阵各列的二范数之和，保存最大值对应传感矩阵中的列索引，并与上一次的索引集合并，即
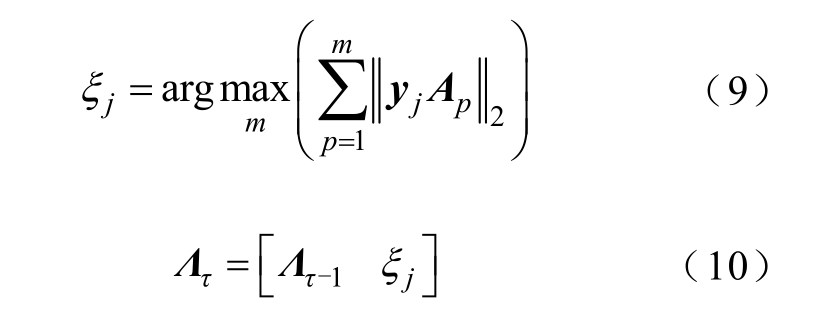
（5）通过最小二乘法求出相关系数，更新残差为
（6）求出重构的中间信号，并计算中间信号的相对方均根误差（RRMSE）和重构信噪比（SNR）。
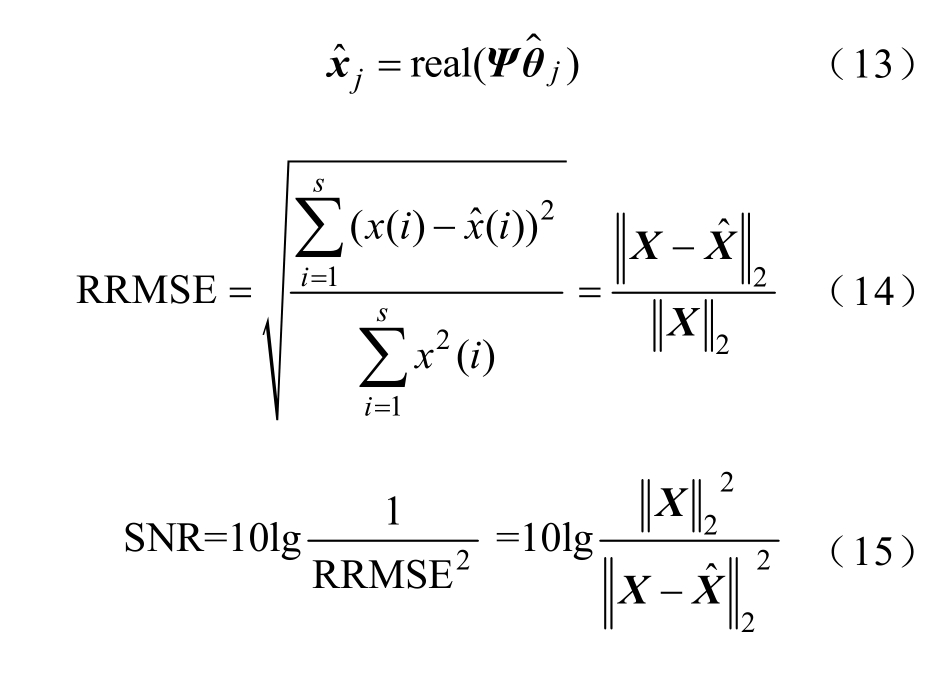
（7）若重构信噪比小于所设定的最低重构信噪比 SNR def ，则通过K-SVD 字典学习算法更新字典原子，执行步骤（4），若重构信噪比满足要求，则输出使用的字典原子和重构结果。
2 基于云边协同的配电网分区和电能质量数据压缩存储方法
云计算[20]是一种能够帮助分析大规模数据的技术。它不需要在本地维护计算硬件、数据存储和相关软件。不过由于云平台和各个终端在物理上相距很远，响应时间慢也经常发生。边缘计算[21-22]作为补充云计算系统的一种创新方式被引入。因为边缘接近终端设备，所以不仅可以减少数据处理的网络延迟，还可以减少原始数据与存储中心之间所需的带宽。因此，通过云平台和边缘平台的协同工作，系统的性能将会得到极大的提升[23-24]。
本文中，基于云边协同框架，在Matlab 仿真平台编写基于 DCS-SOMP 算法的边缘采集算法对PSCAD 中产生的电能质量数据采集，将重构过程中产生的稀疏字典原子和测量值通过建立与远程云端的连接上传至阿里云端服务器。在云端主要进行三种操作：①配电网电能质量数据的压缩存储；②完备稀疏字典的构建；③配电网的双阈值动态分区。云端服务器将动态分区的结果及时发送至边缘，边缘算法获取到新的分区信息后调整计算资源，对新的分区中含有的电能质量进行数据采集，再次上传至云端服务器。从而实现“云端”与“边缘”的相互协同。其原理如图3 所示。
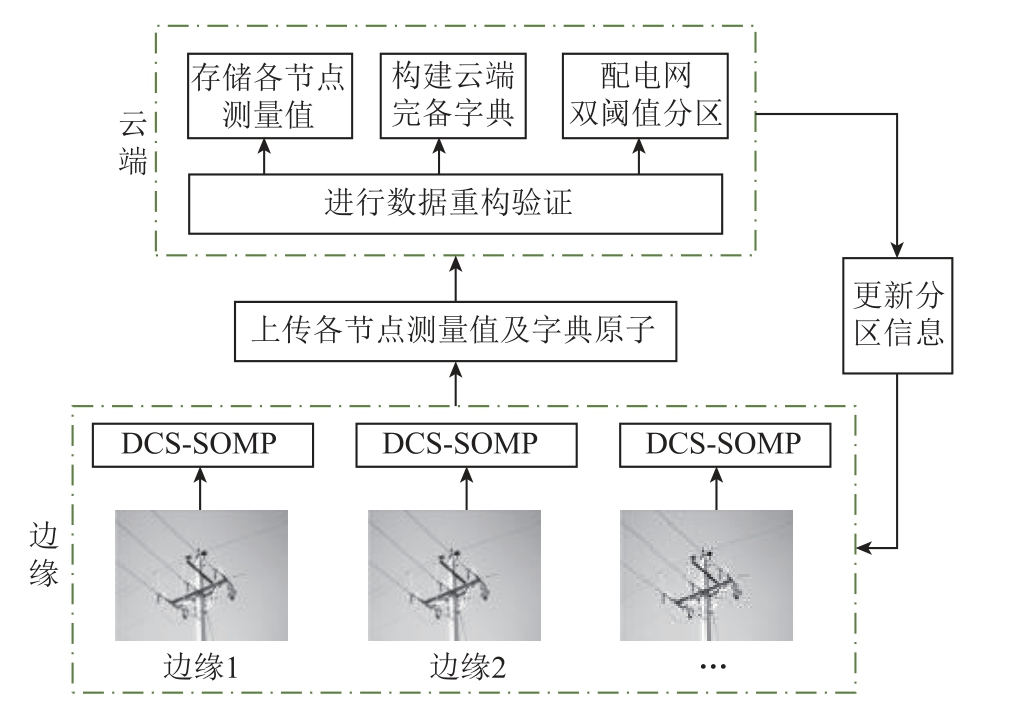
图3 云边协同原理
Fig.3 Principle of cloud-side collaboration
2.1 基于云边协同的数据存储
在云边协同架构下，当采用DCS-SOMP 边缘算法对某一分区中s 个节点的电能质量数据同时进行压缩采集时，分区内各节点的电能质量数据共用相同的字典原子，设定各节点数据长度为n，上传字典原子个数为τ ，则有
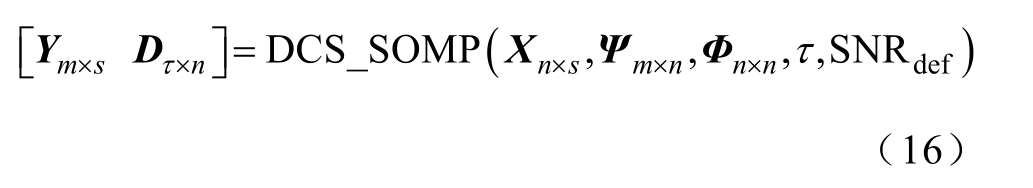
式中， Ym× s 为各节点的测量值； Xn× s 为各节点的原始信号；Dτ×n 为上传云端的字典原子。通过调低测量矩阵的长度m 和上传云端字典原子个数τ 的值，上传云端的测量值与字典原子所占的存储量也将变低。另外，为了保证云端数据在使用时能够被准确、快速地调用，云端对各边缘上传的字典原子进行整合生成完备字典Dk ×n ，其中k 为完备字典的总原子数。当调用此分区数据时，首先由式（17）求出该分区数据对应的稀疏表示系数 θn×s 。
然后通过式（18）恢复得出该分区的原始信号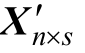
为
通过云端完备字典的建立，各边缘仅需上传测量值便可实现数据的压缩存储，使云端数据的存储空间进一步降低，完备字典的构建步骤如下：
（1）计算边缘节点新上传的字典原子 di 与云端初始稀疏字典Dk ×n 中第k 个原子 kD 的相关度 ri, k ，即
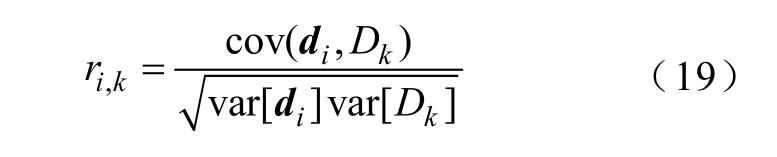
若产生的每一个 ri, k 的值均低于某一阈值，说明上传至云端的字典原子 di 与云端字典Dk ×n 整体相关性较弱，则将该字典原子扩充为云端稀疏字典的原子。
（2）将各分区上传的字典原子组合为过完备稀疏字典，并进行正则化，降低各字典原子间的相干性。
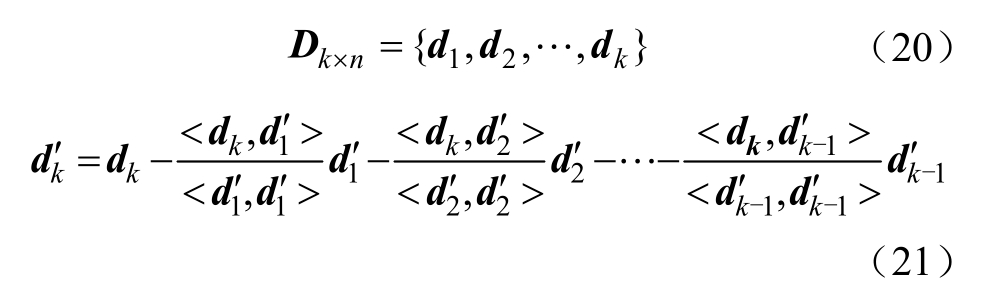
（3）将过完备字典进行归一化更新字典原子。
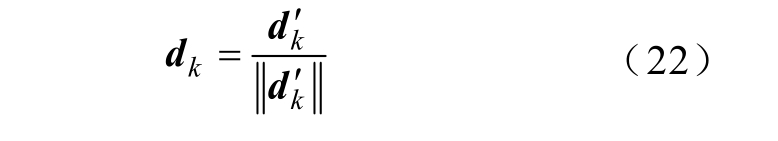
（4）结合过完备稀疏字典，通过分布式压缩感知算法从上传的测量值中恢复出原始数据，验证数据存储的可恢复性，并得到各节点对应的稀疏系数θ j， j∈[1, s]，最终将各节点电能质量数据的测量值作为存储数据实现压缩存储。
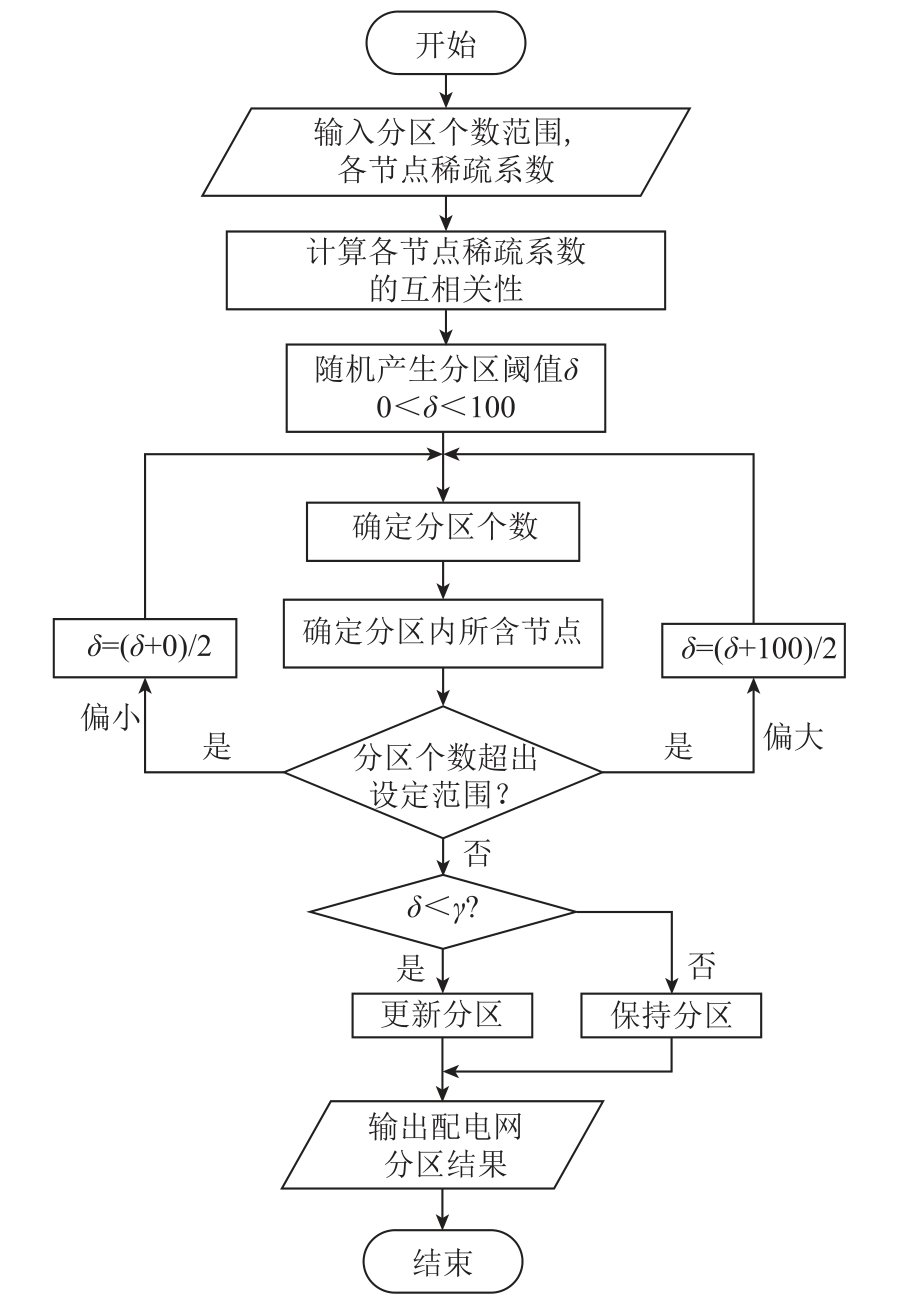
图4 配电网分区流程
Fig.4 Flow chart of distribution network zoning
2.2 基于云边协同的配电网双阈值动态分区原理
随着越来越多的分布式电源以及电力电子器件接入电网，配电网间的谐波变得更加分散化、全网化，对配电网电能质量造成了严重影响[25-27]。如何对配电网谐波污染范围进行有效划分，对配电网的运行、调控以及谐波治理具有重要意义[28]。由于本文以傅里叶正交矩阵为初始稀疏字典对电能质量数据进行稀疏分解，因此通过DCS-SOMP 算法获取的各节点对应的稀疏系数反映了原始电能质量数据中不同频率成分的谐波所占有能量的大小。对各节点稀疏系数互相关度进行分析即转换为对原始电能质量数据各次谐波含有率的互相关度进行分析，基于该原理的配电网分区可以更好地体现出各节点电能质量数据所含谐波的传递关系，也有利于在配电网中更有针对性地治理谐波污染。
此外，在配电网分区过程中，分区阈值的选择方式对分区结果产生重要影响。文献[29-30]均是通过人为设定固定的耦合度阈值对配电网进行分区，不过由于配电网中电能质量数据是时刻变化的，采用固定阈值可能会导致在谐波污染划分时结果不准确。若分区阈值设定过高则将导致分区数量过多，使分区失去优势；若分区阈值设定过小，则导致分区数量过少，分区效果变差，并且人为干预阈值也难以实现。因此本文基于云边协同架构，采用双阈值动态分区的策略，首先限定分区数量的范围，然后通过分析各节点电能质量数据稀疏特性间的互相关度得出配电网分区的动态阈值δ ，为避免分区结果不稳定以及分区信息更新过于频繁，对分区阈值γ加以限定。其实现流程如图4 所示，实现步骤如下：
（1）分区参数初始化。输入2.1 节中得到的各节点电能质量数据的稀疏系数 θ j， j∈[1, s]，设定分区阈值γ ，分区个数的范围 Γ ∈ [ p, q]，其中p 为分区个数上限，q 为分区个数下限。
（2）求解各节点电能质量稀疏系数间的互相关度：
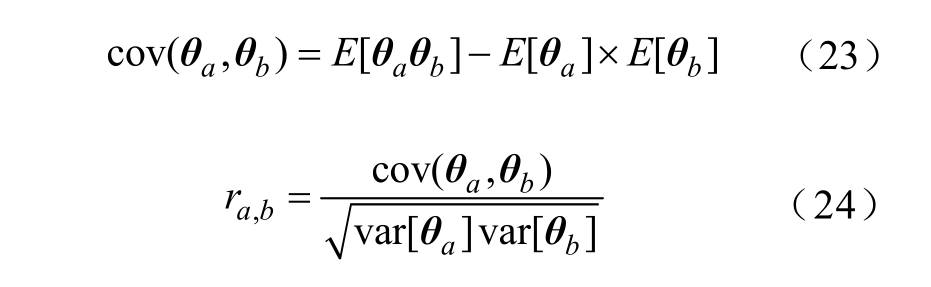
其中， a, b∈ [1, s]。
（3）随机产生阈值δ 并进行分区，若分区数量属于Γ ，则通过二分法对分区阈值δ 的值进行更新，直至满足分区个数要求。
（4）若δ γ＜ ，则确定分区，反之则保持现有分区状态。
（5）输出配电网分区数量及每个分区所属节点情况。
3 实验与仿真分析
3.1 配电网的动态分区
为验证本文所提出方法的合理性，在PSCAD 中搭建IEEE 14 节点配电网模型，如图5 所示，该模型由3 台发电机、14 条母线和3 台变压器构成，变压器一次侧母线电压为35kV，二次侧母线电压为10kV。在该配电网模型中第6～14 节点放置时变谐波源和时变负荷源，在多污染源分散分布的情况下进行配电系统运行仿真。
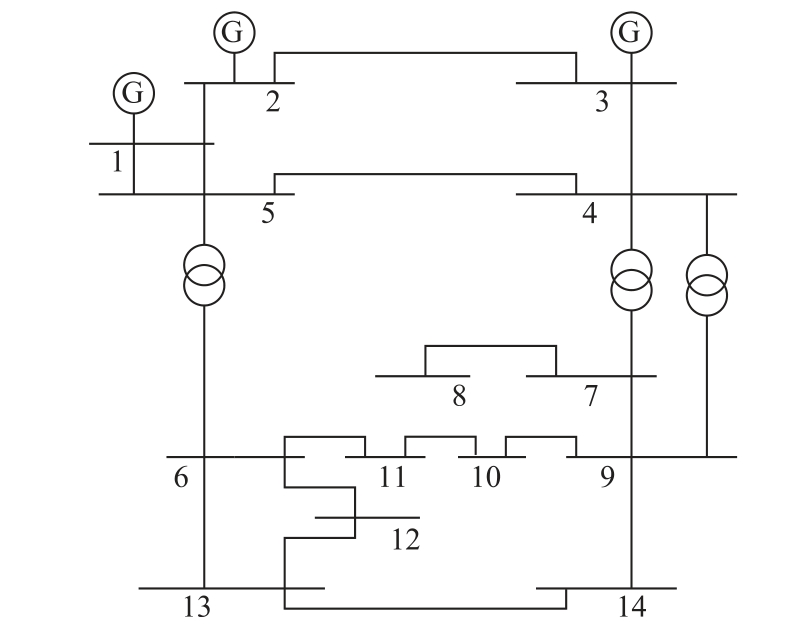
图5 IEEE 14 节点配电网模型
Fig.5 IEEE 14 node distribution network model
配电网中各节点电能质量数据对应的稀疏特性如图6 所示。
图6 配电网各节点电能质量数据稀疏特性
Fig.6 Sparse characteristics of power quality data in each node of distribution network
由于电源节点所受谐波影响较小，所以在讨论分区时仅讨论配电网中4～14 节点电能质量数据，各节点电能质量数据稀疏系数之间的互相关度见表1。
表1 配电网中各节点电能质量数据稀疏系数互相关度
Tab.1 Correlation of sparse coefficients of power quality data of each node in distribution network
节点互相关度r（%）4 5 6 7 8 9 10 11 12 13 14 4 100 77.717 85.137 99.905 93.612 99.812 95.344 96.075 96.429 96.146 95.307 5 77.717 100 98.829 78.619 53.919 79.091 59.839 62.920 64.671 63.235 59.681 6 85.137 98.829 100 86.170 65.566 86.658 70.921 73.664 75.208 73.942 70.779 7 99.905 78.619 86.170 100 93.810 99.984 95.711 96.529 96.932 96.608 95.669 8 93.612 53.919 65.566 93.810 100 93.753 99.711 99.314 99.006 99.264 99.727 9 99.812 79.091 86.658 99.984 93.753 100 95.737 96.598 97.027 96.681 95.692 10 95.344 59.839 70.921 95.711 99.711 95.737 100 99.916 99.789 99.897 100 11 96.075 62.920 73.664 96.529 99.314 96.598 99.916 100 99.971 99.999 99.907 12 96.429 64.671 75.208 96.932 99.006 97.027 99.789 99.971 100 99.980 99.774 13 96.146 63.235 73.942 96.608 99.264 96.681 99.897 99.999 99.980 100 99.888 14 95.307 59.681 70.779 95.669 99.727 95.692 100 99.907 99.774 99.888 100
设定IEEE 14 节点配电网系统分区数量为3～5个，分区阈值γ 为95，系统产生动态阈值δ 为91.75，该IEEE 14 节点配电网系统被划分为4 个区域，分区结果见表2。
表2 配电网分区结果
Tab.2 The results of distribution network zoning
分区结果 所含节点区域Ⅰ 5, 6区域Ⅱ 4, 7, 9区域Ⅲ 8区域Ⅳ 10, 11, 12, 13, 14
3.2 配电网电能质量数据的压缩存储
以分布式压缩感知算法为边缘算法，对每个区域中电能质量数据进行采集，将对应的字典原子和测量值上传云端，在云端实现数据的精确恢复与压缩存储。以对上述IEEE 14 节点配电网系统进行1 次电能质量数据采集为例，其原始数据总大小为254.379 kbit，采用云边协同架构向云端传送的测量值大小为5.08 kbit，稀疏字典原子大小为51.835 kbit，压缩比约为50，边缘算法压缩采集时间为0.105s。由于稀疏字典原子在云端的作用仅为构建完备字典，因此在完备字典构建完成之后云端仅储存测量值即可，可以在保证数据重构精度的前提下实现由云端对原始数据的压缩存储，数据在云端重构的时间为0.006s。配电网各分区的电能质量信号在云端的重构效果如图7 所示。
图7 云端各分区电能质量数据重构情况
Fig.7 Reconstruction of power quality data of each partition in the cloud
3.3 算法性能分析
在假定各节点电能质量信号稀疏度为10 的情况下，对配电网中各分区电能质量数据分别采用正交匹配追踪[31]、广义正交匹配追踪（Generalized OMP, GOMP）[32]、正则化匹配追踪（Regularized OMP, ROMP）[33]、阶段正交匹配追踪（Stagewise OMP, StOMP）[34]、压缩采样匹配追踪（Compressive Sampling MP, CoSaMP）[35]和DCS-SOMP 重构算法进行压缩采集，对比分析各区域内在不同压缩比情况下采用以上重构算法的重构信噪比的变化情况，如图8 所示。
从图8 中可以明显看出，在进行压缩采样时，随着压缩比的不断增加，除DCS-SOMP 重构算法外，采用其他重构算法进行压缩采集时的重构信噪比都呈下降趋势。在压缩比上升为 40 时，采用ROMP 和CoSaMP 重构算法甚至出现了重构失真的现象。DCS-SOMP 重构算法在处理如区域Ⅲ含单一节点电能质量数据时性能最好，重构信噪比保持在145dB 左右，在面临多节点电能质量数据进行压缩采集时，其重构信噪比随着采集节点的增多呈下降趋势。不过通过对比分析各个分区内电能质量数据的重构效果，DCS-SOMP 重构算法的性能都明显优于其他几种重构算法。
此外，在对电能质量数据压缩存储时，数据在稀疏字典下的稀疏性也对边缘上传到云端的数据量具有重要影响。数据越稀疏，上传到云端的稀疏字典原子个数就越少，数据的存储量就更少。在压缩比为20 的情况下，对比分析各区域内在不同稀疏度的情况下采用以上几种重构算法的重构信噪比的变化情况，实验结果如图9 所示。
图8 重构信号信噪比随压缩比变化趋势
Fig8 SNR of reconstructed signal changes with compression ratio
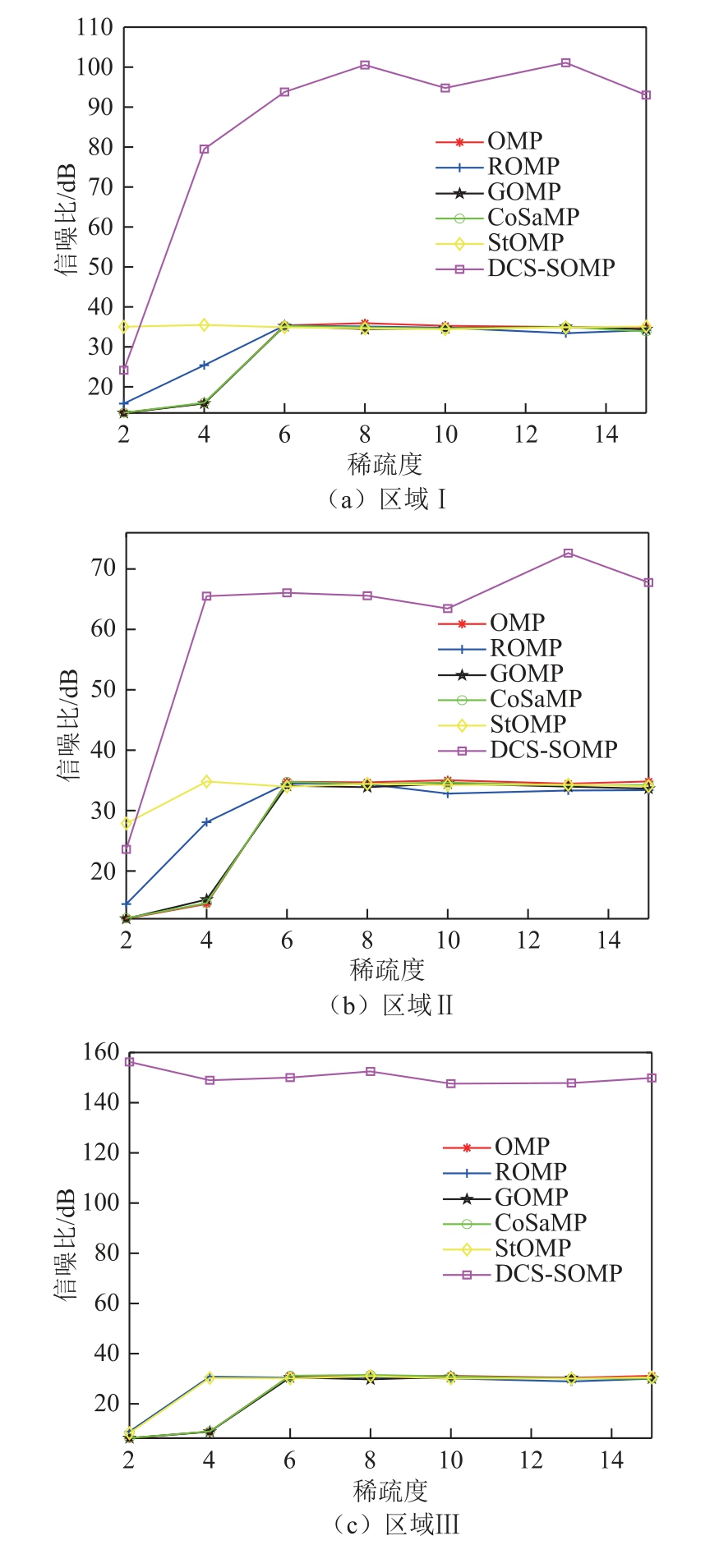
从图9 可以明显看出，随着稀疏度的不断增加，上述各重构算法的重构信噪比呈明显上升的趋势，在一定范围内达到平衡，其中DCS-SOMP 重构算法的上升速度最快。通过对比分析，除DCS-SOMP 重构算法外，其他几种重构算法的重构信噪比最终保持在32dB 左右，而DCS-SOMP 重构算法在各个分区中的重构信噪比都高于其他几种重构算法，且在处理单一节点电能质量数据时，重构性能最优。当对多节点电能质量信号进行同时采集时，分布式压缩感知算法每次向云端服务器上传的是分区内所有节点电能质量数据共用的字典原子，而压缩感知算法进行采集时，向云端上传的字典原子则是分区内每个节点电能质量数据对应的字典原子，其上传的字典原子个数远多于分布式压缩感知。
从图9 还可以看出，在假定各节点电能质量数据的稀疏度为2 时对区域Ⅲ中电能质量数据进行采集，仅DCS-SOMP 算法可以实现无失真重构，在处理其他区域的电能质量数据时，仅DCS-SOMP 和StOMP 两种重构算法可以实现精确重构。综合以上描述，采用DCS-SOMP 重构算法对电能质量数据处理时，不仅可以适应形式复杂的单一节点电能质量数据，还可以以更高压缩比和准确度同时存储多个节点的电能质量数据。
此外，本文通过对配电网中各分区电能质量数据分别采用稀疏度为4，信号压缩比为20 的DCSSOMP 重构算法，基于db4 小波基4 层分解的数据压缩算法[36]、基于Haar 小波基3 层分解的数据压缩算法[37]和FFT 软阈值滤波的数据压缩算法[38]进行采集，得到各分区中不同数据压缩采集算法的重构信噪比如图10 所示。
从图10 中可以看出，采用小波分解的电能质量数据压缩采集算法的重构信噪比基本保持不变，而采用FFT 软阈值的电能质量数据压缩方法在对第Ⅲ和Ⅳ分区进行压缩采集时均出现了失真现象，表明其在数据压缩时的鲁棒性较差。相比之下，采用DCS-SOMP 重构算法进行电能质量数据的压缩采集重构准确度显然更高。因采用FFT 软阈值电能质量数据出现失真现象，在评价压缩比性能时不再考量，则上述几种算法在对各分区电能质量数据采集时的压缩比情况如图11 所示。
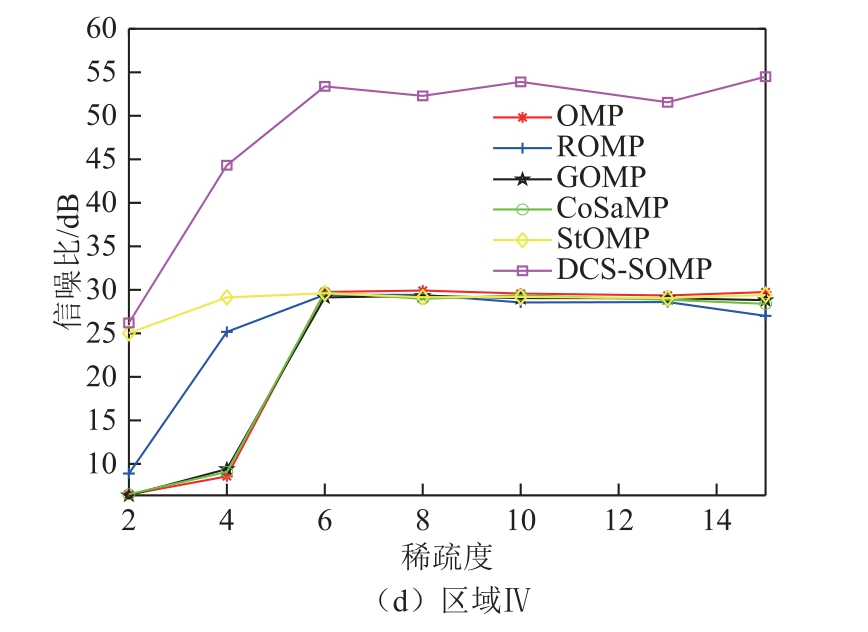
图9 重构信号信噪比随稀疏度变化趋势
Fig.9 SNR of reconstructed signal changes with the sparsity
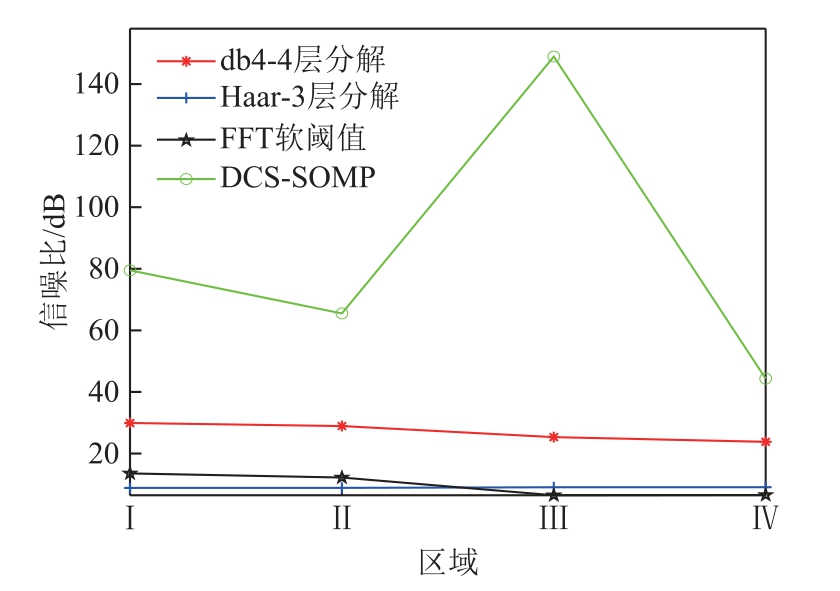
图10 数据压缩采集算法的重构信噪比情况
Fig.10 Reconstruction SNR of data compression acquisition algorithm
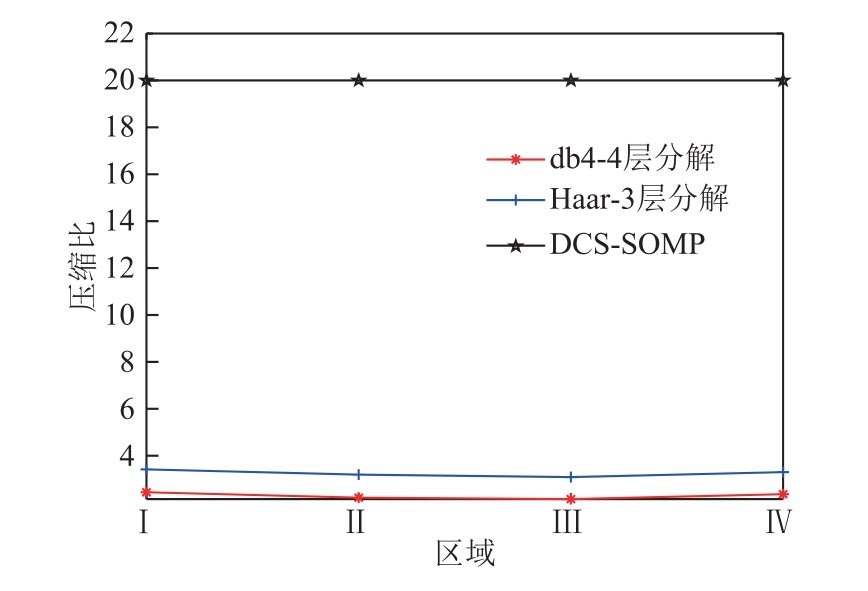
图11 数据压缩采集算法的压缩比情况
Fig.11 Compression ratio of data compression acquisition algorithm
从图11 可以明显看出，采用DCS-SOMP 算法进行数据压缩时，压缩比明显高于采用小波基分解的电能质量数据压缩采集方法，表明本文所提出算法不仅可实现以高压缩比对电能质量数据采集，还可以以较高信噪比精确重构。
4 结论
针对配电网中电能质量数据日益增多且易受到谐波污染的问题，本文提出了一种基于分布式压缩感知和边缘计算的压缩采集方法，通过该方法不仅可以实现对配电网各节点电能质量数据的高效压缩和精确重构，还可以实现对配电网谐波污染情况的分区，为配电网谐波的治理以及电能质量数据存储提供了新的参考方向。本文的主要结论有：
1）基于SOMP 算法和K-SVD 字典学习算法，提出了一种分布式压缩感知算法DCS-SOMP，实现了在低测量值和高压缩比条件下对配电网中电能质量数据的高效压缩与精确重构。
2）基于PSCAD 和Matlab 仿真平台，分析了将分布式压缩感知作为云边协同架构下边缘算法的优势，通过与压缩感知进行对比分析，论证了该方法理论上的优势与可行性。
3）基于云边协同架构，提出了双阈值动态分区策略，并在实验中得到验证。
[1] 周国亮, 宋亚奇, 王桂兰, 等. 状态监测大数据存储及聚类划分研究[J]. 电工技术学报, 2013, 28(增刊2): 337-344.Zhou Guoliang, Song Yaqi, Wang Guilan, et al.Research of condition monitoring big data storage and clustering[J]. Transactions of China Electrotechnical Society, 2013, 28(S2): 337-344.
[2] Zhao Wenjing, Shang Liqun, Sun Jinfan. Power quality disturbance classification based on timefrequency domain multi-feature and decision tree[J].Protection and Control of Modern Power Systems,2019, 4(4): 337-34.
[3] 林楚乔, 佟辉, 于温方, 等. 基于泛在电力物联网的配电网智能化状态监测与故障处理平台设计[J].东北电力大学学报, 2019, 39(4): 1-4.Lin Chuqiao, Tong Hui, Yu Wenfang, et al. Design of intelligent state monitoring and fault handling platform for distribution network based on ubiquitous power internet of things[J]. Journal of Northeast Electric Power University, 2019, 39(4): 1-4.
[4] 刘颖英, 冯丹丹, 林才华, 等. 电能质量综合评估研究现状及发展趋势[J]. 电力系统保护与控制,2020, 48(4): 167-176.Liu Yingying, Feng Dandan, Lin Caihua, et al. Current status and development trend of power quality comprehensive assessment[J]. Power System Protection and Control, 2020, 48(4): 167-176.
[5] 陈雷, 郑德忠, 廖文喆. 基于压缩感知的含扰动电能质量信号压缩重构方法[J]. 电工技术学报, 2016,31(8): 163-171.Chen Lei, Zheng Dezhong, Liao Wenzhe. Method based on compressed sensing for compression and reconstruction of power quality signals with disturbances[J]. Transactions of China Electrotechnical Society, 2016, 31(8): 163-171.
[6] 于华楠, 杜瑶, 马聪聪. 电力系统信号与数据的压缩传感技术综述[J]. 仪器仪表学报, 2017, 38(8):1943-1953.Yu Huanan, Du Yao, Ma Congcong. Survey of compressed sensing technology for signal and data of power system[J]. Chinese Journal of Scientific Instrument, 2017, 38(8): 1943-1953.
[7] 李剑飞, 陈隆道. 应用于电力谐波分析的改进插值算法[J]. 电力系统自动化, 2019, 43(8): 138-146.Li Jianfei, Chen Longdao. Improved interpolation algorithm applied to power harmonic analysis[J].Automation of Electric Power Systems, 2019, 43(8):138-146.
[8] 黄南天, 彭华, 徐殿国, 等. 主动配电网电能质量信号高效压缩[J]. 电工技术学报, 2015, 30(增刊2):181-188.Huang Nantian, Peng Hua, Xu Dianguo, et al. High efficiency power quality data compression in active distribution network[J]. Transactions of China Electrotechnical Society, 2015, 30(S2): 181-188.
[9] 陈杨. 基于多小波的数据压缩研究及其在电力远程通信中的应用[D]. 沈阳: 东北大学, 2015.
[10] 魏雪琴. 电能质量数据压缩的研究[D]. 合肥: 安徽大学, 2013.
[11] 陈思伟, 高翠云, 胡翀. 基于相似度分段及重采样的自适应波形数据压缩[J]. 电子测量与仪器学报,2019, 33(4): 178-185.Chen Siwei, Gao Cuiyun, Hu Chong. Adaptive waveform data compression based on similarity segmentation and resampling[J]. Journal of Electronic Measurement and Instrumentation, 2019, 33(4): 178-185.
[12] 刘嫣, 汤伟, 刘宝泉. 基于压缩感知的电能质量扰动数据稀疏分析与改进重构算法[J]. 电工技术学报, 2018, 33(15): 3461-3470.Liu, Yan, Tang Wei, Liu Baoquan. Data sparse analysis and improved reconstruction algorithm of power quality disturbance based on compressed sensing[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3461-3470.
[13] 于华楠, 代芳琳, 苏天恺. 基于压缩感知的三相电能质量扰动信号压缩及分类新方法[J], 吉林大学学报:工学版, 2016, 46(3): 964-971.Yu Huanan, Dai Fanglin, Su Tiankai. New compression and classification method of three phase power quality disturbance signal based on compressed sensing[J]. Journal of Jilin University: Engineering and Technology Edition, 2016, 46(3): 964-971.
[14] 杨羊. 基于分布式压缩感知的气象传感网数据收集技术研究[D]. 南京: 南京信息工程大学, 2017.
[15] Wang Rui, Qin Jiani, Du Linfeng, et al. A new image fusion method based on compressed sensing[C]//IET International Conference on Smart and Sustainable City, Shanghai, China, 2013, DOI: 10.1049/cp.2013.2025.
[16] 于华楠, 李永鑫, 王鹤. 基于过完备字典设计的电力系统扰动定位方法[J]. 电工技术学报, 2020,35(7): 1444-1453.Yu Huanan, Li Yongxin, Wang He. Disturbance location method of power system based on overcomplete reconstruction dictionary design[J].Transactions of China Electrotechnical Society, 2020,35(7): 1444-1453.
[17] 张真真. 基于稀疏表示与字典学习的图像去噪算法研究[D]. 开封: 河南大学, 2018.
[18] 杨柳, 彭江, 王同勋, 等. 中国电网电能质量数据概率分析模型及特性评[J]. 全球能源互联网(英文),2018, 1(3): 391-395.Yang Liu, Peng Jiang, Wang Tongxun, et al.Compliance verification and probabilistic analysis of state-wide power quality monitoring data[J]. Global Energy Interconnection, 2018, 1(3): 391-395.
[19] 秦奇波, 杨峰. 调制宽带转换器中一种改进的SOMP 算法[J]. 电子信息对抗技术, 2015, 30(6): 10-14.Qin Qibo, Yang Feng. An improved SOMP algorithm for modulated wideband converter[J]. Electronic Information Warfare Technology, 2015, 30(6): 10-14.
[20] Ren Jinke, Yu Guanding, He Yinghui, et al.Collaborative cloud and edge computing for Latency minimization[J]. IEEE Transactions on Vehicular Technology, 2019, 68(5): 5031-5044.
[21] Wang Rui, Li Miao, Peng Limei, et al. Cognitive multi-agent empowering mobile edge computing for resource caching and collaboration[J]. Future Generation Computer Systems, 2020, 102: 66-74.
[22] Yuan Peiyan, Cai Yunyun, Huang Xiaoyan, et al.Collaboration improves the capacity of mobile edge computing[J]. IEEE Internet of Things Journal, 2019,6(6): 10610-10619.
[23] He Qiang, Cui Guangming, Chen Feifei, et al. A gametheoretical approach for user allocation in edge computing environment[J]. IEEE Transactions on Parallel and Distributed Systems, 2020, 31(3): 515-529.
[24] Woo-Joong Kim, Kyung-No Joo, Chan-Hyun Youn.Short-term time-varying request model based chunk caching scheme for live streaming in mobile edgecloud environment[J]. IEEE Access, 2019, 7: 177148-177163.
[25] 邵振国, 黄伟达. 考虑出力不确定性的分布式电源谐波传播计算[J]. 电工技术学报, 2019, 34(增刊2):674-683.Shao Zhenguo, Huang Weida. A calculation method of harmonic propagation considering the uncertainty of distributed generation[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 674-683.
[26] 赵仁德, 李乾, 徐海亮, 等. 脉冲宽度调制并网变换器电网背景谐波电流的抑制[J]. 电工技术学报,2018, 33(增刊2): 558-566.Zhao Rende, Li Qian, Xu Hailiang, et al. Grid background harmonic current suppression for gridconnected PWM converters[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 558-566.
[27] 张俊敏, 刘开培, 汪立, 等. 基于主瓣宽度多谱线插值的高精度快速谐波分析算法[J]. 电工技术学报, 2018, 33(增刊1): 121-128.Zhang Junmin, Liu Kaipei, Wang Li, et al. A precise and rapid algorithm for harmonic analysis based on multi-spectrum-line in main lobe width interpolation FFT[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 121-128.
[28] 张逸, 王攸然, 刘航, 等. 基于监测数据相关性分析的用户谐波责任划分方法[J]. 电力系统自动化,2020, 44(2): 189-199.Zhang Yi, Wang Youran, Liu Hang, et al.Determination method of user harmonic responsibility based on correlation a nalysis of monitoring data[J].Automation of Electric Power Systems, 2020, 44(2):189-199.
[29] 石磊磊, 贾清泉, 孙海东, 等. 基于数据驱动的电能质量分区治理策略[J]. 中国电机工程学报, 2019,39(4): 992-1001.Shi Leilei, Jia Qingquan, Sun Haidong, et al. Regional abatement strategy for power quality based on data driven[J]. Proceedings of the CSEE, 2019, 39(4): 992-1001.
[30] 于浩, 贾清泉, 李珍国, 等. 基于时间序列模式匹配的电能质量区域化治理[J]. 中国电机工程学报,2019, 39(13): 3788-3799.Yu Hao, Jia Qingquan, Li Zhenguo, et al.Regionalization control for power quality based on time series pattern matching[J]. Proceedings of the CSEE, 2019, 39(13): 3788-3799.
[31] 战非. 基于压缩感知OMP 算法对稀疏信号重构的研究[J]. 电子设计工程, 2017, 25(1): 71-74.Zhan Fei. A research on sparse signal reconstruction based on compressed sensing OMP algorithm[J].Electronic Design Engineering, 2017, 25(1): 71-74.
[32] 刘国海, 丁灵卫, 沈跃, 等. 广义正交匹配追踪电能质量信号重构方法[J]. 电测与仪表, 2019, 56(10):69-74.Liu Guohai, Ding Lingwei, Shen Yue, et al. Power quality signal reconstruction method based on generalized orthogonal matching pursuit[J]. Electrical Measurement & Instrumentation, 2019, 56(10): 69-74.
[33] 廖勇, 周昕, 沈轩帆, 等. 一种基于改进ROMP 的MIMO-OFDM 信道估计方法[J]. 电子学报, 2017,45(12): 2848-2854.Liao Yong, Zhou Xin, Shen Xuanfan, et al. A channel estimation method based on improved regularized orthogonal matching pursuit for MIMO-OFDM systems[J]. Acta Electronica Sinica, 2017, 45(12):2848-2854.
[34] Donoho D, Tsaig Y, Drori I, et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2012, 58(2):1094-1121.
[35] 余林, 肖儿良, 简献忠. SA-CoSaMP 算法在电能质量扰动信号识别中的应用[J]. 电子测量技术, 2018,41(21): 1-7.Yu Lin, Xiao Erliang, Jian Xianzhong. Application of SA-CoSaMP algorithm in power quality disturbance signal identification[J]. Electronic Measurement Technology, 2018, 41(21): 1-7.
[36] 肖嘉耀. 基于db4 小波变换的电能质量数据压缩算法[J]. 福建电脑, 2013, 29(6): 117-119.Xiao Jiayao. Power quality data compression algorithm based on db4 wavelet transform[J]. Fujian Computer, 2013, 29(6): 117-119.
[37] 葛哲学, 沙威. 小波分析理论与 MATLAB R2007实现[M]. 北京: 电子工业出版社, 2007.
[38] 张乐平, 丁泽俊, 夏锐, 等. 结合二代小波与快速傅里叶变换的电能质量数据压缩算法[J]. 南方电网技术, 2013, 7(3): 89-93.Zhang Leping, Ding Zejun, Xia Rui, et al. A power quality data compression algorithm in combination of second generation wavelet packets and fast Fourier transform[J]. Southern Power System Technology,2013, 7(3): 89-93.