0 引言
对于无接触网城轨列车采用感应电能供电（Inductive Power Supply, IPS）技术，通过电磁感应将电能以非接触网的方式从电源侧传递到一个或多个负载侧。电能在传输过程中出现电能质量扰动[1-3]，谐波信号中含有高次谐波与间谐波是电能质量出现扰动的主要原因。为了尽可能减少包含间谐波的谐波信号对电能质量扰动的干扰，要求监测站点不间断、高采样率进行谐波信号数据的采集[4]，进而对含间谐波的谐波信号进行分析、评估与治理。
压缩感知（Compressed Sensing, CS）理论的提出[5-6]，突破了Nyquist 采样定理无法对高次谐波与间谐波采样、消耗大量的存储空间和硬件资源的缺陷，成为处理信号领域中一个新的研究热点。在CS理论下处理含间谐波的谐波信号时，如何使压缩重构后的信号具有高信噪比、高精度成为CS 理论研究的重点[7-8]。
目前常用的重构算法主要有以下三类：①以匹配追踪（Matching Pursuit, MP）为代表的贪婪算法，主要代表算法是压缩采样匹配追踪（Compressed Sample Matching Pursuit, CoSaMP）[9]；②以针对基追踪（Base Pursuit, Basis Pursuit, BP）问题的凸优化恢复算法，主要代表有梯度投影稀疏重建（Gradient Projection Sparse Reconstruction, GPSR）算法[10]、谱投影梯度（Spectral Projected Gradient, SPG）算法[11]等；③以迭代阈值为代表的组合恢复算法[12]等。但采用IPS 技术供电时谐波环境复杂，非同步采样导致出现频谱泄漏和栅栏效应问题[4]，致使现有恢复算法重构精度差、误差大、时间长。文献[13]运用CS理论对短时电能质量扰动信号进行压缩重构；文献[14] 提出一种改进的后向子空间匹配追踪（Backward Subspace Matching Pursuit, BSMP）算法，但该算法迭代终止条件取决于残差能量与压缩信号能量的比值ε ；文献[15]指出ε 变化范围较大；文献[16]提出了一种本征时间尺度分解（Intrinsic Timescale Decomposition, ITD）与改进内积的压缩感知重构算法相结合的变流器电压信号重建方法。以上研究为电能质量信号的重构提供了理论依据，但未考虑栅极效应和频谱泄漏问题，从而在算法重构的过程中出现稀疏度过度估计、精度难以保证等问题。
因此，本文主要讨论含间谐波的谐波信号首先在加窗后的快速傅里叶变换（ Fast Fourier Transformation, FFT）下消除短程频谱泄漏，且加窗后FFT 变换下的信号具有高稀疏性，进而提出一种可以消除栅极效应和长范围频谱泄漏的多谱线插值修正的谱投影梯度（Spectral Projected Gradient with Line Interpolation Correction, SPG-LIC）重构算法。该算法首先分离出原始信号中的基波信号（即50Hz）；然后在谱投影梯度算法重构信号之前用多谱线插值修正（Line Interpolation Correction, LIC）算法消除长范围的频谱泄漏及栅极效应，进一步降低信号的稀疏度K 并进行预估；最后通过实验仿真表明SPG-LIC 算法与现有的多种重构算法相比，有效提高了信号重构精度与信噪比，降低了重构误差，缩短了重构时间。
1 谐波在FFT 加窗下的稀疏性
目前，国内外学者对于谐波信号的稀疏性研究主要集中在以小波变换为代表的正交基和以冗余字典为代表的非正交基两个方面[4,7]。考虑到算法的复杂性以及硬件方面的难以实现程度，快速傅里叶变换（Fast Fourier Transformation, FFT）在工程中被广泛应用。
1.1 FFT
FFT 是离散傅里叶变换（Discrete Fourier Transformation, DFT）的快速算法[17-18]，在CS 理论下对谐波信号进行FFT 稀疏变换，可使测量矩阵由N 维降至M 维（M≪ N），进行压缩时计算量大大降低，重构时间大大缩短。
定义：若原始信号x 在稀疏基Ψ 下可稀疏表示为x =Ψ s，s 为稀疏向量且包含的大部分元素（K个）值均小于某一很小的正数ε（ε 通常取0.1）时，则认为原始信号为K——稀疏信号。
在IPS 技术下产生的谐波信号数学模型为
式中， hA 、 fh 和 hφ 为谐波（间谐波）分量参数，共含H 个谐波（间谐波）分量； w( t ) 为含高斯白噪声的间谐波信号，其均值为0，方差为 2σ ；λ 为参数，可改变高斯白噪声的幅值。
对谐波信号以采样频率 fs 进行N 点采样，其离散序列为
1.2 加窗后的FFT 变换
为减少短程频谱泄漏，保证信号的稀疏性，首先对含有间谐波的谐波信号进行加窗处理。由于汉宁窗运算简单，间谐波泄漏误差小，便于计算仿真，因此本文采用汉宁窗。对 fh ( n )在加窗后频域下进行FFT 可得
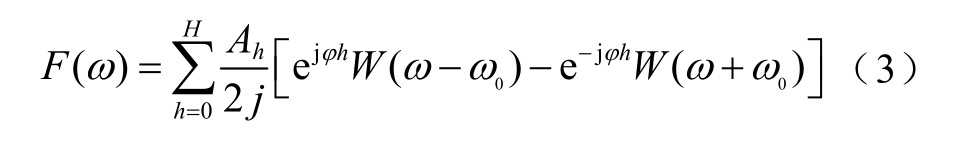
提取加窗后含间谐波信号的一个分量并将其离散化，在FFT 基下的稀疏表示系数为
式中，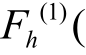
( k )和 
( k )分别为其中两条对称的短程泄漏谱线，其幅度谱为
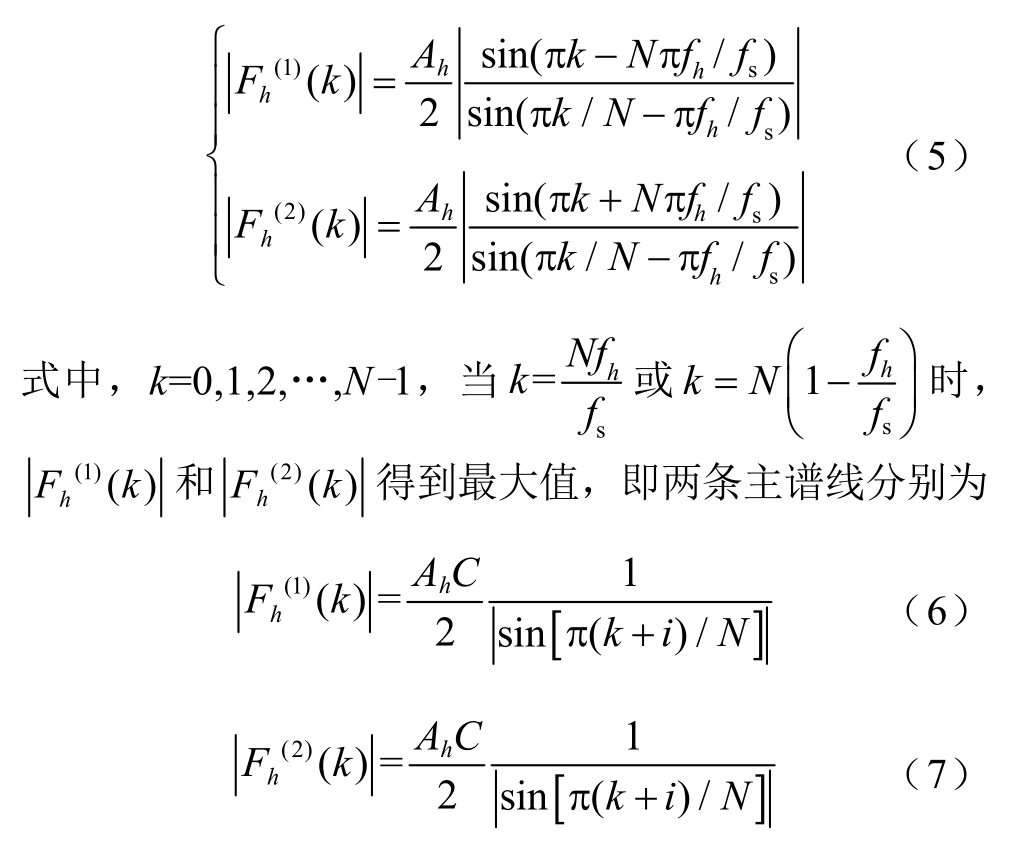
式中， C =sin( πk ); i= 0, ± 1, ± 2,…。当采样点数N 与周期成整数倍关系时，C = 0，泄漏谱线的幅值为0；当采样点数与周期呈非整数倍关系时，泄漏谱线幅值按照
[ π( k + i ) ] sin [ π ( k + i )/N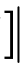
形式衰减。在信号处理理论中，sin c 函数在N＞1 00时具有良好的稀疏性，泄漏谱线能量迅速衰减并接近于零[6]。本文中仿真时间周期T=0.2s，基波频率为50Hz 时，在监测系统数据观测窗口中选取5 个周波，每个周波采集200 ～300个采样点，则采样点总数 N ≥ 1 000，高于信号领域中N＞100时具有稀疏性的要求，因此式（1）在加窗后的FFT 基下具有足够的稀疏性，远远高于CS 理论重构要求。
2 SPG-LIC 重构算法
对含间谐波的谐波信号同步采样时，由于谐波频率偏移、谐波中包含间谐波等情况致使无法同步采样，从而在FFT 计算时出现栅极效应和频谱泄漏[19-20]。栅极效应使采样信号放大，导致相位、幅值等参数远大于原始信号参数；频谱泄漏会影响矩阵的稀疏度K，导致出现稀疏度估计过低或错估的情况；在二者共同作用下，导致重构信号与原始信号之间存在较大误差。为此首先对谐波信号加汉宁窗以减少短程频谱泄漏，再运用LIC 算法来消除长频谱泄漏及栅极效应，最后使用SPG 算法重构原始信号，提高原始信号的重构精度。
2.1 算法原理
由基波-谐波分量的稀疏度性质可知[6]，若滤除原始信号中的基波分量，则信号的稀疏度大幅降低，因此针对含间谐波的谐波信号在加窗FFT 变换后先进行50Hz 的基波滤除，再运用SPG-LIC 算法重构原始信号。
SPG-LIC 算法流程框架如图1 所示。
图1 SPG-LIC 算法流程
Fig.1 Flow chart of SPG-LIC algorithm
SPG-LIC 算法的核心思想是在加汉宁窗后FFT变换的基础上消除短程频谱泄漏，然后运用LIC 算法消除长范围的频谱泄漏及栅极效应，使信号稀疏度进一步提高，最后应用SPG 恢复出具有高稀疏度的重构信号。
2.1.1 谱投影梯度算法
SPG 是一种用于解决基追踪（Basis Pursuit, BP）问题的凸优化方法，采用非单调线性搜索策略，将谱投影梯度和谱步长分别作为搜索方向和步长，具有低复杂度、高重构精度和全局收敛性好的优点[9]。SPG 算法搜索方向和步长无界限约束，但具有收敛性和有限步长终止性，利用式（8）投影算子产生每次迭代搜索的投影梯度路径[21]。
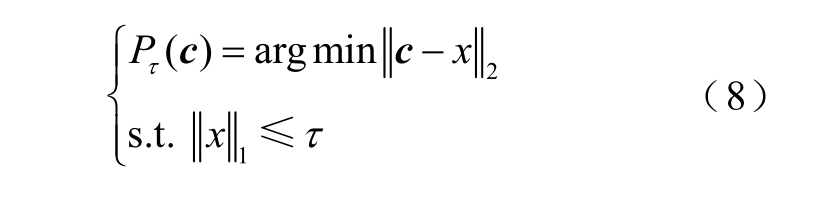
式中，x 为原始信号；c 为一个向量；τ 为1 范数球的半径；P τ ( c )为通过最小二乘法求解后向量c 在Ω上的正交投影，此时Ω=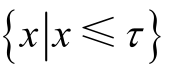 
。
2.1.2 多谱线插值修正算法
由于采用IPS 方式供电时，谐波信号中夹杂有间谐波，出现频谱泄漏而无法同步采样进而影响信号的重构精度[22-23]。为此，本文首先引入加窗后FFT消除短程频谱泄漏的影响，进而保证加窗FFT 后的信号具有高稀疏度；对于长频谱的泄漏及栅极效应，采用多谱线插值修正算法消除。
稳态情况下，对于采样点数为N 的谐波信号，设频谱为 X ( k) ，最大谱线为 k0 ，则可以利用任意两条谱线对频率进行估计，估计频率 f' 为
假设谐波分量的最大峰线和次大峰线对应的谱线标号分别为k1m 和km2 ，则偏移 kδ 量化频率单位后的谱线频率、幅值和相角修正公式分别为
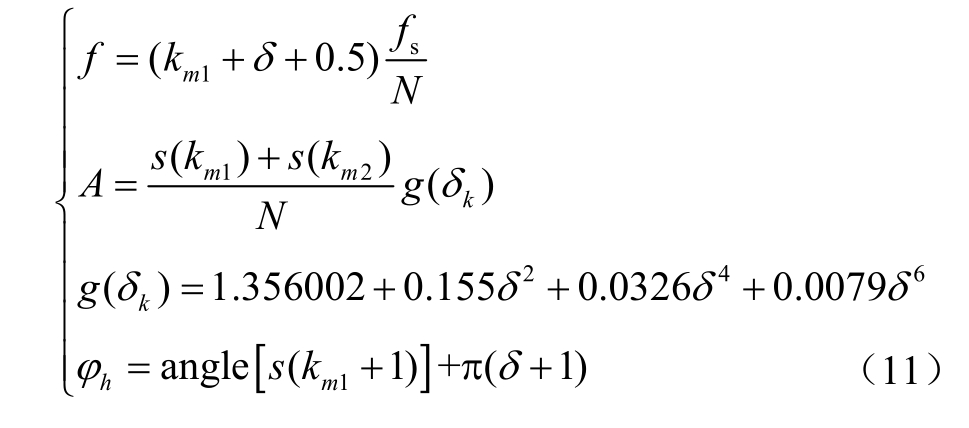
式中，s ( km 1)和s ( km 2)分别为恢复算法得到稀疏向量s 的第k m1和k m2个元素；a ngle [ s ( k m 1+1)]为s 中第km1+1个元素值 s (k m 1+1)的复数角。
2.1.3 稀疏度估计
利用CS 理论对含有高次谐波与间谐波的信号进行压缩重构时，SPG-LIC 算法要求在稀疏度K 已知的前提下才能准确恢复出原始信号。根据先验知识，当信号稀疏度在 K = M /4时，重构效果最好，M为测量矩阵Φ 的维数。
引理：若Φ 满足条件为 (2 K ,δ 2 K )的约束等距（RIP）性质[24]，且预估稀疏值K∗≥ K，则式（12）成立。
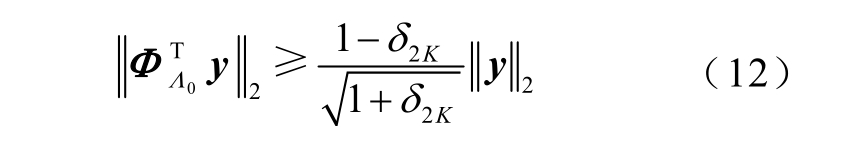
式中，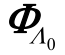 
为矩阵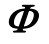
中各列以下标原子为索引构成的子矩阵； 
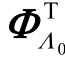为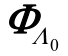 
的转置矩阵。
若上面的命题成立，则逆否命题为：当
，K ∗＜K 也是成立的。根据该逆否命题，首先假设稀疏度估计值 K ∗=M /4，然后逐次增加或递减， 直至不等式
不成立，就可以得到略大于或小于真实稀疏度的估计值。
2.2 SPG-LIC 算法流程
插值后的基波滤除谱投影算法流程如下：
输入：谐波压缩信号 RM y∈ ；测量矩阵 
；感知矩阵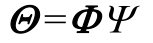
；稀疏度估计值K∗。
输出：原始重构信号 x' 。
初始化：稀疏估计值 s0′b ase=0；残差初始值 r0 = μ；支撑集Λ0=∅；支撑矩阵Ω0 =[]；初始梯度 g0 =-ΘT r 0；初始步长α 0 ∈[α min,αmax]；迭代次数m≥ 1。
循环：
（1）寻找索引λt = arg max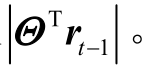
（2）更新支撑集Λ 和支撑矩阵Ω：Λ t =Λt - 1∪{λ t };
为感知矩阵
的第 λt 列的列向量）。
（ 3 ） 最小二乘法更新估计值：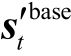 
=
（4）若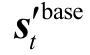 
中所有非零元素相邻，则跳入步骤（6）；否则，在不相邻元素位置上进行谱线插值修正，利用式（9）估计频率 f '，若满足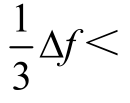
则f′可作为频率估计值，若不满足，利用式（10）、式（11）进行谱线频率、幅值和相角的修正。
（5）更新残差： rt = μ- 
。
（6）若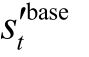 
中所有非零元素满足
≥
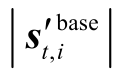，i = 1,2,…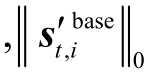 
，则进行下一次循环，t = t+ 1。
（7）当残差
通常取0.1）成立时，结束循环。
循环次数1 ≤ t ≤ M，且残差能量
ε 可根据噪声大小和恢复准确度等实际情况确定。
迭代：
1）线性迭代搜索更新本次迭代估计值。
（1）更新稀疏估计值和残差：
4）当迭代次数 m ≥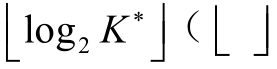
表示下取整）时，终止迭代，输出原始重构信号x′。
3 仿真结果与分析
3.1 重构性能指标
设N 为原始信号长度，M 为采样压缩后信号长度，x 为原始谐波信号，x′为重构信号。为了比较各种算法对谐波信号的重构性能，采用以下指标进行评价，相对方均根误差与重构信噪比越小，表示信号重构成功率越高。
相对方均根误差（Relative Root Mean Square Error, RRMSE）反映原始信号x 与重构信号x′之间差异程度，表达式为
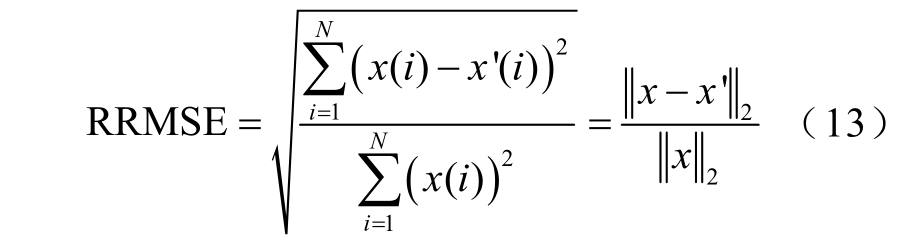
重构信噪比（Signal Noise Ratio, SNR）反映了重构信号中信号与噪声的比例，表达式为
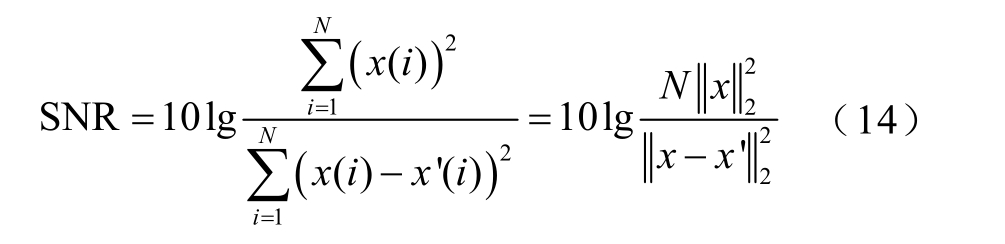
压缩比（Compression Ratio, CR）反映了压缩后与压缩前信号字节数的比值，表达式为
3.2 仿真
以无接触网城轨列车的感应供电模型为研究对象，监测采集原始信号长度N=1 024 的一段谐波信号，其中含有高次谐波信号与间谐波信号。根据引理的逆否命题，可估算出原始信号稀疏度K=76，对信号进行加窗后的FFT 计算及多谱线插值修正处理后，预估出谐波信号稀疏度 K ' =16 ，稀疏度大幅降低，满足重构要求。
3.2.1 谱投影梯度算法仿真
仿真结果表明，SPG 算法对不存在频谱泄漏的谐波信号重构效果较好，稀疏度值估计准确且较小，残差精度远低于规定阈值。假设对工频波加载50Hz的谐波信号进行重构，残差为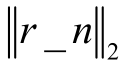
= 3.524 ×1 0-11，稀疏度估计值K ∗= 19，重构信号及频谱如图2 所示。
图2 SPG 算法下三相电压信号重构
Fig.2 Three-phase voltage signal reconstruction algorithm under the SPG
假设运用SPG 算法对工频波加载65.3Hz 的间谐波电压波动信号进行重构，残差为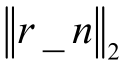
= 0.35，稀疏度预估计值K ∗= 27，重构信号及频谱如图3 所示。对比图2 与图3 可知，当谐波信号中存在间谐波及电压波动时，SPG 算法重构后的信号与原始信号相差较大。
图3 存在频谱泄漏的信号重构
Fig.3 Signal reconstruction with spectral leakage
3.2.2 加窗后的SPG-LIC 算法仿真
1）含谐波扰动信号的重构
提取IPS 技术下感应供电模型中所监测采集到的某段信号，其中含有3 次、5 次、7 次谐波，其信号模型为
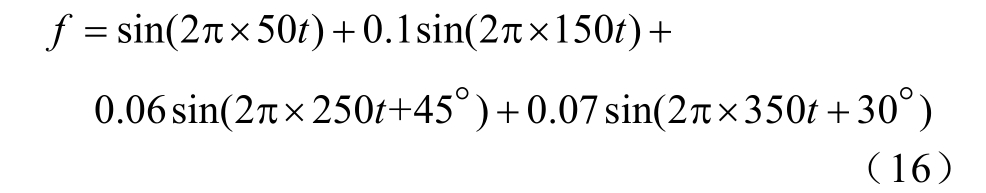
假设信号的稀疏度未知，将其估计为K∗=8 和18，分别进行仿真分析。对压缩采样后长度为M 的数据重复100 次仿真，计算成功重构概率。图4 为成功重构概率曲线。从图中可以看出，在相同的M下，SPG-LIC 算法实现了稀疏度相对较高的重构概率，对信号的稀疏度要求不是很高；BSMP、SPG、OMP 和CoSaMP[5-6]对信号的稀疏度要求较高，信号越稀疏，成功重构概率越高。
图4 含低次谐波扰动信号时不同算法重构概率与M 的关系
Fig.4 Probability of successful recovery of disturbance signal with low harmonic vs. M under different algorithms
2）含高次谐波，间谐波信号的重构
对完成搭建的无接触网城轨列车模型进行监测时，在正常运行列车的某段时间内可以监测到19 次、21 次、25 次及27 次等高次谐波的存在，间谐波频率为153.5Hz、535.6Hz 和925.2Hz，信号模型为
设采样频率为50kHz，原始信号长度N=1 024，通过式（12）与引理的逆否命题，可得到信号稀疏度的预估计值K ∗= 12，对每个M 值重复仿真100次，计算成功重构的概率，得到图5 所示的曲线。
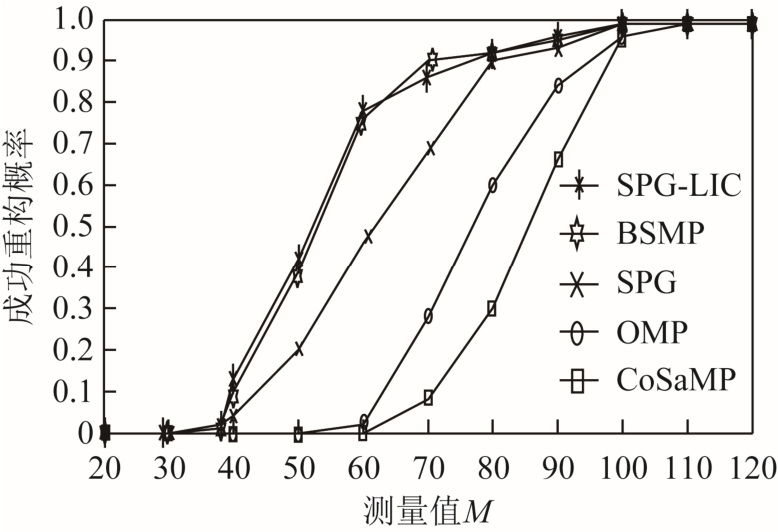
图5 含高次谐波，间谐波时动信号时不同算法重构概率与M 的关系
Fig.5 Probability of successful recovery of disturbance signal with high harmonic and interharmonic vs. M under different algorithms
3.3 信号重构精度分析
对于监测系统中所监测到的高次谐波与间谐波，分别取相同的压缩比，对比不同恢复算法下的重构信噪比与重构精度，测试结果如图6 和图7 所示。由图可知，同一压缩比下的SPG-LIC 算法的重构信噪比高于其他恢复算法，重构误差远低于其他恢复算法。当压缩比 M / N =0.2，信噪比为 110dB时，经式（13）计算验证可得重构信号误差为 6 ×10- 4，由此可知，当SPG-LIC 算法的信噪比高于110dB，其重构信号误差低于 6 ×10-4，重构性能远高于其他恢复算法。
图6 不同恢复算法重构信噪比
Fig.6 SNR of different recovery algorithms
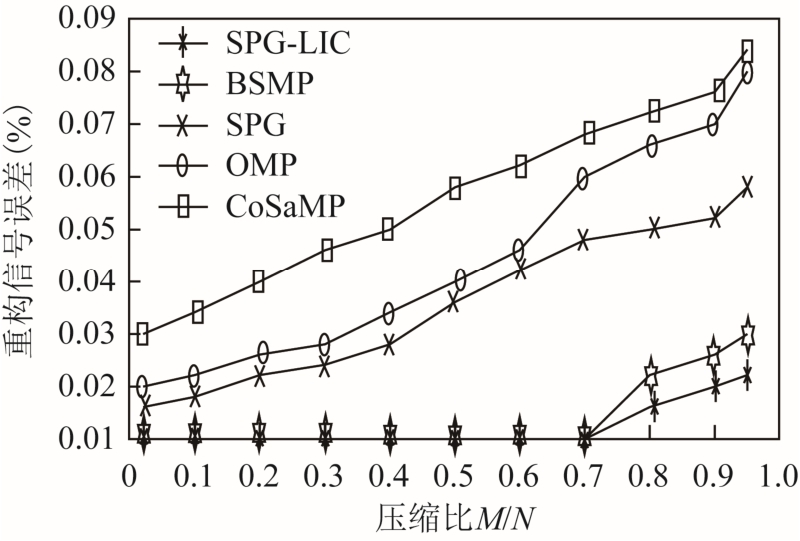
图7 不同恢复算法重构精度
Fig.7 Reconstruction precision of different recovery algorithms
3.4 不同恢复算法的重构时间
信号的准确重构是CS 理论的核心，而信号的稀疏度与精确重构原始信号、信号重构时间密切相关。因此，取相同的测量值M，不同的稀疏度估计值K，分别对比不同的算法重构信号的时间，如图8 所示。从图8 中可以看出，由于SPG-LIC 算法要处理长频谱泄漏及栅极效应，相较于SPG 算法花费时间较长，但优于其他恢复算法，且重构时间远低于预期时间。
图8 不同恢复算法重构时间
Fig.8 Reconstruction time of different recovery algorithms
4 结论
本文针对无接触网城轨列车模型在运行过程中监测到的间谐波与高次谐波信号，在FFT 稀疏变换时加入汉宁窗，消除短范围频谱泄漏，并提出多谱线插值投影梯度（SPG-LIC）算法来抑制长范围频谱泄漏及栅极效应，重构谐波信号并提高信号的重构精度。通过在Matlab 中的仿真结果表明，SPG-LIC算法相比已有的压缩感知恢复算法，具有更短的恢复时间，更少的压缩采样值与更好的信号重构精度，重构信号的信噪比高于110dB 时，重构信号误差小于 6 ×10- 4，远低于国家所规定的标准，为压缩感知在谐波分析中的应用提供了理论方法与依据。
[1] 陈晓静, 李开成, 肖剑, 等. 一种实时电能质量扰动分类方法[J]. 电工技术学报, 2017, 32(3): 45-54.Chen Xiaojing, Li Kaicheng, XiaoJian, et al. A method real-time power quality disturbance classification[J].Transactions of China Electrotechnical Society, 2017,32(3): 45-54.
[2] 王维博, 董蕊莹, 曾文入, 等. 基于改进阈值和阈值函数的电能质量小波去噪方法[J]. 电工技术学报, 2019, 34(2): 211-220.Wang Weibo, Dong Ruiying, Zeng Wenru, et al. A wavelet de-noising method for power quality based on an improved threshold and threshold function[J].Transactions of China Electrotechnical Society, 2019,34(2): 211-220.
[3] 曹玲芝, 刘俊飞, 郑晓婉. 基于EEMD 的HHT 在电能质量多扰动分类识别中的应用[J]. 电气技术,2017, 18(4): 66-70.Cao Lingzhi, Liu Junfei, Zheng Xiaowan.Classification and recognition of power quality multidisturbance based on EEMD-HHT[J]. Electrical Technology, 2017, 18(4): 66-70.
[4] 刘嫣, 汤伟, 刘宝泉. 基于压缩感知的电能质量扰动数据稀疏分析与改进重构算法[J]. 电工技术学报, 2018, 33(15): 34-45.Liu Yan, Tang Wei, Liu Baoquan. Data sparse analysis and improved reconstruction algorithm of power quality disturbance based on compressed sensing[J].Transactions of China Electrotechnical Society, 2018,33(15): 34-45.
[5] Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1280-1306.
[6] Candes E, Wakin M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30.
[7] Chakraborty S, Chatterjee A, Goswami S K, et al.Asparse representation based approach for recognition of power system transients[J]. Engineering Application of Artificial Intelligence, 2014, 30: 137-144.
[8] 杨挺, 武金成, 袁博. 谐波和间谐波检测的压缩感知恢复算法[J]. 中国电机工程学报, 2015, 35(21):5475-5482.Yang Ting, Wu Jincheng, Yuan Bo. The restoration algorithm of compressed sensing to detect harmonic and inter-harmonic[J]. Proceedings of the CSEE, 2015,35(21): 5475-5482.
[9] Needell D, Tropp J A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples[J].Appliedand Computational Harmonic Analysis, 2009,26(3): 301-321.
[10] Figueiredo M A T, Nowak R D, Wright S J. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems[J].IEEE Journal of Selected Topics in Signal Processing,2007, 1(4): 586-597.
[11] Ewout V D B, Friedlander M P. Probing the pareto frontier for basis pursuit solutions[J]. SIAM Journalon Scientific Computing, 2009, 31(2): 890-912.
[12] Beck A, Teboulle M. A fast iterative shrinkagethresholding algorithm for linear inverse problems[J].SIAM Journal on Imaging Sciences, 2009, 2(1): 183-202.
[13] 王学伟, 王琳, 苗桂君, 等. 暂态和短时电能质量扰动信号压缩采样与重构方法[J]. 电网技术, 2012,36(3): 191-196.Wang Xuewei, Wang Lin, Miao Guijun, et al. An approach for compressive sampling and reconstruction of transient and short-time power quality disturbance signals[J]. Power System Technology, 2012, 36(3): 191-196.
[14] 陈雷, 郑德忠, 廖文喆. 基于压缩感知的含扰电能质量信号压缩重构方法[J]. 电工技术学报, 2016,31(8): 163-170.Chen Lei, Zheng Dezhong, Liao Wenzhe. Method based on compressed sensing for compression and reconstruction of power quality signals with disturbances[J]. Transactions of China Electrotechnical Society, 2016, 31(8): 163-170.
[15] Zhang Ruoyu, Zhao Honglin. An improved sparsity estimation variable step-size matching pursuit algorithm[J]. Journal of Southeast University: English Edition, 2016, 32(2): 164-169.
[16] 董唯光, 张晓东, 汤旻安, 等. 基于ITD 与改进内积的压缩感知风电变流器电压信重建方法[J]. 高电压技术, 2018, 44(7): 2338-2345.Dong Weiguang, Zhang Xiaodong, Tang Minan, et al.Voltage signal reconstruction method of wind power converter based on ITD and improved inner product compressed sensing[J]. High Voltage Engineering,2018, 44(7): 2338-2345.
[17] 范满义, 史黎明, 殷正刚, 等. 感应电能传输系统基于阶梯波合成技术的谐波消除和脉冲密度功率调节方法[J]. 中国电机工程学报, 2017, 37(22):6516-6523.Fan Manyi, Shi Liming, Yin Zhenggang, et al.Harmonic elimination and power regulation with pulse density modulation based on staircase waveform for multilevel inverters in inductive power transfer system[J]. Proceedings of the CSEE, 2017, 37(22):6516-6523.
[18] 荣文帅, 蔡志远. 断路器同步分断短路电流零点预测方法研究[J]. 电工技术学报, 2019, 34(15): 3167-3174.Rong Wenshuai, Cai Zhiyuan. Research on zero prediction method of synchronous breaking short circuit current of breaker[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3167-3174.
[19] 翟晓军, 周波. 一种改进的插值FFT 谐波分析算法[J].中国电机工程学报, 2016, 36(11): 2952-2958.Zhai Xiaojun, Zhou Bo. An improved interpolated FFT algorithm for harmonic analysis[J]. Proceedings of the CSEE, 2016, 36(11): 2952-2958.
[20] 王保帅, 肖霞. 一种用于谐波分析的高精度多谱线插值算法[J]. 电工技术学报, 2018, 33(3): 553-562.Wang Baoshuai, Xiao Xia. A high accuracy multispectrum-line interpolation algorithm for harmonic analysis[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 553-562.
[21] Ghahremani M, Ghassemian H. A compressedsensing-based pan-sharpening method for spectral distortion reduction[J]. IEEE Transactions on Geoscience & Remote Sensing, 2016, 54(4): 2194-2206.
[22] 李剑飞, 陈隆道. 应用于电力谐波分析的改进插值算法[J]. 电力系统自动化, 2019, 43(8): 138-146.Li Jianfei, Chen Longdao. Improved interpolation algorithm applied to power harmonic analysis[J].Automation of Electric Power Systems, 2019, 43(8):138-146.
[23] 张建忠, 耿治, 徐帅, 等. 一种有源电力滤波器的改进自适应谐波检测算法[J]. 电工技术学报, 2019,34(20): 4323-4333.Zhang Jianzhong, Geng Zhi, Xu Shuai. et al. An improved adaptive harmonic detection algorithm for active power filter[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4323-4333.
[24] Yang Lu, Guo Wenbin, Xing Wang, et al. Probabilistic greedy pursuit for streaming compressed spectrum sensing[J]. The Journal of China Universities of Posts and Telecommunications, 2013, 18(5): 15-21.