0 引言
近年来,电力系统混沌振荡的控制问题作为一个理论性与实践性共同需要考虑的问题得到了众多学者的关注[1-5]。针对电力系统混沌控制问题,目前众多学者已经针对简单的二阶及四阶电力系统模型提出了各种混沌控制方法[6-11]。1999 年,印度学者针对典型三母线电力系统建立了颇为实用的七阶电力系统动力学模型[12],该模型是目前电力系统模型中最为复杂的一个动力学模型。通过逐步忽略电力系统中的建模因素并对该模型进行化简,就可以得到目前的绝大多数电力系统动力学模型,例如可以得到六阶模型、四阶模型以及二阶模型[12]。因此作为描述三母线电力系统动态行为的系统模型,该模型本身具有很大程度的代表性。随后,学者们针对七阶电力系统进行了更进一步研究。文献[13-16]主要利用该系统模型分析了电力系统分岔及混沌现象对电力系统稳定性造成的各种不利影响。然而由于系统模型的复杂性,导致许多适用于简单系统的控制方法并不能直接用于控制这样复杂的动力学系统,因此对于如何控制这一复杂系统目前仍然缺少比较有效的方法。文献[17]针对该系统提出了新颖的固定时间协同控制方法,为该系统的混沌控制问题提供了思路,然而所给出的控制器中包含复杂系统函数的导数,降低了其工程实用性。
总体而言,电力系统混沌控制领域还存在诸多问题,主要问题有:①目前控制电力系统混沌时所采用的模型均是一些简单低阶电力系统模型[6-11],所设计的控制器普适性较差;②诸多的控制器设计方法只从非线性控制的角度出发进行控制器设计,而很少考虑电力系统的实际运行状况[9-10];③诸多文献针对混沌电力系统所设计的控制输入高度依赖于电力系统模型[6-11],从而降低了控制器的实用性。
针对问题①,本文直接针对七阶电力系统模型进行研究,力图使所设计的控制器具有一定的普适性;针对问题②,本文考虑电力系统的实际运行状况并为其引入储能装置的动态模型,力图构建含有储能装置的受控电力系统;针对问题③,本文基于扩张状态观测器进行控制器设计,力图降低控制器对受控系统模型的依赖性,从而使所设计的控制器具有一定的工程实用性。
作为自抗扰控制的重要组成部分,基于扩张状态观测器的控制方法因其对系统模型的依赖性低而具有重要的工程实用价值[18-20]。另外,由于自身的强鲁棒性,滑模变结构控制策略作为一种非常实用的方法被用于许多实际系统的控制[21-26],而电力系统正是工程实际系统,因此结合扩张状态观测器为七阶混沌电力系统设计滑模变结构控制器,从而抑制整个系统中的混沌振荡,具有重要的工程化意义。
1 扩张状态观测器及控制器设计
1.1 扩张状态观测器设计
考虑受控的一阶非线性系统
式中,x为系统(1)的状态变量; f ( x) 为任意可微的已知非线性函数;g ( x) 为控制增益函数,g ( x) ≠0 ;u 为待设计的控制输入。
对于式(1),令 y =f ( x),则式(1)表述为
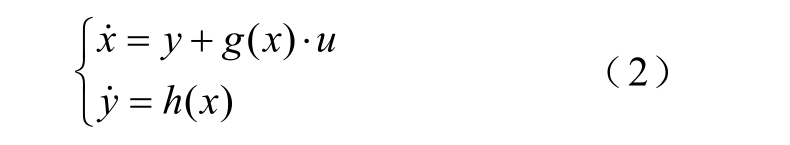
式中,h(x)为函数 f ( x) 的导数。
假设函数 h ( x) 有界,则可以针对式(2)设计二阶扩张状态观测器为[20]
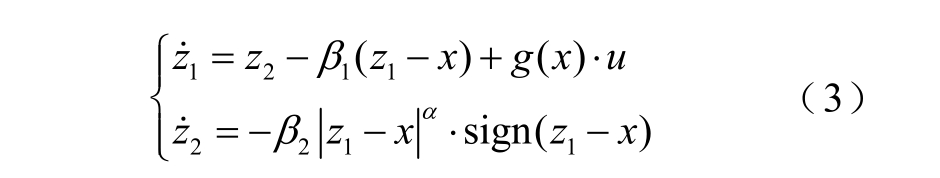
式中, 1z 及 z2 为扩张状态观测器的状态变量,分别表示式(2)中状态变量x与y 的观测值; 1β 、 2β 及α 为待设计的常值参数,并且满足 β1 0>,β 2 0> ,0≤ α≤1 。
在扩张状态观测器(3)的观测作用下, z1 、 z2分别以一定的精度逼近状态变量x 与y,设观测误差为 e1 = x - z1,e 2 = y - z2,则必然存在正的常数 d 1、d 2,使得不等式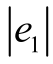 ≤ d1和
≤ d1和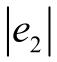 ≤ d2成立。
≤ d2成立。
1.2 控制器设计
为了得到控制器的表达式,首先给出所需要的引理及定理。
定理1:对于0<m < 1,设正定函数V≥ 2β > 0,则总有
证明:定理1 重新表述为:对于0< m< 1,如果V≥2β,则恒有:f (V ) = V m - βm - (2 m - 1 )(V - β)m ≥ 0。首先证明函数 f (V )在V≥2β时为增函数,由于f (V )关于V 的导数为

其中

定理2:设V 为连续正定函数,如果其满足微分方程不等式(4),则函数V 将在有限时间内实现一致终结有界稳定,其最终稳定至原点的邻域{V V=2β }之内,即{V V≤2β }。
式中,k>0 。
证明:对于微分方程不等式  ≤-k (V m -βm ),当V≥2β时,由定理1 可得
≤-k (V m -βm ),当V≥2β时,由定理1 可得

设变量w 收敛至0 的时间为 st ,对式(7)两边积分可得
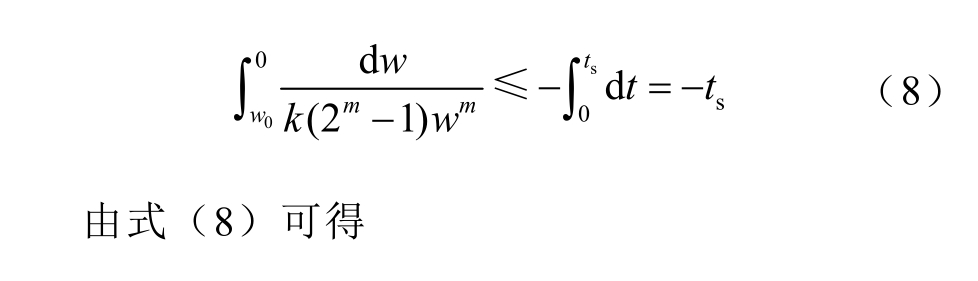
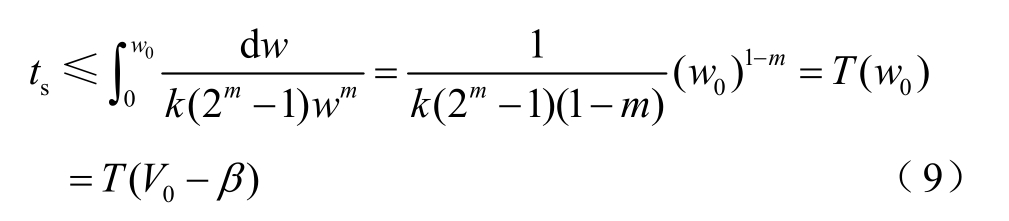
式中, w0 为w 的初始值; V0 为V 的初始值。
式(9)表明正定函数V 将在T (V 0 )的有限时间内 稳 定 至 原 点 的 邻 域 =2β }之 内, 即 有
=2β }之 内, 即 有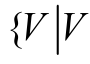 ≤2β },并且该邻域的大小可以通过改变β 值进行人为调节。
≤2β },并且该邻域的大小可以通过改变β 值进行人为调节。
引理1[27]:对于任意χ ∈R 及任意常数ε>0 ,总有
定理3:对于式(1),设其控制目标为原点,如果控制输入的表达式设为式(10),则x将以有限时间收敛于原点的邻域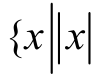 = 2
= 2 之内, 即
之内, 即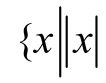 ≤ 2
≤ 2 ,且 γ= {K μ ε [
,且 γ= {K μ ε [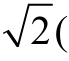 K - d2)]}2。
K - d2)]}2。
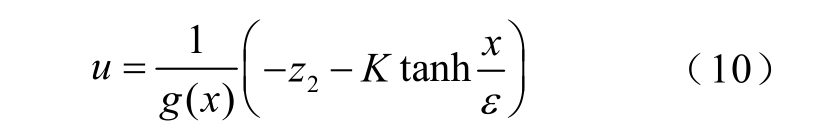
证明:对于式(2),如果控制输入为式(10),则式(2)中的第一个式子表述为
构造李雅普诺夫函数: W =x 2 2,求取该函数关于时间的导数,并考虑到引理1 的不等式,将其表达为
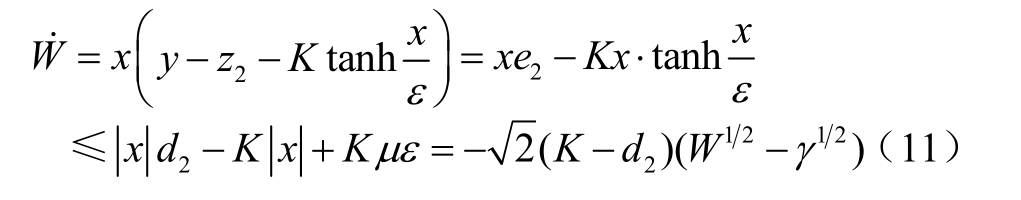
式中, γ= {K μ ε [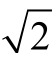 ( K - d2)]}2。
( K - d2)]}2。
对于式(11),如果选取参数K,使得 K> d 2,则由定理 2 可得W 将最终收敛至原点的邻域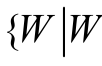 =2γ }之内,即有{
=2γ }之内,即有{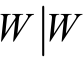 ≤2γ },这表明变量x将收敛于原点的邻域
≤2γ },这表明变量x将收敛于原点的邻域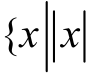 = 2
= 2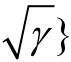 之内, 即
之内, 即 ≤
≤  ,并且邻域的大小与参数ε 成正比。为了使邻域尽可能小以获得比较高的控制精度,应尽可能减小ε 参数的值。值得说明的是,参数ε 的选取会对控制器的控制效果具有重要的影响。该参数的取值不能太小,这是因为当ε 的值太小时tanh( x )ε越逼近符号项sign( x) ,会使控制器出现抖振;然而该取值也不能太大,由定理3 可知,ε 取值太大时会使控制精度变差。具体参数选取时,参数ε 的选取应该在保证控制精度的基础上不至于使控制输入出现抖振为宜。
,并且邻域的大小与参数ε 成正比。为了使邻域尽可能小以获得比较高的控制精度,应尽可能减小ε 参数的值。值得说明的是,参数ε 的选取会对控制器的控制效果具有重要的影响。该参数的取值不能太小,这是因为当ε 的值太小时tanh( x )ε越逼近符号项sign( x) ,会使控制器出现抖振;然而该取值也不能太大,由定理3 可知,ε 取值太大时会使控制精度变差。具体参数选取时,参数ε 的选取应该在保证控制精度的基础上不至于使控制输入出现抖振为宜。
2 基于扩张状态观测器的混沌控制器设计
考虑七阶电力系统模型[12-17],为该模型引入储能装置的动态模型[28],进而得到十阶受控电力系统动力学模型为

式中, mδ 与 sm 分别为发电机的功角与转差;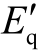 与dE′分别为发电机q 轴与d 轴的暂态电动势;Efd 为发电机励磁电动势; Lδ 与 LV 分别为负载母线电压的相角与幅值;P es1 为接入发电机母线的储能装置吸收的有功功率; Pes2 与Qes 分别为接入负载母线的储能装置吸收的有功功率及无功功率;T es 为储能装置时间常数; upes1 为接入发电机母线的储能装置控制输入;u pes2 与 uqes 分别为接入负载母线的储能装置控制输入;Kpes1 、Kpes2 与Kqes 分别为对应的控制增益。
与dE′分别为发电机q 轴与d 轴的暂态电动势;Efd 为发电机励磁电动势; Lδ 与 LV 分别为负载母线电压的相角与幅值;P es1 为接入发电机母线的储能装置吸收的有功功率; Pes2 与Qes 分别为接入负载母线的储能装置吸收的有功功率及无功功率;T es 为储能装置时间常数; upes1 为接入发电机母线的储能装置控制输入;u pes2 与 uqes 分别为接入负载母线的储能装置控制输入;Kpes1 、Kpes2 与Kqes 分别为对应的控制增益。
受控系统式(12)的变量中, Pg 、 I d、 I q、V t、P、Q 均是状态变量的函数,变量之间的具体耦合关系详见文献[12-17],系统其他变量均为常值参数。常值参数中, Pm = 1.363,V r ef = 1.12,Q 0 =0.6,其他参数取值均引自文献[14]的表1。受控系统式(12)的初值选为

控制器投入运行前,令u pes1 = 0,uqes = 0,u p es2 = 0,则 Pes1 = 0, Qe s = 0, Pe s2 = 0,在给定系统参数及初值条件下七阶电力系统呈现混沌振荡状态,混沌吸引子如图1 所示。

图1 七阶电力系统混沌吸引子
Fig.1 Chaotic attractor in seven dimensional power system
稳定运行的电力系统中绝不允许混沌吸引子的出现。为抑制系统中的混沌振荡,必须使得整个受控电力系统恢复到同步运行状态并将其负载母线电压控制到额定值。这样,受控电力系统式(12)的控制目标设定为 (δ m , s m ,δ L , VL ) = (0,0,0,1),由此确定系统的输出为 y 1 = δm, y 2= δL , y3 = VL。
观察受控电力系统式(12),可以看出有功功率Pe s1响应状态变量 s m的变化、无功功率Qe s响应状态变量 δ L的变化、有功功率 Pe s2及无功功率Qe s共同响应状态变量 VL 的变化。利用这种规律性,就可以为系统设计控制器。为了利用滑模控制方法对系统式(12)进行控制,设计滑模函数为

式中, k1 、 k2 、 k3 、M 均为正的常数。
结合式(12)与式(13),得到三个滑模函数关于时间的导数为

式中,![]() f pes1、f qes及f pes2为含有复杂系统函数导数的表达式,即
f pes1、f qes及f pes2为含有复杂系统函数导数的表达式,即
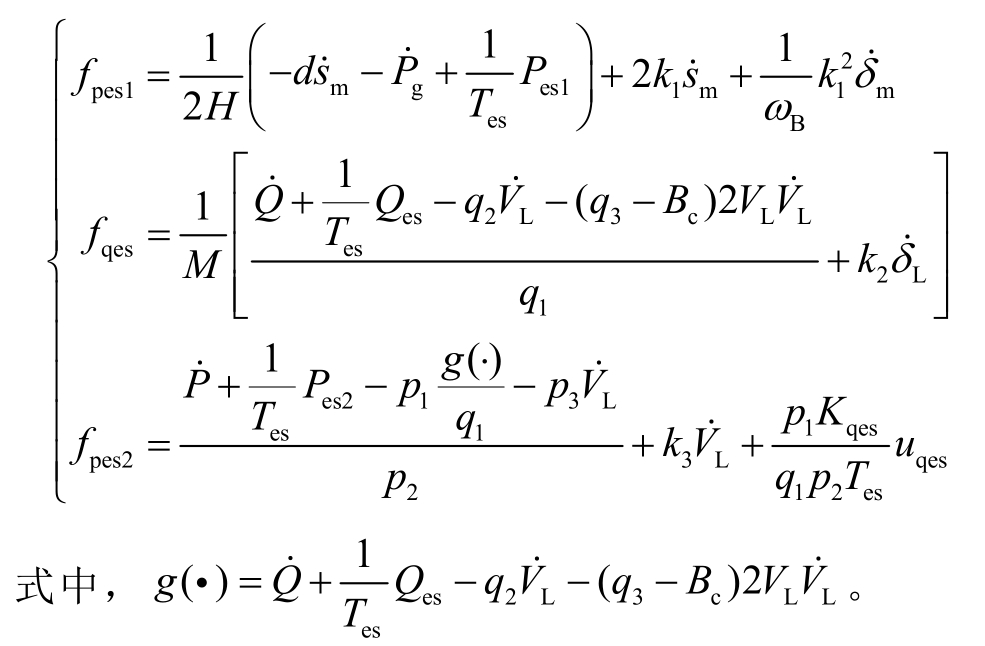
注意到式(14)中的三个方程都具有式(1)的形式,根据为式(1)设计扩张状态观测器的方法可以将式(14)的第一个方程表述为

假设函数 1h 有界,则根据上述扩张状态观测器及控制器的设计方法,为式(15)设计的扩张状态观测器及控制器表述为

假设函数 2h 有界,则为式(17)设计的扩张状态观测器及控制器表述为

假设函数 3h 有界,则为式(19)设计的扩张状态观测器及控制器表述为
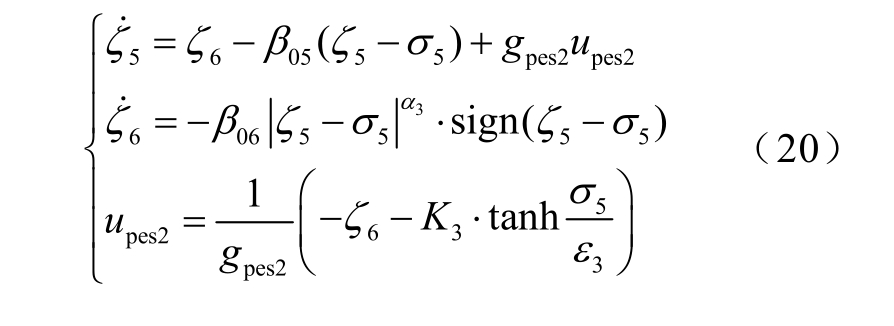
这样,受控电力系统的动力学模型相当于由结合受控十阶电力系统式(12)及观测器式(16)、式(18)和式(20)得到的一个十六阶的动力学系统模型。值得注意的是,按照常规方法设计控制器时控制输入中必然含有复杂的系统函数导数项f pes1、f qes及 f pes2;而基于扩张状态观测器设计的式(16)、式(18)及式(20)中的控制输入却不包含这些复杂系统函数导数信息。
3 控制效果数值仿真
本文通过仿真验证所设计观测器及控制器的有效性。观测器式(16)、式(18)及式(20)的初始值取为 ζ1 (0) = 0, ζ2 (0) = 0, ζ3 (0) = 0, ζ4 (0) = 0,ζ5 (0) = 0, ζ6 (0) = 0。储能装置常值参数为Kpes1 = 5,K pes2 = 5, Kqes = 5, Tes = 1。观测器及控制器参数取为 β01 = 10,β 02 = 10,β 03 = 10,β 04 = 10,β 05 = 10,β06 = 10, α1 =0.5,α2 =0.5, α 3 =0.5,K1 = 10,K2 = 10,K 3 = 10,k 1 = 5,k 2 = 5,k 3 = 5,ε 1 = 0.01,ε2 = 0.01,ε 3 = 0.01,M= 50。在电力系统运行过程中,让所设计的控制器在第20s 投入运行,则可以得到图2~图7 的数值仿真结果。图2 给出了所设计的滑模函数及其观测值,在控制器的控制作用下,系统式(12)的状态到达滑模面,并且观测器可以很好地观测到滑模函数的值。图3 给出了控制器投入运行后七阶电力系统的时域响应波形,每个状态变量均恢复到平衡态,即恢复到稳定运行状态,这时整个电力系统的混沌振荡得到有效抑制。图4 给出了控制器投入运行后储能装置的时域波形。定性来说,状态变量 Pes1 及Qes 的稳态值为正值,状态变量 Pes2 的稳态值为负值,这说明接入发电机母线处的储能装置从电力系统中吸收了一部分有功功率,接入负载母线处的储能装置为负载母线提供了一部分有功功率而从负载母线吸收了一部分无功功率,从而使整个系统的混沌振荡得到控制。重点说明的是,为了满足本文储能装置的时域响应要求,需要综合考虑储能装置最大充放电功率、装置容量、平滑调节效果以及经济性要求来选择合适的储能装置[29]。图5 给出了控制器投入运行后扩张状态观测器的时域波形,其每个状态变量也均能够恢复至稳定状态。图6 给出了受控电力系统由混沌吸引子沿着特定轨线逐渐演化为相空间中不动点的演化过程。具体地,图6a 与图6b 分别表明系统状态在 δm -sm 相平面与 δL-VL相平面中逐渐演化为不动点O1 (0,0)与O2(0,1)。当然,如果绘制出其他相平面或者相空间,仍然可以得到系统状态由混沌吸引子演化为相平面或相空间中的不动点。图7 则给出了所设计的控制输入的波形,控制输入波形比较平滑,没有出现滑模控制中广泛存在的抖振现象。
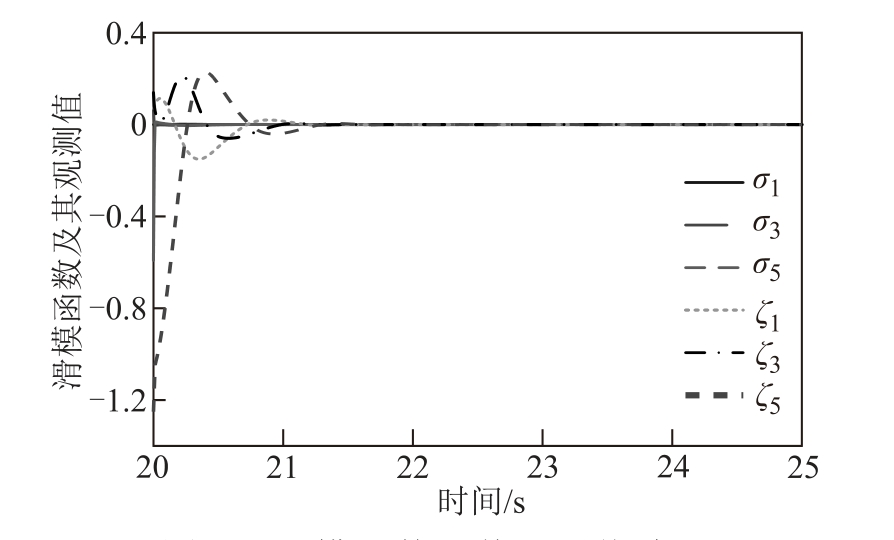
图2 滑模函数及其观测值波形
Fig.2 Sliding mode functions and their observed values
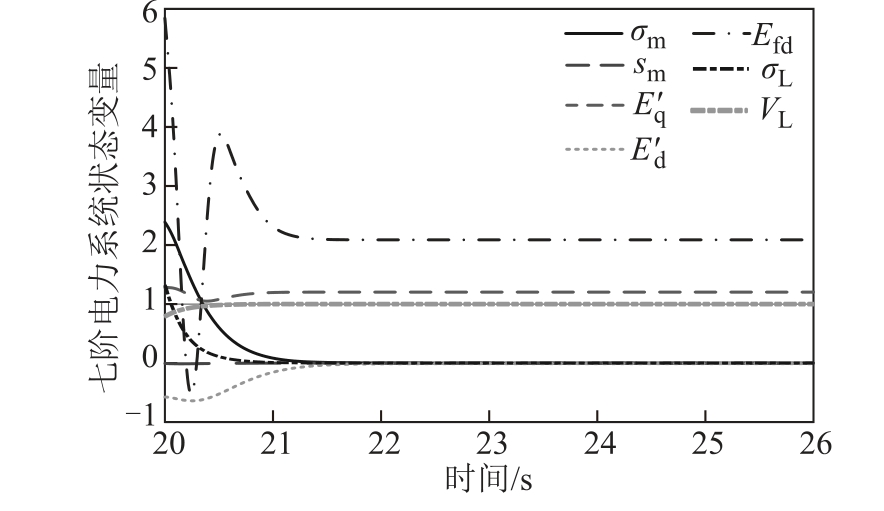
图3 控制器投入运行后七阶电力系统的时域响应波形
Fig.3 Time responses of the seven-dimensional power system after controllers are put into operation

图4 控制器投入运行后储能装置的时域响应波形
Fig.4 Time responses of energy storage devices after controllers are put into operation

图5 控制器投入运行后扩张状态观测器的时域响应波形
Fig.5 Time responses of extended state observers after controllers are put into operation
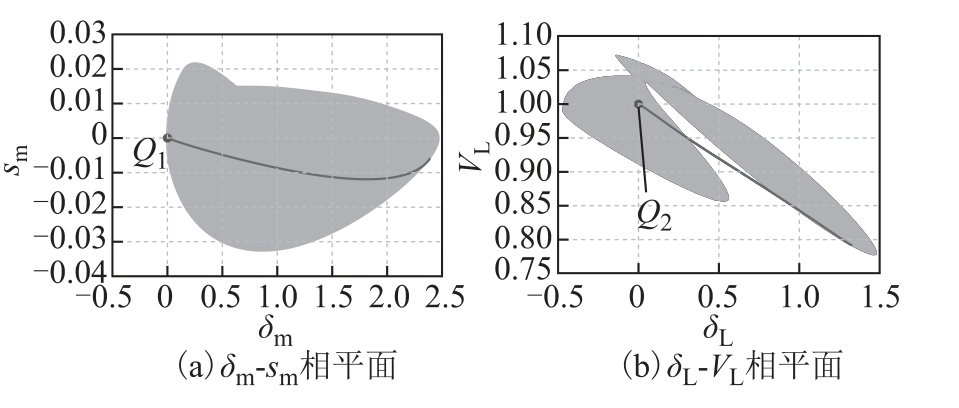
图6 受控电力系统状态演化过程
Fig.6 State evolution process of the controlled power system

图7 七阶电力系统控制输入
Fig.7 Control inputs for seven-dimensional power system
4 结论
1)基于已有的扩张状态观测器设计方法,为一阶非线性系统设计的控制器能够使其状态变量以有限时间收敛于原点的邻域之内,并且邻域的大小可以通过改变相应的常值参数进行人为调节。
2)为七阶电力系统引入储能装置的动态模型,从而调节系统中的有功功率及无功功率,并设计相应的滑模变结构控制器,使电力系统恢复到同步运行,并将其负载母线电压控制到额定值,能够有效抑制整个电力系统的混沌振荡。经过本文给出的基于扩张状态观测器的滑模变结构控制器的设计过程,受控电力系统本质上形成了一个复杂的十六阶电力系统动力学系统模型。当所设计的控制器投入运行之后,受控电力系统的十六个状态变量均能够恢复到平衡态,这时电力系统也就恢复到了稳定运行状态。
3)为七阶混沌电力系统所设计的控制输入不包含受控电力系统复杂系统函数的导数,大大减少了控制输入对于受控系统模型的依赖性,从而有效提升了所设计控制器的工程实用性。
[1] Srivastava K N, Srivastava S C. Elimination of dynamic bifurcation and chaos in power systems using FACTS devices[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications,1998, 45(1): 72-78.
[2] Harb A M, Abdel-Jabbar N. Controlling Hopf bifurcation and chaos in a small power system[J].Chaos, Solitons and Fractals, 2003, 18(5): 1055-1063.
[3] Ginarsa I M, Soeprijanto A, Purnomo M H.Controlling chaos and voltage collapse using an ANFIS-based composite controller-static var compensator in power systems[J]. International Journal of Electrical Power & Energy Systems, 2013,46: 79-88.
[4] 王宝华, 杨成梧, 张强. 电力系统分岔与混沌研究综述[J]. 电工技术学报, 2005, 20(7): 1-8.Wang Baohua, Yang Chengwu, Zhang Qiang.Summary of bifurcation and chaos research in electric power system[J]. Transactions of China Electrotechnical Society, 2005, 20(7): 1-8.
[5] 李文磊. 不确定混沌电力系统的鲁棒自适应跟踪控制[J]. 电机与控制学报, 2007, 11(2): 170-173.Li Wenlei. Robust adaptive control of chaotic power systems with uncertainty[J]. Electric Machines and Control, 2007, 11(2): 170-173.
[6] Ni Junkang, Liu Chongxin, Liu Kai, et al. Variable speed synergetic control for chaotic oscillation in power system[J]. Nonlinear Dynamics, 2014, 78(1):681-690.
[7] 闵富红, 马美玲, 翟炜, 等. 基于继电特性函数的互联电力系统混沌控制[J]. 物理学报, 2014, 63(5): 1-8.Min Fuhong, Ma Meiling, Zhai Wei, et al. Chaotic control of the interconnected power system based on the relay characteristic function[J]. Acta Physica Sinica, 2014, 63(5): 1-8.
[8] Ni Junkang, Liu Ling, Liu Chongxin, et al. Fixed-time dynamic surface high-order sliding mode control for chaotic oscillation in power system[J]. Nonlinear Dynamics, 2016, 86(1): 401-420.
[9] Wang Jiangbin, Liu Chongxin, Wang Yan, et al. Fixed time integral sliding mode controller and its application to the suppression of chaotic oscillation in power system[J]. Chinese Physics B, 2018, 27(7): 1-8.
[10] Ma Caoyuan, Liu Jianhua, Wang Chonglin. Chaos of a power system model and its control[J]. Journal of Vibration and Control, 2012, 18(14): 2176-2185.
[11] Ni Junkang, Liu Ling, Liu Chongxin, et al. Fast fixedtime nonsingular terminal sliding mode control and its application to chaos suppression in power system[J].IEEE Transactions on Circuits and Systems II:Express Briefs, 2017, 64(2): 151-155.
[12] Rajesh K G , Padiyar K R . Bifurcation analysis of a three node power system with detailed models[J].International Journal of Electrical Power & Energy Systems, 1999, 21(5): 375-393.
[13] Yu Yixin, Jia Hongjie, Wang Chengshan. Chaotic phenomena and small signal stability region of electrical power systems[J]. Science in China Series E Technological Sciences, 2001, 44(2): 187-199.
[14] Yu Yixin, Jia Hongjie, Li Peng, et al. Power system instability and chaos[J]. Electric Power Systems Research, 2003, 65(3): 187-195.
[15] 贾宏杰, 余贻鑫, 李鹏. 电力系统环面分岔与混沌现象[J]. 中国电机工程学报, 2002, 22(8): 6-10.Jia Hongjie, Yu Yixin, Li Peng. Torus bifurcation and chaos in power systems[J]. Proceedings of the CSEE,2002, 22(8): 6-10.
[16] 贾宏杰, 余贻鑫, 李鹏, 等. 电力系统混沌现象与不同失稳模式之间的关系[J]. 中国电机工程学报,2003, 23(2): 1-4.Jia Hongjie, Yu Yixin, Li Peng, et al. Relationships of power system chaos and instability modes[J].Proceedings of the CSEE, 2003, 23(2): 1-4.
[17] Wang Jiangbin, Liu Ling, Liu Chongxin, et al. Fixedtime synergetic control for a seven-dimensional chaotic power system model[J]. International Journal of Bifurcation and Chaos, 2019, 29(10): 1-14.
[18] Li Shihua, Yang Jun, Chen Wenhua, et al. Generalized extended state observer based control for systems with mismatched uncertainties[J]. IEEE Transactions on Industrial Electronics, 2012, 59(12): 4792-4802.
[19] Huang Yi, Luo Z W, Svinin M, et al. Extended state observer based technique for control of robot systems[C]//The 4th World Congress on Intelligent Control and Automation, Shanghai, 2002: 2807-2811.
[20] 韩京清, 张荣. 二阶扩张状态观测器的误差分析[J].系统科学与数学, 1999(4): 465-471.Han Jingqing, Zhang Rong. Error analysis of the second order ESO[J]. Journal of Systems Science and Mathematical Sciences, 1999(4): 465-471.
[21] 罗德荣, 贺锐智, 黄守道, 等. 单定子双转子盘式对转永磁同步电机动态滑模控制[J]. 电工技术学报, 2019, 34(9): 1806-1814.Luo Derong, He Ruizhi, Huang Shoudao, et al.Dynamic sliding mode control for single stator dual rotor disc counter-rotating permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1806-1814.
[22] 李鹏瀚, 王杰, 吴飞. 双馈风电机组次同步控制相互作用的反馈线性化滑模变结构抑制[J]. 电工技术学报, 2019, 34(17): 3661-3671.Li Penghan, Wang Jie, Wu Fei. Sub-synchronous control interaction mitigation for DFIGs by sliding mode control strategy based on feedback linearization[J].Transactions of China Electrotechnical Society, 2019,34(17): 3661-3671.
[23] 张迪, 魏艳君, 杨宗丰, 等. 不平衡电网电压下基于滑模变结构控制的双馈风电系统转子侧变流器控制策略[J]. 电工技术学报, 2016, 31(17): 121-131.Zhang Di, Wei Yanjun, Yang Zongfeng, et al. Slidingmode control for rotor-side converters of DFIG-based wind-power generation system under unbalanced grid voltage conditions[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 121-131.
[24] 王德贵. 永磁同步电机调速系统的模糊趋近律滑模控制[J]. 电气技术, 2015, 16(3): 10-14.Wang Degui. Sliding mode control based on fuzzy reaching law of PMSM drive system[J]. Electrical Engineering, 2015, 16(3): 10-14.
[25] 张国荣, 侯立凯, 彭勃, 等. 柔性多状态开关反馈线性化滑模控制[J]. 电力系统自动化, 2020, 44(1):126-133.Zhang Guorong, Hou Likai, Peng Bo, et al. Feedback linearization sliding mode control strategy for soft open point [J]. Automation of Electric Power Systems,2020, 44(1): 126-133.
[26] 龚鸿, 王渝红, 李媛, 等. D-STATCOM 的输入-输出反馈线性化滑模变结构控制[J]. 电力系统自动化, 2016, 40(5): 102-108.Gong Hong, Wang Yuhong, Li Yuan, et al. An inputoutput feedback linearized sliding mode control for DSTATCOM[J]. Automation of Electric Power Systems,2016, 40(5): 102-108.
[27] Polycarpou M M, Ioannou P A. A robust adaptive nonlinear control design[J]. Automatica, 1996, 32(3):423-427.
[28] Fang Jiakun, Yao Wei, Chen Zhe, et al. Design of antiwindup compensator for energy storage-based damping controller to enhance power system stability[J]. IEEE Transactions on Power Systems,2014, 29(3): 1175-1185.
[29] 万乐. 风电场储能装置容量及最大充放电功率的确定[J]. 江西电力职业技术学院学报, 2012, 25(2): 17-20.Wan Le. Determination of capacity and maximum charge and discharge power of energy storage device in wind farm[J]. Journal of Jiangxi Vocational and Technical College of Electricity, 2012, 25(2): 17-20.