0 引言
干式变压器体积小、质量轻,具有抗短路能力和良好的电气性能,在工程中得到了广泛应用。干式变压器绕组一般由环氧树脂整体浇注而成,导热性能比较差,绕组内部的产热和散热情况不均衡,加之负载过大、运行时间长等因素,致使热点问题突出。变压器温升过高不仅会加速绝缘老化,诱发绕组匝间短路造成电击穿等事故,长期过热运行还会造成结构件烧损或者机械变形损伤[1]。
精准预估大功率变压器在漏磁影响下的绕组和结构件损耗,模拟运行工况下的变压器温升特性,对于提升变压器磁热设计并降低局部过热危害具有重要的意义。由于箔式绕组具有特殊的薄片结构,在漏磁场影响下,绕组表面电流密度分布极不均匀,端部具有明显的趋肤效应,损耗的总量增加和不均匀分布一直是工程难点问题[2]。文献[3]和文献[3]的方法广泛应用于变压器绕组损耗计算中,这些方法利用解析式求解简化几何中的微分方程来表征趋肤效应和邻近效应。随着三维有限元分析方法(Finite Element Method, FEM)的引入与计算机数值计算的快速发展,基于A-V-A 和T-ψ 等涡流场有限元法[5-7]逐步在工程上得到采用,以解决导体区域的非线性和电导率各向异性的涡流损耗计算问题。
对于变压器的温度场计算,工程上一般采用GB/T 1094.7—2008 和IEEE Standard C57.91—2011标准中的经验公式[8],根据变压器容量和散热方式给定不同的温度系数来计算变压器瞬态热点温升,操作快速简单但是计算精度较低,且未考虑变压器结构对温度分布的影响。基于热点类比理论的热路模型[9-10]更加符合变压器实际的传热过程,通过计算热容、热阻等参数,将变压器结构等效为热路计算模型,适用于热点温度的精确计算,但是参数的选取基于大量的实验结果,建模过程复杂,工作量大。针对变压器内部的热点分布,国内外学者系统地研究了数值模拟算法[11-13]。为了提高有限元法在求解温度场流-固耦合问题的效率,在求解流体问题时多采用有限体积法[14-15],该方法也是目前变压器温升分布和计算的研究热点。
本文建立了考虑变压器绕组层间气道结构的三维电磁场和温度场计算模型,基于三维瞬态场有限元仿真得到了漏磁通影响下绕组和结构件上的非均匀损耗分布。建立了磁-热-流耦合模型,将磁场节点损耗密度映射至三维流体场中,考虑磁性材料的温度效应,对变压器进行温度场仿真计算,同时通过热电偶多路温度测试仪对变压器进行温升测试实验,验证仿真模型的合理性与准确性。
1 变压器物理模型与实验样机
1.1 样机参数及磁场计算模型
以一台型号为SCB10-2500kV·A/10kV 的双绕组干式变压器为例,建立了如图1 所示的干式变压器三维电磁场模型。干式变压器低压侧为箔式绕组结构,由气道分割为内外三层,高压侧为扁铜线绕组结构,由气道分割为内外两层,轴向分为上下四段,结构件由Q235B 低导磁钢板构成。建模时可忽略机座、垫块和树脂等对磁场分布影响很小的部件,同时考虑到扁铜线难以实现三维精细化建模,电磁计算时直接简化为整块计算,样机具体参数见表1。
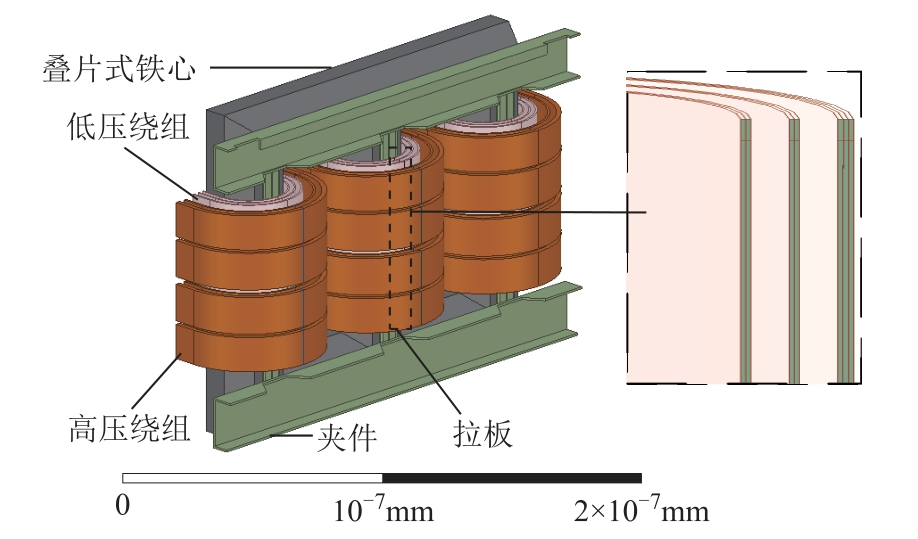
图1 干式变压器磁场计算模型
Fig.1 Magnetic field calculation model of dry-type transformer
表1 样机参数
Tab.1 Parameters of prototype model

?
1.2 温升测试系统
本文对额定负载条件下的变压器功率损耗和温升变化进行了测试实验,温升测试系统包括热电偶多路温度测试仪、红外线热成像仪、热敏风速仪和皮托管流量计等,变压器温升测试平台如图2 所示。采用电力测量分析仪对变压器起动和稳态工况下的电流、电压和阻抗等数据进行了记录。在绕组关键区域埋设热电偶,实时监测并记录变压器运行过程中每一时刻各测温点的温升变化。

图2 变压器温升测试平台
Fig.2 The test platform of temperature rise
2 多物理场耦合数值计算
变压器三维电磁-流体-温度场的耦合计算流程如图3 所示。通过三维瞬态电磁场和流体场计算,得到每个模型网格单元的损耗密度和节点空气流速,通过流体、能量和传导方程的耦合迭代,自动计算出流固耦合面上的对流换热系数,从而进行热场分析。最后根据温升计算结果更新绕组的电阻率,直到迭代过程中相邻两步之间的最大温差小于0.01K。
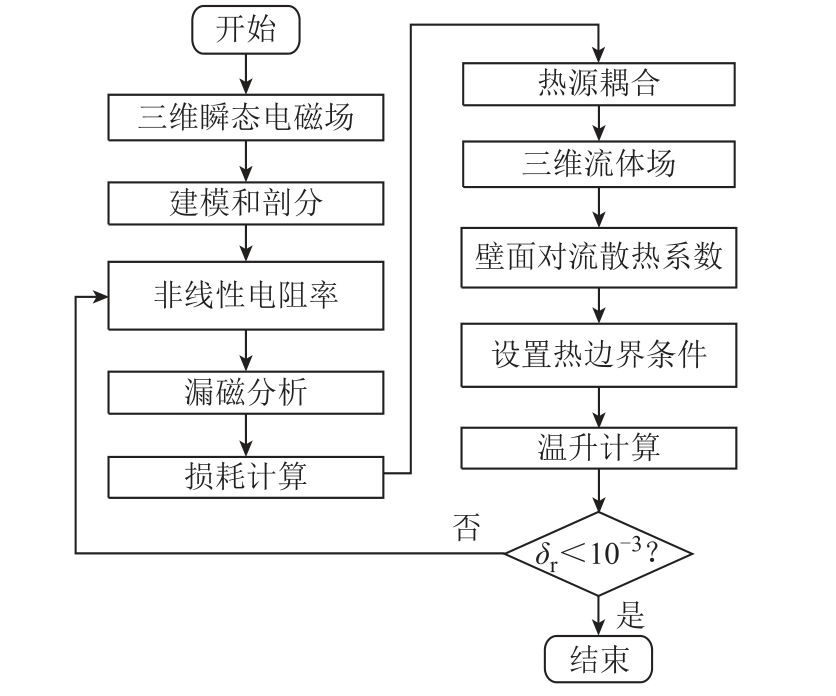
图3 磁-热-流体耦合计算流程
Fig.3 Magnetic-thermal-fluid coupling calculation flow chart
2.1 A-V-A 涡流场计算方法
变压器高压侧为扁铜线绞线结构,绕组损耗主要取决于流经绕组的电流及自身的电阻值,通常忽略其涡流效应。低压侧箔式绕组具有面积大、厚度薄的特点,绕组层间漏磁场使得表面电流分布极不均匀。A-V-A 组合位计算法就是在导体涡流区采用磁矢量位A 和电标量位V,导体区域之外仅采用磁矢量位A,对应求解干式变压器涡流场问题的有限元边值问题控制方程为[16]

式中,v 为磁阻率;σ 为电导率;Jsl 和Jsh 分别为低压绕组和高压绕组的源电流密度。模型中的箔式绕组和结构件可视作涡流区,铁心、高压绕组和周围介质构成非涡流区。
2.2 流体-温度场基本方程
环氧树脂浇注式干式变压器的铁心表面、绕组气道及绕组绝缘外表面与外界空气之间均存在对流换热过程。本文基于Fluent 流体场计算软件求解流-固耦合面的对流换热系数,在热交换过程中,单元表面传热系数h 一般由努赛尔(Nusselt)数进行求解[17],即

式中,kair 为空气热导率;Lp 为变压器本身高度。努赛尔数Nu 综合考虑了对流和热传导的作用,是瑞利数Ra 的特征函数,即

式中,Gr 和Pr 分别为格拉晓夫数和普朗特数,二者用于自然对流流体中;β 为空气热膨胀系数;∆T为变压器表面和外部环境的温差;μair 为空气运动粘度。
变压器铁心与绕组表面、高低压绕组内外表面,以及绕组与绝缘挡板之间同时辐射和吸收热量。本文基于面到面的热辐射模型,采用斯蒂芬-玻耳兹曼方程[18]分析变压器辐射传热过程。斯蒂芬-玻耳兹曼方程为
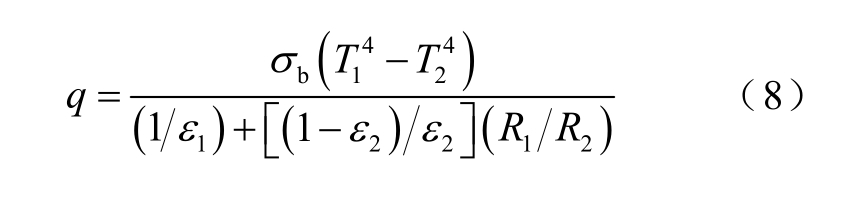
式中,q 为热流率;ε1 和ε2 分别为相邻两个面的发射率;σb 为黑体常数;R1 和R2 分别为两个辐射面的半径;T1 和T2 为两个辐射面的热力学温度。
干式变压器磁-热-流耦合模型主要考虑变压器高低压绕组的电导率随温度变化曲线,在一般的温度范围内,电导率和温度呈线性关系,即
式中, 0T 为参考温度(K);σ Cu 为铜材料电导率(S/m);0σ 为参考温度下的电导率,σ20℃=5.8×107S/m;ζ 为铜材料温度补偿斜率,ζCu = 0.003 93/℃。采用Ansys软件的间接耦合分析功能,基于Ansys Maxwell 的后处理Python 语言建立电磁计算环境和Fluent 流体分析的双向耦合。根据电磁场数据计算绕组涡流损耗,再通过Fluent 二次开发脚本导入热源,求解温度场,并在后处理器中提取绕组温度数据,计算本次迭代的铜材电导率。在下一次迭代开始时,使用新的电磁参数计算下一步电磁损耗,并开启循环迭代过程。
3 计算结果与分析
3.1 变压器电磁损耗分析
为了模拟变压器额定负载试验情况,假设三相电流对称,高、低压侧额定电流值分别为 83.3A、3 608.4A,相位相差180°,绕组电导率设置为温度变化函数。图4 为干式变压器C 相绕组截面磁力线分布情况,绕组漏磁场分布基本呈上下对称,高低压绕组主空道内磁力线分布最密,漏磁场强度最大且以轴向分量为主。在绕组端部磁力线比较密集且部分磁力线发生弯曲使绕组端部产生横向漏磁。按照经验公式,绕组主空道最大漏磁感应强度计算式为
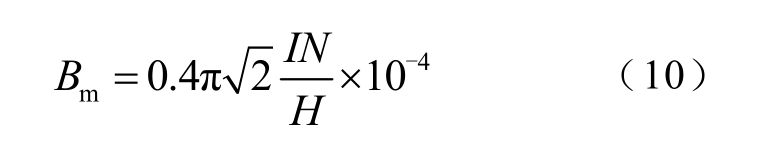
式中,I 和N 分别为绕组电流和匝数;H 为磁路长度,在本模型中表示绕组有效高度。代入相应数据计算得到变压器模型主空道最大电磁感应强度Bm =6.901×10-2T,与有限元方法计算的最大漏磁数值比较,误差控制在2.8%,满足计算精度要求。
低压箔式绕组电流密度分布云图如图5 所示,绕组表面电流密度分布极不均匀,中间部分电流密度值稳定在 2.42×106 A/m2,绕组端部出现显著的涡流效应,电流密度最大值为6.15×106A/m2,高达设计值的2.5 倍。高压绕组段间漏磁的存在使得最外层绕组中部电流密度增大,波峰幅值高达3.42×106A/m。

图4 变压器漏磁场分布
Fig.4 Transformer leakage magnetic field distribution
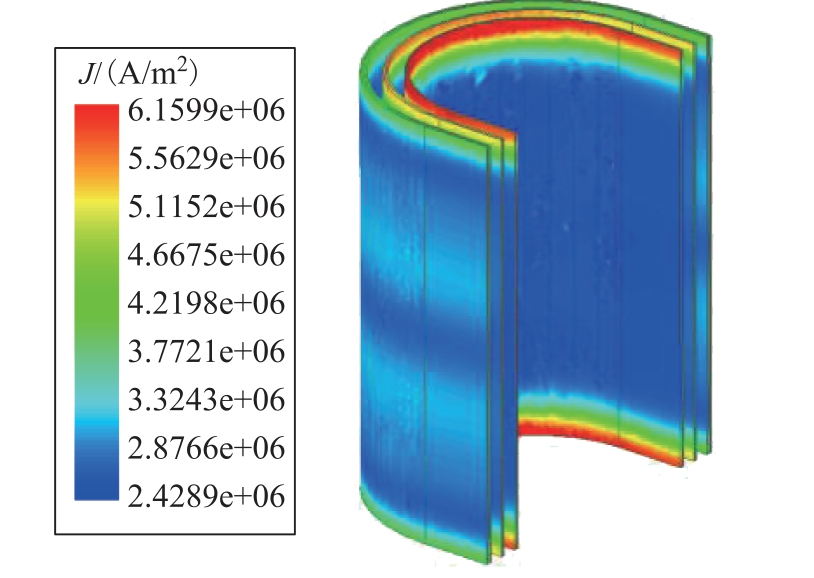
图5 低压箔式绕组电流密度分布云图
Fig.5 Foil winding current density distribution
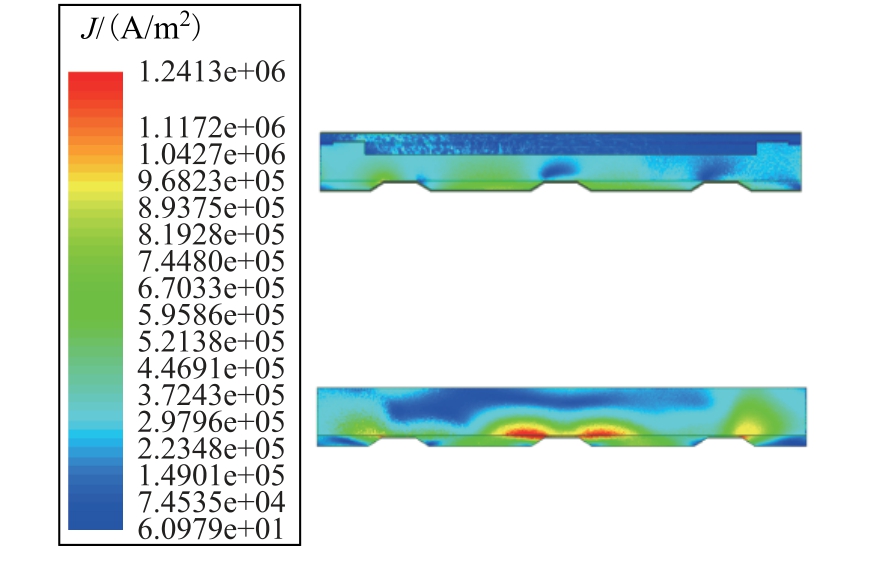
图6 夹件电流密度分布云图
Fig.6 Distribution map of current intensity on clamp
通过漏磁场计算得到上下夹件和拉板的电流密度分布,如图6 和图7 所示。由于高低压绕组之间气道较宽,磁场在端部比较发散,部分漏磁通过夹件形成回路产生涡流。靠近铁心一侧的钢板受到漏磁的影响较大,涡流损耗较为集中。绕组两端部分横向漏磁通穿入拉板形成环流,工程中对拉板进行开槽处理以减少局部涡流效应,图7a 和图7b 分别给出未开槽和开槽结构拉板表面电流密度分布,结果表明开槽结构明显改善了拉板表面环流分布,同时也降低了涡流损耗。

图7 拉板涡流密度分布云图
Fig.7 Distribution map of current intensity on pull plate
3.2 变压器温度场计算模型
不同于电磁场模型,绕组外部包裹的环氧树脂等绝缘材料以及高低压绕组之间的绝缘挡板对温度场影响很大,应该考虑在内。图8 给出了求解负载绕组温升的三维温度场求解域模型,本文只对变压器中间相绕组进行建模,考虑到散热结构的对称性,将其简化为1/4 对称模型进行求解。在建模过程中,考虑夹件结构对风道流速的影响,忽略对变压器散热影响较小的基座部分。
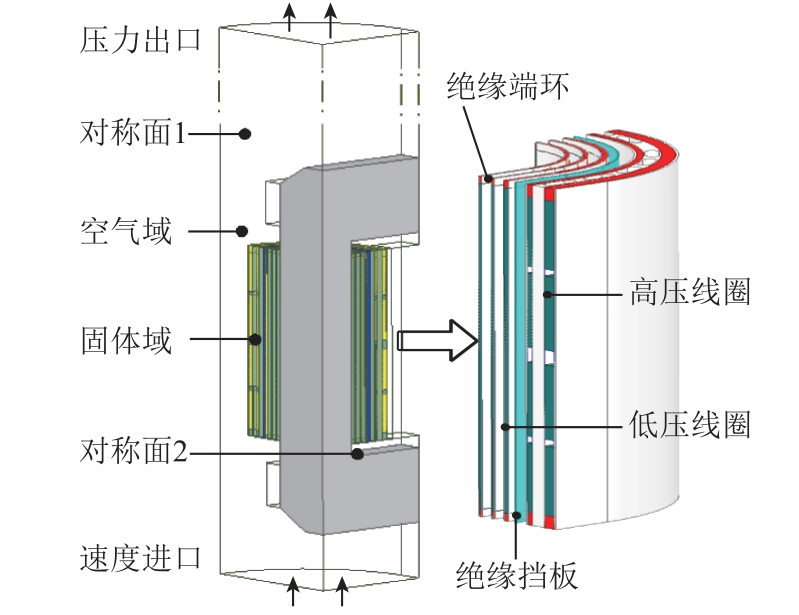
图8 变压器温度场模型
Fig.8 Transformer temperature field model
考虑绕组存在层间纸绝缘无法进行精细化建模,本文参考文献[19]建立了高压绕组等效模型如图9所示,在绕组外侧将导线外绝缘与环氧树脂一起等效,等效绝缘的导热系数计算公式为
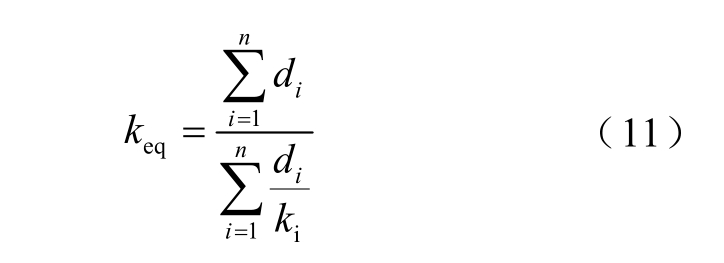
式中,keq 为等效绝缘的导热系数;di 为槽内各绝缘材料的等效厚度;ki 为相应绝缘材料的导热系数。硅钢片、复合聚酯漆、玻璃纤维网格布、树脂和铜导线的导热系数分别为18.0W/(m·K)、0.23W/(m·K)、0.21W/(m·K)、0.276W/(m·K)和398W/(m·K)。

图9 高压绕组等效模型
Fig.9 Transformer temperature field model
3.3 稳态温度场计算结果分析
将电磁损耗计算结果按照网格节点耦合至热场中作为初始热源,模拟空载和满载运行条件下的变压器稳态温升分布,参考实验测试环境,将初始环境温度设置为293K,空气压强指定为标准大气压强101 325Pa,为减少流体场迭代步数,将初始入口速度设置为0.01m/s。图10 给出空气域气流分布和对称面平面流速,可以看出,外部气体从变压器下侧面进入,绕组表面温度较高且气道宽度较窄,导致空气流速较高,但是在结构件和铁轭部分,流通路径受到阻碍,气流流速下降。
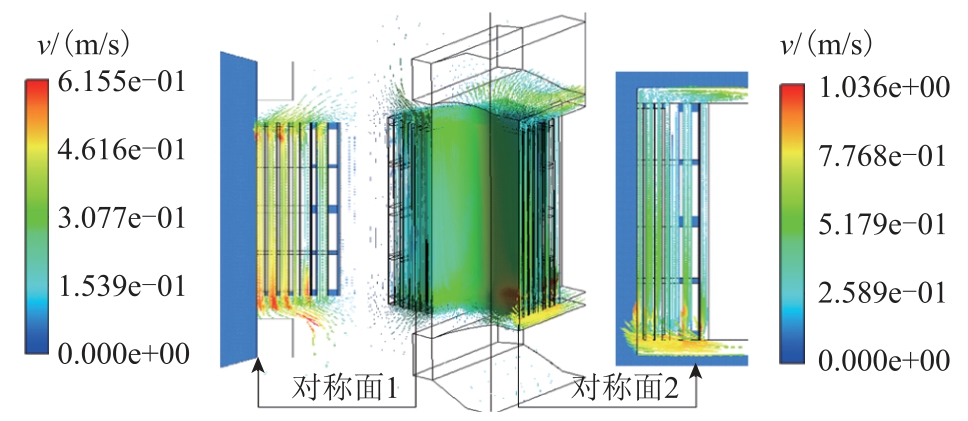
图10 变压器内部流体流速分布
Fig.10 Velocity distribution inside the transformer
图11 给出了变压器整体及绕组温升分布结果,对流散热过程中空气的黏度随温度的升高而变大,受到自身黏度和壁面摩擦的影响,在冷却表面处气体速度逐渐减小,形成换热薄层。壁面粘滞力的加强导致换热层的厚度增加,不利于散热,变压器温升随轴向高度的增加呈上升趋势。高压绕组温度分布规律呈现为四个波峰和五个波谷,四段绕包线沿轴向温度差梯度较大,但每一个绕包线的温差较小,高温区为最外层第一个绕包线,最高温度可达145℃,此时绝缘材料由于热膨胀会发生变形和绝缘破损,容易引发绕组短路故障。波谷产生的原因是绕包线之间留有中空气道,被树脂填充,导热性比较差,致使空气道部分温度下降。
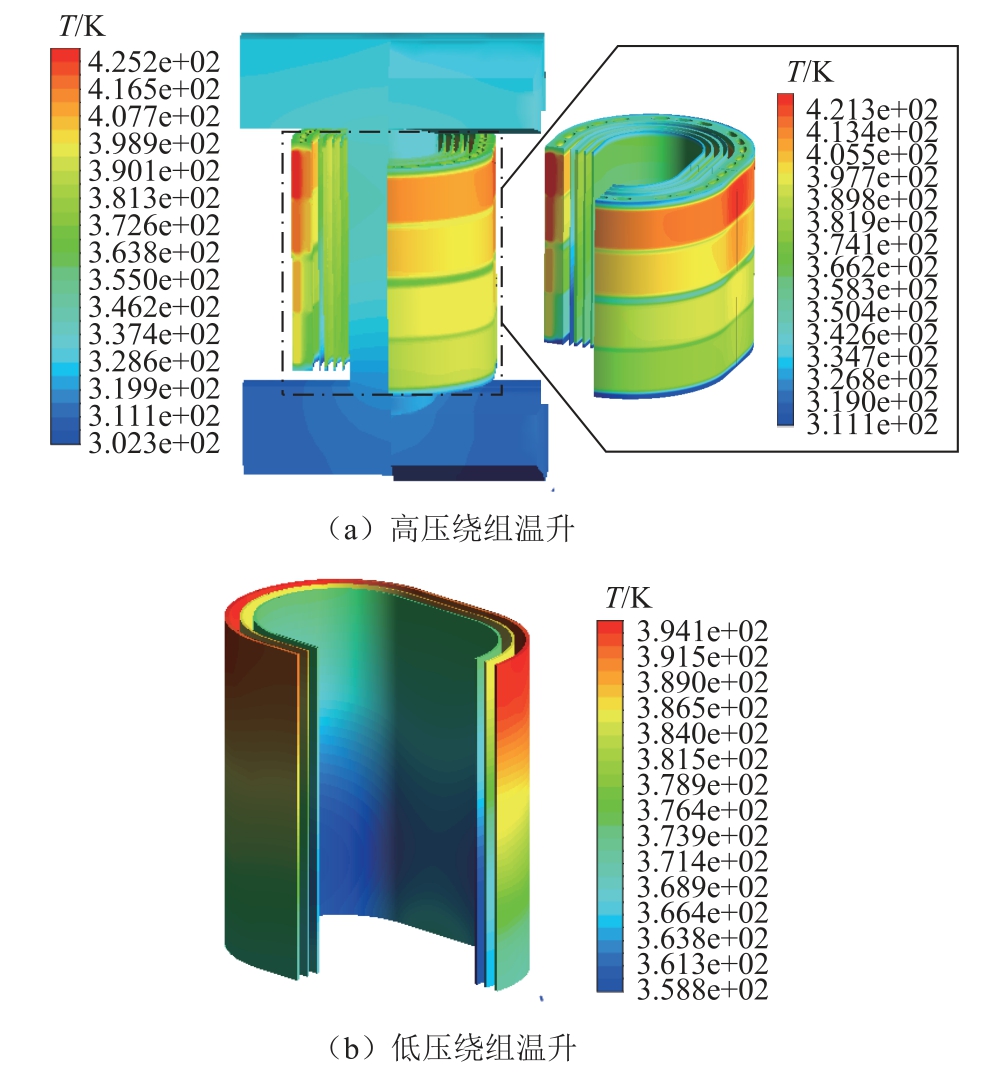
图11 变压器温升分布结果
Fig.11 Transformer temperature rise distribution result
低压箔式绕组高温区出现在外层绕组中上段,最高温度可达121℃,这是由于最外层绕组电磁损耗最大,且受到高压侧较强的热辐射影响。主空道设计绝缘挡板不仅起到电气隔离的作用,同时也降低了高低压绕组之间的热辐射效应。内层绕组部分热量辐射至铁心表面,绕组温度偏低,最低温度为85℃。铁轭上方的矩形绕组区散热困难,上下端部由于涡流损耗的存在会出现局热过热。
结构件温度分布如图12 所示,夹件和拉板的热点温度出现在绕组端部对应区域,相比环境温度的最高温升大约为42K 和37K,温升产生的原因一部分来自局部涡流损耗,一部分来自高温绕组的热辐射。与拉板开槽结构相比,未开槽结构热点更为集中,长期过热容易引发结构件变形或损坏。
3.4 变压器温升测试结果
为了验证变压器多物理场耦合仿真模型的合理性与准确性,本文进行变压器稳态短路温升试验。选取高低压绕组径向不同位置分析其温度变化规律,热电偶埋设位置如图13 所示,测温点位置沿着高、低压绕组轴向15%~85%的高度等距均匀分布。红外线热像仪可以更加直观地观察变压器整体的温升变化过程。经过8h 的运行,变压器各测温点在1h 周期内的温升变化小于1K,此时认为变压器处于稳态运行。
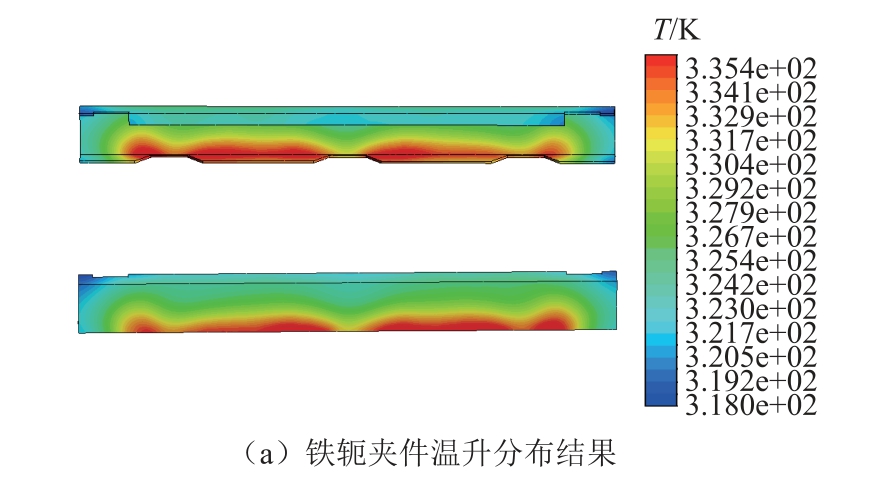
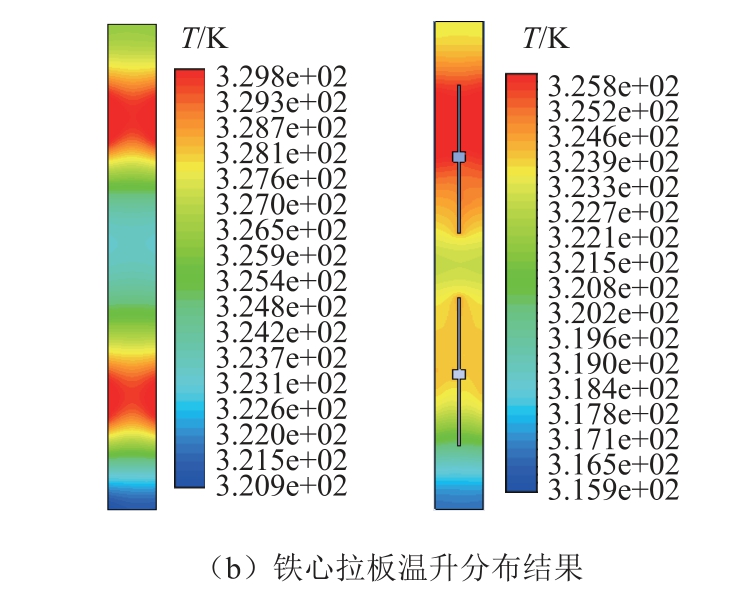
图12 结构件温升分布结果
Fig.12 Temperature rise distribution on structures
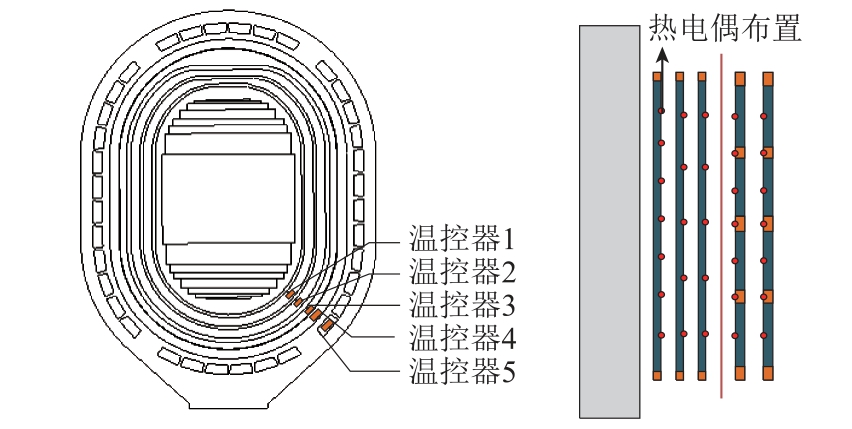
图13 热电偶埋设位置
Fig.13 Thermocouple buried positions

图14 红外线温升测试结果
Fig.14 Infrared temperature rise test results
图14 为红外热像仪成像结果,可以看出,上夹件在靠近绕组的底部区域温度均比较高,维持在70℃左右,高压绕组外表面最热温度高达142℃。图15给出了高、低压绕组对应轴向位置的试验值与仿真值对比结果,可以看到绕组整体温度仿真结果与试验结果吻合得较好,高压侧和低压侧大部分测试点的温度误差控制在±3%和±3.7%以内。温度误差较大的点主要集中在高、低压绕组的底端区域,计算值明显高于实测值,造成误差的原因是建模过程中对夹件结构过于简化,忽略了夹件孔洞和空槽设计对通风散热的影响,该区域测温点仿真值与试验值温度误差控制在±6%,满足工程精度需要。在误差允许范围内验证了计算方法的合理性与准确性。
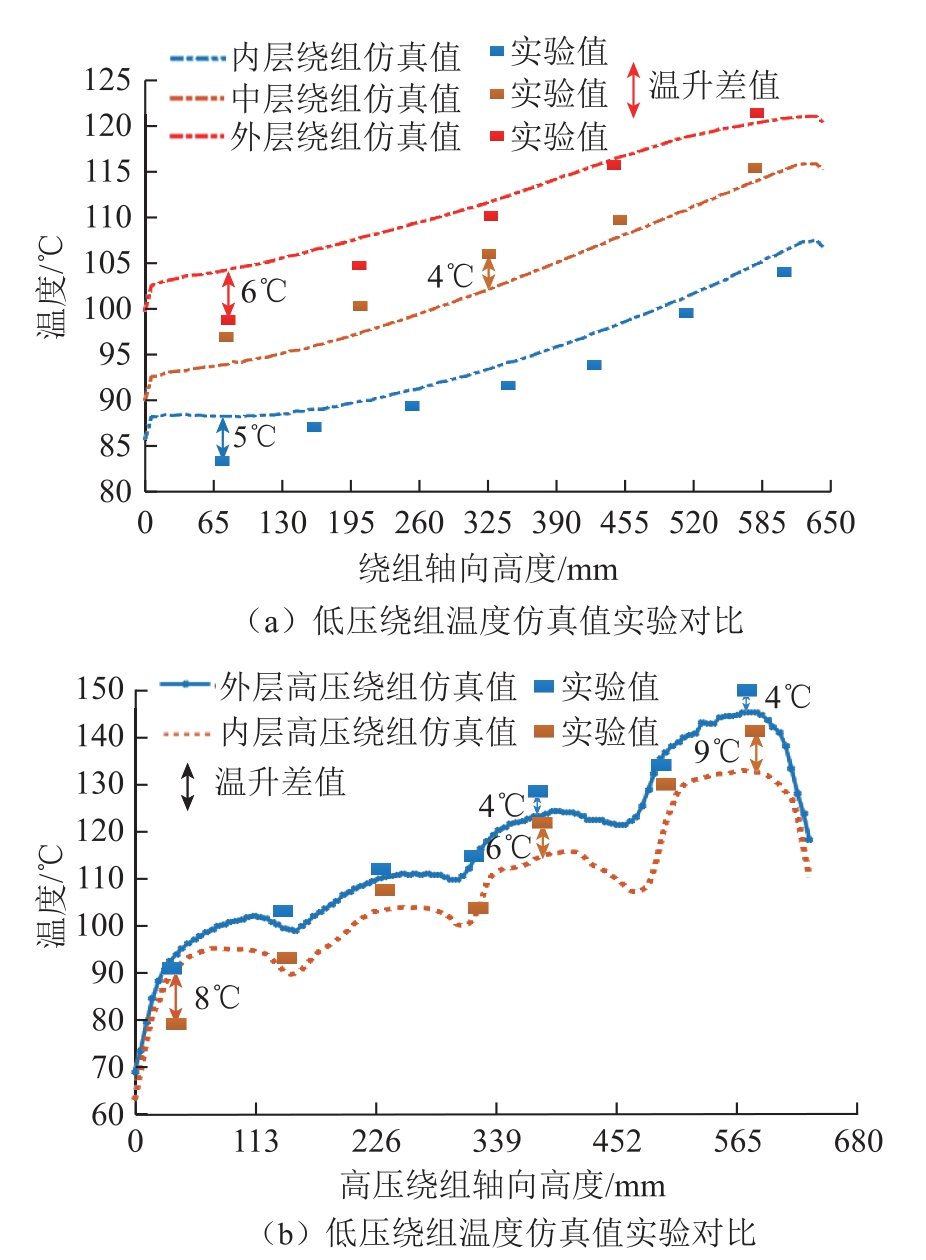
图15 绕组温升仿真值与实验值对比结果
Fig.15 Comparison of simulated and experimental values on winding temperature
4 高压最热饼温度预测
高压饼式绕组结构比较复杂,单根扁铜线外部由聚酯漆薄膜包裹,层间由玻璃纤维绝缘布隔开,绕组外部整体由环氧树脂浇注而成。由于绝缘材料的导热系数非常小,在多导热介质区域的边界层处温度会发生明显的梯度变化。为了预测高压绕组最热饼位置,以变压器C 相绕组为研究对象,建立精细化二维轴对称温度场模型。绕组温升计算可以近似简化为二维轴对称圆柱坐标系中的传热问题[20],绕组部分在导体区域、绝缘区域和边界区域的温度场控制方程分别为
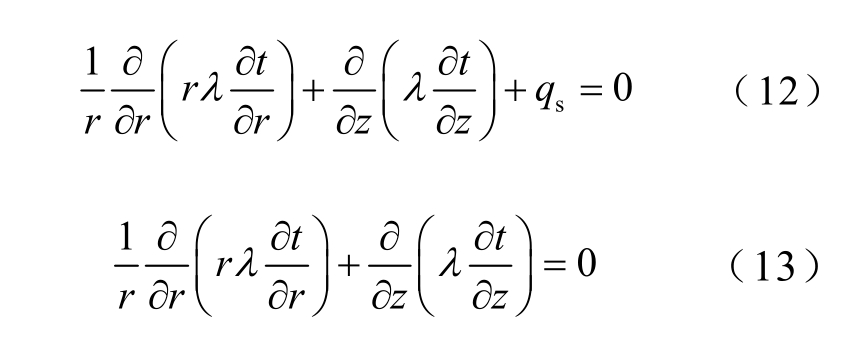
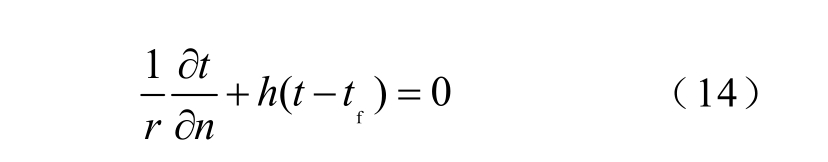
式中,qs 为热源密度;h 为散热系数;t 和tf 分别为物体上的温度和周围介质温度。
图16 给出了变压器二维温度场分布结果和高压最热饼位置预测结果。可以看出二维温升计算结果和三维结果分布基本一致,高压最热饼出现在最外层第一个绕包线的中间两列上部区域,与绕组绝缘表面的温度差达到5℃,最高温度高达150℃,树脂型干式变压器的耐热等级为F 级,可承受的耐热极限为155℃,变压器长期满载运行条件下该区域极易发生绝缘开裂和绕组短路等故障,在初期设计研发阶段应该重点关注。
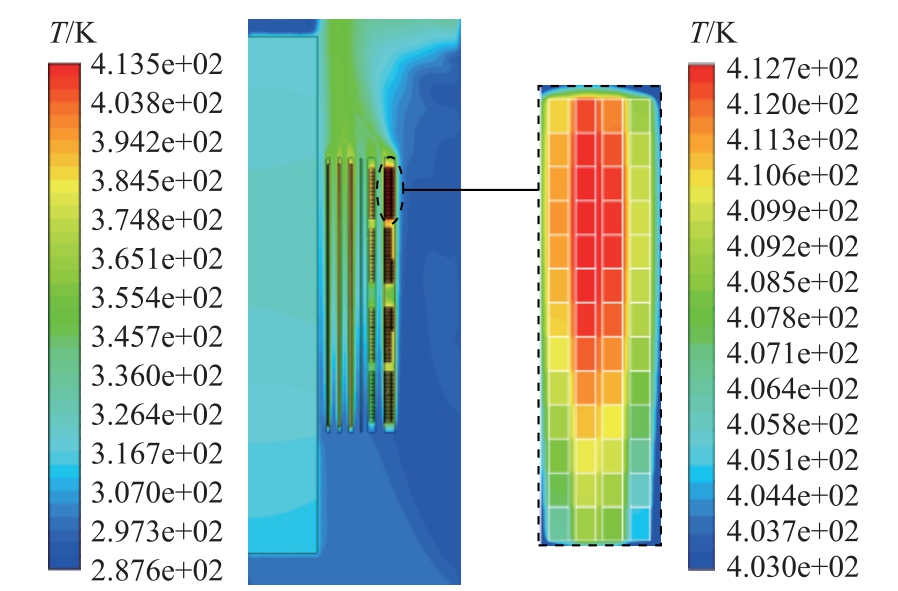
图16 变压器温升分布及最热饼位置预测
Fig.16 Transformer temperature rise distribution and hottest disk position prediction
5 结论
本文基于有限元计算方法,建立了变压器三维电磁场模型并进行漏磁场分析与计算。采用磁-热-流体多物理场耦合方法计算流-固耦合面对流换热系数,并实现变压器温升计算和绕组热点预测,得到以下结论:
1)考虑大容量干式变压器漏磁场影响下的绕组和结构件涡流效应更加符合变压器实际运行状态下的损耗计算和热源分布。
2)变压器低压箔式绕组高温区域位于最外层中上端,最高温度达121℃,高压饼式绕组最热点区域位于外层第一个绕包线中间两列,最热温度可高达150℃,与表面存在5℃左右的温度差。
3)变压器上、下结构件和拉板在漏磁场影响下,表面产生涡流效应,同时在绕组高温辐射下,产生局部过热,最高温升相比于环境温度高达42K。
4)考虑材料温度效应的多物理场耦合方法,克服了传统磁路法损耗计算不准确的问题,能够更好地研究变压器内部热点分布。通过变压器稳态短路温升测试实验,验证了仿真结果的合理性与准确性。
[1] 王有元, 刘玉, 王施又, 等. 电热老化对干式变压器中环氧树脂特性的影响[J]. 电工技术学报, 2018,33(16): 250-260.Wang Youyuan, Liu Yu, Wang Shiyou, et al. The effect of electrothermal aging on the properties of epoxy resin in dry-type transformer[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 250-260.
[2] Diaz G, Mombello E. Semianalytic integral method for fast solution of current distribution in foil winding transformers[J]. IEEE Transactions on Magnetics,2015, 51(9): 1-9.
[3] Dowell P L. Effects of eddy currents in transformer windings[J]. Proceedings of the IEEE, 1966, 113(8):1387-1394.
[4] Ferreira J A. Improved analytical modeling of conductive losses in magnetic components[J]. IEEE Transactions on Power Electronics, 1994, 9(1): 127-131.
[5] 程志光, 李琳, 高生. 电气工程涡流问题的分析与验证[M]. 北京: 高等教育出版社, 2001.
[6] 孟张文, 郑晓钦, 吴新振. 多相感应电机三维电磁分析与损耗计算[J]. 电工技术学报, 2018, 33(增刊2):81-87.Meng Zhangwen, Zheng Xiaoqing, Wu Xinzhen.Three-dimensional electromagnetic analysis and loss calculation of multiphase induction motors[J].Transactions of China Electrotechnical Society, 2018,33(S2): 81-87.
[7] 李龙女, 李岩, 刘晓明. 高压自耦变压器肺叶磁屏蔽特性的数值计算与分析[J]. 电工技术学报,2017(22): 140-149.Li Longnü, Li Yan, Liu Xiaoming. Numerical calculation and analysis of lobe-type magnetic shielding in high voltage auto-transformer [J].Transactions of China Electrotechnical Society, 2017,32(22): 140-149 .
[8] IEC 60076—7—2005 Power transformers-part 7:loading guide for oil-immersed power transformers[S].Switzerland:IEC Central Office, 2005.
[9] 罗汉武, 陈连凯, 姜国义, 等. 涉及环境条件的电力变压器热路模型及其应用[J]. 高电压技术, 2018,44(11): 3561-3568.Luo Hanwu, Chen Liankai, Jiang Guoyi, et al. Thermal circuit model of the transformer considering environment factors and its application[J]. High Voltage Technology, 2018, 44(11): 3561-3568.
[10] 傅晨钊, 汲胜昌, 王世山, 等. 基于有限元法的电缆变压器绕组的暂态热路模型研究[J]. 电工技术学报, 2003, 18(2): 77-82.Fu Chenzhao, Ji Shengchang, Wang Shishan, et al. A study of transient thermal circuit model for the cable transformer coil based on finite element method[J].Transactions of China Electrotechnical Society, 2003,18(2): 77-82.
[11] Wang Qingyu, Wang Haoran, Peng Zongren, et al. 3-D coupled electromagnetic-fluid-thermal analysis of epoxy impregnated paper converter transformer bushings[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(1): 630-638.
[12] Liao Caibo, Ruan Jiangjun, Liu Chao, et al. 3-D coupled electromagnetic-fluid-thermal analysis of oilimmersed triangular wound core transformer[J]. IEEE Transactions on Magnetics, 2014, 50(11): 1-4.
[13] Liu Chao, Gong Ruohan, Ruan Jiangjun, et al.Temperature rise of a dry-type transformer with quasi-3D coupled-field method[J]. IET Electric Power Applications, 2016, 10(7): 598-603.
[14] Rodriguez G R, Garelli L, Storti M, et al. Numerical and experimental thermo-fluid dynamic analysis of a power transformer working in ONAN mode[J].Applied Thermal Engineering, 2017, 112: 1271-1280.
[15] 朱高嘉, 刘晓明, 李龙女, 等. 永磁风力发电机风冷结构设计与分析[J]. 电工技术学报, 2019, 34(5):60-67.Zhu Gaojia, Liu Xiaoming. Li Longnü, et al. Design and analysis of the ventilation structure for a permanent magnet wind generator[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 60-67.
[16] 程志光, 高桥则雄, 博扎德·弗甘尼, 等. 电气工程电磁热场模拟与应用[M]. 北京: 科学出版社, 2009.
[17] Rodriguez G R, Garelli L, Storti M, et al. Numerical and experimental thermo-fluid dynamic analysis of a power transformer working in ONAN mode[J].Applied Thermal Engineering, 2017, 112: 1271-1280.
[18] Lee M, Abdullah H A , Jofriet J C , et al. Temperature distribution in foil winding for ventilated dry-type power transformers[J]. Electric Power Systems Research, 2010, 80(9): 1065-1073.
[19] 王小飞, 代颖, 罗建. 基于流固耦合的车用永磁同步电机水道设计与温度场分析[J]. 电工技术学报,2019, 34(增刊1): 22-29.Wang Xiaofei, Dai Ying, Luojian. Waterway design and temperature field analysis of vehicle permanent magnet synchronous motor based on fluid-solid coupling[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 22-29.
[20] Dejan S, Matti L, Hasse N. Dynamic thermal modelling of power transformers[J]. IEEE Transaction on Power Delivery, 2005, 20(1): 197-204.