0 引言
永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）正越来越多地被应用到电梯、电动汽车、伺服系统等领域，同时人们对其性能的要求也越来越高[1-5]。但是，永磁同步电机及其控制系统内变频电源电压输出波形的谐波含量丰富，波形畸变较大的问题引起了国内外学者关注。
文献[6]将 Boost 变换器应用到单电感双输出的电路中，推导和分析了电路的交叉影响特性。文献[7]为了降低变换器级联的损耗问题，将Boost 变换器应用到二次型变换器中，同时提高了变换器的效率。文献[8]在解决变换器开关应力问题的同时，将Boost 变换器应用到高增益变换器中，提高了变换器的效率。文献[9-11]将Boost 电路作为功率因数校正变换器，进行了相关的研究。但是少有学者将 Boost 变换器引用到变频电源系统拓扑结构中。
在永磁同步电机及其系统的研究方向上，目前诸多学者主要对控制策略及控制算法的提升进行了研究。文献[12]针对永磁同步电机由于变频器的非线性特性给电机电流中引入大量低次谐波，从而导致的电机损耗问题，提出了一种基于补偿电压的算法，能够有效抑制5 次和7 次谐波。文献[13]对变频器谐波给电机带来的损耗进行了研究，最后提出了谐波损耗系数，但对于如何降低电机铁损耗及谐波损耗系数，未从变频器角度做深入研究和说明。文献[14]针对中压变频驱动装置中高次谐波对电机存在影响这一问题进行了相关研究。通过大量的仿真数据并综合考虑了基波压降和有功损耗等问题，给出了滤波器参数的简化公式，但是未对其理论与仿真进行相关实验验证。文献[15]将谐振控制器应用到同步旋转坐标系下的PI 控制器中，以实现对高次谐波的控制，但其研究内容仅限于电网频率，未对变频的情况进行研究。上述研究内容主要集中在电机控制算法与系统控制策略等领域，少有学者考虑变频电源系统内部拓扑结构对输出电压波形谐波给电机产生的影响。
在前人研究基础上，本文提出一种在变频电源整流和逆变环节中加入Boost 变换器的改进控制方法。将Boost 变换器引入变频电源的整流环节和逆变环节之间，并建立改进后的变频电源系统仿真模型。优化结果显示，引入Boost 变换器后，变频电源的输出电压波形质量得到有效提升。在此基础上，分析考虑变频电源输出电压谐波含量对永磁电机铁损耗的影响。最后，设计、制作一台小型变频电源，并搭建实验测试平台，对本文所提方法的有效性进行了验证。
1 PMSM 数学模型及控制系统
1.1 PMSM 控制拓扑及Boost 电路参数计算
随着电力电子开关器件和电机控制技术的发展，晶闸管、MOSFET 和IGBT 等电力电子开关器件也能更好地应用于PMSM 控制系统中。高频率开关器件应用的同时也使永磁同步电机变频调速系统性能越好，越稳定。
永磁电机变频控制系统中常见的拓扑结构如图1 所示。三相交流电经过整流桥变为直流电，直流母线电压经过三相逆变器输出，驱动电机工作。
图1 永磁电机变频驱动器系统拓扑结构
Fig.1 Topology of permanent magnet motor frequency converter driver system
永磁同步发电机、二极管整流桥和逆变电路均具有较强的非线性。而目前的控制策略多为普通的比例积分PI 控制。PI 控制器具有设计简单和适应性好等特点。电机的运行状态发生改变，会导致逆变器的直流侧母线电压发生波动。而PI 调节是一种基于目标误差的控制器，能够保证系统在某一运行状态附近的稳态特性，但正因为如此，其本身忽略了系统的动态性能。当直流母线电压波动以后，电机的运行性能就会发生改变。
1.2 PMSM 数学模型
为了使永磁同步电机能够达到控制性能的需求，需要更加准确的数学模型，永磁同步电机的数学模型包括：电压方程、磁链方程、转矩方程。为了建立合理的数学模型，需要做如下假设：①忽略电动机中的涡流和磁滞损耗，磁路饱和忽略不计；②不考虑转子上的阻尼绕组，PMSM 定子绕组对称且空间上互差120°；③忽略磁路饱和及电机参数的变化，假设三相电流是对称的正弦波。
最终得到两相旋转坐标系下的电压方程为
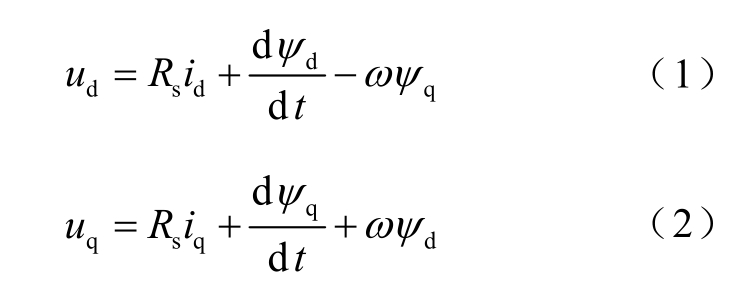
式中，ud、uq 分别为d、q 轴上的电压，id、iq 分别为d、q 轴上的电流， dψ 、 qψ 分别为d、q 轴上的磁链；ω 为角频率。
磁链方程为
式中，Ld、Lq 为d、q 轴上的电感； rψ 为转子永磁体磁链。
电磁转矩方程为
式中， pn 为PMSM 的极对数。
式（5）代入式（6）得到
因此可以发现当转子磁链不变的情况下，PMSM 的转矩仅受d、q 轴电流影响，当d、q 轴电感分量相等时，PMSM 的电磁转矩方程为
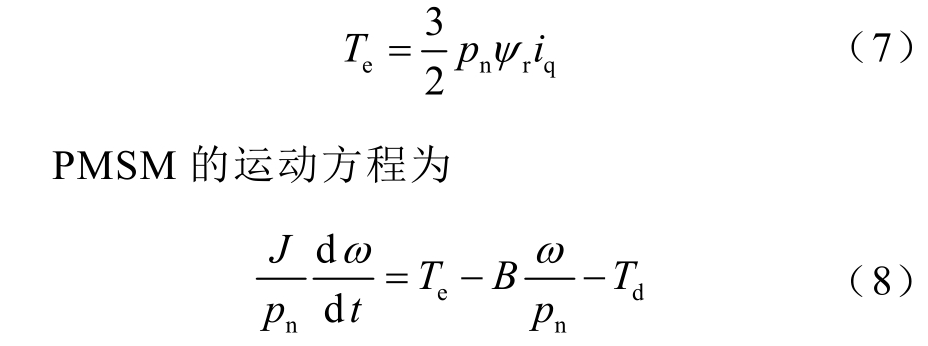
式中，J 为PMSM 的转动惯量；Td 为PMSM 的负载转矩；B 为PMSM 的黏滞摩擦系数。
1.3 PMSM 控制系统
永磁电机矢量控制中常见的控制方式是id=0 的控制方式。此时，从永磁电机的端口看进去，永磁电机等效为一台他励直流电机。id=0 的控制系统框图如图2 所示。
id=0 的控制系统是由外环为转速环、内环为电流环组成。实际速度ω 与给定速度ω*的误差经过PI 调节器输出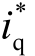
。在内环中，经过Clarke 变换和Park 变换将电流采样得到的三相静止坐标系下的iA、iB、iC 变换为两相旋转坐标系下相互垂直并且独立的id 和iq。
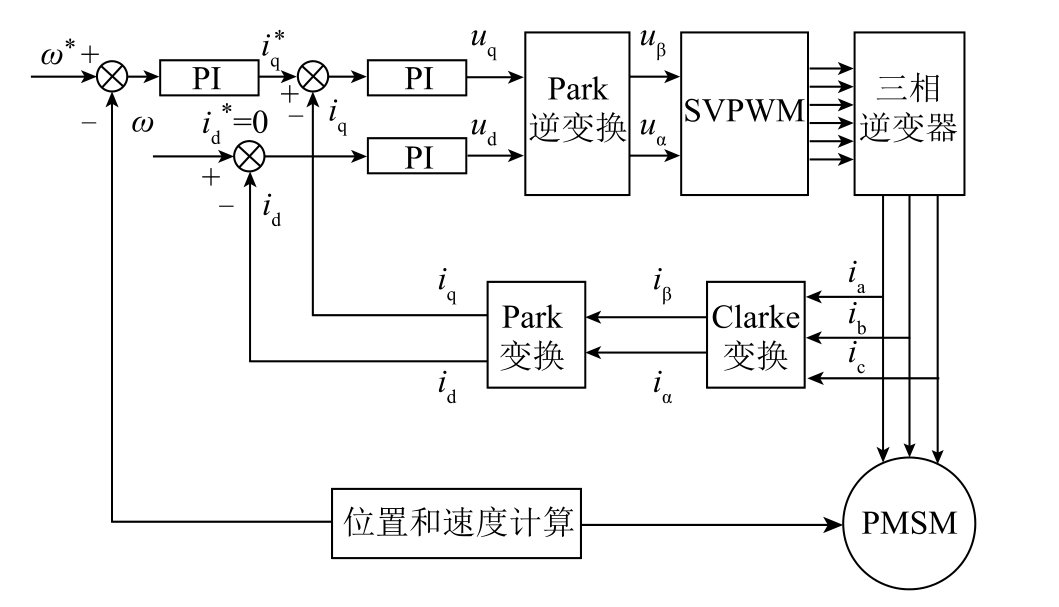
图2 id=0 系统控制框图
Fig.2 The sketch of id=0 system control sketch
反馈电流id 和iq 与给定电流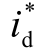
和
的误差经过PI 调节器得到d、q 轴电压ud、uq。经过Park 变换得到αβ 静止坐标系下的uα 和uβ，然后在SVPWM模块中以计算扇区为基础，计算出导通时间，进而控制逆变桥臂的导通和关断实现对电动机的控制。
1.4 Boost 电路参数计算
Boost 的引入位置是在整流环节和逆变环节之间。考虑到Boost 的性质是直流变换器，最终的输出依然是直流，将Boost 归为AC-DC 之中。引进Boost 后的AC-DC 环节如图3 所示。图3 中点画线线框内为引入的Boost 环节，对于Boost 环节采用闭环控制。将Boost 的直流输出采样，用作反馈控制，Boost 采用PI 闭环控制，保证Boost 的直流输出稳定在设定值，不产生较大的波动。
图3 引入Boost 环节的AC-DC 环节
Fig.3 AC-DC link with Boost chopper
Boost 的电路原理如图4 所示。建模之后可以由式（9）求得占空比。
式中， oV 为输出电压； Vin 为输入电压。
电路中滤波电感的选择与负载电流的变化和设定的工作状态相关。设定电路的工作状态要满足电
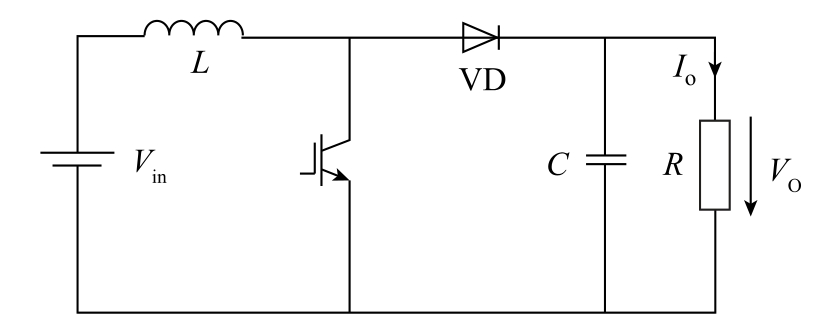
图4 Boost 斩波电路原理
Fig.4 Boost chopper circuit schematic diagram
感的电流工作在连续状态，则临界电感可以表示为
式中，f 为电路工作频率。
而对于滤波电容的选择直接关系到直流输出中纹波电压的大小。
式中， ΔU 为电压纹波。
1.5 傅里叶分解与谐波成分分析
对于系统内的正弦电压，可以对其进行傅里叶级数分解，得到电网基波频率分量的同时，还能得到一系列高于电网频率的分量。对于电压波形，在满足狄里赫利条件时，可以分解为
式中，nω0 为n 次谐波频率；t 为时间；φ为初相位；An 为n 次谐波的幅值。频率与基波频率的比值为对应谐波次数。
通用变频器多为交直交变频器，采用三相整流桥进行整流，以六脉冲整流为常见形式，其波形特点决定其主要的谐波次数为6k+1 和6k-1 次，其中的主要成分是5 次与7 次谐波。在不损失基波幅值的前提下，通过控制和优化策略，最大程度消除或抑制高次谐波。
2 控制系统仿真平台搭建
PMSM 系统总图如图5 所示，前级为AC-DC 整流部分，后级为DC-AC 逆变部分。通过示波器观测三相电压波形，通过三相电压的波形质量可以直观地看出引入Boost 环节对于系统的提升。
图6 是图5 中AC-DC 部分的展开。该部分为三相电源的整流部分，三相电源经此整流为直流，经过直流母线输出至逆变级输入端口。
图5 变频系统仿真结构总图
Fig.5 General structure diagram of frequency conversion system simulation
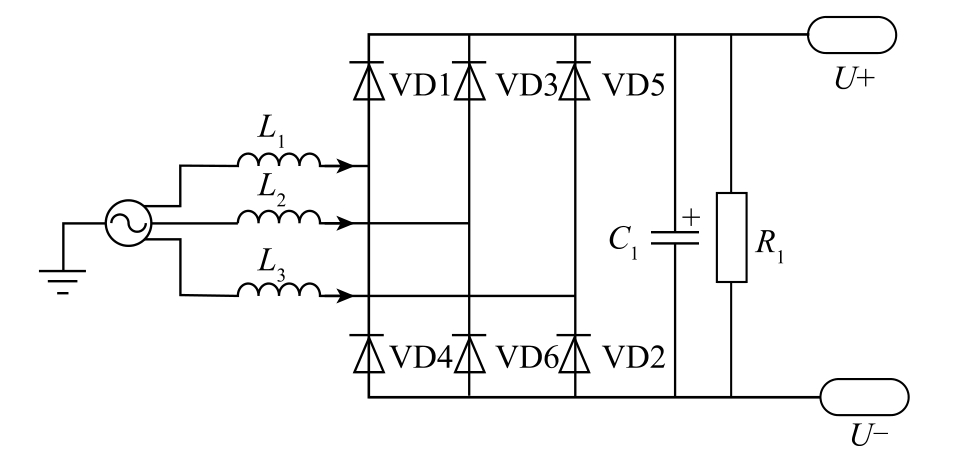
图6 AC-DC 整流部分仿真系统图
Fig.6 AC-DC rectifier part simulation system diagram
逆变级在仿真中采用IGBT 作为开关管，其门级控制信号可编程逻辑控制器芯片作为控制部分。直流母线经逆变输入端口输入直流电流，IGBT 在控制信号的驱动下进行开关动作，直流逆变为三相交流，驱动PMSM 电机工作。控制部分，逆变输出通过采样采集输出电压Ua、Ub、Uc 用作闭环控制，保证三相电压的稳定输出。
图7 中门级驱动信号部分由可编程控制器的模块产生。采集三相输出电压经过坐标变换后产生信号波，输出给DSP，通过与三角波比较产生驱动信号驱动IGBT，完成电源逆变，DC-AC 逆变仿真PWM驱动控制部分如图8 所示。
3 引入Boost 前后的电路与有限元仿真
为了验证所提理论的有效性，建立了小功率下的控制仿真及实物实验，进行对比验证，从数据和波形两方面进行分析。同时为了证明本文方法能够同样适用于其他功率永磁同步电机，特在同样的电压谐波优化前提下建立了140kW 电机的有限元分析，结果表明电机铁损耗有效降低，该方法同样适用。
3.1 引入Boost 前后的电路仿真分析
建立小型变频电源的仿真模型，按照式（8）和式（9）计算，要求Boost 环节输入电压为35V，电流输出为2A，电压输出为50V，开关频率为20kHz，纹波小于 0.5V，并且相应微调电感和电容，则L=330mH，C=1 230μF，占空比为D=0.32。
通过对上述拓扑的数学模型分析搭建仿真环境与仿真平台，观察仿真结果，逆变输出电压波形如图9 所示。
图7 DC-AC 逆变及控制环节仿真系统图
Fig.7 DC-AC inverter and control simulation system
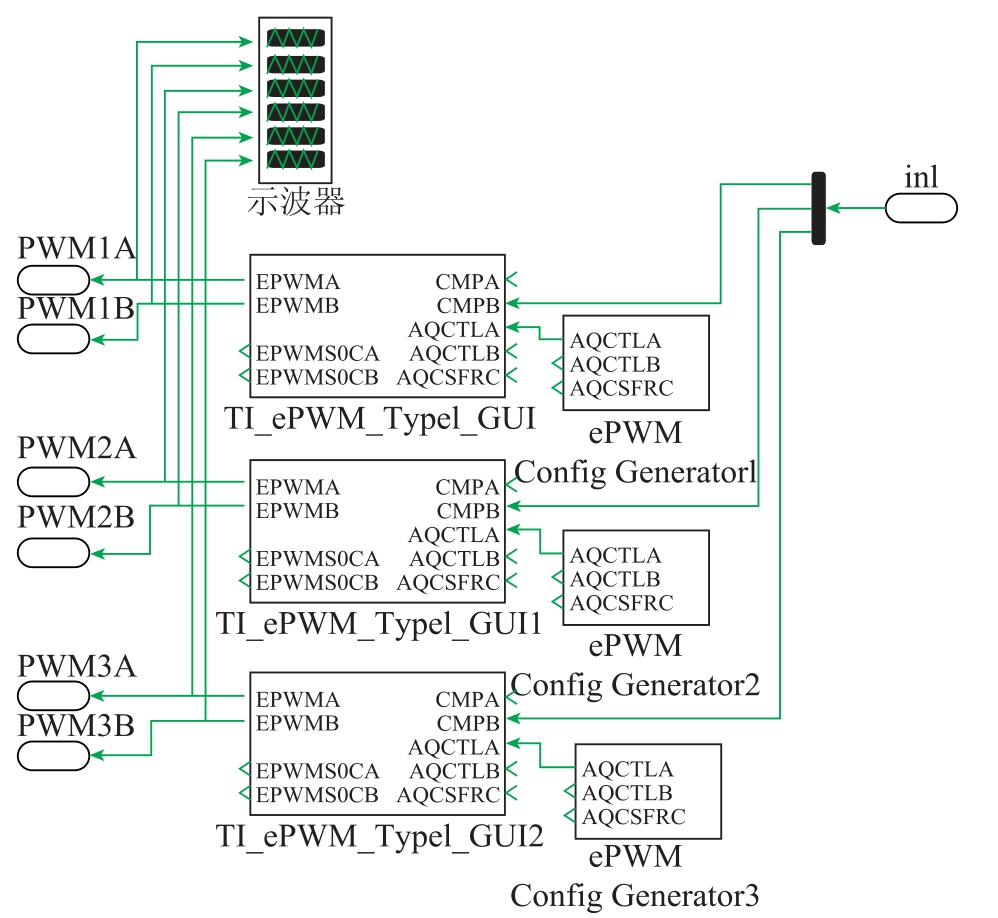
图8 DC-AC 逆变仿真PWM 控制部分
Fig.8 PWM control part of DC-AC inverter simulation
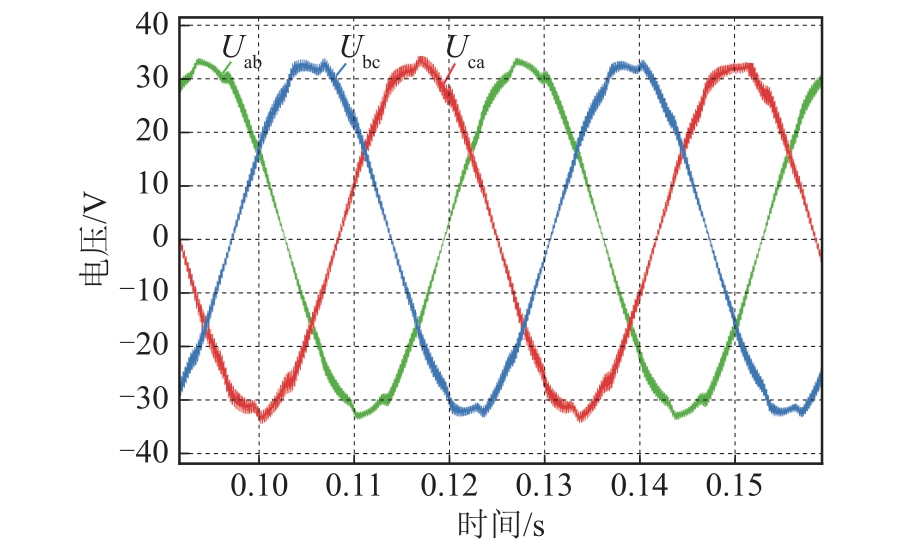
图9 逆变输出电压波形
Fig.9 Inverter output voltage waveforms
观察波形可以看出，电压已经产生了一定程度的畸变，并且在变频器不改变滤波器参数的情况下，电压曲线的毛刺现象明显，作为PMSM 电机的电源，其电源质量开始下降。
上述系统在引入Boost 后的线电压输出波形如图10 所示。可以发现，在加入Boost 电路之后的电压输出波形的质量已经有很大提升，并且电压波形的毛刺现象也有很大程度的减少，电机的电源质量得到了显著提高。
图10 引入Boost 电路后逆变环节电压输出波形
Fig.10 Voltage output waveforms of inverter link after Boost circuit is introduced
3.2 引入Boost 前后铁损耗的有限元仿真分析
为了比较优化前后谐波对于电机铁损耗的影响，通过有限元分析，建立对永磁同步电机的仿真分析模型，对永磁同步电机的铁损耗的数值和分布进行研究分析。电机参数见表1。
表1 永磁电机部分设计参数
Tab.1 Part of design parameters for PM motor
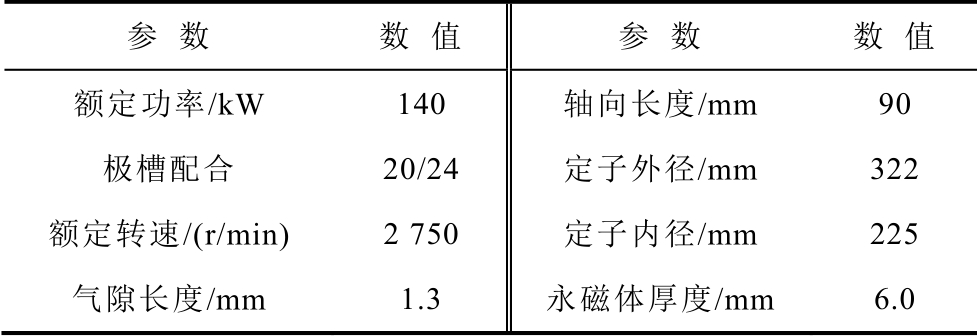
参 数 数 值 参 数 数 值额定功率/kW 140 轴向长度/mm 90极槽配合 20/24 定子外径/mm 322额定转速/(r/min) 2 750 定子内径/mm 225气隙长度/mm 1.3 永磁体厚度/mm 6.0
优化前，电源波形THD 为8.7%，为永磁同步电机供电时，永磁同步电机的定子铁损耗为1 260.3W，损耗的分布情况如图11a 所示，损耗在槽底处较为集中。优化后，电源波形THD 为3.4%，同样条件下，仿真得到铁损耗的分布如图11b 所示，铁损耗降低为1 179.4W，参数的永磁同步电机进行仿真，主要对比分析了优化前和优化后，谐波对于永磁同步电机的损耗的影响。
图11 定子铁损耗分布对比
Fig.11 Distribution comparison diagram of stator iron loss
谐波优化前后的THD 由8.7%降低到3.4%，同时损耗由1 260.3W 降低为1 179.4W。优化后，铁损耗有效降低，降低百分比为6.4%。
4 实验验证
按照Boost 的仿真分析，本次建立了48W 的变频器实验平台如图12 所示，其输出端电压有效值24V，最大输出电流为2A。
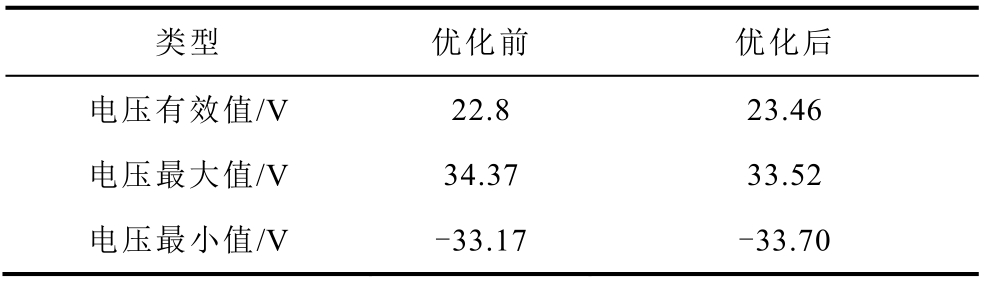
无Boost 环节输出端电压波形如图13 所示。在相同实验条件下，引入Boost 环节，最终得到的波形如图14 所示。输出端电压波形得到了改善，电源的质量得到提升。同样对其进行傅里叶分析，分析结果表明THD 降低为3.43%。优化前后，电压波形数据对比见表2。
图12 变频器实验平台
Fig.12 Inverter experimental platform
图13 无Boost 环节输出端电压波形
Fig.13 No Boost output voltage waveform
图14 引入Boost 环节输出端电压波形
Fig.14 Output voltage waveform with Boost
表2 优化前后电压各项数值对比
Tab.2 Comparative of voltage values
?
对比引入Boost 前后的傅里叶分析结果，可以发现电源质量得到提升，引入Boost 后波形质量提升了60.4%。优化前后各次谐波的幅值对比如15 图所示。
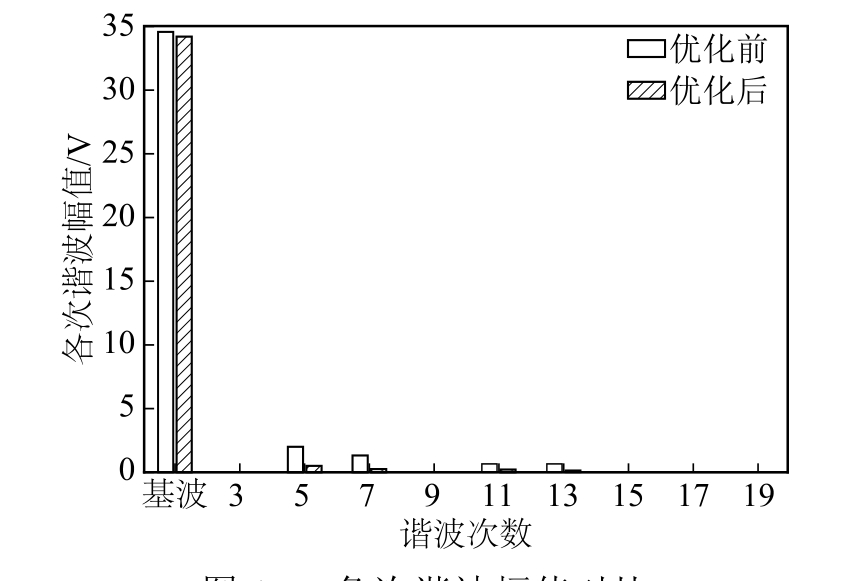
图15 各次谐波幅值对比
Fig.15 Comparison of harmonic amplitudes
对比两次实验分析结果，可以看出，在引入Boost 环节之后电源的质量得到了提升，有效降低了谐波含量。5 次、7 次、11 次、13 次谐波相比之前分别降低了72.5%、81.3%、77.6%、76.0%。电压波形畸变率由优化前8.7%降低为3.4%，但同时基波幅值有所降低，相比优化前，基波幅值降低了0.8%。
5 结论
针对永磁同步电机负载波动时变频器输出电压波形畸变和毛刺问题，提出在整流和逆变环节中间设置Boost 斩波电路的方法，得到如下结论：
1）通过对传统PMSM 变频控制系统的分析与建模，对永磁同步电机变频电源系统进行仿真分析。对引入 Boost 斩波电路前后进行对比分析，引入Boost 变换器后能够有效地提升电源质量，降低电压波形的谐波含量。
2）进行实验验证，通过对实验波形进行傅里叶对比分析，在引入Boost 环节后，输出电压波形的畸变率明显下降，电压波形THD 由8.7%降低为3.4%。
3）在此基础上，分析变频电源拓扑结构优化前后对永磁电机定子附加损耗的影响，结果显示，优化后的永磁电机定子铁损耗降低了6.4%。
[1] Hu Sideng, Liang Zipeng, Wei Zhang, et al. Research on the integration of hybrid energy storage system and dual three-phase PMSM drive in EV[J]. IEEE Transactions on Industrial Electronics, 2018, 65(8):6602-6611.
[2] Zhou Shi, Sun Xiaodong, Cai Yingfeng, et al. Torque analysis and dynamic performace improvement of a PMSM for EVs by skew angle optimization[J]. IEEE Transactions on Applied Superconductivity, 2019,29(2): 1-5.
[3] 杨明, 曹佳, 徐殿国. 基于输入整形技术的交流伺服系统抖动抑制[J].电工技术学报, 2018, 33(21):4979-4986.Yang Ming, Cao Jia, Xu Dianguo. Suppression of vibration of AC servo system based on input shaping technique[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4979-4986.
[4] 朱健, 曹君慈, 刘瑞芳, 等. 电动汽车用永磁同步电机铁心采用非晶合金与硅钢的性能比较[J]. 电工技术学报, 2018, 33(增刊2): 352-358.Zhu Jian, Cao Junci, Liu Ruifang, et al. Comparative analysis of silicon steel and amorphous on the performance of permanent magnet synchronous motors on electric vehicles[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 352-358.
[5] Sun Xiaodong, Hu Chang, Zhu J, et al. MPTC for PMSMs of EVs with multi-motor driven system considering optimal energy allocation[J]. IEEE Transactions on Magnetics, 2019, 55(7): 1-6.
[6] 周述晗, 周国华, 毛桂华, 等. 电流型控制单电感双输出开关变换器稳定性与瞬态特性分析[J]. 电工技术学报, 2018, 33(6): 1374-1381.Zhou Shuhan, Zhou Guohua, Mao Guihua, et al.Stability and transient response analysis of currentmode controlled single-inductor dual-output converter[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1374-1381.
[7] Jorge A, Rodrigo L, Elvia P, et al. Modelling and control of a DC-DC quadratic boost converter with R2P2[J]. IET Power Electronics, 2014, 7(1): 11-22.
[8] 张建丰, 许建平, 周翔, 等. 一种基于辅助网络的软开关二次型Boost 高增益变换器[J]. 电工技术学报, 2017, 32(24): 71-79.Zhang Jianfeng, Xu Jianping, Zhou Xiang, et al. A soft-switched high step-up quadratic boost converter with auxiliary circuit[J]. Transactions of China Electrotechnical Society, 2017, 32(24): 71-79.
[9] 曹勇, 杨飞, 李春晖, 等. 不同耦合系数下的交错并联电流连续模式Boost 功率因数校正变换器的传导电磁干扰[J]. 电工技术学报, 2019, 34(10): 2176-2186.Cao Yong, Yang Fei, Li Chunhui, et al. Conducted electromagnetic interference of interleaved continuous current mode Boost power factor correction converter with different coupling coefficients[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2176-2186.
[10] 陈正格, 许建平, 杨平, 等. 变占空比控制二次型Boost 功率因数校正变换器[J]. 电工技术学报, 2016,31(16): 72-82.Chen Zhengge, Xu Jianping, Yang Ping, et al.Variable duty cycle control quadratic Boost power factor correction converter[J]. Transactions of China Electrotechnical Society, 2016, 31(16): 72-82.
[11] 任小永, 白雷, 惠琦, 等. 一种快速动态响应低电压纹波功率因数校正变换器的控制策略[J]. 电工技术学报, 2019, 34(14): 2936-2945.Ren Xiaoyong, Bai Lei, Hui Qi, et al. Control strategy of power factor correction converter for fast dynamic response and low output voltage ripple[J].Transactions of China Electrotechnical Society, 2019,34(14): 2936-2945.
[12] 纪世忠. 一种永磁同步电机谐波电流抑制算法[J].电力电子技术, 2019, 53(4): 109-114.Ji Shizhong. A novel harmonic current suppression algorithm for permanent magnet synchronous motor[J]. Power Electronics, 2019, 53(4): 109-114.
[13] 佟文明, 孙静阳, 段庆亮, 等. 永磁同步电动机空载铁耗研究[J]. 电工技术学报, 2017, 21(5): 51-57.Tong Wenming, Sun Jingyang, Duan Qingliang, et al.No-load iron loss of permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2017, 21(5): 51-57.
[14] 沈启平, 韩雪岩. 变频器供电下定子磁动势引起的永磁同步电机转子损耗分析[J]. 电工技术学报,2016, 31(4): 51-57.Shen Qiping, Han Xueyan. Rotor loss analysis of the permanent magnet synchronous machine caused by stator magnetomotive force with converter powering[J]. Transactions of China Electrotechnical Society,2016, 31(4): 51-57.
[15] Liserre M，Teodorescu R，Blaabjerg F．Multiple harmonics control for three-phase grid converter systems with the use of PI-RES current controller in a rotating frame[J]. IEEE Transactions on Power Electronics, 2006, 21(3): 836-841.