0 引言
近年来,内置式永磁同步电机(Interior Permanent Magnet Synchronous Machine, IPMSM)以其功率密度高、效率高、调速范围宽等优良性能,在工业传动系统、电动汽车等领域中得到了广泛的应用。目前IPMSM 的典型控制方法,如矢量控制和预测控制,都需要在稳态和动态条件下获得可靠的转子位置信息。但在电机轴上安装位置传感器增加了控制系统的体积、成本及复杂度。为了克服机械传感器的缺点,IPMSM 无位置传感器技术已经成为当前的研究热点[1-2]。最早的无传感器方案基于反电动势估计原理,这些方案在电机运行高速时,可以很好地检测到转子的位置,但在起动及低速时却会失效。这是因为此时反电动势的值太低不足以获得与转子位置相关的可靠信息[3-4]。
为了拓宽无位置传感器的运行范围,基于电机磁路不对称性质的信号注入法被提出,这些方法是将特殊的电压或电流信号叠加在基频激励信号上,从电机的电流响应中检测出转子凸极。这些方法可以获得良好的零、低速位置检测性能。信号注入法分为高频电压信号注入法[5-6]、高频电流信号注入法[7]和电压脉冲注入法[8]等。其中,高频旋转正弦电压注入法因其稳定性强、收敛时间短、收敛点不包括q 轴和收敛点不易发散等优点得到了广泛的应用[9-10]。但传统旋转注入法在解调过程中需要解调函数、同步轴旋转滤波器、低通和带通滤波器等多个环节,不仅增加了算法复杂度,还降低了系统的带宽[11]。与此同时,旋转注入法的位置估计精度易受磁路饱和及交叉耦合效应(以下简称为交叉饱和效应)影响[12]。基于以上问题,学者们已经进行了一些研究。
1)优化注入及解调算法
为了在保留旋转注入法优势的前提下,提高注入频率,减少滤波器的使用,近年来,许多学者提出将高频方波信号注入静止坐标系。文献[13]提出了一种将高频方波电压注入α 轴的无传感器控制策略,这种方法不仅像旋转注入法一样稳定,还像脉振注入法一样简单。然而,这种方法会引起直流偏置误差,需要进行人工补偿。文献[14]提出了正交的方波电压注入方法,补偿了由高通滤波器带来的相位延迟,增加了系统的带宽,但是其解调过程与传统旋转注入法中基于同步轴旋转变换的解调算法类似,包含大量与解调信号相乘的计算过程,计算量大。文献[15]针对正交方波注入方法提出了一种新的解调算法,对一个周期内的四个采样点采用了四种不同的解调公式。这种方法需要精确地知道采样点数,对电流传感器的快速性要求较高。
2)补偿电感误差
为了补偿因电机电感参数变化造成的误差,首先需要对电感参数进行辨识,常见的辨识方法主要有离线法和在线法。其中,离线法需要先由基于理想模型的有限元分析[16]或实验测量和计算[17]得到电感参数离线查询表,并通过离线表进行电感误差的计算和补偿[13,18]。但在电机实际运行中,注入信号幅值与频率,电机工作点、温度、振动及噪声、永磁体退磁等因素都会导致电感参数的变化,进而影响离线表的准确度。因此,基于离线表的补偿方式不能实时适应电感参数的变化,可能会导致错误的补偿。
许多学者也提出了基于电机动态模型和现代控制理论的电感参数在线辨识方法,例如电流导数和电压估算法[19]、递归最小二乘法[20]、仿射投影算法[21-22]和模型参考自适应法[23]等,这些方法适用于在矢量控制或者基于反电动势预估的中高速无传感器控制方法中对电感参数进行在线辨识,缺少注入高频电压时的算法收敛性分析,不能直接用于高频信号注入法。除此之外,交叉饱和效应还与注入信号的类型、幅值及频率有关[19],因此,需要针对不同信号注入法的特点设计不同的在线辨识方案。文献[24]提出了一种基于高频脉振电压注入三相静止坐标系的电感误差在线辨识方法,但没有对不同负载下的动态特性进行验证。文献[25]提出了一种动态电感辨识方法,但这种方法只适用于传统的高频正弦信号注入法。综上所述,在优化解调算法的同时研究适合于不同注入方法及工况下的电感误差在线辨识算法具有实际应用价值。
本文提出了一种考虑了交叉饱和效应的IPMSM 无传感器优化方法。首先,采用基于离散电流的特征分析方法,对高频正交方波注入法的信号分离及解调算法进行了优化,不仅消除了滤波器带来的幅值衰减和相位滞后,并且计算量小、实时性高。然后,提出了针对旋转方波注入法的电感误差在线辨识方法,并将辨识结果补偿到位置估算中,提高了位置观测精度。
1 考虑磁路饱和的IPMSM 高频电压模型
IPMSM 在d、q 轴上的电压方程为
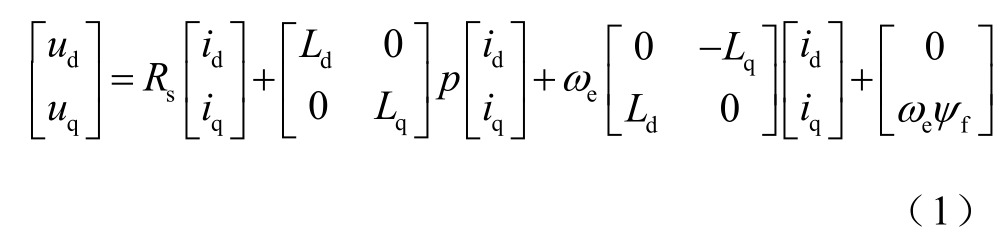
式中,ud、uq 和id、iq 分别为d、q 轴电压和电流;Ld、Lq 分别为d、q 轴电感;Rs 为定子电阻; fψ 为永磁体磁链;ωe 为电机转子电角速度;p 为微分算子。
在高频电压信号注入法中,当注入载波电压的频率远高于基波频率时,定子电阻Rs 上的压降、反电动势及旋转电压都可以忽略不计,在这种情况下,IPMSM 的定子绕组可以看作是纯电感。另外式(1)中的第二项是对高频电流求导,其值远远大于其他项[24],因此,IPMSM 中高频信号的电磁关系可以简化为

式中,udh、uqh 和idh、iqh 分别为d、q 轴高频电压和电流分量。
在电机的实际运行过程中,随着电流的增大,d、q 轴磁链容易饱和,导致Ld、Lq 的变化。与此同时,由于d、q 轴磁链之间存在共磁路,产生的互感Ldq、Lqd也会随着磁链饱和程度的变化而变化。因此,考虑到交叉饱和效应,式(2)被重新表示为
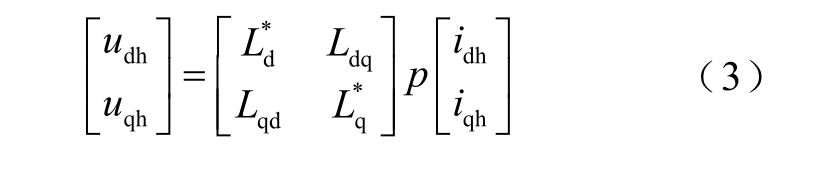
式中,Ldq 和Lqd 为与交叉耦合效应相关的互感,Ldq 通常被认为与 Lqd 相同[12]; L*d =Ld+Δ Ld, L*q=Lq+Δ Lq,“Δ ”代表因磁路饱和引起的变化。
然后,借助坐标变换矩阵T(θe),即
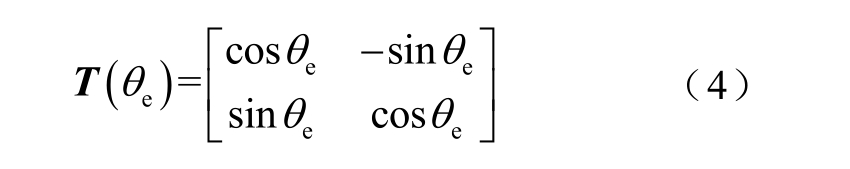
IPMSM 的高频电压方程可以从两相旋转坐标系变换到两相静止坐标系。即

式中,uαh、uβh 和iαh、iβh 分别为α、β 轴高频电压和电流分量。L 1 = (  /2, L 0 = (
/2, L 0 = ( 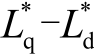 )/2,θm与Ldq,
)/2,θm与Ldq, 和
和 有关,称为交叉饱和角,为
有关,称为交叉饱和角,为
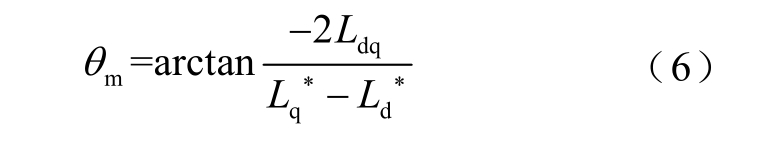
2 所提出的IPMSM 低速无传感器优化方法
本文提出了一种基于离散电流特征分析和电感误差在线辨识的IPMSM 无传感器优化方法。首先,设计了梳状数字滤波器(Comb Digital Filter,CDF)用于高频感应电流提取,相比传统的一阶高通滤波器,提取出的感应电流信号没有相位偏移。然后,通过判断中间电流分量的大小,采用不同的算法解调出转子位置,消除了传统解调环节中的低通滤波器和解调函数,解调算法简单,计算量小,且不受采样点的影响。最后,设计了针对正交方波注入的电感误差在线补偿算法,进一步提高了位置估计精度。
本文提出的无传感器优化方法的总体框图如图1 所示,主要包括高频电压注入、高频电流提取、转子位置解调和电感误差在线补偿四个部分。算法的实现流程如下:①将高频电压信号与矢量控制中Park 逆变换输出的α 轴、β 轴电压叠加,送入SVPWM;②通过电流传感器检测出三相电流,经过Clarke 变换得到iα 和iβ,然后通过CDF 分离出高频响应电流iαh 和iβh;③应用本文提出的转子位置解调方法得到转子位置初定值θetemp;④对由于电感误差造成的交叉饱和角θm 进行在线辨识,并将辨识结果补偿到转子位置初定值中,得到估计的转子位置角。

图1 所提出的无传感器控制的原理框图
Fig.1 Principle block diagram of proposed sensorless control
2.1 高频电压注入
由式(5)可知,注入高频电压信号之后,所得的高频电流响应中包含转子位置角,因此,可以将两个正交的高频方波电压注入α 轴和β 轴,如图2 所示,然后利用高频电流信号的特征解调出转子位置。
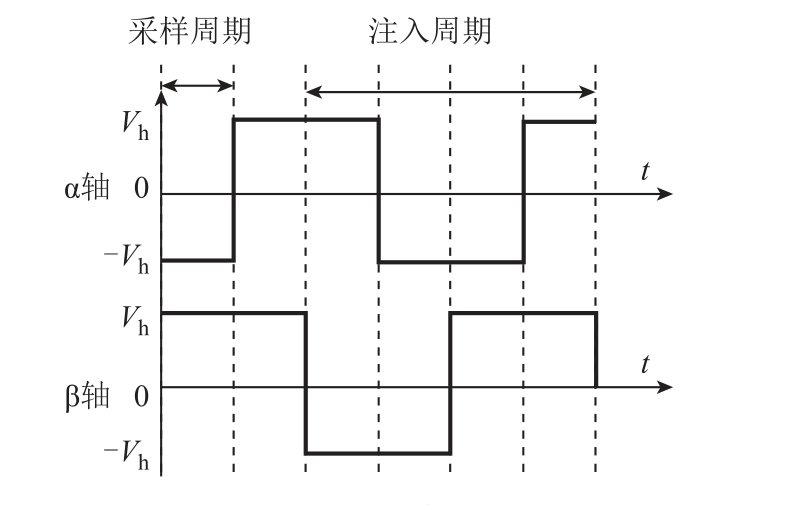
图2 注入的方波电压类型
Fig.2 The type of injected square-wave voltage
为了便于分析和计算,将注入的两个正交方波电压经傅里叶分解为

式中,Vh 为注入电压的幅度; m 为谐波的次数;ωh 为注入方波信号的频率,也是电压经傅里叶分解后得到的一次谐波频率,ωh 的大小是采样频率的1/4。
2.2 高频电流提取
为了消除基波电流的影响,提取出高频响应电流,首先需要对采样得到高频电流进行频率分析。
由于数字系统的离散特性,得到高频电流响应之后,需要根据采样频率和注入电压频率的关系将系统数学模型从连续模式转换为离散模式。由于在本文提出的方波注入法中,注入的方波频率为采样频率的1/4,因此式(7)中的ωht 可以变换为
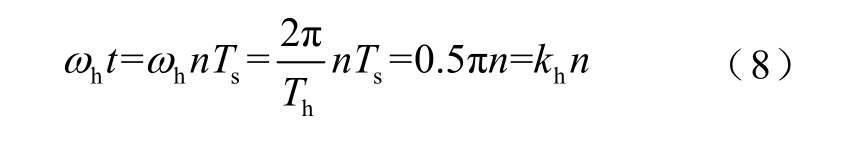
式中,n 为采样点数,可以是任意正整数;kh 为采样得到的离散高频信号的数字频率。
联立式(5)、式(7)和式(8),可以得到数字系统下的高频响应电流为


式中,iαh[n]、iβh[n]分别为α、β 轴下高频电流的离散值;k1 和k2 分别为
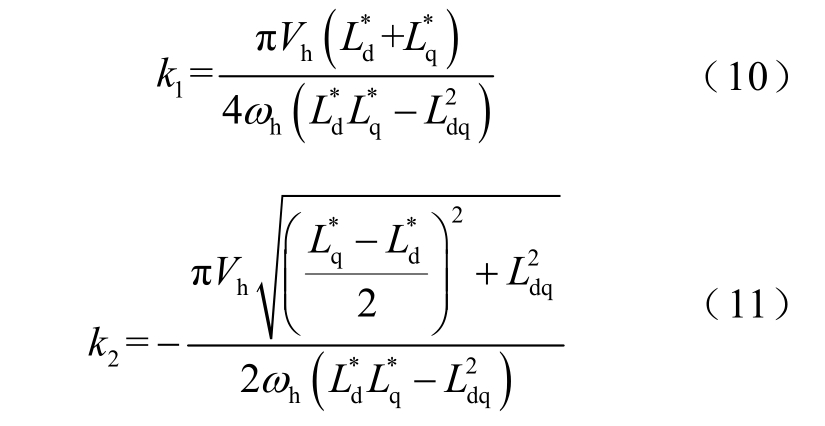
在电机低速运行中,需要考虑用于矢量控制的基波分量,假设α、β 轴定子电流为
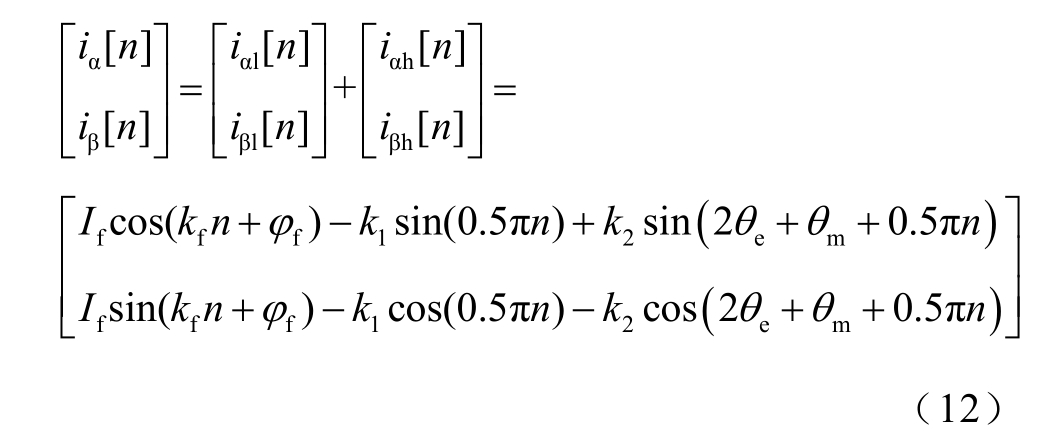
式中,iαl[n]、iβl[n]为基波电流的离散值;If、kf、φf分别为基波电流的幅值、数字频率和相位。当电机运行在300r/min 及以下的低速区时,kf ≪kh。
由式(9)可知,高频电流分量iαh[n]、iβh[n]的数字频率单一且为0.5π,因此可以采用适合单一数字频率信号提取的四阶CDF 来实现高频信号提取。
基于四阶滑动平均滤波原理,本文设计的四阶CDF 的传递函数为

图3 为本文设计的四阶CDF 的幅相特性曲线。由图3 可知,CDF 对于数字频率为0.5π 的信号没有幅值衰减和相位滞后。因此,所提出的高频电流提取方法没有传统高通滤波器的幅相偏移问题。
在 300r/min 及以下的零低速运行区域,在20kHz 的采样频率下,基波电流的数字频率 kf ≤0.0015π,经过计算,四阶CDF 滤波后,基波电流的衰减大于40dB,满足系统要求。

图3 四阶CDF 的幅相特性曲线
Fig.3 Amplitude phase characteristic curve of fourth order CDF
2.3 转子位置解调
在得到高频电流响应iαh[n]、iβh[n]后,由式(9)可知,iαh[n]、iβh[n]受转子位置θe 调制,因此,可以通过对离散电流信号进行处理,解调出转子位置角。然而,iαh[n]、iβh[n]同时与采样点数n 和交叉饱和角θm 有关,要精确得到θe 必须消除n 和θm 的影响。
本文所提算法需要假设在两个采样周期(即PWM 周期)内,θe 保持不变,但实际上电机在低转速下仍会转动一定的角度,当采样频率为20kHz 时,两个采样周期内位置转动的电角度为θdelay=2ωeTs。可知θdelay在电机转速低于300r/min 时低于0.009rad,该误差非常小,可以被忽略。同时,由于采样周期很短,可以假设在相邻采样周期内电动机的电感参数保持不变,即θm 不变。本算法采用单PWM 更新模式,PWM 载波频率等于采样频率,如果转速更高,或者PWM 周期更长,则需要考虑转速对位置估计的影响并进行补偿。
将式(9)中的采样点n 替换为n-1 得到上一时刻的α、β 轴高频电流分量后,可以对相邻采样时刻的高频电流进行加减运算,得到

式中,iαh[n-1]、iβh[n-1]分别为上一时刻的高频电流分量。
由式(14)可知以下规律:①i1[n]的值仅与n 有关,且i1[n]的值在0 和±2k1 之间跳变;②i2[n]、i3[n]是n、θe 和θm 的三角函数;③i1[n]、i2[n]、i3[n]的周期均为4。
由i1[n]的表达式可以看出,当n=4m 和n=4m+2时i1[n]=0,其中m 为正整数。此时可以推导出
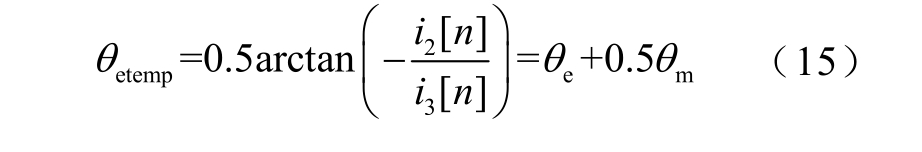
同理,当n=4m+1 和n=4m+3 时|i1[n]|=2k1,此时可以推导出

因此,通过判断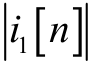 的大小,可以选择不同的位置计算公式,从而消除采样点数n 对位置估算的影响。
的大小,可以选择不同的位置计算公式,从而消除采样点数n 对位置估算的影响。
转子位置初定值的计算过程如图4 所示。首先,通过电流采样得到离散电流iα[n]、iβ[n],并利用四阶CDF 提取出高频离散电流iαh[n]、iβh[n],然后通过相邻采样周期的高频电流iαβh[n]和iαβh[n-1],结合式(15)和式(16),当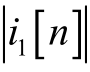 >δ 时(本文考虑工程裕度,设置判断值δ 为1),应用式(16),否则应用式(15),从而得到转子位置初定值。所提方法在解调中没有使用低通滤波器和解调函数,没有传统方法中滤波器带来的幅值衰减和相位滞后,解调过程仅包含一个判断环节和三个加法运算,计算量小,实时性高。
>δ 时(本文考虑工程裕度,设置判断值δ 为1),应用式(16),否则应用式(15),从而得到转子位置初定值。所提方法在解调中没有使用低通滤波器和解调函数,没有传统方法中滤波器带来的幅值衰减和相位滞后,解调过程仅包含一个判断环节和三个加法运算,计算量小,实时性高。

图4 转子位置初定值计算过程
Fig.4 Calculation process of tentative value of rotor position
2.4 补偿因电感变化造成的估计误差
在式(15)和式(16)中仍然含有交叉饱和角θm,会影响位置估计的精度,降低无位置控制的动态性能。因此,本文采用在线的方法对交叉饱和效应进行补偿。首先,为了对电感参数进行定性分析,本文采用两种方法对电感进行了离线测量,一种是传统的磁链电流法[26],另一种是文献[13]中使用的针对高频注入法的电感测量法。在两种测量方法中,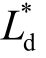 随着
随着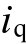 的变化均很小,约等于0.3mH。这是因为本文所使用的电机控制方法是id=0 的矢量控制方法,d 轴电流波动很小,并且d 轴等效气隙较大,较不易饱和。这与文献[24]中得出的结论一致。在这种情况下,式(3)中的ΔLd 可以看作为0。与d 轴电感不同,随着q 轴电流的增大,ΔLq 呈负向增大,
的变化均很小,约等于0.3mH。这是因为本文所使用的电机控制方法是id=0 的矢量控制方法,d 轴电流波动很小,并且d 轴等效气隙较大,较不易饱和。这与文献[24]中得出的结论一致。在这种情况下,式(3)中的ΔLd 可以看作为0。与d 轴电感不同,随着q 轴电流的增大,ΔLq 呈负向增大,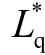 明显减小,这是因为q 轴的等效气隙比较短,且q轴电流随负载变大显著增加,从而由电枢反应引起的磁路饱和程度较高。同时根据交叉耦合的性质以及实际的测量验证:在电机正转运行时,即当iq>2A时,Ldq 的值为负;当电机反转运行时,即iq<-2A时,Ldq 的值为正。
明显减小,这是因为q 轴的等效气隙比较短,且q轴电流随负载变大显著增加,从而由电枢反应引起的磁路饱和程度较高。同时根据交叉耦合的性质以及实际的测量验证:在电机正转运行时,即当iq>2A时,Ldq 的值为负;当电机反转运行时,即iq<-2A时,Ldq 的值为正。
基于以上分析,并结合2.3 节中推导出的离散高频电流与电感之间的关系,可以对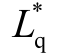 和Ldq 进行在线辨识,联立式(10)和式(11)可得
和Ldq 进行在线辨识,联立式(10)和式(11)可得

式中,本文采用空载时用磁链电流法得到的Ld 作为已知参数参与计算,并在整个运算中保持不变。k1和k2 可以由式(14)中得到的电流分量i1[n]、i2[n]、i3[n]计算得出,k1 和k2 的推导公式为
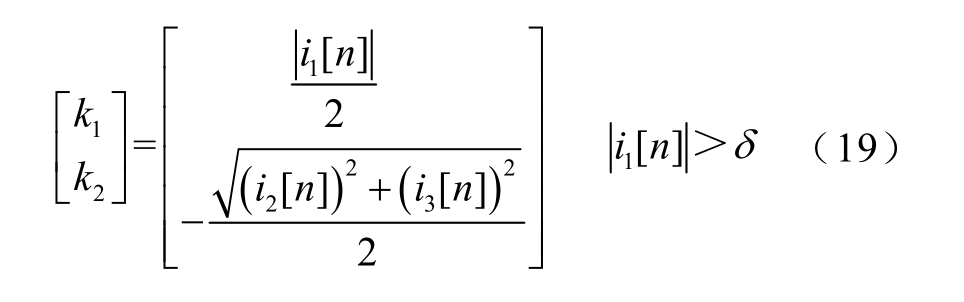
根据式(17)~式(19)识别出电感参数后,可以根据式(6)计算出交叉饱和角θm。θm 的计算流程如图5 所示。最后,将计算出的θm 补偿到转子位置初定值中,可以得到转子位置估计值的最终值和由交叉饱和角引起的估计误差为
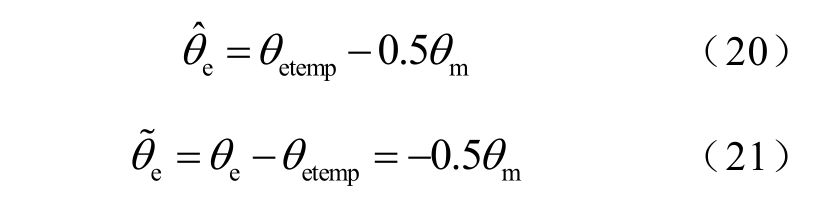
式中,上标“ˆ”和“~”分别代表估计值和误差值。

图5 交叉饱和角的计算流程
Fig.5 The calculation process of the cross-saturation angle
3 实验结果
为验证本文提出的基于方波信号注入法的IPMSM 无位置检测方法的可行性,在基于矢量控制的IPMSM 控制平台上进行了实验研究,实验中所采用的电机参数见表1。
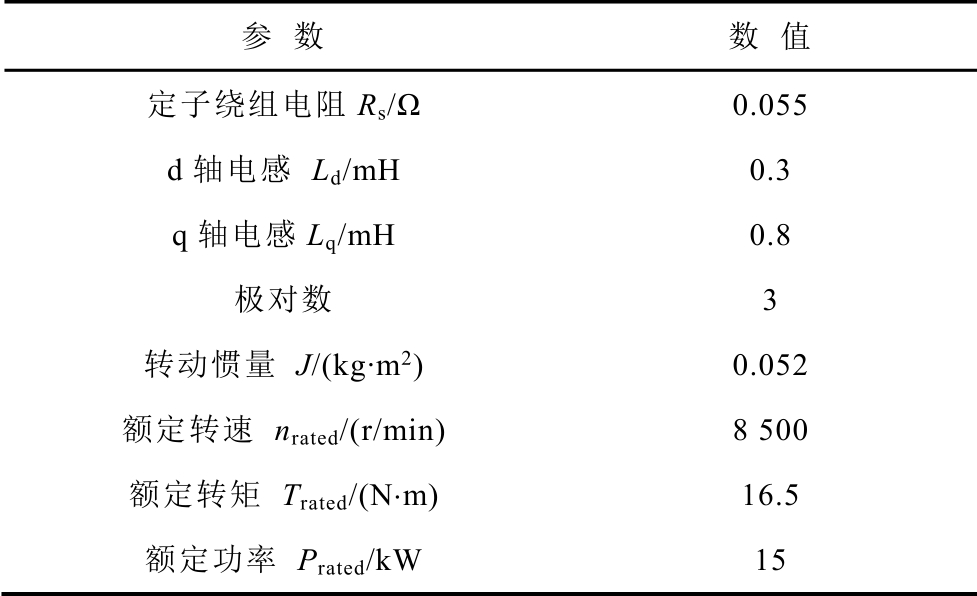
表1 IPMSM 参数
Tab.1 The parameters of the IPMSM
参 数 数 值定子绕组电阻Rs/Ω 0.055 d 轴电感 Ld/mH 0.3 q 轴电感Lq/mH 0.8极对数 3转动惯量 J/(kg·m2) 0.052额定转速 nrated/(r/min) 8 500额定转矩 Trated/(N⋅m) 16.5额定功率 Prated/kW 15
实验采用TI 公司的TM320F28335 作为主控制器,采用型号为LT108—S7/SP8 的霍尔传感器作为电流传感器。为了验证位置检测精度,通过安装一个型号为TS2225N1112E102 的多摩川旋转变压器检测转子位置,与观测值进行比较。DSP 系统时钟设为 150MHz,PWM 开关频率及采样频率均为20kHz,采用单采样更新模式。注入的正交高频电压的幅度和频率分别为10V 和5kHz。测试系统配有编码器,可以提供实际的转子位置进行比较。另一个IPMSM 与实验用IPMSM 同轴固定,以产生负载转矩。电机采用id=0 的矢量控制方法,采用无传感器控制策略进行实验,实验平台如图6 所示。在实验平台上进行电感和转子位置误差辨识实验和稳态、动态条件下的无位置运行实验。

图6 IPMSM 实验平台
Fig.6 IPMSM experimental platform
3.1 电感及转子误差辨识实验
应用2.4 节方法得到 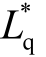 和Ldq 与iq 的关系如图7所示。实验时设置电机的转速为100r/min,电机的d 轴控制电流为0,电机在不同负载下运行,此时q 轴电流在10~50A 之间变化。每隔10A 取一个实验点。
和Ldq 与iq 的关系如图7所示。实验时设置电机的转速为100r/min,电机的d 轴控制电流为0,电机在不同负载下运行,此时q 轴电流在10~50A 之间变化。每隔10A 取一个实验点。
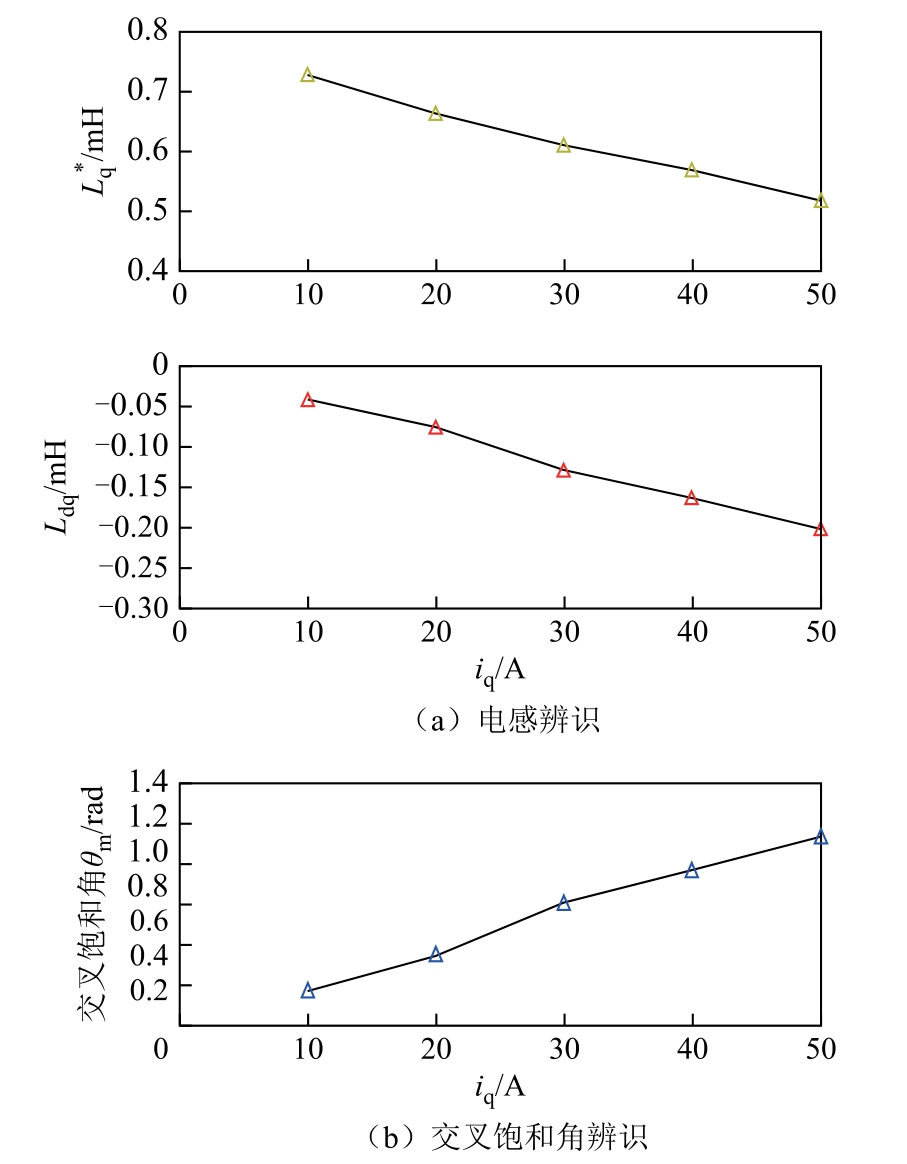
图7 电感参数和交叉饱和角辨识波形
Fig.7 Experimental waveforms of inductance and rotor position error identification
由图7a 可以看出, 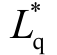 在10A 时的估计值为0.767mH,与表1 的给定值比较接近,但是随着q 轴电流的增大,
在10A 时的估计值为0.767mH,与表1 的给定值比较接近,但是随着q 轴电流的增大, 明显减小。此外,电机还受交叉耦合效应的影响,随着iq 的增加,Ldq 的变化趋势为负向增大。由图7b 可以看出,交叉饱和角θm 随着iq的增加而增加,实验结果与2.4 节分析一致。
明显减小。此外,电机还受交叉耦合效应的影响,随着iq 的增加,Ldq 的变化趋势为负向增大。由图7b 可以看出,交叉饱和角θm 随着iq的增加而增加,实验结果与2.4 节分析一致。
3.2 无传感器运行实验
为了验证本文所提方法的估计性能,进行了稳态、动态条件下的无位置运行实验。图8 为电动机以100r/min、4N·m 负载下稳定运行时利用2.4 节所提方法对θm 进行补偿和没有补偿时的转子位置估计结果。由图8 可以看出,在没有对θm 进行补偿时,预估误差有一个直流偏置,大小约0.25rad,这降低了位置估计的精度。当应用本文提出的补偿方法后,该直流偏置被消除,估计误差在0rad 附近。
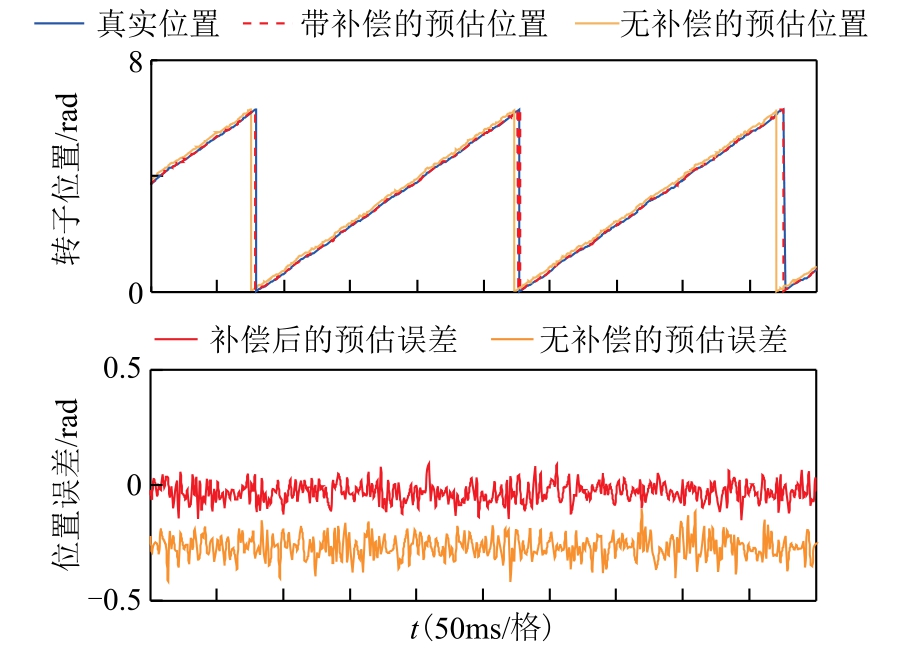
图8 稳态下的位置估计结果
Fig.8 Position estimation results in steady state
其次,设置IPMSM 在不同负载条件下进行动态性能测试,图9 为在转速300r/min 时,不同条件下的无位置传感器控制的负载动态性能曲线。图9a为没有补偿因电感变化造成的位置估计误差时的电机动态性能曲线,负载转矩在t1 时刻从2N⋅m 变为6N⋅m,在t2 时刻变为10N⋅m。图9b 为应用了2.4节所提电感误差在线补偿方法下的电机动态性能曲线。负载转矩在t3 时刻从2N⋅m 变为6N⋅m,在t4时刻变为10N⋅m。图9a 和图9b 的两个实验使用了相同PI 参数,确保此时两个实验的区别仅为电机的位置误差 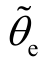 。
。
从图9 可以看出在没有电感误差补偿的情况下,加大负载之后位置误差的绝对值明显增大,相比图9b,图9a 的转子位置估算不准,导致磁场定向不准,系统动态性能恶化。而在图9a 中,由于应用了误差补偿方法,位置误差仅在负载突变的瞬间有0.1rad 左右的波动,然后很快恢复稳定状态,电机运转平稳。实验结果表明,所提出的补偿方法可以提高转子位置估计精度,在负载变化的情况下实现良好的动态性能。

图9 不同负载下无传感器控制的动态性能
Fig.9 Dynamic performance with sensorless control under different loads
4 结论
本文提出了一种考虑交叉饱和效应的低速无传感器优化方法,通过向电机定子绕组注入正交的高频方波信号,并深入分析离散模型中高频电流与转子位置、电感参数的关系,提取转子位置角。在分离和解调环节中,没有滤波器带来的幅相偏移,算法结构简单,计算量小;在补偿环节中,通过在线对电感参数变化引起的估计误差进行辨识,提高了检测精度。实验证明本文提出的方法具有良好的位置估计效果,可以实时补偿因为电感变化造成的估计误差,在负载变化时位置误差变化不大,动态跟踪性能良好。
[1] Sul S, Kwon Y, Lee Y. Sensorless control of IPMSM for last 10 years and next 5 years[J]. CES Transactions on Elecreical Machines and Systems, 2017, 1(2):91-99.
[2] 刘计龙, 肖飞, 沈洋, 等. 永磁同步电机无位置传感器控制技术研究综述[J]. 电工技术学报, 2017,32(16): 76-88.Liu Jilong, Xiao Fei, Shen Yang, et al. Positionsensorless control technology of permanent-magnet synchronous motor—a review[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 76-88.
[3] Song Xinda,Fang Jiancheng,Han Bangcheng, et al.Adaptive compensation method for high-speed surface PMSM sensorless drives of EMF-based position estimation error[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1438-1449.
[4] Zhao Yue,Zhang Zhe,Qiao Wei, et al. An extended flux model-based rotor position estimator for sensorless control of salient-pole permanent-magnet synchronous machines[J]. IEEE Transactions on Power Electronics, 2015, 30(8): 4412-4422.
[5] Kim S I, Im J H, Song E Y, et al. A new rotor position estimation method of IPMSM using all-pass filter on high-frequency rotating voltage signal injection[J].IEEE Transactions on Industrial Electronics, 2016,63(10): 6499-6509.
[6] 张航, 刘卫国, 彭纪昌, 等. 基于方波电压信号注入的表贴式永磁同步 电机饱和凸极性响应分析及转子位置估计[J]. 电工技术学报, 2017, 32(16): 106-114.Zhang Hang, Liu Weiguo, Peng Gichang, et al.Saturation Saliency response analysis and rotor position estimation based on square-wave voltage signal injection for surface-mounted permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 106-114.
[7] 刘颖, 周波, 冯瑛, 等. 基于脉振高频电流注 入SPMSM 低速无位置传感器控制[J]. 电工技术学报, 2012, 27(7):139-145.Liu Ying, Zhou Bo, Feng Ying, et al. Sensorless control of SPMSM based on high frequency current signal injection in the direct axis at low and zero speed[J]. Transactions of China Electrotechnical Society, 2012, 27(7): 139-145.
[8] 黄科元, 陈忠强, 黄守道. 一种基于电感饱和效应的电流差值检测永磁同步电机转子初始位置的方法[J]. 电工技术学报, 2018, 32(7): 1508-1515.Huang Keyuan, Chen Zhongqiang, Huang Shoudao.A initial rotor position estimation method for PMSM based on inductance saturation effect[J]. Transactions of China Electrotechnical Society, 2018, 32(7): 1508-1515.
[9] Huang Zhaobin, You Linru, Wang Zhaodong.Sensorless initial rotor position identification for nonsalient permanent magnet synchronous motors based on dynamic reluctance difference[J]. IET Power Electronics,2014, 9(7): 2336-2346.
[10] Zhang Xing, Li Haoyuan, Yang Shuying, et al.Improved initial rotor position estimation for PMSM drives based on HF pulsating voltage signal injection[J]. IEEE Transactions on Industrial Electronics, 2018, 65(6): 4702-4713.
[11] Xu Peilin, Zhu Ziqiang. Carrier signal injection-based sensorless control for permanent magnet synchronous machine drives with tolerance of signal processing delays[J]. IET Electric Power Applications, 2017,11(6): 1140-1149.
[12] Li Haoyuan, Zhang Xing, Yang Shuying, et al. Unified graphical model of high frequency signal injection methods for PMSM sensorless control[J]. IEEE Transactions on Industrial Electronics, 2019, DOI:10.1109/TIE. 2019. 2924863.
[13] Liu J M, Zhu Z Q. Sensorless control strategy by square-waveform high-frequency pulsating signal injection into stationary reference frame[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(2): 171-180.
[14] Wang Gaolin, Xiao Dianxun, Zhang Guoqiang, et al.Sensorless control scheme of IPMSMs using hf orthogonal square-wave voltage injection into stationary reference frame[J]. IEEE Transactions on Power Electronics, 2019, 34(3):2573-2584.
[15] 姜燕, 刘思美, 罗德荣, 等. 基于高频正交方波电压注入的永磁同步电机初始位置辨识[J]. 电工技术学报, 2019, 34(19): 4006-4016.Jiang Yan, Liu Simei, Luo Derong, et al. Rotor initial position identification based on the HF orthogonal square-wave voltage injection[J].Transactions of China Electrotechnical Society, 2019, 34(19): 4006-4016.
[16] Wang Shuo, Kang Jinsong, Degano M, et al. An accurate wide-speed range control method of ipmsm considering resistive voltage drop and magnetic saturation[J]. IEEE Transactions on Industrial Electronics, 2019, DOI: 10.1109/TIE.2019.2912766.
[17] Wang Qiwei, Zhang Guoqiang, Wang Gaolin, et al.Offline parameter self-learning method for generalpurpose PMSM drives with estimation error compensation[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 11103-11115.
[18] Liu J M, Zhu Z Q. Novel sensorless control strategy with injection of high-frequency pulsating carrier signal into stationary reference frame[J]. IEEE Transactions on Industry Applications, 2014, 50(4):2574-2583.
[19] Bui M X, Faz Rahman M, Guan D, et al. A new and fast method for on-line estimation of d and q axes inductances of interior permanent magnet synchronous machines using measurements of current derivatives and inverter DC-bus voltage[J]. IEEE Transactions on Industrial Electronics, 2019, 66(10):7488-7497.
[20] Feng Guodong, Lai Chunyan, Kar N C. A novel current injection-based online parameter estimation method for PMSMs considering magnetic saturation[J].IEEE Transactions on Magnetics, 2016, 52(7): 1-4.
[21] Dang Dongquang, Rafaq M S, Choi H H, et al. Online parameter estimation technique for adaptive control applications of interior PM synchronous motor drives[J]. IEEE Transactions on Industrial Electronics,2016, 63(3): 1438-1449.
[22] Rafaq M S, Mwasilu F, Kim J, et al. Online parameter identification for model-based sensorless control of interior permanent magnet synchronous machine[J].IEEE Transactions on Power Electronics, 2017, 32(6):4631-4643.
[23] Liu Kan, Zhu Z Q, Zhang Qiao, et al. Influence of nonideal voltage measurement on parameter estimation in permanent-magnet synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2012, 59(6): 2438-2447.
[24] Tang Qipeng, Shen Anwen, Luo Xin, et al. PMSM sensorless control by injecting HF pulsating carrier signal into ABC frame[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3767-3776.
[25] 李峰, 车进, 刘大铭, 等. IPMSM 动态电感辨识方法及转子位置估计误差补偿策略[J]. 电工技术学报, 2018, 33(23): 5418-5426.Li Feng, Chen Jin, Liu Daming, et al. Dynamic inductance identification method and rotor position estimation error compensation strategy for IPMSM[J].Transactions of China Electrotechnical Society, 2018,33(23): 5418-5426.
[26] Stumberger B, Stumberger G, Dolinar D, et al.Evaluation of saturation and cross-magnetization effects in interior permanent-magnet synchronous motor[J]. IEEE Transactions on Industry Applications,2003, 39(5): 1264-1271.