0 引言
特高压直流输电（Ultra-High Voltage Direct Current,UHVDC）在单极大地回路运行方式下引起的接地极附近交流电网变压器直流偏磁问题增多[1-3]。多年来，我国针对接地极入地电流的影响及防治开展了大量研究，但大地电性结构模型不准确造成的直流偏磁电流（DC Biasing Current, DCBC）计算值偏离实测值的问题尚未解决，准确评估接地极入地电流对交流电网的影响仍是一个难题。
由于早期对大地电阻率探测技术和反演算法研究不足，在进行大地建模时将大地电阻率看作单一电阻率值[4]。虽便于进行数值计算，但其过于理想，横向纵向的大地结构和参数的变化并未予以考虑，工程计算中一般不采用。随着深层大地电性探测技术的发展，开展对深层大地电性及其构造的探测，在进行大地建模时采用水平分层模型[5-7]。水平分层模型在一定程度上可反映大地电阻率随深度变化的情况，其模型简单，适合采用解析法对其进行计算研究，但需研究的接地极入地电流影响范围较广，大地电性及其构造复杂，或者存在湖泊、海洋，需要大地电性及其构造的三维分布特性。采用大地电磁测深（Magnetotelluric Sounding，MT）剖面延拓[8-9]模型可以反映大地电性结构横向、纵向及垂向的分布特性，但建立此模型时通过人工识别MT 剖面颜色获取大地电阻率数据存在误差。并且一些接地极近区没有阵列式测点[10-11]数据，只有部分MT 剖面，然而二维MT 剖面只能反映测线位置的大地电阻率，并不能反映测线之间未知区域的大地电阻率，直接延拓剖面建立三维大地电性结构模型，会使模型的准确性降低，进而影响接地极评估的准确度。
针对上述问题，本文采用±800 kV 扎青直流输电工程扎鲁特接地极周边 MT 剖面数据对未知区域的电阻率进行Kriging 预测[12-14]。利用多种子区域生长法[15-17]建立接地极近区大地电性结构模型，计算得到接地极近区交流系统各厂站的中性点电位，结合电网结构参数计算偏磁电流[18]。通过与实测值比较，验证了模型的准确性，为评估高压直流输电工程接地极对交流电网的影响提供了更加精确的模型。
1 大地电阻率原始数据
1.1 数据资料
为研究地下结构的发展演化，同时进行矿产资源的开发，我国开展了《深部探测技术与实验研究专项》，得到了不同深度电阻率数据及MT 剖面图，为大地建模提供参考。此外，西北院《扎鲁特-青州±800kV 特高压直流输电工程扎鲁特±800kV 换流站接地极初步设计》初步设计报告及图样（第一卷）、专题研究报告（第二卷），吉林大学实测松南、辽北地区及下辽河盆地内七条大地电磁剖面数据，也为扎鲁特接地极近区大地电性结构建模提供了基础数据。
1.2 MT 剖面数据处理
由于深部探测计划的测点过于稀疏，一些研究区域内不存在测点，需要从MT 剖面中提取大地电阻率作为大地电性结构建模的原始数据。采用某一密度的网格进行采样，以使整个MT 剖面彩图成为N ×N 个像素点。通过分层量化，将采样后获得的每个像素的灰度值从模拟值转换为离散值。
图例中每个点的灰度对应一个电阻率，将彩图每个点的灰度与图例每个点的灰度逐一对比，灰度相同时得到该点的电阻率，完成原始大地电阻率数据点的提取。
2 大地电性结构建模
2.1 Kriging 法预测大地电阻率
Kriging 法利用待预测点附近的实测数据来估计待预测点的属性值，只有当区域化变量具有空间相关性和随机性时才能够使用 Kriging 法进行预测。
将大地电阻率作为区域化变量，设点 xi ( i=1,2,⋅⋅⋅, n)处大地电阻率为 Z i，则预测点 x0 处电阻率Z0的 Kriging 预测结果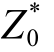
是已知采样点电阻率Z i (i = 1,2, ⋅⋅⋅, n)的加权和，即
式中，λ i为待定权重系数；n 为电阻率采样点数量。
针对无偏条件，区域化变量 Z ( x )的数学期望为常数，即 ∀ x，有 E[ Z ( x) ]=k（k 为常数）。
针对估计方差最小的条件
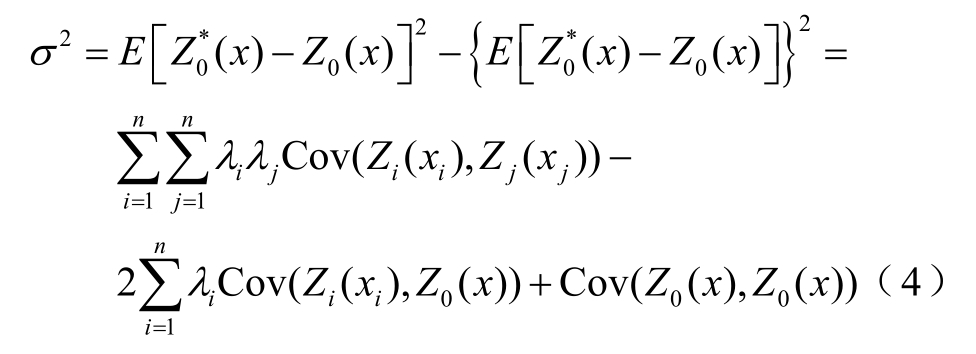
式中，σ 2 为方差；Cov 为协方差。
应用拉格朗日乘数法求条件极值， 令
其中μ 为Lagrange 函数因子，对 iλ 求偏导，进一步推导可得线性方程组
式中，x 为电阻率实测点位置坐标；h 为空间距离；Var[·]为方差。
将从MT 剖面提取的电阻率作为原始数据点，MT 剖面之间电阻率未知点作为预测点，在原始数据点中搜索与预测点相距h 的点对[ Z ( xi ), Z ( xi + h)]，并统计点对个数N，计算变异函数 v ( h )的估计值v* ( h) 为
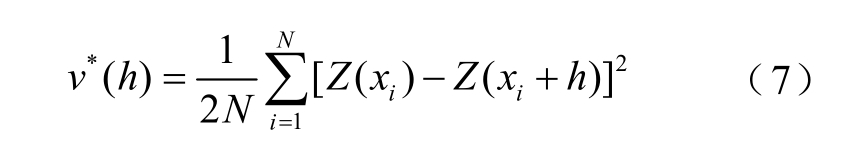
式中，Z ( xi )为实测点的电阻率；Z ( xi + h)为与 Z ( xi)空间相距h 的实测点电阻率； N 为空间间隔为h 的实测点对数量。
利用变异函数估计值绘制实验空间变异函数散点图，采用式（8）所示的球型变异函数拟合这些实验空间变异函数数据点，从而得到理论变异函数为
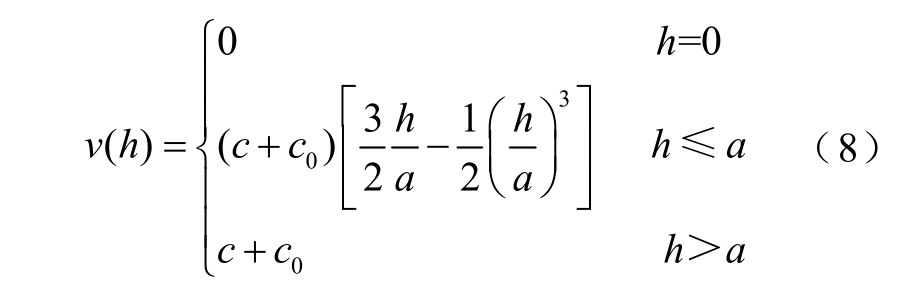
式中，c 为偏基台值；a 为变程； c0 为块金值；v 为大地电阻率空间预测值。
由协方差函数和变异函数的关系，进一步整理得
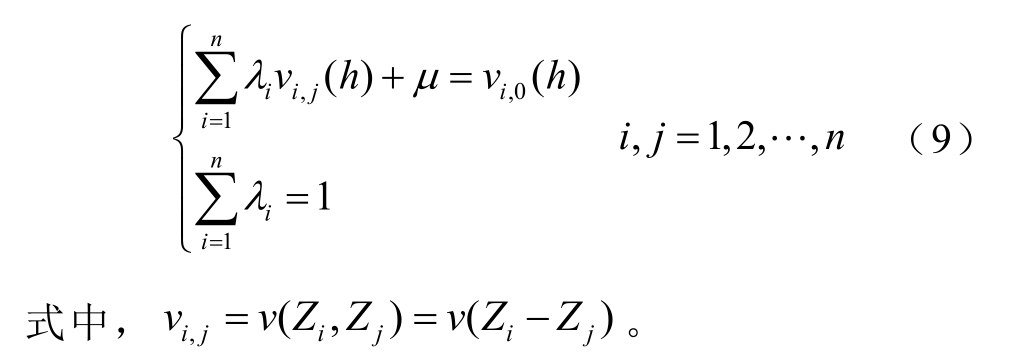
求解式（9），得到一组加权系数 λ1, … , λn ，代入式（1）计算预测点的电阻率。
2.2 大地电阻率模型
预测得到大地电阻率后形成大地电性结构散点模型，在Matlab 中采用多种子区域生长法将散点大地电性结构进行区块化处理，从第二层开始，每隔26 个点选择一个种子点，阈值设定为200 Ω⋅m 。生长方式采用图1 所示的26 邻域进行判别，若种子点与26 个邻域点的电阻率差值在阈值范围内，则沿x、y、z 三个生长方向进行区域生长，进而形成规则形状区块，每个区域的电阻率设置为26 个邻域点的平均值，将电阻率相同的区域进行合并，记录每个区块各个顶点坐标及相邻顶点间隔的散点数量。
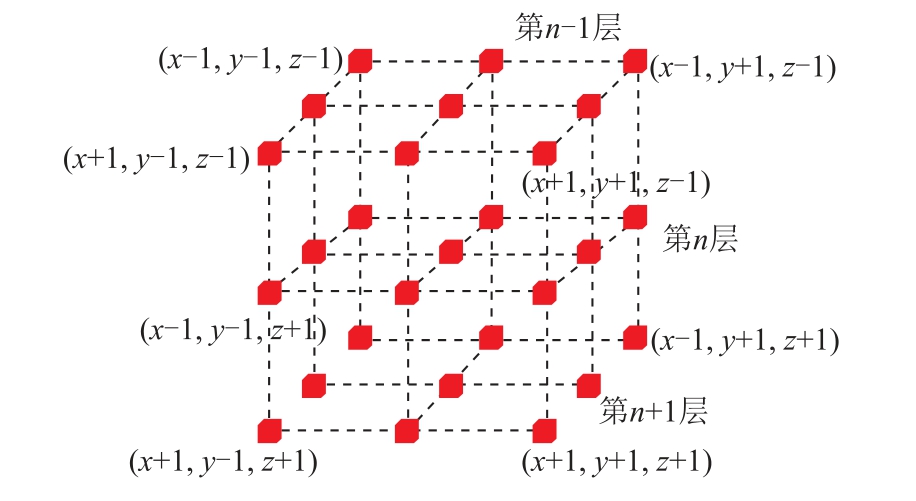
图1 26 邻域生长方式
Fig.1 26 neighborhood growth mode
由每个区块各个顶点坐标及相邻顶点间隔的散点数量以及散点之间的空间距离确定每个区块的大小。在Ansys 中，采用4 面体10 节点Solid 98单元作为计算单元，最终建立大地电性结构模型。考虑到接地极和大地电性结构模型尺寸之间存在巨大的差异，入地直流电流分布和接地极形状关系不大，故将接地极简化为点电流源施加在模型上表面中心处。
3 算例分析
考虑到计算可靠性，以及Ansys 在复杂建模方面比其他软件具有更强的灵活性，因此运用Ansys建立三维大地电性结构模型计算UHVDC 扎鲁特接地极近区的地电位。
3.1 Kriging 大地电性结构模型
将扎鲁特接地极近区的阿鲁科尔沁旗-威远堡、哈拉道口-海城、扎鲁特-昌图、科右中旗-辽源、瓦房店-营城子、科右后旗-乾安、北票-西绍根MT 剖面以100 行×100 列的竖直网格进行划分，同样用网格对图例进行剖分，提取剖面交叉点三原色与图例各点逐一进行比对得到大地电阻率原始数据。将MT 剖面第1 行所有节点大地电阻率汇总定义为第1 层数据，第2 行所有节点大地电阻率汇总定义为第2 层数据，以此类推，获得100 层大地电阻率原始数据，统计各层数据见表1。将标准差与平均值的比值定义为变异系数，由表1 可知大地电阻率的变异系数较大，说明大地电阻率的空间变异受随机因素的影响较大。
表1 MT 剖面大地电阻率统计特征（部分）
Tab.1 Statistical characteristics of earth resistivity of seven MT section surfaces（part）
层数电阻率/( Ω⋅m )变异系数平均值 标准差1 1 683.1 3 301.8 1.96 10 1 369.3 2 275.9 1.66 21 1 653.6 2 557.8 1.55 35 1 746.5 2 756.7 1.58 39 1 745.1 2 753.5 1.58 54 1 625.6 2 578.5 1.59 68 1 560.3 2 479.3 1.59 83 1 452.3 2 327.7 1.60 95 1 343.4 2 155.6 1.60 100 1 256.6 2 026.6 1.61
利用式（7）计算实验空间变异函数的估计值，绘制成散点图如图2a 所示，“·”为实验变异函数丢弃值，“+”为理论变异函数分组计算得到的平均值。根据穿过尽可能接近平均值（蓝色点）位置的原则，利用式（8）理论球型变异函数拟合这些平均点得到理论空间变异函数曲线如图2b 所示。
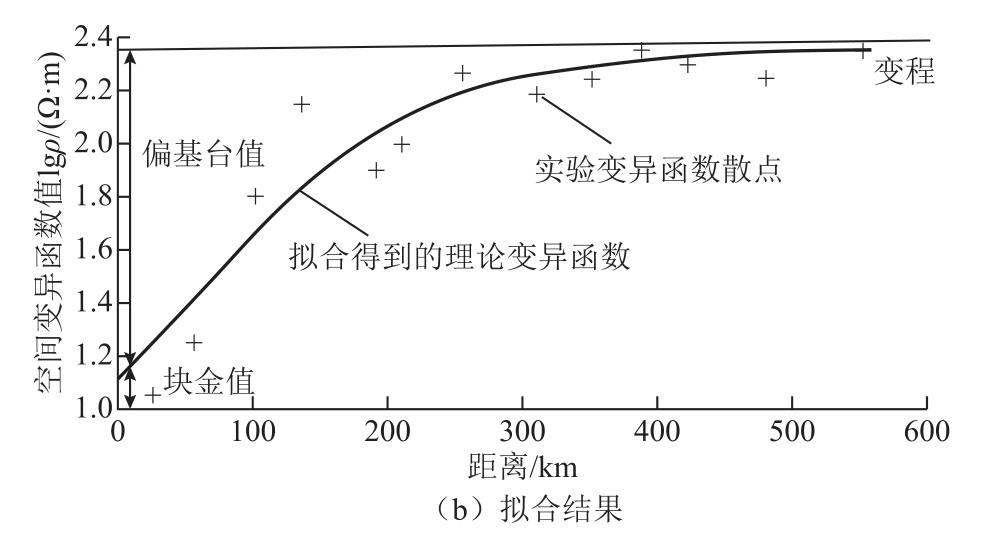
图2 变异系数拟合（球型变异函数曲线）
Fig.2 Fitting of variogram(spherical variogram curve)
理论变异函数参数见表2，将MT 剖面间的点作为预测点，求解式（9）得到权重系数，进而计算预测点电阻率。对于每层大地电阻率数据点，采用随机抽样方式，80%作为训练集、20%作为测试集，假定测试集中的电阻率未知，用训练集拟合出变异函数估计测试集中的电阻率，进而检验用变异函数估计值拟合得到的理论变异函数准确性，部分层平均误差（Mean Error，ME）、均方根误差（Root Mean Square Error，RMSE）和标准化均方根误差（Root Mean Square Standard Error，RMSDE）见表2，表2中各项指标均较小，证明拟合得到的理论变异函数准确度较高，可用于大地电阻率预测。
表2 大地电阻率的变异函数参数及其拟合精度（部分）
Tab.2 Variation function parameters of earth resistivity and its model fitting accuracy（part）
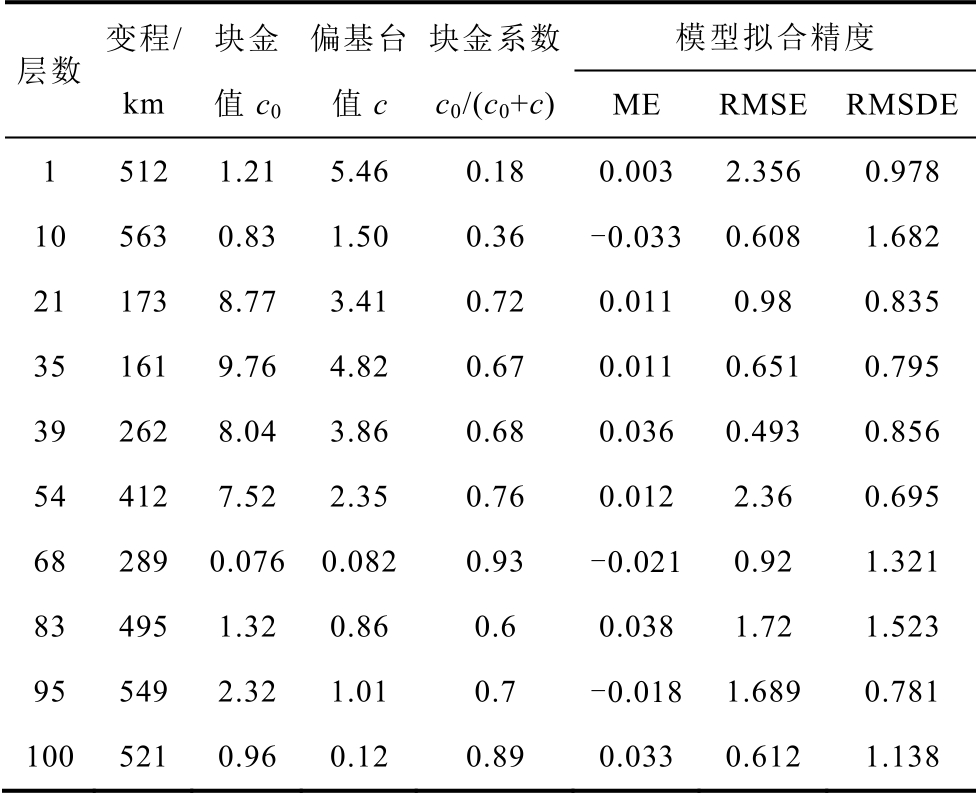
层数变程/km块金值c0偏基台值c块金系数c0/(c0+c)模型拟合精度ME RMSE RMSDE 1 512 1.21 5.46 0.18 0.003 2.356 0.978 10 563 0.83 1.50 0.36 -0.033 0.608 1.682 21 173 8.77 3.41 0.72 0.011 0.98 0.835 35 161 9.76 4.82 0.67 0.011 0.651 0.795 39 262 8.04 3.86 0.68 0.036 0.493 0.856 54 412 7.52 2.35 0.76 0.012 2.36 0.695 68 289 0.076 0.082 0.93 -0.021 0.92 1.321 83 495 1.32 0.86 0.6 0.038 1.72 1.523 95 549 2.32 1.01 0.7 -0.018 1.689 0.781 100 521 0.96 0.12 0.89 0.033 0.612 1.138
除第1 层和10 层块金系数较小外，其余各层块金系数均在0.6 以上，表明大地电阻率的空间变异性受结构性因素影响，加之前文已证明的大地电阻率空间变异受随机因素影响，所以满足使用Kriging法的前提条件，因此Kriging 法可用于预测大地电阻率。利用原始大地电阻率散点和Kriging 法预测得到的大地电阻率散点，通过多种子区域生长法最终建立如图3 所示大地电性结构模型。
图3 整体区块模型
Fig.3 Overall block model
3.2 地电位及偏磁电流计算
在大地模型边界处电压自由度约束设置为0V，以表征模型零电位边界条件。模型采用整体精细智能网格剖分并结合整体网格细化控制。仿真计算时分别在MT 剖面沿拓模型和Kriging 大地模型点电流源处施加2 500A 和6 250A 的电流作为接地极入地电流，计算地电位。扎鲁特接地极近区的电网结构如图4 所示。利用Kriging 法建立的大地电性结构模型计算得到的接地极近区各厂站变压器中性点电位（m1～m42），如图5 所示。
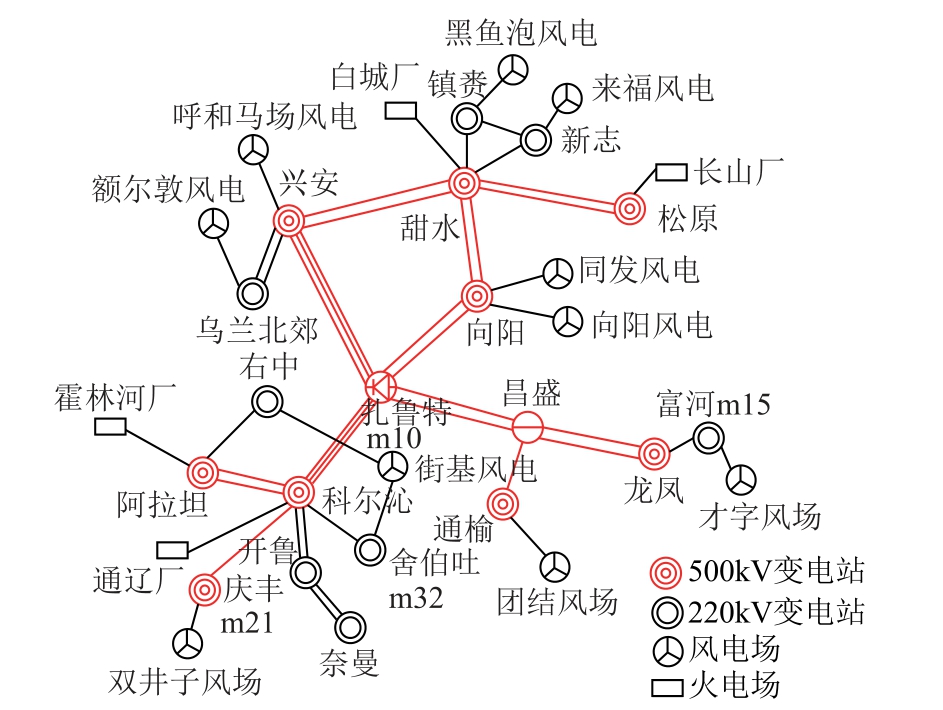
图4 接线图（部分）
Fig.4 Wiring diagram (part)
图5 地表电位计算结果（6250A）
Fig.5 Calculation results of surface potential（6250A）
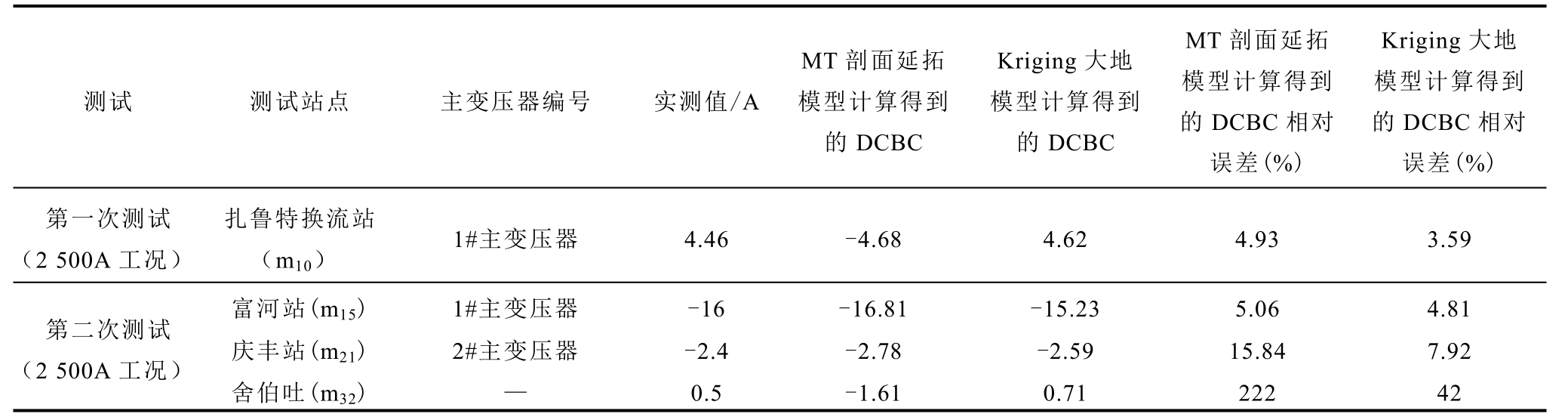
结合电网结构参数，对扎青工程3 次单极大地回路运行方式下的扎鲁特端电网偏磁电流进行了测量。第一次10 回配套工程中仅扎鲁特-科尔沁3 回投运，各站均未加装DCBC 治理装置，接地极入地电流2 500A，偏磁电流以流入大地为正。第二次与第一次投运线路和工况相同，但扎鲁特换流站内各变压器装设1Ω DCBC 治理装置。第三次10 回配套工程中仅扎鲁特-科尔沁3 回、扎鲁特-向阳2 回投运，接地极入地电流6 250A，扎鲁特换流站各变压器装设1Ω DCBC 治理装置，母线电抗器装设3Ω DCBC 治理装置，富河站变压器装设2Ω DCBC 治理装置。DCBC 实测值与两种模型的计算值对比见表3，相比于MT 剖面延拓模型计算得到的DCBC相对误差，利用Kriging 法预测得到的大地电阻率数据建立的模型DCBC 的误差更小，证明了利用Kriging 法预测得到的大地电阻率建立的接地极近区大地电性结构模型比简单的MT 剖面延拓模型更加准确。
表3 实测值和计算值
Tab. 3 Measured and calculated values
?
（续）
?
4 结论
本文对大地电性结构建模经过“散点-区块-整合”过程。利用地质统计学Kriging 法计算MT 剖面之间未知的大地电阻率，形成整体区域的三维散点模型。应用多种子区域生长法，将散点大地电性结构模型转化为区块大地电性结构模型，减小建模工作量。分别利用MT 剖面延展得到的三维大地电性结构模型和Kriging 三维大地电性结构模型，在接地极注入入地电流计算地电位，结合电网结构参数得到±800kV 扎青工程扎鲁特接地极近区各厂站偏磁电流。利用两种建模方法计算得到的偏磁电流与实测值比较，证明利用Kriging 预测数据建立的三维大地电性结构模型计算地电位更准确。
[1] 郝黎明, 王东来, 卢铁兵, 等. 计及金属回流线影响的±500kV 高压直流输电线路地面合成电场计算分析[J]. 电工技术学报, 2019, 34(12): 2468-2476.Hao Liming, Wang Donglai, Lu Tiebing, et al.Calculation and analysis og ground-level total electric field under ±500kV HVDC lines considering the influence of metal return lines[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2468-2476.
[2] 滕予非, 李小鹏, 林圣, 等. 特高压直流系统接地极线路阻抗监视系统适应性研究[J]. 电工技术学报, 2019, 34(19): 4154-4161.Teng Yufei, Li Xiaopeng, Lin Sheng, et al.Adaptability analysis of fault supervision system for long electrode line of UHVDC[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4154-4161.
[3] 陈剑, 刘春明, 王茂海, 等. 广义有限差分法在静态电磁场计算中的应用[J].电工技术学报, 2018,33(7): 1579-1587.Chen Jian, Liu Chunming, Wang Maohai, et al.Application of the generalized finite difference method to static electromagnetic problems[J].Transactions of China Electrotechnical Society, 2018,33(7): 1579-1587．
[4] Zou J, Liu Y Q, Yuan J S, et al. Analysis of the toroidal HVDC grounding systems in horizontal multilayer soils[J]. IEEE Transactions on Magnetics, 2006, 42(4):1435-1438.
[5] Li Wei, Pan Zhuohong, Lu Hailiang, et al. Influence of deep earth resistivity on HVDC ground-return currents distribution[J]. IEEE Transaction on Power Delivery, 2012, 10(18): 1835-1842．
[6] 刘春明, 林晨翔, 王小宁, 等. 海岸效应对电网地磁感应电流的影响[J]. 电网技术, 2017, 41(8): 2716-2722.Liu Chunming, Lin Chenxiang, Wang Xiaoning, et al.Impact of coast effect on geomagnetically induced current in power grid[J]. Power System Technology,2017, 41(8): 2716-2722．
[7] 刘春明, 林晨翔, 王璇, 等. 大地电导率横向变化对地磁暴感应电场 H 极化及地磁感应电流的影响[J]. 电工技术学报, 2016, 31(24): 113-119.Liu Chunming, Lin Chenxiang, Wang Xuan, et al.Evaluating the influence of lateral change of conductivity on the “H Polarization” of induced geoelectric field and geomagnetically induced current[J]. Transactions of China Electrotechnical Society, 2016, 31(24): 113-119.
[8] 刘连光, 姜克如, 李洋, 等. 直流接地极近区三维大地电阻率模型建立方法[J]. 中国电机工程学报,2018, 38(6): 1622-1630, 1898.Liu Lianguang, Jiang Keru, Li Yang, et al. Threedimensional earth resistivity structure modelling around DC ground electrode[J]. Proceedings of the CSEE, 2018, 38(6): 1622-1630, 1898.
[9] 陶瑞祥, 王泽忠. 基于有限元的电场区域分解法的广义极小残量迭代算法[J]. 电工技术学报, 2018,33(2): 225-231.Tao Ruixiang, Wang Zezhong. Generalized minimal residual iteration method for finite based domain decomposition technique for electric field problem[J].Transactions of China Electrotechnical Society, 2018,33(2): 225-231.
[10] 董树文, 李廷栋, 陈宣华, 等. 我国深部探测技术与实验研究进展综述[J]. 地球物理学报, 2012,55(12): 3884-3901.Dong Shuwen, Li Tingdong, Chen Xuanhua, et al.Progress of deep exploration in mainland China: A review[J]. Chinese Journal of Geophysics, 2012,55(12): 3884-3901.
[11] 董树文, 李廷栋. Sino Probe—中国深部探测实验[J].地质学报, 2009, 83(7): 895-909.Dong Shuwen, Li Tingdong. Sino Probe: the exploration of the deep interior beneath the Chinese continent[J]. Acta Geologica Sinica, 2009, 83(7): 895-909.
[12] 李晓军, 王长虹, 朱合华. Kriging 插值方法在地层模型生成中的应用[J]. 岩土力学, 2009, 30(1): 157-162.Li Xiaojun, Wang Changhong, Zhu Hehua, et al.Kriging interpolation and its application to generating stratum model[J]. Rock and Soil Mechanics, 2009,30(1): 157-162.
[13] Oliver M A, Webster R. Kriging: a method of interpolation for geographical information systems[J].International Journal of Geographical Information Science, 1990, 4(3): 313-332.
[14] Pang Su, Li Tianxuan, Wang Yengdong, et al. Spatial interpolation and sample size optimization for oil copper (Cu) investigation in cropland soil at county scale using Co-Kriging[J]. Agricultural Sciences in China, 2009, 8(11): 1369-1377.
[15] 闫东阳, 明冬萍. 基于自动多种子区域生长的遥感影像面向对象分割方法[J]. 工程科学学报, 2017,39(11): 1735-1742.Yan Dongyang, Ming Dongping. Object-oriented remote sensing image segmentation based on automatic multispeed region growing algorithm[J].Chinese Journal of Engineering, 2017, 39(11): 1735-1742.
[16] 孔俊, 王佳男, 谷文祥, 等. 基于区域的自动种子区域生长法的彩色图像分割算法[J]. 东北师大学报(自然科学版), 2008, 40(4): 47-51.Kong Jun, Wang Jianan, Gu Wenxiang, et al.Automatic SRG based region for color image segmentation[J]. Journal of Northeast Normal University(Natural Science Edition), 2008, 40(4): 47-51.
[17] Frank Y Shih, Cheng S X. Automatic seeded region growing for color image segmentation[J]. Image and Vision Computing, 2005, 30(23): 877-886.
[18] 程佩芬, 李崇涛, 傅闯, 等. 基于状态空间法的高压直流输电系统电磁暂态简化模型的解析算法[J].电工技术学报, 2019, 34(6): 1230-1239.Cheng Peifen, Li Chuntao, Fu Chuang, et al. An analytic solution for simplified electromagnetic transient model of HVDC transmission system based on state space method[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1230-1239.