0 引言
在国家加紧建设能源互联网的大环境下,坚强智能电网作为能源互联网的重要组成部分,其涵盖的源、网、荷、储发挥着日益重要的作用[1]。电磁热储能系统作为主要储能手段,承担缓解弃风弃光,促进新能源消纳和移峰填谷的作用,使电网能源的分布更加合理,目前已成为国内的研究热点[2]。
在实际系统中,谐振电路作为电磁向热转换的实现环节,其中的加热管体随着结构尺寸、控制电路输出波形、实时工况的变化,电流会显著变化,不同值的电流会使加热管体中导磁性金属管处在不同的磁化曲线工作点。电流较大会使工作点进入非线性区,使得加热管体的电感产生变化,在谐振电路中电容不变的状态下会影响电压与电流相位,导致谐振电路大幅偏离工作点,影响系统功率。为避免以上问题发生,对在非线性状态下由动态电感构成的谐振电路的机理研究是十分重要的。
文献[3]对电磁热储能系统的温度场、流体场和控制电路进行了仿真分析,但未考虑系统中主要能量转换电路即谐振电路的参数特性。文献[4]通过实验测量磁心材料特性参数,结合电磁场分析,采用多元非线性回归算法建立了动态电感模型。文献[5]通过简化有限元计算模型,利用Simpson 数值微分公式计算了磁心不同饱和程度下的动态电感;文献[6-7]使用解析法求解了类电磁热储能系统加热管体的电感值,其中文献[7]考虑了电流因趋肤效应和涡流影响而分布不均对电感计算造成的影响;但文献[5-7]对于涉及串联谐振电容的谐振电路缺乏指导性。文献[8]提出了一种有限元与解析计算相结合的方法计算具有圆形横截面的任意形状的线圈电感,其准确性高,计算速度快,但没有考虑频率变化所带来的电流分布不均的影响。文献[9-11]采用数值计算方法对变压器直流偏磁下动态电感进行计算,提高了该种情况下的计算效率与准确性,但变压器的工作频率相较电磁热储能系统偏低,计算分析方法有所出入。文献[12-16]针对动态电感在无位置传感器控制电机时的作用和改善并网逆变器控制效果进行了研究。其他文献的研究主要集中在电感参数的计算方法及其等效模型的建立[17-20]。
针对现有文献只考虑动态电感,未将可与其构成谐振电路的谐振电容综合考虑的情况,本文对12.85kHz/50kW 的电磁热储能系统进行研究。先提出了谐振电路的计算分析流程,再对加热管体进行了有限元计算与分析,得出其动态电感函数,适配了合适的电容,最后进行样机实验。验证了本文阐述的谐振电路分析计算方法的准确性。
1 谐振电路分析
电磁热储能系统的结构如图1 所示。三相交流电经过整流滤波后通过H 桥进行移相斩波,将高频方波电压作用在谐振电路两端,图中R 为加热管体的电阻分量。
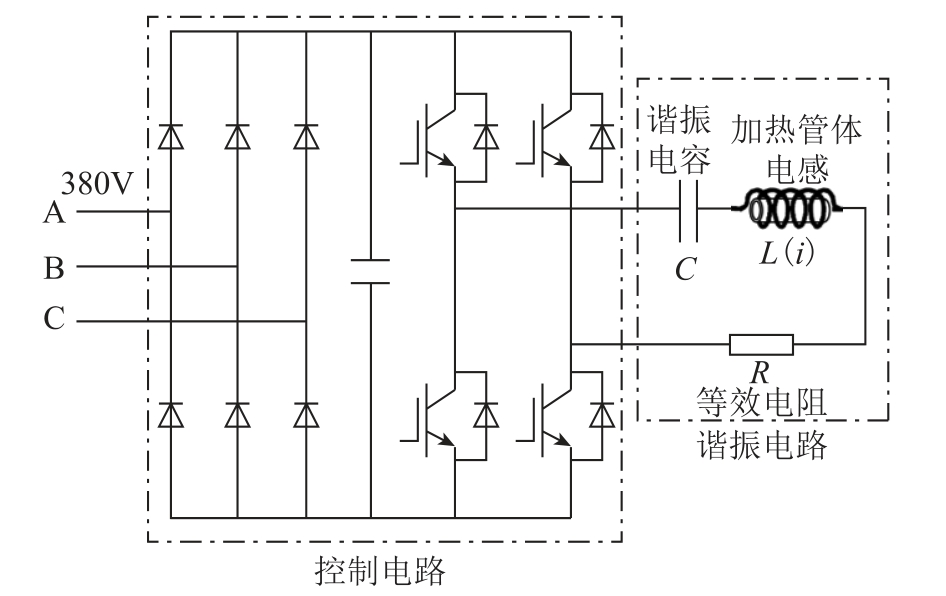
图1 电磁热储能系统结构
Fig.1 The structure diagram of electromagnetic thermal energy storage system
谐振电路计算分析流程如图2 所示。对加热管体简化模型进行有限元计算,得到求解域内的磁共能随电流变化的曲线数据;使用该数据,通过泰勒展开法得到准确的磁链随电流变化函数;最后进行求导,得到动态电感,继而通过对谐振电路的基波分析,得到谐振电容。对谐振电路进行仿真与实验验证谐振电路波形参数及电磁热储能系统的功率和效率。

图2 谐振电路计算分析流程
Fig.2 The calculation and analysis flow chart of resonance circuit
1.1 加热管体动态电感的计算方法
麦克斯韦方程中表示的电磁感应作用为
式中,B 为磁通密度;E 为电场强度;l 为闭合积分回路;S 为闭合积分回路l 所限定的面积。
定义闭合积分回路l 所交链的磁链Ψ为
由式(1)与式(2)可得静止媒质下,回路端电压u 与磁链Ψ、回路电流i 的关系为
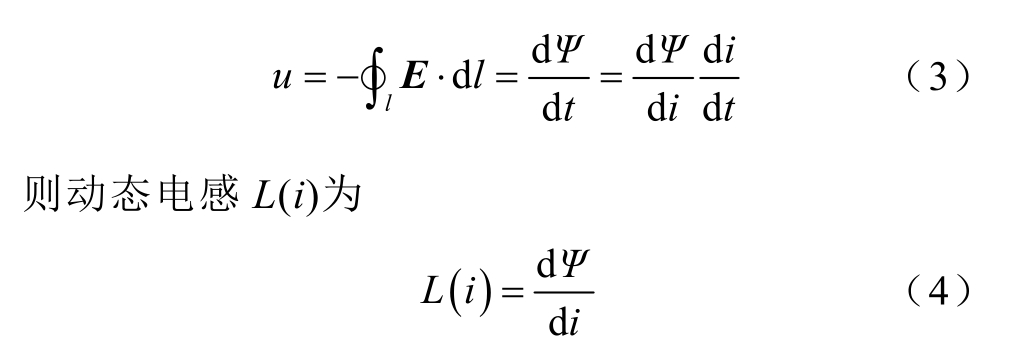
由式(3)可得,闭合回路在电流增至终值时,磁场能量W 为
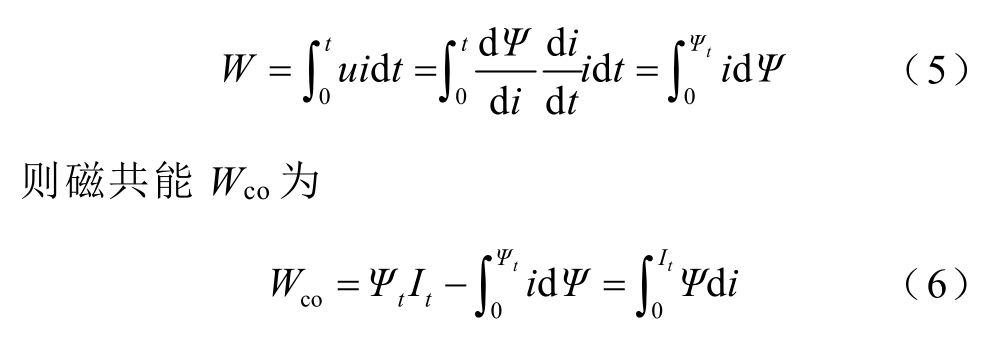
式中,It 与Ψt 分别为电流终值和电流终值对应的磁链。磁共能、磁链与电流的关系如图3 所示。
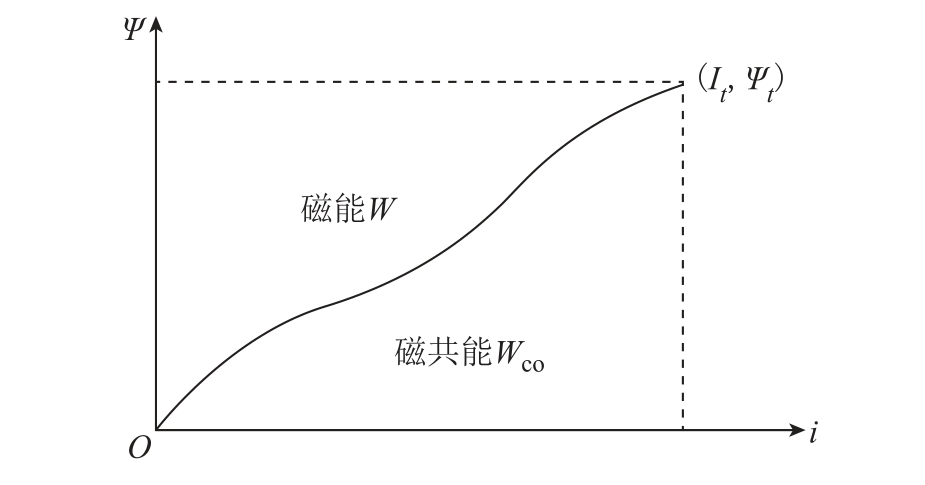
图3 磁共能、磁链与电流关系
Fig.3 Magnetic coenergy, flux linkage and current diagram
以i=0 处泰勒展开磁链与电流的函数关系为

式中,Ψ (0)、L(0)等均为电流为0 时所对应的磁链、电感及其各阶导数值。
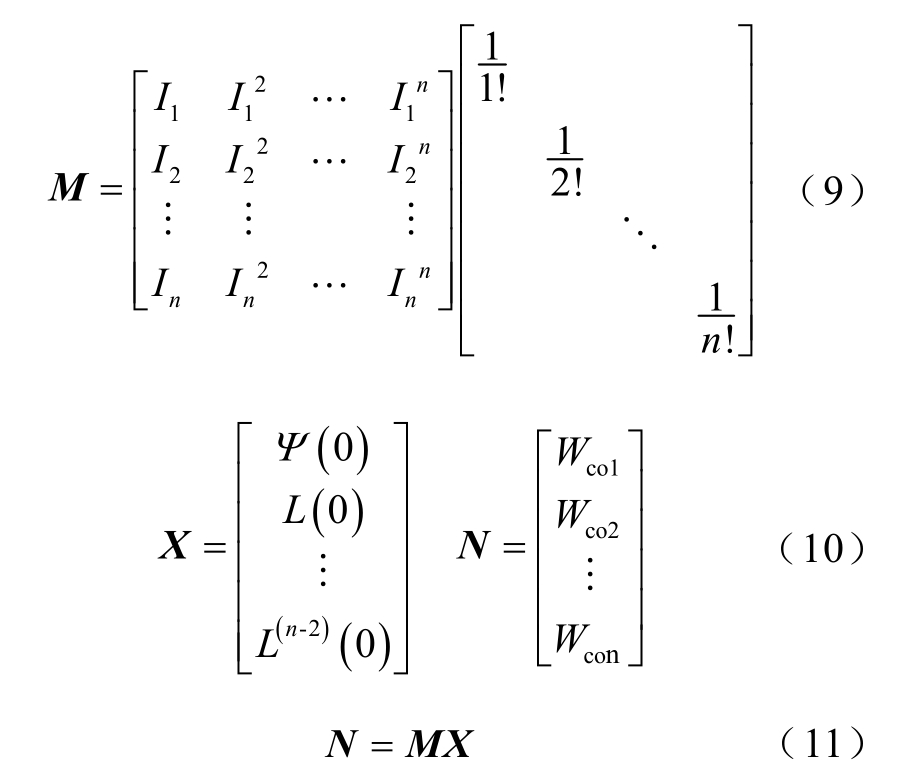
式中,M 为n×n 系数矩阵;X 为n×1 待求矩阵;N为n×1 磁共能矩阵。将已求解出的(I,Wco)值代入M和N 矩阵,可得Ψ (0)及其各阶导数的值,并准确地描述Ψ (i)函数,从而得出准确的动态电感L(i)。
1.2 加热管体有限元简化模型建立
加热管体模型图及轴对称截面结构如图4 所示。Ω0 为空气区域,Ω1 为线圈区域,Ω2 为10 号钢(导磁性金属管)区域。
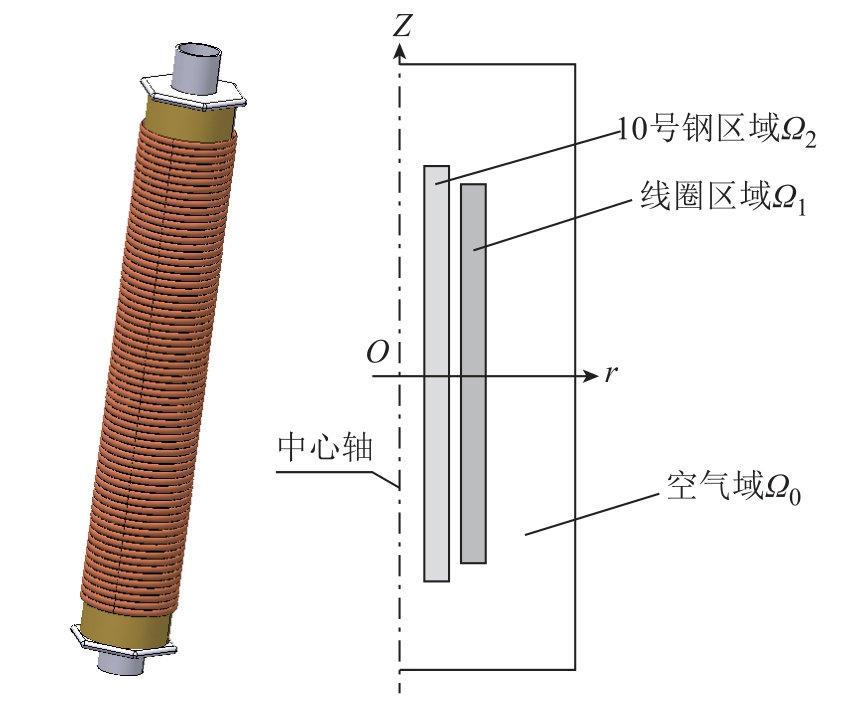
图4 加热管体模型图和结构图
Fig.4 The model diagram and structure diagram of heating tube
为得到加热管体的磁共能与电流值,本文依照实际加热管体建立有限元计算模型[21-24]。因加热管体为严格的轴对称结构,所以采用二维有限元计算,更加快速、准确;考虑导磁性金属管磁化工作点的变化,使用瞬态求解器进行计算;由于流经管体电流的三次及以上谐波含量低,波形近似正弦,采用正弦电流激励;管体端盖与接头远离线圈,该部分结构对计算影响极小故而忽略;PVC 材料的电磁特性与空气相近,将PVC 材质结构作为空气处理;管体线圈由高频导线绕制,则设置为线圈内部电流密度分布均匀,并忽略高频导线绝缘。对于求解的空气域,其轴向、辐向尺寸均为管体尺寸的2 倍。对加热管体按电磁准静态场问题求解,管体模型满足的场域方程和边界条件如下。
场域方程
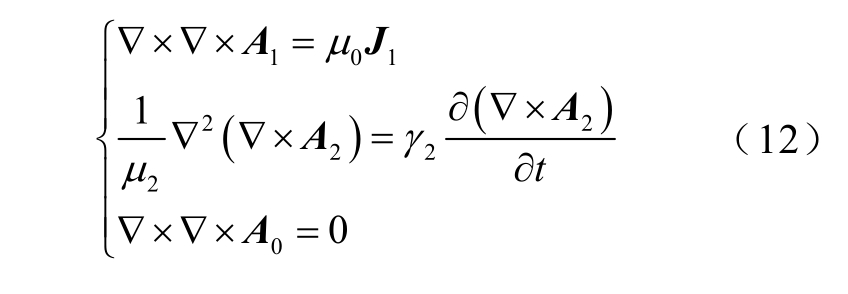
式中,J 为电流密度;A 为各区域的矢量磁位;μ 为各区域的磁导率;γ 为区域的电导率。
空气与导磁性金属管间边界方程
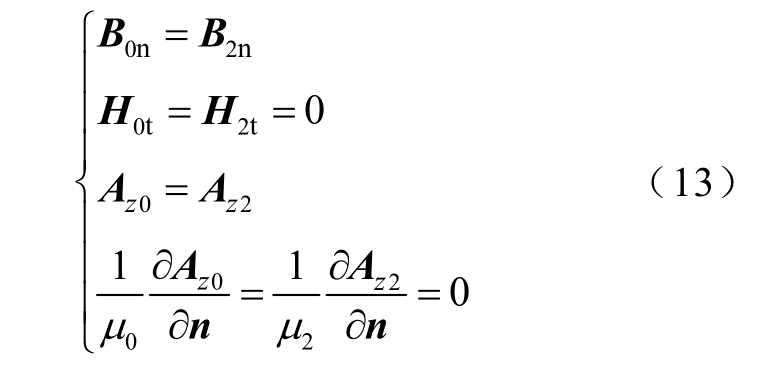
式中,Bn、Ht 和Az 分别为各区域的磁密法向分量、磁场强度切向分量和矢量磁位z 轴分量。
加热管体的工作频率处于10~20kHz 范围内,需要考虑趋肤效应。在趋肤效应影响下,电流在辐向分布接近指数函数关系,则在有限元计算网格划分时,将10 号钢区域在辐向上划分成多个并联的部分,并参考电流分布方式,按照指数关系对各个部分的尺寸进行设置。
1.3 动态电感计算方法的优化
对简化的模型进行瞬态有限元计算,得到准确的磁共能随电流变化曲线,通过曲线对磁共能和电流函数关系进行准确描述是动态电感计算的重点。由加热管体动态电感计算的原理可知,越多的(I,Wco)点参与计算,经过泰勒展开后的所得到的Wco(i)函数关系与实际越吻合,但这意味参与求解的矩阵阶数增大,极大影响计算效率。为使求解精度高,求解速度快,需要尽可能减少泰勒展开的阶数,同时还要保证计算值与实际值的误差满足要求,当式(14)即n>|i-x|-1 成立时,能够满足上述要求。
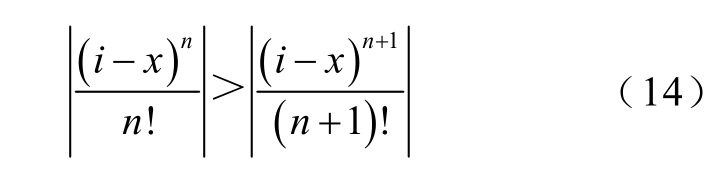
式中,i 为电流变量;x 为泰勒展开点;n 为泰勒展开阶数。若i 的取值范围为[a, b],则max(|i-x|-1)的最小值在x=(a+b)/2 处取得,令n=max(|i-x|),则n也为最小值。对于求解动态电感来说,i 在中值处泰勒展开可减小展开阶数,相较i 在取值范围两端处展开,使阶数减少一半,提高了计算效率同时也不损失精度。
1.4 谐振电容的确定
当控制器的H 桥开关频率为fs,开关周期为Ts时,谐振电路的模型如图5 所示。
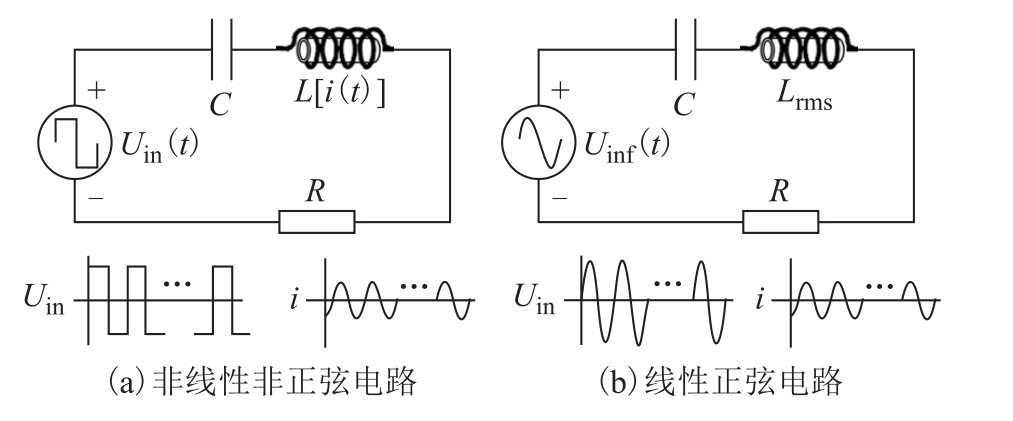
图5 谐振电路模型
Fig.5 The model of resonant circuit
图5a 中,谐振电容C 与电阻分量R 为定常量,动态电感L[i(t)]随电流i(t)变化而变化,谐振电路的电压输入Uin(t)为幅值为U 的方波,占空比d 由控制方式决定。谐振电路的电压方程为
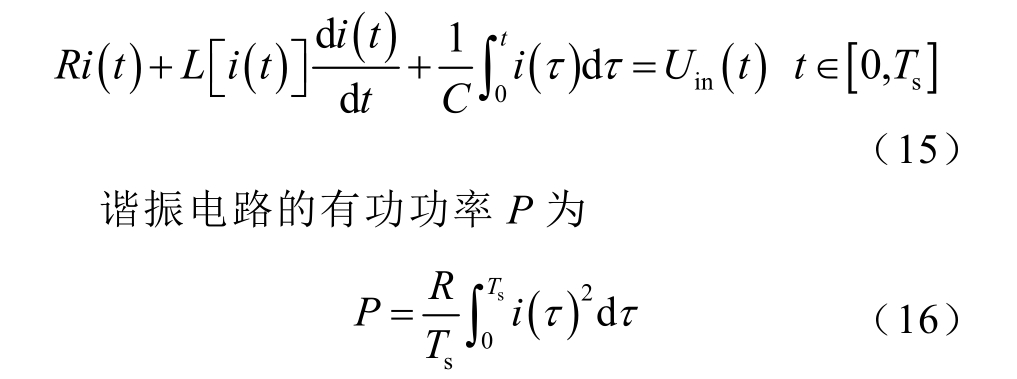
由于加热管体中的导磁性金属管工作在数百摄氏度的高温下,其电阻率在这一温度区间内几乎不变,通过实验可计算出电阻分量R 的值。
由于谐振电路中的电流和电容电压近似为正弦量,因此在对该电路分析时,只考虑基波量,如图5b所示。谐振电路的基波电压Uinf(t)和电流i(t)分别为
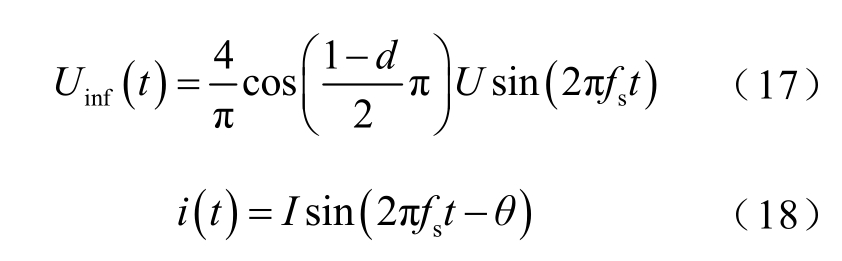
根据所求出的动态电感函数L(i),求取电感的有效值Lrms,联立式(20)、式(21)求得电磁热储能系统有功功率为50kW 时所适配的电容C 和功率因数角θ。

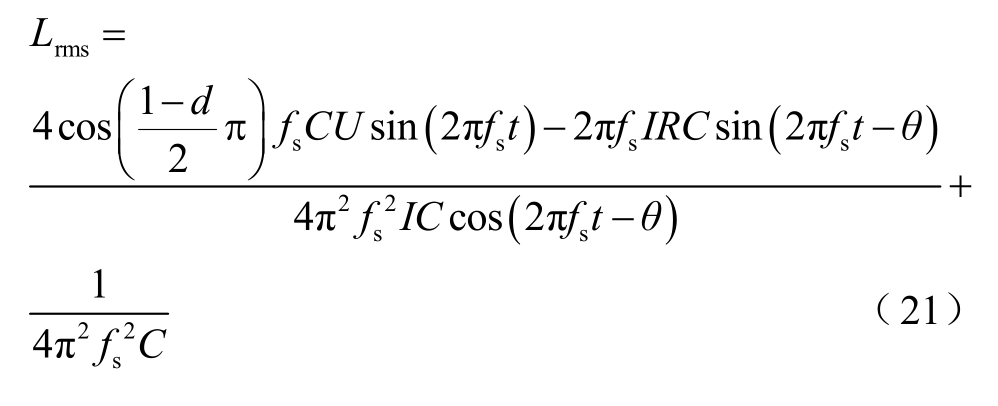
2 数值计算分析
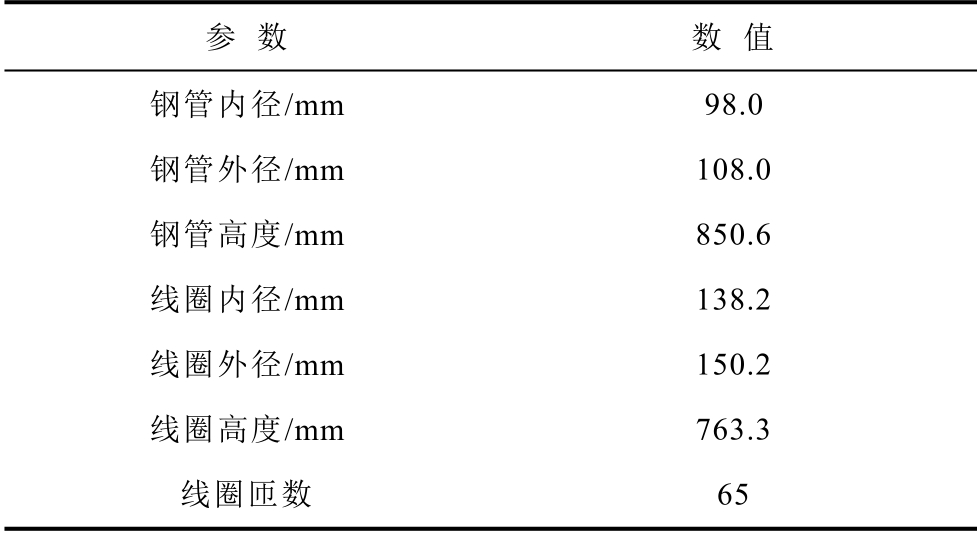
根据前面提出的加热管体有限元计算方程与优化后的动态电感计算方法,依照实际加热管体建立简化计算模型,通过计算得到其动态电感。选取的加热管体基本参数见表1。导磁性金属管所用的10号钢磁化曲线如图6 所示。
表1 加热管体基本参数
Tab.1 Basic parameters of heating tube
参 数 数 值钢管内径/mm 98.0钢管外径/mm 108.0钢管高度/mm 850.6线圈内径/mm 138.2线圈外径/mm 150.2线圈高度/mm 763.3线圈匝数 65
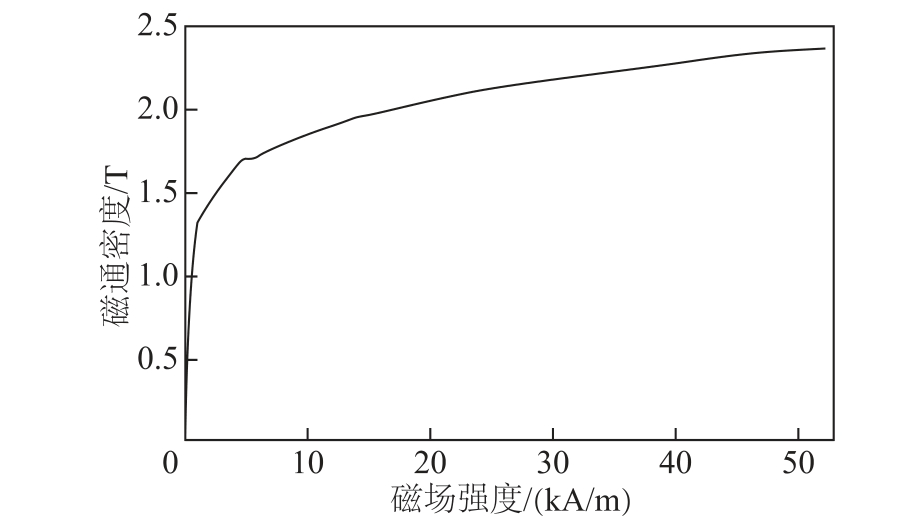
图6 10 号钢磁化曲线
Fig.6 10# steel magnetization curve
简化后的有限元计算模型如图7 所示,将10 号钢管区域按指数关系划分为10 层,其中最小厚度为0.115mm,公比为1.034,其余各层厚度见表2。激励为频率是12.85kHz 的正弦电流。
有限元计算结果如图8 所示,10 号钢在当前工况下趋肤效应显著,在距外壁0.5mm 范围内有电流,尤其在距外壁0.2mm 的范围内,磁通密度和电流密度的变化规律与0.2~0.5mm 处有明显变化,说明靠近外壁处已经出现磁饱和,磁化工作点在钢管辐向上分布不均匀,反映了加热管体动态电感计算的必要性。
表2 导磁性金属管区域剖分各层厚度
Tab.2 Thick of each parts of magnetically conductive metal pipe area

层数 厚度/mm 1 0.115 2 0.150 3 0.196 4 0.255 5 0.333 6 0.434 7 0.565 8 0.737 9 0.961 10 1.254

图7 有限元计算模型
Fig.7 The finite element calculation model

图8 10 号钢管外壁区域磁通密度、电流密度分布曲线
Fig.8 Magnetic flux density and current density distribution curve of 10# steel pipe outer wall area
计算所得的磁共能随电流变化曲线如图9 所示。磁共能随电流呈单增变化趋势,且斜率逐渐变大。在磁共能与电流曲线上选择计算点时,应遵循的规则为:在曲线斜率大、极值或最值点附近区域多取点;在斜率小,平缓区域可较少取点。
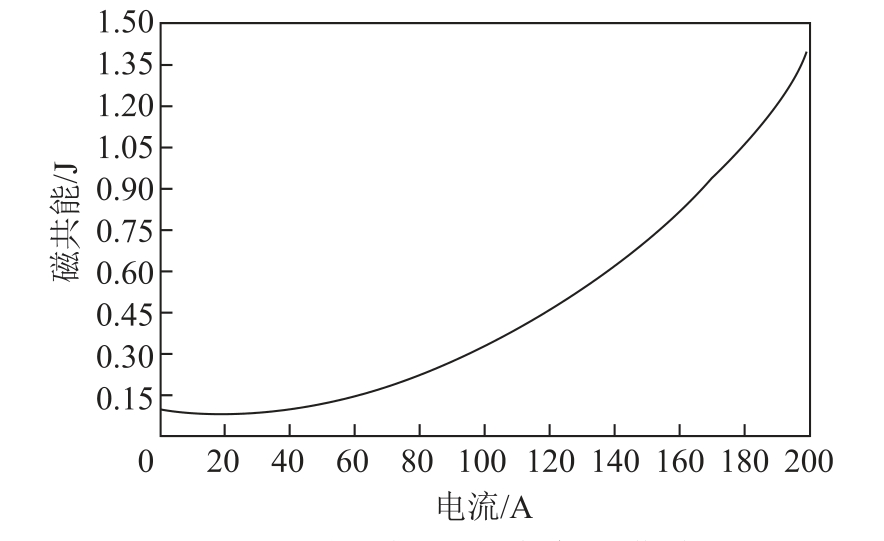
图9 磁共能随电流变化曲线
Fig.9 The curve of magnetic coenergy change with current
计算点的数量决定了磁共能对电流函数展开的阶数。计算点数量为M,展开阶数为N,M=N。当M=N=2 时,表示磁共能与电流呈线性关系,此时磁链恒定,所得动态电感为0,静态电感随电流增大而减小;当M=N=3 时,表示磁共能与电流呈二次方关系,此时磁链与电流呈线性关系,动态电感为常数,对于本文研究对象,此时动态电感恒为79.5μH;当M=N=101 时,式(14)成立,在此阶数下展开的函数可准确描述磁共能与电流的变化关系。由图10可知,随着展开阶数的增加,函数关系表现为随着电流的增大,动态电感随之缓慢增大,当电流接近终值时,动态电感陡然增大。
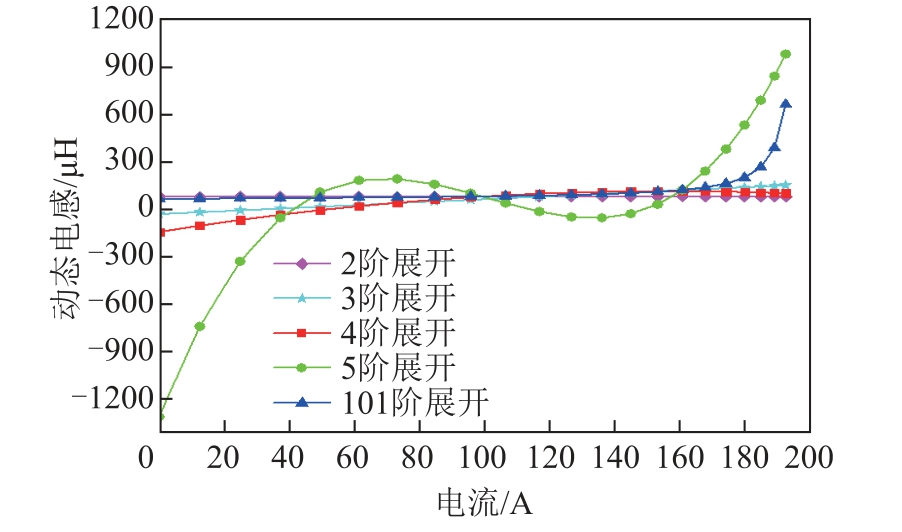
图10 动态电感随电流变化曲线
Fig.10 The curves of dynamic inductance change with current
以101 阶展开所得的动态电感与电流的变化函数为准选择谐振电容。根据1.4 节,得出电感有效值为92μH,将此值代入式(20)和式(21),得到谐振电容C 的值约为2.4μF,功率因数角为39.5°。对101 阶展开所得的动态电感和2.4μF 的谐振电容构成的谐振电路添加在控制电路输出侧进行仿真计算,得到谐振电路电压电流波形如图11 所示。
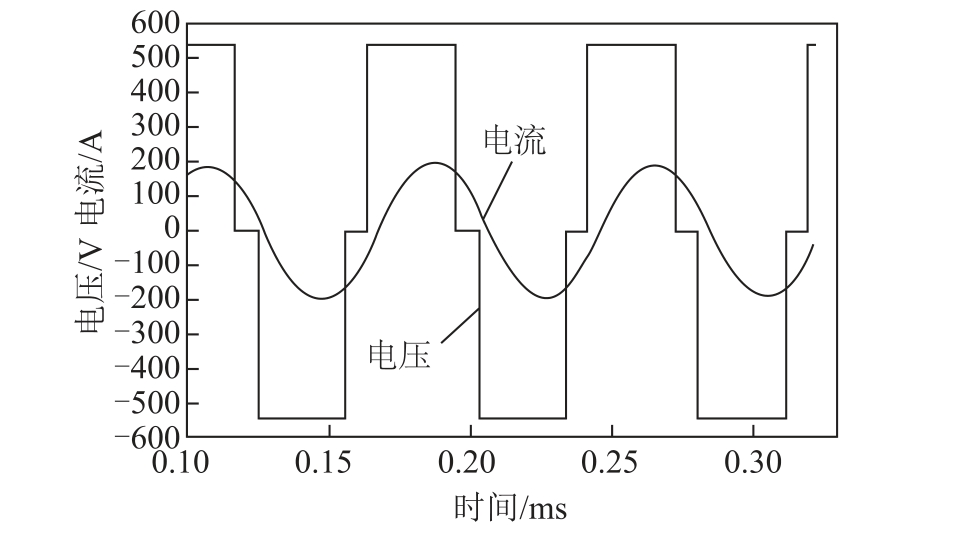
图11 谐振电路仿真波形
Fig.11 The simulation waveforms of resonant circuits
由图11 可看出谐振电路在稳定运行时,功率因数角为40°,电流幅值为191A,电流波形接近正弦,此时电路输出的有功功率为47.7kW。
3 实验验证
本文使用功率分析仪PW6001 搭配高精度闭口电流传感器对工作频率在12.85kHz 的50kW 电磁热储能系统进行测量。图12、图13 为实验所用的加热管体和控制器(含2.4μF 谐振电容)。一个管体和一个控制器构成一个运行单元,图中为双单元并行,本实验只对其中一个运行单元的谐振电路进行测量。

图12 电磁热储能系统样机
Fig.12 Electromagnetic thermal energy storage system prototype

图13 电磁热储能系统控制电路
Fig.13 The control circuit of Electromagnetic thermal energy storage system
测量谐振电路及加热管体的电压电流波形如图14 所示,谐振电路电流波形正弦度良好,幅值为198A,有效值为131.9A,电压有效值480.3V,功率因数角为40.4°,输出的有功功率为48.2kW。将仿真数据与实验数据对比发现本文所提出的谐振电路分析计算方法是比较准确的。图15 为测量控制器效率,控制器的效率为 97.2%,其损耗基本来源于IGBT 的通态损耗。

图14 谐振电路实验波形
Fig.14 The experiment waveforms of resonant circuits
图15 控制电路实验效率
Fig.15 The experiment efficiency diagram of control circuit
使用桶径为620mm,水深为650mm 的圆柱水桶进行电磁热储能系统循环加热水实验,测量时间为 270s,水温上升 14.9K,水的比热容取 4.2×103J/(kg·K)时,电磁热储能系统的效率为91.6%。
对动态电感的测量方案如下:
(1)通过功率分析仪测定的谐振电路有功功率和电流有效值推算出电路的电阻量R。
(2)在5MHz 采样频率下对谐振电路两端的电压Urlc、加热体两端的电压Url 和电路电流i 数据进行采集。
(3)将电路电流i 的数据和电阻量R 的乘积记为Ur,将加热体电压Url 与Ur 做差得到动态电感上的电压Ul。
(4)基于Lagrange 中值定理,在动态电感电压Ul 波形上进行取值,得到电压值U,并在此段电压波形对应的电流波形区间上求取斜率,此斜率可视作di/dt,两者相除,得到此时电流所对应的电感值。测量方案的示意图如图16 所示。

图16 动态电感测量方案示意图
Fig.16 The schematic diagram of dynamic inductance measurement scheme
通过实验数据计算所得的动态电感随电流的变化曲线与计算出的动态电感与电流函数关系如图17 所示。经比较,发现动态电感的实际变化规律与计算值所描述的规律相吻合。

图17 动态电感计算值与实验值
Fig.17 Dynamic inductance calculated and experimental values
动态电感计算值与实验值误差呈现中间低、向两端逐渐增高的趋势,是由于从中值处进行磁共能展开而导致的。中值邻域的计算精度高,误差在5%以内,两端的计算值与测试值偏差大,但二者的变化趋势仍相吻合。
4 结论
本文针对电磁热储能系统中的谐振电路,通过有限元计算及磁共能函数展开法,得出加热管体的动态电感,并计算适配合适的谐振电容,构成了谐振电路,最后进行了实验验证,得出以下结论:
1)运行在高频、大电流工况的加热管体中磁性材料磁导率的非线性,对管体电感量有较大影响,在更大功率电流,更高频率的应用场合,更加需要着重考虑。
2)提出了基于有限元计算及磁共能函数展开法求解加热管体动态电感的方法,并优化了函数的求解过程。通过实验验证了方法的准确性。
3)基于基波分析法,对涉及动态电感的谐振电路中的谐振电容进行了计算,并通过实验验证了选型的准确性,使电磁热储能系统的运行功率为50kW,电热转换效率达到91.6%。
4)本文提出的涉及动态电感的谐振电路的计算分析方法及模型可以作为其他高频率大功率大电流的谐振环节设计分析的参考,但模型的简化需要依照实际的结构和材料特性来设定。
[1] 葛维春, 张艳军, 高超, 等. 基于风电消纳能力态势划分的源荷储系统分阶段优化策略[J]. 电力系统自动化, 2019, 43(15): 26-33.Ge Weichun, Zhang Yanjun, Gao Chao, et al. Phased optimal strategy of source-load-storage system based on state partition of accommodation capacity of wind power[J]. Automation of Electric Power Systems,2019, 43(15): 26-33.
[2] 陈柏翰, 冯伟, 孙凯, 等. 冷热电联供系统多元储能及孤岛运行优化调度方法[J]. 电工技术学报,2019, 34(15): 3231-3243.Chen Bohan, Feng Wei, Sun Kai, et al. Multi-energy storage system and islanded optimal dispatch method of CCHP[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3231-3243.
[3] 焦永刚, 张凤阁, 殷孝雎. 大功率电磁热储能系统感应加热仿真研究[J]. 电气工程学报, 2015, 10(9):8-14.Jiao Yonggang, Zhang Fengge, Yin Xiaoju.Simulation research on induction heating technology of high power electromagnetic thermal energy storage system[J]. Journal of Electrical Engineering, 2015,10(9): 8-14.
[4] 林苏斌, 陈为. 共模扼流圈磁心磁场特性分析及其动态电感模型[J]. 中国电机工程学报, 2015, 35(21):5614-5622.Lin Subin, Chen Wei. Dynamic inductance model and magnetic field analysis of common mode choke[J].Proceedings of the CSEE, 2015, 35(21): 5614-5622.
[5] 张鹏飞, 邹军, 伍小刚, 等. 一种快速准确计算共模扼流圈动态电感的方法[J]. 电工技术学报, 2018,33(19): 4458-4467.Zhang Pengfei, Zou Jun, Wu Xiaogang, et al. Fast and precise method for calculating dynamic inductance of common mode chock[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4458-4467.
[6] 赵志衡, 李春峰, 李建辉, 等. 电磁成形用螺线管线圈电感的研究[J]. 哈尔滨工业大学学报, 2000,32(5): 64-66.Zhao Zhiheng, Li Chunfeng, Li Jianhui, et al.Inductance of solenoid coil sued for electromagnetic forming[J]. Journal of Harbin Institute of Technology,2000, 32(5): 64-66.
[7] Ooi B L, Xu D X. Modified inductance calculation with current redistribution in spiral inductors[J]. IEE Proceedings - Microwaves, Antennas and Propagation,2003, 150(6): 445-450.
[8] Li H, Banucu R, Rucker W M. Accurate and efficient calculation of the inductance of an arbitrary-shaped coil using surface current model[J]. IEEE Transactions on Magnetics, 2015, 51(3): 1-4.
[9] 潘超, 金明权, 蔡国伟, 等. 基于漏感辨识的变压器交直流混合运行保护方法[J]. 电工技术学报,2018, 33(4): 771-780.Pan Chao, Jin Mingquan, Cai Guowei, et al. Protection for transformer in AC-DC hybrid operation mode based on leakage inductance identification[J].Transactions of China Electrotechnical Society, 2018,33(4): 771-780.
[10] 王泽忠, 谭瑞娟, 李书连, 等. 基于动态电感-励磁电流曲线的特高压变压器空载直流偏磁计算[J].电工技术学报, 2017, 32(10): 154-161.Wang Zezhong, Tan Ruijuan, Li Shulian, et al. DCbias calculation for UHV transformer in no-load based on the curve of the relationship between dynamic inductance and exciting current[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 154-161.
[11] 史海涛, 王建元, 蔡国伟, 等. 变压器电磁耦合模型中动态电感的计算方法[J]. 电工电能新技术,2015, 34(8): 69-74.Shi Haitao, Wang Jianyuan, Cai Guowei, et al.Dynamic inductance computation in electromagnetic coupled model of transformer[J]. Advanced Technology of Electrical Engineering and Energy,2015, 34(8): 69-74.
[12] 曲兵妮, 宋世潮, 宋建成, 等. 考虑小电感区电感变化量的开关磁阻电机开关角优化方法[J]. 电机与控制学报, 2019, 23(2): 87-93.Qu Bingni, Song Shichao, Song Jiancheng, et al.Switch angle optimization method for switched reluctance motor considering the inductance variation in small inductance period[J]. Electric Machines and Control, 2019, 23(2): 87-93.
[13] Tanpo S, Takahashi R, Ohishi K S, et al. Online identification method of static & dynamic inductance of IPMSM for fine position sensorless control[C]//IEEE 5th International Symposium on Sensorless Control for Electrical Drives, Hiroshima, 2014: 1-6.
[14] 李伟, 张勇军, 肖雄. 实时电感辨识的模型预测并网逆变器控制方法[J]. 电工技术学报, 2018, 33(15):3450-3460.Li Wei, Zhang Yongjun, Xiao Xiong. The model predictive grid-connected inverter control method based on real-time inductance identification[J].Transactions of China Electrotechnical Society, 2018,33(15): 3450-3460.
[15] Zhang Xulong, Wang Feng, Wu Xuanqin. Low-speed direct-driven sensorless control including zero-speed for switched reluctance motor based on dynamic inductance model[C]//IEEE 17th International Conference on Electrical Machines and Systems(ICEMS), Hangzhou, 2014: 763-767.
[16] 李峰, 车进, 刘大铭, 等. IPMSM 动态电感辨识方法及转子位置估计误差补偿策略[J]. 电工技术学报, 2018, 33(23): 5418-5426.Li Feng, Che Jin, Liu Daming, et al. Dynamic inductance identification method and rotor position estimation error compensation strategy for IPMSM[J].Transactions of China Electrotechnical Society, 2018,33(23): 5418-5426.
[17] Escarela-Perez R, Campero-Littlewood E, Arjona-Lopez M A, et al. Comparison of two techniques for two-dimensional finite-element inductance computation of electrical machines[J]. IEE Proceedings-Electric Power Applications, 2005, 152(4): 855-861.
[18] 倪筹帷. 多导体段的电感参数计算方法[D]. 北京:华北电力大学, 2018.
[19] Ni Chouwei, Zhao Zhibin, Cui Xiang. Inductance calculation method based on induced voltage[J]. IEEE Transactions on Magnetics, 2017, 53(6): 1-4.
[20] Zhang Jun, Ouyang Ziwei, Duffy M C, et al. Leakage inductance calculation for planar transformers with a magnetic shunt[J]. IEEE Transactions on Industry Applications, 2014, 50(6): 4107-4112.
[21] 唐新灵. 高压大功率压接型IGBT 器件并联芯片瞬态电流特性研究[D]. 北京: 华北电力大学, 2017.
[22] 井永腾, 王宁, 李岩, 等. 电磁-热-流弱耦合的变压器绕组温升研究[J]. 电机与控制学报, 2019,23(10): 41-48.Jing Yongteng, Wang Ning, Li Yan, et al. Research on temperature rise of transformer windings with electromagnetic-thermal-flow weak coupling[J].Electric Machines and Control, 2019, 23(10): 41-48.
[23] 唐新灵, 崔翔, 赵志斌, 等. 压接式IGBT 动态测试平台杂散电感的提取(英文)[J]. 中国电机工程学报, 2017, 37(2): 652-663.Tang Xinling, Cui Xiang, Zhao Zhibin, et al.Extraction of stray inductance in press pack IGBTs’dynamic testing platform[J]. Proceedings of the CSEE,2017, 37(2): 652-663.
[24] 倪光正. 工程电磁场原理[M]. 北京: 高等教育出版社, 2002.