0 引言
高压直流输电线路的电磁环境主要由空间离子流场和合成电场构成。对离子流场的数值仿真涉及求解连续性方程。学者们提出了多种计算方法用于求解连续性方程,这些方法可分为两类:一类是基于流线运动轨迹的欧拉类方法,将原问题求解域分解为若干条特征线,进而求解每根线上离子密度分布。这类方法从最初基于Deutsch 假设的特征线方法[1-3],发展为去除Deutsch 假设影响的迭代特征线方法[4-5]。由于该类方法仅计算沿线离子密度,计算速度快,但线间的离子密度靠线性插值获得,精度较低。第二类方法是基于网格剖分的拉格朗日类方法,这类方法通过添加人工粘性项或者使用迎风差分格式获得光滑稳定的数值解,例如上流迎风有限元方法[6]和有限体积法[7]。这类方法往往采用较为复杂的形状函数和测试函数,虽然能获得较高精度,但计算复杂度高,耗时长。
T. Takuma 等于1981 年提出迎风有限元方法[8],该方法实际上是一种基于迎风单元的有限差分方法。该方法采用显式差分格式,将连续性方程转换为每个节点处的一元二次方程,使得整个求解过程变得简单、易于操作;同时该方法获得的数值解沿对流速度方向递减,具有极佳的数值稳定性。这些优点使迎风有限元方法成为离子流问题求解中广为使用的一种方法[9-13]。
迎风有限元方法也存在若干缺点:采用一阶迎风差分格式,计算精度较低;方法本身未强加通量守恒特性,由于连续性方程的误差具有累积效应,使得数值解的通量守恒误差较大[14]。针对这些问题,本文提出一种基于误差传递方程的修正方法,有效减小截断误差,改善数值解的通量守恒特性。
1 高压直流输电线路空间离子流模型
1.1 泊松方程-连续性方程耦合系统
离子流问题对应的数学模型[15]为

式中,φ为导线电荷和空间电荷共同作用产生的合成电位(V);ρ+、ρ-分别为正、负离子密度(C/m2);R 为正负电荷复合系数(m3/s);e 为电子电量,e=1.6×10-19C;V +、V -分别为正、负离子的速度矢量,即

式中,μ+、μ-分别为正、负离子迁移率,本文统一取为1.5×10-4m2/(V⋅s)。方程式(1)也称为泊松-连续性方程耦合系统,对应的边界条件为

泊松方程-连续性方程耦合系统的求解包含两个循环[16-17]:外循环根据边界条件(3)导线表面电场修正导线表面电荷分布;内循环在已知导线表面电荷分布的前提下,迭代求解泊松方程和连续性方程构成的非线性系统。1.2 节将专门介绍内循环求解的连续性方程及相应的边界条件。
1.2 连续性方程及其边界条件
内循环求解的边值问题由方程组(1)以及边界条件(4)构成。

注意到正、负离子对应的连续性方程形式上完全对称,式(5)可以统一表示为
式中,V 为对流速度;σ为反应项系数。正离子情况对应的方程系数为
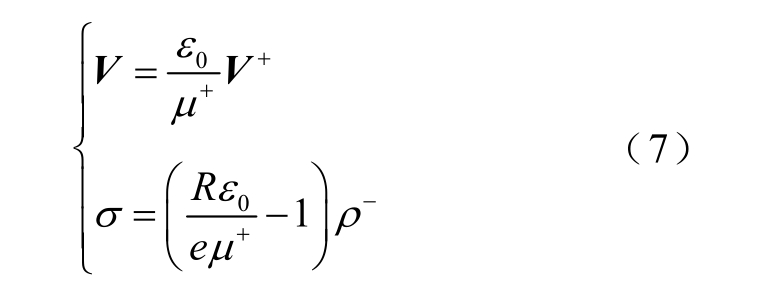
负离子情况对应的方程系数为
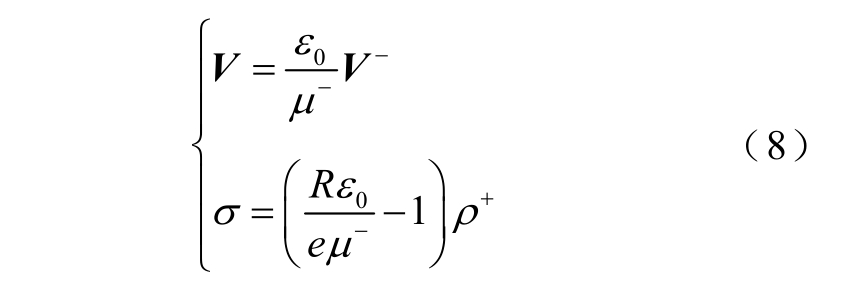
连续性方程对应的边界条件为
本文目标即是求解由式(6)和式(9)构成的边值问题。
2 基于误差传递方程的修正方法
本文方法的主要思路是:使用迎风有限元方法求解一般性问题;根据当前计算结果,推导数值解满足的误差传递方程,并使用迎风有限元求解相应的误差传递方程。将两次计算结果之和作为修正后的数值解。下面将详细介绍误差传递方程的推导与求解。
2.1 误差传递方程推导
为方便说明,以图1 所示节点示意图为例,将节点0 的相邻节点分为两类
式中,A+为节点0 以及相应的上游节点;A-为下游节点构成的集合。将偏微分方程式(6)离散为代数方程的方法可分为两类。

图1 节点示意图
Fig.1 Configuration around node
一类是显式离散

为简化表示,记Pi 为第i 个节点电荷密度的数值解, iρ 为第i 个节点电荷密度的真解,定义节点误差为
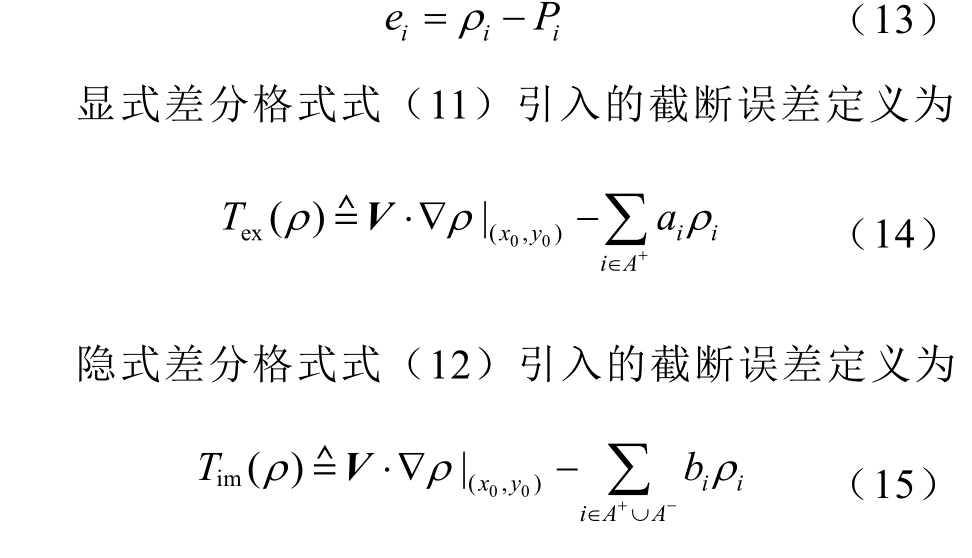
真解在任一点处均精确满足原方程式(6),将式(13)代入式(6)得到关于节点误差e 的方程为
将未知项ei 置于方程左侧,已知项Pi 置于右侧,整理得到关于e0 的一元二次方程为

将式(18)代入式(17)可得

式(20)左侧表示由上游节点传递给下游节点的误差,右侧表示数值解在节点0 处的残差。减小节点0 处局部网格尺寸,只能减小残差,而不能减小来自上游节点的误差,因此误差会在下游节点累积,数值解的整体通量守恒特性被破坏。
本文提出的修正方法将原始数值解P0 与该点处误差e0 之和作为修正后的解:修正前节点0 处数值解为P0,对应截断误差为Tex(ρ);修正后数值解为P0+e0,对应截断误差为Tim(ρ)+Tim(e)-Tex(e)。这里显式差分格式(式(11))对应迎风差分格式,而隐式差分格式对应基于梯度恢复技术具有超收敛特性的差分格式[19]。考虑到恢复得到的梯度具有高阶精度,关系为
即修正后截断误差远小于直接使用迎风差分格式后的截断误差,因此通过误差传递方程式(20)对原数值结果进行修正的确可以改善精度。
2.2 误差传递方程求解
2.1 节基于一般性问题(6)推导了相应的误差传递方程式(20)。本节将以实际问题(5)中的正离子为例,说明如何求解该方程。
记正、负离子浓度的数值解为 ,节点误差为
,节点误差为 ,而真实的正、负离子密度分布为
,而真实的正、负离子密度分布为
 对应反应项系数σ可写为
对应反应项系数σ可写为
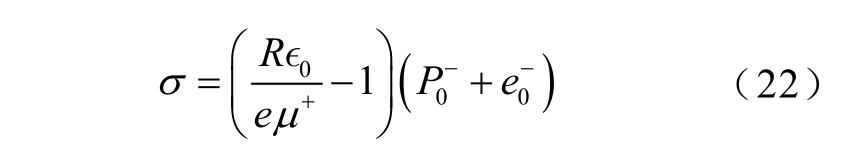
为保证关于  的误差传递方程式(20)可解,需要该一元二次方程对应的特征多项式非负,即
的误差传递方程式(20)可解,需要该一元二次方程对应的特征多项式非负,即
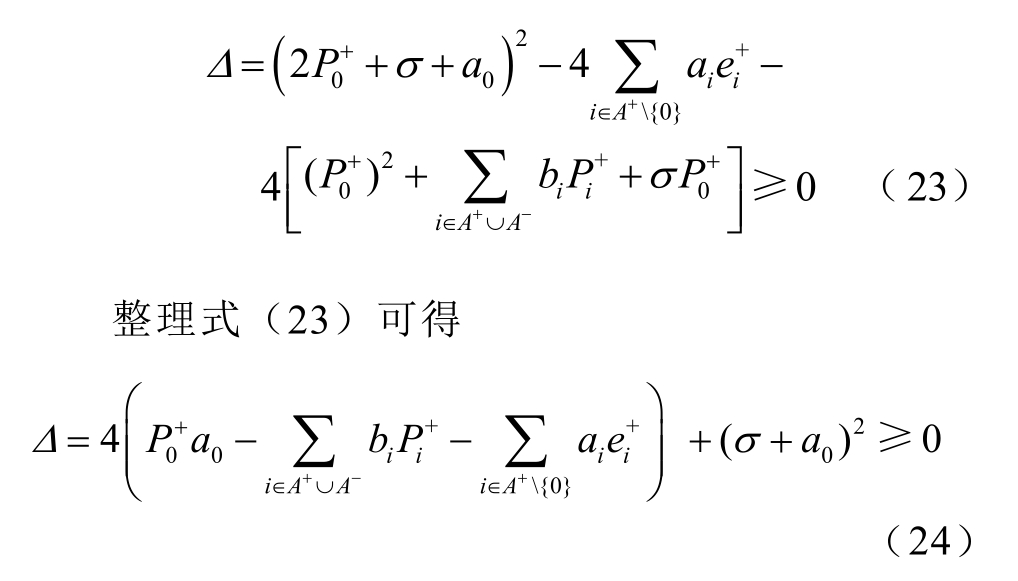
将式(14)和式(15)代入式(24),则有
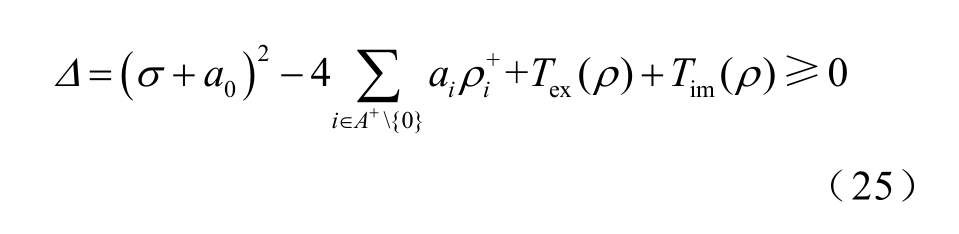
由于显式差分格式(11)为迎风差分格式,因此有

因此随着网格尺寸缩小,误差传递方程必然存在实数解为

因此选取r1 为对当前节点的误差估计,即
以上介绍了每个节点处误差传递方程的求解方法。在实际应用中,顺着流线方向顺序建立并求解定义在各节点处的关于误差的一元二次方程。如果当前节点对应的误差传递方程不存在实数解,则将该节点所处的局部区域进行加密,直至相应的误差传递方程存在实数解。
2.3 修正方法流程
针对泊松-连续性方程耦合系统式(1)的高精度计算方法具体流程如下:
(1)第k 步,根据前一步得到的正负离子密度计算(k-1)ρ+、(k -1)ρ-空间电位(k)φ 。
(2)使用基于迎风单元的有限差分方法计算连续性方程,得到新的数值电荷分布(k)P+、(k)P-。
(3)根据误差传递方程,给出正、负离子数值解的误差估计(k)e+和(k)e-。
(4)根据步骤(3)得到的误差估计对计算结果进行修正,得到修正后的电荷空间分布为(k)ρ+和(k)ρ-。
(5)比较第k-1 步计算结果与第k 步计算结果之间差异,如果大于阈值,k=k+1,返回步骤(1);如果小于阈值,输出结果。

图2 平行板模型下精度对比
Fig.2 Comparison of the maximum error under different methods
3 数值算例验证
3.1 平行板模型
平行板模型的上下极板位于y=±0.5m 处,上极板注入竖直向下离子流 2μA/m2,电场强度为20kV/m;下极板接地。该模型几何形状对称,存在解析解[20]。将空间电场设为已知量,那么待求解问题简化为连续性方程,即
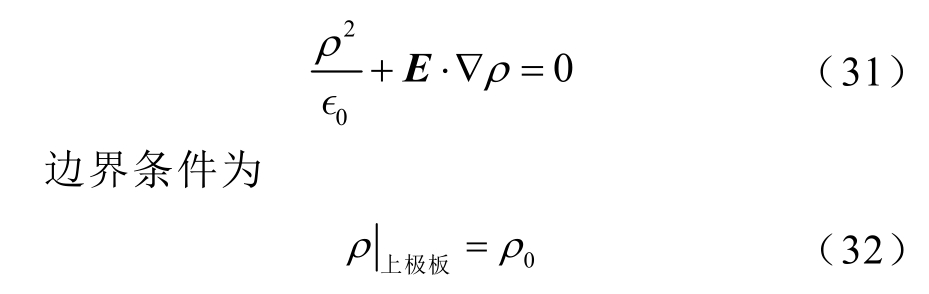
使用规则的三角网格剖分,数值解的相对误差与网格尺寸的关系如图2 所示。在相同网格下,修正方法的精度要远高于直接使用迎风有限元的计算精度:网格尺寸为1/128 时,迎风有限元方法对应的最大相对误差为1.1%,而修正方法对应的最大相对误差仅为0.08%;随着网格尺寸缩小,修正方法误差的收敛阶数高于迎风有限元方法,在该算例中修正方法的收敛阶数为1.5 阶,而原方法的误差收敛阶数为1 阶。
3.2 ±800kV 六分裂高压直流输电线路模型
本节将修正方法应用于电压等级为±800kV 的六分裂高压直流输电线路[21],模型的几何信息如图3 所示。
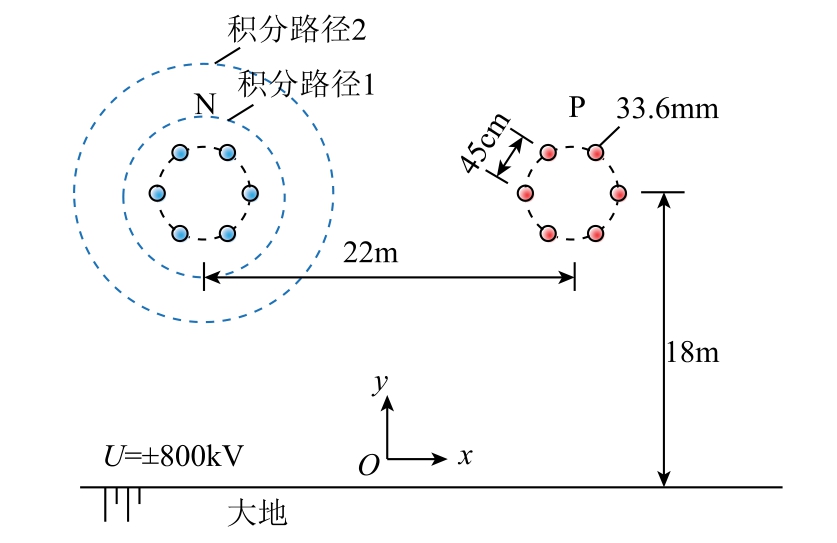
图3 ±800kV 六分裂高压直流输电线路模型
Fig.3 Configuration of the ±800kV six-bundle HVDC transmission line model
真实线路模型具有两个典型特征:分裂导线半径远小于整体计算区域的尺寸,大量网格集中在导线附近,而远离导线区域网格分布稀疏;导线附近电荷密度衰减剧烈,在远离导线区域电荷变化平缓。
仿真中导线表面起晕电场设置为
图 4 所示为两种方法得到的地面附近离子流分布,相差不大,且都位于测量结果范围内。为进一步比较导线与地面之间区域的计算精度,选取一系列围绕负极性导线的同心圆为积分路径,由于空间电荷具有通量守恒特性,通过各个积分路径的电晕电流通量应该相同。将通过负极性导线表面的电晕电流通量作为基准值,比较不同路径下通量误差,±800kV 高压直流输电线路不同积分路径通量守恒误差对比如图5 所示。由图5 可知,如果使用迎风有限元计算连续性方程,随着积分路径的半径逐渐扩大,通量误差逐渐增长至10%,将网格点数由11 312 点增加至23 988 点,并不能有效减小通量误差。如果使用修正方法求解连续性方程,可以将通量误差限制在2%以下。另外可以看到修正方法在进行了若干网格加密操作后耗时仅为 210s,不超过相同网格下原方法计算时长的两倍,即本文提出的修正方法能够付出较少的计算代价,有效提高计算精度,抑制误差的传递,使数值解满足通量守恒特性。

图4 ±800kV 高压直流输电线路地面离子流分布对比
Fig.4 Comparison of the ion density distribution on the ground level under different methods

图5 ±800kV 高压直流输电线路不同积分路径通量守恒误差对比
Fig.5 Comparison of the current flux error on different paths under different methods
4 结论
本文提出一种基于误差传递方程的修正方法,结合误差的传递特性,给出误差的合理估计,并对原数值解进行修正。该方法计算复杂度与迎风有限元方法相同,均为O(n),保持了迎风有限元方法计算简单这一特性的同时,使修正后的解具有更高精度,符合通量守恒特性,可广泛应用于离子流问题的求解。
本文仅对迎风有限元计算结果进行修正,修正后截断误差近似为Tex(e)。通过反复使用该方法,不断求解误差传递方程并进行修正,理论上可以将截断误差缩小至Tim(ρ),即通过若干次显式差分格式的计算,获得隐式差分格式的精度,相关结论有待进一步的验证。
[1] Maruvada P S, Janischewskyj W. Analysis of corona losses on DC transmission lines: I-unipolar lines[J].IEEE Transaction on Power Apparatus and Systems,1969, P45-88(5): 718-731.
[2] 田冀焕, 邹军, 刘杰, 等. 高压直流双回输电线路合成电场与离子流计算[J]. 电网技术, 2008, 32(2):61-70.Tian Jihuan, Zou jun, Liu Jie, et al. Calculation of total electric field and ionic current density of double-circuit HVDC transmission lines[J]. Power System Technology, 2008, 32(2): 61-70.
[3] 乔骥, 邹军, 袁建生, 等. 采用有限差分求解高压直流输电线路空间离子流场的新方法[J]. 电工技术学报, 2015, 20(6): 85-91.Qiao Ji, Zou Jun, Yuan Jiansheng, et al. A new finite difference based approach for calculating ion flow field of HVDC transmission lines[J]. Transactions of China Electrotechnical Society, 2015, 20(6): 85-91.
[4] Qiao Ji, Zhang Pengfei, Zhang Jiangong, et al. An iterative flux tracing method without deutsch assumption for ion-flow field of AC/DC hybrid transmission lines[J]. IEEE Transaction on Magnetics,2018, 54(3): 1-4
[5] 乔骥, 徐志威, 邹军, 等. 一种消除Deutch 假设的高精度迭代特征线方法求解高压直流输电线路离子流场[J]. 电工技术学报, 2018, 33(19): 4419-4425.Qiao Ji, Xu Zhiwei, Zou Jun, et al. A high-accuracy iterative method of characteristics without deutsch assumption for calculating ion-flow field of HVDC overhead lines[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4419-4425.
[6] Liu Jie, Zou Jun, Tian Jihuan, et al. Analysis of electric field, ion flow density, and corona loss of same-tower double-circuit HVDC lines using improved FEM[J].IEEE Transaction on Power Delivery, 2009, 24(1):482-483.
[7] Li Xin. Numerical analysis of ionized fields associated with HVDC transmission lines including effect of wind[D]. Manitoba: The University of Manitoba, 1997.
[8] Takuma T, Ikeda T, Kawamoto T. Calculation of ion flow fields of HVDC transmission lines by the finite element method[J]. IEEE Transaction on Power Systems, 1982, 1(12): 4802-4810.
[9] 甄永赞, 崔翔, 卢铁兵, 等. 离子流场中导体充电电位的计算[J]. 中国电机工程学报, 2011, 31(27): 8-13.Zhen Yongzan, Cui Xiang, Lu Tiebing, et al.Calculating charged electric potential of the conductor in ionized field[J]. Proceedings of the CSEE, 2011,31(27): 8-13.
[10] Huang Guodong, Ruan Jiangjun, Du Zhiye, et al.Highly stable upwind FEM for solving ionized field of HVDC transmission line[J]. IEEE Transaction on Magnetics, 2012, 48(2): 719-722.
[11] 杨扬, 陆家榆, 杨勇. 基于上流有限元法的同走廊两回±800kV 直流线路地面合成电场计算[J]. 电网技术, 2012, 36(4): 22-27.Yang Yang, Lu Jiayu, Yang Yong. Calculation of total electric field at the ground level under double-circuit±800kV DC transmission lines arranged on same corridor with upstream FEM method[J]. Power System Technology, 2012, 36(4): 22-27.
[12] 乔冀, 葛小宁, 邹军. 采用通量线-有限元混合方法求解有风条件下直流输电线路离子流场[J]. 电工技术学报, 2019, 34(5): 910-916.Qiao Ji, Ge Xiaoling, Zou Jun. A flux-tracing hybrid method for calculating ion-flow field of HVDC overhead lines in presence of wind[J]. Transaction of China Electrotechnical Society, 2019, 34(5): 910-916.
[13] 袁海燕, 傅正财. 基于有限元法的±800kV 特高压直流输电线路离子流场计算[J]. 电工技术学报. 2010,25(2): 139-146.Yuan Haiyan, Fu Zhengcai. Corona ionized field analysis of ±800kV HVDC transmission lines[J].Transaction of China Electrotechnical Society, 2010,25(2): 139-146.
[14] Qiao Ji, Zou Jun, Zhang Jiangong, et al. Ion-flow field calculation of HVDC overhead lines using a high-order stabilization technique based on Petrov-Galerkin method[J]. IET Generation, Transmission and Distribution, 2018, 12(5): 1138-1189.
[15] 乔骥. 交直流并行线路离子流与混合电场计算方法及应用研究[D]. 北京: 清华大学, 2018.
[16] Arthur J B, Zoltan J C, James F. Interfacing the finiteelement method with the method of characteristic field models[J]. IEEE Transactions on Industry Applications,1989, 25(3): 533-538.
[17] Tian Yi, Huang Xinbo, Tian Wenchao. Hybrid method of calculation of ion-flow fields of HVDC transmission lines[J]. IEEE Transaction on Dielectrics and Electrical Insulation, 2016, 23(5): 2830-2839.
[18] Qin Yuehui. Discrete error transport equation for error estimation in CFD[D]. Michigan: Michigan State University, 2004.
[19] Zienkiewicz O C, Zhu J Z. The super convergent patch recovery and a posteriori error estimates. Part 1: the recovery technique[J]. International Journal for Numerical Methods in Engineering, 1992, 33: 1331-1364.
[20] Martin M. Generation and measurement of dc electric fields with space charge[J]. Journal of Applied Physics,1981, 52(5): 3135-3144.
[21] Yin Han, Zhang Bo, He Jinliang, et al. Time domain finite volume method for ion-flow field analysis of bipolar high voltage direct current transmission lines[J]. IET Generation, Transmission and Distribution, 2012, 6(8): 785-791.