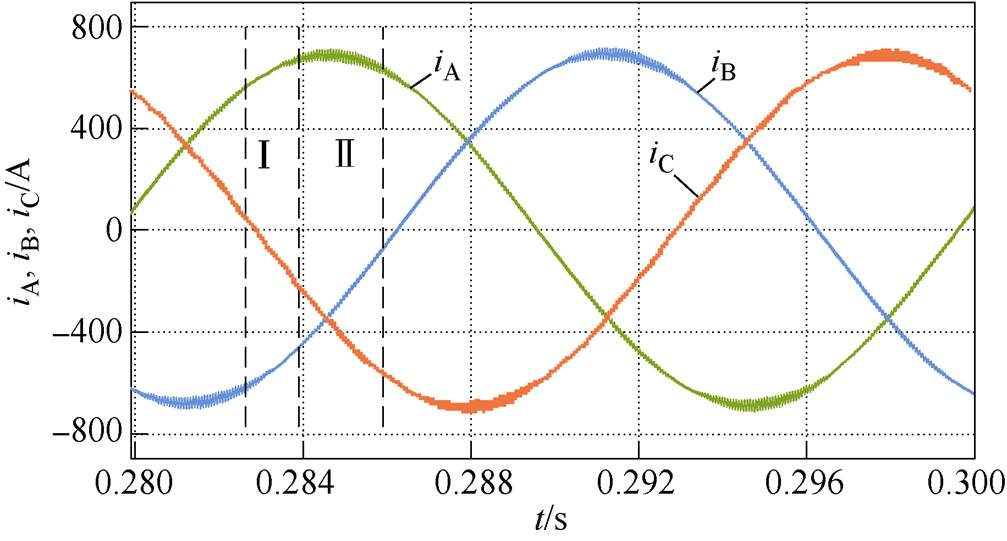
图1 采用固定开关频率的三相电流波形
Fig.1 Three-phase current waveforms with constant switching frequency
摘要 与广泛使用的固定开关频率脉宽调制(CSFPWM)策略相比,采用可变开关频率脉宽调制(VSFPWM)可在一定程度上消减电流功率谱密度尖峰,从而降低电机的窄带噪声和系统的传导电磁干扰(EMI)。该文首先基于坐标变换推导出感应电机定子电流纹波峰值的解析表达式,在此基础上提出一种减少开关损耗的VSFPWM策略:在满足最大纹波峰值的约束条件下,根据定子电流纹波与调制比及相位的关系,得到一种可变开关频率的确定方法,通过改变开关频率降低逆变器开关损耗。最后对所提出的调制策略进行理论分析和仿真验证,并搭建了15kW感应电机对拖实验平台,通过分析定子电流及MOSFET的温升情况,验证了可变开关频率脉冲宽度调制(PWM)策略的可行性和有效性。
关键词:感应电机 可变开关频率脉宽调制 电流纹波 开关损耗
按照直流侧电源特性,逆变器分为电压源型逆变器(Voltage Source Inverter, VSI)和电流源型逆变器[1]。由于结构简单、控制灵活、适应性强等优势,三相VSI已被广泛应用于电机驱动系统[2],其中,空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)因其输出电流波形好、直流侧电压利用率高且易于数字控制器实现等优点,成为应用于三相VSI最为广泛的调制算法[3-6]。目前,大多数三相VSI采用固定开关频率的调制方法,这种方法虽然简单且易于实现,但从频谱分析可知,高频谐波峰值基本集中在开关频率的整数倍附近,因其高频、带宽窄的特性,会引起电机振动,产生刺耳的窄带噪声[7-8]。为削减窄带噪声、减少电机振动以及抑制电磁干扰,一些学者基于统计和实验经验引入了随机脉冲宽度调制(Pulse Width Modulation, PWM)技术[8-10],随机PWM的开关频率在原固定开关频率上下某个频段(如2kHz)随机出现,但随机化产生的开关频率均值等于原固定频率,因而不能减少系统的开关损耗。
电流纹波是设计和控制三相逆变器的重要参数,电流纹波峰值会影响电机的最大转矩峰值和噪声幅度,对于关注输出电流最大偏差的应用,电流纹波要求通常定义为电流最大纹波峰值。对于固定开关频率脉宽调制(Constant Switching Frequency Pulse-Width-Modulation, CSFPWM),产生的电流纹波并不是均匀分布,如图1所示,在某些区域如Ⅰ区,三相电流纹波均小于最大纹波峰峰值,在该区域无需使用和Ⅱ区相同的开关频率。文献[11]通过计算共模电压表达式确定三相电流纹波最小有效值(Root Mean Square, RMS),提出了一种基于电流纹波最小RMS值的最优调制方法,但其采用的仍是固定开关频率。文献[12]介绍了单相逆变器基于时域的电流纹波分析,提出了两种具有可变开关频率脉宽调制(Variable Switching Frequency Pulse Width Modulation, VSFPWM)方案。文献[13]首次提出了一种使用戴维南等效电路的三相逆变器电流纹波预测方法,基于该电流纹波预测方法,一种应用于三相VSI的VSFPWM被提出[14]。进一步的实验结果表明,采用VSFPWM的电磁兼容性(Electro- magnetic Compatibility, EMC)更好、开关损耗更低、逆变器效率更高[15-16]。此外,相同的电流纹波分析已扩展到五相[17]和七相[18]逆变器。文献[19-20]对多相VSI的电流纹波峰峰值进行了比较。文献[21]对电流预测方法进行了总结。文献[22]提出了一种使用dq变换的新型电流纹波预测方法,该方法考虑了绕组电感的变化,使之更为通用。

图1 采用固定开关频率的三相电流波形
Fig.1 Three-phase current waveforms with constant switching frequency
前面所提出的电流纹波预测方法都是基于整个基波周期进行的,同时需要大量的在线实时计算,本文利用电流纹波矢量在三相实轴上的投影,得到三相电流纹波的表达式,通过对电流纹波的分析,发现三相电流纹波峰值在每个扇区内呈现相同的变化趋势,提出了一种基于电流纹波峰值的VSFPWM策略,该调制策略采用查表法,不需要对三相电流进行在线实时估计,保证不超过最大纹波峰值的同时,在电流纹波峰值较小处,通过降低开关频率,减少系统开关损耗,提高逆变器效率;并且该方法与随机PWM具有相同的优点,可削弱电机的声学噪声和抑制传导电磁干扰(Electromagnetic Inter- ference, EMI)。
带感应电机负载的三相VSI如图2所示,其中,Udc为直流母线电压;SA、SB和SC分别表示ABC三相桥臂开关状态,SA,B,C=1时,表示上桥臂导通,下桥臂关断;SA,B,C=0时,表示上桥臂关断,下桥臂导通。则三相桥臂对地输出电压uAO、uBO和uCO可分别表示为
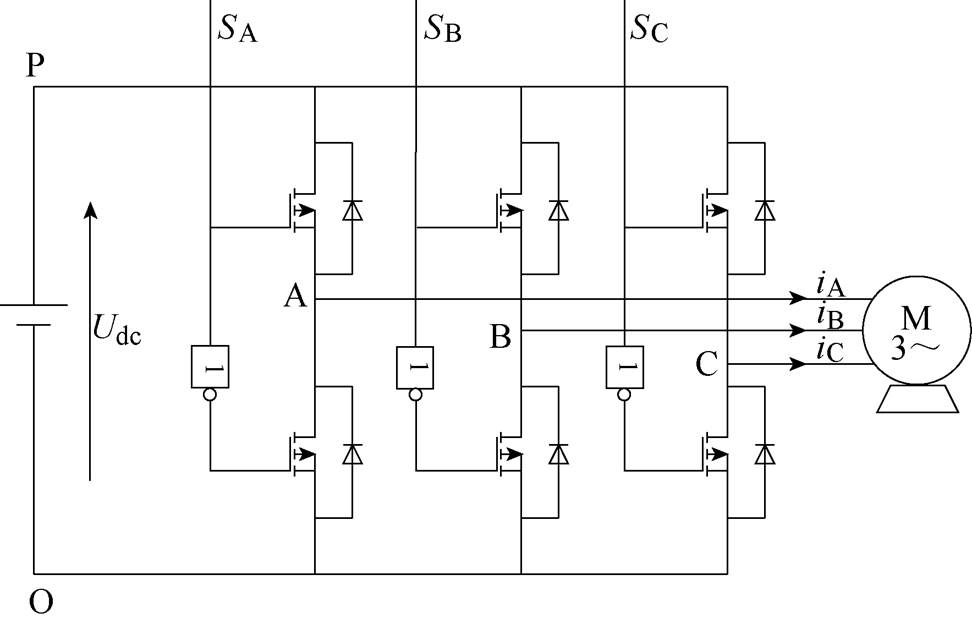
图2 带感应电机负载的三相VSI
Fig.2 Scheme of a PWM-VSI connected to a induction motor
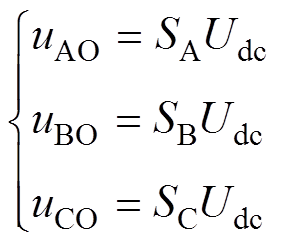 (1)
(1)根据SA,B,C取值不同,三相VSI具有8个开关状态,分别对应8个电压矢量,其中包含6个非零电压矢量(V1~V6)和两个零电压矢量(V0和V7)。这八种电压空间矢量如图3所示,在SVPWM中,参考电压矢量Vref是由相邻两个基本电压矢量进行合成的,因此在一个开关周期内,不同电压矢量作用时会产生不同的电压纹波矢量DV,从而在感应电机的定子绕组中产生电流纹波。
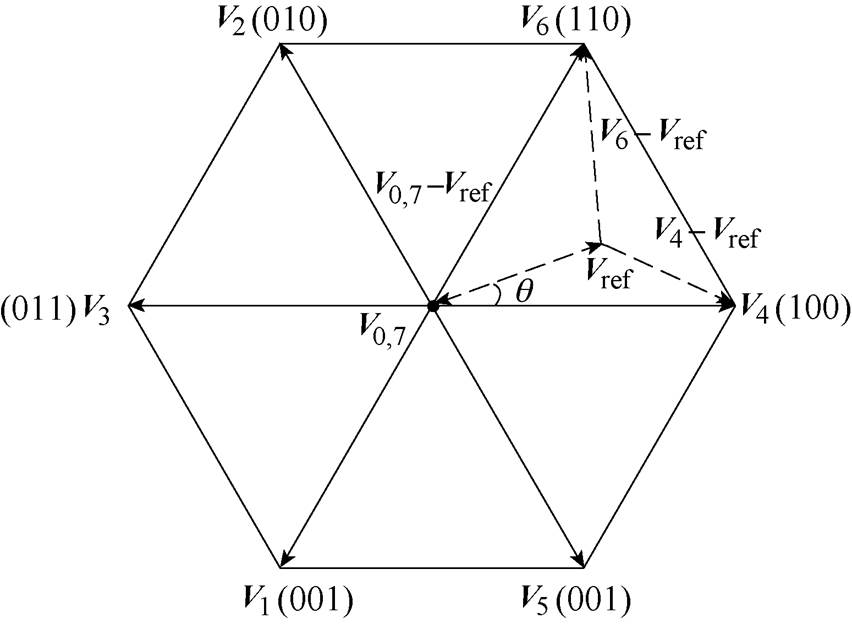
图3 电压空间矢量
Fig.3 Space voltage vector
定义电压纹波矢量DV和电流纹波矢量DI分别为
 (2)
(2)式中,Vi为当前时刻所使用的基本电压矢量;Ii为电流矢量的实际值;Iref为参考电流矢量。
图4为感应电机的T形等效电路模型,图4中,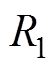 为定子电阻;
为定子电阻; 和
和 分别为折算到定子侧的转子漏感及电阻;
分别为折算到定子侧的转子漏感及电阻; 和
和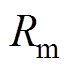 则分别为励磁电感和励磁电阻;
则分别为励磁电感和励磁电阻; 为定子侧感生的反电动势。由附录对感应电机的分析可知,输出电流纹波可表示为
为定子侧感生的反电动势。由附录对感应电机的分析可知,输出电流纹波可表示为
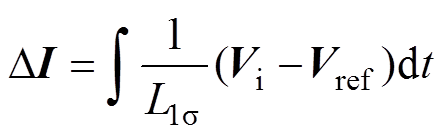 (3)
(3)式中,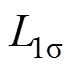 为定子漏感。
为定子漏感。
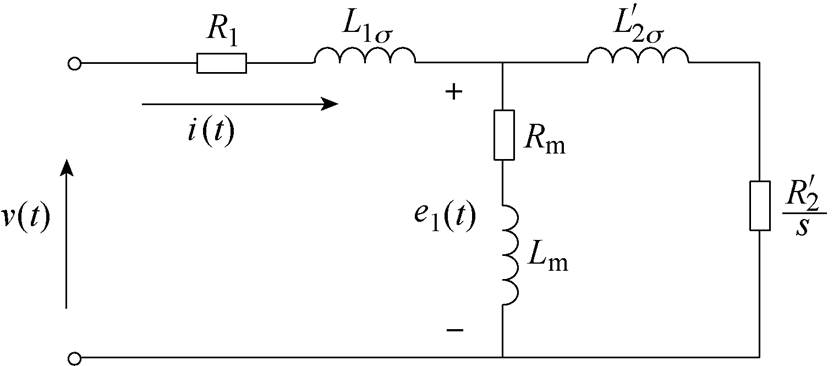
图4 感应电机T形等效电路模型
Fig.4 T-type equivalent circuit of induction motor
以第Ⅰ扇区为例,电流纹波矢量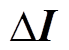 在一个开关周期中的轨迹如图5所示,由于电流纹波矢量在实轴(即A相相轴)的投影是A相电流纹波的瞬时值,故一个开关周期内的A相电流波形如图5右侧波形所示。
在一个开关周期中的轨迹如图5所示,由于电流纹波矢量在实轴(即A相相轴)的投影是A相电流纹波的瞬时值,故一个开关周期内的A相电流波形如图5右侧波形所示。
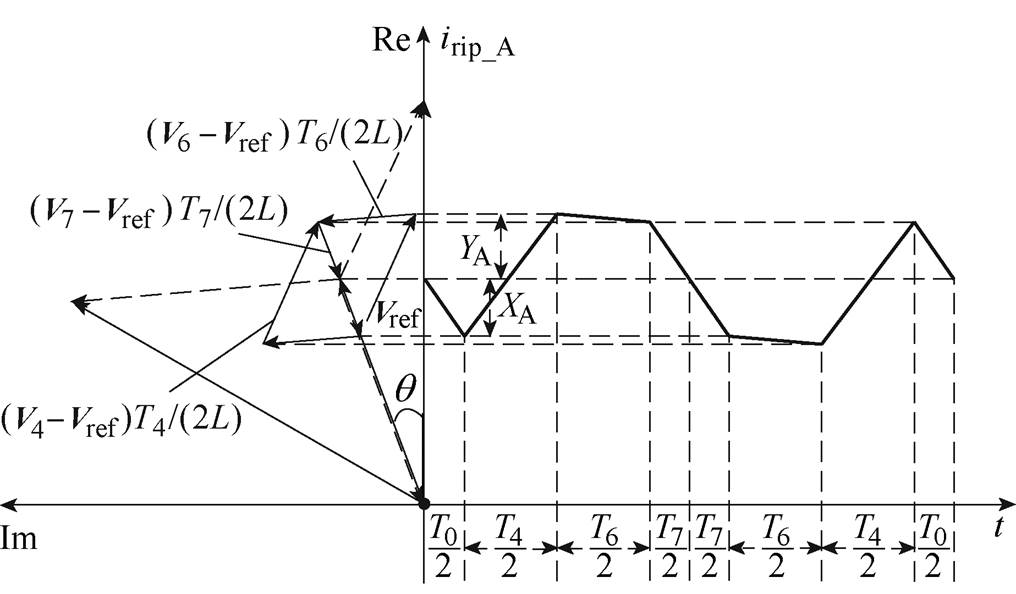
图5 电流纹波轨迹和A相电流波形
Fig.5 The current ripple vector locus and phase-A current waveform
由于电流纹波矢量轨迹的对称性,分析仅集中在开关周期的前半部分,由图5可知,前半个开关周期A相电流纹波DiA分为4段,则零矢量V0作用产生的纹波XA和有效矢量V4作用产生的纹波YA分别为
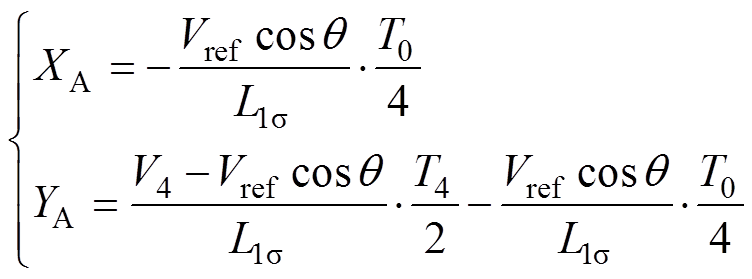 (4)
(4)式中,V4和Vref分别是V4和Vref的模;T0为零矢量V0,7的总作用时间;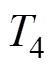 为有效矢量V4的作用时间,有
为有效矢量V4的作用时间,有
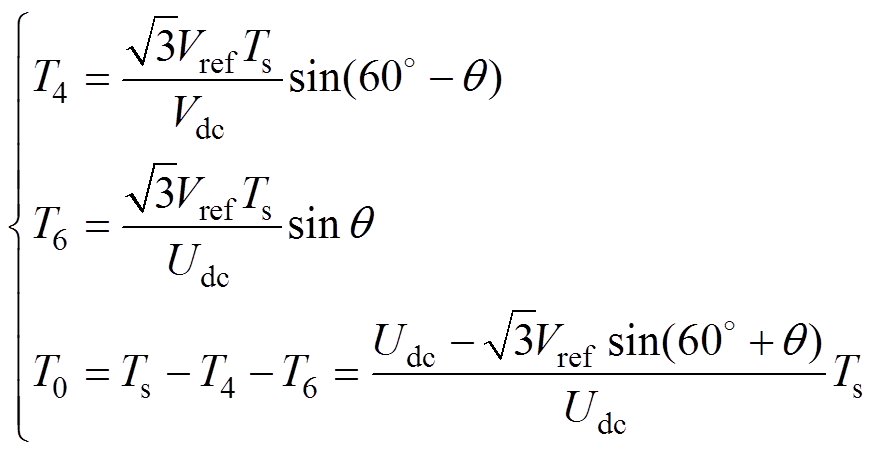 (5)
(5)
式中,Ts为开关频率;T6为有效矢量V6的作用时间。
令 ,对电流纹波
,对电流纹波 和
和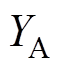 以
以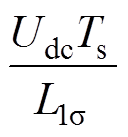 进行归一化,得
进行归一化,得
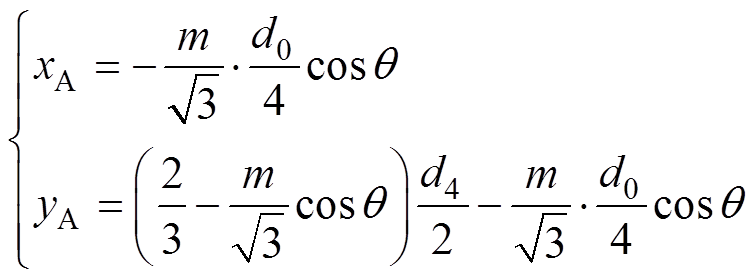 (6)
(6)其中
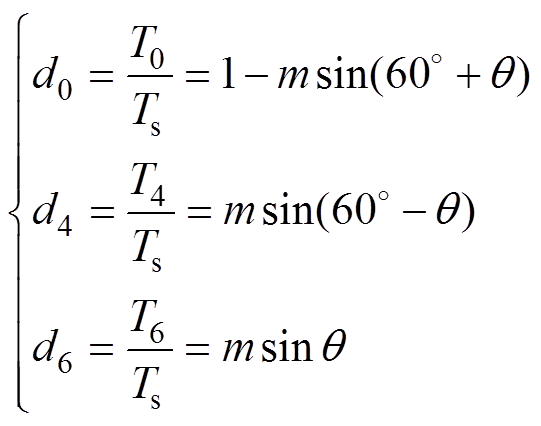 (7)
(7)
同理,将电流纹波矢量分别投影到B相相轴和C相相轴,得到 、
、 和
和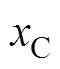 、
、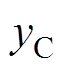 ,其具体表达式见表1。则一个开关周期内归一化后三相电流纹波峰值的最大值
,其具体表达式见表1。则一个开关周期内归一化后三相电流纹波峰值的最大值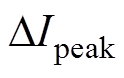 定义为
定义为
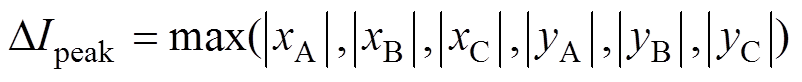 (8)
(8)表1 前半个开关周期电流纹波峰值表达式
Tab.1 The analytical expression of current ripple of the first half of the switching cycle

峰 值表达式 xA yA xB yB xC yC
扇区Ⅰ归一化后电流纹波最大峰值如图6所示。图6a显示了SVPWM下第Ⅰ扇区归一化的电流纹波峰值最大值随调制比 和相位
和相位 变化的三维图;图6b是当调制比
变化的三维图;图6b是当调制比 分别为0.3, 0.5, 0.7和1.0时,
分别为0.3, 0.5, 0.7和1.0时,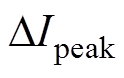 随着相位
随着相位 变化的波形。随着调制比增大,电流纹波峰值最大值逐渐增加。当调制比大于0.5后,电流纹波峰值最大值在整个扇区的变化幅度急剧上升,且均在
变化的波形。随着调制比增大,电流纹波峰值最大值逐渐增加。当调制比大于0.5后,电流纹波峰值最大值在整个扇区的变化幅度急剧上升,且均在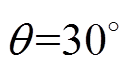 处取得最大。最终,在m =1.0,
处取得最大。最终,在m =1.0,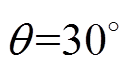 处取得整个线性调制区内的
处取得整个线性调制区内的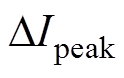 最大值。同时从图6可以看出,第Ⅰ扇区任意调制比下的电流纹波峰值最大值总是在相位
最大值。同时从图6可以看出,第Ⅰ扇区任意调制比下的电流纹波峰值最大值总是在相位 、
、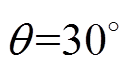 或
或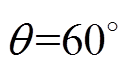 处取得最大,其中,
处取得最大,其中, 和
和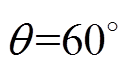 处的电流纹波峰值最大值相等,整个扇区电流纹波峰值最大值变化曲线关于
处的电流纹波峰值最大值相等,整个扇区电流纹波峰值最大值变化曲线关于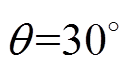 对称。
对称。
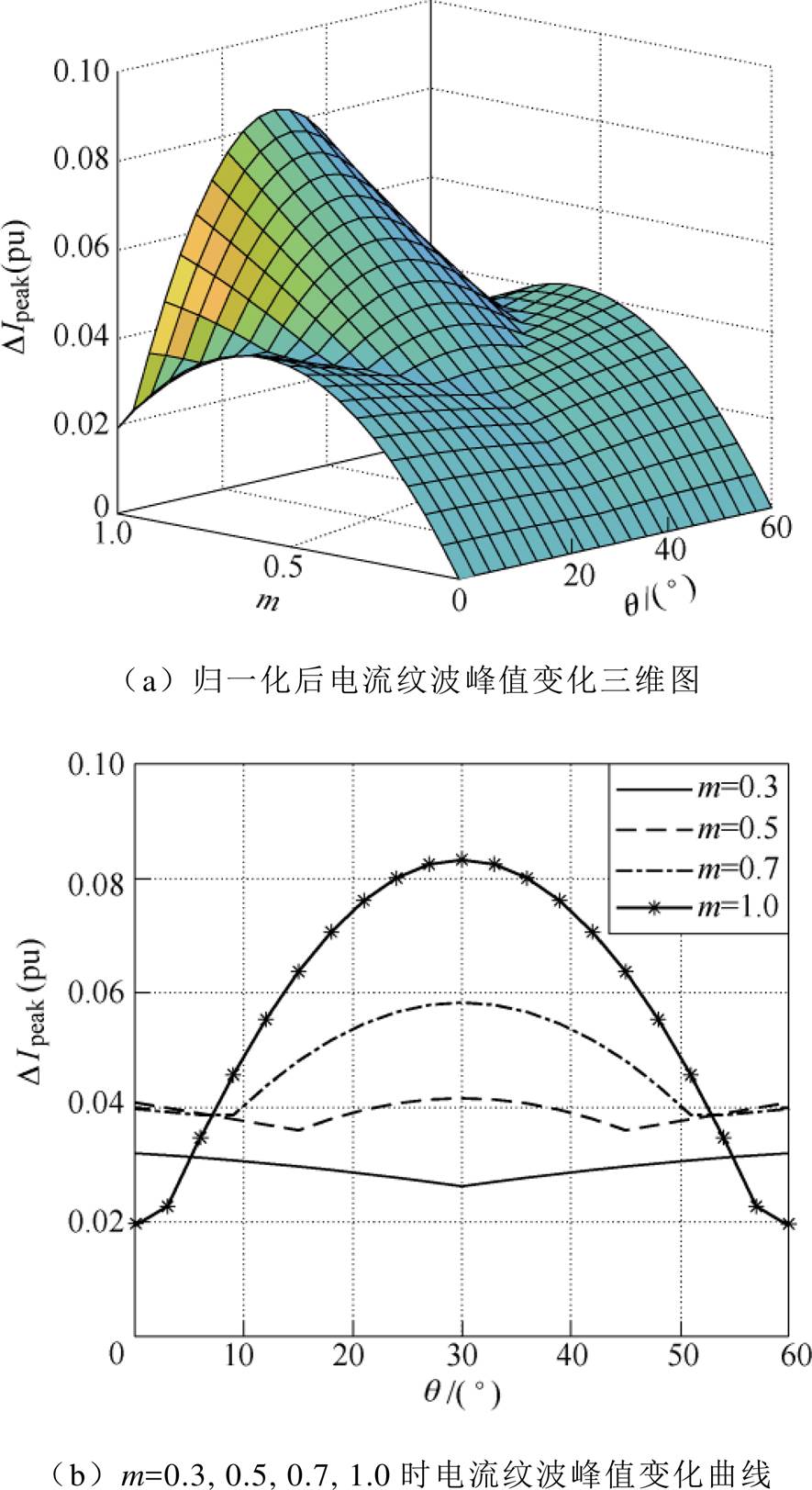
图6 扇区Ⅰ归一化后电流纹波最大峰值
Fig.6 Maximum normalized current ripple peak value in sector Ⅰ
另外五个扇区可得到和第Ⅰ扇区相同的电流纹波峰值变化曲线,A相电流纹波有效值 可表示为
可表示为
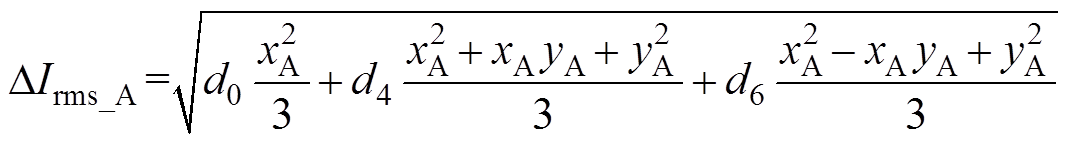 (9)
(9)整个基波周期内的电流纹波有效值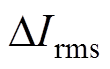 可表示为
可表示为
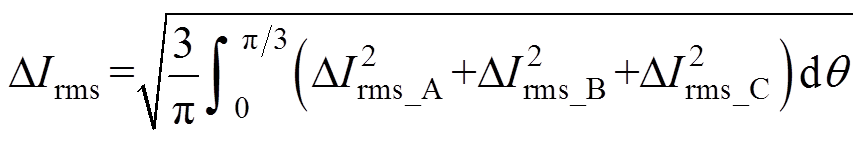 (10)
(10)
图7显示了整个基波周期内电流纹波有效值与调制比之间的关系,随着调制比的增加,电流纹波有效值逐渐增加,与文献[11]的分析结果一致。
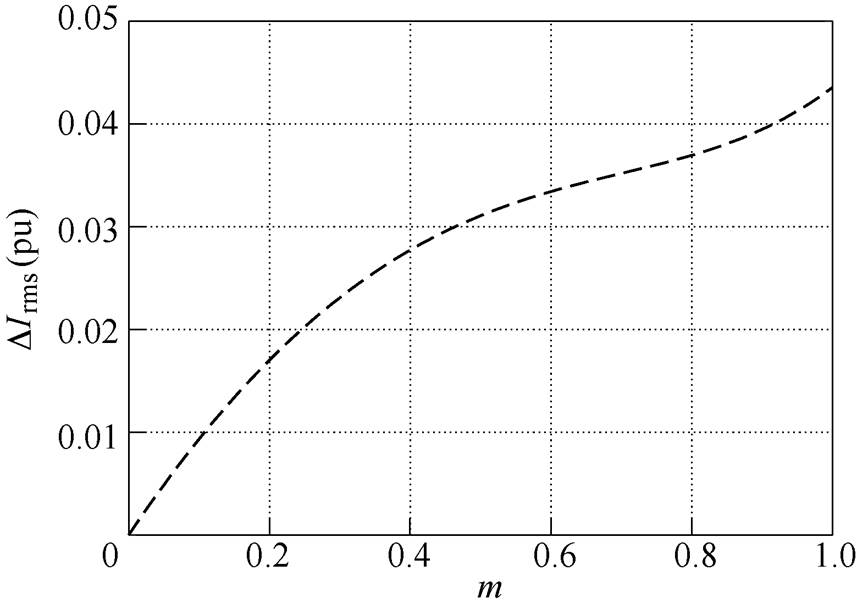
图7 整个周期内归一化电流纹波RMS
Fig.7 Normalized current ripple RMS value over one cycle
如第1节分析可知,电流纹波随调制比和相位的变化会呈现不同的峰值,因此,在保证不超过系统要求的最大纹波峰值的约束条件下,可以在峰值较小处降低开关频率,从而减少系统的开关损耗,这种调制方法称为VSFPWM。
第1节的纹波分析是在固定开关频率下进行的,假设开关周期 是
是 的函数,将电流纹波峰值以
的函数,将电流纹波峰值以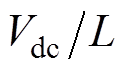 进行归一化,
进行归一化,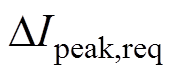 为系统要求最大归一化电流纹波峰值,则有
为系统要求最大归一化电流纹波峰值,则有
 (11)
(11)由图6可知,当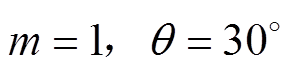 时,
时,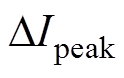 取得最大值,即此时对应最高开关频率
取得最大值,即此时对应最高开关频率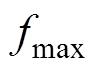 。为保证系统的稳定运行,需限定最低开关频率
。为保证系统的稳定运行,需限定最低开关频率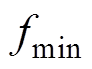 ,因此可变频率PWM的开关频率函数
,因此可变频率PWM的开关频率函数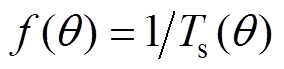 可表示为
可表示为
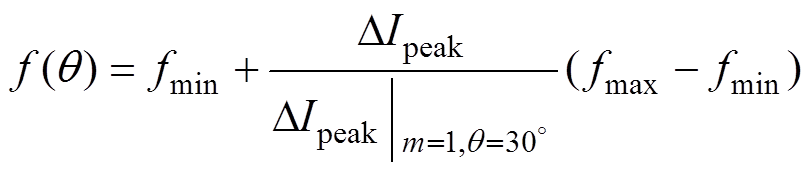 (12)
(12)
由第1节分析可知,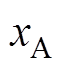 、
、 、
、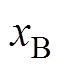 、
、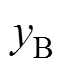 、
、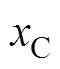 和
和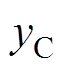 均是正弦函数,则
均是正弦函数,则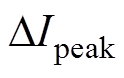 是正弦函数的集合,同时
是正弦函数的集合,同时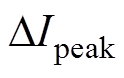 在每个扇区的变化趋势相同,故
在每个扇区的变化趋势相同,故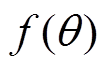 是周期信号,其周期为基波周期的1/6,因此所提出的VSFPWM属于正弦周期频率调制,由文献[23-25]可知,相比于CSFPWM,正弦周期频率调制可以有效地扩展谐波频谱,使原集中于载波周期整数倍处的能量分散到其附近频段,从而降低载波信号频谱峰值,达到削弱窄带噪声的效果。
是周期信号,其周期为基波周期的1/6,因此所提出的VSFPWM属于正弦周期频率调制,由文献[23-25]可知,相比于CSFPWM,正弦周期频率调制可以有效地扩展谐波频谱,使原集中于载波周期整数倍处的能量分散到其附近频段,从而降低载波信号频谱峰值,达到削弱窄带噪声的效果。
假设一个开关周期的开关损耗与电流线性相关,并且忽略电流纹波对开关损耗的影响,一个开关周期内的平均开关损耗可表示为
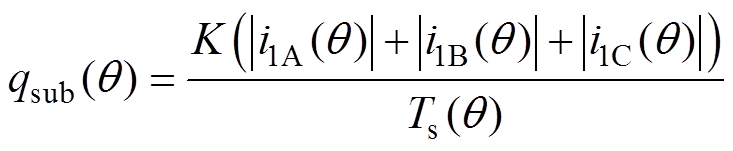 (13)
(13)式中,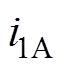 、
、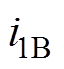 、
、 分别为三相基波瞬时电流;
分别为三相基波瞬时电流;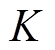 为一个常数,取决于直流母线电压和功率器件的动作时间。
为一个常数,取决于直流母线电压和功率器件的动作时间。
假设系统的功率因数为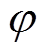 ,则式(13)可重写为
,则式(13)可重写为
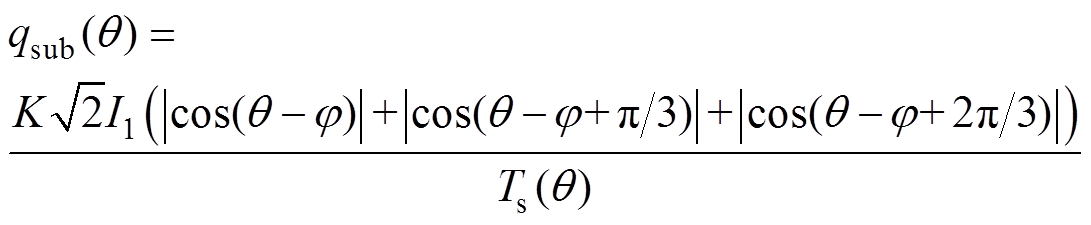 (14)
(14)其中
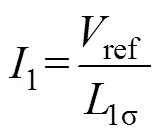
整个基波周期内的平均开关损耗为
 (15)
(15)将固定开关频率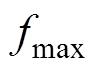 和可变频率函数
和可变频率函数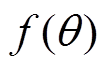 分别代入到式(14)和式(15)中,可分别得到固定频率调制平均开关损耗
分别代入到式(14)和式(15)中,可分别得到固定频率调制平均开关损耗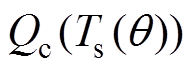 和可变频率调制的平均开关损耗
和可变频率调制的平均开关损耗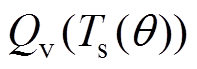 分别为
分别为
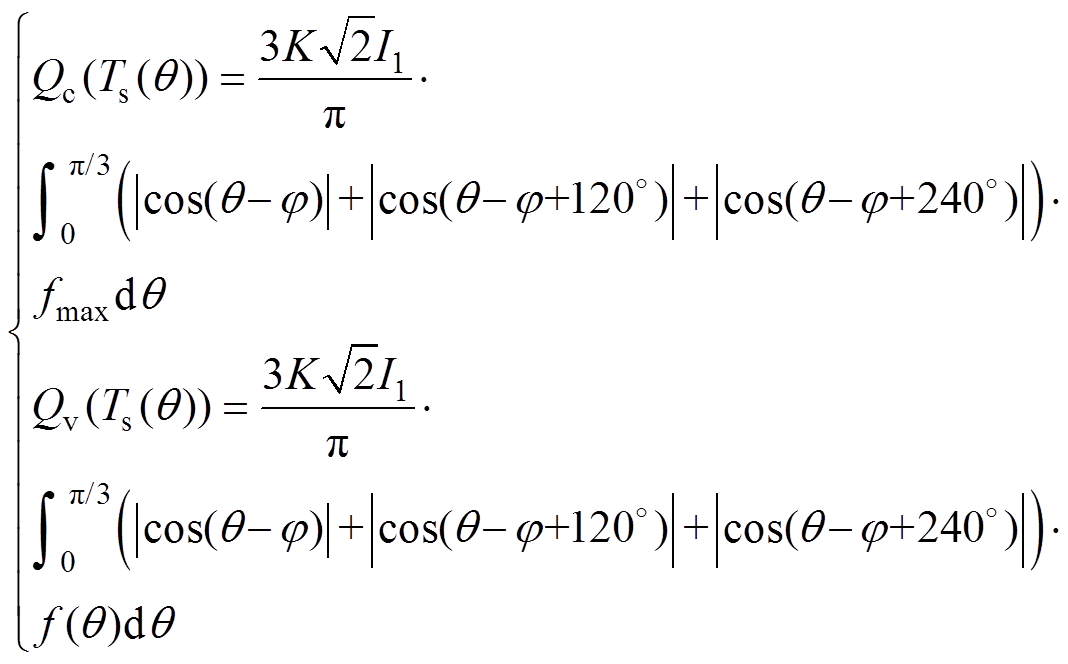 (16)
(16)
相对固定开关频率,减少的开关损耗所占比例可表示为
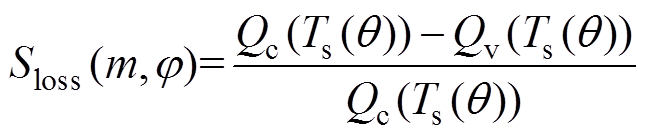 (17)
(17)假设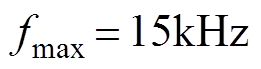 、
、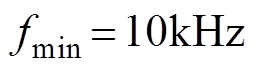 ,图8显示了可变开关频率PWM在不同调制比和功率因数下减少的开关损耗百分比,m =1.0时,能减少10%的开关损耗,调制比越小,减少的开关损耗越多;m =0.3时,能减少21%左右的开关损耗。
,图8显示了可变开关频率PWM在不同调制比和功率因数下减少的开关损耗百分比,m =1.0时,能减少10%的开关损耗,调制比越小,减少的开关损耗越多;m =0.3时,能减少21%左右的开关损耗。
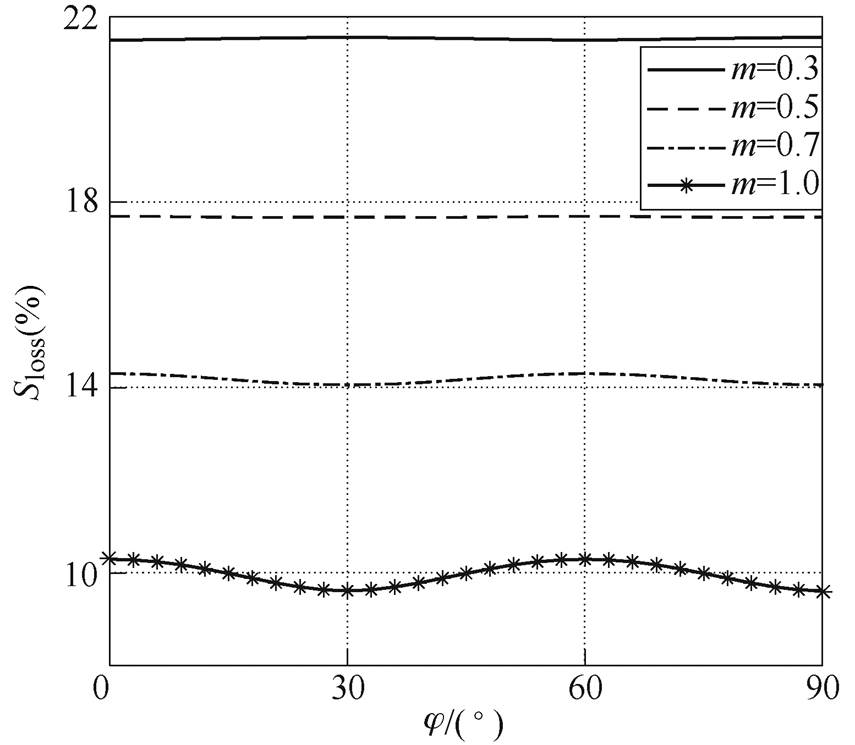
图8 m=0.3, 0.5, 0.7及1.0时Sloss随j 变化
Fig.8 Sloss with respect to of position space vector (j ) when m=0.3, 0.5, 0.7 and 1.0 respectively
为验证所提出的VSFPWM在电流纹波方面的变化,同时与文献[22]提出的另一种VSFPWM(用VSFPWM[22]表示)进行比较,在Matlab/Simulink中对其进行了模拟仿真。图9是m =0.5和m =0.9时对应的VSFPWM与VSFPWM[22]以及CSFPWM下A相相电流纹波的变化以及开关频率波形之间的对比。
由图9a可知,当m =0.5时,相对于CSFPWM而言,VSFPWM的开关频率降低了接近20%,且形状和图6b一致,相应地,电流纹波在一定程度上有所增加;相比于VSFPWM[22],VSFPWM增加的电流纹波较大。当m =0.9时,VSFPWM的开关频率相对CSFPWM降低较少,其电流纹波只是略有增加;而VSFPWM[22]的开关频率变化范围极大,最低达到了6kHz以下,故增加的电流纹波相对较大,在扇区切换处尤为明显,如图9b所示。
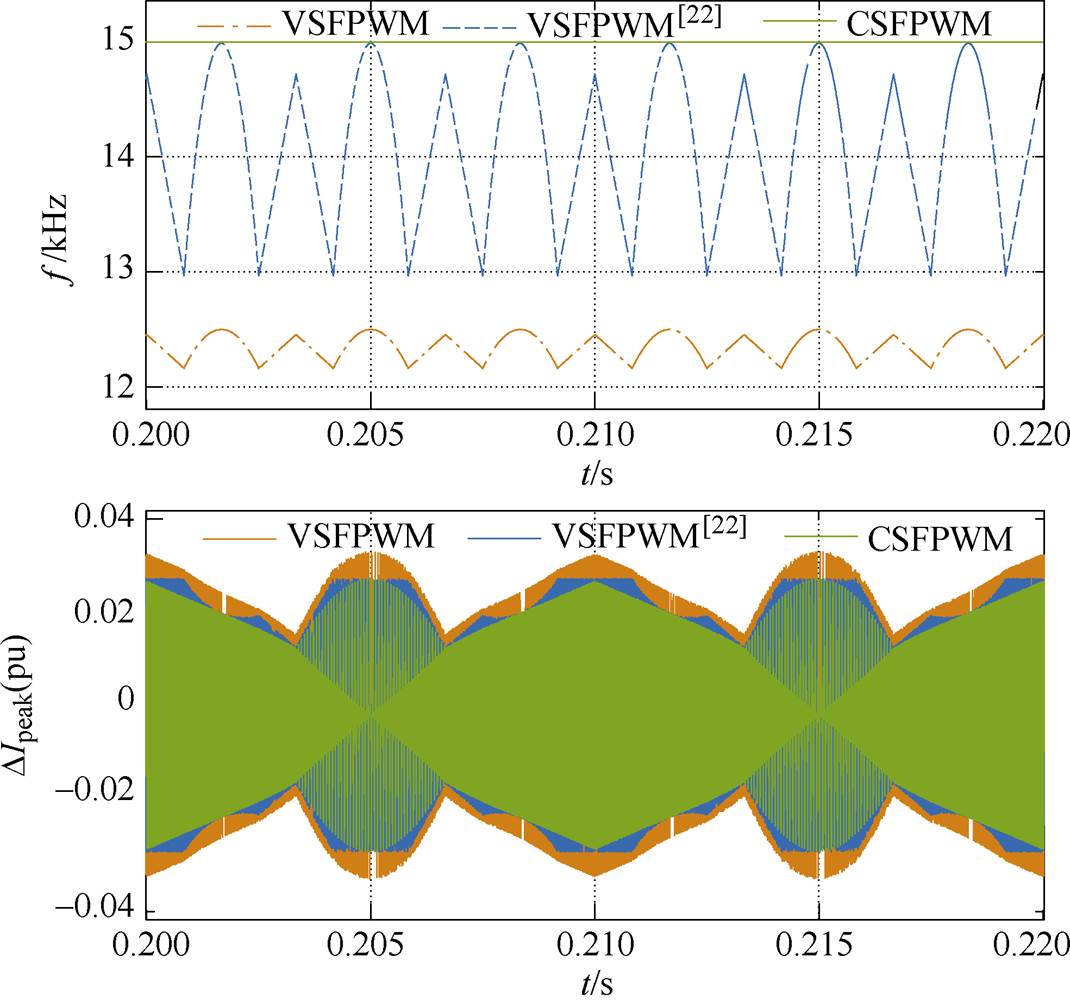
(a)m=0.5
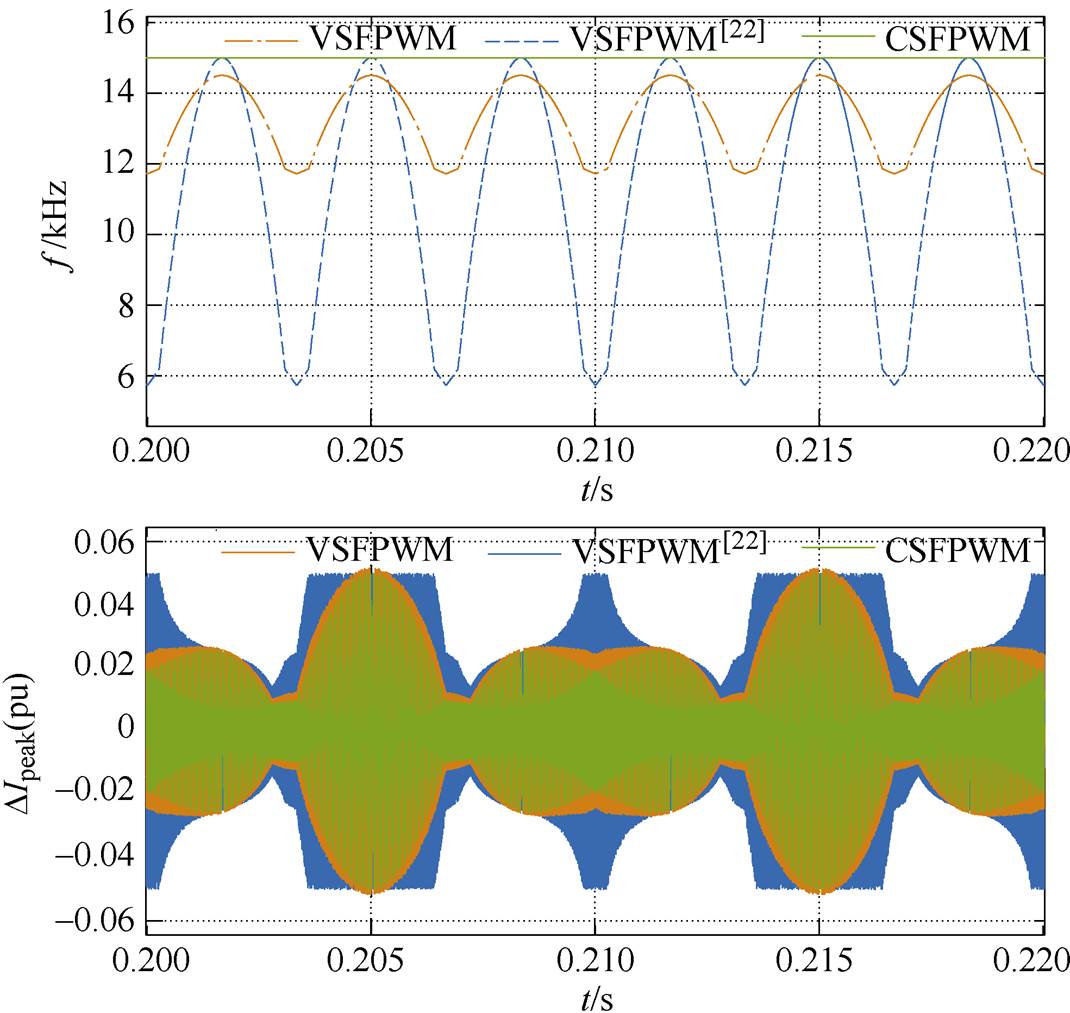
(b)m=0.9
图9 三种调制下A相电流纹波以及开关频率对比
Fig.9 Comparison of phase-A current ripple and switching frequency between CSFPWM, VSFPWM and VSFPWM[22]
为验证提出的VSFPWM是否能够降低开关损耗,并与VSFPWM[22]进行对比,根据英飞凌提供的数据手册,在Simulink中建立了AIKQ120N60CT的开关损耗模型,并进行仿真得到表2,其中,整个表格在输出电流为460A,感应电机稳定工作1s后的工况下测得。由表2可知,开关损耗仿真结果与图8完全吻合,任意调制比下,VSFPWM的开关损耗较CSFPWM均有不同程度减少,且调制比越小时,开关损耗减少得越多。VSFPWM[22]则与本文所提出的VSFPWM相反,随着调制比的增大,开关损耗减少得越多,当m<0.6时,减少比例均在10%以下,并且当调制比m=0.65时,VSFPWM[22]与本文提出的VSFPWM减少的开关损耗基本相等。
以m =0.7为例,对三种调制下A相电流分别进行快速傅里叶分析(Fast Fourier Transform, FFT)分析。m =0.7时CSFPWM和VSFPWM高频谐波对比如图10所示,相比于CSFPWM,VSFPWM和VSFPWM[22]下的A相电流总谐波畸变率(Total Harmonic Distortion, THD)分别增加了0.12%和0.2%。但VSFPWM载波频率处谐波含量峰值却比CSFPWM降低了0.1%,VSFPWM[22]则是降低了0.2%,两种VSFPWM均将原来集中在开关频率倍频处的高频谐波峰值分散到开关频率变化的频段内,使之谐波能量得以分散扩展,而VSFPWM[22]扩展地更均匀。
表2 m=0.3, 0.5, 0.7及1.0时开关损耗
Tab.2 Switching energy losses when m=0.3, 0.5, 0.7 and 1.0 respectively

调制比m开关损耗/J减少比例(%) CSFPWMVSFPWMVSFPWM[22]VSFPWMVSFPWM[22] 0.32 3661 8832 18820.417.52 0.52 3871 9692 22617.516.74 0.72 3842 0191 92715.3119.17 1.02 4272 1471 80011.5325.83
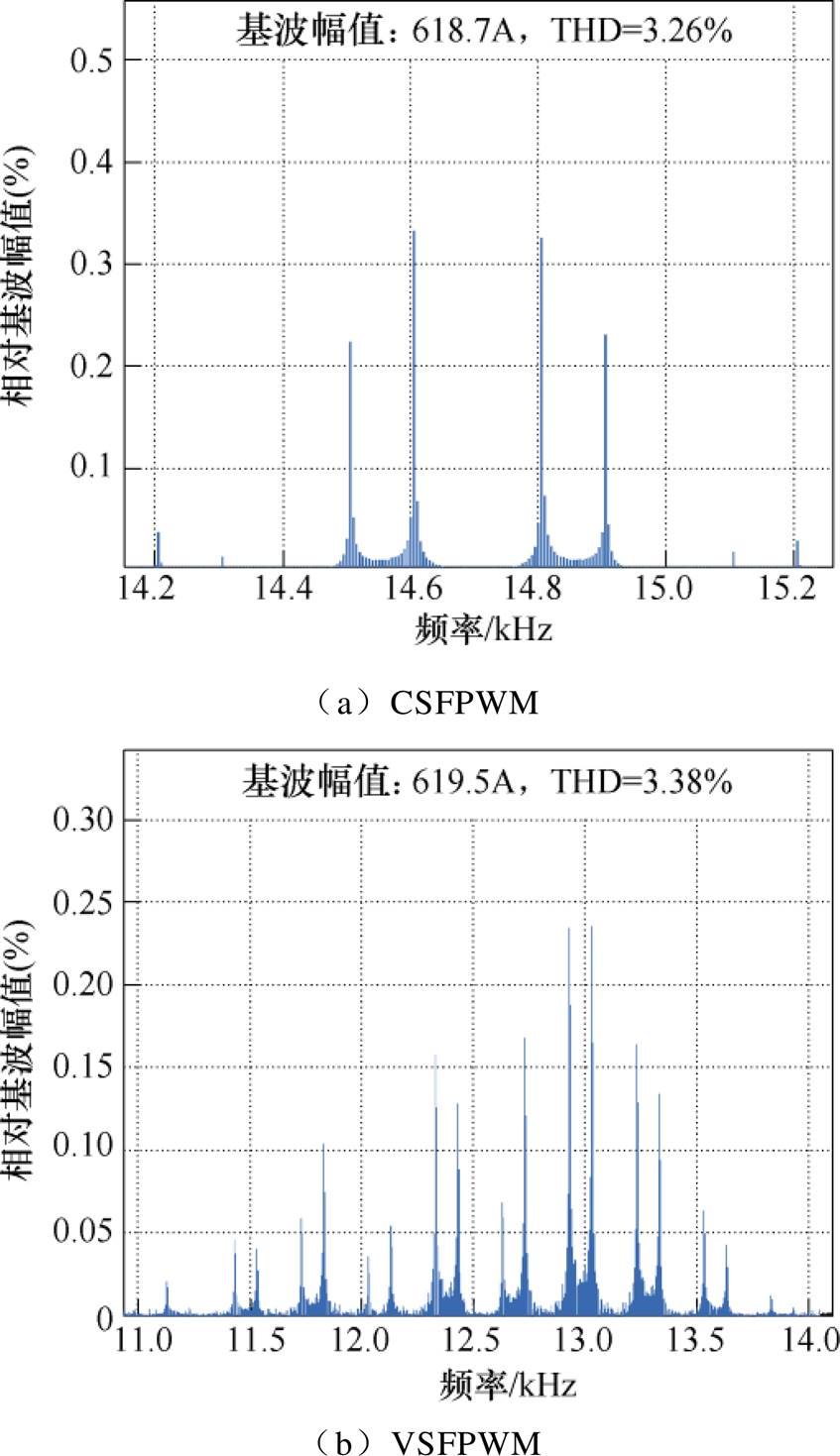
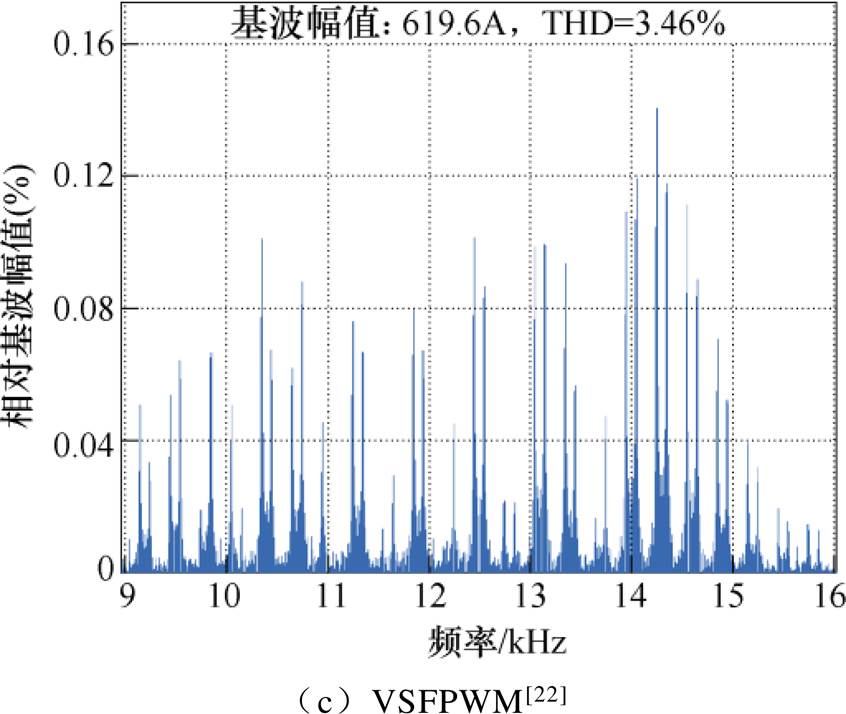
图10 m=0.7时三种调制下高频谐波对比
Fig.10 Comparison of high frequency harmonic between CSFPWM and VSFPWM and VSFPWM[22] when m=0.7
为验证VSFPWM的有效性,搭建了如图11所示的感应电机对拖实验平台,并进行对拖实验。该平台采用TI的TMS320F28069作为主控芯片,选取MOSFET作为开关器件,CSFPWM固定开关频率设为15kHz,VSFPWM开关频率通过软件查表获得,感应电机转速设定为3 000r/min,定子电流为300A。如图11所示,左边感应电机采用恒压频比控制,作为发电机拖动右边的感应电机运行,其中,感应电机的参数见表3。

图11 感应电机对拖实验平台
Fig.11 The dragging platform for Induction motor
表3 感应电机参数
Tab.3 Induction motor parameters

参 数数 值 额定功率P/kW15 定子漏感L1s/mH19.32 转子漏感L1s/mH21.43 励磁电感Lm/mH1.1 定子电阻R1/mW11.09 转子电阻R1/mW6.89
图12为所提出的VSFPWM的控制流程,利用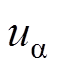 和
和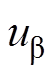 计算出此时的调制比m和相位
计算出此时的调制比m和相位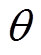 ,然后通过查表获得变化的开关频率,并应用于PWM模块中。利用查表法对VSFPWM[22]进行实验,以便与本文所提出的VSFPWM进行对比。
,然后通过查表获得变化的开关频率,并应用于PWM模块中。利用查表法对VSFPWM[22]进行实验,以便与本文所提出的VSFPWM进行对比。
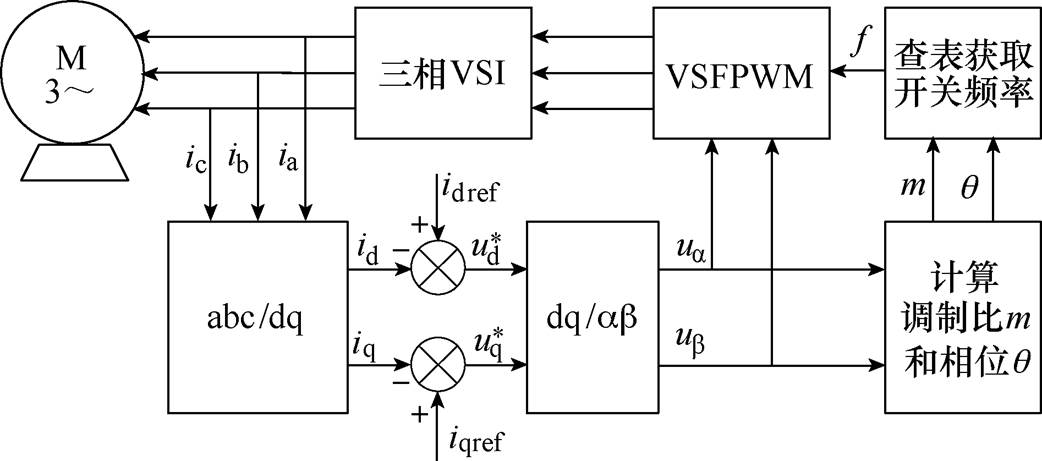
图12 VSFPWM调制流程图
Fig.12 Flow diagram of VSFPWM
本文在调制比m=0.3, 0.5, 0.7及1.0时,分别对采用CSFPWM和VSFPWM的定子电流进行测量、分析,得到两种调制算法下定子电流相位分别等于0°和90°处的纹波峰峰值,见表4。由第1节分析可知,第Ⅱ扇区和第Ⅰ扇区的电流纹波峰值变化相同,故90°对应的纹波峰值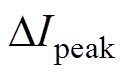 与第Ⅰ扇区30°处峰值相等。由表4可知,提出的VSFPWM在每个调制比以及相位处的电流纹波峰峰值都有不同程度的增加,但都不超过CSFPWM对应的最大电流纹波峰峰值,即48A,满足VSFPWM提出的约束条件。VSFPWM[22]在调制比较小(
与第Ⅰ扇区30°处峰值相等。由表4可知,提出的VSFPWM在每个调制比以及相位处的电流纹波峰峰值都有不同程度的增加,但都不超过CSFPWM对应的最大电流纹波峰峰值,即48A,满足VSFPWM提出的约束条件。VSFPWM[22]在调制比较小(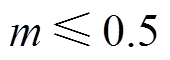 )时,其电流纹波均比VSFPWM小;但当
)时,其电流纹波均比VSFPWM小;但当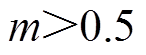 时,其电流纹波随着调制比的增大而急剧增加,m =1.0时定子电流出现严重畸变,电流纹波峰峰值均远远超过CSFPWM最大值。
时,其电流纹波随着调制比的增大而急剧增加,m =1.0时定子电流出现严重畸变,电流纹波峰峰值均远远超过CSFPWM最大值。
表4 m=0.3, 0.5, 0.7及1.0时电流纹波峰峰值
Tab.4 Current ripple peak-to-peak value when m=0.3, 0.5, 0.7 and 1.0 respectively

电流纹波峰值/A 调制比mCSFPWMVSFPWMVSFPWM[22] 0°90°0°90°0°90° 0.3162424321628 0.5243232362836 0.7324040484856 1.02448404872112
表5列出了三种调制算法下的定子电流THD,虽然VSFPWM在m=0.3, 0.5, 0.7及1.0的THD均比CSPWM大,但增幅均很小;m =0.7时THD增加最大,也仅增加了0.38%。当m<0.5时,VSFPWM[22]增加的THD小于VSFPWM;当m>0.5时,随着调制比的增加,VSFPWM[22]的THD也相应地增加,且增幅越来越大。
表5 m=0.3, 0.5, 0.7及1.0时A相电流THD
Tab.5 THD of phase-A current when m=0.3, 0.5, 0.7 and 1.0 respectively

调制比mTHD(%) CSFPWMVSFPWMVSFPWM[22] 0.33.093.153.14 0.52.973.133.21 0.73.193.575.70 1.03.563.6618.59
为验证所提出的VSFPWM在减少开关损耗方面的效果,利用FLUKE热成像仪对控制器的MOSFET进行温升实验。本文通过比较系统达到稳定后的60s前后MOSFET表面温度,间接反映两种调制算法的开关损耗大小关系,CSFPWM、VSFPWM和VSFPWM[22]温升对比如图13所示。其中,由于当调制比m =0.3时,定子电流很难一直保持为300A,故m =0.3的温升实验定子电流保持为250A,从图13可以看出,三种调制算法在m =0.3时温升明显低于其他三种工况。
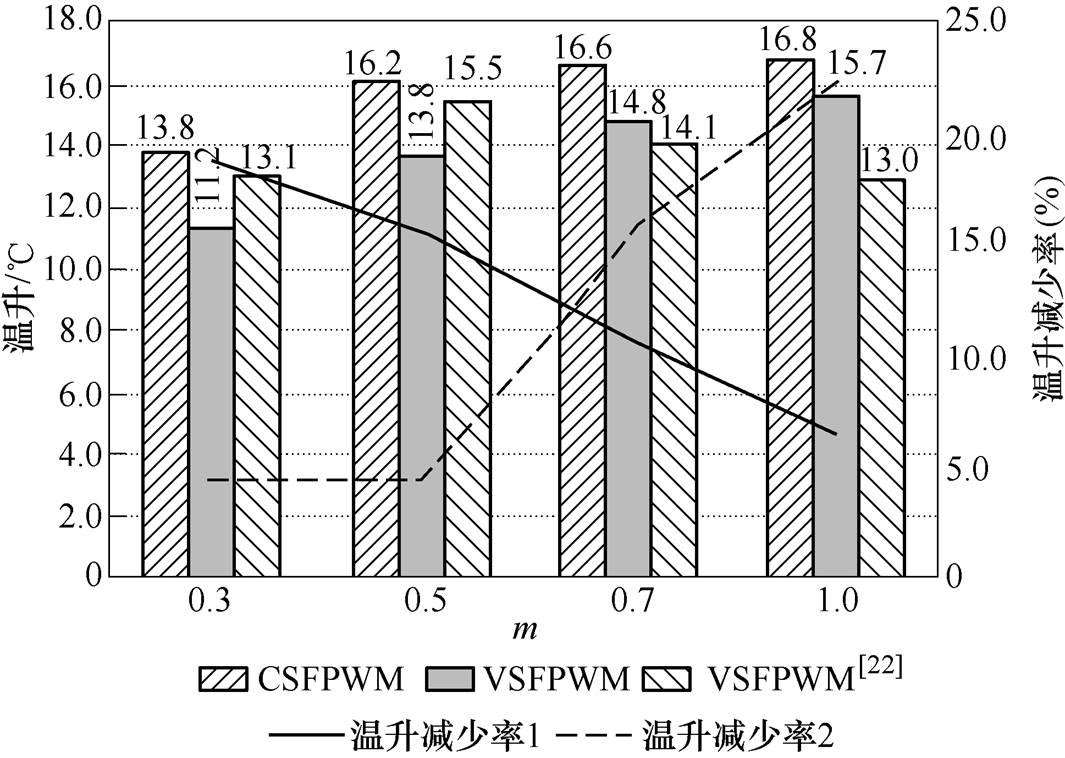
图13 CSFPWM、VSFPWM和VSFPWM[22]温升对比
Fig.13 Comparison of temperature rise between CSFPWM, VSFPWM and VSFPWM[22]
由于定子电流基波幅值始终保持为恒定值(除m =0.3外,定子电流有效值都始终保持为300A),开关损耗基本只与开关频率相关,因此随着调制比的增加,CSFPWM基本不变,而VSFPWM的温升越来越大,且均小于前者,VSFPWM[22]的温升则是越来越小。图13中,实折线反映的是VSFPWM的温升减少率,虚折线则反映的是VSFPWM[22]的温升减少率,分别用于反映使用VSFPWM和VSFPWM[22]减少的开关损耗百分比。对于VSFPWM,当调制比m =0.3时,温升减少率达到了18.8%;调制比m =1.0时,温升减少率只有6.55%。对于VSFPWM[22]而言,当m<0.5时,温升减少率基本不变,维持在4.3%;当m>0.5时,随着调制比增加,温升减少率逐渐增加,m =1.0时取得最大值,达到了22.62%。考虑到散热、测量等引起的误差,实验结果和2.2节的分析基本吻合。
以m =1.0为例,对采集的三种调制算法定子电流进行功率谱密度(Power Spectral Density, PSD)分析,如图14所示。由图14a可知,CSFPWM的功率谱在开关频率(15kHz)即其倍频处出现较高的尖峰,这些尖峰会引起电机的窄带噪声和增加系统传导EMI。图14b显示VSFPWM的最高尖峰出现在13.5kHz附近,证明其降低了开关频率的平均值。同时VSFPWM在开关频率及其倍频处的尖峰分布明显较CSFPWM范围更宽,且开关频率的1~3倍频处峰值分别降低了5dB/Hz、7dB/Hz和8dB/Hz。VSFPWM[22]的PSD非常平稳,基本没有明显尖峰,如图14c所示,故其电机噪声较前两种最小。
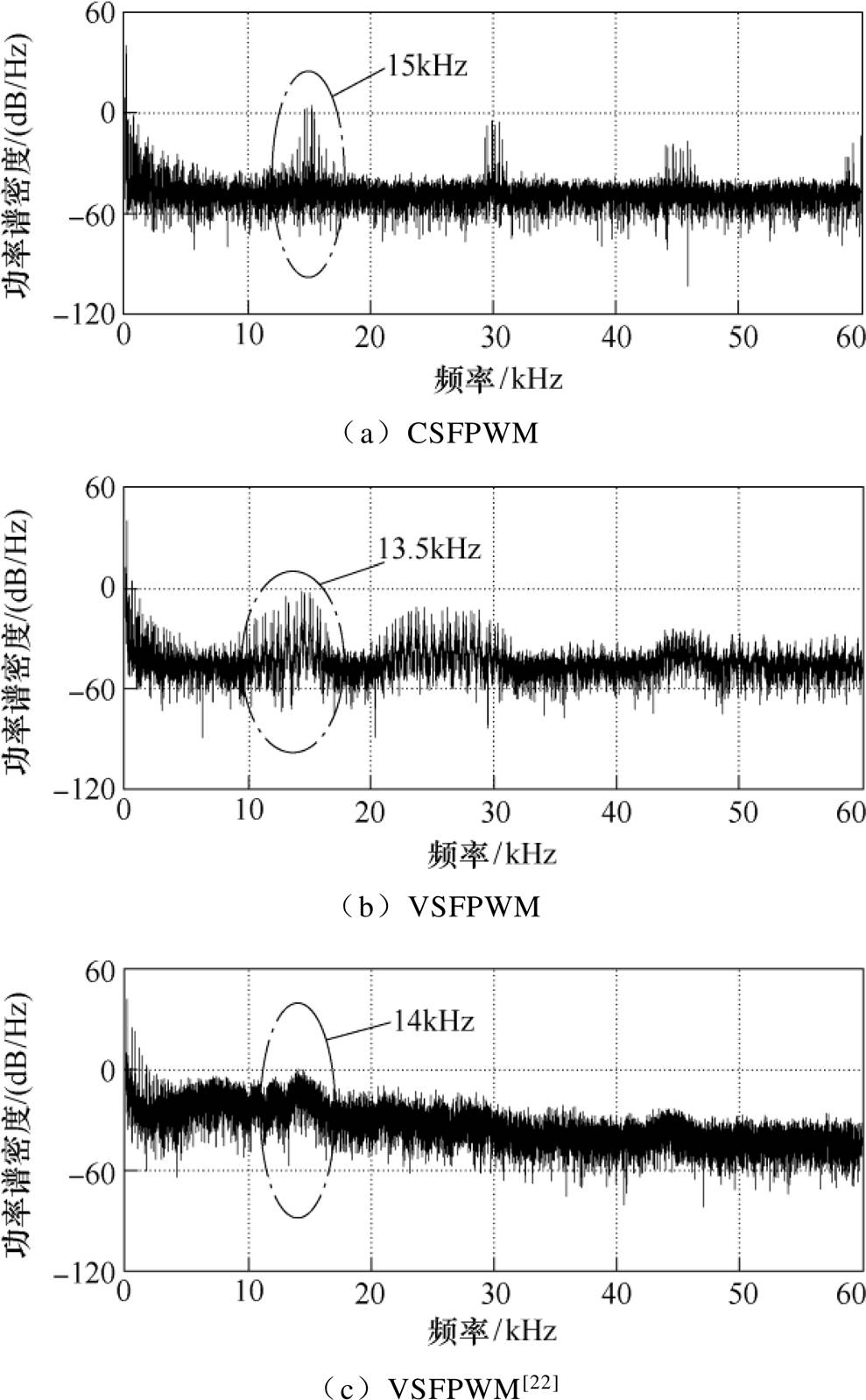
图14 m=1.0时电流PSD对比
Fig.14 Comparison of PSD when m=1.0
综合上述纹波峰峰值、温升情况以及PSD三个方面的实验分析与比较,当m<0.5时,VSFPWM[22]的电流纹波峰值和THD均小于本文所提出的VSFPWM,但其开关损耗减少得较少;当m>0.5时,虽然VSFPWM[22]减少的开关损耗比本文提出的VSFPWM多,PSD抑制效果更好,但其电流THD和电流纹波峰值远远大于本文VSFPWM,且随着调制比的增加,其电流波形畸变越严重。本文提出的VSFPWM在不超过系统要求的最大纹波峰值的情况下,通过改变开关频率,减少了逆变器开关损耗,且电流THD增幅很小,同时能够降低电机的窄带噪声,证明了该调制算法的有效性。
本文针对感应电机恒压频比控制系统,利用坐标变换推导出定子电流纹波表达式,在此基础上提出了减少开关损耗的VSFPWM策略。理论和实验证明,该策略能够在保证不超过最大电流纹波峰值的条件下,一定程度上减少了开关损耗,且对电流THD的影响较小,同时削弱了开关频率倍频处的PSD峰值,降低了电机的窄带噪声。该策略采用查表法进行对开关频率的修改,不需要进行在线估计计算,简单且易于数字实现,具有很好的通用性。
由图4可得
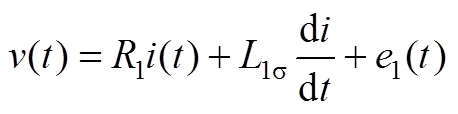 (A1)
(A1)式(A1)在一个开关周期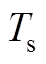 内的平均值可表示为
内的平均值可表示为
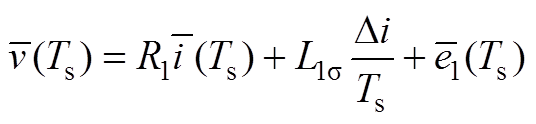 (A2)
(A2)
其中
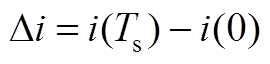
令电压误差为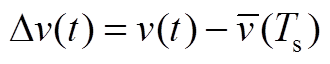 ,则
,则
 (A3)
(A3)
由于定子漏抗远远大于定子电阻,同时在一个开关周期内,转速变化很小,反电动势基本不变,因此第一项和第三项可忽略,得
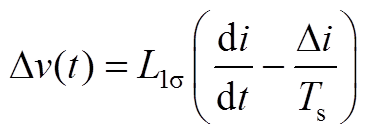 (A4)
(A4)因此电流纹波可表示为
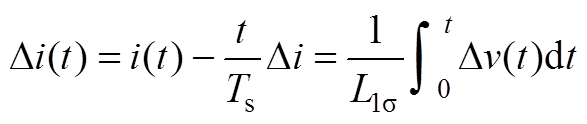 (A5)
(A5)
参考文献
[1] 苗轶如, 刘和平, 华泽玺, 等. 基于直流侧储能电感电流最优给定的三相电流源型逆变器控制策略[J]. 电工技术学报, 2019, 34(2): 349-362.
Miao Yiru, Liu Heping, Hua Zexi, et al. Control strategy for three-phase current source inverter based on optimal given value of DC storage inductance current[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 349-362.
[2] 曾正, 邵伟华, 宋春伟, 等. 电压源逆变器典型控制方法的电路本质分析[J]. 中国电机工程学报, 2016, 36(18): 4980-4989, 5123.
Zeng Zheng, Shao Weihua, Song Chunwei, et al. Circuit-based analysis of typical control schemes of voltage-source inverter[J]. Proceedings of the CSEE, 2016, 36(18): 4980-4989, 5123.
[3] 郭磊磊, 金楠, 申永鹏. 一种基于优化电压矢量选择的电压源逆变器模型预测共模电压抑制方法[J].电工技术学报, 2018, 33(6): 1347-1355.
Guo Leilei, Jin Nan, Shen Yongpeng. A mode predictive common-mode voltage suppression method for voltage source inverter based on optimum voltage vector selection[J]. Transactions of China Electro- technical Society, 2018, 33(6): 1347-1355.
[4] 董帅, 张千帆, 王睿, 等. SVPWM控制时双向Z源逆变器电容电压纹波分析[J]. 电工技术学报, 2017, 32(24): 107-114.
Dong Shuai, Zhang Qianfan, Wang Rui, et al. Analysis of capacitor voltage ripple for bi-directional Z-source inverters based on SVPWM[J]. Transactions of China Electrotechnical Society, 2017, 32(24): 107-114.
[5] 陆原, 胡丙辉, 张军伟, 等. 基于SVPWM调制的三段式算法研究[J]. 电力系统保护与控制, 2016, 44(6): 68-75.
Lu Yuan, Hu Binghui, Zhang Junwei, et al. A three- segment algorithm research based on SVPWM modulation[J]. Power System Protection and Control, 2016, 44(6): 68-75.
[6] 陈招兵, 王榕生. SVPWM逆变器谐波数值分析[J].电气技术, 2018, 19(3): 60-64, 69.
Chen Zhaobing, Wang Rongsheng. Numerical analysis of harmonic for space vector modulation of full voltage range[J]. Electrical Engineering, 2018, 19(3): 60-64, 69.
[7] Binojkumar A C, Kumar B, Narayanan G. Variable- switching frequency PWM technique for induction motor drive to spread acoustic noise spectrum with reduced current ripple[J]. IEEE Transactions on Industry Applications, 2016, 52(5): 3927-3938.
[8] 刘和平, 刘庆, 张威, 等. 电动汽车用感应电机削弱振动和噪声的随机PWM控制策略[J]. 电工技术学报, 2019, 34(7): 1488-1495.
Liu Heping, Liu Qing, Zhang Wei, et al. Random PWM technique for acoustic noise and vibration reduction in induction motors used by electric vehicles[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1488-1495.
[9] 许杰, 聂子玲, 朱俊杰. 一种低电磁干扰载波斜率随机分布脉宽调制技术[J]. 中国电机工程学报, 2017, 37(14): 4175-4183, 4297.
Xu Jie, Nie Ziling, Zhu Junjie. A random slope PWM with low electromagnetic interference[J]. Proceedings of the CSEE, 2017, 37(14): 4175-4183, 4297.
[10] 刘洋, 王庆义, 赵金. 基于矢量控制系统的双随机PWM技术研究[J]. 中国电机工程学报, 2010, 30(36): 98-102.
Liu Yang, Wang Qingyi, Zhao Jin. Dual randomized PWM based on vector control system[J]. Proceedings of the CSEE, 2010, 30(36): 98-102.
[11] Casadei D, Serra G, Tani A, et al. Theoretical and experimental analysis for the RMS current ripple minimization in induction motor drives controlled by SVM technique[J]. IEEE Transactions on Industrial Electronics, 2004, 51(5): 1056-1065.
[12] Mao Xiaolin, Ayyanar R, Krishnamurthy H K. Optimal variable switching frequency scheme for reducing switching loss in single-phase inverters based on time-domain ripple analysis[J]. IEEE Transactions on Power Electronics, 2009, 24(4): 991-1001.
[13] Jiang Dong, Wang Fei. Current-ripple prediction for three-phase PWM converters[J]. IEEE Transactions on Industry Applications, 2014, 50(1): 531-538.
[14] Jiang Dong, Wang Fei. Variable switching frequency PWM for three-phase converters based on current ripple prediction[J]. IEEE Transactions on Power Electronics, 2013, 28(11): 4951-4961.
[15] Cao Wenchao, Wang Fred, Jiang Dong. Variable switching frequency PWM strategy for inverter switching loss and system noise reduction in electric/ hybrid vehicle motor drives[C]//28th Annual IEEE Applied Power Electronics Conference and Exposition, Long Beach, CA, USA, 2013: 773-780.
[16] Xu Zhuxian, Xu Fan, Jiang Dong, et al. A high temperature traction inverter with reduced cooling and improved efficiency for HEV applications[C]// IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 2013: 2786-2792.
[17] Grandi G, Loncarski J. Evaluation of current ripple amplitude in five-phase PWM voltage source inver- ters[C]//IEEE EUROCON, Zagreb, Croatia, 2013: 1073-1080.
[18] Grandi G, Loncarski J. Analysis of peak-to-peak current ripple amplitude in seven-phase PWM voltage source inverters[J]. Energies, 2013, 6(9): 4429-4447.
[19] Grandi G, Loncarski J, Rossi C. Comparison of peak-to-peak current ripple amplitude in multiphase PWM voltage source inverters[C]//15th European Conference on Power Electronics and Applications, Lille, France, 2013: 1-10.
[20] Grandi G, Loncarski J, Dordevic O. Analysis and comparison of peak-to-peak current ripple in two- level and multilevel PWM inverters[J]. IEEE Transa- ctions on Industrial Electronics, 2015, 62(5): 2721- 2730.
[21] Jiang Dong, Wang Fei. A general current ripple prediction method for the multiphase voltage source converter[J]. IEEE Transactions on Power Electro- nics, 2014, 29(6): 2643-2648.
[22] Yang Fei, Taylor A R, Bai H, et al. Using d-q trans- formation to vary the switching frequency for interior permanent magnet synchronous motor drive systems[J]. IEEE Transactions on Transportation Electrification, 2015, 1(3): 277-286.
[23] 原庆兵. 永磁同步电机系统的周期频率调制策略研究[D]. 哈尔滨: 哈尔滨工业大学, 2016.
[24] David G, Josep B, Alfonso S, et al. Conducted EMI reduction in power converters by means of periodic switching frequency modulation[J]. IEEE Transa- ctions on Power Electronics, 2007, 22(6): 2271-2281.
[25] Chen Nan, Yu Shengbao, Gao Lihui, et al. Sup- pressing interference peak in an active power filter via periodic carrier frequency modulation based on a spectrum analysis approach[J]. IEEE Transactions on Electromagnetic Compatibility, 2019, 61(6): 1-11.
Variable Switching Frequency Pulse Width Modulation for Induction Motors Based on Current Ripple Peak Value
Abstract Compared with the widely used constant switching frequency pulse-width-modulation (CSFPWM) method, variable switching frequency pulse width modulation (VSFPWM) can be used to reduce current power spectral density (PSD) peak values to a certain extent, thereby reducing the narrowband noise of induction motor and suppressing the conducted EMI. In this paper, the analytical expression of stator current ripple peak of induction motor is derived based on coordinate transformation. According to the expression, a VSFPWM strategy for reducing switching loss is proposed, that is, the switching frequency varies within a fundamental cycle to reduce the switching loss of a two-level inverter while maintaining the current ripple peak value within a predefined limit. The theoretical analysis and simulation are carried out, and a 15kW induction motor control platform is built. By analyzing the stator current and the temperature rise of MOSFETs, the feasibility and effectiveness of the variable switching PWM modulation strategy are verified.
keywords:Induction motor, variable switching frequency pulse width modulation, current ripple, switching losses
中图分类号:TM346
DOI: 10.19595/j.cnki.1000-6753.tces.191209
重庆市教委科学技术研究资助项目(KJ1600944)。
收稿日期2019-09-22
改稿日期 2019-12-29
黄 鹏 男,1994年生,硕士研究生,研究方向为电机控制及PWM技术。E-mail: 1269024748@qq.com(通信作者)
刘和平 男,1957年生,教授,博士生导师,研究方向为电力传动及其控制技术。E-mail: engineer@cqu.edu.cn
(编辑 崔文静)