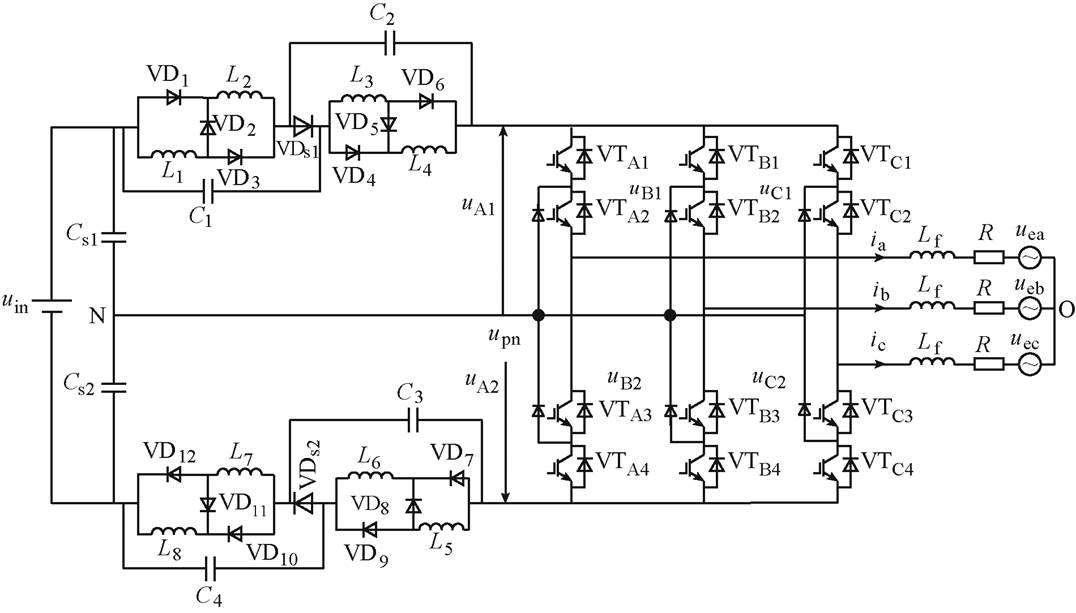
图1 准Z源并网逆变器拓扑
Fig.1 Topology of quasi-Z source grid-connected inverter
摘要 该文将无源控制（PBC）引入到一种准Z源三电平并网逆变器上，该方法无需对逆变器系统进行线性化处理，就可实现良好的并网控制。首先，讨论逆变器拓扑的工作原理，推导出逆变器整体数学模型，给出无源E-L（Euler-Lagrange）方程形式；然后，验证逆变器系统具有严格的无源特性，通过采用合适的阻尼注入和控制率，加速逆变器系统达到期望点，得到逆变器并网电流解耦的无源控制规律，设计出逆变器的无源控制系统，并结合正弦脉宽调制（SPWM）算法驱动逆变器的开关动作；最后，在Matlab/Simulink软件仿真平台和硬件平台上进行实验，实验结果表明，该文基于E-L模型的无源控制策略具有动态特性好、鲁棒性强等优点。
关键词：准Z源逆变器 三电平逆变器 无源控制 E-L模型 端口受控耗散哈密顿模型
在微电网系统中，并网逆变器是其重要组成部分，逆变器性能的高低直接影响到微电网系统的品质[1-2]。传统的并网逆变器系统多采用电压源逆变器，运用DC-DC+DC-AC双级式交换电路的并网策略，增加了系统的复杂程度和成本。Z源逆变器的提出，为逆变器并网提供了新途径。
Z源逆变器的上下桥臂可以同时导通，通过插入直通矢量，避免加入PWM响应时间，增加了系统安全性和抗电磁干扰性[3-5]。随着对Z源逆变器的深入研究，文献[4-9]提出了准Z源的新拓扑。
多电平逆变器由于输出电压电平数的增加，输出波形畸变率减小，降低了滤波器的成本。开关管关断时承受电压减半，系统损耗降低。用中点钳位（Neutral-Point-Clamped, NPC）型结构实现准Z源三电平逆变器，可以充分发挥两者优势，在光伏发电、直驱式风力发电、燃料电池等应用中，前景更加广阔[10]。
随着现代控制和智能控制的理论发展，反馈线性化、滑模变结构和无差拍控制等多种非线性控制应用到并网逆变器的控制系统中[11]。这些控制方法都能够在不同程度上改进并网逆变器的缺陷，但自身也存在一定的不足[12]。文献[13]提出准PR控制，该控制算法可以很好地抑制谐振频率的峰值，提高系统鲁棒性，但其设计参数难以确定。文献[14]提出无差拍控制，具有良好的稳定特性和动态特性，但其能量转换效率低下。文献[15]提出滑模变结构控制策略，提高系统稳定性，但其控制器结构复杂、滑模系数不易确定。由于无源控制（Passivity-Based Control, PBC）对参数变化和外来扰动具有鲁棒性和适应性，为了实现电力电子变换器的非线性控制，无源控制已经应用到并网逆变器的控制中，并取得了较好的控制效果[16-20]，但这些文献中均采用基于端口受控耗散哈密顿（Port Controlled Hamiltonian with Dissipation, PCHD）模型的无源控制，且它们的控制对象分别为标准Z源逆变器、电压源换流器-高压直流输电系统、三相四线电压型PWM整流器、准Z源T形三电平逆变器和隔离型直通Z源逆变器。基于PCHD 模型的无源控制方法缺乏必要的物理意义，直接求解偏微分方程难度大、计算量大、实现困难。
由于基于E-L（Euler-Lagrange）模型的无源控制方法设计简单、物理意义明确、全局稳定性且无奇异点及反对称矩阵简化了无源控制律，因此，本文创新性地将基于 E-L 模型的无源控制运用到准Z源逆变器控制中。首先，分析了准Z源逆变器拓扑的稳态工作原理，提高了直流母线输出电压峰值，并降低了电容电压；然后，建立并网逆变器的数学模型，证明其严格无源性，选择合适的能量函数和注入阻尼，得到电流解耦的无源控制规律，设计出无源控制系统框图；最后，通过Matlab/Simulink软件仿真和硬件实验结果表明，相比于其他的控制策略，该控制策略具有动态特性好、鲁棒性强、可调参数少和电流畸变率低等特点。
本文针对目前并网逆变器双极式结构和输出电压范围窄等问题，提出了一种单极式准Z源并网逆变器工作拓扑，如图1所示。
图1 准Z源并网逆变器拓扑
Fig.1 Topology of quasi-Z source grid-connected inverter
这种逆变器拓扑结构采用了只有1个电压为uin的直流输入电源，Cs1和Cs2为分压电容，且Cs1=Cs2。准Z源网络部分由L1、L2、VD1～VD3，L3、L4、VD4～VD6，L5、L6、VD7～VD9，L7、L8、VD9～VD12组成4路开关电感单元，形成上、下对称结构，有利于维持分压电容中性点平衡，进一步提高升压能力。Lf、R分别为单相线路的等效电感、电阻，uea、ueb、uec为电网A、B、C三相交流电压。
准Z源网络的加入，使得逆变器可以工作在直通状态，形成了并网逆变器独特的升压机制。
准Z源逆变器通过切换半直通与非直通状态的两种工作方式来获得升压效果。为了便于分析，假定开关电感单元中，各个电感电容相等。并网逆变器具有直通状态与非直通状态两种工作状态。
1.2.1 直通状态
在此运行方式下，逆变桥被短接，上下直通等效电路如图2所示。
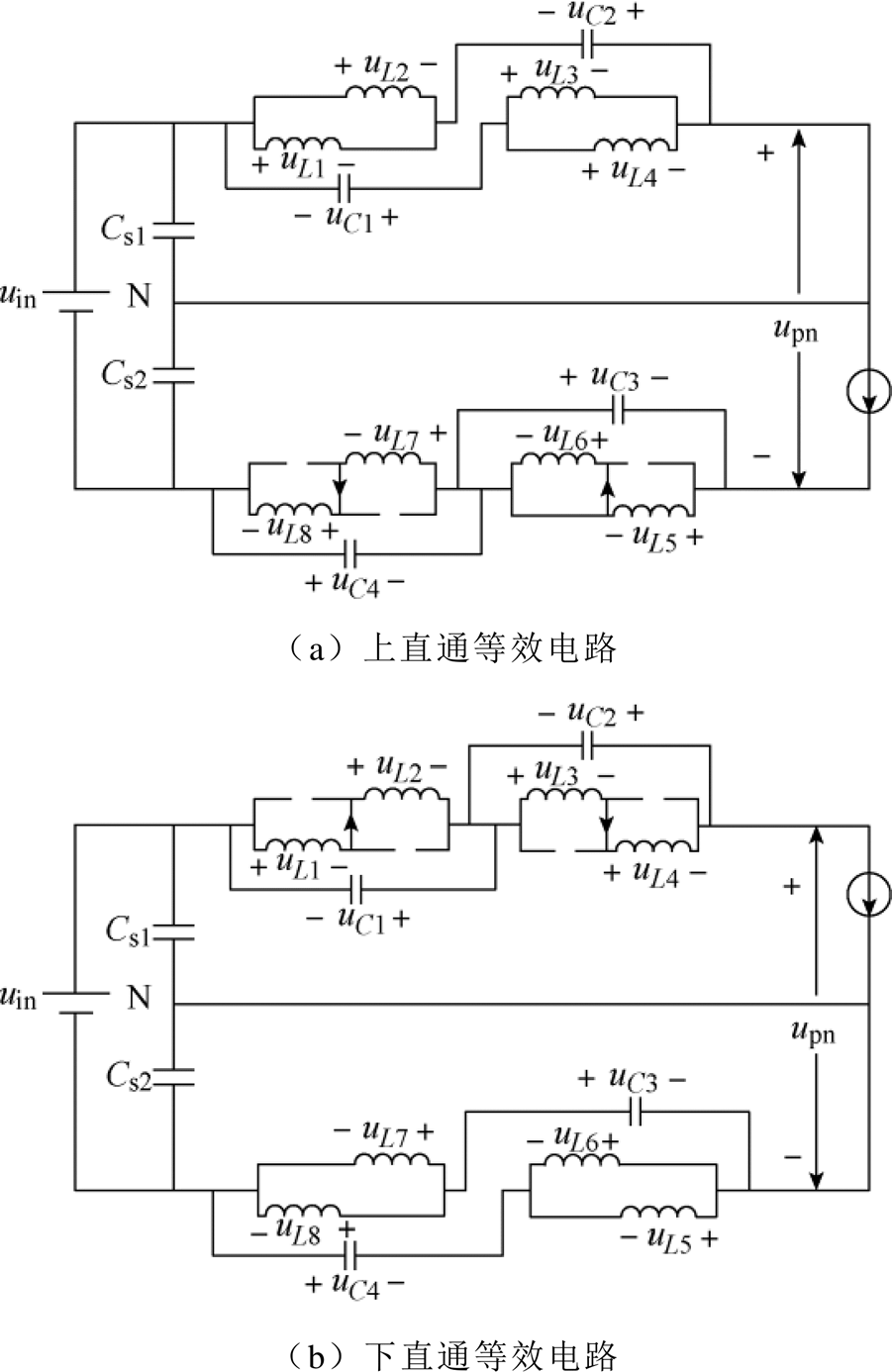
图2 直通等效电路
Fig.2 Shoot-through equivalent circuit
为了保证输出电压平衡，两者在单位周期内作用时间等于T0。由电路对称性可得
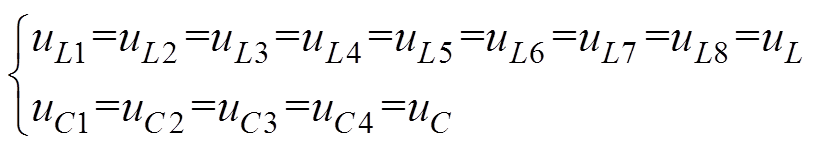（1）若不计IGBT的电压损失，根据基尔霍夫定律，可以得到
（2）
1.2.2 非直通状态
在此运行方式下，逆变桥和负载等效为两个电流源。此时VDs1、VDs2导通，此方式的运行状态如图3所示。
由图3可得
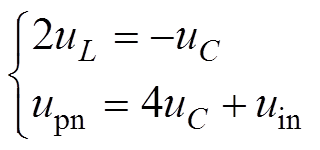（3）设开关动作周期为Ts。依据伏秒平衡原理，由式（2）和式（3）可得
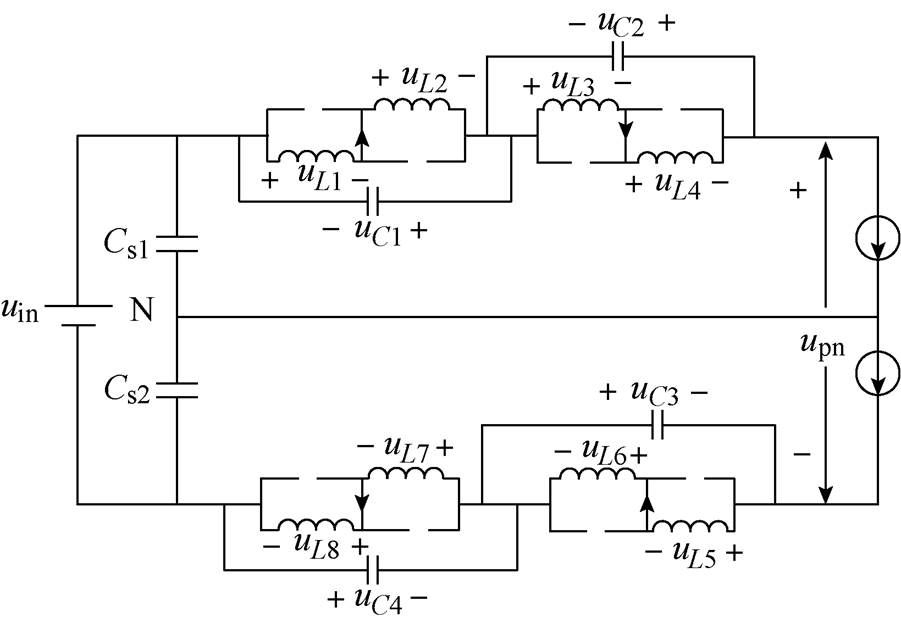
图3 非直通等效电路
Fig.3 Non shoot-through equivalent circuit
（4）联立式（2）～式（4），可以得到电容电压和直流母线电压表达式为
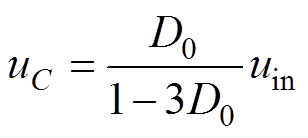（5）
（6）式中，D0为直通占空比，D0=T0/Ts。
图4为准Z源拓扑与传统Z源拓扑升压因子比较。由图4可见，在相同的直通占空比下，准Z源拓扑具有更高的升压能力。在D0=0.3时，传统Z源拓扑的升压比B仅为2.5，而准Z源拓扑的升压比达到13。新拓扑的升压能力远高于传统Z源拓扑。
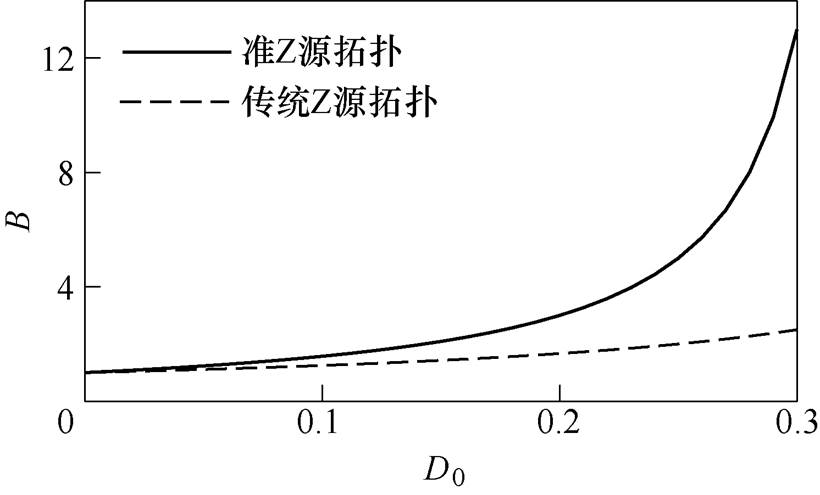
图4 准Z源拓扑与传统Z源拓扑升压因子比较
Fig.4 Comparison of Boost factor for new quasi-Z source topology and traditional Z source topology
逆变器输出相电压的基波幅值为
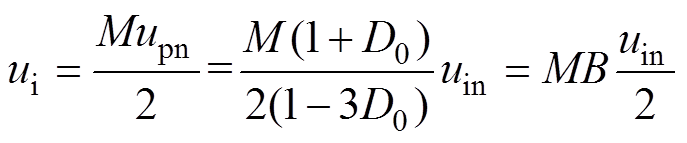（7）式中，M为逆变器的调制比；B为升压比，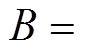
。
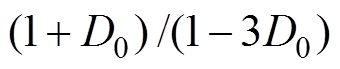根据准Z源并网逆变器的特点，可以将其分为直流升压侧和三相并网逆变侧两个部分。下面对其进行各自建模分析，然后再进行综合建模分析。
设上开关电感单元中电感电流为iL1，电容电压为uC1；下开关电感单元中电感电流为iL2，电容电压为uC2。直流母线上面负载电流为iload1，下面负载电流为iload2。
不考虑电感寄生电阻和电容串联电阻，定义状态变量x=[iL1iL2uC1uC2]T、控制变量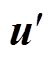
=[uiniload1iload2]T。
非直通状态有
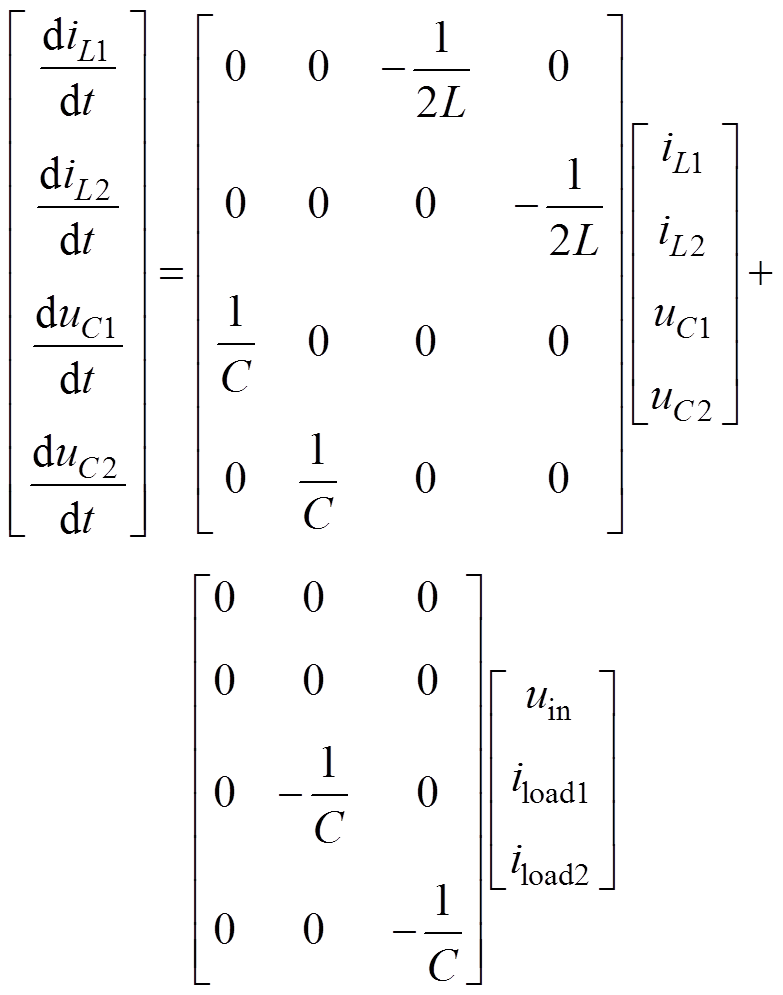（8）上直通状态时有
（9）
下直通状态时有
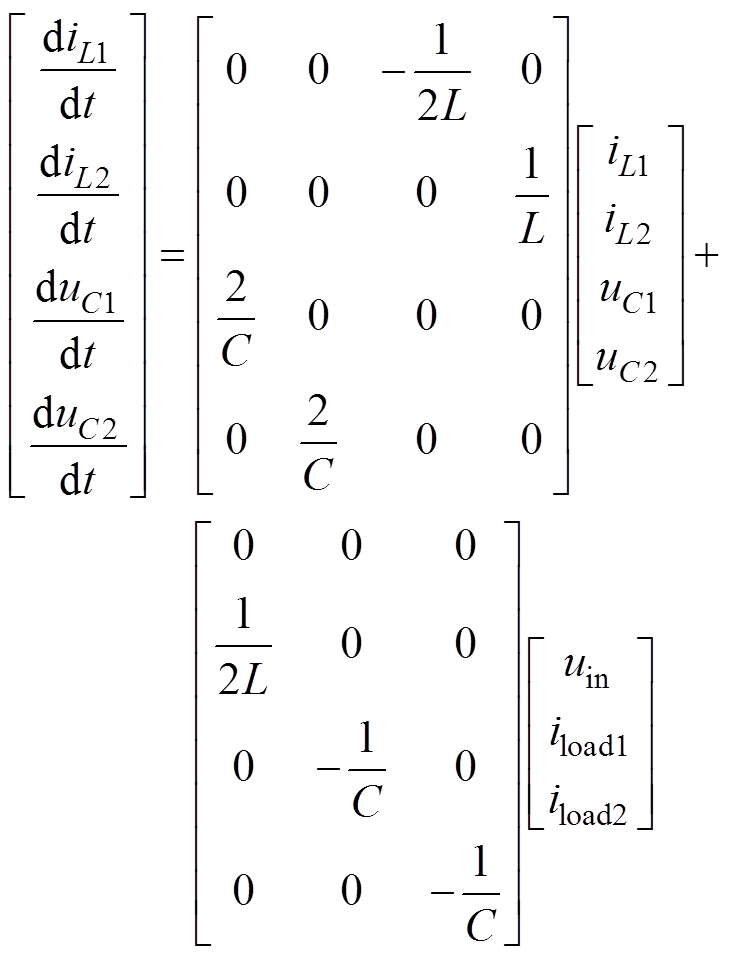（10）若要推导出单位开关周期内的平均状态方程，需将3个方程按照各自占空比进行分段加权计算，从而可得
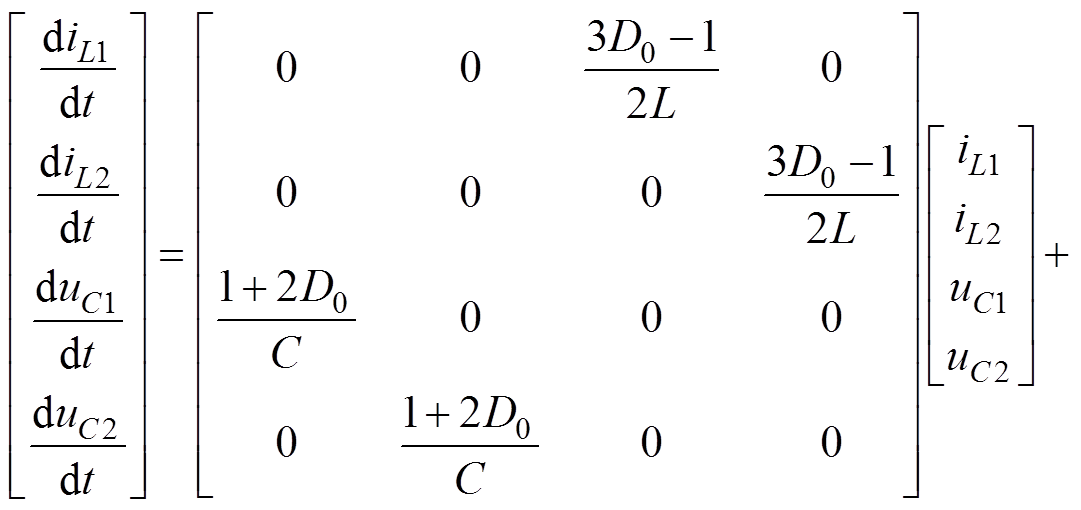
（11）由于准Z源网络的完全对称性，iL1=iL2=iL，uC1= uC2=uC，iload1=iload2=iload，则原4阶方程可简化为2阶方程，即为
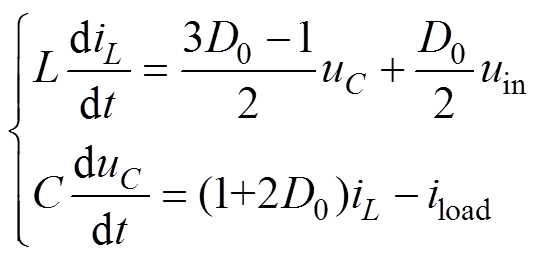（12）
并网三相逆变桥拓扑结构如图5所示。三相并网逆变器开关函数定义为
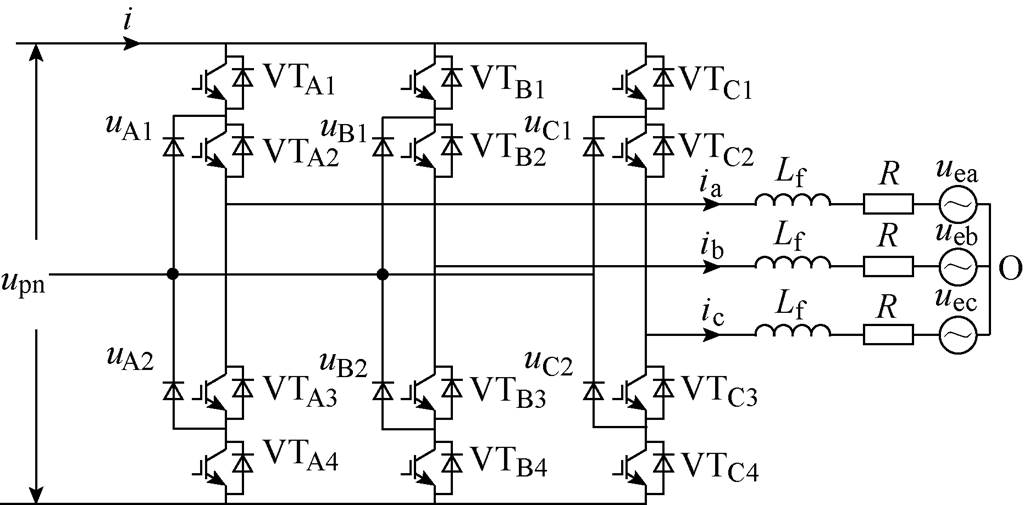
图5 三相并网逆变器拓扑结构
Fig.5 Three-phase grid-connected inverter topology
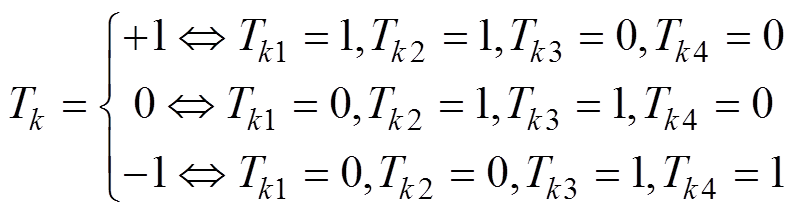（13）式中，k=A, B, C。
根据开关函数定义和并网逆变器拓扑结构，得到并网逆变器在同步旋转dq坐标系下的微分方程为
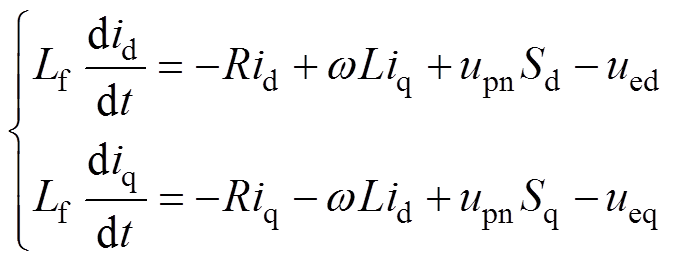（14）式中，Sd、Sq、id、iq、ued、ueq和w 分别为开关函数、线路电流、电网侧电压在d、q轴上的分量和两相旋转角频率。
根据式（13），得到三相逆变器桥臂输入电流i为
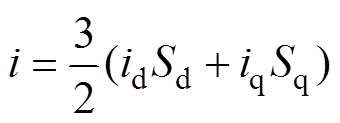（15）联立式（5）和式（6），可推出直流母线峰值电压和电容电压关系为
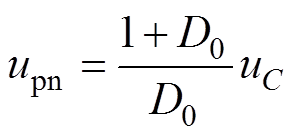（16）
联合式（12）、式（14）和式（16），推导出准Z源并网逆变器的数学模型为
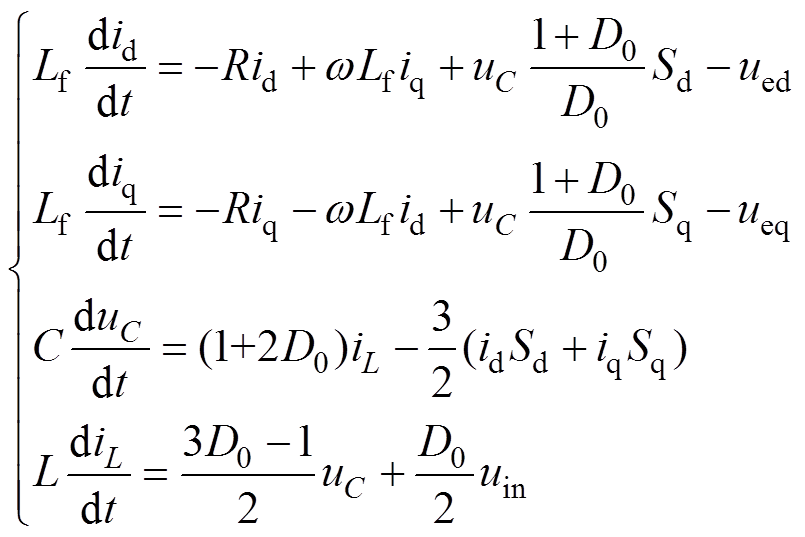（17）将式（17）写成无源控制要求的E-L方程为
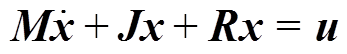（18）
其中
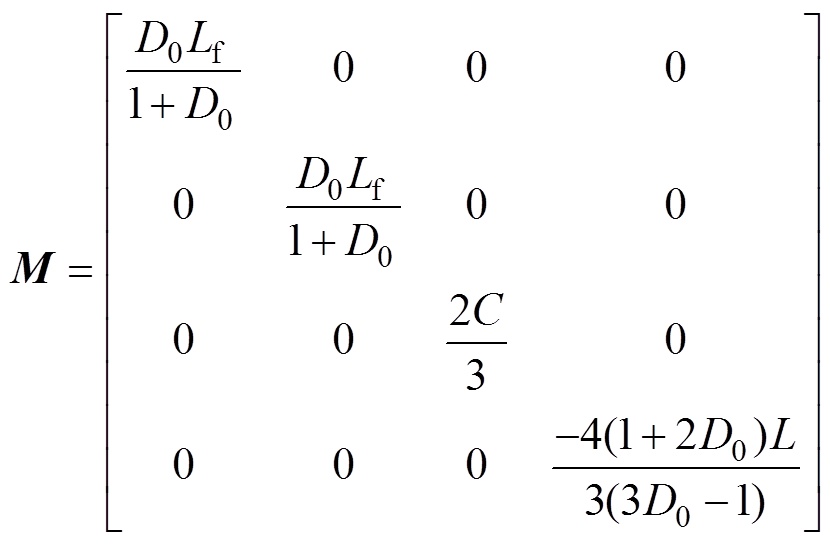
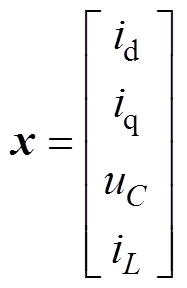
式中，M为储能元件组成的正定的对角阵；J为系统内部互联结构的反对称矩阵，J=-JT；R为反映系统耗散的对称正定矩阵；u表示系统与外部能量交换。
可以选择不同能量函数和注入阻尼，设计出不同无源控制方法。
若存在半正定能量函数H(x)和正定函数Q(x)，对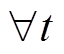
＞0，有不等式[11]为
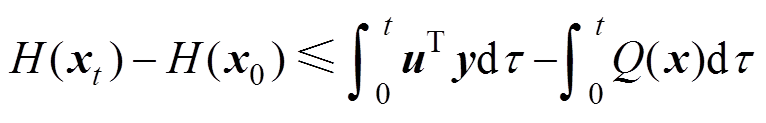（19）或
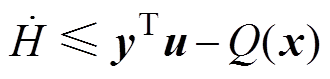（20）
对系统输入u、输出y及能量供给率yTu成立，则系统是严格无源的。能量函数可设为
，那么
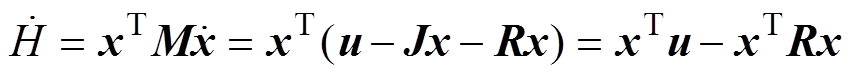（21）令y=x，Q(x)=xTRx，式（21）与式（20）表达是一致的，因此，证明了并网逆变器系统是严格无源的，而严格无源的系统一定是渐近稳定系统[10]。
选择系统的误差存储能量函数为
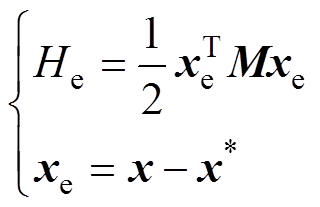（22）式中，x*为系统的期望平衡点；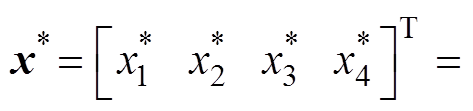
。
对于E-L模型的无源控制器，为了使xe快速趋于0，可以注入阻尼使得系统快速收敛到期望点。注入的阻尼耗散项为
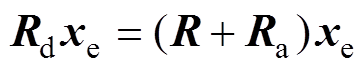（23）式中，Ra为对角线矩阵，Ra=diag(Ra1,Ra2,Ra3,Ra4)。
所以式（18）可以写成
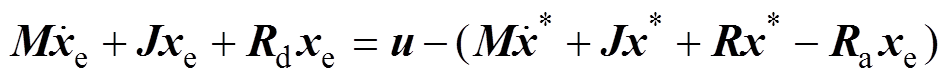（24）选取控制律为
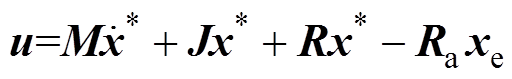（25）
可以使得
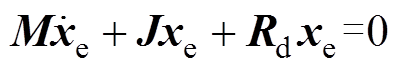（26）使得误差存储能量函数导数为
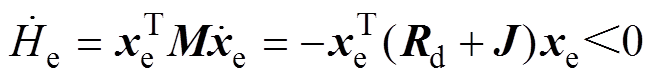（27）
联立式（25）和式（18），可以得到开关函数为
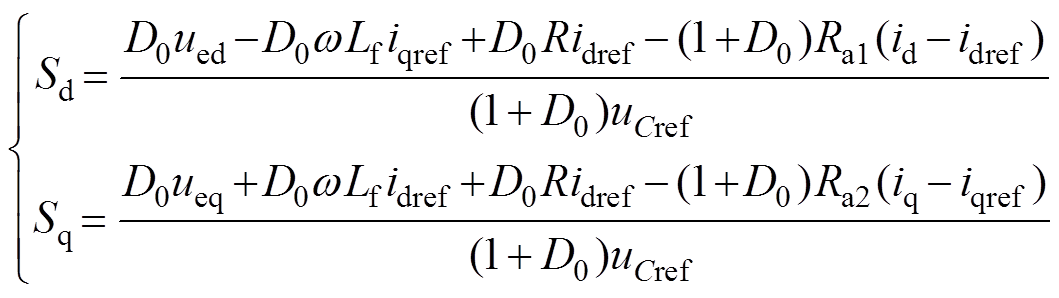（28）将式（28）代入式（17）可得
（29）
由式（29）可以看出，有阻尼注入且由控制律式（28）得到的系统存在强耦合。为了解决耦合问题，将式（24）变形为
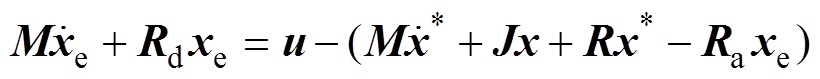（30）选取新的控制律为
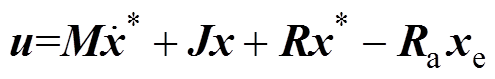（31）
可以使得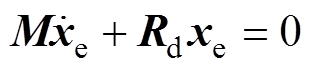
，误差能量函数导数为
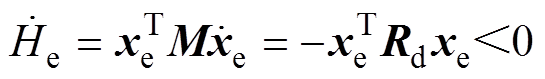（32）联立式（31）和式（18），得到新的开关函数为
（33）
将新的开关函数代入系统dq轴数学模型可得
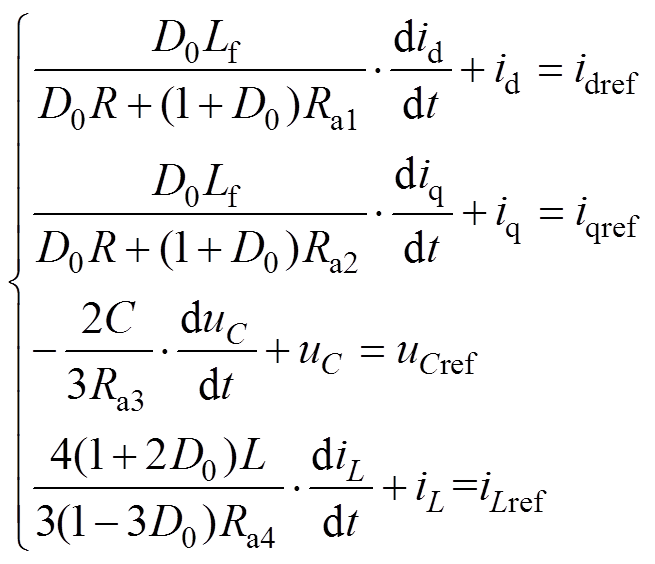（34）观察式（34）可知，式（33）即为电流解耦的无源控制律。若选择合适阻尼Ra1、Ra2、Ra3和Ra4，则id、iq、uC和iL可以快速稳定于其参考值idref、iqref、uCref和iLref。
综上所述，可得到E-L模型下准Z源并网逆变器的无源控制系统如图6所示。图6中，upnref为直流母线电压参考值。
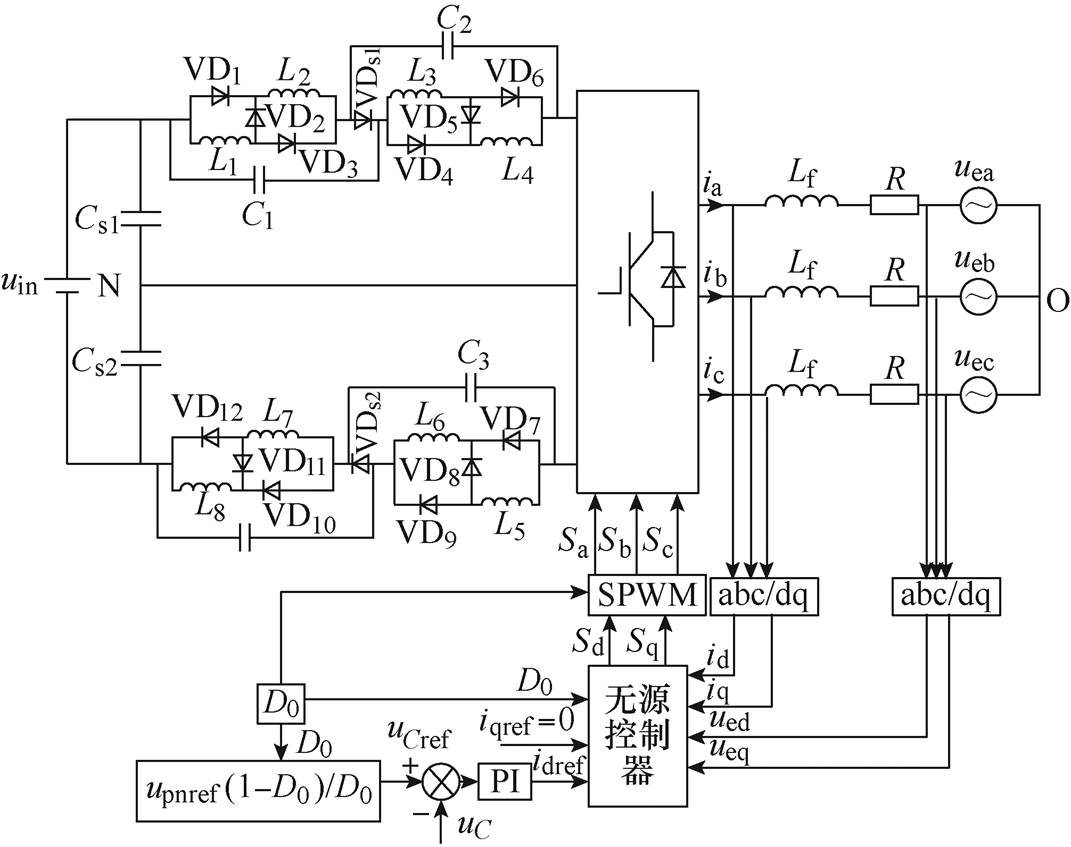
图6 准Z源并网逆变器的无源控制系统
Fig.6 Passivity-based control system of new quasi-Z source grid-connected inverter
由无源控制规律式（31），系统系数矩阵依赖于逆变器系统的数学模型。系统内阻容易受环境影响，进而改变能量函数，影响系统鲁棒性和快速响应性等指标。
假设线路的内阻由环境变化引起的内阻变化为DR，则式（30）变化为
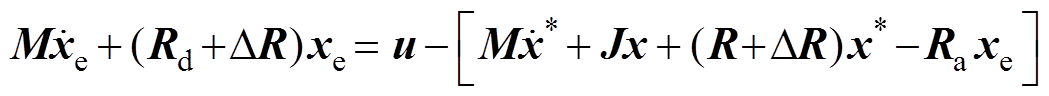（35）如果选择控制律为
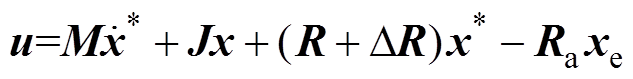（36）
可以使得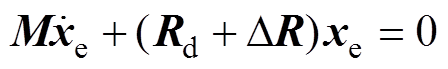
，那么DR难以直接测得。若计算的时候，以R代替R+DR，那么可以测得
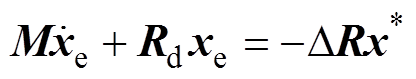（37）由式（22）和式（37）可得
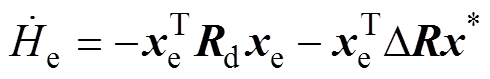（38）
由式（38）可以看出，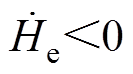
依赖于DR，所以选取尽量大的Ra，可以提高无源控制器控制性能，降低系统参数对控制性能的影响。
为了验证上文中的理论分析，在Matlab环境中对准Z源并网逆变器无源控制系统进行仿真。
系统参数为：直流电压uin=300V，准Z源网络中电容、电感分别是800mF、10mH，分压电容为Cs1= Cs2=2 200mF，idref计算PI调节器的比例系数、积分系数为KP=10、KI=5。线路中等效电感、电阻分别为5mH、1W。直通占空比D0=0.1，电网相电压有效值为220V，频率f =50Hz。
若期望的q轴电流iqref=0A，图7为采用不同注入阻尼下开关函数Sd的波形。由图7可见，当注入阻尼变大时，开关函数趋于稳定的时间延长。当Ra=5W 时，Sd趋于稳定的时间约为0.05s；当Ra= 10W 时，Sd大约在0.1s趋于稳定；特别地，当Ra≥ 20W 时，Sd趋于稳定的时间超过0.1s。
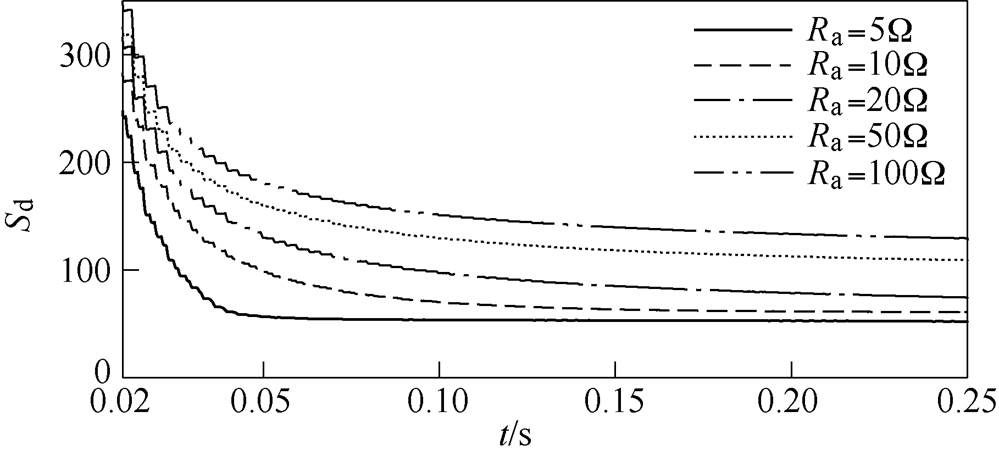
图7 不同注入阻尼下系统开关函数Sd
Fig.7 System switching function Sd under different injection damping
图8为不同注入阻尼下无源控制器内部d轴电流。由图8可见，Ra≤10W 时，在0.25s时，id还不能够稳定，并趋于发散；当Ra≥20W 时，id趋于稳定的时间大约在0.05s。随着注入阻尼的变大，系统动态稳定性越来越高。
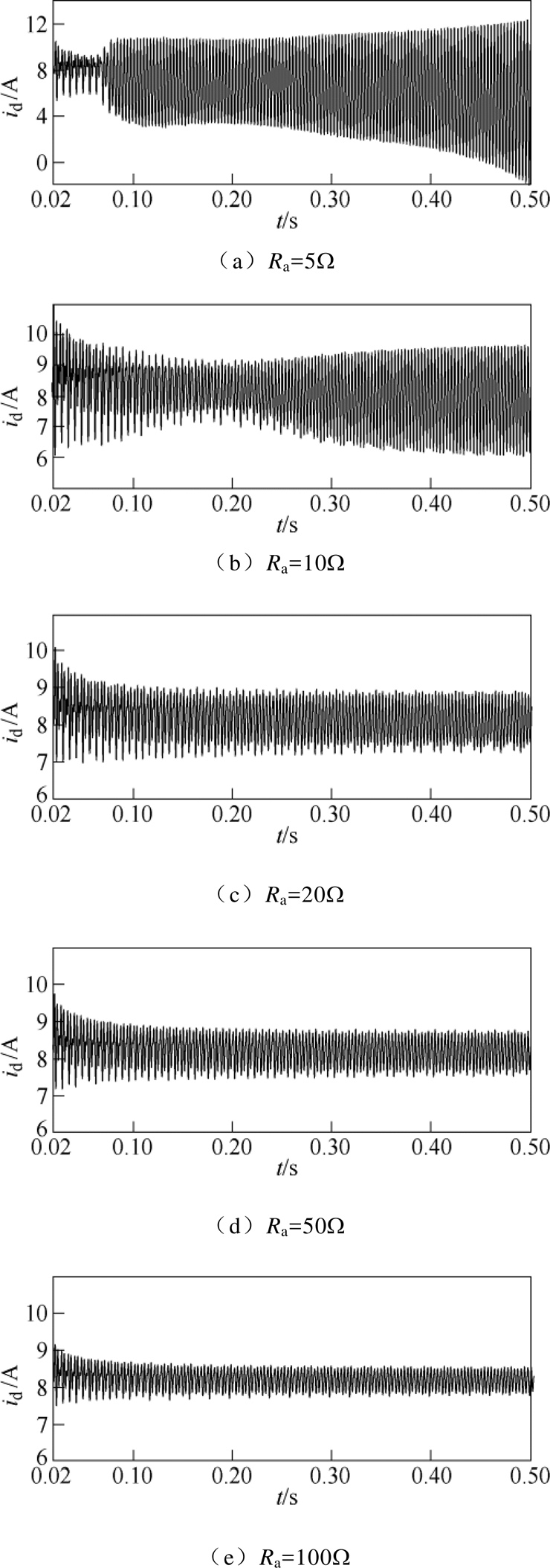
图8 不同注入阻尼情况下d轴电流波形
Fig.8 d-axis current waveformsunder different injection damping
因此，从系统的快速响应性和动态稳定性两方面考虑，本文选取Ra1=Ra2=20W。
图9为准Z源逆变器直流母线输出电压波形。由图9可见，uin=300V、D0=0.1时，直流母线输出峰值电压大约为470V，上下直通时电压约为235V。若是采用传统Z源逆变器，则输出电压最大只能达到375V。因此，拓扑扩大了电压输出范围，适用范围更广。
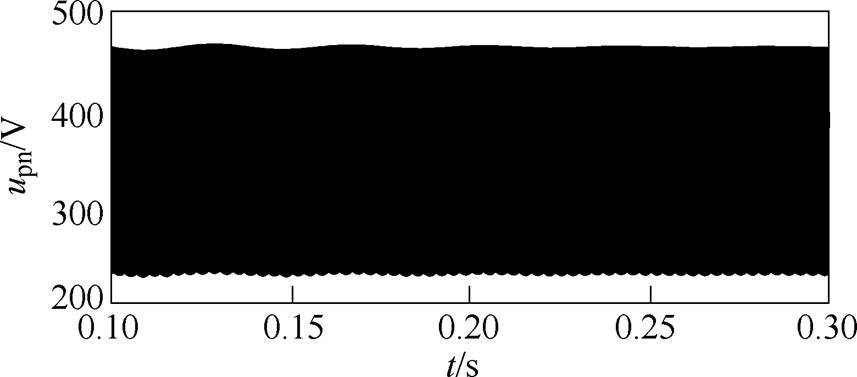
图9 准Z源逆变器的直流母线输出电压波形
Fig.9 DC bus output voltage waveform of new quasi-Z source inverter
准Z源逆变器产生的相电压和线电压波形如图10所示。仿真中，D0=0.1，升压比B约为1.57。所以理论上逆变器输出的相电压共±Buin/2、0三种电平，即±235V、0。理论上逆变器输出的线电压共±Buin、±Buin/2、0五种电平，即±470V、±235V、0V。仿真结果与理论一致。
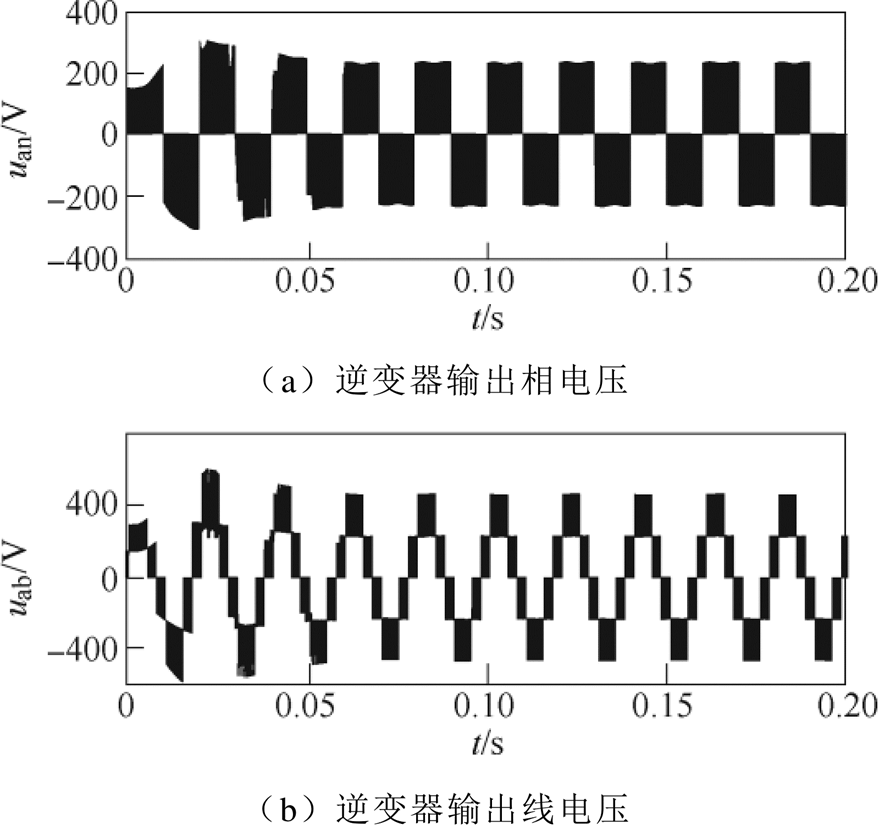
图10 准Z源逆变器输出电压波形
Fig.10 Output voltage waveforms of new quasi-Z source inverter
图11为逆变器a相4路开关PWM信号。图11中，0～1ms时间内，VTA2导通，VTA4关断。当VTA1=1、VTA3=1时，a相上直通；当VTA1、VTA3不全为1时，a相非直通。插入直通矢量，实现并网逆变器的升压机制。
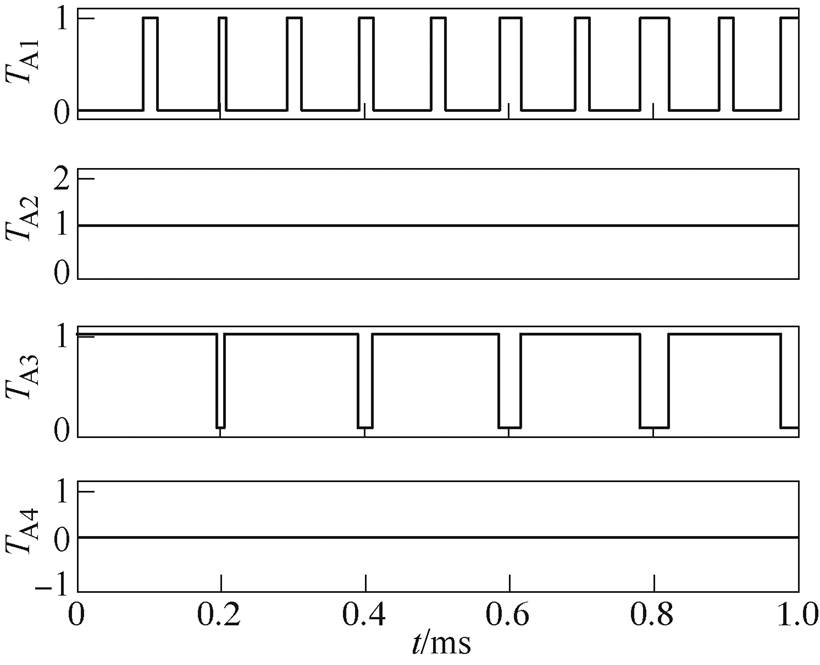
图11 a相4路开关PWM信号
Fig.11 a-phase 4-way switch PWM signals
图12为无源控制器内部的输出量Sd和Sq，其为从电网侧提取电压电流信号量，进行标幺化处理，经过abc/dq变换和无源控制规律得到，并作为正弦脉宽调制（Sinusoidal Pulse Width Modulation, SPWM）的输入信号。
为了说明本文所提基于E-L模型的无源控制优势，将本文基于E-L模型的无源控制、基于电压矢量的双闭环PI控制及基于PCHD模型的无源控制进行仿真比较。
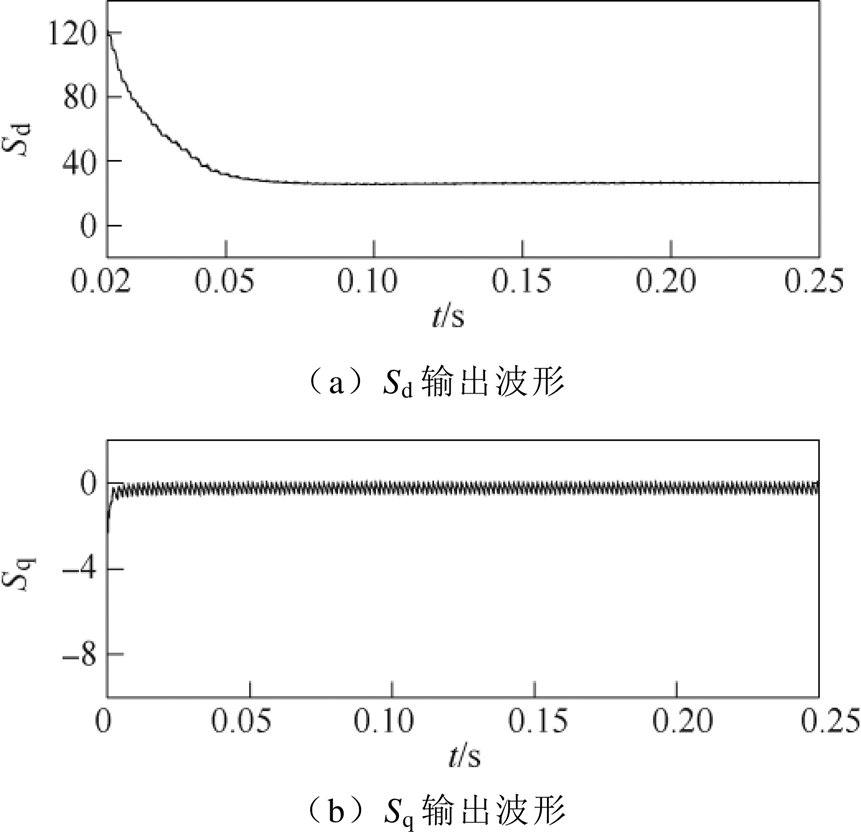
图12 无源控制器的输出变量
Fig.12 Outputvariables of passivity-based controller
图13为两种不同控制策略下电容电压。由图13可见，在本文所提无源控制下，电容电压约在0.03s时趋于稳定，保持在40V上下波动；而在双闭环PI控制下，电容电压的稳定时间大约0.09s。本文的无源控制下电容电压的超调量远低于传统的双闭环PI控制，因此，本文无源控制的响应更快、稳定性更高。
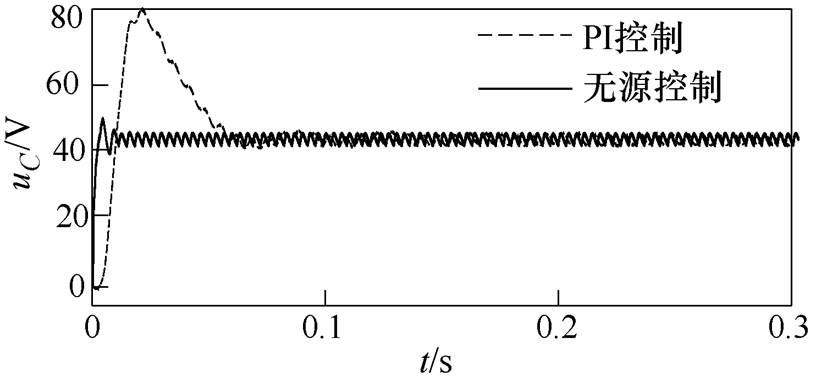
图13 两种不同控制策略下电容电压
Fig.13 Capacitor voltages under two different control strategies
图14为不同控制策略下的并网电压电流。由图14可见，三种控制策略都可以实现电压电流同相位，但PI控制下，电流波形比较粗糙，这将影响微电网系统的电能质量；而在无源控制下，电流曲线光滑，纹波较低，且本文基于E-L模型的无源控制性能要稍好于基于E-L模型的无源控制性能。
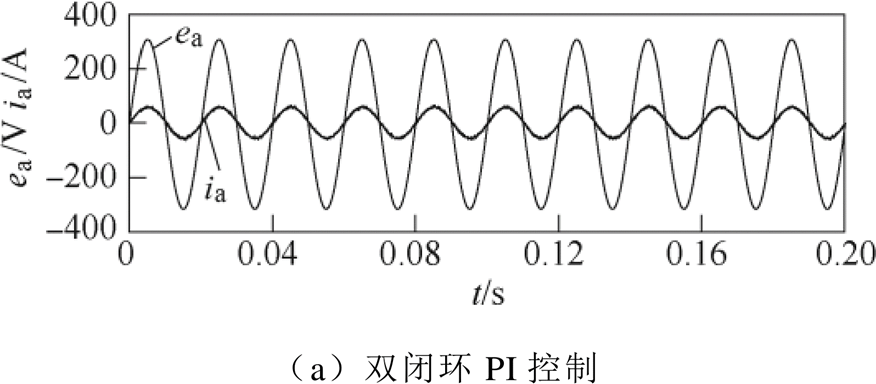
图14 不同控制策略下并网电压电流
Fig.14 Grid-connected voltages and currents under different control strategies
图15为不同控制策略下并网电流的快速傅里叶变换（Fast Fourier Transform, FFT）分析曲线。由图15可见，E-L模型的无源控制下电流谐波畸变率仅达1.03%，远低于双闭环PI控制下电流谐波畸变率4.79%和PCHD模型无源控制下电流谐波畸变率3.17%。E-L模型的无源控制下电流基波幅值为31.49A，大于双闭环PI控制下电流基波幅值29.95A和PCHD模型的无源控制下电流基波幅值30.24A。另外，双闭环PI控制中内、外环都采用PI控制，其控制参数难以整定。
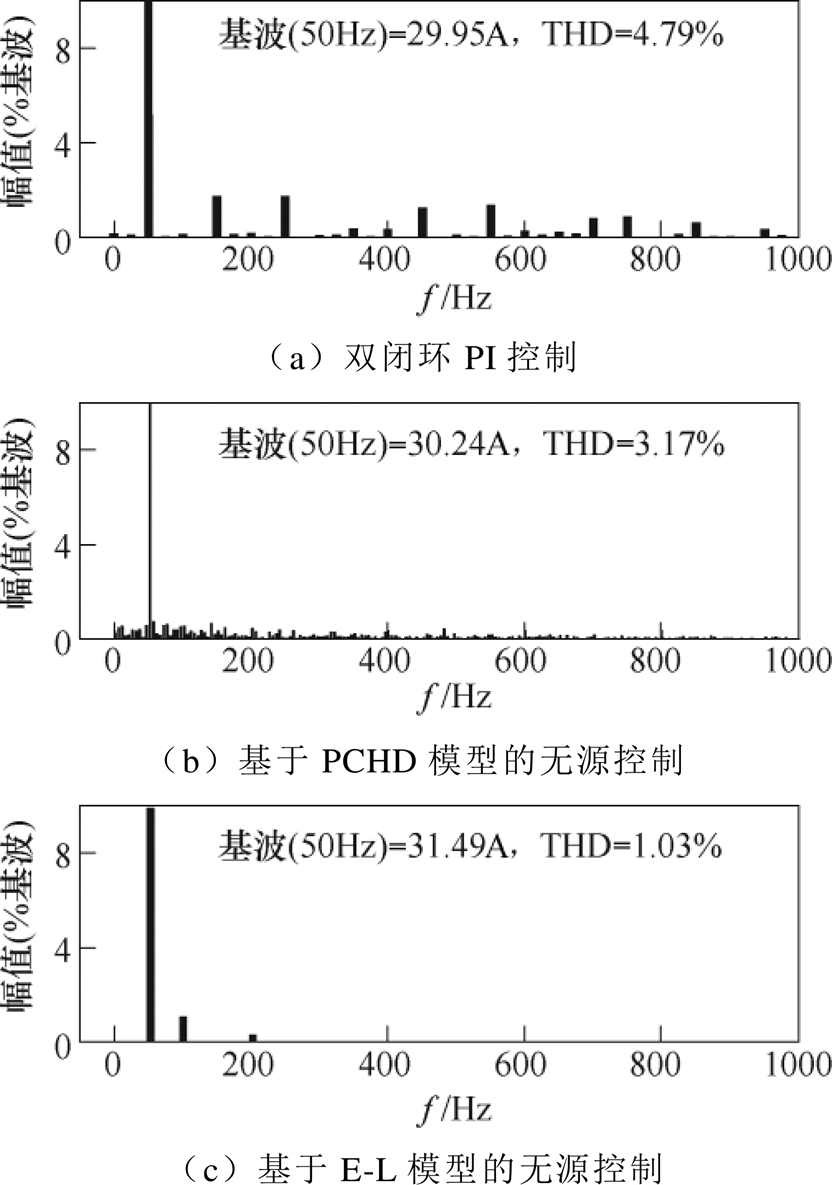
图15 不同控制策略下并网电流的FFT分析曲线
Fig.15 FFT analysis curves of grid-connected current under different control strategies
本文还制作了硬件实验平台如图16所示。图16中，直流稳压电源提供直流输入，TMS320F28335型的DSP产生控制信号；实际系统的参数取值均与软件仿真系统参数相同；逆变器输出经过滤波器接到电阻负载上。在此硬件平台上，进行并网逆变器的控制策略验证。
图16 硬件实验平台
Fig.16 Hardware experiment platform
图17为在两种不同模型的无源控制策略下示波器上显示的电容电压uC。实验中，输入电压uin= 300V、直通占空比D0=0.1。由图17可见，电容电压都能稳定在42V左右，但在PCHD模型的无源控制下电容电压波动大，而在E-L模型的无源控制下电容电压波动小，因此，本文的无源控制系统的稳定性更强，这有利于保护电容。
图17 两种不同模型的无源控制策略下电容电压
Fig.17 Capacitor voltages under passivity-based control strategies based on two different models
图18为准Z源逆变器输出的相电压和线电压。D0=0.1时，升压比B≈1.57。当uin=300V时，逆变器输出的线电压有±470V、±235V和0五种电平，逆变器输出的相电压有±235V和0三种电平。这与之前的理论分析一致。
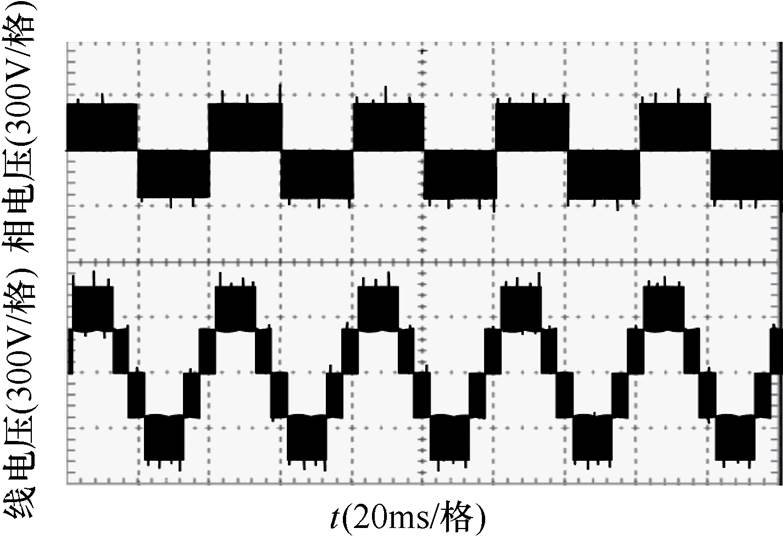
图18 准Z源逆变器的输出电压
Fig.18 Output voltage of new quasi-Z source inverter
图19为三种不同控制策略下a相电压和并网电流。图19中，设置期望的输出电流幅值idref=30A，iqref=0A。由图可见，不同控制策略下都能实现较高功率因数并网，但本文基于E-L模型的无源控制下电流畸变率最低。
图19 不同控制策略下a相电压和电流
Fig.19 a-phase voltage and current under different control strategies
本文提出一种准Z源三电平并网逆变器，其直流母线输出电压大幅提高，电容承受电压降低。本文建立了逆变器系统的状态方程，给出E-L模型的方程形式，并证明了其严格无源性。采用了阻尼注入的方法，得到这种逆变器的无源控制规律，并设计基于这种逆变器的无源控制系统。最后通过软件仿真和实验得到如下结论：
1）对于准Z源并网逆变器，本文设计的基于E-L模型的无源控制器，与其他两种控制器相比，具有结构简单、可调参数少、控制性能优良等特点。
2）对于基于E-L模型的无源控制器，通过选取合适的阻尼参数，可以显著地提高控制系统的动态特性和鲁棒性。
3）在本文基于E-L模型的无源控制策略下，并网电压电流同相位，且电流畸变率低于其他两种控制策略下电流谐波畸变率。
参考文献
[1] Rajakaruna S. Steady-state analysis and designing impedance network of Z-source inverters[J]. IEEE Transactions on Industrial Electronics, 2010, 57(1): 2483-2491.
[2] 曾正, 杨欢, 赵荣祥, 等. 多功能并网逆变器研究综述[J]. 电力自动化设备, 2012, 32(8): 5-15.
Zeng Zheng, Yang Huan, Zhao Rongxiang, et al. Overview of multi-functional grid-connected inver- ters[J]. Electric Power Automation Equipment, 2012, 32(8): 5-15.
[3] Peng Fangzheng. Z-source inverter[J]. IEEE Transa- ctions on Industry Applications, 2003, 39(2): 504- 510.
[4] 汤雨, 谢少军, 张超华. 改进型Z源逆变器[J]. 中国电机工程学报, 2009, 29(30): 28-34.
Tang Yu, Xie Shaojun, Zhang Chaohua. Improved Z-source inverter[J]. Proceedings of the CSEE, 2009, 29(30): 28-34.
[5] Tang Yu, Xie Shaojun, Zhang Chaohua. Improved Z-source inverter with reduced Z-source capacitor voltage stress and soft-start capability[J]. IEEE Transactions on Power Electronics, 2009, 24(2): 409-415.
[6] 蔡春伟, 曲延滨, 盛况. 增强型Z源逆变器[J]. 中国电机工程学报, 2011, 31(增刊1): 259-266.
Cai Chunwei, Qu Yanbin, Sheng Kuang, et al. Enhanced Z-source inverter[J]. Proceedings of the CSEE, 2011, 31(S1): 259-266.
[7] 周玉斐, 黄文新, 赵健伍, 等. 一种高升压比的Z源逆变器[J]. 电工技术学报, 2013, 28(9): 239-246.
Zhou Yufei, Huang Wenxin, Zhao Jianwu, et al. A high gain Z-source inverter[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 239-246.
[8] 侯世英, 肖旭, 张闯, 等. 改进型Z源逆变器[J]. 电力自动化设备, 2011, 31(8): 24-28.
Hou Shiying, Xiao Xu, Zhang Chuang, et al. Improved Z source inverter[J]. Electric Power Automation Equipment, 2011, 31(8): 24-28.
[9] 徐聪, 程启明, 李明, 等. Z源逆变器及其多种改进拓扑结构的比较[J]. 电网技术, 2014, 38(10): 2926-2931.
Xu Cong, Cheng Qiming, Li Ming, et al. A comparative simulation study on Z-source inverter and its various improvement topllogies[J]. Power System Technology, 2014, 38(10): 2926-2931.
[10] 王久和, 黄立培, 杨秀媛. 三相电压型PWM整流器的无源性功率控制[J]. 中国电机工程学报, 2008, 28(21): 20-25.
Wang Jiuhe, Huang Lipei, Yang Xiuyuan. Power control of three-phase Boost-type PWM rectifier based on passivity[J]. Proceedings of the CSEE, 2008, 28(21): 20-25.
[11] 王久和, 穆小斌. 基于无源性的光伏并网逆变器电流控制[J]. 电工技术学报, 2012, 27(11): 176-182.
Wang Jiuhe, Mu Xiaobin. Current control strategy of photovoltaic grid-connected inverter based on passivity[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 176-182.
[12] 陆翔, 谢运祥, 桂存兵. 基于无源和滑模变结构控制想结合的VIENNA整流器控制策略[J]. 电力自动化设备, 2014, 34(10): 110-115.
Lu Xiang, Xie Yunxiang, Gui Cunbing. Passivity and sliding mode control based on a combination of VIENNA rectifiers[J]. Electric Power Automation Equipment, 2014, 34(10): 110-115.
[13] 雷亚雄, 李建文, 李永刚. 基于准PR调节器电流双闭环LCL三相并网逆变器控制[J]. 电力系统保护与控制, 2014, 42(12): 44-50.
Lei Yaxiong, Li Jianwen, Li Yonggang. Control strategy of three-phase LCL grid-connected inverter based on quasi-PR adjuster[J]. Power System Pro- tection and Control, 2014, 42(12): 44-50.
[14] 黄天富, 石新春, 魏德冰, 等. 基于电流无差拍控制的三相光伏并网逆变器的研究[J]. 电力系统保护与控制, 2012, 40(11): 36-41.
Huang Tianfu, Shi Xinchun, Wei Debin, et al. Study on three-phase photovoltaic grid-connected inverter based on current deadbeat control[J]. Power System Protection and Control, 2012, 40(11): 36-41.
[15] Bo Xu, Xiao Hongran. Sliding mode control for three-phase quasi-Z-source inverter[J]. IEEE Access, 2018(6): 60318-60328.
[16] 程启明, 张强, 程尹曼, 等. 基于PCHD模型的光伏Z源并网逆变器无源控制[J]. 高电压技术, 2016, 42(9): 2723-2732.
Cheng Qiming, Zhang Qiang, Cheng Yinman, et al. Passivity based control of PV Z-source grid- connected inverter based on PCHD model[J]. High Voltage Engineering, 2016, 42(9): 2723-2732.
[17] 钱甜甜, 苗世洪, 刘子文, 等. 基于PCHD模型的VSC-HVDC的无源控制与辅助改进滑模控制[J]. 电工技术学报, 2016, 31(3): 138-144.
Qian Tiantian, Miao Shihong, Liu Ziwen, et al. Passive control and auxiliary sliding mode control strategy for VSC-HVDC system based on PCHD model[J]. Transactions of China Electrotechnical Society, 2016, 31(3): 138-144.
[18] 王久和, 张巧杰, 李萍, 等. 基于PCHD模型的三相四线电压型PWM整流器无源控制[J]. 电工技术学报, 2015, 30(14): 354-361.
Wang Jiuhe, Zhang Qiaojie, Li Ping, et al. Passivity based control of three-phase four-wire voltage source PWM rectifier based on PCHD model[J]. Transa- ctions of China Electrotechnical Society, 2015, 30(14): 354-361.
[19] 程启明, 李涛, 程尹曼, 等. 基于受控耗散Hamiltonian系统模型的光伏准Z源T型三电平并网逆变器控制策略[J]. 电工技术学报, 2019, 34(8): 1718-1727.
Cheng Qiming, Li Tao, Cheng Yinman, et al. Control strategy of PV quasi-Z-source T-type three-level inverter based on port controlled Hamiltonian with dissipation mode[J]. Transactions of China Electro- technical Society, 2019, 34(8): 1718-1727.
[20] Lü Youdong, Yu Haisheng, Liu Xudong. Switching control of sliding mode and passive control for DC-link voltage of isolated shoot-through Z-source inverter[C]//Conference of Chinese Automation Congress (CAC), Xi'an, China, 2018: 2687-2692.
Passivity-Based Control Strategy of Quasi Z-Source Three-Level Grid-Connected Inverter
Abstract In this paper, passivity-based control (PBC) is introduced into a new quasi-Z source three-level grid-connected inverter. This method can achieve good grid-connected control without linearizing the inverter system. Firstly, the working principle of the new inverter topology is discussed, the overall mathematical model of the new inverter is derived, and the passive Euler-Lagrange (EL) equation form is given. Then, it is verified that the inverter system has strict passive characteristics. By adopting the appropriate damping injection and control rate, the inverter system is accelerated to reach the desired point, the PBC law of decoupling grid-connected current is obtained, and the PBC system of the new inverter is designed. This system can drive the switch action of the new inverter in combination with SPWM modulation algorithm. Finally, the results on the Matlab/Simulink software platform and hardware platform show that the PBC strategy based on EL model has good dynamic characteristics and strong robustness.
keywords：Quasi-Z source inverter, three-level inverter, passivity-based control, E-L model, port controlled hamiltonian with dissipation model
中图分类号：TM464
DOI: 10.19595/j.cnki.1000-6753.tces.191173
国家自然科学基金项目（61573239）和上海市电站自动化技术重点实验室项目（13Z2273800）资助。
收稿日期 2019-09-08
改稿日期 2019-11-05
程启明 男，1965年生，教授，硕士生导师，研究方向为电力系统自动化、发电过程控制、先进控制及应用。E-mail: chengqiming@sina.com（通信作者）
江 畅 男，1996年生，硕士研究生，研究方向为电力系统自动化、电机控制等。E-mail: 1009722953@qq.com
（编辑 陈 诚）