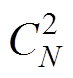 ,一旦相数N>3时,双绕组耦合电感的数量将急剧增加,大大限制了这种等效方法的推广。
,一旦相数N>3时,双绕组耦合电感的数量将急剧增加,大大限制了这种等效方法的推广。摘要 为了解决多相交错并联磁集成双向DC-DC变换器中单磁心耦合电感结构不对称、成本高和设计比较困难等问题,提出一种基于双绕组耦合电感的多相交错并联双向DC-DC变换器。该文以四相交错并联双向DC-DC变换器为例,采用四个双绕组耦合电感代替单磁心耦合电感,详细研究所提变换器的稳态和暂态性能。同时,变换器运行时由于相电路参数差异可能引起相间不均流问题,使得重载相过载发热,进而影响到整个变换器的运行可靠性。为此,该文提出一种基于相电流解耦的均流控制策略来解决这个问题。最后,通过仿真和样机实验验证了所提拓扑和均流控制方法的优越性、可靠性和实用性。
关键词:双向DC-DC变换器 耦合电感 稳态和暂态性能 均流控制策略 相电流解耦
交错并联技术不仅可以降低开关器件的电流应力,还可以减少总的输出电流纹波,提高整个系统的功率[1-3]。交错并联双向DC-DC变换器广泛应用于电动汽车、航空电源、不间断电源、可再生能源发电等需要能量双向流动的场合[4-7]。
交错并联并不会减少每一相的电感电流纹波。另外,在大功率应用的场合,交错并联的相数会越来越多,这就导致了电感的数量和体积都在成倍地增加。通过在交错并联电路中引入磁集成和反向耦合技术,不仅可以减少体积,还同时满足了电路对稳态和暂态性能的要求[7]。文献[8]首次提出了等效电感、稳态电感和暂态电感的概念。文献[9-10]又对交错并联磁集成双向DC-DC变换器中耦合电感的设计和制作、耦合电感的对称化等进行了深入的研究。
然而,随着相数的增加,将所有相电感绕制在同一副磁心的设计变得愈发困难。当前,单磁心耦合电感的研究和设计存在的问题有:①多相耦合电感面临着磁通密度分布不均匀、结构不对称的问题;②多相耦合电感磁心的选型和设计存在很大的困难;③多相耦合电感的结构比较复杂,导致准确磁路和电路模型的建立比较困难。
另外一种实现多相耦合的思路是采用双绕组耦合电感的组合[12]。双绕组耦合电感制作比较简单,一般不存在不对称和直流偏磁等问题,并且现在对双绕组耦合电感的准确磁路和电路模型的建立以及加工制作技术都比较成熟[13]。在文献[14]中,三相耦合电感被三个双绕组耦合电感等效替代,将这种等效替代方法拓展到N相时,耦合电感数量是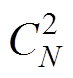 ,一旦相数N>3时,双绕组耦合电感的数量将急剧增加,大大限制了这种等效方法的推广。
,一旦相数N>3时,双绕组耦合电感的数量将急剧增加,大大限制了这种等效方法的推广。
在传统的交错并联双向DC-DC变换器中,由于每一相的寄生参数不一致,开关管等器件参数不完全相同以及占空比抖动等都会造成相间不均流现象,可能使得某些模块承担更多负载电流,从而致使重载相发热问题严重,进而导致整个电路不能正常工作[15]。
传统的均流控制策略可以分为有源均流法和下垂法两大类[16]。有源均流法是指各个模块之间有相互联系并且存在均流母线的控制方法,又可以分为主从法和平均法;反之,没有相互联系并且不存在均流母线的控制方法称之为下垂法,又可以将其分为串联电阻法和输出电流反馈法。文献[17]提出了一种改进的下垂法,其中,电流内环采用自适应的PI控制方法,电压外环采用I-V下垂控制方法,大大提高了变换器的暂态响应。文献[18]提出一种适用于多相Buck变换器的无传感器电流共享算法,通过测试估算每相的寄生电阻参数,进而计算出实现各相之间电流分配的占空比,补偿控制回路和功率变换器中由于寄生参数不匹配和占空比丢失带来的误差,无需检测每相电流也能实现良好的电流分配。文献[19]设计了一种基于输入电容电压纹波的无传感器电流共享自动调节控制器,利用输入电容电压纹波值之间的差异来指示各相的电流分布状态。每相的占空比被自动调整,使输入电容电压纹波值之间的差异最小,从而实现无电流传感器的相间均流。
传统的多相交错并联双向DC-DC变换器的均流控制方法,国内外研究已经十分成熟,但是针对多相交错并联耦合电感双向DC-DC变换器的均流控制方法,国内外并不多见。文献[20]针对两相交错磁集成双向DC-DC变换器,提出了离散滑模控制方法,但是当离散滑模控制应用于更高阶的复杂系统时,控制器的设计将会变得极其困难,所以目前针对多相交错并联耦合电感双向DC-DC变换器的滑模控制,理论并不成熟。
针对现有的文献,本文提出一种基于双绕组耦合电感的多相交错并联双向DC-DC变换器。以四相为例,本文详细分析了所提拓扑的工作模态、稳态和暂态性能。为了解决所提拓扑中存在的相间不均流问题,本文提出了一种基于相电流解耦的均流控制策略,大大简化了多相交错并联耦合电感DC-DC变换器中均流环路的设计。最后,通过仿真和实验验证了所提拓扑和均流控制策略的优越性、可靠性和实用性。
本文所提的基于耦合电感的四相交错并联双向DC-DC变换器主电路拓扑如图1所示。VH、VL分别为所提拓扑的高压侧电压和低压侧电压;v1、v2、v3、v4为每一相的电感电压;i1、i2、i3、i4为每一相的电感电流。该变换器采用交错并联控制来控制开关管的开通和关断,即S1、S3、S5、S7的导通顺序按照相位依次相差90°,而S2、S4、S6、S8分别与S1、S3、S5、S7互补导通。S1、S3、S5、S7占空比相等,均为D,S2、S4、S6、S8的占空比则为 =1-D。
=1-D。
本文主要研究反向耦合电感,并且所提拓扑中的双绕组耦合电感都是完全相同的,所以双绕组耦合电感的自感L1=L2=L3=L4=L,互感都为M,且耦合系数-1<k=M/L<0。因为所研究的拓扑对称,每一相的工作原理相似,不失一般性,本文仅仅分析第一相运行在Buck模式下的工作情况。
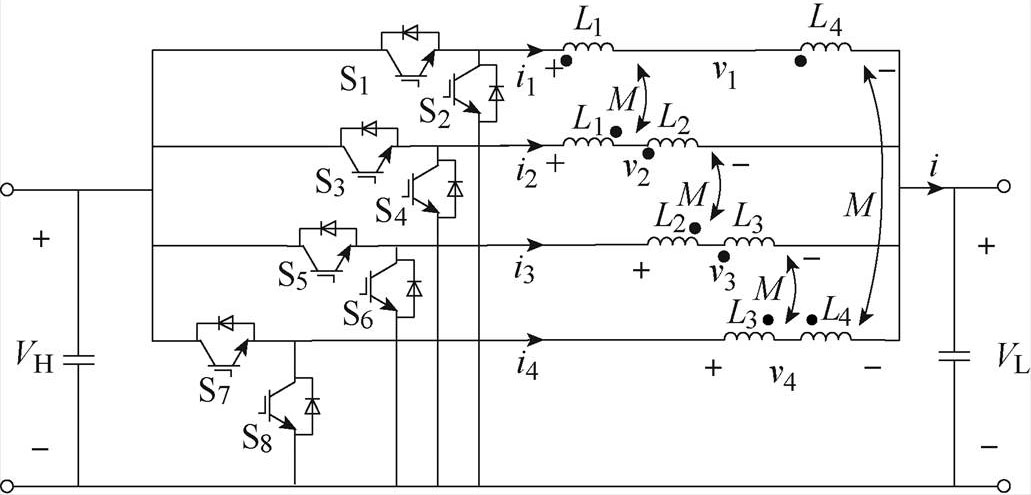
图1 主电路拓扑
Fig.1 Topology of main circuit
由图1可知,电感电压和电流的关系为
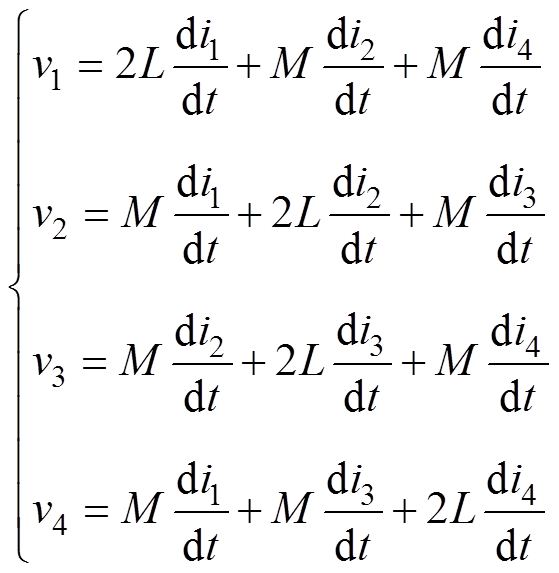 (1)
(1)耦合电感的电压和电流波形如图2所示。D= VL/VH,va=VH-VL>0,vb=-VL<0,则va=-( )vb。当占空比D处于不同的区间范围时,该变换器的工作状况会发生变化。本文以0.25<D<0.5为例来进行详细分析。
)vb。当占空比D处于不同的区间范围时,该变换器的工作状况会发生变化。本文以0.25<D<0.5为例来进行详细分析。
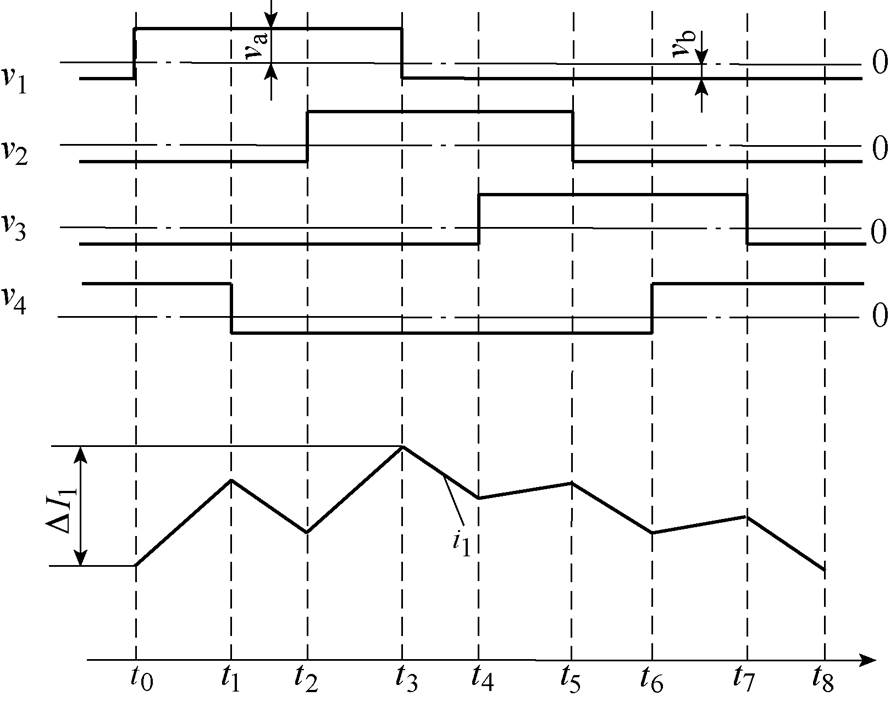
图2 耦合电感的电压和电流波形
Fig.2 Voltage and current waveforms of coupled inductors
模态1(t0, t1):v1=v4=va,v2=v3=vb,结合式(1)可得
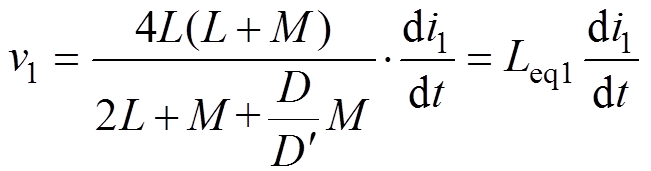 (2)
(2)式中,Leq1为工作模态1下的等效电感。
同理可以得到在不同占空比区间范围内,变换器在8个工作模态下的等效电感见表1。
表1 不同占空比下的等效电感
Tab.1 The equivalent inductance under different duty cycle

Leq12(L+M) Leq22(L+M) Leq32(L+M) Leq42(L+M) Leq52(L+M) Leq62(L+M) Leq72(L+M) Leq82(L+M)
根据以上分析可知,在各个占空比区间内,电感电流i1的变化只与v1有关,与v2、v3和v4无关。因此,在一个周期内各个工作模态下,每一相的模态电感相当于实现了等效解耦,即分别等效于非耦合情况下的独立电感。从表1可以看出,等效电感在每个模态下是变化的,所以基于耦合电感的四相交错并联双向DC-DC变换器是一个复杂的非线性系统。
在耦合情况下,当变换器工作在0.25<D≤0.5的稳态情况时,耦合电感的电压和电流波形如图2所示。从图2可知,每一相的稳态相电流纹波是模态1、2、3的电流变化量之和,因此稳态相电流纹波(峰-峰值)DI1为
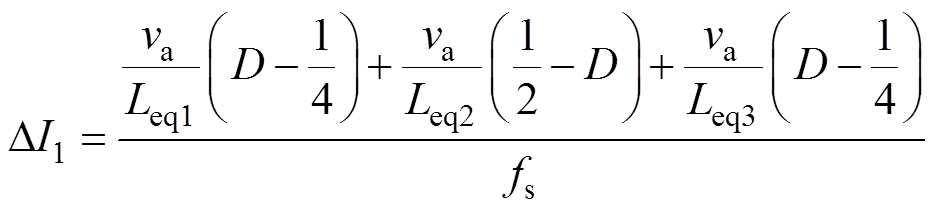 (3)
(3)式(3)可以进一步化简为
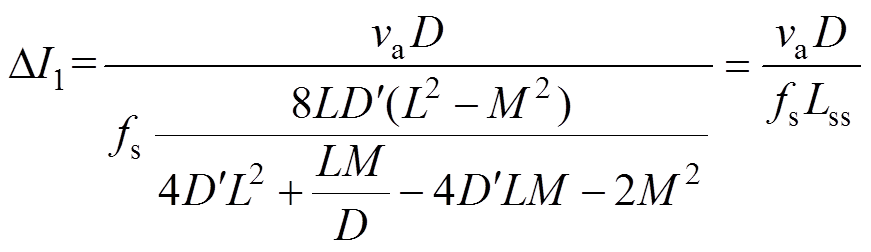 (4)
(4)
其中
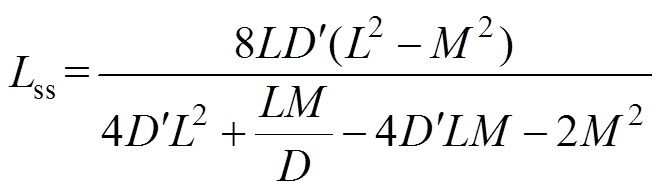
式中,fs为开关频率;Lss为耦合情况下变换器的等效稳态电感。
同理,在非耦合情况(即每相采用独立电感,下同)下,传统的四相交错并联双向DC-DC变换器的稳态相电流纹波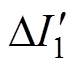 为
为
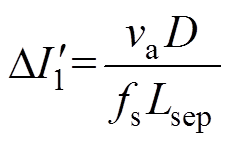 (5)
(5)式中,Lsep为非耦合情况下变换器的独立电感。
由式(4)和式(5)可以看出,变换器在耦合和非耦合情况下的稳态相电流纹波的差异是由于Lss和Lsep的不同引起的。
同理,可以得到所提变换器在不同占空比下的等效稳态电感见表2。
本文所提变换器的另一重要特性就是动态性能。当负载或输入电压突然变化时,占空比需要快速动态调整,从而使变换器的输出电压稳定。暂态相电流波形如图3所示,当四相交错并联耦合电感双向DC-DC变换器工作在0.25<D≤0.5的Buck 运行模式下时,如果占空比D突然增加了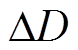 ,可以看出,虚线部分的相电流暂态增量Di1为
,可以看出,虚线部分的相电流暂态增量Di1为
表2 不同占空比下的等效稳态电感
Tab.2 The equivalent steady-state inductance under different duty cycle

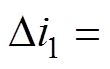
 (6)
(6)
式中,TS为开关周期。式(6)可以进一步化简为
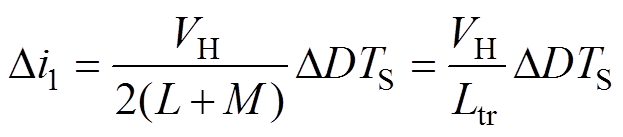 (7)
(7)其中
Ltr=2(L+M)
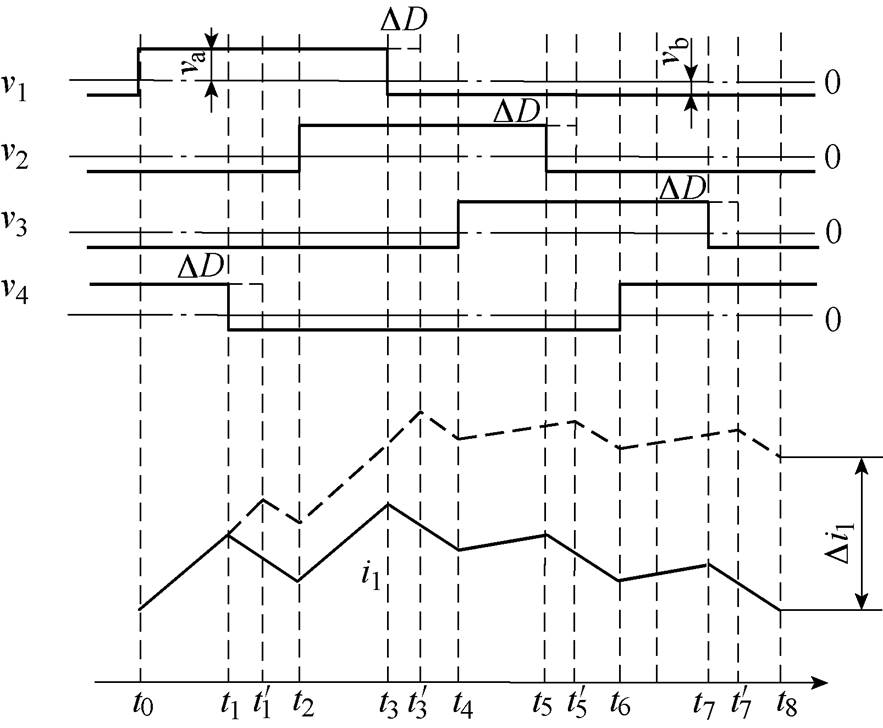
图3 暂态相电流波形
Fig.3 Transient-state phase current waveforms
同理,可以得到在非耦合情况下,当占空比D增加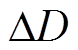 时,变换器的相电流暂态增量
时,变换器的相电流暂态增量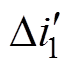 为
为
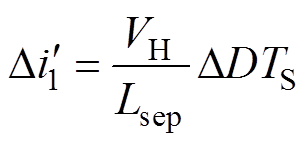 (8)
(8)由式(7)和式(8)可以看出,变换器在耦合和非耦合情况下的暂态相电流增量差异是由于Ltr和Lsep的不同引起的,因此,称Ltr为所提拓扑的等效暂态电感。
同理,可以得到所提变换器在其他占空比下的等效暂态电感,均为2(L+M)。
根据式(4)和式(5)可知,在耦合和非耦合情况下,变换器的稳态相电流纹波之比为
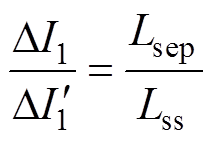 (9)
(9)为了更便于比较,假设变换器的暂态相电流响应速度在耦合和非耦合情况下是相同的,即Lsep= Ltr=2(L+M)。根据式(9)可以得到在耦合和非耦合情况下,变换器的稳态相电流纹波之比见表3,其三维图如图4a所示。
表3 两种情况下的稳态相电流纹波之比
Tab.3 Ratio of steady-state phase current ripple in two cases

通过图4a可知,在耦合情况下,变换器的稳态相电流纹波远远小于非耦合情况。图4a关于D=0.5对称,即当占空比等于0.5+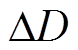 或者0.5-
或者0.5-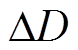 时,使用反向耦合电感对稳态相电流纹波的减少作用是相同的。同时,在耦合情况下,互感系数k越小以及占空比D越接近于0.25、0.5、0.75,稳态相电流纹波减小的效果越明显。
时,使用反向耦合电感对稳态相电流纹波的减少作用是相同的。同时,在耦合情况下,互感系数k越小以及占空比D越接近于0.25、0.5、0.75,稳态相电流纹波减小的效果越明显。
根据式(7)和式(8)可知,在耦合和非耦合情况下,变换器的暂态相电流响应速度之比为
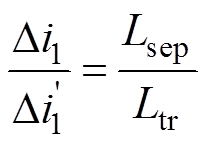 (10)
(10)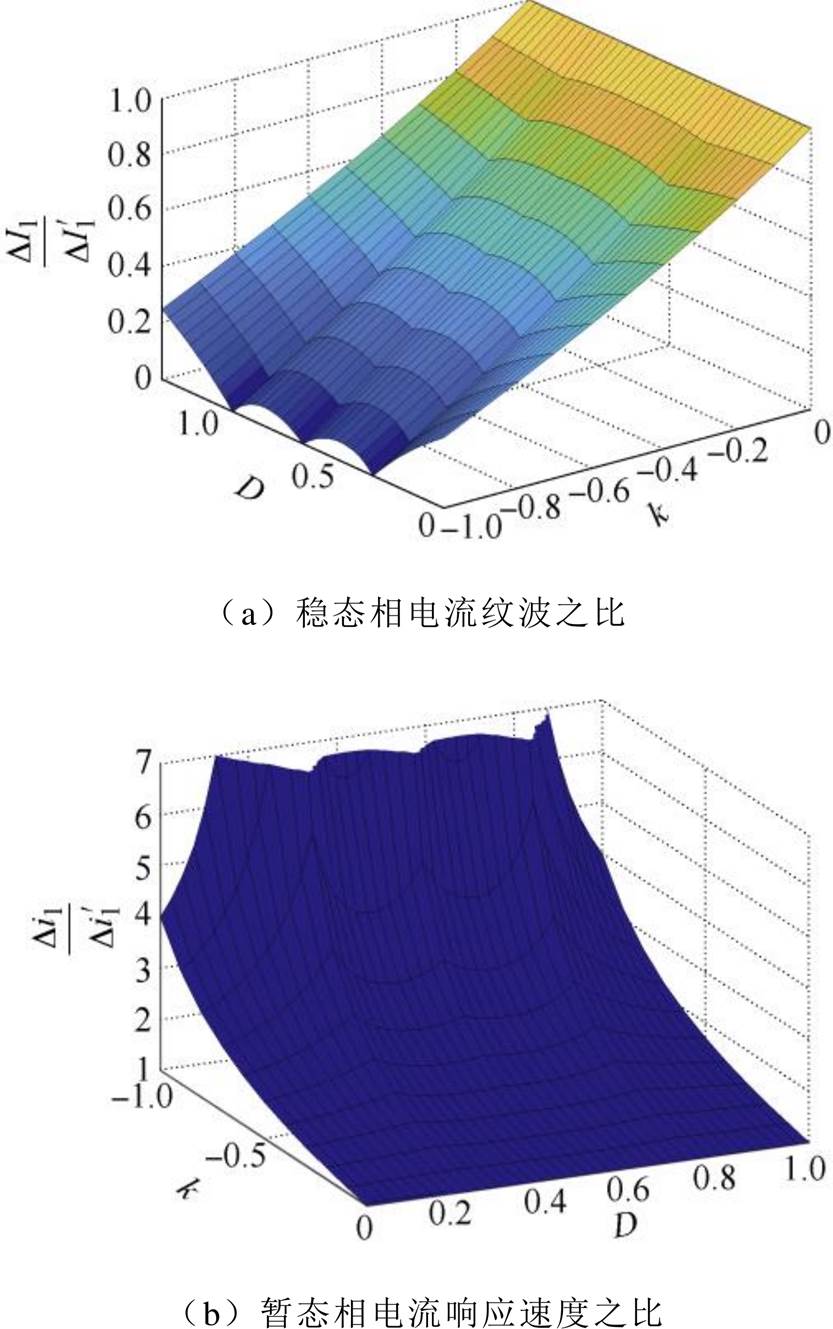
图4 耦合与非耦合情况下的稳态相电流纹波之比与暂态相电流响应速度之比
Fig.4 Ratio of steady-state phase current ripple and transient-state phase current response speed in two cases
为了更便于比较,假设变换器的稳态相电流纹波在耦合和非耦合情况下是相同的,即Lsep=Lss。根据式(10)可以得到两种情况下变换器的暂态相电流响应速度之比见表4,其三维图如图4b所示。
表4 两种情况下的暂态相电流响应速度之比
Tab.4 Ratio of transient-state phase current response speed in two cases

通过图4b可知,在耦合情况下,变换器的暂态相电流响应速度远远大于非耦合情况。图4b关于D=0.5对称,即当占空比等于0.5+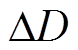 或者0.5-
或者0.5- 时,使用反向耦合电感对暂态相电流响应速度的增强作用是相同的。同时,在耦合情况下,互感系数k越小以及占空比D越接近于0.25、0.5、0.75,暂态相电流响应速度的提升效果越明显。
时,使用反向耦合电感对暂态相电流响应速度的增强作用是相同的。同时,在耦合情况下,互感系数k越小以及占空比D越接近于0.25、0.5、0.75,暂态相电流响应速度的提升效果越明显。
交错并联耦合电感双向DC-DC变换器的设计难点主要是相间存在耦合关系,如果直接用传统的小信号建模的方法来求传递函数,得到的传递函数很复杂,调节器的设计将会变得非常困难。因此,本文提出一种基于相电流解耦的均流控制策略,大大简化了电流调节器的设计。
四相交错并联耦合电感双向DC-DC变换器在Buck运行状态下的动态结构如图5所示,图中,r为变换器每一相等效寄生电阻之和(包括电感的寄生电阻、线路的阻抗等),Ro为输出端的负载,iz为电路输出的四相电流之和,iC为流过输出端电容的电流,io为输出端电流响应,Vi为稳态输入电压,vi为输入电压扰动,vo为输出电压响应,dm、vLm、iLm分别为第m相的开关管占空比、电感电压、电感电流,m =1、2、3、4。通过图5可以看出,由于电感的耦合作用,相电流之间互有影响而不是相互独立。如果按照传统的电流调节器进行设计,将导致电流内环的设计变得极其困难,不利于实际应用。
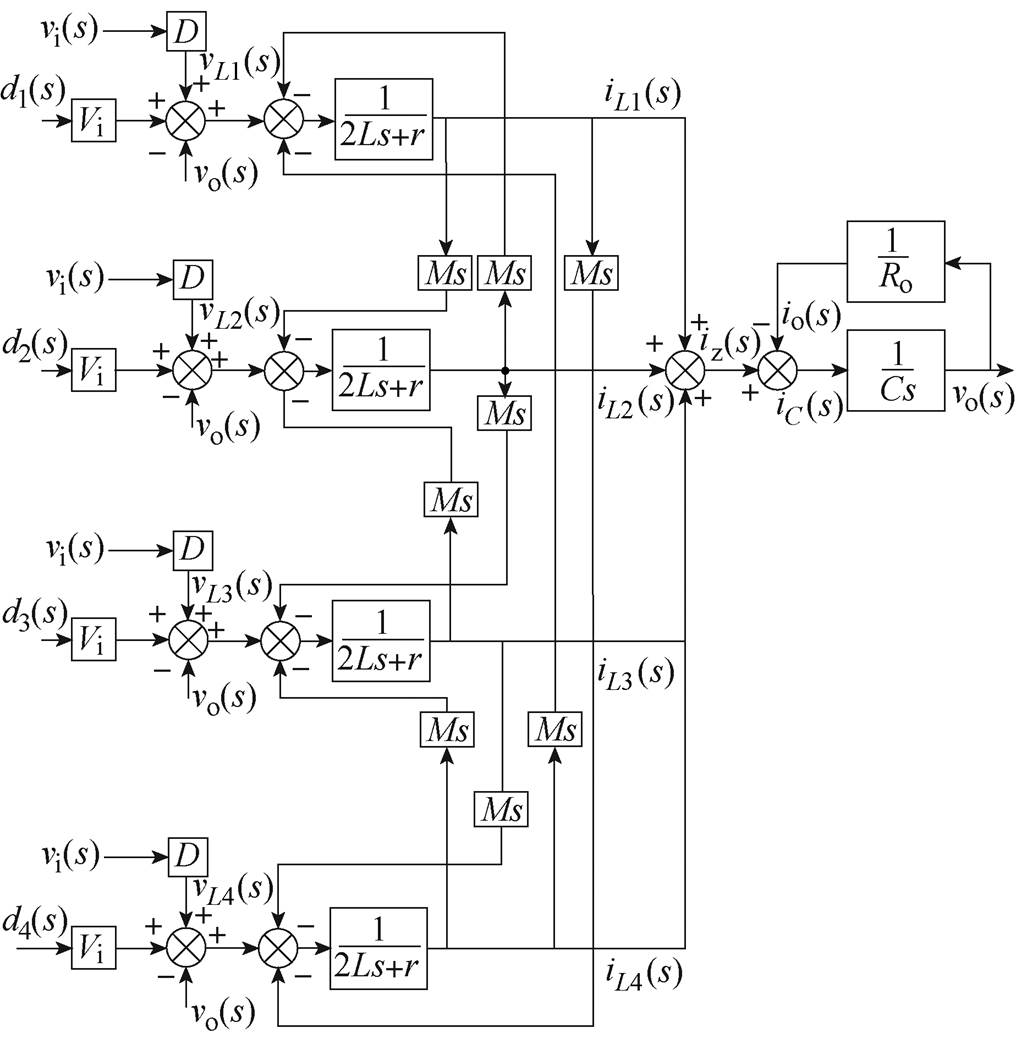
图5 所提拓扑在Buck运行状态下的动态结构
Fig.5 Dynamic block diagram of the proposed topology in Buck mode
根据图1可以写出电路的相电压和相电流在频域的方程式为
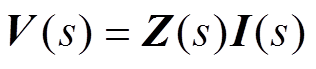 (11)
(11)其中,阻抗矩阵Z(s)为
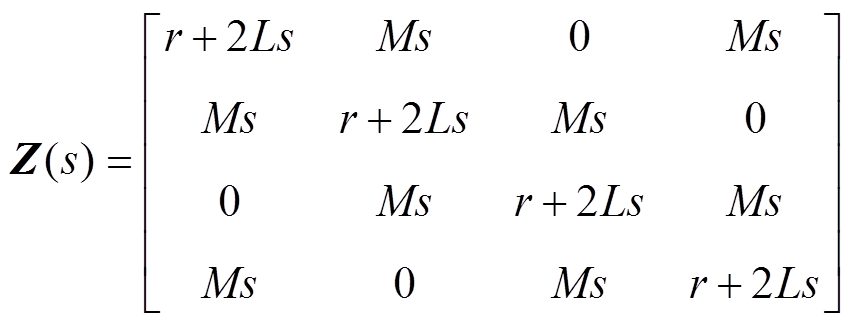 (12)
(12)
所提拓扑的简化电流环控制框图如图6所示,图中,vi(s)为输入电压扰动,vo(s)为输出电压扰动,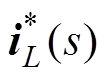 为相电流给定值向量,iL(s)为输出相电流向量,Vi为输入电压,导纳矩阵Y(s)为式(12)中阻抗矩阵Z(s)的逆矩阵。在传统的四相变换器(即各相采用独立电感)中,相间不存在耦合关系,导纳矩阵Y(s)是一个四阶的对角阵,对应的调节器矩阵WCEA(s)也是一个对角阵。然而多相耦合变换器中,导纳矩阵Y(s)不再是一个对角阵,即相电流之间存在耦合作用,这就导致了电流调节器的设计变得极其复杂。在多相交错并联耦合电感双向DC-DC变换器中,只要导纳矩阵Y(s)满足相似对角化的条件,就可以将其进行相似对角化,相似对角化后得到的对角阵就相当于传统交错变换器中的导纳矩阵Y(s),从而实现了相电流的解耦功能,大大简化了电流调节器的设计。
为相电流给定值向量,iL(s)为输出相电流向量,Vi为输入电压,导纳矩阵Y(s)为式(12)中阻抗矩阵Z(s)的逆矩阵。在传统的四相变换器(即各相采用独立电感)中,相间不存在耦合关系,导纳矩阵Y(s)是一个四阶的对角阵,对应的调节器矩阵WCEA(s)也是一个对角阵。然而多相耦合变换器中,导纳矩阵Y(s)不再是一个对角阵,即相电流之间存在耦合作用,这就导致了电流调节器的设计变得极其复杂。在多相交错并联耦合电感双向DC-DC变换器中,只要导纳矩阵Y(s)满足相似对角化的条件,就可以将其进行相似对角化,相似对角化后得到的对角阵就相当于传统交错变换器中的导纳矩阵Y(s),从而实现了相电流的解耦功能,大大简化了电流调节器的设计。
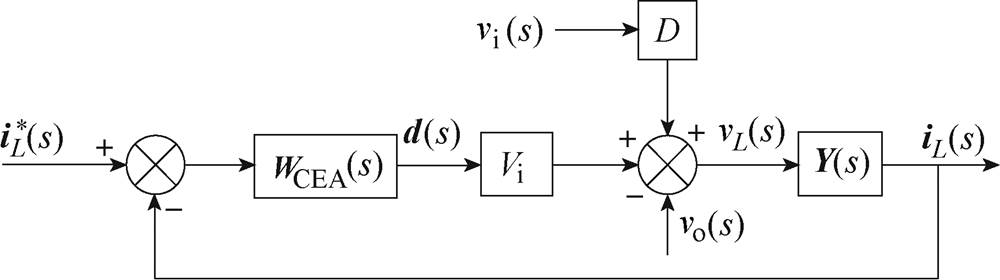
图6 简化的电流环控制框图
Fig.6 Simplified current-loop control diagram
根据式(12)可以看出阻抗矩阵Z(s)是实对称矩阵,所以其导纳矩阵Y(s)也一定是实对称矩阵,可以将其导纳矩阵Y(s)进行相似对角化,结果为
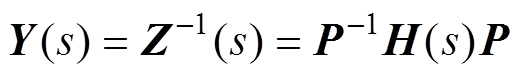 (13)
(13)其中
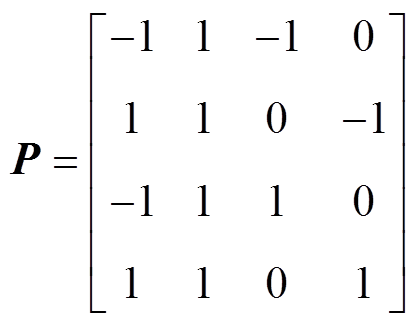
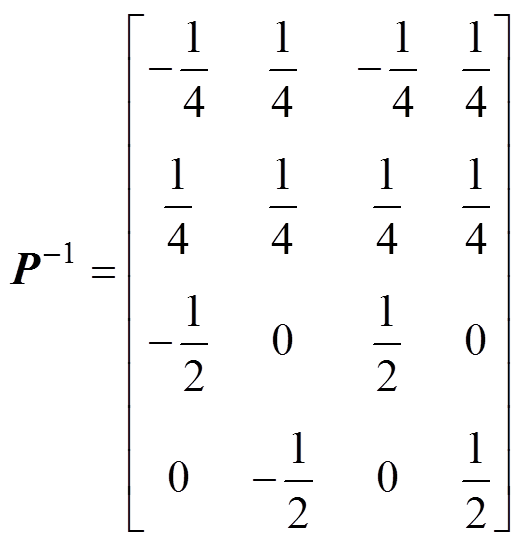
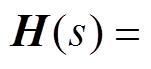
通过式(13)可以看出,解耦后的矩阵H(s)是个四阶的对角阵,相电流之间已不存在耦合关系,所以每一相的电流调节器可以独立进行设计。相对于解耦前相电流存在耦合关系,解耦后大大减少了均流环的设计难度和工作量。
本文所提拓扑进行相电流解耦后的电流环控制框图如图7a所示,通过控制理论可以将其进一步转化成如图7b所示的等效框图。图7b中,电流环调节器WCEA(s)也是一个四阶对角阵。通过图7b可以看出,解耦后相当于将原先的电流给定值 转化成新的给定值
转化成新的给定值 ,解耦后新的变量
,解耦后新的变量 是相互独立的,不存在耦合关系。忽略系统扰动量,可以将电流环框图进一步简化,如图7c所示,解耦后四个新的电流环是彼此独立的,图中,W1(s)、W2(s)、W3(s)、W4(s)分别是需设计的四个相电流调节器,G1(s)、G2(s)、G3(s)、G4(s)是解耦后四阶对角阵H(s)中的对应的对角元素。
是相互独立的,不存在耦合关系。忽略系统扰动量,可以将电流环框图进一步简化,如图7c所示,解耦后四个新的电流环是彼此独立的,图中,W1(s)、W2(s)、W3(s)、W4(s)分别是需设计的四个相电流调节器,G1(s)、G2(s)、G3(s)、G4(s)是解耦后四阶对角阵H(s)中的对应的对角元素。
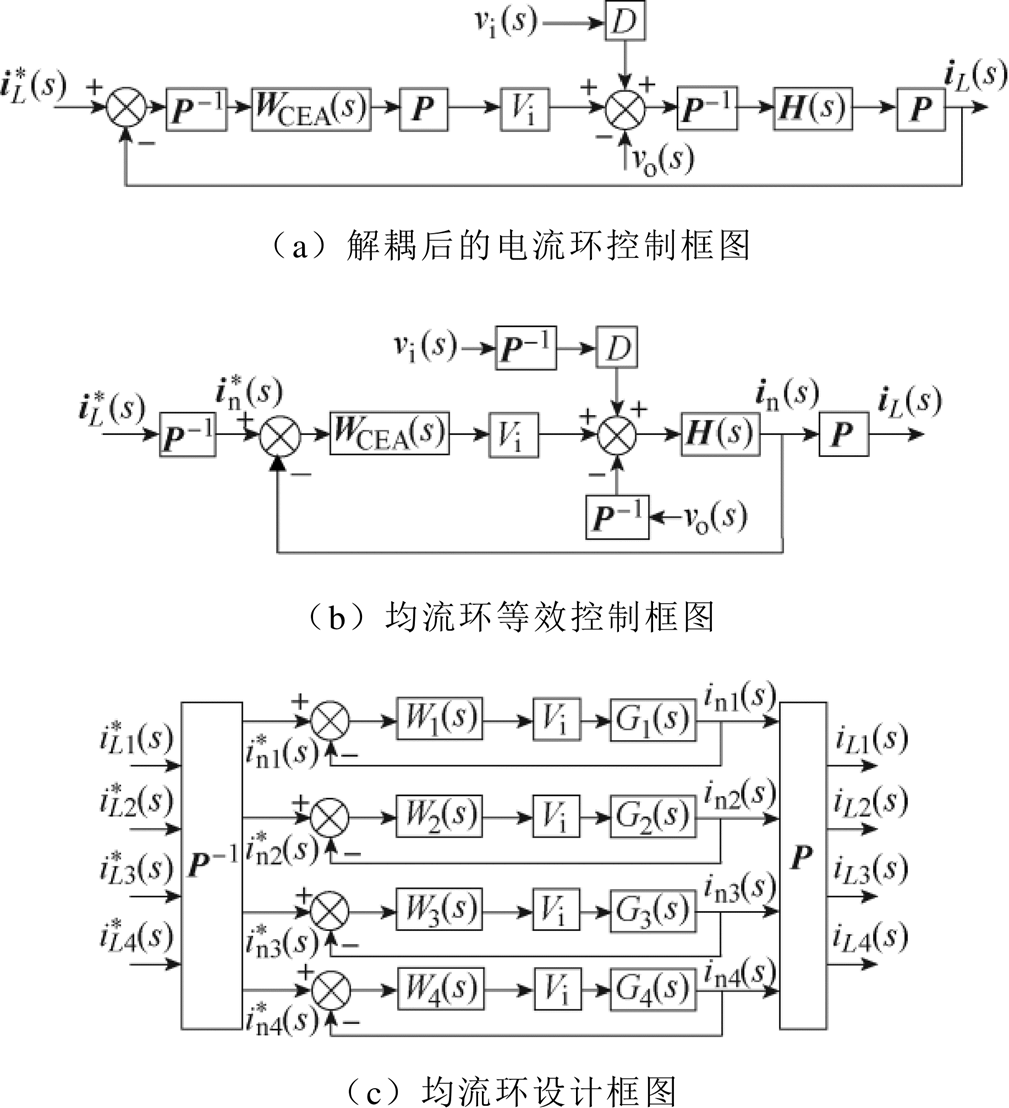
图7 相电流解耦的均流环控制框图
Fig.7 Phase-decoupled current sharing control diagram
在实际应用中,为了实现变换器的输出电压控制,一般是对系统进行电压电流双闭环控制,即在均流环基础上加入电压控制外环。在设计电压外环时,本文采用的是公共电压外环设计方法。
所提拓扑的公共电压外环控制框图如图8所示。图8a所示是系统的电压电流双闭环控制框图,可以将其中的均流环进一步简化成如图8b所示的电流内环等效框图。然后用电流调节器将四个电流内环校正成相同的形式,如图8c所示。为了简化电压外环的设计,以电路空载为例,对公共电压外环进行设计,空载情况下简化的电压外环框图如图8d所示。图中,WVEA(s)为电压环调节器。
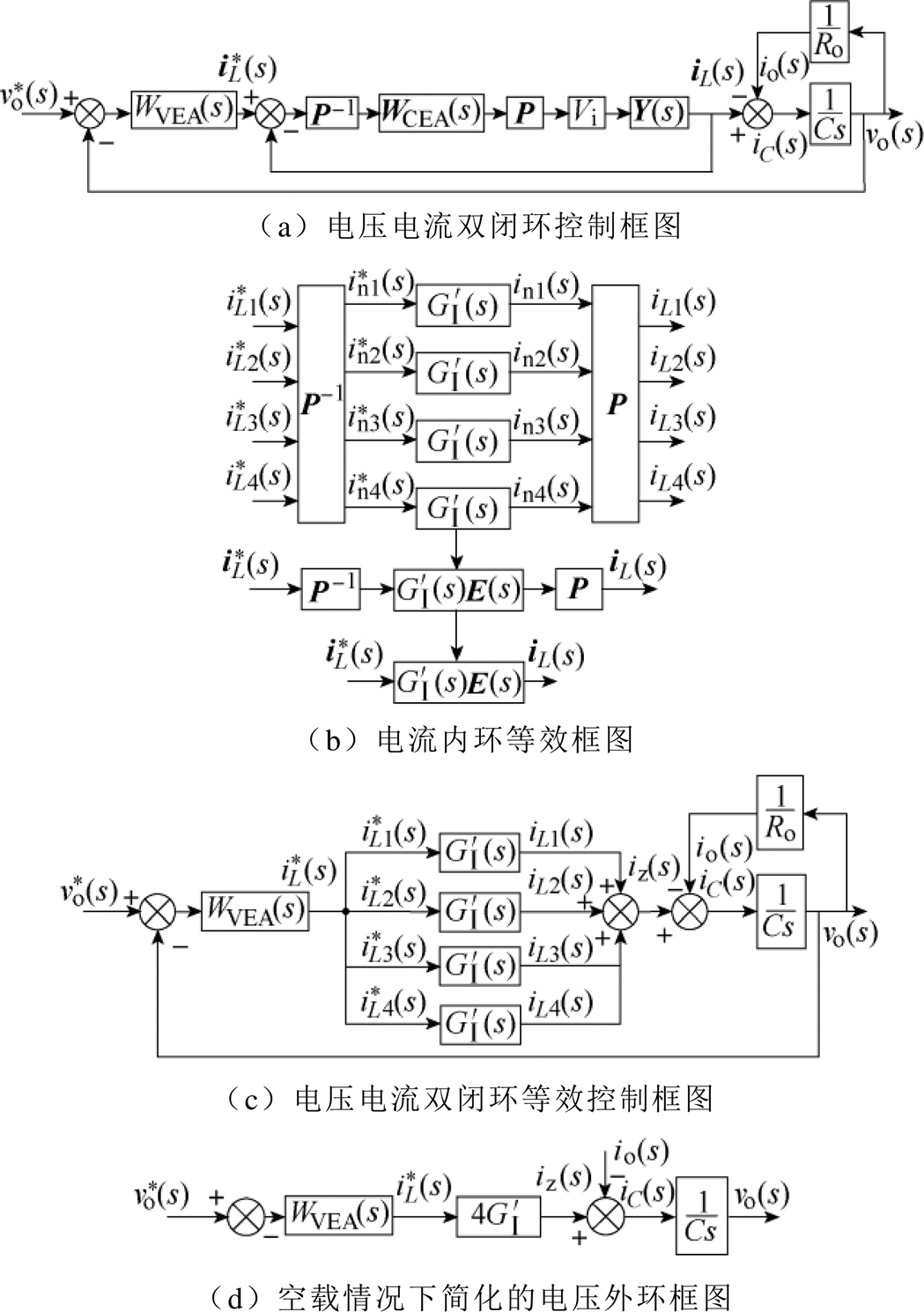
图8 公共电压外环控制框图
Fig.8 Diagram of public outer voltage control loop
通过以上分析可以看出,本文所采用的电压外环控制方法设计比较简单,实现起来也比较容易,大大简化了多相耦合变换器的电压外环控制器的设计。
基于耦合电感的四相交错并联双向DC-DC变换器可以双向运行,本文所提的均流控制方法同样适用于Boost模态。所提拓扑在Boost运行状态下的动态结构如图9所示,图中,d1、d2、d3、d4分别为开关管S2、S4、S6、S8的占空比,其稳态值都为D,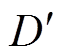 =1-D为开关管S1、S3、S5、S7的稳态占空比。
=1-D为开关管S1、S3、S5、S7的稳态占空比。
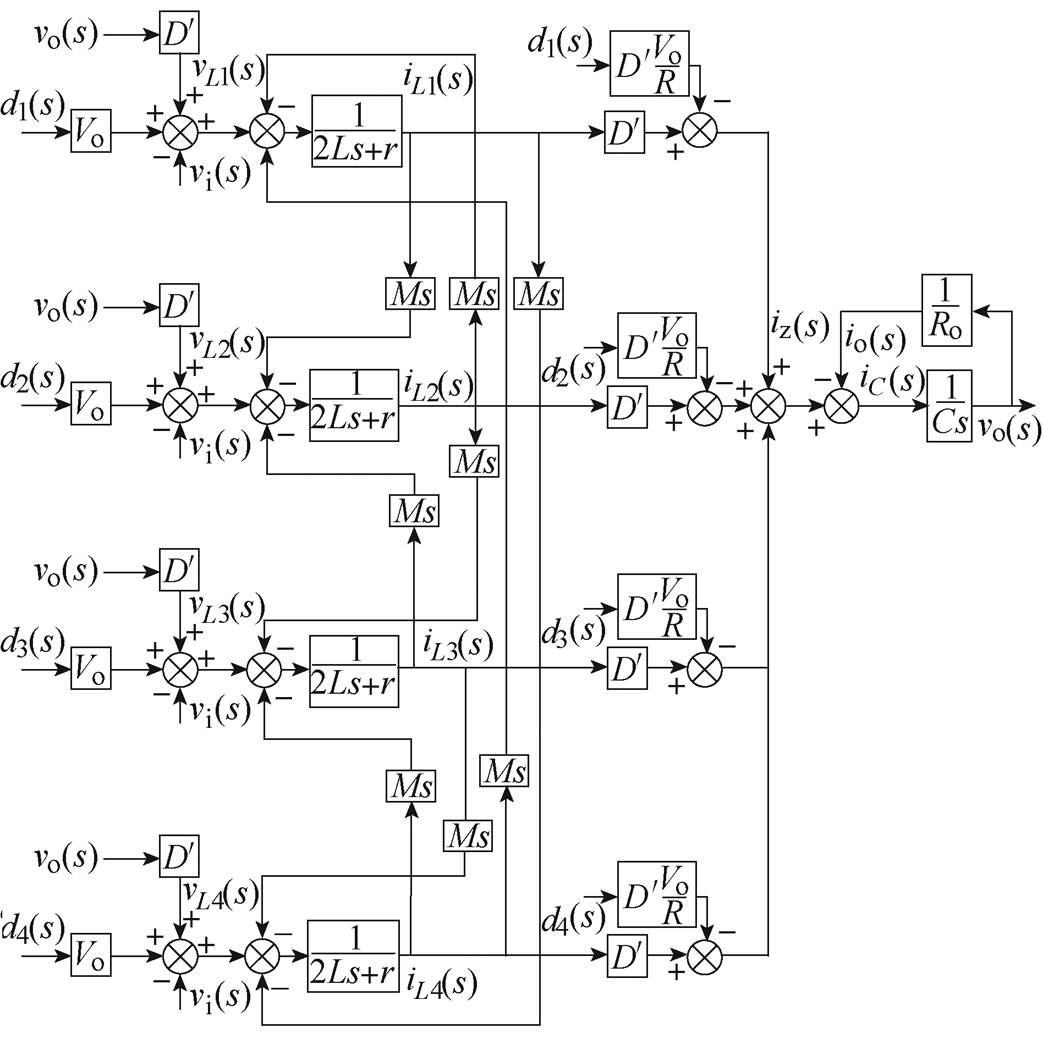
图9 所提拓扑在Boost运行状态下的动态结构
Fig.9 Dynamic block diagram of the proposed topology in Boost mode
通过对比图5和图9可以看出,忽略系统的输入输出电压扰动,所提拓扑在Boost运行状态下的电流环路和在Buck运行状态下的电流环路相同,电压环路也仅仅多了一个比例系数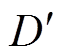 。因此变换器Boost模态下的电压电流调节器的设计思路完全可以按照Buck模态下调节器的设计思路来进行,其中,Buck模态下的电流调节器参数不用修改,就可以直接适用于Boost模态,电压调节器比例系数稍作修改,也同样适用于Boost模态,体现了所提均流控制方法的优越性和实用性。
。因此变换器Boost模态下的电压电流调节器的设计思路完全可以按照Buck模态下调节器的设计思路来进行,其中,Buck模态下的电流调节器参数不用修改,就可以直接适用于Boost模态,电压调节器比例系数稍作修改,也同样适用于Boost模态,体现了所提均流控制方法的优越性和实用性。
本节将以所提拓扑在Buck运行状态为例,详细进行系统的电压电流双闭环设计。主电路参数见表5。
3.4.1 电流调节器设计
根据式(13)和图7c可知,未使用电流调节器校正前,四个独立的并联电流回路开环传递函数分别是ViG1(s)、ViG2(s)、ViG3(s)、ViG4(s),表示为
表5 主电路参数
Tab.5 Main circuit parameters

参 数数 值 输入电压Vi/V50 输出滤波电容C/mF1 000 开关频率fs/kHz20 双绕组耦合电感自感L/mH220 双绕组耦合电感互感M/mH-176 相内等效寄生电阻r/W0.1
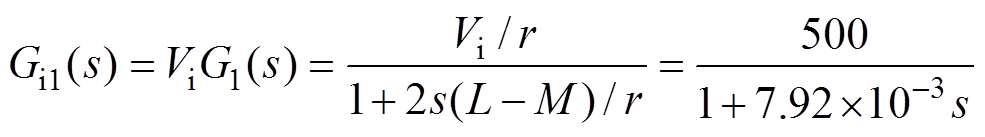 (14)
(14)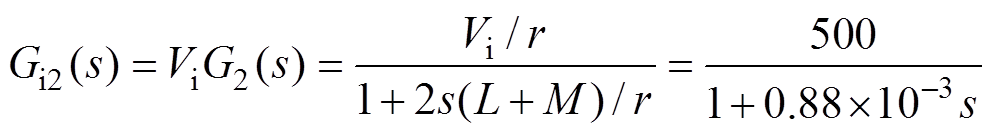 (15)
(15)
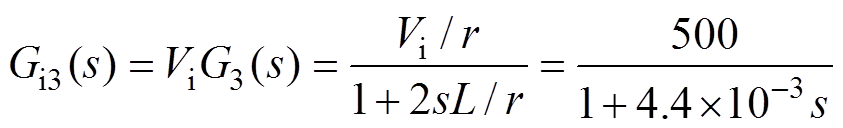 (16)
(16)
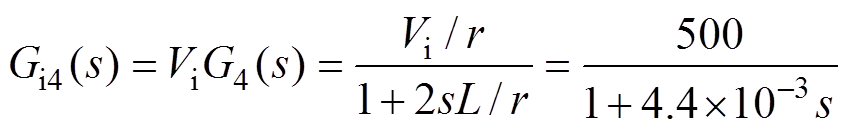 (17)
(17)由于本节采用的是公共电压外环的设计思路来设计电压闭环调节器,所以需要把四个电流环校正成相同的传递函数。可以看出,未校正前四个独立的并联电流回路传递函数是一阶惯性环节。为了实现电流内环快速的动态响应功能,使用电流调节器将电流回路的开环传递函数校正成I型系统,四个电流调节器分别为
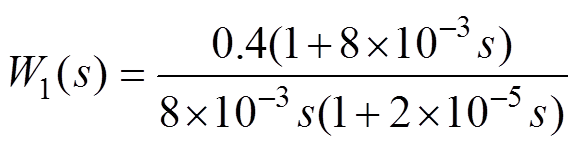 (18)
(18)
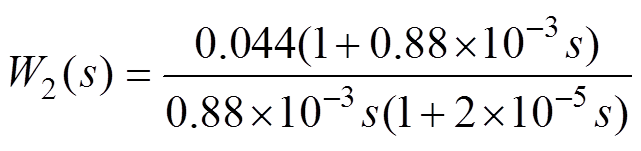 (19)
(19)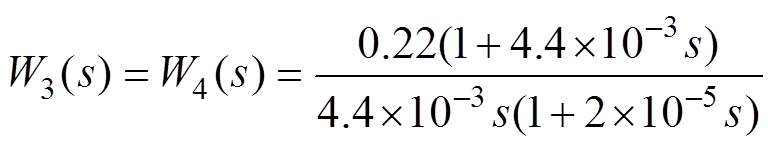 (20)
(20)
校正后的四个独立的并联电流回路开环传递函数均为
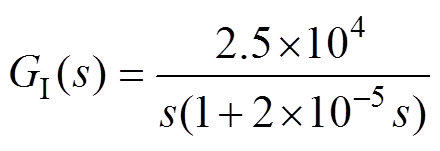 (21)
(21)校正后电流环的开环传递函数伯德图如图10a所示,可以看出,校正后的电流开环传递函数的相位裕度为65.5°,剪切频率为3 620Hz,所以校正后的系统是稳定的,并且动态响应很快,完全满足 要求。

图10 校正后的开环传递函数伯德图
Fig.10 Bode diagrams of open-loop transfer function after correction
校正后,四个独立的并联电流回路闭环传递函数均为
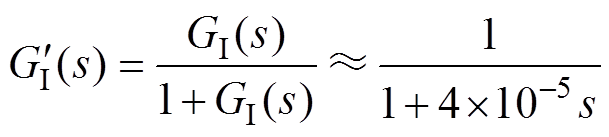 (22)
(22)3.4.2 电压调节器设计
根据图8d可知,在空载情况下,忽略系统其他扰动,未校正前电压回路的开环传递函数为
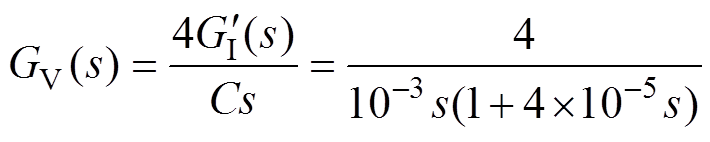 (23)
(23)为了满足电压外环的无静差调节、抗干扰性能强的要求,用电压调节器将电压回路的开环传递函数校正成II型系统。此时,电压调节器为
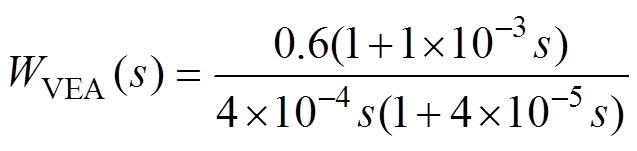 (24)
(24)
使用电压调节器校正后的电压外环开环传递函数为
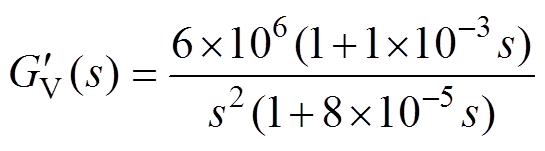 (25)
(25)校正后电压环的开环传递函数伯德图如图10b所示,从中可以看出,校正后的电压开环传递函数的相位裕度为55.8°,剪切频率为886Hz,所以校正后的系统是稳定的,并且抗干扰性能好,完全可以满足要求。
为了验证以上理论分析的正确性,首先搭建了所提拓扑的PSIM仿真模型,进行仿真验证。以Buck运行状态为例,仿真参数见表5。
假设变换器在耦合/非耦合情况下的暂态性能是相同的,即Ltr=Lsep=2(L+M)=88mH。在占空比为0.6时,在耦合/非耦合两种情况下,即变换器使用耦合电感/独立电感时的稳态相电流仿真波形如图11所示,可以看出,变换器在耦合和非耦合情况下其稳态相电流纹波之比为1.63/6.68=0.244,理论值为0.246,两者基本相同,验证了第2.1节的理论分析。
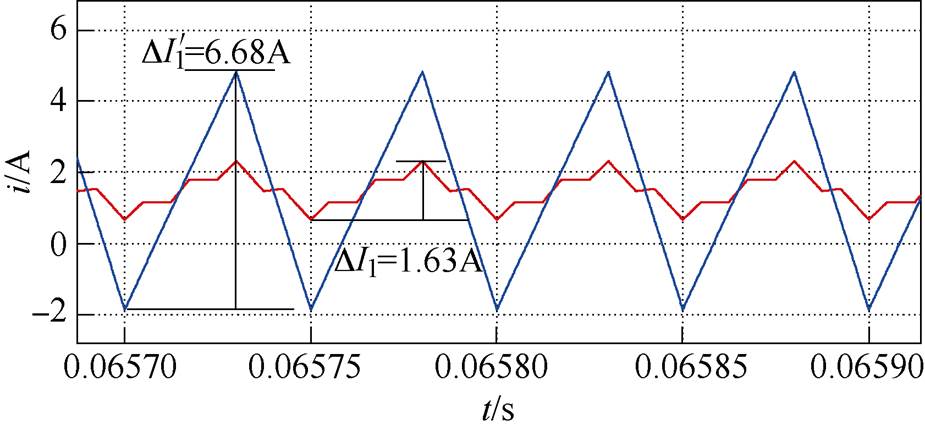
图11 耦合/非耦合情况下的稳态相电流仿真波形
Fig.11 Steady-state phase current simulation waveforms under coupled and uncoupled cases
为了验证所提的闭环均流控制策略,四相变换器第二相和第三相分别串联0.3W 和0.15W 的小电阻,来模拟相间的电流不平衡。占空比为0.6时,所提拓扑的各相电流仿真波形如图12所示,可以看出,开环控制时四相电流不平衡现象明显,同时也说明了闭环均流控制的必要性。

图12 D=0.6时四相电流仿真波形
Fig.12 Simulation waveforms of four phase currents at D=0.6
采用本文所提的电压电流双闭环控制策略时的仿真波形如图13所示。图13a为所提拓扑各相的电流波形。通过对比图13a以及图12可知,在电压电流双闭环控制时,给定输出电压30V、负载为5W 情况下,四相电流平均值均为1.5A左右,均流效果良好,说明了本文所提的电压电流双闭环控制策略的正确性。
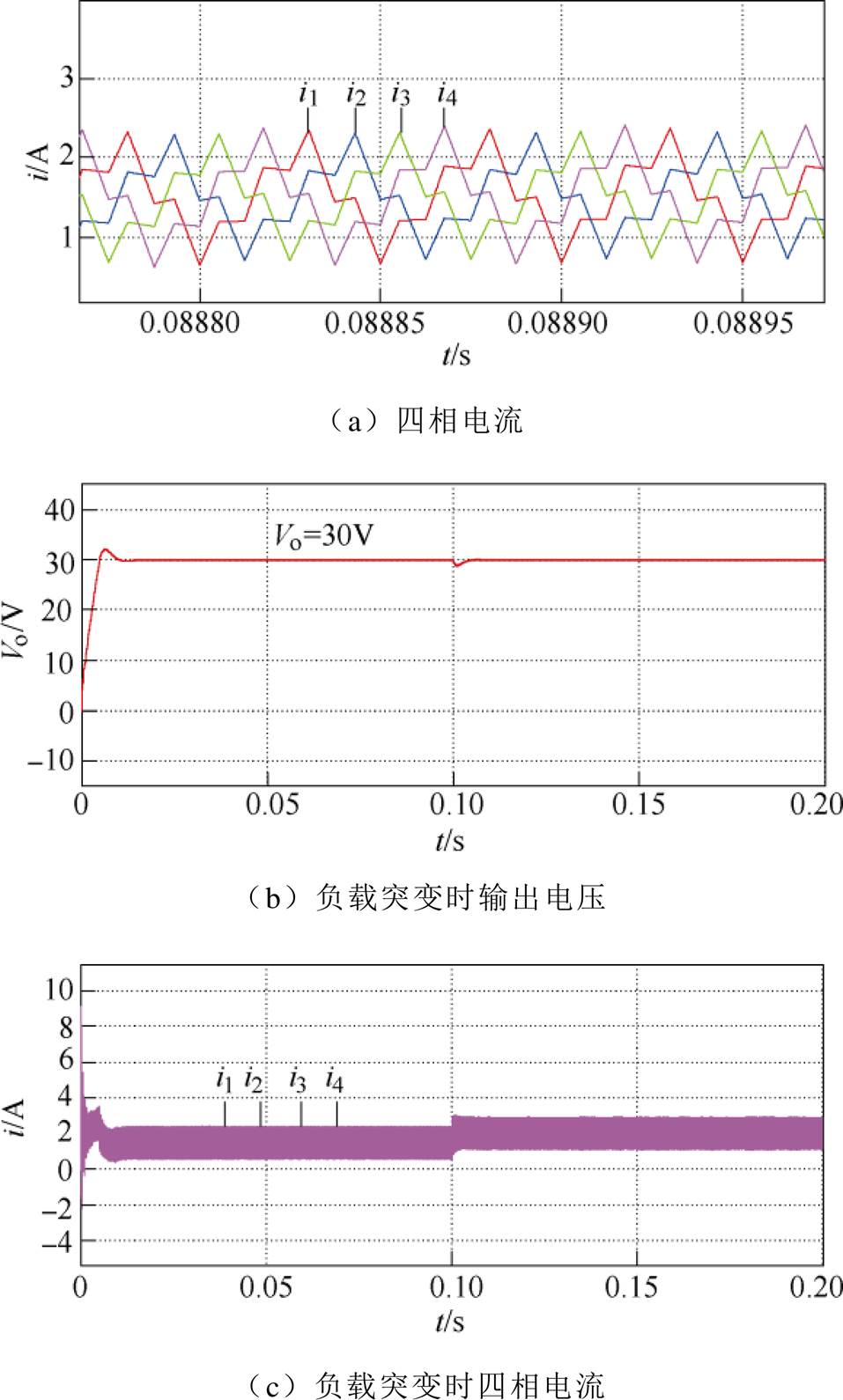
图13 电压电流双闭环控制时的仿真波形
Fig.13 Simulation waveforms when the voltage and current double closed-loop is used
为了检验双闭环控制时系统的抗干扰能力,进行了负载突变仿真,当负载在0.1s时由5W→3.7W突变时(即功率由180W→243W突变),仿真波形如图13b和图13c所示。输出电压经短的暂态很快维持在30V,四相电流平均值均由1.5A跃变至2A,电流的均流效果依然良好。输出电压和四相电流都能起到反馈作用,响应速度都很快,并且稳定性良好,抗干扰性能强,实现了无静差调节。说明了本文所提的电压电流双闭环控制策略的正确性和可行性。
为了验证本文所提理论分析的正确性,以基于耦合电感的四相交错并联双向DC-DC变换器为例制作了一台实验样机,样机平台如图14所示。其中实验样机主电路设计参数和仿真相同,见表5;双绕组耦合电感的实测参数见表6。从表6可以看出,双绕组耦合电感的自感L≈220mH,互感M≈-176mH,耦合系数k=-0.8。

图14 实验样机平台
Fig.14 Experimental prototype platform
表6 双绕组耦合电感参数
Tab.6 Parameters of two-winding coupled inductors

耦合电感一次侧自感/mH二次侧自感/mH互感/mH 1221223-174 2220225-175 3222217-174 4217217-182
采用TI公司的DSP TMS320F28335来实现对变换器主电路的控制,相关的实验波形如图15~图19所示。
4.2.1 稳态/暂态性能比较验证
与仿真类似,在比较验证稳态性能时,理想情况下独立电感的设计值为88mH,实验中所用的独立电感参数分别为88mH、89mH、90mH和90mH。当四相变换器工作在Buck模式下,在占空比D=0.4和0.6时,在耦合/非耦合情况下的稳态相电流实验波形如图15所示。
与图11的仿真波形相比可以看出,实验和仿真的电流纹波大小稍有偏差,这是由电感加工误差、电路分布参数影响等造成的。
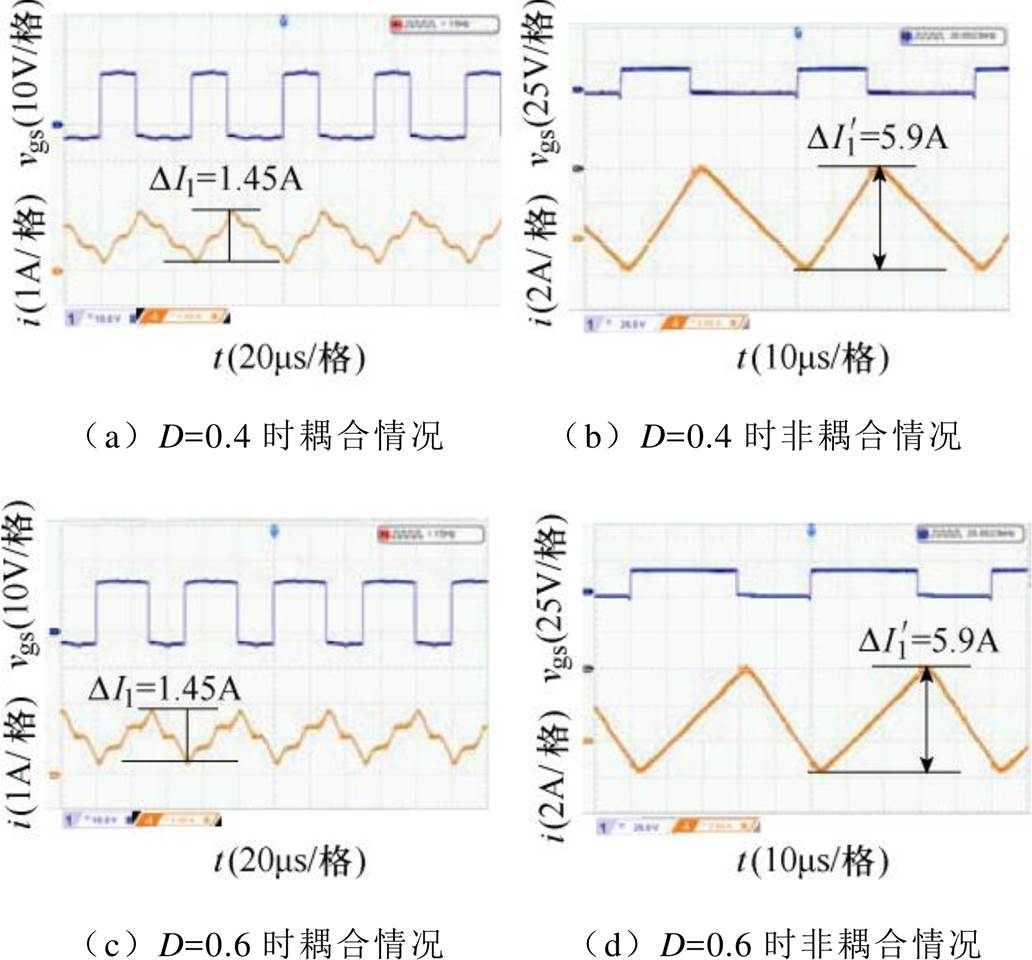
图15 稳态相电流波形
Fig.15 Steady-state phase current waveforms
耦合/非耦合情况下稳态相电流纹波之比的理论值和实验值见表7。通过表7可以看出,实验值和理论值以及仿真值很接近,验证了第2.1节的理论分析。
表7 耦合和非耦合情况下稳态相电流纹波之比
Tab.7 Ratio of steady-state phase current ripple under coupled and uncoupled cases

d 实验值理论值 0.40.2410.246 0.60.2410.246
假设四相变换器在耦合和非耦合情况下的稳态性能是相同的,即
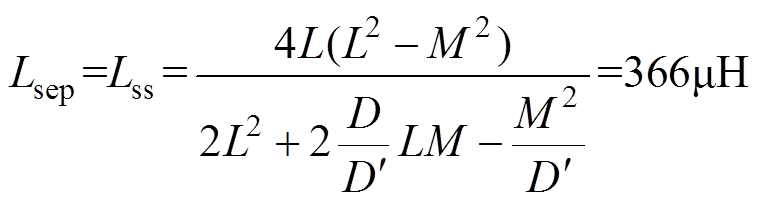 (26)
(26)理想情况下独立电感的设计值为366mH,实验中所用的独立电感参数分别为373mH、372mH、370mH和371mH。当四相变换器工作在Buck模式下,占空比从0.4变为0.48时,在耦合情况下和非耦合情况下的暂态相电流实验波形如图16所示。
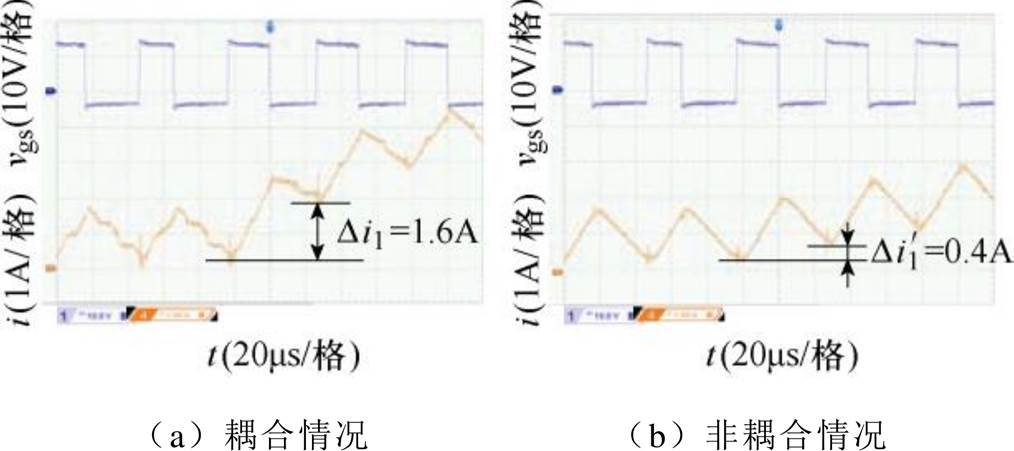
图16 暂态相电流波形
Fig.16 Transient-state phase current waveforms
耦合/非耦合情况下暂态相电路响应速度之比的理论值和实验值见表8,通过表8可以看出,实验值和理论值很接近,验证了第2.2节的理论分析。
表8 耦合和非耦合情况下暂态相电流响应速度之比
Tab.8 Ratio of transient-state phase current response speed under coupled and uncoupled cases

d 实验值理论值 0.4→0.4844.15
4.2.2 闭环及均流实验验证
为了验证所提闭环均流控制策略的正确性,与仿真设置相同,实验时将变换器的第二相和第三相分别串联0.3W 和0.15W 的小电阻,来模拟相间电流的不平衡。
当输入电压为50V、负载为5W、占空比为0.6时,所提拓扑的四相电流波形如图17所示。通过图17可知,四相电流的平均值分别为1.8A、1.1A、1.3A、1.75A。在开环情况下,与图12的仿真波形基本相同,四相电流不平衡现象明显。
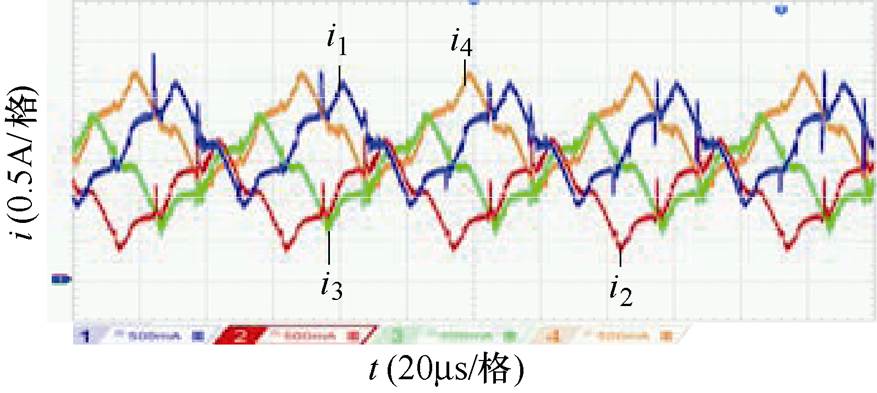
图17 D=0.6时四相电流波形
Fig.17 Four phase current waveforms at D=0.6
当采用本文所提出的均流控制策略、单电流环控制时的电压电流波形如图18所示。由于实验中所使用的示波器只有四路测量通道,为了更好地观察实验波形,图18a、图18b分别给出了四相电流以及三相电流和输出电压的波形。通过对比图18a、图18b以及图17可知,在单电流环控制时,给定电流1.5A,负载为5W 的情况下,四相电流平均值均为1.5A左右,均流效果良好,说明了所提均流控制策略的正确性。
为了检验单电流环控制时系统的抗干扰能力,进行了负载突变实验。如图18c和图18d所示,当负载由4.7W→2.5W→4.7W 突变时(即功率由170W→90W→170W突变),四相电流响应速度很快,抗干扰性能强,并且稳定性很好,同时四相电流均流效果良好。在负载突变实验中输出电压由28V→15V→28V变化,但是响应比较慢,这是由于单电流闭环控制无法实现输出电压的反馈控制,同时也说明了双闭环控制的必要性。
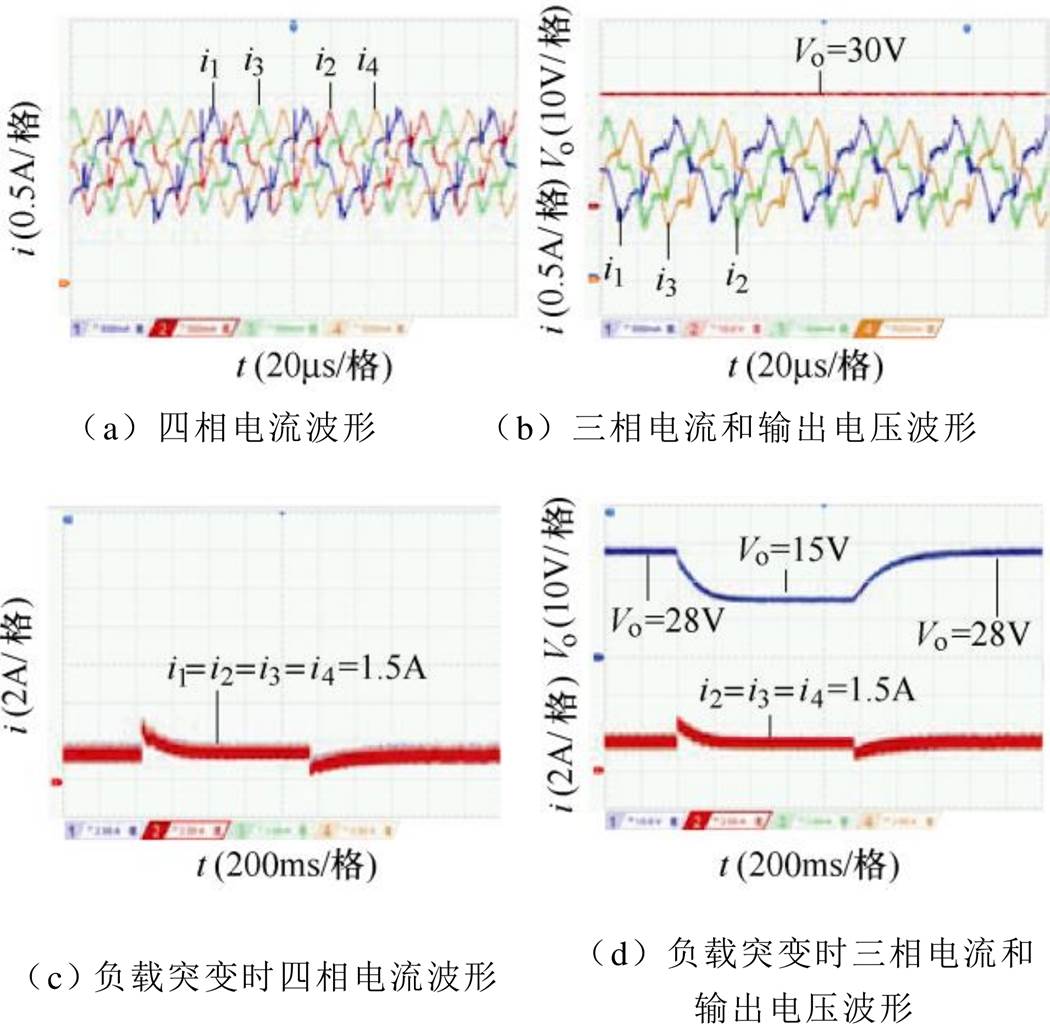
图18 单电流环控制时电压电流波形
Fig.18 Voltage and current waveforms when the single current closed-loop is used
采用本文所提的电压电流双闭环控制策略时的实验波形如图19所示。通过对比图19a、图19b以及图17可知,在电压电流双闭环控制时,给定输出电压30V、负载为5W 情况下,输出电压为30V,同时四相电流均为1.5A左右,均流效果良好,同时实验波形和图13a的仿真波形基本相同,说明了本文所提的电压电流双闭环控制策略的正确性。
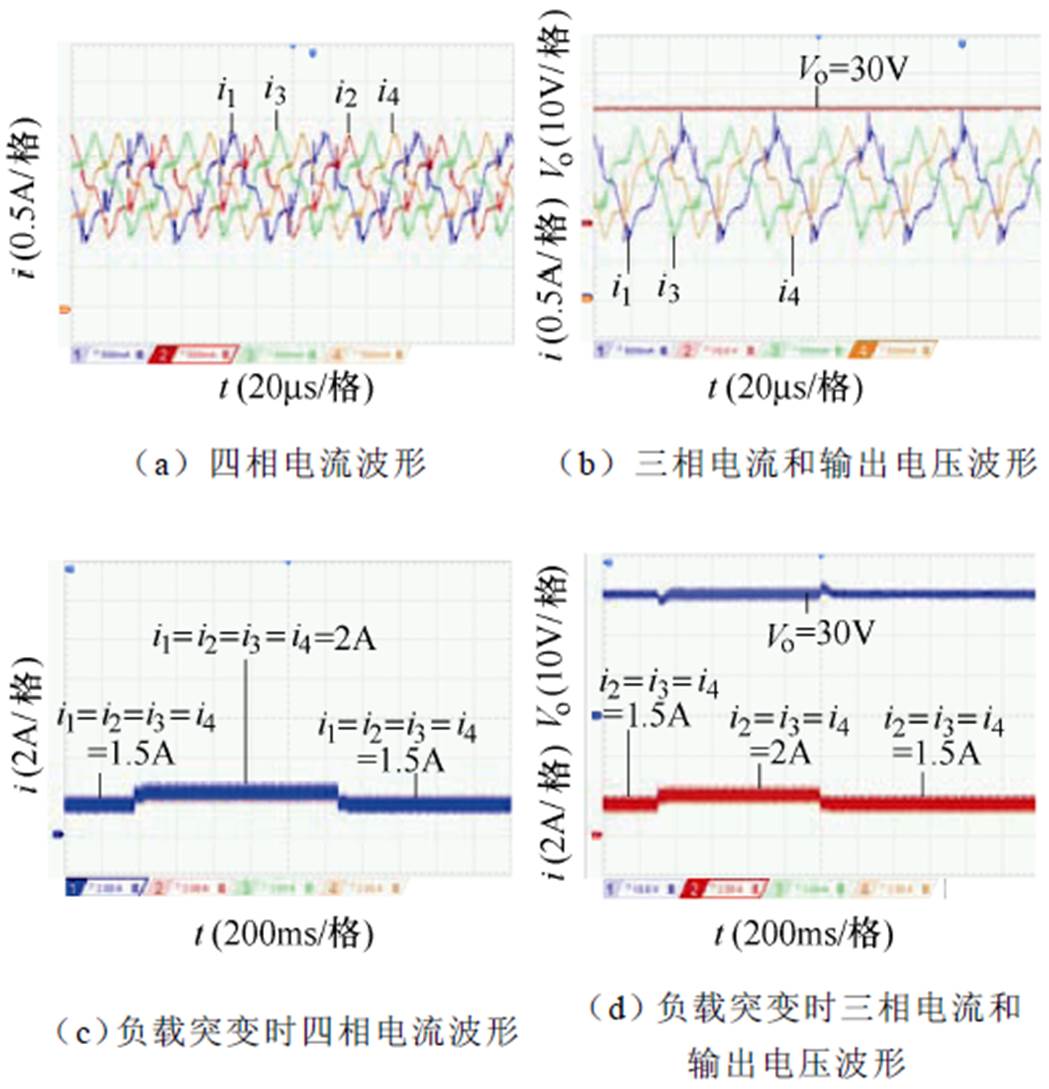
图19 电压电流双闭环控制时电压电流波形
Fig.19 Voltage and current waveforms when the voltage and current double closed-loop is used
为了检验双闭环控制时的系统抗干扰能力,进行了负载突变实验,实验波形如图19c和图19d所示,当负载由5W→3.7W→5W 突变时(即功率由180W→243W→180W突变),输出电压一直维持在30V左右,四相电流平均值由1.5A→2A→1.5A变化,电流的均流效果依然良好。同时在负载突变时,实验波形和图13b、图13c的仿真波形基本相同,说明了本文所提的电压电流双闭环控制策略的正确性和可行性。
本文主要对基于耦合电感的四相交错并联双向DC-DC变换器及其均流控制策略进行了研究。详细分析了所提拓扑的等效电感、稳态和暂态性能、均流控制策略以及电压电流双闭环控制方法。通过理论分析以及仿真和样机实验,可以得出以下结论:
1)和传统拓扑相比,所提拓扑在保持暂态性能的同时,通过增大等效稳态电感,大大减小了稳态相电流纹波。
2)所提拓扑具有良好的拓展性,当拓展到N相时,双绕组耦合电感的数量是N。
3)通过使用本文所提的基于相电流解耦的均流控制方法,解耦后大大减小了均流环的设计难度。
4)所提的均流控制方法具有良好的拓展性,不仅可以用于本文所提的拓扑,其他类型的多相交错并联双向DC-DC变换器只要导纳矩阵Y(s)满足相似对角化的条件,就可以使用本文所提的均流控制方法。
目前电力电子变换器正在朝着高频化发展,后续的研究中,可以将软开关技术应用到本文所提拓扑中,以减少高频应用时的开关损耗。
参考文献
[1] 赵清林, 刘会峰, 袁精, 等. 基于移相补偿的全桥LLC谐振变换器交错并联技术[J]. 电工技术学报, 2018, 33(12): 2777-2787.
Zhao Qinglin, Liu Huifeng, Yuan Jing, et al. An interleaved full-bridge LLC resonant converter with phase shift compensation[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2777-2787.
[2] 杨玉岗, 吴晗, 关婷婷. 交错并联LLC谐振变换器的磁集成均流特性[J]. 电工技术学报, 2019, 34(12): 2529-2538.
Yang Yugang, Wu Han, Guan Tingting. Magnetic integrated current sharing characteristics of inter- leaved LLC resonant converter[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2529- 2538.
[3] 曹勇, 杨飞, 李春晖, 等. 不同耦合系数下的交错并联电流连续模式Boost功率因数校正变换器的传导电磁干扰[J]. 电工技术学报, 2019, 34(10): 2176- 2186.
Cao Yong, Yang Fei, Li Chunhui, et al. Conducted electromagnetic interference of interleaved conti- cuous current mode Boost power factor correction converter with different coupling coefficients[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2176-2186.
[4] Zhang Yun, Gao Yongping, Li Jing, et al. Interleaved switched-capacitor bidirectional DC-DC converter with wide voltage-gain range for energy storage systems[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 3852-3869.
[5] 陆治国, 祝万平, 刘捷丰, 等. 一种新型交错并联双向DC/DC变换器[J]. 中国电机工程学报, 2013, 33(12): 39-46.
Lu Zhiguo, Zhu Wanping, Liu Jiefeng, et al. A novel interleaved parallel bidirectional DC/DC converter[J]. Proceedings of the CSEE, 2013, 33(12): 39-46.
[6] 罗全明, 闫欢, 支树播, 等. 一种交错控制高增益 ZCT Boost换器[J]. 中国电机工程学报, 2013, 33(12): 18-23.
Luo Quanming, Yan Huan, Zhi Shubo, et al. An interleaved high step-up zero-current-transition Boost converter[J]. Proceedings of the CSEE, 2013, 33(12): 18-23.
[7] 王议锋, 崔玉璐, 马小勇, 等. 一种交错并联双Buck全桥型双向并网逆变器[J]. 电工技术学报, 2019, 34(21): 4529-4539.
Wang Yifeng, Cui Yulu, Ma Xiaoyong, et al. An interleaved dual-Buck full-bridge type bidirectional grid-connected inverter[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4529-4539.
[8] 杨玉岗, 李涛, 冯本成. 交错并联磁集成双向 DC/DC变换器的设计准则[J]. 中国电机工程学报, 2012, 32(30): 37-45.
Yang Yugang, Li Tao, Feng Bencheng. Design criterion for interleaving and magnetically integrated bidirectional DC/DC converters[J]. Proceedings of the CSEE, 2012, 32(30): 37-45.
[9] Wong Pit-Leong, Xu Peng, Yomg B, et al. Performance improvements of interleaving VRMs with coupling inductors[J]. IEEE Transactions on Power Electronics, 2006, 16(4): 499-507.
[10] Yang Yugang, Guan Ting, Zhang Shuqi. More symmetric four-phase inverse coupled inductor for low current ripples & high-efficiency interleaved bidirectional Buck/Boost converter[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(3): 1952- 1966.
[11] 杨玉岗, 李龙华, 冯本成. 三相交错并联变换器中耦合电感的对称化[J]. 电工技术学报, 2013, 28(7): 177-183.
Yang Yugang, Li Longhua, Feng Bencheng. Symmetry of coupling inductance in 3-phase interleaving converter[J]. Transactions of China Electrotechnical Society, 2013, 28(7): 177-183.
[12] 王磊, 郭瑞, 杨玉岗. 多相电压调理模块的矩阵化多自由度耦合磁件[J]. 电工技术学报, 2018, 33(12): 2801-2811.
Wang Lei, Guo Rui, Yang Yugang. Array integrated magnetic inductance with multi-degree-of-freedom used for multiphase VRM[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2801-2811.
[13] Yang Yugang, Ma Jie, Ho C N, et al. A new coupled-inductor structure for interleaving bidire- ctional DC-DC converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(3): 841-849.
[14] Pan Tengteng, Wang Yubin, Qu Zengbin, et al. Research on high power interleaved bidirectional DC/DC converter with coupling technique[C]//ITEC Asia-Pacific, Harbin, China, 2017: 1-6.
[15] Cho Y, Koran A, Miwa H, et al. An active current reconstruction and balancing strategy with DC-link current sensing for a multi-phase coupled-inductor converter[J]. IEEE Transactions on Power Electro- nics, 2012, 2(4): 1697-1705.
[16] 梁锋. DC/DC变换器并联均流与交错控制研究[D]. 北京: 清华大学, 2004.
[17] Wang Haojie, Han Minxiao, Han Renke, et al. A decentralized current-sharing controller endows fast transient response to parallel DC/DC converters[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 4362-4372.
[18] Gordillo J, Aguilar C. A simple sensorless current sharing technique for multiphase DC-DC Buck con- verters[J]. IEEE Transactions on Power Electronics, 2016, 32(5): 3480-3489.
[19] Huang Wangxin, Qahouq J A. Input voltage ripple- based sensorless current sharing autotuning controller for multiphase DC-DC converters[J]. IEEE Transa- ctions on Industry Applications, 2016, 52(5): 4117- 4125.
[20] 陈丹丹. 交错并联磁集成双向DC/DC变换器的离散滑模控制研究[D]. 阜新: 辽宁工程技术大学, 2014.
Multi-Phase Interleaved Bidirectional DC-DC Converter with Coupled Inductors and Current Sharing Control Strategy
Abstract With the increase of phase number, multi-phase interleaved and magnetically integrated bidirectional DC-DC converter with single-core coupled inductor has several problems, such as asymmetrical parameters, high manufacturing cost, difficult design of the multi-phase magnetic core, and so on. In this paper, a multi-phase interleaved bidirectional DC-DC converter with two-winding coupled inductors is proposed. Taking four-phase interleaved bidirectional DC-DC converter as an example, this paper uses four two-winding coupled inductors instead of single-core coupled inductors. The steady-state and transient performance is then studied in detail. Meanwhile, the difference in phase circuit parameters may cause uneven current among phases, which makes excessive thermal and device stress in heavy-load phase, thereby deteriorating the whole system reliability. Therefore, a phase-decoupled current sharing control strategy is proposed. Finally, simulation and the prototype experiment have verified the superiority, reliability and practicability of the proposed converter and current sharing control strategy.
keywords:Bidirectional DC-DC converter, coupled inductors, steady-state and transient-state performances, current sharing control strategy, decoupling of phase currents
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.191167
国家自然科学基金(51277115)和山东省自然科学基金(ZR2018MEE037)资助项目。
收稿日期2019-09-10
改稿日期 2020-04-14
苏 冰 男,1994年生,硕士研究生,研究方向为电力电子变换器拓扑与控制技术、软开关技术。E-mail: subing86@163.com
王玉斌 男,1967年生,教授,研究方向为电力电子变换器拓扑与控制技术、直流微电网控制及稳定性、软开关技术等。E-mail: yb_wang@sdu.edu.cn(通信作者)
(编辑 崔文静)