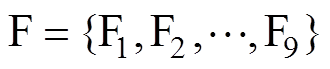 ;第二层为指标层,为各故障类型所对应的具体指标,如绝缘受潮所对应的指标可表示为
;第二层为指标层,为各故障类型所对应的具体指标,如绝缘受潮所对应的指标可表示为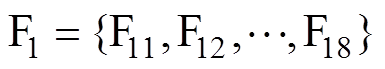 。
。摘要 为了客观科学地评估变压器状态,建立变压器状态评估层次指标体系,提出一种基于变权灰云模型的变压器状态层次评估方法。首先,针对传统灰色聚类白化权函数不能描述信息随机性的缺陷,利用云模型改进传统白化权函数构建灰云模型,有效地反映出评估等级信息的模糊性、灰性和随机性;并利用指标云模型代替指标值计算云关联度,更好地体现变压器状态信息的不确定性。然后,利用关联规则和灰云聚类得到变压器故障层状态,采用变权融合得到变压器整体状态,综合考虑变压器故障层状态和整体状态,得到最终的评估结果。最后,通过实例分析验证该方法的有效性和优越性。
关键词:变压器 状态评估 云模型 变权理论 灰云聚类 云关联度
电力变压器是整个电力系统中电能传输和转换的核心设备,其运行可靠性直接关系到电力系统的安全和稳定[1]。对变压器实行状态检修可以提高维修效率和设备的可靠性,使检修工作更加合理化和科学化,而实现状态检修的关键是对变压器进行科学、有效的状态评估[2-3]。
变压器结构复杂、状态指标繁多、且状态信息存在不确定性,针对变压器的这些特点,国内外学者引入了众多评估算法评估变压器状态。文献[4-5]构建了以模糊数学为基础的电力变压器状态评估模型,并通过实例证明了该方法的有效性,但是该方法本身所需要的模糊判断矩阵需要专家根据经验确定,并且仅考虑了信息不确定性中的模糊性,忽略了随机性。文献[6-8]运用灰色聚类法对变压器状态进行评估,综合考虑了变压器评估因素的模糊性和灰色性,但其白化权函数需依赖专家经验确定,主观性太强,并且传统白化权函数不能有效表示灰色系统中信息的随机性,存在着较大的改进空间。还有一些学者运用集对分析[9]、理想点法[10-11]等方法评估变压器状态,取得了一定的成果,但这些方法均只考虑了信息不确定性中的模糊性,而忽略了随机性。为此,文献[12-14]构建了基于云模型的变压器状态评估模型,充分考虑了不确定性中的模糊性和随机性,得到了较为准确的评估结果,但在计算云关联度时仅考虑了等级云的不确定性,没有考虑指标本身的不确定性,需对其进一步改进。
根据上述分析,本文提出了基于变权灰云模型的变压器状态层次评估方法。首先,为了充分表征指标本身的不确定因素对计算结果的影响,构建了一种能够将指标值模糊离散化的指标云模型,并将此模型与利用云模型改进灰色聚类白化权函数得到的灰云模型相结合,提出一种基于指标云模型的云关联度计算方法,以便更好地体现变压器状态评估过程中的不确定性;其次,对变压器状态进行分层评估,确定故障层状态时涉及到的指标权重利用关联规则计算,尽可能地避免了专家主观意见对权重准确性的影响,同时确定整体状态时,采用变权理论计算故障层各故障权重;最后,综合考虑变压器故障层状态和整体状态,得到最终的评估结果。
电力变压器是一种结构复杂、多参量的系统,表征其状态的指标繁多[15]。为了更加准确地评估变压器状态,本文根据《油浸式变压器(电抗器)状态评价导则》[16]和变压器故障类型与状态指标间关联性强的特点,构建层次型变压器状态评估指标体系[9, 15, 17],如图1所示。第一层为故障层,共分为9类故障,可表示为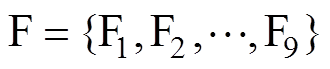 ;第二层为指标层,为各故障类型所对应的具体指标,如绝缘受潮所对应的指标可表示为
;第二层为指标层,为各故障类型所对应的具体指标,如绝缘受潮所对应的指标可表示为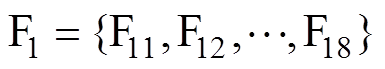 。
。
为了便于评估变压器状态,本文参考《油浸式变压器(电抗器)状态评价导则》,将变压器的状态等级划分为严重、异常、注意、正常四种。
由于反映变压器状态的指标具有不同的量纲和标度,为了方便计算,采用相对劣化度的方式对各指标做标准化处理,有
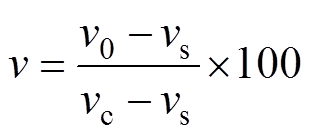 (1)
(1)式中,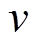 为指标量化值,其取值范围为[0, 100];
为指标量化值,其取值范围为[0, 100];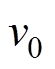 为指标的试验实测值;
为指标的试验实测值;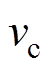 为指标的初始值;
为指标的初始值; 为指标的警示值。如果计算得到的指标量化值
为指标的警示值。如果计算得到的指标量化值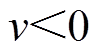 ,则令
,则令 ;如果
;如果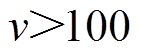 ,则令
,则令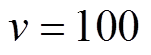 ;若给出指标注意值
;若给出指标注意值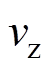 ;则
;则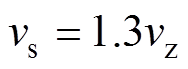 (正劣化)或
(正劣化)或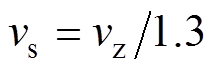 (负劣化)[9]。
(负劣化)[9]。
正态云模型[18-21]是一种有效集成信息随机性和模糊性,并实现定性概念与定量数值之间的不确定性转换的模型。可用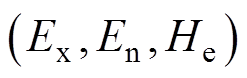 表示,有
表示,有
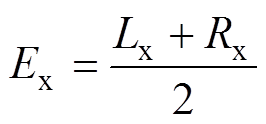 (2)
(2) (3)
(3)
 (4)
(4)
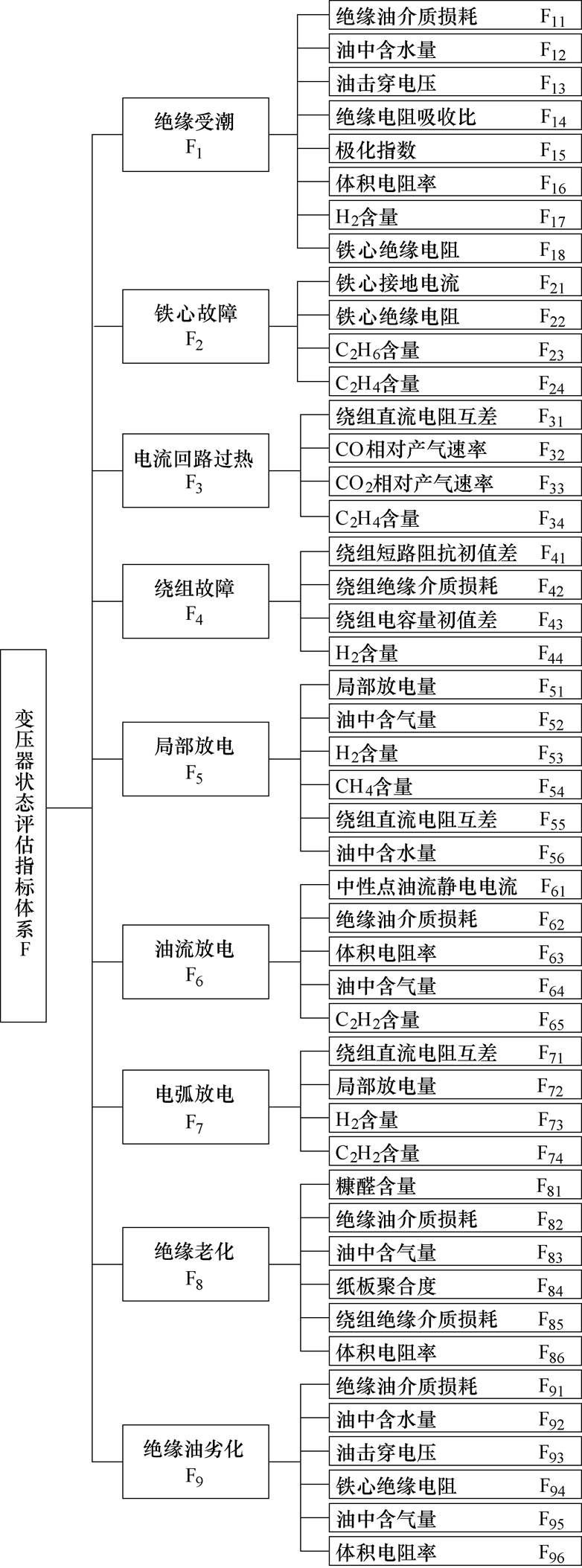
图1 变压器状态评估指标体系
Fig.1 Assessing index system of transformer condition
式中,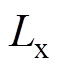 、
、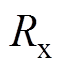 分别为正态云模型的左、右界值;云期望
分别为正态云模型的左、右界值;云期望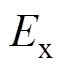 为最能代表定性概念的值;云熵
为最能代表定性概念的值;云熵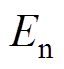 为对属性概念不确定性的度量;云超熵
为对属性概念不确定性的度量;云超熵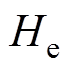 为熵的熵,代表熵的离散程度,也代表云滴的凝聚程度;
为熵的熵,代表熵的离散程度,也代表云滴的凝聚程度; 为大于0的常数。
为大于0的常数。
正态云模型符合统计学上的“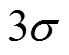 准则”,即位于区间
准则”,即位于区间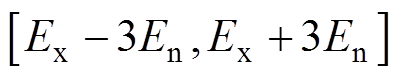 之外的云滴元素为小概率事件,将其忽略并不影响云模型整体特征[22]。其生成算法步骤如下:
之外的云滴元素为小概率事件,将其忽略并不影响云模型整体特征[22]。其生成算法步骤如下:
(1)生成以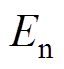 为期望、
为期望、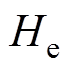 为标准差的正态随机数
为标准差的正态随机数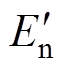 。
。
(2)生成以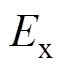 为期望、
为期望、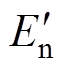 为标准差的正态随机数
为标准差的正态随机数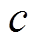 。
。
(3)计算 ,令
,令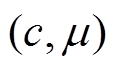 为一个云滴。
为一个云滴。
(4)重复上述步骤,直到产生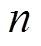 个云滴为止。
个云滴为止。
通过上述正态云模型生成算法,生成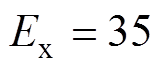 ,
,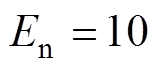 ,
,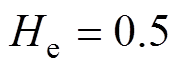 的云滴图,云滴数为500,如图2所示。图中,云滴包络线分别为云模型的内外关联度曲线
的云滴图,云滴数为500,如图2所示。图中,云滴包络线分别为云模型的内外关联度曲线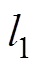 、
、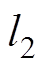 ,位于中间位置的曲线为正态云模型的期望曲线
,位于中间位置的曲线为正态云模型的期望曲线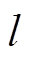 ,三者的表达式分别为
,三者的表达式分别为
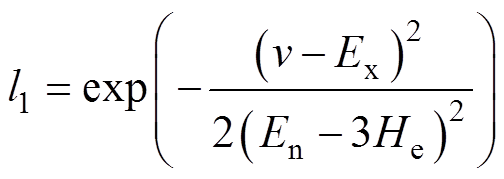 (5)
(5)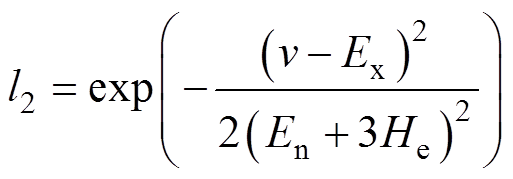 (6)
(6)
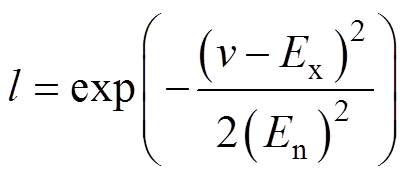 (7)
(7)

图2 正态云模型
Fig.2 Normal cloud model
由图2可知,在正态云模型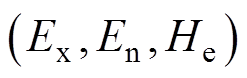 中,对于某一云关联度固定值而言,可由不同的指标量化值通过该正态云模型计算得到。对于左半边云而言,这些指标值中存在一个最大指标量化值
中,对于某一云关联度固定值而言,可由不同的指标量化值通过该正态云模型计算得到。对于左半边云而言,这些指标值中存在一个最大指标量化值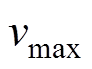 和一个最小指标量化值
和一个最小指标量化值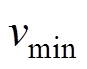 ;对于右半边云而言,也存在一个最大指标量化值
;对于右半边云而言,也存在一个最大指标量化值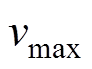 和一个最小指标量化值
和一个最小指标量化值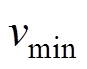 ,并且
,并且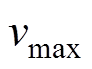 和
和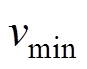 在内外关联度曲线上。因此,指标云约束区间计算步骤如下:
在内外关联度曲线上。因此,指标云约束区间计算步骤如下:
(1)将指标量化值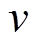 代入正态云模型的期望曲线表达式中,求出云关联度
代入正态云模型的期望曲线表达式中,求出云关联度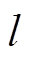 。
。
(2)计算云关联度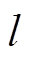 所对应的最大指标值
所对应的最大指标值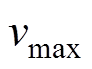 和最小指标值
和最小指标值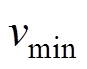 。令
。令 ,当
,当 时,有
时,有
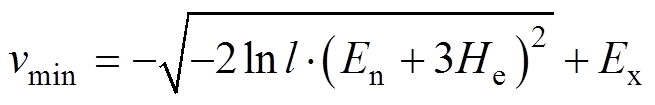 (8)
(8)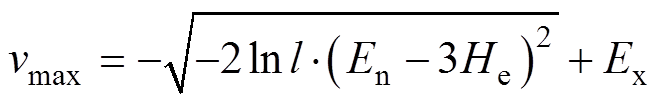 (9)
(9)
当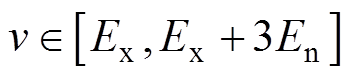 时,则有
时,则有
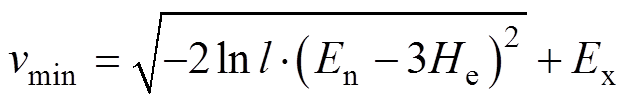 (10)
(10)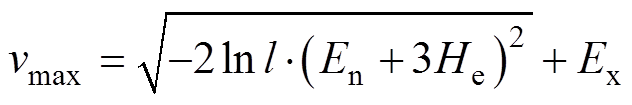 (11)
(11)
特别地,当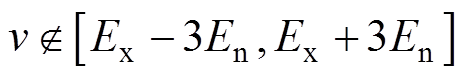 时,
时,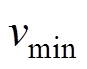 和
和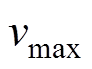 不存在,即不存在指标云模型。
不存在,即不存在指标云模型。
(3)根据最小指标值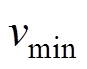 和最大指标值
和最大指标值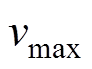 确定指标云约束区间为
确定指标云约束区间为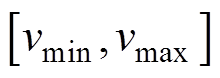 。
。
将指标云约束区间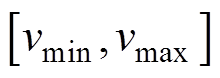 中的边界值
中的边界值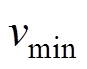 和
和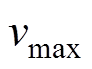 分别作为正态云模型的左、右界值,则可由式(2)~式(4)计算指标云模型
分别作为正态云模型的左、右界值,则可由式(2)~式(4)计算指标云模型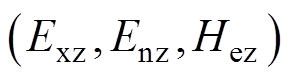 中的各个参数,指标云期望
中的各个参数,指标云期望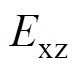 、指标云熵
、指标云熵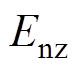 和指标云超熵
和指标云超熵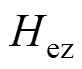 分别为
分别为
 (12)
(12)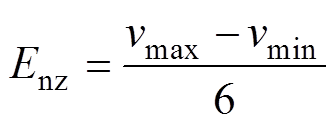 (13)
(13)
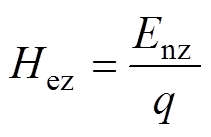 (14)
(14)
式中,q为常数,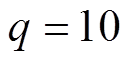 [23]。
[23]。
图3所示为基于变权灰云模型的变压器状态评估流程,具体步骤如下:
(1)根据相关标准,选取变压器状态指标,构建变压器状态评估层次型指标体系。
(2)划分变压器状态等级,对指标试验实测值进行标准化处理得到指标量化值。
(3)对指标初始值、注意值和警示值标准化处理,构建变压器状态评估等级灰云模型。
(4)构建各指标云模型,并结合评估等级灰云模型,计算各指标与各评估等级的云关联度。
(5)利用关联规则计算指标权重,并采用灰云聚类计算故障层各故障的评估分数,从而确定故障层状态。
(6)利用变权理论计算故障层各故障变权重,通过加权融合计算变压器整体评估分数,并确定变压器整体状态。
(7)综合考虑变压器故障层状态和整体状态,确定最终的评估结果。
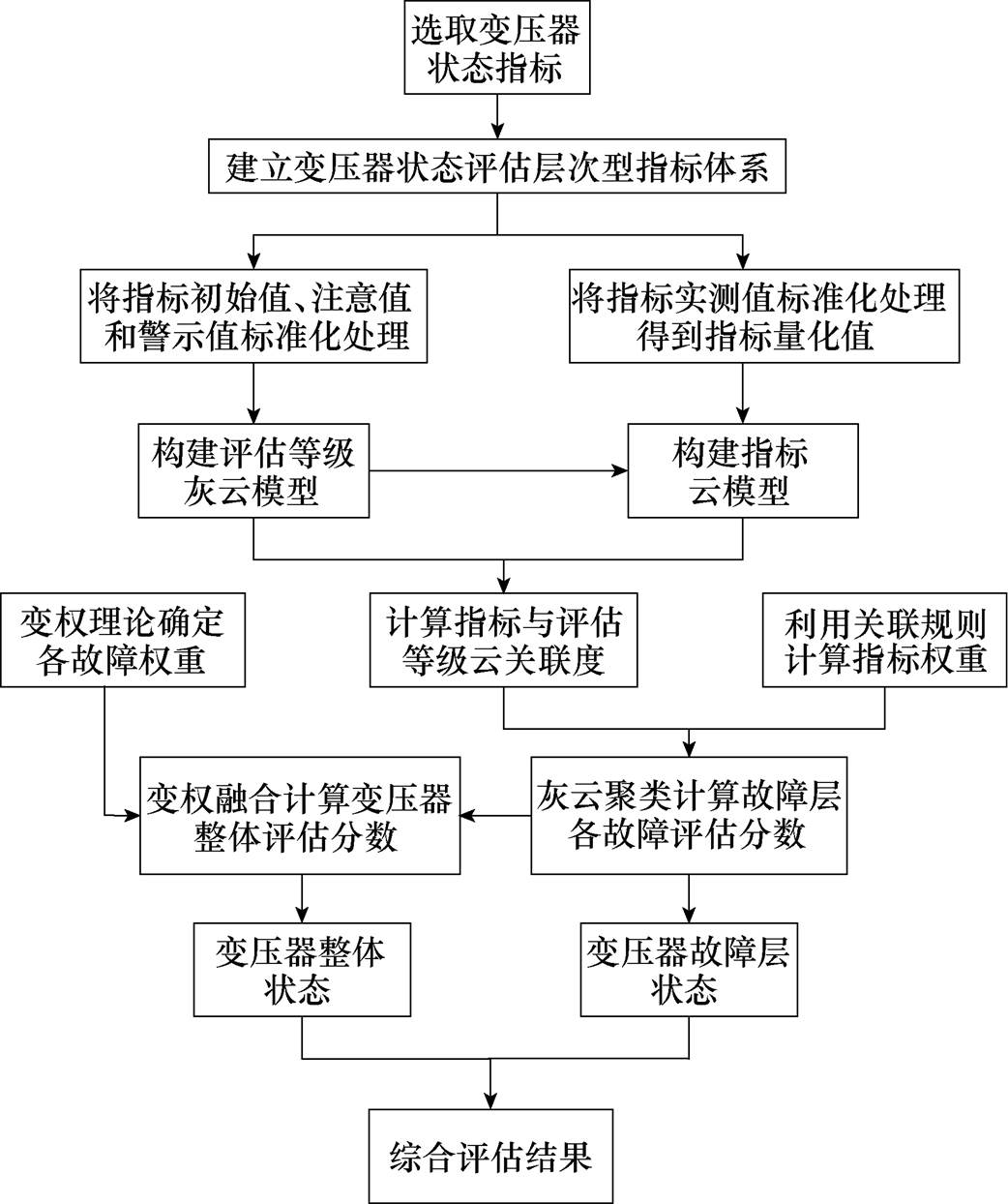
图3 基于变权灰云模型的变压器状态评估流程
Fig.3 Flow chart of an assessment method for condition of transformer based on weight-varying gray cloud model
将正态云模型引入到灰色聚类白化权函数中,得到正态灰云白化权函数,简称灰云模型,它可以充分发挥云模型在处理模糊性和随机性信息方面的优势,弥补传统白化权函数无法兼顾随机性信息的弊端[24]。
若故障 中指标
中指标 关于第
关于第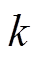 等级的白化权函数为
等级的白化权函数为
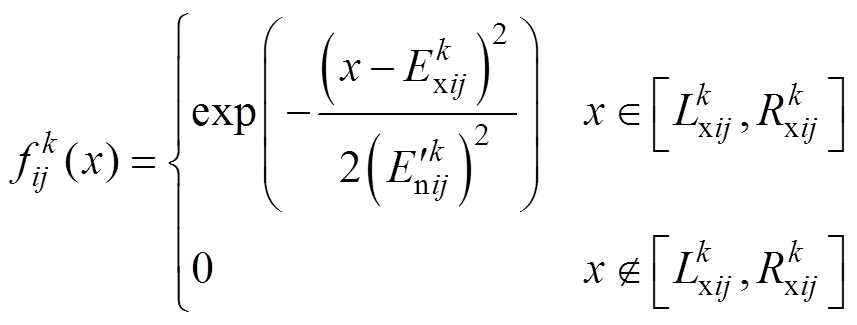 (15)
(15)则称其为适中测度灰云模型,记为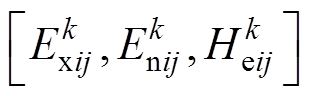 。
。
若故障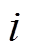 中指标
中指标 关于第
关于第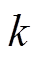 等级的白化权函数为
等级的白化权函数为
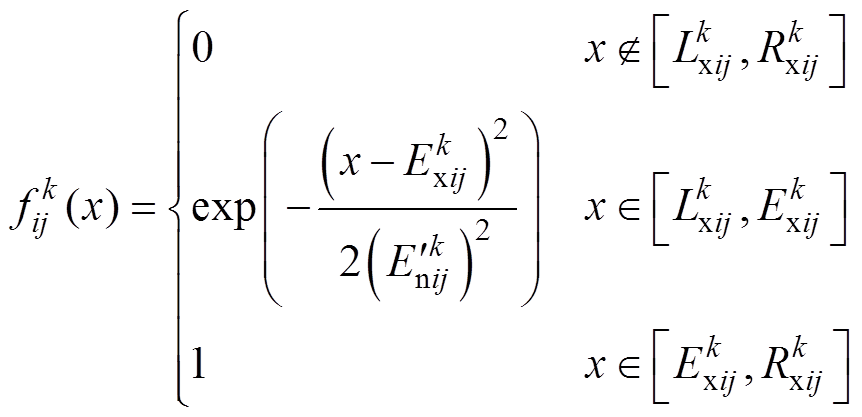 (16)
(16)称其为上限测度灰云模型,记为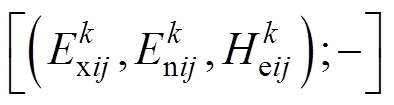 。
。
若故障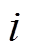 中指标
中指标 关于第
关于第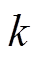 等级的白化权函数为
等级的白化权函数为
 (17)
(17)称其为下限测度灰云模型,记为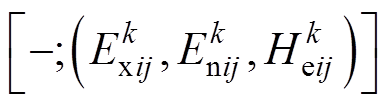 。式中,x为评估指标变量;
。式中,x为评估指标变量;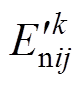 为以
为以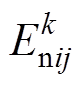 为期望、
为期望、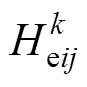 为标准差的正态随机数;
为标准差的正态随机数;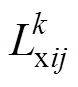 、
、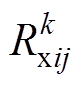 分别为故障
分别为故障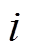 中指标
中指标 第
第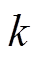 等级灰云模型的左、右边界。
等级灰云模型的左、右边界。
本文根据变压器指标初始值、注意值和警示值与状态等级的关系,并结合式(2)~式(4),确定变压器状态等级灰云模型数字特征,见表1。表中,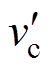 、
、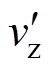 和
和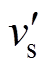 是分别采用如式(1)所示的相对劣化度的方式对指标初始值、注意值和警示值进行标准化处理后,得到的量化值,取
是分别采用如式(1)所示的相对劣化度的方式对指标初始值、注意值和警示值进行标准化处理后,得到的量化值,取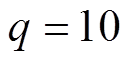 。变压器状态等级{1, 2, 3, 4}={严重, 异常, 注意, 正常}。
。变压器状态等级{1, 2, 3, 4}={严重, 异常, 注意, 正常}。
表1 等级灰云模型数字特征确定方法
Tab.1 The method for digital feature determination of level grey cloud model

模型严重异常注意正常
图4所示为某指标所对应的四个等级灰云模型,其中,严重状态为下限测度灰云模型,异常、注意状态为适中测度灰云模型,正常状态为上限测度灰云模型。各白化权函数值描述了指标量化值关于各评估等级的云关联度。
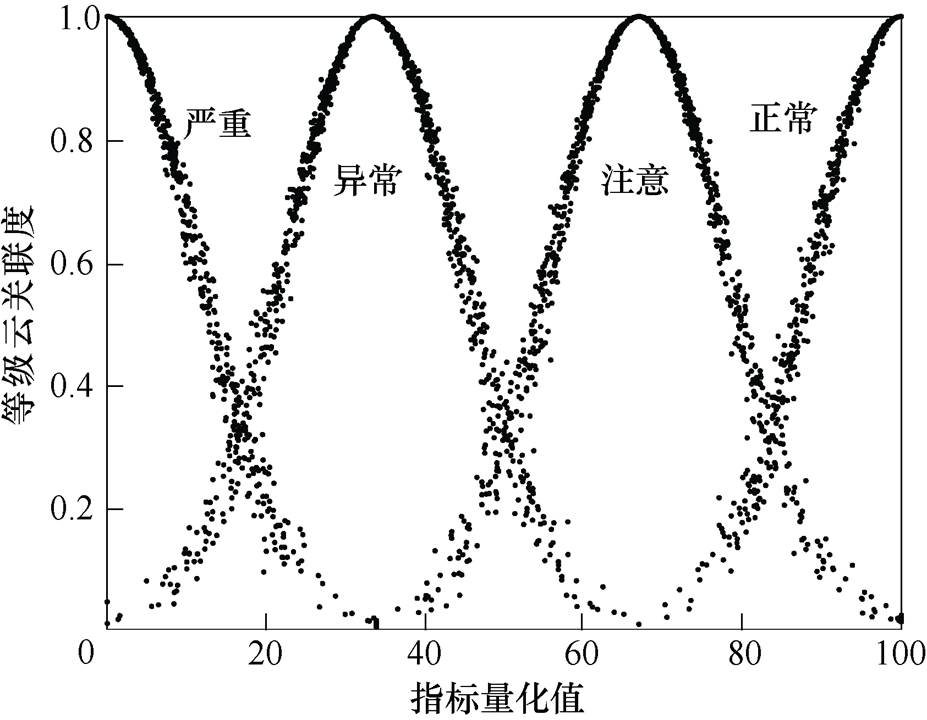
图4 四等级灰云模型
Fig.4 Four-level gray cloud model
作为指标与等级灰云之间关联程度的度量,云关联度的计算准确度将直接影响指标等级判定结果的准确性,通过查阅相关文献[12-14],学者们基于对云模型的理解,提出了两种云关联度计算方法:
(1)取点法。取点法是指先构建等级灰云模型图,然后找出已知指标数据与第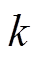 等级灰云模型的
等级灰云模型的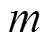 (
( )个交点云滴,则取
)个交点云滴,则取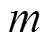 个云滴的均值作为该指标与第
个云滴的均值作为该指标与第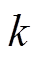 等级的云关联度。但通过这种方法确定云关联度,有时可能会出现取空值的现象,从而导致最终的评估结果不准确。
等级的云关联度。但通过这种方法确定云关联度,有时可能会出现取空值的现象,从而导致最终的评估结果不准确。
(2)基于指标量化值云关联度计算方法。基于指标量化值计算云关联度法是将指标量化值代入相应等级灰云白化权函数中,求出该指标与第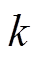 等级的云关联度。这种方法解决了计算云关联度时可能取空值这一问题,但其仅考虑了等级云的不确定性,没有考虑指标本身因试验条件不同、电气试验测试与运行条件不同造成的测量误差以及相关标准制定时主观因素带来的不确定性[25]。
等级的云关联度。这种方法解决了计算云关联度时可能取空值这一问题,但其仅考虑了等级云的不确定性,没有考虑指标本身因试验条件不同、电气试验测试与运行条件不同造成的测量误差以及相关标准制定时主观因素带来的不确定性[25]。
本文为更好地体现变压器状态信息的不确定性,以兼顾等级灰云模型和指标云模型不确定性为目标,提出一种基于指标云模型的云关联度计算方法。计算步骤如下:
(1)根据第2节中指标云模型构建方法,构建故障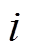 中指标
中指标 量化值
量化值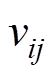 关于第
关于第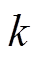 等级灰云的指标云模型为
等级灰云的指标云模型为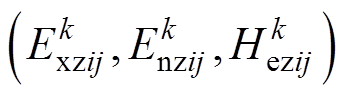 。
。
(2)计算故障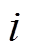 中指标
中指标 关于第
关于第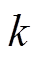 等级的云关联度
等级的云关联度 。如果
。如果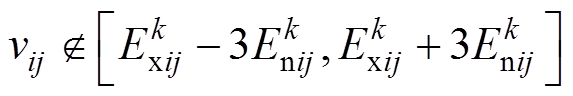 ,则可直接判定该指标与第
,则可直接判定该指标与第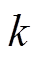 等级的云关联度为0。如果
等级的云关联度为0。如果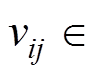
 ,先以
,先以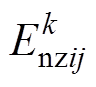 为期望、
为期望、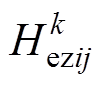 为标准差生成正态随机数
为标准差生成正态随机数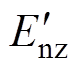 ,再以
,再以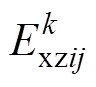 为期望、
为期望、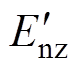 为标准差生成正态随机数
为标准差生成正态随机数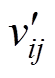 ,利用
,利用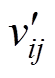 替换评估指标变量
替换评估指标变量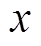 ,代入到式(15)~式(17)所示的等级灰云模型中,计算故障
,代入到式(15)~式(17)所示的等级灰云模型中,计算故障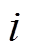 中指标
中指标 关于第
关于第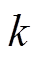 等级的白化权函数值
等级的白化权函数值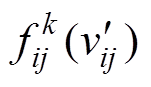 ,由于灰云模型具有随机性,每一次计算结果并不相同,所以重复上述过程,生成
,由于灰云模型具有随机性,每一次计算结果并不相同,所以重复上述过程,生成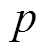 个正态随机数
个正态随机数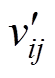 ,得到
,得到 个白化权函数值,计算其期望
个白化权函数值,计算其期望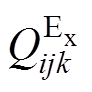 ,并将故障
,并将故障 中指标
中指标 关于各等级的白化权函数期望值归一化处理,得到故障
关于各等级的白化权函数期望值归一化处理,得到故障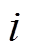 中指标
中指标 关于第
关于第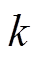 等级的云关联度
等级的云关联度 ,有
,有
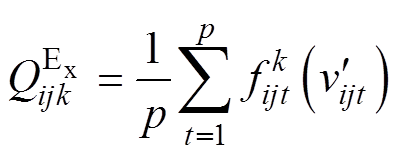 (18)
(18)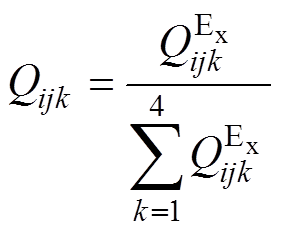 (19)
(19)
式中, 为第
为第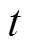 次计算的白化权函数值;
次计算的白化权函数值;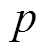 为正整数,其值越大,云关联度的随机性就越小,考虑计算工作量和效率,取
为正整数,其值越大,云关联度的随机性就越小,考虑计算工作量和效率,取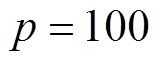 。
。
随着智能电网和物联网的建设,大数据技术也越来越成熟[26]。本文借鉴大数据思想,根据文献[9]整理的1 242组已知故障类型的变压器故障统计数据,采用关联规则[8]中的置信度计算故障层故障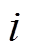 中指标
中指标 的权重wij,结果见表2;利用灰云聚类[24]计算故障层故障
的权重wij,结果见表2;利用灰云聚类[24]计算故障层故障 关于第
关于第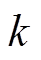 等级的聚类云关联度
等级的聚类云关联度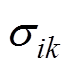 ,有
,有
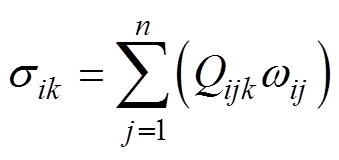 (20)
(20)式中,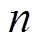 为故障
为故障 中所包含指标的个数。
中所包含指标的个数。
利用加权法[14]得出故障层故障 的评估分数
的评估分数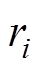 ,有
,有
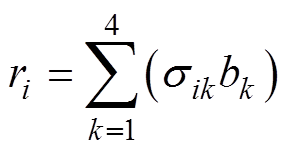 (21)
(21)式中,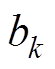 为第
为第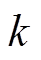 等级得分值,对变压器状态的四个等级分别赋予分值25、50、75、100。
等级得分值,对变压器状态的四个等级分别赋予分值25、50、75、100。
表2 故障层各指标权重
Tab.2 Index weights of fault layers
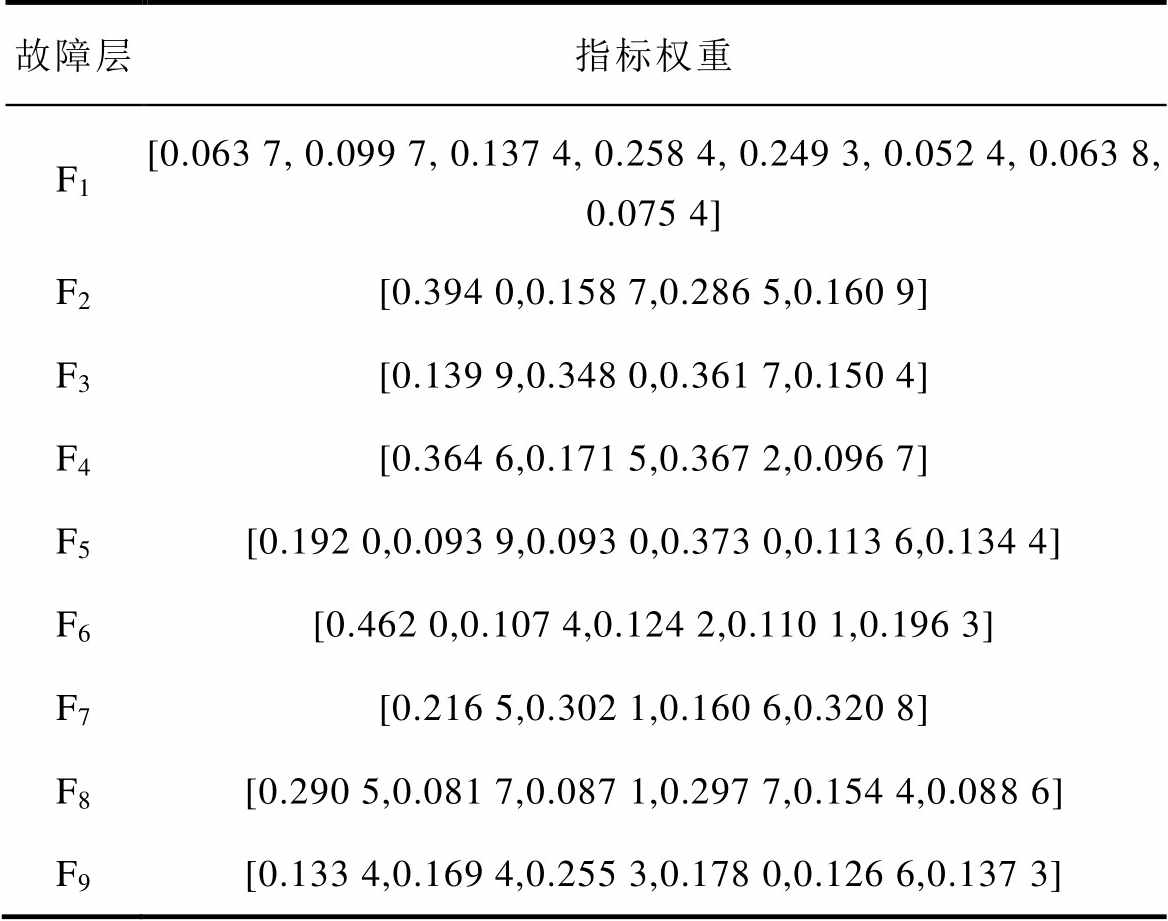
故障层指标权重 F1[0.063 7, 0.099 7, 0.137 4, 0.258 4, 0.249 3, 0.052 4, 0.063 8, 0.075 4] F2[0.394 0,0.158 7,0.286 5,0.160 9] F3[0.139 9,0.348 0,0.361 7,0.150 4] F4[0.364 6,0.171 5,0.367 2,0.096 7] F5[0.192 0,0.093 9,0.093 0,0.373 0,0.113 6,0.134 4] F6[0.462 0,0.107 4,0.124 2,0.110 1,0.196 3] F7[0.216 5,0.302 1,0.160 6,0.320 8] F8[0.290 5,0.081 7,0.087 1,0.297 7,0.154 4,0.088 6] F9[0.133 4,0.169 4,0.255 3,0.178 0,0.126 6,0.137 3]
再根据“50%关联度”规则[14]确定变压器各等级界限依次为[25, 37.5]、(37.5, 62.5)、(62.5, 87.5)、(87.5, 100]。最后利用所得评估分数确定变压器故障层状态。
为更加准确地反映变压器真实状态,将变权理论[27]引入到变压器综合状态评估中,有
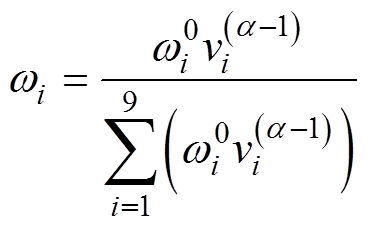 (22)
(22)式中,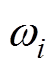 、
、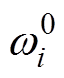 和
和 分别为故障
分别为故障 的变权重、常权重和评估量化值,
的变权重、常权重和评估量化值, 由故障
由故障 中各指标量化值和相应指标权重加权融合得到,
中各指标量化值和相应指标权重加权融合得到,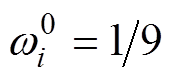 ;
;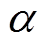 为均衡函数,其取值决定各故障对评估结果影响的大小。当
为均衡函数,其取值决定各故障对评估结果影响的大小。当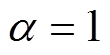 时,等同于定权模式;当
时,等同于定权模式;当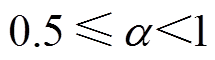 时,表示对均衡性要求不高;当
时,表示对均衡性要求不高;当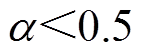 时,表示不能容忍某些故障的严重缺陷。考虑到变压器发生任一故障都会影响系统稳定性,根据实际情况,取
时,表示不能容忍某些故障的严重缺陷。考虑到变压器发生任一故障都会影响系统稳定性,根据实际情况,取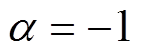 。
。
利用加权融合求得变压器整体评估分数z为
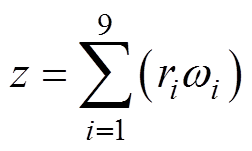 (23)
(23)根据变压器各等级界限确定变压器整体状态,并结合故障层状态得到变压器综合评估结果。
以某台运行年限为10年的220kV变压器(SFPS9-150000/220)为例(实例1),其2011年试验数据及相关指标初始值、注意值见表3[28]。
表3 实例1试验数据
Tab.3 Test datas of example 1

指标初始值注意值实测值 油击穿电压/kV584055 油中含水量/(mg/L)3.5258.9 绕组电容量初值差(%)151.4 糠醛含量/(mg/L)00.20.21 H2含量/(mL/L)6.115016.6 C2H6含量/(mL/L)2.3654.7 C2H4含量/(mL/L)4.8507.3 油中含气量(%)133.2 绕组短路阻抗初值差(%)131.2 C2H2含量/(mL/L)050 CH4含量/(mL/L)8.710018.5 绝缘电阻吸收比21.31.9 极化指数2.51.52.2 CO相对产气速率/(%/月)010012 CO2相对产气速率/(%/月)020031 体积电阻率/(109W·m)6056 绕组绝缘介质损耗(%)0.170.80.76 绕组直流电阻互差(%)141.5 绝缘油介质损耗(%)0.543.6 局部放电量/pC3050072 纸板聚合度1 000250265 中性点油流静电电流/mA0.0210.07 铁心接地电流/A0.010.10.02 铁心绝缘电阻/MW1 0001001 000
由于指标繁杂仅以绝缘老化为例进行计算分析,故障层绝缘老化状态评估的计算步骤如下:
(1)先利用式(1)对变压器绝缘老化中各指标实测值进行标准化处理;然后对指标初始值、注意值和警示值标准化处理,根据表1中方法确定各评估指标等级灰云模型的数字特征,结果见表4。
(2)根据3.3节中所提出的方法计算绝缘老化中指标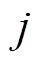 与第
与第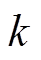 等级的云关联度Q8jk(绝缘老化为故障8),再利用式(20)计算绝缘老化与各等级的聚类云关联度
等级的云关联度Q8jk(绝缘老化为故障8),再利用式(20)计算绝缘老化与各等级的聚类云关联度 ,结果见表5。
,结果见表5。
(3)将 代入式(21)中,可得绝缘老化的评估分数
代入式(21)中,可得绝缘老化的评估分数 ,在区间(37.5, 62.5]范围内,可判定故障层绝缘老化为异常状态。
,在区间(37.5, 62.5]范围内,可判定故障层绝缘老化为异常状态。
同理可确定故障层其他故障的评估分数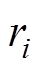 及评估结果,再根据式(22)得到各故障的变权重w = [0.038 4, 0.026 4, 0.029 4, 0.035 0, 0.033 7, 0.047 6, 0.026 8, 0.701 4, 0.061 3],将各故障评估分数
及评估结果,再根据式(22)得到各故障的变权重w = [0.038 4, 0.026 4, 0.029 4, 0.035 0, 0.033 7, 0.047 6, 0.026 8, 0.701 4, 0.061 3],将各故障评估分数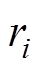 代入式(23)可得变压器整体评估分数z。分别采用本文方法、取点法、基于指标量化值云关联度计算方法和文献[8]中的灰色聚类法对该算例进行计算,实例1的评估分数和结果对比见表6。
代入式(23)可得变压器整体评估分数z。分别采用本文方法、取点法、基于指标量化值云关联度计算方法和文献[8]中的灰色聚类法对该算例进行计算,实例1的评估分数和结果对比见表6。
表4 绝缘老化各评估指标等级灰云模型
Tab.4 Level gray cloud models for assessment indices of insulation aging

指标严重异常注意正常 F81[-; (0,7.692 3,0.769 2)][30.769 2,10.256 4,1.025 6][61.538 5,12.820 5,1.282 1][(100,12.820 5,1.282 1); -] F82[-; (0,8.510 6,0.851 1)][31.383 0,10.461 0,1.046 1][62.766 0,12.411 4,1.241 1][(100,12.411 4,1.241 1); -] F83[-; (0,10.344 8, 1.034 5)][32.758 6,10.919 5,1.092 0][65.517 3,11.494 3,1.149 4][(100,11.494 3,1.149 4); -] F84[-; (0,2.381 0,0.238 1)][26.785 7,8.928 6,0.892 9][53.571 5,15.476 2,1.547 6][(100,15.476 2,1.547 6); -] F85[-; (0,9.195 4,0.919 5)][31.896 6,10.632 2,1.063 2][63.793 1,12.069 0,1.206 9][(100,12.069 0,1.206 9); -] F86[-; (0,0.684 9,0.068 5)][25.513 7,8.504 6,0.850 5][51.027 4,16.324 2,1.632 4][(100,16.324 2,1.632 4); -]
表5 绝缘老化云关联度计算值
Tab.5 Cloud correlation calculation value of insulation aging
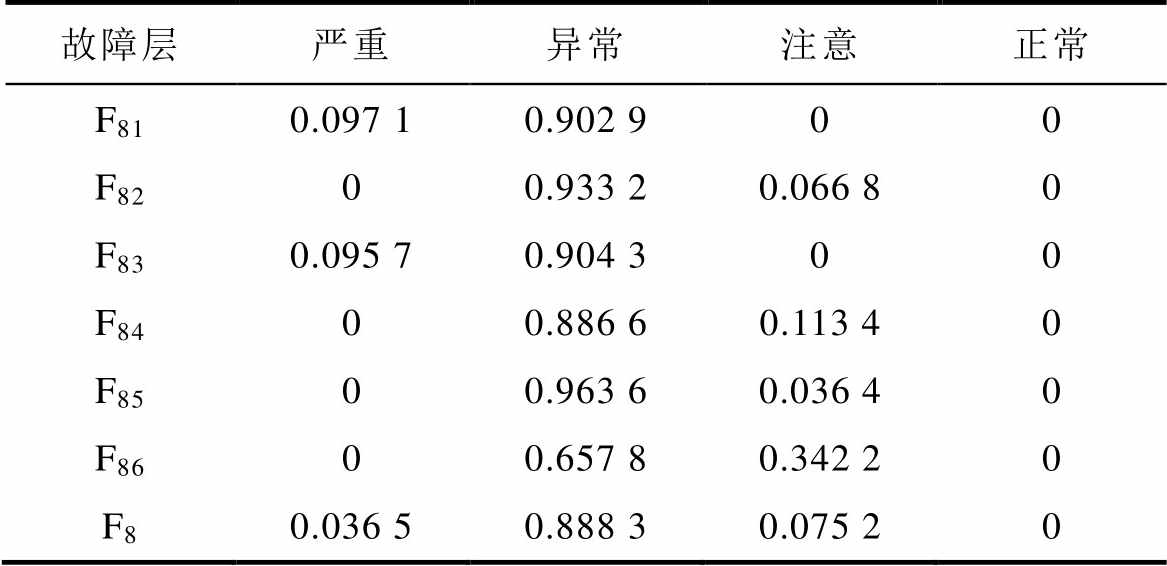
故障层严重异常注意正常 F810.097 10.902 900 F8200.933 20.066 80 F830.095 70.904 300 F8400.886 60.113 40 F8500.963 60.036 40 F8600.657 80.342 20 F80.036 50.888 30.075 20
由表6可知,本文所提出的方法将绝缘老化判定为异常状态,绝缘受潮、油流放电和绝缘油劣化判定为注意状态,其余故障类型均判定为正常状态,同时将变压器整体状态判定为异常状态,因此初步判定变压器绝缘存在非正常老化的迹象。停电后,对变压器进行试验与详细论证,确定该变压器是因为在夏天的时候运行温度过高以及负荷过重造成绝缘的非正常老化,与本文所提方法判定结果一致,表明该方法的有效性。
表6 实例1的评估分数和结果对比
Tab.6 Assessment scores and results comparison of example 1

F1F2F3F4F5F6F7F8F9综合评分 本文方法87.400 098.762 596.762 590.062 591.650 083.355 098.090 050.965 077.920 062.167 5 评估结果注意正常正常正常正常注意正常异常注意异常 取点法91.267 599.850 099.490 087.937 592.997 592.075 099.707 549.897 587.292 562.680 0 评估结果正常正常正常正常正常正常正常异常注意注意 “指标量化值”87.560 098.850 096.997 590.170 091.810 083.485 098.235 051.102 577.900 062.290 0 评估结果正常正常正常正常正常注意正常异常注意异常 灰色聚类87.975 0100.00100.0091.425 094.037 579.505 0100.0035.412 575.087 551.230 0 评估结果正常正常正常正常正常注意正常严重注意异常
由表3中指标实测值数据可知,绝缘老化中糠醛含量和油中含气量已略微超过注意值,其余指标已接近注意值,根据油浸式变压器状态评价导则可以确定绝缘老化和变压器整体状态为异常状态;绝缘受潮、油流放电和绝缘油劣化中部分指标出现了不同程度的劣化,其变化趋势朝接近注意值方向发展,依据评价导则可以确定其状态为注意状态。根据表6的评估结果,本文方法均判断正确,其他三种方法均出现不同程度的误判现象,例如,取点法将绝缘受潮和油流放电误判为正常状态,将整体状态误判为注意状态。
为进一步验证本文方法的有效性,另搜集整理了三个故障类型已知的220kV变压器实测样本,分别为实例2、实例3(SFPS9-150000/220)、实例4(SFPS9-150000/220),相关实测数据见表7。具体的计算过程与实例1相同,不再赘述,其评估结果见表8~表10。
由表8~表10的计算结果可知,取点法错估了实例2变压器的整体状态,并且对变压器故障层状态共误判6次;“指标量化值”法错估了实例4变压器的整体状态,对实例3变压器故障层状态误判1次,并且在实例1中误将故障层绝缘受潮故障判为正常状态;灰色聚类法错估了实例2和实例4变压器的整体状态,并且对变压器故障层状态共误判3次;本文所提出的方法通过等级灰云和指标云的双重软化作用,对各实例的变压器故障层状态和整体状态进行评估,得到的结果均与实际状态相符。这说明本文所述方法在处理变压器状态等级边界信息时有着更为优异的表现,从而得到更为准确的评估结果,进而能为变压器状态检修提供更为合理的决策。
表7 实例2~4的试验数据
Tab.7 Test datas of examples 2 to 4

指标实例2实例3实例4 油击穿电压/kV56.75537 油中含水量/(mg/L)4.512.130.5 绕组电容量初值差(%)51.41.4 糠醛含量/(mg/L)0.0080.050.02 H2含量/(mL/L)140359166.23 C2H6含量/(mL/L)19.7925.3 C2H4含量/(mL/L)16.3523.1 油中含气量(%)1.61.61.6 绕组短路阻抗初值差(%)3.51.21.1 C2H2含量/(mL/L)000 CH4含量/(mL/L)27.318.513.81 绝缘电阻吸收比1.751.610.89 极化指数2.162.031.07 CO相对产气速率/(%/月)201213 CO2相对产气速率/(%/月)513158 体积电阻率/(109W·m)48558.83 绕组绝缘介质损耗(%)0.790.360.26 绕组直流电阻互差(%)3.71.51.2 绝缘油介质损耗(%)1.461.74.86 局部放电量/pC677261 纸板聚合度850900980 中性点油流静电电流/mA0.080.070.05 铁心接地电流/A0.063.80.04 铁心绝缘电阻/MW800200300
表8 实例2的评估结果
Tab.8 Assessment results of example 2

评估方法综合评分评估结果故障层误判个数 本文方法61.196 3异常0 取点法63.785 0注意2 指标量化值60.858 2异常0 灰色聚类63.557 8注意1 实际状态对变压器检查后发现,其运行出口处有短路情况出现,经过短路电流冲击后,绕组发生变形,且相关指标接近或略微超过注意值,变压器判定为异常状态
表9 实例3的评估结果
Tab.9 Assessment results of example 3

评估方法综合评分评估结果故障层误判个数 本文方法35.822 5严重0 取点法28.735 0严重1 指标量化值36.167 1严重1 灰色聚类29.742 0严重2 实际状态经检查,发现油箱底部有少量金属粉末,在电磁力作用下使铁轭与垫脚或箱底形成不稳定多点接地,导致铁心过热,且相关指标远远超过注意值,变压器判定为严重状态
表10 实例4的评估结果
Tab.10 Assessment results of example 4

评估方法综合评分评估结果故障层误判个数 本文方法37.465 9严重0 取点法32.730 0严重3 指标量化值37.634 6异常0 灰色聚类38.389 9异常0 实际状态经检查,发现绝缘受潮和绝缘油劣化中的大部分相关指标略微或远远超过注意值,且发生两种故障,变压器判定为严重状态
本文建立了以故障类型为基础的层次型变压器状态评估指标体系,并提出一种融合变权理论和灰云模型的变压器状态层次评估方法。
1)采用灰云模型代替传统的灰色聚类白化权函数,兼顾了评估等级信息的模糊性、灰性和随机性的特点,具有更强的普适性和代表性。
2)利用指标云模型代替指标值计算云关联度,通过对原来的指标量化值进行模糊离散化处理,更好地体现变压器状态信息的不确定性。
3)建立以故障类型为基础的层次型变压器状态评估指标体系,利用关联规则和灰云聚类得到故障层状态,再根据变权融合得到变压器综合状态,逐层评估使结果更加科学准确。
4)实例对比分析表明,该方法不仅能得到满意的状态评估结果,还能进一步找出导致该状态的具体原因,验证了该方法的有效性和实用性。
参考文献
[1] 李秀广, 李军浩, 吴旭涛, 等. 不同冲击电压下变压器油击穿特性研究[J]. 电机与控制学报, 2018, 22(3): 82-87, 94.
Li Xiuguang, Li Junhao, Wu Xutao, et al. Research onthe breakdown characteristics of transformer oil under oscillatory impulse voltage[J]. Electric Machines and Control, 2018, 22(3): 82-87, 94.
[2] 邹阳, 何倩玲, 蔡金锭. 基于组合赋权-双基点法的变压器油纸绝缘状态综合评估[J]. 电工技术学报, 2019, 34(20): 4400-4408.
Zou Yang, He Qianling, Cai Jinding. Comprehensive evaluation of transformer oil-paper state based on combined weight-double base point method[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4400-4408.
[3] 刘志文, 董旭柱, 吴争荣, 等. 考虑灵活定义约束的配电网检修计划双层优化方法[J]. 电工技术学报, 2018, 33(10): 2208-2216.
Liu Zhiwen, Dong Xuzhu, Wu Zhengrong, et al. A bi-level optimization method for distribution network maintenance schedule considering flexible definition- constraint condition[J]. Transactions of China Elec- trotechnical Society, 2018, 33(10): 2208-2216.
[4] 张晶晶, 许修乐, 丁明, 等. 基于模糊层次分析法的变压器状态评估[J]. 电力系统保护与控制, 2017, 45(3): 75-81.
Zhang Jingjing, Xu Xiule, Ding Ming, et al. A condition assessment method of power transformers based on fuzzy analytic hierarchy process[J]. Power System Protection and Control, 2017, 45(3): 75-81.
[5] 祝顺才, 蔡金锭. 基于模糊-灰色聚类的油纸绝缘状态综合诊断[J]. 仪器仪表学报, 2017, 38(3): 718-725.
Zhu Shuncai, Cai Jinding. Comprehensive diagnosis of oil-paper insulation status based on fuzzy gray clustering[J]. Chinese Journal of Scientific Instru- ment, 2017, 38(3): 718-725.
[6] Song Renjie, Liu Ruiying, Ma Dongmei. Hierarchy evaluation method for power transformer condition based on fuzzy and grey clustering analysis[J]. ICIC Express Letters, Part B: Applications, 2017, 8(1): 19-26.
[7] 刘庆珍, 张晓燕, 蔡金锭. 基于降维技术与K- means聚类的油纸绝缘状态综合灰评估[J]. 电力系统保护与控制, 2019, 47(8): 62-70.
Liu Qingzhen, Zhang Xiaoyan, Cai Jinding. Com- prehensive grey evaluation for oil-paper insulation based on dimension reduction techniques and K- means cluster[J]. Power System Protection and Control, 2019, 47(8): 62-70.
[8] 宋人杰, 刘瑞英, 王林. 灰色定权聚类和变权模式在变压器状态评估中的应用研究[J]. 电工电能新技术, 2017, 36(3): 75-80.
Song Renjie, Liu Ruiying, Wang Lin. Application of grey fixed weight clustering and variable weight model in transformer condition evaluation[J]. Advanced Technology of Electrical Engineering and Energy, 2017, 36(3): 75-80.
[9] 谢龙君, 李黎, 程勇, 等. 融合集对分析和关联规则的变压器故障诊断方法[J]. 中国电机工程学报, 2015, 35(2): 277-286.
Xie Longjun, Li Li, Cheng Yong, et al. A fault diagnosis method of power transformers by integr- ated set pair analysis and association rules[J]. Proceedings of the CSEE, 2015, 35(2): 277-286.
[10] 张宁, 蔡金锭. 基于模糊物元-逼近理想点法的油纸绝缘状态评估[J]. 电工技术学报, 2018, 33(22): 5381-5389.
Zhang Ning, Cai Jinding. Evaluation of oil-paper insulation condition based on fuzzy matter element- technique for order preference by similarity to ideal solution method[J]. Transactions of China Electro- technical Society, 2018, 33(22): 5381-5389.
[11] 蔡金锭, 叶荣, 刘庆珍. 基于改进TOPSIS和时域特征量的油纸绝缘状态分类分级评估[J]. 电机与控制学报, 2020, 24(1): 86-94.
Cai Jinding, Ye Rong, Liu Qingzhen. Oil-paper insulation classification and grading assessment based on improved TOPSIS and time-domain characteristic parameters[J]. Electric Machines and Control, 2020, 24(1): 86-94.
[12] 张镱议, 廖瑞金, 杨丽君, 等. 基于云理论的电力变压器绝缘状态评估方法[J]. 电工技术学报, 2012, 27(5): 13-20.
Zhang Yiyi, Liao Ruijin, Yang Lijun, et al. An assessment method for insulation condition of power transformer based upon cloud model[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 13-20.
[13] 孙睿. 配网变压器运行状态评估的云模型研究[J]. 电气技术, 2018, 19(2): 84-86, 91.
Sun Rui. Study on cloud model of network transformer operation state evaluation[J]. Electrical Engineering, 2018, 19(2): 84-86, 91.
[14] 刘云鹏, 许自强, 付浩川, 等. 采用最优云熵改进可拓云理论的变压器本体绝缘状态评估方法[J]. 高电压技术, 2020, 46(2): 397-405.
Liu Yunpeng, Xu Ziqiang, Fu Haochuan, et al. Insulation condition assessment method of power transformer based on improved extension cloud theory with optimal cloud entropy[J]. High Voltage Engineering, 2020, 46(2): 397-405.
[15] 何怡刚, 陈铭, 张大波, 等. 基于古林法和层次可拓的变压器状态评估[J]. 电力系统保护与控制, 2018, 46(21): 38-44.
He Yigang, Chen Ming, Zhang Dabo, et al. Trans- former condition assessment based on A. J. Klee method and extension hierarchy[J]. Power System Protection and Control, 2018, 46(21): 38-44.
[16] 国家电网公司. 油浸式变压器(电抗器)状态评价导则Q/GDW 10169—2016[S]. 北京: 中国电力出版社, 2017.
[17] Li Lee, Xie Longjun, Zhang Deng, et al. Condition assessment of power transformers using a synthetic analysis method based on association rule and variable weight coefficients[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2013, 20(6): 2052-2060.
[18] 杨德友, 崔冬晓, 蔡国伟. 基于云智能控制器的燃料电池最大功率跟踪策略[J]. 电工技术学报, 2018, 33(14): 3362-3370.
Yang Deyou, Cui Dongxiao, Cai Guowei, et al. A maximum power point tracking technology for fuel cells using cloud model based intelligent controller[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3362-3370.
[19] 贾清泉, 艾丽, 董海艳, 等. 考虑不确定性的电压暂降不兼容度和影响度评价指标及方法[J]. 电工技术学报, 2017, 32(1): 48-57.
Jia Qingquan, Ai Li, Dong Haiyan, et al. Uncertainty description and assessment of incompatibility & influence index for voltage sags[J]. Transactions of China Electrotechnical Society, 2017, 32(1): 48-57.
[20] 阎洁, 李宁, 刘永前, 等. 短期风电功率动态云模型不确定性预测方法[J]. 电力系统自动化, 2019, 43(3): 17-23.
Yan Jie, Li Ning, Liu Yongqian, et al. Short-term uncertainty forecasting method for wind power based on real-time switching cloud model[J]. Automation of Electric Power Systems, 2019, 43(3): 17-23.
[21] 刘敦楠, 张潜, 李霄彤, 等. 基于云模型与模糊Petri网的电力市场潜在危害行为识别[J]. 电力系统自动化, 2019, 43(2): 25-37.
Liu Dunnan, Zhang Qian, Li Xiaotong, et al. Identification of potential harmful behaviors in electricity market based on cloud model and fuzzy Petri net[J]. Automation of Electric Power Systems, 2019, 43(2): 25-37.
[22] 夏鹏, 刘文颖, 张尧翔, 等. 考虑风电高阶不确定性的分布式鲁棒优化调度模型[J]. 电工技术学报, 2020, 35(1): 189-200.
Xia Peng, Liu Wenying, Zhang Yaoxiang, et al. A distributionally robust optimization scheduling model considering higher-order uncertainty of wind power[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 189-200.
[23] 张银燕, 李弼程. 基于MIN-MAX云重心推理的目标威胁评估方法[J]. 系统仿真学报, 2014, 26(2): 411-418.
Zhang Yinyan, Li Bicheng. Method of target threat assessment based on cloudy MIN-MAX center of gravity reasoning[J]. Journal of System Simulation, 2014, 26(2): 411-418.
[24] 杨哲, 杨侃, 刘朗, 等. 组合赋权模糊熵-灰云聚类二维河流健康评价[J]. 华中科技大学学报: 自然科学版, 2018, 46(5): 90-94.
Yang Zhe, Yang Kan, Liu Lang, et al. Two dimensional river health evaluation based on fuzzy entropy-gray cloud clustering and combination weighting method[J]. Journal of Huazhong University of Science and Technology: Nature Science Edition, 2018, 46(5): 90-94.
[25] 梁永亮, 李可军, 牛林, 等. 变压器状态评估多层次不确定模型[J]. 电力系统自动化, 2013, 37(22): 73-78.
Liang Yongliang, Li Kejun, Niu Lin, et al. A multilayer uncertain transformer condition assessment model[J]. Automation of Electric Power Systems, 2013, 37(22): 73-78.
[26] Shen Hongtao, Tao Peng, Zhao Pei, et al. Massive power device condition monitoring data feature extraction and clustering analysis using MapReduce and graph model[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(2): 221-230.
[27] 祝顺才, 蔡金锭, 王岭. 基于变权-模糊综合评判法的绝缘状态诊断研究[J]. 电气技术, 2017, 18(4): 16-21.
Zhu Shuncai, Cai Jinding, Wang Ling. Study on insulation condition diagnosis based on the variable weight-fuzzy comprehensive evaluation method[J]. Electrical Engineering, 2017, 18(4): 16-21.
[28] 谢荣斌, 张登, 林福昌,等. 基于关联规则与变权重的变压器状态评估方法[J]. 高压电器, 2014, 50(1): 133-138.
Xie Rongbin, Zhang Deng, Lin Fuchang, et al. Transformer condition assessment using association rules and variable weight[J]. High Voltage Apparatus, 2014, 50(1): 133-138.
Hierarchical Assessment Method of Transformer Condition Based on Weight-Varying Grey Cloud Model
Abstract In order to objectively and scientifically evaluate the transformer condition, a hierarchical index system for transformer condition evaluation was established, and a hierarchical assessment method for transformer condition based on weight-varying grey cloud model was proposed. Firstly, the cloud model was used to improve traditional whitening weight function to build grey cloud model. Compared with the traditional grey clustering whitening weight function, the grey cloud model could effectively reflect fuzziness, greyness and randomness for information of evaluation level. To better reflect the uncertainty of the transformer status information, the cloud correlation was calculated using index cloud model instead of index value. Then, the condition of transformer fault layer was obtained by association rules and grey cloud clustering. The overall condition of transformer was obtained by weight-varying fusion. To acquire the final evaluation result, the condition of transformer fault layer and the overall condition were considered comprehensively. Finally, the case studies verified that the proposed method is effective and superior.
keywords:Transformer, condition assessment, cloud model, weight-varying theory, gray cloud clustering, cloud correlation
中图分类号:TM411
DOI: 10.19595/j.cnki.1000-6753.tces.190827
国家自然科学基金(51477040)、天津市自然科学基金(19JCZDJC32100)和河北省自然科学基金(E2018202282)资助项目。
收稿日期2019-07-05
改稿日期 2020-06-03
杜 江 男,1972年生,博士,副教授,研究方向为电机、变压器及其智能化技术。E-mail: dj@hebut.edu.cn(通信作者)
孙铭阳 男,1995年生,硕士研究生,研究方向为电机、变压器及其智能化技术。E-mail: 1020222947@qq.com
(编辑 崔文静)