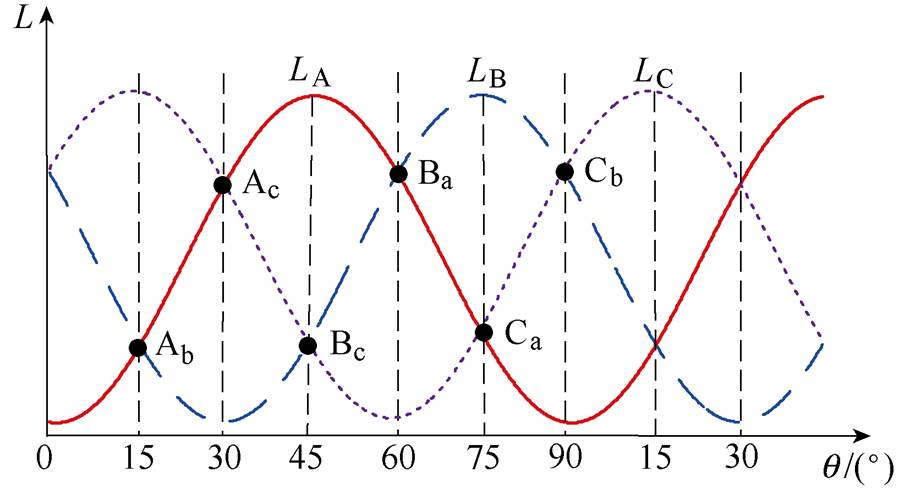
图1 三相绕组电感随转子位置角度的变化曲线
Fig.1 Curves of three phase winding inductance varying with rotor position angle
摘要 开关磁阻电机在磁路饱和情况下,其导通相电感会随导通相电流的变化而变化,针对传统相电感法转子位置估算精度受磁路饱和影响大的问题,提出一种基于相电感非饱和区定位的开关磁阻电机无位置传感器控制方法。建立开关磁阻电机的相电感函数,阐述确定相电感非饱和区的方法,提出相电感非饱和区定位点的基本概念并分析其相关特点,研究根据两相邻定位点来估算电机转子位置角度的具体实现方法。最后通过仿真与实验验证了上述方法的可行性。
关键词:开关磁阻电机 电感非饱和区 定位点 位置估算
开关磁阻电机(Switched Reluctance Motor, SRM)具有结构简单、可靠性高、容错能力强等优点[1-2],被广泛应用于纺织机械、矿山装备等诸多领域。开关磁阻电机要实现高精度调速控制,就必须准确获取转子的实时位置信息。传统获取转子位置信息主要利用位置传感器,但使用位置传感器不仅会增加调速系统的体积、成本及加工复杂度,同时也降低了调速系统在一些特定环境下的工作可靠性。因此开展开关磁阻电机无位置传感器研究具有重要的现实意义[3-4]。
近年来,国内外针对开关磁组电机无位置传感器控制已开展了广泛研究。文献[4-5]通过建立增量电感与转子位置角度之间的关系模型,并由采集的电压、电流值来实时计算增量电感,再根据增量电感来实现对转子位置的估算。该方法增量电感受相绕组磁路饱和的影响较大,因此只适用于电机轻载情况。文献[6]通过检测相电流梯度的过零信号来确定电感最大值处的位置角度,并据此实现对转子位置的估算;该算法原理简单、实时性高,但转子位置估算精度易受开通角和相电流变化的影响。针对上述问题,文献[7]提出电流斜率检测和电感斜率过零点检测相结合的方法,该方法有效地避免了开通角对转子位置估算精度的影响,具有较高的容错性。文献[8]则提出一种简化磁链法,通过预先存储换相点的磁链-角度值,在电机运行时只需将检测的磁链值与存储的换相点磁链值进行比较,即可实现对电机位置的估算,该方法因换相点磁链同样受磁路饱和影响,故同样只适用于电机轻载情况。文献[9]提出一种基于五点磁链模型的转子位置估算方法,其选取的五点磁链值可在线获取,算法简单、易实现;但该方法中选取的五点磁链值会随磁路饱和程度而发生变化,从而影响转子位置估算精度。文献[10]提出一种改进型简化磁链位置估算方法,通过检测7.5°处的磁链值并进行算术平均处理后计算出转子位置估算角度;该方法中的算术平均法不能消除因磁路饱和造成的转子位置估算的误差,因此只适用于磁路非饱和情况。文献[11]提出一种改进型的脉冲电流峰值位置估算方法,通过均值采样法计算出相电流峰值,再由相电流峰值估算点实现对转子位置的估算;该方法中的相电流峰值估算点只在磁路非饱和状态下具有很高的精度,因此不适合与磁路饱和状态下的转子位置估算。文献[12]提出一种基于非导通相电流双阈值的转子位置估算方法,可实现电机静止起动;该方法未考虑绕组压降与反电动势的影响且相电流阈值的设定受电机运行状态影响,因而其位置估算精度不高。针对该问题,文献[13-14]通过对非导通相采取脉冲斩波控制,由采集的感应电流斜率差来估算相电感,再根据离线构建的相电感-角度模型来计算出相应的转子位置角度值;该方法有效地克服了绕组电阻压降和反电动势对估算精度的影响,可实现全周期的位置估算,但模型构建过程繁琐、复杂。文献[15]通过对相电感坐标进行变换,使得三相电感可以近似由单位正弦函数表示,在保证精度的前提下简化了位置估算模型,可实现中低转速下的转子位置估算,但该方法也没有考虑磁路饱和因素,只适合电机轻载情况。
针对目前开关磁阻电机转子位置估算在磁路饱和时存在估算精度低的问题,提出一种基于相电感非饱和区定位的开关磁阻电机无位置传感器控制方法,该方法能有效克服磁路饱和对转子位置角度估算精度的影响,并且具有算法简单、实时性高等特点。文中阐述了利用相电感非饱和区定位点确定开关磁阻电机转子位置角度的具体实现方法,并通过仿真和实验对该方法的正确性进行了验证。
本文以三相6/4结构开关磁阻电机为例,设各相绕组的参数一致,则各相绕组电感随转子位置角度的变化规律相同,只是相位错开一定的角度。在磁路非饱和时,三相绕组电感LA、LB和LC随转子位置角度q 的变化曲线如图1所示。可见,在一个机械周期90°内,三相电感曲线有六个交点,其交点角度分别为15°、30°、45°、60°、75°和90°,在磁路达到临界饱和之前,上述各交点的位置角度基本保持不变。

图1 三相绕组电感随转子位置角度的变化曲线
Fig.1 Curves of three phase winding inductance varying with rotor position angle
以功率为4kW、额定电压为380V的开关磁阻电机为例,利用ANSYS Maxwell软件构建电机仿真模型,并以A相为导通相,B、C相为非导通相,得到其导通相与非导通相电感曲线交点随导通相电流变化的关系曲线,如图2所示。图中,该电机的临界饱和电流为9A,可见,当A相电流值小于等于9A时,其相电感曲线相互重合,它与B、C相电感曲线的交点位置基本保持不变;而当A相电流大于9A时,随着A相电流的逐步增大,电感值逐步减小,电感曲线逐步下移,从而导致该电感曲线与B、C相电感曲线的交点也随之逐步下移。如果此时仍按照磁路非饱和时的相电感交点位置角度来估算电机转子的位置角度,则势必会造成较大的误差。
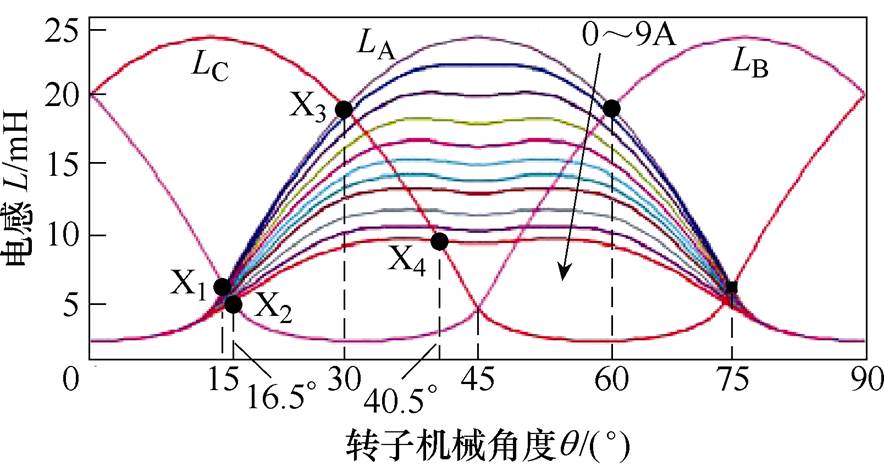
图2 导通相与非导通相电感曲线交点随导通相电流变化曲线
Fig2 The change diagram of the intersection point between the conduction phase and the non conduction phase inductance curves with the conduction phase current
针对本文提出的基于相电感非饱和区定位点来确定开关磁阻电机的转子位置角度,需要先确定电机各相绕组的相电感函数,根据斜率差法可得三相开关磁阻电机电感表达式[16]为
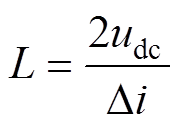 (1)
(1)式中,udc为直流母线电压;Di为开关管开通与关断期间的相电流斜率差。
根据式(1)可计算出开关磁阻电机全周期内不同位置角度的一系列电感值,采用数值拟合方法可得到相应函数关系,其傅里叶级数展开式可表示[16]为
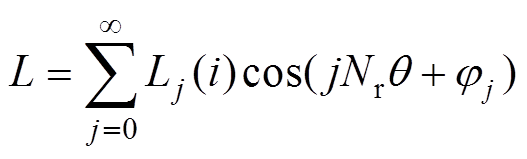 (2)
(2)式中,Nr为转子级数;Lj(i)为基波及各次谐波项的系数函数;jj为初相位。
以三相开关磁阻电机为例,在一个转子电气周期内,将开关磁阻电机第一个导通相称为A相,随后导通相称为B相,最后导通相称为C相。为简化分析计算,忽略式(2)中的高次项后,可得三相开关磁阻电机各相简化电感函数分别为
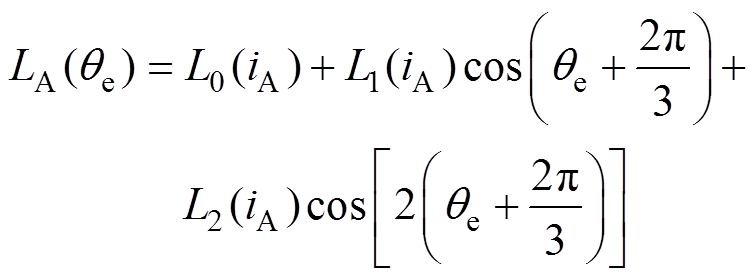 (3)
(3)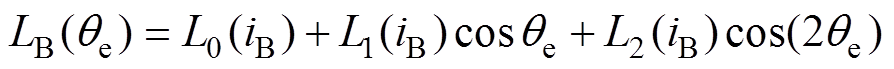 (4)
(4)
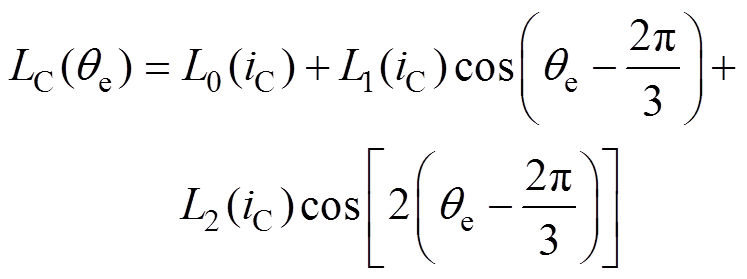 (5)
(5)
式中,LA(qe)、LB(qe)、LC(qe)分别为三相开关磁阻电机A、B、C相电感函数;qe为电机转子电气角度;L0(i)、L1(i)和L2(i)分别为相电感各分量的系数函数。
根据文献[17],L0(i)、L1(i)和L2(i)可分别表示为
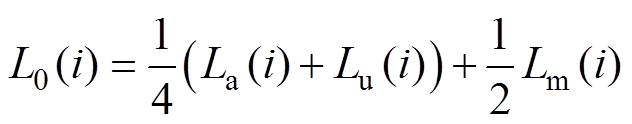 (6)
(6)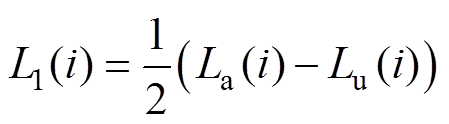 (7)
(7)
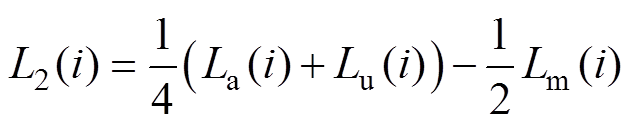 (8)
(8)
式中,La为最大相电感值;Lu为最小相电感值;Lm为最大电感与最小电感的中间值;i为注入脉冲响应电流。
根据式(3)~式(5),当开关磁阻电机导通相电流大于临界饱和电流时,其三相电感曲线如图3所示。以A相绕组为例,当开关磁阻电机运行在电动机状态时,其在一个相电感周期内的导通区间为对应相电感的上升阶段,并在相电感达到峰值之前关断,之后其电感值将采用注入高频脉冲方式来获取,由于脉冲注入电流小于其临界饱和电流,故相电感进入下降阶段后的电感值将不受磁路饱和的影响。本文将从相电感峰值到最小值之间的相电感下降区间确定为相电感非饱和区,并利用该区间的电感来实现对电机转子位置角度的估算。
由于在相电感非饱和区,其相电流iA、iB和iC均小于其临界饱和电流,根据文献[17]可知,此时各相电感系数函数L0(i)、L1(i)和L2(i)与导通相电流大小无关且为常数,即
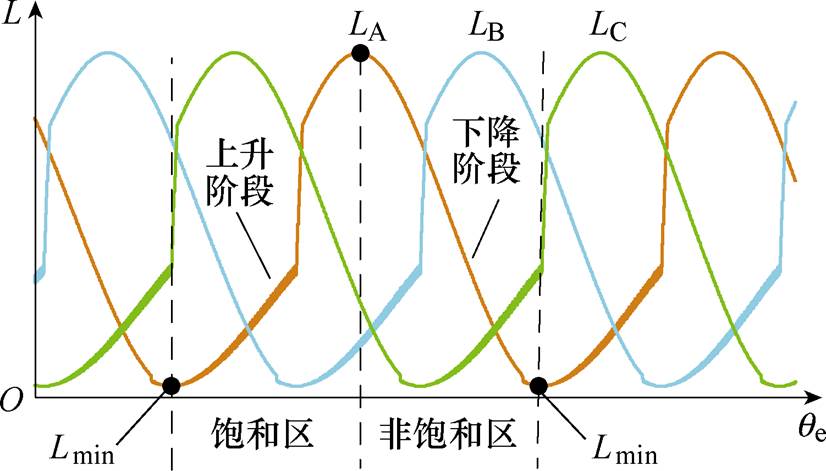
图3 三相开关磁阻电机相电感曲线
Fig.3 Phase inductance curves of three-phase SRM
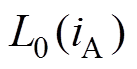 =
=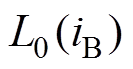 =
=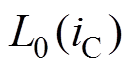 (9)
(9)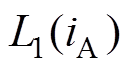 =
=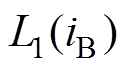 =
=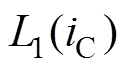 (10)
(10)
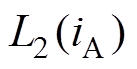 =
=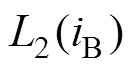 =
=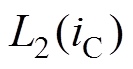 (11)
(11)
由式(3)~式(11),有
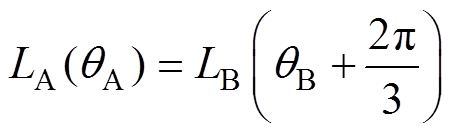 (12)
(12)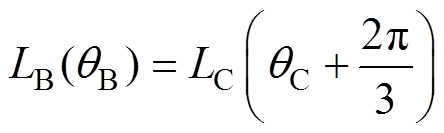 (13)
(13)
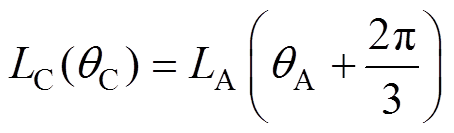 (14)
(14)
可见,在相电感非饱和区内,对于电感值相等的任意两相邻相电感,其对应的位置角度差均为2p/3,因此本文将在相电感非饱和区内相电感值相等时所对应的位置点(qe, L(qe))定义为定位点,转子位置估算定位点的确定如图4所示。根据定位点的定义,若在相电感非饱和区内取定位点的相电感值L(qe)=L0(i)-L2(i),可得三相开关磁阻电机各相电感在定位点处的具体位置角度为
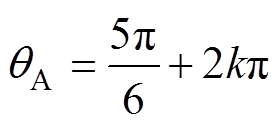 (15)
(15) (16)
(16)
 (17)
(17)
式中,qA、qB、qC分别为电机三相电感在电感值为L0(i)-L2(i)的定位点处的位置角度;k为整数。
由于两相邻相电感定位点之间的电气角度Dqe= 2p/3,故根据电机转子机械角度与电气角度间的关系,可得对应的机械角度为
 (18)
(18)式中,Dqn为两相邻相电感定位点间的机械角度。
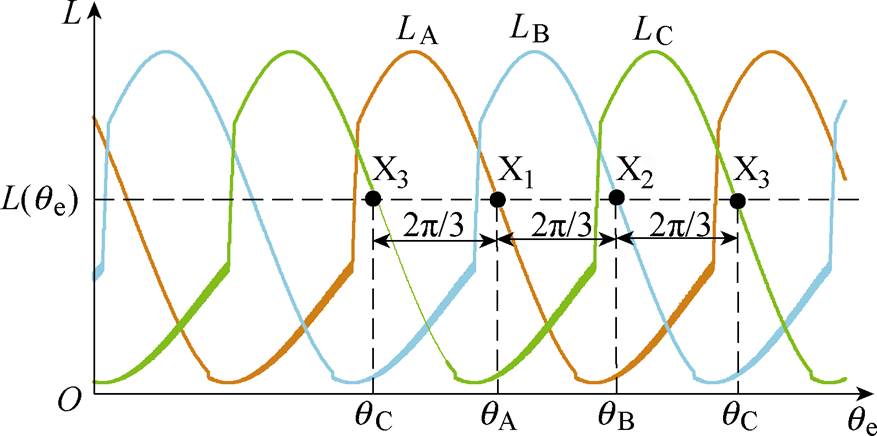
图4 转子位置估算定位点的确定
Fig.4 Determination of rotor position estimation location point
对三相6/4结构的开关磁阻电机来说,其Nr=4,则Dqn=p/6。
根据上述确定的两相邻相电感定位点间的机械角度Dqn,再确定电机转子转过上述两定位点对应区间的时间Dtn,则可确定电机转子在第n个区间的平均转速为
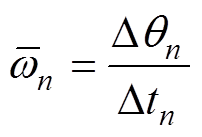 (19)
(19)鉴于开关磁阻电机属惯性负载,因而当其转子从第n个区间旋转至第n+1个区间时,其转速可认为基本保持恒定,为此可根据电机在第n个区间的平均转速,估算出电机转子在下一个对应区间,即第n+1个区间任意时刻的位置角度qn+1(t),具体为
 (20)
(20)
式中,qn+1(t)为电机转子在第n+1个区间任意时刻t的位置角度;qn+1(t0)为电机转子在第n+1个区间起始时刻t0的位置角度。
以三相6/4规格开关磁阻电机为例,确定一个区间的起始位置角度q(t0)方法为:取定位点电感值为L0-L2,则由式(15)~式(17)可知,在一个电气周期内三相电感对应各区间的起始位置角度值q(t0)分别为5p/6、3p/2和p/6;具体确定是哪个位置角度的方法为:在电机起动运行后,实时检测三相电感值,根据表1所示相电感定位点位置的逻辑关系来判断出第一个相电感下降区定位点的位置角度,当A相电感满足第k+1次获取的电感值小于第k次电感值,且k+1次电感值等于L0-L2时,则可由表1判断出此时相电感定位点为X1,其交点位置角度为5p/6,此后各相电感定位点的位置角度在此基础上按2p/(3Nr)的关系递增。在确定好一个区间的起始位置角度后,即可根据式(20)计算出该区间内任意时刻的电机转子位置角度。
表1 相电感定位点位置的逻辑关系
Tab.1 Logical relation of positive location of line inductance

相电感逻辑关系相电感交点相电感交点位置角度/(°) LA(k)<LA(k+1), LA(k)=L0-L2X15p/6 LB(k)<LB(k+1), LB(k)=L0-L2X23p/2 LC(k)<LC(k+1), LC(k)=L0-L2X3p/6
为验证上述理论分析的正确性,采用Matlab/ Simulink构建三相6/4结构开关磁阻电机控制系统仿真模型。该控制系统的基本原理框图如图5所示,包括转速控制外环和电流控制内环。其中转速控制外环采用PI控制,电流控制内环采用电流斩波控制。基本工作原理为给定转速nref与估算转速nest之差经过PI控制得到斩波电流给定Iref,再通过采集实际电流经电流斩波控制输出相应的功率变换器脉冲信号,从而完成对电机转速的跟踪。转子位置估算方法:通过采集三相电流与母线电压值来计算对应的相电感值,先确定当前计算的相电感值是否处于下降区,当确定为下降区后,判断当前电感值是否等于定位点处的电感值,最后通过对相电感定位点的确定来实现电机转子速度与位置角度的估算。
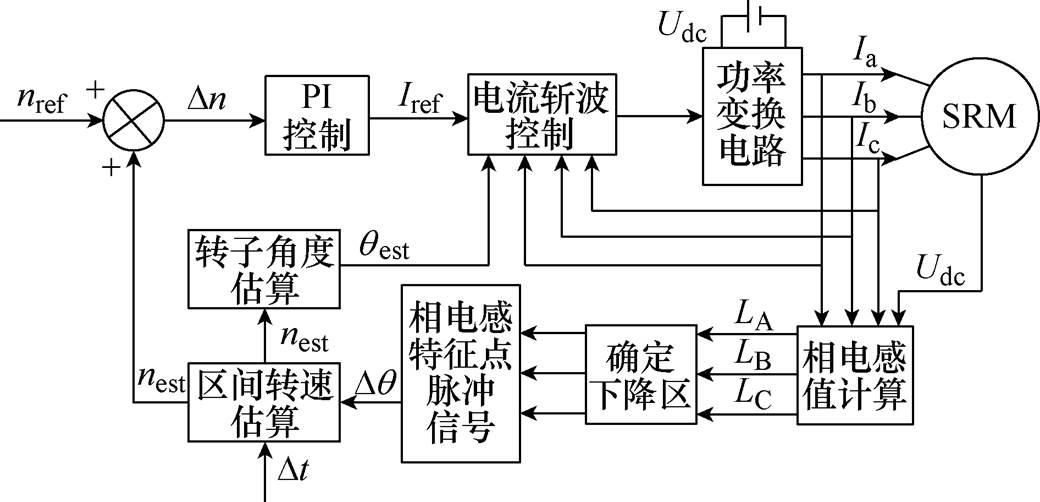
图5 无位置传感器控制系统原理框图
Fig.5 Implementation schematioc of sensorless control system
电机仿真参数设置如下:电机功率为4kW,临界饱和电流为9A,电流斩波频率为20kHz,非导通相脉冲注入频率为20kHz,占空比为15%。为说明电机在磁路非饱和及磁路饱和两种情况下基于相电感定位点估算转子位置角度的效果,分别针对上述两种情况进行仿真研究。
为了验证在磁路非饱和情况下基于相电感非饱和区定位点估算转子位置角度的效果,在临界饱和电流9A左右,任取电机导通相电流分别为7A、10A和16A,转速为600r/min的条件下进行仿真验证,得到相应的仿真波形分别如图6~图8所示,仿真结果见表2。
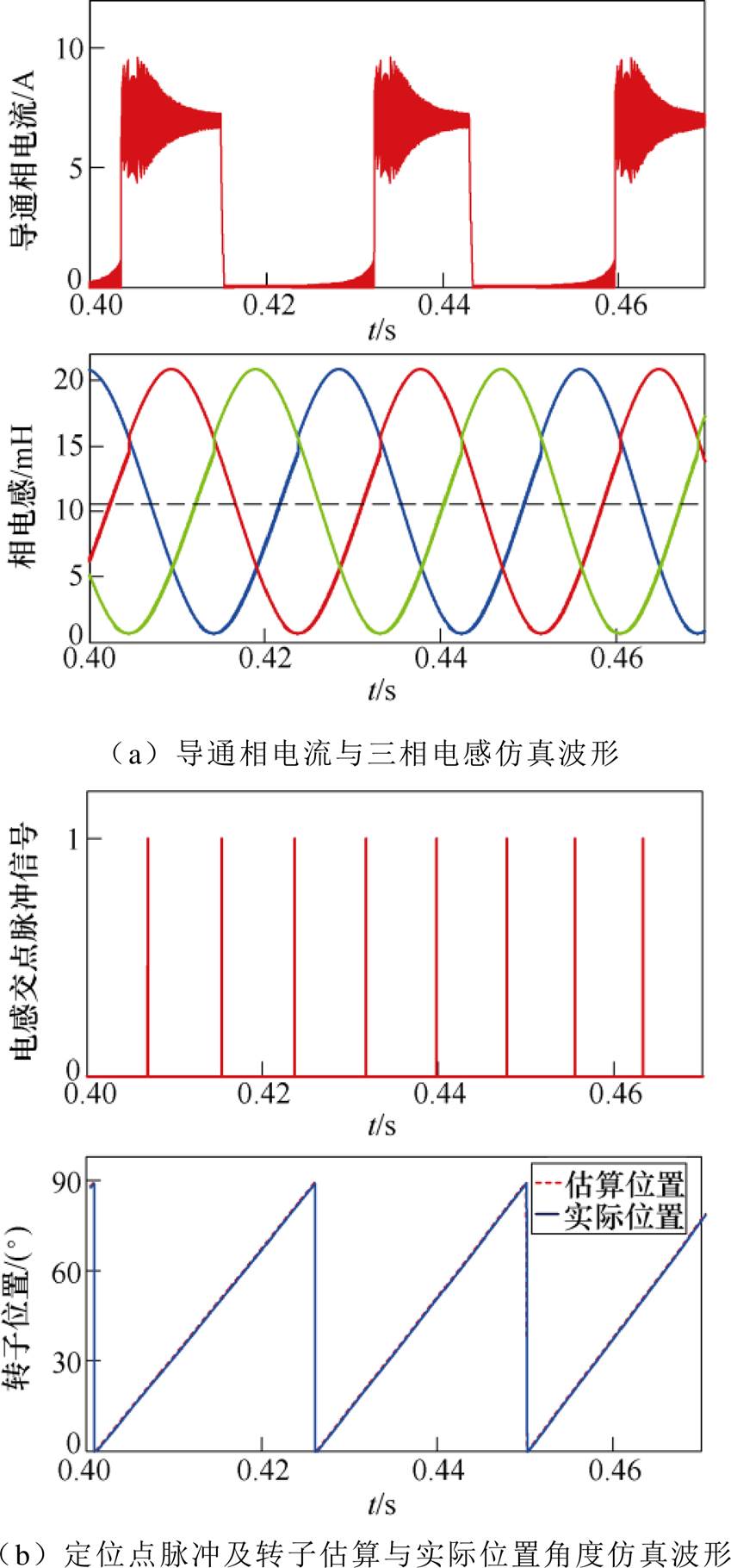
图6 电流为7A时的仿真波形
Fig.6 Simulation waveforms of current is 7A
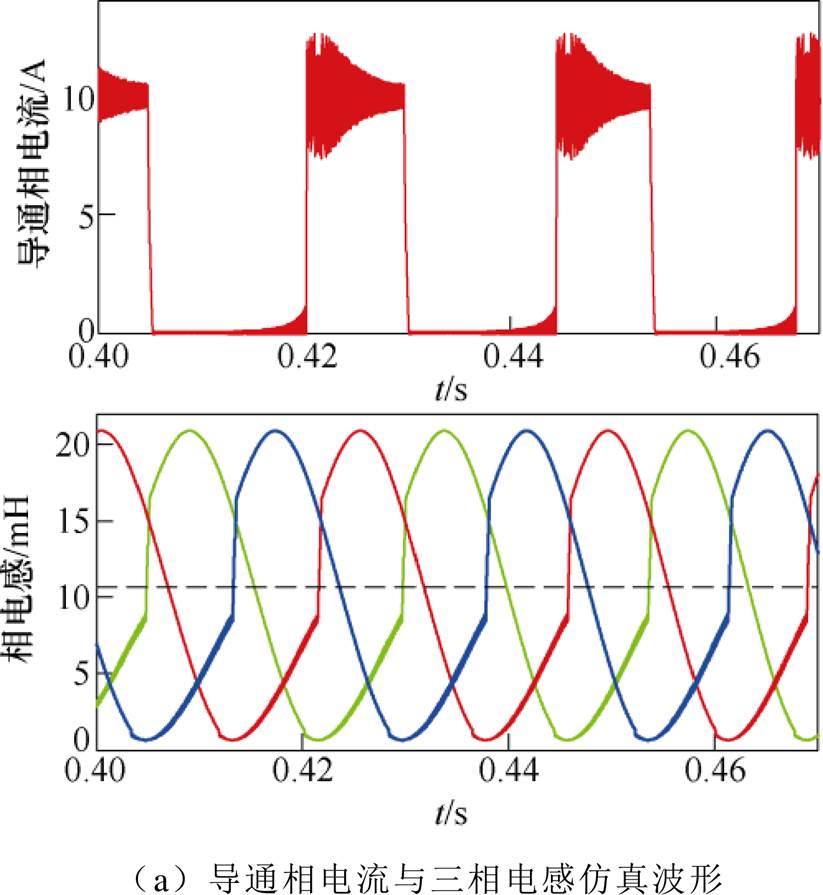
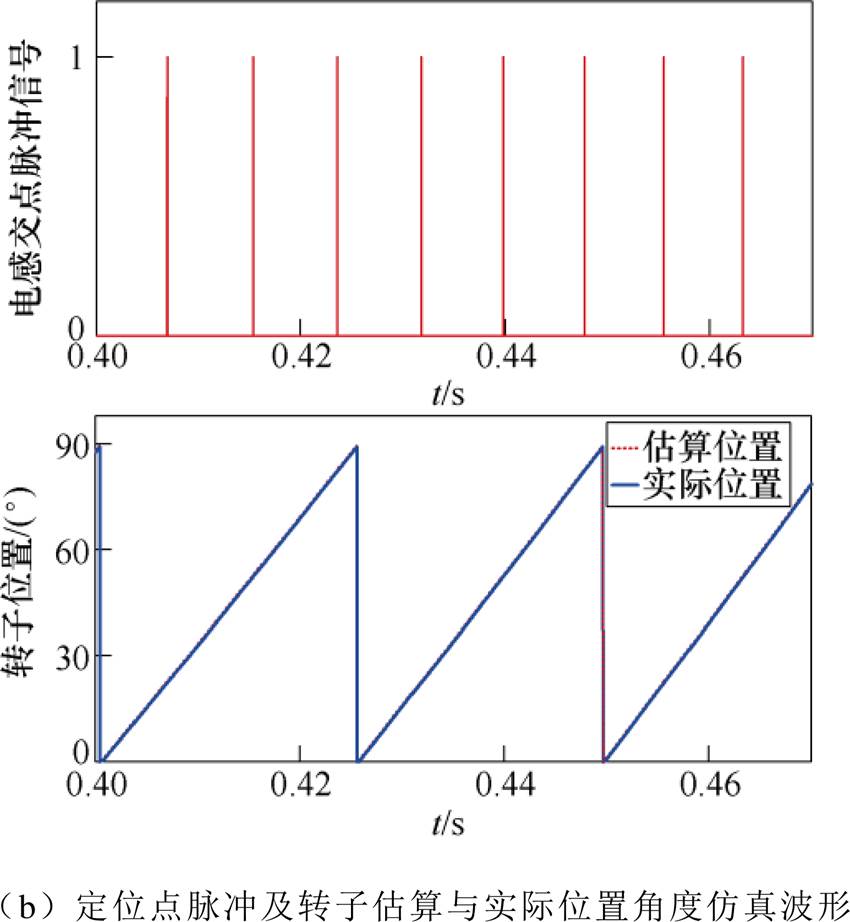
图7 电流为10A时的仿真波形
Fig.7 Simulation waveforms of current is 10A
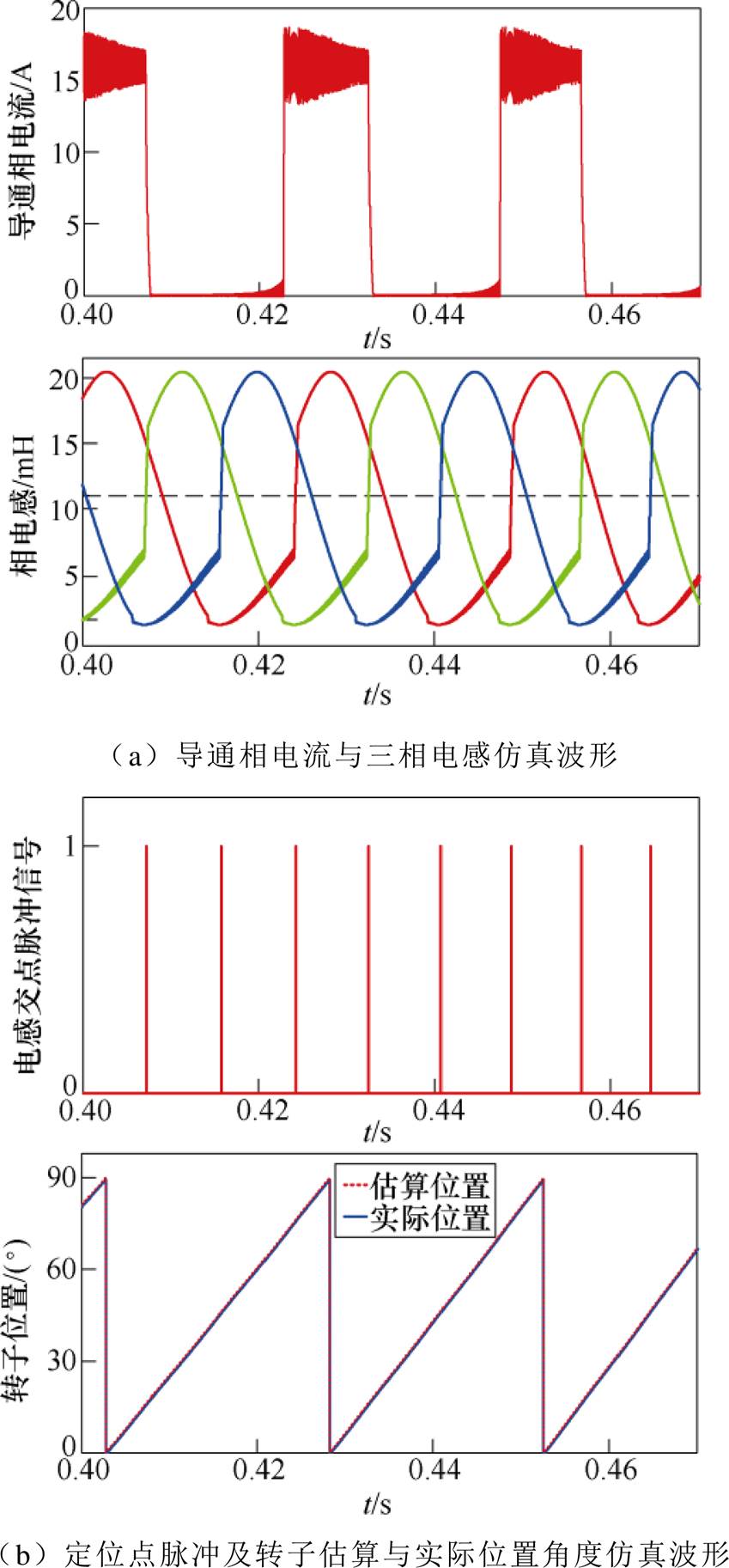
图8 电流为16A时的仿真波形
Fig.8 Simulation waveforms of current is 16A
表2 不同相电流条件下的位置角度估算误差
Tab.2 Estimation errors of position angle under different phase current conditions

电流/A最大角度误差/(°) 70.9 100.9 160.9
从图6可见,在磁路非饱和条件下,其相电感曲线形状能基本保持规则的正弦波,电机转子位置角度的估算波形能够较好地跟踪实际波形;另外从表2可见,此时转子位置的估算角度与其实际角度间的最大偏差为0.9°。
在大于临界饱和电流9A的情况下,从图7和图8可见,电机导通相电流大于其临界饱和电流时,相电感曲线在其导通区间内发生了较大变形,且随着相电流的增大,变形更为严重。但从图中可见,在相电感下降区,其相电感曲线依旧能保持与非磁路饱和时一样的规则正弦波,因此对应于相电感下降区定位点的脉冲信号之间的间隔能依旧保持不变,电机转子位置角度的估算波形与实际波形也均基本保持吻合。另外从表2可知,对应于两种不同饱和相电流下的转子位置估算角度与其实际角度间的最大偏差均控制在0.9°。
为进一步验证本文所提电机转子位置估算方法的可行性,以TMS320F28335 DSP为系统控制核心研制了一套实验装置,实验系统实物如图9所示。该实验系统装置包括一台4kW三相6/4结构开关磁阻电机、转矩控制器、制动器、扭矩传感器等,其中SRM的主要技术参数见表3。为了与仿真结果进行对比分析,实验中相关参数设置与仿真时一致。同样,为说明该方法在磁路非饱和及饱和状态下的转子位置估算效果,实验分恒转速和变转速两种情况进行。

图9 实验系统实物
Fig.9 Hardware of the experimental system
表3 SRM主要技术参数
Tab.3 SRM main technical parameters

参 数数 值 额定功率/kW4 电源电压/V380 额定转矩/(N·m)32 额定转速/(r/min)1 200 电感中间值Lm/mH10.3
保持电机转速一定,通过改变电机导通相电流,来验证在导通相电流变化时对转子位置角度估算精度的影响。取电机转速为600r/min,因电机导通相临界饱和电流为9A,故分别在9A左右取导通相电流为7A、10A和16A进行实验,得到相应的实验波形分别如图10~图12所示,实验结果见表4。可见,当导通相电流小于临界饱和电流时,其相电感曲线接近正弦波;而当导通相电流大于临界饱和电流时,相电感曲线在导通区内已发生变形,且随着相电流的增大,变形更为严重,但在相电感曲线的下降区内,其曲线基本不受影响。另外从表4可见,在三种不同导通相电流下,其电机转子位置角度估算的最大偏差均为1.0°。

图10 相电流为7A时的实验波形
Fig.10 Experimental waveforms with phase current of 7A
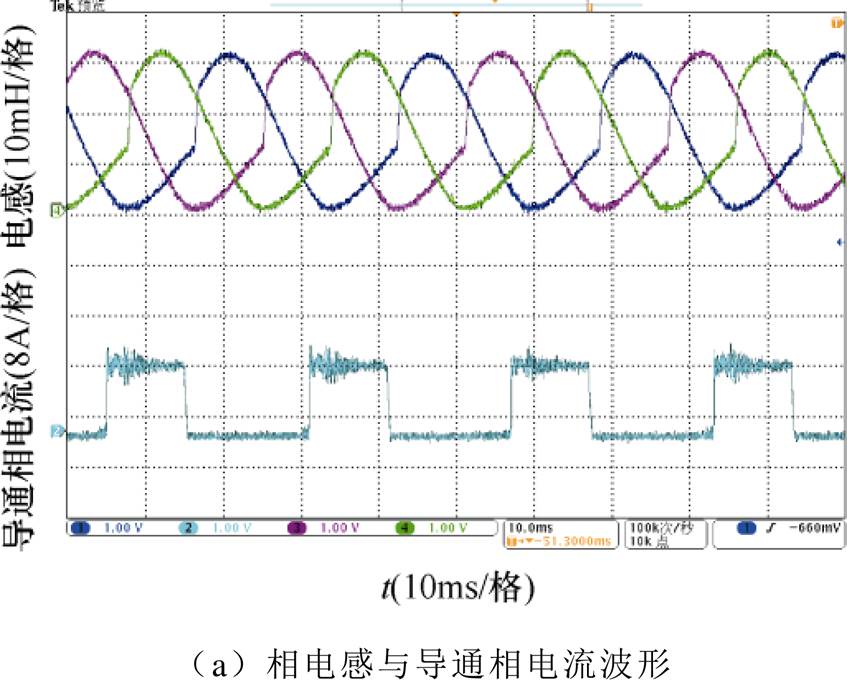
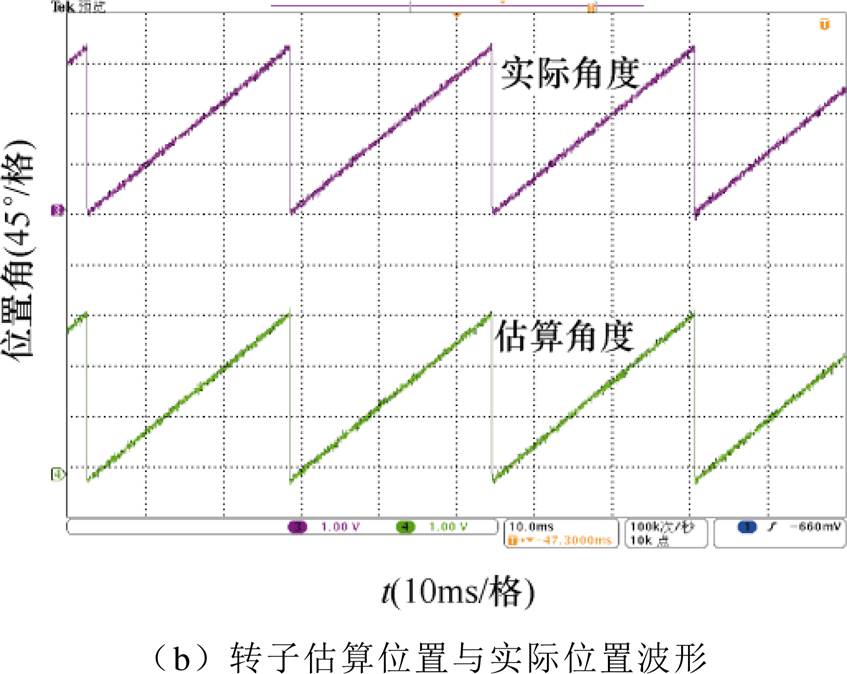
图11 相电流为10A时的实验波形
Fig.11 Experimental waveforms with phase current of 10A
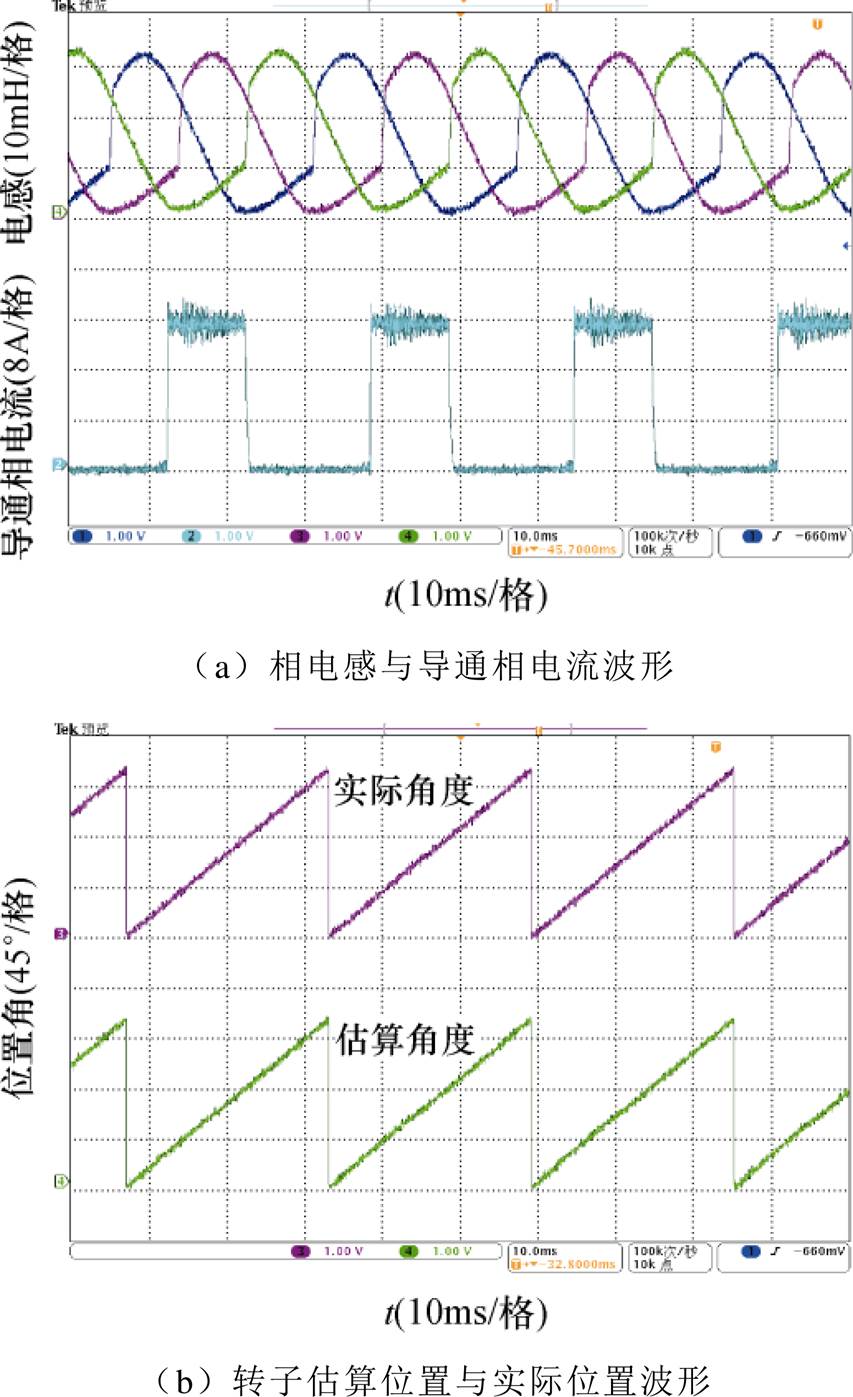
图12 相电流为16A时的实验波形
Fig.12 Experimental waveforms with phase current of 16A
表4 不同相电流条件下的位置角度估算误差
Tab.4 Position angle estimation error under different phase current conditions

电流/A最大角度误差/(°) 71.0 101.0 161.0
保持电机导通相电流一定,通过改变电机转速来验证不同转速对转子位置角度估算精度的影响。取电机导通相电流为16A,分别取转速为900r/min和1 200r/min进行实验,得到相应的实验波形分别如图13和图14所示,实验结果见表5。可见,当电机转速分别为900r/min和1 200r/min时,其电机转子位置角度估算的最大偏差分别为1.4°和2.0°。
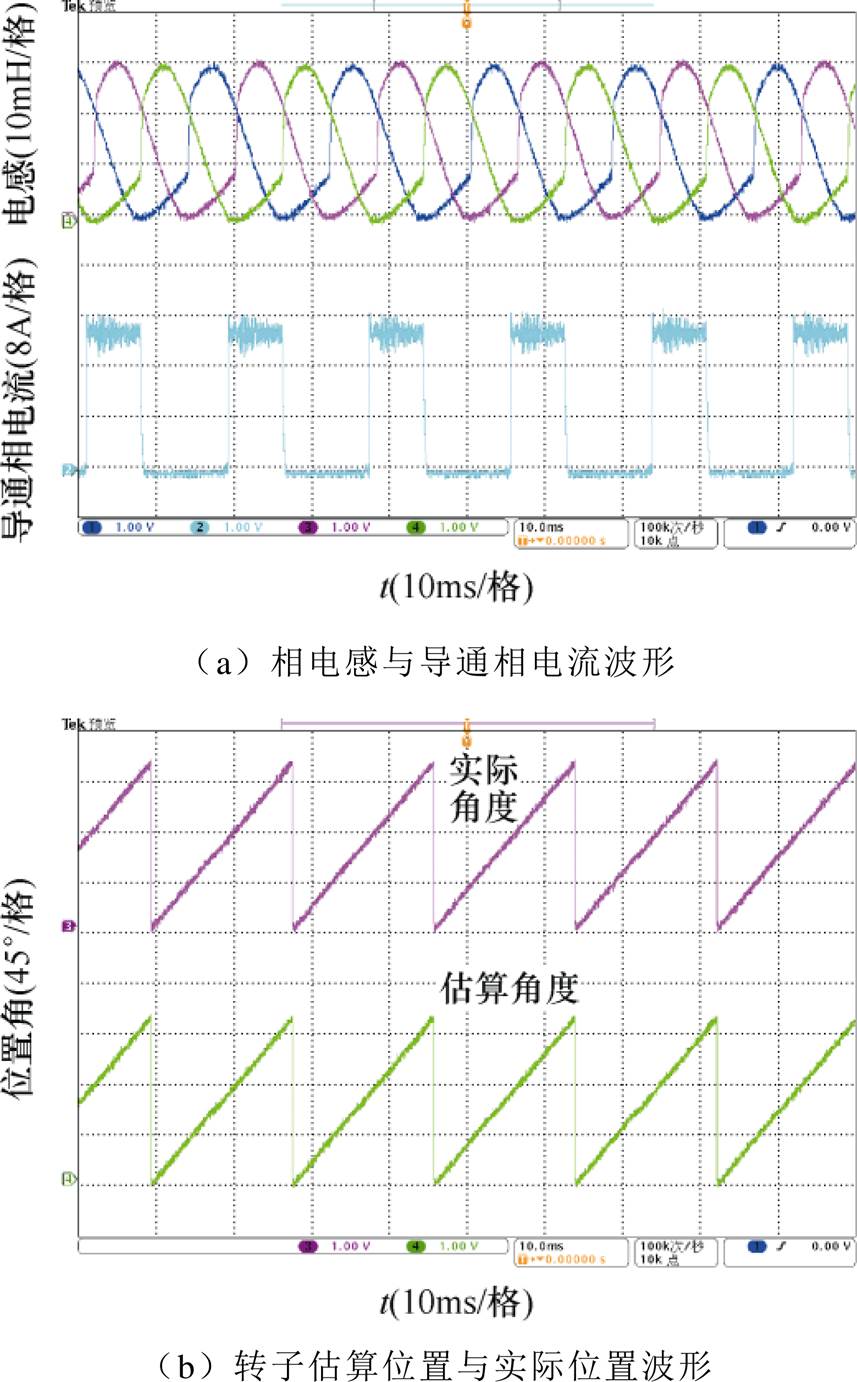
图13 电机转速为900r/min时的实验波形
Fig.13 Experimental waveforms with motor speed of 900r/min
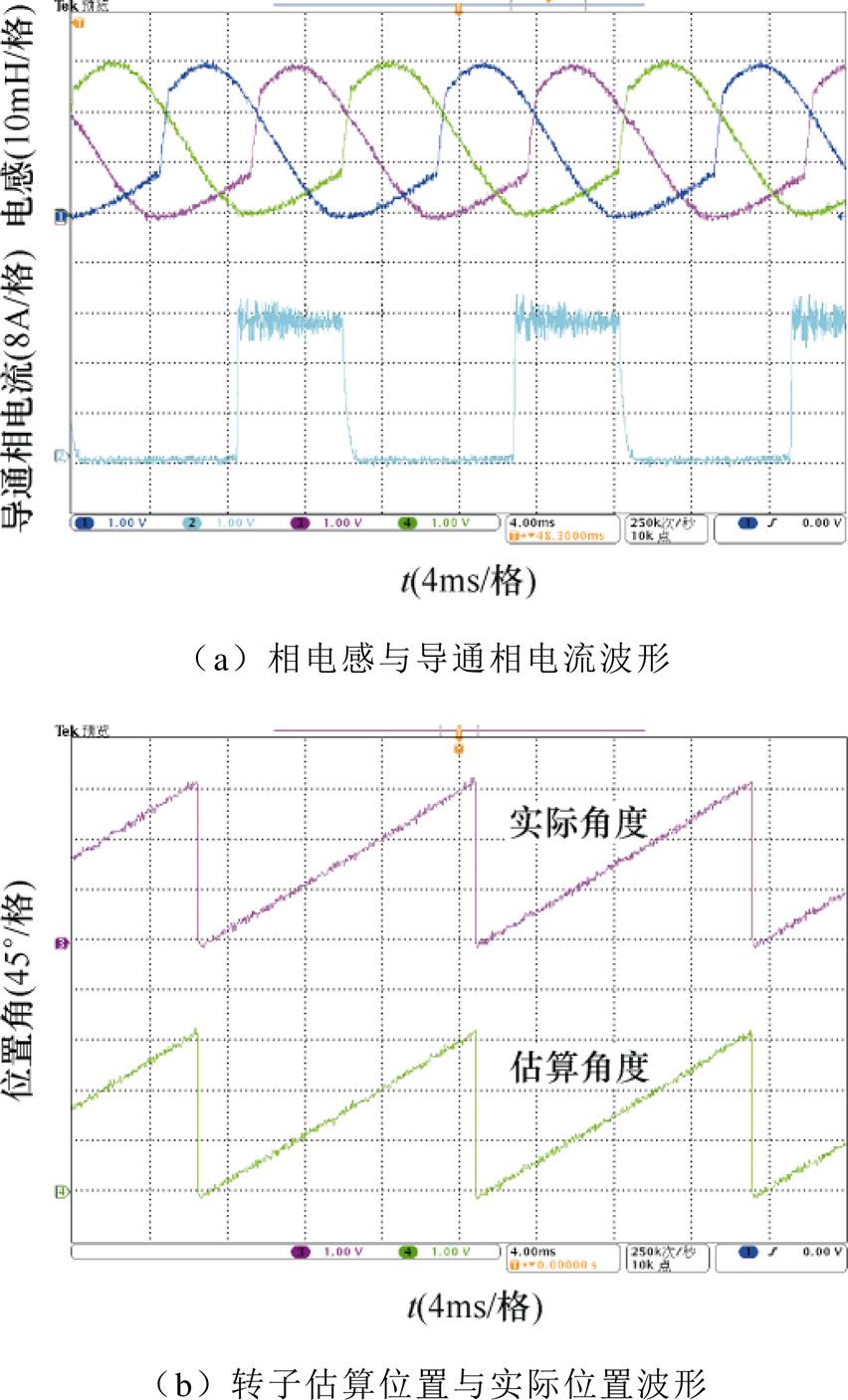
图14 电机转速为1 200r/min的实验波形
Fig.14 Experimental waveforms with motor speed of 1 200r/min
表5 不同电机转速条件下的位置角度估算误差
Tab.5 Position angle estimation error under different motor speed conditions

转速/(r/min)最大角度误差/(°) 9001.4 1 2002.0
根据上述仿真与实验结果,得到如下结论:
(1)在电机转速一定的情况下,不管其导通相电流是否大于其临界饱和电流,转子位置角度估算值与实际值之间的偏差基本保持不变,因而说明本文所提出的方法能有效克服磁路饱和对转子位置角度估算精度的影响。
(2)在电机导通相电流一定的情况下,随着电机转速的提高,转子位置估算精度将随之下降。原因在于随着电机转速的增加,在单位时间内导通相绕组注入的高频脉冲数量会相应减少,由此降低了相电感获取的精度,从而导致转子位置角度估算误差的增加。
针对目前开关磁阻电机在无位置传感控制方面存在受磁路饱和影响而导致转子位置估算精度不高的问题,提出一种基于相电感非饱和区定位的开关磁阻电机无位置传感器控制方法。阐述了利用相电感非饱和区定位点确定开关磁阻电机转子位置角度的具体实现方法,并通过仿真和实验对该方法的正确性进行了验证。结果表明该方法能够有效克服磁路饱和对转子位置估算精度的影响,适合于受磁路饱和影响的开关磁阻电机无位置传感器控制领域,具有较好的应用价值。
参考文献
[1] Gan Chun, Wu Jianhua, Hu Yihua, et al. Online sensorless position estimation for switched reluctance motors using one current sensor[J]. IEEE Transa- ctions on Power Electronics, 2016, 31(10): 7248- 7263.
[2] Fahimi B, Emadi A, Sepe R B. A switched reluctance machine-based starter/alternator for more electric cars[J]. IEEE Transactions on Energy Conversion, 2004, 19(1): 116-124.
[3] Ofori E, Husain T, Sozer Y, et al. Pulse-injection based sensorless position estimation method for a switched reluctance machine over a wide speed range[J]. IEEE Transactions on Industry Application, 2015, 51(5): 3867-3876.
[4] Gao Hongwei, Salmasi F R, Ehsani M. Inductance model-based sensorless control of the switched reluctance motor drive at low speed[J]. IEEE Transa- ctions on Power Electronics, 2004, 19(6): 1568-1573.
[5] Ehsani M, Fahimi B. Elimination of position sensors in switched reluctance motor drives: state of the art and future trends[J]. IEEE Transactions on Industrial Electronics, 2015, 49(1): 40-47.
[6] Gallegos-Lopez G. A new sensorless method for switched reluctance motor drives[J]. IEEE Transa- ctions on Industrial Application, 1998, 34(4): 832- 840.
[7] 蔡骏, 邓智泉. 一种具有容错功能的开关磁阻电机无位置传感器控制方法[J]. 中国电机工程学报, 2012, 32(36): 109-116.
Cai Jun, Deng Zhiquan. A fault-tolerant sensorless control method for switched reluctance motors[J]. Proceedings of the CSEE, 2012, 32(36): 109-116.
[8] 邱亦慧, 詹琼华, 马志源, 等. 基于简化磁链法的开关磁阻电机间接位置检测[J]. 中国电机工程学报, 2001, 21(10): 59-62.
Qiu Yihui, Zhan Qionghua, Ma Zhiyuan, et al. The indirect position sensing of SRM on the basis of simplified flux method[J]. Proceedings of the CSEE, 2001, 21(10): 59-62.
[9] 张磊, 刘闯, 王云林, 等. 开关磁阻电机改进型简化磁链无位置传感器技术[J]. 电机与控制学报, 2013, 17(11): 13-19.
Zhang Lei, Liu Chuang, Wang Yunlin, et al. Sensor- less technology of switched reluctance motor based on the improved simplified flux method[J]. Electric Machines and Control, 2013, 17(11): 13-19.
[10] 张磊, 刘闯, 王云林, 等. 开关磁阻电机磁链特性检测与位置信号估计[J]. 电机与控制学报, 2013, 17(2): 28-33.
Zhang Lei, Liu Chuang, Wang Yunlin, et al. Flux linkage characteristic detection of switched relu- ctance motor and the position estimate[J]. Electric Machines and Control, 2013, 17(2): 28-33.
[11] 罗德荣, 李亚雄, 李孟秋, 等. 基于单阈值的开关磁阻电机无位置传感器技术[J]. 湖南大学学报: 自然科学版, 2017, 44(2): 94-100.
Luo Derong, Li Yaxiong, Li Mengqiu, et al. Sensorless technology of switched reluctance motor based on the single threshold[J]. Journal of Hunan University: Natural Sciences, 2017, 44(2): 94-100.
[12] 张磊, 刘闯, 王云林, 等. 一种具有容错功能的开关磁阻电机初始位置估计方法[J]. 电工技术学报, 2014, 29(7): 125-132.
Zhang Lei, Liu Chuang, Wang Yunlin, et al. A fault-tolerant initial position estimation method for switched reluctance motors[J]. Transactions of China Electrotechnical Society, 2014, 29(7): 125-132.
[13] 蔡骏, 邓智泉. 基于全周期电感法的开关磁阻电机无位置传感器控制技术[J]. 电工技术学报, 2013, 28(2): 145-154.
Cai Jun, Deng Zhiquan. Sensorless control of switched reluctance motors based on full-cycle inductance method[J]. Transactions of China Electro- technical Society, 2013, 28(2): 145-154.
[14] 蔡骏, 邓智泉. 基于电感线性区模型的开关磁阻电机无位置传感器技术[J]. 中国电机工程学报, 2012, 32(15): 114-123.
Cai Jun, Deng Zhiquan. Sensorless control of switched reluctance motors based on phase inductance model in model in linear regions[J]. Proceedings of the CSEE, 2012, 32(15): 114-123.
[15] 蔡骏, 邓智泉. 基于相电感综合矢量法的开关磁阻电机初始位置估计[J]. 中国电机工程学报, 2013, 33(12): 145-151.
Cai Jun, Deng Zhiquan. Initial position estimation of switched reluctance motors based on synthetic vectors of phase inductance[J]. Proceedings of the CSEE, 2013, 33(12): 145-151.
[16] 李孟秋, 陈欣, 任修勇, 等. 基于典型位置电感的开关磁阻电机无位置传感器控制策略[J]. 中国电机工程学报, 2017, 37(13): 3901-3908.
Li Mengqiu, Chen Xin, Ren Xiuyong, et al. Sensor- less control of switched reluctance motor based on the typical positions of three-phase inductance[J]. Proceedings of the CSEE, 2017, 37(13): 3901-3908.
[17] 蒯松岩, 王鹏飞, 成静红, 等. 基于变系数电感模型开关磁阻电机四象限无位置传感器技术[J]. 电工技术学报, 2014, 29(7): 114-124.
Kuai Songyan, Wang Pengfei, Cheng Jinghong, et al. Four-quadrant sensorless technology of switched reluctance motors based on variable coefficients inductance model[J]. Transactions of China Electro- technical Society, 2014, 29(7): 114-124.
Sensorless Control Method for Switched Reluctance Motors Based on Locations of Phase Inductance Characteristic Points
Abstract A method for estimating the rotor position angle of a switched reluctance motor is proposed, using two adjacent phase inductance characteristic points. When a switched reluctance motor (SRM) appears magnetic saturation, its conduction phase inductances change with the changing conduction phase currents. The accuracy of estimating rotor position using the traditional phase inductance method is susceptible to the influence of magnetic saturation. Therefore, this paper proposes a sensorless position control method for SRM based on the locations of characteristic phase inductance points. The function is established for the phase inductance of an SRM versus its position. The method for determining the non-saturated section of the phase inductance curve is explained. The concept of the characteristic inductance points is presented, and the realization method of estimating the rotor angle of the motor is analyzed. Finally, the feasibility of the proposed method is verified by simulation and experiment.
keywords:Switched reluctance motor, inductive unsaturated zone, location point, position estimation
中图分类号:TM352
DOI: 10.19595/j.cnki.1000-6753.tces.191077
长株潭国家自主创新示范区专项(2017XK2303)和湘潭市科技专项(CXY-ZD20172001)资助项目。
收稿日期 2019-08-27
改稿日期 2019-10-12
匡斯建 男,1992年生,硕士研究生,研究方向为电力电子与电力传动。E-mail: 826037796@qq.com
张小平 男,1966年生,博士,教授,硕士生导师,研究方向为电力电子与电力传动、智能控制等。E-mail: zxp836@163.com(通信作者)
(编辑 陈 诚)