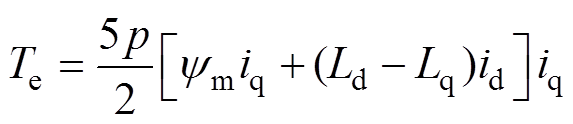（1）摘要 为了解决传统最大转矩电流比（MTPA）控制方法中高频信号注入不够灵活的难题，该文提出一种频率可变型内嵌式永磁同步电机（IPMSM）MTPA控制方法。该方法通过在空间矢量脉宽调制（SVPWM）中改变各电压矢量的作用时间，产生频率可变的高频信号，并将其直接注入到逆变器中实现MTPA。由于该方法是在SVPWM算法中实现的，所以注入信号的频率随着电机转速的变化而改变，使得信号频率的选择更加灵活。同时，由于信号直接注入到逆变器中，使注入信号的频率不干扰电机中的固有谐波且不受转速、电流环的带宽限制。实验和仿真结果表明，该方法能准确地跟踪MTPA点，并且对转矩和速度变化具有较强的鲁棒性。
关键词：内嵌式五相永磁同步电机 空间电压矢量信号调制 最大转矩电流比控制 频率可变型信号注入
内嵌式永磁同步电机（Interior Permanent-Magnet Synchronous Motor, IPMSM）由于转矩密度高、调速区域宽与功率密度高等优势[1-3]，已逐渐成为工业应用领域中不可或缺的一类电机。IPMSM因其转子磁路结构不对称，而产生磁阻转矩。同时，最大转矩电流比（Maximum-Torque-Per-Ampere, MTPA）控制可充分利用这部分磁阻转矩，进而使电机的转矩输出能力和系统效率都得到最大程度的优化。所以在IPMSM的控制方法中，MTPA已成为最常采用的控制策略[4-6]。
现有的MTPA控制方法主要分为两种：一种是依赖参数的MTPA，包括查表法和公式法[7-9]。查表法被广泛应用于实际工程应用中，该方法通过转矩方程将不同转矩下所对应的d、q轴电流绘制成表，用在线查表的方式给定MTPA电流值，但这需要大量时间来进行离线测试且会占用控制芯片的大量存储空间；公式法利用电机的模型及参数，通过对转矩方程求导并令其等于零，从而计算出MTPA控制时所对应的定子电流角，但电机的参数会受磁饱和、温度等因素的影响，所以这种方法的精度较差且计算量大。另一种是不依赖参数的MTPA方法。其中，最典型的是高频辅助信号注入法，该方法一般在电流中注入高频信号，通过响应信号的变化找到MTPA点，但传统的高频信号注入法在变负载或变速时跟踪性能会下降。文献[10-11]通过将高频小幅值扰动信号注入到电流角中，在机械功率响应信号中提取出反应转矩变化信息的信号，再经过高频信号处理过程找到MTPA对应的定子电流角。在文献[12]中，提出了一种基于极值搜索算法的MTPA方法。由于MTPA点是恒转矩曲线上唯一的极小值，由此构造出一个关于电流幅值的目标函数并对其进行极值分析，找到MTPA点，但该搜索算法的收敛时间较长。文献[13]在定子磁链同步坐标系上提出了一种考虑磁饱和效应的数学模型来实现MTPA控制，同时也提出了一种确定模型参数的方法。而文献[14-15]改进了信号注入的方式，提出了一种虚拟信号注入的方法，通过注入一个虚拟高频小幅值信号跟踪MTPA点，该方法不依赖电机参数且不向电机中注入任何实际信号，避免了实际信号注入带来的损耗增加等问题。文献[16]将虚拟信号注入技术扩展至无位置MTPA控制下，通过定义一个虚拟q轴电感值，同时实现IPMSM的无传感器MTPA控制，并提出了一种基于虚拟信号注入的高频信号处理技术，用于准确跟踪虚拟q轴电感的变化。然而，由于在电流矢量中注入的高频信号没有考虑d轴的交叉耦合效应，则会导致最终结果的准确性受到影响。在以上通过信号注入来实现MTPA的控制方法中，都必须适当选择注入信号的频率。因此，这些方法的性能会受到诸如位置/速度传感器等硬件的限制[17-20]。文献[21]中，将信号直接注入逆变器中来控制电机，本质上是一种开环注入方式，可以忽略电流内环的带宽限制及调制效果。与目前的MTPA控制方法相比，它具有高精度、参数独立、易于实现等优点。然而，在宽调速场合，因其只注入固定频率的信号会导致MTPA跟踪精度下降。
为了解决上述问题，本文将信号注入与空间矢量脉宽调制（Space Vector Pulse Width Modulation, SVPWM）方法进行结合，提出一种频率可变型MTPA控制方法。在该算法中，注入高频信号的频率与电机运行频率呈倍数关系。因此，无论转速如何变化，注入的高频信号都不会干扰电机的基波电流。此外，通过将可变频率信号注入的算法固化到SVPWM中，增加了算法的可靠性和灵活性，可根据不同的转速范围选择不同的频率注入，也可将注入信号的频率控制在一个合适的范围内。
当不考虑磁饱和效应时，IPMSM在d-q轴同步坐标系下的转矩方程为
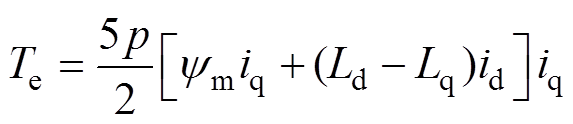（1）其中
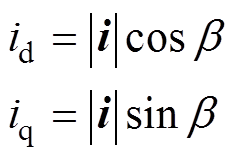
式中，id、iq分别为d、q轴定子电流；Ld、Lq分别为d、q轴定子电感；ym为永磁磁链；p为电机极对数；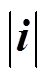
为定子电流的幅值；b 为定子电流角。
在稳态输出转矩确定的条件下，都有能够满足其要求的d、q轴电流组合。但对于MTPA点来说，所对应的只是电流幅值最小的点，可将其转化为如下的极值问题，即
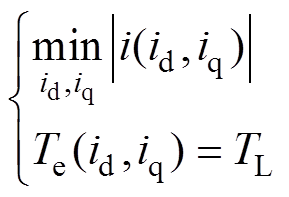（2）理论上，通过转矩表达式（1）和电机参数的标称值，可以预先计算出不同的负载转矩TL在MTPA控制时所对应的d、q轴电流。但由于电机参数会随着环境的变化而改变，则无法保证该类方法的准确度。
图1所示为在dq轴同步坐标系中定子电流矢量、定子电压矢量和定子磁链矢量的相位关系。IPMSM可被视作感性负载，即电压矢量超前于电流矢量，忽略电阻的影响，认为电压矢量超前磁链矢量90°，同时由于定子磁链矢量角d 与定子电流矢量角b 之间偏差小于90°（b -d＜90°
，则在输出转矩稳定的情况下，定子电流角与磁链幅值的变化是相反的，即
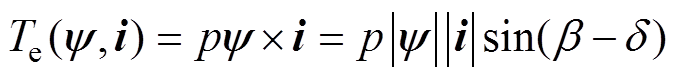（3）式中，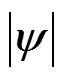
、d 分别为定子磁链的幅值与角度。
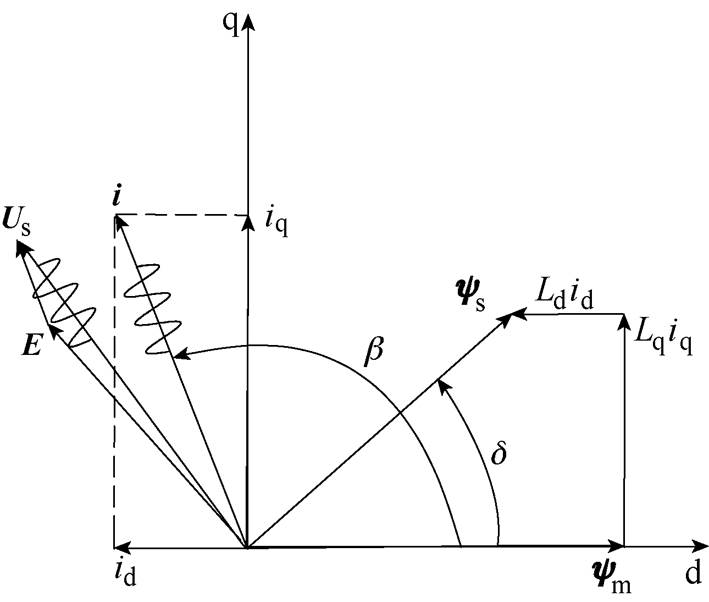
图1 同步旋转坐标系矢量控制
Fig.1 Vector control in synchronous rotating reference frame
图2所示为恒转矩条件下电流幅值与电流角之间的关系，从图2中看出，电流幅值具有唯一的极小值。同时，在B点处，即MTPA点，定子电流幅值最小；相应地，A、C两点分别为定子电流角小于MTPA角和大于MTPA角的情况。在A点附近，磁链幅值具有与电流幅值相同的变化趋势，在C点附近，它们具有相反的变化趋势。而只有在MTPA点处，无论磁链幅值如何变化，电流幅值均增大。
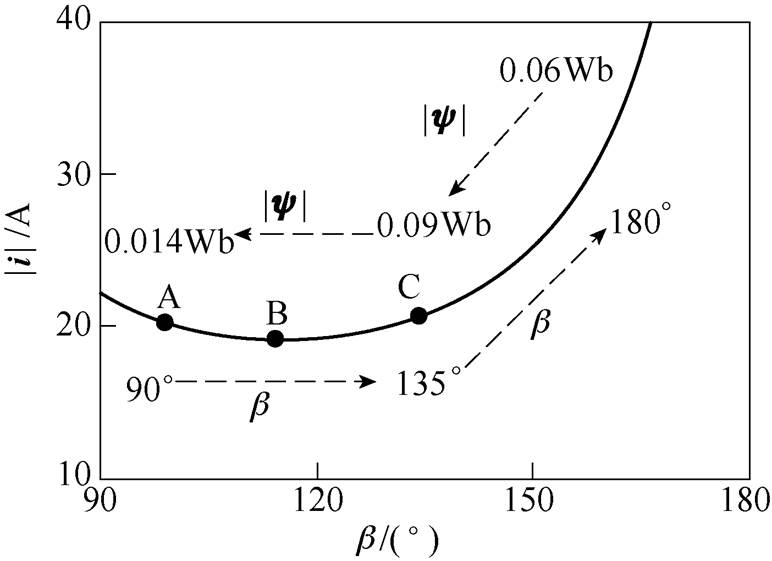
图2 恒转矩曲线上电流幅值与电流角的关系
Fig.2 Relationship between current amplitude and current angle on constant torque curve
从图2可得到定子磁链幅值与定子电流幅值之间的关系为
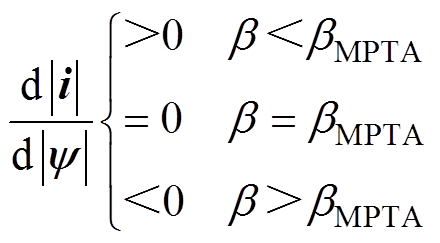（4）式（4）即可用做MTPA的判据，来实现MTPA点跟踪。
本文通过改进后的SVPWM将高频信号注入电压矢量中，实现可变频率的信号注入。基波空间平面电压矢量合成如图3所示，在五相电压源逆变器中，共有32个空间矢量，这些矢量在基波电压子平面与3次谐波子平面均有相等的大矢量、中矢量、小矢量和零矢量，其中包括30个非零矢量和2个零矢量，三组矢量的幅值比为1.6182
1.6181。在中矢量与大矢量的作用时间比为0.618时，谐波子平面的谐波电压合成分量为零。这些矢量将空间分为10个扇区，在最常用的相邻最近四矢量SVPWM矢量合成方法中，通常在一个扇区中选择中矢量、大矢量及零矢量共6个矢量来合成参考矢量，一般将两个中矢量合成的电压矢量与两个大矢量合成的参考矢量相叠加，即为所需要的目标矢量。
以第一扇区为例，参考式（5），对参考电压矢量信号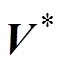
进行采样，采用频率为fs（Ts=1/fs），两个中矢量V16与V29的作用时间分别为TM1与TM2，两个大矢量V25的V24的作用时间分别为TL1和TL2，且大矢量的作用时间与中矢量的作用时间之比为1.618。
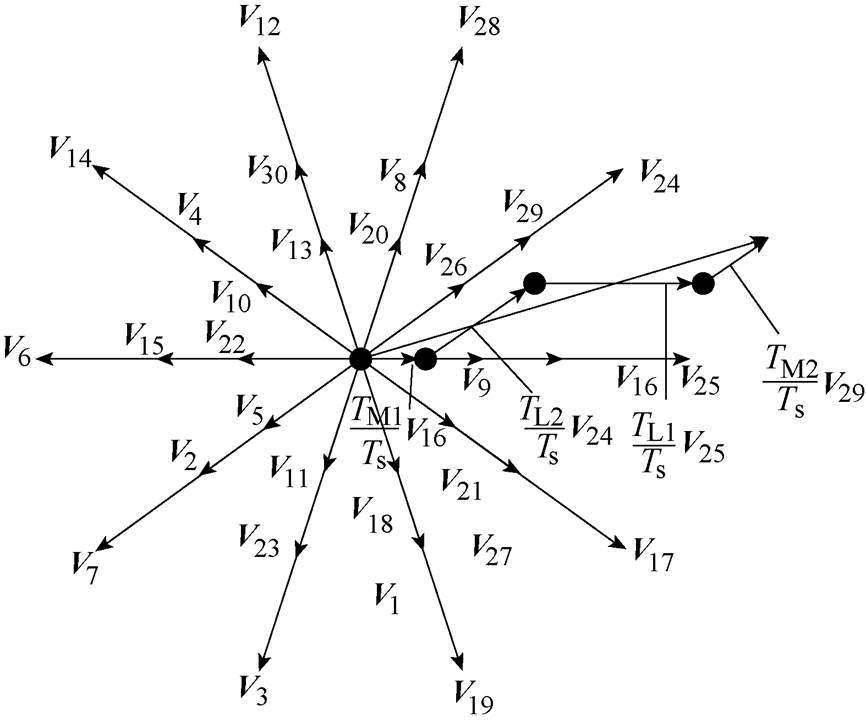
图3 基波空间平面电压矢量合成
Fig.3 Synthesis of voltage vector in fundamental space
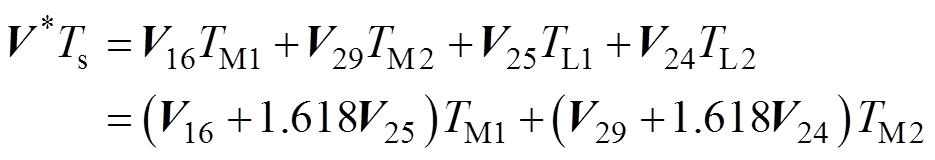（5）由式（5）可以看出，通过改变中矢量的作用时间即增大TM1或减小TM2，能够给参考电压矢量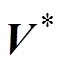提供一个矢量相位的滞后；同理，减小TM1或增大TM2，能够给参考电压矢量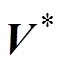提供一个矢量相位的超前。因此，在各个扇区中分别对相邻两个中矢量的作用时间进行调制，可以在电压矢量角度中注入一个扰动信号，即
（6）其中
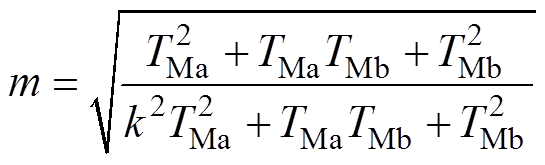
式中，TMa、TMb为各扇区中相邻两个中矢量的作用时间；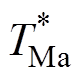
、
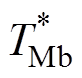为对其进行调制过后的作用时间；k为增益系数，用来改变注入信号的幅值；m为一个比例系数，目的是维持电压矢量的幅值不变，否则会改变外部注入信号的准确性。
改变相邻矢量作用时间使参考矢量相位超前如图4所示，在每个扇区中的前半部分，增加TMa同时减少TMb，即在每个扇区的前半部分使参考电压矢量的相位超前；在后半部分减小TMa同时增加TMb，即在每个扇区的后半部分使参考电压矢量的相位滞后，通过电压矢量相位在扇区中的不断变化产生扰动信号。
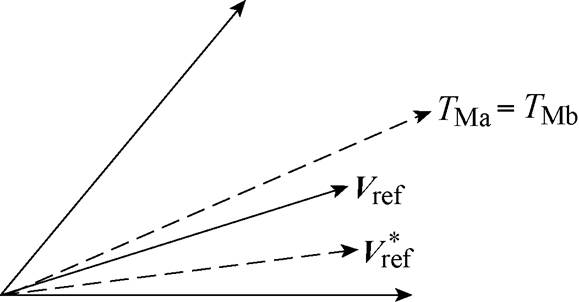
图4 改变相邻矢量作用时间使参考矢量相位超前
Fig.4 Adjust the adjacent vector action time to make the reference vector phase ahead
通过这种方式可得到如图5所示的信号注入前后ab 轴电压波形，图5中，实线为信号注入前的Va、Vb 波形，点画线为信号注入后的Va、Vb 波形。从图中可以看出，注入信号后的电压曲线与注入前相比，出现了明显的周期性波动。而且由于参考电压矢量在10个扇区中旋转，因此，形成一个10倍电周期的波动，其频率为基波电频率的10倍。以此类推，在每隔两个扇区对V16、V8、V4、V2、V1共五个中矢量进行作用时间上的改变，可实现一个周期内5次波动，即5倍于基波电频率的变频；同样地，改变V16、V6与单独改变V16可分别实现2次波动与1次波动，即2倍变频与1倍变频。因此，针对不同的速度，可选择不同频率的注入信号，有利于提升跟踪精度。
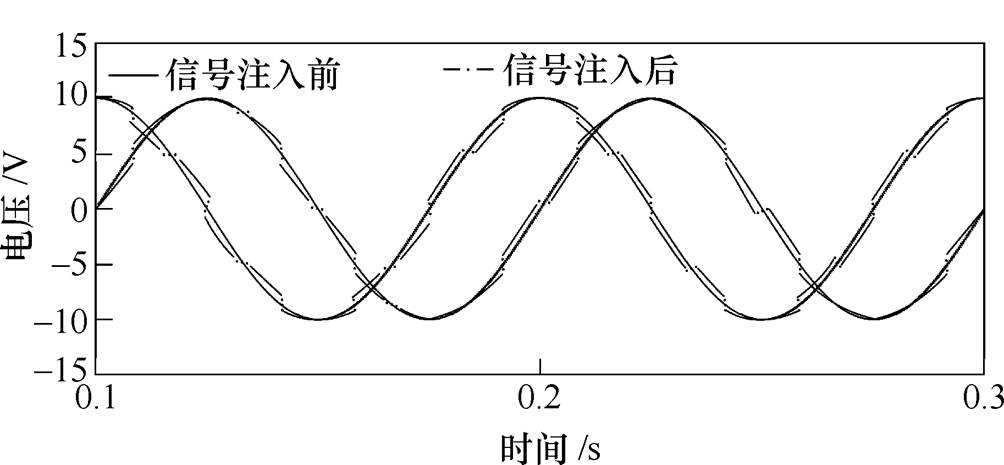
图5 信号注入前后电压波形
Fig.5 Waveforms of voltage before and after signal injection
经过变频SVPWM算法作用后，电压矢量会产生一个高频信号，由上述分析可知，磁链矢量中会出现一个相应的高频信号。电机在恒转矩运行时，磁链角d 与电流角b 的变化都会导致磁链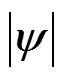幅值与电流幅值的相应变化。
值得注意的是，注入信号的幅值应足够小，以保证注入信号不引起速度或者转矩的脉动。在本文中，增益系数k=1.3，且电压角变化的幅度控制在4.5°左右。如果效果不明显，可将k增大到1.5。由于电压矢量直接由逆变器调制不经过控制回路，则理论上注入信号的频率仅仅受逆变器开关频率的限制。同时，因控制过程中需要始终保证3次谐波最小，因此3次谐波产生的转矩可忽略不计，变频算法只作用于基波平面。
对高频信号的处理模块如图6所示，利用改进后的SVPWM改变电压矢量作用时间使其波动，使得磁链形成相同的波动，从而形成主动的注入信号，不需要对磁链信号进行滤波和计算，其表达式为
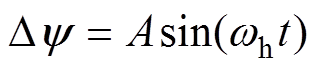（7）式中，Dy 为高频磁链扰动信号；A为所注入的高频信号的幅值；wh为所注入的高频信号的频率。
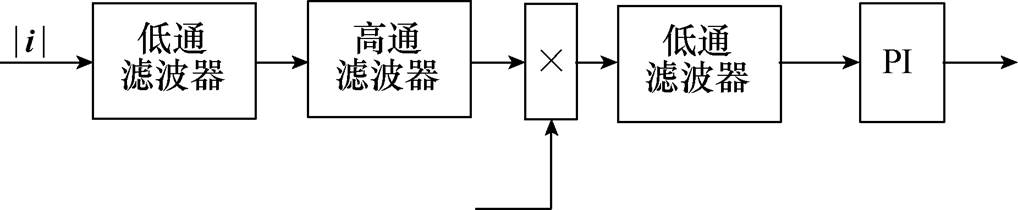
图6 信号处理模块
Fig.6 Schematic of the MTPA detector
在电流幅值处的扰动可经过泰勒展开为
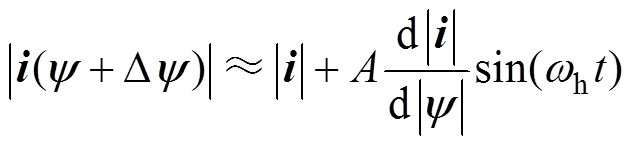（8）将其依次通过一个时间常数为TLPF的一阶低通滤波器和一个时间常数为THPF的一阶高通滤波器后，从电流幅值中提取出与wh相关的特定频率的信号，乘以Dy 可得
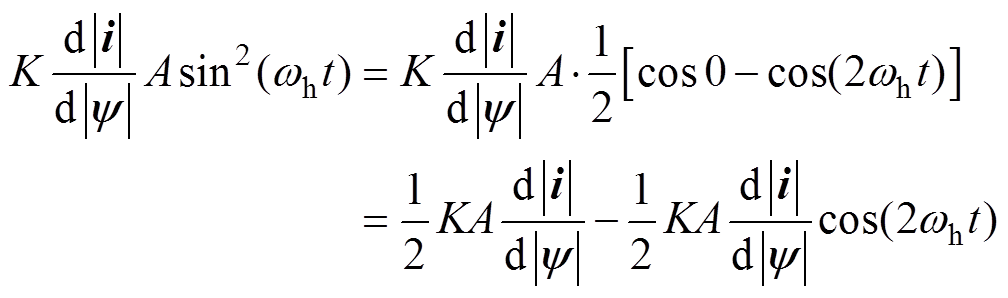（9）
式中，K为带通滤波器在wh处的增益系数。
将式（9）中的结果通入截止频率为wh的一阶低通滤波器中，可提取出所需要的信号即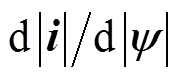
，记其为MTPA因子e。将其送入纯积分器中可得到MTPA角。积分器中时间常数的选取将影响最终输出值的收敛速度和波动情况。
图7给出了所提出的MTPA跟踪方法的IPMSM驱动控制策略。图7中，速度控制回路与电流控制回路为传统的双闭环控制。速度控制回路输出电流幅值的大小，参考定子电流矢量角度由MTPA控制策略获得。
图7 所提出的MTPA追踪方法的控制策略
Fig.7 Control scheme with proposed MTPA tracking method
为了验证所提出算法的合理性和正确性，结合电机设计参数，根据图7利用Matlab搭建电机的仿真模型，进行仿真验证。
图8给出了在400r/min及4N·m负载转矩下，电机电流幅值、MTPA因子及电流角的仿真结果。从图8中可以看出，在电流幅值最低处达到MTPA点，当b＜bMTPA时，MTPA因子为正；b＞bMTPA时，MTPA因子为负，这与理论分析式（4）相符合。
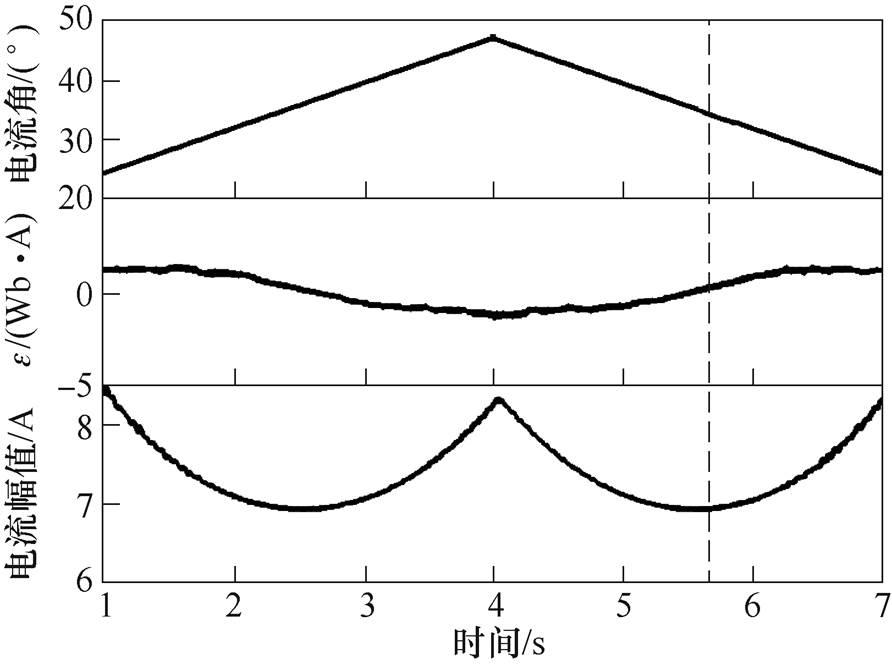
图8 电流幅值、MTPA因子与电流角在400r/min及4N·m负载转矩下的波形
Fig.8 Waveforms of current amplitude, MTPA criterion value, and current angle at 400r/min and 4N·m load torque
图9为转速200r/min、负载转矩为3N·m时，在5s处由id=0控制向MTPA控制切换的电流与磁链仿真结果。从图9中可以看出，在采用该方法实现MTPA后，相电流幅值从6.3A下降到5.6A，由于此时为10倍频信号注入，则扰动信号使磁链在一个电周期内有10次波动。
为了进一步证明所提出的方法对MTPA点跟踪精度的准确性，电机运行在400r/min、4N·m时，电流角从0°手动调整到45°，然后在6s时加入频率可变型信号注入算法，其结果如图10所示。从图10中可以看出，所提出的方法寻找的MTPA控制时对应的定子电流角为33.3°，与实际的MTPA角32.8°只相差0.5°，跟踪性能良好。
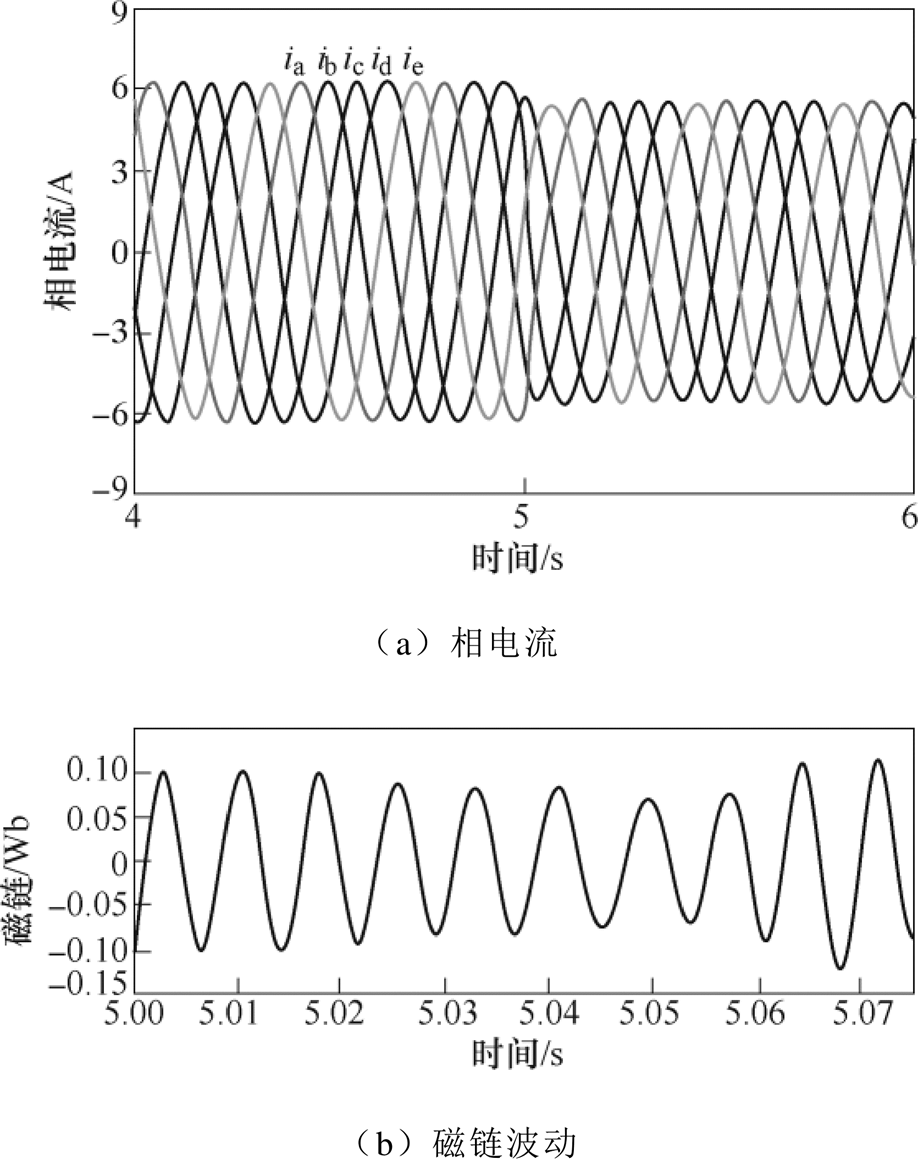
图9 变频信号注入方式的仿真结果
Fig.9 Simulation results of variable frequency signal injection method
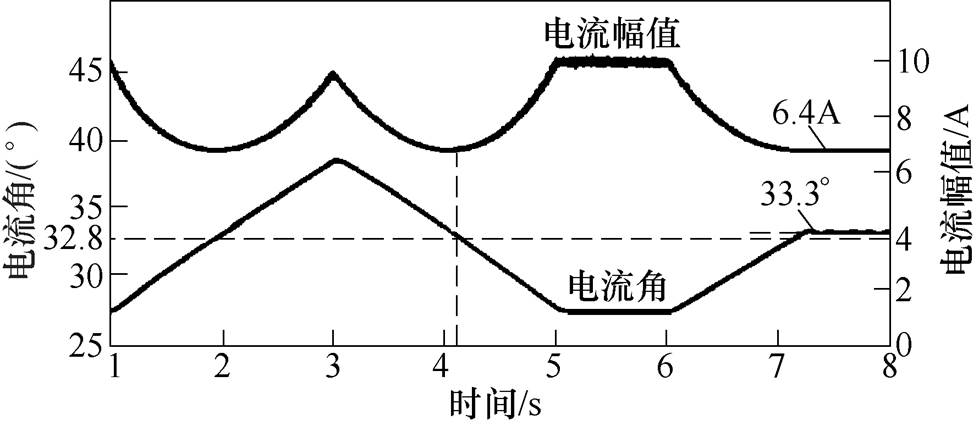
图10 在400r/min转速和4N·m负载转矩下的电流角与电流幅值
Fig.10 Current angle and current amplitude at 400r/min and 4N·m load torque
图11为负载转矩在8N·m下，将转速从600r/min增大到900r/min再回到700r/min的仿真结果。可以看出，当速度变化时，无论是对速度还是定子电流角，该方法的平稳性与跟踪精度都较好，这也说明了所提出的方法对转矩和速度的变化都具有鲁棒性。
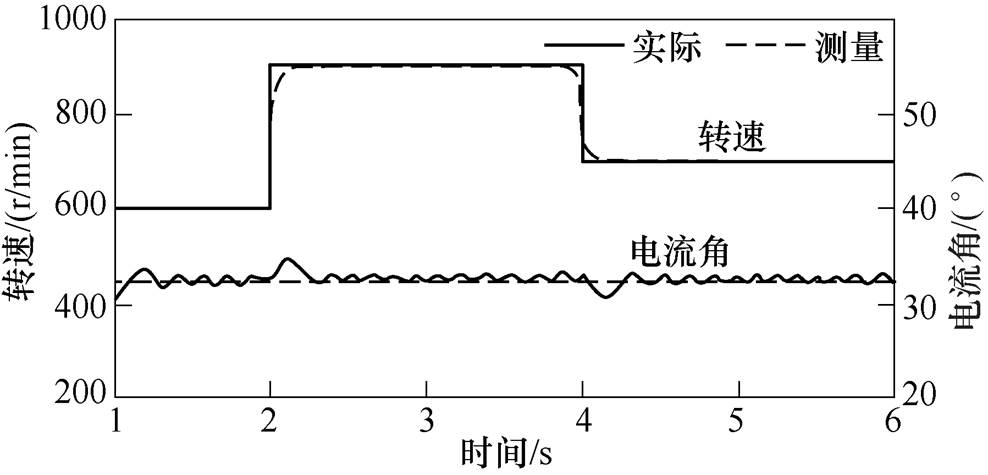
图11 速度突变时的仿真结果
Fig.11 Simulation results of speed step response
为了验证所提出的基于改进SVPWM的MTPA控制方法的可行性，搭建了如图12所示的五相IPMSM控制系统实验平台。在所构建的实验系统中，电机由磁粉制动器进行加载，转矩由高精度转矩传感器（T8-20-B4A/20NM）进行测量，由于信号注入到空间矢量，则注入信号的最大频率仅受逆变器的开关频率限制。在该实验中，逆变器的开关频率为10kHz，电流传感器的采样率为2kHz，且注入信号的频率与基波电频率呈倍数关系。其中所测试电机的参数见表1。
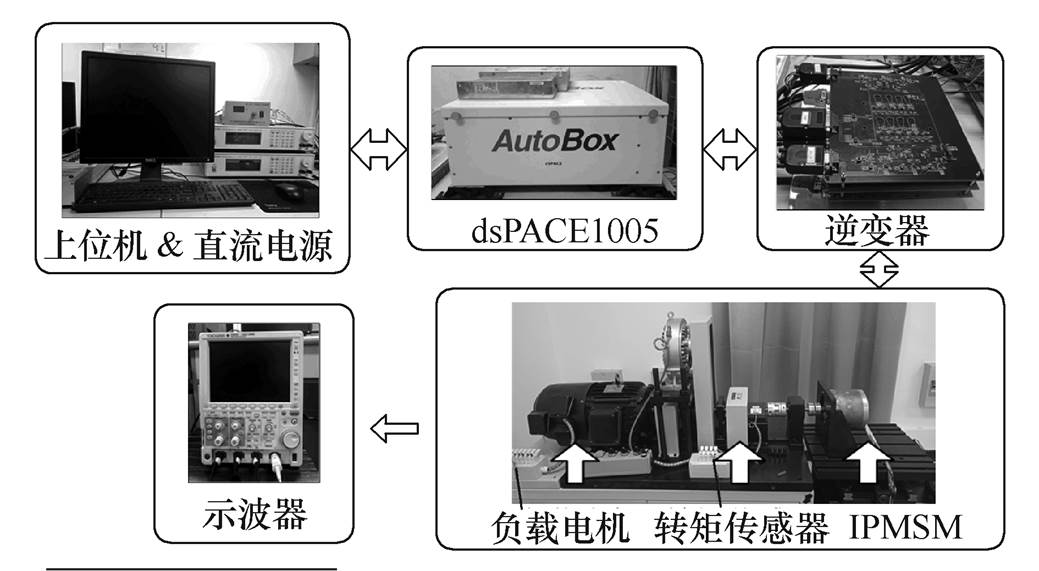
图12 五相IPMSM控制系统实验平台
Fig.12 Experiment platform of control system for FP-IPMSM
表1 内嵌式永磁同步电机参数
Tab.1 IPMSM parameters
参 数数 值 极对数4 相电阻/W0.8 d轴电感/mH17 q轴电感/mH5.3 基波永磁磁链/Wb0.111 额定转速/(r/min)1 500
在电机转速达到200r/min时，在5s处将id=0控制切换为MTPA控制，其相电流与转矩的实验结果如图13所示。由图13可以看出，在输出转矩恒为3N·m的情况下，相电流由6.3A下降到5.3A。说明所提出的方法可以在负载突变的情况下实现MTPA。
为了在实验中更好地证明跟踪性能，在电机运行于转速400r/min和负载转矩4N·m工况下，手动将电流角由0°调整到45°，40s后加入频率可变型MTPA算法，结果如图14所示。由图14可以看出，理论计算值的MTPA点电流幅值与角度分别为7A和33.2°，而实验最终稳定的电流幅值与角度分别为6.8A和33.9°。MTPA电流角相差仅0.7°，说明该方法能够很好地跟踪MTPA点。
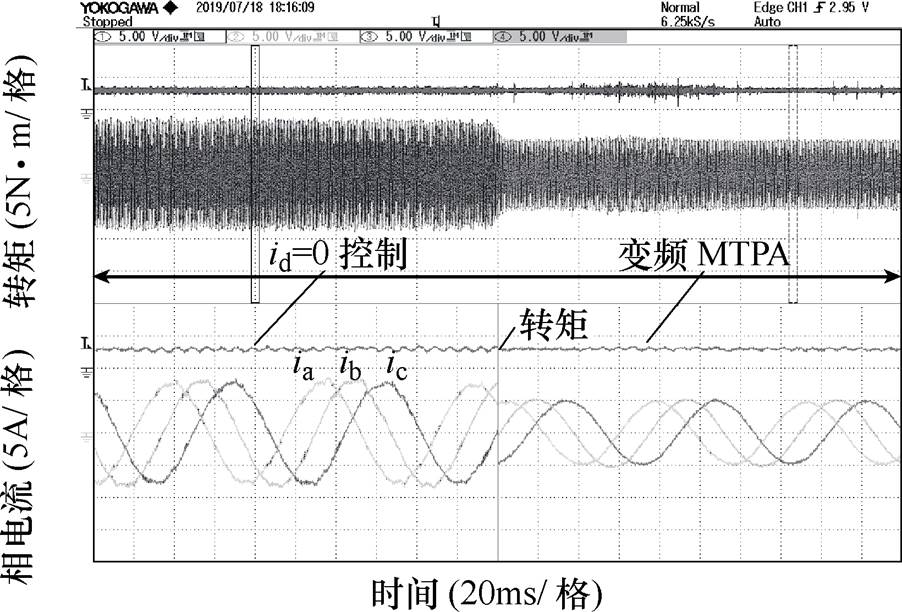
图13 所提出的方法跟踪MTPA点效果
Fig.13 Exact MTPA points and proposed MTPA tracking results
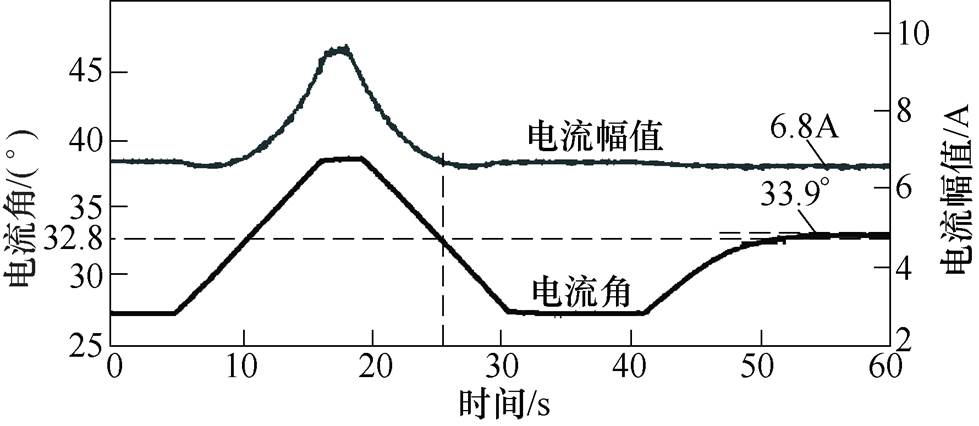
图14 在400r/min转速和4N·m负载转矩下的电流角与电流幅值
Fig.14 Current angle and current amplitude at 400r/min and 4N·m load torque
图15为转速从300r/min到600r/min突变时，该方法对转速跟踪与d轴电流变化的实验结果。其中d轴电流恒为-4.8A，且在变速时有一个小的波动后很快恢复。可以看出，所提出方法不仅实现了MTPA控制，同时在转速突变时具有较强的鲁棒性。
图16为电机转速为200r/min时，在所提出的算法作用下，转矩由3N·m突减至2N·m的相电流波形。由图16可以看出，电流由5.2A下降到3.6A，且响应速度较快，说明该算法在转矩变化时具有较好的鲁棒性与快速性。
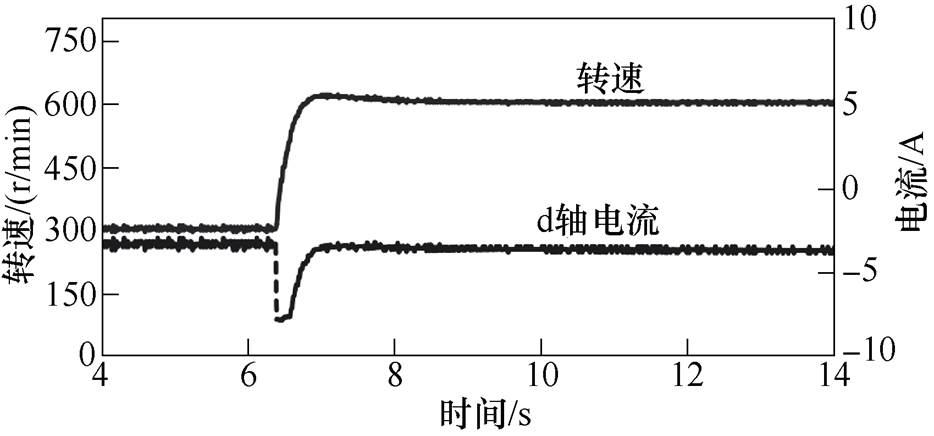
图15 转速突变时的实验结果
Fig.15 Experimental results of speed step response
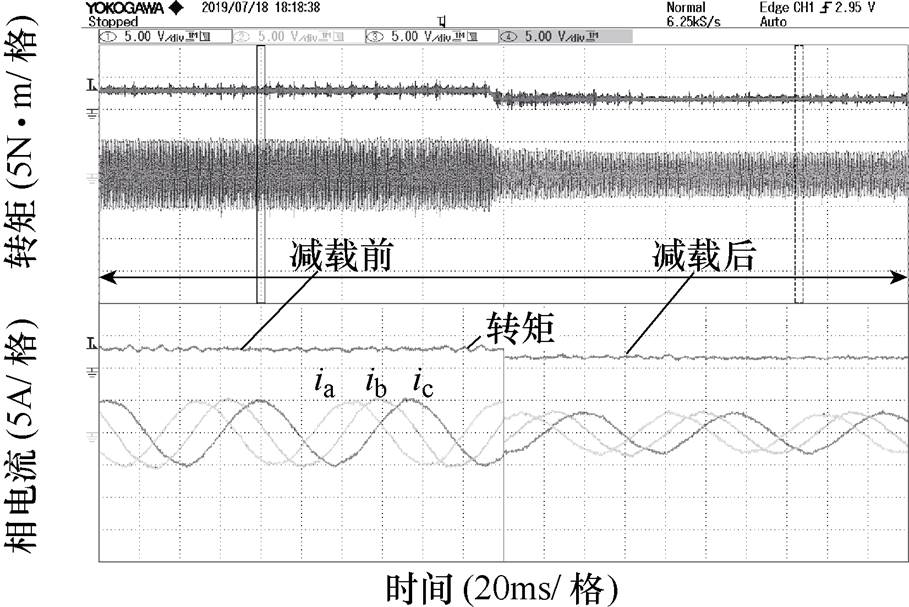
图16 转矩突变时测量相电流幅值的变化
Fig.16 Measured phase current amplitude and torque response to a step load torque change
本文在基于SVPWM的基础上，提出了一种能够在线跟踪MTPA点的频率可变型信号注入方法。该方法通过改变空间电压矢量的作用时间实现倍频信号注入，对定子电流与磁链中的响应信号进行采样和分析，从而实现MTPA控制。与一般的高频信号注入方法相比，频率可变型信号注入方式与电机转速相关，同时所注入的高频信号与电机中的固有信号不发生相互作用，该方法不仅简化了系统结构，而且易于实现。本文对该方法进行了仿真与实验验证，结果表明，该方法能够在不依赖电机参数的情况下对MTPA点进行较好的跟踪，并且在不同工况下具有较强的鲁棒性。
参考文献
[1] 刘自程, 李永东, 郑泽东. 多相电机控制驱动技术研究综述[J]. 电工技术学报, 2017, 32(24): 17-29.
Liu Zicheng, Li Yongdong, Zheng Zedong. Control and drive techniques for multiphase machines: a review[J]. Transactions of China Electrotechnical Society, 2017, 32(24): 17-29.
[2] 毛亮亮, 王旭东. 一种新颖的分段式优化最大转矩电流比算法[J]. 中国电机工程学报, 2016, 36(5): 1404-1412.
Mao Liangliang, Wang Xudong. Research on a novel segmented optimum maximum torque per ampere algorithm[J]. Proceedings of the CSEE, 2016, 36(5): 1404-1412.
[3] Hu Yihua, Gan Chun, Cao Wenping, et al. Flexible fault-tolerant topology for switched reluctance motor drives[J]. IEEE Transactions on Power Electronics, 2016, 31(6): 4654-4668.
[4] Ahn Kukhyun, Bayrak Alparslan Emrah, Papalambros Panos Y. Electric vehicle design optimization: inte- gration of a high-fidelity interior permanent magnet motor model[J]. IEEE Transactions on Vehicular Technology, 2015, 64(9): 3870-3877.
[5] Patel Vipulkumar I, Wang Jiabin, Nugraha Dian Tresna, et al. Enhanced availability of drivetrain through novel multiphase permanent-magnet machine drive[J]. IEEE Transactions on Industrial Electronics, 2015, 63(1): 469-480.
[6] 刘璐, 杜旭东, 王晓年. 考虑磁饱和的感应电机MTPA转矩控制[J]. 电工技术学报, 2017, 32(23): 42-50.
Liu Lu, Du Xudong, Wang Xiaonian. MTPA torque control of induction on motor considering magnetic saturation[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 42-50.
[7] 王伟, 王淑红, 张一博, 等. 内置式永磁同步电动机弱磁控制策略的研究[J]. 西北工业大学学报, 2018, 36(5): 970-977.
Wang Wei, Wang Shuhong, Zhang Yibo, et al. Study on magnetic flux weakening control strategy of interior permanent magnet synchronous motor[J]. Journal of Northwestern Polytechnical University, 2018, 36(5): 970-977.
[8] Hoang Khoa Dang, Aorith Hawa K A. Online control of IPMSM drives for traction applications con- sidering machine parameter and inverter nonlin- earities[J]. IEEE Transactions on Transportation Electrification, 2015, 1(4): 312-325.
[9] 李峰, 夏超英. 考虑磁路饱和的IPMSM电感辨识算法及变参数MTPA控制策略[J]. 电工技术学报, 2017, 32(11): 136-144.
Li Feng, Xia Chaoying. Inductance identification algorithm and variable-parameters MTPA control strategy for IPMSM considering magnetic circuit saturation[J]. Transactions of China Electrotechnical Society, 2017, 32(11): 136-144.
[10] 康劲松, 王硕. 基于Newton-Raphson搜索算法的永磁同步电机变电感参数最大转矩电流比控制方法[J]. 电工技术学报, 2019, 34(8): 1616-1625.
Kang Jinsong, Wang Shuo. Newton-Raphson based searching method for variable-parameters inductance maximum torque per ampere control used for IPMSM[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1616-1625.
[11] 钟志宏, 方晓春, 林飞, 等. MTPA控制下逆变器- IPMSM系统直流侧电压稳定性研究[J]. 电工技术学报, 2017, 32(21): 34-43.
Zhong Zhihong, Fang Xiaochun, Lin Fei, et al. DC voltage stability studies with IPMSM system under the control of MTPA[J]. Transactions of China Elec- trotechnical Society, 2017, 32(21): 34-43.
[12] Antonello Riccardo, Carraro Matteo, Zigliotto Mauro. Maximum-torque-per-ampere operation of anisotropic synchronous permanent-magnet motors based on extremum seeking control[J]. IEEE Transactions on Industrial Electronics, 2014, 61(9): 5086-5093.
[13] Inoue Tatsuki, Inoue Yukinori, Morimoto Shigeo, et al. Mathematical model for MTPA control of permanent-magnet synchronous motor in stator flux linkage synchronous frame[J]. IEEE Transactions on Industry Applications, 2015, 51(5): 3620-3628.
[14] Sun Tianfu, Wang Jiabin, Chen Xiao. Maximum torque per ampere (MTPA) control for interior permanent magnet synchronous machine drives based on virtual signal injection[J]. IEEE Transactions on Power Electronics, 2015, 30(9): 5036-5045.
[15] Chen Qian, Zhao Wenxiang, Liu Guohai, et al. Extension of virtual-signal-injection-based MTPA control for five-phase IPMSM into fault tolerant operation[J]. IEEE Transactions on Industrial Elec- tronics, 2019, 66(2): 944-955.
[16] Tang Qipeng, Shen Anwen, Luo Pan, et al. IPMSMs sensorless MTPA control based on virtual q-axis inductance by using virtual high frequency signal injection[J]. IEEE Transactions on Industrial Elec- tronics, 2019, DOI: 10.1109/TIE.2018.2890487.
[17] Kim Sungmin, Yoon Young-Doo, Sul Seung-Ki, et al. Maximum torque per ampere (MTPA) control of an IPM machine based on signal injection considering inductance saturation[J]. IEEE Transactions on Power Electronics, 2013, 28(1): 488-497.
[18] 薛诚, 宋文胜, 冯晓云. 五相永磁同步电机多目标优化直接转矩控制算法[J]. 中国电机工程学报, 2016, 36(6): 1695-1704.
Xue Cheng, Song Wensheng, Feng Xiaoyun. A direct torque control algorithm of five-phase permanent- magnet machines with multi-objective optimi- zation[J]. Proceedings of the CSEE, 2016, 36(6): 1695-1704.
[19] Jung Sung-Yoon, Hong Jinseok, Nam Kwanghee. Current minimizing torque control of the IPMSM using Ferrari’s method[J]. IEEE Transactions on Power Electronics, 2013, 28(12): 5603-5617.
[20] Sun Tianfu, Wang Jiabin, Koc Mikail, et al. Self- learning MTPA control of interior permanent-magnet synchronous machine drives based on virtual signal injection[J]. IEEE Transactions on Industry Appli- cation, 2016, 52(4): 3062-3070.
[21] Liu Guohai, Wang Jian, Zhao Wenxiang, et al. A novel MTPA control strategy for IPMSM drives by space vector signal injection[J]. IEEE Transactions on Industrial Electronics, 2017, 64(12): 9243-9252.
Variable Frequency Maximum-Torque-Per-Ampere Control for Five-Phase Permanent-Magnet Motor Based on Space Voltage Vector Injection
Abstract In order to solve the problem that the high-frequency signal injection is not flexible enough in the traditional maximum-torque-per-ampere (MTPA) control method, a novel signal injection method with variable frequency is proposed. The proposed method changes the action time of each voltage vector in space vector pulse width modulation (SVPWM) to generate a variable frequency signal, and directly injects the signal into the inverter to realize the MTPA. Since the variable frequency signal injection method is implemented in SVPWM algorithm, the frequency of the injected signal changes with the motor speed, which makes the selection of the signal frequency more flexible. Additionally, since the signal is directly injected into the inverter, the frequency of the injected signal does not interfere with the inherent harmonics in the motor. Hence, the bandwidth limitations of the current loop can be eliminated. The proposed method simplifies the part of signal analysis without reducing the tracking performance of MTPA points. Finally, the experimental and simulation results show that the method can accurately track MTPA points, and has robustness to torque and speed changes.
keywords：Interior five-phase permanent-magnet synchronous motor, space-vector signal modu- lation, maximum-torque-per-ampere control, variable frequency signal injection
中图分类号：TM351; TM341
DOI: 10.19595/j.cnki.1000-6753.tces.191079
国家自然科学基金(51877098，51707083)和江苏省高校优势学科项目资助。
收稿日期 2019-08-27
改稿日期 2019-09-20
刘国海 男，1964年生，教授，博士生导师，研究方向为电动机系统及其控制，包括电气传动自动化、复杂过程的智能控制等。E-mail: ghliu@ujs.edu.cn
陈 前 男，1986年生，副教授，研究方向为永磁电动机设计与控制。E-mail: chenqian0501@ujs.edu.cn（通信作者）
（编辑 陈 诚）