
图1 磁通反向直线旋转永磁电机拓扑结构
Fig.1 Flux reversal linear rotary permanent magnet machine
摘要 该文通过在三维磁路结构中增加可变磁阻单元,建立磁通反向直线旋转永磁电机的三维非线性等效磁路模型,首先采用磁节点法推导此电机定子、动子的磁阻表达式;其次采用二维有限元法确定可变磁阻单元磁阻的变化规律,其磁阻值随动子的直线和旋转运动位置的不同从0到无穷大周期性变化;然后采用分割的方法推导电机气隙磁导的表达式;最后通过迭代的方法对其空载气隙磁通密度等电磁特性进行计算分析,与三维有限元法相比,计算时间大大降低。此模型可以将定子铁心材料的饱和、永磁的局部漏磁、极间漏磁考虑在内,其反电动势、齿槽转矩/直线定位力的计算结果与三维有限元法和实验测量的结果基本保持一致,验证了此等效磁路模型的正确性和有效性。
关键词:等效磁路模型 磁通反向直线旋转永磁电机 可变磁阻 静态特性
有限元法、解析法和磁路法是进行电机结构设计和电磁特性计算时常用的三种方法,文献[1-3]中分别采用此三种方法对游标电机的电磁性能进行计算,可以看出,在进行电磁特性分析时有限元法耗时较长,子域解析法推导过程较为复杂,磁路法耗时少、计算简单。近年来,国内外众多学者针对各种不同类型的电机提出了多种新型的磁路计算模 型[4-18]。文献[4]中建立了将永磁的端部漏磁和磁桥的局部饱和考虑在内的混合转子永磁电机的等效磁路模型,将永磁主磁路和漏磁分开,并采用迭代算法对其进行求解。根据定、转子相对位置不同时的磁场分布情况,建立了磁通切换电机[5]集中参数磁路模型,推导出其节点磁动势矩阵及电机各主要电磁参数的解析表达式并进行计算和分析。为了进行盘式横向磁通永磁无刷电机和双转子结构永磁磁阻电机结构的参数优化及电磁特性的分析,建立了变网络等效磁路模型[6-7],可以将铁心饱和及非线性考虑在内,通过对磁化曲线进行插值处理,使得铁心的磁导率为非线性,更贴合实际情况。采用分布磁路法对六相圆筒式直线感应电机的磁路进行计算,并对其饱和特性进行分析[8],在此基础上,进一步通过有限元法考虑了磁性槽楔作用下的齿槽效应,通过计及磁性槽楔作用的卡氏系数对感应电动机的分布磁路模型进行修正,对考虑磁路饱和效应的磁性槽楔感应电动机的电磁特性进行分析,计算精度与有限元数值计算相当[9]。文献[10-14]建立了轴向磁通电机、永磁同步电机、内置永磁电机、绕线型同步电机和表贴式轴向永磁同步电机的磁路模型,将结构尺寸、磁饱和、漏磁和转子位置考虑在内,并采用迭代法进行精确的计算,对其电磁特性进行了分析。针对直线旋转电机的结构特点[15],通过采用解析计算和磁路模型相结合的方法,对直线旋转电机的气隙磁场进行快速、准确的分析计算。文献[16]建立了在负载条件下,可变磁通记忆电机的等效磁路,通过对永磁负载工作线分析,其与有限元法计算的结果基本一致。针对直线磁通切换永磁电机[17]、双轴向磁通永磁电机[18]的结构特点,分别建立了三维磁路模型,通过增加可变磁阻单元,准确获取其气隙磁通密度。可见,通过采用不同的方法将定转子局部饱和、永磁体的局部漏磁、端部效应等考虑在内,建立电机的等效磁路模型,不仅可以提高计算精度,而且提升了电机结构设计及优化的效率。
磁通反向直线旋转永磁电机(Flux Reversal Linear Rotary Permanent Magnet Motor, FR-LRPMM)是典型的三维磁路结构,本文建立了一种三维非线性等效磁路模型(Equivalent Magnetic Circuit Model, EMCM),此模型在传统EMCM的基础上,添加了可变磁阻单元,首先采用二维有限元法确定了其变化规律;然后采用磁节点法推导了电机定子、动子铁心的磁阻表达式,运用分割法确定了其三维气隙磁导的表达式;最后通过建立三维非线性EMCM对其磁通分布和电磁特性进行计算分析,并制作样机。
图1为磁通反向直线旋转永磁电机的拓扑结 构[19-20],其轴向有3个相同的定子单元,通过非导磁材料连接。在旋转方向有两个电周期,在直线方向有一个电周期。在定子极的表面有两个永磁极和两个铁极交替排列,动子极在轴向错开22.5°交错排列。为了降低计算的复杂度,将定子Ⅰ单元作为本文的分析对象。

图1 磁通反向直线旋转永磁电机拓扑结构
Fig.1 Flux reversal linear rotary permanent magnet machine
定子和动子区域可以划分为定子极、定子轭部、定子齿、动子极和动子轭部。当磁路被细分为更小的单元时,每一个磁路单元都有独立的磁阻单元,图2为其一个磁阻单元,Rmr和Rmq分别为其径向和周向的磁阻分量。
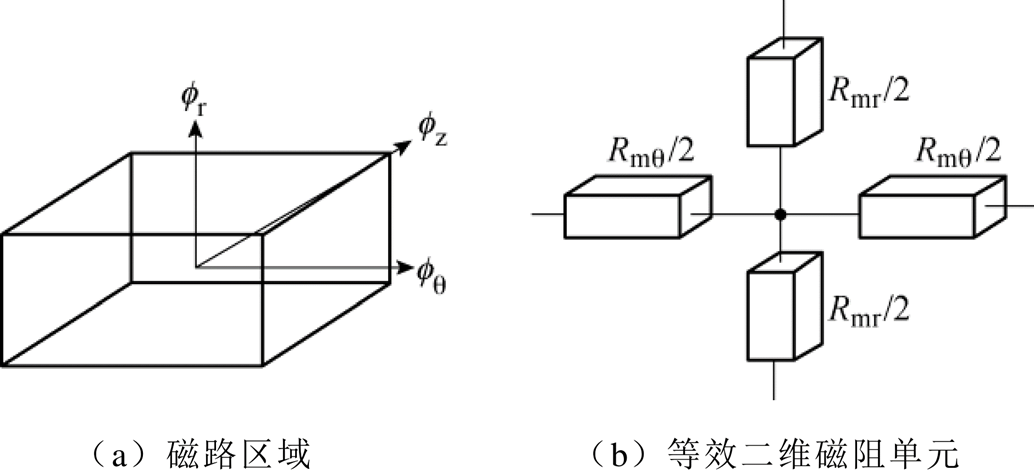
图2 磁阻单元
Fig.2 Reluctance unit
图3和图4分别为定子和动子单元的基本结构。周向和轴向磁阻的表达式分别为
 (1)
(1)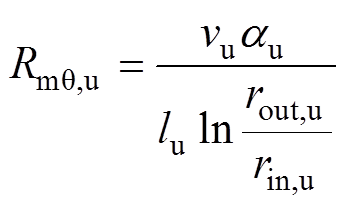 (2)
(2)
式中,vu为磁阻率;lu为电机轴向的长度;au为定动子极的弧度;rin,u和rout,u分别为内、外铁心半径。在图3 S_Ⅰ区域中:au=asⅠ,rout,u=RS_Ⅰ,rin,u=RS_Ⅱ;在S_Ⅱ区域中:au=asⅡ,rout,u=RS_Ⅱ,rin,u=RS_Ⅲ;在S_Ⅲ区域中:au=asⅢ,rout,u=RS_Ⅲ,rin,u=RS_Ⅳ。在图4 R_Ⅰ区域中:au=arⅠ,rout,u=Rr_Ⅰ,rin,u=Rr_Ⅱ;在R_Ⅱ区域中:au=arⅡ,rout,u=Rr_Ⅱ,rin,u=Rr_Ⅲ。

图3 定子单元基本结构
Fig.3 Basic structure of stator unit
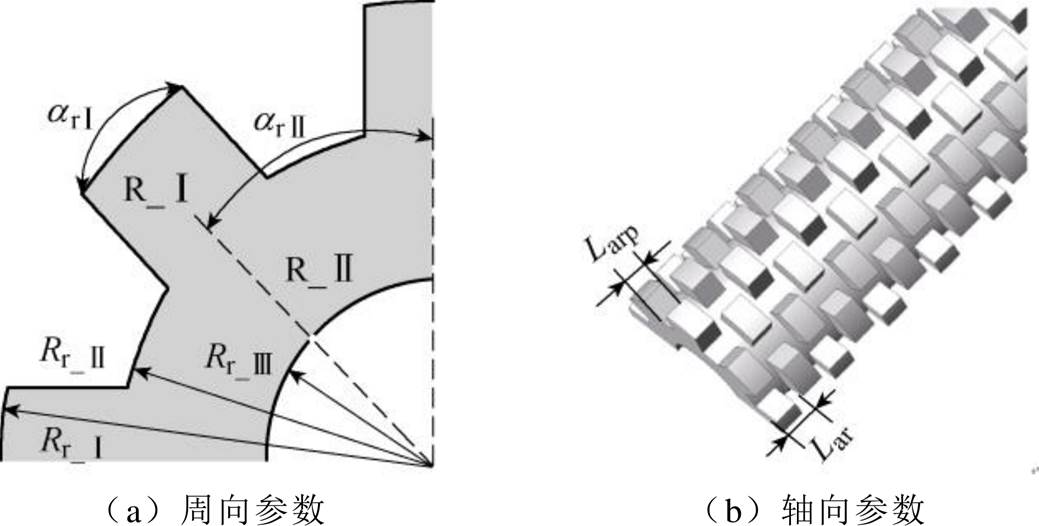
图4 动子单元基本结构
Fig.4 Basic structure of mover unit
图5为电机磁通密度云图,其中,图5a为定子永磁极和铁极的排列分布,图5b为定子永磁极和铁极的磁通密度云图,图5c和图5d分别为其定子和动子磁通密度云图。从图中可以看出,当定子极与动子极在周向的一个平面内时,在定子铁极、定子极内部和动子极上存在局部饱和现象。
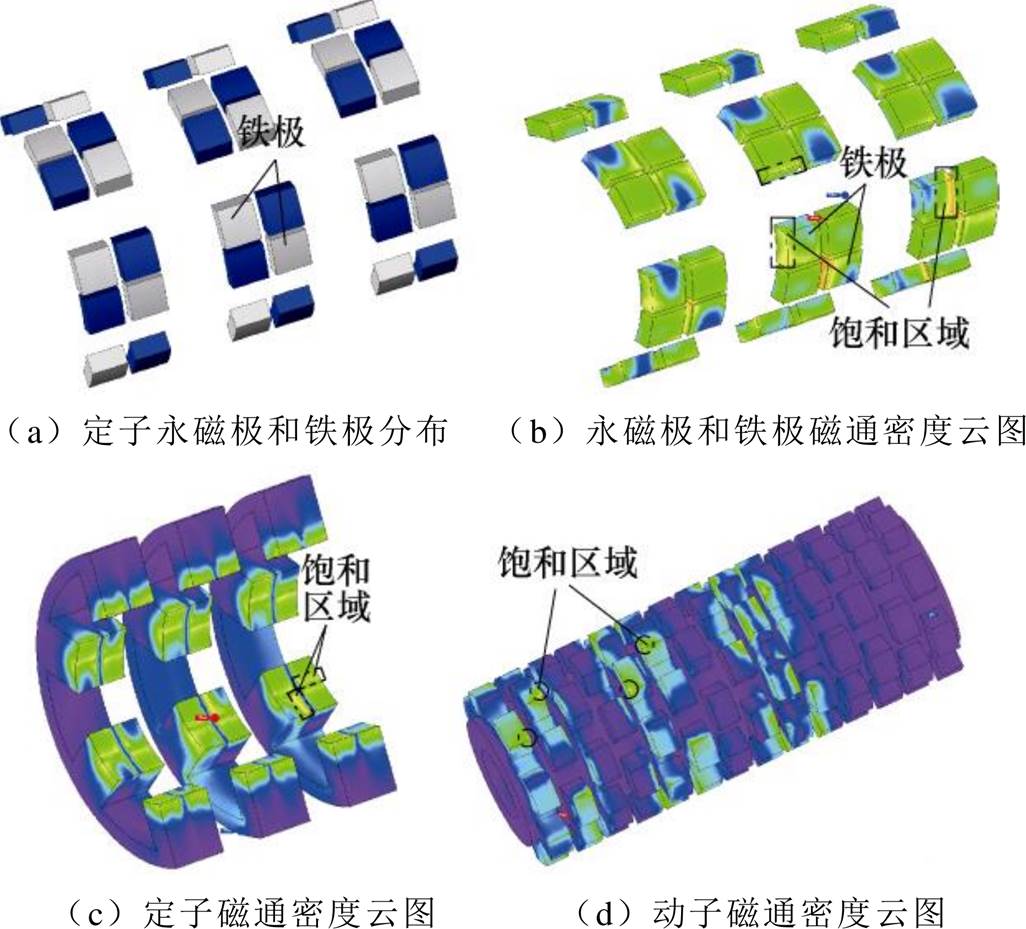
图5 电机磁通密度云图
Fig.5 Magnetic field contour distribution in the motor
由于定子极和动子极表面不是等磁势面,磁链和铁磁表面与等磁势表面不垂直,因此可以通过对其二维模型的分析,建立电机磁路模型。图6是电机的周向结构,当电机在旋转运动时定动子单元会出现饱和的区域(见图6①②③),为了减少计算时间,将旋转运动方向上一个动子极距的距离作为分析对象,分析其空载磁路和气隙磁导。图7为其单层磁通切换结构的空载等效磁路。Rsfe、Rsh、Rsy、Rpfe、Rrh和Rry分别为定子铁极、定子极、定子轭部、永磁极与铁极间漏磁阻、动子极和动子轭部磁阻,Rg为定子永磁极和动子铁极之间的局部漏磁阻,Rg1~Rg4为气隙磁阻。
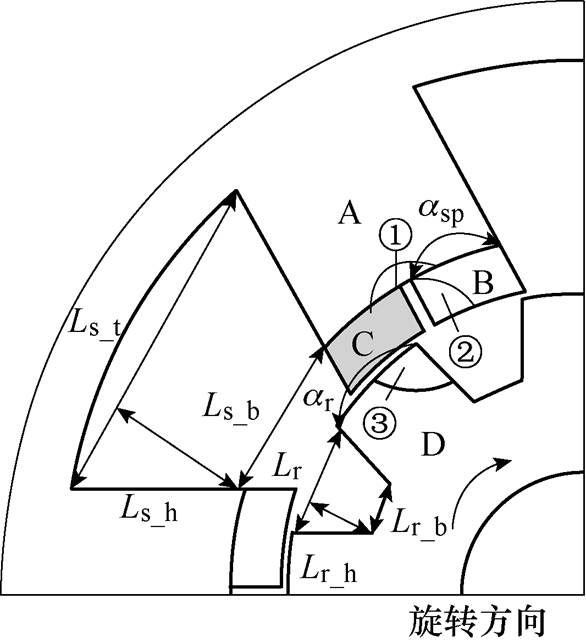
图6 定子区域模型
Fig.6 stator section model
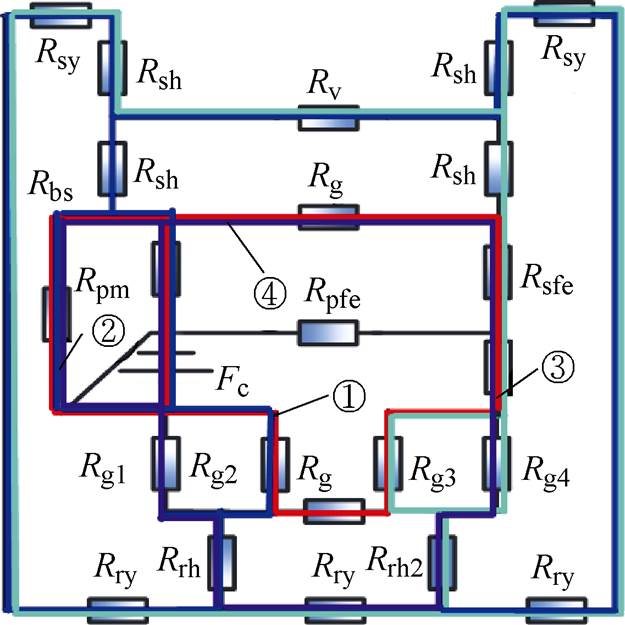
图7 空载等效磁路
Fig.7 No-load equivalent magnetic circuit
在图7中,①、②、③、④分别为定子极中心线、定子铁极中心线、定子永磁极中心线和定子槽中心线同动子极中心线一致时空载等效磁路。本文中采用磁通叠加的方法计算磁路,因此,漏磁路①、④可以作为单独分析对象计算。图8为旋转运动时一个电周期内FR-LRPMM单层磁通切换结构的EMCM,它可以将漏磁路、局部饱和及可变磁阻考虑在内。图9为FR-LRPMM单个定子极区域的三维非线性EMCM,在定子单元的周向和轴向均增加了可变磁阻单元。其中,漏磁路是由定子与动子的相对位置决定的,图8和图9中局部饱和磁阻分别为定子永磁极与铁极间的局部漏磁阻Rg、定子齿饱和磁阻(见图6 ②)和动子极饱和磁阻(见图6 ③),定子齿磁阻Rsfe、动子极磁阻Rrh分别由定子齿不饱和磁阻与定子饱和磁阻、动子极不饱和磁阻与动子饱和磁阻并联得到。
在EMCM中,定子极、定子轭部、动子极和动子轭部的磁阻为常数,气隙磁阻为非线性的,它与动子的旋转位置角a 有关,因此分别进行计算。
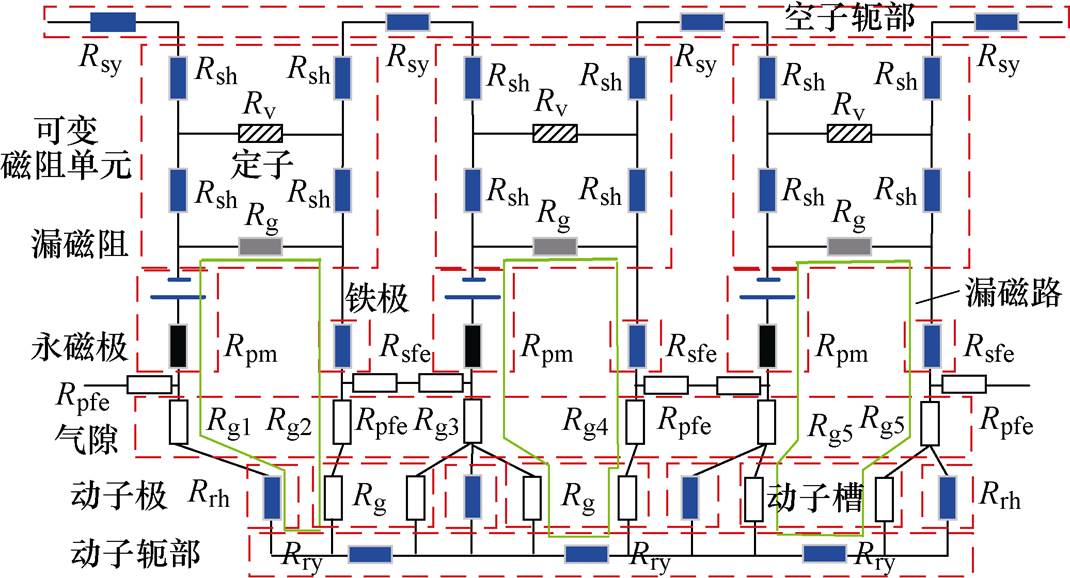
图8 非线性可变磁阻EMCM
Fig.8 Nonlinear variable reluctance EMCM
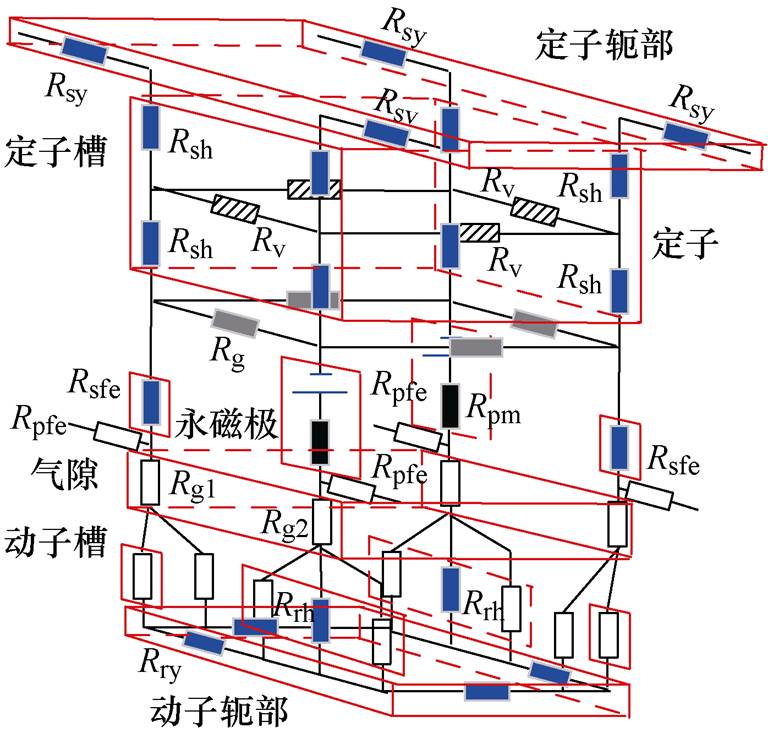
图9 单个定子极区域的三维非线性EMCM
Fig.9 3D nonlinear EMCM of a single stator pole region
永磁体等效磁动势和磁阻的表达式为
 (3)
(3)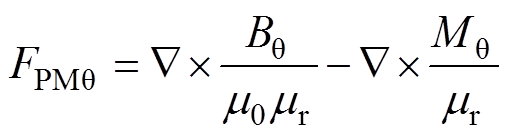 (4)
(4)
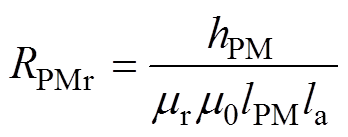 (5)
(5)
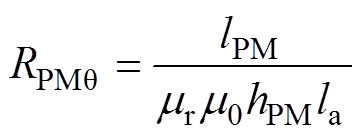 (6)
(6)式中,m0为空气的磁导率;mr为永磁体的相对磁导率;Br、Bq 分别为永磁体的径向和周向磁感应强度;Mr、Mq 分别为永磁体的径向和周向剩余磁化强度;hPM、lPM、la分别为永磁体的高、宽和轴向长度。
铁磁材料磁阻的表达式为
 (7)
(7)式中,ai为通过磁阻曲线拟合的多项式常数值;rm为磁通区域的磁阻系数;Bu为铁磁材料的磁感应强度;lj为磁通区域的长度;Aj为垂直于磁通的区域的面积。
在磁阻模型中,气隙的磁阻模型的轴向长度的表达式为
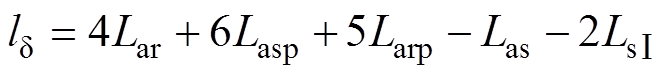 (8)
(8)式中,Lasp为定子极的轴向长度;Las为定子Ⅰ的轴向长度;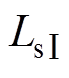 为定子Ⅰ和定子Ⅱ间的轴向长度;Larp为动子极的轴向长度;Lar为轴向极距。
为定子Ⅰ和定子Ⅱ间的轴向长度;Larp为动子极的轴向长度;Lar为轴向极距。
图9中,根据可变虚拟槽模型,饱和磁阻的径向和周向饱和磁阻的表达式[21]为
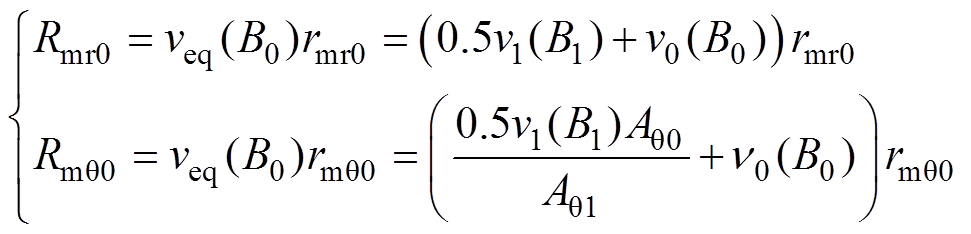 (9)
(9)式中,rmr0、rmq0分别为开口槽区域的径向和周向磁导系数。
图10为可变磁阻单元随着动子旋转位置的不同阻值的变化波形,其阻值从0到无穷大周期性变化。当动子位置处于磁链的最大值时,在位置( )处的阻值为无穷大。在旋转运动时,可变磁阻Rv的表达式为
)处的阻值为无穷大。在旋转运动时,可变磁阻Rv的表达式为
 (10)
(10)式中,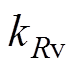 为采用有限元法确定的经验系数;n为旋转转速;p为周向极对数。
为采用有限元法确定的经验系数;n为旋转转速;p为周向极对数。
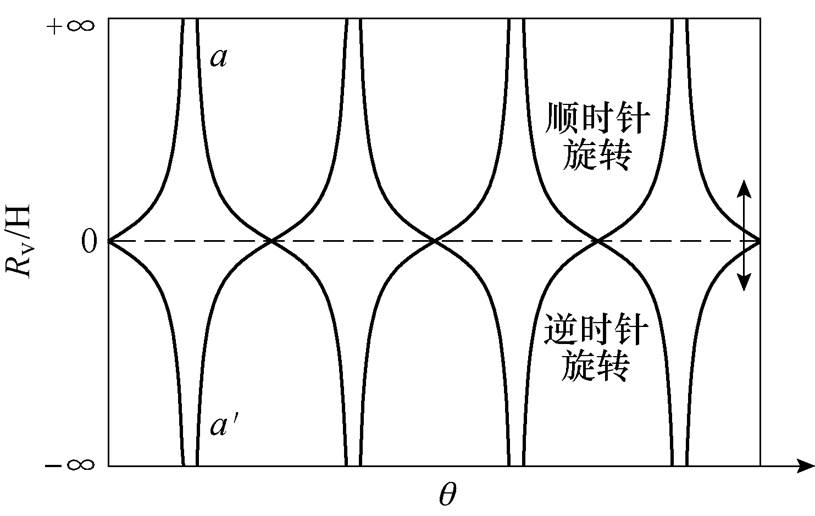
图10 可变磁阻的磁阻波形
Fig.10 Waveforms of variable reluctance
由于定子铁极和永磁极在周向和轴向的距离较小,部分磁通在铁极和永磁极上可以形成局部回路,采用许克变换可以得到局部漏磁的表达式为
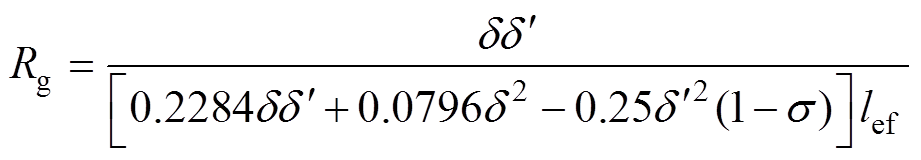 (11)
(11)其中
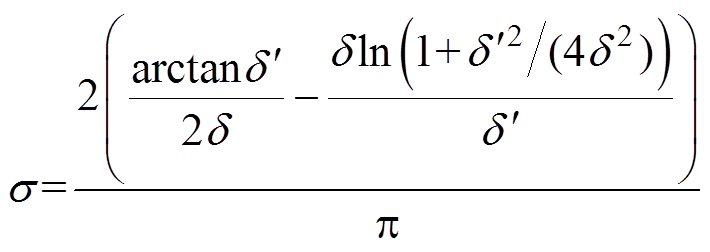
式中,d 为气隙的径向长度;在周向上,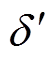 =aSⅡ- 2aS Ⅲ,在轴向上,
=aSⅡ- 2aS Ⅲ,在轴向上,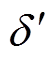 =Las-2Lasp。
=Las-2Lasp。
永磁漏磁阻的表达式为
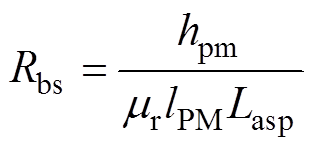 (12)
(12)由于永磁体材料位于定子极的表面,定子槽对气隙磁场的影响比动子槽对气隙磁场的影响小。图11是定子和动子极的相对位置结构。由于气隙磁路随着动子位置的不同而改变,根据定子极中心线和动子极中心线的角度不同将其一个动子极距范围划分为a到b,b到c,c到d,d到e,e到f,f到a6个部分,即(0, (ts-br)/2),((ts-br)/2, (ts-bs+br)/2),((ts-bs+br)/2, (ts+bs-br)/2),((ts+bs-br)/2, (ts+br)/2),((ts+br)/2, ts-tr/2), (ts-tr/2, 2p)。
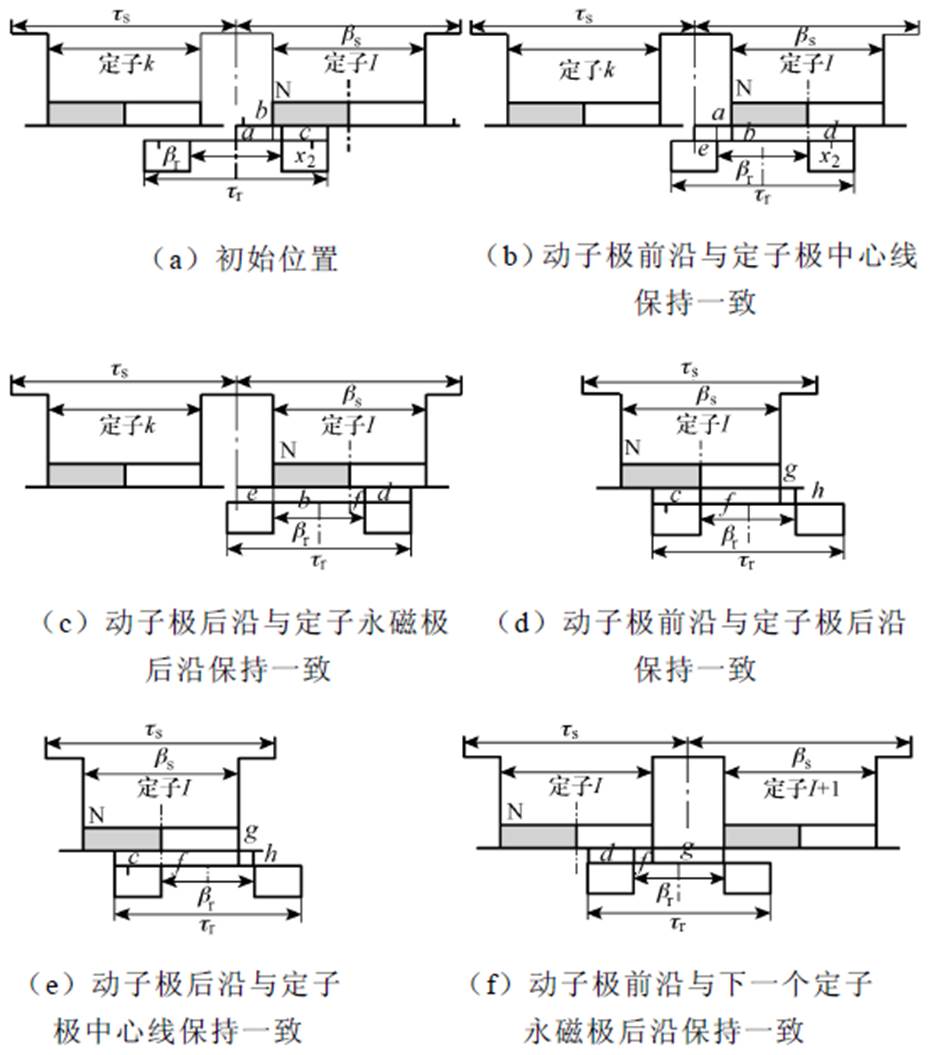
图11 定子和动子极的相对位置
Fig.11 Relative position between stator and mover poles
气隙部分可以被划分为a、b、c、d、e、f、g和h共8个子区域。a=[(ts-br)/2-a]Rsi,b=( br/2-a)Rsi,c=bsRsi/(2-b),d=bsRsi/(2-f),e=(tr-br)Rsi/(2-c),f = brRsi-b,g=brRsi-f,h=tsRsi/(2-g)。其中,tr、bs、ts和br分别为动子极距、定子极弧弧度、定子极距、动子极弧度,Rsi为定子内径。
为了提高计算精度,气隙磁导修正系数Kc的表达式为
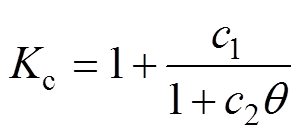 (13)
(13)式中,系数c1和c2为三维有限元法计算的气隙磁导率的最大和最小磁链的位置。由此可以得到定子、动子气隙磁导率修正系数Kcrfe和Kcsfe。
漏磁系数Kc-pm的表达式为
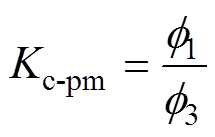 (14)
(14)式中,f1、f3为流过定子极的磁链量。由此可以得到永磁自漏磁Kcpm和永磁铁极漏磁系数Kcpmfe。
在a、e区域中,没有磁链;在b、f区域中,磁链为直线;在c、d和g区域中,磁链由直线和圆弧组成;在h区域中,定子槽与动子槽相对应,根据定子和动子极的磁通分界点(x1=hps/b1,x2= hpr/b2),可以将磁链分为三个平行的部分:一条直线部分和两个圆弧部分,一个直线和一个圆弧部分,一个直线部分,其中,hps和hpr分别为定子和动子极高。
在a、b、c、d、e、f、g和h区域中气隙磁导的表达式分别为
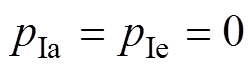 (15)
(15)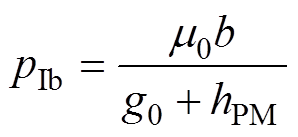 (16)
(16)
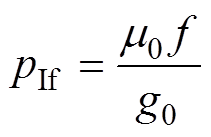 (17)
(17)
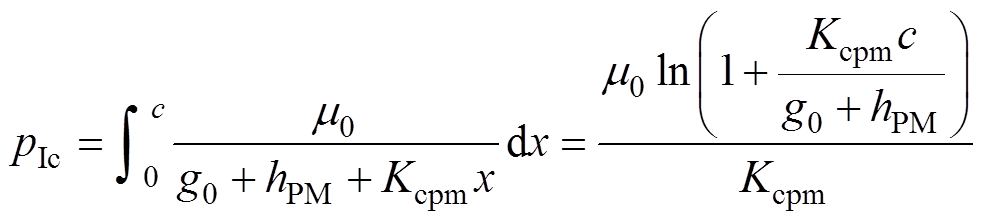 (18)
(18)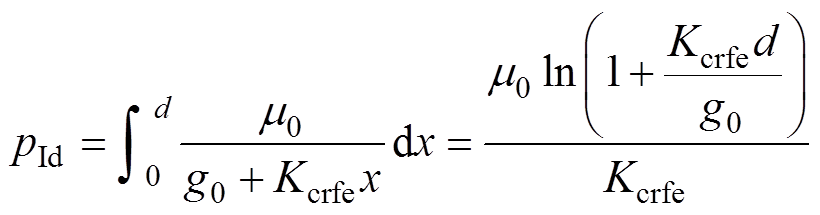 (19)
(19)
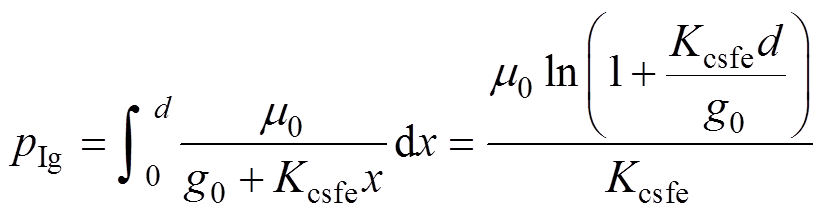 (20)
(20)
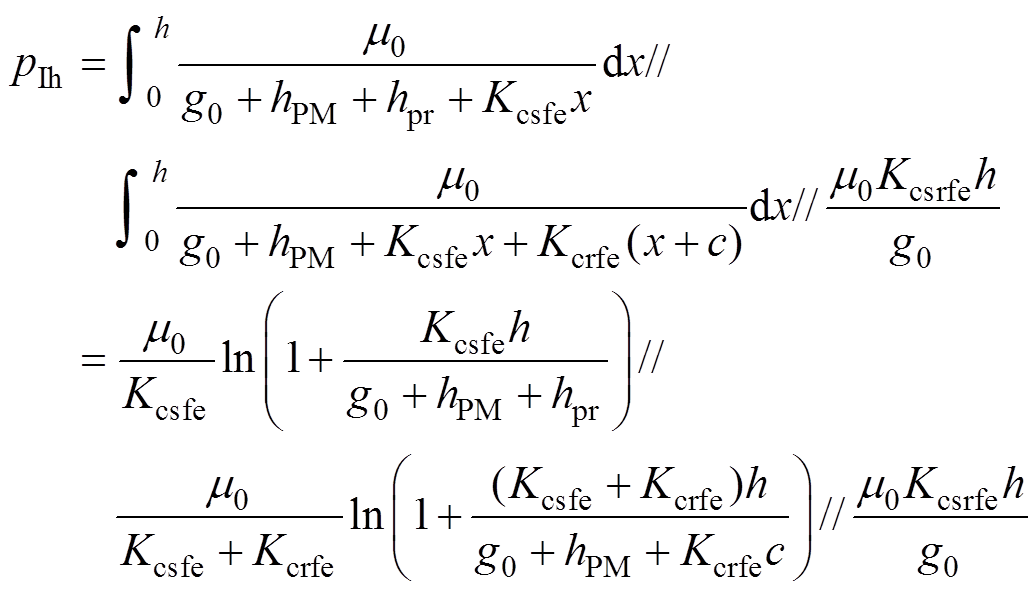 (21)
(21)式中,g0为气隙的宽度。
因此,气隙磁导的表达式为
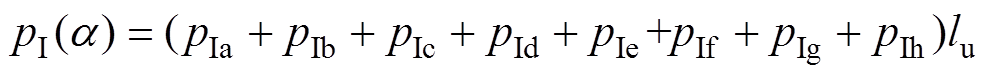 (22)
(22)根据空载磁路、铁磁磁阻、气隙磁导,磁通反向直线旋转永磁电机气隙磁链的计算误差作为迭代计算的参考值进行迭代计算,通过推导得到磁通密度、反电动势、齿槽转矩的表达式。
图12是采用传统磁路模型、EMCM和三维有限元模型计算的气隙磁通密度波形。从图中可以看出,采用EMCM和有限元法计算的结果基本一致,但由于采用传统磁路法计算的磁通密度波形没有考虑局部饱和的影响,在气隙磁通密度的峰值处的计算结果有较大的差距。
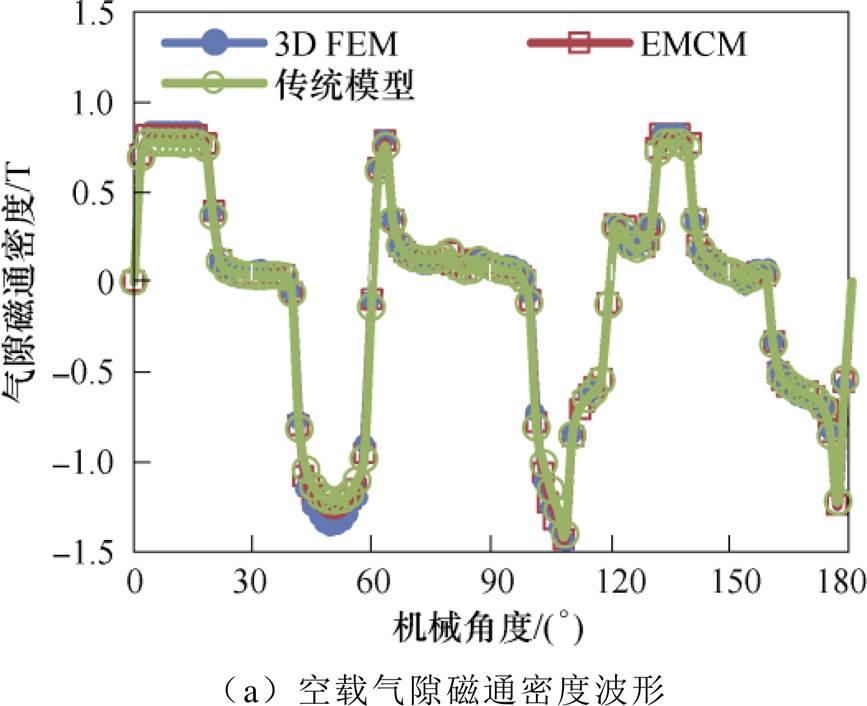
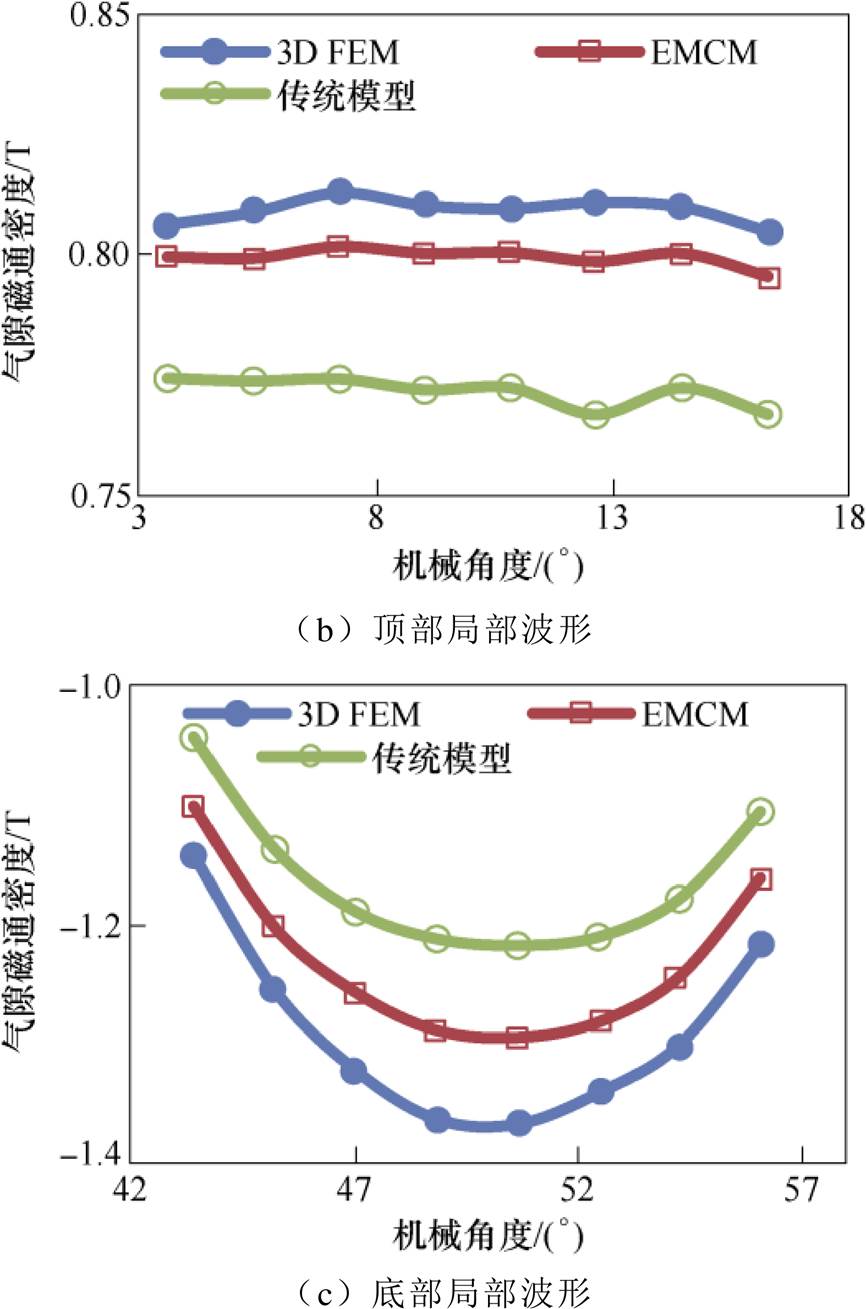
图12 采用传统磁路法、EMCM和三维有限元法计算的空载气隙磁通密度波形
Fig.12 No-load air-gap magnetic flux density waveforms analyzed by traditional magnetic circuit method, improved EMCM and 3D FEM
根据仿真结果,制作了一台FR-LRPMM样机,如图13所示,其主要设计参数见表1。通过采用三维非线性EMCM、三维有限元法和实验对FR-LRPMM的反电动势、齿槽转矩/直线定位力进行计算分析,图14为A相空载反电动势波形的对比结果及其谐波分析(n=1 500r/min),可以看出,EMCM和有限元法计算的反电动势波形基本一致,但测量值低于仿真结果,主要是由于样机加工过程的误差造成的。由谐波分析的波形可以看出,基波和2次谐波约占65%。
图15和图16分别是齿槽转矩波形和直线定位力波形对比,从图15中可以看出,采用有限元法、EMCM计算的齿槽转矩波形的幅值(0.088N·m,0.085N·m)与测量值(0.087N·m)基本保持一致,验证了EMCM进行结构设计的正确性。FR-LRPMM随着动子轴向位置的不同,直线定位力的脉动不同,从图16中可以看出,采用三维有限元法计算的直线定位力波形幅值(13.34N)略大于EMCM计算的结果(11.6N),验证了EMCM的正确性。但其测量值的幅值为18.4N,约为计算值的1.6倍,这主要是因为采用有限元法和EMCM计算直线定位力时,周向磁场产生的周向力的轴向分力合力为0,直线定位力由齿槽力和端部力构成,但由于FR-LRPMM的三维磁路结构及加工误差,造成了永磁电机漏磁的增大,直线运动时周向磁场产生的周向力的轴向分力增大,进而增大了直线定位力。

图13 FR-LRPMM样机
Fig.13 Prototype of FR-LRPMM
表1 FR-LRPMM的主要设计参数
Tab.1 Main design parameters of FR-LRPMM

参 数数 值 定子直径/mm120 气隙宽度/mm0.6 单定子轴向宽度/mm21 定子极周向宽度/mm21 永磁体周向宽度/mm9.9 定子内径/mm110 定子轭部厚度/mm5 动子极周向弧度/(°)22.5 动子直径/mm60.2 轴直径/mm24 动子轭部厚度/mm10 定子模块间距离/mm17.5 永磁体轴向宽度/mm9.5 动子极高/mm8.1 永磁体厚度/mm5.2 动子极轴向宽度/mm7.5
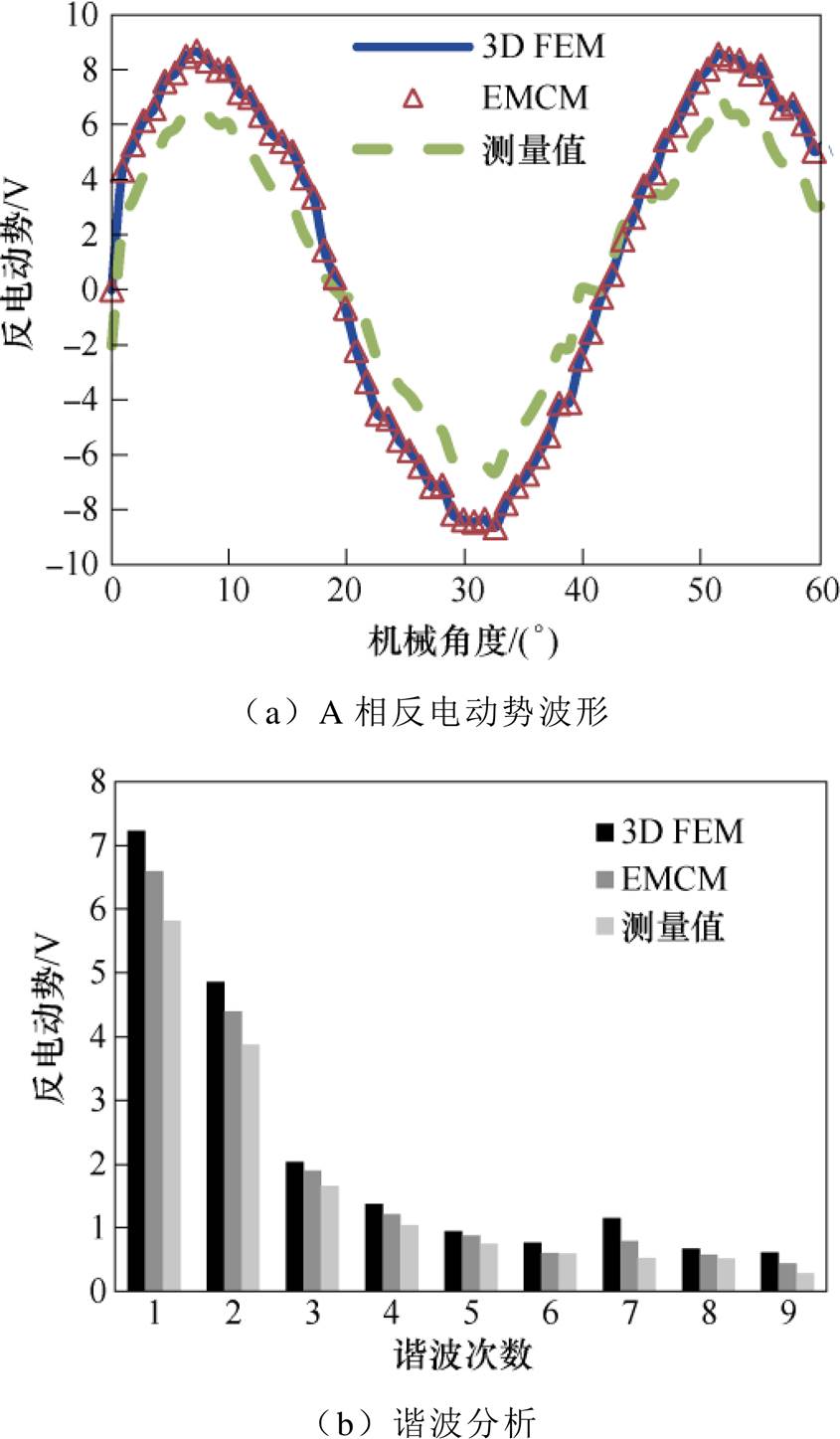
图14 A相反电动势波形及其谐波分析
Fig.14 Waveforms of A phase back EMF and its harmonic analysis
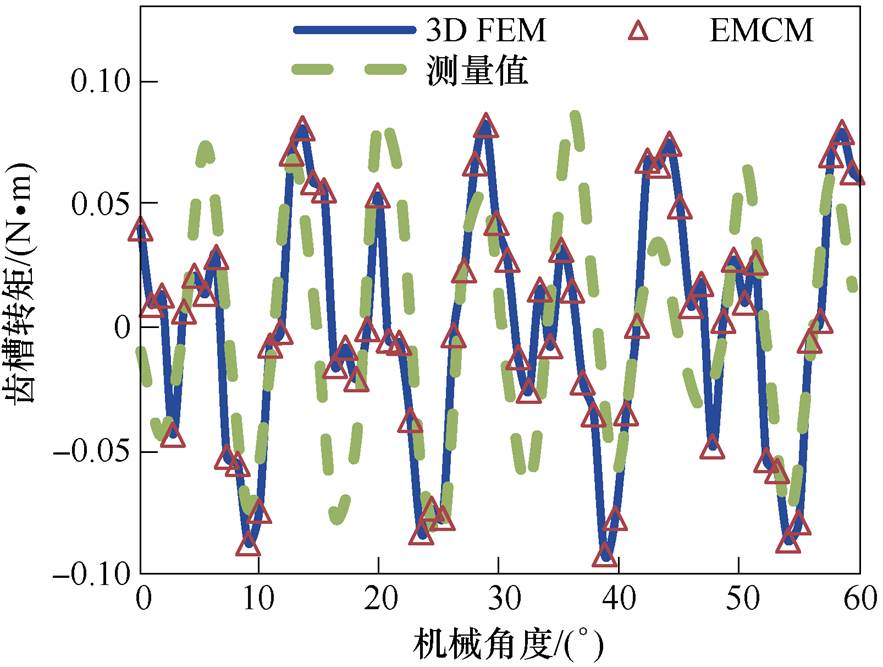
图15 齿槽转矩波形
Fig.15 Waveforms of cogging torque
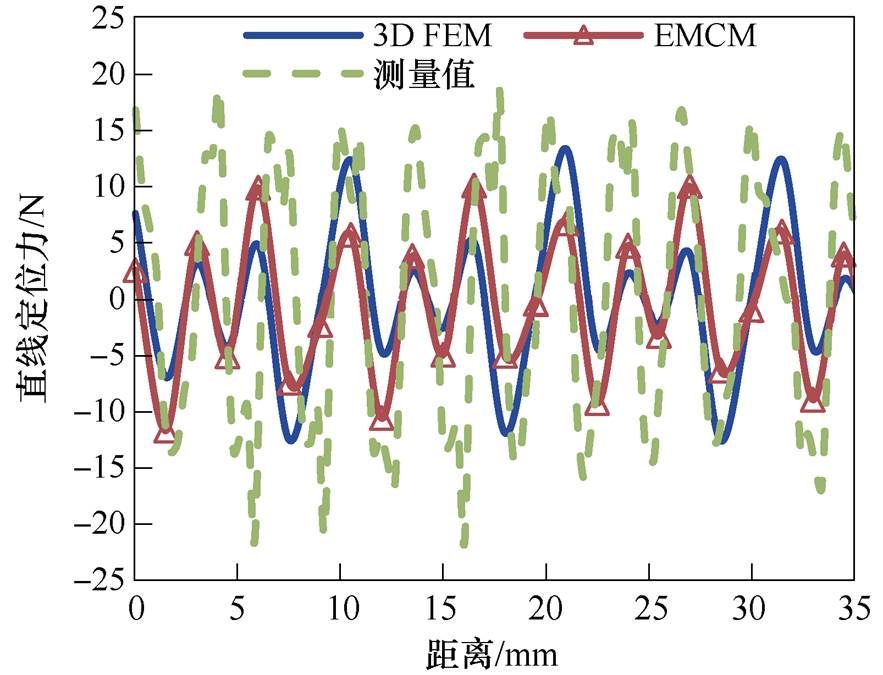
图16 直线定位力波形
Fig.16 Waveforms of detent force
为了降低FR-LRPMM结构设计的时间,提高其开发效率,本文通过在定子周向和轴向增加可变磁阻单元,建立了FR-LRPMM的三维非线性EMCM,并对其气隙磁通密度波形进行对比分析,采用EMCM计算的结果与三维有限元法计算的结果基本一致,与传统磁路法相比,提高了磁场的计算精度。根据计算结果制作了样机,采用EMCM对其电磁特性进行分析,其反电动势、齿槽转矩/直线定位力的计算结果与有限元法、试验测量的结果基本保持一致,验证了此方法是对此类电机进行结构设计和电磁特性分析的一种快速有效的方法。
参考文献
[1] 谢颖, 黑亮声, 华邦杰, 等. 新型永磁游标电机的设计与研究[J]. 电机与控制学报, 2019, 23(2): 68-74.
Xie Ying, Hei Liangsheng, Hua Bangjie, et al. Design and analysis of a new vernier permanent-magnet motor[J]. Electric Machines and Control, 2019, 23(2): 68-74.
[2] 杨玉波, 刘国鹏, 陈鹏, 等. 基于子域法的游标混合电机电磁性能解析计算[J]. 电机与控制学报, 2019, 23(9): 9-17.
Yang Yubo, Liu Guopeng, Chen Peng, et al. Electro- magnetic performance investigation of vernier hybrid machine[J]. Electric Machines and Control, 2019, 23(9): 9-17.
[3] Liu Guohai, Ding Ling, Zhao Wenxiang, et al. Nonlinear equivalent magnetic network of a linear permanent magnet vernier machine with end effect consideration[J]. IEEE Transactions on Magnetics, 2018, 54(1): 8100209.
[4] Xu Gaohong, Liu Guohai, Jiang Shan, et al. Analysis of a hybrid rotor permanent magnet motor based on equivalent magnetic network[J]. IEEE Transactions on Magnetics, 2018, 54(4): 8202109.
[5] 张继鹏, 陈鹏, 苏锦智, 等. 一种三维磁路永磁电机的集中参数磁路模型[J]. 电机与控制学报, 2015, 19(4): 21-27.
Zhang Jipeng, Chen Peng, Su Jinzhi, et al. One lumped parameter magnetic circuit model for permanent magnet machines with three-dimensional flux paths[J]. Electric Machines and Control, 2015, 19(4): 21-27.
[6] 徐衍亮, 吴巧变, 宫晓. 新型盘式横向磁通永磁无刷电机的变网络等效磁路模型[J]. 电工技术学报, 2016, 31(17): 147-153.
Xu Yanliang, Wu Qiaobian, Gong Xiao. Network- varying equivalent magnetic circuit modeling of novel disk transverse-flux permanent magnet brush- less machine[J]. Transactions of China Electro- technical Society, 2016, 31(17): 147-153.
[7] Du Jinhua, Xue Yuntian, Liu Quanwei, et al. Improved analytical model for inductance calcu- lations of a dual-rotor permanent magnet reluctance machine based on magnetic networks[J]. IEEE Transactions on Industrial Applications, 2018, 54(6): 5822-5832.
[8] 黄垂兵, 马伟明, 许金, 等. 六相圆筒式直线感应电机磁路计算及饱和特性分析[J]. 电工技术学报, 2018, 33(5): 1032-1039.
Huang Chuibing, Ma Weiming, Xu Jin, et al. Magnetic circuit calculation and saturation characteristics analysis of six phase cylindrical linear induction motor[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1032-1039.
[9] 刘治鑫, 王东, 余中军, 等. 基于磁性槽楔修正模型的感应电动机气隙磁场的分布磁路法[J]. 电工技术学报, 2019, 34(15): 3112-3123.
Liu Zhixin, Wang Dong, Yu Zhongjun, et al. Distributed magnetic circuit method for calculating air-gap magnetic field of induction motor based on modified model considering the effect of magnetic slot wedges[J]. Transactions of China Electro- technical Society, 2019, 34(15): 3112-3123.
[10] Ojaghlu Pourya, Vahedi Abolfazl, Totoonchian Farid. Magnetic equivalent circuit modelling of ring winding axial flux machine[J]. IET Electric Power Appli- cations, 2018, 12(3): 293-300.
[11] Hanic Ana, Zarko Damir, Kuhinek Dalibor, et al. On-load analysis of saturated surface permanent magnet machines using conformal mapping and magnetic equivalent circuits[J]. IEEE Transactions on Energy Conversion, 2018, 33(3): 915-924.
[12] Yeo Han-Kyeol, Lim Dong-Kuk, Jung Hyun-Kyo. Magnetic equivalent circuit model considering the overhang structure of an interior permanent-magnet machine[J]. IEEE Transactions on Magnetics, 2019, 55(6): 8201404.
[13] Lee Jae-Jun, Lee Ju, Kim Kwang-Soo. Design of a WFSM for an electric vehicle based on a nonlinear magnetic equivalent circuit[J]. IEEE Transactions on Applied Superconductivity, 2018, 28(3): 5206304.
[14] Hemeida Ahmed, Lehikoinen Antti, Rasilo Paavo, et al. A simple and efficient quasi-3D magnetic equivalent circuit for surface axial flux permanent magnet synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2019, 66(11): 8318-8333.
[15] Bao Jing, Gysen B L J, Lomonova E A. Hybrid analytical modeling of saturated linear and rotary electrical machines: integration of fourier modeling and magnetic equivalent circuits[J]. IEEE Transa- ctions on Magnetics, 2018, 54(11): 8109905.
[16] Song Jun-Young, Lee Jin-Hwan, Kim Dae-Woo, et al. Analysis and modeling of permanent magnet variable flux memory motors using magnetic equivalent circuit method[J]. IEEE Transactions on Magnetics, 2017, 53(11): 8208905.
[17] Wei Yao, Zhao Mei, Yang Hongyong, et al. Electromagnetic characteristic of a novel linear flux switching machine with three-dimensional magnetic circuit[J]. IEEE Transactions on Applied Super- conductivity, 2019, 29(2): 0600505.
[18] Tong Wenming, Wang Shuai, Dai Shanhong, et al. A quasi-three-dimensional magnetic equivalent circuit model of a double-sided axial flux permanent magnet machine considering local saturation[J]. IEEE Transactions on Energy Conversion, 2018, 33(4): 2163-2173.
[19] Guo Kaikai, Fang Shuhua, Lin Heyun, et al. 3-D analytical analysis of magnetic field of flux reversal linear-rotary permanent magnet actuator[J]. IEEE Transactions on Magnetics, 2017, 53(6): 8202205.
[20] Guo Kaikai, Guo Youguang. Key parameter design and analysis of flux reversal linear rotary permanent magnet actuator[J]. IEEE Transactions on Applied Superconductivity, 2019, 29(2): 0600405.
[21] Perho J. Reluctance network for analyzing induction machines[M]. Finland: Helsinki University of Tech- nology, 2002.
3D Nonlinear Equivalent Magnetic Circuit Model Analysis of a Flux Reversal Linear Rotary Permanent Magnet Machine
Abstract An improved 3D nonlinear equivalent magnetic circuit model (EMCM) of a flux reversal linear rotary permanent magnet machine (FR-LRPMM) was established by adding a variable reluctance unit to 3D magnetic circuit structure. The magnetic reluctance expressions of the stator and mover sections were derived by magnetic nodal method. The reluctance of the variable-reluctance unit was derived by 2D finite element method (FEM), which changed from 0 to infinity periodically with different locations of the mover when it was in linear or rotary motion. The 3D air-gap permeance expression was derived by segmentation method. The electromagnetic characteristics, such as no-load air gap flux density, were calculated and analyzed by an iterative method. Compared with the 3D FEM, the calculation time of this proposed model is reduced greatly. The proposed model could take in account the saturation of the stator core material, PM local flux leakage and pole-pole flux leakage. The analyzed results of the electromagnetic characteristics, including the back EMF, cogging torque and detent force, are consistent with those of 3D FEM and test measurement, which verifies the improved EMCM.
keywords:Equivalent magnetic circuit model, flux reversal linear rotary permanent magnet machine, reluctance-varying, static characteristic
中图分类号:TM302
DOI: 10.19595/j.cnki.1000-6753.tces.191258
国家自然科学基金(51905003)、中国博士后科学基金(2019M652161)、安徽省自然科学基金(1908085QE207)和安徽理工大学青年教师科学研究基金重点(QN2018107)资助项目。
收稿日期 2019-09-28
改稿日期 2020-01-09
郭凯凯 男,1987年生,博士,讲师,研究方向为永磁电机结构设计及其控制系统。E-mail: guokai0072000@gmail.com(通信作者)
郭有光 男,1965年生,教授,博士生导师,研究方向为电机设计、电磁场数值计算和新材料在电磁装置上的应用等。E-mail: Youguang.guo-1@uts.edu.au
(编辑 崔文静)