0 引言
高空核爆电磁脉冲（High-Altitude Electro- magnetic Pulse, HEMP）是核爆炸除核辐射、热辐射和冲击波外的第四种效应。图1为400km高空核爆炸产生的HEMP在地面电场强度分布示意图[1]，其最大电场强度为39kV/m，覆盖范围可达2 200km。大范围强电磁脉冲会在输配电线路上耦合产生过电压，引起线路绝缘子串闪络，直接威胁到电网的安全稳定。
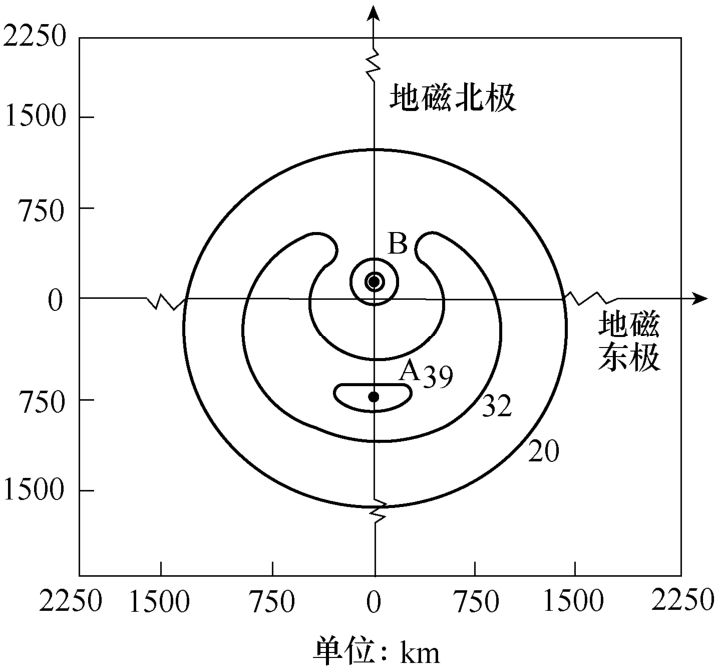
图1 400km高空核爆炸地面HEMP电场强度分布
Fig.1 Electrical field configuration on the ground of a 400km high altitude nuclear explosion
针对HEMP与传输线的耦合方法[2-4]，目前应用最为广泛的是传输线理论[5]。基于传输线理论，场与传输线间的耦合作用可简化为传输线方程，并有三种表现形式，包括Taylor模型、Agrawal模型和Rachidi模型[6]。三种模型表现形式不同，但模型相互等价[7]。文献[8-11]应用传输线理论分析了高空核爆电磁脉冲激励下传输线网络的暂态感应电压，并改进了Carson地阻抗公式，给出了适用于更高频率的地阻抗表达式。地阻抗参数是传输线方程中重要的线路参数，目前主要有Carson、Sunde公式等取值方式。
此外，基于麦克斯韦方程的天线理论也用于分析HEMP与导线的耦合，天线理论是传输线理论的高频拓展，模型更为准确[6]。结合细线假设，文献[12]应用天线理论推导了无限长架空线受场激励时导线感应电流的解析表达式。当导线长度有限时，由于需考虑导线两端边界条件，感应电流无法解析表达，需通过数值迭代方法求解[13-14]。在分析受入射场激励下有限长架空导线感应电流时，天线理论和传输线理论具有相同的表现形式[12]。传输线理论推导的感应电流具有解析解，且仅与线路参数及频率有关。而天线理论推导的感应电流无解析解，需通过迭代方法求解，且还与场的入射角有关。天线理论是传输线理论在高频段的改进，虽然模型更为精确，但表达式复杂，且无解析解，不便于直接应用[9]。
架空输配电线路由于分布范围广，成为了高空核爆电磁脉冲的直接攻击对象。美国能源局针对高空核爆炸对电网的潜在威胁已做了大量的研究[1,15]。文献[1]考虑了地线接地情况，计算了高空核爆炸下半无限长架空输配电线路感应电压；文献[15]将架空输配电线路等效为无限长线路，研究了美国四种电压等级输配电线路在高空核爆炸下绝缘子闪络的可能性。文献[1,15]均将架空输配电线路视为无限长线，并未考虑激励场强度的变化，而实际线路长度有限，且不同线路位置处，激励场强度不同。另外，输配电线路长度可达上百千米，杆塔数目上百，直接分析实际输配电线路感应电压时，存在计算时间长、收敛困难的问题。
受电磁场激励时，传输线上的感应浪涌峰值并不会随着传输线长度持续增加。当传输线长度达到有效耦合长度（Effective Coupling Length, ECL）时，感应浪涌峰值不再随传输线长度增加[16]。本文首先利用传输线理论，结合电路方法求解多导体传输线网络受HEMP激励时节点的暂态感应电压。同时应用有效耦合长度概念，建立架空输配电线路的简化模型，从而降低计算复杂度。最后，应用多导体传输线网络受HEMP激励时暂态响应的求解方法，基于输配电线路简化模型，分析在400km高空核爆炸下绝缘子的闪络情况。
1 HEMP与架空多导体线路耦合模型
基于传输线理论，架空多导体线路可视为多导体传输线，HEMP与传输线的耦合模型可用传输线方程表示。本节将给出HEMP激励下的多导体传输线方程具体表达式，并分析相应的线路参数取值。
1.1 多导体传输线网络结构配置
图2为含n个节点的架空多导体传输线网络受HMEP激励的示意图，各节点处导线均通过线性电阻R接地。其中，HEMP以入射角ψ 入射，且与第1条传输线的夹角，即方位角为φ，入射波的极性角为α。每条传输线由m个导体构成，记第k条传输线高度为hk，长度为lk，导体半径为rk，且与第1条传输线的夹角为αk。导体电导率为σw，土壤电导率为σg，相对介电常数为εg。
图2 受HEMP激励的架空多导体传输线网络模型
Fig.2 Configuration of overhead multi-conductor transmission line network with the excitation of HEMP
为方便描述各节点位置，以节点1的垂直接地点为原点，并以第1条传输线沿线方向为x轴方向，建立全局直角坐标系（x, y, z）。由此，可确定其他n-1个节点的空间坐标。同时，以第k条线路首端点为原点，第k条传输线沿线方向为xk轴方向，建立局部直角坐标系（xk, yk, zk）。局部坐标系xk轴方向与全局坐标系x轴方向夹角为αk。
1.2 HEMP激励下多导体传输线方程
应用传输线理论，受HEMP激励的第k条多导体传输线上的感应电压向量V(x)，电流向量I(x)[6]可表示为
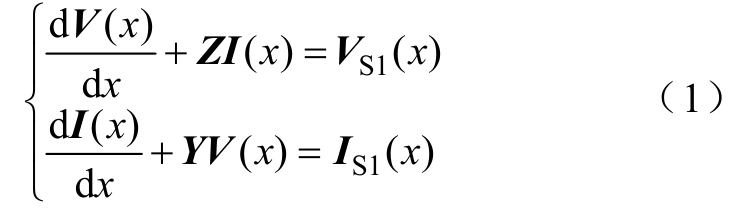
式中，Z和Y分别为多导体传输线单位长度阻抗和导纳矩阵，且为m×m矩阵；VS1和IS1分别为HEMP激励源等效的分布电压源和电流源向量，并满足
式中，
为HEMP总磁场Hex沿y轴方向的分量；
分别总电场Eex沿x、z轴方向的分量；且 总场由入射场 Hin 、Ein 和地面反射场 Href 、Eref 叠 加构成；h为第k条多导体传输线的m个导体高度组成的向量。位于有损耗大地上方的多导体传输线，其单位长度阻抗Z和导纳Y参数可表示为图3所示的电路形式。
图3 多导体传输线单位长度阻抗和导纳示意图
Fig.3 Circuit model of the per unit impedance and admittance of multi-conductor transmission line
由图3可知，单位长度阻抗由三部分组成：内阻抗、外阻抗及地阻抗。单位长度导纳由外电导和地电纳组成。单位长度阻抗Z和导纳Y矩阵可分别表示为
式中，Zi为多导体传输线内阻抗矩阵，为对角阵；Zg为多导体传输线单位长度地阻抗矩阵；Yg为地导纳矩阵；L和C分别为多导体传输线单位长度电感和电容矩阵。
Zi的第k个对角元素[6]可表示为
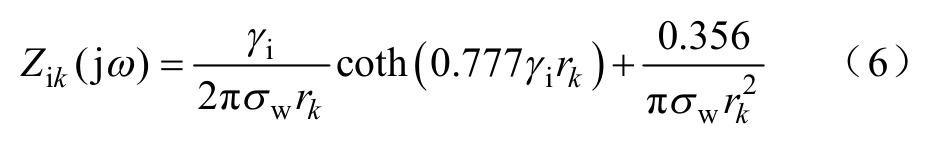
其中
式中，σw为导体电导率；μ0为真空磁导率；rk为导体半径；ε0为真空介电常数。
由于各导体间存在相互耦合作用，L和C均为满秩矩阵。电感矩阵L对角元素为导体自电感，非对角元素为导体间的互电感。对于第k个导体，其自电感及与第l个导体间的互电感可分别表示为
式中，hk和hl分别为第k、l个导体的对地高度；dkl为第k个和第l个导体的间距。
单位长度电容C=P-1，P为多导体传输线的电位系数矩阵，其对角元素Pkk为第k个导体的自电位系数，非对角元素Pkl为第k个导体与第l个导体间的互电位系数，可分别表示为
图4为第k个导体自地阻抗及与第l个导体间的互地阻抗示意图，其近似表达式分别为[6]
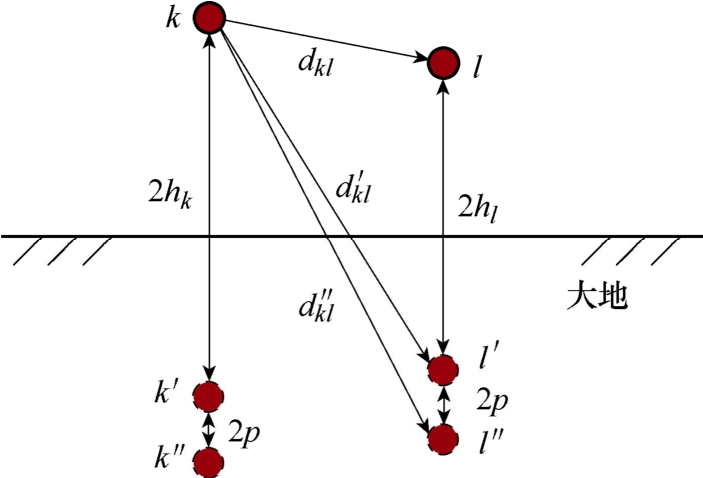
图4 多导体传输线地阻抗示意图
Fig.4 Ground impedance of multi-conductor transmission line
图4中，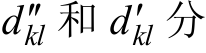
别为第k个导体距离第l个导体在良导体大地和有损耗大地条件时的镜像导 体的距离。p为大地趋肤深度，且
为土壤传播常数，并满足 
其中，σg为土壤电导率，εg为土壤相对介电常数。由于地导纳Yg较外电导小，因而可以忽略Yg。
2 HEMP激励下多导体传输线网络感应电压求解
本节将采用时频域结合的方法来求解HEMP激励下传输线网络暂态感应电压。频域方法不仅能够充分考虑场线耦合作用，同时也能考虑大地及导体的趋肤效应。首先通过求解HEMP激励下的传输线方程，推导出多导体传输线频域形式的PI等效型电路模型及电路参数。然后对频域形式的等效电路，应用节点电压法求得传输线网络各节点处的感应电压频域解。最后采用反傅里叶变换（Inverse Fast Fourier Transform, IFFT），求得感应电压时域解。
2.1 HEMP激励下多导体传输线PI型等效电路
直接求解传输线方程式（1）便可得HEMP激励下传输线上的感应电压、电流。但对于多导体传输线网络，由于各传输线在节点处相互耦合，直接求解传输线方程较为困难。本文将采用电路方法求解传输线上的感应电压。
通过求解式（1）可获得第k条传输线的端口特性矩阵Φ11、Φ12、Φ21、Φ22，并由此可将其表示为等效的PI型电路模型，图5为第k条传输线的PI型等效电路。其中，Vi、Ii分别为传输线首端i处感应电压、电流向量，Vj、Ij分别为传输线末端j处感应电压、电流向量。
图5 HEMP激励下多导体传输线PI型等效电路
Fig.5 PI-type equivalent circuit of the multi-conductor transmission line with HEMP excited
图5中，Ya、Yb、Yc分别为表征传输线端口特性的导纳矩阵，ISa、ISb分别为HEMP激励源等效的集中电流源向量，且与传输线端口特性矩阵满足
式中，U为单位矩阵；lk为第k个导体长度。
2.2 HEMP激励下多导体传输线网络感应电压时域解
HEMP激励下的传输线网络中每条多导体传输线均可表示为频域形式的PI型等效电路，由此可形成PI型等效电路网络。由于各节点处，导体均通过线性电阻接地，因此PI型等效电路中只含有线性元件。求解HEMP激励下传输线网络的感应电压由此可转化为对PI型电路网络的求解。
通过观察频域形式的PI型等效电路网，可得到节点导纳矩阵Y(jω)和节点电流源向量Isc(jω)。对于含n个节点的传输线网络，Y(jω)为nm×nm维矩阵，Isc(jω)为nm维向量。应用节点电压法可获得各节点处的感应电压频域解为
对式（16）进行IFFT变换，可获得感应电压的时域解式为
式中，ξ 为傅里叶变换。
3 方法验证
为验证HEMP激励下多导体传输线网络感应电压求解方法的正确性，计算图6所示的含4个节点，3条线路的传输线网络在HEMP激励下各节点的感应电压，并与文献计算结果[8]进行对比。
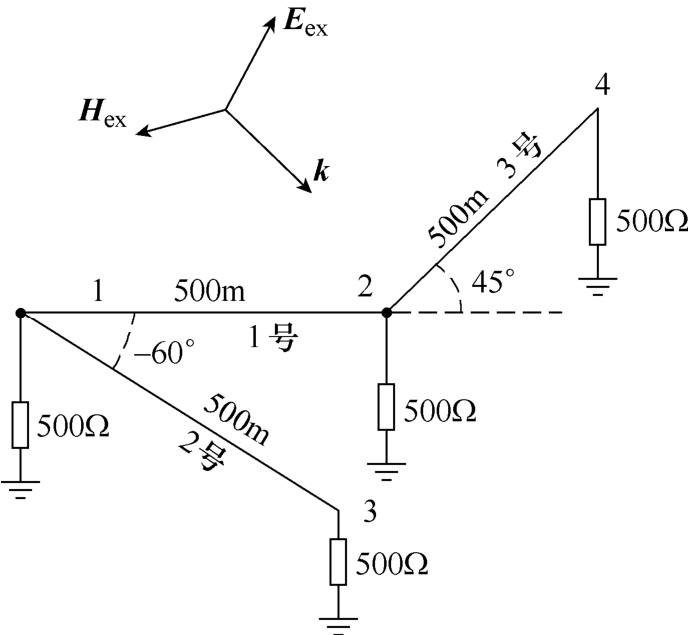
图6 含4个节点3条传输线的多导体传输线 网络配置示意图
Fig.6 Configuration of the multi-conductor transmission line network with four nodes and three lines
图中HEMP入射波为垂直极化波，即α =0°，入射角ψ =50°，方位角φ =20°，入射波表达式为
式中，Emax=50kV/m，k=1，β1=4×106，β2=4.76×108。图6中，各线路长度l=500m，各节点处导线均通过500Ω 线性电阻接地。第2条线路与第1条线路的夹角为-60°，第3条线路与第1条线路的夹角为45°。每条线路包含3个导体，各导体分布如图7所示，导体半径r=4mm，土壤电导率δg=0.5mS/m，相对介电常数εg=5，导体电导率为δw=5.97×106S/m。
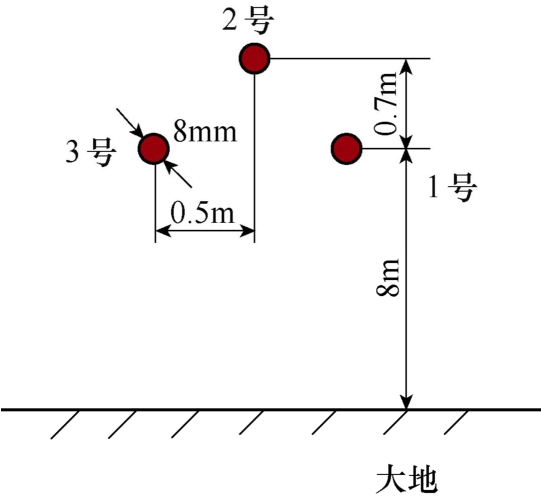
图7 导体分布示意图
Fig.7 Configuration of the conductors
图8为第1号导体在节点1和节点3处的感应电压仿真结果，并与Carson方法、D'Amore方法计算结果[8]进行了对比。由图8可以看出，仿真结果与文献结果基本吻合。此外，仿真结果恰好位于Carson方法与D'Amore方法计算结果之间。由于本文采用Sunde地阻抗公式，相较于Carson地阻抗公式，考虑了土壤中的位移电流，因而适用于更高频率的场线耦合。而D'Amore方法通过推导麦克斯韦方程组，得到了更为精确的阻抗计算公式，计算结果也更为准确，但其计算复杂，不便于使用。三种方法计算结果的变化趋势一致，且本文计算结果与Carson方法计算结果较为接近，而D'Amore方法考虑了更高频率的耦合效应，节点感应电压幅值更大。
图8 节点1、3感应电压仿真及文献结果对比
Fig.8 Calculated induced voltage at node one and three and results from the literature
为了更突出地体现三种方法由于采用不同地阻抗计算方法，而造成的感应电压计算结果的差异，分别计算了土壤电导率δg=0.2mS/m、2mS/m时，各节点最大感应电压，计算结果见表1。
表1 不同土壤电导率下各节点感应电压最大值
Tab.1 Maximum induced voltage with different earth conductivity
最大电压/kV σg=0.2mS/m σg=2mS/m 节点 Carson 本文 D'Amore Carson 本文 D'Amore 1 -380 -381 -408 -343 -344 -355 2 394 406 470 198 197 200 3 459 469 536 252 252 256 4 177 181 195 70 70 68
由表1可知，不同土壤电导率下，仿真结果基本位于Carson方法计算结果与D'Amore方法计算 结果之间，且仿真结果与Carson方法计算结果接近，而D'Amore方法计算结果幅值偏高。此外，随着土壤电导率的增加，三种方法计算的节点感应电压的最大值都将下降。
4 HEMP激励下架空输配电线路绝缘子闪络情况分析
HEMP可在广泛分布的架空输配电线上感应出过电压，导致绝缘子串发生闪络，造成短路故障，从而威胁电网的安全运行。目前我国110kV及以上输电线路输送距离可达上百千米，低压配电线路长度也可达几十千米。由于多导体传输线PI型等效电路的导纳参数，其频域波形以固定周期高频振荡，且振荡周期与线路长度成反比。随着线路长度的增加，波形振荡周期迅速下降，为防止波形畸变，需要减小频域分析步长。如果按照实际长度建立架空输配电线路模型，将存在求解规模大、求解速度慢、收敛困难的问题。为解决上述困难，本节将利用有效耦合长度概念，建立架空输配电线路的简化模型，并结合传输线网络感应电压求解方法，分析400km高空核爆炸下，国内四种电压等级输配电线路绝缘子串的闪络情况。
4.1 架空输配电线路模型
图9为架空输配电线路模型，架空线路含n个杆塔，各个杆塔均经线性电阻R与杆塔相连，图10为导线与杆塔连接的示意图。相邻杆塔间的架空线路可视为一条多导体传输线，图9共有n+1条传输线，其中第i-1个杆塔与第i个杆塔间距离为L。由于相线与杆塔绝缘，则连接电阻R为无穷大，且相线首末两端空载。地线经杆塔接地则连接电阻R为杆塔接地电阻，即为10Ω。
图9 输配电线路等效模型
Fig.9 Model of the power transmission and distribution line
图10 杆塔等效模型
Fig.10 Model of the tower
文献[16]指出随着线路长度的增加，传输线上的感应电压最大值先增大随后保持不变，使线路感 应电压最大值不再增大的线路长度被称为有效耦合长度。分析HEMP激励下架空输配电线路绝缘子闪络问题，仅需关注架空线路上的最大感应电压。因此可应用ECL将长距离的架空输配线路等效为短距离线路，等效原则为线路仿真长度L需大于有效耦合长度Lecl。
4.2 高空核爆炸下架空输配电线路感应电压
为仿真高空核爆炸下，架空输配电线路最大感应电压，将输配电线路置于图1中的最大电场强度A点处，并计算此时线路上的感应电压。图1中，A点电场强度为39kV/m，HEMP电磁波入射角Ψ =28°。
图11为国内四种不同电压等级架空输配电线路的导线分布示意图，其中，配电线路电压等级有10kV、35kV；输电线路电压等级有110kV、500kV。根据输配电线路仿真长度确定原则，仿真长度需要大于线路有效耦合长度Lecl=266m。对于500kV及110kV线路，其档距为500m，因此选择档数为2；35kV线路档距为350m，选择档数为2；10kV线路档距为50m，选择档数为5。土壤相对介电常数εg= 10，土壤电导率为δg=0.01S/m。
图11 国内架空输配电线路导线布置示意图
Fig.11 Configuration of the conductor of power transmission and distribution line in China
图12为四种电压等级架空输配电线路首端点各相线感应电压曲线。由图12可知，随着电压等级的升高，导线高度的增加，架空线路上的感应电压 逐步增大。同时地线对架空线路上的感应电压水平也有较大的影响，由于10kV配电线路无地线，线路感应电压水平高于35kV配电线路。
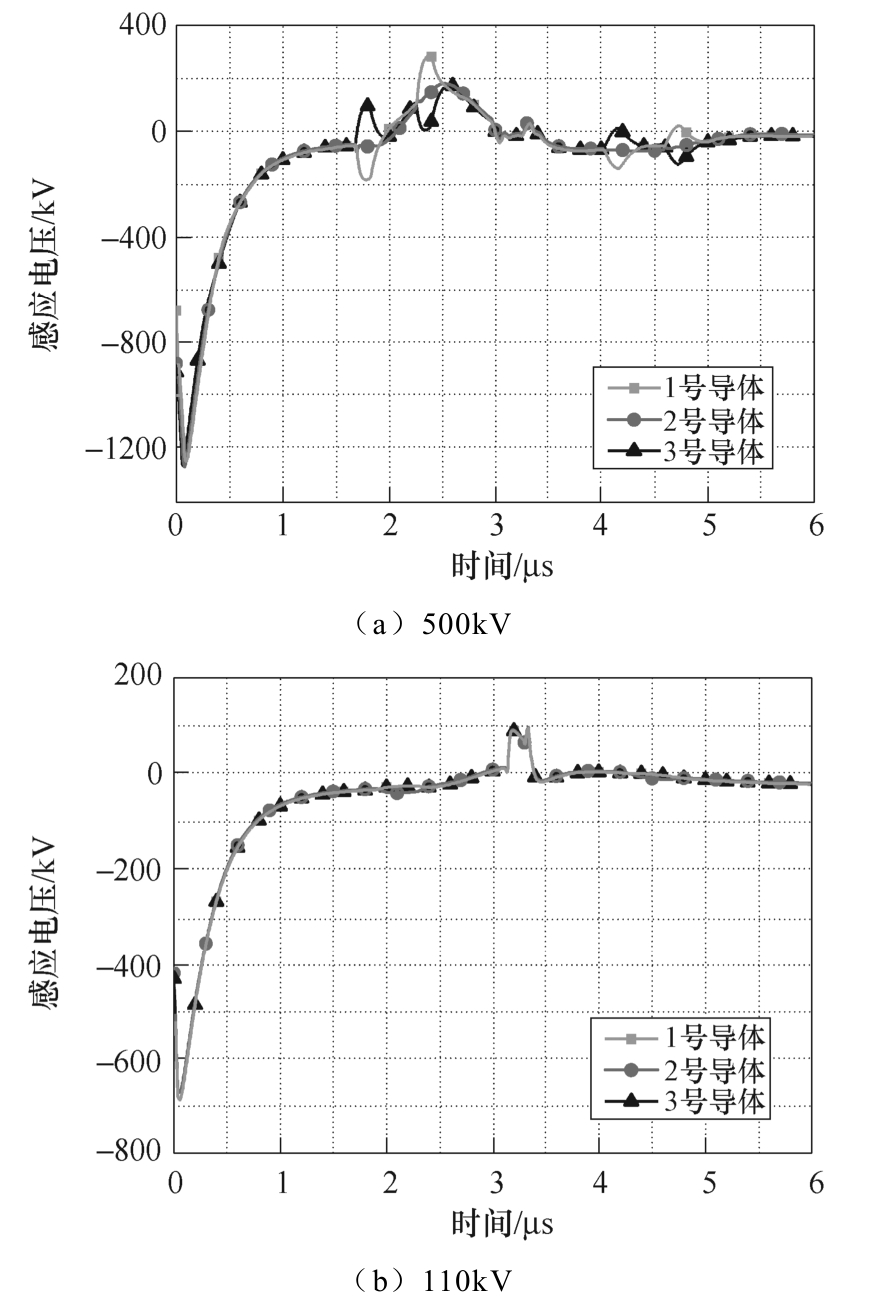
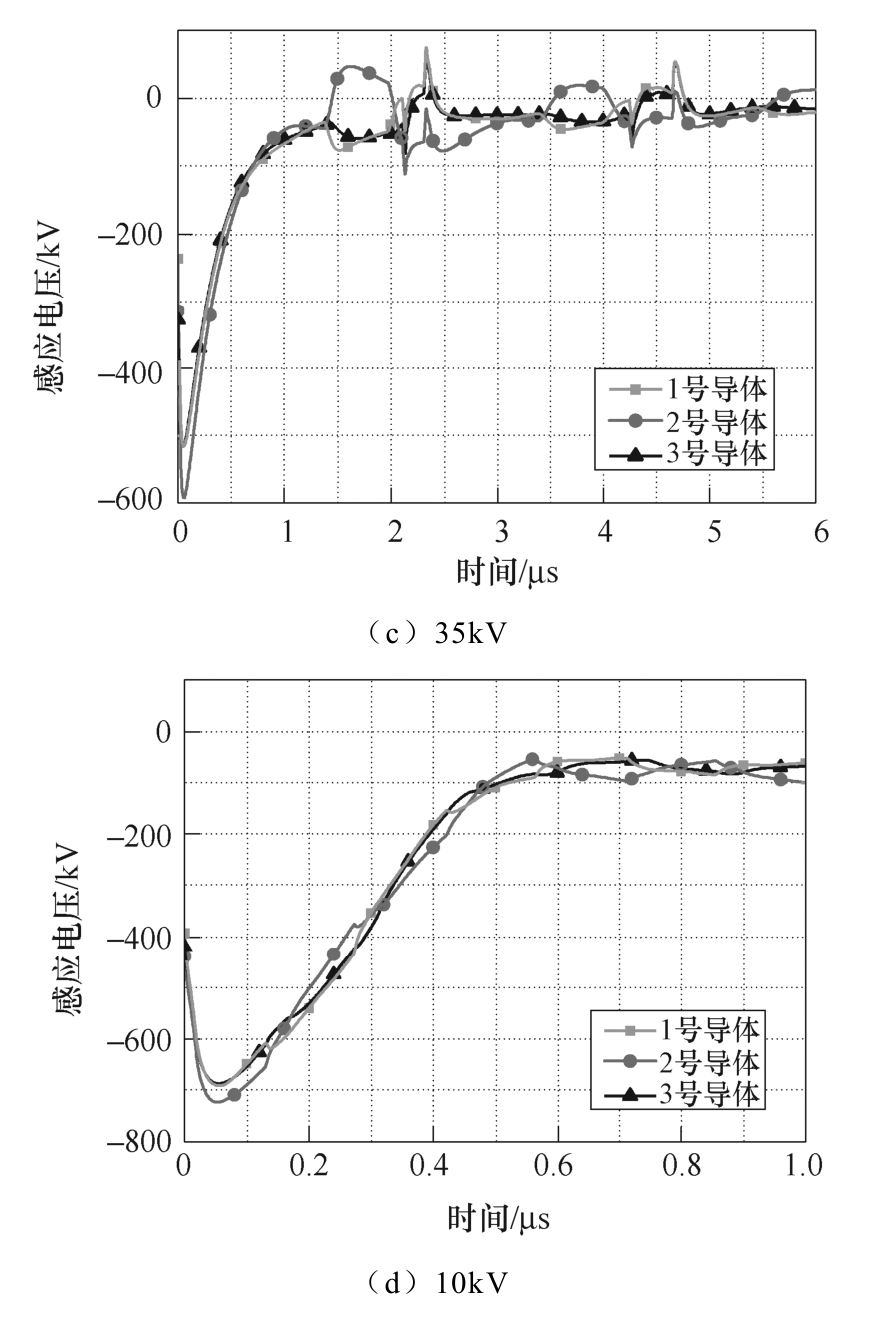
图12 400km高空核爆炸下，架空输配电线路 首端点感应电压
Fig.12 Transient induced voltage of the overhead power lines with excitation of 400km nuclear explosion
4.3 高空核爆炸下架空输配电线路绝缘子闪络可能性
目前对于标准雷电波形激励下，绝缘子串是否 闪络已有较多的研究。其中波头相交法广泛运用于判断绝缘子串是否闪络，即通过判断绝缘子串两端暂态过电压波形与绝缘子串伏秒特性曲线是否相交来判定。由图12可知，HEMP在架空输配电线路上感应出的暂态脉冲具有上升时间快（ns级），持续时间短（μs级）的特点，不同于已熟悉的雷电波产生的感应脉冲。而目前对于HEMP波形下的绝缘子串闪络电压（Critical Flashover Voltage, CFO），可获取的数据非常少。但实验结果表明，HEMP波形下的绝缘子串闪络电压与标准雷电波形下的闪络电压有一定关系，其中25/300ns波形下绝缘子串闪络电压为1.2/50μs标准雷电波形闪络电压的1.5～2.0倍[17]。
文献[18]给出了标准雷电波形下绝缘子串50%放电电压的经验公式为
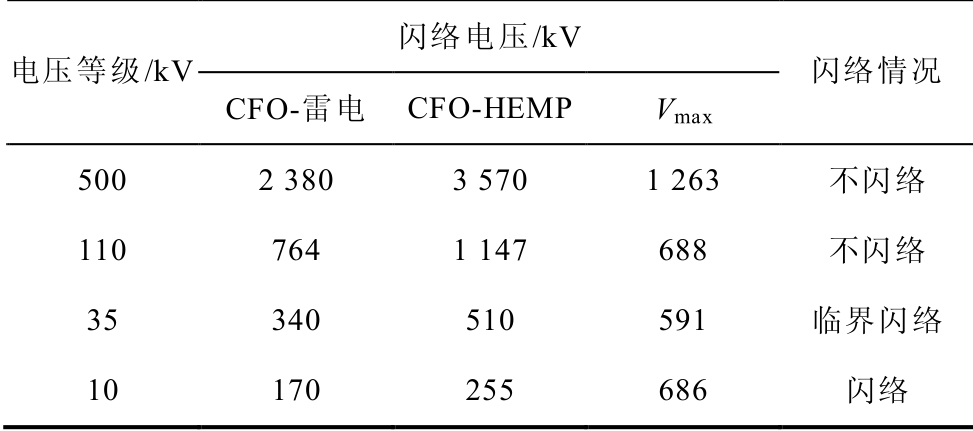
由式（19）可得标准雷电波形下各电压等级架空输配电线路绝缘子串的闪络电压，即CFO-雷电，见表2。其中，CFO-HEMP表示HEMP波形下的绝缘子串闪络电压，且为1.5倍CFO-雷电，Vmax为各电压等级架空输配线路最大感应电压。
表2 HEMP激励下四种电压等级线路绝缘子闪络情况
Tab.2 Flashover possibility of four kinds of power line insulators with HEMP excited
闪络电压/kV 电压等级/kV CFO-雷电 CFO-HEMP Vmax 闪络情况 500 2 380 3 570 1 263 不闪络 110 764 1 147 688 不闪络 35 340 510 591 临界闪络 10 170 255 686 闪络
由表2可知，500kV和110kV输电线路最大感应电压小于绝缘子串闪络电压，并且有1.5～2.0倍的裕度。因而高空核爆炸下，架空输电线路绝缘子串不会发生闪络。对于35kV的高压配电线路，线路最大感应电压略大于绝缘子串闪络电压，因而35kV配电线路绝缘子串处于临界闪络状态。而10kV配电线路最大感应电压为绝缘子串闪络电压的3倍左右，因而10kV线路易发生闪络。
5 结论
HEMP在地面上的最大电场强度可达39kV/m，本文通过分析国内四种典型电压等级输配电线路在最强电场处绝缘子闪络情况，得出以下结论：
1）随着架空线路高度的增加，即电压等级的抬升，线路感应过电压逐步增大。
2）地线能够有效降低架空线路上的感应电压。虽然10kV线路高度较低，但因10kV线路没有架设地线，线路最大感应电压仍高于35kV线路。此外，由于110kV线路架设双地线，其感应电压与10kV线路基本一致。
3）500kV、110kV线路由于架设双地线，导线高度对感应电压的增大作用有限，且线路绝缘子耐压水平较高，HEMP不会造成绝缘子闪络，并有较大安全裕度。
4）35kV高压配电线路导线高度低且架设单地线，感应电压较小，但由于绝缘子耐压水平较低，HEMP激励下线路最大感应电压与绝缘子耐压水平接近，绝缘子处于临界闪络水平。
5）10kV低压配电线路虽然导线高度低，但由于没有架设地线且绝缘子耐压水平低，HEMP激励下线路产生较高的过电压会造成绝缘子闪络。
上述结论表明，高空核爆炸主要对架空配电线路造成电磁危害，会在配电线路上感应出较高过电压，引起绝缘子闪络。输电线路由于绝缘子耐压水平高，且架设双地线，基本不受HEMP影响。因此，预防HEMP主要是针对架空配电线路而言，初步研究表明以下措施可抑制HEMP的影响，后续将对各措施具体抑制效果做进一步研究。
1）增加绝缘子串数量。通过增加线路绝缘子串数目，而提高线路耐HEMP的绝缘水平。
2）架设地线。由于地线对HEMP感应能量起到分流作用，地线可降低线路感应电压。仿真结果也表明地线对减小线路感应电压有明显作用。
3）减小杆塔接地电阻。通过改善杆塔接地装置，增加接地极面积，以减小杆塔接地电阻，增加HEMP能量经大地释放的通路，降低线路感应电压。
4）安装线路保护器（避雷器）。线路保护器与绝缘子串并联，当线路产生过电压后保护器动作释放HEMP能量，从而保护绝缘子串，避免线路跳闸。
[1]Kruse V J, Liu T K, Tesche F M, et al. Flashover vulnerability of transmission and distribution lines to high-altitude electromagnetic pulse (HEMP)[J]. IEEE Transactions on Power Delivery, 1990, 5(2): 1164- 1169.
[2]公延飞, 郝建红, 蒋璐行, 等. 有损大地上传输线HEMP响应的研究[J]. 电工技术学报, 2018, 33(21): 4901-4908. Gong Yanfei, Hao Jianhong, Jiang Luhang, et al. The research for the transient response of overhead transmission line on lossy ground excited by HEMP[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4901-4908.
[3]卢斌先, 郝晓飞, 罗艳华, 等. HEMP场激励下交直流高压输电线耦合响应[J]. 电工技术学报, 2011, 26(1): 141-146. Lu Binxian, Hao Xiaofei, Luo Yanhua, et al. Probability distribution of coupling responses of HVAC and HVDC externally excited by HEMP[J]. Transactions of China Electrotechnical Society, 2011, 26(1): 141-146.
[4]文刚, 齐世举, 姜勤波, 等. 大地水平分层电导率对架空线缆HEMP响应的影响[J]. 电工技术学报, 2016, 31(1): 91-95. Wen Gang, Qi Shiju, Jiang Qinbo, et al. Impact of horizontal stratified earth conductivity on overhead cable HEMP response[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 91-95.
[5]Tesche F M, Ianoz M V, Karlsson T. EMC analysis methods and computational models[M]. New York: Wiley, 1996.
[6]Farhad Rachidi, Sergey Tkachen. 电磁场与传输线的相互作用[M]. 谢彦召, 译. 北京: 清华大学出版社, 2013.
[7]谢彦召, 王赞基, 王群书. 地面附近架高线缆HEMP响应计算的Agrawal和Taylor模型比较[J]. 强激光与粒子束, 2005, 17(4): 576-580. Xie Yanzhao, Wang Zanji, Wang Qunshu. Com- parison of agrawal and taylor models for response calculations of aboveground cable excited by HEMP[J]. High Power Laser and Particle Beams, 2005, 17(4): 576-580.
[8]Marcello D Amore, Maria Sabrina Sarto. Theory of field-excited networks[J]. IEEE Transactions on Electromagnetic Compatibility, 1996, 38(3): 212-219.
[9]Amore M D, Sarto M S. A new efficient procedure for the transient analysis of dissipative power networks with nonlinear loads[J]. IEEE Transactions on Power Delivery, 1996, 11(1): 533-539.
[10]Amore M D, Sarto M S. Time response of a network containing field-excited multiconductor lossy lines with nonlinear loads[C]//IEEE International Sympo- sium on Electromagnetic Compatibility, Dallas, 1993: 436-441.
[11]Amore M D, Sarto M S. A new formulation of lossy ground return parameters for transient analysis of multiconductor dissipative lines[J]. IEEE Transa- ctions on Power Delivery, 1997, 12(1): 303-313.
[12]Tesche F M. Comparison of the transmission line and scattering models for computing the NEMP response of overhead cables[J]. IEEE Transactions on Electromagnetic Compatibility, 1992, 34(2): 93-99.
[13]Sergei Tkatchenko, Farhad Rachidi, Michel Ianoz. Electromagnetic field coupling to a line of finite length: theory and fast iterative solutions in frequency and time domains[J]. IEEE Transactions on Electromagnetic Compatibility, 1995, 37(4): 509- 518.
[14]Sergei Tkatchenko, Farhad Rachidi, Michel Ianoz. High-frequency electromagnetic field coupling to long terminated lines[J]. IEEE Transactions on Electromagnetic Compatibility, 2001, 43(2): 117-129.
[15]Tesche F M, Barnes P R. A multiconductor model for determining the response of power transmission and distribution lines to a high altitude electromagnetic pulse (HEMP)[J]. IEEE Transactions on Power Delivery, 1989, 4(3): 1955-1964.
[16]Xie Haiyan, Du Taijian, Zhang Maoyu, et al. Theoretical and experimental study of effective coupling length for transmission lines illuminated by HEMP[J]. IEEE Transactions on Electromagnetic Compatibility, 2015, 57(6): 1529-1538.
[17]Burrage L M, Veverka E F, Shaw J H, et al. Impact of the steep front, short duration impulse on electric power system insulation-final report[R]. 1991.
[18]马钦国, 米凯, 石磊, 等. 750kV输电线路防雷保护措施的研究[J]. 电网与清洁能源, 2014, 30(12): 67-77. Ma Qinguo, Mi Kai, Shi Lei, et al. Research on lightning protection in 750kV transmission lines[J]. Power System and Clean Energy, 2014, 30(12): 67-77.