0 引言
风能因其清洁永续的优点得到了快速的发展，我国的风电场大多采用集中式接入，电能通过双馈风电场送出变外送至系统[1-2]。目前双馈风电场送出变仍采用常规变压器保护，其原理是根据变压器两侧或三侧电流、电压的频率在故障前后相同，从而利用差动保护原理辨别区内和区外故障[3]。在双馈风电场容量占比较小时，电力系统保护的配置与整定值的计算不考虑其短路电流特性，而是简单地将风电场视为一个负荷，或将风力发电机作为同步发电机处理。但大规模的双馈风电场接入后，当电网发生故障时，双馈风电机组将向短路点提供短路电流[4]。由于双馈风电场的短路电流特性有别于常规的同步发电机[5-7]，基于传统电力系统故障的保护动作性能无法得到保证。风电接入电网后，故障的快速、正确切除已成为保证电网安全运行的重要因素[4]。
变压器是电力系统中最重要的设备之一，变压器保护能否正确动作对整个电力系统的安全稳定具有很大的影响。目前双馈风电场送出变保护主要以差动保护为主，但如何准确有效地区分变压器励磁涌流和内部故障电流，一直是变压器差动保护的难点。变压器励磁涌流的波形特征受多种因素的影响，致使以涌流波形为依据的防止空载投入误动的措施不能保证变压器差动保护不误动，随着变压器容量的增大、制造工艺的改进以及系统中容性设备的增加，2次谐波制动的可靠性问题日益突出，差动电流中2次谐波的含量与铁心饱和并不具备一一对应的关系，也就是说铁心饱和并不一定表现为2次谐波含量的增加，暂态过程中差动电流所分解得到的2次谐波也不一定是由铁心饱和造成的[8]。另外由于双馈风电场短路电流特性也会导致基于傅里叶算法提取工频相量的传统差动保护动作特性受到影 响。文献[9]指出具备低电压穿越能力的双馈风电场短路电流频率会发生偏移，傅里叶算法无法准确提取2次谐波，导致2次谐波分量被放大，从而使比率差动元件被2次谐波制动元件闭锁。文献[10]根据傅里叶原理，推导了信号频率偏移时2次谐波幅值以及2次谐波制动分量比的表达式，表明2次谐波幅值将会随时间以二倍频波动，并结合仿真实验分析了双馈风电场短路电流特性对变压器比率差动、2次谐波制动以及差动速断保护的影响。文献[11]分析了频率偏移对风电场主变压器差动保护动作特性的影响，指出具备低电压穿越能力的双馈风电机组短路电流频率不再保持工频，导致比率差动和2次谐波制动均无法保证快速动作。
很多专家和学者在风电机组的短路电流特性、风电场送出变压器保护的适应性等方面开展了系统、全面的研究工作，并取得了一系列研究成果。其中，对风电场送出变压器保护的性能分析主要集中在频率偏移对风电场主变压器差动保护动作特性的影响上。但是鲜有学者提出提高双馈风电场送出变差动保护的速动性与可靠性的保护新方案。因此，急需开发适用于双馈风电场送出变的新型保护。
本文针对双馈风电场短路电流频率偏移导致送出变传统差动保护无法快速准确动作的问题，提出了一种双馈风电场送出变差动保护新方案，该方案根据变压器等效电路，推导出励磁电感计算公式，计算出一定时间间隔内励磁电感的方差，根据励磁电感在不同情况下的数值特征制定判据，基于励磁电感的励磁涌流识别方法利用变压器饱和和非饱和状态下励磁电感的不同，判断铁心工作的状态，进而判别励磁涌流。该方法识别励磁涌流特征明确，能够快速、可靠地区分励磁涌流和各种内部故障，将励磁涌流闭锁判据与三段式比率差动和差动速断相结合构成双馈风电场送出变差动保护新方案。在Matlab/Simulink中搭建带撬棒（Crowbar）保护的双馈感应风机的风电场以及送出变差动保护仿真模型，仿真分析差动保护新方案的适应性。
1 双馈风电机组短路电流特性分析
当电网发生轻微故障时，机端电压跌落程度较轻，风机的Crowbar保护电路不投入，其短路电流特性主要与双侧变流器的控制策略相关。当电网故障导致机端电压严重跌落时，风机检测到转子过电流，投入Crowbar电路将转子侧的变流器短接，在此期间，变压器保护来不及动作。此后双馈风机相当于异步发电机，直到故障消失后，Crowbar保护电路退出[12]。
1.1 三相对称故障
三相对称故障时，短路电流解析式为
式中，As、Bs、Cs为对称故障时定子电流系数，详细表达式如附录式（A1）所示；系数表达式（A1）中，Rr、Lr分别为双馈风机转子电阻和电感；Lm为定转子绕组互感；
Lm+Lσs ，其中，Lσs、Lσr分别为定、转子漏感；Rs、Ls分别为双馈风机定子电阻和电感；s为转差率， 
其中，ω1为同步转速，ωr为转子转速；τs、τc分别为投入Crowbar电路后定、转子侧的时间衰减常数，
为Crowbar电阻值；Um为故障时刻机端电压幅值；K为电压跌落程度系数；α为故障时刻定子电压的初相角。
1.2 不对称故障
不对称短路故障时，短路电流的分析可表示为正序和负序两部分的叠加，短路电流正序分量的求解方法与三相短路电流的求解方法相同，短路电流分别为
式中，
为短路电流负序分量系数，详细表达式如附录式（A2）所示；Isc-abc1为短路电流正序分量；Isc-abc2为短路电流负序分量；系数表达式（A2）中，
为负序电压；α1为故障时刻定子负序电压的初相角。
由式（1）～式（3）可知，Crowbar保护电路动作后，对称故障和不对称故障时，短路电流均由衰减直流分量、强制基频分量和衰减的转速频率分量组成。故障初期短路电流主要由衰减的转速频率分量构成，其频率与当前的转速相关。双馈风电机组的转速一般为0.7～1.3(pu)，因此短路电流的频率将在35～65Hz之间变化。
2 短路电流经变压器变换
由于双馈风电场送出变通常采用Y-d11联结方式，这种联结方式的变压器在高压侧或低压侧短路时，故障侧和非故障侧的电压、电流在相位和幅值上都不相同，为了校核变压器保护的动作性能，需对这种联结方式的变压器故障进行分析计算。
2.1 三相对称故障
根据式（1）的短路电流表达式推导出变压器星形侧三相短路时A、B、C三相的短路电流，其中，A相短路电流表达式为
式中，
为对称故障时A相的电流系数，详细表达式如附录式（A3）所示，其中，
为星形侧A相的短路电流；星形侧B相短路电流
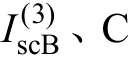相短路电流 
的初相位分别滞后星形侧A相短路电流120°和240°，故可根据星形侧A相短路电流表达式写出
的表达式。
星形侧三相短路时，三角形侧A、B、C三相的短路电流表达式为
式中，IΔa、IΔb、IΔc分别为三角形侧A、B、C三相的电流；IYA、IYB、IYC分别为星形侧A、B、C三相的电流；nB为变压器的电压比。据式（5）得
式中，
为三角形侧A相的短路电流；三角形侧B相短路电流
C相短路电流
的初相位分别滞后三角形侧A相的短路电流120°和240°，故可根据三角形侧A相短路电流表达式写出
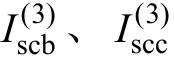的表达式。
对比式（4）和式（6）可知，当双馈风电场送出变星形侧发生三相短路时，短路电流经变压器传变后，三角形侧短路电流比星形侧短路电流超前 30°，幅值是星形侧短路电流的 nB倍。
2.2 不对称故障
以变压器星形侧A、B两相短路故障为例，根据式（2）写出变压器星形侧不对称短路时A、B、C三相的短路电流表达式为
式中，
分别为星形侧A、B两相短路时A、B、C三相的短路电流；
分别为不对称 故障时的电流系数，如附录式（A4）所示。
将式（7）代入式（5）可求解出星形侧A、B两相短路时，三角形侧A、B、C三相的短路电流表达式为
式中，
分别为三角形侧A、B、C三相的短路电流；
各系数的计算公式如附录 式（A5）所示。
根据式（8）可知，当变压器高压侧发生不对称故障时，三相短路电流经变压器变换后，三角形侧A、B、C三相的短路电流与星形侧短路电流相比幅值和相位均不同。
3 双馈风电机组短路电流特性对DFT的影响分析
双馈风电场送出变保护主要是通过傅里叶算法对故障发生后2～3个周期内数据进行处理，傅里叶算法对含有与基频相近的间谐波抑制效果较差，导致傅里叶算法无法准确提取工频相量，故障后傅里叶算法工频相量计算值会发生波动，代入保护动作方程，将会对各保护产生不同程度的影响[13]。
3.1 三相对称故障
三相短路故障时，短路电流经滤波处理后，认为衰减直流分量与高次谐波已经被滤除，以A相短路电流为例，对星形侧和三角形侧的短路电流分别进行离散傅里叶变换（Discrete Fourier Transform, DFT）基频相量计算，计算式为
式中，N为基频周期内的采样点数；n为谐波次数；XRe 为经DFT计算后的实部；XIn为经DFT计算后的虚部。
由所求得的实、虚部可进一步计算出n次谐波分量的幅值和相位分别为
分别将式（4）和式（6）的A相短路电流代入式（9），得到星形侧和三角形侧的A相短路电流经过DFT基频相量实部虚部计算结果为
其中
式中，
分别为三相 短路时星形侧A相短路电流经DFT基频相量计算后的实部、虚部、实部误差以及虚部误差；
分别为三相短路时三角形侧 A相短路电流经DFT基频相量计算后的实部、虚部、实部误差以及虚部误差。
3.2 不对称故障
根据式（9）对星形侧和三角形侧的短路电流分别进行离散傅里叶（DFT）基频相量计算，星形侧和三角形侧计算结果分别为
其中
式中，
分别为A、B 两相短路时星形侧A相短路电流经DFT基频相量计算后的实部、虚部、实部误差以及虚部误差；
分别为两相短路时三角形侧A相短路电流经DFT基频相量计算后的实部、虚部。
分析式（12）～式（15），
中含有ωr+ω1的衰减频率分量；
中含有ωr- ω1的衰减频率分量；同步发电机 的短路电流中不含有衰减的转速频率分量，短路电流经DFT计算出来的相量实部和虚部都是常数，而双馈风电场的短路电流中含有衰减的转速频率分量，三相短路时星形侧短路电流经DFT相量计算后， 存在
的偏差，三角形侧存在
的偏差，两相短路时星形侧、三角形侧短路 电流经DFT相量计算也都存在偏差，代入保护动作方程，将会对双馈风电场送出变的差动保护的动作性能产生影响。
3.3 仿真验证及分析
分别将对称故障、不对称故障时星形侧、三角形侧经DFT相量计算的实部和虚部，即式（11）～式（14）代入式（10），可求得星形侧、三角形侧短路电流经DFT提取工频相量的幅值和相位。为了验证双馈风电机组的短路电流经DFT变换后的计算表达式的正确性，在Matlab/Simulink上建立带Crowbar保护的双馈风电机组仿真模型，双馈风机额定功率为1.5MW，功率因数为0.9，额定电压为575V，额定转速为1.2(pu)，基准功率为额定视在功率，基准电压为额定电压，单台1.5MW双馈风机的仿真参数见表1。
表1 单台1.5MW双馈风机的仿真参数
Tab.1 Simulation parameters of single 1.5MW DFIG
（单位: pu） 参 数 数 值 定子电阻 0.023 转子电阻 0.016 撬棒阻值 0.005 定子漏感 0.18 转子漏感 0.16 定转子互感 2.9
1s时发生三相短路故障，机端电压跌落至额定电压的90%，1.01s故障消失，鉴于篇幅有限，本文只给出对称故障时星形侧短路电流的幅值和相位仿真值与理论值对比如图1和图2所示。
图1 短路电流基频幅值理论值与仿真值对比
Fig.1 Short-circuit current base frequency amplitude theoretical value and simulation value comparison chart
图2 短路电流基频相位理论值与仿真值对比
Fig.2 Comparison of theoretical and simulated values of the fundamental phase angle of short-circuit current
根据式（11），分别画出三相短路故障时，星形侧的短路电流经DFT向量计算后的幅值与相位的曲线，并将其分别与相应的仿真波形进行对比验证，由图1和图2可知，对称故障时星形侧短路电流的幅值和相位理论波形与仿真波形基本吻合，验证了双馈风电机组的短路电流经DFT基频计算表达式的正确性。图1中，在没有发生故障之前，理论波形与仿真波形基本完全重合，短路电流的幅值一直维持在0.997(pu)左右，在1s时发生故障后，短路电流增大到2.571(pu)，由于故障后风电短路电流频率偏移，导致DFT算法产生计算偏差，使短路电流经DFT计算后的幅值波动较大，但此时，理论计算波形与实际仿真波形还是相对比较接近的，随着时间的推移，风电短路电流逐渐衰减，所以理论计算波形与实际仿真波形的幅值也在逐渐衰减。由图2可知，在故障发生后，经DFT工频相量理论计算与实际仿真的相位波形也基本保持一致，但二者都在-85.37°～137.3°之间波动。由于DFT相量计算带来的偏差，致使短路后DFT相量计算值存在波动，将其代入差动保护判据，会对差动保护中的2次谐波元件、比率差动元件以及差动速断元件产生不同程度的影响，继而有可能导致双馈风电场送出变的差动保护无法正确动作。
4 差动保护原理
本文第3节通过理论分析和仿真验证了双馈风电机组的短路电流频率偏移特性会对DFT工频相量计算产生偏差，从而对风电场送出变差动保护的动作性能产生影响，基于此，本文提出了一种基于励磁电感计算的双馈风电场送出变差动保护。
风电场送出主变压器使用电力变压器微机保护，差动保护逻辑包括比率差动元件、涌流闭锁元件和差动速断元件[14]三个部分，变压器差动保护流程如图3所示。
图3 变压器差动保护流程
Fig.3 Flow chart of transformer differential protection
（1）差动速断。差动速断保护是当发生严重的区内故障时，快速地切除故障点。当三相差流中有任何一相满足差动速断保护动作条件时，差动速断保护动作。
（2）比率差动。比率差动保护一般采用三折线比率制动保护，其保护动作方程为
式中，Iop为差动保护动作电流；Iop.min为最小动作电流；Ires为制动电流；Ires.min为最小制动电流；In 为变压器二次侧额定电流；k1为比率差动系数。
（3）励磁涌流闭锁。励磁涌流时励磁电感数值在较大值与较小值之间波动，当发生内部故障时，励磁电感数值较小并且不会发生波动；在正常运行与外部故障时，励磁电感数值较大，根据变压器不同运行状况下励磁电感的数值特征制定励磁涌流判据[15]。
1）根据如图4所示的Y/Δ联结三相变压器T形等效电路，形成三相回路方程，即
式中，uA、uB、uC分别为变压器星形侧A、B、C三相电压；
分别为变压器三角形侧A、B、 C三相绕组电流；LA、LB、LC分别为变压器星形侧A、B、C三相漏感；RA、RB、RC分别为变压器A、B、C三相电阻；RmA、RmB、RmC分别为变压器A、B、C三相励磁电阻；LmA、LmB、LmC分 别为变压器A、B、C三相励磁电感；ip为三角形绕组中的环流；t为时间。
图4 三相变压器T形等效电路
Fig.4 T-shaped equivalent circuit diagram of three-phase transformer
2）由于励磁电阻、电阻、漏感均远小于励磁电感。对式（16）进行化简并离散化，得到A、B、C三相的励磁电感分别为
其中
式中，
为第k个采样点
离散值；
为第k+1个采样点离散值；
为第k个采样点
离散值；
为第k+1个采样点离散值；
为第k个采样点
离散值；
为第k+1个采样点离散值；ΔT为一个工频周期。
3）求解A相Δt时间内的励磁电感的方差为
式中，LmA(k)为A相k时刻的励磁电感；
为A相Δt时间内的励磁电感的平均值；
为A相Δt时间内的励磁电感的方差；m为Δt时间内的采样点数。同理可求B相和C相Δt时间内的励磁电感的方差。
4）当A、B、C三相任意一相Δt时间内的励磁电感的方差大于励磁涌流门槛值时，判别为发生励磁涌流，闭锁三段式比率差动为
式中，ε为励磁涌流整定值。
5 差动保护在双馈风电场中的适应性分析
为了验证双馈风电场送出变差动保护新方案的适应性，以图5所示双馈风电场送出系统为例，在Matlab/Simulink建立带Crowbar保护的双馈风电场仿真模型。其中，双馈风电机组单台装机容量为1.75MV·A，共20台机，总装机容量为35MV·A，系统短路容量为380MV·A，风电场短路容量比为9.2%，转差率为0.2。风电场出口电压等级为575V，经箱式升压变压器升压至35kV，再经风电场主变压器升压至110kV，而后经13.4km输电线路将电能送至110kV系统。
图5 双馈风电场送出系统
Fig.5 Equivalent circuit diagram of doubly fed wind farm delivery system
风电场主变压器送出变压器与差动保护参数见表2。
表2 双馈风电场送出变压器与差动保护参数
Tab.2 Double fed wind farm outgoing transformer and differential protection parameters
参 数 数 值 额定容量/(MV·A) 65 联结方式 Yd11 高压侧 NU /kV 110 低压侧 nU/kV 35 星形侧二次侧额定电流 NI/A 2.84 三角形侧二次侧额定电流 nI/A 4.47 最小动作电流 n0.5I 最小制动电流 res.minI nI 差动速断电流 n8I 比率制动系数 1k 0.5
利用Simulink中搭建的双馈风电场以及送出变差动保护模型，分别对不同运行状态下的双馈风电场送出变差动保护新方案进行适应性分析，并对比仿真分析传统差动保护与新方案的动作特性，鉴于篇幅有限，本文只给出三角形侧发生A相匝间短路时差动保护新方案与传统差动保护的仿真结果以及动作情况如图6～图10所示。其他仿真结果见表3。根据仿真实验分析的方法确定计算励磁电感方差的数据窗为Δt=0.02s ，A、B、C三相励磁涌流整定值均为ε=300。
图6 三角形侧A相匝间短路时三相比率差动动作特性
Fig.6 Three-phase ratio differential action characteristic of triangle side A phase-to-turn short circuit
图7 三角形侧A相匝间短路时三相励磁电感瞬时值
Fig.7 Instantaneous value of three-phase magnetizing inductance when the Δ side A phase is short-circuited between turns
图8 2次谐波制动动作特性
Fig.8 Two harmonic braking action characteristics
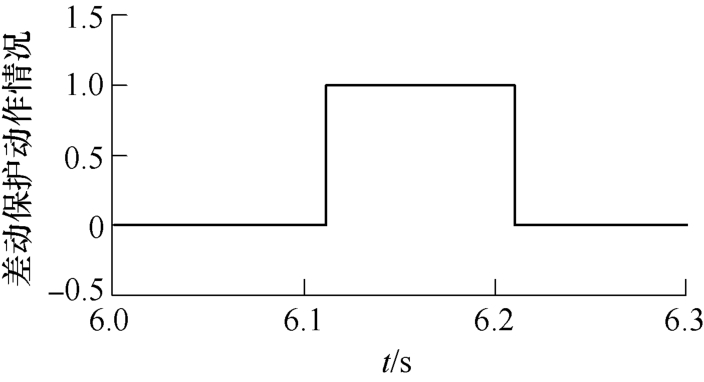
图9 传统差动保护动作情况
Fig.9 Traditional differential protection action
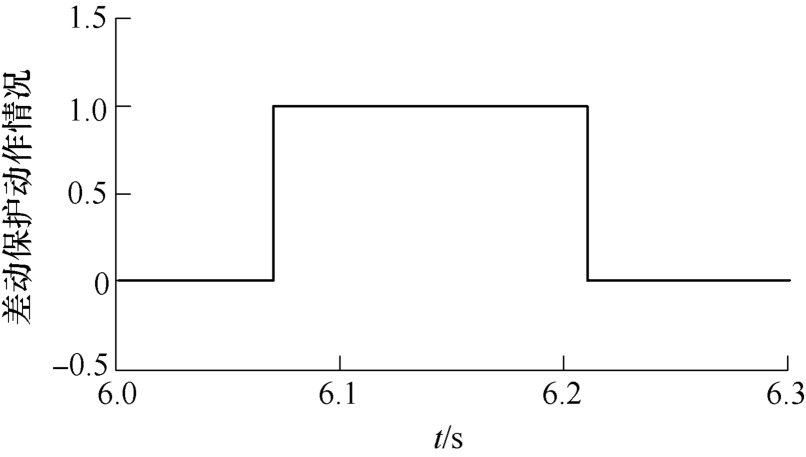
图10 励磁电感直接计算差动保护动作情况
Fig.10 Traditional differential protection action
双馈风电机组转速为1.2(pu)，在6.05～6.2s时送出变三角形侧发生A相匝间短路，短路匝数比为50%，发生故障后，检测到转子侧过电流，投入Crowbar电路将转子侧短接。A、B、C三相的差动速断动作值都小于差动速断整定值，差动速断元件不动作。从图6可知，在故障发生后，差动电流与 制动电流经DFT相量计算后的幅值都具有一定的波动，并且在故障期间存在制动量大于差动量的情况。在故障前期A、C相比率差动动作量大于制动量，在6.09～6.118s之间，A相动作量小于制动量，而在6.118～6.2s之间，A相动作量大于制动量，在6.094～6.111s之间，C相动作量小于制动量，而在6.111～6.2s之间，C相动作量大于制动量，在故障期间B相动作量都小于制动量。从故障发生起一周期内A、B、C相励磁电感瞬时值结果如图7所示，计算出的瞬时励磁电感变化幅度较小，其数值也相对较小，这表明了匝间短路时变压器铁心未饱和，励磁电感数值基本保持不变。其中，根据式（18）计 算出A、B、C三相一周期内的励磁电感方差值分别 为
均小于励磁涌流门槛值，励磁涌流闭锁元件不动作。传统差动保护中根据2次谐波分量比是否小于励磁涌流整定值来判断是否发生励磁涌流，本文取2次谐波分量比整定值为0.15，从图8可知，在6.05～6.114s之间，2次谐波分量比大于整定值，将比率差动元件闭锁，在6.114～6.118s之间，虽然2次谐波分量比小于整定值，但是A相动作量小于制动量，所以差动保护依然无法正确动作，在6.114～6.2s之间，C相比率差动动作量大于制动量且2次谐波分量比小于整定值，差动保护动作。在故障发生初期，由于双馈风电场侧的短路电流频率发生偏移，2次谐波制动元件将会闭锁差动保护，随着故障时间的推移，风电场侧的短路电流会逐渐衰减，从而导致2次谐波分量比减小，然而在此期间，差动保护的动作性能无法得到保证，差动保护保护的动作时间将会被延长。根据图9和图10对比分析传统差动保护与新方案的动作情况可知，传统差动保护在6.118s动作，即在故障发生后68ms才动作，新方案差动保护在6.07s动作，即故障发生后20ms动作。
鉴于篇幅有限，将仿真分析验证差动保护新方案适用性的其他仿真结果见表3。分析表3可知，除了星形侧三相短路、星形侧A、B两相短路、星形侧三相接地短路这三种运行状态下，传统差动保护动作时间略小于新方案动作时间外，其他运行状态下差动保护新方案动作时间都小于传统差动保护。当发生空载合闸于故障时，传统差动保护2次谐波制动分量比大于整定值，将比率差动闭锁，保护不能准确动作，而新方案的励磁电感方差小于励磁涌流门槛值，A、C相的比率制动在故障期间动作量大于制动量，差动保护动作。
进一步对比分析表3的仿真结果，得到双馈风电场送出变保护的影响因素。
表3 各种运行状态下差动保护动作结果
Tab.3 Differential protection action results under various operating conditions
励磁电感方差/H 动作结果 动作时间/s 案例 故障类型 差动 速断 比率 差动 mA L Δ mB L Δ mC L Δ 传统 差动 差动 新方案 传统 差动 差动 新方案 1 正常运行 不动 不动 0.800 0.794 0.796 不动 不动 无 无 2 区外三相故障 不动 不动 0.870 0.900 0.908 不动 不动 无 无 3 三角形侧A相匝间短路（匝比50%） 不动 A、C相动作 0.385 0.221 0.311 动作 动作 0.068 0.02 4 三角形侧A相匝间短路（匝比34%） 不动 A、C相动作 0.348 0.304 0.365 动作 动作 0.086 0.02 5 空载合闸 不动 B、C相动作 110.59 528.40 214.58 不动 不动 无 无 6 空载合闸于A相匝间短路 不动 A、C相动作 44.152 228.800 53.427 不动 动作 无 0.02 7 星形侧A相匝间短路（匝比50%） 不动 A、C相动作 0.275 0.193 0.385 动作 动作 0.048 0.02 8 星形侧三相短路 不动 A、B、C相动作 0.304 0.356 0.222 动作 动作 0.018 0.02 9 星形侧A、B两相短路 不动 A、B相动作 0.574 0.056 0.796 动作 动作 0.014 0.02 10 星形侧三相接地短路 不动 A、B、C相动作 0.331 0.481 0.371 动作 动作 0.018 0.02 11 短路容量比为4.6% （三角形侧A相匝间短路） 不动 A、C相动作 0.797 0.300 0.710 动作 动作 0.044 0.02 12 转速为1.1(pu) （三角形侧A相匝间短路） 不动 A、C相动作 1.269 2.177 5.002 动作 动作 0.029 0.02
（1）故障位置。对比分析案例3和案例7差动保护的动作性能仿真结果可知，当变压器发生区内故障时，故障位置在送出变近双馈风电场侧时，双馈风电场侧短路电流较大，对送出变的差动保护影响较大，导致差动保护的动作时间延迟较长，若故障位置在送出变远离风电场侧时，因双馈风电场侧的短路电流较小，所以差动保护动作时间延迟较短，不管是近风电场侧还是远风电场侧，传统差动保护动作的时间都大于差动保护新方案的动作时间。
（2）故障类型。对比分析案例8和案例9差动保护的动作性能仿真结果可知，当发生对称短路故障时，双馈风电场的短路电流频率偏移较明显，对送出变差动保护影响较大，相比于对称故障，不对称故障对送出变差动保护的影响较小，传统差动保护的动作时间略小于差动保护新方案的动作时间。
（3）短路容量比。对比分析案例3和案例11差动保护的动作性能仿真结果可知，双馈风电场接入系统的短路容量比一般不超过10%，其容量占系统短路容量的比例越大，对送出变差动保护的影响也越大，短路容量比越大，传统差动保护动作的时间越长，且都大于差动保护新方案。
（4）运行工况。对比分析案例3和案例12差动保护的动作性能仿真结果可知，当转速与同步转速相差越大时，双馈风电场频率与基频相差也越大，对送出变差动保护的影响也越显著，传统差动保护的动作时间长；反之，对送出变的差动保护影响较小，且传统差动保护的动作时间都大于差动保护新方案。
6 结论
本文在理论分析双馈风电场送出变两侧短路电流中的衰减转速频率分量会使DFT相量计算产生偏差的基础上，提出了一种适用于双馈风电场送出变的差动保护新方案，并结合仿真分析验证了送出变两侧的短路电流经傅里叶算法计算的正确性以及差动保护新方案的适用性，得到如下结论：
1）理论推导与仿真结果均表明双馈风电场短路电流经变压器变换后，送出变两侧的短路电流中的衰减转速频率分量会导致傅里叶算法无法准确提取基频相量。
2）仿真结果表明基于傅里叶算法提取工频量的双馈风电场送出变传统差动保护的比率制动保护元件和2次谐波制动元件均无法保证快速动作，差动保护的动作时间将会被延长。
3）仿真结果表明变压器空载合闸于故障时传统差动保护不能准确动作，而差动保护新方案却能准确动作，并且该新方案能较好地提高双馈风电场送出变差动保护的速动性与可靠性，改善了风电场短路电流频率偏移导致差动保护不能准确动作的问题。
附 录
其中
其中
其中
[1]张保会, 王进, 李光辉, 等. 具有低电压穿越能力的风电接入电力系统继电保护的配合[J]. 电力自动化设备, 2012, 32(3): 1-6. Zhang Baohui, Wang Jing, Li Guanghui, et al. Coordination of relay protection for wind power connected to power system with low voltage ride through capability[J]. Power Automation Equipment, 2012, 32(3): 1-6.
[2]欧阳金鑫, 唐挺, 郑迪, 等. 低电压穿越控制下双馈风电机组短路电流特性与计算方法[J]. 电工技术学报, 2017, 32(22): 216-224. Ouyang Jinxin, Tang Ting, Zheng Di, et al. Short- circuit current characteristics and calculation method of doubly-fed wind turbines under low voltage ride- through control[J]. Transactions of China Electro- technical Society, 2017, 32(22): 216-224.
[3]王增平, 李菁, 郑涛, 等. 考虑变流器限流与GSC电流的双馈风力发电机暂态全电流计算与分析[J]. 电工技术学报, 2018, 33(17): 4123-4135. Wang Zengping, Li Jing, Zheng Tao, et al. Calcu- lation and analysis of transient full current of doubly-fed wind turbines considering current limiter and GSC current[J]. Transactions of China Electro- technical Society, 2018, 33(17): 4123-4135.
[4]文玉玲, 晁勤, 吐尔逊·依布拉音. 风电场对电网继电保护的影响[J]. 电网技术, 2008, 32(14): 15-18. Wen Yuling, Chao Qin, Tulson Yibrayin. Influence of wind farm on grid relay protection[J]. Power System Technology, 2008, 32(14): 15-18.
[5]陈实, 邰能灵, 范春菊, 等. 考虑风力发电的配电网弱馈线路自适应电流保护[J]. 电工技术学报, 2017, 32(3): 65-73. Chen Shi, Tai Nengling, Fan Chunju, et al. Adaptive current protection of weak feed lines in distribution network considering wind power generation[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 65-73.
[6]廉茂航, 任永峰, 韩鹏, 等. 双馈风电系统中VRB储能型网侧九开关变换器[J]. 电工技术学报, 2018,33(6): 1197-1207. Lian Maohang, Ren Yongfeng, Han Peng, et al. The VRB energy storage network side nine-switch converter in the doubly-fed wind power system[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1197-1207.
[7]郭鹏, 文晶, 朱丹丹, 等. 基于源-荷互动的大规模风电消纳协调控制策略[J]. 电工技术学报, 2017, 32(3): 1-9. Guo Peng, Wen Jing, Zhu Dandan, et al. Large-scale wind power consumption coordination control strategy based on source-load interaction[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 1-9.
[8]李家羊, 岑韬, 张磊, 等. 提高柔性直流输电换流阀阀控系统性能的方法研究[J]. 电气技术, 2017, 18(12): 152-156. Li Jiayang, Cen Tao, Zhang Lei, et al. Research on the method of improving the performance of flexible DC transmission converter valve control system[J]. Electrical Engineering, 2017, 18(12): 152-156.
[9]韩璐, 李凤婷, 王春艳, 等. 风电接入对继电保护的影响综述[J]. 电力系统保护与控制, 2016, 44(16): 163-169. Han Lu, Li Fengting, Wang Chunyan, et al. An overview of the impact of wind power access on relay protection[J]. Power System Protection and Control, 2016, 44(16): 163-169.
[10]张保会, 王进, 郝治国, 等. 风电接入对继电保护的影响(三)——风电场送出变压保护性能分析[J]. 电力自动化设备, 2013, 33(3): 1-8. Zhang Baohui, Wang Jin, Hao Zhiguo, et al. Impact of wind farm integration on relay protection(3): performance analysis for wind farm outgoing trans- former protection[J]. Power Automation Equipment, 2013, 33(3): 1-8.
[11]姜达军, 张罗马, 高丙团, 等. 风电场短路电流频率不一致性及其对纵差保护的影响[J]. 电气应用, 2017, 36(5): 32-38. Jiang Dajun, Zhang Luoma, Gao Bingtuan, et al. Frequency inconsistency of short circuit current in wind farms and its effect on longitudinal differential protection[J]. Electrical Application, 2017, 36(5): 32-38.
[12]李建林, 许洪华, 胡书举. 风力发电系统低电压运行技术[M]. 北京: 机械工业出版社, 2008.
[13]李菁, 郑涛, 赵裕童, 等. 双馈风电短路电流特性对距离保护的影响分析[J]. 电力系统保护与控制, 2017, 45(6): 37-47. Li Jing, Zheng Tao, Zhao Yutong, et al. Influence of short circuit current characteristics of DFIG on distance protection[J]. Power System Protectiion and Control, 2017, 45(6): 37-47.
[14]王维俭. 发电机变压器继电保护应用[M]. 北京: 中国电力出版社, 2005.
[15]焦在滨, 马涛, 屈亚军, 等. 基于励磁电感参数识别的快速变压器保护[J]. 中国电机工程学报, 2014, 34(10): 1658-1666. Jiao Zaibin, Ma Tao, Qu Yajun, et al. Fast trans- former protection based on excitation inductance parameter identification[J]. Proceedings of the CSEE, 2014, 34(10): 1658-1666.