0 引言
直流配电系统因可以高效、灵活地接入新能源电源与直流负荷且供电半径及容量大，成为配电网研究热点之一[1]。然而，直流配电系统故障时换流器自身控制保护动作速度快[2-3]，故障有效信息短、等值阻抗时变，传统基于固定频率下幅值、相位故障特征保护难以在多分支、分段结的配网中准确识别故障区域。如何利用有限的故障暂态信息快速有选择地切除故障，成为直流配电系统保护所面临的新挑战。
目前，柔性直流配电系统保护方案仍处于理论研究阶段，通常借鉴交流和直流输电系统的保护方案进行配置和整定。根据保护原理可将现有直流保护分为双端量和单端量保护。双端量保护基于通信可实现全线速动，文献[4-5]研究了差动保护在直流配电系统中的应用，其不受分布式电源和故障电流大小的影响。文献[6]利用限流电抗器两侧暂态电压的比值构成纵联保护，具有良好的抗过渡电阻能力。双端量保护需要同时比较线路两端的信息，对于暂态信息而言，需要高质量的信道和较严格的同步信号，将其广泛配置于直流配网中存在一定的难度。
单端量保护无需考虑通信问题。文献[7-8]研究了传统电流、电压以及微分保护在直流配电系统中的应用，其动作速度快，但配电系统结构复杂，相邻区域保护定值整定困难，大多依赖于仿真计算。文献[9-10]研究了行波保护应用于直流配网中的技术问题，依靠行波通过边界元件时不同的故障特性进行保护，动作速度快，但由于配电线路通常较短，对采样率要求较高，并且不一定每条线路都有滤波电抗作为边界元件，其应用范围受限。文献[11-12]将距离保护应用于直流配电网中，依赖于一次系统的特殊结构或装置，并且易受测量、计算误差和过渡电阻的影响，造成保护误动或者拒动。可见，现有单端量保护定值整定困难、易受过渡电阻和换流器自身故障控制等因素的影响，适用范围受限。
本文针对柔性直流配电系统中故障有效信息短、故障等效阻抗时变，同时系统分支多、难以准确识别故障区域的问题，将系统故障后产生的高频分量看作在故障点引入高频源，分析故障高频信号在换流器不同开关过程中的通路，通过分析简化，建立了不受控制策略影响的换流器高频恒定阻抗等效模型。在此基础上，提出一种高频突变量距离保护，该方法利用本地量测得到的故障前后几ms的电气量信息，快速提取高频分量，利用高频电压、电流以及高频阻抗进行计算，同时结合保护的整定配合实现故障区域的识别。在PSCAD/EMTDC仿真平台上搭建六端柔性直流配电系统模型进行仿真。实验结果表明，所提保护方法能够正确识别故障区域，具有良好的速动性和选择性，同时具有较好的耐受过渡电阻和噪声的能力。
1 柔性直流配电系统暂态高频阻抗特性分析
1.1 柔性直流配电系统结构
本文参考贵州、张北小二台等柔性直流配电工程，搭建六端柔性直流配电系统作为研究对象。该直流系统通过两个基于钳位双子模块的模块化多电平换流器（Clamp Double Submodule-Modular Multilevel Converter, CDSM-MMC）与中压交流系统相连，CDSM-MMC在故障后能快速闭锁，清除系统中的故障电流[13]。光伏、直流负荷和储能装置通过直流变换器（DC-DC）接入±10kV直流配电系统，DC-DC采用双向全桥（Dual Active Bridge, DAB）变换器的基本结构，DAB中的高频变压器能够实现两侧的电气隔离。中压交流系统通过Z型变压器经高阻接地，六端柔性直流配电系统结构如图1所示。
配电线路两端配有隔离开关和电压、电流监测点，故障后换流器闭锁清除故障电流，保护识别故障区域，跳开故障区段快速隔离/分段开关。由于直流配电系统中一般采用高阻接地的运行方式，当系统发生单极接地故障时，不会出现严重的过电流现象，保护不需要快速动作，因此本文主要针对双极短路故障进行研究分析。
1.2 柔性直流配电系统故障暂态高频阻抗
在柔性直流配电系统中，系统发生故障后，故障点的电压会由正常工作电压瞬间跌落至较低水平，产生一个类似于阶跃信号的电压波形。对该故障信号进行频谱分析可得到它的全频域信息，信号频率越高，其频谱密度越大[14]，因此故障暂态电压 信号可以看作在故障点瞬间加入了高频电压源。如图1中在t =0时刻k点发生金属性故障时，引入的高频故障突变量状态如图2所示。
图1 六端柔性直流配电系统结构
Fig.1 Structure diagram of six-terminal flexible DC distribution system
图2 系统故障突变量状态
Fig.2 State diagram of system fault component
图2中，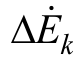
表示故障产生的高频源， 
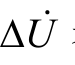表示母线处测得的高频电压值，Δi表示电路中的高频 电流，Zk表示故障线路的高频阻抗，ZS表示系统等值阻抗，其中包括换流器等值阻抗。本文基于系统中的高频阻抗，通过提取本地量测得的故障暂态电气量中的高频信息进行计算，识别故障区域并进行保护的整定。系统故障后由于受电力电子装置控制影响，换流器阻抗时变，因此，保护的关键在于对换流器高频阻抗进行等值。
1.3 换流器高频恒定阻抗等效模型
随着电力电子器件的发展，目前MMC和DC- DC成为柔性直流系统的主要实现形式[15]。本文仅以CDSM-MMC和DC-DC为例，进行换流器高频阻抗等效模型的推导。需要说明的是，本文所提等效方法的适用性不局限于这两种换流器拓扑。
1.3.1 CDSM-MMC高频恒定阻抗等效模型
图3所示为CDSM-MMC闭锁前直流侧简化等效电路。图中，L0为桥臂电感，C0为子模块电容，Rarm为桥臂电阻，npi、nni（i=a, b, c）分别为三相上、下桥臂投入的子模块数量；LZ为交流侧Z型变压器的等效电抗，Rg为接地电阻。
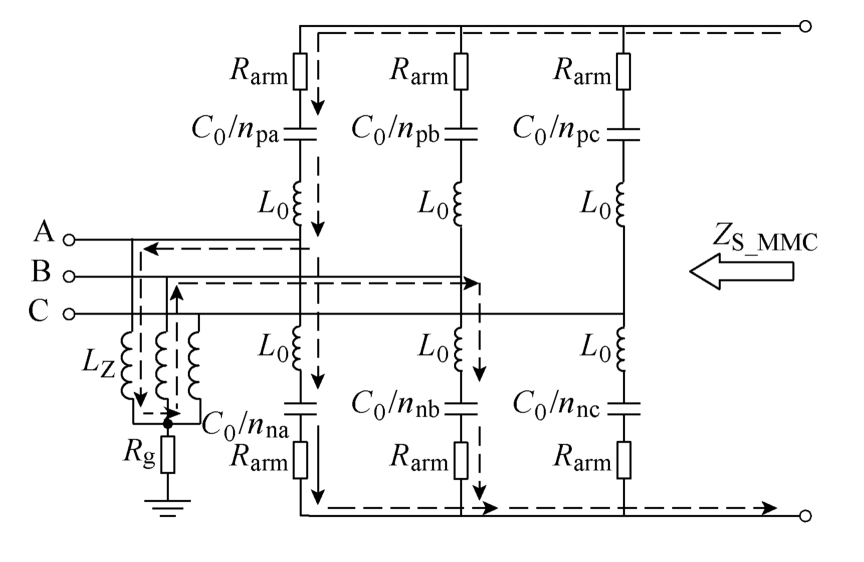
图3 CDSM-MMC闭锁前直流侧简化等效电路
Fig.3 DC-side simplified equivalent circuit of the CDSM-MMC before blocking
图3中虚线表示直流侧发生故障后a、b两相间的部分高频电流回路，每两个回路之间可构成一个惠斯通电桥，以其中一个惠斯通电桥为例，分析系统故障后桥臂开关状态以及交流侧对CDSM-MMC等效模型的影响。CDSM-MMC中，A、B两相间的故障高频回路如图4所示。
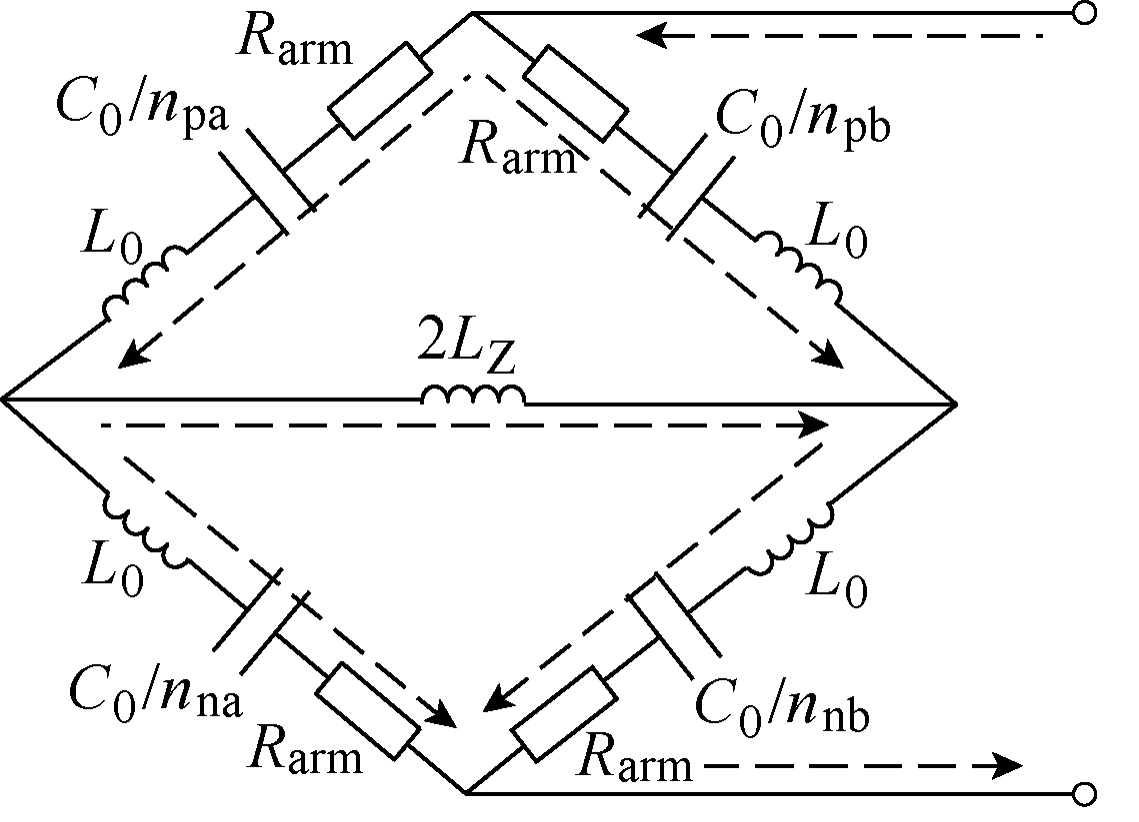
图4 CDSM-MMC故障高频回路
Fig.4 High frequency circuit after CDSM-MMC failure
CDSM-MMC中每个相单元的上、下桥臂分别有N个子模块，任意时刻上、下桥臂投入的子模块之和恒等于N[16]。假设上桥臂投入n个子模块，则下桥臂投入的子模块数为N-n，忽略桥臂中IGBT的导通电阻，以a相为例，此时上、下桥臂的阻抗分别为
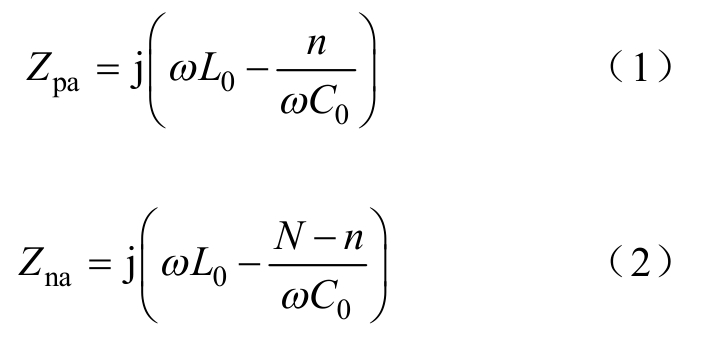
本文所用仿真模型中MMC为五电平（N=2），其中，L0=15mH，C0=0.5mF，按照n=N的极端情况计算，在f =1kHz时
利用高频量对保护进行分析，f≫82Hz。其中桥臂电抗参数是根据系统电压等级和换流器容量确定的[17]。文献[18]指出，子模块参数改变必须遵守C0/N保持恒定不变的原则，因此在同一电压等级下，当子模块数发生变化时，上述分析结论仍成立。
由上述分析可知，在数kHz的高频下有
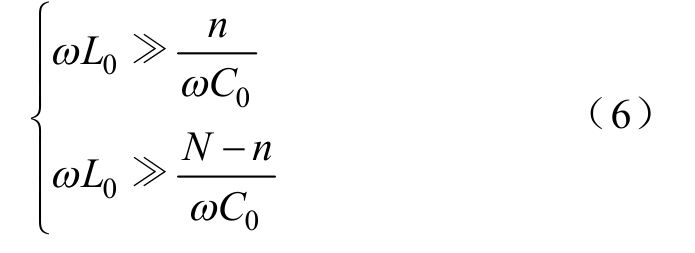
根据式（1）、式（2）和式（6）可得
b、c两相的阻抗分析与a相相同，由此可知，在高频下电桥的四个臂阻抗近似相等，电桥达到平衡，LZ所在的中间支路没有电流流过，因此，交流侧阻抗对高频回路的影响可以忽略。同时可以看出在高频下CDSM-MMC中上、下桥臂子模块的投切状态对其高频阻抗影响不大，可忽略回路中电力电开关状态所带来的非线性影响，通过简化得到直流侧发生故障时CDSM-MMC直流侧高频恒定阻抗等效模型如图5所示。
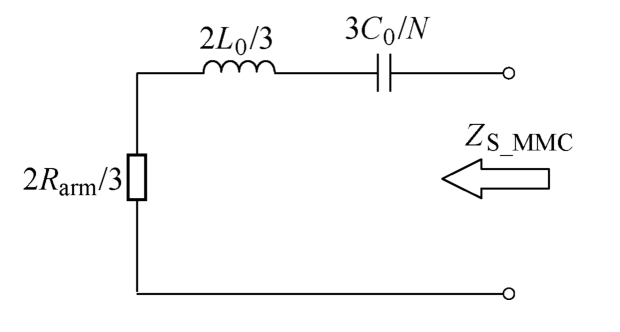
图5 CDSM-MMC直流侧高频阻抗等效模型
Fig.5 DC-side high frequency impedance equivalent model of the CDSM-MMC
CDSM-MMC的高频等值阻抗可以表示为
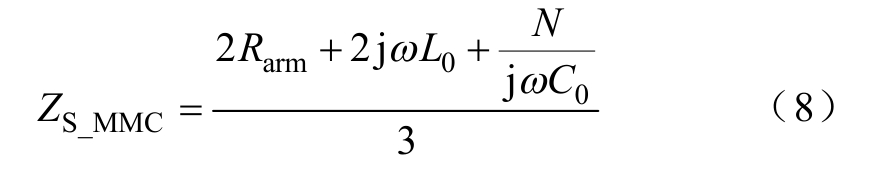
1.3.2 DC-DC高频恒定阻抗等效模型
直流配电系统中±10kV直流线路通过多层DAB模块实现与低压直流的连接，多个DAB模块在低压侧并联，中压侧则采用串联连接，可以提高系统的耐压水平[19]，其具体结构如附图1所示。首先对DC-DC中单个DAB模块的故障高频回路进行等效分析。在DAB模块工作过程中，两侧H桥的开关频率相同，对角开关管同时导通[20]，单个DAB模块故障高频回路如图6所示，系统直流侧发生双极短路故障时，在高频下得到两种故障回路。图中C0、C1分别表示中压直流侧和低压直流侧出口电容，L表示换流器出口电抗，Zl表示线路高频阻抗。
图6 单个DAB模块故障高频回路
Fig.6 Fault high frequency circuit of a single DAB module
分析图6中的高频回路可知，IGBT不管处于哪种开关状态，高频电流在DAB模块的一次侧和二次侧都会两次经过开关器件。本文采用短窗提取系统直流侧故障高频分量，短窗内系统故障电压（电流）变化产生的暂态信号的强度要远高于高频变压器等效开关频率，因此换流器等效开关频率的影响可以忽略。首先根据变压器的原理将理想高频变压器部分等效成一个T型等效电路，并把系统参数都折算到变压器的高压侧，得到如图7所示的单个DAB模块直流侧高频阻抗等效模型。
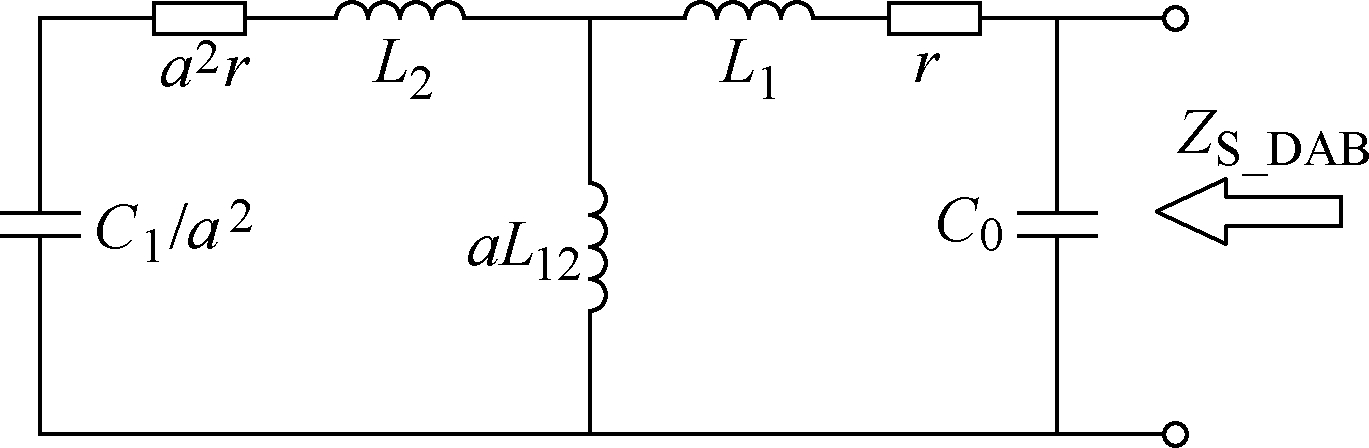
图7 单个DAB模块直流侧高频阻抗等效模型
Fig.7 DC-side high frequency impedance equivalent model of a single DAB module
图7中，a为变压器的电压比，r为桥臂开关器件的导通电阻，L1、L2和L12为变压器T型等效电路的阻抗参数。将系统参数代入可得 L1=L2= 0.106 1mH，L12=53.025 1mH。由于L12的计算值大约为L1（L2）的500倍，在等效时为使计算更加简便，可将L12所在支路忽略，此时单个DAB模块的高频等值阻抗为
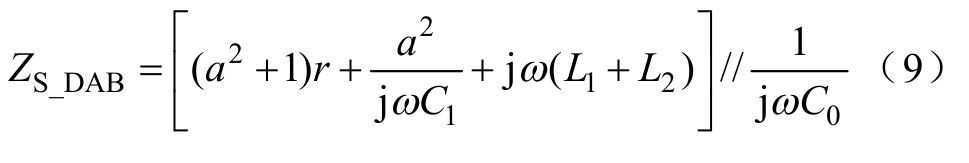
从中压直流端口看进去的DC-DC为10个DAB模块串联，现已求得单个DAB模块的高频等效阻抗，那么DC-DC换流器的高频阻抗就可以用10个DAB等效阻抗串联来表示，即
由式（8）、式（9）可以看出，CDSM-MMC和DAB型DC-DC的高频等值阻抗仅与其自身的参数以及频率有关，与电力电子器件的开关过程以及开关状态无关。在特定频率下，换流器的等值阻抗为恒定值，解决了阻抗时变问题，为保护研究奠定了基础。
2 基于高频突变量的距离保护
2.1 高频突变量保护原理
首先以图1中1号、3号和4号换流器间的线路为例，分析直流配电系统高频突变量距离保护原理，图8给出了直流线路不同位置短路时电压高频故障分量在系统中的分布。
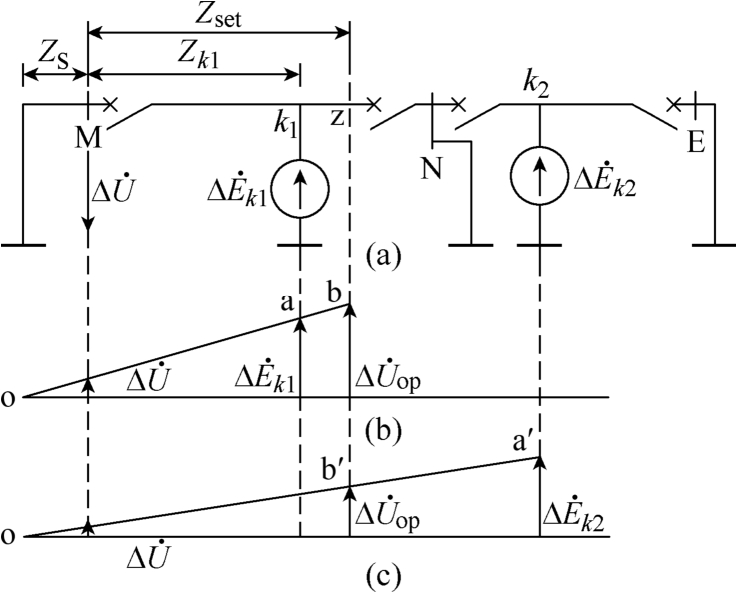
图8 不同位置短路时电压高频故障分量的分布
Fig.8 Distribution of voltage high-frequency fault components when short-circuited at different positions
当k1点发生双极短路故障时，母线M保护安装处的高频故障分量电流、电压可以分别表示为
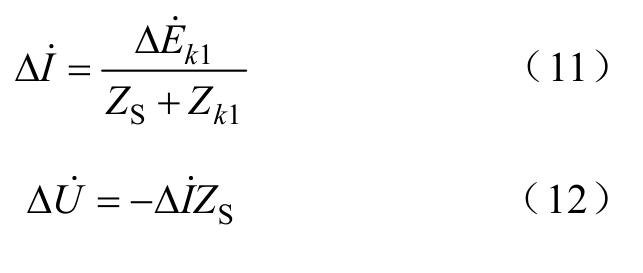
高频故障分量距离元件的高频工作电压为
式中，Zset为保护的高频阻抗整定值；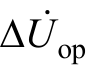
对应图8 中z点的高频电压。
在保护区内k1点短路时，如图8b所示，b点 （
的末端）在o点与a点（
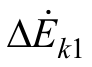的末端）连线的延长线上，这时有
。
在正向区外k2点短路时，如图8c所示，b′点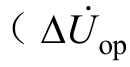 
的末端）在o点与a′点（
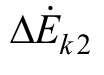的末端）的连线上，
。
根据上述分析可知，比较高频工作电压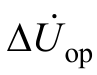 
与高频电源电动势幅值的大小就能够区分区内与区外 故障。线路发生金属性故障时，故障点电压在几ms内降为零，该电压可以用非故障状态下短路点电压值构造阶跃来代替，故障附加状态下高频电源电动势的大小可以用所构造的阶跃电压中提取出来的高 频分量
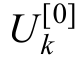表示。假定故障前为空载，短路点电压 的大小等于保护安装处母线电压的大小，高频故障分量距离元件的动作判据可以表示为
满足式（14）判定为区内故障，保护动作；不满足式（14），判定为区外故障，保护不动作。
2.2 高频突变量距离保护的整定计算
参照交流系统中距离保护的配置方式和整定计算，高频突变量距离保护采用阶梯延时配合的两段式配置方式。下面分别针对保护Ⅰ、Ⅱ段的整定原则进行分析。
2.2.1 不同电路结构对保护安装处高频测量阻抗的影响
系统中的分支会影响保护安装处所测得的高频阻抗。因此，以图9所示不同系统结构对高频测量阻抗的影响为例分析直流分支对于整定的影响。
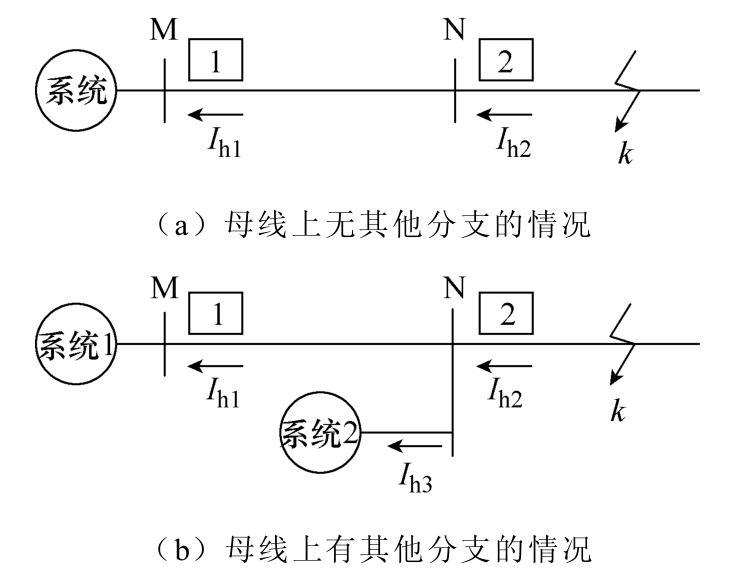
图9 不同系统结构对高频测量阻抗的影响
Fig.9 Influence of different system structures on high frequency measurement impedance
图9a为电路母线上无其他分支的情况，在k点发生双极短路故障时，保护1和2处测得的高频阻抗ZS_M和ZS_N分别为
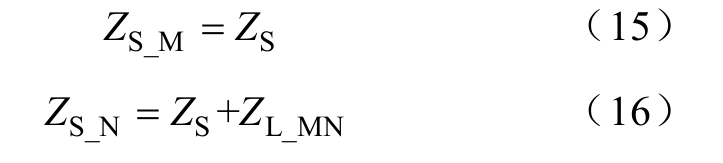
式中，ZS为母线M处所连系统的高频等值阻抗，ZL_MN为线路MN的高频阻抗。
图9b为当k点发生故障后，故障点高频源所产生的电流流经母线N时，一部分经线路MN流向系统1，另一部分流向系统2所在支路，保护2处所测得的高频阻抗为两条支路阻抗的并联，可以表示为
式中，ZS1和ZS2分别表示系统1和系统2的高频等值阻抗。保护1处的高频测量阻抗和第一种情况测得的结果相同，上述分析中的ZS_M和ZS_N等价于式（13）中的ZS。
2.2.2 高频突变量距离保护Ⅰ、Ⅱ段的整定
距离保护Ⅰ段为速动保护段，无时间延时，按照躲开相邻线路出口故障整定为
式中，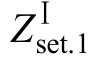 
为距离Ⅰ段的线路高频整定阻抗；LMN为被保护线路的长度；z1为被保护线路单位长度的阻抗；
为可靠系数，由于距离保护为欠量保护，所以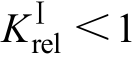
，考虑到互感器误差和参数测量误差等 因素，一般取0.80～0.85。
距离保护Ⅱ段线路阻抗整定值需要与相邻线路距离保护Ⅰ段配合。若保护2的Ⅰ段线路阻抗整定 值为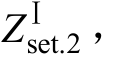 
则保护1的Ⅱ段线路整定阻抗为
式中，
距离保护Ⅱ段可靠系数，一般取0.8。
距离保护Ⅱ段，应该能够保护线路的全长，本线路末端短路时，应该有足够高的灵敏度。考虑各种误差因素，要求灵敏系数满足
如果
不满足要求，则距离保护Ⅱ段应改为 与相邻线路的保护Ⅱ段相配合，计算的方法与上面类似，此处不再赘述。
保护Ⅱ段的动作延时，应该比与之配合的相邻线路保护动作时间大一个时间级差 tΔ，即
式中，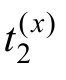
为与本保护配合的相邻线路保护段（x为 Ⅰ段或Ⅱ段）的最大动作时间。
系统发生故障后，换流器阀级保护动作，CDSM- MMC能在几ms内闭锁并清除故障，电流变为零[21]。DAB模块闭锁后的工频电流回路如图10所示。DC- DC中的IGBT闭锁后，首先进入电容放电阶段，此时二极管承受反压无法导通，电流通路如图10中的点画线所示。当电容电压第一次经过零点后，二极管将满足导通条件，此时电感电流将通过H桥的反并联二极管进行续流，电容支路被旁路，如图10中虚线所示。根据系统中的参数计算以及仿真实验可知，故障后电路中的电流将会持续100ms以上，直流变换器故障后工频电流仿真如图11所示。同时考虑换流器闭锁消除故障电流时间、快速开关动作速度等因素，将保护Ⅱ段的动作延时取为20ms。若故障后距离Ⅰ段未动作切除故障，在经过保护Ⅱ段20ms的延时后，电路中仍可以检测到直流电流。
图10 DAB模块闭锁后的工频电流回路
Fig.10 Power frequency current loop after blocking of DAB module
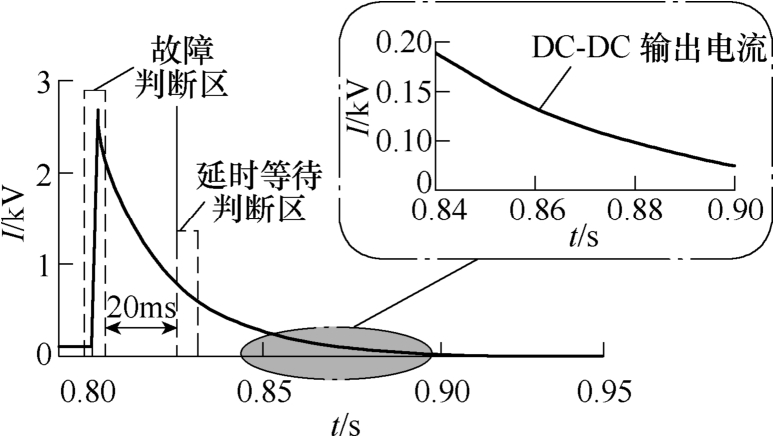
图11 直流变换器故障后工频电流仿真
Fig.11 Simulation diagram of power frequency current after DC converter failure
高频突变量距离保护Ⅰ、Ⅱ段是通过提取故障前后3ms时间窗长内的暂态高频量来判断系统中故障的发生，换流器闭锁以后，回路中的故障高频电流无法流通，高频量迅速减少。保护Ⅱ段经20ms 延时后，无法再利用电路中的高频信息对故障状态进行判断。为了区分本级线路末端与下级线路出口处故障，需要为保护Ⅱ段增加一个补充判据——延时等待判据，保护Ⅱ段利用故障瞬间产生的高频量检测到故障，经20ms延时后利用延时等待判据判断回路中是否还存在电流。若是下级线路出口故障，下级线路保护Ⅰ段能迅速动作将故障切除，延时等待判据不满足条件，保护Ⅱ段可靠返回；若本级线路末端发生故障，经20ms延时后延时等待判据仍能满足条件，保护Ⅱ段动作。根据对换流器故障特性的分析，将延时等待判据整定为
式中，IN为系统正常运行时的额定电流；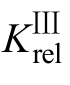
为可 靠系数，一般取1.15～1.25。
在求得线路整定阻抗后，根据式（11）可以计算出保护安装处距离元件保护Ⅰ、Ⅱ段的高频工作电压幅值，然后根据式（12）比较Ⅰ、Ⅱ段高频工作电压整定值与高频电源电动势的大小来判断是否发生故障。若满足保护Ⅰ段动作条件，则Ⅰ段瞬时动作切除故障，Ⅱ段可靠返回；若Ⅰ段不满足，Ⅱ段满足动作条件。则经Ⅱ段延时后检测延时等待判据是否满足要求，若满足延时等待判据，保护Ⅱ段动作；若不满足，保护Ⅱ段可靠返回。
对于本文所研究的系统，可以采用低电压过电流保护来检测故障，作为故障启动判据。差动保护和高频距离保护相互配合进行故障识别。近端故障时两者都满足条件，由于距离保护Ⅰ段无需通信，能够快速无延时动作。差动保护在忽略通信延时的情况下能实现全线速动，远端故障一般由差动保护切除，动作延时为10ms。高频距离保护Ⅱ段可作为差动的备用，延时20ms动作。若上述保护失灵均未动作，则低电压过电流保护延时50ms动作，无选择性地断开线路上所有的隔离开关。各保护的动作区域与延时保护方案配合如图12所示。
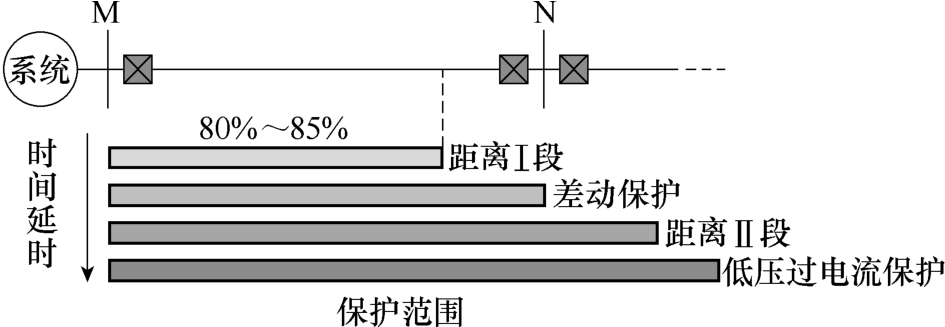
图12 保护方案配合
Fig.12 Protection scheme coordination diagram
3 仿真与验证
为验证所提保护新原理的可行性，在PSCAD中搭建了如图1所示的六端柔性直流配电系统，系统的具体参数见附录。仿真过程中所用的采样频率为10kHz，仿真步长为10μs，系统在0.8s时发生故障。计算时采用小波变换进行高频分量的提取，所选小波变换的中心频率fc=2Hz，带宽频率fb=10Hz。利用di/dt在0.3ms内快速检测出故障，确定故障时刻，考虑不同系统故障后换流器闭锁时间的差异，同时保留一定裕度，将数据窗长取为故障时刻前后各3ms。
3.1 换流器直流侧高频阻抗等效模型验证
根据1.3节中的分析，在所搭建的模型中对CDSM- MMC和DC-DC高频等值阻抗模型的准确性进行了仿真验证。通过小波变换对故障后换流器出口处测得的电压和电流进行频域变换，相同频率下电压和电流的比值即为换流器在该频率下的阻抗计算值，利用式（8）～式（10）分别求得换流器的高频阻抗理论值，将换流器高频阻抗的计算值与理论值进行比较，得到如图13所示的结果。
根据仿真结果可以看出，MMC高频等效模型在500～3 500Hz范围内，DC-DC高频等效模型在500～1 700Hz范围内高频阻抗计算值和理论值的吻合度很高，误差小。该仿真结果验证了本文推导的换流器直流侧高频阻抗等效模型的有效性。依据 两种换流器阻抗计算值和理论值的仿真结果，本文选取1～1.6kHz（每隔100Hz）频率范围作为距离保护研究频段。
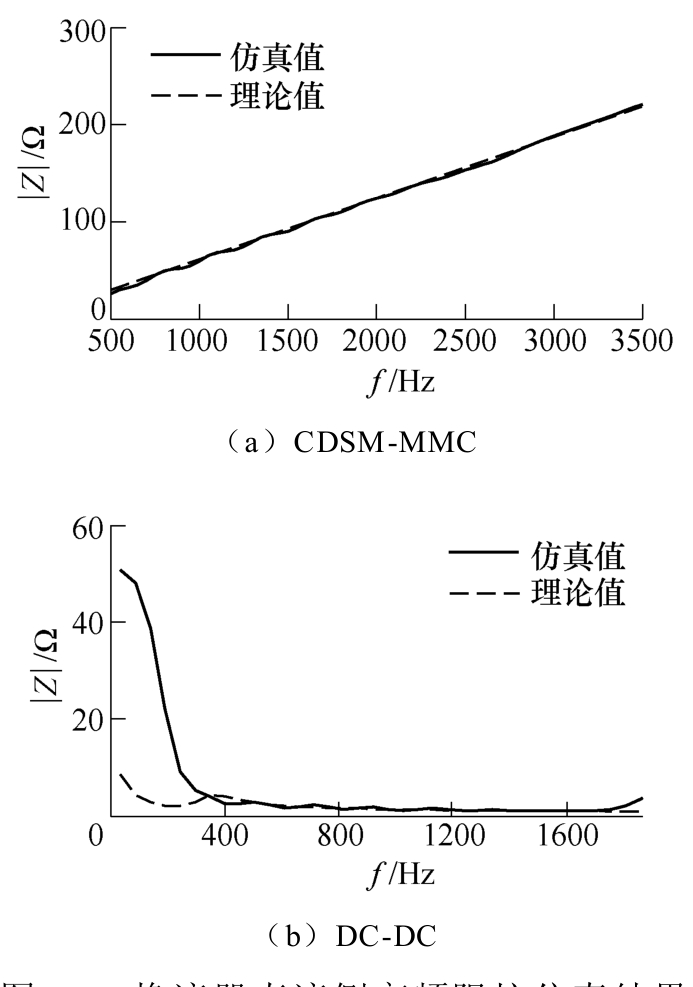
图13 换流器直流侧高频阻抗仿真结果
Fig.13 Simulation results of the DC-side high frequency impedance of the converter
3.2 直流线路不同位置故障仿真结果
对图1所示的柔性直流配电系统不同位置的故障进行仿真，系统分别在k1、k2和k3点（k1位于线路13的中点，k2位于线路13上距离该线路左侧母线95%处，k3位于线路34上距离该线路左侧母线5%处）发生双极短路故障时线路13和34两端距离保护元件的Ⅰ、Ⅱ段整定值与高频电源电动势比较情况如图14～图16所示。
图14 线路13上k1点发生故障
Fig.14 Failure at point k1 on the line13
当k1点发生故障时，故障位于线路13保护区内，保护13和31的Ⅰ、Ⅱ段整定值均大于高频电源电动势，由于Ⅱ段有延时，故障后Ⅰ段满足条件快速动作，Ⅱ段可靠返回；保护34和43的距离保护整定值均小于高频电源电动势，线路34上的保护能够可靠不动作。
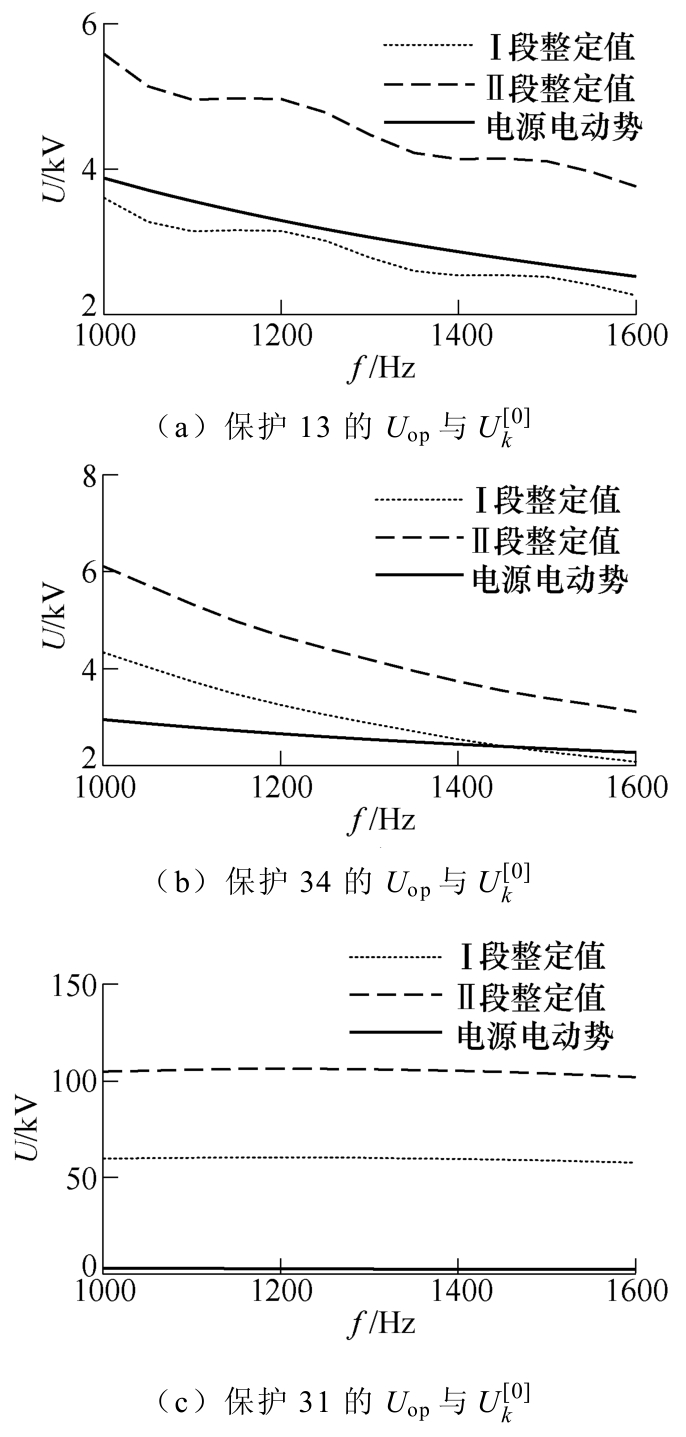
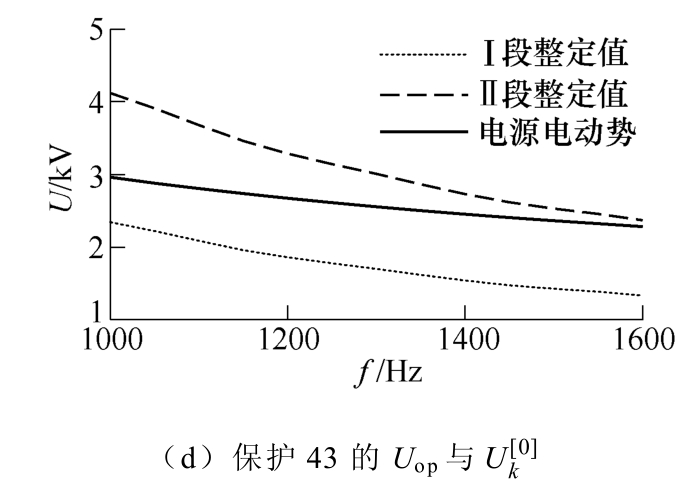
图15 线路13上k2点发生故障 Fig.15 Failure at point k2 on the line13
图16 线路34上k3点发生故障
Fig.16 Failure at point k3 on the line34
当k2点发生故障时，故障位于线路13上，但靠近保护31，保护13的Ⅰ段整定值小于高频电源电动势，不动作，Ⅱ段整定值大于电源电动势，并且在经过Ⅱ段延时后，延时等待判据满足条件，保护Ⅱ段动作；保护31的Ⅰ、Ⅱ段整定值均大于电源电动势，Ⅰ段能够快速可靠动作；对于保护34来说，该故障属于反方向故障（利用电流极性可以判断），无需比较高频电压关系；由于保护31在故障后快速动作故障电流消失，保护43的Ⅱ段能够可靠返回。
当k3点发生故障时，保护34和43的Ⅰ、Ⅱ段整定值都大于高频电源电动势，Ⅰ段可以无延时动作切除故障电流；保护13的Ⅱ段整定值大于高频电源电动势，但由于保护34的Ⅰ段瞬间动作切断了故障，此时延时等待判据不满足动作条件，故其保护Ⅱ段不动作；保护31通过电流极性识别反向故障，可靠不动作。
在本文所研究的六端柔性直流配电系统每条线路的不同位置设置双极短路故障点，如图1所示。在每个故障点设置金属性故障、非金属性故障（过渡电阻10Ω）以及在所测得的电压、电流中随机加入30dB高斯噪声，统计系统中各保护的动作情况，表1给出了不同位置、不同类型故障保护动作情况。
表1 不同位置、不同类型故障保护动作情况
Tab.1 Protecting action of different position and different types
注：表中的百分数表示故障点到本线路左侧母线的距离，“√”表示保护动作，“×”表示保护不动作。
保护情况 保护45 保护54 保护65 保护56 故障类型 Ⅰ段 Ⅱ段 Ⅰ段 Ⅱ段 Ⅰ段 Ⅱ段 Ⅰ段 Ⅱ段k5(35%) √ × √ × × × × × k6(88%) × √ √ × × × × × k7(95%) × × × × × √ √ × 金属性 故障 k8(60%) × × × × √ × √ × k5(35%) √ × √ × × × × × k6(88%) × √ √ × × × × × k7(95%) × × × × × √ √ × 过渡 电阻 k8(60%) × × × × √ × √ × k5(35%) √ × √ × × × × × k6(88%) × √ √ × × × × × k7(95%) × × × × × √ √ × 30dB 噪声 k8(60%) × × × × √ × √ ×
表1中未列出的线路也均针对上述几种故障类型和故障情况做了仿真，所得结果显示系统中不同位置发生双极短路故障时，在10Ω 过渡电阻和30dB噪声情况下，保护仍能快速有选择性地准确识别故障区域，说明该保护方法能够耐受一定的过渡电阻，同时具有抗噪声能力，仿真结果验证了本文所提保护方法的可行性和有效性。
4 结论
本文针对柔性直流配电系统，基于系统故障时所产生的暂态电气量信息，通过分析故障高频信号在换流器开关过程中的回路，建立了换流器高频阻抗等效模型，解决了故障等值阻抗时变的问题。在此基础上，提出了一种基于高频突变量的距离保护新方法。该方法利用本地量测信息进行故障区域识别，无需通信，算法简单，具有良好的速动性和选择性，同时具有较好的耐受过渡电阻和噪声的能力。大量仿真结果表明，该方法能够快速准确识别故障区域，在柔性直流配电系统中具有良好的适用性。
附录 仿真系统参数
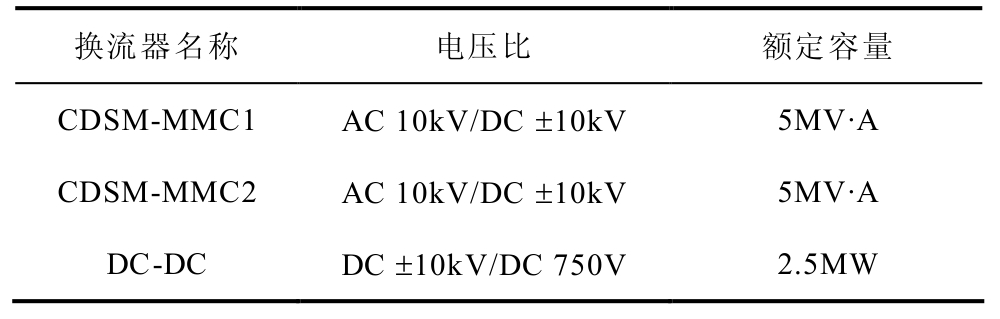
附表1 换流器参数
App.Tab.1 Parameters of converters
?
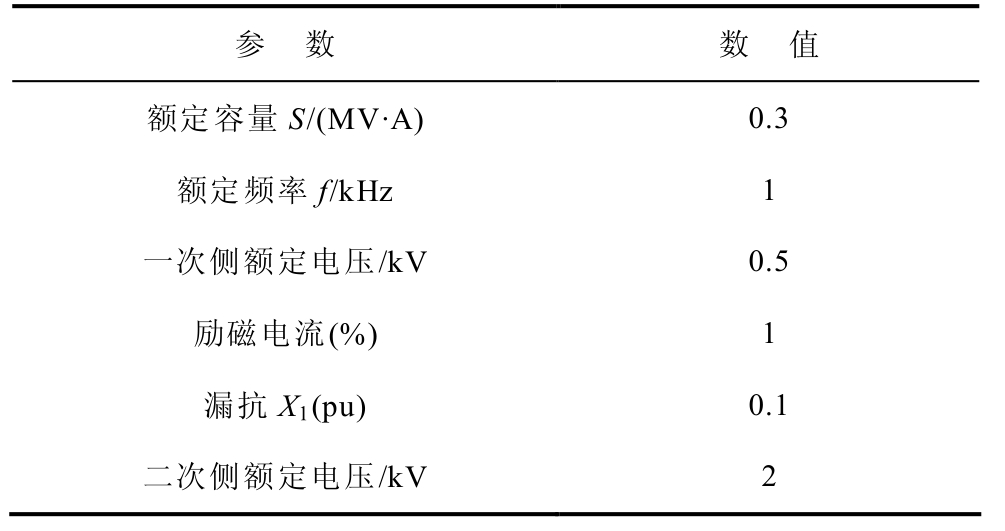
附表2 高频变压器参数
App.Tab.2 Parameters of high-frequency transformer
?
附表3 直流线路参数
App.Tab.3 Parameters of DC lines
线路(Line) 长度/km 电阻/(Ω/km) 电感/(mH/km) 电容/(10-9F/km)12 2.50 0.066 9 0.685 7 8.34 23 1.75 0.066 9 0.685 7 8.34 36 3.00 0.066 9 0.685 7 8.34 14 3.50 0.066 9 0.685 7 8.34 45 2.75 0.066 9 0.685 7 8.34 56 3.75 0.066 9 0.685 7 8.34
附图1 DAB型DC-DC拓扑结构
App.Fig.1 Topology of DAB type DC-DC
[1]李露露, 雍静, 梁仕斌, 等. 民用低压直流供电系统保护综述[J]. 电工技术学报, 2015, 30(22): 133- 143. Li Lulu, Yong Jing, Liang Shibin, et al. A review of civil low voltage DC distribution system pro- tection[J]. Transactions of China Electrotechnical Society, 2015, 30(22): 133-143.
[2]戴志辉, 葛红波, 严思齐, 等. 柔性直流配电网故障分析[J]. 电工技术学报, 2018, 33(8): 1863-1874. Dai Zhihui, Ge Hongbo, Yan Siqi, et al. Fault analysis of flxible DC distribution system[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(8): 1863-1874.
[3]李斌, 何佳伟. 柔性直流配电系统故障分析及限流方法[J]. 中国电机工程学报, 2015, 35(12): 3026- 3036. Li Bin, He Jiawei. DC fault analysis and current limiting technique for VSC-based DC distribution system[J]. Proceedings of the CSEE, 2015, 35(12): 3026-3036.
[4]时伯年, 赵宇明, 孙刚. 柔性直流配电网保护方案研究及实现[J]. 南方电网技术, 2015, 9(9): 11-16. Shi Bonian, Zhao Yuming, Sun Gang. Research and implementation of protection scheme for MMC DC distribution network[J]. Southern Power System Technology, 2015, 9(9): 11-16.
[5]Monadi M, Zamani M A, Koch-Ciobotaru C, et al. A communication-assisted protection scheme for direct- current distribution networks[J]. Energy, 2016, 109: 578-591.
[6]嵇康, 邰能灵, 刘剑, 等. 基于暂态电压的多端柔性直流线路保护方案[J]. 电力科学与技术学报, 2018, 33(1): 3-10. Ji Kang, Tai Nengling, Liu Jian, et al. Protection scheme for multi-terminal VSC-HVDC lines based on transient voltage[J]. Journal of Electric Power Science and Technology, 2018, 33(1): 3-10.
[7]王艳婷, 张保会, 范新凯. 柔性直流电网架空线路快速保护方案[J]. 电力系统自动化, 2016, 40(21): 13-19. Wang Yanting, Zhang Baohui, Fan Xinkai. Fast protection scheme for overhead transmission lines of VSC-based HVDC grid[J]. Automation of Electric Power Systems, 2016, 40(21): 13-19.
[8]刘鑫蕊, 谢志远, 孙秋野, 等. 低压双极性直流微网故障分析及保护方案[J]. 电网技术, 2016, 40(3): 749-755. Liu Xinrui, Xie Zhiyuan, Sun Qiuye, et al. Fault analysis and protection for LV bipolar DC micro- grid[J]. Power System Technology, 2016, 40(3): 749-755.
[9]Azizi S, Sanaye-Pasand M. A traveling-wave-based methodology for wide-area fault location in multi- terminal DC systems[J]. IEEE Transactions on Power Delivery, 2014, 29(6): 2552-2560.
[10]董新洲, 王珺, 施慎行. 配电线路单相接地行波保护的原理与算法[J]. 中国电机工程学报, 2013, 33(10): 154-160, 6. Dong Xinzhou, Wang Jun, Shi Shenxing. Principle and algorithm of traveling waves based single- phase-to-ground protection for distribution lines[J]. Proceedings of the CSEE, 2013, 33(10): 154-160, 6.
[11]李猛, 贾科, 毕天姝, 等. 适用于直流配电网的测距式保护[J]. 电网技术, 2016, 40(3): 719-724. Li Meng, Jia Ke, Bi Tianshu, et al. Fault distance estimation-based protection for DC distribution networks[J]. Power System Technology, 2016, 40(3): 719-724.
[12]Yang J, Fletcher J E, O'Reilly J. Multiterminal DC wind farm collection grid internal fault analysis and protection design[J]. IEEE Transactions on Power Delivery, 2010, 25(4): 2308-2318.
[13]徐殿国, 李彬彬, 周少泽. 模块化多电平高压变频技术研究综述[J]. 电工技术学报, 2017, 32(20): 104-116. Xu Dianguo, Li Binbin, Zhou Shaoze. Overview of the modular multilevel converter based high voltage motor drive[J]. Transactions of China Electro- technical Society, 2017, 32(20): 104-116.
[14]李军, 万文军, 刘志刚. 一种阶跃函数在矩形时间窗口频域特性的分析方法[J]. 电力自动化设备, 2013, 33(11): 111-116, 122. Li Jun, Wan Wenjun, Liu Zhigang. Method for analyzing frequency-domain characteristics of step function in rectangular time window[J]. Electric Power Automation Equipment, 2013, 33(11): 111- 116, 122.
[15]李斌, 李晔, 何佳伟. 具有直流故障清除能力的MMC子模块关键性能研究[J]. 中国电机工程学报, 2016, 36(8): 2114-2122. Li Bin, Li Ye, He Jiawei. Research on the key properties of MMC sub-modules with DC fault eliminating capability[J]. Proceedings of the CSEE, 2016, 36(8): 2114-2122.
[16]范志华, 苗世洪, 刘子文, 等. 模块化多电平换流器子模块故障特性分析与解耦控制策略[J]. 电工技术学报, 2018, 33(16): 3707-3718. Fan Zhihua, Miao Shihong, Liu Ziwen, et al. Modular multilevel converter sub-module fault characteristics analysis and decoupling control strategy[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(16): 3707-3718.
[17]杨用春, 肖湘宁, 郭世枭, 等. 基于模块化多电平变流器的统一电能质量调节器工程实验装置研究[J]. 电工技术学报, 2018, 33(16): 3743-3755. Yang Yongchun, Xiao Xiangning, Guo Shixiao, et al. Research of unified power quality conditioner engineering experiment device based on modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3743-3755.
[18]徐政, 肖晃庆, 张哲任. 模块化多电平换流器主回路参数设计[J]. 高电压技术, 2015, 41(8): 2514- 2527. Xu Zheng, Xiao Huangqing, Zhang Zheren. Design of main circuit parameters of modular multilevel converters[J]. High Voltage Engineering, 2015, 41(8): 2514-2527.
[19]姜山, 范春菊, 黄宁, 等. 电力电子变压器直流端口极间短路故障特性分析[J]. 中国电机工程学报, 2018, 38(5): 1301-1309. Jiang Shan, Fan Chunju, Huang Ning, et al. Fault characteristic analysis of DC pole-to-pole fault in power electronic transformer[J]. Proceedings of the CSEE, 2018, 38(5): 1301-1309.
[20]季振东. 级联型电力电子变压器关键技术研究[D].南京: 东南大学, 2015.
[21]郝瑞祥, 杨晓峰, 薛尧, 等. 一种具有直流故障限流能力的模块化多电平换流器[J]. 电工技术学报, 2017, 32(6): 172-180. Hao Ruixiang, Yang Xiaofeng, Xue Yao, et al. A novel modular multilevel converter with DC fault current limiting capability[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 172-180.