0 引言
同步相量测量装置（Phasor Measurement Unit, PMU）因其同步性与快速性，已成为监测电力系统动态过程的有效工具之一[1-4]。如何测试和校准PMU在静态和动态条件下的测量精度是该装置能否广泛应用的关键问题。为此，国内外发布了PMU测试标准用于规定PMU在静动态条件下的量测性能[5-7]，标准通过建立表征电力系统典型静动态过程的信号数学模型，并设置比实际电力系统更大的信号参数变化范围，以使PMU在实验室更苛刻的测试条件下通过测试校准得到精确的量测量，从而保证PMU应用于实际系统时，能更好地跟踪系统的动态变化。
目前，为得到PMU的量测性能，国内外应用的PMU测试系统之一为基于高精度信号源的测试系统[8-10]，该类测试系统根据PMU测试标准中信号的理论数学模型生成与GPS（global position system）同步的测试信号与基准量测量，因此信号源的精度应保证所发信号的幅值、频率等参数与理论模型参数之间的误差小于标准要求4倍以上[11]，对信号源的精度要求很高。部分信号源在经数模转换器（Digital-to-Analog Convertor, DAC）与功率放大器等模块将数字量同步输出为模拟量的过程中，产生较大的随信号参数变化而变化的难以精确补偿的误差，无法作为测试信号源。
因此，为解决在缺乏高精度信号源的条件下无法提供满足校准要求的基准值的问题，IEEE标准委员会、美国国家标准技术研究院（National Institute of Standard and Technology, NIST）、美国德州农机大学等研究机构提出了基于PMU校准器的测试系 统[12-14]。该类测试系统将信号源生成的PMU测试标准规定的测试信号同时发送给PMU校准器和待测PMU，将校准器的量测量作为基准值，与待测PMU的量测量进行比较，从而得出待测PMU的测量误差。因此，该类测试系统无需高精度且与GPS同步的信号源。作为PMU测试误差分析参考值的提供设备，校准器的测量精度应高于标准要求4倍以上[11]。因此，如何保证PMU校准器的测量精度是该类测试系统的关键与难点。
算法性能与硬件精度是直接关系到PMU校准器精度的主要因素。其中，硬件可通过选用高精度、高成本的板卡来满足精度要求；而算法则是PMU校准器研究的重点与难点。
近年来，国内外学者提出了多种相量计算方法，包括离散傅里叶变换（Discrete Fourier Transform, DFT）及其改进算法[15-17]、卡尔曼滤波[18]、最小二乘法[19]和频域动态模型法[20]等。但上述算法均针对实际PMU装置开发，强调算法的通用性与实时性，故其精度难以满足标准对校准器测量精度的要求。有文献提出了适用于PMU校准器的相量算法[12-13]，但仍基于静态相量模型，动态条件下测量精度难以满足国内PMU标准[5]。因此，亟需提出一种适用于国内外PMU静态和动态测试的高精度量测算法。
本文建立了PMU静态和动态测试通用相量拟合模型，提出了适用于PMU校准器的基于非线性拟合的高精度相量计算方法，能够为不同静态和动态过程提供基准量测量。通过硬件选型搭建了PMU校准器，为验证搭建的PMU校准器的测量精度，从算法仿真与实验测试两方面对其进行了验证。
1 PMU静态和动态测试相量拟合模型
1.1 相量拟合模型与求解方法可行性分析
PMU校准器用于PMU实验室测试与校准，与商用PMU相比有两个特点：①在进行PMU静态和动态测试时，信号源根据PMU标准规定的测试项目发出测试信号，即测试信号类型在测试时已知，这使得在算法中建立与测试信号对应的信号数学模型成为可能；②PMU校准器无需进行实时测量，不要求快速的响应时间，只要测量结果带有时标，即可作为校准基准值，这使得通过采用较长的时间窗与复杂的迭代拟合算法以提高测量精度成为可能。本节基于第一个特点，建立了PMU静态和动态测试相量拟合模型。
PMU国内外标准将PMU测试分为稳态测试与动态测试[5-7]。稳态测试主要模拟电力系统在稳态条件下的不同运行工况；动态测试主要模拟电力系统不同动态过程，包括模拟功率振荡的调制测试、模拟失步的频率斜坡测试等（各测试类型的目的详见附录）。通过分析，本文建立两类通用相量拟合模型，包括适用于稳态和频率斜坡测试的拟合模型、适用于调制测试的拟合模型。
1.2 稳态与频率斜坡测试相量拟合模型
理论上，稳态测试信号的幅值、频率和初相角为常数；频率斜坡测试信号的幅值为常数，频率线性增加或减小。因此，建立拟合模型为
式中，Xm为相量幅值；fn为额定频率（50Hz）；φ0为初相角；Δf为频率偏移量，表征信号源实际所发信号的频率偏离额定频率fn的情况；Rf为频率线性变化速率，一方面表征信号频率在频率斜坡测试中线性变化；另一方面表征信号频率在稳态测试中信号源因同步误差导致的频率波动。
该模型中，Xm、Δf、Rf、φ0为四个待求解的参数，构成待求参数向量p=[XmΔf Rf φ0]。由p可得到该模型的相量、频率和频率变化率的理论值分别为
式中，
和rf(t)分别为t时刻的相量、频率 和频率变化率的理论值；幅值X(t)与相位θ (t)的表达式分别为
此外，稳态测试中还包括谐波测试与带外测试，其测试信号是在稳态基波信号上分别叠加多个谐波和间谐波干扰信号，若将上述干扰信号加入拟合模型，则式（1）变为
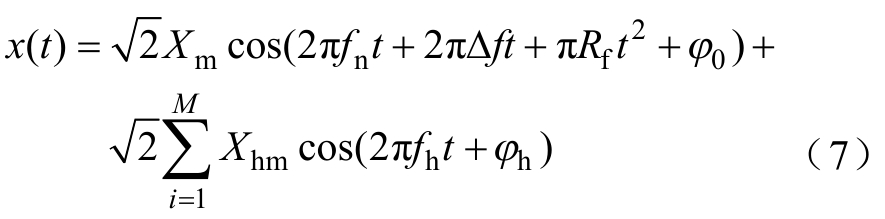
式中，Xhm、fh和φh分别为谐波或间谐波的幅值、频率和初相角；M为谐波和间谐波信号的个数。
若用式（7）作为含干扰信号的拟合模型，则待求解参数为3M+4个，多个待拟合谐波和间谐波参数的存在会严重影响基波参数的拟合精度。例如，谐波测试中需同时测试PMU在2～25次谐波条件下的测量精度，则待求解参数为76个。
因此，基于PMU校准器无需实时测量与快速响应的特点，本文采用高阶带通数字滤波器滤除谐波和带外测试信号等干扰信号。所采用的滤波器需在有效滤除干扰信号的同时，不对PMU测量频带范围内信号（45～55Hz）产生影响。
1.3 调制测试相量拟合模型
调制测试中信号的幅值或相位以一定频率发生正弦变化，且基频会发生偏移，则其拟合模型为
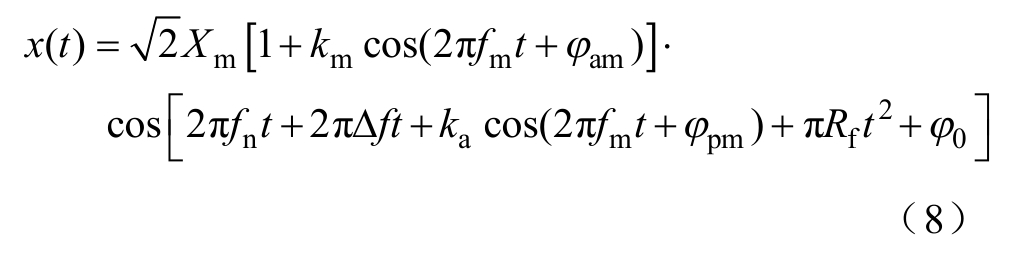
式中，km为幅值调制深度；ka为相位调制深度；fm 为调制频率；φam为幅值调制初相角；φpm为相位调制初相角。Δf的设置作用与其在式（1）中一致。 相位不发生调制时，Rf用以表征频率的微小波动；相位发生调制时，频率和频率变化率也会随之进行正弦调制，由ka与fm表征，此时Rf表征频率的非正弦微小波动。
在PMU标准中，调制测试分为三类，包括：幅值调制（Amplitude Modulation, AM）测试（km≠0, ka=0），待求解参数向量p=[XmkmfmφamΔf Rf φ0]；相位调制（Phase Modulation, PM）测试（km=0, ka≠0），待求解参数向量p=[XmfmφpmΔf kaRf φ0]；幅值相位同时调制测试（km≠0, ka≠0），待求参数向量p=[XmfmkmφamΔf kaφpmRfφ0]。该拟合模型在t时刻的相量、频率和频率变化率的理论值分别为
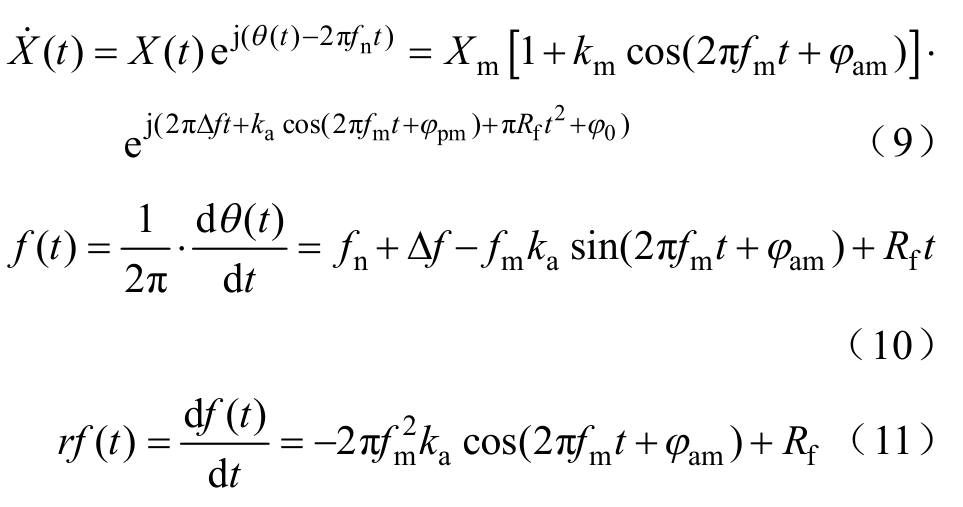
其中
2 非线性拟合相量测量方法
2.1 最优化模型
根据1.1节PMU校准器的第二个特点，提出了基于非线性最小二乘法的迭代求解方法，以求解拟合模型中的参数向量p。首先，构造残差二次方和最小的最优化模型分别为
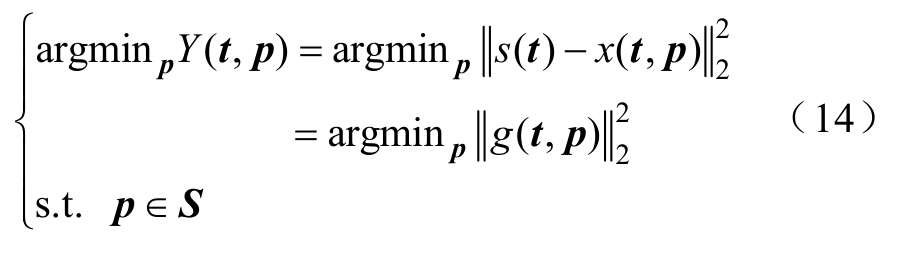
式中，t为计算窗内的时间向量，即
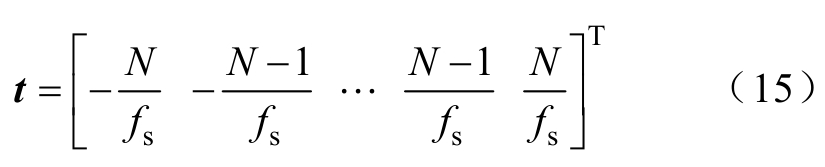
式中，fs为信号采样频率，每个计算窗内有2N+1个采样点，N为正整数；s(t)为计算窗内测试信号的采样值；Y(t, p)为目标函数；x(t, p)为计算窗内拟合模型求得的拟合值；g(t, p)=s(t)-x(t, p)表示残差；||·||2为2范数；S表示边界约束，定义了参数向量可行值的范围。式（14）表示用相量拟合模型拟合测试信号采样值s(t)，并在限定区域S内搜索到使残差二次方和最小的局部最优参数向量。
2.2 拟合参数初始值与边界约束设置方法
由式（14）可以看出，目标函数是严格非线性且非凸的，因此，给定拟合参数的初始值后，利用最优化求解方法（见2.3节），拟合参数将迭代收敛于局部最小值而非全局最小值。从而导致给定拟合参数不同的初始值，最优化求解方法将生成不同的局部最优值。因此，为保证解的唯一性，需合理地设置拟合参数初始值和约束条件。
初始值设置恰当与否对算法的迭代收敛速度和相量的量测精度有较大影响。因此，应尽量使p的初始值p(0)接近其理论值。由于测试信号是根据PMU测试标准规定发出的，因此各参数的理论值及变化范围是已知的。
对于在测试过程中为定值的参数，直接将其理论值设为待拟合参数的初始值。例如，标准规定AM 测试的km=0.1，ka=0rad，Rf=0Hz/s，因此可令 
测试信号的额定电压
为57.73V，令
对于在测试过程中在a～b范围内变化的待拟合参数，若其初始值为ε，则初始值和真实值之间的最大差值为|ε -a|或|ε -b|。为使最大差值最小，ε 应为(a+b)/2。仍以AM测试为例，初相角可在-π ～ π 范围内任意变化，因此初始值应为0rad，即 
频率偏移范围为-0.5～0.5Hz，因此Δf (0)= 0Hz；调制频率的变化范围为0.01～5Hz，
所以，AM拟合模型中待拟合参数的初始值p(0)= [57.73 0.1 2.5 0 0 0 0]。
为使目标函数近似为凸函数，拟合参数可行值范围S可约束在参数额定值附近，即需设置待拟合参数在迭代过程中的上下边界。待拟合参数的上下边界由用于发送测试信号的信号发生器的精度和测试信号的参数变化范围决定的。具体地，待拟合参数的上下边界应略大于信号源的不确定度，例如，若信号源在额定频率下的频率不确定度为0.002Hz，那么Δf的上下界可设为±0.01Hz。在此基础上，参数的上下边界还应包含参数的变化范围。例如，标准规定幅值扫描测试的信号幅值变化范围为0.1～2.0倍的额定幅值Xn，因此Xm的上下界可分别设为0.08Xn和2.02Xn。
2.3 相量非线性拟合求解方法
式（14）中，参数向量p的求解是一个非线性拟合问题，需对相量模型x(t, p)进行一阶泰勒级数展开并将其线性化，转化为线性最小二乘问题[21]，其正规方程最终为
式中，Δp为参数向量p的增量；J为雅可比矩阵，即
在迭代过程中，通过式（16）求出Δp，不断更新参数向量p，最终使残差g(t, p)的二次方和最小，从而得到参数向量的局部最优测量值。
本节仍以AM测试为例说明相量非线性拟合求解方法，此时s(t)为AM信号的采样值，p=[XmkmfmφamΔf Rfφ0]。拟合模型x(t, p)为
由式（16）可知，为求解增量Δp，需先求得雅可比矩阵J。AM信号的雅可比矩阵为
其中
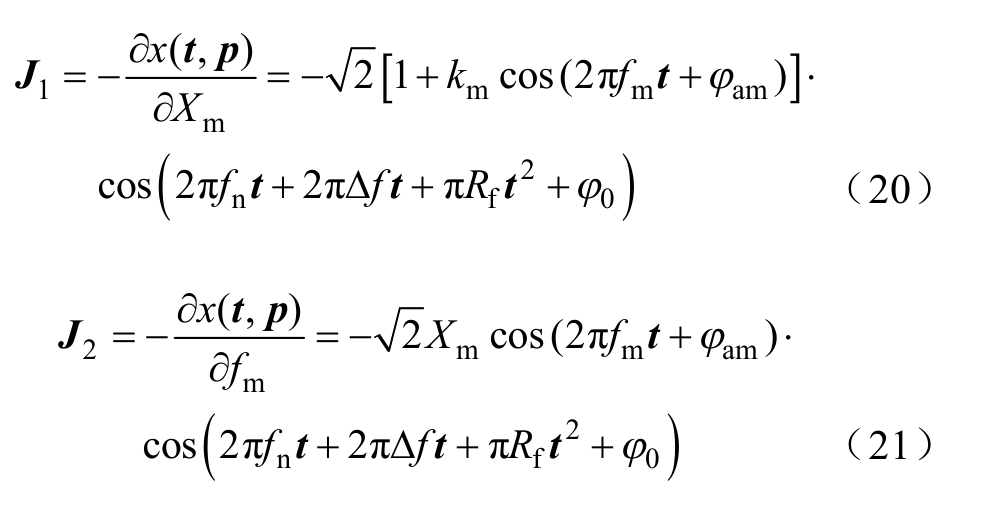
Ji（i＞2）表达式与式（20）和式（21）类似，不再赘述。将p(k)代入J中得到J(k)（k为迭代次数，k≥0）。
由式（16）可知，为求得增量Δp，需对矩阵JTJ求逆。因此，JTJ应为正定矩阵，以保证相量测量算法收敛于局部最小值。为此，引入了衰减系数μ（μ≥0），其初始值μ (0)=1×10-3。令
式中，I为单位矩阵。对A(k)进行三角分解，判断其是否正定，若非正定矩阵，令μ(k)=4μ(k)，重新分解直至正定。此时式（16）变为
由式（23）求解参数向量p(k)的增量Δp(k)为
判断相量算法是否满足迭代终止条件为
式（25）中，ε1为指定的小正数，该式用于判断增量Δp(k)中每个元素的绝对值是否均小于ε1。式（26）中，K为最大迭代次数，该式用于判断相量算法的迭代次数是否超过预设的最大迭代次数。
若满足其中一个终止条件，则相量算法迭代结束，参数向量的最终拟合结果为
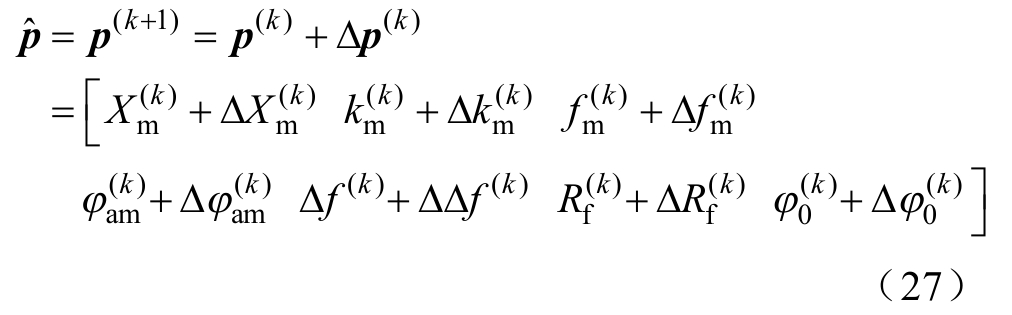
否则，根据式（19）～式（24）重新计算，直至收敛或超过最大迭代次数为止。
重新迭代时需更新μ(k)的值，更新的标准是判断目标函数 Y(t, p(k+1))的值较 Y(t, p(k))是增加还是减小，若增加则增大μ(k)的值；反之，则减小μ(k)的值。具体地，令
若ρ (k)＞0，表明相量的拟合残差g(t, p)在减小，相量算法逐渐收敛，因此减小衰减系数避免相量算法在最优解附近振荡，令
式中，ν为增益系数，本文中令ν=3。此时，按式（27）更新参数向量p，更新时应保证参数向量在边界约束S范围内。
若ρ (k)≤0，表明相量拟合残差g(t, p)在增大，这显然与求解目标相反，因此，此时所得增量Δp(k)是无效的，令
为使相量拟合残差向减小的方向移动，增大衰减系数从而使算法更快接近最优解，令
得到ˆp后，将量测量的时标打在计算窗（t =0s）中，则由式（9）～式（11）可知AM测试信号在 该计算窗内的相量
频率fc与频率变化率rfc为
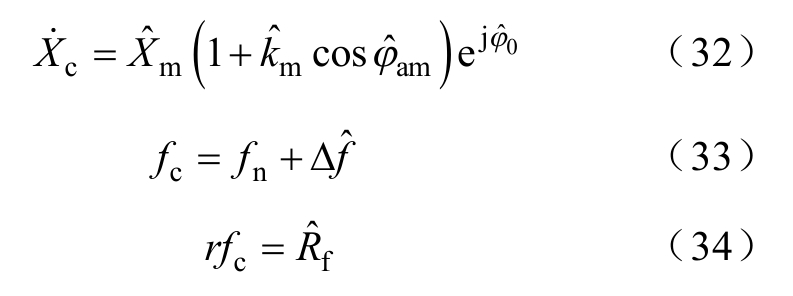
以上为AM测试条件下，相量测量的求解方法，其他测试条件下的相量求解过程同上，不再赘述。
由于相量算法在较短时间间隔内对电压电流信号进行量测（时间间隔最大为40ms[18]），相邻计算窗内待拟合参数变化不会太大，因此可将当前计算窗的参数拟合结果作为下一计算窗的参数拟合初始值，即
式中，
当前计算窗的参数拟合结果；
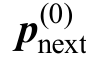为 下一计算窗内待拟合参数的初始值。这样可使下一计算窗内的待拟合参数的初始值接近其理论值，进而使非线性拟合相量测量算法更快收敛，提高量测精度和计算速度。
2.4 随机噪声抑制方法
校准器采样信号中不可避免地会出现噪声。噪声可能来源于信号源所发出的实际信号，也可能由校准器采集系统产生。噪声的存在增加了算法的计算时间，并降低了量测精度，因此，应采取措施抑制随机噪声对校准器量测精度的影响。
为此，测试了信号中叠加不同信噪比（Signal- to-Noise Ratio, SNR）的高斯白噪声时，所提测量方法在不同计算窗长条件下的相量测量精度，不同信噪比与计算窗条件下的幅值误差（Amplitude Error, AE）如图1所示。
图1 不同信噪比与计算窗条件下的幅值误差
Fig.1 Maximum AE for different SNR and TL
可以看出，相量的幅值误差随着信噪比的增大而减小，这表明可选择高性能的硬件搭建校准器以降低系统的随机噪声，从而提高量测精度。当信噪比确定时，幅值误差随着计算窗的增加而减小，这表明可以在软件算法上增加计算窗的长度以抑制随机噪声，进而提高量测精度。但是，由0.06～0.1s这一区间可以看出，当计算窗越来越长时，幅值误差降低的幅度越来越小，但是计算时间越来越长，因此应根据实际的硬件系统，在保证精度满足校准要求的前提下，提高计算速度。文献[22]指出配电网侧噪声在60dB左右，PMU实验室测试环境较好，噪声一般更小。因此算法采用0.08s的时间窗，可满足校准要求。
2.5 非线性拟合相量测量方法的实现
2.5.1 软件实现
所提适用于校准器的非线性拟合相量测量方法的流程如图2所示。校准器根据测试信号类型选择拟合模型，其中，若为谐波和带外测试，需进行数字带通滤波；根据所选模型设置待拟合参数p的初 始值和约束条件；由非线性最小二乘法迭代求解拟合参数向量p；根据求得的
按式（2）～式（4）或式（9）～式（11）计算出测试信号的相量、频率和频率变化率。
图2 非线性拟合相量测量方法的流程
Fig.2 Flowchart of the proposed estimation method
2.5.2 硬件实现
PMU校准器主要由GPS同步授时模块、信号采集模块和控制器模块3部分组成。本文选用美国国家仪器公司（National Instruments, NI）的PXIe- 6682H板卡、PXIe-4300板卡、PXIe-8135RT控制器搭建PMU校准器。
PXIe-6682H是同步授时板卡，该板卡能接受GPS信号并将其以秒脉冲（Pulse Per Second, PPS）形式输出。PXIe-4300是一个16位且输入量程为±10V的电压采集板卡，最大采样率为250kHz。由于测试信号的额定电压为57.73V[18]，因此还需使用与PXIe-4300配套的电压衰减模块NI TB4300B，该电压衰减接线盒可提供300V/10V、150V/10V、60V/10V和30V/10V四种电压传变量程。PXIe- 8135RT是一个嵌入式控制器，该控制器含有8个扩展插槽，可用于安装PXIe-6682和PXIe-4300等板卡。将提出的非线性拟合相量测量方法在PXIe- 8135RT控制器的嵌入式系统中编程实现，搭建了PMU校准器。
3 仿真与实验验证
3.1 仿真测试
为验证所提初始值与参数约束条件的设置方法的必要性，进行了如下仿真测试。仿真测试类型为幅值调制测试，Xm=50，fm=5Hz，且在信号中叠加SNR为60dB的高斯白噪声，测试条件为：①任意设置p的初始值且无约束条件；②按2.2节所述设置初始值和约束条件。任意初始值且无约束条件下的幅值误差如图3所示，初始值和约束条件符合要求时的幅值误差如图4所示。
图3 任意初始值且无约束条件下的幅值误差
Fig.3 Amplitude error without complying with the proposed measures
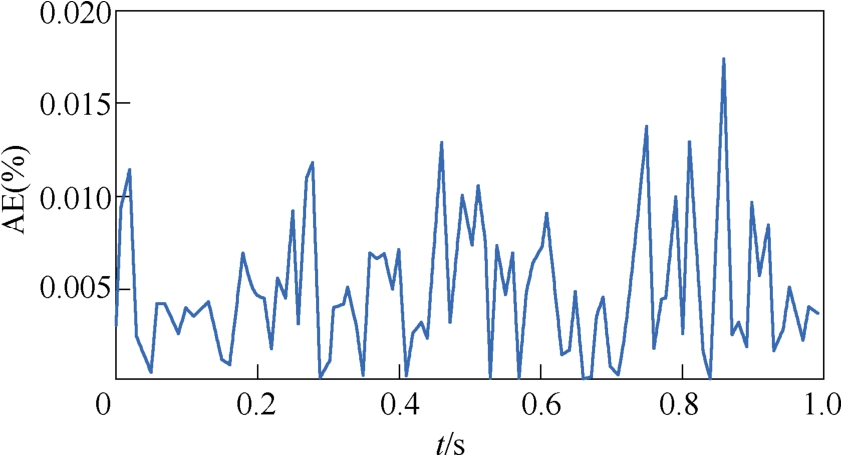
图4 初始值和约束条件符合要求时的幅值误差
Fig.4 Amplitude error complying with the proposed measures
由图3可知，当待拟合参数初始值设置不当且无约束时，所提量测算法收敛于不同的局部最小值，导致部分量测误差非常大。但是，由图4可以看出，当合理设置初始值和约束条件后，即便测试信号含噪声，量测精度仍很高，图中幅值误差最大值在0.02%以下，低于标准要求0.2%的10倍以上。
为验证所提相量测量算法在各测试类型下的测量精度，根据PMU测试标准[5]对算法在各静态和动态信号下进行了仿真测试（测试条件详见附表1），算法的仿真参数为：信号采样率为10kHz，计算窗长为0.08s（4个周波），ε1=1×10-5，最大迭代次数K= 100，计算频率为50Hz；带通数字滤波器阶数为5 000阶，通带为42～58Hz，阻带小于28Hz，大于72Hz。
将所提算法的量测精度与文献[15]提出的改进DFT（Improved DFT, IDFT）算法以及标准要求进行了对比，各参数仿真测量最大误差见表1。表1中PE（phase error）为相位误差，FE（frequency error）为频率误差，RFE（ROCOF error）为频率变化率误差，Std为标准规定的误差要求，PMU标准对带外测试的RFE没有要求，在表1中用N/A表示。
表1 仿真测试最大误差结果
Tab.1 Maximum errors results of simulation
最大AE(%) 最大PE/(°) 最大FE/Hz 最大RFE/(Hz/s) 测试 类型 Std IDFT 本文算法 Std IDFT 本文算法 Std IDFT 本文算法 Std IDFT 本文算法 幅值扫描测试 0.2 3.3×10-8 5.3×10-8 0.2 1.3×10-11 1.2×10-8 0.002 3.3×10-13 4.5×10-14 0.01 3.6×10-13 5.2×10-13 频率扫描测试 0.2 5.6×10-8 1.7×10-8 0.2 0.090 1.2×10-8 0.002 1.2×10-13 2.3×10-12 0.01 9.7×10-13 1.6×10-11 谐波测试 0.4 0.165 0.002 0.4 0.103 4.8×10-5 0.004 0.008 3.2×10-6 0.02 0.539 3.7×10-6 带外测试 0.5 5.283 0.002 1 3.642 2.4×10-6 0.025 0.185 1.4×10-6 N/A — — AM 0.2 0.135 5.4×10-7 0.3 0.010 4.9×10-5 0.025 0.001 4.3×10-8 0.1 0.050 8.7×10-7 PM 0.2 4.7×10 -4 3.9×10-8 0.5 0.074 5.2×10-7 0.3 0.030 5.0×10-7 3 1.100 4.8×10-7 AM+PM 0.2 0.135 6.7×10-7 0.5 0.076 1.0×10-6 0.3 0.031 5.6×10-7 3 1.163 9.0×10-7 频率斜坡测试 0.2 1.6×10-6 8.9×10-8 0.5 0.101 5.8×10-6 0.01 1.0×10-4 1.8×10-9 0.2 1.5×10-7 8.7×10-9
可以看出，IDFT算法在信号的幅值、频率和频率变化率上均为定值时，能获得精确的量测量，此时两种算法的误差相差不大。但是，当幅值或相位发生调制等非线性变化或频率偏移基频较大时，精度较差，未高于标准要求4倍以上，无法作为校准时的参考值。
本文所提方法在各种测试条件下测量精度均较高，普遍比标准要求小5～6个数量级。其中，谐波与带外测试表明，本文采用的数字滤波器可有效消除干扰信号，并且对基频相量产生的影响可忽略，其精度仍高于标准两个数量级。
3.2 PMU校准器实验测试
为验证实际PMU校准器整体测量精度，采用高精度信号源Omicron-CMC256plus对其进行了测试，PMU校准器实验测试最大误差结果见表2。
可以看出，相比仿真结果，两种算法的整体精度均有所下降，这是由硬件系统的误差及信号中的随机噪声所致。IDFT算法特性与表1基本一致，但稳态测试时的频率变化率误差较大，已超出标准要求。这是由于该算法中频率变化率是由相位的二次差分所得，放大了相位量测中的误差。而本文所提算法可直接求解频率和频率变化率，避免了此问题。
本文方法应用于实际硬件装置后，在静态与动态条件下的测量精度如下：①静态（无干扰信号）：AE≤0.005%，PE≤0.017°，FE≤9.5×10-5Hz，RFE≤ 6.3×10-5Hz/s，均低于标准20倍以上；②静态（有干扰信号）：AE≤0.016%，PE≤0.012°，FE≤2.2× 10-4Hz，RFE≤6.1×10-4Hz/s，均低于标准12倍以上；③动态：AE≤0.014%，PE≤0.016°，FE≤1.7× 10-4Hz，RFE≤0.003Hz/s，幅值低于标准14倍，相位低于标准30倍，频率和频率变化率则低近3个数量级。可以看出，所研制的PMU校准器在静态和动态条件下的量测精度均满足高于标准4倍以上的校准要求，可用于PMU实验室测试与校准。为验证所搭建的PMU校准器的实用效果，用PMU校准器对国内某厂家的PMU进行了测试（测试结果见附录）。
表2 PMU校准器实验测试最大误差结果
Tab.2 Maximum errors results of PMU calibrator experiment tests
最大AE(%) 最大PE/(°) 最大FE/Hz 最大RFE/(Hz/s) 测试类型 Std IDFT 本文算法 Std IDFT 本文算法 Std IDFT 本文算法 Std IDFT 本文算法 幅值扫描测试 0.2 0.008 0.005 0.2 0.021 0.017 0.002 3.2×10-4 9.5×10-5 0.01 0.011 6.3×10-5 频率扫描测试 0.2 0.005 0.004 0.2 0.094 0.010 0.002 3.6×10-4 4.1×10-5 0.01 0.075 3.1×10-5 谐波测试 0.4 0.170 0.016 0.4 0.115 0.012 0.004 0.008 2.0×10-4 0.02 0.547 6.1×10-4 带外测试 0.5 5.436 0.015 1 3.655 0.010 0.025 0.243 2.2×10-4 N/A — — AM 0.2 0.141 0.009 0.3 0.033 0.012 0.025 0.002 4.3×10-5 0.1 0.056 5.9×10-5 PM 0.2 0.007 0.008 0.5 0.085 0.008 0.3 0.030 1.7×10-4 3 1.102 0.003 AM+PM 0.2 0.142 0.014 0.5 0.086 0.010 0.3 0.031 1.4×10-4 3 1.169 0.003 频率斜坡测试 0.2 0.009 0.005 0.5 0.102 0.016 0.01 4.2×10 -4 1.5×10-4 0.2 0.018 3.7×10-4
4 结论
本文提出了一种适用于PMU校准器的高精度相量测量方法。该方法根据PMU标准规定的测试信号建立了两种非线性拟合模型，并给出了相量理 论值计算公式。构造了残差二次方和最小的最优化模型，提出了非线性拟合相量计算方法，提出了待求相量参数初始值设置方法与约束条件，保证了相量算法解的唯一性。进一步地，通过硬件选型，搭建了PMU校准器。通过仿真与实验测试表明，校准器的精度均高出标准要求10倍以上，部分达100倍以上，达到了校准要求，可用于PMU的测试与校准。
附 录
1. 静态和动态测试条件与测试目的
各测试类型及其对应的测试条件见附表1。
附表1 PMU校准器测试条件
App.Tab.1 PMU calibrator test conditions
测试类型 测试条件 测试目的 幅值扫描测试 信号频率为50Hz，幅值变化范围0.1Xn～2.0Xn 检测PMU在额定频率下不同的输入电压和电流条件下的相量量测精度 频率扫描测试 信号幅值为额定值Xn，基波频率变化范围为45～55Hz 实际电力系统大多数时间都在非额定频率运行，因此该测试用于检测PMU在频率偏移条件下的相量修正能力 谐波影响测试 基波幅值为额定值Xn，基波频率为49.5Hz、50Hz和50.5Hz，谐波幅值为0.1Xn，谐波频率为2～25次谐波 用于检测PMU在额定频率附近对谐波的免疫能力 带外测试 基波幅值为额定值Xn，基波频率为49.5Hz、50Hz和50.5Hz，谐波幅值为0.1Xn，带外信号频率| f-f0|≥Fs/2，Fs=50Hz或100Hz 带外信号会使相量在上传主站时发生频率混叠现象，该测试用于检测PMU对于带外信号的免疫能力 幅值调制测试 基波频率为49.5Hz、50Hz和50.5Hz，幅值调制深度为0.1Xn，幅值调制频率0.1～5Hz 相位调制测试 基波频率为49.5Hz、50Hz和50.5Hz，相位调制深度为0.1rad，相位调制频率0.1～5Hz 幅值相位 同时调制测试 基波频率为49.5Hz、50Hz和50.5Hz，幅值调制深度为0.1Xn，相位调制深度为0.1rad，调制频率0.1～5Hz 用于检测PMU在电力系统功率振荡条件下的相量量测精度
（续）
测试类型 测试条件 测试目的 频率斜坡测试 信号幅值为额定值Xn，信号频率从45Hz线性变化至55Hz，频率的线性变化速率范围为0.5～2Hz/s 当电力系统中发电机发生失步时，电力信号频率将发生变化，该测试用于检测PMU在频率持续变化时的量测精度
2. 商用PMU测试结果
考虑到厂家的保密要求，测试的PMU设备厂家与型号在文中并未公开。由于PMU测试类型较多，因此只给出了测试条件最苛刻的幅值相位以5Hz同时调制的测试结果。为表明所研制的校准器的准确性和有效性，将分析结果与基于高精度信号源的PMU测试系统的测试结果进行了对比。具体过程如下：
（1）实验方案：利用信号源发出幅值相位以5Hz同时调制的信号，同时给校准器和待测PMU，待两者量测完毕，提取量测量进行误差分析。
（2）实验接线与测试场景如附图1所示。
附图1 实验接线与测试场景
App.Fig.1 Connection and practical testing scene
（3）使用的实验设备：OMICRON-CMC256plus，国内某厂家PMU，研制的PMU校准器、计算机。
（4）幅值相位同时调制测试结果如附图2所示。
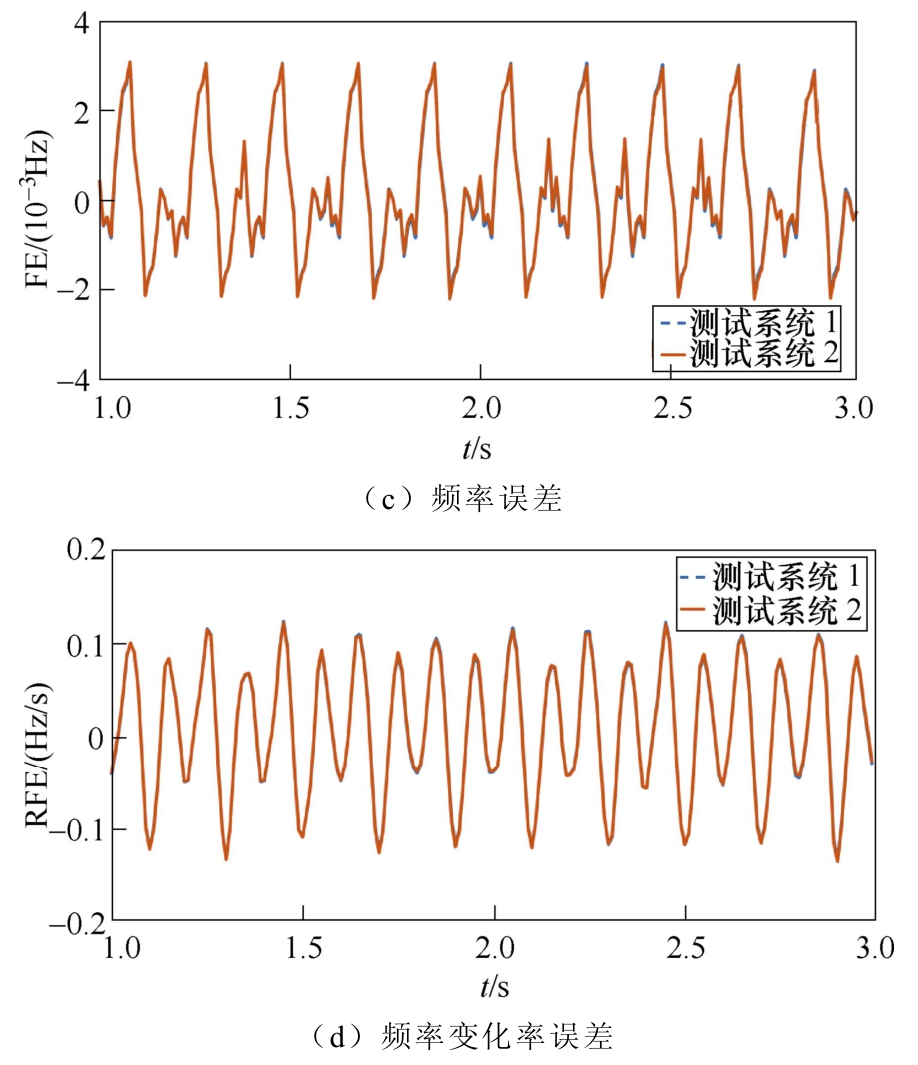
附图2 幅值相位同时调制测试结果
App.Fig.2 Test results of amplitude and phase modulation
附图2中，测试系统1表示基于高精度信号源的测试系统，测试系统2表示本文所研制的基于PMU校准器的测试系统。可以看出，该PMU装置的幅值、相位、频率与频率变化率误差随时间呈现周期性变化，这是由于输入相量的幅值和相位被调制导致的。根据附表1中的调制测试的标准要求，可以看出该厂商的PMU的测量精度较高，相位、频率与频率变化率精度比标准要求高10倍以上。而且，两套测试系统的测试结果非常类似，特别是频率与频率变化率的测试结果几乎完全重叠。这也验证了本文提出PMU校准器的测量精度完全满足PMU实验室校准的要求。
[1]罗深增, 李银红, 石东源. 广域测量系统可观性概率评估及其在PMU优化配置中的应用[J]. 电工技术学报, 2018, 33(8): 1844-1853. Luo Shenzeng, Li Yinhong, Shi Dongyuan. Wide area monitoring system observability probabilistic evaluation and it’s application in optimal PMU placement[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1844-1853.
[2]邵雅宁, 唐飞, 刘涤尘, 等. 一种适用于WAMS量测数据的系统暂态功角稳定评估方法[J]. 电力系统保护与控制, 2015, 43(6): 33-39. Shao Yaning, Tang Fei, Liu Dichen, et al. An approach of transient angle stability assessment in power system for WAMS measured data[J]. Power System Protection and Control, 2015, 43(6): 33-39.
[3]王臻, 李承, 林志芳, 等. 考虑高斯有色噪声的FOMC-HTLS-Adaline算法在低频振荡模式辨识中的研究[J]. 电工技术学报, 2017, 32(6): 21-30. Wang Zhen, Li Cheng, Lin Zhifang, et al. Research on low frequency oscillation mode identification based on FOMC-HTLS-Adaline algorithm considering colored gaussian noises[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 21-30.
[4]姜涛, 贾宏杰, 李国庆, 等. 基于广域量测信息相关性的电力系统同调辨识[J]. 电工技术学报, 2017, 32(1): 1-11. Jiang Tao, Jia Hongjie, Li Guoqing, et al. Cross- correlation coefficient-based coherency identification in Bulk power system using wide-area measure- ments[J]. Transactions of China Electrotechnical Society, 2017, 32(1): 1-11.
[5]Q/GDW 1131-2014 电力系统实时动态监测系统技术规范[S]. 北京: 国家电网公司, 2015.
[6]IEEE Std. C37.118.1-2011. IEEE standard for synchro-phasor measurements for power systems[S]. 2011-10.
[7]IEEE standard for synchro-phasor measurements for power systems-amendment 1: modification of selected performance requirements[S]. IEEE Std C37.118.1a- 2014, 2014-04.
[8]Pogliano U, Braun J P, Voljč B, et al. Software platform for PMU algorithm testing[J]. IEEE Transactions on Instrumentation & Measurement, 2013, 62(6): 1400-1406.
[9]Grando F L, Denardin G W, Moreto M. Test platform for analysis and development of phasor measurement units (PMU)[C]//IEEE International Conference on Industry Applications, Curitiba, 2017: 1-6.
[10]毕天姝, 刘灏, 杨奇逊. PMU算法动态性能及其测试系统[J]. 电力系统自动化, 2014, 38(1): 62-67. Bi Tianshu, Liu Hao, Yang Qixun. Dynamic performance of PMU algorithm and its testing system[J]. Automation of Electric Power Systems, 2014, 38(1): 62-67.
[11]Caldwell D. ANSI/NCSL Z540.3: 2006: Require- ments for the calibration of measuring and test equipment[S]. 2006.
[12]Tang Y, Stenbakken G N. Calibration of phasor measurement unit at NIST[J]. IEEE Transactions on Instrumentation & Measurement, 2013, 62(6): 1417- 1422.
[13]Kilter J, Palu I, Almas M S, et al. Experiences with dynamic PMU compliance testing using standard relay testing equipment[C]//Innovative Smart Grid Technologies Conference, Washington, DC, 2015: 103-110.
[14]Trinchera B, Serazio D, Pogliano U. Asynchronous phase comparator for characterization of devices for PMUs calibrator[J]. IEEE Transactions on Instru- mentation & Measurement, 2017, 66(6): 1139-1145.
[15]金涛, 陈毅阳, 段小华, 等. 基于改进DFT的电力系统同步相量测量算法研究[J]. 电工技术学报, 2017, 32(17): 1-10. Jin Tao, Chen Yiyang, Duan Xiaohua, et al. Research on synchronous phasor measurement algorithm of power system based on improved DFT[J]. Transactions of China Electrotechnical Society, 2017, 32(17): 1-10.
[16]Xia Tao, Liu Yilu. Single-phase phase angle measurements in electric power systems[J]. IEEE Transactions on Power Systems, 2010, 25(2): 844-852.
[17]Romano P, Paolone M. Enhanced interpolated-DFT for synchrophasor estimation in FPGAs: theory, implementation, and validation of a PMU proto- type[J]. IEEE Transactions on Instrumentation & Measurement, 2014, 63(12): 2824-2836.
[18]刘洁波, 黄纯, 江亚群, 等. 基于强跟踪泰勒-卡尔曼滤波器的动态相量估计算法[J]. 电工技术学报, 2018, 33(2): 433-441. Liu Jiebo, Huang Chun, Liu Yaqun, et al. Dynamic phasor estimator based on strong tracking Taylor- Kalman filter[J]. Transactions of China Electro- technical Society, 2018, 33(2): 433-441.
[19]Belega D, Fontanelli D, Petri D. Dynamic phasor and frequency measurements by an improved Taylor weighted least squares algorithm[J]. IEEE Transa- ctions on Instrumentation & Measurement, 2015, 64(8): 2165-2178.
[20]符玲, 韩文朕, 麦瑞坤, 等. 利用频域信息滤除衰减直流的同步相量测量算法[J]. 中国电机工程学报, 2016, 36(18): 4923-4929. Fu Ling, Han Wenzheng, Mai Ruikun, et al. Phasor estimator based on frequency-domain information considering decaying DC components[J]. Pro- ceedings of the CSEE, 2016, 36(18): 4923-4929.
[21]Horio M, Morimoto J, Tabuchi T. A method for nonlinear least squares problem[J]. Technical Bulletin of Tokushima Bunri University, 2008, 75: 81-95.
[22]Zhan Lingwei, Liu Yong, Culliss J, et al. Dynamic single-phase synchronized phase and frequency estimation at the distribution level[J]. IEEE Transa- ctions on Smart Grid, 2015, 6(4): 2013-2022.