0 引言
近年来，太阳能发电随着技术进步和成本降低，其装机容量也在快速增长，已成为全球能源转型的重要领域之一。截至2016年第一季度，全国太阳能发电装机容量达到5 031万kW[1]。为了防止电网故障时光伏电源大规模脱网给电网安全稳定运行带来危害，在光伏电源并网运行的相关规程中，明确要求大中型光伏电站需具备低电压穿越能力[2]。光伏电源由于其自身发电方式、电路拓扑结构和低电压穿越控制策略的特殊性，其故障特性远区别于传统同步电机。大量光伏电源实施低电压穿越运行后，其馈出的复杂短路电流将会给电网的继电保护带来诸多不利影响，可能导致保护误动或拒动，进而威胁电力系统的安全稳定运行。因此，深入开展光伏电源的短路电流特性分析，建立短路电流的理论解析计算模型，对准确评估其对电网继电保护的影响，改进和完善保护性能具有重要的现实意义。
文献[3-7]重点针对光伏电源的稳态故障电流特性和计算方法开展研究，但未考虑光伏电源的暂态故障特性，因此所得结论仅适用于稳态短路分析。文献[8]首先建立了逆变型分布式电源（Inverter Interfaced Distributed Generator, IIDG）在单电压外环控制策略下的故障分析数学模型，进而提出了含IIDG的配电网故障分析方法。但目前IIDG通常采用电压外环电流内环的双环控制策略[9-10]，并不能直接简化为单电压外环控制策略进行故障特性分析。文献[11-13]以故障期间直流母线电压恒定为假设前提，对光伏电源的故障暂态和稳态特性开展了研究。但光伏电源在故障工况下，其输出的电磁功率将发生大幅变化，导致直流母线电压波动，进而会影响输出故障电流，因此上述近似分析方法有待完善。为防止故障期间不平衡有功功率造成直流母线电压过电压，光伏电源直流母线一般均装设有卸荷电路[14]。文献[15-16]在计及直流卸荷电路影响的前提下，利用数字仿真，对光伏电源的故障暂态特性开展了研究，但主要局限于定性分析，缺乏必要的理论分析支持。
针对上述问题，本文在考虑故障期间直流母线电压波动以及卸荷电路影响的基础上，提出了光伏电源故障暂态和稳态电流的理论求解方法及计算模型，通过数字仿真，验证了其正确性。以此为基础，对影响光伏电源短路电流特性的主要因素进行了分析，为含光伏电源的电网继电保护研究和控制器设计提供参考。
1 光伏电源拓扑及低穿控制策略
1.1 光伏电源拓扑结构及逆变器控制策略
大功率光伏电源的逆变器拓扑结构一般分为单级式和双级式[9]。其中，双级式结构的逆变器将最大功率点跟踪（Maximum Power Point Tracing, MPPT）[17]和并网控制策略分隔开来，简化了控制系统的设计难度，因此较多地应用在实际中[9]，光伏电源拓扑结构如图1所示。光伏阵列产生直流电，经DC-DC电路升压后连至直流母线，再经DC-AC变换器和滤波电路接入电网。其中，DC-DC电路除升压作用外，还用于控制光伏阵列输出电压，以实现光伏电源的MPPT功能。
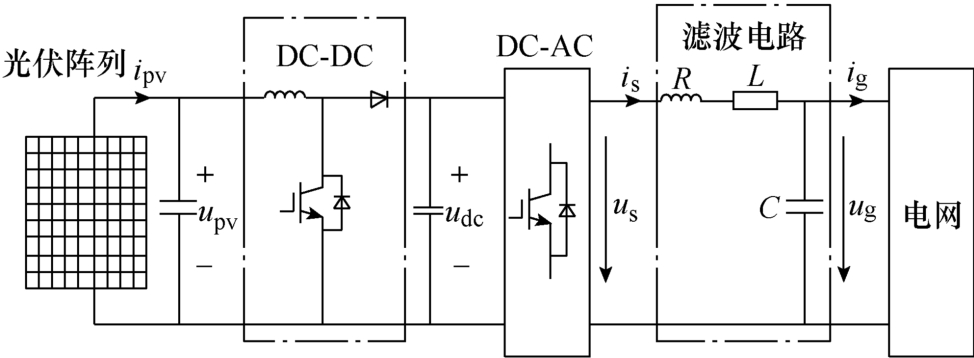
图1 光伏电源拓扑结构
Fig.1 Topology of PV power
光伏电源的输出功率通常采用矢量解耦控制方法[9]，一般将电网正序电压定向于d轴，其输出功率方程为
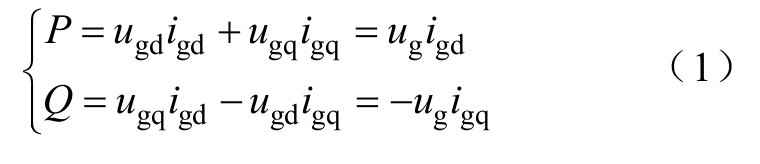
式中，P和Q分别为光伏电源输出有功和无功功率； ugd 和ugq分别为并网点d轴和q轴电压分量；igd和gqi分别为输出d轴和q轴电流分量；ug为并网点电压。
正常情况下，光伏电源在单位功率因数工况下运行，同时采用电压外环、电流内环的双环控制策略。此时在d、q轴两相旋转坐标系下，其逆变器控制方程为
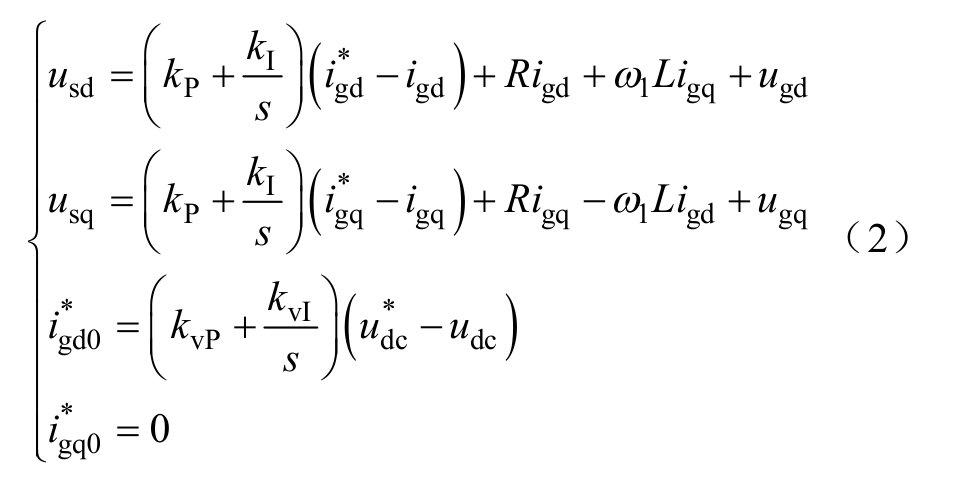
式中，上标*代表控制器指令值；kvP和 kvI分别为电压外环控制器的P、I参数；kP、kI分别为电流内 环控制器的P、I参数；usd和usq分别为光伏电源端口d轴和q轴电压分量；udc为逆变器直流母线电压；
分别为正常情况下输出d轴和q轴电流指令值。
在故障情况下，光伏电源需具备低电压穿越能力[2]，满足系统的无功支撑要求。同时为保证直流母线电压在故障期间依旧具备一定的调节能力，故障期间光伏电源电压控制外环不闭锁。此时，光伏电源的低电压穿越运行控制方程为
式中，UT为故障后网侧正序电压幅值；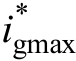
为输出电流限幅值；
为故障后输出d轴和q轴电流指令值。
另外，在不对称故障情况下，光伏电源普遍采用基于正序电压测量的平衡（无负序分量）输出电流控制策略[18]。其中，首先由快速锁相环（Phase- Locked Loop, PLL）测得故障电压中正序分量的幅值和相位[19]，再根据式（3）获得输出正序有功和无功电流的指令值，而后光伏电源的输出电流基于电流内环控制环节快速跟踪指令值，因此不对称故障下的光伏电源同样不会输出负序故障电流。
1.2 直流卸荷电路控制策略
当电压跌落程度较深时，光伏电源有功输出受限，而在故障后短时内，光伏阵列的输出功率因DC-DC电路的稳压作用基本保持不变。为防止有功功率不平衡造成直流母线过电压，目前的普遍做法是在直流母线侧增设直流卸荷电路[11]，其投切控制是基于直流母线电压越限与否的判断，直流母线侧卸荷电路控制原理如图2所示。卸荷电路的开关信号由直流电压差值经PI和脉宽调制（Pulse Width Modulation, PWM）环节调制得到，该做法可有效降低直流侧电压的波动。
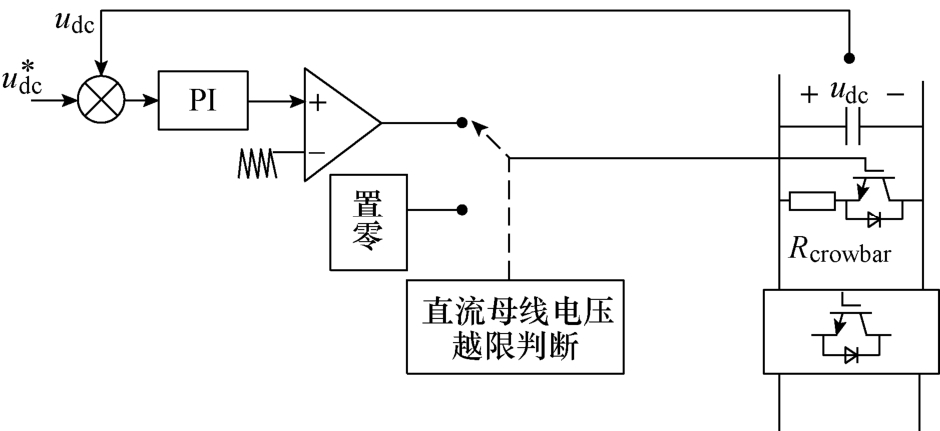
图2 直流母线侧卸荷电路控制原理
Fig.2 The control principle of relieving circuit on DC bus side
2 光伏电源故障特性理论分析方法及计算模型
2.1 计及直流母线电压波动的故障电流计算模型
2.1.1 对称故障情况
当电网发生故障时，直流母线电压由于功率不平衡存在波动变化，将直接影响短路电流特性。根据电容储能特性和能量守恒原则，可知直流母线电容电压方程为
式中，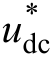
为直流母线电容额定电压；C为直流母线电容；t0为故障发生时刻；P0为光伏阵列输入有功功率；Pg为光伏电源输出有功功率；Pcrow为直流卸荷电路消耗功率。
令 Δudc为故障期间直流母线电压的故障分量，为保证直流母线和逆变器安全运行，一般规定直流母线侧最大允许电压不超过1.1倍额定电压[20]，此时若将式（4）两边取二次方，可忽略其中 Δudc的二次方项。由此可得直流母线故障分量电压方程为
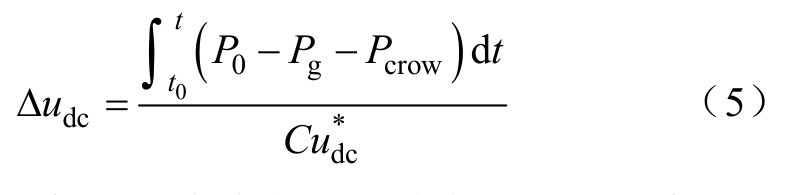
忽略逆变器和滤波电路的功率损耗，逆变器的电压外环控制框图如图3所示。
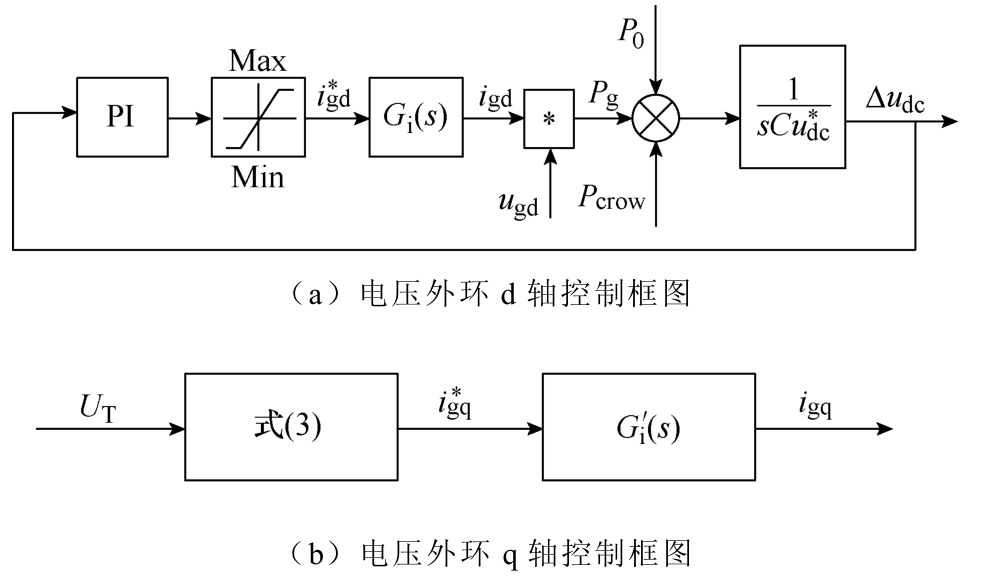
图3 逆变器电压外环控制框图
Fig.3 Control block diagram of inverter of the voltage external link
图3中，对于电流控制内环i()Gs和i()Gs′ ，为获得较快的电流跟随特性，一般设计成典型I型系统，同时要保证其截止频率在等效开关频率的1/10以内[21]。本文选取等效开关频率为15 000Hz，截止频率为fc=1000Hz 。此时的衰减时间常数 τ= 1/(2πfc)= 0.16ms，即输出有功电流能在数ms内跟踪其指令值，无功电流的快速跟踪性同理可证。因此可近似认为故障期间
联立式（1）、式（2）、式（5）和式（6），直流母线故障分量电压方程可改写为
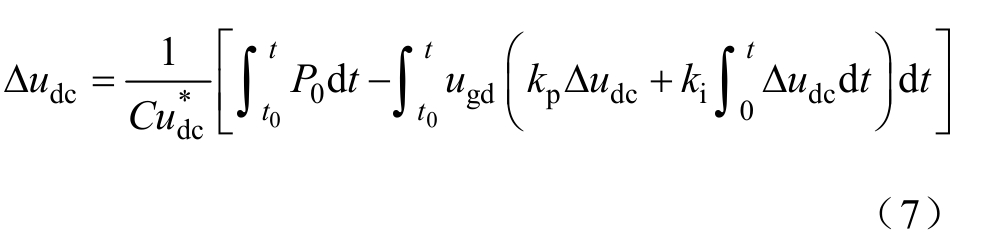
故障短时内，可近似认为光伏阵列输出功率保持不变。对式（7）两边取关于时间的二阶导数，可得
式中，D2为二阶微分因子；D为一阶微分因子；ugd为跌落后的电网d轴电压，其值在故障期间为常数。
由于故障瞬间输出电流连续，即
故式（8）的定解条件为
式中，δ为正序电网电压的跌落深度。
式（9）为典型的二阶常系数齐次微分方程，其特征方程为
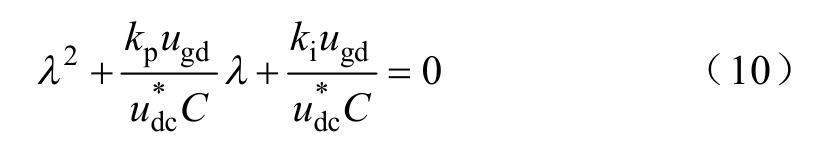
式（10）的特征根理论上存在两个互异实根和两个共轭复根两种情况，以下分别进行详细分析。
1）特征方程存在两个互异实根
由式（8）、式（9）可得直流母线电压的故障分量的解析表达式为
其中
将式（11）代入式（3）中，可得光伏电源d轴和q轴输出电流分别为
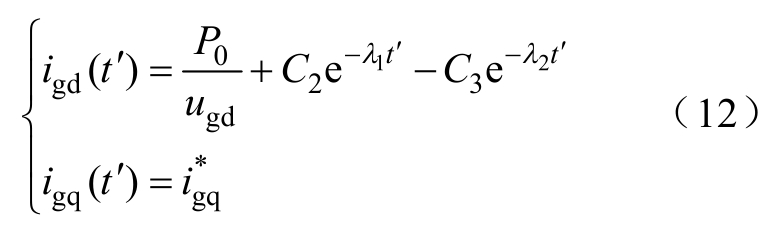
式中，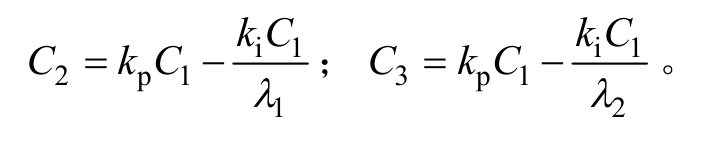
归算到三相坐标系下为
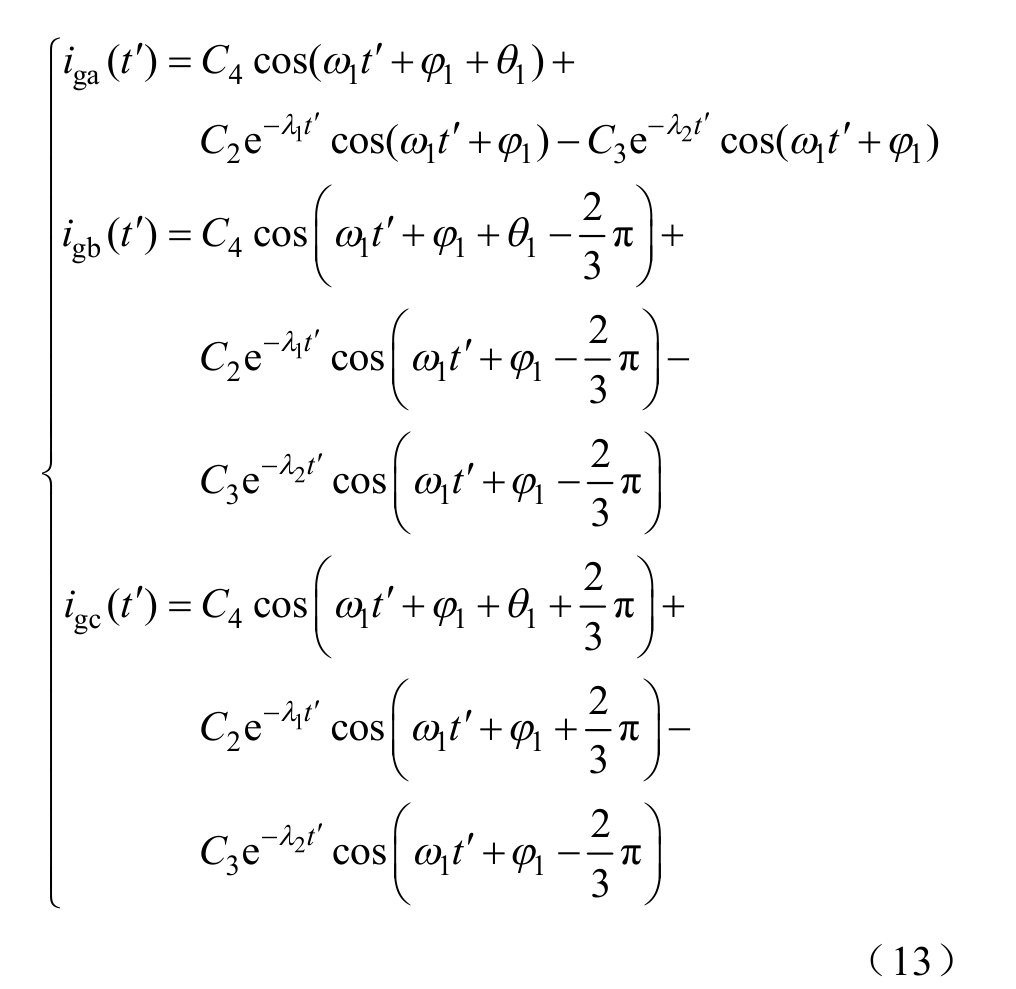
式中，φ1为故障前A相电流初相位；θ1= 
由式（12）和式（13）可知，当特征方程存在两个互异实根时，相较于传统同步电机，光伏电源的故障电流中不含衰减直流分量，而含有稳态基频分量和两种自由基频分量。其中，两种自由基频分量的初值和衰减时间常数均不同，且相位相反。初值大的自由基频分量衰减速度较快，相位与稳态分量相反；而初值小的自由基频分量衰减速度较慢，相位与稳态分量相同。分析可知，此时光伏电源故障期间的d轴电流和相电流包络线会呈现先增后减的变化特征，在后续数字仿真中对该情况进行了验证。
2）特征方程存在两个共轭复根
根据式（8）、式（9），解得直流母线电压的故障分量的解析表达式为
式中，
同样将式（14）代入式（3）中，可得光伏电源d轴和q轴输出电流分别为
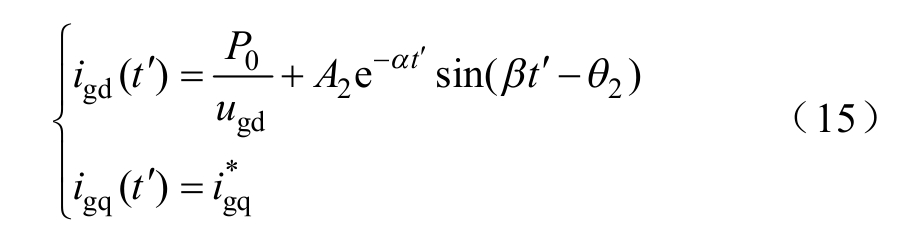
式中，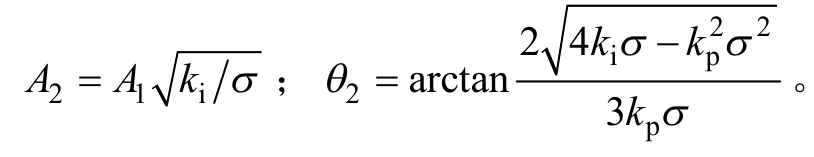
归算到三相坐标系下为
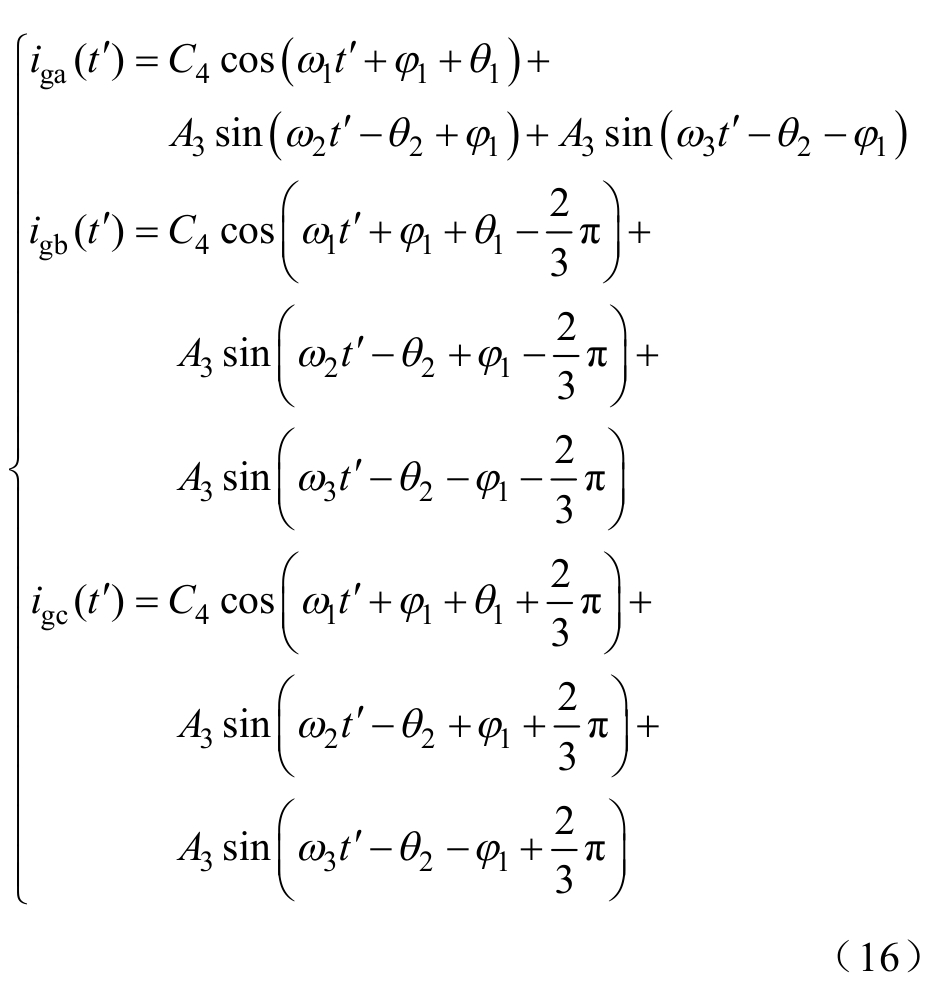
式中，
由式（15）和式（16）可知，当特征方程存在两个共轭复根时，光伏电源的故障电流中含有稳态基频分量和两种自由非基频交流分量，而不含衰减直流分量和自由基频分量。其中，两种自由非基频交流分量的初值和衰减时间常数相同，频率和相位不同。二者的叠加为某固定频率的衰减交流分量，此时光伏电源故障期间d轴电流和相电流包络线会呈现先增后振荡衰减的情况，这与传统同步电机故障特性存在明显差异。
2.1.2 不对称故障情况
不对称故障下，光伏电源输出的正序电流与负序故障电压会产生二倍频功率，其中二倍频有功功率会引起直流母线的二倍频电压波动，其经过电压外环中的PI环节产生二倍频的d轴指令电流，此时q轴指令电流不受影响。二倍频dq电流经dq/abc坐标系变化后即为三相电流中的正序三倍频和负序基频电流，但负序基频电流会被抑制，其产生机理如图4所示。
由图4可知，由于产生的二倍频功率仅引起三倍频相电流，而对正序基频相电流无影响，因此正序基频相电流的求解方法与对称故障时一致。由式（12）和式（15）可知，稳态正序基频电流的d轴 分量为
轴分量为
此时同样将负序电压定向于负序d轴，即令
基于此可求得光伏 电源输出稳态二倍频有功功率为
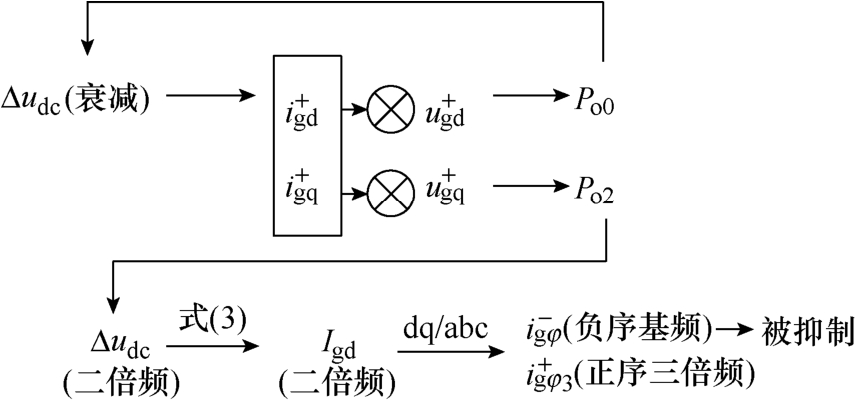
图4 3次谐波产生机理
Fig.4 Generation mechanism of third harmonic
式中，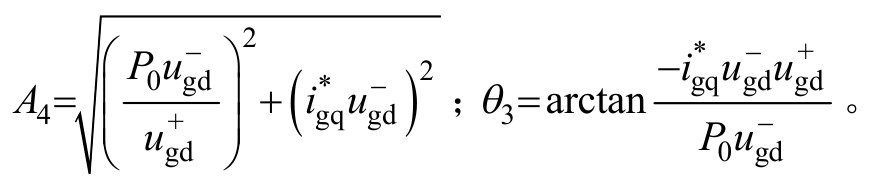
进而求得稳态直流母线二倍频电压分量为
此时光伏电源输出稳态d轴二倍频电流为
其中
由于无负序基频电流，归算到三相静止坐标系下的正序三倍频相电流为
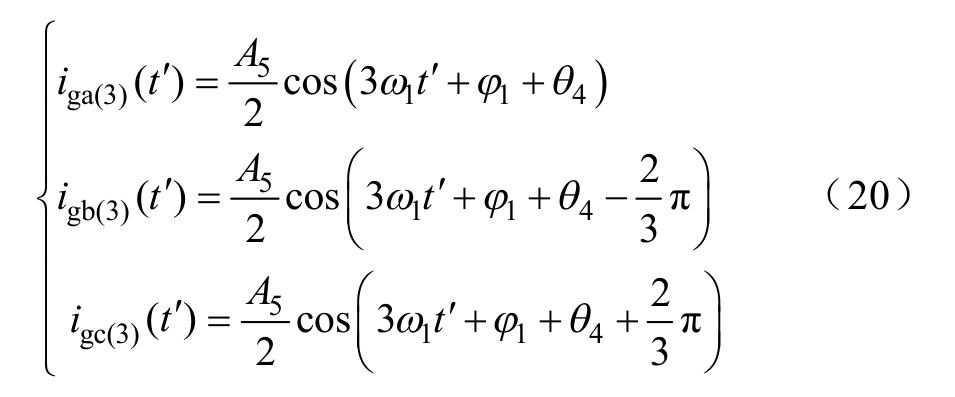
2.2 故障稳态数学模型
目前所采用的继电保护主要是利用短路电流的基频分量构成，其中以稳态基频电流占据主导地位。以下将根据所推导的光伏电源故障特性解析表达式（13）和式（16），分别针对电流未达到限幅值（非严重故障）和达到限幅值（严重故障）两种情况，建立光伏电源的稳态基频电流等效计算模型。
1）电流未达到限幅值
根据故障电流计算模型中的式（13）和式（16），同时虑及光伏电源d轴电流定向于并网点电压的控 制策略[7]，即 ugd=UT，此时故障电流两种形态解下的d、q轴稳态值和相电流稳态值均为
2）电流达到限幅值
此时故障电流d轴分量取值将受限幅值影响，由式（3）可知d、q轴稳态值和相电流稳态值为
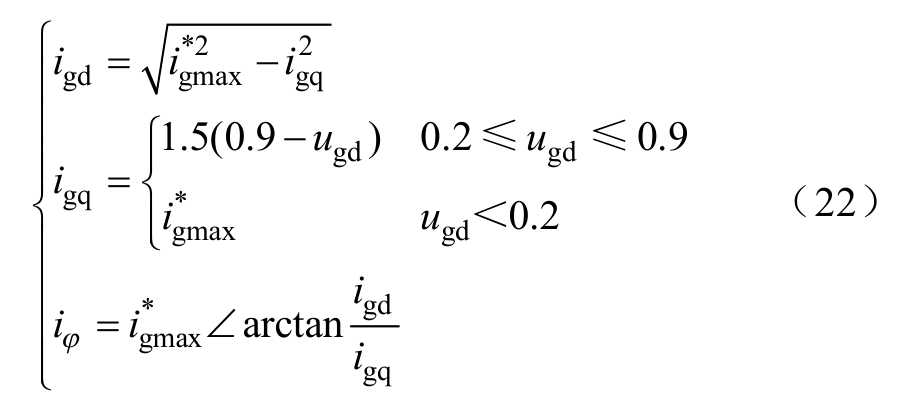
由上述解析表达式（21）和式（22）可知，光伏电源基波稳态分量的幅值和相位主要取决于电压跌落程度和短路前负荷水平。电压跌落程度越浅，负荷程度越轻，基波幅值越小；电压跌落程度越深，负荷程度越重，基波幅值越大。而基波相位呈现较大的波动范围（0°～90°变化）。负荷程度越轻，故障后电压跌落程度越深，相位越大（最大可达到 90°）；电压跌落越小，短路前有功输出越大时，基波相位将随之降低（最小值为0°）。解析表达式（21）和式（22）同时表明，在短路电流计算中，当故障期间电流未达到限幅值时，光伏电源可视为幅值和相位均受控的压控电流源模型。当电流达到限幅值时，在短路计算中可视为仅相位受控的压控电流源模型。
2.3 卸荷电路对故障电流特性的影响分析
当光伏电源并网点电压严重跌落时，直流母线电压将在故障后短时内迅速升至限幅值，触发直流卸荷电路投入。但在直流卸荷电路投入前，光伏电源的输出电流会更早达到限幅值。因为直流母线电压的越限时间取决于母线电容充电的速度，母线电容充电为物理过程且母线电容一般很大，因此该过程一般持续几百ms以上。而输出电流对其指令值具有ms级的快速跟踪性，同时其有功限幅值因光伏电源的无功支撑要求变得较低，甚至会低于正常运行电流，整个越限过程不会超过几十ms。越限后，光伏电源输出电流将一直保持在限幅值，因此直流卸荷电路的投入实际上对光伏电源的故障暂态特性没有影响。而当光伏电源的输出电流达到限幅值时，电压外环的控制策略将由控制直流母线电压恒定切换至控制输出电流限幅，此时相应的d轴电流将不再随直流母线电压变化，而是和q轴电流一起在限幅值达到稳定。此后光伏电流的输出电流幅值和相位均不再变化，即进入了故障稳态。因此光伏电源的输出电流达到限幅值可认为是其进入故障稳态的标志，而卸荷电路的投入是晚于该时刻的，故卸荷电路对故障稳态特性分析也是无影响的。后文会对此展开进一步的仿真验证。
3 光伏电源故障特性计算模型仿真验证
本文基于PSCAD/EMTDC仿真平台搭建如图5所示的含光伏电源的系统模型，以验证上述理论分析的正确性。其中，光伏阵列额定功率为0.6MW，实际输入功率为0.55MW，交流侧额定电压为0.69kV，直流母线额定电压为2.5kV，输出电流限幅值为1.2(pu)，直流母线电压限幅值为1.1(pu)，直流母线电容为8 000μF，卸荷电路电阻为15Ω [17]，滤波电阻为0.5mΩ，滤波电感为0.011mH。线路AB和BC分别长2km和1.6km。故障发生时刻为2s。
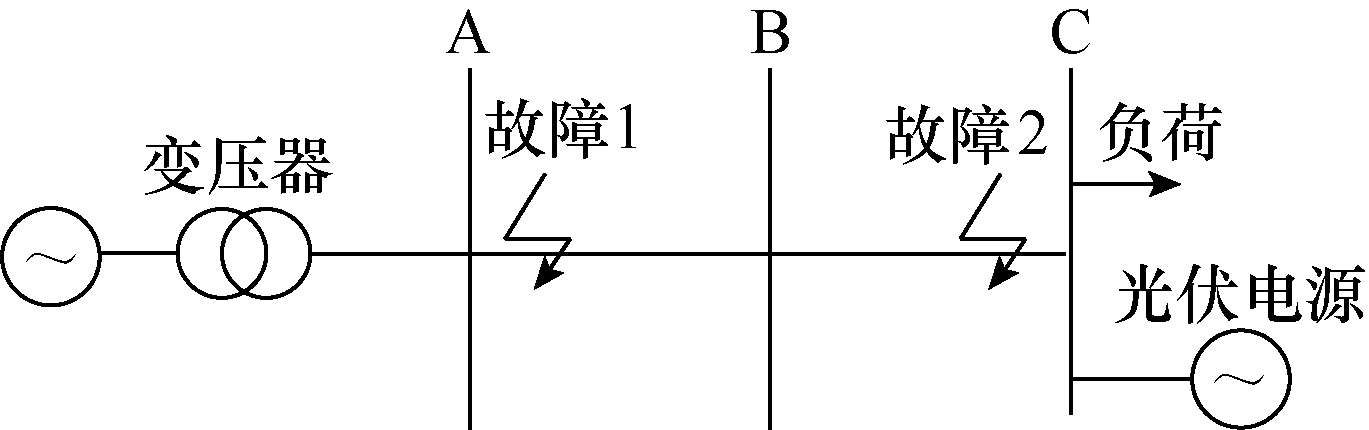
图5 含光伏电源的大电网仿真模型
Fig.5 The simulation model of Large power grid including PV power supply
由式（10）可知，故障电流解析解的形式与PI调节参数、直流母线电容值等有关。在实际应用中，PI调节器取值除需考虑控制器的稳定性要求外，还需考虑控制器的跟踪速度和跟踪精度，两者具有一定的矛盾性，不同厂家有不同的做法，故目前对控制器参数尚未形成统一的设置要求。本节通过绘制如图3a所示的电压控制外环的开环传递函数伯德图，在保证控制系统稳定性的前提下，分别选取 kp=3, ki=50和 kp=3, ki=200两组参数进行数字 仿真验证。其中，前者代表式（10）存在两个互异实根的情况，后者代表式（10）存在两个共轭复根的情况。同时，仿真还选取了不同的电压跌落深度和故障类型作为外部变量，其实际物理背景是针对光伏电源外部的不同位置和类型的短路故障，由于光伏电源主要采用负序电流抑制控制策略，故无论是对称还是不对称故障，其短路电流中只包含正序分量，而不同类型和位置短路故障的影响，主要体现在机端正序电压的跌落深度上。实际仿真选取了正序电压跌至85%和70%的三相对称故障以及正序电压跌至85%的两相相间故障情况。
需要说明的是，在第2节的理论分析中，关于光伏电源故障特性的已求解变量主要包括直流母线电压故障分量（见式（11）、式（14）和式（18））、d轴和q轴电流分量（见式（12）、式（15）和式（19））以及三相短路电流（见式（13）、式（16）和式（20））。针对这些变量，本节给出了其同时包含理论计算曲线和仿真曲线的波形，并对理论曲线和仿真曲线进行了分析比较，以充分地验证理论分析结果的正确性，详见下述。
3.1 直流卸荷电路未投入
首先以对称故障下并网点电压跌至85%为例进 行仿真，此时卸荷电路不投入。当 kp=3, ki=50时， 理论分析表明，此时式（10）存在两个互异实根。光伏电源母线电压故障分量波形如图6所示。图7和图8分别为光伏电源输出d、q轴电流波形和A相电流波形。
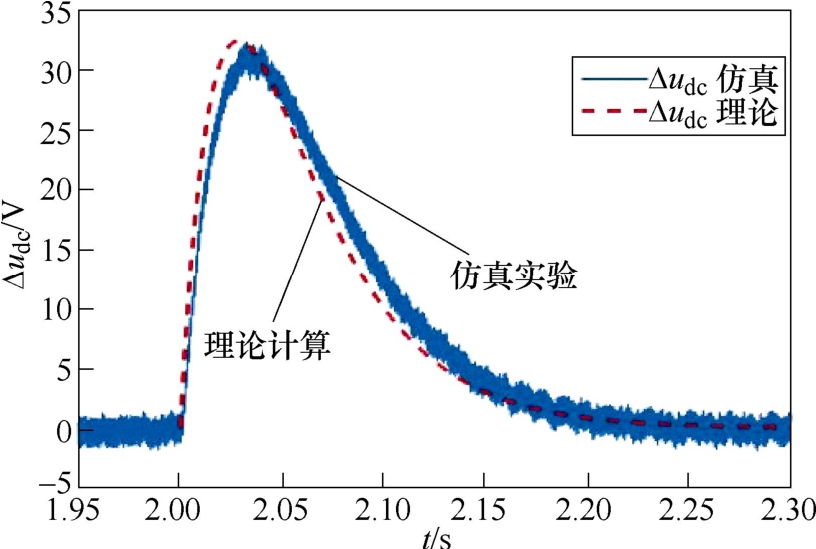
图6 直流母线电压故障分量波形（kp=3, ki=50）
Fig.6 The waveforms of DC bus voltage fault component (kp=3, ki=50)
图7 d、q轴输出电流波形（kp=3, ki=50）
Fig.7 The waveforms of output current of d and q axis (kp=3, ki=50)
图8 A相输出电流波形（kp=3, ki=50）
Fig.8 The waveforms of A phase output current (kp=3, ki=50)
由图7可知，在故障暂态过程中，输出d轴电流先迅速上升后逐渐衰减至稳定，上升和衰减过程 中未出现振荡情况，说明其暂态分量仅包含衰减的直流量，与理论表达式（12）相吻合。而输出q轴电流在故障发生后短时内迅速升至指令值0.075(pu)，与前述分析一致。由图6可知，直流母线电压先因逆变器输入有功功率大于输出有功功率，短时内电压上升。随着逆变器输出d轴有功电流上升，逆变器输出功率大于光伏阵列输入功率，直流母线电压在电压外环控制下渐渐回落至稳定值。整个过程理论曲线和仿真曲线基本吻合，验证了理论解析模型的正确性。
当kp=3,ki=200时，式（10）将存在两个共轭复根。光伏电源母线电压故障分量波形如图9所 示。图10和图11分别为光伏电源输出d、q轴电流波形和A相电流波形。
图9 光伏电源母线电压故障分量波形（kp=3, ki=200）
Fig.9 The waveforms of DC bus voltage fault component (kp=3, ki=200)
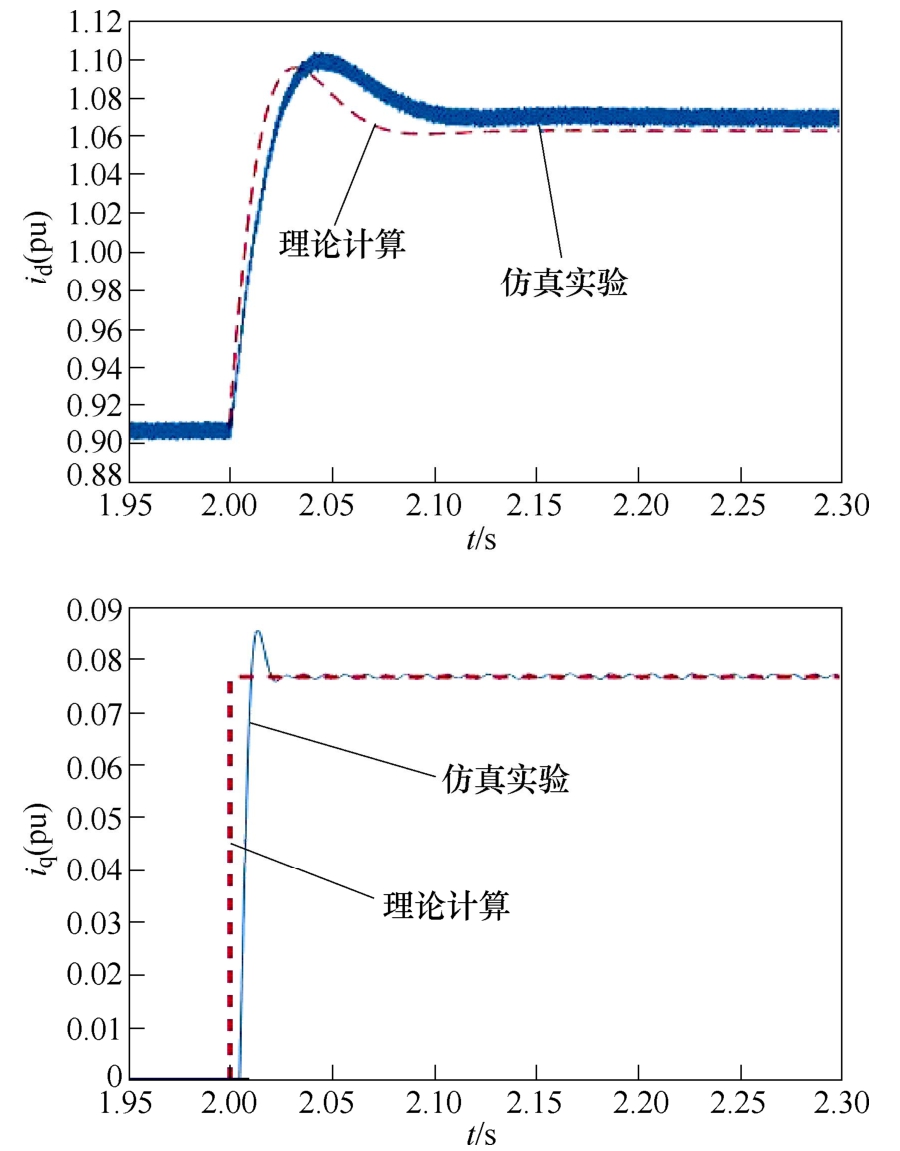
图10 光伏电源输出d、q轴电流波形（kp=3, ki=200）
Fig.10 The waveforms of output current of d and q axis (kp=3, ki=200)
由图10可知，在此种情况下，输出d轴电流在衰减过程中出现振荡情况，说明其暂态分量包含衰减的交流量，与理论表达式（15）相吻合。由图9可知，直流母线电压在回落至稳定值的过程中，由于直流母线电压和输出电流交互影响，同样出现振荡情况。整个过程理论曲线和仿真曲线基本吻合，验证了光伏电源在另一种状态下的故障电流理论解的正确性。
图11 A相输出电流波形（kp=3, ki=200）
Fig.11 The waveforms of A phase output current (kp=3, ki=200)
3.2 直流卸荷电路投入
以对称故障下并网点电压跌至70%为例进行仿 真，卸荷电路将在故障后投入运行。当 kp=3, ki= 50时，光伏电源卸荷电路投入下的输出d、q轴电 流波形如图12所示，图13为卸荷电路投入时A相电流波形。
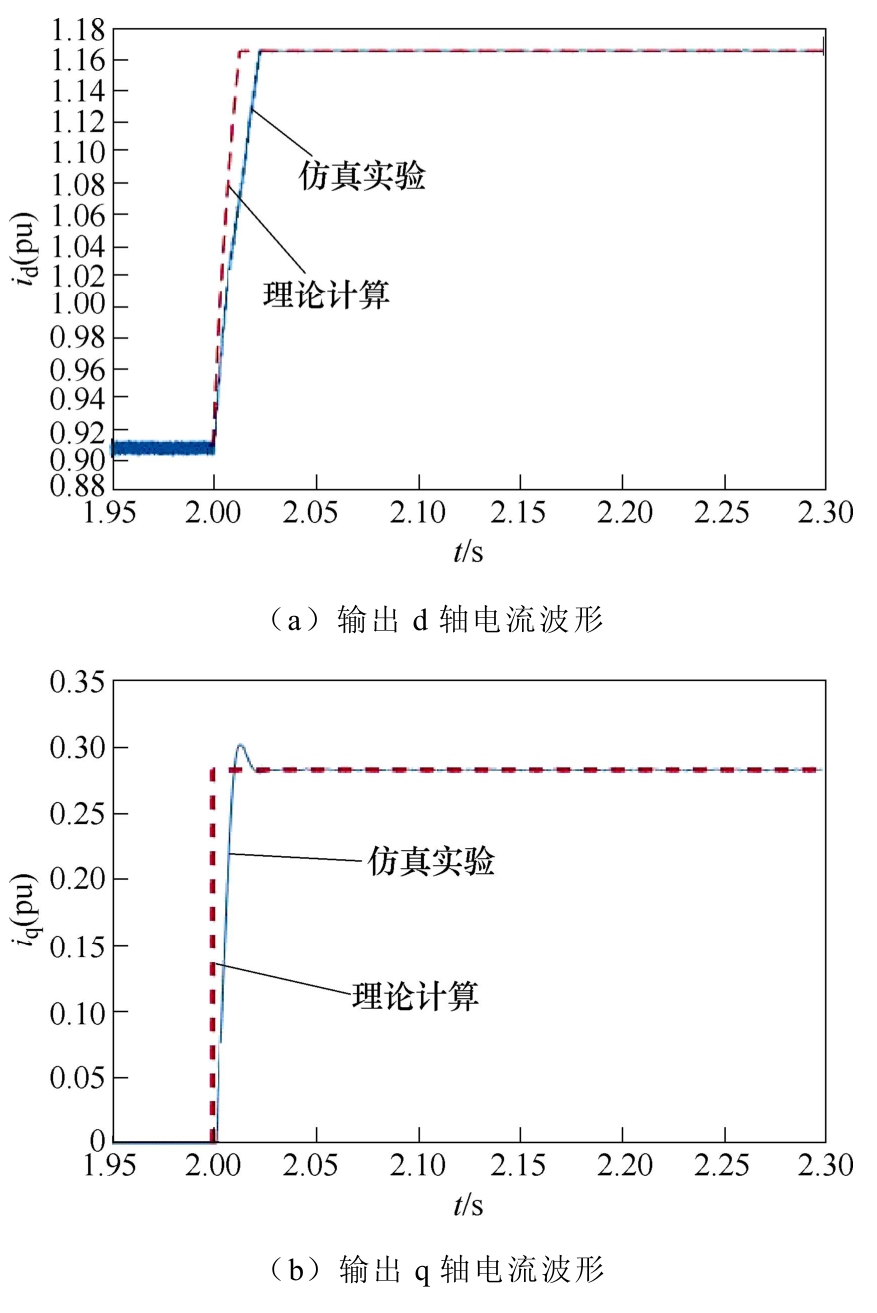
图12 卸荷电路投入下的输出d、q轴电流波形
Fig.12 The waveforms of output current of d and q axis when relieving circuit input
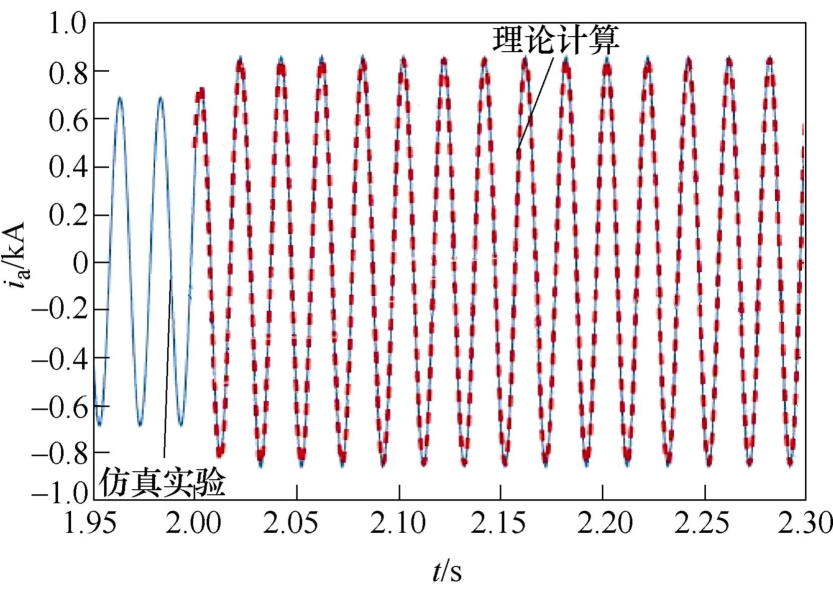
图13 卸荷电路投入时A相电流波形
Fig.13 The waveforms of A phase output current when relieving circuit input
由图12可知，当并网点电压跌落较深时，因输 出电流限幅值为1.2(pu)，输出d轴电流迅速升至 1.17(pu)后维持稳定，理论曲线与仿真曲线基本吻合，说明理论方法在电流限幅作用时仍适用于其故障过程的分析。而输出q轴电流在故障发生后短时内迅速升至指令值0.28(pu)，与理论计算值相同。由图13可知，光伏电源输出相电流升至1.2(pu)的限幅值后稳定，且理论曲线与仿真曲线同样吻合。
3.3 不对称故障
以AB两相故障下并网点正序电压跌至85%为 例进行仿真，此时卸荷电路不投入运行。当 kp=3,ki=50时，光伏电源两相短路时输出d轴电流波形如图14所示，图15为两相短路时光伏电源输出A相电流波形。
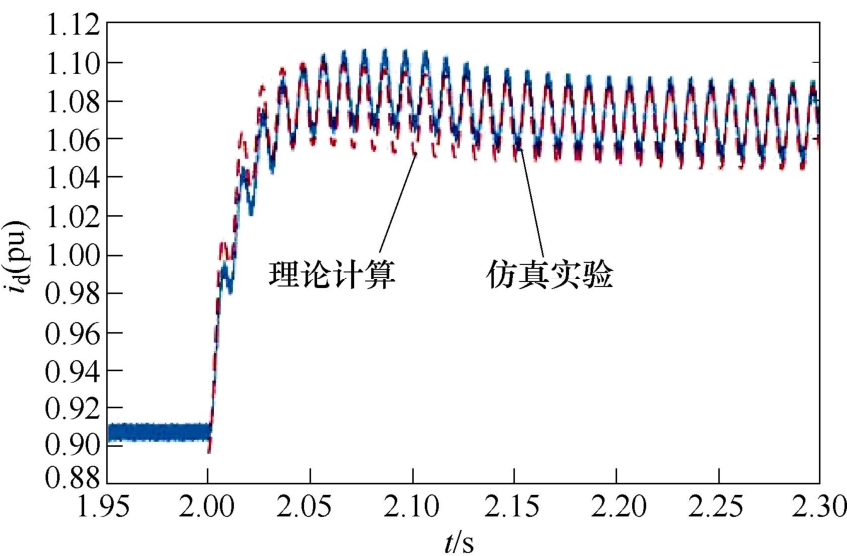
图14 两相短路时输出d轴电流波形
Fig.14 The waveforms of output current of d axis in phase to phase short circuit fault
由图14可知，故障后d轴电流直流量升至1.07(pu)，且d轴稳态电流中含有两倍频的交流量，其幅值约为0.04(pu)，远小于直流量。在图15中，由于相稳态电流中的三倍频分量很小，相稳态电流基本仍为50Hz的正弦波。同时，图14和图15中的理论曲线和仿真曲线都基本吻合，验证了不对称 故障下光伏电源故障电流计算模型的正确性。
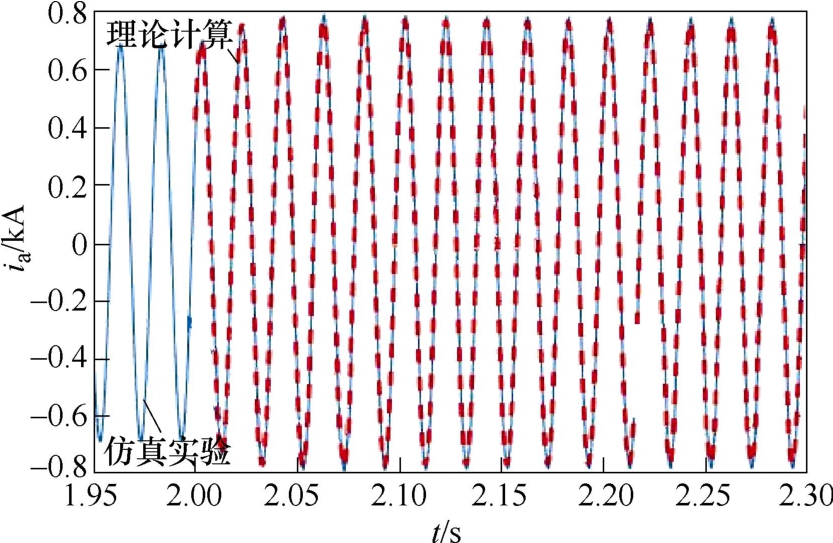
图15 两相短路时光伏电源输出A相电流波形
Fig.15 The waveforms of phase A current in phase to phase short circuit fault
4 光伏电源故障特性的影响因素分析
由上文分析可知，在给定的直流母线电容和额定电压条件下，光伏电源的故障特性与PI控制器参数、故障电压跌落深度、光伏电源负载情况有关，以下基于单一变量法对各参数的影响情况进行分析。
1）PI调节器参数
以下选取了10种不同的PI调节参数（取值范围见文献[5-16]）下的故障情况，并控制其他影响因素不变。其中，并网点额定线电压有效值为690V，故障后并网点线电压有效值为317V（0.46(pu)），光伏阵列额定功率为0.6MW，输入功率0.15MW（0.25(pu)），直流母线额定电压为2.5kV，直流母线电容为8 000μF。光伏电源故障特性指标PI调节器参数影响情况见表1。
由表1可知，对于自由分量频率，只有当比例调节参数kp取值较小或积分调节参数ki取值较大时，才会出现自由分量频率远离基频的情况。当kp和ki参数在一定范围内时，自由分量频率为基频或接近基频。
对于衰减时间常数，当自由分量频率为非基频时，随着比例调节参数kp增大，自由分量衰减加快，暂态过程缩短，而积分调节参数ki对衰减时间常数影响不大。当自由分量为基频时，考虑到暂态时长主要由衰减速度慢的自由分量决定，可以发现随着比例调节参数kp增大，暂态时长更长，而随着积分调节参数ki增大，暂态时长更短。
对于自由分量峰值，当自由分量频率为基频时，相较于传统同步电机自由基频分量由大到小衰减的现象，光伏电源的自由基频分量总体则会增大，其原因在于两种自由基频分量中，幅值较大的自由分量与稳态基频分量相位相反，而幅值较小的自由分量与稳态分量相位相同。此外，随着比例调节参数kp增大，自由分量峰值逐渐减小，而随着积分调节参数ki增大，自由分量峰值逐渐增大。当自由分量为非基频时，随着比例调节参数kp增大，自由分量峰值逐渐增大，随着积分调节参数ki增大，自由分量峰值逐渐减小。PI调节参数对光伏电源故障电流稳态值无影响。
表1 PI调节器参数影响情况
Tab.1 The influence of PI regulator parameters
注：自由分量频率在两种故障电流状态解（见2.1小节）下分别为基频和两种非基频，衰减时间常数在两种故障电流状态解下分别为非单一和单一，同时暂态时长主要取决于较长的衰减时间常数。
kp ki 自由分量 频率/Hz 自由分量 衰减时间 常数/ms 电流是否 限幅 自由分量 峰值(pu) 稳态值 (pu) 2 200 57.8 42.2 76.9 否 0.20 0.85 4 200 57.5 42.5 38.5 否 0.23 0.85 7 200 53.7 46.3 22 否 0.41 0.85 8 200 50 23.9 16.1 否 0.86 1.26 0.85 10 200 50 40.5 9.5 否 0.12 0.51 0.85 2 10 50 148.1 51.9 否 0.21 0.61 0.85 2 40 53 47 76.9 否 0.24 0.85 2 100 55.4 44.6 76.9 否 0.21 0.85 2 250 58.8 41.2 76.9 否 0.2 0.85 2 500 62.7 37.3 76.9 否 0.2 0.85
2）故障电压跌落深度
以下选取了五种不同并网点故障电压跌落深度下的故障情况，并控制其他影响因素不变。其中，PI 调节参数kp= 2 ,ki= 2 00，光伏阵列额定功率为0.6MW，输入功率0.15MW（0.25(pu)），直流母线额定电压为2.5kV，直流母线电容为8 000μF。光伏电源故障特性指标的故障电压跌落深度影响情况见表2。
表2 故障电压跌落深度影响情况
Tab.2 The Influence of fault voltage sag depth
故障电压 跌落深度 (%) 自由分量 频率/Hz 自由分量 衰减时间 常数/ms 电流 是否 限幅 自由分量峰值 (pu) 稳态值 (pu) 10 60.6 39.4 39.5 否 0.02 0.28 20 60 40 44.4 否 0.04 0.35 30 59.5 40.5 50.8 否 0.08 0.47 50 58.1 41.9 71.4 否 0.18 0.78 70 56.3 43.7 119 是 0.4 1.2 80 55.3 44.7 177.6 是 0.67 1.2
由表2可知，当自由分量频率为非基频时，随着电压电压跌落程度越深，自由分量频率越靠近基频，衰减时间常数越大。当故障电流未达到限幅值时，衰减时间常数越大意味着暂态时间越长。但当故障电流达到限幅值时，暂态时长主要取决于故障电流升至限幅值的速度，其暂态时长与衰减时间常数关系不大，且会明显短于故障电流未达到限幅值的情况。
对于自由分量峰值，随着故障电压跌落程度加深，自由分量幅值不断增大，且故障电流稳态值不断增大直至达到限幅值。
3）电源负载情况
以下选取了四种不同光伏阵列输入功率下的故障情况，并控制其他影响因素不变。其中，正常并网点线电压有效值为690V（1.0(pu)），故障后并网点线电压有效值为317V（0.46(pu)），PI调节参数 kp=2,ki=200，直流母线额定电压为2.5kV，直流母线电容为8 000μF。光伏电源故障特性指标的电源 负载情况影响情况见表3。
由表3可知，自由分量频率和衰减时间常数与光伏电源负载情况无关。但随着光伏电源负载增大，自由分量峰值按负载增大的比例逐渐增大，同时故障电流稳态值不断增大直至达到限幅值。
表3 电源负载情况影响情况
Tab.3 The Influence of power source load
电源负载 情况 自由分量频率/Hz 自由分量衰减时间常数/ms 电流 是否 限幅 自由分量峰值(pu) 稳态值(pu) 空载 （0） — — 否 — 0.66 轻载 （25%） 57.8 42.2 76.9 否 0.2 0.85 轻载 （35%） 57.8 42.2 76.9 否 0.28 1 半载 （50%） 57.8 42.2 76.9 是 0.41 1.2 重载 （75%） 57.8 42.2 76.9 是 0.61 1.2 满载 （100%） 57.8 42.2 76.9 是 0.81 1.2
5 结论
为全面评估光伏电源故障特性的影响，本文提出了虑及故障期间直流母线电压波动的光伏电源故障电流解析方法和计算模型，利用仿真结果验证了其正确性，并对影响短路电流特性的主要因素进行了分析，得到以下结论：
1）光伏电源的结构参数和控制参数均会影响其故障暂态特性，不同参数设计下故障电流可能含自由基频量或自由非基频量，故障特征差别较大。当特征方程存在两个互异实根时，光伏电源的故障电流暂态分量由两种衰减自由基频分量构成，其初值和衰减时间常数均不同，但相位相反。当特征方程存在两个共轭复根时，故障电流暂态分量为两种衰减的自由非基频交流分量，其初值和衰减时间常数相同，频率和相位不同。
2）随着故障电压跌落深度越深和光伏电源负载越重，故障电流的自有分量峰值越大，暂态波动越剧烈。PI调节参数很大程度上影响自由分量的频率特性，当比例调节参数kp取值较小或积分调节参数ki取值较大时，自由分量频率将远离基频。同时当PI参数参考表1在一定范围内取值时，自有分量频率为基频，且自由分量峰值较小，整个暂态过程趋于平稳。
3）故障电压跌落较深时，直流卸荷电路的投入时刻会晚于输出电流达到限幅值的时刻。因此若直流卸荷电路投入，则意味着输出电流已达到限幅值，且直流卸荷电路对故障电流的暂态和稳态特性均没有影响。
4）光伏电源基波稳态分量的幅值和相位主要取决于电压跌落程度和短路前负荷水平。电压跌落程度越深，负荷程度越重，基波幅值越大。而基波相位呈现较大的波动范围。负荷程度越轻，故障后电压跌落程度越深，功角越大。
5）在稳态短路电流计算时，逆变型电源可等值为压控电流源。同时，当故障期间电流未达到限幅值时，逆变型电源在短路计算中可视为幅值和相位均受控的压控电流源模型。当电流达到限幅值时，逆变型电源在短路计算中可视为仅相位受控的压控电流源模型。
上述分析结论可为继电保护性能评估、整定计算以及逆变器控制参数设计提供参考。
[1]范士雄, 蒲天骄, 刘广一, 等. 主动配电网中分布式发电系统接入技术及其进展[J]. 电工技术学报, 2016, 31(增刊2): 92-101. Fan Shixiong, Pu Tianjiao, Liu Guangyi, et al. Technologies and its trends of grid integration of distributed generation in active distribution network[J]. Transactions of China Electrotechnical Society, 2016, 31(S2): 92-101.
[2]GB/T 19964-2012. 光伏发电站接入电力系统技术规定[S]. 2012.
[3]李松峰, 牟龙华, 郭文明, 等. 基于虚拟阻抗的恒压恒频微电源的故障控制策略[J]. 电工技术学报, 2018, 33(3): 581-590. Li Songfeng, Mu Longhua, Guo Wenming, et al. Fault control strategy of U/f controlled micro sources based on virtual impedance[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 581-590.
[4]李娟, 高厚磊, 朱国防. 考虑逆变类分布式电源特性的有源配电网反时限电流差动保护[J]. 电工技术学报, 2016, 31(17): 74-83. Li Juan, Gao Houlei, Zhu Guofang. Inverse-time current differential protection in active distribution network considering characteristics of inverter- interfaced distributed generations[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 74- 83.
[5]焦彦军, 梁宵, 蒋晨阳. 计及LVRT控制策略的光伏电站并网配电网故障分析方法[J]. 电力系统自动化, 2016, 40(20): 92-99. Jiao Yanjun, Liang Xiao, Jiang Chenyang. Failure analysis method in distribution network considering LVRT control strategy of grid-connected photo- voltaic station[J]. Automation of Electric Power Systems, 2016, 40(20): 92-99.
[6]郭金学, 南东亮, 郝红岩, 等. 光伏电站接入对距离保护和重合闸的影响[J]. 电气技术, 2017, 18(11): 25-31, 38. Guo Jinxue, Nan Dongliang, Hao Hongyan, et al. Effects of PV power station on distance protection and automatic reclosing[J]. Electrical Engineering, 2017, 18(11): 25-31, 38.
[7]贾科, 顾晨杰, 毕天姝, 等. 大型光伏电站汇集系统的故障特性及其线路保护[J]. 电工技术学报, 2017, 32(9): 189-198. Jia Ke, Gu Chenjie, Bi Tianshu, et al. Fault characteristics and line protection within the collection system of a large-scale photovoltaic power plant[J]. Transactions of China Electrotechnical Society, 2017, 32(9): 189-198.
[8]Baran M E, Markaby I. Fault analysis on distribution feeders with distributed generators[J]. IEEE transa- ctions on power systems, 2005, 20(4): 1757-1764.
[9]刘东冉, 陈树勇, 马敏, 等. 光伏发电系统模型综述[J]. 电网技术, 2011, 35(8): 47-52. Liu Dongran, Chen Shuyong, Ma Min, et al. A review on models for photovoltaic generation system[J]. Power System Technology, 2011, 35(8): 47-52.
[10]张雅静, 郑琼林, 马亮, 等. 采用双环控制的光伏并网逆变器低电压穿越[J]. 电工技术学报, 2013, 28(12): 136-141. Zhang Yajing, Zheng Qionglin, Ma Liang, et al. LVRT of photovoltaic grid-connected inverter adopting dual-loop control[J]. Transactions of China Electrotechnical Society, 2013, 28(12): 136-141.
[11]孔祥平, 张哲, 尹项根, 等. 含逆变型分布式电源的电网故障电流特性与故障分析方法研究[J]. 中国电机工程学报, 2013, 33(34): 65-74. Kong Xiangping, Zhang Zhe, Yin Xianggen, et al. Study on fault current characteristics and fault analysis method of power grid with inverter interfaced distributed generation[J]. Proceedings of the CSEE, 2013, 33(34): 65-74.
[12]Kong Xiangping, Zhang Zhe, Yin Xianggen. Fault current study of inverter interfaced distributed generators[J]. Distributed Generation & Alternative Energy Journal, 2015, 30(3): 6-26.
[13]熊飞, 吴俊勇, 郝亮亮, 等. 不对称电压跌落下逆变电源的多目标控制策略[J]. 电工技术学报, 2017, 32(1): 107-116. Xiong Fei, Wu Junyong, Hao Liangliang, et al. Multi-objective control strategies of grid interface inverter under unbalanced voltage sags[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(1): 107-116.
[14]张明光, 陈晓婧. 光伏并网发电系统的低电压穿越控制策略[J]. 电力系统保护与控制, 2014, 42(11): 28-33. Zhang Mingguang, Chen Xiaojing. A control strategy of low voltage ride-through for grid-connected photovoltaic power system[J]. Power System Protection and Control, 2014, 42(11): 28-33.
[15]毕天姝, 刘素梅, 薛安成, 等. 逆变型新能源电源故障暂态特性分析[J]. 中国电机工程学报, 2013, 33(13): 165-171. Bi Tianshu, Liu Sumei, Xue Ancheng, et al. Fault characteristics of inverter-interfaced renewable energy sources[J]. Proceedings of the CSEE, 2013, 33(13): 165-171.
[16]李斌, 张慧颖, 段志田, 等. 逆变型电源控制策略对其故障暂态的影响分析[J]. 电力系统及其自动化学报, 2014, 26(12): 1-7, 27. Li Bin, Zhang Huiying, Duan Zhitian, et al. Analysis of the effect of control strategy on the fault transient characteristics of inverter-based distributed gener- ators[J]. Proceedings of the CSU-EPSA, 2014, 26(12): 1-7, 27.
[17]邢珊珊, 田素立, 王振华, 等. 光伏MPPT系统电压控制器的优化设计[J]. 电力系统保护与控制, 2016, 44(12): 114-118. Xing Shanshan, Tian Suli, Wang Zhenhua, et al. Optimized design of the voltage controller of PV MPPT system[J]. Power System Protection and Control, 2014, 44(12): 114-118.
[18]Timbus A V. Control strategies for distributed power generation systems operating on faulty grid[C]//IEEE International Symposium on Industrial Electronics, Montreal, Canada, 2006: 1601-1607.
[19]Guo Xiaqiang, Wu Weiyang, Chen Zhe. Multiple- complex coefficient- filter-based phase-locked loop and synchronization technique for three-phase grid- interfaced converters in distributed utility net- works[J]. IEEE Transaction on Industrial Electro- nics, 2011, 58(4): 1194-1204
[20]梁海峰, 冯燕闯, 刘子兴, 等. 基于无差拍控制的光伏电站低电压穿越技术的研究[J]. 电力系统保护与控制, 2013, 41(21): 110-115. Liang Haifeng, Feng Yanchuang, Liu Zixing, et al. Research on low voltage ride through of photovoltaic plant based on deadbeat control[J]. Power System Protection and Control, 2013, 41(21): 110-115.
[21]Erickson R W, Maksimovic D. Fundamentals of power electronics[M]. Berlin: Springer Science & Business Media, 2007.